Abstract
In this study, we analyze how the octahedral tilts and rotations of thin films of LaNiO3 and LaAlO3 grown on different substrates, determined using synchrotron X-ray diffraction-measured half-integer Bragg peaks, depend upon the total film thickness. We find a striking difference between films grown on SrTiO3 and LaAlO3 substrates which appears to stem not only from the difference in epitaxial strain state but also from the level of continuity at the heterointerface. In particular, the chemically and structurally discontinuous LaNiO3/SrTiO3 and LaAlO3/SrTiO3 interfaces cause a large variation in the octahedral network as a function of film thickness whereas the rather continuous LaNiO3/LaAlO3 interface seems to allow from just a few unit cells the formation of a stable octahedral pattern corresponding to that expected only given the applied biaxial strain.
Keywords: Perovskite, nickelate, thin film, heterostructure, X-ray diffraction, structure
Owing to the highly directional and electronically localized nature of the d orbital wave functions, transition metal oxides (TMOs) often exhibit a strong coupling between the lattice and other degrees of freedom.1
Many TMOs stabilize in the perovskite structure with the formula unit ABO3.2 The lattice can be visualized as a network of corner-sharing O6 octahedra with the B cation situated in the center of each. One octahedron represents the perovskite pseudocubic (pc) unit cell (u.c.) and can be seen as the functional unit. In almost all perovskites, however, the primitive unit cell is larger than this as the lattice is distorted, most commonly through antiferrodistortive rotations and tilts of the O6 units, doubling the unit cell in real space. These often subtle rotations of oxygen octahedra carry direct implications for the wider physics of the material affecting, for example, magnetic exchange and electronic hopping.3−7 In the family of rare earth nickelates, RNiO3, for instance, the Ni—O—Ni bond angle determines the temperature of their famous metal-to-insulator transition.8,9
From the wide range of available chemistries given by the distortion of the octahedral functional unit, a correspondingly wide range of materials functionalities emerges. One main challenge is in the development of new approaches by which the octahedral network can be engineered.
In bulk systems, octahedral engineering is largely understood within an empirical framework, for example, via the tolerance factor.10 Then, for a given ABO3 compound further tuning the octahedral lattice can be achieved by chemical or isotope substitution,8,11,12 nonhomogenous deformations such as bending,13 nonequilibrium excitation with light,14 or by pressure effects, either hydrostatic15 or internal.16
In epitaxial perovskite oxide heterostructures, direct and static lattice tuning can be achieved without relying on external stimuli or chemistry through heterostructure effects both brought about by the substrate and by the heterointerfaces with the other functional layers.17,18
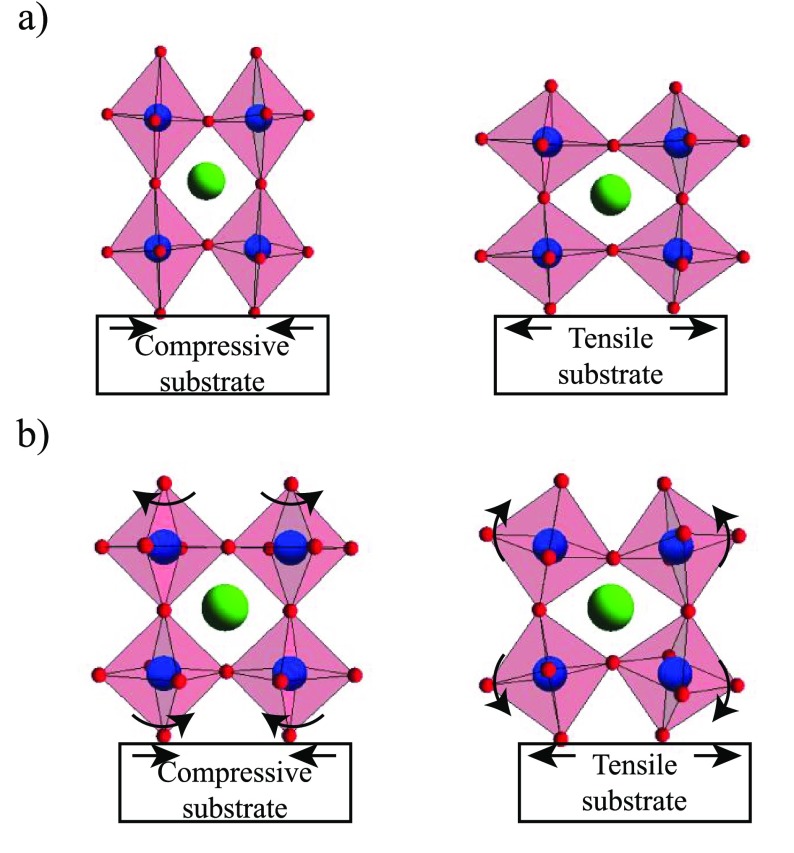
The primary mechanism of heterostructure engineering of the lattice is through epitaxial strain imposed by the substrate. Figure 1 illustrates schematically the expected effect of the biaxial strain when considering either pure bond length modifications (panel a) or pure rotations of octahedra (panel b). In reality, a combination of the two responses would most likely be expected. The effect of heterostructuring, however, goes beyond simple biaxial strain as, very often, the substrate itself has a characteristic octahedral network, which can affect the film through the interfacial coupling of distortions. This added texturing should also bring a thickness-dependent modulation to the film structure, even with the retention of complete biaxial strain that is usually observed up to much higher thickness limits. As many functional properties, often unavailable in bulk, stem from heterointerfaces, the study of the lattice structure toward the ultrathin limit is highly appealing from the perspective of tailor-made nanoscale materials and may reveal new engineering routes.
Figure 1.
A simplified schematic of the response to biaxial strain through (a) pure bond length modifications and (b) pure oxygen octahedral rotations.
Today, an entire field of research is dedicated to measuring collective lattice distortions. Structural modulations have often been observed at heterointerfaces to vary on a length scale of 3–8 pseudocubic unit cells.19−25 Our previous work on LaNiO3 thin films, utilizing TEM and ab initio calculation, found that the film structure has a tendency to adopt the structure of the LaAlO3 substrate close to the interface with strong distortions on the film surface.23 This coexistence of different structures was shown to be the likely origin for a thickness-dependent conductivity enhancement in those ultrathin films, illustrating how important the lattice distortion can be for the physical properties of TMOs.
One of the primary challenges in further developing tools and approaches to measure distortions of the octahedral functional unit itself lies in the fact that they usually stem only from displacements of light oxygen atoms which, when combined with the fact that heterostructuring tends to involve low sample volumes, make their detection rather arduous. Here we describe an approach to quantify rotational distortions of the perovskite octahedral functional unit by synchrotron X-ray diffraction. Our results show that this technique is well-suited to this type of problem even when the film thickness is as low as 2 nm. Resulting from our analysis, a striking contrast in behavior is observed when the heterointerface is quite structurally and chemically continuous (i.e., between very similar materials) versus when it is rather discontinuous. In the latter case, a thickness-dependence of the collective distortion is uncovered and a potential control knob for octahedral distortion magnitude is revealed.
The approach employed here leverages the fact that distortions of the functional unit double the real space unit cell and, therefore, halve the reciprocal space periodicity, producing extra peaks at half-integer points when probed by X-ray diffraction (XRD). This method of obtaining the precise pattern of tilts and rotations of the octahedra was introduced by Glazer along with a convenient shorthand to describe this collective distortion.26 First, a definition of the functional unit distortion is that α and β are the rotation magnitudes of the octahedron around the a- and b-axes, respectively, often referred to as “tilts”, while γ represents the rotation magnitude around the c-axis. A schematic definition can be found in the Supporting Information. Glazer notation uses three labels, each of one letter and one superscript symbol, to describe the rotations around the three respective crystallographic axes. The superscript “0” denotes no rotation around that axis, “–” denotes an out-of-phase rotation (adjacent octahedra rotate in the opposite direction), and “+” denotes an in-phase rotation (all octahedra rotate in the same direction). If more than one label has the same letter, then it means that the rotations around those axes are equal in magnitude. For example, the common Glazer system a–a–a– represents out-of-phase-rotations around the three axes, all of the same magnitude, that is, α = β = γ. By recording which half-integer Bragg peaks (HIBP) are present and which are absent, the sample symmetry is readily reasoned.
As a further step, the magnitudes of the tilts and rotations can be obtained by more detailed analysis of the relative intensities of the HIBP in XRD.27 This method has been successfully applied to perovskite systems to examine the effect of biaxial strain28,29 and symmetry mismatch30 as well as more complex systems such as multicomponent superlattices24,31 and structures that include cation displacements.32 In an original study, May and co-workers illustrated how a typical perovskite, LaNiO3, adapts its NiO6 network to the epitaxial strain from the substrate. In particular, the authors found that when compressive (tensile) strain is applied, the in-plane rotation increases (decreases) in magnitude whereas the out-of-plane tilts decrease (increase) in magnitude, as sketched in Figure 1. In that work, the films were 20–40 pc u.c. in thickness (1 pc u.c. ≈ 3.85 Å). Here, we apply a rather similar approach to films close to the ultrathin limit demonstrating for the first time to our knowledge how distortions evolve from ultrathin to thin films depending on the substrate, providing important information on the interfacial strain, structural, and chemical effects potentially giving new engineering tools for future material designs.
Because of the possibility that ultrathin films may allow the stabilization of more extreme octahedral rotations, the simulation aspect of this work was adapted and generalized from the one employed in the past and details of this can be found in the Supporting Information.
The systems investigated were tensile LaNiO3 on (001)-oriented SrTiO3 (STO) substrate and compressive LaNiO3 grown on (001)-oriented LaAlO3 substrate, both series of various film thicknesses, as low as 5 u.c. (20 Å), as well as the analogous compressive system of LaAlO3 on SrTiO3 substrate. Table 1 summarizes the room-temperature structural properties of the bulk materials involved.
Table 1. Summary of Bulk, Room Temperature, Structural Parameters of the Materials Used33,34.
| LaNiO3 | LaAlO3 | SrTiO3 | |
|---|---|---|---|
| pc lattice parameter | 3.838 Å | 3.789 Å | 3.905 Å |
| space group | R3̅c | R3̅c | Pm3m |
| Glazer system | a–a–a– | a–a–a– | a0a0a0 |
| O6 rotation/tilt α = β = γ | 5.2° | 5.6° | 0° |
The growth and characterization for the LaNiO3 and LaAlO3 samples can be found in the Experimental Section, Supporting Information, and elsewhere.35−37
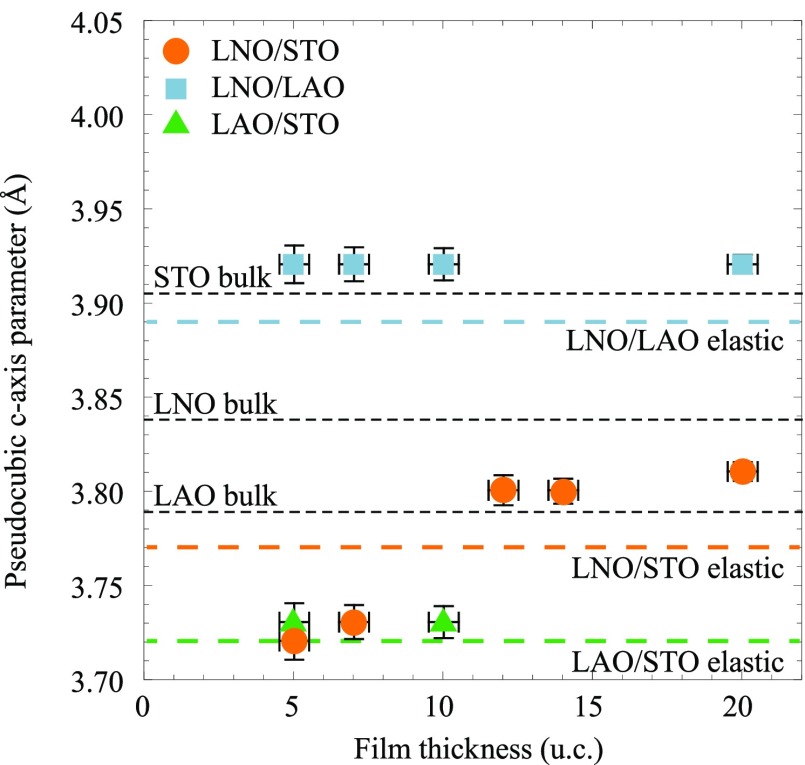
For all samples, the film thickness was obtained by recording a specular CTR (described in the Experimental Section and shown in Supporting Information) and using a specialized simulation to extract the number of unit cells and the c-axis parameter through fitting the finite thickness fringes.38Figure 2 displays the results of this analysis.
Figure 2.
Pseudocubic c-axis lattice parameter as a function of total film thickness for the three heterostructure types, LaNiO3/SrTiO3, LaNiO3/LaAlO3, and LaAlO3/SrTiO3. Bulk lattice parameters for all materials are denoted by the black dashed line. The wider dashed lines show the film c-axis parameters that would be expected for a given heterointerface assuming only a volume change governed by the Poisson ratio (νLNO = 0.34 from ref (39) and νLAO = 0.22 from ref (40)). Error bars derive from the reliability of fitting the finite thickness fringes in InteractiveXRDFit, which increases with film thickness.
The out-of-plane lattice parameters primarily reflect the strain state of the films where LaNiO3/SrTiO3 and LaAlO3/SrTiO3, both under tensile strain, see a reduction in their c-axis parameter as compared to the bulk state, whereas the opposite effect is observed in LaNiO3/LaAlO3 samples, which are compressively strained. Indeed, the measured c-axis parameters are close to that predicted by elastic theory for almost all the samples. The LaNiO3/LaAlO3 series does not display a thickness dependence of the c-axis parameter over the range examined. The LaNiO3/SrTiO3 series, on the other hand, shows an overall decrease of the out-of-plane lattice parameter as the thickness of the film is reduced. The two samples of LaAlO3/SrTiO3 are entirely consistent with a previous report on the thickness-dependence of the c-axis parameter where a strong modulation due to the electrostrictive effect and intermixing is observed for films of less than 4 u.c. and a relaxation of the lattice parameter back to that of bulk LaAlO3 is seen for films over 40 u.c.41 The two thicknesses of LaAlO3/SrTiO3 measured here, however, belong to a thickness regime where the c-axis parameter was found by Cancellieri and co-workers to be constant at between 3.73–3.74 Å.41 The variation of c-axis parameter with thickness for the LaNiO3/SrTiO3 series seen here cannot be reasoned in the same way as the LaAlO3/SrTiO3 series was previously. In the case of LaNiO3/SrTiO3, there is no two-dimensional (2D) electron system at the interface and the film remains fully strained to the substrate for all the thicknesses studied, as confirmed by analyzing the in-plane diffraction peaks. The intriguing thickness dependence of the c-axis in the LaNiO3/SrTiO3 series, however, be may correlated with a strong thickness-dependence of the lattice of oxygen octahedral distortions, as will be discussed.
To access information
about the rotations and tilts of the oxygen
octahedral network, a series of off-specular CTRs were recorded around
6–10 half-integer Bragg peaks (HIBPs) belonging to different
families of diffraction planes. All measurements reported were carried
out at room temperature. For all samples, all HIBPs of the form 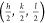 with h, k, l odd
integers were observed except those that
satisfy h = k = l, which are forbidden. No intensity was observed at conditions where
one of the h, k, or l is an even integer, peaks that would arise from in-phase rotations
of octahedra only, thus no orthorhombicity is present. This confirms
that all the films adhere to the Glazer system a–b–c–, at lowest possible symmetry.
As these samples are biaxially strained, it is reasonable to increase
the symmetry to a–a–c–, reflecting the assumed equivalence of the two in-plane directions.
This assumption is justified by the observation of equivalent intensities
in all four quadrants
with h, k, l odd
integers were observed except those that
satisfy h = k = l, which are forbidden. No intensity was observed at conditions where
one of the h, k, or l is an even integer, peaks that would arise from in-phase rotations
of octahedra only, thus no orthorhombicity is present. This confirms
that all the films adhere to the Glazer system a–b–c–, at lowest possible symmetry.
As these samples are biaxially strained, it is reasonable to increase
the symmetry to a–a–c–, reflecting the assumed equivalence of the two in-plane directions.
This assumption is justified by the observation of equivalent intensities
in all four quadrants 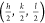 ,
, 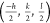 ,
, 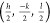 , and
, and 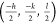 . The condition
α = β will henceforth
be enforced.
. The condition
α = β will henceforth
be enforced.
In order to obtain the magnitudes of the octahedral
tilts and rotations,
it was necessary to compare measured and simulated relative diffraction
intensities of HIBPs. The measured intensity for a given peak was
taken as the integrated intensity of a Gaussian that has been fitted
to the data including a linear slope offset and a constant background,
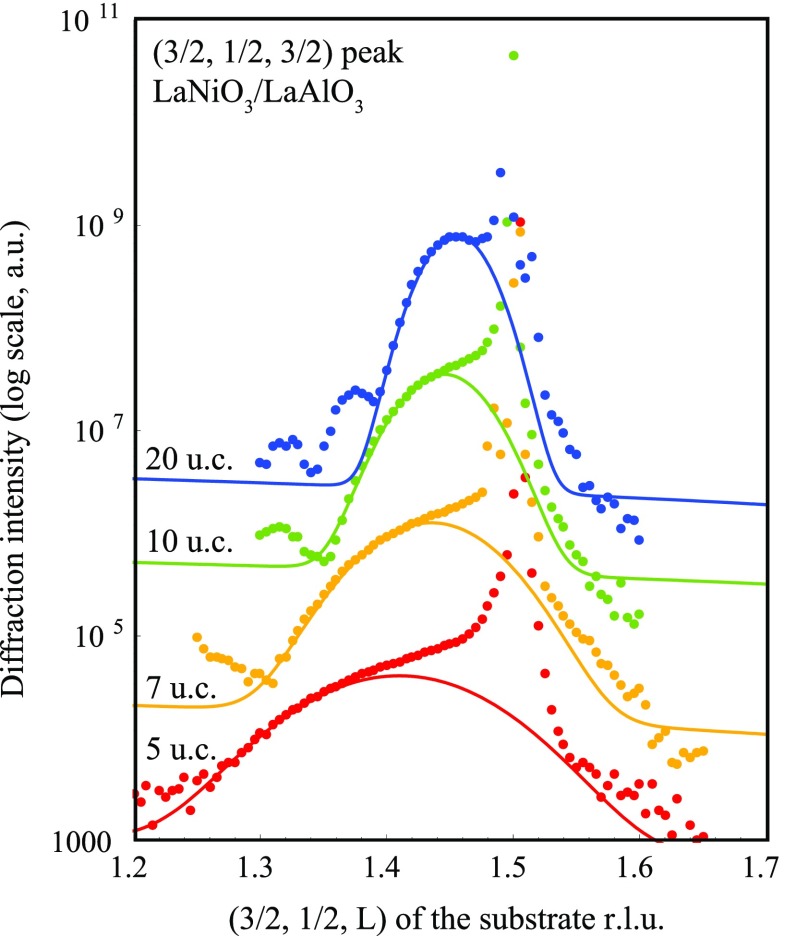
as shown in the Supporting Information. Figure 3 shows the evolution
of the diffraction intensity close to the 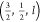 reflection for the series of LaNiO3/LaAlO3 samples and illustrates the fits that are
obtained. When the thickness is reduced to only 5 u.c. (2 nm), the
intensity is still clear and easily quantifiable, even when directly
adjacent to the much stronger substrate contribution. This represents
a serious technical achievement as this intensity derives only from
small displacements of light oxygen atoms in a film only 2 nm in thickness.
Also observed are the oscillations resulting from the finite thickness
effect in the films, confirming the high crystalline quality of the
oxygen sublattice.
reflection for the series of LaNiO3/LaAlO3 samples and illustrates the fits that are
obtained. When the thickness is reduced to only 5 u.c. (2 nm), the
intensity is still clear and easily quantifiable, even when directly
adjacent to the much stronger substrate contribution. This represents
a serious technical achievement as this intensity derives only from
small displacements of light oxygen atoms in a film only 2 nm in thickness.
Also observed are the oscillations resulting from the finite thickness
effect in the films, confirming the high crystalline quality of the
oxygen sublattice.
Figure 3.
Diffraction intensity close to the 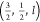 reflection as an example of half integer
Bragg peaks for the series of LaNiO3/LaAlO3 samples
showing the evolution with film thickness. Solid lines are the fits
to the data of a Gaussian function plus a linear slope and a constant
background. The data was vertically displaced for clarity.
reflection as an example of half integer
Bragg peaks for the series of LaNiO3/LaAlO3 samples
showing the evolution with film thickness. Solid lines are the fits
to the data of a Gaussian function plus a linear slope and a constant
background. The data was vertically displaced for clarity.
The simulated diffraction intensity was computed from given atomic positions, where only the oxygen positions are considered, as the cations do not contribute to these HIBPs. Simulating the atomic positions was done on a Mathematica 9 notebook with the only input parameters being the Glazer rotation system (i.e., how each octahedron rotates with respect to its neighbors), assuming the oxygen octahedra to be rigid. The tilt and rotation magnitudes are always defined with respect to the internal symmetry axes of the octahedron and not to the original, unrotated Cartesian reference frame. To avoid possible issues arising from the non-Abelian nature of the SO(3) group, the Rodrigues formula for three-dimensional rotations around a vector is applied iteratively around the three internal axes of octahedral symmetry, each time by an increment of the total rotation angle of that axis. More detail on this process is given in the Supporting Information. After the rotation operation on one octahedron is complete for a given set of input angles, α, β, γ, the full unit cell can be built by generating seven additional octahedra, rotated by the same magnitude of angles but in different directions depending upon the Glazer rotation system.
After obtaining a simulated doubled perovskite unit cell in three dimensions, the diffracted intensity can be calculated from the structure factor for the comprising 24 oxygen atoms via
where dp expresses the relative domain population of four geometrically equivalent domains and with the structure factor being given by
where 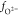 is the form factor for the 2– oxygen ion and the nth oxygen is situated at (xn, yn, zn) in coordinates relative to the doubled unit cell. The domains indexed
by p arise due to the equivalence of the final atomic
positions when the octahedron undergoes rotations of the type (α,
β, γ), (−α, β, γ), (α,
−β, γ) and (α, β, – γ).
is the form factor for the 2– oxygen ion and the nth oxygen is situated at (xn, yn, zn) in coordinates relative to the doubled unit cell. The domains indexed
by p arise due to the equivalence of the final atomic
positions when the octahedron undergoes rotations of the type (α,
β, γ), (−α, β, γ), (α,
−β, γ) and (α, β, – γ).
Once both the simulated and experimental intensities have been obtained they are normalized to the same half integer (h, k, l) usually the one corresponding to the highest experimental intensity, giving two comparable sets. If the normalized simulated intensity for the nth diffraction peak is Isim(h, k, l)n and the normalized experimentally measured intensity for the nth diffraction peak is Iexp(h, k, l)n then the residual sum of squares (RSS) is defined as
and from this, the input parameters (α, β, γ, and the dp) can be varied until the RSS is minimized, determining the best fit structure. This was done for the two samples of LaAlO3/SrTiO3, the series of LaNiO3/SrTiO3, and the series of LaNiO3/LaAlO3 and the resultant rotation magnitudes are plotted in Figure 4. More detail on the fitting procedure is shown in the Supporting Information.
Figure 4.
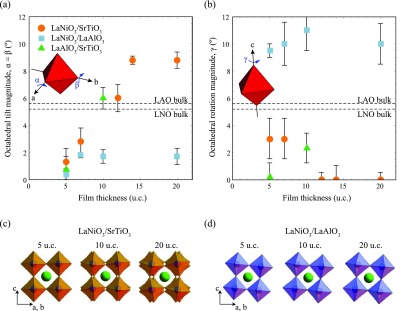
Oxygen octahedral tilt (a) and rotation (b) magnitudes as a function of total film thickness in pc u.c. for the three types of heterostructure system analyzed. Dashed lines indicate the octahedral tilt and rotation magnitudes for the bulk materials LaNiO3 and LaAlO3 (SrTiO3 having no room-temperature octahedral distortions). The uncertainties are generated as described in the Supporting Information. An inset on each of the figures illustrates the relevant Glazer angles, α, β, and γ. Panels c and d are side view sketches of the octahedral tilt systems determined for, respectively, the LaNiO3/SrTiO3 and LaNiO3/LaAlO3 films, with the true measured angles. Three representative thicknesses of each series are shown. A strong evolution with thickness is seen for LaNiO3/SrTiO3 (panel c), whereas in panel d there is little variation with thickness for the LaNiO3/LaAlO3 series.
For the thicker (>14 u.c.) LaNiO3 samples, on both SrTiO3 and LaAlO3 substrate, the angles reflect what would be expected from only considering the effect of biaxial strain, as sketched in panel b of Figure 1. On SrTiO3, the strain is tensile so the LaNiO3 oxygen octahedra would be expected to straighten their equatorial Ni—O—Ni bonds laterally to maximize the in-plane space, meaning a rotation around the c-axis toward a smaller γ of nearly 0°. The α and β, on the other hand, are much larger at almost 9°. The octahedra reduce their out-of-plane extension by increasing α and β to account for the tetragonal distortion stemming from tensile biaxial strain.
The opposite situation is observed for the compressive LaNiO3/LaAlO3; here, γ is forced to around 10° by in-plane restriction while α and β decrease to accommodate the new tetragonal distortion that is longer out-of-plane than in-plane. These Glazer rotation magnitudes would therefore likely be found for continually increasing thickness until strain relaxation, where the bulk of 5.2° would be preferred. A previous report finds, for slightly thicker LaNiO3 on both LaAlO3 and SrTiO3 substrates, Glazer angles that are in good agreement with what we see here.27 Theoretical calculations on LaAlO3 films also reproduce these higher thickness, biaxially strained structures and LaNiO3 would be expected to be similar.29,42
Now we perform the same analysis on films with thicknesses as low as 5 u.c. (2 nm) and in doing so, we have unveiled a striking behavior toward the atomic limit that suggests that the nature of the specific heterointerface plays a role in determining the film structure far beyond the simple consideration of biaxial strain.
First, in the case of the films on LaAlO3 substrate, the structure similar to the thicker LaNiO3/LaAlO3 films holds down to the lowest thicknesses measured, 5 u.c., similar to how the c-axis parameter appears to be independent of the total thickness, as shown in Figure 2. In our previous work, we found that although the depth-resolved structure of LaNiO3 films on LaAlO3 substrate varies the depth-averaged structure is independent of the total film thickness, as is observed here.23
By contrast, the octahedral rotations in films on SrTiO3 substrate depend much more strongly on the total thickness. In particular, as the thickness is decreased, the α- and β-tilts tend toward 0°, which, it should be noted, is the room temperature tilt angle in the cubic SrTiO3 substrate. It is therefore likely that the film structure is inclined to adopt the same out-of-plane tilts as the substrate through octahedral coupling at the heterointerface. The effect of the interfacial octahedral coupling reduces when the thickness increases to 12–15 u.c., the same length scale over which the c-axis parameter changes in the same system. The actual interfacial coupling length could be much less than 12 u.c., however, as it should be kept in mind that these measurements are sensitive to the entire film thickness and so give an average structure. Indeed, several studies find an interfacial coupling of the octahedral tilt magnitudes over around four unit cells.43−45 Other works also find a highly distorted surface structure extending over around 2 u.c. which, although it would contribute to the macroscopic measurements reported here, does not become relevant unless films even thinner than those measured in this work, the so-called ultrathin regime, are investigated.23,46 Interesting behavior emerges in ultrathin films. LaNiO3 films are found to become insulating under 6 u.c. thickness when grown on SrTiO3 substrate but retain metallicity until as thin as 3 u.c. on LaAlO3 substrate.36,47 This thickness-dependent metal–insulator transition is not fully understood but the substrate effect may be related to the type of interfacial structural coupling observed here.
The α = β tilts determined for the two LaAlO3/SrTiO3 films compare well to those obtained from a microscopy study20 and fit well with the LaNiO3/SrTiO3 series, suggesting that LaAlO3 and LaNiO3 react to the SrTiO3 interface in a similar way (except for the 2D electron system). This is most likely as a result of their structural similarities in bulk (both are rhombohedral with a similar distortion magnitude), as summarized in Table 1. Comparing the bulk similarities of LaNiO3 and LaAlO3 also aids in the understanding of the LaNiO3/LaAlO3 interface.
In the case of the LaNiO3 films on LaAlO3 substrate, the two materials are much closer in lattice parameter and the interface has, nominally, no polar discontinuity, no A-site discontinuity, and no symmetry discontinuity so the LaNiO3 can adopt a more stable, low energy, structure. In the LaNiO3/SrTiO3 system, however, there are chemical, polar, and symmetry discontinuities so it could be that the LaNiO3 is more frustrated and has to respond to the interface in a more complex way as the thickness is increased, first by octahedral coupling and then by accommodating the biaxial strain. Such interface effects are not unusual.18,21,48 Although strain relaxation on the scale of the thicknesses measured here can be ruled out by the in-plane coherency of the diffraction peaks between the substrate and the film, there is still the possibility that the LaNiO3/SrTiO3 interface has a higher propensity to develop point defects and this may have an effect as well. Regardless of the origin, the smooth evolution of the thickness dependence of the octahedral rotations in the LaNiO3/SrTiO3 system may have an application in atomic-scale structural engineering through integration in a superlattice structure. This is especially appealing given the strong relationship between the Ni—O—Ni bond angle and electronic and magnetic properties of rare earth nickelates in general.
In summary, a simulation designed to give the Glazer rotation system and angles through fitting half integer Bragg peaks measured by synchrotron X-ray diffraction was used for three different perovskite oxide heterostructures; LaNiO3/LaAlO3, LaNiO3/SrTiO3, and LaAlO3/SrTiO3.
LaNiO3/LaAlO3 appears to be a system where the compatibility between the two component materials leads to a general film structure that is independent of the total film thickness and the Glazer rotation angles reflect an almost pure biaxial strain effect.
LaNiO3/SrTiO3 and LaAlO3/SrTiO3 are very similar, possibly owing to the corresponding similarity between bulk LaNiO3 and LaAlO3. In the LaNiO3/SrTiO3 system, the stark differences between the ideal film structure and the substrate are such that the film appears to accommodate the heterointerface in a complex and thickness-dependent way, first by undoing the octahedral tilting to match the substrate and then for thicker films by octahedral rotation to fill the tetragonality imposed by biaxial strain.
This demonstrated ability of using layer thickness as a tool to control the atomic positions on such a fine scale is certainly appealing from a materials engineering standpoint and is likely to be generalizable to many perovskite/perovskite systems with a high level of structural and chemical discontinuity.
Experimental Section
The substrates used were SrTiO3 and LaAlO3, both (001)-oriented and distributed by Crystec GmbH. The SrTiO3 is treated by the manufacturer to obtain a TiO2 terminated surface while the LaAlO3 is annealed in flowing oxygen at 1000 °C to obtain an AlO2 terminated surface.
The LaNiO3 films were grown by radio frequency off-axis magnetron sputtering at a temperature of 510 °C and in a 7:2 Ar/O2 mix at a pressure of 0.24 mbar. The LaAlO3 films were grown by pulsed laser deposition in a pressure of 8 × 10–5 mbar at a temperature of 800 °C and a laser repetition rate of 1 Hz with a postannealing stage in 200 mbar of oxygen at 530 °C for an hour. Characterization can be found in the Supporting Information.
The XRD measurements took the form of crystal truncation rods (CTRs) and were performed at the Materials Science beamline X04SA, Surface Diffraction endstation at the Swiss Light Source, Paul Scherrer Institut.49 The samples were mounted on a hexapod in a 6-circle diffractometer and, for all off-specular conditions, the incident angle was fixed at 4°. The two-dimensional Pilatus-II pixel detector was used to capture the diffracted beam. All measurements were carried out at room temperature and under flowing helium and at photon energies between 13 and 15.5 keV.
Acknowledgments
The authors wish to thank Steve May for invaluable help and advice in the development of the simulation described herein and Marco Lopes and Sébastien Muller for technical support. This work was supported by the Swiss National Science Foundation through Division II. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Program (FP7/2007-2013)/ERC Grant Agreement 319286 (Q-MAC).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.9b01772.
Additional sample characterization. Details on the simulation of atomic positions. The determination of the experimental intensities and associated coherence thickness. The goodness of the simulation fits and a summary of the output structural parameters. Supplementary structural parameters (Ni—O—Ni bond angle and Ni—O bond lengths) (PDF)
Author Present Address
∥ (M.G.) Physik Institut, University of Zürich, 190 Winterthurerstrasse, 8057 Zürich, Switzerland.
The authors declare no competing financial interest.
Supplementary Material
References
- Khomskii D. I.Transition Metal Compounds; Cambridge University Press: Cambridge, 2014. [Google Scholar]
- Mitchell R. H.Perovskites: Modern and Ancient; Almaz: Thunder Bay, 2003. [Google Scholar]
- Rondinelli J. M.; Spaldin N. a. Substrate Coherency Driven Octahedral Rotations in Perovskite Oxide Films. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82 (11), 113402. 10.1103/PhysRevB.82.113402. [DOI] [Google Scholar]
- Rondinelli J. M.; May S. J.; Freeland J. W. Control of Octahedral Connectivity in Perovskite Oxide Heterostructures: An Emerging Route to Multifunctional Materials Discovery. MRS Bull. 2012, 37 (03), 261–270. 10.1557/mrs.2012.49. [DOI] [Google Scholar]
- Islam M. A.; Rondinelli J. M.; Spanier J. E. Normal Mode Determination of Perovskite Crystal Structures with Octahedral Rotations: Theory and Applications. J. Phys.: Condens. Matter 2013, 25 (17), 175902. 10.1088/0953-8984/25/17/175902. [DOI] [PubMed] [Google Scholar]
- Balachandran P. V.; Rondinelli J. M. Interplay of Octahedral Rotations and Breathing Distortions in Charge-Ordering Perovskite Oxides. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 054101. 10.1103/PhysRevB.88.054101. [DOI] [Google Scholar]
- Pavarini E.; Biermann S.; Poteryaev A.; Lichtenstein A. I.; Georges A.; Andersen O. K. Mott Transition and Suppression of Orbital Fluctuations in Orthorhombic 3 d 1 Perovskites. Phys. Rev. Lett. 2004, 92, 4–7. 10.1103/PhysRevLett.92.176403. [DOI] [PubMed] [Google Scholar]
- Medarde M. L. Structural, Magnetic and Electronic Properties of RNiO3 Perovskites (R Equals Rare Earth). J. Phys.: Condens. Matter 1997, 9 (8), 1679–1707. 10.1088/0953-8984/9/8/003. [DOI] [Google Scholar]
- Catalan G. Progress in Perovskite Nickelate Research. Phase Transitions 2008, 81 (7–8), 729–749. 10.1080/01411590801992463. [DOI] [Google Scholar]
- Goodenough J. B. Electronic and Ionic Transport Properties and Other Physical Aspects of Perovskites. Rep. Prog. Phys. 2004, 67 (11), 1915–1993. 10.1088/0034-4885/67/11/R01. [DOI] [Google Scholar]
- Dabrowski B.; Kolesnik S.; Baszczuk A.; Chmaissem O.; Maxwell T.; Mais J. Structural, Transport, and Magnetic Properties of RMnO3 perovskites (R = La, Pr, Nd, Sm,153Eu, Dy). J. Solid State Chem. 2005, 178 (3), 629–637. 10.1016/j.jssc.2004.12.006. [DOI] [Google Scholar]
- Medarde M.; Lacorre P.; Conder K.; Fauth F.; Furrer A. Giant 16O-18O Isotope Effect on the Metal-Insulator Transition of RNiO3 Perovskites (R = Rare Earth). Phys. Rev. Lett. 1998, 80, 2397–2400. 10.1103/PhysRevLett.80.2397. [DOI] [Google Scholar]
- Koirala P.; Mizzi C. A.; Marks L. D. Direct Observation of Large Flexoelectric Bending at the Nanoscale in Lanthanide Scandates. Nano Lett. 2018, 18 (6), 3850–3856. 10.1021/acs.nanolett.8b01126. [DOI] [PubMed] [Google Scholar]
- Subedi A.; Cavalleri A.; Georges A. Theory of Nonlinear Phononics for Coherent Light Control of Solids. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89 (22), 1–5. 10.1103/PhysRevB.89.220301. [DOI] [Google Scholar]
- Xiang H. J.; Guennou M.; Íñiguez J.; Kreisel J.; Bellaiche L. Rules and Mechanisms Governing Octahedral Tilts in Perovskites under Pressure. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96 (5), 1–11. 10.1103/PhysRevB.96.054102. [DOI] [Google Scholar]
- Herklotz A.; Wong A. T.; Meyer T.; Biegalski M. D.; Lee H. N.; Ward T. Z. Controlling Octahedral Rotations in a Perovskite via Strain Doping. Sci. Rep. 2016, 6, 1–7. 10.1038/srep26491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang H. Y.; Iwasa Y.; Kawasaki M.; Keimer B.; Nagaosa N.; Tokura Y. Emergent Phenomena at Oxide Interfaces. Nat. Mater. 2012, 11 (2), 103–113. 10.1038/nmat3223. [DOI] [PubMed] [Google Scholar]
- Zubko P.; Gariglio S.; Gabay M.; Ghosez P.; Triscone J.-M. Interface Physics in Complex Oxide Heterostructures. Annu. Rev. Condens. Matter Phys. 2011, 2 (1), 141–165. 10.1146/annurev-conmatphys-062910-140445. [DOI] [Google Scholar]
- Aso R.; Kan D.; Shimakawa Y.; Kurata H. Atomic Level Observation of Octahedral Distortions at the Perovskite Oxide Heterointerface. Sci. Rep. 2013, 3, 1–6. 10.1038/srep02214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gazquez J.; Stengel M.; Mishra R.; Scigaj M.; Varela M.; Roldan M. A.; Fontcuberta J.; Sánchez F.; Herranz G. Competition between Polar and Nonpolar Lattice Distortions in Oxide Quantum Wells: New Critical Thickness at Polar Interfaces. Phys. Rev. Lett. 2017, 119 (10), 1–6. 10.1103/PhysRevLett.119.106102. [DOI] [PubMed] [Google Scholar]
- Borisevich A. Y.; Chang H. J.; Huijben M.; Oxley M. P.; Okamoto S.; Niranjan M. K.; Burton J. D.; Tsymbal E. Y.; Chu Y. H.; Yu P.; et al. Suppression of Octahedral Tilts and Associated Changes in Electronic Properties at Epitaxial Oxide Heterostructure Interfaces. Phys. Rev. Lett. 2010, 105 (8), 1–4. 10.1103/PhysRevLett.105.087204. [DOI] [PubMed] [Google Scholar]
- Jia C. L.; Mi S. B.; Faley M.; Poppe U.; Schubert J.; Urban K. Oxygen Octahedron Reconstruction in the SrTiO3/LaAlO3 Heterointerfaces Investigated Using Aberration-Corrected Ultrahigh-Resolution Transmission Electron Microscopy. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79 (8), 2–5. 10.1103/PhysRevB.79.081405. [DOI] [Google Scholar]
- Fowlie J.; Gibert M.; Tieri G.; Gloter A.; Íñiguez J.; Filippetti A.; Catalano S.; Gariglio S.; Schober A.; Guennou M.; et al. Conductivity and Local Structure of LaNiO$_3$ Thin Films. Adv. Mater. 2017, 29 (18), 1605197. 10.1002/adma.201605197. [DOI] [PubMed] [Google Scholar]
- May S. J.; Smith C. R.; Kim J. W.; Karapetrova E.; Bhattacharya A.; Ryan P. J. Control of Octahedral Rotations in (LaNiO3)n/ (SrMnO3)m Superlattices. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83 (15), 2–5. 10.1103/PhysRevB.83.153411. [DOI] [Google Scholar]
- Moon E. J.; Balachandran P. V.; Kirby B. J.; Keavney D. J.; Sichel-Tissot R. J.; Schlepütz C. M.; Karapetrova E.; Cheng X. M.; Rondinelli J. M.; May S. J. Effect of Interfacial Octahedral Behavior in Ultrathin Manganite Films. Nano Lett. 2014, 14 (5), 2509. 10.1021/nl500235f. [DOI] [PubMed] [Google Scholar]
- Glazer A. M. Simple Ways of Determining Perovskite Structures. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1975, 31 (6), 756–762. 10.1107/S0567739475001635. [DOI] [Google Scholar]
- May S. J.; Kim J.-W.; Rondinelli J. M.; Karapetrova E.; Spaldin N. a.; Bhattacharya a.; Ryan P. J. Quantifying Octahedral Rotations in Strained Perovskite Oxide Films. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82 (1), 014110. 10.1103/PhysRevB.82.014110. [DOI] [Google Scholar]
- Rotella H.; Lüders U.; Janolin P.-E.; Dao V. H.; Chateigner D.; Feyerherm R.; Dudzik E.; Prellier W. Octahedral Tilting in Strained LaVO3 Thin Films. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85 (18), 184101. 10.1103/PhysRevB.85.184101. [DOI] [Google Scholar]
- Johnson-Wilke R. L.; Marincel D.; Zhu S.; Warusawithana M. P.; Hatt A.; Sayre J.; Delaney K. T.; Engel-Herbert R.; Schlepütz C. M.; Kim J.-W.; et al. Quantification of Octahedral Rotations in Strained LaAlO3 Films via Synchrotron X-Ray Diffraction. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88 (17), 174101. 10.1103/PhysRevB.88.174101. [DOI] [Google Scholar]
- Kan D.; Wakabayashi Y.; Tajiri H.; Shimakawa Y. Interfacially Engineered Oxygen Octahedral Rotations and Their Impact on Strain Relief in Coherently Grown SrRuO3 Films. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94 (2), 1–6. 10.1103/PhysRevB.94.024112. [DOI] [Google Scholar]
- Kinyanjui M. K.; Lu Y.; Gauquelin N.; Wu M.; Frano A.; Wochner P.; Reehuis M.; Christiani G.; Logvenov G.; Habermeier H. U.; et al. Lattice Distortions and Octahedral Rotations in Epitaxially Strained LaNiO3/LaAlO3 Superlattices. Appl. Phys. Lett. 2014, 104 (22), 221909. 10.1063/1.4881557. [DOI] [Google Scholar]
- Brahlek M.; Choquette A. K.; Smith C. R.; Engel-Herbert R.; May S. J. Structural Refinement of Pbnm -Type Perovskite Films from Analysis of Half-Order Diffraction Peaks. J. Appl. Phys. 2017, 121 (4), 045303. 10.1063/1.4974362. [DOI] [Google Scholar]
- García-Muñoz J. L.; Rodríguez-Carvajal J.; Lacorre P.; Torrance J. B. Neutron-Diffraction Study of RNiO3 (R = La,Pr,Nd,Sm): Electronically Induced Structural Changes across the M. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 46 (8), 4414–4425. 10.1103/PhysRevB.46.4414. [DOI] [PubMed] [Google Scholar]
- Müller K. A.; Berlinger W.; Waldner F. Characteristic Structural Phase Transition in Perovskite-Type Compounds. Phys. Rev. Lett. 1968, 21 (12), 814–817. 10.1103/PhysRevLett.21.814. [DOI] [Google Scholar]
- Scherwitzl R.; Zubko P.; Lichtensteiger C.; Triscone J. M. Electric-Field Tuning of the Metal-Insulator Transition in Ultrathin Films of LaNiO3. Appl. Phys. Lett. 2009, 95 (22), 222114. 10.1063/1.3269591. [DOI] [Google Scholar]
- Scherwitzl R.; Gariglio S.; Gabay M.; Zubko P.; Gibert M.; Triscone J. M. Metal-Insulator Transition in Ultrathin LaNiO3 Films. Phys. Rev. Lett. 2011, 106 (24), 3–6. 10.1103/PhysRevLett.106.246403. [DOI] [PubMed] [Google Scholar]
- Cancellieri C.; Reyren N.; Gariglio S.; Caviglia A. D.; Fête A.; Triscone J. M. Influence of the Growth Conditions on the LaAlO3/SrTiO3 Interface Electronic Properties. Epl 2010, 91 (1), 17004. 10.1209/0295-5075/91/17004. [DOI] [Google Scholar]
- Lichtensteiger C. InteractiveXRDFit : A New Tool to Simulate and Fit X-Ray Diffractograms of Oxide Thin Films and Heterostructures. J. Appl. Crystallogr. 2018, 51 (6), 1745–1751. 10.1107/S1600576718012840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masys; Jonauskas V. Elastic Properties of Rhombohedral, Cubic, and Monoclinic Phases of LaNiO3 by First Principles Calculations. Comput. Mater. Sci. 2015, 108 (PA), 153–159. 10.1016/j.commatsci.2015.06.034. [DOI] [Google Scholar]
- Luo X.; Wang B. Structural and Elastic Properties of LaAlO3 from First-Principles Calculations. J. Appl. Phys. 2008, 104 (7), 073518. 10.1063/1.2990068. [DOI] [Google Scholar]
- Cancellieri C.; Fontaine D.; Gariglio S.; Reyren N.; Caviglia A. D.; Fête A.; Leake S. J.; Pauli S. A.; Willmott P. R.; Stengel M.; et al. Electrostriction at the LaAlO3/SrTiO3 Interface. Phys. Rev. Lett. 2011, 107 (5), 1–4. 10.1103/PhysRevLett.107.056102. [DOI] [PubMed] [Google Scholar]
- Hatt A. J.; Spaldin N. A. Structural Phases of Strained LaAlO3 Driven by Octahedral Tilt Instabilities. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82 (19), 1–5. 10.1103/PhysRevB.82.195402. [DOI] [Google Scholar]
- Aso R.; Kan D.; Shimakawa Y.; Kurata H. Control of Structural Distortions in Transition-Metal Oxide Films through Oxygen Displacement at the Heterointerface. Adv. Funct. Mater. 2014, 24 (33), 5177–5184. 10.1002/adfm.201303521. [DOI] [Google Scholar]
- Liao Z.; Gauquelin N.; Green R. J.; Müller-Caspary K.; Lobato I.; Li L.; van Aert S.; Verbeeck J.; Huijben M.; Grisolia M. N. Metal – Insulator-Transition Engineering by Modulation Tilt-Control in Perovskite Nickelates for Room Temperature Optical Switching. Proc. Natl. Acad. Sci. U. S. A. 2018, 115 (38), 9515. 10.1073/pnas.1807457115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao Z.; Huijben M.; Zhong Z.; Gauquelin N.; Macke S.; Green R. J.; Van Aert S.; Verbeeck J.; Van Tendeloo G.; Held K.; et al. Controlled Lateral Anisotropy in Correlated Manganite Heterostructures by Interface-Engineered Oxygen Octahedral Coupling. Nat. Mater. 2016, 15 (4), 425–431. 10.1038/nmat4579. [DOI] [PubMed] [Google Scholar]
- Kumah D. P.; Malashevich A.; Disa A. S.; Arena D. A.; Walker F. J.; Ismail-Beigi S.; Ahn C. H. Effect of Surface Termination on the Electronic Properties of LaNiO3 Films. Phys. Rev. Appl. 2014, 2 (5), 1–7. 10.1103/PhysRevApplied.2.054004. [DOI] [Google Scholar]
- Son J.; Moetakef P.; Lebeau J. M.; Ouellette D.; Balents L.; Allen S. J.; Stemmer S. Low-Dimensional Mott Material: Transport in Ultrathin Epitaxial LaNiO3 Films. Appl. Phys. Lett. 2010, 96 (6), 062114. 10.1063/1.3309713. [DOI] [Google Scholar]
- Vailionis A.; Boschker H.; Liao Z.; Smit J. R. A.; Rijnders G.; Huijben M.; Koster G. Symmetry and Lattice Mismatch Induced Strain Accommodation near and Away from Correlated Perovskite Interfaces. Appl. Phys. Lett. 2014, 105 (13), 131906. 10.1063/1.4896969. [DOI] [Google Scholar]
- Willmott P. R.; Meister D.; Leake S. J.; Lange M.; Bergamaschi A.; Böge M.; Calvi M.; Cancellieri C.; Casati N.; Cervellino A.; et al. The Materials Science Beamline Upgrade at the Swiss Light Source. J. Synchrotron Radiat. 2013, 20 (5), 667–682. 10.1107/S0909049513018475. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.