Role of Rostral Fastigial Neurons in Encoding a Body-Centered Representation of Translation in Three Dimensions

Abstract

Many daily behaviors rely critically on estimates of our body motion. Such estimates must be computed by combining neck proprioceptive signals with vestibular signals that have been transformed from a head- to a body-centered reference frame. Recent studies showed that deep cerebellar neurons in the rostral fastigial nucleus (rFN) reflect these computations, but whether they explicitly encode estimates of body motion remains unclear. A key limitation in addressing this question is that, to date, cell tuning properties have only been characterized for a restricted set of motions across head-re-body orientations in the horizontal plane. Here we examined, for the first time, how 3D spatiotemporal tuning for translational motion varies with head-re-body orientation in both horizontal and vertical planes in the rFN of male macaques. While vestibular coding was profoundly influenced by head-re-body position in both planes, neurons typically reflected at most a partial transformation. However, their tuning shifts were not random but followed the specific spatial trajectories predicted for a 3D transformation. We show that these properties facilitate the linear decoding of fully body-centered motion representations in 3D with a broad range of temporal characteristics from small groups of 5–7 cells. These results demonstrate that the vestibular reference frame transformation required to compute body motion is indeed encoded by cerebellar neurons. We propose that maintaining partially transformed rFN responses with different spatiotemporal properties facilitates the creation of downstream body motion representations with a range of dynamic characteristics, consistent with the functional requirements for tasks such as postural control and reaching.

SIGNIFICANCE STATEMENT Estimates of body motion are essential for many daily activities. Vestibular signals are important contributors to such estimates but must be transformed from a head- to a body-centered reference frame. Here, we provide the first direct demonstration that the cerebellum computes this transformation fully in 3D. We show that the output of these computations is reflected in the tuning properties of deep cerebellar rostral fastigial nucleus neurons in a specific distributed fashion that facilitates the efficient creation of body-centered translation estimates with a broad range of temporal properties (i.e., from acceleration to position). These findings support an important role for the rostral fastigial nucleus as a source of body translation estimates functionally relevant for behaviors ranging from postural control to perception.

Introduction

Activities such as running to catch a ball involve many tasks including estimating our heading direction, maintaining balance during movement, and reaching to grasp an object. Each task relies critically on estimating how our body moves in three-dimensional (3D) space. However, this poses computational challenges. Because individual sensors provide ambiguous information about body movement, such estimates must be computed by integrating information from multiple sources (Green and Angelaki, 2010). For example, to distinguish trunk from head motion, vestibular and neck proprioceptive signals must be combined (Mergner et al., 1991; Brooks and Cullen, 2009; Luan et al., 2013). However, integrating these signals appropriately requires that vestibular signals be transformed from a head- to a body-centered reference frame (Manzoni et al., 1999; Kleine et al., 2004; Shaikh et al., 2004; Chen et al., 2013).

Several studies have implicated the cerebellum in these computations. In particular, recent work suggests the rostral fastigial nucleus (rFN) as a candidate for computing estimates of passive or “unexpected” body motion (Brooks and Cullen, 2009, 2013; Brooks et al., 2015) and distributing them to brainstem regions involved in postural control (Batton et al., 1977; Homma et al., 1995) as well as via the thalamus to cerebral cortical areas involved in motor control and self-motion perception (Asanuma et al., 1983; Middleton and Strick, 1997; Meng et al., 2007). But do rFN cells indeed encode explicit representations of body motion? In support of this notion, many rFN neurons combine dynamic vestibular and neck proprioceptive signals during horizontal-plane rotations precisely as required to differentiate body from head motion (Brooks and Cullen, 2009). However, so far this has only been shown under conditions when no vestibular reference frame transformation was required (i.e., when head and body motion axes remained parallel). Other studies provided evidence for a transformation of vestibular estimates of translational (Shaikh et al., 2004) or rotational (Kleine et al., 2004) motion toward body-centered coordinates in the rFN, but for most neurons the transformation was only partial. This could suggest that the computations to estimate body motion remain incomplete in the rFN. Alternatively, they might be expressed only at the population level.

A key limitation in distinguishing these possibilities is that previous studies examined cell tuning properties only for a restricted set of motions across head orientations in the horizontal plane. Thus, they neither measured neural tuning in 3D nor characterized how that tuning changes across head-re-body orientations in multiple planes. This has at least two important consequences. First, many rFN neurons possess complex spatiotemporal convergence (STC) properties (Zhou et al., 2001; Shaikh et al., 2005a) whereby their spatial tuning for translation in any given plane need not reflect a simple projection of their full 3D tuning (Chen-Huang and Peterson, 2006). Consequently, conclusions about reference frames based solely on tuning properties in a single plane might either underestimate or overestimate the true extent of transformation. Second, and more importantly, if a representation of body motion indeed exists in the rFN, then cells in this region must reflect a transformation of vestibular signals fully in 3D (i.e., across head-re-body orientations in any plane). The ideal computations for this transformation predict cell properties should shift away from head-centered tuning along a precise spatial trajectory that depends both on a given cell's 3D spatial tuning and the plane of head reorientation.

Here, we investigated the evidence for these computations by examining how 3D spatial tuning for translational motion varied with changes in head orientation in both horizontal and vertical planes. We show that rFN cell spatiotemporal tuning properties indeed reflect a 3D transformation of vestibular signals. Furthermore, they do so across the neural population in a specific fashion that facilitates the creation of body-centered motion estimates with a broad range of dynamic properties, consistent with the functional requirements for different behaviors ranging from postural control to heading perception (Lockhart and Ting, 2007; Chen et al., 2011a, 2016).

Materials and Methods

Animal preparation.

Data reported here were collected from 2 juvenile male rhesus monkeys (Macaca mulatta) weighing 4–8 kg that were prepared for chronic recording of eye movements and single-unit activity. In a first surgery, the animals were chronically implanted with a circular delrin head-stabilization ring (7 cm diameter) that was anchored to the skull using hydroxyapatite-coated titanium inverted T-bolts and neurosurgical acrylic (Green et al., 2007). Supports for a removable delrin recording grid (3 × 5 cm) were stereotaxically positioned inside the ring and secured to the skull with acrylic. The grid consisted of staggered rows of holes (spaced 0.8 mm apart) and was positioned inside the ring such that it was slanted in the horizontal plane by 10° from left to right to provide access to medial recording regions in the cerebellar and vestibular nuclei. In a second surgery, animals were chronically implanted with a scleral eye coil for recording eye movements in 2D (Robinson, 1963). Surgeries were performed under anesthesia and aseptic conditions. After surgical recovery, animals were trained to fixate and pursue visual targets within a ±1.5° window for fluid reward using standard operant conditioning techniques. All surgical and experimental procedures were approved by the institutional animal research review board (Comité de déontologie de l'expérimentation sur les animaux) and were in accordance with national guidelines for animal care.

Experimental setup.

During experiments, monkeys were comfortably seated in custom-built primate chairs. To prevent changes in body position, the animal's torso was secured with shoulder belts and a waist restraint and his limbs were gently attached to the chair with straps. The head was secured in different positions with respect to the body by means of a custom-built head restraint system mounted on top of the primate chair that attached to the monkey's head stabilization ring implant at three points via set screws. The restraint system's positioning mechanism allowed the head to be manually reoriented and locked in different head-on-trunk positions along three independent orthogonal axes (Fig. 1A). In particular, the head could be reoriented in vertical planes toward nose-down (pitch reorientation by up to 45°; Fig. 1Aii,Dii) and right/left-ear-down (roll reorientation by up to 30°; Fig. 1Aiii,Diii) about horizontal axes located at approximately the level of the second cervical vertebra. The head could also be reoriented in the horizontal plane about a vertical axis passing through the head center (yaw axis reorientation by up to 45°; Fig. 1Aiv,Div).

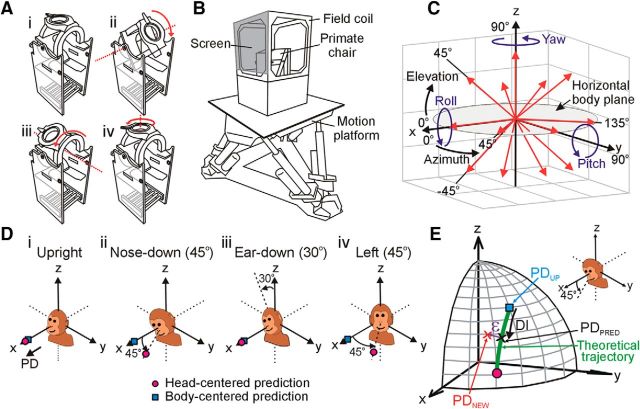
Figure 1.

Experimental methods. A, Custom primate chairs allowed testing of cell tuning with the head upright and facing forward (Ai) as well as after manual repositioning of the head relative to the body in the vertical plane by up to 45° toward nose-down (Aii) or 30° toward right-ear-down (Aiii) and in the horizontal plane by 45° to the left (Aiv). B, Schematic illustration of the motion delivery system. The primate chair and eye movement monitoring system (field coil) were mounted on top of a 6 degree-of-freedom motion platform (Moog). C, Illustration of the 13 axes along which sinusoidal translation stimuli (red arrows; 0.5 Hz, ±9 cm) and the 3 axes about which sinusoidal rotation stimuli (blue arrows; 0.5 Hz, ±22°/s) were applied. Motion directions described in spherical coordinates (azimuth and elevation) were defined in a body-centered reference frame. D, Cell tuning was characterized with the head upright (Di), after vertical plane head reorientation either by 45° toward nose-down (Dii) or 30° toward ear-down (Diii) and after horizontal plane reorientation 45° to the left (Div). The predicted preferred translation tuning (PD) for body-centered (blue squares) versus head-centered (pink circles) encoding of motion is illustrated for a cell with a head upright PD along the x axis (0° azimuth, 0° elevation). E, Schematic representation of the theoretically predicted trajectory of PDs (green curve) between body-centered (blue square) and head-centered (pink circle) coding predicted for an example cell with an upright PD (PD_UP) of (45°, 45°). The cell's tuning reflects a new PD (PD_NEW; red x) of (25°, 30°) when the head is reoriented by 45° toward nose-down (Inset). The extent of shift from PD_UP to PD_NEW along the “ideal” (green) trajectory was quantified by a displacement index (DI; x corresponds to a DI of 0.5). The extent of shift orthogonal to this trajectory was quantified by an angular error ε (purple arrow indicates an ε of −8.5°) defined as the angle between PD_NEW (red x) and the closest point along the ideal trajectory (PD_PRED; black x).

The primate chair was secured on top of a 6 degree-of-freedom motion platform (6DOF2000E, Moog) that was used to provide 3D translational and rotational movement stimuli (Fig. 1B). Platform motion was measured with a navigational sensor composed of a three axis linear accelerometer and a three axis angular velocity sensor (Tri-Axial Navigational IMU, Kistler). Eye movements were measured with a three-field magnetic search coil system (24 inch cube; Riverbend Instruments) that was mounted on a frame attached to the motion platform such that the monkey's head was centered within the magnetic field. Visual point targets were back-projected onto a vertical screen mounted in front of the animal (25.5 cm distance) using a laser and an x-y mirror galvanometer system (Cambridge Technology). Stimulus presentation, reward delivery, and data acquisition were controlled with custom scripts written in the Spike2 software environment using the Cambridge Electronics Design (model power 1401) data acquisition system. Eye coil voltage signals and 3D linear accelerometer and angular velocity measurements of platform motion were antialias filtered (200 Hz, 4-pole Bessel; Krohn-Hite), digitized at a rate of 833.33 Hz, and stored using the Cambridge Electronics Design system.

Neural recordings.

Single-unit extracellular recordings in the rostral fastigial and vestibular nuclei (rFN and VN) were performed with epoxy-coated, etched tungsten microelectrodes (5–7 mΩ, FHC) that were inserted into the brain using 26-gauge guide tubes that were passed via the recording grid through small predrilled burr holes in the skull. Electrodes were then advanced using a remote-controlled mechanical microdrive (Hydraulic Probe Drive; FHC) mounted on top of the head-stabilization ring. Neural activity was amplified, filtered (30 Hz to 15 kHz), and isolated online using a time-amplitude dual window discriminator (BAK Electronics). Single-unit spikes triggered acceptance pulses from the window discriminator that were time-stamped and stored using the event channel of the Cambridge Electronics Design data acquisition system. In addition, raw neural activity waveforms were digitized at 30 kHz and stored using the Cambridge Electronics Design system for off-line spike discrimination.

In initial penetrations, the abducens nuclei were localized bilaterally. The recording regions of interest in the rFN and VN were subsequently identified based on their stereotaxic locations relative to the abducens nuclei and fourth ventricle and their characteristic response properties (Dickman and Angelaki, 2002; Shaikh et al., 2005a). We focused exclusively on cells responsive to motion stimuli but not to eye movements, known as “vestibular-only” (VO) neurons. Cells were characterized as eye-movement-insensitive by their failure to exhibit changes in modulation during horizontal and vertical smooth pursuit (0.5 Hz, ±10 cm) as well as during saccades and fixation (up to ±20° horizontally and vertically). Translation-sensitive VO neurons were recorded in the rFN ∼2.3–4.5 mm above the abducens nuclei within ±4 mm of the midline and anterior to pursuit- and saccade-related neurons encountered in the caudal FN (Büttner et al., 1991). VO neurons responding to translation stimuli were also recorded in the rostral portions of the medial and lateral VN (medial part), within ±5.5 mm of the midline and at a similar depth to abducens neurons where they were typically found intermingled with neurons having sensitivity to eye movements. VO cell responses to vestibular stimuli were recorded in darkness and fixation was uncontrolled. However, in postrecording analyses, we confirmed that none of the neurons reported here exhibited responses to vestibular stimulation during translation (i.e., response gains and phases; see below) that were consistently correlated with eye position.

After a translation-sensitive VO neuron in either the rFN or VN was isolated, its spatial tuning was first characterized with the head facing straight ahead in an upright orientation (Fig. 1Di) by recording responses to sinusoidal translation (0.5 Hz, ±9 cm, ±0.09 G) along 13 different axes. These axes were defined in body-centered coordinates and described by different combinations of azimuth and elevation angles in increments of 45° spanning 3D space (Fig. 1C, red arrows). To improve spatial resolution, responses were also often recorded for motion along 4–6 additional axes that were chosen based on the cell's preferred directional tuning. These included the maximum and minimum response directions predicted for a head-centered encoding of translation after head reorientation in vertical and horizontal planes (see below), as well as additional directions (typically at 30° and 60° to the cell's preferred direction [PD] in elevation/azimuth) that were predicted to exhibit large gain or phase differences for head- versus body-centered spatial tuning. After characterizing spatial tuning for translation most neurons were also tested for rotation sensitivity during sinusoidal rotation (0.5 Hz, 22 deg/s) about x, y, and z axes defined in a body-centered reference frame with an origin centered in the head (i.e., in roll, pitch, and yaw; see Fig. 1C, blue arrows).

To examine the extent to which neural responses reflected a head- versus body-centered encoding of self-motion, the spatial tuning for translation was subsequently characterized in additional head orientations (Fig. 1D). In particular, the head was first repositioned relative to the body in the vertical plane in either pitch (45° nose-down) or roll (30° right-ear-down) depending on the cell's preferred upright response direction and on the axis of reorientation that was predicted to result in larger differences between head- versus body-centered tuning (i.e., the axis further away from the cell's preferred response direction; Fig. 1Dii vs Fig. 1Diii). Responses to translation were then characterized in the new static head-on-trunk orientation for the same set of body-centered translation directions that were examined with the head upright. The head was then returned to upright and retested along one or more directions close to its preferred response direction to confirm cell isolation. If cell isolation was maintained, the spatial tuning for translation was then characterized after the head was repositioned relative to the body in the horizontal plane (45° left). To maximize the use of partial datasets, we prioritized testing across elevations in the cell's preferred upright azimuth direction after vertical plane head reorientation and across azimuth directions in the horizontal plane (0° elevation) after horizontal plane reorientation.

Data analysis.

Data analysis was performed offline using custom scripts written in MATLAB (The MathWorks). The neuron's instantaneous firing rate (IFR) was computed as the inverse of the interspike interval and assigned to the middle of that interval. For each motion direction in each head orientation, the gain and phase of the neural IFR response to the stimulus were determined by fitting both the response and stimulus with a sine function over 5–20 well-isolated cycles using a nonlinear least-squares (Levenberg-Marquardt) minimization algorithm. For translational stimuli, response gain was expressed in units of spikes/s/G (where G = 9.81 m/s²) and phase as the difference (in degrees) between peak neural modulation and peak linear acceleration. For rotational stimuli, gain was expressed in units of spikes/s/deg/s and phase as the difference in peak neural firing and peak angular velocity.

Tuning profiles were visualized by plotting response gains as a function of the azimuth and elevation of translation direction (e.g., Fig. 3A–C). To obtain a precise estimate of the PD for translation, in each head orientation we fit gains and phases across directions using a 3D spatiotemporal convergence (STC) model (Chen-Huang and Peterson, 2006) that is more general than cosine tuning and can account for the observation that many rFN and VN cells reflect responses to motion stimuli with dynamic properties that depend on stimulus direction (Siebold et al., 1999; Angelaki and Dickman, 2000; Shaikh et al., 2005a; Chen-Huang and Peterson, 2006). Using this model, 3D tuning functions describing cell gain, G(α, β), and phase, φ(α, β), across directions in azimuth (α) and elevation (β) are given by the following equations:

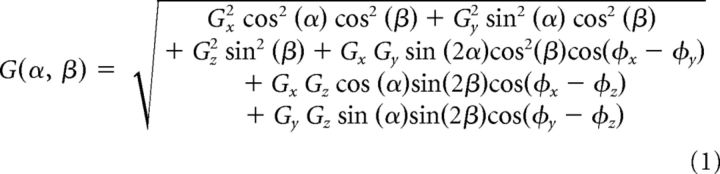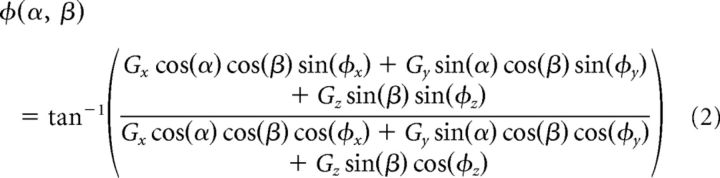where G_x, G_y, G_z and φ_x, φ_y, φ_z are gain and phase parameters, respectively, along orthogonal x, y, and z axes (for details, see Chen-Huang and Peterson, 2006). The fitting procedure allowed estimation for each head orientation of the cell's maximum response gain, phase, and direction (i.e., the PD). We also calculated the ratio of the minimum to maximum response gain (STC tuning ratio). This ratio provides a measure of the extent to which a cell's response reflects simple cosine-tuned changes in gain across movement directions (STC ratio = 0) versus dynamic properties that depend on stimulus direction, consistent with a convergence of vestibular signals that differ in terms of both spatial tuning (i.e., PD) and response phase relative to the stimulus (STC ratio > 0) (Angelaki, 1991; Chen-Huang and Peterson, 2006).

Figure 3.

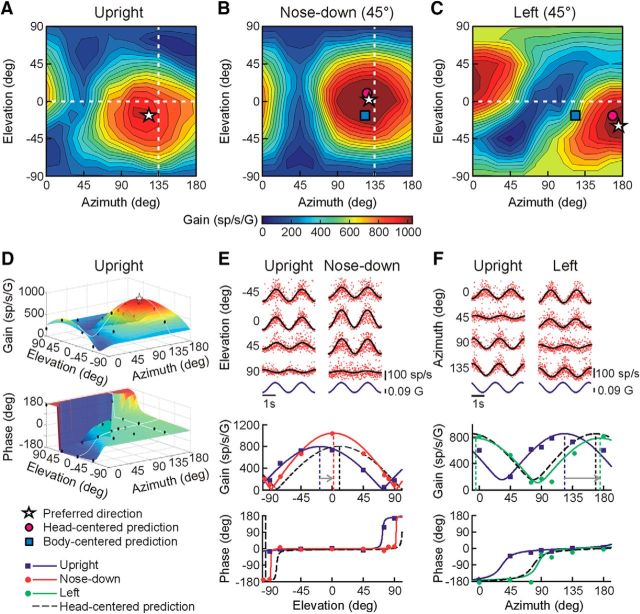
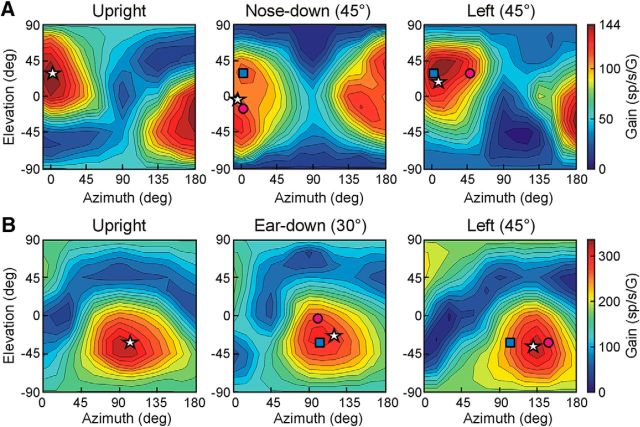
Example of a head-centered cell in the rFN. A–C, Contour plots illustrating the cell's 3D spatial tuning for translation with the head upright (A) as well as after vertical plane head reorientation toward 45° nose-down (B) and after horizontal plane reorientation 45° to the left (C). In all plots, azimuth and elevation are expressed in body-centered coordinates. Star: PD; pink circle: predicted PD for head-centered tuning; blue square: predicted PD for body-centered tuning. D, The cell's preferred translation direction (star) for each head orientation was estimated by fitting a 3D STC model (colored surface) to cell response gain and phase data (black circles) across stimulus directions (here illustrated for the upright orientation). E, Instantaneous firing rates (IFRs; top) and STC model fit to gains and phases across elevations (bottom) for an azimuth angle of 135° (i.e., along dashed white line in B) with the head upright (blue lines and symbols) and after reorientation toward nose-down (red lines and symbols). F, IFRs (top) and STC model fit to gains and phases across azimuth angles (bottom) for 0° elevation (i.e., along dashed white line in C) with the head upright (blue lines and symbols) and after reorientation to the left (green lines and symbols). Dashed black curves in E and F show the predictions for head-centered tuning.

All neurons were fit with a 3D STC model for the head upright. However, for several neurons (16 of 66 neurons recorded across multiple head orientations), only partial datasets, with insufficient data to fit a full 3D STC model, were obtained after head reorientation in either the vertical or horizontal plane. Neurons with partial datasets after vertical plane reorientation were included in our analyses only if we were able to complete testing across all elevations in the vertical plane passing closest to their preferred azimuth direction (N = 12/66). Similarly, partial datasets after horizontal plane reorientation were included only if we were able to complete testing across all azimuth directions in the horizontal plane (i.e., elevation 0°; N = 4/66). For such partial datasets, preferred tuning in elevation or azimuth was estimated by fitting responses across motion directions in that plane using a 2D STC model (Angelaki, 1991).

To examine the extent to which neurons reflected a head- versus body-centered encoding of heading direction, we quantified how spatial tuning varied with changes in head orientation using two approaches. Because spatial tuning in the current study was defined in body-centered coordinates, cells encoding translation in a body-centered reference frame were predicted to exhibit similar tuning across all head-re-body orientations (e.g., Fig. 1D, blue squares). In contrast, head-centered cells were predicted to exhibit tuning shifts with changes in head position (e.g., Fig. 1D, pink circles) that could be predicted based on the cell's PD and the amplitude and plane of head reorientation. Thus, in a first approach, we quantified the extent of shift in spatial tuning after head reorientation in each plane using a 3D displacement index (DI), defined as the ratio of the actual shift in PD compared with that predicted for head-centered tuning (ΔPD_actual/ΔPD_{head-centered}). No shift in PD with changes in head orientation (i.e., body-centered tuning) therefore yielded a DI of 0, whereas a PD shift consistent with the predictions for head-centered encoding yielded a DI of 1. For a head-centered cell, reorientation in any vertical plane that is not perfectly aligned with its preferred azimuth direction (e.g., head reorientation in the plane through azimuth direction 0° toward nose-down for a cell with a preferred azimuth of 45°) will give rise to tuning shifts in both elevation and azimuth in body-centered coordinates, each of which may be smaller in amplitude than the angle of head reorientation. For example, for a head-centered cell with an upright PD of 45° in azimuth and 45° in elevation, the predicted shift for head reorientation 45° toward nose-down is −36.6° in elevation and −14.6° in azimuth (Fig. 1E, pink circle). Thus, in contrast to previous studies, which have quantified vestibular reference frame transformation extent by examining tuning shifts exclusively in a single plane (e.g., shifts in azimuth for head/eye reorientation in the horizontal plane) (Kleine et al., 2004; Shaikh et al., 2004; Fetsch et al., 2007; Chen et al., 2013), the 3D DI we used took into account observed and predicted shifts in azimuth and elevation simultaneously for head reorientation in each of the vertical and horizontal planes. For a given cell PD and head reorientation axis, the predicted shift in either azimuth or elevation considered individually could be quite small. However, a key advantage of computing an index that takes into account shifts in both coordinates simultaneously is that predicted tuning shift magnitudes depend only on head reorientation amplitude and the proximity of the cell's PD to the head reorientation axis. Thus, for an appropriate choice of head reorientation axis (i.e., choice of an axis as distant as possible from alignment with the cell's PD; see above), this approach ensures that actual shifts need never be compared with very small predicted values.

In brief, to compute this index, we started from the cell's PD when upright and facing forward and used a 3D rotation matrix to compute the new PD that would be predicted for a head-centered encoding of translation after reorienting the head in a given plane (i.e., the new PD consistent with a DI of 1). In addition, we calculated a “trajectory” of the predicted PDs that would be obtained if the neuron's tuning shift reflected only a fraction of the full shift predicted for a head-centered cell, consistent with a representation intermediate between head- and body-centered encoding (Fig. 1E, green trace). Specifically, predicted PDs were calculated for angular displacements in the range of −50% to 150% of the actual change in head orientation (in steps of 0.1%), corresponding to the PDs for DIs in the range of −0.5 to 1.5. While DI values between 0 and 1 are consistent with a partial shift away from head-centered tuning toward body-centered coordinates, the PDs corresponding to DIs greater than 1 or less than 0 were also computed to account for a few cells that showed shifts that were either larger than, or in the opposite direction to, the predictions for head-centered tuning. The cell's DI for head reorientation in a given plane was then obtained by computing the dot product between the actual PD observed after head reorientation (Fig. 1E, PD_NEW, red cross) and each of the predicted PDs along the trajectory (Fig. 1E, green trace) to find which predicted PD (corresponding to a particular DI) was the closest match to that experimentally observed (Fig. 1E, PD_PRED, black cross). Importantly, there was no a priori reason to assume that the actual PD would fall along the theoretically predicted trajectory of PDs for a reference frame transformation between head- and body-centered coordinates. Therefore, we also estimated the “goodness of match” between the observed PD (Fig. 1E, red cross) and closest predicted PD (Fig. 1E, black cross). This was done by computing the magnitude of the angular error, ε, between these two directions as ε = cos⁻¹(${\stackrel{\rightharpoonup }{PD}}_{NEW}·{\stackrel{\rightharpoonup }{PD}}_{PRED}$) with clockwise versus counterclockwise angular deviations away from the ideal PD trajectory from head- to body-centered defined as positive and negative errors, respectively (Fig. 1E, purple).

To facilitate the interpretation of DIs and ε values despite differences in neural sensitivities to motion stimuli (i.e., signal-to-noise ratio) across neurons and neural populations, we established the significance of tuning shifts by computing confidence intervals (CIs) for each DI and error estimate, ε, using a bootstrap method based on resampling of residuals (Efron and Tibshirani, 1993). In brief, bootstrapped tuning functions for each head orientation were obtained by resampling (with replacement) the residuals of the STC model fit to the data, adding the resampled residuals to the model predicted response to create a new synthetic dataset, and then fitting this dataset with the STC model to obtain a new set of model parameters. This process was repeated 1000 times to produce a distribution of tuning functions for each head orientation and a corresponding distribution of DIs and ε values from which 95% CIs could be derived (percentile method). A DI or ε estimate was considered significantly different from a particular value if its 95% CI did not include that value.

To assess the specificity with which observed spatial tuning shifts followed the theoretical trajectories predicted for neurons effecting a vestibular head-to-body reference frame transformation, we also examined how our measured DIs and ε values compared with those predicted by chance. In particular, for each recorded cell (having a particular PD) and head reorientation case characterized experimentally for that cell, we examined the distributions of DIs and ε values that would result from 10,000 random tuning shifts from head-centered toward body-centered coordinates. These were obtained by rotating the cell's PD expressed in head coordinates about randomly chosen axes within ±90° of the actual head reorientation axis and through amplitudes randomly chosen from 0 up to a maximum of twice the actual angle of head reorientation. The DIs and ε values for all tuning shifts were then computed in body coordinates for comparison with our experimental results. In principle, completely random rotations could be about axes spanning 3D space with amplitudes up to 180°. However, we constrained the axes to be within ±90° of the head reorientation axis to ensure that tuning shifts were not in the opposite direction to those appropriate for effecting the transformation (i.e., producing completely unrealistic DIs). Similarly, maximum rotation amplitudes were constrained to twice the actual head reorientation angle as we found that this was sufficient to achieve DIs in the range of 0 to 1 for ≈70%-90% of axes capable of producing DIs in that range. On average, such random shifts produced broad distributions of DIs and ε values quite different from those observed in our experimental populations, and included ε values associated with DIs well outside those measured experimentally. Thus, to be able to make a more meaningful direct comparison between our measured ε values and those predicted by random shifts, we examined how large the ε values would be expected to be by chance for a population of cells having similar DI distributions to those recorded experimentally. To achieve this, from the distributions created for each recorded cell and head reorientation case, we randomly sampled a DI and ε combination from among all those combinations in which the DI fell within ±0.1 of the DI that was actually measured. Across all cells and head reorientation cases, this yielded a DI distribution similar to that of our experimental data and a corresponding distribution of ε values. This sampling procedure was repeated 1000 times to yield average DI and ε distributions for random tuning shifts that we compared with our experimental data.

The DI analysis provided an estimate of the extent of transformation toward body-centered coordinates. However, DIs could vary continuously between 0 and 1 and were calculated separately for each plane of head reorientation. Thus, we used a second analysis to assess whether a given cell could be considered significantly more consistent with a head- versus body-centered encoding of translation, and to examine the extent to which its tuning properties reflected a full 3D transformation toward body-centered coordinates. In particular, we simultaneously fit the data acquired across multiple head orientations with body- and head-centered reference frame models. For comparison with our DI analyses, we first fit the data across two head orientations (upright and after vertical plane reorientation toward nose/ear-down, or upright and after horizontal plane reorientation to the left). To examine the evidence for a full 3D reference frame transformation at the level of individual neurons we then extended the analysis to fit data across all three head orientations (upright, nose/ear-down and left). Each 3D STC model incorporated three gain (G_x, G_y, G_z) and three phase (φ_x, φ_y, φ_z) parameters along orthogonal coordinate axes (see Eqs. 1, 2). To take into account significant gain changes across head orientations that were revealed by our analyses, we also included a gain scaling factor that was used to scale the three gain parameters (G_x, G_y, G_z) in each of the nose/ear-down and left orientations relative to those in the upright orientation. This scaling factor was set based on the gains associated with the tuning functions obtained for each individual head orientation and was not a free parameter in our head- versus body-model fitting analysis. Head versus body reference frame models were distinguished by the fact that gains, G, and phases, φ, were expressed in terms of x, y, and z axes and azimuth (α) and elevation angles (β) defined either in head- or body-centered coordinates.

For each model, we estimated the goodness-of-fit by computing the correlation (R) between the best-fitting function and the data. Because the two models are themselves correlated, we removed the influence of this correlation by computing partial correlation coefficients (ρ) according to the following formulas:

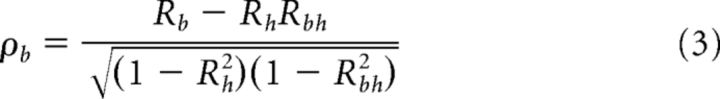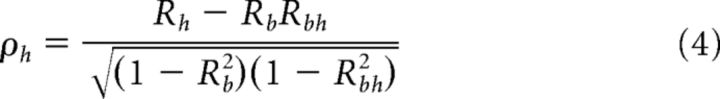where R_b and R_h are the simple correlation coefficients between the data and the body- and head-centered models, respectively, and R_bh is the correlation between the two models. Partial correlation coefficients ρ_b and ρ_h were then normalized using Fisher's r-to-Z transform so that conclusions regarding significant differences in model fits could be drawn on the basis of comparisons of Z scores, independent of the number of data points (Angelaki et al., 2004; Smith et al., 2005; Fetsch et al., 2007). To visualize the results of this analysis, we constructed a scatterplot of the Z scores for the head-centered versus body-centered model and separated the plot into regions where the fit of one model was significantly better than that of the other (e.g., see Fig. 7). In particular, a cell was considered significantly better fit by one model than the other if the Z score for that model was > 1.645 and exceeded the Z score for the other model by 1.645 (equivalent to a p value of <0.05).

Figure 7.

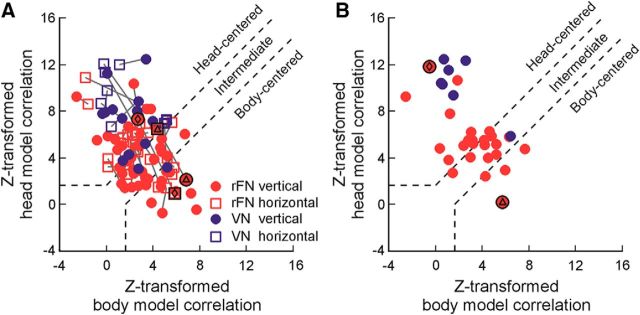
Correlation with head-centered and body-centered models. A, B, Scatter plots of head- versus body-centered model partial correlation coefficients (Z-transformed) when neural response gains and phases for rFN (red) and VN (blue) cells were fit with each model across either (A) 2 head orientations (circles denote upright and after vertical plane reorientation; squares denote upright and after horizontal plane reorientation) or (B) all 3 head orientations (upright and after vertical and horizontal plane reorientations). Significance regions are based on the difference between head- and body-centered Z scores corresponding to p < 0.05 (top left, head- centered; bottom right, body-centered; middle diagonal region, not significantly better correlated with either model and classified as “intermediate.”) Gray lines in A link data points associated with the same cell for head reorientation in different planes. Diamonds and triangles in A indicate the example cells in Figures 8A and B, respectively, which were classified differently for vertical versus horizontal plane reorientations. The diamond and triangle in B indicate the example head- and body-centered cells of Figures 3 and 4, respectively.

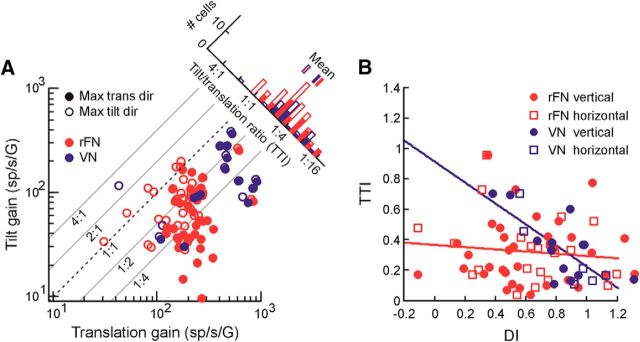
The translation stimuli we used to investigate reference frame transformations exclusively stimulated the otolith organs. However, recent studies have emphasized that, because the otoliths respond equivalently to tilts relative to gravity and translations (i.e., they encode the net gravito-inertial acceleration [GIA]), otolith afferent signals must be combined nonlinearly with canal signals to resolve this “tilt/translation ambiguity” and accurately estimate translation (Angelaki et al., 2004; Green and Angelaki, 2004; Yakusheva et al., 2007; Laurens et al., 2013). To assess the extent to which evidence for a head to body reference frame transformation in individual neurons was correlated with tilt/translation disambiguation, neural responses to upright pitch and roll rotation stimuli were expressed in terms of the linear acceleration stimulus sensed by the otoliths along the x and y head axes, respectively, due to tilt relative to gravity. This yielded tilt response gains in units of spikes/s/G where G = 9.81 m/s² and phases defined relative to linear acceleration. A 2D STC model was used to estimate tilt gains and phases across all azimuth directions in the horizontal plane based on those measured along the x and y axes (0° and 90° azimuth). The extent of GIA- versus translation-encoding behavior for each cell was then quantified using a “tilt/translation” index (TTI) computed as the ratio of a cell's response gain during head tilt to its response gain during translation. A TTI of 1 (equivalent gains for tilt and translation) thus indicates GIA-encoding behavior, like an otolith afferent, whereas a TTI of 0 reflects a pure translation-encoding cell.

Neural population decoding.

To test whether the properties of our rFN cells were sufficient to achieve a purely body-centered representation of translation in 3D, we examined whether such a representation could be linearly decoded from our rFN population. Specifically, we examined the capacity to construct a population of fully body-centered “output units” (for illustrative purposes, 13 units with PDs along axes spaced at 45° intervals in azimuth and elevation; e.g., Fig. 1C) from a simple linear weighted combination of the tuning functions of the subset of our rFN cells characterized across all three head orientations (N = 25).

To facilitate the choice of decoding weights across a broad range of head reorientations relative to the body (i.e., up to ±90° toward nose-up/down, right/left-ear-down, and left/right), we made several simplifying assumptions to predict the tuning functions of our neurons in untested head orientations based on those characterized experimentally. In particular, we assumed that the vertical- and horizontal-plane DI values that we obtained for each cell were the same for all amplitudes of head reorientation in that plane (i.e., the extent of transformation was independent of the amplitude of head reorientation) and that DIs in the tested vertical plane (i.e., nose-down or ear-down) generalized to other vertical planes. Similarly, ε values and head-orientation-dependent gain changes measured in the tested vertical plane were assumed to generalize to reorientations in any vertical plane. Importantly, while these are assumptions that could not be confirmed by our present dataset, we also examined the impact of randomly assigning DI (and ε and gain change) values to the untested vertical plane orthogonal to the tested one (i.e., either nose-down or ear-down). Values were chosen based on our measured distributions and randomly assigned so as to maintain similar proportions of head- and body-centered cells to those observed experimentally. This alternative approach yielded similar results and the same general conclusions.

In addition, to extrapolate measured gain changes across a range of head orientations, we assumed that gain changes scale linearly with reorientation amplitude, consistent with approximately linear or monotonic gain-scaling as a function of static postural signals (e.g., eye, head, or hand position) observed for many cells in cortical regions (Andersen et al., 1990; Brotchie et al., 1995; Buneo et al., 2002; Chang et al., 2009). Because it is unclear how ε values should change with head reorientation amplitude and because for a majority of reorientations (74%) ε values for rFN cells were found to be statistically indistinguishable from zero, in initial analyses we assumed ε amplitudes were fixed at the measured value (in degrees) across all head reorientation angles for each plane. Another potential option would have been simply to set all nonsignificant ε values to zero. However, to provide a more conservative estimate of decoding performance, we opted instead not to eliminate ε values entirely, even if they were statistically insignificant. In additional analyses, we also investigated the impact of global increases in ε on the facility with which body-centered representations can be decoded.

In a first analysis, we examined the capacity to decode body-centered representations based solely on the spatial tuning properties of our recorded neurons across head orientations without taking response phase into account. For simplicity, cell gains were approximated as cosine-tuned across directions with a PD corresponding to their maximum gain direction. Similarly, we assumed “output” body-centered units with cosine-tuned directional responses. Decoding weights were then chosen based on a multiple linear regression analysis that modeled the 3D spatial tuning of each output neuron as a weighted combination of the predicted tuning functions of our rFN neurons across 13 head orientations that included upright and ±30° and ±60° angular head deviations from upright toward nose-up/down, right/left-ear-down, and left/right. The capacity to decode fully body-centered representations (i.e., DI and ε close to zero) was then evaluated by calculating the DIs and ε values of our output units across several head orientations in each plane, including ±30°, ±45°, ±60°, ±75°, and ±90°.

In a second analysis, the full spatiotemporal response properties of each recorded cell (i.e., gains G_x, G_y, G_z and phases φ_x, φ_y, φ_z in Eqs. 1, 2) were included. Decoding weights were chosen in a similar fashion to our first analysis, except that in the regression analysis both response gain and phase were taken into account. In addition, to relax the requirement for cosine-tuned spatial tuning on our output units we used a weighted least-squares approach, in which tuning parameters contributing to defining the gain and phase in the output unit's PD were weighted more heavily than those contributing to response components 90° out of phase and spatially orthogonal to the PD. This approach allowed for moderate levels of STC in our output layer (i.e., 82%–100% STC ratios < 0.5; mean STC ratio = 0.2–0.3) similar to those observed in our recorded rFN cells (91% < 0.5; mean STC ratio of 0.27). To examine the range of temporal characteristics that could be successfully decoded in our body-centered output units, we repeated this regression analysis assuming phases in the PD of our output units ranging from −135° to 45° relative to acceleration.

An additional goal of our decoding analysis was to address how close the tuning properties of rFN cells are to reflecting fully transformed vestibular signals by exploring how many cells were required to decode fully body-centered representations. In particular, we were specifically interested in the facility with which body-centered representations, functionally relevant for behaviors such as postural control, could be obtained from linear combinations of very small groups of cells that plausibly activate the same muscle group, and whether particular cell properties are associated with this capacity. Because the population of cells we recorded across all three head orientations was too sparsely distributed across spatial directions to adequately address these questions, we constructed a synthetic population of 500 neurons having distributions of vertical and horizontal plane DIs, ε values, PD response phases, and STC characteristics similar to those of our recorded rFN cells. We found no systematic relationship between cell PD and other tuning characteristics (i.e., response phase, DI, etc.) and thus assumed that the rFN population reflects similar distributions of these characteristics across all spatial directions. In addition, for simplicity, PDs for the 500 neurons were distributed uniformly across 3D space. Although this was not true for our actual recorded population (see Fig. 2), the simplification of uniformly distributed PDs had no impact on our general conclusions as long as we assumed a sufficiently large cell population was available for decoding in each direction (e.g., at least 30 cells with PDs within ±45° of that direction and a distribution of properties similar to those of our recorded rFN neurons).

Figure 2.

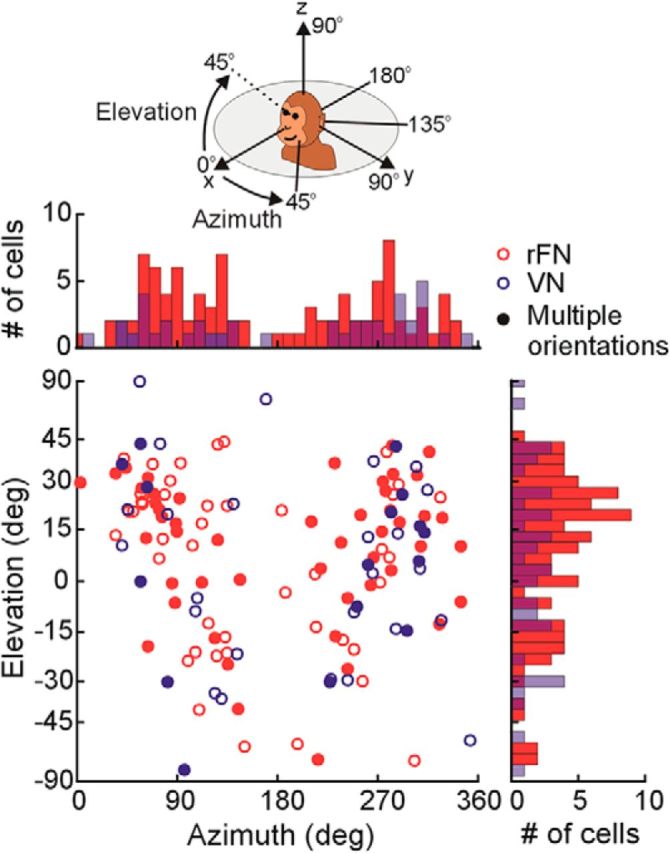
Distribution of preferred translation directions of rFN (red; N = 95) and VN (blue; N = 46) cells. Each data point in the scatter plot indicates the preferred azimuth (abscissa) and elevation (ordinate) with elevation angle spacing scaled according to Lambert's equal area projection of the spherical stimulus space. Histograms along the top and right sides of the plot show marginal distributions. Filled symbols denote cells for which tuning functions were characterized across multiple head orientations.

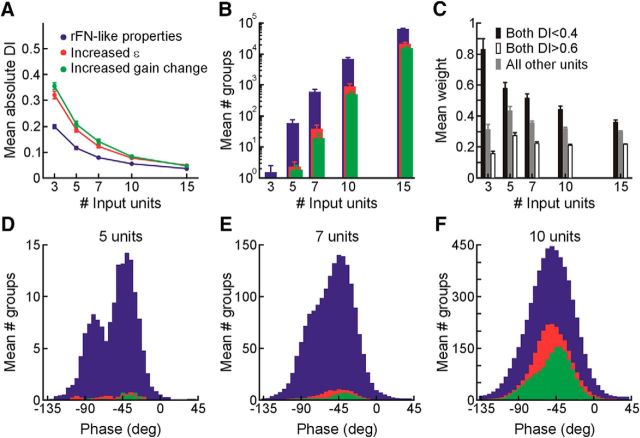
We then examined all (∼60,000) possible subsets of 3 cells and 200,000 possible subsets of 5, 7, 10, or 15 neurons having PDs within ±45° of one of 13 tested translation directions (i.e., aligned with the 13 axes defined in Fig. 1C) and evaluated the capacity to decode body-centered representations of motion with different temporal properties in that direction using cell populations of different sizes. Because it was possible to decode representations with DIs close to 0, yet characterized by other properties not consistent with a head-orientation-invariant, body-centered estimate of motion (i.e., substantial ε values or changes in gain or phase with changes in head orientation), further analysis was limited to decoded representations meeting the following criteria across head orientations up to ±90° in each vertical and horizontal plane: (1) average ε values <15% of the angular change in head orientation; (2) average gain changes relative to upright of <15%; and (3) average phase changes relative to upright of <10°. The influence of ε on decoding ability was also examined by evaluating the impact of increasing the existing value of ε for each synthetic cell by an amplitude randomly chosen in the range of 8°-16°. Similarly, the influence of head-orientation-dependent gain changes on decoding ability was examined by increasing the existing extent of gain increase or decrease by an amplitude randomly chosen in the range of 0.5%–1% per degree of change in head angle. The capacity to decode body-centered representations from each of the increased ε and gain change populations was then evaluated using the same approach and sets of criteria as for our rFN-like cell population.

Statistical analysis.

All statistical tests were performed using MATLAB (The MathWorks). To establish CIs on the estimates of neural response gain and phase obtained from sine function fits to the firing rate modulation for a given motion stimulus and direction (see above), we used a bootstrap method in which bootstrapped gain and phase estimates were obtained by resampling (with replacement) the response cycles used for the sine function fits 600 times. A cell was considered to exhibit a significant modulation for a given motion stimulus if at the time of peak response (estimated from the nonbootstrapped fit across all response cycles) 95% CIs on the firing rate modulation were greater than a minimum of 2 spikes/sinusoidal cycle.

The significance of changes in response tuning was evaluated by using a bootstrap method based on resampling of residuals (Efron and Tibshirani, 1993) to create distributions of 1000 tuning functions for each head orientation. These were used to compute corresponding distributions of DIs, ε values, PD response gain and phase changes, and STC ratio changes from which 95% CIs could be derived (for details, see above). A given parameter was considered significantly different from a particular value if the 95% CI did not include that value.

To test whether tuning functions across head orientations were statistically better correlated with a head- versus a body-centered tuning model (two models that are themselves correlated), we computed partial correlation coefficients for each model fit to the data (see Eqs. 3, 4), which were subsequently normalized using Fisher's r-to-Z transform. A cell was considered significantly better fit by a given model if the Z score for that model exceeded the Z score for the other by 1.645 (equivalent to a p value of <0.05; for details, see above).

To test for significant differences between DI distributions (a subset of which were non-Gaussian), we used the nonparametric Wilcoxon rank-sum test. To test for a significant difference between our measured ε distributions and the broader distributions produced by random tuning shifts, we used the Kolmogorov–Smirnov test. The Wilcoxon signed rank test was used to compare distribution medians to specific values (e.g., DI medians to either 0 or 1). Hartigan's Dip Test (Hartigan and Hartigan, 1985) was used to test distributions for multimodality. We tested the uniformity of PDs (i.e., circular distributions of azimuth and elevation angles) in our sampled neural populations using Rao's spacing test (Berens, 2009). Correlations between DI and other cell tuning properties (e.g., ε, STC ratio) were evaluated using linear regression. For all statistical tests, p values of < 0.05 were considered statistically significant.

Results

Using a motion platform (Fig. 1B) to provide passive movement stimuli, we recorded from 95 rostral fastigial neurons (32 in Monkey A, 63 in Monkey B) and 46 vestibular nucleus neurons (33 in Monkey A, 13 in Monkey B) that were responsive to translational motion but insensitive to eye movements. To characterize spatial tuning, neural responses were collected as monkeys were sinusoidally translated along a minimum of 13 axes distributed throughout 3D space (Fig. 1C). Responses were plotted as a function of translation direction in azimuth and elevation to construct 3D tuning functions (e.g., Fig. 3A) and precise estimates of the preferred direction (PD) for translation were computed by fitting neural responses with a 3D STC model (see Materials and Methods; Fig. 3D).

As shown in Figure 2, the PDs spanned 3D space when the head was upright and facing forward. In elevation, the distribution of PDs was largely concentrated within ± 45° and slightly biased toward upward translational motion (Rao's spacing test, p < 0.001; mean elevation: 8.44°). PDs were also broadly distributed in azimuth but, similar to previous reports, rFN cells showed a preference for lateral (y axis) translation (i.e., azimuth close to 90° or 270°) (Zhou et al., 2001; Green et al., 2005; Shaikh et al., 2005a). The majority of rFN and VN cells tested (54 of 61 rFN and 27 of 27 VN) also responded for rotational motion about at least one of the cardinal (x, y, z) axes (bootstrap test; 95% CIs did not include response gains <0.045 spikes/s/deg/s, equivalent to a modulation of 2 spikes/cycle).

Quantification of reference frames by spatial tuning shifts

To investigate the extent to which neurons encoded translational motion in head- versus body-centered coordinates, the two reference frames were dissociated by comparing spatial tuning with the head upright with that after reorientation in both the vertical and horizontal planes (Fig. 1D). Motion directions were defined in a coordinate frame fixed to the body. Thus, the spatial tuning of neurons encoding a body-centered estimate of heading direction should be invariant to changes in head-re-body orientation (e.g., Fig. 1D, blue squares). In contrast, cells encoding translation in a head-centered frame (i.e., as the vestibular sensors) should exhibit systematic shifts in preferred tuning with changes in head orientation (Fig. 1D, pink circles). Reference frames were assessed for a subset of 49 rFN and 17 VN neurons whose tuning functions were characterized across multiple head orientations.

To quantify the spatial shift of tuning functions across the neural populations, we computed DIs for each cell and plane of head reorientation (i.e., vertical and horizontal). In contrast to previous studies in which tuning shifts in motion-sensitive neurons were measured in a single plane (i.e., only in azimuth for horizontal-plane changes in head orientation) (Kleine et al., 2004; Shaikh et al., 2004; Fetsch et al., 2007; Chen et al., 2013), we quantified PD shifts fully in 3D (i.e., in both azimuth and elevation) such that DI values provided information about the extent of shift along the theoretically predicted 3D spatial “trajectory” for a transformation toward body-centered tuning (see Materials and Methods; Fig. 1E, green trace). A DI of 1 indicates a tuning shift equivalent to that predicted for head-centered encoding of translation, whereas a DI of 0 indicates no shift, consistent with body-centered encoding. Importantly, to assess how closely observed tuning shifts followed the prediction for a 3D transformation, we also quantified the angular displacement away from the ideal predicted trajectory (Fig. 1E, angular deviation error, ε).

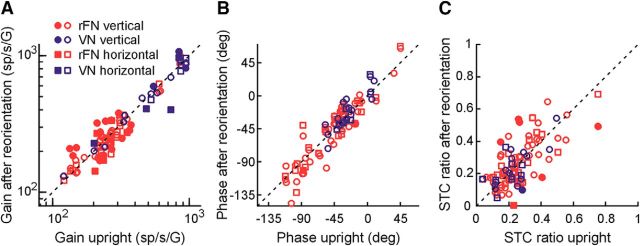
Similar to previous observations limited to the horizontal plane (Shaikh et al., 2004), head-centered and body-centered estimates of heading direction were both found in the rFN. For example, with the head upright and forward the preferred translation direction for the neuron in Figure 3 was 123.5° in azimuth and −16.6° in elevation (Fig. 3A, white star). However, after vertical-plane head reorientation 45° toward nose-down, the cell's PD shifted by 19.5° in elevation and 3.9° in azimuth. This is close to the predictions for head-centered encoding of translation, as illustrated in the contour plot of Figure 3B (star closer to pink circle than blue square) and STC model fits to the data across elevations in the preferred azimuth direction (Fig. 3E, bottom; red curve closer to black dashed curve than to blue curve). Similarly, after head reorientation 45° to the left the cell's PD shifted by 51.2° in the same direction as the head (Fig. 3C,F). These properties are consistent with encoding of translation in a mainly head-centered reference frame as reflected in DIs close to 1 (DI_vert = 0.74; DI_hor = 1.14) and small ε values (ε_vert = −0.54°; ε_hor = −12.8°).

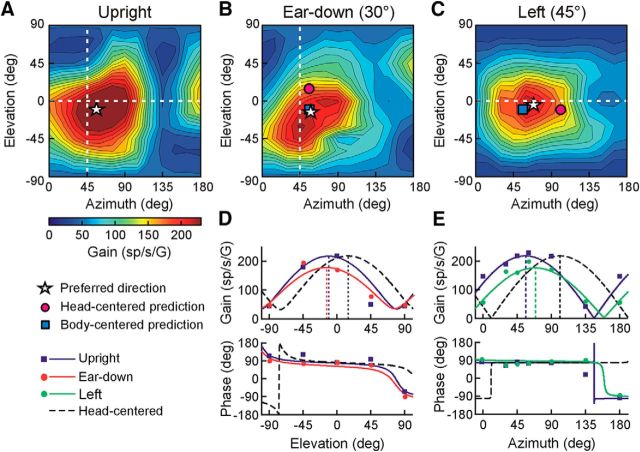
In contrast, the tuning properties of other cells were consistent with the predictions for body-centered encoding of translation. For example, the neuron in Figure 4 maintained similar tuning both after head reorientation toward right-ear-down in the vertical plane (Fig. 4B) and after leftward head reorientation in the horizontal plane (Fig. 4C). For both vertical and horizontal reorientations, neither the DIs (DI_vert = −0.11; DI_hor = 0.25) nor the ε values (ε_vert = −1.4°; ε_hor = 6.1°) were statistically different from zero (bootstrap test; 95% CIs included 0). Thus, the tuning properties of this neuron reflected translation signals that had undergone a full 3D reference frame transformation toward body-centered coordinates.

Figure 4.

Example rFN neuron with body-centered tuning. A–C, Contour plots illustrating the cell's 3D spatial tuning for translation with the head upright (A) as well as after vertical plane head reorientation 30° toward right-ear-down (B) and after horizontal plane reorientation 45° to the left (C). Star: PD; pink circle: predicted PD for head-centered tuning; blue square: predicted PD for body-centered tuning. D, STC model fit to gains and phases across elevations for an azimuth angle of 45° (i.e., along dashed white line in B) with the head upright (blue lines/symbols) and after reorientation toward ear-down (red lines/symbols). E, STC model fit to gains and phases across azimuth angles for 0° elevation (i.e., along dashed white line in C) with the head upright (blue lines/symbols) and after reorientation to the left (green lines/symbols). Dashed black curves in D and E show the predictions for head-centered tuning.

Unlike the example cells in Figures 3 and 4, however, many rFN cells exhibited responses that were neither purely head- nor body-centered. This is shown in Figure 5A, B, which summarizes the distributions of DIs for all rFN and VN cells tested for head reorientations in each plane. Whereas rostral VN cells were more consistently head-centered for reorientation in both vertical (Fig. 5A, blue) and horizontal planes (Fig. 5B, blue) with median DI values close to 1 (DI_vert = 0.83, DI_hor = 0.99), DI values for rFN cells were broadly distributed. DIs for some rFN cells were statistically indistinguishable from 0 (vertical-plane: 23%; horizontal-plane: 22%; bootstrap test, 95% CI included 0) and others indistinguishable from 1 (vertical-plane: 36%; horizontal-plane: 37%; bootstrap test, 95% CI included 1). However, the DIs for many other cells fell between these two values. This is reflected in distributions that were not significantly bimodal (Hartigan's Dip Test; rFN vertical: p = 0.54; rFN horizontal: p = 0.72) with median vertical- and horizontal-plane DIs of 0.55 and 0.66, respectively, that were significantly greater than 0 (Wilcoxon signed rank tests; p < 0.0001), less than 1 (Wilcoxon signed rank tests; p < 0.0001), and significantly lower than the corresponding DIs for VN cells (Wilcoxon rank-sum test; vertical, p = 0.0065; horizontal, p = 0.043). There was no significant difference in the DI distributions for reorientation in vertical versus horizontal planes for either cell population (Wilcoxon rank-sum test; rFN: p = 0.62; VN: p = 0.22). Thus, consistent with previous observations limited to the horizontal plane (Shaikh et al., 2004), rFN cell responses to translation were on average significantly more transformed toward body-centered coordinates than those in the rostral VN.

Figure 5.

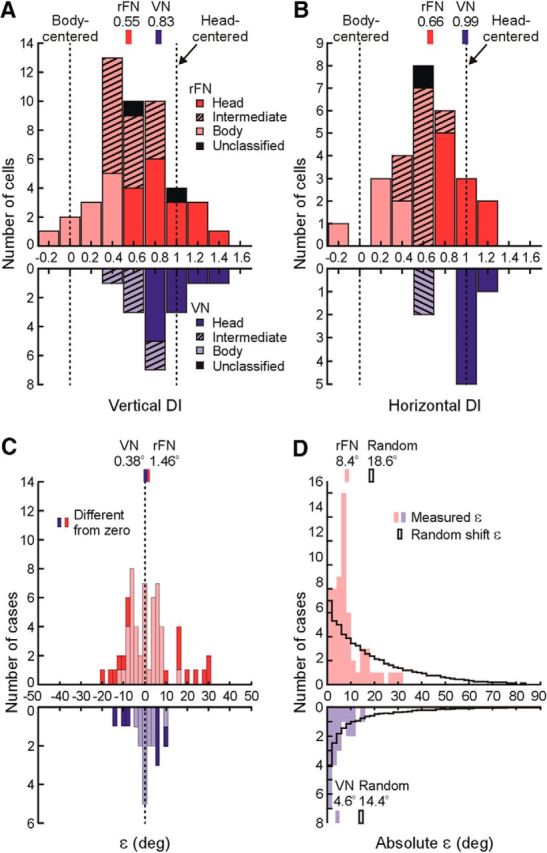
Distribution of DIs and ε values. DI values of 0 and 1 indicate tuning shifts consistent with body- and head-centered encoding of translation, respectively. A, DI distribution for vertical-plane head reorientation. B, DI distribution for horizontal-plane head reorientation. rFN (red; vertical, N = 47; horizontal, N = 27) and VN (blue; vertical, N = 16; horizontal, N = 8) cell DIs are classified based on bootstrapped DI 95% CIs as body-centered (pale colors), head-centered (dark colors), or intermediate (hatched). Cells for which bootstrapped DI CIs included both 0 and 1 were labeled as unclassified (black; N = 2 for rFN vertical; N = 1 for rFN horizontal). Vertical red and blue bars above the plots indicate the medians of each population. C, Distribution of ε values across vertical and horizontal head reorientations. Dark colors denote a significant difference from zero (N = 16 of 62 cases for rFN; N = 7 of 20 cases for VN). Vertical red and blue bars above the plot indicate the means of each population. D, Distributions of measured absolute ε values across vertical and horizontal head reorientations (pale red, rFN; pale blue, VN) superimposed on the distributions of absolute ε values predicted for random tuning shifts (black outlines) producing similar DI distributions to those measured experimentally. Vertical colored and black outlined bars above the plot indicate the means of each distribution.

Importantly, however, despite broad distributions in the extent of tuning shifts exhibited by rFN cells, these shifts were not random. Indeed, they typically fell along the 3D spatial trajectories that were theoretically predicted for a transformation from head- to body-centered coordinates. This is indicated by the finding that the ε values (i.e., angular deviations away from the “ideal” trajectory) for most rFN cells were small (Fig. 5C) and similar to those of VN cells. In particular, they were less than 10° in 76% of all head reorientation cases for rFN cells and 85% for VN cells, and for 72% of all reorientation cases they were not significantly different from zero (bootstrap test; 95% CIs included 0). While this result might be expected for cells with tuning close to either head- or body-centered (i.e., either untransformed or fully transformed cells), particularly relevant is that 74% of reorientation cases characterized by significant shifts toward “intermediate” tuning (i.e., a partial transformation) reflected insignificant ε values. There was no significant correlation between transformation extent (DI) and ε for reorientation in either plane (vertical: r = 0.28, p = 0.09; horizontal: r = 0.36, p = 0.09). Furthermore, on average, our measured ε amplitudes were significantly smaller than those predicted for random tuning shifts producing similar DI distributions to those measured experimentally (Fig. 5D; Kolmogorov–Smirnov test; rFN: p < 10⁻⁶; VN: p = 0.005).

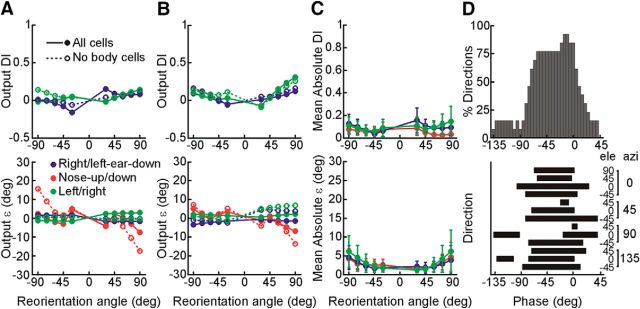
In addition to examining spatial tuning shifts, we also examined how other aspects of cell responses varied across head-re-body positions. In particular, posture-dependent changes in response gain (i.e., “gain-fields”) have been theoretically predicted (Zipser and Andersen, 1988; Pouget and Sejnowski, 1997; Xing and Andersen, 2000; Deneve et al., 2001; Salinas and Sejnowski, 2001; Smith and Crawford, 2005; Blohm et al., 2009) and experimentally observed (Andersen et al., 1990; Brotchie et al., 1995; Batista et al., 1999; Buneo et al., 2002; Avillac et al., 2005; Mullette-Gillman et al., 2005; Chang et al., 2009; Chang and Snyder, 2010; DeSouza et al., 2011; Chen et al., 2013; Rosenberg and Angelaki, 2014) in cell populations thought to reflect intermediate stages in the computation of reference frame transformations. We first evaluated the evidence for such changes in response dynamics by examining how rFN and VN cell response gains and phases in the PD (obtained from STC model fits) varied with head orientation. In contrast to previous observations suggesting an absence of gain-field properties (Kleine et al., 2004; Shaikh et al., 2004), we found that many cells exhibited increases or decreases in maximum response gain for head reorientation in one or both planes that reached significance in 39% of rFN cells and 35% of VN cells (bootstrap analysis, 95% CIs on changes did not include 0). However, these changes were typically small (average 13% change from upright or 0.36% per degree of change in head angle for rFN and 0.24%/° for VN; Fig. 6A). Other aspects of response dynamics remained invariant across head orientations. In particular, we found no systematic dependence of response phase on head orientation in either the horizontal or vertical planes (Fig. 6B). Similarly, while the ratio of minimum to maximum response gain (STC ratio) varied to a limited extent with changes in head orientation, these changes were significant in only a minority of cells (<11%; Fig. 6C; bootstrap analysis, 95% CIs on changes did not include 0). No significant correlation was found between either response phase and DI (rFN vertical: r = 0.12, p = 0.40; rFN horizontal: r = 0.23, p = 0.36; VN vertical: r = 0.44, p = 0.09; VN horizontal: r = 0.45, p = 0.26) or STC ratio and DI (rFN vertical: r = 0.16, p = 0.27; rFN horizontal: r = 0.18, p = 0.36; VN vertical: r = 0.28, p = 0.29; VN horizontal: r = 0.28, p = 0.5) for reorientation in either vertical or horizontal planes.

Figure 6.

Dependence of tuning function parameters on head orientation. Tuning parameters after head reorientation in the vertical (circles) and horizontal (squares) planes are plotted versus the corresponding values with the head upright and straight forward relative to the body. A, Gain along the maximum response direction. B, Phase along the maximum response direction. C, STC ratio. Filled symbols denote parameter values that were significantly different after head reorientation compared with upright. Red denotes rFN cells. Blue denotes VN cells. Dashed line indicates unity slope.

Classification of individual neurons in 3D

The population data of Figure 5 provide evidence that, in contrast to rostral VN cells, many rFN cells reflect a transformation toward body-centered coordinates. The fact that rFN DI distributions were similar for head reorientation in both vertical and horizontal planes supports the hypothesis that such a transformation takes place in 3D. However, this first analysis provided little insight as to whether a full 3D transformation was reflected at the level of individual neurons. To address this question, we performed a second model-fitting analysis that assessed whether the tuning of each cell was best explained by a body- versus a head-centered model.

In this analysis, an STC model characterized by gain and phase parameters along either body- or head-centered axes (see Materials and Methods) was fit to the data across multiple head orientations. For comparison with the DI results, we first fit each model to the data separately for head reorientation in each of the vertical and horizontal planes (i.e., across two head orientations at a time). The goodness of fit of each model was quantified using a partial correlation analysis (Angelaki et al., 2004; Smith et al., 2005; Fetsch et al., 2007). To simplify interpretation, partial correlation coefficients were normalized using Fisher's r-to-Z transform and those corresponding to the head-centered model were plotted versus those for the body-centered model (Fig. 7A). Cells in the upper-left region of the plot reflect a significantly better fit by the head-centered model, whereas those in the lower-right region reflect a significantly better fit by the body-centered model. Cells in the central diagonal region were not better fit by one model compared with the other and were classified as “intermediate.” Gray lines join the results obtained for the same neuron for head reorientation in the vertical (filled circles) versus the horizontal planes (open squares).

Using this classification approach, we found that 40% (19 of 47) of rFN neurons were better fit by the head-centered model and 23% (11 of 47) by the body-centered model for vertical head reorientation, whereas 36% (17 of 47) reflected intermediate tuning (Fig. 7A, filled red circles). Similarly, for horizontal plane head reorientation, 63% (17 of 27) of rFN neurons were consistent with head-centered tuning while 18.5% (5 of 27) were body-centered and 18.5% (5 of 27) were intermediate (Fig. 7A, open red squares). In contrast, 88% (14 of 16) and 100% (8 of 8) of VN neurons were classified as head-centered for vertical and horizontal plane head reorientation, respectively.

Particularly notable, however, is that the conclusions regarding reference frames for individual rFN neurons were often dependent on the plane of head reorientation examined (i.e., Fig. 7A, gray lines joining the same neuron often cross boundaries). Figure 8 provides particularly striking examples of this. Whereas the neuron in Figure 8A was classified as head-centered for vertical plane head reorientation, it exhibited body-centered tuning for horizontal plane reorientation (Fig. 7A, diamond symbols joined by gray line). Conversely, the cell in Figure 8B was classified as body-centered for vertical plane head reorientation but head-centered for horizontal plane reorientation (Fig. 7A, triangle symbols joined by gray line). More generally, across the rFN population, 32% (8 of 25) reflected different tuning properties for reorientation in vertical versus horizontal planes, exhibiting head-centered tuning for reorientation in one plane but body-centered or intermediate tuning for reorientation in the other plane. Thus, even if a cell appeared to be body-centered for horizontal plane reorientations, as shown in previous studies (Kleine et al., 2004; Shaikh et al., 2004), it was not necessarily fully body-centered in 3D. Conversely, cells classified in previous studies as head-centered may actually have reflected an at least partial transformation for reorientation in vertical planes.

Figure 8.

Tuning functions of two example rFN neurons for which the conclusions regarding reference frame differed for vertical versus horizontal plane head reorientations. A, Example rFN cell exhibiting tuning better correlated with head-centered encoding of translation after vertical plane head reorientation (45° nose-down, DI = 0.76), but body-centered encoding of translation for horizontal plane reorientation (45° left, DI = 0.13; see Fig. 7A, diamonds). B, Example rFN cell exhibiting body-centered encoding of translation for vertical plane head reorientation (30° right-ear-down, DI = 0.19), but closer to head-centered tuning for horizontal plane reorientation (45° left, DI = 0.61; see Fig. 7A, triangles). Star: PD; pink circle: predicted PD for head-centered tuning; blue square: predicted PD for body-centered tuning.

To examine the evidence for a full 3D reference frame transformation at the level of individual rFN neurons, we then extended the model-fitting analysis to fit data across all three head orientations simultaneously. Figure 7B shows the results of this analysis for the subset of neurons (25 rFN, 7 VN) in which it was possible to collect full datasets across all three head orientations. Whereas all VN cells with one exception were head-centered in 3D, similar proportions of rFN cells were classified as either head-centered or intermediate (48% head-centered; 36% intermediate). Strikingly, however, and in keeping with the results above, only 4 neurons (16%) were classified as statistically closer to body-centered in 3D. Of these, only 2 cells (8%) were characterized by DIs < 0.4 in both horizontal and vertical planes. Thus, while the computations necessary for a reference frame transformation in 3D were reflected across the population of rFN neurons, a complete 3D transformation was typically not observed at the level of individual cells.

Population decoding of body-centered representations

Although few individual rFN neurons encoded a fully body-centered representation of translation in 3D, previous studies have demonstrated that reference frame transformations can be computed by combining activities of sufficient numbers of cells across a neural population that encodes sensory information in heterogeneous reference frames (Zipser and Andersen, 1988; Pouget and Sejnowski, 1997; Xing and Andersen, 2000; Deneve et al., 2001; Salinas and Sejnowski, 2001; Smith and Crawford, 2005; Blohm et al., 2009). To confirm this for our rFN neurons, we examined whether we could decode fully body-centered representations of translation from a simple weighted linear sum of the tuning functions of the subset of rFN neurons (N = 25) recorded across all three head orientations.

We first examined this capacity using simplified representations of our rFN cells that took into account their preferred spatial tuning across head reorientations (including DIs, ε values, and gain changes in each plane) but did not include their temporal properties and assumed cosine-tuned gains across directions (i.e., no STC; see Materials and Methods). As expected, we found that with a weighted linear sum of these simplified rFN tuning functions, it was indeed possible to construct fully body-centered output units. This is exemplified by the example output unit in Figure 9A (solid lines and filled circles), which maintained a close to body-centered representation of y axis (90° azimuth, 0° elevation) motion (DI and ε values close to 0) across changes in head orientation of up to ±90° in each of the pitch (nose-up/down), roll (left/right-ear down), and yaw (left/right) planes. A similar capacity to decode body-centered representations was found even when only the cells classified as “head-centered' and “intermediate” were included (Fig. 9A, dotted lines and open circles). Most importantly, when we extended our analysis to include the full spatiotemporal tuning characteristics of our neurons (i.e., their full STC tuning including response phases across directions), we found that it was possible not only to construct output units with close to body-centered tuning across 13 motion axes spanning 3D space (Fig. 9B,C), but with changes in the decoding weights such outputs units could exhibit a broad spectrum of temporal characteristics ranging from phases leading translational acceleration to lagging translational velocity (Fig. 9D). Thus, our recorded rFN population could be used to provide downstream regions with body-centered estimates of translational acceleration, translational velocity, or a broad range of intermediate dynamic properties as required for different behavioral tasks.

Figure 9.

Decoding body-centered motion in 3D from the recorded rFN population. A, B, DI (top) and ε (bottom) as a function of head reorientation angle toward nose-up/down (red), right/left-ear-down (blue), and left/right (green) for an output unit with a PD along the y axis (90° azimuth, 0° elevation). The output unit was decoded from a weighted linear sum of either (A) simplified cosine-tuned representations of the preferred spatial tuning properties of our recorded rFN cells (i.e., STC properties/phases were not taken into account) or (B) tuning functions that incorporated their full spatiotemporal tuning characteristics. The decoded body-centered unit in B has a phase lag of 15° relative to acceleration in its PD. Filled symbols and solid lines represent decoding performance using all rFN cells recorded across 3 head orientations (N = 25) as inputs. Open symbols and dashed lines represent decoding performance using all cells, with the exception of those classified as body-centered (N = 21). DIs are shown only for ear-down and left/right head reorientation because the DI is undefined for nose-up/down reorientation about an axis aligned with the output unit's PD (i.e., no tuning shift is predicted for nose-up/down reorientation for this unit and thus any observed shift is described by ε). C, Average decoding performance (mean absolute DI and ε) across 13 motion directions (spaced at 45° intervals in azimuth and elevation; Fig. 1C) for each head orientation and plane using the full STC tuning properties of all rFN cells recorded across 3 head orientations. Means were computed using the DI and ε values for each direction associated with the output phase at which the best decoding performance (lowest regression mean-squared error) was obtained. Error bars indicate standard deviation (SD) in DI and ε values across directions for reorientations in each plane. D, Distribution of phases relative to translational acceleration that could be successfully decoded across directions. The percentage of motion directions for which body-centered representations having each phase could be decoded (top) and the range of phases decoded for each motion direction (bottom) are illustrated for all decoded representations meeting the following criteria across head angles up to ±90° for reorientation in each plane: (1) average absolute DI < 0.15; (2) average absolute ε < 15% the angular change in head orientation angle; (3) average gain changes relative to upright of <15%; and (4) average phase change relative to upright <10°.

To gain further insight into the facility with which fully transformed translation estimates could be obtained from rFN cells, in a second analysis we investigated how many cells were required to decode body-centered representations in 3D. In particular, we reasoned that if the rFN plays a functional role in supplying information about body motion for tasks such as postural control, then rFN cells might reflect particular characteristics that would facilitate the decoding of body-centered representations from simple linear combinations of the tuning functions of very small groups of cells that plausibly activate the same muscle group. The population of cells we recorded across all three head orientations was too sparsely distributed across spatial directions to reflect the range of response properties in each direction required to adequately address this question. Thus, we constructed a synthetic population of 500 neurons (input units) with PDs spanning 3D space and distributions of tuning properties similar to those of our recorded population. We then examined decoding ability with input unit groups of different sizes (3, 5, 7, 10, and 15 units) across motion directions (see Materials and Methods).

Of all (∼60,000) possible groups of 3 input units and 200,000 randomly chosen possible groups of 5, 7, 10, or 15 units with PDs within ±45° of each output direction, we examined the relationship between DI and input unit group size only for those decoded representations that met several additional criteria for body-centered motion estimation in each plane of head reorientation across head reorientation angles up to ± 90°. These included the following: (1) average ε values of <15% the angular change in head orientation; (2) average gain changes relative to upright of <15%; and (3) average phase changes of <10° relative to upright. The capacity to decode body-centered representations was examined across 13 motion directions spanning 3D space (e.g., Fig. 1C). This analysis yielded similar results for most directions, with the exception of up-down (i.e., 90° elevation) where we found that it was substantially easier to decode body-centered representations in 3D with very small numbers of input units. Consequently, we focused our further analysis and report here on the more conservative estimates of decoding performance obtained across the other 12 directions.

As expected, average DI across all directions, head orientations, and planes decreased as the number of input units used for decoding increased (Fig. 10A). However, for groups with 5 or more units, this decrease largely reflected an increase in the number of combinations yielding decoded representations with low DIs (e.g., DIs < 0.15, Fig. 10B). With 3 units, only a few groups across a subset of motion directions (4 of 12) yielded body-centered representations with average DIs < 0.15 across all head orientations in each plane. However, the capacity to decode body-centered representations increased rapidly with the number of input units. With as few as 5 units, on average 56 ± 22 SE groups in each direction (range 3–263) yielded decoded representations with mean DIs in each plane of <0.15, and this number rose rapidly to 578 ± 141 SE (range 112–1645) for 7 unit groups and 6759 ± 1054 SE (range 2333–14807) for 10 unit groups.

Figure 10.

Decoding performance as a function of the number of synthetic input units and specific tuning properties. A, Mean output DI across directions, head reorientation angles, and planes plotted as a function of input unit group size. For each direction, average DIs were calculated based on the representations decoded from the 100 groups that yielded the lowest DIs while also meeting the following output criteria for decoding across head angles of up to ±90° for reorientation in each plane: (1) average absolute ε <15% the angular change in head orientation angle; (2) average gain changes relative to upright of <15%; and (3) average phase change relative to upright <10°. For each input unit group, only the DI at the phase yielding the best decoding performance (lowest regression mean-squared error) was included in the average. The plot shows the mean (±standard error [SE]) of the average DI values across the 12 motion directions (excluding 90° elevation) that yielded similar performance (see Results). Blue denotes decoding performance for input units with properties similar to those of our recorded rFN neurons. Red denotes decoding performance for input units with ε values for reorientation in each plane increased by 8° to 16°. Green denotes decoding performance for input units with “gain-field” sensitivities in units of percentage gain change per degree of head angle increased by 0.5%/° to 1%/° (see Materials and Methods). B, Number of input unit groups of each size (mean ± SE across 12 directions) that yielded decoded representations meeting the criteria in A and having average absolute DIs < 0.15 across head angles up to ±90° for reorientation in each plane. Red, blue, and green denote decoding using input units with tuning properties as described in A. C, Average decoding weight amplitudes for input units in the groups that yielded successful body-centered representations (as defined by the criteria in A and B). Weights are classified according to input unit tuning characteristics. Black denotes tuning closer to body-centered (both horizontal and vertical-plane DIs < 0.4). White denotes closer to head-centered (both DIs > 0.6). Gray denotes intermediate tuning (i.e., all other units). The plot shows the mean (±SE) of the average decoding weights across 12 motion directions. D–F, Distributions of phases that could be successfully decoded to yield body-centered representations (according to the criteria in A and B) for 5 unit (D), 7 unit (E), and 10 unit (F) input groups. For each direction, histograms reflect the phase distributions associated with a maximum of 800 input unit groups (with lowest output DIs) but including all group and weight combinations yielding body-centered representations (i.e., with different decoding weights each group could contribute to decoding across multiple phases). Each histogram is the average of the histograms computed individually for 12 motion directions. Red, blue, and green denote decoding using input units with tuning properties as described in A.

Unsurprisingly, most such 5 and 7 unit groups (on average, 92% of 5 unit groups and 85% of 7 unit groups) contained at least one input unit having both horizontal and vertical DIs < 0.4. However, many groups (73% of 5 unit, 64% of 7 unit) contained only 1 such input unit. Furthermore, it is important to emphasize that all synthetic input units used in these analyses either reflected DIs > 0.2 in one or more planes or failed to meet other criteria for consistent coding of body-centered motion (i.e., ε, gain change or phase change criteria; see above and Materials and Methods). Thus, although very few (40 of 500 or 8%) of the input units spanning 3D space had both vertical and horizontal-plane DIs < 0.4 (2 of 500 had both DIs < 0.2), linear combinations of small groups of units having a distributed range of tuning properties (i.e., from more body-centered to more head-centered) yielded output representations substantially closer to fully body-centered. The contribution of input units with a range of tuning properties was further reflected in the distribution of decoding weights (Fig. 10C). Although decoding weight amplitudes were on average significantly larger for input units that were closer to body-centered (both horizontal- and vertical-plane DIs < 0.4) than head-centered (both DIs > 0.6; Wilcoxon rank-sum test; p < 0.0001) or intermediate (DI in at least one plane between 0.4 and 0.6 or one DI < 0.4 and the other > 0.6; Wilcoxon rank-sum test; p < 0.0001), on average units in all categories made a significant contribution (Wilcoxon signed rank tests, p ≤ 0.0001).

Perhaps most importantly, with as few as 5–7 input units, it was possible to decode body-centered representations having response phases in their PD ranging from lagging translational velocity to leading acceleration (Fig. 10D–F). This suggests that combining small populations of units not only permitted the creation of close to fully body-centered representations, but facilitated the creation of such representations with a broad range of temporal properties.

Would these results be obtained with any neural population characterized by a range of reference frames and temporal properties? The computations to transform sensorimotor signals between reference frames that rotate relative to each other in 3D involve nonlinear multiplicative interactions between tuned neural activity and postural signals that provide information about the relative alignment of the different frames (e.g., head vs body) (Blohm et al., 2009; Crawford et al., 2011). An appropriate integration of such “gain-modulated” neural activities produces the tuning shifts required to complete the transformation. In keeping with these requirements, theoretical studies predict that cell populations involved in intermediate stages of such a transformation exhibit prominent gain-field properties accompanied by partial tuning shifts to an extent that depends on the network topology (e.g., feedforward vs including feedback loops) and the degree of integration of gain-modulated signals (Zipser and Andersen, 1988; Salinas and Abbott, 1995, 1996; Pouget and Sejnowski, 1997; Xing and Andersen, 2000; Deneve et al., 2001; Blohm et al., 2009). Similarly, although the extent to which tuning shifts follow “ideal” trajectories in 3D has not been characterized explicitly in most such studies (but see Blohm et al., 2009, their Fig. 7), one might predict that if the transformation involves the progressive integration of gain-modulated signals across a series of stages, neurons involved in “earlier” stages of the computations would reflect tuning shifts that appear more random (i.e., follow the ideal trajectory between frames less precisely and reflect larger ε values) than those at “later” stages. Notably, however, despite reflecting a distribution of intermediate reference frames, our rFN cells neither exhibited the prominent gain-field properties, nor substantial ε values one might predict at intermediate stages in the computations.

Thus, to gain further insight into whether these particular properties of our neurons were related to the facility with which body-centered representations could be decoded from small cell groups, we examined the impact of increasing input unit ε values (by 8° to 16°) to yield an increase in the average absolute ε value across our synthetic population from 8.4° to 20.4°. Similarly, we increased the size of head-orientation-dependent gain changes (by 0.5% to 1% per degree of change in head angle) to yield an average value of 1.1%/°. This is similar to or lower than values previously reported for posture-dependent gain fields in cortical areas that have been implicated in reference frame transformations; for example: ≈1%/° eye position in the lateral intraparietal area (LIP) and 1%/°–3%/° in parietal area 7a (Andersen et al., 1985, 1990); 1.7%/° head/body-re-world position in area 7a (Snyder et al., 1998); and 2%/° hand position and 3.4%/° eye position in the parietal reach region (PRR) (Chang et al., 2009). In each case, we performed the same analysis as for our rFN-like input unit population and examined decoding ability for all possible groups of 3 input units and 200,000 randomly chosen possible groups of 5, 7, 10, or 15 units.

As illustrated in Figure 10A, B, D–F, decoding ability with 3–10 units deteriorated significantly when either the average ε value (red) or gain sensitivity to head orientation (green) of our input units was increased, as reflected by significantly larger DIs (Wilcoxon rank-sum tests, p < 0.0001) and lower numbers of input unit combinations yielding successfully decoded body-centered motion representations (Wilcoxon rank-sum tests; 5–15 units: p < 0.0002). This was accompanied by a substantial reduction in the range of phases over which body-centered representations could be decoded (Fig. 10D–F). Both observations suggest that the low ε and gain change amplitudes observed in our experimentally recorded rFN population contribute to the facility with which body-centered representations with a broad range of temporal properties can be constructed from the activities of small cell groups in this area.

Relationship between body-centered tuning and tilt/translation discrimination

The above analyses are consistent with the hypothesis that the rFN plays a key role in encoding and distributing body-centered motion representations. However, it remains unclear whether there exists a further relationship between what motions are being represented and the reference frame in which they are encoded. In particular, because otolith afferents respond identically to tilts relative to gravity and translations (i.e., they signal the net gravito-inertial acceleration [GIA]) (Fernández and Goldberg, 1976a,b; Angelaki and Dickman, 2000), estimating translational motion relies on a series of computations that involve a convergence of otolith and semicircular canal signals (Merfeld et al., 1993, 1999; Mergner and Glasauer, 1999; Bos and Bles, 2002; Merfeld and Zupan, 2002; Zupan et al., 2002; Green and Angelaki, 2004, 2007). Recent studies have emphasized an important role for the rFN in encoding a population-level representation of the output of such computations with many cells reflecting activity that more closely encodes translation than the net GIA (Angelaki et al., 2004; Green et al., 2005; Shaikh et al., 2005b). However, it remains unknown whether the same cells that more closely encode translation also reflect a transformation toward body-centered tuning. We hypothesized that while head-centered neurons might reflect little processing and encode the net GIA (i.e., like otolith afferents), cells that have been transformed toward body-centered coordinates may also reflect the computations to estimate translation.

To investigate this issue, we compared neural responses to tilt with those due to translation across our neural populations both in their horizontal-plane direction of maximum gain for translation as well as in their estimated maximum gain direction for tilt. Both rFN and VN neurons reflected a distribution of properties ranging from “GIA-like” (i.e., similar responses to tilt and translation) to more translation-encoding (i.e., no response to tilt). However, most cells exhibited larger responses to translation with 82% of cells having responses to translation that were at least twice as large as their responses to tilt along their preferred translation direction (Fig. 11A) and 59% doing so along their preferred tilt direction. To quantify the extent to which each cell exhibited GIA- versus translation-encoding properties, we computed a tilt/translation index (TTI) defined as the ratio of response tilt gain to translation gain. Thus, a TTI of 1 indicates sensory otolith-like or GIA-encoding properties, whereas a TTI of 0 indicates translation-encoding behavior. TTIs tended to fall between 0 and 1 for both rFN (mean 0.31 ± 0.21 SD in preferred translation direction; mean 0.55 ± 0.34 SD in preferred tilt direction) and VN cells (mean 0.36 ± 0.20 SD in preferred translation direction; mean 0.56 ± 0.66 SD in preferred tilt direction) consistent with a processing of sensory signals toward estimates of translational motion (Angelaki et al., 2004; Green et al., 2005; Shaikh et al., 2005b).

Figure 11.

Relationship between cell responses to translation versus tilt and extent of reference frame transformation. A, Comparison of response gains for translation versus tilt (expressed in units of spikes/s/G) along the horizontal plane direction of maximum response to translation (filled symbols) and to tilt (open symbols). Top right, Histogram showing the distribution of the TTI (tilt/translation gain ratio) for rFN (red) and VN (blue) cells. Filled bars denote the maximum translation gain direction. Open bars denote the maximum tilt gain direction. Bars above the plot indicate mean values. B, Relationship between each cell's TTI in the horizontal-plane direction of maximum translation gain and its DIs for vertical plane (filled circles) and horizontal plane (open squares) head reorientation. Linear regressions are shown for rFN cells (red, r = −0.11, p = 0.42) and VN cells (blue, r = −0.74, p = 0.0003).

Next, to assess the relationship between a cell's ability to distinguish translation from tilt and its transformation toward body-centered tuning, we compared each cell's TTI in its preferred translation direction with its DIs for vertical and horizontal plane head reorientation. As shown in Figure 11B, we found no significant correlation for rFN cells (r = −0.11, p = 0.42), suggesting that the extent of processing of sensory signals toward an estimate of translation was unrelated to the extent to which these signals were transformed toward body-centered coordinates. In contrast, rostral VN cells showed a significant negative correlation between DI and TTI (r = −0.74, p = 0.0003), suggesting a trend for translation-encoding neurons to reflect head-centered tuning. No significant correlation was found for either rFN or VN cells, however, when cell TTIs were instead estimated based on tilt and translation sensitivities in the cell's preferred horizontal plane tilt direction (data not shown; rFN: r = 0.08, p = 0.53; VN: r = −0.31, p = 0.20).

Discussion

Estimates of body motion are critical for many behaviors, including postural control (Maurer et al., 2006; Macpherson et al., 2007), locomotion (Bent et al., 2004; Fitzpatrick et al., 2006), navigation (Yoder and Taube, 2014), spatial perception and memory (Gu et al., 2007; Klier and Angelaki, 2008; Clemens et al., 2011), and voluntary movement (Bockisch and Haslwanter, 2007; Moreau-Debord et al., 2014; Blouin et al., 2015). Vestibular signals are essential for such estimates but must be transformed into body-centered coordinates.

Here, we characterized, for the first time, the extent of this transformation at the neural level across multiple planes of head reorientation in 3D. In contrast to brainstem cells in the rostral VN, which maintained mainly head-centered coding, many deep cerebellar rFN neurons reflected vestibular coding that was profoundly influenced by changes in head-re-trunk position in both vertical and horizontal planes. Notably, while most neurons reflected only a partial transformation, their tuning shifts were not random but followed the specific spatial trajectories predicted for a 3D transformation toward body-centered coordinates. Consequently, while few individual neurons reflect fully body-centered tuning in 3D, such a representation can nonetheless be decoded through a simple linear combination of a small population (5–7) of rFN cells. These results thus confirm that the spatially transformed vestibular signals required to compute estimates of body motion are indeed encoded by cerebellar neurons.

Role of the rFN in computing body-centered motion

Compatible with previous studies, which examined rFN vestibular reference frames in 2D (Kleine et al., 2004; Shaikh et al., 2004), we found a broad distribution of displacement indices, consistent with reference frames ranging between head- and body-centered. Notably, for some cells the DIs differed substantially for head reorientation in different planes. Consequently, conclusions regarding reference frames often depended on the plane examined. This emphasizes the importance of examining reference frames fully in 3D and suggests that a significant percentage of cells classified as head- or body-centered in previous studies might actually have reflected intermediate tuning. Indeed, when examined across multiple planes, only 16% of cells were consistent with body-centered encoding of translation in 3D, supporting previous conclusions of a mixed representation in the rFN (Kleine et al., 2004; Shaikh et al., 2004).

While these findings may seem to suggest that the rFN occupies only an intermediate stage in the transformations, several lines of evidence nonetheless lead us to conclude that rFN cells are actually quite close to fully transformed. In particular, the transformation of sensorimotor signals between reference frames that rotate relative to each other in 3D (e.g., see Blohm et al., 2009; Crawford et al., 2011) requires nonlinear multiplicative interactions between tuned activity encoded in one frame (e.g., head-centered) and postural information (e.g., head-re-body orientation) that varies with changes in the alignment of the original frame and a new one (e.g., body-centered). An appropriately weighted combination of such “gain-modulated” signals is required to complete the transformation. While different models have been proposed to demonstrate how neural populations might effect such transformations (Zipser and Andersen, 1988; Salinas and Abbott, 1995; Pouget and Sejnowski, 1997; Xing and Andersen, 2000; Deneve et al., 2001; Blohm et al., 2009), a common element is the presence of intermediate layers of cells with “gain-field” properties and output stages that reflect an appropriately weighted combination of their activities.

Several observations suggest that rFN cells more closely reflect an output stage of such computations (e.g., “population output” units in Blohm et al., 2009). First, unlike theoretical “intermediate layer” cells, head-orientation-dependent gain changes in rFN neurons were typically very small (e.g., Fig. 6A; mean 0.36% per degree of head angle), consistent with previous reports (Kleine et al., 2004; Shaikh et al., 2004). Second, although most cells reflected only a partial transformation toward body-centered coordinates, their tuning shifts were not random. Instead, they tended to shift along the specific spatial trajectories theoretically predicted for a 3D transformation. Both observations suggest that rFN cells reflect a late stage in the computations, after gain-modulated vestibular signals have already been substantially integrated. Indeed, our analyses showed that a simple linear combination of the tuning functions of as few as 5–7 units with distributions of properties similar to our rFN cells could be used to decode fully body-centered motion representations in 3D. Furthermore, the facility with which such representations could be decoded from small cell groups was reduced when average shifts away from the ideal 3D trajectory (i.e., ε values) or head-orientation-dependent gain changes of the input units were increased.

The notion that the rFN occupies a late stage in the head-to-body reference frame transformation is also compatible with previous findings implicating upstream regions of the anterior vermis that project to the rFN in transforming vestibular signals toward body-centered coordinates (Manzoni et al., 1998, 1999). While translation responses in this region have yet to be characterized, during head tilts elicited by a wobble stimulus changes in head-re-body position in the horizontal plane were accompanied not only by spatial tuning shifts but also changes in response gain, phase, and STC (Manzoni et al., 1999). Furthermore, inactivation of this region resulted in a failure to appropriately modulate postural responses with changes in head position (Manzoni et al., 1998). Both observations suggest the anterior vermis as a likely candidate for effecting the transformation of vestibular estimates of translation.

Functional role of self-motion estimates in the rFN

If rFN cells are close to being fully transformed, then why should they exhibit a broad distribution of tuning shifts? One possibility is that there is simply no need to complete the transformation at the level of individual neurons. Indeed, distributed representations may have many advantages, including enabling downstream regions to read out a variety of representations in different reference frames (Salinas and Abbott, 1995; Pouget and Sejnowski, 1997) and/or to perform optimal multisensory integration (Deneve et al., 2001; McGuire and Sabes, 2009). Here, we propose an additional interpretation suggested by the temporal properties of our neurons. Specifically, the maintenance of a range of partially transformed responses with different spatiotemporal properties facilitates the creation of downstream representations with a broad range of dynamic characteristics. In keeping with this proposal, we found that linear combinations of the tuning functions of small groups of neurons permitted the construction of body-centered representations with temporal characteristics ranging from leading translational acceleration to lagging velocity. Importantly, this is consistent with the functional requirements for tasks such as postural control, which depends on body-centered estimates of translational acceleration, velocity, and position (Jeka et al., 2004; Lockhart and Ting, 2007).

Indeed, the rFN projects to brainstem regions that mediate vestibulospinal reflexes (Batton et al., 1977; Homma et al., 1995) and has long been implicated in postural control and locomotion by lesion studies (Sprague and Chambers, 1953; Thach et al., 1992). Recent work suggests that at least one aspect of its contribution involves computing estimates of body motion (Kleine et al., 2004; Shaikh et al., 2004; Brooks and Cullen, 2009). Compatible with this, we show that small groups of rFN neurons (that in principle could activate the same muscle group) can provide body-centered translation estimates with a broad range of temporal properties, as required to contribute to leg muscle-activation patterns during postural corrections (Lockhart and Ting, 2007; Welch and Ting, 2008).

The rFN is also ideally poised to distribute self-motion estimates to cortical regions via the thalamus (Asanuma et al., 1983; Middleton and Strick, 1997; Meng et al., 2007). Indeed, parietal areas implicated in self-motion perception carry translational signals with a broad distribution of temporal properties (Chen et al., 2010, 2011a,b), and at least two such regions (parietoinsular vestibular cortex [PIVC] and ventral intraparietal area [VIP]) reflect a head-to-body vestibular reference frame transformation (Chen et al., 2013). Although so far shown only for the horizontal plane, average tuning was more body-centered than in the rFN, with VIP reflecting the most complete transformation. Notably, PIVC receives vestibular signals from thalamic areas that receive rFN inputs (Akbarian et al., 1992; Meng et al., 2007) and in turn projects to VIP (Lewis and Van Essen, 2000), raising the possibility that the transformation seen in PIVC and VIP reflects the convergence of partially transformed signals in the rFN over the course of their transmission to these areas.

Compatible with previous observations, we found that translation-sensitive rFN cells were typically not GIA-encoding but instead were substantially more responsive to translation than tilt (Angelaki et al., 2004; Green et al., 2005). Furthermore, tilt/translation discrimination extent was uncorrelated with DI, pointing to a strong role for the rFN in signaling translation independent of the reference frame. While estimates of body translation are essential for tasks such as navigation and maintaining postural equilibrium, such tasks also require information about the body's movement relative to the reference of gravity (i.e., world-centered estimates) (Fitzpatrick et al., 2006). Future work that varies both head orientation relative to the body and body orientation relative to gravity will be important in distinguishing between body- versus world-centered translation coding in the rFN and further elucidating the likely functional roles of motion representations in this region.