Suppressed Sensory Response to Predictable Object Stimuli throughout the Ventral Visual Stream

Abstract

Prediction plays a crucial role in perception, as prominently suggested by predictive coding theories. However, the exact form and mechanism of predictive modulations of sensory processing remain unclear, with some studies reporting a downregulation of the sensory response for predictable input whereas others observed an enhanced response. In a similar vein, downregulation of the sensory response for predictable input has been linked to either sharpening or dampening of the sensory representation, which are opposite in nature. In the present study, we set out to investigate the neural consequences of perceptual expectation of object stimuli throughout the visual hierarchy, using fMRI in human volunteers. Participants of both sexes were exposed to pairs of sequentially presented object images in a statistical learning paradigm, in which the first object predicted the identity of the second object. Image transitions were not task relevant; thus, all learning of statistical regularities was incidental. We found strong suppression of neural responses to expected compared with unexpected stimuli throughout the ventral visual stream, including primary visual cortex, lateral occipital complex, and anterior ventral visual areas. Expectation suppression in lateral occipital complex scaled positively with image preference and voxel selectivity, lending support to the dampening account of expectation suppression in object perception.

SIGNIFICANCE STATEMENT It has been suggested that the brain fundamentally relies on predictions and constructs models of the world to make sense of sensory information. Previous research on the neural basis of prediction has documented suppressed neural responses to expected compared with unexpected stimuli. In the present study, we demonstrate robust expectation suppression throughout the entire ventral visual stream, and underlying this suppression a dampening of the sensory representation in object-selective visual cortex, but not in primary visual cortex. Together, our results provide novel evidence in support of theories conceptualizing perception as an active inference process, which selectively dampens cortical representations of predictable objects. This dampening may support our ability to automatically filter out irrelevant, predictable objects.

Introduction

Our environment is structured by statistical regularities. Making use of such regularities by anticipating upcoming stimuli is of great evolutionary value, as it enables the agent to predict future states of the world and prepare adequate responses, which in turn can be executed faster or more accurately (Hunt and Aslin, 2001; Kim et al., 2009; Bertels et al., 2012). Our brains are exquisitely sensitive to these statistical regularities (Turk-Browne et al., 2009, 2010; Schapiro et al., 2012, 2014). Indeed, it has been suggested that a core operational principle of the brain is prediction (Bubic et al., 2010) and prediction error minimization (Friston, 2005). Statistical learning is an automatic learning process by which statistical regularities are extracted from the environment (Turk-Browne et al., 2010), without explicit awareness or effort by the observer (Fiser and Aslin, 2002; Brady and Oliva, 2008), even under concurrent cognitive load (Garrido et al., 2016). These statistical regularities can be used to form predictions about upcoming input, with effects of statistical learning being evident even 24 h after exposure (Kim et al., 2009).

The neural consequences of perceptual predictions have been investigated extensively, but conflicting results have emerged. For example, Turk-Browne et al. (2009) reported larger neural responses to predictable than random sequences of stimuli in human object-selective lateral occipital complex (LOC). However, contrary to this notion, neurons in monkey inferotemporal cortex, the putative homolog of human LOC (Denys et al., 2004), showed reduced responses to expected compared with unexpected object stimuli (Meyer and Olson, 2011; Kaposvari et al., 2018). This is in line with findings in human primary visual cortex (V1), which revealed that visual gratings of an expected orientation elicit a suppressed neural response compared with gratings of an unexpected orientation (Kok et al., 2012a; St. John-Saaltink et al., 2015). Even though there is superficial agreement between these studies, the exact form of expectation suppression, in terms of the underlying effect of expectations on the neural representations of stimuli, appeared to be opposite. Kok et al. (2012a) observed the strongest suppression in voxels that were tuned away from the expected stimulus, resulting in a sparse, sharpened population code. Electrophysiological studies in macaques, on the other hand, have reported a positive scaling of expectation suppression with image preference (Meyer and Olson, 2011), suggesting that sensory representations are dampened for expected stimuli (Kumar et al., 2017).

In sum, several discrepancies remain concerning the neural basis of perceptual expectation, which may be related to differences in species (macaque vs human), measurement technique (spike rates vs fMRI BOLD), and cortical hierarchy (early vs late). In the current study, we set out to examine the existence and characteristics of expectation suppression throughout the visual hierarchy, using a paradigm that closely matches a set of previous studies on object prediction in macaque monkeys (Meyer and Olson, 2011; Ramachandran et al., 2016). This allowed us to better compare and generalize between species, methods, and different levels of the cortical hierarchy. First, we exposed participants to pairs of sequentially presented object images in a statistical learning paradigm. Next, we recorded neural responses, using whole-brain fMRI, to expected and unexpected object image pairs. By contrasting responses to expected and unexpected pairs, we probed whether a suppression of expected object stimuli is evident throughout the ventral visual stream, and in particular in object-selective cortex. Moreover, by investigating expectation suppression as a function of image preference and voxel selectivity, we contrasted sharpening with dampening (scaling) accounts of expectation suppression.

In brief, our results show that expectation suppression is ubiquitous throughout the human ventral visual stream, including object-selective LOC. Furthermore, we found that expectation suppression positively scales with object image preference and voxel selectivity within object-selective LOC. This suggests that object predictions dampen sensory representations in object-selective regions.

Materials and Methods

Participants

Twenty-four healthy, right-handed participants (17 female, aged 23.3 ± 2.4 years, mean ± SD) were recruited from the Radboud research participation system. The sample size was based on an a priori power calculation, computing the required sample size to achieve a power of 0.8 to detect an effect size of Cohen's d ≥ 0.6, at α = 0.05, for a two-tailed within-subjects t test. Participants were prescreened for MRI compatibility, had no history of epilepsy or cardiac problems, and had normal or corrected-to-normal vision. Written informed consent was obtained before participation. The study followed institutional guidelines of the local ethics committee (CMO region Arnhem-Nijmegen, The Netherlands). Participants were compensated with 42 euro for study participation. Data from one subject were excluded because of excessive tiredness and poor fixation behavior. One additional subject was excluded from all ROI-based analyses because no reliable object-selective LOC mask could be established due to subpar fixation behavior during the functional localizer.

Experimental design and statistical analysis

Stimuli and experimental paradigm

Main task.

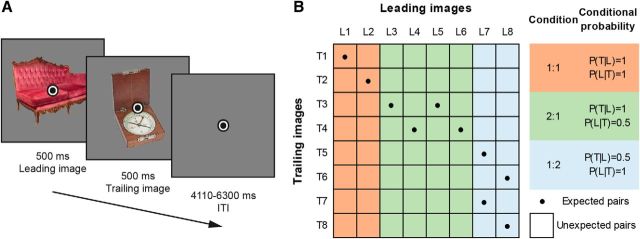
Participants were exposed to two object images in quick succession. Each image was presented for 500 ms without interstimulus interval, and an intertrial interval of 1500–2500 ms during behavioral training and 4110–6300 ms during fMRI scanning (for a single trial, see Fig. 1A). A fixation bull's-eye (0.5° visual angle in size) was presented throughout the run. For each participant, 16 object images were randomly selected from a pool of 80 stimuli (see also Stimuli). Eight images were assigned as leading images (i.e., appearing first on trials), whereas the other eight images served as trailing images, occurring second. Image pairs and the transitional probabilities between them were determined by the transitional probability matrix depicted in Figure 1B, based on the transition matrix used by Ramachandran et al. (2016). The expectation manipulation consisted of a repeated pairing of images in which the leading image predicted the identity of the trailing image, thus over time making the trailing image expected given the leading image. Importantly, the transitional probabilities governing the associations between images were task-irrelevant because participants were instructed to respond, by button press, to any upside-down versions of the images, the occurrence of which was not related to the transitional probability manipulation and could not be predicted. Upside-down images (target trials) occurred on ∼9% of trials. Participants were not informed about the presence of any statistical regularities and instructed to maintain fixation on the central fixation bull's-eye. Trial order was fully randomized.

Figure 1.

Paradigm overview. A, A single trial, with two example images and superimposed fixation bull's-eye. Leading images and trailing images were presented for 500 ms each, without interstimulus interval, followed by an intertrial interval of 4110–6300 ms (fMRI session; 1500–2500 ms during behavioral training). Participants responded to upside-down images by button press; the image at either position (leading or trailing) could be upside-down. B, Image transition matrix determining image pairs. Eight leading images (L1–L8) and eight trailing images (T1–T8) were used for each participant. Conditional probability conditions are highlighted, and their respective conditional probabilities during training are listed on the right: orange represents the 1:1 condition; green represents the 2:1 condition; blue represents the 1:2 condition. Cells with dots represent expected image pairs. Empty cells represent unexpected pairs.

During behavioral training, only expected image pairs were presented on a total of 1792 trials, split into 8 blocks with short breaks in between blocks. Thus, during this session the occurrence of image L1 was perfectly predictive of image T1 (i.e., P(T1|L1) = 1; Fig. 1B). Apart from these trials, which constituted the 1:1 conditional probability condition, there were also trials with a 2:1 and 1:2 image pairing. In the 2:1 conditional probability condition, the leading image was perfectly predictive of the trailing image (e.g., P(T3|L3) = 1), but two different leading images predicted the same trailing image, thereby reducing the conditional probability of the leading image given a particular trailing image (i.e., P(L3|T3) = 0.5). Last, the 1:2 condition consisted of a reduced predictive probability of the trailing image given the leading image, as such image L7, for instance, was equally predictive of images T5 and T7 (i.e., P(T5|L7) = 0.5 and P(T7|L7) = 0.5).

On the next day, participants performed one additional behavioral training block, consisting of 224 trials, and another 48 practice trials in the MRI during acquisition of the anatomical image. The task during the subsequent fMRI experiment was identical to the training session, except that also unexpected image pairs occurred. Nonetheless, the expected trailing image was still most likely to follow a given leading image, namely, on 56.25% of trials compared with 6.25% for each unexpected trailing image (1:1 condition). It is important to note that each trailing image was only (un)expected by virtue of its temporal context (i.e., by which leading image it was preceded). Thus, each trailing image served both as an expected and unexpected image depending on context. Additionally, trial order was fully randomized, thus rendering systematic effects of trial history unlikely. In sum, any difference between expected and unexpected occurrences cannot be explained in terms of different base rates of the trailing images, adaptation or trial history. Because intertrial intervals were longer in the fMRI session, and responses to upside-down images therefore occurred at a lower rate, potentially reducing participants' vigilance, the percentage of upside-down images was increased to ∼11% of trials. As during the behavioral training session, in the main fMRI task, participants were not informed about the presence of transitional probabilities, and there was no correlation between the image transitions and the occurrence of upside-down images. In total, the MRI main task consisted of 512 trials, split into four equal runs, with an additional three resting blocks (each 12 s) per run. Feedback on behavioral performance (percentage correct and mean response time) was provided after each run. To ensure adequate fixation on the fixation bull's-eye, an infrared eye tracker (SensoMotoric Instruments) was used to record and monitor eye positions.

Functional localizer.

The main task was followed by a functional localizer, which was used for a functional definition of object-selective LOC for each participant, and to determine image preference for each voxel within visual cortex in an expectation neutral context. Finally, localizer data served as independent training data for the multivoxel pattern analysis (see Data analysis, Multivoxel pattern analysis). In a block design, each object image was presented four times, each time flashing at 2 Hz (300 ms on, 200 ms off) for 11 s. The used stimuli were the same object images as shown during the fMRI main task. Additionally, a globally phase-scrambled version of each image (Coggan et al., 2016) was shown twice, also flashing at 2 Hz for 11 s. The order of object images and scrambles was randomized. Participants were instructed to fixate the bull's-eye and respond by button press whenever the fixation bull's-eye dimmed in brightness.

Questionnaire.

Following the fMRI session, participants filled in a brief questionnaire probing their explicit knowledge of the image transitions. Knowledge of each of the eight image pairs was tested by presenting participants with one leading image at a time, instructing them to select the most likely trailing image.

Categorization task.

Finally, outside the scanner, participants performed a categorization task. During this task, participants indicated, by button press, whether the trailing image would fit into a shoebox (yes/no decision), similar to Dobbins et al. (2004) and Horner and Henson (2008). This task was aimed at assessing any implicit reaction time (RT) or accuracy benefits due to incidental learning because the statistical regularities, learned during the previous parts of the experiment, could be used to predict the correct response before the trailing image appeared. For each participant, the same images and transitions were used as during their fMRI task. Furthermore, it was ensured that half of the trailing images in each conditional probability condition (1:1, 1:2, 2:1) fit into a shoebox, whereas the other half did not fit. A brief practice block was used to make sure that participants correctly classified the object images and understood the task. Participants were not informed about the intention behind this task, nor were they instructed to make use of the statistical regularities, to avoid influencing their behavior. A full debriefing took place after the categorization task.

Stimuli.

Object stimuli were taken from Brady et al. (2008) and consisted of a large collection of diverse full-color photographs of objects. Of this full set of images, a subset of 80 images was selected; 40 objects fitting into a shoebox, and 40 objects not fitting into a shoebox. Images spanned ∼5° × 5° visual angle and were presented in full color on a mid-gray background. During training, stimuli were displayed on an LCD screen and back-projected during MRI scanning (EIKI LC-XL100 projector; 1024 × 768 pixel resolution, 60 Hz refresh rate), visible using an adjustable mirror. Because images were drawn at random per participant, each image could occur in any condition or position, thereby eliminating potential effects induced by individual image features.

fMRI data acquisition

Functional and anatomical images were collected on a 3T Skyra MRI system (Siemens), using a 32-channel headcoil. Functional images were acquired using a whole-brain T2*-weighted multiband-8 sequence (TR/TE = 730/37.8 ms, 64 slices, voxel size 2.4 mm isotropic, 50° flip angle, A/P phase encoding direction). Anatomical images were acquired with a T1-weighted MP-RAGE (GRAPPA acceleration factor = 2, TR/TE = 2300/3.03 ms, voxel size 1 mm isotropic, 8° flip angle).

Data analysis

Behavioral data analysis.

Behavioral data from the categorization task was analyzed in terms of RT and accuracy. All RTs exceeding 3 SD above mean and <200 ms were excluded as outliers (2.0% of trials). Because unexpected trailing image trials during the categorization task may require a change in the response, any differences in RT and accuracy between the expected and unexpected conditions may reflect a combination of surprise and response adjustment, thereby inflating possible RT and accuracy differences. Therefore, only unexpected trials requiring the same response as the expected image were analyzed, yielding an unbiased comparison of the effect of expectation. RTs for expected and unexpected trailing image trials were averaged separately per participant and subjected to a paired t test. The error rate was also calculated separately for expected and unexpected trailing image trials per subject and analyzed with a paired t test. Additionally, the effect size of both differences was calculated in terms of Cohen's d_z (Lakens, 2013). All SEs of the mean presented here were calculated as the within-subject normalized SE (Cousineau, 2005) with Morey's (2008) bias correction.

fMRI data preprocessing.

fMRI data preprocessing was performed using FSL 5.0.9 (FMRIB Software Library; Oxford, UK; www.fmrib.ox.ac.uk/fsl; RRID:SCR_002823) (Smith et al., 2004). The preprocessing pipeline included brain extraction (BET), motion correction (MCFLIRT), temporal high-pass filtering (128 s), and spatial smoothing for univariate analyses (Gaussian kernel with FWHM of 5 mm). No smoothing was applied for multivariate analyses, nor for the voxelwise image preference analysis. Functional images were registered to the anatomical image using FLIRT (BBR) and to the MNI152 T1 2 mm template brain (linear registration with 12 df). The first eight volumes of each run were discarded to allow for signal stabilization.

Univariate data analysis.

To investigate expectation suppression across the ventral visual stream, voxelwise GLMs were fit to each subject's run data in an event-related approach using FSL FEAT. Separate regressors for expected and unexpected image pairs were modeled within the GLM. All trials were modeled with 1 s duration (corresponding to the duration of the leading and trailing image combined) and convolved with a double gamma hemodynamic response function. Additional nuisance regressors were added, including one for target trials (upside-down images), instruction and performance summary screens, first-order temporal derivatives for all modeled event types, and 24 motion regressors (six motion parameters, the derivatives of these motion parameters, the squares of the motion parameters, and the squares of the derivatives; comprising FSL's standard + extended set of motion parameters). The contrast of interest for the whole-brain analysis compared the average BOLD activity during unexpected minus expected trials (i.e., expectation suppression). Data were combined across runs using FSL's fixed effect analysis. For the across-participants whole-brain analysis, FSL's mixed effect model FLAME 1 was used. Multiple-comparison correction was performed using Gaussian random-field based cluster thresholding, as implemented in FSL, using a cluster-forming threshold of z > 3.29 (i.e., p < 0.001, two-sided) and a cluster significance threshold of p < 0.05. An identical analysis was performed to assess the influence of the different conditional probability conditions (see Main task), except that the expected and unexpected event regressors were split into their respective conditional probability conditions (1:1, 1:2, 2:1), thus resulting in a GLM with six regressors of interest.

Planned ROI analyses.

Within each ROI (V1 and LOC; see ROI definition), the parameter estimates for the expected and unexpected image pairs were extracted separately from the whole-brain maps. Per subject, the mean parameter estimate within the ROIs was calculated and divided by 100 to yield an approximation of mean percentage signal change compared with baseline (Mumford, 2007). These mean parameter estimates were in turn subjected to a paired t test and the effect size of the difference calculated (Cohen's d_z). For the conditional probability manipulation, a similar ROI analysis was performed, except that the resulting mean parameter estimates were subjected to a 3 × 2 repeated-measures ANOVA with conditional probability condition (1:1, 2:1, 1:2) and expectation (expected, unexpected) as factors. For this analysis, we calculated η-squared (η²) as a measure of effect size.

Multivoxel pattern analysis (MVPA).

MVPA was performed per subject on mean parameter estimate maps per trailing image. These maps were obtained by fitting voxelwise GLMs per trial for each subject, following the “least-squares separate” approach outlined by Mumford et al. (2012). In brief, a GLM is fit for each trial, with only that trial as regressor of interest and the remaining trials as one regressor of no interest. This was done for the functional localizer and main task data. The resulting parameter estimate maps of the functional localizer were used as training data for a multiclass SVM (classes being the eight trailing images), as implemented in Scikit-learn (SVC; RRID:SCR_002577) (Pedregosa et al., 2011). Decoding performance was tested per subject on the mean parameter estimate maps from the main task data for each trailing image, split into expected and unexpected image pairs. The choice to decode mean parameter estimate maps, instead of single-trial estimates, was made after observing that image decoding performance when decoding individual trials was close to chance, indicating a lack of sensitivity to detect potential differences between expected and unexpected image pairs. This decision was based on an independent MVPA collapsed over expected and unexpected image pairs, without inspection of the contrast of interest. Expected image pair trials are by definition more frequent, which may in turn yield a more accurate mean parameter estimate. Thus, stratification by random sampling was used to balance the number of expected and unexpected image pairs per trailing image, thereby removing potential bias. In short, for each iteration (n = 1000), a subset of expected trials was randomly sampled to match the number of unexpected occurrences of that trailing image. Finally, decoding performance was analyzed in terms of mean decoding accuracy. To this end, the class with the highest probability for each test item was chosen as the predicted class and the proportion of correct predictions calculated. Mean decoding performances for expected and unexpected image pairs were subjected to a two-sided, one-sample t test against chance decoding performance (chance level = 12.5%). If decoding was above chance for the expected and unexpected image pairs, decoding performances between expected and unexpected pairs were compared by means of a paired t test and the effect size was calculated. In short, the classifier was used to distinguish between the eight trailing images, after being trained on the single-trial parameter estimates from the functional localizer. The performance of the classifier was tested on the per-image parameter estimates from the main task split into the expected and unexpected condition.

Image preference analysis.

For the voxelwise image preference analysis, the single-trial GLM parameter estimate maps (as outlined in Multivoxel pattern analysis) were used. Within each participant, the parameter estimate maps of the functional localizer were averaged for each trailing image, thus yielding an average activation map induced by each trailing image in an expectation free, neutral context. The same was done for the main task data, but for expected and unexpected occurrence of each trailing image separately. Then, for each voxel, trailing images were ranked according to the response they elicited during the functional localizer. These rankings were applied to the main task data, resulting in a vector per voxel, consisting of the mean activation (parameter estimate) elicited by the trailing images during the main task, ranked from the least to most preferred image based on the context neutral, independent functional localizer data. This was done separately for expected and unexpected occurrences of each trailing image. Within each ROI, the mean parameter estimates of expected and unexpected image pairs per preference rank were calculated. For each ROI, linear regressions were fit to the ranked parameter estimates: one for expected and one for unexpected pairs. A positive regression slope would thus indicate that the ranking from the functional localizer generalized to the main task, which was considered a prerequisite for any further analysis. This was tested by subjecting the slope parameters across subjects to a two-tailed one sample t test, comparing the obtained slopes against zero. Furthermore, this analysis assumes a linear relation between the response parameter estimates and preference rank. Of note, a strong nonlinear relationship, in either of the expectation conditions, could pose a problem for the interpretation of the resulting slope parameter. Therefore, we tested for linearity, by comparing the model fit between the linear model and a second-order polynomial model. The data were deemed sufficiently linear if the fit of the linear model was superior to the fit of the nonlinear model as index by a smaller Bayesian information criterion (BIC) (Schwarz, 1978). If these requirements were met for the expected and unexpected conditions, the difference between slope parameters was compared by a two-tailed paired t test. If the amount of expectation suppression (i.e., unexpected − expected) indeed scales with image preference (i.e., dampening), then we should find the slope parameter for the unexpected condition regression line to be significantly larger than for the expected condition. The opposite prediction, a larger slope parameter for the expected condition, is made by the sharpening account. For this comparison, the effect size was also calculated in terms of Cohen's d_z.

The rationale of this analysis is that a dampening mechanism suppresses responses in highly active neurons (i.e., those neurons that are tuned toward the expected feature) more than in less active neurons (those that are tuned away). Thus, when responses within a voxel are strong to a particular image, more neurons can be suppressed by dampening than when a less preferred image is shown. Because a neural sharpening mechanism, opposite to dampening, would particularly suppress less active neurons compared with highly active ones, the reverse pattern would be evident under sharpening.

In addition to the ROI-based approach, we also performed a whole-brain version of the image preference analysis to provide an overview of where dampening or sharpening might be evident beyond our a priori defined ROIs. The analysis was identical to the ROI-based approach, outlined above, except for that the amount of expectation suppression per voxel and preference rank was calculated to display results across the whole brain. Regressions were thus fit to expectation suppression as function of image preference rank for each voxel and subject. The fit was constrained to voxel in which the response to expected and unexpected stimuli showed a significant positive slope with preference rank, thereby indicating that the image preference ranking generalized from the localizer to the main task. Unlike in the ROI-based approach, the data were spatially smoothed using a Gaussian kernel with FWHM of 8 mm. The slope parameters across subjects were tested against zero in each voxel. Because in this analysis expectation suppression was expressed as a function of image preference rank, from least to most preferred, positive slopes indicate support for dampening, whereas negative slopes are evidence for sharpening.

Bayesian analyses.

To assess whether any nonsignificant results constituted a likely absence of an effect, or rather indicated a lack of statistical power to detect possible differences, corresponding Bayesian tests were performed. All Bayesian analyses were performed in JASP (JASP Team, 2017) (RRID:SCR_015823) using default settings. Paired and one-sample t tests used a Cauchy prior width of 0.707 and repeated-measures ANOVAs used a prior with the following settings: r scale fixed effects = 0.5, r scale random effects = 1, r scale covariates = 0.354. The number of samples of the RM ANOVA was increased to 100,000 and Bayes factors for the inclusion of the respective factors are reported (BF_inclusion), which yields the evidence for the inclusion of that factor averaged over all models in which the factor is included (Wagenmakers et al. (2017). Interpretations of the resulting Bayes factors are based on the classification by Lee and Wagenmakers (2013).

ROI definition.

The two a priori ROIs (object-selective LOC and V1) were defined per subject based on data that was independent from the main task. To obtain object-selective LOC, GLMs were fit to the functional localizer data of each subject, modeling object image and scrambled image events separately with a duration corresponding to their display duration. First-order temporal derivatives, instruction, and performance summary screens, as well as motion regressors were added as nuisance regressors. The contrast, object images minus scrambles, thresholded at z > 5 (uncorrected; i.e., p < 1e-5), was used to select regions per subject selectively more activated by intact object images compared with scrambles (Kourtzi and Kanwisher, 2001; Haushofer et al., 2008). The threshold was lowered on a per-subject basis, if the LOC mask contained <300 voxels in native volume space. The individual functional masks were constrained to anatomical LOC using an anatomical LOC mask obtained from the Harvard-Oxford cortical atlas (RRID:SCR_001476), as distributed with FSL. Finally, a decoding analysis of object images (also see Multivoxel pattern analysis) was performed using a searchlight approach (6 mm radius) on the functional localizer data, using a k-fold cross-validation scheme with four folds. This MVPA yielded a whole-brain map of object image decoding performance, based on which the 200 most informative LOC voxels (in native volume space) in terms of image identity information were selected from the previously established LOC masks. This was done to ensure that the final masks contain voxels, which best discriminate between the different object images. Freesurfer 6.0 (recon-all, RRID:SCR_001847) (Dale et al., 1999) was used to extract V1 labels (left and right) per subject based on their anatomical image. Subsequently, the obtained labels were transformed back to native space using mri_label2vol and combined into a bilateral V1 mask. The same searchlight approach mentioned above was used to constrain the anatomical V1 masks to the 200 most informative V1 voxels concerning object identity decoding. To verify that our results were not unique to the specific (but arbitrary) ROI size, we repeated all ROI analyses with ROI masks ranging from 50 to 300 voxels in steps of 50 voxels.

Software

FSL 5.0.9 (FMRIB Software Library; Oxford, UK; www.fmrib.ox.ac.uk/fsl, RRID:SCR_002823) (Smith et al., 2004) was used for preprocessing and analysis of fMRI data. Additionally, custom MATLAB (The MathWorks, RRID:SCR_001622) and Python (Python Software Foundation, RRID:SCR_008394) scripts were used for additional analyses, data extraction, statistical tests, and plotting of results. The following toolboxes were used: NumPy (RRID:SCR_008633) (van der Walt et al., 2011), SciPy (RRID:SCR_008058) (Jones et al., 2001), Matplotlib (RRID:SCR_008624) (Hunter, 2007), PySurfer (RRID:SCR_002524) (https://pysurfer.github.io/), Mayavi (RRID:SCR_008335) (Ramachandran and Varoquaux, 2011), and Scikit-learn (RRID:SCR_002577) (Pedregosa et al., 2011). Whole-brain results are displayed using Slice Display (Zandbelt, 2017) using a dual-coding data visualization approach (Allen et al., 2012), with color indicating the parameter estimates and opacity the associated z statistics. Additionally, PySurfer was used to display whole-brain results on an inflated cortex, with surface labels from the Desikan-Killiany atlas (Desikan et al., 2006). Bayesian analyses were performed using JASP version 0.8.1.1 (RRID:SCR_015823) (JASP Team, 2017). Stimulus presentation was done using Presentation software (version 18.3, Neurobehavioral Systems, RRID:SCR_002521).

Results

Expectation suppression throughout the ventral visual stream

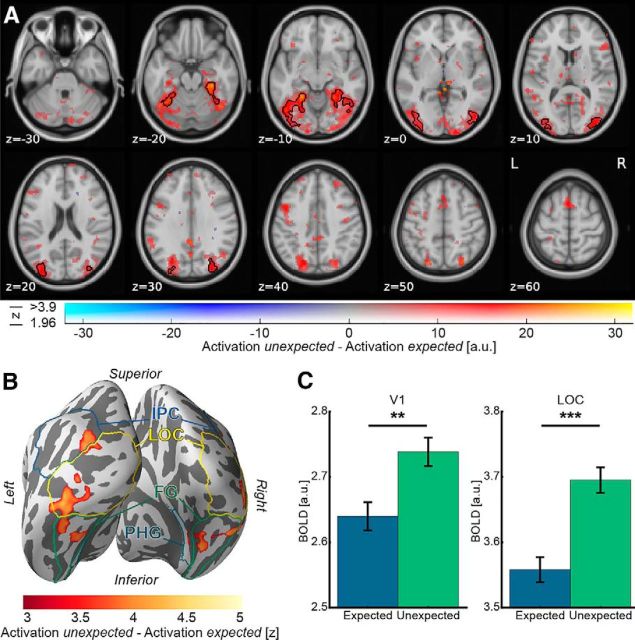
We first examined expectation suppression within our a priori defined ROIs, V1 and object-selective LOC. We observed a significantly larger BOLD response to unexpected compared with expected image pairs, both in V1 (t₍₂₁₎ = 3.20, p = 0.004, Cohen's d_z = 0.68; Fig. 2C) and object-selective LOC (t₍₂₁₎ = 5.03, p = 5.6e-5, Cohen's d_z = 1.07; Fig. 2C). To ensure that the results are not dependent on the (arbitrarily chosen) mask size of the ROIs, the analyses were repeated for ROIs of sizes between 50 and 300 voxels (691–4147 mm³); the direction and statistical significance of all effects were identical for all ROI sizes.

Figure 2.

A, Expectation suppression throughout the ventral visual stream. Displayed are parameter estimates for unexpected image pairs minus expected pairs overlaid on the MNI152 2 mm template. Color represents the parameter estimates: red-yellow clusters represent expectation suppression; opacity represents the associated z statistics. Black contours outline statistically significant clusters (Gaussian random field cluster corrected), which include significant expectation suppression in superior and inferior divisions of LOC, temporal occipital fusiform cortex, and posterior parahippocampal gyrus. B, Expectation suppression displayed on an inflated cortex reconstruction. z statistics of the expectation suppression contrast (cluster thresholded) are displayed. Visible are large clusters showing significant expectation suppression in LOC, fusiform gyrus (FG), inferior parietal cortex (IPC), and posterior parahippocampal gyrus (PHG). C, Expectation suppression within V1 and object-selective LOC. Displayed are parameter estimates ± within-subject SE for responses to expected and unexpected images pairs. In both ROIs, V1 (left bar plot) and LOC (right bar plot), BOLD responses to unexpected image pairs were significantly stronger than to expected image pairs. **p < 0.01. ***p < 0.001.

A whole-brain analysis, investigating effects of perceptual expectation across the brain, revealed an extended statistically significant cluster (Fig. 2A, black contours) of expectation suppression across the ventral visual stream. As also evident in Figure 2B, cortical areas showing significant expectation suppression included large parts of bilateral object-selective LOC, bilateral fusiform gyrus, bilateral inferior parietal cortex, and right posterior parahippocampal gyrus. Thus, there is substantial support for a widespread expectation suppression effect across the ventral visual stream.

Next, we assessed the neural effect of the conditional probability conditions within V1 and LOC. Although this analysis confirmed a weaker response for expected items in V1 (F_(1,21) = 6.39, p = 0.020, η² = 0.233) and LOC (F_(1,21) = 19.50, p = 2.4e-4, η² = 0.481), there was no significant modulation by conditional probability, nor an interaction between conditional probability and expectation in either V1 (conditional probability: F_(2,42) = 2.02, p = 0.145, η² = 0.088; interaction: F_(2,42) = 1.19, p = 0.315, η² = 0.053) or LOC (conditional probability: F_(2,42) = 1.90, p = 0.162, η² = 0.083; interaction: F_(2,42) = 0.92, p = 0.407, η² = 0.042). Bayesian analyses yielded very strong support for the effect of expectation in LOC (BF_Incl. = 35.403) but provided moderate evidence that conditional probability did not have an effect (BF_Incl. = 0.327), and neither did the interaction of expectation and conditional probability (BF_Incl. = 0.290). In V1, results remained inconclusive as there was only anecdotal evidence against an effect of expectation (BF_Incl. = 0.426) and conditional probability (BF_Incl. = 0.373), but moderate evidence against an effect of the interaction (BF_Incl. = 0.172). Thus, because there is no evidence for an effect of the conditional probability manipulation, we collapse across the three different conditional probability conditions for all subsequent analyses.

Perceptual expectations dampen sensory representation in LOC

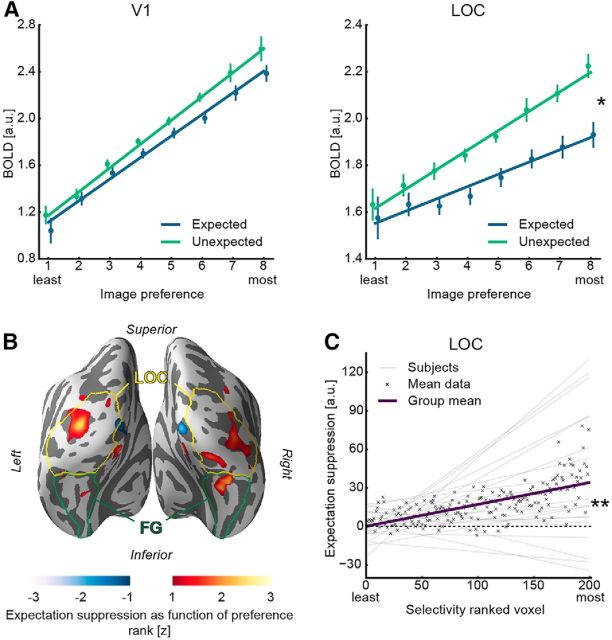
To examine whether sharpening or dampening of sensory representations underlies the observed expectation suppression effect in V1 and LOC, an image preference analysis was conducted. In short, BOLD responses were regressed on image preference rank, with dampening predicting a steeper slope for unexpected compared to expected images and sharpening predicting the opposite (for details, see Materials and Methods). First, we tested whether the relation between voxel-level BOLD responses and image preference rank was better described by a linear model than a polynomial model. There was higher model evidence for linear compared with nonlinear response profiles in both areas and conditions (V1, expected: BIC_linear = 97.02 < BIC_polynomial = 97.25; V1, unexpected: BIC_linear = 95.85 < BIC_polynomial = 96.09; LOC, expected: BIC_linear = 94.82 < BIC_polynomial = 95.01; LOC, unexpected: BIC_linear = 94.99 < BIC_polynomial = 95.28). Furthermore, results depicted in Figure 3A reveal positive slopes within V1 (expected: t₍₂₁₎ = 9.11, p = 9.6e-9, Cohen's d_z = 1.94; V1 unexpected: t₍₂₁₎ = 9.90, p = 2.3e-9, Cohen's d_z = 2.11), as well as in LOC (expected: t₍₂₁₎ = 3.39, p = 0.003, Cohen's d_z = 0.72; LOC unexpected: t₍₂₁₎ = 7.14, p = 4.8e-7, Cohen's d_z = 1.52), confirming that the image preference ranking from the functional localizer data generalized to the main task. This indicates a stable, reproducible sensory code and allows for an analysis of the difference in slopes between expected and unexpected image pairs. Crucially, image preference slopes were significantly steeper for unexpected than expected image pairs in LOC (t₍₂₁₎ = 2.18, p = 0.041, Cohen's d_z = 0.47). This means that the amount of expectation suppression (i.e., Fig. 3A, the difference in the two regression lines) increased with the image preference rank in object-selective LOC. A control analysis confirmed that the results were independent of the number of voxels in the ROI mask (mask sizes 50–300 voxels). There was no statistically significant difference in slopes between the expectation conditions in V1 (t₍₂₁₎ = 1.20, p = 0.242, Cohen's d_z = 0.26), regardless of the number of voxels in the ROI mask (50–300 voxels). To explore whether there was evidence for the absence of dampening in V1, a Bayesian t test was performed on the difference of the image preference slopes (unexpected vs expected) in the V1 ROI. This analysis yielded a BF₁₀ < 1/3 for all V1 ROI sizes, except for the 200 voxel mask (BF₁₀ = 0.423). Together, this suggests that there is moderate evidence for the absence of dampening in V1.

Figure 3.

A, Image preference analysis results in V1 and object-selective LOC. Parameter estimates ± within-subject SE are displayed as a function of voxelwise image preference, ranked from the least to the most preferred image rank based on the functional localizer. Superimposed is the mean regression line fit of the subjectwise regressions for expected and unexpected image pairs separately (see Materials and Methods). Left line plot represents responses to expected and unexpected image pairs within the V1 ROI. The fitted regression lines for expected and unexpected are parallel (i.e., no difference in slopes). Right plot represents image preference results for object-selective LOC, showing a steeper slope for the unexpected image pair regression line compared with the corresponding expected image pair regression line. B, Image preference analysis results displayed on an inflated cortex reconstruction. z statistic (uncorrected) of expectation suppression as function of image preference rank is shown: red represents more suppression for preferred stimuli (dampening); blue represents less suppression for preferred stimuli (sharpening). Visible are clusters showing a dampening effect largely in bilateral LOC and, to a lesser extent, in fusiform gyrus (FG). C, Expectation suppression (unexpected − expected) as function of voxel selectivity, ranked from the least to the most selective voxels, in object-selective LOC. Displayed are the linear models per subject, the mean linear model (group mean), and the mean data for each selectivity ranked voxel. The amount of expectation suppression increases as a function of voxel selectivity. *p < 0.05. **p < 0.01.

To provide an additional overview of the localization of the dampening effect beyond our a priori ROIs, we performed a whole-brain analysis of the image preference analysis. Results depicted in Figure 3B, using a liberal threshold, suggest clusters of dampening to be primarily located in LOC and to a lesser degree in fusiform gyrus.

After showing a dampening of representations in object-selective LOC, we further explored whether this dampening at the voxel level is likely to reflect neural dampening, as also evident in Meyer and Olson (2011) and Kumar et al. (2017). A key problem is that, under certain conditions, a neural sharpening mechanism can produce voxel level dampening, as also suggested by Alink et al. (2017) in the case of repetition suppression. Thus, we performed an additional analysis in which we analyzed expectation suppression (i.e., unexpected − expected) as a function of voxel selectivity (i.e., slope of the response amplitude to preference ranked images). We reasoned that, under a dampening account, selective voxels, showing strong responses to some, but weak responses other stimuli, are, on average, more likely to yield strong expectation suppression than low selectivity voxels. Sharpening on the other hand predicts the opposite pattern because highly selective voxels should be less suppressed by sharpening, or even enhanced in their response, because more activated neurons are, on average, tuned toward the expected stimulus, compared with voxels with lower selectivity. For this analysis, we first established a voxel selectivity ranking. The rank was based on the slope of activity regressed onto image preference during the localizer for each voxel. The rationale is that voxels that are more selective in their response yield a larger slope parameter because the activity elicited by different images shows a larger difference than in voxels with low selectivity (i.e., those that respond similarly to different images). After obtaining the slope parameter of image preference per voxel, we ranked voxels by this slope coefficient, reflecting voxel selectivity during the localizer. Next, we regressed expectation suppression during the main task onto voxel selectivity rank. As explained above, we reasoned that dampening predicts a positive slope for this regression, whereas sharpening would predict a negative slope. Results from LOC (Fig. 3C) showed a significant positive slope of expectation suppression with voxel selectivity (t₍₂₁₎ = 3.00, p = 0.007, Cohen's d_z = 0.64), demonstrating that highly selective voxels are more suppressed by expectation than less selective ones. These effects were present for all LOC ROI mask sizes from 50 to 300 voxels. Thus, also the selectivity analysis provides evidence that neural responses are dampened by expectations in LOC. Results in V1 were inconclusive with no significant effect of voxel selectivity on expectation suppression (t₍₂₁₎ = 1.80, p = 0.086, Cohen's d_z = 0.38) and only weak anecdotal evidence for the absence of an effect in the corresponding Bayesian t test (BF₁₀ = 0.887).

In another complementary analysis, we reasoned that, if the reduced activity for expected items is associated with a reduction of noise (sharpening), it is expected to be associated with an increase in classification accuracy in a MVPA (Kok et al., 2012a). Conversely, a dampening of the representation is predicted to be associated with a decrease in classification accuracy for expected image pairs (Kumar et al., 2017). Generally, image identity could be classified well above chance (12.5%) in V1 (expected: 27.9%, t₍₂₁₎ = 10.89, p = 4.3e-10, Cohen's d_z = 2.32; unexpected: 30.2%, t₍₂₁₎ = 15.70, p = 4.5e-13, Cohen's d_z = 3.35), and LOC (expected: 18.5%, t₍₂₁₎ = 5.69, p = 1.2e-5, Cohen's d_z = 1.21; unexpected: 19.5%, t₍₂₁₎ = 6.76, p = 1.1e-6, Cohen's d_z = 1.44). While a trend toward better decoding performance for unexpected images was visible in both ROIs, in line with dampening of the sensory response, this difference was not statistically significant (V1: t₍₂₁₎ = 1.93, p = 0.067, Cohen's d_z = 0.41; LOC: t₍₂₁₎ = 1.16, p = 0.260, Cohen's d_z = 0.25). Bayesian t tests of this difference also remained inconclusive in both ROIs (V1: BF₁₀ = 1.073; LOC: BF₁₀ = 0.403).

Expectation facilitates image categorization

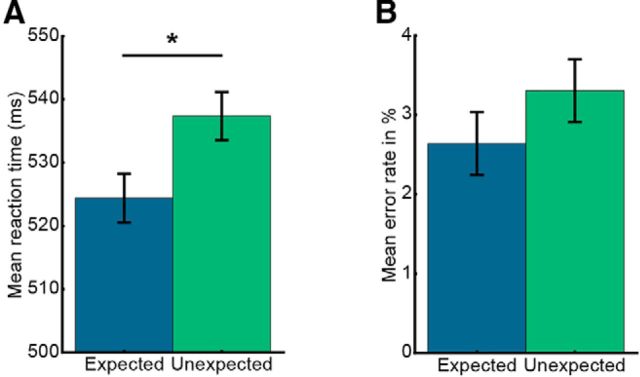
To assess whether concurrent to the described neural effects also behavioral benefits of expectation are evident, data from the categorization task were analyzed. Results demonstrate that participants categorized expected trailing images faster (524.4 ± 3.8 ms, mean ± SE) than unexpected items (537.4 ± 3.8 ms; t₍₂₁₎ = 2.40, p = 0.026, Cohen's d_z = 0.51; Fig. 4A). A similar, albeit not statistically significant trend (t₍₂₁₎ = 1.19, p = 0.247, Cohen's d_z = 0.25) was visible in terms of error rates (Fig. 4B). Analysis of the questionnaires showed that, on average, participants correctly identified 4.0 ± 2.3 (mean ± SD) of the eight image pairs.

Figure 4.

Behavioral data analysis from the categorization task indicates incidental learning of image transitions. Data are mean ± within-subject SE. A, Mean RT to expected and unexpected trailing images. RTs were significantly faster to expected trailing images compared with unexpected images. B, The corresponding mean error rates. *p < 0.05.

Spatial extent of expectation suppression

In a post hoc analysis, we investigated whether the expectation suppression effect in V1 and LOC was spatially unspecific or constrained to regions activated by the object stimuli. The reasoning was that a spatially unspecific effect indicates that at least part of the observed expectation suppression may be due to arousal changes in response to unexpected compared with expected trailing images, while a constrained effect may point toward a spatially specific top-down modulation. To investigate this, the amount of expectation suppression was compared between voxels significantly activated by object stimuli and those that were not. The split into activated and not activated voxels was performed using data from the functional localizer, with activated voxels being defined as all voxels within anatomically defined V1 and LOC, respectively, which exhibited a significant activation by object images (z > 1.96; i.e., p < 0.05, two-sided), whereas nonactivated voxels were defined as voxels displaying no significant activation, nor deactivation (−1.96 < z < 1.96). ROI masks were constrained to gray matter voxels. In both ROIs, activated and nonactivated voxels showed evidence of expectation suppression (V1, activated voxels: t₍₂₁₎ = 3.01, p = 0.007, Cohen's d_z = 0.64; V1, nonactivated voxels: t₍₂₁₎ = 2.17, p = 0.041, Cohen's d_z = 0.46; LOC, activated voxels: t₍₂₁₎ = 4.11, p = 0.0005, Cohen's d_z = 0.88; LOC, nonactivated voxels: t₍₂₁₎ = 2.51, p = 0.021, Cohen's d_z = 0.53). In LOC, expectation suppression was significantly stronger in voxels that were activated by the stimuli than in nonactivated voxels (t₍₂₁₎ = 2.20, p = 0.039, Cohen's d_z = 0.47). However, in V1, this difference was not statistically significant (t₍₂₁₎ = 1.09, p = 0.286, Cohen's d_z = 0.23). A Bayesian analysis of V1 data remained inconclusive, yielding only anecdotal evidence for the absence of a difference between activated and nonactivated voxels (BF₁₀ = 0.379).

Discussion

We set out to investigate the neural effects of perceptual expectation and demonstrated that, after incidental learning of transitional probabilities of object images, expectation suppression is evident throughout the human ventral visual stream. Importantly, the amount of expectation suppression scaled positively with image preference and voxel selectivity in LOC, suggesting that dampened sensory representations underlie expectation suppression in object-selective areas, in line with results from monkey IT (Meyer and Olson, 2011; Kumar et al., 2017).

Dampening of sensory representation in object-selective cortex

The suppression of expected stimuli, evident throughout the ventral visual stream in the present study, extends and supports previous research showing expectation suppression in early visual areas (Alink et al., 2010; Kok et al., 2012a; St. John-Saaltink et al., 2015) and monkey IT (Meyer and Olson, 2011; Kaposvari et al., 2018). The observed suppression may constitute an efficient and adaptive processing strategy, which filters out predictable, irrelevant objects from the environment. Conversely, the stronger response to unexpected objects may serve to render unexpected stimuli more salient. This surprise response to unexpected stimuli may draw attention toward these stimuli, as also reasoned by Meyer and Olson (2011). Such capture of attention is adaptive because unexpected events may provide particularly relevant information. It is important to note that the used paradigm did not manipulate attention toward expected or unexpected stimuli in a top-down fashion. Indeed, unexpected and expected stimuli were only distinguishable by the context in which they occurred. Therefore, if unexpected stimuli do indeed automatically capture attention (Brockmole and Boot, 2009; Howard and Holcombe, 2010), then any attentional modulation must temporally follow the expectation effect, and not vice versa.

Given the absence of a neutral condition, we cannot differentiate whether the observed expectation suppression effect constitutes a suppressed response for expected stimuli, or an enhanced response to unexpected ones, or both. Although there is evidence for both expectation suppression and surprise enhancement (Kimura and Takeda, 2015; Kaposvari et al., 2018), the present data cannot speak to this issue but only concerns the relative difference between expected and unexpected stimuli.

We showed that the amount of expectation suppression scales with image preference in object-selective LOC, as also demonstrated in monkey IT (Meyer and Olson, 2011). Scaling indicates that expectation suppression in object-selective areas does not merely signal an unspecific surprise response, but rather that sensory representations are dampened by expectations because the neural population most responsive to the expected stimulus is also most suppressed. Accordingly, we also demonstrated that expectation suppression scales positively with voxel selectivity. This result further supports the dampening account of expectation because selective voxels contain more highly responsive neurons, tuned toward the expected stimulus features, which are also most suppressed by dampening. Although there are some scenarios in which neural sharpening could account for some of the results presented here in isolation, the joint set of observations can only be accounted for by a dampening process at the neural level. Thus, our results lend support to the notion that neural responses are dampened by expectations in object-selective LOC. Functionally, a dampening of sensory representations is in line with an adaptive mechanism, which filters out behaviorally irrelevant, predictable objects from the environment.

If expectation suppression, and the underlying representational dampening in LOC, represents an adaptive neural strategy, one might expect behavioral benefits to correlate with the neural effects. Although we observed behavioral benefits for expected stimuli during the categorization task, the present study cannot answer whether expectation suppression is associated with behavioral benefits because during the fMRI task, and central to the interpretation above, expectations were task-irrelevant. Task-relevant predictions, necessary to investigate this question, may in turn change the underlying neural dynamics. Indeed, it has been suggested that, at least in early visual areas, attention can reverse the suppressive effect of expectation (Kok et al., 2012b).

Although we did observe expectation suppression in V1, we did not find conclusive evidence for, or against, dampening or sharpening. These results cannot be explained by the absence of image preference in V1 for the used stimuli, as the preference ranking itself was reliable. Because a stimulus unspecific suppression was evident in V1, it is possible that object-specific expectations were resolved at a higher level in the cortical hierarchy and only the results of the prediction (expected or unexpected) were relayed to V1 as feedback. Alternatively, a dampening effect may exist in V1, albeit of a smaller magnitude than in LOC, yielding an effect below detection threshold for the present study. Suppression in V1 may also have arisen due to spatially unspecific effects across V1, such as arousal changes, after the resolution of expectations in higher cortical areas. This interpretation is supported by the fact that expectation suppression was not significantly larger in stimulus-driven than non–stimulus-driven voxels.

Finally, the present results are at odds with a previous study that observed a sharpening of the sensory population response in V1 by expectation (Kok et al., 2012a). Although we did not find evidence for a sharpening of responses in V1, we did observe dampening in LOC, in line with studies of monkey electrophysiology (Meyer and Olson, 2011; Kumar et al., 2017). Thus, our data show that the disagreement in previous studies, suggesting sharpening in human V1 (Kok et al., 2012a) and dampening in monkey IT (Meyer and Olson, 2011; Kumar et al., 2017), are unlikely to be caused by differences between species or recording methods. We briefly discuss three factors that may account for the opposite results. First, Kok et al. (2012a) and the present study used different stimuli (grating vs object stimuli), tailored to investigate the population response in different areas of the visual hierarchy (V1 vs LOC). Given that we did not find evidence for sharpening in V1, the opposite results cannot be explained by a general difference between the sensory areas, but rather an interaction between stimulus type and sensory area. Second, we induced expectations by prolonged exposure before scanning, whereas in Kok et al. (2012a), expectations were learned and updated during the experiment. Interestingly, while expectation suppression has been shown in monkey IT when expectations were induced by long-term exposure (Meyer and Olson, 2011; Kaposvari et al., 2018), this effect was not found when expectations were induced during the experiment (Kaliukhovich and Vogels, 2011, 2014). Finally, there are differences between the studies in task demands. In the current study, we examined neural activity elicited by expected and unexpected nontarget stimuli (i.e., stimuli that did not require a response by the observer). On the other hand, all stimuli in Kok et al. (2012a) were target stimuli, requiring a discrimination judgment by the observers. Given that attentional selection is known to sharpen stimulus representations (Serences et al., 2009), this difference in task setup could explain the opposite results.

Prediction errors and predictive coding

Within a hierarchical predictive coding framework, prior expectations about an upcoming stimulus act as top-down signals predicting the bottom-up input based on generative models of the agent (Friston, 2005). These predictions are then compared with the actual bottom-up input, resulting in a mismatch signal, the prediction error. Expectation suppression, as evident in the present data, and previously observed by others (Kok et al., 2012a; den Ouden et al., 2012; e.g., Blank and Davis, 2016), matches the properties of a prediction error signal. That is, the ensuing prediction error is smaller for expected compared with unexpected trailing images because the mismatch between prediction and input is smaller, thus resulting in expectation suppression, as evident here throughout the ventral visual stream. Furthermore, a dampening of object representations in LOC can well be explained within predictive coding as a result of the stronger and prolonged resolution of prediction errors elicited by unexpected images.

Alternatively, our results could partially be explained by changes in arousal, potentially reflecting globally enhanced responses following surprising stimuli. This explains why expectation suppression in V1 was spatially unspecific, and some suppression was evident in non–stimulus-driven voxels in LOC. However, such unspecific upregulation of activity cannot readily account for the stimulus-specific and spatially specific response modulations in LOC, while predictive coding explains these effects well.

No systematic modulation of expectation suppression by conditional probability

The present results do not provide evidence for a systematic modulation of expectation suppression by conditional probabilities. This is somewhat surprising given that a modulation has been demonstrated in monkey TE (Ramachandran et al., 2016). Furthermore, it is only by virtue of the difference in conditional probability that a trailing image can be considered expected or unexpected. Thus, by its nature, expectation suppression should be sensitivity to conditional probability. We believe that this null result may be due to a lack of sensitivity of the associated analysis. The complexity of the transition matrix and the relatively small difference in conditional probability between the conditions, as well as the split of the available data into the three conditions may have all led to a reduction in sensitivity. Thus, to further elucidate the nature of expectation suppression, future research in humans is required, possibly using simplified paradigms or extended exposure to the image transitions.

In conclusion, our results demonstrate that expectation suppression is a widespread neural mechanism of perceptual expectation in the ventral visual stream, which increases with image preference and voxel selectivity. Perceptual expectations thus lead to a dampening of sensory representations in object-selective cortex, possibly supporting our ability to filter out irrelevant, predictable objects.