Synaptic Excitation in Spinal Motoneurons Alternates with Synaptic Inhibition and Is Balanced by Outward Rectification during Rhythmic Motor Network Activity

Abstract

Regular firing in spinal motoneurons of red-eared turtles (Trachemys scripta elegans, either sex) evoked by steady depolarization at rest is replaced by irregular firing during functional network activity. The transition caused by increased input conductance and synaptic fluctuations in membrane potential was suggested to originate from intense concurrent inhibition and excitation. We show that the conductance increase in motoneurons during functional network activity is mainly caused by intrinsic outward rectification near threshold for action potentials by activation of voltage and Ca²⁺ gated K channels. Intrinsic outward rectification facilitates spiking by focusing synaptic depolarization near threshold for action potentials. By direct recording of synaptic currents, we also show that motoneurons are activated by out-of-phase peaks in excitation and inhibition during network activity, whereas continuous low-level concurrent inhibition and excitation may contribute to irregular firing.

SIGNIFICANCE STATEMENT Neurons embedded in active neural networks can enter a high-conductance state. High-conductance states were observed in spinal motoneurons during rhythmic motor behavior. Assuming no change in intrinsic conductance, it was suggested that the high-conductance state in motoneurons originated from balanced inhibition and excitation. In this study, we demonstrate that intrinsic outward rectification significantly contributes to the high-conductance state. Outward rectification balances synaptic excitation and maintains membrane potential near spike threshold. In addition, direct synaptic current recordings show out-of-phase excitation and inhibition in motoneurons during rhythmic network activity.

Introduction

Neurons in large-scale networks tend to fire with irregular interspike intervals. Theoretically, irregular firing most readily occurs in response to concurrent inhibition and excitation produced by uncorrelated intense activity in large numbers of afferents forming weak synapses (Gerstein and Mandelbrot, 1964). Experimental evidence suggests that background synaptic activity is high in cortical pyramidal cells in vivo (Paré et al., 1998) and leads to increased variability of interspike intervals (Holt et al., 1996; Destexhe et al., 2003). Functional roles for concurrent inhibition and excitation have been proposed for sensory cortices (Shadlen and Newsome, 1994, 1998; Mariño et al., 2005; Monier et al., 2008; Dehghani et al., 2016; Kremkow et al., 2016). Theoretically, the balanced state in networks favors fast response times (van Vreeswijk and Sompolinsky, 1996) and is efficient for coding (Denève and Machens, 2016), and the associated variable interspike intervals reduce accumulation of correlated activity (Averbeck et al., 2006; Renart et al., 2010). Concurrent inhibition and excitation also provides for sensitive regulation of postsynaptic gain (Chance et al., 2002). In cortical circuits, concurrent inhibition and excitation is associated with the occurrence of up states (Shu et al., 2003) and orientation selectivity in local microcircuits (Marino et al., 2005). The dynamic interplay between inhibition and excitation plays a fundamental role in processing sensory stimuli in local sensory cortical microcircuits (Wehr and Zador, 2003; Wilent and Contreras, 2005; Monier et al., 2008; Kremkow et al., 2016).

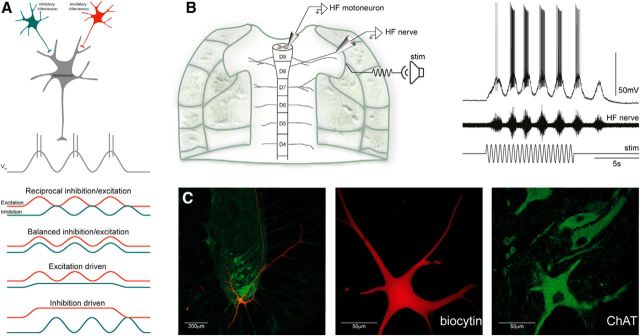
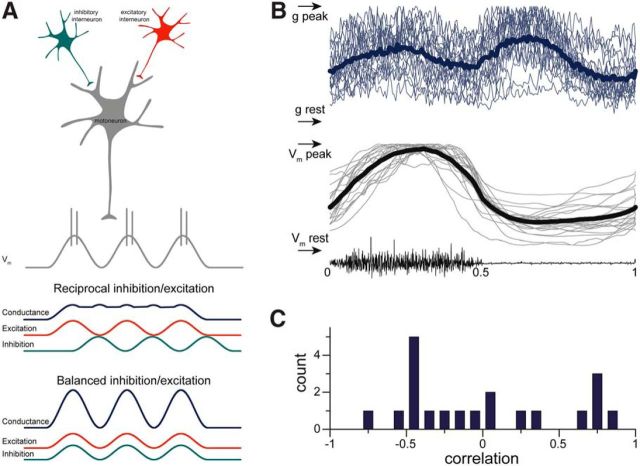
In contrast, the presence and role of concurrent inhibition and excitation in spinal motor function is not well established but could be the course of the high-conductance states in motoneurons during network activity (Alaburda et al., 2005). It is widely accepted that spinal motoneurons are activated by out-of-phase reciprocal inhibition and excitation during rhythmic behaviors (Brown, 1914; Jankowska et al., 1965). Nevertheless, the same rhythmic depolarization in membrane potential of motoneurons can be achieved by other combinations of inhibition and excitation (Fig. 1A). The reciprocal activation is supported experimentally by direct recordings of synaptic currents in small-scale spinal networks (Russell and Wallen, 1983; Dale, 1985; Kotaleski et al., 1999; Gabriel et al., 2009). The same type of recordings from motoneurons in the neonatal spinal cord in rats found either rhythmic excitation or rhythmic inhibition (Hochman and Schmidt, 1998). Furthermore, irregular firing, increased conductance, and synaptic fluctuations in membrane potential in turtle motoneurons during network activity are indicative of concurrent inhibition and excitation (Alaburda et al., 2005; Berg et al., 2008; Guzulaitis et al., 2016). However, because of technical limitations, concurrent activation was deduced indirectly from estimates of the total conductance rather than by direct recordings of synaptic currents (Berg et al., 2007; Petersen et al., 2014). As in cortical neurons (Anderson et al., 2000; Mariño et al., 2005; Priebe and Ferster, 2005), the ratio between inhibition and excitation in motoneurons was obtained from current-clamp (CC) recordings assuming ignorable changes in nonsynaptic conductance. Quite clearly, however, and unlike estimates from voltage clamp (VC; Borg-Graham et al., 1998; Shu et al., 2003; Wehr and Zador, 2003; Monier et al., 2008), uncontrolled voltage changes in current clamp pose serious limitations in identifying the origin and dynamics of conductance changes during rhythmic network activity. In the present study, we implement whole-cell recordings from hip flexor motoneurons in an ex vivo preparation from the adult turtle (Fig. 1B). With current-clamp and voltage-clamp recordings, we show that intrinsic conductances contribute significantly to the high-conductance state during sensory-induced fictive scratching. We also show that synaptic inhibition and excitation peaks out of phase during scratching.

Figure 1.

Experimental paradigm. A, Schematic representation of four hypothetical patterns of excitatory (red) and inhibitory (blue) synaptic input for motoneurons (gray) during rhythmic motor activity. Premotor excitatory and inhibitory interneurons may be active in-phase (reciprocal) or out-of-phase (balanced). Alternatively, only excitatory or inhibitory interneurons could provide oscillatory synaptic input to motoneurons. B, Left, Alternative activation patterns were examined with whole-cell recordings from motoneurons in an ex vivo spinal cord–carapace preparation from the adult turtle. Right, In the ex vivo preparation, mechanical stimulation of the carapace (loudspeaker) was used to induce rhythmic scratch network activity. C, A subset of the presumed motoneurons recorded from was filled with biocytin for histological verification. These neurons, recorded in the lateral part of the ventral horn, turned out to be ChAT-positive cells, i.e., motoneurons. ChAT, Choline acetyl transferase.

Materials and Methods

Ethical approval.

The surgical procedures complied with Danish legislation and were approved by the controlling body under The Ministry of Justice.

An ex vivo carapace–spinal cord preparation.

Surgical procedures were described previously (Alaburda and Hounsgaard, 2003; Guzulaitis et al., 2013). Briefly, turtles were placed on crushed ice 2 h before surgery to induce drowsiness and reduce stress and pain by hypothermia. In this way, the head and neck could be protracted using minimal force. Brain functions were terminated immediately after decapitation by crushing the head. The blood was substituted by perfusion through the heart with a Ringer's solution containing (mm) 100 NaCl, 5 KCl, 30 NaHCO₃, 2 MgCl₂, 3 CaCl₂, and 10 glucose, saturated with 95% O₂ and 5% CO₂ to obtain pH 7.6. Transverse cuts were made at D9–D10 and D3 spinal cord segments (Fig. 1B). The hip flexor (HF) nerve innervating the puboischiofemoralis internus, pars anteroventralis muscle was exposed and cut.

Scratching was initiated by mechanically stimulating turtle carapace with a fire-polished glass rod mounted to the membrane of a loudspeaker controlled with a function generator (loudspeaker in Fig. 1B). Only responses with three or more bursts in the HF nerve were used for later analysis.

Slice preparation.

Adult turtles were anesthetized by intravenous injection of propofol (30 mg/kg, B. Braun). The head was crushed immediately after decapitation. After intracardiac perfusion of Ringer's solution, the lumbar enlargement (D8–S2 segments) of the spinal cord was removed. The lumbar enlargement was cut into slices (600 μm thick) with a microtome (MicroM slicer HM 650V) equipped with cooling unit (CU65) set at 2°C.

Recordings.

Whole-cell recordings from motoneurons were performed with a Multiclamp 700B amplifier (Molecular Devices). Patch pipettes were filled with a solution containing (mm) 122 K-gluconate, 2.5 MgCl₂, 5.6 Mg-gluconate, 5 K-HEPES, 5 H-HEPES, 5 Na₂ATP, 1 EGTA, 0.3 CaCl₂, and 2.5 biocytin. The pH was adjusted to 7.4 with KOH. The electrode resistance was 4–6 MΩ. Recordings were accepted if neurons had a stable membrane potential more negative than −50 mV. VC experiments were performed on motoneurons when access resistance was low (R_a < 20 MΩ) and possible to compensate by 60–80%. Recordings were sampled at 20 kHz with a 16-bit analog-to-digital converter (Digidata 1322A, Molecular Devices), displayed by means of Axoscope and Clampex software (Molecular Devices), and stored on a hard disk for later analysis.

The electroneurogram (ENG) of the HF nerve was recorded with a differential amplifier (Iso-DAM8, World Precision Instruments) using a suction electrode. The bandwidth was 100 Hz to 1 kHz.

Identification of motoneurons.

Motoneurons were identified by their location in the ventral horn, size (via R_m), height of action potentials (APs), and/or spiking relationship with nerve activity. A subset of neurons in the ex vivo preparation and spinal cord slices were filled with biocytin for histological processing (Fig. 1C). Lumbar segments were removed en bloc from the ex vivo preparation, kept in PBS with 4% paraformaldehyde for 24–48 h at 4°C, and subsequently rinsed with and stored in PBS. Fixed slices or spinal segments were mounted in an agar mount and sectioned transversely into 100-μm-thick slices using a microtome (VT1000 S, Leica). The slices were incubated in a blocking solution (PBS, 0.1% Triton X-100, and 5% donkey serum) for 4 h at 4°C and later for 24–48 h at 4°C with a goat polyclonal antibody directed against ChAT (choline acetyl transferase; 1:250, Millipore). The slices were washed three times with PBS-T (PBS and 0.1% Triton X-100) and incubated for 12–24 h at 4°C with secondary antibodies Alexa Fluor 647 (Alexa647) conjugated with donkey anti-goat antibodies (1:500, Jackson ImmunoResearch Laboratories) and cyanine-3 (Cy3) conjugated with streptavidin (1:500, Jackson ImmunoResearch Laboratories). After three washes with PBS, the slices were mounted and coverslipped using ProLongGold antifade reagent (Invitrogen) and cured overnight at 4°C before microscopy.

Micrographs of neurons were produced using a confocal microscope (LSM 700 with diode lasers, Zeiss) on a Axiolmager M2 using a 20×/0.8 Plan-Apochromat objective (Zeiss). The fluorophores were excited/detected at the following wavelengths: Cy3 at 555/560–800 nm, Alexa647 at 643/560–800 nm. Images were handled with ZEN 2011 software (Zeiss) in the LSM and 8-bit TIFF format.

Data analysis.

Conductance of motoneurons was calculated from Ohm's law:

The mean change in conductance was determined as follows. Hyperpolarizing current pulses at 5 Hz were injected into motoneurons before and during scratching (Fig. 2A,E). Responses of motoneurons were aligned (Fig. 2B,F, light color traces), and the mean V_m was calculated (Fig. 2B,F, dark color traces). Conductance was calculated from the mean V_m before (50–10 ms before pulse onset) and at the end (50–90 ms from pulse onset) of pulse injection. Conductance of motoneurons was estimated also in VC mode (Fig. 2C) where holding V_m was switched between −70 and −60 mV at 5 or 10 Hz. Conductance was calculated from the I_m needed to hold the neuron at a certain membrane potential. Episodes where the holding potential was changed were aligned (Fig. 2D, light yellow), and the mean was calculated (Fig. 2D, dark yellow). Conductance was calculated from two I_m values just before a change in the holding potential (25–40 ms before changing holding potential).

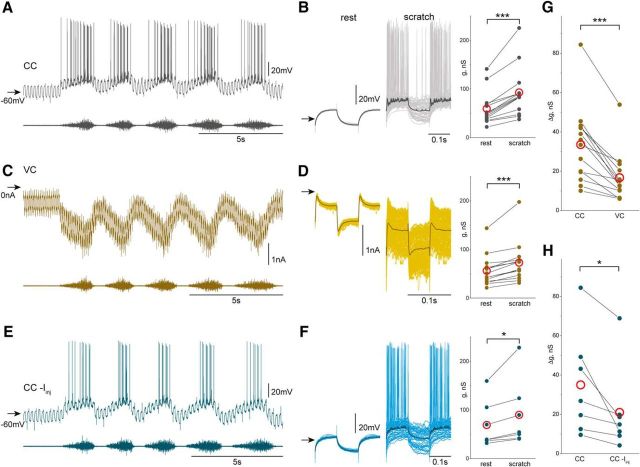
Figure 2.

Voltage-dependent conductance increase during scratching. A, A train of short (100 ms) hyperpolarizing current pulses were injected into a motoneuron just before and during scratching in CC mode. B, V_m during current pulses was aligned (light gray) and averaged (dark gray). The V_m deflection caused by current injection is larger at rest than during scratching, indicating conductance increase during scratching (n = 14, p = 1.2 × 10⁻⁴, Wilcoxon signed rank test). C, The conductance of the same motoneuron was evaluated during scratching when V_m was hyperpolarized in VC recordings. Holding V_m was changed between −70 and −60 mV at 10 Hz. D, Episodes of I_m at the two V_m levels were aligned (light yellow) and averaged (dark yellow). The difference in I_m at the two V_m levels is larger during scratching than at rest, indicating conductance increase during scratching (n = 14, p = 1.2 × 10⁻⁴, Wilcoxon signed rank test). E, F, Conductance also increased during scratching when V_m was hyperpolarized by a steady hyperpolarizing holding current in CC recordings (n = 7, p = 0.016, Wilcoxon signed rank test). G, Smaller conductance increase (Δg) was observed during scratching when motoneurons were hyperpolarized in VC recordings (n = 14, p = 1.2 × 10⁻⁴, Wilcoxon signed rank test). H, In line, smaller Δg during scratching was also found with the hyperpolarizing holding current in CC recordings (n = 7, p = 0.016, Wilcoxon signed rank test). Red open circles in B, D, and F–H represent mean.

The method proposed by Borg-Graham et al. (1998) was used to find temporal changes in conductance. Different DCs were injected into a motoneuron during several successive scratch episodes (Fig. 3A). V_m of motoneurons was low-pass filtered (Gaussian, 5 Hz), and cycles of scratching were normalized in relation to HF nerve activity. To determine the onset and offset of HF bursts, the ENG activity was rectified and low-pass filtered (Gaussian, 5 Hz). The onset of HF activity was defined as 0 (or 1) and the offset as 0.5. V_m during the active and the quiescence HF phases were divided into 100 equal segments each, and the mean of at least three successive scratch cycles was calculated (Fig. 3B). Conductance at each time point was calculated from the I/V relationship by using Ohm's law. The mean inhibitory and excitatory conductances were estimated as described previously (Berg et al., 2007) from the following:

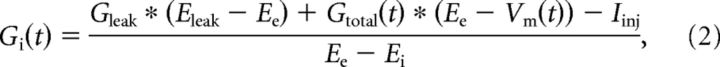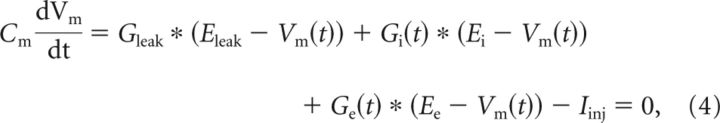ignoring rapid changes in membrane potential. In addition, it was assumed that G_leak does not change and all changes in conductance are of synaptic origin. Since minimal synaptic activity is present before each scratch episode, G_leak was set as resting conductance for each motoneuron individually and E_leak was taken as resting V_m (−59.56 ± 4.3 mV). Resting conductance was calculated as slope of I/V when subthreshold currents were injected into motoneurons. E_e is the reversal potential for excitatory synaptic input and was set to E_e = 0 mV. E_i is the reversal potential for inhibitory synaptic input and was set to E_i = −65 mV.

Figure 3.

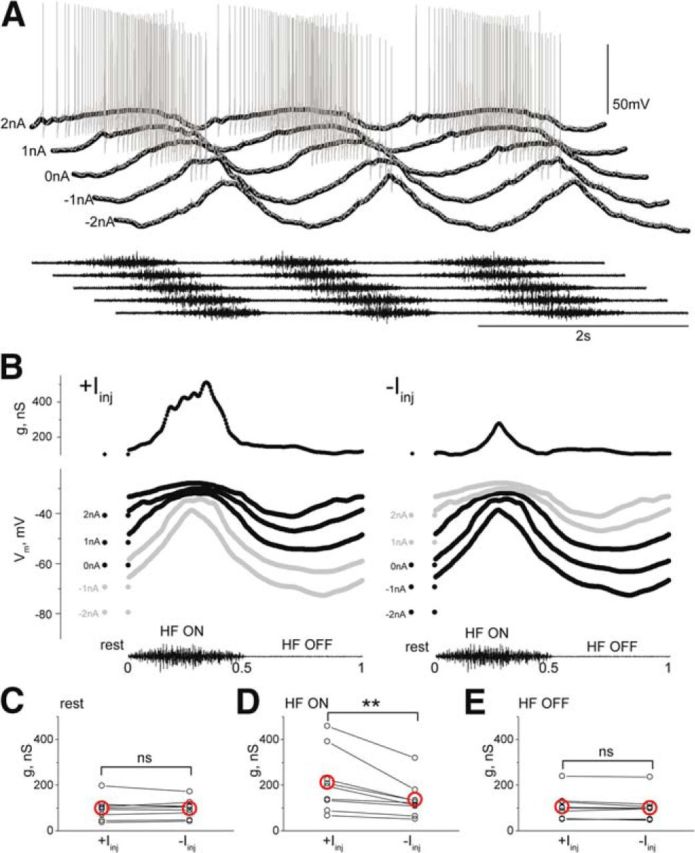
V_m-dependent conductance associated with depolarization. A, Five successive scratch episodes in a motoneuron recorded with holding currents of 2, 1, 0, −1, and −2 nA. From the top: V_m of motoneuron during scratching at different DC injections (gray, raw recordings; black, low-pass filtered); HF nerve activity during scratching. B, The middle graph shows aligned and normalized depolarizing V_m waves obtained from the low-pass filtered sweeps of the records in A. The top graph shows conductance during depolarizing waves obtained from the three most depolarized V_m records (left) and from the three most hyperpolarized records (right). From the top: conductance of the motoneuron; normalized and averaged V_m; HF nerve activity. C, The conductance at rest is unaffected by holding current (n = 9, p = 1, Wilcoxon signed rank test). D, In contrast, the estimated conductance in the HF ON phase, i.e., during depolarization, is higher with the depolarizing holding current than with the hyperpolarizing holding current (n = 9, p = 0.004, Wilcoxon signed rank test). E, The conductance in the HF OFF phase is unaffected by the holding current (n = 9, p = 0.13, Wilcoxon signed rank test). Red open circles in C–E represent mean.

V_m oscillations were induced in motoneurons by injecting a sine-wave current through the recording electrode (Fig. 4A). Conductance was calculated from low-pass filtered (Gaussian, 5 Hz) V_m traces by Ohm's law in subthreshold (Fig. 4, gray) and suprathreshold (Fig. 4, black) voltage ranges.

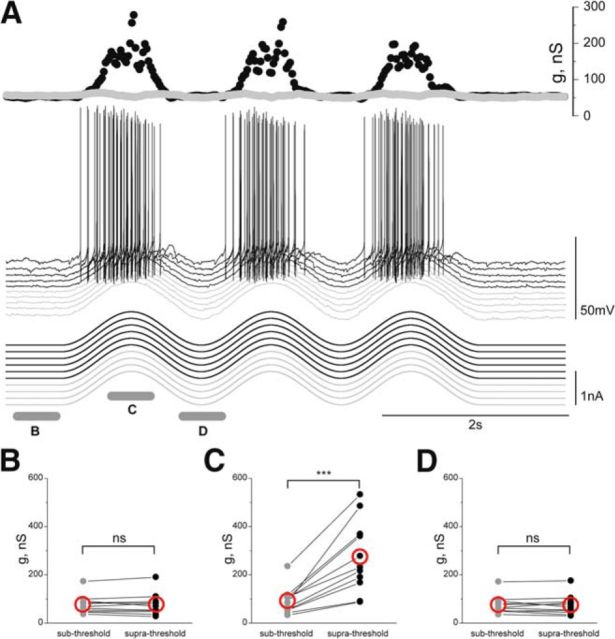
Figure 4.

Intrinsic conductance in motoneurons during current-induced, scratch-like depolarizing waves. A, Ten successive sweeps of scratch-like depolarizing waves in a motoneuron (middle) was obtained by injecting sine-wave currents with a different holding current (bottom). Conductance was calculated from subthreshold sweeps (gray traces) and from superthreshold sweeps (black traces). From the top: motoneuron conductance in the suprathreshold range (black) and the subthreshold range (gray); V_m of motoneuron; current injected into the motoneuron. B, The resting conductance does not depend on the holding current (n = 11, p = 1, Wilcoxon signed rank test). C, Conductance during depolarization is higher in the suprathreshold range than in the subthreshold voltage range (n = 11, p = 9.8 × 10⁻⁴). D, The conductance in the hyperpolarized phase does not depend on holding current (n = 11, p = 0.64, Wilcoxon signed rank test). Red open circles in B–D represent mean.

The resting I/V was obtained either in CC mode when different current steps were injected (Fig. 5A) or in VC mode when cells were depolarized slowly (∼10 mV/s) from −70 to −10 mV (Fig. 5D). To obtain I/V relationships from CC recordings, V_m was taken as the mean over the last 200 ms of 500 ms current pulse injections. In VC recordings, I_m was averaged over 1 mV depolarization. Rectification was quantified as the increase in conductance at depolarized levels compared with hyperpolarized levels. Hyperpolarized levels were subthreshold in CC mode (Fig. 5A) and between −70 and −50 mV in VC mode (Fig. 5D). Depolarized levels were suprathreshold in CC mode and between −20 and −10 mV in VC mode.

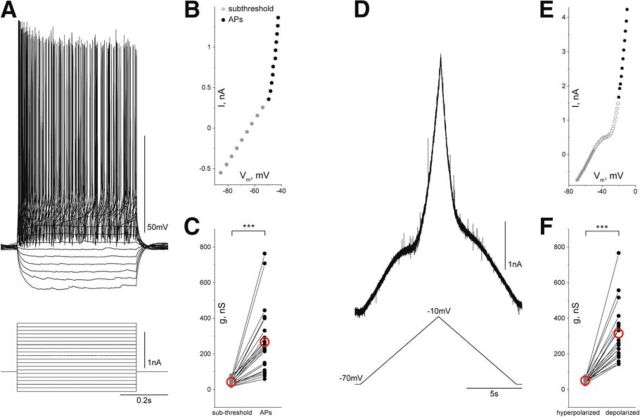
Figure 5.

Outward rectification in spinal motoneurons. A, Superimposed sweeps of responses to 0.5 s current pulses from −0.5 to +1.5 nA injected into a motoneuron. B, The I/V plot obtained from the sweeps in A shows piecewise linear segments with shallow slope in the subthreshold range (gray dots) and a steep slope in the suprathreshold range (black dots). C, Conductance in the subthreshold I/V range is significantly lower than in the suprathreshold I/V range (n = 22, p = 4.8 × 10⁻⁷, Wilcoxon signed rank test). D, I/V plots were obtained also in VC mode when motoneurons were slowly depolarized (≈10 mV/s). E, The I/V curve obtained in VC mode also shows two piecewise linear segments. F, Conductance at depolarized V_m levels increases when compared with hyperpolarized V_m levels (n = 20, p = 1.9 × 10⁻⁶, Wilcoxon signed rank test). Red open circles in C and F represent mean.

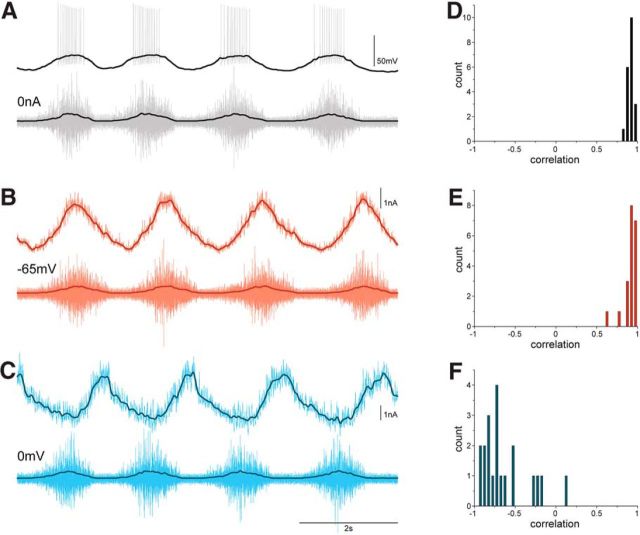
To find the relationship between V_m and the motor output, the HF nerve activity was rectified and both V_m and the rectified HF nerve activity was low-pass filtered (Gaussian, 5 Hz; see Fig. 8A). Correlation (Pearson) was calculated between the filtered signals (see Fig. 8D). Only motoneurons with a high correlation coefficient (r > 0.8) were considered to be HF motoneurons and presented in this study. The same procedure was performed for VC recordings when V_m of motoneurons was clamped at −65 mV and at 0 mV (see Fig. 8B,C). Currents recorded at −65 mV were inverted. Inward currents recorded at −65 mV were considered as excitatory synaptic inputs, and outward currents recorded at 0 mV were considered as inhibitory synaptic inputs.

Figure 8.

V_m, excitation, and inhibition are tightly related to motor output A, A motoneuron recorded in CC mode during scratching (gray traces). Low-pass-filtered traces of V_m and HF nerve activity are shown in black. B, The same motoneuron recorded in VC mode at −65 mV (light red traces, currents inverted). Low-pass-filtered I_m and HF nerve activity are shown in dark red. C, Finally, the motoneuron recorded in VC mode at 0 mV (light blue traces). Low-pass-filtered I_m and HF nerve activity are shown in dark blue. D, Motoneurons with high correlation between V_m and HF nerve activity were selected in the study (n = 20). E, Cumulative histogram of correlation coefficients between excitation, i.e., I_m recorded at −65 mV, and HF nerve activity (n = 20). F, Cumulative histogram of correlation coefficients between inhibition, i.e., I_m recorded at 0 mV, and HF nerve activity (n = 20). From the top: V_m (A) or I_m recorded at −65 mV (inverted; B) and at 0 mV (C); HF nerve activity.

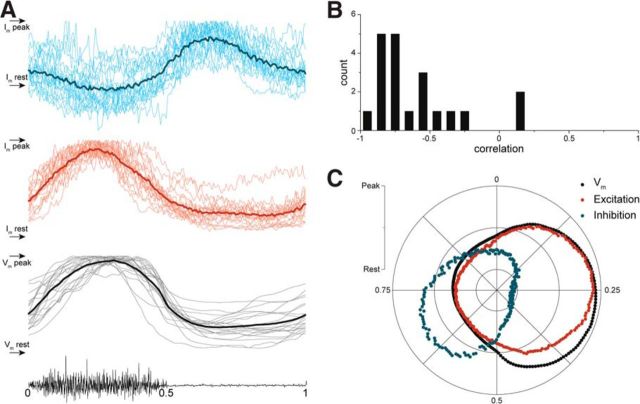
To find the relationship between excitation and inhibition, V_m but not I_m was low-pass filtered (Gaussian, 5 Hz) and normalized as described above (see Fig. 9). Currents recorded at −65 mV were inverted. The correlation (Pearson) between currents recorded at −65 mV and at 0 mV was calculated.

Figure 9.

Inhibition and excitation alternate in HF motoneurons during scratching A, V_m of motoneurons recorded in CC mode during scratching was normalized with respect to HF nerve activity (gray traces). The same normalization was applied for currents recorded in VC mode at −65 mV (red traces, signals are inverted) and at 0 mV (blue traces; n = 20, light color traces depict records of each motoneuron, and dark color traces depict mean). From the top: normalized I_m recorded at 0 mV; inverted and normalized I_m recorded at −65 mV; normalized V_m of motoneurons recorded in CC mode; HF nerve activity. B, Excitatory input is negatively correlated with inhibitory input in the majority of recorded HF motoneurons. C, The circular plot shows that excitatory currents are closely related to V_m, whereas inhibitory currents are out of phase with both excitation and V_m.

Synaptic intensity, i.e., synaptic conductance, was estimated by Ohm's law from two VC recordings when the motoneuron was recorded at −65 mV and at 0 mV. To pool data for all recorded motoneurons, synaptic intensity was normalized.

Experimental design and statistical analysis.

Red-eared turtles (Trachemys scripta elegans; n = 42) of either sex were used in this study. Animals of 10–15 cm carapace length were obtained from Nasco (Fort Atkinson, WI).

Data were analyzed statistically using the two-tailed Wilcoxon signed rank test (OriginLab). The level of significance is indicated as n.s. p > 0.05; *p < 0.05; **p < 0.01; ***p < 0.001. Data are presented as mean ± SD.

Drugs.

The following drugs were bath applied when indicated: tetrodotoxin (TTX; 2 μm; Tocris), tetraethylammonium chloride (TEA; 1 mm; Sigma-Aldrich), apamin (100 nm; Tocris), nimodipine (20 μm; Sigma-Aldrich), and Bay-K8644 (2 μm; Tocris).

Results

Conductance increase during network activity is voltage dependent

With whole-cell recordings, we first compared the average increase in membrane conductance in motoneurons during scratch network activity in CC and in VC. In CC recordings, motoneuron conductance was estimated from the voltage deflection in response to current pulses injected through the recording electrode. As reported before (Alaburda et al., 2005; Guzulaitis et al., 2016) and illustrated in Figure 2A, the amplitude of V_m deflections measured at rest was clearly reduced during scratching. To quantify the conductance increase during scratching, V_m episodes during current injections were aligned (Fig. 2B, light gray traces) and averaged (Fig. 2B, dark gray traces). In all motoneurons tested, the conductance during scratching (92.6 ± 49.7 nS, n = 14) was higher than the conductance at rest (59.1 ± 33.5 nS, n = 14, p = 1.2 × 10⁻⁴, Wilcoxon signed rank test; Fig. 2B, right).

To test whether the increase in conductance was voltage dependent, the same motoneurons were recorded in VC mode. The V_m was switched between −60 and −70 mV at 10 Hz (Fig. 2C). Episodes of I_m were aligned (Fig. 2D, light yellow) and averaged (Fig. 2D, dark yellow). In all motoneurons tested, the conductance during scratching (72.5 ± 41.3 nS, n = 14) was higher than the conductance at rest (55.9 ± 31.5 nS, n = 14, p = 1.2 × 10⁻⁴, Wilcoxon signed rank test; Fig. 2D, right). However, the conductance increase (Δg) in CC mode (33.5 ± 19.1 nS, n = 14) was higher than in VC mode (16.6 ± 12.3 nS, n = 14, p = 1.2 × 10⁻⁴, Wilcoxon signed rank test; Fig. 2G). These experiments demonstrated that the conductance increase during scratching was reduced when V_m of motoneurons was maintained at a hyperpolarized level and that the additional conductance increase depended on depolarization of V_m. This was substantiated by the finding that the conductance increase during scratching in CC recordings was reduced by a steady hyperpolarizing current that shifted the resting membrane potential from −50 mV (Fig. 2A) to −60 mV (Fig. 2E). With a hyperpolarizing holding current, motoneuron conductance during scratching (89.4 ± 66.2 nS, n = 7) was higher than the conductance at rest (68.5 ± 47.7, n = 7, p = 0.016, Wilcoxon signed rank test; right of Fig. 2F, right). However, the conductance increase (Δg) during scratching was substantially lower with hyperpolarizing holding current (20.9 ± 21.8 nS, n = 7) than without a holding current (35 ± 26.4 nS, n = 7, p = 0.016, Wilcoxon signed rank test; Fig. 2H).

Voltage-dependent conductance is present during depolarization

The finding that part of the conductance increase during scratching was related to depolarization prompted further experimental analysis. A continuous measure of conductance was adopted to relate conductance change to the scratch cycle. V_m of motoneurons was recorded during successive scratch episodes at different levels of steady polarizing holding currents (Fig. 3A). To reduce the influence of trial-to-trial variability on conductance estimates, the recordings were normalized to the HF nerve activity cycle (Fig. 3B). Motoneuron conductance shown at the top in Figure 3B was calculated either from the three most depolarized V_m levels (Fig. 3B, left) or from the three most hyperpolarized V_m levels (Fig. 3B, right). It is evident that conductance is higher during the HF ON phase with depolarizing holding currents (210.9 ± 133.1 nS, n = 9) than with hyperpolarizing holding currents (135.5 ± 78.2 nS, n = 9, p = 0.004, Wilcoxon signed rank test; Fig. 3D). In contrast, conductance at rest (Fig. 3C) and conductance during the HF OFF phase (Fig. 3E) was similar when calculated from recordings obtained with a hyperpolarizing or a depolarizing holding current. This finding demonstrates that the voltage-sensitive conductance is present during the depolarizing wave of the scratch cycle.

To find out whether the voltage-sensitive conductance during scratching is related to the synaptic input or to intrinsic properties of motoneurons, we simulated scratch-like voltage trajectories by injecting current with a sinusoidal waveform into motoneurons at different levels of steady holding currents (Fig. 4A). Conductance was calculated in the subthreshold range (Fig. 4A, gray) and when the motoneuron generated APs during the depolarizing waves (Fig. 4A, black). No detectable change in conductance was observed at rest (Fig. 4B) or during the hyperpolarizing phase (Fig. 4D) with different levels of holding currents. However, a clear conductance increase was observed during the depolarizing phase when motoneurons generated APs (Fig. 4C). The conductance in the subthreshold range during depolarizing waves (91.5 ± 55.7 nS, n = 11) increased about three times (273.2 ± 148.3 nS, n = 11, p = 9.8 × 10⁻⁴, Wilcoxon signed rank test) in the suprathreshold voltage range. These experiments show that a depolarizing wave, traversing the same voltage range in the cell body as during scratching, recruits a substantial conductance even in the absence of increased synaptic activity.

Outward rectification in spinal motoneurons

To characterize the nature of the intrinsic conductance increase recruited during scratching, we investigated the rectifying properties in the voltage range near threshold for APs. First, current pulses of different amplitude were injected into motoneurons in the ex vivo preparation (Fig. 5A). The I/V relationship was established from the mean of V_m at the end of each injected current pulse. Two fairly linear ranges of I/V were obtained (Fig. 5B). The slope of the I/V curve in the suprathreshold range (Fig. 5B, black circles) was much steeper than the slope in the subthreshold range (Fig. 5B, gray circles). Consequently, the conductance of motoneurons in the subthreshold range (41.7 ± 16.9 nS, n = 22) was much smaller than the conductance in the suprathreshold range (266 ± 188 nS, n = 22, p = 4.8 × 10⁻⁷, Wilcoxon signed rank test; Fig. 5C).

The conductance responsible for the outward rectification near threshold for APs was pursued in motoneurons in thin slices from the spinal cord. Likely contributors are conductances activated by APs. This was tested from I/V curves obtained before and after block of sodium channels by application of TTX (2 μm). TTX application removes APs during depolarizing current pulses and linearizes the I/V relationship. The conductance increase in the suprathreshold range (237.4 ± 149.5 nS, n = 7) was reduced (110.5 ± 73.9 nS, n = 7, p = 0.03, Wilcoxon signed rank test) when APs were blocked. However, a conductance increase remained at depolarized V_m levels after eliminating APs. This shows that additional non-AP-related conductances contribute to the rectifying conductance increase.

Outward rectification in the suprathreshold voltage range, independent of APs, was also supported by VC experiments. Motoneurons in the ex vivo preparation were slowly depolarized from −70 to −10 mV (Fig. 5D) to inactivate sodium channels and avoid APs. The I/V plot obtained from VC ramps (Fig. 5E) shows that outward rectification is present even when APs are not generated. The conductance at hyperpolarized V_m levels was much smaller (49.2 ± 13.4 nS, n = 20) than the conductance at depolarized V_m levels (313.7 ± 158.1 nS, n = 20, p = 1.9 × 10⁻⁶, Wilcoxon signed rank test; Fig. 5F).

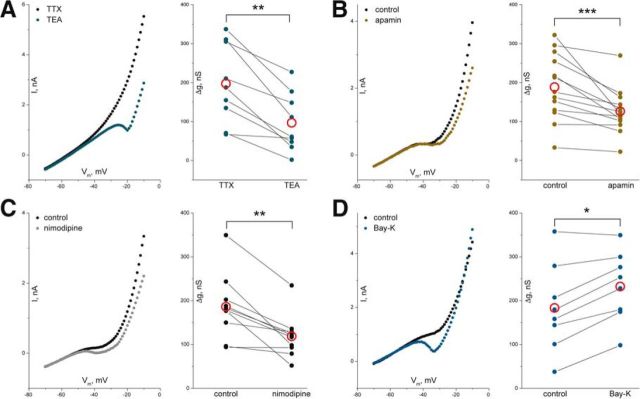
Potassium conductances contributing to outward rectification

Slow ramps in VC mode were used in motoneurons in thin spinal cord slices to identify conductances contributing to outward rectification during depolarization. The role of K_V channels was investigated by application of the antagonist TEA. To avoid spiking and increase in transmitter release, the experiments were performed in the presence of TTX. The slope of the I/V curve at depolarized levels and outward rectification was reduced by TEA (1 mm; Fig. 6A).

Figure 6.

Potassium conductances contribute to outward rectification A, I/V curves from motoneurons were obtained in spinal cord slices during slowly depolarizing VC ramps. Application of TEA, a blocker of K_V channels, does not change the I/V slope at hyperpolarized levels but reduces the slope at depolarized levels (left). Rectification, i.e., the conductance increase at depolarized levels, is smaller after blocking K_V channels (right; n = 9, p = 0.004, Wilcoxon signed rank test). B, C, Rectification was also reduced after blocking K_Ca (SK) channels with apamin (B; n = 13, p = 2.4 × 10⁻⁴, Wilcoxon signed rank test) and after blocking L-type Ca channels with nimodipine (C; n = 10, p = 0.002, Wilcoxon signed rank test). D, Facilitation of L-type Ca channels with Bay-K8644 increased rectification (n = 8, p = 0.016, Wilcoxon signed rank test). Red open circles represent mean.

An additional fraction of the outward rectification was mediated by SK potassium channels. Application of the specific SK channel blocker apamin (100 nm) significantly reduced outward rectification (Fig. 6B). A similar reduction in outward rectification was observed by application of nimodipine (20 μm), an antagonist of L-type Ca channels (Fig. 6C). This could imply that SK channels are activated by intracellular Ca²⁺ accumulation attributable to activation of L-type Ca channels during depolarization. The increased rectification induced by the agonist of L-type Ca channels, Bay-K8644 (2 μm), supports this possibility (Fig. 6D).

To summarize, our findings suggest that K_V and SK channels contribute to voltage-dependent outward rectification in motoneurons. In addition, we demonstrated that SK channels are activated by Ca²⁺ influx though L-type Ca channels.

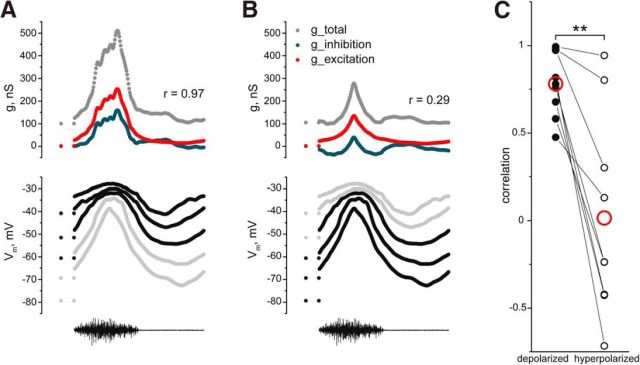
Inhibition and excitation calculated from total conductance depends on V_m

So far, we demonstrated that high-conductance states in motoneurons have a voltage-dependent intrinsic component. Although often ignored (Anderson et al., 2000; Mariño et al., 2005; Priebe and Ferster, 2005; Berg et al., 2007), intrinsic conductance can lead to overestimation of the level of concurrent synaptic inhibition and excitation (Guillamon et al., 2006). Here we explore how this aspect may influence the validity of estimates of the ratio between inhibitory and excitatory synaptic conductance from CC recordings in motoneurons during scratch episodes. As in Figure 3, total conductance was obtained from scratch episodes recorded either at depolarizing holding currents (Fig. 7A) or hyperpolarizing holding currents (Fig. 7B). Assuming no change in intrinsic conductance, we calculated inhibitory and excitatory conductances from the total conductance. High correlation (0.78 ± 0.18, n = 9) between inhibition and excitation was found when conductance was measured at depolarized V_m levels. However, the correlation decreased significantly to 0.01 ± 0.57 (n = 9, p = 0.004, Wilcoxon signed rank test) when inhibition and excitation were extracted from episodes recorded with hyperpolarizing holding currents (Fig. 7C).

Figure 7.

Correlation of estimated synaptic conductance for inhibition and excitation depends on the holding current A, Low-pass filtered V_m during successive scratch episodes recorded in CC mode at five levels of the holding current (data from Fig. 3). Synaptic conductance for inhibition (blue, top) and excitation (red, top) estimated from the total conductance (gray, top) were obtained from the three most depolarized V_m traces assuming constant leak conductance. B, Synaptic conductance for inhibition (blue) and excitation (red) were estimated from total conductance (gray) obtained from the three most hyperpolarized V_m traces assuming constant leak conductance. In A and B, from the top: total conductance (gray) and excitatory (red) and inhibitory (blue) conductance; V_m of motoneuron at different holding current injections (black traces were used for conductance estimation, and gray traces were omitted); HF nerve activity. C, The correlation between the estimated synaptic excitatory and inhibitory conductance is significantly reduced by the hyperpolarizing holding current (n = 9, p = 0.004, Wilcoxon signed rank test). Red open circles represent mean.

Synaptic currents in spinal motoneurons during rhythmic motor network activity

Rather than extracting the pattern of synaptic inhibition and excitation indirectly from conductance measurements, whole-cell patch-clamp permits inhibitory and excitatory synaptic currents to be recorded directly. First, spinal motoneurons were recorded in CC mode to obtain the V_m pattern during scratching (Fig. 8A). HF nerve activity and V_m of motoneurons were low-pass filtered (Fig. 8A, black traces), and the correlation between the two filtered signals was calculated. To obtain recordings from a homogeneous pool of motoneurons, we only considered motoneurons with high correlation (r > 0.8) between V_m and HF nerve activity (Fig. 8D; r = 0.9 ± 0.04, n = 20).

Next, motoneurons were recorded in VC mode at −65 mV (Fig. 8B) and at 0 mV (Fig. 8C) during successive scratch episodes. Inward current recorded at −65 mV was inverted and taken to be the excitatory synaptic input transmitted to the cell body. Likewise, the outward current recorded at 0 mV was taken to be the inhibitory synaptic current transmitted to the cell body. Again, the correlation between inhibitory or excitatory synaptic currents and the HF nerve signal was obtained from the low-pass filtered records. Inward currents recorded at −65 mV were positively correlated with HF nerve activity (Fig. 8E; r = 0.89 ± 0.08, n = 20). Outward currents recorded at 0 mV were negatively correlated with HF nerve activity (Fig. 8F; r = −0.59 ± 0.27, n = 20).

These experiments show that HF motoneurons, i.e., motoneurons in which V_m is highly correlated with HF motor nerve activity, receive in-phase excitatory synaptic input and out-of-phase inhibitory synaptic input during scratching. Note, however, that both excitatory and inhibitory synaptic activity is continuously present throughout the scratch cycle (see noise in raw traces in Fig. 8B,C).

Alternating inhibitory and excitatory inputs in HF motoneurons

To link the pattern of inhibition and excitation to the scratch cycle, we normalized all intracellular recordings to the HF nerve activity (Fig. 9A). As expected, we found that the excitatory synaptic input (red traces, inverted) correlates well with V_m (gray traces), whereas the inhibitory synaptic input (blue traces) peaks out of phase with V_m and excitation (Fig. 9A). In addition, inhibitory and excitatory currents are negatively correlated (r = −0.59 ± 0.32, n = 20; Fig. 9B). The relationship between V_m (black), excitation (red), and inhibition (blue) during the scratch cycle is summarized in the circular plot in Figure 9C.

The balanced model proposed previously (Berg et al., 2007) implies that V_m of motoneuron is tightly correlated with the conductance change (Fig. 10A). In contrast, the reciprocal model suggests that synaptic conductance is not well correlated with V_m but rather depends on the relative intensity of inhibition and excitation. Here we calculated conductance increase in motoneurons from VC recordings at −65 mV and at 0 mV during successive scratch episodes. This conductance is taken to represent the intensity of synaptic input during scratching. In our experiments, synaptic conductance in HF motoneurons peaks twice during the scratch cycle, i.e., in phase and out of phase with V_m depolarization (Fig. 10B). In addition, the correlation between conductance and V_m varies from negative to positive in different HF motoneurons (0 ± 0.52, n = 20; Fig. 10C). This finding supports reciprocal rather than balanced synaptic inhibition and excitation in motoneurons during scratching.

Figure 10.

Synaptic intensity does not correlate with V_m. A, The synaptic conductance during V_m oscillations predicted by the balanced and the reciprocal inhibition and excitation models. B, Synaptic conductance calculated from VC recordings peaks twice during the scratch cycle (n = 20; light color traces depict records of each motoneuron, and dark color lines depict mean). From the top: synaptic conductance calculated from VC recordings at −65 mV and at 0 mV; V_m of motoneuron; HF nerve activity. C, Correlation between synaptic conductance and V_m varies from positive to negative.

Discussion

The high-conductance state in motoneurons in an ex vivo carapace–spinal cord preparation from the turtle was investigated with whole-cell recordings. We show that voltage-dependent outward rectification detected in somatic recordings contributes to the high-conductance state during scratch network activity. In thin spinal cord slices, TEA-sensitive, voltage-activated K⁺ conductance and apamin-sensitive, Ca²⁺-dependent K⁺ conductance contribute significantly to the depolarization-induced outward rectification. During functional network activity, the outward rectification opposes depolarization beyond the threshold for APs and may serve to balance excitatory synaptic currents near threshold for APs. In doing so, the intrinsic, high-conductance state curtails regular repetitive spiking and promotes irregular firing of APs activated by synaptic transients. In addition, by performing whole-cell voltage clamp, we found that inhibition and excitation peaks out of phase in spinal motoneurons during scratching.

The high-conductance state in motoneurons during motor network activity is readily observed in CC recordings with high-resistance sharp electrodes (Alaburda et al., 2005; Berg et al., 2007; Guzulaitis et al., 2016). As in other neurons (Anderson et al., 2000, 2001; Mariño et al., 2005; Priebe and Ferster, 2005), arguments for the proposal that the conductance increase is caused exclusively by synaptic activity are indirect and assume unchanged intrinsic conductance (Berg et al., 2007; Petersen et al., 2014). With the improved voltage control and current passing capabilities provided by whole-cell recording, the origin of conductance changes during network activity can be analyzed more directly (Borg-Graham et al., 1998; Monier et al., 2008). As observed in cortical neurons (Waters and Helmchen, 2006; Monier et al., 2008), we find a dramatic increase in motoneuron input conductance in a suprathreshold range of V_m both in thin slices and during network activity ex vivo. In current clamp, this conductance increase is a potential for error in synaptic conductance estimates. Theoretically, spike-related conductance increase leads to overestimation of the balance between inhibition and excitation (Guillamon et al., 2006). This is confirmed experimentally in the present study, i.e., the estimated correlation between inhibitory and excitatory synaptic conductance during the scratch cycle shifted from in-phase to out-of-phase by application of a hyperpolarizing holding current (Fig. 7). Interestingly, estimates of inhibition and excitation with this method showed out-of-phase synaptic input to motoneurons during locomotor-like network activity in neonatal rodents (Endo and Kiehn, 2008). This is probably because less depolarized drive potentials, as indicated by the paucity of spiking, do not reach the activation level for outward rectification.

Previous work on cat spinal motoneurons demonstrated that APs and repetitive firing is accompanied by increased input conductance (Schwindt and Calvin, 1973). Part of this increase was subsequently shown to include two spike-independent intrinsic components activated by depolarization, i.e., a voltage-gated persistent inward current balanced by outward rectification (Schwindt and Crill, 1977; Li and Bennett, 2007). As we confirm here, part of the outward rectification is Ca²⁺ dependent (Li and Bennett, 2007). Therefore, the high-conductance state during network activity may be further deepened by enhanced SK conductance by direct Ca²⁺ entry and facilitation of L-type Ca channels (Alaburda and Hounsgaard, 2003). We suggest that outward rectification stabilizes membrane potential of spinal motoneurons near threshold for APs by balancing intrinsic inward currents and excitatory synaptic input.

Direct recordings of synaptic current during scratching have shown that excitation is highly correlated with hip flexor nerve activity, whereas inhibition is negatively correlated with synaptic excitation and nerve activity. This demonstrates out-of-phase rather than balanced activation of motoneurons. The half-center model and reciprocal inhibition between half-centers was inferred a century ago (Brown, 1914), but direct recordings of out-of-phase inhibition and excitation during behavior were obtained only in small-scale spinal networks (Russell and Wallen, 1983; Dale, 1985; Gabriel et al., 2009; Kishore et al., 2014). Recordings from motoneurons embedded in a larger-scale network reveal either rhythmical inhibitory or rhythmical excitatory inputs in different motoneurons (Hochman and Schmidt, 1998). In the present study, we show that the same motoneurons receive both rhythmical excitatory and rhythmical inhibitory synaptic input during scratching and that synaptic excitation and synaptic inhibition peak out-of-phase.

Regular firing in spinal motoneurons is quenched during network activity (Berg et al., 2008; Guzulaitis et al., 2016). Several factors may contribute to irregular firing. First, the long-lasting spike AHP, essential for regular firing in motoneurons (Hounsgaard, 2017), is attenuated during network activity (Brownstone et al., 1992; Berg et al., 2008). Second, intense synaptic bombardment increases fluctuations in membrane potential (Calvin and Stevens, 1967; Alaburda et al., 2005; Guzulaitis et al., 2016). Finally, we find that inhibitory synaptic input is present throughout the scratch cycle (noise in raw recording in Fig. 8C) with considerable overlap between inhibition and excitation (Fig. 9C). Therefore, residual inhibitory input may increase synaptic fluctuations in membrane potential and irregular firing during scratching.