Cofilin drives rapid turnover and fluidization of entangled F-actin

Significance

When an animal cell moves or divides, a disordered network of actin filaments (F-actin) builds mechanical scaffolds to drive cell-shape changes. Actin filaments are undergoing continual cycles of assembly and disassembly, known as turnover, but it is unknown how these dynamics impact the mechanical properties of actin-filament-based networks. Here, we show that actin-filament turnover dynamics contribute to mechanical stress relaxation. Additionally, we identify the factors necessary to generate a nonequilibrium steady state of dynamic actin filaments that provides a picture of their regulation in vivo.

Abstract

The shape of most animal cells is controlled by the actin cortex, a thin network of dynamic actin filaments (F-actin) situated just beneath the plasma membrane. The cortex is held far from equilibrium by both active stresses and polymer turnover: Molecular motors drive deformations required for cell morphogenesis, while actin-filament disassembly dynamics relax stress and facilitate cortical remodeling. While many aspects of actin-cortex mechanics are well characterized, a mechanistic understanding of how nonequilibrium actin turnover contributes to stress relaxation is still lacking. To address this, we developed a reconstituted in vitro system of entangled F-actin, wherein the steady-state length and turnover rate of F-actin are controlled by the actin regulatory proteins cofilin, profilin, and formin, which sever, recycle, and assemble filaments, respectively. Cofilin-mediated severing accelerates the turnover and spatial reorganization of F-actin, without significant changes to filament length. We demonstrate that cofilin-mediated severing is a single-timescale mode of stress relaxation that tunes the low-frequency viscosity over two orders of magnitude. These findings serve as the foundation for understanding the mechanics of more physiological F-actin networks with turnover and inform an updated microscopic model of single-filament turnover. They also demonstrate that polymer activity, in the form of ATP hydrolysis on F-actin coupled to nucleotide-dependent cofilin binding, is sufficient to generate a form of active matter wherein asymmetric filament disassembly preserves filament number despite sustained severing.

The capacity of the cytoskeletal protein actin to dynamically assemble into short-lived, semiflexible filaments (F-actin) underlies its fundamental role in cell motility, morphogenesis, division, and mechanics (1). More than 100 actin-binding proteins control the formation and differential regulation of F-actin networks, yielding architectures and turnover rates tuned for specific cellular processes (2). Accordingly, the actin cortex, a thin F-actin meshwork anchored just beneath the plasma membrane, is thought to be the primary determinant of cell shape and mechanics (3, 4). In vivo measurements place cortical actin turnover on the 10- to 100-s timescale (5, 6), and while turnover is known to modulate cortical tension and flows (7), a mechanistic understanding of how turnover regulates cortical mechanics is currently lacking.

Rheological measurements of F-actin networks reconstituted with purified proteins provide significant insight into the mechanics of living cells by enabling architectural and compositional control and are sufficient to capture aspects of cellular mechanical response (8). Guided by decades of reconstitution experiments, a quantitative theoretical understanding has emerged for how static microscopic parameters like actin-filament density, length, and stiffness contribute to the viscoelastic mechanics of entangled F-actin solutions and cross-linked F-actin networks (9–11). Suppression of filament bending fluctuations by entanglements or cross-links transiently stores stress energy, giving rise to elasticity on the timescale of seconds. Diffusive, snake-like reptation of filaments (in entangled solutions) or cross-link unbinding (in networks) sets the timescale for stress relaxation, t_relax. While the response of networks on timescales longer than t_relax is complicated by a broad spectrum of timescales related to the unbinding of multiple cross-links, relaxation is expected to be nearly Maxwellian in entangled solutions, with response dominated by a simple viscosity (9, 12). However, the contribution of dynamic F-actin turnover to stress relaxation remains largely unknown.

F-actin turnover requires sequential disassembly, nucleotide exchange, and assembly and is limited in vitro primarily by slow disassembly kinetics (13, 14). However, all of these reactions are tightly regulated in vivo, with the actin-binding proteins cofilin and profilin playing particularly important roles (15, 16). Cofilin binds cooperatively and preferentially to ADP–F-actin (17–19), allosterically accelerates release of inorganic phosphate (P_i) (18–20), and severs filaments at boundaries between clusters of cofilin-bound and -unbound subunits (20–23). Profilin, in turn, competes with cofilin for binding to ADP-bound monomers (24), catalyzes exchange of ADP for ATP (25), blocks assembly at pointed ends (26, 27), and promotes the rapid elongation of barbed ends by formin proteins (28), which are responsible for generating the long cortical filaments important for mechanics in living cells (29). Additionally, interplay between the mechanical and the biochemical couplings of the cortex to the bulk cytoplasm constrain cortex structure and stability in vivo (30, 31).

Here, we use purified cofilin, profilin, and formin to reconstitute rapid F-actin turnover at steady state. We then combine filament-level measurements of length and turnover rate with fluorescence recovery after photobleaching (FRAP) and microrheology to systematically study the impact of nonequilibrium turnover on the dynamics and mechanics of entangled actin-filament solutions in vitro. The choice of entangled solutions, which are structurally and biochemically isotropic, enables a quantitative assessment of stress-relaxation mechanisms. Our work lays the foundation for elucidating the influence of F-actin turnover on the mechanics of more physiological network architectures.

Results

Independent Control of F-Actin Length and Turnover at Steady State in Vitro.

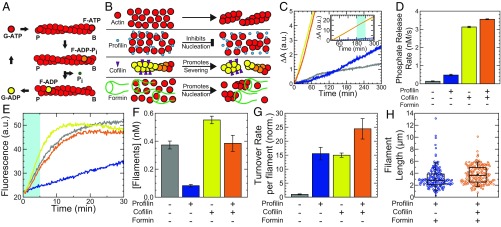
Nucleotide hydrolysis is intimately coupled to actin polymer dynamics (2), as shown in Fig. 1A. Upon incorporation into filaments, ATP-bound globular actin (ATP–G-actin) monomers undergo a conformational change, becoming ATP–F-actin. ATP is rapidly and stochastically hydrolyzed on the filament, converting ATP–F-actin to ADP–P_i–F-actin (orange). The P_i is subsequently released on a much slower timescale (∼300 s), resulting in ADP–F-actin (yellow). ADP–F-actin converts to ADP–G-actin upon dissociation from the filament, and the cycle is completed by exchange of the bound ADP nucleotide with free ATP in solution. Importantly, it is the effective irreversibility of the ATP-hydrolysis step that confers nonequilibrium dynamics to this set of coupled reactions, generating a directed turnover cycle with a steady-state flux of monomers. Monitoring the production of P_i in solution with a coupled-enzyme reaction gives a direct measure of bulk turnover (32).

Fig. 1.

Independent control of F-actin length and turnover at steady state in vitro. (A) Schematic of the actin-turnover cycle. B and P denote filament barbed and pointed ends, respectively. (B) Schematic of important biochemical activities of actin, profilin, cofilin, and formin. (C) Time course of P_i production for 1.5 µM Mg–ATP–actin alone (gray), with 4.5 µM profilin (R_p = 3; blue), with 0.75 µM cofilin (R_c = 0.5; yellow), or with 4.5 µM profilin and 0.75 µM cofilin (orange), all in the presence of 0.2 mM 2-amino-6-mercapto-7-methylpurine ribonucleoside and 1 U/mL purine nucleoside phosphorylase. (C, Inset) Extended vertical axis showing the linear increase in all samples at long times. (D) Bulk P_i-release rate from linear fits to the P_i-release time course 3–4 h after polymerization is initiated, as indicated by portion shaded in light blue (C, Inset). Error bars indicate SEM; n = 4 for the profilin + cofilin condition, and n = 2 for each of the others. (E) Typical time courses of seeded assembly reactions in which 0.25 µM Mg–ATP–actin monomers (10% pyrene-labeled) are added to 0.5-µM unlabeled actin seeds formed in the absence of additional proteins (gray), with 1.5 µM profilin (R_p = 3; blue), with 0.25 µM cofilin (R_c = 0.5; yellow), or with 1.5 µM profilin and 0.25 µM cofilin (orange). (F) Steady-state filament concentrations calculated using linear fits to the seeded assembly time courses during the time window shaded in light blue in E. Error bars indicate SEM; n = 6, 6, 5, and 6 per condition, from left to right. (G) Single-filament turnover rates calculated from the data in D and F and rescaled by actin concentration for actin alone, with R_p = 3, with R_c = 0.5, or with R_p = 3 and R_c = 0.5. Data are normalized (norm.) by the single-filament turnover rate for actin alone (gray). Error bars denote propagation of error from the mean filament concentration and mean bulk phosphate release-rate measurement for each condition. (H) Length distribution of Alexa 488–phalloidin-labeled filaments from source solutions containing 11.9 µM actin, R_p = 3, R_f = 0.01, and either no cofilin (R_c = 0; blue) or 6.95 µM cofilin (R_c = 0.5; orange). Each length distribution is composed of 100 filaments from each of two independent samples, for a total of 200 filaments per condition. a.u., arbitrary units.

F-actin turnover is regulated in part by the actin binding proteins profilin and cofilin (Fig. 1B) (18, 19, 33). We measured turnover (P_i production; Fig. 1C) in solutions assembled from 1.5 µM Mg–ATP–actin alone (gray trace), or copolymerized with either 4.5 µM profilin (mole ratio profilin:actin = R_p = 3; blue), 0.75 µM cofilin (R_c = 0.5; yellow), or 4.5 µM profilin and 0.75 µM cofilin (R_p = 3 and R_c = 0.5; orange). All traces are initially nonlinear as actin is assembled, but become linear once steady state is reached (Fig. 1C and SI Appendix, Fig. S1). Measurements of steady-state P_i production indicate that a molar excess of profilin:actin (R_p = 3) is sufficient to increase the bulk turnover rate approximately threefold over actin alone (Fig. 1D). Optimal concentrations of cofilin (R_c = 0.5) accelerate bulk turnover ∼20-fold, consistent with previous work (18). The combined effects of profilin and cofilin increase bulk turnover ∼23-fold (red), qualitatively consistent with previous results (33).

To extract how profilin and cofilin affect the turnover rate of individual filaments, we first determined the number of filaments. Unlabeled actin was assembled to steady state in the presence of regulatory proteins. Fluorescent pyrene–actin was then added, and the initial rate of the fluorescence increase was proportional to the number of elongating filaments present (Fig. 1 E and F and SI Appendix, section I.g.ii) (34).

Consistent with its role in inhibiting spontaneous nucleation (15), profilin (R_p = 3) reduces the filament concentration at steady state approximately fivefold (Fig. 1 B, E, and F). By contrast, cofilin (R_c = 0.5) increases the filament concentration ∼50%, qualitatively consistent with its severing activity (21) (Fig. 1 B, E, and F). In the presence of both profilin and cofilin, the filament concentration is comparable to that for actin alone. By dividing the bulk phosphate release rate by the filament density, we obtained the turnover rate for individual filaments (Fig. 1G). Relative to actin alone, we found that profilin and cofilin are each sufficient to increase the turnover rate of actin ∼15-fold. In the presence of both profilin and cofilin, turnover increases ∼24-fold, qualitatively consistent with previous results (33).

Filament length is controlled by varying the filament nucleation rate through changes in the concentration of the formin mDia1, which nucleates and processively elongates actin filaments (35–37) (Fig. 1B). Fluorescence imaging revealed that, for fixed concentrations of actin and profilin, the mean filament length at steady state can be varied from 21 to 3 µm by increasing the formin concentration from 0 to ∼1 µM (SI Appendix, Fig. S2). Remarkably, the presence of the severing protein cofilin had little effect on the steady-state length distribution in the presence of profilin and formin (Fig. 1H). Indeed, 11.9 µM Mg–ATP–actin polymerized to steady state in the presence of profilin (R_p = 3; 35.7 µM) and formin (R_f = 0.01; 119 nM) had very similar length distributions in the absence or presence of cofilin, with mean values of 3.1 and 3.7 µm, respectively (Fig. 1H). This is reminiscent of the constant time-averaged length of formin-associated filaments amid cofilin severing reported during assembly (38, 39), but now at steady state. In this work, we use the term steady state to describe the temporal invariance of the system on the 10 s of minutes timescale with respect to monomer–polymer ratio (SI Appendix, Fig. S1), turnover (Fig. 1C), and mechanics. It is possible that the filament length distribution is still evolving on much longer timescales (40). Together, these data demonstrate that nucleation during assembly sets the steady-state F-actin length distribution nearly independent of cofilin-mediated severing and increased filament turnover dynamics.

Cofilin Enhances Reaction-Limited Reorganization Dynamics in Entangled Actin Solutions.

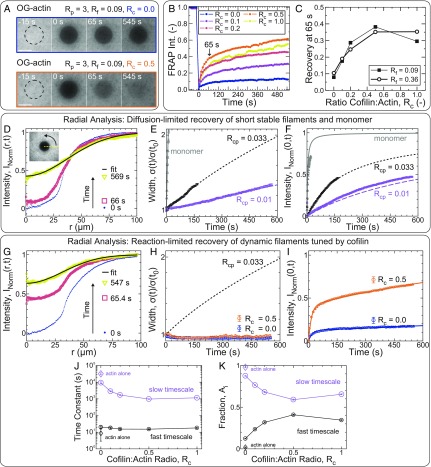
To explore the consequences of severing and turnover on the dynamic redistribution of F-actin, we performed FRAP measurements on entangled solutions of 11.9 µM actin (5% Oregon Green-labeled) assembled with a constant molar excess of profilin (R_p = 3) and a range of cofilin and formin concentrations. Before photobleaching, the fluorescence signal was nearly spatially uniform (Fig. 2A). The postbleach recovery of actin fluorescence we observed across a range of cofilin concentrations is qualitatively described by two phases: a relatively rapid recovery in the first ∼60 s and a slower recovery thereafter (Fig. 2B). The degree of fast actin recovery was sensitively tuned by cofilin (Fig. 2C), with a maximal increase of approximately fivefold. In the absence of cofilin, the average fluorescence intensity of the bleached region recovered to ∼8% of the prebleach value within ∼1 min, whereas the recovery was 40% at optimal cofilin concentration (Fig. 2 A and B, red). A similar trend was observed at two different formin concentrations, suggesting that the fluorescence recovery is insensitive to changes in filament length in the regime probed.

Fig. 2.

Cofilin enhances reaction-limited reorganization dynamics in entangled actin solutions. (A–K) Unless otherwise indicated, all samples are polymerized from 11.9 µM Mg–ATP–actin [5% Oregon Green (OG)-labeled]. (A) Confocal fluorescence time-lapse micrographs for samples with R_p = 3, R_f = 0.09, and R_c = 0 (Upper) or R_c = 0.5 (Lower) at steady state. Dashed black circles denote the region exposed to the bleaching laser. Time is relative to the end of the 4-s bleach. (Scale bars: 50 µm.) (B and C) FRAP analysis of the bleached region for samples with variable cofilin and formin concentrations (all with R_p = 3). (B) Time course of the normalized fluorescence intensity (Int.) averaged across the bleached region for entangled solutions with R_c as indicated in the key and R_f = 0.09. (C) Actin fluorescence intensity recovered within 65 s of bleaching (denoted by arrow in B) as a function of cofilin concentration with either R_p = 0.09 (filled squares) or R_p = 0.36 (open circles). Each point represents a single experiment. (D–K) Radial FRAP analysis of actin assembled in the presence of either capping protein (D–F: R_cp = 0.01 or 0.033; R_p = R_c = R_f = 0) or profilin, formin, and variable cofilin (G–K: R_p = 3; R_f = 0.09; R_c as indicated; R_cp = 0). Gray lines (E and F) and open triangles (E and F) refer to 0.52 µM unassembled Ca–ATP actin monomer (53% Oregon Green-labeled) in G buffer in the absence of regulatory proteins. (D and G) Normalized, azimuthally averaged fluorescence intensity profiles at different times postbleach assembled in the presence of capping protein (D: R_cp = 0.01; R_p = R_c = R_f = 0) or cofilin (G: R_cp = 0; R_p = 3; R_c = 0.5; R_f = 0.09). Solid black line is a Gaussian fit to the last profile. D, Inset depicts the azimuthal averaging process. Time evolution of the normalized profile widths and postbleach intensities at the center of the bleached regions, as extracted from the Gaussian fits, are plotted in E and H, and F and I, respectively. (E, F, H, and I) Symbols are parameters obtained from Gaussian fits to radial profiles [squares: R_p = R_c = R_f = 0 with R_cp = 0.01 (lavender) or 0.033 (black); circles: R_cp = 0, R_p = 3, R_f = 0.09, with R_c = 0 (orange) or 0.5 (blue); triangles (gray): monomer with R_p = R_c = R_f = R_cp = 0]. (E, F, and H) Lines are the width (E and H) or central intensity (F) trajectories expected for dilute, monodisperse solutions of diffusing particles. The solid gray line (E and F) is a fit-free prediction for monomer-sized spheres, while the short-dashed black and long-dashed lavender lines are fits to the width time course for samples with R_cp = 0.033 and 0.01, respectively (E). Lines in F are predictions (not fits) for either monodisperse solutions of monomers (gray) or cylinders (black and lavender) with the effective lengths obtained from E. (I) Solid lines are double-exponential fits to the central intensity recovery trajectories of samples with cofilin. Time constants (J) and amplitude fractions (K) obtained from double-exponential fits like those in I are plotted as a function of R_c. Large lavender and small black symbols denote the fit parameters associated with the slow and fast timescales, respectively. (J and K) Solid lines are a guide to the eye. Disconnected diamonds are parameters obtained from a double-exponential fit for an actin-only sample (R_c = R_p = R_f = R_cp = 0).

We considered two plausible physical explanations for the observed cofilin-dependent fluorescence recovery. In the first scenario, the dominant source of recovery is through the lateral diffusion of short and relatively stable filaments. We reason that if cofilin significantly reduces the typical steady-state filament length in our system, this would result in a similar decrease in the characteristic diffusion timescale, yielding faster recovery. In the second scenario, recovery relies on rapid diffusion of monomers and/or oligomers, whose concentration is limited by the kinetics of filament disassembly, that rapidly assemble onto existing filaments within the bleached region. Recovery is reaction-limited in this case and would be enhanced by cofilin-dependent increases in the rates of reactions related to actin turnover. Analysis of the spatiotemporal evolution of radial intensity profiles has previously enabled the contribution of diffusion- and reaction-limited recovery mechanisms to be distinguished in cells (41, 42). Crucially, diffusion-limited recovery requires broadening of the intensity profile, whereas the profile width remains constant for reaction-limited recovery by spatially homogeneous reactions (42).

To develop intuition for the spatiotemporal signatures of filament diffusion in our entangled solutions, we first performed FRAP measurements on two model systems for which we expected the recovery to be purely diffusion-limited (Fig. 2 D–F): (i) short, relatively stable filaments assembled in the presence of capping protein, and (ii) unassembled actin monomer. Photobleaching of these samples yielded images similar to those in Fig. 2A, from which we calculated radial intensity profiles by azimuthally averaging intensities about the bleach center (Fig. 2 D, Inset and SI Appendix, section I.e.iii). We observed both fluorescence recovery at the bleach center as well as significant profile broadening for each of our model-diffusive systems (Fig. 2D and SI Appendix, Fig. S3A), qualitatively consistent with diffusion-limited recovery. We characterized this time-dependent profile broadening (Fig. 2E) and intensity recovery (Fig. 2F) quantitatively by fitting the radial profiles at each time-point to Gaussians, though we note that our conclusions are robust to the exact method of analysis (SI Appendix, Figs. S3 and S4, Tables S1–S3, and section I.e.iii). For unassembled actin monomers, we found excellent agreement between the diffusive timescale we measured experimentally from the evolution of the profile width (3.49 ± 0.13 s; gray triangles in Fig. 2E and SI Appendix, Fig. S5A) and a fit-free width evolution prediction for monomer-sized spheres in dilute solution (3.3 s; gray line in Fig. 2E and SI Appendix, section I.e.iii), which validates our analysis methodology. Conversely, fitting the experimental width evolution from samples assembled in the presence of different capping protein concentrations enabled us to extract characteristic diffusion times for each concentration (Fig. 2E, solid magenta and lavender lines), from which we can estimate effective filament lengths (SI Appendix, Table S4 and section I.e.iii). By using the characteristic diffusion times from Fig. 2E, the recovery of fluorescence intensity at the bleach center predicted by single-species diffusion-limited recovery models was furthermore in reasonable quantitative agreement with that measured experimentally (Fig. 2F and SI Appendix, section I.e.iii). Taken together, these data demonstrate that the evolution of the radial intensity profile width quantitatively captures in vitro actin fluorescence recovery kinetics in diffusion-limited samples.

To determine the contribution of lateral filament diffusion to the cofilin-dependent enhancement in the fluorescence recovery of entangled samples, we next performed the same radial analysis on the entangled samples assembled in the presence of profilin, formin, and a range of cofilin concentrations (Fig. 2 G–I). In contrast to the diffusion-limited samples, here, we saw no significant broadening of the radial profile width during recovery (Fig. 2 G and H). In particular, the normalized profile width for entangled samples in the presence of optimal cofilin concentrations (R_c = 0.5) remained near 1 (and comparable to that for R_c = 0; Fig. 2H) over a time window during which the intensity recovered by 60% (Fig. 2I). While it is difficult to reconcile the discrepancy between the recovery kinetics of samples assembled with and without cofilin (Fig. 2I) with the nearly indistinguishable width evolution (Fig. 2H) in the context of diffusion-limited recovery, these data are fully consistent with a scenario in which recovery is limited by spatially homogeneous reactions, the rates of which are regulated by cofilin (SI Appendix, section I.e.iii). The experimental recovery time courses were well fit by a model with two reactions on well-separated timescales (∼20 and >1,000 s; Fig. 2J), but not by one with a single reaction (SI Appendix, Fig. S6), indicating that at least two reactions contributed to the observed recovery. The presence of small but systematic deviations in the residuals (SI Appendix, Fig. S6B) suggests that the two-reaction model provides only a phenomenological description and, thus, that the extracted timescales are effective rather than fundamental. We note, however, that the value of the fast timescale was approximately fivefold slower than the characteristic timescale for monomer diffusion across the bleached region and nearly independent of cofilin concentration (Fig. 2J and SI Appendix, Tables S1 and S2), consistent with a recovery reaction that consumes but is not kinetically limited by the availability of fluorescent monomer. In contrast, the fraction of the total recovery associated with the fast timescale was cofilin-dependent, increasing more than threefold at optimal concentrations relative to samples without cofilin (Fig. 2K and SI Appendix, Tables S1 and S2). Taken together, these data strongly suggest that actin FRAP in the presence of nonequilibrium turnover is reaction-limited and that cofilin-dependent changes in actin FRAP arise from modulation of the rates of at least two spatially homogeneous reactions rather than from the lateral diffusion of short stable filaments.

Cofilin Fluidizes Entangled F-Actin Solutions.

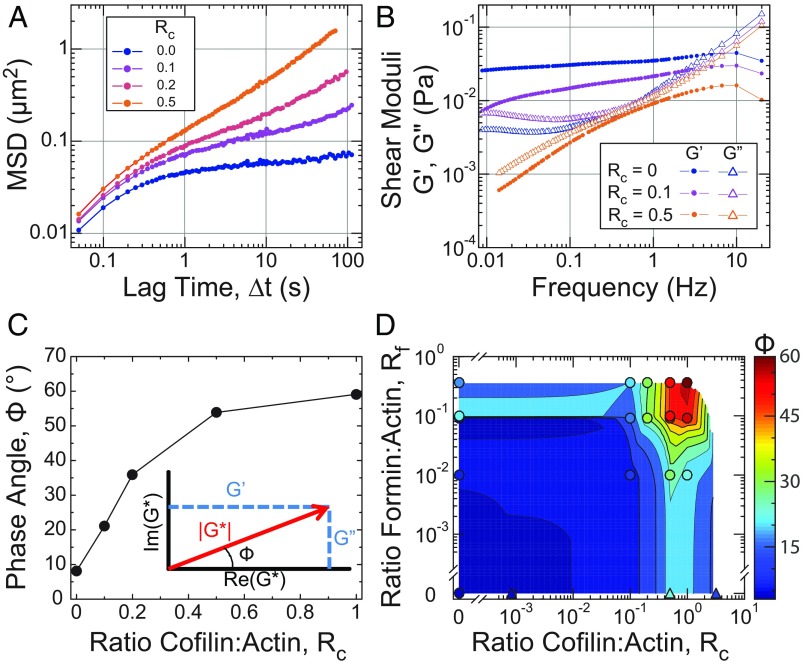
To measure the frequency-dependent viscoelasticity of entangled F-actin solutions with constant filament length and density, but varying amounts of cofilin-mediated turnover, we employed microrheolgy. A concentration of 11.9 µM Mg–ATP–actin was assembled with profilin (R_p = 3), formin (R_f = 0.09), varying amounts of cofilin, and 1-µm-diameter fluorescent polystyrene beads for 95 min to reach steady state (SI Appendix, Fig. S7). The bead diameter was more than twice the typical mesh size, which we estimated to be ξ ∼ 440 nm at this actin concentration (SI Appendix, Table S6 and section IV.a.iv), so that bead motions were significantly constrained by the entangled solution. Bead centroids were obtained from fluorescence images and tracked over time to obtain the ensemble-averaged mean-squared displacements (MSDs) as a function of lag time (∆t). In the absence of cofilin, MSDs were characteristic of semidilute, entangled F-actin solutions (Fig. 3A, blue). Bead motions at lag times <0.3 s were dominated by actin-filament bending fluctuations (11), whereas at longer times, the MSD approached a plateau value that reflected the local elastic modulus (43).

Fig. 3.

Cofilin-mediated turnover tunes the steady-state fluidity of entangled F-actin solutions. All microrheology measurements are of steady-state entangled actin solutions polymerized from 11.9 µM Mg–ATP–actin (0% or 5% Oregon-Green labeled) with R_p = 3 (35.7 µM), R_f = 0.09 (1.07 µM), and R_c as indicated, except for D, where R_f is as indicated, and R_p = 0 for samples denoted by triangles. (A) Ensemble-averaged MSD of 1-µm-diameter beads with R_c as indicated in the key. Each point is calculated from at least 1,000 displacements from a single sample. (B) Real and imaginary components of the complex shear modulus (G′ and G′′, respectively) for the R_c = 0, 0.1, and 0.5 samples from A, denoted by filled circles (G′) and open triangles (G″), respectively. (C) Phase angle (Φ) evaluated at 0.1 Hz for conditions with R_c as indicated. (C, Inset) Geometric relationship between the magnitude of the complex shear modulus (|G*|; red), its real and imaginary components (G′ and G″; blue), and the phase angle (Φ), shown in the complex plane. (D) State diagram displaying the phase angle (Φ; color) evaluated at 0.1 Hz for entangled solutions with R_f and R_c as indicated and R_p = 3 (circles) or 0 (triangles). In most cases, each point represents a single sample, although some are the average of multiple samples. The heatmap represents a 2D interpolation of the discrete data points.

The generalized Stokes–Einstein relationship is used to obtain the frequency-dependent elastic, G′, and viscous, G″, moduli (43–45). In the absence of cofilin, the elastic modulus was nearly constant and much larger than the viscous modulus at frequencies between ∼1 and 0.01 Hz (Fig. 3B, blue), consistent with previous measurements on entangled F-actin solutions (43, 46).

Increasing concentrations of cofilin raised the magnitude and modified the time dependence of the MSD. The plateau in the MSD was truncated by the emergence of a gradual upturn at lag times >10 s for R_c = 0.1 (Fig. 3A, cyan). The location of the upturn shifted toward shorter lag times as R_c increased, with the MSD approaching diffusive scaling (∼∆t^1.0) at the longest lag times for R_c = 0.5. This increased bead mobility reflected dramatic changes in the local viscoelasticity (Fig. 3B). At moderate cofilin concentration (R_c = 0.1; cyan), the elastic modulus systematically decayed from 1 to 0.01 Hz, resulting in a low-frequency cross-over, where, presumably, the viscous modulus becomes dominant at frequencies <0.01 Hz. At higher cofilin concentrations (R_c = 0.5), the elastic and viscous modulus are similar in magnitude and decay with time. A parameterization of the frequency-dependent viscoelasticity is the phase angle Φ(ω) ≡ arctan(G″(ω)/G′(ω)), which is 0° and 90° for purely elastic and viscous materials, respectively. Calculating Φ at 0.1 Hz, we found that it increased from 10° to 60° as the cofilin concentration was increased from R_c = 0 to R_c = 1 (Fig. 3C). Thus, increased cofilin concentration resulted in a transition between a viscoelastic solid to a viscoelastic fluid. Since cofilin does not significantly reduce the filament length (Fig. 1H) or concentration (SI Appendix, Fig. S8, Table S5 and S6, and section IV.a), the fluidization likely resulted from elevated actin filament turnover.

To explore how the fluidity of actin solutions can be regulated by changes to filament length and turnover dynamics, we measured Φ at 0.1 Hz over a range of cofilin and formin concentrations (Fig. 3D). For all filament lengths (formin concentrations) examined, the addition of sufficient cofilin increased the phase angle. The most fluid-like samples were those with short filaments (highest formin concentration) undergoing rapid turnover (high cofilin concentration). While fluidization of entangled F-actin solutions by shortening the steady-state filament length has been appreciated (46), we demonstrate that fluidization can be achieved by accelerating steady-state turnover without reducing the average length of filaments.

Rapid Cofilin-Mediated Turnover Is a Single-Timescale Mode of Stress Relaxation.

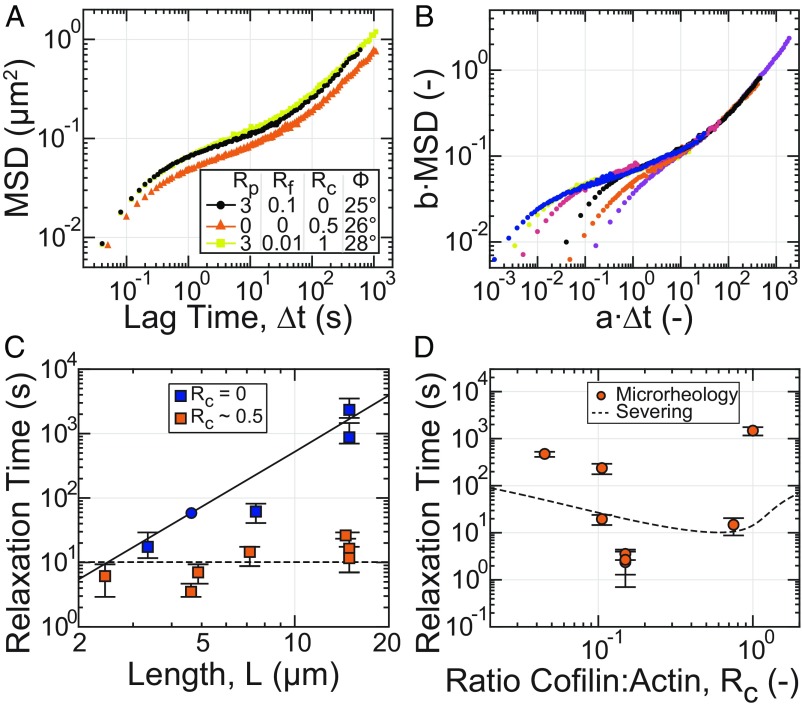
To compare the mechanism of enhanced fluidity that arises from accelerated filament turnover to shortened filament length, we compared the MSD of microscopically distinct F-actin solutions that have identical values of Φ at 0.1 Hz (Fig. 4A). Specifically, we compared samples with long filaments and fast turnover (yellow, orange) to one with short filaments and slow turnover (black). Interestingly, these samples are rheologically indistinguishable at all timescales probed. Thus, an entangled solution of relatively long filaments undergoing rapid turnover (yellow) is mechanically equivalent to a solution of relatively short, stable filaments (black), and stress relaxation is dominated by a single time scale (10).

Fig. 4.

Rapid cofilin-mediated turnover is a single-timescale mode of stress relaxation and dominates reptation. All microrheology measurements are of steady-state entangled actin solutions polymerized from 11.9 µM Mg–ATP–actin (0% or 5% Oregon-Green labeled) with R_p = 3 (35.7 µM) and R_f and R_c as indicated, except for the sample denoted by triangles in A and C, where R_p = 0. (A) Ensemble-averaged MSD for samples with similar values of the phase angle (Φ) evaluated at 0.1 Hz. (B) Collapse of MSD curves at long times to a reference sample of short stable filaments (A and B, black; C, circle) after rescaling lag time and MSD by shift factors a and b, respectively. (C) Dependence of relaxation time, estimated from the shift factor a, on filament length with (orange) and without (blue) cofilin. Data points represent individual samples. Error bars represent estimated uncertainty in relaxation time determination. The blue circle denotes the reference sample. The solid curve is the relaxation time predicted for reptation alone. The dashed line is a fit of the length-independent severing-based model to the cofilin-containing data. (D) Dependence of relaxation time on R_c for samples with R_p = 3 and R_f = 0.0092. Data points represent individual samples. Error bars represent estimated uncertainty in relaxation time determination. The dashed line is the relaxation time dependence on cofilin concentration predicted by the severing-based model using the severing rate inferred from the fit in C, an association constant for cofilin:F-actin binding of 1/K_a = 10 µM and a cofilin-binding cooperativity parameter of ω = 7.5 (17).

To estimate the stress-relaxation time scale over varying filament lengths and dynamics, we used an approach inspired by time–temperature superposition (47). For many samples, the stress-relaxation time exceeded those that can be directly measured with microrheology. The relaxation timescale was, instead, determined by rescaling the MSDs by a shift-factor b, and ∆t by a shift-factor a, such that the long-time behavior superposed to a sample with a stress-relaxation time within our observation window (black, Fig. 4 A and B and SI Appendix, Fig. S9), for which the relaxation time, τ_ref, could be directly inferred (SI Appendix, Fig. S10). The estimated relaxation timescale for each sample i is then given by τ_i = τ_ref/a_i. The successful superposition of the long-timescale MSDs for entangled solutions with a wide variety of formin and cofilin concentrations (Fig. 4B) validated the use of this approach.

We examined the dependence of the relaxation time on filament length (SI Appendix, Fig. S11 and section I.h.ii). In the absence of cofilin, the stress relaxation time increased as a function of L, consistent with L³ (Fig. 4C, blue). This is consistent with stress relaxation occurring via lateral filament diffusion along its length, or reptation, as expected for entangled F-actin solutions (9, 10, 12, 48). By contrast, at optimal cofilin concentrations, the relaxation time was reduced at all filament lengths and exhibits a much weaker sublinear or even absence of dependence on filament length (Fig. 4C, red). This indicates that cofilin-mediated turnover accelerated stress relaxation in entangled solutions by a single timescale mechanism that dominated over reptation.

We explored how changing the severing rate can modulate the stress-relaxation time. As the cofilin molar ratio was increased from 0.05 to 0.15, the relaxation time decreased nearly ∼200-fold from 600 to ∼3 s (Fig. 4D). As the cofilin ratio was increased further to 1, the relaxation time increased back to ∼1,000 s. We compared this trend to a model of stress relaxation in entangled solutions with variable filament severing (20) (Fig. 4D, dashed line; SI Appendix, section III). While the simple model did predict a biphasic dependence of the relaxation time on cofilin concentration, more work is required to develop a model which captures the full features of the experimental data. Importantly, these data underscore how nonequilibrium severing activity can decouple mechanical stress relaxation from material structure, as all of these samples in Fig. 4D contain actin filaments at the same density and nearly the same length.

To understand the mechanism of cofilin-mediated stress relaxation observed in Fig. 4 C and D, we explored a simple physical model which explicitly incorporated filament severing and which captured the weak dependence of the relaxation time on filament length. Our choice to focus on severing as the dominant stress-relaxation mechanism was motivated by the observation that cofilin-mediated severing (i) reduces the combined length of stress-bearing filaments, as described below; and (ii) precipitates the enhanced disassembly of ADP-rich filament portions, which in turn elevates actin turnover. Assuming an initial steady-state length distribution $P_L^{SS}$, we approximated the residual stress at time t following application of a step strain as proportional to the residual polymer of length exceeding the entanglement length L_e: $\sigma \left(t\right)\sim {\displaystyle \sum _{L=L_e}^{\infty }L{P}_L\left(t\right)}$. The distribution P_L(t) of residual stressed filaments with length L evolved according to $\frac{d}{dt}{P}_L=k_s\left[-\left(L-1\right)P_L+2{\displaystyle {\sum }_{M=1}^{\infty }{P}_{L+M}}\right]$ due to severing alone at a rate k_s and neglecting depolymerization, which represents a valid approximation for large lengths L and M. This time evolution is analogous to that used to describe the rheology of worm-like micelles (49), but neglecting filament-annealing reactions, which we expect to be suppressed here by depolymerization and the presence of formin (50). We emphasize that P_L(t) represents the distribution of “stressed” filaments, and not the instantaneous filament length distribution $P_L^{SS}$, which remained constant due to depolymerization and subsequent stress-free elongation. This model is solvable for exponential $P_L^{SS}$ (SI Appendix, section II) and yields a stress that decays with a characteristic timescale τ_relax ∼ (k_sL_e) ⁻¹, which depends on polymer density (through the entanglement length), but not filament length (SI Appendix, Fig. S12), consistent with our results in Fig. 4C.

A fit of this model to the relaxation times measured with varying cofilin concentration (Fig. 4D, dashed line) predicted a severing rate of 3.3 × 10⁻⁴ in units of per monomer (or subunit) per second (subunit⁻¹·s⁻¹) at optimal concentrations, ∼12-fold higher than reported (22). We speculated that this discrepancy could arise from enhanced severing in the presence of steric constraints from filament entanglements (51, 52). Including enhanced disassembly of barbed ends exposed by severing in the evolution of P_L could further reduce this discrepancy. One can define a lengthscale $L_d\sim \sqrt{k_{\text{disassembly}}/k_s}$, at which the time between severing events is comparable to the time for depolymerization of fragments of length L_d. If this length exceeds the entanglement length, then the rate of stress relaxation is expected to increase by a factor L_d/L_e. Taken together, these modeling results demonstrate how severing activity results in the weak dependence of mechanical relaxation on filament length in Fig. 4C.

Discussion

Here, we show that cofilin-mediated turnover tunes the steady-state fluidity of entangled solutions of F-actin. Cofilin-mediated severing does not appreciably reduce the mean filament length or number density at steady state, factors known to control mechanics and filament mobility. Instead, the enhanced fluidity arises from nonequilibrium actin turnover catalyzed by cofilin-mediated filament disassembly.

Our work extends the emerging microscopic understanding of cofilin-mediated actin disassembly (23), providing a microscopic model of how a steady-state length is achieved in the presence of cofilin activity (Fig. 5). The textbook view of actin turnover is treadmilling, wherein barbed-end elongation proceeds at the turnover rate and is exactly balanced at steady state by pointed-end disassembly. A treadmilling-based mechanism predicts that the relaxation time would be linear in L, which is the strongest dependence with which our data are reasonably consistent (Fig. 4C). However, the 8-nm/s treadmilling velocity we obtained by extrapolating turnover measurements (Fig. 1) to 11.9 µM total actin was ∼100-fold too slow to account for the observed relaxation times (SI Appendix, section IV.c).

Fig. 5.

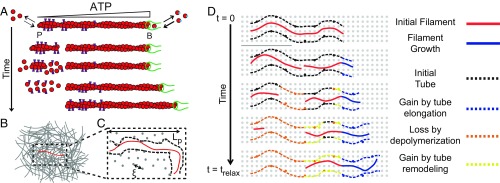
Microscopic model of cofilin-mediated actin turnover and stress relaxation. (A) Microscopic dynamics of the test filament regulated by cofilin, profilin, and formin. Cofilin binds and severs ADP-rich filament regions, creating unstable ADP-rich filaments which depolymerize from both ends. The additional G-actin is incorporated onto the stable ATP-barbed end, restoring the length lost from severing. (B) Cartoon of a test filament (red) entangled with other filaments (gray) in a semidilute actin solution. (C) Representation of tube model. Entanglements (black) between the test chain and background filaments constrain test chain fluctuations to a tube (black dashed line) and thereby store stress. The entanglement length is set by solution mesh size (gray dots) and filament persistence length. (D) Tube memory, and thus stress, decays by depolymerization (orange) and tube remodeling (yellow) after severing of the test filament and background filaments, respectively. Polymerization (blue) is stress-free, so a newly created tube does not contribute.

Instead, nonequilibrium ATP hydrolysis directs cofilin severing and enables asymmetric kinetics for both assembly and disassembly of severed fragments (Fig. 5A). Cofilin binds with an ∼40-fold higher affinity to ADP–F-actin than either ADP–Pi–or ATP–actin (18, 24), preferentially directing severing away from the filament barbed end (20, 22). Importantly, the two fragments formed upon filament severing differ in their nucleotide composition. The fragment with the newly created barbed end was ADP-rich throughout, resulting in its rapid disassembly from both pointed and barbed ends, at a combined rate on the order of ∼0.1 µm/s (SI Appendix, section IV.b). In contrast, the fragment with the preexisting barbed end retained an ATP gradient along its length and was thus stable, independent of the presence of the formin. This stable fragment continued to elongate, and by consuming monomer released through the rapid disassembly of unstable severed fragments, it quickly regenerated length lost through severing (Fig. 5A). Thus, severing coupled to asymmetric dynamics of assembly and disassembly generated by nonequilibrium ATP hydrolysis preserves steady-state filament length while catalyzing turnover.

The possibility for nonequilibrium effects to fluidize materials is of great interest in understanding active biological materials. The mechanical response of entangled F-actin solutions is typically dominated by filament length and density and understood in terms of a tube model (Fig. 5 B and C), wherein stress relaxes by filament reptation. Our results demonstrate that rapid turnover catalyzed by cofilin can fluidize these solutions without diffusion-mediated filament translation. The enhanced stress relaxation arises from rapid disassembly of large filament portions, while filament assembly and tube remodeling occur stress-free (Fig. 5D). In contrast to other active processes (e.g., myosin motors), here, the nonequilibrium activity primarily affects changes in filament constituents, rather than generating local forces. This suggests that the bead motions are likely still dominated by thermal forces and validating our use of the generalized Stokes–Einstein relation.

It will be interesting to explore the effects of severing-mediated stress relaxation in more physiological cross-linked networks of F-actin. Consistent with suppression of cofilin binding (21), saturation of actin networks with cross-linkers or the side-binding protein tropomyosin inhibits disassembly in vitro (53, 54). However, more sparsely distributed attachment points give both sufficient space to allow cofilin binding and actually accelerate severing (52), suggesting an important role for cross-link density in tuning severing and thereby fluidity.

F-actin turnover has been considered an important mechanism to support the fluidization of the actin cortex in vivo (4). In contrast to polarized, branched networks like lamellipodia with spatially segregated zones of filament assembly and disassembly (55–57), the fluidization we describe here occurs via spatially uniform assembly and disassembly. In vivo, phospho-regulation of cofilin activity could enable rapid and spatially resolved modulation of both turnover and mechanics. Furthermore, the decoupling of relaxation time and filament length expands control of network mechanical response by removing a physical design constraint. Exploring how the results found here impact cortex turnover at physiological temperature and concentrations will be an exciting area of future study, providing insight into how cells exploit cofilin-mediated nonequilibrium turnover to differentially tune the dynamics and mechanics of actin networks to enable diverse physiological function.

Materials and Methods

Mg–ATP–actin (5% Oregon Green-labeled) was polymerized for 95 min in the presence of regulatory proteins and 1-µm-diameter polystyrene beads to reach steady state and imaged on a spinning-disk confocal microscope. Details of all experimental methods and analysis can be found in SI Appendix (58–84). To facilitate interpretation by persons with red–green color-perception deficiencies, data were plotted by using well-separated colors from the Ametrine colormap (85).

Supporting Information.

Details regarding experimental methods, analysis, modeling, and physical estimates, as well as six tables, 12 figures, and four movies, are available in SI Appendix.