Multiplexed Population Coding of Stimulus Properties by Leech Mechanosensory Cells

Abstract

Sensory coding has long been discussed in terms of a dichotomy between spike timing and rate coding. However, recent studies found that in primate mechanoperception and other sensory systems, spike rates and timing of cell populations complement each other. They simultaneously carry information about different stimulus properties in a multiplexed way. Here, we present evidence for multiplexed encoding of tactile skin stimulation in the tiny population of leech mechanoreceptors, consisting of only 10 cells of two types with overlapping receptive fields. Each mechanoreceptor neuron of the leech varies spike count and response latency to both touch intensity and location, leading to ambiguous responses to different stimuli. Nevertheless, three different stimulus estimation techniques consistently reveal that the neuronal population allows reliable decoding of both stimulus properties. For the two mechanoreceptor types, the transient responses of T (touch) cells and the sustained responses of P (pressure) cells, the relative timing of the first spikes of two mechanoreceptors encodes stimulus location, whereas summed spike counts represent touch intensity. Differences between the cell types become evident in responses to combined stimulus properties. The best estimation performance for stimulus location is obtained from the relative first spike timing of the faster and temporally more precise T cells. Simultaneously, the sustained responses of P cells indicate touch intensity by summed spike counts and stimulus duration by the duration of spike responses. The striking similarities of these results with previous findings on primate mechanosensory afferents suggest multiplexed population coding as a general principle of somatosensation.

SIGNIFICANCE STATEMENT Multiplexing, the simultaneous encoding of different stimulus properties by distinct neuronal response features, has recently been suggested as a mechanism used in several sensory systems, including primate somatosensation. While a rigorous experimental verification of the multiplexing hypothesis is difficult to accomplish in a complex vertebrate system, it is feasible for a small population of individually characterized leech neurons. Monitoring the responses of all four mechanoreceptors innervating a patch of skin revealed striking similarities between touch encoding in the primate and the leech: summed spike counts represent stimulus intensity, whereas relative timing of first spikes encodes stimulus location. These findings suggest that multiplexed population coding is a general mechanism of touch encoding common to species as different as man and worm.

Introduction

Encoding of sensory stimuli has been intensively studied across species and sensory systems. Nevertheless, several open questions remain, in particular regarding the encoding of complex stimuli comprising combined stimulus properties. Traditionally, neural coding has been discussed in terms of dichotomies: (1) rate encoding versus temporal encoding (Theunissen and Miller, 1995), (2) encoding by individual cells versus population coding (Sakurai, 1996), and (3) encoding of single stimulus properties versus multiplexing (Panzeri et al., 2010).

These three pairs of hypotheses have recently been discussed for the somatosensory pathway of the primate hand (Saal and Bensmaia, 2014). Based mainly on evidences from somatosensory cortex, Saal and Bensmaia (2014) concluded that populations of mixed cell types encode different properties of tactile stimuli in a multiplexed way, using both rate coding and temporal response features. In our study, we tested the three pairs of hypotheses for a much smaller somatosensory system, the tiny population of leech mechanoreceptors.

Each patch of leech skin is innervated by only four individual mechanoreceptor cells, which are sensitive to mechanical stimulation: two T (“touch”) cells and two P (“pressure”) cells with overlapping receptive fields (Nicholls and Baylor, 1968). Constant pressure stimulation triggers in P cells sustained spiking activity, whereas T-cell responses adapt rapidly and mainly indicate stimulus changes (Carlton and McVean, 1995; Lewis and Kristan, 1998). These mechanoreceptors provide the sensory input for the local bend reflex (Kristan et al., 2005), which we can use to scrutinize their encoding properties. This reflex causes the leech body wall to bend away from tactile stimulation, depending on touch intensity, location, and duration. The few mechanoreceptors discriminate stimulus location more finely than the human finger tip, causing different behavioral reactions for stimuli that are only 500 μm apart (Baca et al., 2005; Thomson and Kristan, 2006).

Thomson and Kristan (2006) investigated the encoding of touch location by spike counts versus response latencies of P cells and found that only the latency difference of two P cells encodes stimulus location precisely enough to explain the behavioral performance. Their results agree with evidence for latency coding of location-specific information in other systems such as rat somatosensory cortex (Foffani et al., 2004) and human tactile afferents (Johansson and Birznieks, 2004). However, when Thomson and Kristan (2006) induced specific latency differences via current injection to P cell somata, the resulting local bend movements were not as precisely localized as during skin stimulation. These results suggest that the leech uses additional information to regulate the exact position of muscle responses to local touch.

In this study, we aimed at completing the picture of leech mechanosensory encoding that underlies the surprisingly precise local bend reflex:

First, we investigated responses of T cells in addition to P cells. The two cell pairs innervating each patch of skin must, together, transmit all information about this tactile stimulus available to the animal.

Second, in addition to spike counts and response latencies, we considered interspike intervals, properties of the T-cell burst at stimulus onset and combinations of response features as additional candidate codes. Like Thomson and Kristan (2006), we compared the encoding performances of individual cells and cell pairs for all response features.

Third, we analyzed the encoding of three stimulus properties, location, intensity, and duration, as well as their combinations. Although intensity and duration have been shown to shape behavioral responses of the leech (Baca et al., 2005), their encoding by mechanosensory cells has not been studied so far.

When considering combinations of stimulus properties and multiple response features in both cell types, leech tactile encoding strikingly resembles published findings obtained in the primate (Saal and Bensmaia, 2014): whereas each sensory cell responds ambiguously to different combinations of stimulus properties, a tiny population of four cells—two cell pairs of different types—cooperatively encodes stimulus combinations. Relative spike timing encodes stimulus location, whereas combined spike counts represent stimulus intensity in a multiplexed way.

Materials and Methods

Physiology.

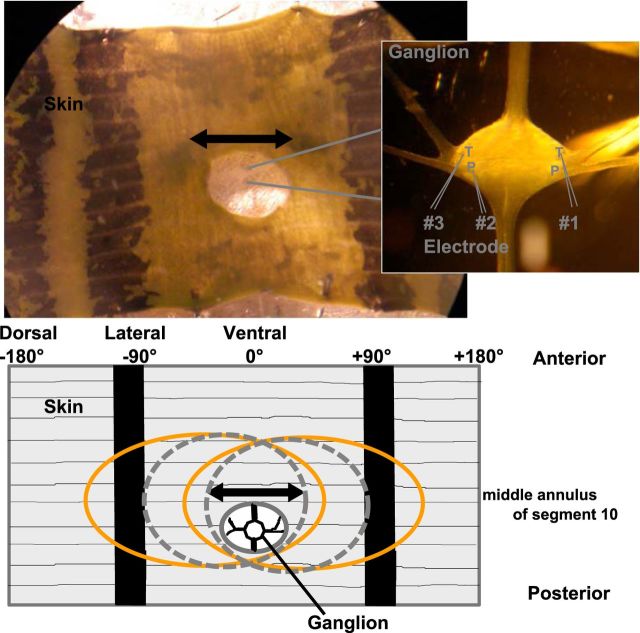
We used adult, hermaphrodite medicinal leeches (Hirudo verbana) from Biebertaler Leech Breeding Farm. The leeches weighed 1–2 g and were kept at room temperature in tanks with ocean sea salt (1:1000) diluted with purified water. Animals were anesthetized with ice-cold saline (Muller et al., 1981) before and during dissection. Experiments were performed at room temperature. In total, 70 preparations were used for this study. The body-wall preparation (Fig. 1) consisted of midbody segments 9–11, with corresponding ganglia of the ventral nerve cord. Innervation of segment 10 remained unaffected. Because the leech nervous system is highly repetitive (Kristan et al., 2005), and to our knowledge, no indication for differences in mechanoreception between midbody ganglia has previously been reported, we assume that our results apply to the entire midbody region of the leech. The body wall was flattened and pinned out with the ectodermal side of the skin facing upward in a plastic Petri dish coated with a silicone elastomere (Sylgard; Dow Corning). In the area of the fifth annulus (counted from anterior) of segment 10, a hole was cut into the skin to provide access to the ventral side of the ganglion, where mechanosensory cell somata are located (Kristan et al., 2005). The skin was stimulated at the middle annulus (third annulus of segment 10), which was identified by location of the sensilla (Blackshaw et al., 1982).

Figure 1.

Photograph of the body-wall preparation and sketch of the receptive fields of mechanoreceptors. Inset (right), A photomicrograph of the ganglion is shown with higher-magnification. Responses of up to three mechanosensory cells (T, P) were recorded intracellularly (positions of cell bodies and electrodes are marked in the inset), while the skin was stimulated mechanically by the poker (see Materials and Methods). The double-arrow line indicates the stimulation area at the middle annulus of the 10th segment. Ventral midline (the middle between the two black stripes on the skin) is defined as 0°. Stimulus locations to the right were denoted as a positive number of degrees and to the left as negative degrees. The left end of the preparation marks −180°, the right side +180°, black stripes are approximately at −90° and +90°. The sketch of the body wall preparation below the photograph shows the approximate locations and extents of the receptive fields of the full population of mechanoreceptors responding to mechanical stimulation at the ventral midline: two T cells (dashed gray) and two P cells (orange).

The ventral midline of each preparation was defined as 0°. Because stimulus locations to the left are denoted as negative and to the right as positive numbers of degrees, the preparation spans from −180° to +180° (Fig. 1). While stimulating the skin mechanically, we performed single, double, or triple intracellular recordings from P and T cells (Nicholls and Baylor, 1968). These cells have been well studied and are easily identifiable based on their location in the ganglion, their size and electrical properties (Nicholls and Baylor, 1968; Kristan et al., 2005). We used glass electrodes with resistances between 20 and 40 MΩ, filled with potassium acetate (3M). For numbers of recorded cells and cell pairs, see Table 1. The experimental rig consisted of mechanical micromanipulators type MX-1 (Narishige Group), amplifiers (model SEC-05X and BA1S) from NPI Electronic, and the data were acquired via an interface BNC-2090 with NI PCI-6036E board from National Instruments. Neuronal responses were recorded (sample rate 10 kHz) and analyzed using MATLAB software (MathWorks).

Table 1.

Details of stimulation protocols and numbers of recorded cells for seven different estimation tasks analyzed in this study

Estimation task	Stimulus properties			Numbers of cells
	Location, degrees	Intensity, mN	Duration, ms	T cells	TT pairs	P cells	PP pairs	TP pairs
Location	−20°, −15°, −10°, −5°, 0°, 5°, 10°, 15°, 20°	10, 50	200	10	5	10	5	—
Intensities low	0	10, 20, 30, 40, 50	200	14	7	24	12	—
Intensities high	0	10, 20, 50, 70, 100	200	27	8	23	5	11
Duration	0	60	50, 200, 500	10	—	12	—	—
Duration and intensity	0	20, 60	50, 200, 500	10	—	12	—	—
Location and intensity	−20 , 0°, +20	10, 50	200	10	5	10	5	—
Location and intensity, 15 combinations	−20°, −10°, 0°, +10°, +20°	10, 20, 50	200	10	5	10	5	—

Stimulation.

For applying pressure stimuli onto the skin, we used a Dual-Mode Lever Arm System (Aurora Scientific, Model 300B; Baca et al., 2005; Thomson and Kristan, 2006) with a poker tip size of 1 mm². The stimulus was varied in intensity (10–100 mN) and location (−20° to +20°, relative to ventral midline, in 5° steps). Tactile stimulation lasted 200 ms (Lewis and Kristan, 1998; Thomson and Kristan, 2006), except in the duration encoding experiments, in which stimulus durations of 50, 200, and 500 ms were combined with intensities of 20 and 60 mN at 0°. Table 1 summarizes the combinations of varied and fixed tactile stimulus parameters (location, intensity, duration) for all seven encoding tasks analyzed in this study. All combinations of stimulus properties used for one encoding task were presented 8–15 times in pseudorandomized order.

Analyzed response features.

The spike time was defined as the time of maximum spike amplitude. The neuronal responses were quantified using response features defined for single cells, as well as for both cells of the simultaneously recorded cell pair.

1. Spike count (C): total number of spikes elicited in a single cell during the stimulation.

2. Spike count difference (CD): signed difference of spike counts of a cell pair (left − right cell).

3. Summed spike count (SC): sum of spike counts of a cell pair.

4. Latency (L): time between stimulus onset and first spike of one cell.

5. Latency difference (LD, also called relative latency): signed time difference of the first spikes of a cell pair (left − right cell).

6. First interspike interval (I, 1st ISI): time interval between the first and second spike of one cell.

7. First ISI difference (ID): signed interval difference of the ISIs of a cell pair (left − right cell).

8. Response duration (RD): time difference between the first spike and the last spike of the elicited neuronal response.

9. Burst spike count (BC): number of spikes of one cell in the first burst after stimulus onset.

10. Burst duration (BD): time difference between first and last spike of one cell in the first burst after stimulus onset.

Bursts were identified based on the distribution of ISIs according to the definition by Oswald et al., 2007. If this distribution was bimodal, we defined a threshold, separating burst ISIs from longer ISIs (Oswald et al., 2007). According to this definition, we found that T cells generated a single burst at stimulus onset (see Figs. 3, 5; Nicholls and Baylor, 1968; Baltzley et al., 2010), whereas P cells did not produce bursts. Therefore, the analysis of burst spike counts and durations are shown in Figures 4, 6, and 8 only for T cells.

Figure 3.

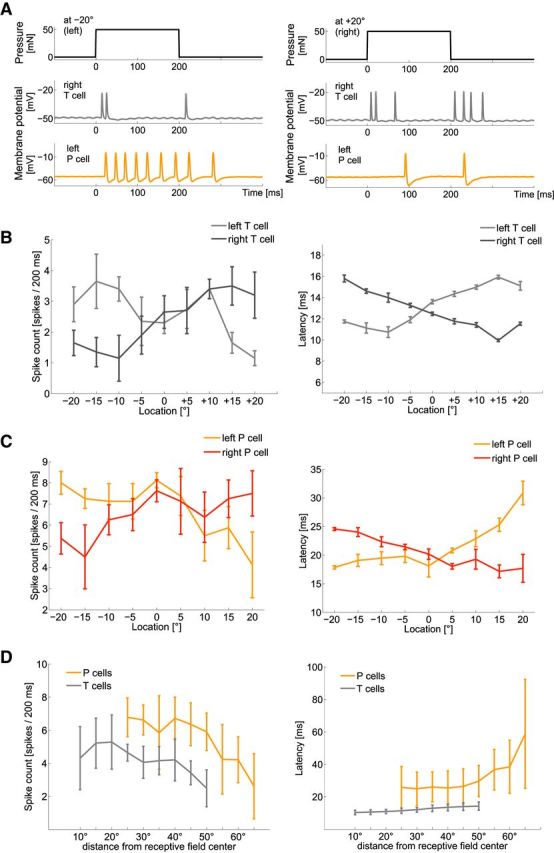
Influences of touch location on neuronal responses of mechanoreceptors. A, Typical example of simultaneously intracellularly recorded responses of a right T cell (gray) and left P cell (orange) to a pressure stimulus of 50 mN for 200 ms at −20° (left) and +20° (right). B, Spike count and latency (mean and SD) of a typical T-cell double-recording with 10 repeated presentations of estimation task “location” (Table 1): a stimulus intensity of 50 mN applied for 200 ms at varied locations. Ventral midline is defined as 0°, stimulus locations to the right as positive and to the left as negative numbers of degrees. C, Spike count and latency (mean and SD of 10 responses) of a typical P-cell double-recording responding to the same stimulation as used in B. D, Dependencies of spike count and latency on stimulus location (mean and SD of the mean activity of 10 T cells and 10 P cells responding to 8–10 stimulus repetitions). Responses of left and right cells were pooled, displaying distances from receptive field centers rather than absolute stimulus locations on the body wall. The curves of both cell types are shifted relative to each other, because the receptive field centers of P cells are at −45° and 45°, and of T cells at −30° and 30° (Lewis and Kristan, 1998). Hence, stimulation of both cell types from −20° to +20° around the midline led to larger distances from receptive field centers of P cells than of T cells.

Figure 5.

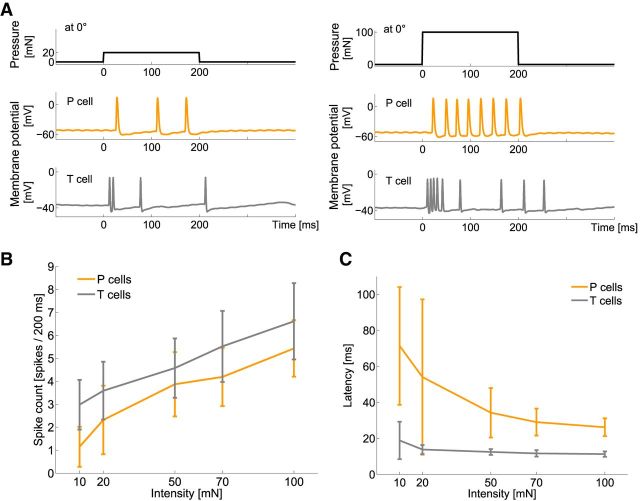
Influences of stimulus intensity on neuronal responses of mechanoreceptors. A, Typical example of simultaneously, intracellularly recorded responses of a T cell (gray) and a P cell (orange) to a mechanical stimulus of 20 mN (left) and 100 mN (right) for 200 ms at 0° (ventral midline). B, C, Dependencies of B spike count and C latency on stimulus intensity. Mean and SD of 27 T cells (gray) and 22 P cells (orange) with 10 stimulus repetitions each, for intensities of 5–100 mN applied at 0° (Table 1, estimation task intensities high).

Figure 4.

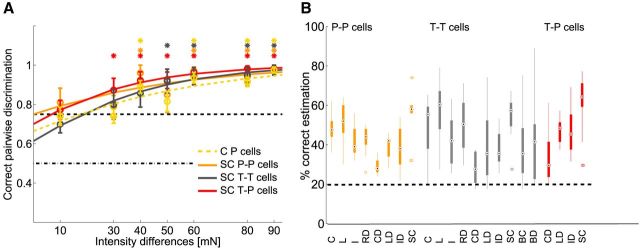
Estimation results for stimulus location. A, Pairwise discrimination results for tactile stimulation at 0° compared with stimulus locations between 5° and 40°. Responses of T and P cells (5 TT and 5 PP cell double-recordings, 8–10 stimulus presentations for each cell) were analyzed for two stimulus intensities, 10 and 50 mN. The black dashed lines show chance level and 75% threshold. Asterisks indicate mean values that are significantly (p < 0.05, t test) above threshold. B, Classification result for nine locations of a 50 mN pressure stimulus. Black dashed line shows chance level, black dots mark the median values, and circles indicate statistical outliers (see Material and Methods). Response features: C, spike count; L, latency; I, first ISI; RD, response duration; CD, spike count difference; LD, latency difference; ID, first ISI difference; SC, summed spike count; BC, burst spike count; BD, burst duration.

Figure 6.

Estimation results for stimulus intensity. A, Pairwise discrimination of responses to 10 mN steps of stimulus intensities between 20 and 100 mN. Black dashed lines show chance level and 75% threshold. Asterisks indicate mean values that are significantly (p < 0.05, t test) above threshold. Response features see B. B, Classification results for five stimulus intensities between 10 and 100 mN (Table 1, estimation task intensities high), which were applied at 0° for 200 ms. The black dashed line shows chance level, black dots mark the median values, and circles indicate statistical outliers (see Material and Methods). Response features: C, spike count; L, latency; I, first ISI; RD, response duration; CD, spike count difference; LD, latency difference; ID, first ISI difference; SC, summed spike count; BC, burst spike count; BD, burst duration.

Figure 8.

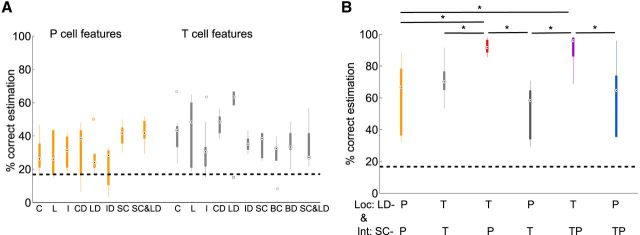
Estimation results for combination of location and intensity. A, Estimation results for combination of three locations (−20°, 0°, 20°) and two intensities (10 and 50 mN; Table 1, estimation task: location and intensity). C, Spike count; L, latency; I, first ISI; CD, spike count difference; LD, latency difference; ID, first ISI difference; SC, summed spike count; BC, burst spike count; BD, burst duration. Black dashed lines show chance level black dots mark median values, and circles indicate statistical outliers. B, Results for combination of summed spike count (SC) for intensity estimation (Int) and latency difference (LD) for location estimation (Loc) for the same location and intensity estimation task as in A. P-cell pairs in orange; T-cell pairs in light gray. Pooled data analysis: P cell SC and T cell LD in red, and T cell SC and P cell LD in dark gray; SC of P cell and T cell pooled data with LD of T cells in purple and with LD of P cells in blue. In the top row of the x-axis labels, the cells used for location estimation based on latency differences are listed; the second row shows cells used for intensity estimation based on summed counts. Asterisk indicates significant difference between estimation results (p < 0.05, Kruskal–Wallis test).

Stimulus estimation.

The aim of stimulus estimation is to calculate how well the value of a stimulus property can be estimated based on a specific response feature (Theunissen and Miller, 1995). The main idea of this approach is that the experimenter tries to solve the same task as the nervous system, answering the question “which stimulus was present?” based solely on the spike responses of the mechanoreceptors innervating the stimulated patch of skin. We used two stimulus estimation approaches based on a maximum likelihood method (Aldrich, 1997): pairwise discrimination and stimulus classification (see below). In both approaches, a “leave one out” validation was applied (Quian Quiroga and Panzeri, 2009).

For a fair comparison of the different response features A–J, we processed all of them in the same way, even though they differed considerably in their statistical properties (e.g., spike count can only have integer numbers <20, whereas latency is a continuous variable). Therefore, we used response feature ranks rather than absolute values for stimulus estimation. The underlying assumption of this approach is that response features depend in a monotonic way on stimulus properties and therefore, similar responses have a high probability of being triggered by the same stimulus. We confirmed this assumption for our datasets, and found that spike counts increase with increasing stimulus intensity as well as with decreasing distance from the receptive field center (see Figs. 5B, 3D), whereas latencies (see Figs. 5C, 3D) and first ISIs decrease in either case.

The idea of stimulus estimation is illustrated in Figure 2: in an experiment with N different stimuli (Fig. 2A; N = 3; Table 1 shows experimental parameters), each stimulus was presented M (Fig. 2; M = 4) times. For each stimulus #i, M − 1 responses were used as stimulus class S_i in the training dataset (Fig. 2B), whereas the remaining response was used as the test data (Fig. 2C).

Figure 2.

Sketch of the stimulus estimation process, consisting of training and test phases. In this example, three stimuli of different intensities (A) were applied four times: for each of the stimuli, three response traces were included in the corresponding stimulus response class S₁, S₂, or S₃ of the training dataset (B, top row, vertical lines indicate spike times), the remaining trace was used as test data (C, top row). B, Training: the analyzed response feature, here spike count, was determined for each trace in the training dataset. These numbers were sorted, and divided into three commensurate quantile classes (Q₁, Q₂, Q₃) according to their ranks. We determined how often each possible spike count was contained in each quantile class Q_i. For each spike count value, the index i of the most probable quantile class Q_i determined to which rank class R_i all responses showing this spike count were assigned. The rank class look table gives the definitions of (R₁, R₂, R₃) and line 5 shows the rank classes for each of the responses shown in line 1. The rank class matrix (B, bottom left) shows how many of the traces contained in each stimulus response class (S₁, S₂, S₃) were assigned to each of the three rank classes (R₁, R₂, R₃). The rank class matrix is used to create a stimulus estimation table (B, bottom right), giving for each rank class the stimulus, which has most probably elicited the response (maximum likelihood). C, Test: each trace in the test dataset is assigned to one of the rank classes based on the rank-class look table constructed in the training. Applying the stimulus estimation table, this rank class determines the estimated stimulus for each test response trace. The comparison of estimated and presented stimuli for all response traces leads to the percentage of correct estimations.

(1) In the fist step of the training phase (Fig. 2B), the values of the response feature investigated (Fig. 2, spike count) obtained in all N × (M − 1) training responses were sorted and divided into N quantile classes Q_{1..N} of equal sizes, according to their ranks (Fig. 2B).

For the analysis of response feature combinations, this step was performed for both features, so that two training datasets and two corresponding sets of quantile classes were generated. Response features A–C and H–J (spike count, response duration, and burst features) were sorted in ascending order; features D–G (latency and ISI features) in descending order.

(2) We counted for each possible response feature value (Fig. 2B, spike counts from 1 to 6) how often it was contained in each quantile class Q_{1..N} and determined the index i of the quantile class with the highest number of occurrences (in Fig. 2B, a spike count of 3 was contained most often in Q₂). Applying the maximum likelihood principle, we assigned all responses sharing the same most probable quantile class Q_i to rank classes R_i (in Fig. 2B, all response traces with spike counts of 3 or 4 are assigned to R₂). Hence, whereas S_i contained all the (unsorted) response feature values that were evoked by stimulus #i, R_i could contain values belonging to any of the stimulus classes S_{1,..N} (in Fig. 2B, rank class R₂ contains two responses from S₂, and one response each from S₁ and S₃). In case of continuous response features like latencies or interspike intervals, the lookup table defined value ranges for the assignment of the most probable rank class. In rare cases (1.33% of all responses) in which two or more quantile classes had equal probabilities of eliciting one specific response feature value, both corresponding rank classes were included into the look table.

When response feature combinations (e.g., spike counts and latencies) were considered, a rank look table was generated for each response feature separately. Because increases in spike counts usually correlated with decreases in latencies and interspike intervals (Figs. 3, 5, 7; Thomson and Kristan, 2006), we sorted spike counts in ascending order, whereas latencies and interspike intervals were sorted in descending order. For each response trace, the two rank numbers obtained for the two features were summed, leading to a single number. For the example shown in Figure 2, each of the response traces would obtain a rank class number between 1 and 3 for its spike count and a second number between 1 and 3 for its latency, leading to summed rank class numbers between 2 and 6.

Figure 7.

Influences of the stimulus duration on neuronal responses of mechanoreceptors. A, Spike count (mean and SD) for P cells (orange; N = 12) and T cells (gray; N = 10) for stimuli of 20 and 60 mN with 50, 200, and 500 ms duration, applied at 0° stimulus location (Table 1, estimation task duration). B, Classification results for 60 mN stimulus intensity with three durations (50, 200, and 500 ms). The black dashed line shows chance level, black dots mark the median values, and circles indicate statistical outliers (see Material and Methods). Response features: C, spike count; L, latency; I, first ISI; RD, response duration. P-cell features are shown in orange; T-cell features in gray. C, Classification results for two intensities (20 and 60 mN) in combination with three durations (50, 200, and 500 ms; Table 1, estimation task duration and intensity). For response features and legend see B.

(3) After determining the rank class R_i for each of the responses in the training dataset (Fig. 2B), we calculated the rank class matrix for the response feature, showing how many traces of each stimulus class S_i were assigned to each of the rank classes R_{1…N}. If the rank-class look table contained two or more rank classes for the specific response feature value, one of them was chosen by chance for the entry into the rank class matrix.

For combined response features, the rank class matrix did not have a square shape. In our example of Figure 2, the combined analysis of spike count and latency would lead to a 3 × 5 matrix, connecting the three stimuli to the five possibilities of summed rank class numbers (see Step 2).

(4) Reading this matrix in the opposite direction, we determined for each rank class R_i, from which stimulus class S_j most responses were obtained. The resulting maximum likelihood assignment table (Fig. 2B, bottom right) was the basis for the stimulus estimation in the test phase. Again, if more than one stimulus classes S_j shared the same maximum probability for triggering a response in R_i, both class numbers were included into the stimulus estimation table.

This procedure was done in the same way for single and for combined response features, leading to the same way of stimulus estimation in the test phase.

(5) In the test phase (Fig. 2C), the remaining response traces were used to estimate the stimuli they were most probably elicited by. For each test response, the response feature (Fig. 2, spike count) value was determined and assignment to one rank class R_i according to the rank look table created during the training phase (Fig. 2B, line 4). With the stimulus estimation table (Fig. 2B, bottom right), we determined the stimulus class S_j with the highest probability of eliciting a response belonging to this rank class R_i (maximum likelihood). The corresponding stimulus #j was the estimated stimulus for this test response (e.g., for the rank class R₂ the stimulus response class S₂ had the highest probability, leading to the assignment of #2 as estimated stimulus for the left-most and middle response traces in Fig. 2C).

(6) Finally, we constructed a confusion matrix (Quian Quiroga and Panzeri, 2009) by repeating this procedure consisting of training and test phase M times, using each of the response traces once as test data. For each response trace, the value of 1 was added to the component of the confusion matrix corresponding to the resulting pair of presented and estimated stimuli. Hence, correct estimations added to the diagonal components, while wrong estimations added 1 at other positions. If two or more stimuli shared the highest probability of eliciting a response in this specific rank class (more than one entry in the estimated stimulus assignment table), the test response was assigned to all of them to equal parts, leading to non-integer numbers in the confusion matrix.

(7) In the last step, we calculated the percentage of correct estimations as the ratio of the summed diagonal components divided by the total number of responses (Fig. 2C, bottom).

This procedure was used in both estimation approaches, pairwise discrimination and classification (see below), for all response features A–H individually and in all possible pairwise combinations for all cells. For T cells, we additionally analyzed burst spike count (I) in combination with burst duration (J) and with latency difference (E) as feature pairs.

Pairwise discrimination.

The pairwise discrimination deals with the question as to how well two stimuli can be discriminated based on specific response features. This approach reveals the minimum differences between intensities or locations that can be discriminated based on the neuronal responses. For the example shown in Figure 2, we would at first analyze a small intensity difference by comparing only the first two stimuli and their responses, but ignoring stimulus 3. In the next step, the discrimination of a larger intensity difference would be analyzed by comparison of stimuli 1 and 3. Results are represented in Figures 4A and 6A, as mean values of percentages of correct decisions with SEM and fitted with a logistic function. Chance level of pairwise discrimination is always 0.5 and discrimination threshold was defined as 0.75 (75% correct estimation; Johnson and Philips, 1981; Thomson and Kristan, 2006).

Classification.

The idea of the classification approach is to quantify how well a set of N stimuli can be estimated based on a specific response feature (Fig. 2 shows the classification of three stimuli based on the spike counts of the response traces). Chance levels for classification depended on the number of different stimuli. Since in our dataset all stimuli were presented equally often, the chance level for this method was defined as 100/N % (33.33% in Fig. 2). In this study, classification of nine different locations (Fig. 4B), five different intensities (Fig. 6B), three different durations (Fig. 7B), six different combinations of intensities and durations (Fig. 7C), and six different combinations of intensities and durations (Fig. 8A,B) of mechanical stimuli were classified. The exact values of these stimulus properties are given in Table 1. Classification results in Figures 4, 6, 7, and 8 are given in percentage correct and displayed in boxplots, in which black dots mark the median values and box edges the 25th (q₁) and 75th (q₃) percentiles. Whiskers show minimum and maximum data values, which were not considered as outliers. Outliers, determined by the standard MATLAB boxplot function as values x > q₃ + 1.5(q₃ − q₁) or x < q₁ − 1.5(q₃ − q₁), are plotted as individual dots.

For estimation of location-intensity combinations, we used pooled data of P and T cell double recordings (Fig. 8B) to approximate encoding by the full mechanosensory cell population. The five P-cell double-recordings were randomly combined across preparations with the five T-cell double-recordings. In these cases, the response features of the two cell types were combined in the same way as previously described for one cell type (see Stimulus estimation). Briefly, rank class numbers were determined for each cell type separately for estimation of either intensity or location and combined to one number by summation. All following steps of training and test phases were performed in the same way as for separate response features. When performing estimation based on pooled data several times with random combinations, the estimation results were stable and did not show any significant differences across the pooled data groups.

Mutual information.

We computed the mutual information (Quian Quiroga and Panzeri, 2009) of all possible pairs of response features and stimulus properties in bits.

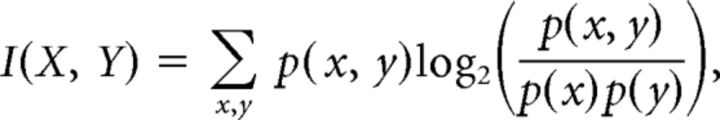where X denotes the stimulus property and Y the observed neuronal response feature. p(x, y) is the joint probability distribution function of X and Y; p(x) and p(y) are the marginal probability distribution of X and Y, respectively. The numbers of repetitions and stimuli influence the maximal information for each response feature. To allow a comparison of results, the values in Tables 2 and 3 are normalized to the maximal information, defined for each case as the information of a 100% correct estimation.

Table 2.

Normalized mutual information of response features with stimulus properties (mean ± SD)

	Cells	Count	Latency	Sum count	Latency diff
Encoding task: 9 locations
Fixed Int & Dur
10 mN, 200 ms	T	0.35 ± 0.12	0.49 ± 0.15	0.30 ± 0.11	0.73 ± 0.12
10 mN, 200 ms	P	0.35 ± 0.07	0.36 ± 0.07	0.25 ± 0.07	0.45 ± 0.12
50 mN, 200 ms	T	0.33 ± 0.04	0.51 ± 0.16	0.28 ± 0.08	0.61 ± 0.09
50 mN, 200 ms	P	0.36 ± 0.04	0.49 ± 0.10	0.33 ± 0.06	0.62 ± 0.09
Encoding task: 5 intensities
Fixed Loc & Dur
0°, 200 ms	T	0.44 ± 0.15	0.46 ± 0.16	0.48 ± 0.15	0.28 ± 0.17
0°, 200 ms	P	0.40 ± 0.09	0.39 ± 0.12	0.47 ± 0.11	0.25 ± 0.11
0°, 200 ms	P-T			0.52 ± 0.18	0.38 ± 0.11
Encoding task: 3 locations and 2 intensities
Fixed time
200 ms	T	0.38 ± 0.14	0.56 ± 0.07	0.36 ± 0.11	0.71 ± 0.08
200 ms	P	0.53 ± 0.14	0.49 ± 0.15	0.52 ± 0.13	0.52 ± 0.20

Bold numbers indicate the response feature with the highest mutual information obtained for the estimation task. Sum, Summed; Diff, difference; Int, Intensity; Loc, location; Dur, duration. Estimation tasks correspond to the stimulation protocols listed in Table 1.

Table 3.

Normalized mutual information of response features with stimulus properties (mean ± SD)

	Cells	Count	Latency	1st ISI	Resp dur
Encoding task: 3 durations
Fixed Int & Loc
60 mN, 0°	T	0.60 ± 0.24	0.11 ± 0.15	0.12 ± 0.12	0.59 ± 0.17
60 mN, 0°	P	0.84 ± 0.11	0.10 ± 0.08	0.18 ± 0.09	0.72 ± 0.12
Encoding task: 3 durations and 2 intensities
Fixed Location
0°	T	0.42 ± 0.13	0.34 ± 0.21	0.32 ± 0.13	0.49 ± 0.12
0°	P	0.50 ± 0.07	0.30 ± 0.7	0.32 ± 0.09	0.53 ± 0.05

Bold numbers indicate the response feature with the highest mutual information obtained for the estimation task. Resp, response; Dur, duration; Int, intensity; Loc, Location; ISI, interspike interval. Estimation tasks correspond to the stimulation protocols listed in Table 1.

Significance tests.

Significant influence of stimulus properties on neuronal response features was identified with the Friedman test (Hollander and Wolfe, 1999) with significance level p < 0.001, which is similar to two-way ANOVA, using ranks rather than the original data values. In this test, the response feature values (e.g., spike count or latency) measured for all stimulus conditions are ranked separately for each cell. Then, ranks obtained for all cells are grouped according to the stimulus condition they were elicited by. The null hypothesis is that the distributions of ranks are identical for all stimuli. If the null hypothesis is rejected, response ranks of at least one stimulus condition differ significantly from the rank distributions obtained for the other stimulus values, showing a significant effect of the stimulus property on the response feature for the set of recorded cells.

Significant differences between pairs of classification results in Figure 8 were tested with the Kruskal–Wallis significance test with p < 0.05 (Gibbons, 1985; Hollander and Wolfe, 1999). This test compares medians of independent samples from two or more groups and is a nonparametric version of the one-way ANOVA.

For pairwise discrimination shown in Figures 4 and 6, a one tailed t test with p < 0.05 was applied to define which discrimination results were significantly above the performance threshold of 75%.

All tests were performed with the MATLAB Statistics Toolbox (MathWorks).

Results

We used three complementary approaches to compare encoding performances of several response features for specific tactile stimulus properties and their combinations. First, pairwise discrimination (Thomson and Kristan, 2006) was used to estimate the minimum difference between stimulus locations or intensities that could be discriminated based on a specific neuronal response feature.

Second, we applied a classification approach to obtain a broader perspective on stimulus encoding. This method was used to quantify how well all experimentally tested stimulus properties and their combinations were represented by a specific neuronal response feature. Thirdly, the results obtained by both estimation approaches were confirmed by calculating the mutual information between stimulus properties and response features. With these three methods, we studied encoding of the mechanical stimulus properties location, intensity, and duration, as well as their combinations.

Encoding of location

In agreement with Thomson and Kristan (2006), we found that response latency and spike count of P cells depend significantly on the location of mechanical stimulation (Friedman test, p < 0.001). Qualitatively, the same dependencies were found for responses of P and T cells (Fig. 3). For touch intensities of 10 mN and of 50 mN, spike counts, latencies, and first interspike intervals of both cell types significantly depended on touch location (Friedman test, p < 0.001). Latency increased and spike count decreased with increasing distance to the center of the receptive field. Remarkably, both cell types show a smaller variance across trials in latencies as compared with spike counts (Fig. 3B,C, shows typical examples).

Encoding performances of several P- and T-cell response features were investigated using two stimulus estimation methods (Fig. 4). For P cells, our results support the finding of Thomson and Kristan (2006) that the latency difference of two cells with overlapping receptive fields is the best encoder of stimulus location. For a stimulus intensity of 50 mN, location differences of 10° could be significantly discriminated (Fig. 4A). For an average leech, with a circumference of 2.5 cm, this corresponds to a distance of ∼0.7 mm. In the more general task of stimulus estimation (Fig. 4B), the latency difference of both P cells allowed correctly assigning 60% of response traces to one of nine classes corresponding to the nine different stimulus locations. Moreover, the mutual information of latency difference and location of a 50 mN stimulus was higher than for any other P-cell response features (Table 2).

When comparing cell types, we found that latencies' differences of T-cell responses encode touch location even more precisely than P-cell responses (Fig. 4; Table 2). This finding was particularly evident for very soft touch stimuli of 10 mN, which could not be discriminated based on P-cell responses, whereas T-cell responses allowed a significant discrimination of location differences as small as 5° (Fig. 4A). When a higher intensity of 50 mN was applied, T-cell latency differences still outperformed P-cell responses, with a lower discrimination threshold of only 5° location difference (Fig. 4A) and a larger percentage of ∼70% correct estimations of stimulus location (Fig. 4B). Hence, encoding of stimulus location depends on stimulus intensity, with the most sensitive mechanoreceptor playing the leading role for soft touch.

Features of the initial transient T-cell response at stimulus onset (Fig. 4B, features BC and BD) and combinations of response features (data not shown) did not improve encoding of stimulus location compared with the latency difference data of the pair of T cells. A smaller set of double recordings of one T and one P cell (data not shown) indicated that location estimation based on the combination of T- and P-cell features fell behind estimates based on latency differences between two T or two P cells.

We conclude that the location of tactile stimulation is most precisely encoded by a temporal population code; the relative timing of the first spikes produced by a pair of cells of the same type.

Encoding of intensity

When varying the pressure of mechanical stimuli applied to a constant position of the skin, we found that elevating stimulus intensity increased spike counts and decreased response latencies of both cell types (Fig. 5). Spike counts, latencies, and first interspike intervals of T and P cells showed significant differences (Friedman test, p < 0.001) for different intensities. Qualitatively, the same dependencies on stimulus intensity were found at different locations. Quantitatively, all stimulus intensities used in this study elicited higher spike numbers and shorter latencies when they were applied closer to a cell's receptive field (data not shown).

Stimulus estimation and mutual information based on single T- or P-cell responses revealed similar results for absolute latencies and spike counts (Fig. 6B; Table 2). For T cells, the spike count obtained during the full stimulus duration of 200 ms led to better estimation results than the spike count during the initial burst after stimulus onset (Fig. 6B, response features C and BC). Summing spike counts of two cells of the same type improved the results (Fig. 6A,B, response features C and SC), whereas the performance of latency differences clearly fell short (Fig. 6; Table 2). Qualitatively, the same results were found for an additional large dataset of P and T cells that were stimulated with a lower range of intensities (Table 1, estimation task intensities low, results not shown). For the ranges of stimulus intensities and locations we used in this study, we did not find a systematic dependency of intensity estimation results on stimulus location (data not shown). Because postsynaptic cells are not able to make use of absolute latencies without an additional reference point, we conclude that spike counts integrated over a small population of cells are the most suitable response feature for encoding intensity.

Concerning the interaction of cell responses, we found that the sum of P and T cell spike counts encoded stimulus intensity at least as well as cell pairs of the same type (Fig. 6). Using the summed spike counts of one P cell and one T cell yielded ∼70% correct estimations of five different intensities and a pairwise discrimination became significant at 30 mN intensity difference (Fig. 6). In summary, the intensity of mechanical skin stimulation is encoded by a spike-count population code, in which responses of different cell types might be combined.

Encoding of duration

To analyze the encoding of stimulus duration, we stimulated the skin with two intensities (20 and 60 mN) for three durations (50, 200, 500 ms). Spike counts of both cell types depended significantly (p < 0.001, Friedman test) on stimulus duration, with longer durations triggering more spikes (Fig. 7A). As expected, no significant dependency could be found for first interspike intervals of both cell types and latencies of P cells. For T cells, the distributions of obtained response latencies were so narrow that a rank-based significance test could not be applied in a meaningful way.

Because the mechanosensory cells are not spontaneously active, their response duration mimics stimulus duration to the first approximation, even though strong stimuli can cause prolonged firing (Fig. 5A), perhaps caused by muscle movement. For both cell types, the spike count and response duration yielded best results for stimulus duration estimation (Fig. 7B). The highest mutual information on stimulus duration was attained by the spike count of sustained spiking P cells, whereas the transient T-cell responses clearly fell short (Table 3). Nevertheless, when stimulus duration was varied in combination with intensity, the combination of stimulus properties (Table 1, estimation task duration and intensity) can best be estimated based on the response duration of P cells, with T cells performing only slightly worse (Fig. 7C). Accordingly, this P-cell response feature also yielded the highest mutual information for the combination of stimulus intensity and duration (Table 3). Because we did not apply this stimulation protocol during double recordings, we are not able to analyze the role of population coding on duration estimation.

Based on the available results, we conclude that the stimulus duration is best encoded by the temporal feature response duration of both cell types or by total spike count of P cells.

Encoding of property combinations

To estimate the individual stimulus properties location and intensity, we identified two different population codes. A temporal feature, the relative latency of two cells of the same type, was found to be the best encoder for the location of tactile skin stimulation. Stimulus intensity was encoded best by a spike count code; the summed spike count of cell pairs.

Because touch intensity and location were found to affect the same response features of T and P cells, the responses of individual cells to combined stimulus properties must be ambiguous. A stimulus of a given intensity elicits more spikes at a shorter latency if it is applied closer to the receptive field center. In addition, at each location, spike counts and latencies depend on the intensity of mechanical stimulation. A response trace with a low latency and a high spike count could be elicited either by a light stimulation close to the receptive field center, or by a stronger pressure applied farther away. Moreover, different stimulus properties interfere for encoding: estimation of stimulus location depends on intensity (Fig. 4A) and spike counts increase more steeply with stimulus duration for higher intensities (Fig. 7A). However, for the stimuli applied in this study we did not find a clear dependency on location for the estimation of stimulus intensity (data not shown).

To test how the leech could solve this ambiguity problem, we stimulated the skin with combinations of two intensities and three locations (Table 1, estimation task location and intensity), while performing T-and P-cell double-recordings (Fig. 8). The resulting six stimuli could be estimated above chance level based on the responses of pairs of the same cell type (Fig. 8A). Similar results were obtained in additional experiments, with up to 15 different stimuli, also for different values of response feature combinations (Table 1 and data not shown). For T-cell pairs, best estimation results for the combined stimulus were attained by latency differences (Fig. 8A, Table 2. For P-cell pairs, the combined stimulus features were best estimated based on summed spike counts or a combination of summed counts and latency differences (Fig. 8A; Table 2). For both cell types, estimation results improved greatly when stimulus properties were estimated separately based on the previously found optimal response features; location with latency differences and intensity with summed spike counts (Fig. 8B, two left-most boxplots).

To strictly test whether the interaction of both cell types improves estimation performance, simultaneous recording of the entire population consisting of both T cells together with both P cells would be necessary. However, due to our technical limitation of maximally three intracellular electrodes, we had to approximate full population responses by pooling recordings across preparations. When analyzing all possible pairs of combined experiments, we found very consistent results across preparations. The six different stimuli could be estimated almost perfectly (median 90% correct; Fig. 8B), when spike counts of both P cells were summed to estimate intensity and T-cell latency differences were used for location estimation. Summing spike counts of all four T and P cells for intensity estimation did not change the result significantly. All other combinations of cell types, response features and stimulus properties led to significantly poorer results (Fig. 8B). Qualitatively, the same results, albeit on a lower level of correct estimations, were found for more difficult tasks involving more stimulus combinations (Table 1, task location and intensity; 15 combinations, results not shown).

In conclusion, we found that mechanoreceptor pairs of both types encode different stimulus properties in a multiplexed way. Without having the opportunity to record from the entire population of mechanoreceptors simultaneously, we could show that combinations of stimulus properties could be estimated well based on the assumption of cell-type-specific tasks and population coding strategies. For our dataset, best stimulus estimation results were obtained when latency differences of the T-cell pair were used for the estimation of touch location in combination with summed spike counts of the P-cell pair for the estimation of stimulus intensity.

Discussion

The leech is able to react surprisingly precisely to tactile stimuli, despite its small nervous system and low numbers of mechanoreceptors (Baca et al., 2005; Kristan et al., 2005; Thomson and Kristan, 2006). Several prior studies examined leech mechanoreceptors and local bend behavior (Kristan, 1982; Lockery and Kristan, 1990; Lockery and Sejnowski, 1992; Lewis and Kristan, 1998; Zoccolan and Torre, 2002; Baca et al., 2005; Thomson and Kristan, 2006; Baltzley et al., 2010), but neither encoding of stimulus property combinations nor the interaction of mechanosensory cell types have been examined yet. In this study, we present evidence that multiplexed population coding of tactile stimulus properties by two mechanoreceptor types provides the basis for the excellent behavioral performance in stimulus discrimination.

Regarding the literature on leech mechanoreception, these results can provide the solution to an open question left by the study of Thomson and Kristan (2006). Analyzing P-cell responses, they found, in agreement with our study, relative latency to be the best encoder for stimulus location. Nevertheless, electric stimulation of P cells simulating their responses to tactile stimuli did not elicit local bend muscle contractions with the same spatial precision as tactile stimuli themselves. Our results suggest that the extremely precisely timed T-cell spikes are required to achieve this behavioral goal.

In a broader perspective, we discuss our results in the context of primate mechanoreception and identify common principles of somatosensory encoding.

Rate coding versus temporal coding

Although rate and temporal coding have traditionally been controversially discussed (Theunissen and Miller, 1995; Shadlen and Newsome, 1998; deCharms and Zador, 2000), recent studies in several sensory systems found evidence that simultaneous usage of both types of encoding represents different stimulus aspects (Panzeri et al., 2010; Ainsworth at al., 2012; Wohrer et al., 2013). In particular, the somatosensory system was found to simultaneously rely on both spike rates and timing (Harvey et al., 2013; Saal and Bensmaia, 2014). Mechanoreceptors of the primate glabrous skin and their downstream cortical targets seem to represent spatiotemporal features of tactile stimuli using temporal response properties (Johansson and Birznieks, 2004; Mackevicius et al., 2012; Harvey et al., 2013; Weber et al., 2013), whereas stimulus intensity is represented by a rate code (Bensmaia, 2008; Harvey et al., 2013). In good accordance with these results, we found evidence that the leech mechanosensory system also uses both types of encoding simultaneously. By means of stimulus estimation methods, we identified a temporal feature—relative latencies—as the best encoder for stimulus location. At the same time, a rate code—summed spike counts—best encoded stimulus intensity. Hence, this study confirms that the general principles of response feature combinations, rather than a dichotomy of spike count versus spike timing, applies to sensory coding.

Individual cells versus population coding

The classical hypothesis, that mechanoreception of the primate glabrous skin is a labeled line code (Abraira and Ginty, 2013; Zeveke et al., 2013), assumes that different receptor types provide input to isolated channels of information transmission for different modalities. However, several recent studies found evidence that signals from different mechanoreceptor types participate in shaping cortical response patterns, causing an integrated perception of several aspects of cutaneous stimulation (Bensmaia, 2008; Abraira and Ginty, 2013; Zeveke et al., 2013; Saal and Bensmaia, 2014). These findings are particularly relevant for natural tactile stimulation in behavioral contexts, because touching and manipulating objects always causes perception shaped by several combined stimulus properties (Johansson and Flanagan, 2009; Saal and Bensmaia, 2014). In particular, SA-I (slowly adapting) and FA-I/RA (rapidly adapting) afferents were shown to provide input to the same target cells in the somatosensory cortex (Saal and Bensmaia, 2014) and both to be involved in overlapping sensory tasks, such as the perception of intensity (Bensmaia, 2008), stimulus shape (Johansson and Birznieks, 2004), and texture (Weber et al., 2013) of tactile stimuli.

The mechanoreceptors of the leech serve the same function as mammalian mechanosensory afferents, i.e., transmitting mechanically induced action potentials to the CNS. They respond strikingly similarly to the afferents of the mammalian glabrous skin, e.g., the human fingertip and rodent paws (Zimermann et al., 2014). P cells resemble SA-I afferents in their sustained, slowly adapting responses to constant mechanical stimulation, whereas T cells share with FA-I afferents the rapid adaptation after stimulus onset and also tend to respond to stimulus offset (leech: Figs. 3A, 5A; Nicholls and Baylor, 1968; Baca et al., 2005; human: Vallbo and Johansson, 1984; Johansson and Flanagan, 2009; Abraira and Ginty, 2013).

Remarkably, these two leech receptor types seem to play very similar functional roles in encoding tactile stimulus properties to their primate counterparts. For humans and monkeys, it was found that estimation of touch intensity requires the integration of several afferents (Johnson, 1974; Muniak et al., 2007; Bensmaia, 2008; but see Arabzadeh et al., 2014). SA-I afferents are essential for intensity estimation of constant mechanical stimuli, but the perceived intensity of vibrating stimuli is approximated best by the weighted sum of activities of all afferent types (Muniak et al., 2007; Bensmaia, 2008). Even though an analysis of optimally weighted response features and cell types remains to be performed for the leech, we found in agreement that summed spike counts of two or more leech mechanoreceptors allowed the best estimation of stimulus intensity, in particular if P-cell responses were included.

Primates and leeches also share a common population coding principle for spatial properties of mechanical skin stimulation, namely relative latencies. In humans, the relative timing of first spikes represents the shape of tactile stimuli, with RA afferents allowing faster decoding than SA-I (Johansson and Birznieks, 2004). In leeches, the location of a small tactile stimulus can be estimated very precisely based on the latency difference of two mechanoreceptors, in particular of the T-cell pair.

Encoding of single stimulus properties versus multiplexing of stimulus properties

Leech mechanoreceptors and primate mechanosensory afferents clearly encode multiple properties of tactile stimuli in a multiplexed way. Each slowly adapting (SA-I and P), and each rapidly adapting (RA and T) cell tunes its spike rate to intensity and, at the same time, its latency to spatial aspects of tactile stimuli. Hence, response features on different temporal scales simultaneously represent complementary information on two different stimulus properties. This finding exactly matches the definition of multiplexing given by Panzeri et al. (2010).

However, our estimation of stimulus property combinations, i.e., stimulus location and intensity, suggests specialization of cell types for encoding one of the stimulus properties with a single response feature. The relative timing of the fast, and temporally precise, first spikes of the T-cell pair provides most information about stimulus location, whereas the summed spike counts of sustained P-cell pair responses indicate stimulus intensity (Fig. 8). In particular, combinations of response features can be predicted much better when responses of both mechanoreceptor types are considered rather than for each cell type separately. Hence, our results suggest that the multiplexed signals of mechanoreceptors may be split for decoding. This hypothesis needs to be tested experimentally on the next level of sensory signal processing, the responses of postsynaptic interneurons in the local bend network. If the leech uses the strategy we identified, we would expect to find coincidence detector interneurons sensitive to relative spike timing of mechanoreceptor pairs on the one hand and temporal integrator interneurons summing inputs from two or more mechanoreceptors over time on the other hand. Further experiments will reveal whether these distinct types of interneurons exist and which inputs they combine. A specialization to one mechanoreceptor type would hint toward a labeled line code, whereas inputs from both mechanoreceptor types to coincidence detector and integrator interneurons would carry multiplexed population coding onto the next network layer.

Previous studies of the primate sensory system typically focused on one stimulus property. To the best of our knowledge, no results were yet published on the encoding of combined intensity and spatial properties of tactile stimuli. However, very good evidence exists that neurons in the somatosensory cortex receive inputs from both SA-I and RA afferents and tune their responses to several (individually analyzed) properties of tactile stimuli, including intensity and spatial features (Saal and Bensmaia, 2014).

Conclusions

Leech mechanoreceptors and afferents of primate glabrous skin share not only their response patterns to tactile stimulation, but also several encoding mechanisms. Despite the great difference in cell numbers, both systems use the same stimulus property-specific population coding strategies. Because these strategies are shared by systems as different as the human fingertip and the leech body wall, they might be general mechanisms underlying somatosensation. The question of combined encoding of multiple stimulus properties, however, requires further analyses, particularly in the context of natural tactile stimuli. When the hand of a primate or the body wall of a moving leech touches an object, it induces a complex, temporally and spatially dynamic mechanical stimulation (Johansson and Flanagan, 2009), comprising several stimulus properties. The experimentally easily approachable, minimalistic system of the leech might help to understand how various stimulus features are integrated into one consistent perception, representing an object touched by a human fingertip.