Abstract
Motivated directly by recent trapped-ion quantum simulation experiments, we carry out a comprehensive study of the phase diagram of a spin-1 chain with XXZ-type interactions that decay as 1/rα, using a combination of finite and infinite-size DMRG calculations, spin-wave analysis, and field theory. In the absence of long-range interactions, varying the spin-coupling anisotropy leads to four distinct and well-studied phases: a ferromagnetic Ising phase, a disordered XY phase, a topological Haldane phase, and an antiferromagnetic Ising phase. If long-range interactions are antiferromagnetic and thus frustrated, we find primarily a quantitative change of the phase boundaries. On the other hand, ferromagnetic (nonfrustrated) long-range interactions qualitatively impact the entire phase diagram. Importantly, for α ≲ 3 long-range interactions destroy the Haldane phase, break the conformal symmetry of the XY phase, give rise to a new phase that spontaneously breaks a U(1) continuous symmetry, and introduce a possibly exotic tricritical point with no direct parallel in short-range interacting spin chains. Importantly, we show that the main signatures of all five phases found could be observed experimentally in the near future.
The study of quantum phase transitions in low-dimensional spin systems has been a major theme in condensed matter physics for many years [1]. A well-known implication of Mermin and Wagner’s famous results [2] on finite temperature quantum systems is that, for a large class of one-dimensional quantum spin systems, long-range order is forbidden even at zero temperature. This absence of classical order promotes quantum fluctuations to a central role, and they often determine the qualitative properties of the quantum ground state. An important example, first conjectured by Haldane [3,4], is that a spin-1 antiferromagnetic Heisenberg chain possesses a disordered phase with an energy gap to bulk excitations, later identified as a symmetry protected topological phase [5,6]. Its spin-1/2 counterpart, despite possessing the same classical limit, has a disordered ground state with gapless excitations, and is described by a conformal field theory (CFT) [7].
Experimentally, such quantum phase transitions have been explored in quasi-1D materials, and more recently using artificial materials designed through the careful control of atomic, molecular, and optical (AMO) systems [8–11]. These AMO systems are usually well isolated from the environment, offer considerable tunability of system parameters, and make possible both measurement and control at the individual lattice-site level. A distinctive feature of AMO systems is that interactions between particles are often long ranged, decaying as a power law with distance (1/rα). The exponent α varies widely amongst different AMO systems, ranging from α = 6 for van de Waals interactions in Rydberg atoms, to α = 3 for polar molecules and magnetic atoms, to α = 0 for atoms coupled to cavities [11–19]. The effect of long-range interactions can be tuned by either changing the dimensionality of the system, e.g., for neutral atoms or molecules in optical lattices, or by directly (and often continuously) altering the value of α, e.g., in trapped ions or cold atoms coupled to photonic crystals [14]. The availability of tunable long-range interactions creates an entirely new degree of freedom—absent in typical condensed-matter systems—for inducing quantum phase transitions, and can potentially lead to novel quantum phases [20–23].
While long-range interacting classical models have been studied in considerable detail for some time [24–28], there is a relative lack of in-depth studies of quantum phase transitions in long-range interacting systems, despite the emerging experimental prospects for studying both their equilibrium and nonequilibrium properties [15–18,29–35]. One reason is that many analytically solvable lattice models become intractable when interactions are no longer short ranged, a well-known example being the spin-1/2 XXZ model. Thus exact analytical studies are either restricted to noninteracting bosonic and fermionic systems with long-range hopping and pairing [33,35–37], or to certain contrived long-range interacting spin models which are difficult to realize in real systems [38–41]. In addition, to properly incorporate long-range interactions in low-energy effective theories, existing field theoretic treatments need to be modified and usually become more complicated [42,43]. While spin-wave theories can be useful in treating long-range interactions [44,45], they are unable to distinguish major differences in quantum phases between integer and half-integer spin chains. Exact numerical studies for long-range interacting spin models are restricted to small system sizes and usually inconclusive [46–49], since the correlation length is generally divergent [32,50]. Approximate numerical techniques such as the density matrix renormalization group (DMRG) method have been adapted to treat long-range interactions [51], but determining complete diagrams with large-system-size calculations remains challenging, and those that exist are primarily for spin-1/2 chains [20,29,52,53].
In this paper, we carry out a comprehensive study of a spin-1 chain with tunable XXZ interactions that decay monotonically as 1/rα, for all α > 0. Our study is largely motivated by imminent trapped-ion-based experiments that can simulate this model with widely tunable index α [54–56]. In the absence of long-range interactions, the choice of spin-1 over spin-1/2 allows us to have four distinct quantum phases by varying the anisotropy of the interactions: a ferromagnetic (FM) phase and an antiferromagnetic (AFM) Ising phase that are both gapped and long-range ordered, a disordered gapless phase (the XY phase), and a gapped and topologically ordered phase (the Haldane phase). By using a combination of DMRG calculations, spin wave analysis, and field theory, we obtain the phase diagram for arbitrary anisotropy and all α > 0, with both ferromagnetic and antiferromagnetic interactions. Our key observation is that when interactions in all spatial directions are antiferromagnetic, long-range interactions are frustrated, leading to primarily quantitative changes to the phase boundaries compared to the short-range interacting chain. Interestingly, we find that the topological Haldane phase is robust under long-range interactions with any α > 0 [48,49,57]. However, when the interactions in the x-y plane become ferromagnetic, we find a number of significant modifications to the phase diagram: (1) The Haldane phase is destroyed at a finite α due to a closing of the bulk excitation gap; (2) the gapless XY phase, described by a CFT with central charge c = 1, disappears when α ≲ 3 due to a breakdown of conformal symmetry [33,35]; (3) the disappearance of the XY phase heralds the emergence of a new phase at α ≲ 3 (continuous-symmetry breaking, or CSB) in which the spins order in the xy plane, spontaneously breaking a U(1) symmetry and possessing gapless excitations (Nambu-Goldstone modes); (4) Novel tricritical points, with no direct analog in short-range interacting 1D models, appear at the intersection of the Haldane, CSB, and XY/AFM phases.
The paper is organized as follows. In Sec. I, we introduce the model Hamiltonian and present complete phase diagrams for the ferromagnetic and antiferromagnetic cases. In Sec. II, we study the boundary of the FM phase, where a spin-wave approximation is found to be asymptotically exact in the large-system limit. In Sec. III, we determine both the XY-to-Haldane and Haldane-to-AFM transition lines accurately using DMRG calculations and use field theory arguments to explain the effect of long-range interactions on the boundary of the Haldane phase. In Sec. IV, we introduce the CSB phase and explain its emergence using spin-wave theory. The boundary between the CSB and XY phases is determined by a numerical calculation of central charge. In Sec. V, we show that all five phases possess distinct signatures that could be observed in near-future trapped ion quantum simulations with chains of 16 spins. Finally, we conclude the paper in Sec. VI and comment on a number of open questions.
I. MODEL HAMILTONIAN AND PHASE DIAGRAMS
We consider the following spin-1 Hamiltonian with long-range XXZ interactions in a 1D open-boundary chain:
| (1) |
Here Jz ∈ (−∞, ∞) and α ∈ (0, ∞) are allowed to vary continuously, and we consider both the Jxy = 1 (antiferromagnetic) and Jxy = −1 (ferromagnetic) cases. We note that, for 0 < α < 1, Eq. (1) does not have a well-defined thermodynamic limit when Jxy and/or Jz is ferromagnetic, since the ground-state energy density diverges. To make the ground-state energy extensive, we may impose an energy renormalization factor Nα−1, first introduced by Kac [58], when taking the thermodynamic or continuum limit (here N is the chain length). For finite-size numerical calculations, we do not need to implement the Kac renormalization for 0 < α < 1 since ground-state properties are unaffected by energy renormalization [59].
Figure 1 shows our full phase diagram for both Jxy = 1 and Jxy = −1, with actual phase boundaries plotted using the results of calculations discussed in the following sections. The nearest-neighbor interaction limit is achieved at α → ∞ (1/α = 0). In this limit, the Hamiltonian in Eq. (1) with Jxy = −1 is equivalent to the one with Jxy = 1, as can be seen by performing a local unitary transformation that flips every other spin in the x-y plane while preserving the spin commutation relations: . The different ground-state phases of this short-range Hamiltonian have been well studied [60–62]. Notably, Haldane first conjectured [3,4] that for λ1 < Jz < λ2, a disordered gapped phase (the Haldane phase) will emerge. At Jz = λ2, the ground state undergoes a second-order phase transition from the Haldane phase to an AFM phase, which belongs to the same universality class as the 2D Ising model. The value λ2 ≈ 1.186 has been found by various numerical techniques including Monte-Carlo [63], exact diagonalization [64], and DMRG [65–67]. At Jz = λ1, a Berezinskii-Kosterlitz-Thouless (BKT) transition intervenes between the Haldane phase and a gapless disordered XY phase at Jz < λ1. The value of λ1 is theoretically predicted to be exactly zero after mapping Eq. (1) (for α = ∞) to a field theory model using bosonization [68]. This prediction is supported by conformal field theory arguments [69] and a level spectroscopy method based on a renormalization group analysis and the SU(2)/Z2 symmetry of the BKT transition [61,70–72]. Numerically, λ1 ≈ 0 has been verified via finite-size scaling [64,73,74] and DMRG [65]. Finally, at Jz = λ0 = −1, a first-order phase transition from the XY phase to a ferromagnetic Ising phase takes place [61,66,75].
FIG. 1.
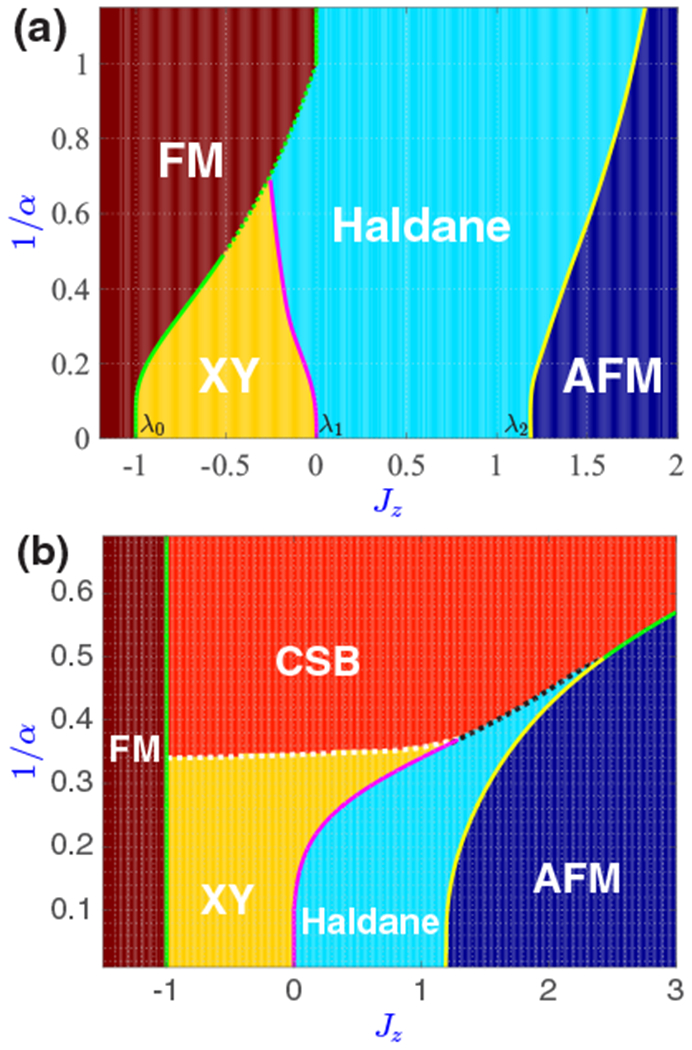
Proposed phase diagram for (a) Jxy = 1 and (b) Jxy = −1. Five different phases are identified: a ferromagnetic (FM) Ising phase, an antiferromagnetic (AFM) Ising phase, a disordered XY phase, a topological Haldane phase, and a continuous symmetry breaking (CSB) phase. At α = ∞, the transition points are denoted by Jz = λ0,1,2 in (a). The FM-to-XY, FM-to-CSB, and CSB-to-AFM transitions are first order (green line); the XY-to-Haldane transition is BKT type with central charge c = 1 (purple line); the Haldane-to-AFM transition is second order with c = 0.5 (yellow line); the CSB-to-XY transition (white dotted line) has c = 1, but is a BKT-like transition corresponding to a universality class different from the XY-to-Haldane transition [83]; the CSB-to-Haldane transition (black dotted lines) appears to be an exotic continuous phase transition not described by a 1+1D CFT. The location of solid transition lines are expected to be accurate in the thermodynamic limit, while the location of dotted transition lines may have a small uncertainty.
We now introduce our results for the long-range interacting case (1/α > 0). For Jxy = 1 and Jz > 0, long-range interactions are frustrated and the Haldane-to-AFM phase transition point λ2(α) increases moderately as α decreases, without changing the universality class of the transition. For sufficiently small Jz < 0, the ferromagnetic long-range interactions along the z direction eventually favor a ferromagnetic ground state, inducing a first-order transition at λ0(α). The magnitude of the critical coupling, |λ0(α)|, decreases monotonically from 1 (at α = ∞) to 0 (for all α ⩽ 1) in the thermodynamic limit. The XY-to-Haldane phase boundary λ1(α) becomes negative for finite α, eventually terminating in a tricritical point at the intersection of FM, Haldane, and XY phases. The entire XY phase (including the XY-to-Haldane phase boundary) has conformal symmetry with c = 1, and the XY-to-Haldane phase boundary remains a BKT transition until it terminates at the tricritical point. We note that the phase diagram [Fig. 1(a)] is similar to Fig. 1 in Ref. [76], which studies the XXZ spin-1 chain with next-nearest-neighbor interactions of tunable strength. This is partially because the frustrated long-range interactions in the x-y plane effectively cancel each other at different ranges, so their influences on the phase boundary are somewhat similar to those from next-nearest-neighbor interactions. However, we point out that the full 1/rα long-range interactions, frustrated or not, will result in power-law decaying correlation functions in the gapped phases (see Ref. [57] for details); such correlations are absent in models with next-nearest-neighbor interactions [76–79].
For Jxy = −1, where long-range interactions in the x-y plane are not frustrated, the phase diagram [Fig. 1(b)] shows a number of important qualitative differences from the nearest-neighbor phase diagram as α is decreased. First, the XY-to-Haldane phase boundary bends significantly toward positive Jz, and we find the Haldane phase to terminate at α ≈ 3 for Jz = 1. Second, we expect the XY phase to disappear for α ≲ 3 due to the breakdown of conformal symmetry [33,35]. Third, for α ≲ 3 a new CSB phase emerges—this is not in violation of the Mermin-Wagner theorem, as it no longer applies for this range of interactions [2,52,80–83]. The CSB-to-AFM phase transition is expected to be first-order, since at large Jz and small α, quantum fluctuations play negligible roles for both the Néel-ordered state and the ordered CSB state. This behavior is similar to the transition between the AFM phase and the large-D phase (where a large positive anisotropy term causes all spins to stay in the state) reported in Refs. [65,66,75]. The Haldane phase has a c = 1 critical phase boundary with the XY phase, a c = 0.5 phase boundary with the AFM phase [67], and a possibly exotic phase boundary with the CSB phase, a boundary that is not described by a 1+1D CFT.
II. FM PHASE AND ITS BOUNDARY
Because the ferromagnetic state with all spins polarized along ±z (or an arbitrary superposition of these two states) is an exact eigenstate of the Hamiltonian for any value of α and Jz, we expect a first-order quantum phase transition at the boundary of the FM phase. The FM state has an energy EFM = Jz Σi>j(i − j)−α, and the phase transition out of this state, defining the critical line Jz = λ0(α), occurs when some other eigenstate with no ferromagnetic order appears with a lower energy. The dependence of λ0 on α can be estimated using the following intuitive argument. For a given Jz < 0, the energy density of the ferromagnetic state in the thermodynamic limit is given by is the Riemann zeta function], which diverges as α → 1. For Jxy = 1, the magnitude of the energy density arising from the term can be at most (the Dirichlet eta function), with this value obtained for any state that is Néel-ordered along some direction in the x-y plane. The competition between the energy of these two classical states gives a critical point Jz ≈ −η(α)/ζ(α), which smoothly varies from Jz = −1 at α = ∞ to Jz = 0 at α = 1. For Jxy = −1, the situation is quite different, because the polarized state along any direction in the x-y plane has an energy density equal to −ζ(α), and thus we naively expect the phase boundary to be at Jz = −1 for all α > 0.
More formally, the boundary can be calculated via a spin-wave analysis. We treat the spin state that is polarized along the +z direction as the vacuum state with no excitations and apply the Holstein-Primakoff transformation (for spin 1) to map spin excitations (spin-waves) into bosons: , . In the weak excitation limit, , we can approximate , and our Hamiltonian becomes
| (2) |
where we have ignored the interaction terms since is assumed. Assuming for the moment periodic boundary conditions, this quadratic Hamiltonian can be diagonalized by Fourier transformation, , with the following dispersion relation (q ≡ 2πk/N) for an infinite system
| (3) |
If ωmin ≡ min ω(q) > 0, then the ground state of Hsw is the vacuum state of all modes k, and for all i, consistent with the approximation . If ωmin < 0, then the ground state has an extensive number of spin excitations and the spin-wave approximation should break down, and we do not expect the polarized state in the z direction to be the quantum ground state. The ωmin = 0 condition thus sets the phase boundary for Hsw. For Jxy = 1, ωmin = ω(q = π) = −Jz ζ(α) − η(α), leading to a critical line of Jz = −η(α)/ζ(α). For Jxy = −1, ωmin = ω(q = 0) = (1 − Jz)ζ(α), leading to a critical line at Jz = −1, independent of α. These results exactly match with the previous intuitive arguments.
We now compare the above spin-wave theory prediction with infinite-size DMRG calculations [84,85] for Jxy = 1. As seen in Fig. 2, the numerical results agree well with the spin-wave theory at large α, and the spin-wave prediction of λ0(α) is asymptotically exact as α → ∞. However, a small but increasing difference in λ0(α) is seen as α decreases. For α ≳ 1.5, our infinite-size DMRG calculations converge well (see appendix A for our numerical treatment of long-range interactions), and we conjecture that it is the spin-wave approximation that starts to break down when α decreases. This is possibly due to stronger effects of interactions between spin-wave excitations as α becomes smaller, so that the spin-wave approximation (which ignores interactions) becomes less and less accurate. While our infinite-size DMRG calculations do not converge well for α ≲ 1.5, the spin-wave prediction should be asymptotically exact as α → 1, since the FM state’s energy is super extensive for α ⩽ 1 and λ0(α ⩽ 1) = 0. As a result, in Fig. 1(a) we have adopted the spin-wave prediction for the FM phase’s boundary, but made the boundary line dotted for 1 < α < 2 to represent a small uncertainty in the transition point [for α > 2 the uncertainty of the transition point is well below the resolution of Fig. 1(a)]. For Jxy = −1, our infinite-size DMRG calculations provide exactly the same transition point λ0(α) = −1 as the spin-wave theory, independent of α [Fig. 1(b)].
FIG. 2.
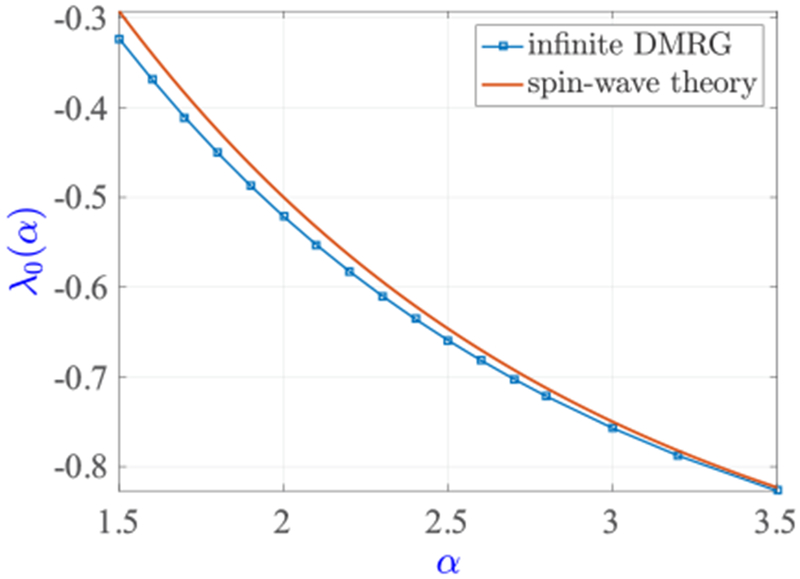
Comparison of the (first-order) transition point λ0(α) out of the FM phase calculated using infinite-size DMRG and spin-wave theory for Jxy = 1. The spin-wave theory predicts λ0(α) = −η(α)/λ(α). The infinite-size DMRG calculations use a bond dimension χ = 100, and increasing χ to 200 does not yield results distinguishable within the resolution of the plot. The transition point is numerically determined by finding the value of Jz at which the ground state energy density obtained from infinite-size DMRG calculations is equal to that of the FM state.
III. HALDANE PHASE AND ITS BOUNDARY
The existence of the Haldane phase in a spin-1 XXZ chain makes the phase diagram much richer than that of a spin-1/2 XXZ chain. We focus first on the XY-to-Haldane phase boundary λ1(α). The transition out of the Haldane phase is signaled by a vanishing of the string-order correlation function when |i − j| → ∞. However, because the phase transition is of the BKT type, changes rather smoothly with Jz and α for a finite |i − j|, and it is very challenging to find the exact transition point numerically. Finite-size scaling using exact diagonalization on small chains must be performed very carefully due to logarithmic corrections in system size [61,86–88], and infinite-size DMRG yields a phase transition point that depends strongly on the bond dimension χ (the dimension of the matrix product states used [89]), since the ground state bipartite entanglement entropy S grows logarithmically with system size N according to CFT: S = c log N + const [90]. As seen in Fig. 3, for χ = 100 and at α = ∞, the string-order correlation function appears to start vanishing at Jz ≈ 0.3, instead of at Jz = 0 as predicted by field theory [68]. However, this is consistent with previous infinite-size DMRG calculation results [65,66]. To extract a more accurate phase boundary, we perform a scaling of χ ranging from 50 to 200 near the XY-to-Haldane phase boundary, following a procedure similar to that in Ref. [65]. We then extract the XY-to-Haldane phase boundary (white line in Fig. 3) by determining the location where vanishes, which now correctly yields Jz ≈ 0 at α = ∞. However, we expect a few percent uncertainty in the transition point due the use of at a finite separation |i − j|, and due to the error in extrapolating .
FIG. 3.
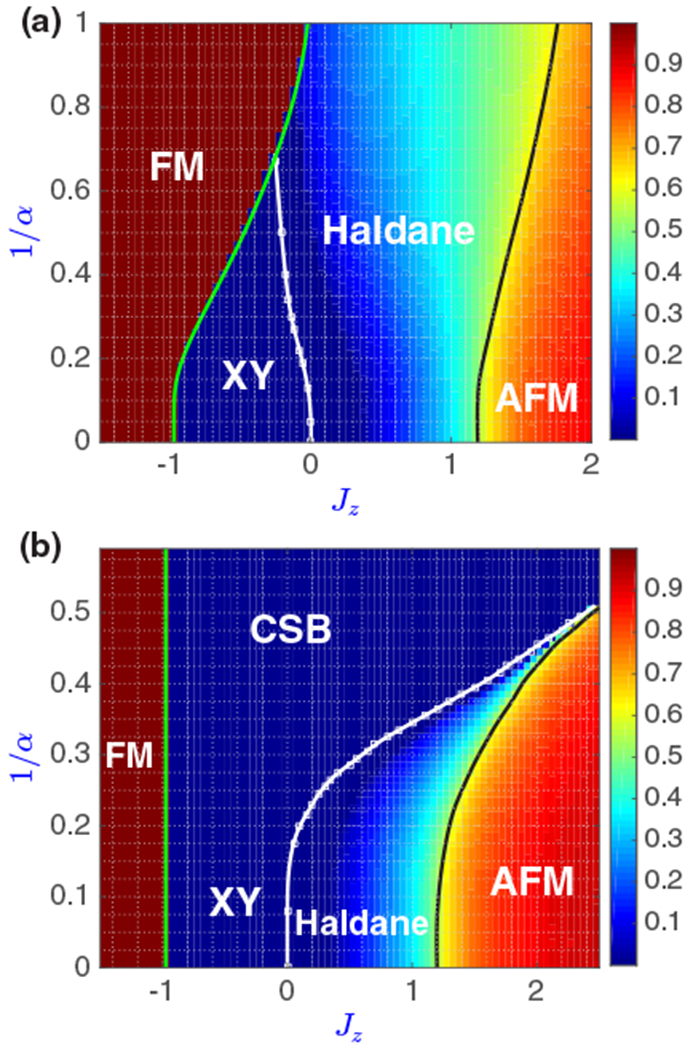
Infinite-size DMRG calculation of for a separation of |i − j| = 500. in the FM phase and deep in the AFM phase for any i and j. As |i − j| → ∞, is finite for the Haldane phase and zero for the XY phase, thus we can use it to locate the XY-to-Haldane phase boundary. (a) Jxy = 1. The FM phase boundary (green line) is given by the spin-wave prediction Jz = −η(α)/ζ(α). (b) Jxy = −1. The FM phase boundary (green line) is exactly at Jz = −1. For both (a) and (b), we vary the bound dimension χ to accurately determine the XY-to-Haldane phase boundary, determining the value of Jz at which vanishes (for a large but finite |i − j|) and then extrapolating to the χ → ∞ limit (white squares fitted by the white line). The black line is the Haldane-to-AFM phase boundary, which is determined from (see Fig. 4).
To explain why long-range interactions bend the XY-to-Haldane phase boundary in opposite directions for ferromagnetic and antiferromagnetic Jxy, we use an effective field theory first proposed by Haldane [3] and developed by Affleck [91]. The proper inclusion of long-range interactions within this field theoretic approach was discussed in detail in Ref. [57]. Here, we give a brief review of this field-theory treatment. Consider first the case of Jxy = Jz = 1. In this case, each spin-1 is mapped to a staggered field and a uniform field . Importantly, we observe that the classical ground state of H is always Néel-ordered for any α > 0, with n2(x) = 1 and l(x) = 0 for any position x. The intuition behind this decomposition is that, in the quantum ground state, n(x) should have only long-wave-length variations with n2(x) ≈ 1, while l(x) ≈ 0 should represent long wave-length perturbations to the direction of n(x) due to quantum fluctuations. Therefore, when working with the Fourier-transformed fields n(q) and l(q), we can expand the Hamiltonian in powers of the momentum q and keep only the leading order terms.
The effective Hamiltonian in the continuum limit and momentum space reads (the lattice spacing is set to 1 for simplicity)
| (4) |
where the cross terms between n and l are ignored because they involve n(q) near q = π. The dispersion relations Ω(q) and ω(q) can be expanded at small q as [92]:
| (5) |
For the n field, we need to keep the q2 term since the zeroth-order term gives a constant due to the approximation n2(x) ≈ 1. The zeroth-order term in q for the l field is the dominant source of quantum fluctuations, and we can ignore higher-order terms in determining whether Heff is gapped or not (they do contribute to the long-distance behavior of correlation functions though [57]). Thus the Hamiltonian is approximately given by . In a coherent-spin-state path-integral representation, the action is quadratic in the field l and it can be integrated out [1,93]. The remaining path integral over the staggered field n defines a 1+1D O(3) nonlinear sigma model, with Lagrangian density (nonlinear constraint n2(x) = 1 implied)
| (6) |
Here the effective coupling g and spin-wave velocity v depend both on α and the lattice spacing (their exact values are not important to us). The coupling strength g flows towards infinity under renormalization group for the above Lagrangian [1,93], suggesting a disordered ground state with an excitation gap. This is corroborated by the variant of the Hamiltonian in the limit, which can be analytically solved and contains a mass gap [91,94]. Now we adopt a phenomenological treatment [95,96] of the above Lagrangian (Eq. 6): The nonlinear constraint n2 = 1 can be approximately removed by introducing a mass gap Δα and a renormalized spin-wave velocity vα. We thereby arrive at a free field theory with the Lagrangian density (written in momentum space)
| (7) |
Since Δα→∞ ≈ 0.41 [97,98] and Δα→0 = 1 (where the Hamiltonian becomes integrable), we infer that Δα should increase as α decreases. This speculation is confirmed by accurate finite-size DMRG calculations of Δα in Ref. [57].
Next, we consider the case of Jxy = 1 but Jz < 1. We can then write
| (8) |
Following Refs. [76] and [91], the anisotropy term above can be treated as a negative mass term to the Lagrangian density in Eq. (7). The precise value of the renormalization factor fα is not important to us, but we expect it to continuously decrease as α becomes smaller, since the staggered field dominates in the Haldane phase and long-range interactions [ in Eq. (8)] are increasingly frustrated as α decreases. The mass gap for the field nz is now smaller than for nx and ny, and reads . Combined with the above discussion that Δα should increase with decreasing α, we require progressively more negative Jz to close the gap and transition into the XY phase as α decreases, thus explaining the shape of the XY-to-Haldane phase boundary in Fig. 3(a).
For Jxy = −1 and Jz < 1, the classical ground state is no longer Néel ordered and the field theory employed above is not valid. However, by rotating every other spin by π about the z axis, we generate a transformed Hamiltonian
| (9) |
Now the classical ground state is Néel ordered (along any direction for Jz = 1). The first term above is isotropic, and gets mapped to
| (10) |
where the roles of ω(q) and Ω(q) are swapped as compared to Eq. (4). For α < 3, Ω(q) in Eq. (5) is now dominated by the nonanalytic term |q|α−1 at small q, and we can no longer obtain the simple free Lagrangian in Eq. (7). In Ref. [57], it is shown that the |q|α−1 term in the dispersion of n(q) in Eq. (10) leads to a renormalization group flow towards a gapless ordered phase spontaneously breaking an SU(2) symmetry for α < αc ≲ 3. For our complete Hamiltonian H′ in Eq. (9), the anisotropy leads instead to a U(1) continuous symmetry breaking phase for (see the next section for further discussions, where is estimated to be 2.9 at Jz = 1). Our infinite-size DMRG calculations in Fig. 3(b) suggest that the Haldane phase terminates at a critical α around 3.1 for Jz = 1, and the XY phase is expected to exist in between the CSB phase and the Haldane phase at Jz = 1 for .
For α > 3, Ω(q) is dominated by q2 and we can once again reduce H′ to the free field Lagrangian Eq. (7), but with a different mass gap , and spin-wave velocity . The anisotropy term in Eq. (9) changes the gap to . Here gα is a renormalization factor due to nonfrustrating long-range interactions in Eq. (9), and should thus increase as α decreases, while hα is a renormalization factor due to frustrating long-range interaction in Eq. (9), and should decrease as α decreases. Together with the expectation that the gap , should decrease with α [47,57] due to the appearance of gapless continuous symmetry breaking phase at α ≲ 3, we conclude that the gap closes at a point with Jz strictly larger than zero in the presence of long-range interactions, again consistent with our numerical results.
We point out that a different field theoretic approach based on non-Abelian bosonization [57,68] can also be employed to predict the qualitative changes to the XY-to-Haldane phase boundary. This technique has been used to predict the XY-to-Haldane phase boundary of a spin-1 XXZ chain with next-nearest-neighbor interactions [76], which is a reasonable approximation to our model when α is large enough that next-nearest-neighbor interactions dominate over the next-longer-range interactions.
We end this section with a brief discussion of the boundary between the Haldane and AFM phases. Both the Haldane and AFM phases are gapped and have finite entanglement entropy in the infinite-system-size limit [99]. Thus we see well-converged results for bond dimensions of χ ⩾ 100 in our infinite-size DMRG calculations. We extract the Haldane-to-AFM phase boundaries using the spin-spin correlation functions (see Fig. 4), and plot them as black lines in Figs. 3(a) and 3(b). Good agreement with existing literature [63–66] is found for the Haldane-to-AFM transition point at α = ∞ (1.15 < Jz < 1.2). The bending of the Haldane-to-AFM phase boundary toward larger Jz for both Jxy = 1 and Jxy = −1 in the presence of long-range interactions can be understood via simple energetic considerations. In the AFM phase, the spins are (nearly) antialigned in the z direction; long-range interactions are strongly frustrated, and the energy at α → 0 is only half of the α = ∞ case for a perfectly Néel ordered state. In the Haldane phase, the AFM order of spin correlations 〈Si · Sj〉 decays exponentially (followed by a small power-law tail [57]), and thus the ground state energy is much less frustrated by the long-range interactions. As a result, we expect the disordered ground state in the Haldane phase to have progressively lower energy than an AFM ordered state as a decreases at a given Jz, and hence a larger (but always finite even for α → 0) Jz is needed to make the transition from the Haldane phase into the AFM phase.
FIG. 4.
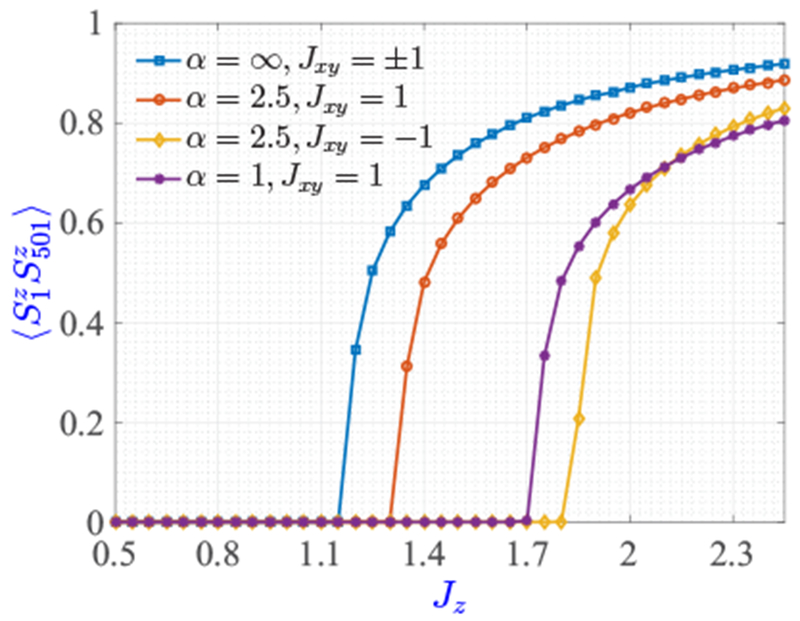
as a function of Jz calculated using infinite-size DMRG for a few different sets of α and Jxy. The Haldane-to-AFM phase transition is clearly observed and we locate the transition point by finding the critical Jz (restricted to Jz > 0) above which . The curves shown look nearly identical when we increase the bond dimension used from 100 to 200.
IV. CSB PHASE AND ITS BOUNDARY
The celebrated Mermin-Wagner theorem rigorously rules out continuous symmetry breaking in 1D and 2D quantum and classical spin systems at finite temperature, as long as the interactions satisfy the convergence condition in the thermodynamic limit (rij and Jij are respectively the distance and coupling strength between sites i and j) [2]. The long-distance properties of 1D spin systems at zero temperature can often be related to those of a 2D classical model at finite temperature; however, in the process of this mapping, the long-range interactions are only inherited by one of the two spatial directions in the classical model, and the Mermin-Wagner convergence condition will be satisfied for interactions decaying faster than 1/r3. Thus we expect no continuous symmetry breaking in the ground state of our Hamiltonian Eq. (1) for α > 3. Indeed, we have found exclusively disordered or discrete (Z2) symmetry breaking phases for α > 3 in our phase diagrams (Fig. 1). Continuous symmetry breaking can (and does) appear when α < 3. To gain a better understanding of the robustness of symmetry breaking states to quantum fluctuations, below we carry out a spin-wave analysis [100]. Similar analysis can be also found in Ref. [44] and [45] for Heisenberg chains with long-range interactions.
We start by considering the Jxy = −1 case, and take the state with all spins polarized along the +x direction as the vacuum state. With this choice of vacuum, and assuming that the density of spin waves is small ( in the following expressions), the Holstein-Primakoff mapping is now , . Under this mapping, and dropping terms that are quartic in bosonic operators (again based on the assumption that , H becomes
| (11) |
| (12) |
| (13) |
where . Hswx can be diagonalized with a Bogoliubov transformation, yielding noninteracting Bogoliubov quasiparticles with a spectrum νk. Importantly, when |ωk| > |μk|, νk > 0 and the vacuum is dynamically stable. When |ωk| < |μk|, νk is imaginary and the system is dynamically unstable indicating that we have made the wrong choice of a classical ground state. Using the expressions for ωk and μk in Eqs. (12) and (13), we find that |ωk| > |μk| is satisfied for all k ≠ 0 modes if and only if −1 ⩽ Jz < ζ(α)/η(α). This is because when Jz < −1, the classical ground state is ferromagnetic in z direction, and when Jz > ζ(α)/η(α) the classical ground state is Néel ordered along the z direction.
Because the Bogoliubov quasiparticles consist of both particles and holes, the ground state of Hswx can have a finite or divergent density of spin excitations, measured by
| (14) |
Expanding the integrand [1 − μ2(q)/ω2(q)]−1/2 above around q = 0 to the lowest order in 1/q, we find that
| (15) |
where Γ(x) is the gamma function. For α > 3, since [1 − μ2(q)/ω2(q)]−1/2 ∝ 1/|q| to leading order in 1/q, the spin-wave density divergesas N → ∞ according to Eq. (14). This means the long-range ferromagnetic order along the x direction is destroyed by quantum fluctuations in the thermodynamic limit; we expect that , and the system will be disordered (either Haldane or XY). For α < 3, instead we have to leading order in q, and the excitation density converges to a finite constant. As a self-consistency condition, we also require to prevent the breakdown of the spin-wave approximation [44,52]. We expect a CSB phase in the parameter region of , with nonvanishing spin order in the x-y plane (i.e., ), and a disordered phase when . By numerically evaluating Eq. (14), which gives in the infinite-size limit [101], we have obtained a phase diagram for Jxy = −1 under spin-wave approximation (Fig. 5).
FIG. 5.
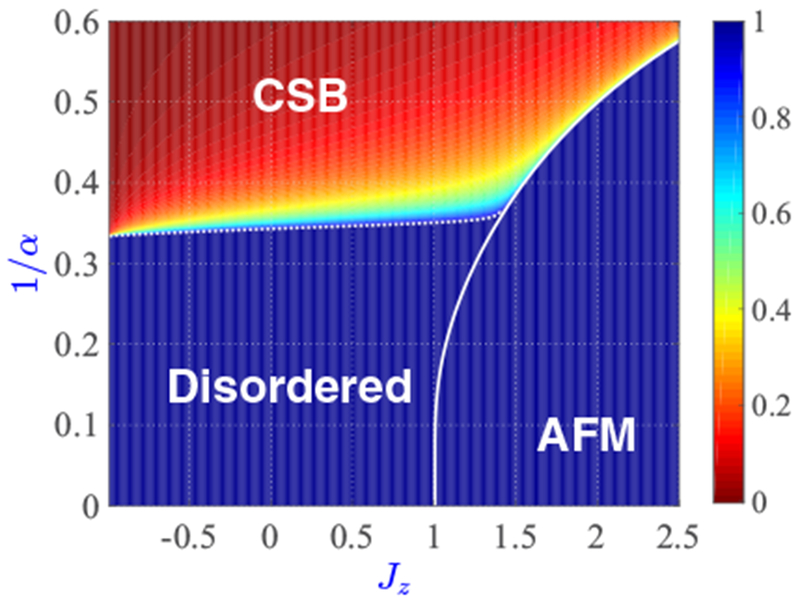
Spin-wave excitation density calculated using Eq. (14) for an infinite-size chain. For Jz > ζ(α)/η(α) (region to the right of the white line), imaginary frequencies appear in the Bogoliubov spectrum, indicating a classical instability toward the AFM phase. The region above the dotted and solid white lines has , and is associated with the CSB phase. The remaining region in the plot has , and is expected to be disordered. The disordered phase can be either the XY or the Haldane phase, but the spin-wave theory cannot distinguish one from the other. For better visibility, we have set for regions without CSB in the plot.
For Jxy = 1 and | Jz| < 1, classically the spins prefer to antialign in the x-y plane. Expanding around this classical state, the spin-wave approximation leads to the same Hamiltonian in Eq. (11) except that we have
| (16) |
| (17) |
As a result, now both μ(q) and ω(q) become fully analytic (in the N → ∞ limit) due to the alternating sign (−1)r in Eqs. (16) and (17). Expanding around q = 0, we have
| (18) |
As a result, will be divergent for any α > 0 due to the 1/|q| singularity in the integrand of Eq. (14). Thus continuous symmetry breaking is forbidden for all α > 0 for Jxy = 1.
Now we confirm the spin-wave prediction of the CSB phase’s boundary using DMRG calculations. Naively, one should calculate the CSB phase’s order parameter . However, we find that in the XY phase decays with a rather slow power law (e.g., η = 0.25 at Jz = 0 and α = ∞). At the maximum separation that we can calculate accurately using either finite or infinite-size DMRG, only shows a crossover from the XY phase to the CSB phase. To faithfully determine the boundary of the CSB phase, we instead calculate the effective central charge ceff as a function of α and Jz. We obtain ceff by calculating the half-chain entanglement entropy S for two chains with different total lengths N1 and N2 using a finite-size DMRG algorithm [102]. Explicitly, for large N1 and N2, we have
| (19) |
In the XY phase (including its boundaries) and at the boundary between the Haldane and AFM phases, we expect 1+1D conformal symmetry in the underlying field theory model [67,69], with ceff being the actual central charge representing the conformal anomaly [90]. In the Haldane, FM, and AFM phases, no 1+1D conformal symmetry exists due to the presence of a gap. Although the CSB phase is gapless, we expect a breakdown of 1+1D conformal symmetry due to the 1/rα long-range interactions that become relevant in the RG sense for α ≲ 3 [33,35,83]. We emphasize that in phases with no conformal symmetry, ceff does not have the meaning of the central charge and is used only as a diagnostic here to numerically find phase boundaries.
We identify the XY-to-CSB phase boundary in Fig. 6 as the place where ceff starts to become appreciably (5–10%) larger than 1. Here we find good agreement with the XY-to-CSB phase boundary predicted by spin-wave theory in Fig. (5) for −1 < Jz ≲ 1. Together with perturbative field theory calculations presented in Ref. [83], we expect the phase boundary in Fig. 6 to be accurate within a few percent. The accuracy of the calculated ceff can be further improved by finite-size scaling, which is however beyond the scope of the current study. The location of the CSB-XY-Haldane tricritical point is estimated to be at α ≈ 2.75 and Jz ≈ 1.35.
FIG. 6.
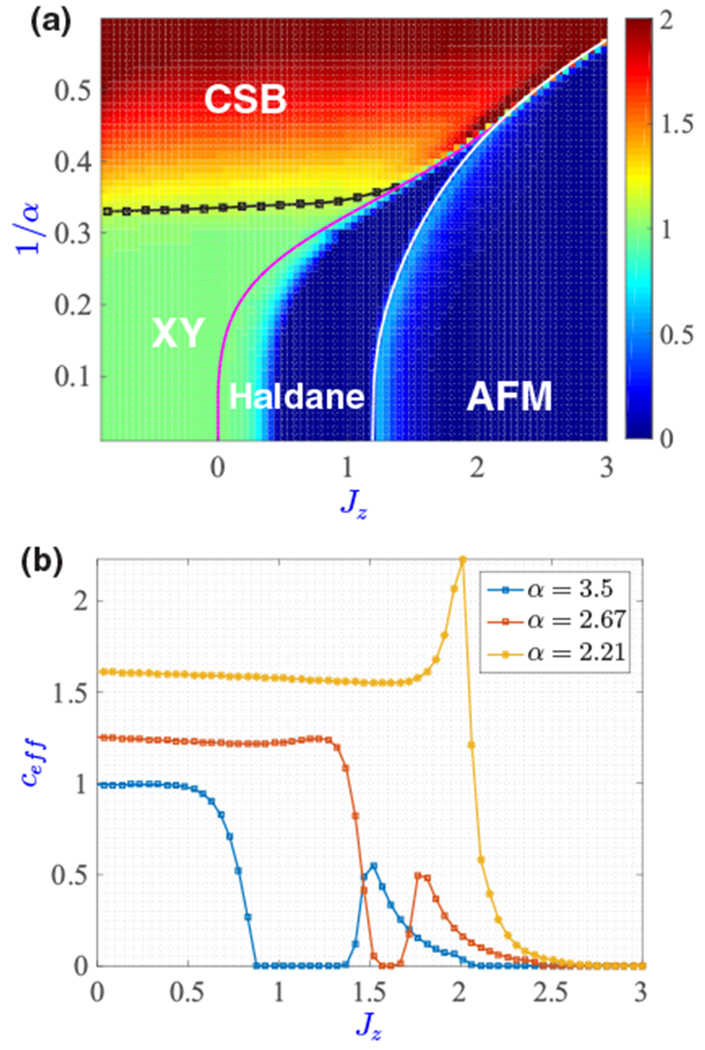
Calculation of the effective central charge ceff as a function of Jz and α for Jxy = −1, extracted from finite-size DMRG calculations with N1 = 100, N2 = 110, and a maximum bond dimension of 500. (a) The black squares (fitted by the black line) show where ceff starts to deviate from 1 when going from the XY to the CSB phase. The purple line and white line are from Fig. 3, and show the boundaries of the Haldane phase. (The calculation of ceff is inaccurate in predicting the location of the XY-to-Haldane transition due to strong finite-size effects [61,86–88].) For better contrast, locations with c > 2 are shown with the color corresponding to c = 2. (b) For our finite-size chains, the XY-to-Haldane BKT phase transition is signaled by a continuous drop of ceff from 1 to 0 (α = 3.5). The Haldane-to-AFM phase transition is identified by a peak with value around 0.5 in ceff (α = 3.5 and α = 2.67). The CSB-to-Haldane transition is expected to be continuous and not associated with a central charge (α = 2.67). The CSB-to-AFM transition has a sharp peak in ceff (α = 2.21), an indication of a first-order transition [67].
From Ref. [83], it follows that the XY-to-CSB transition is a BKT-like transition that belongs to a universality class different from the XY-to-Haldane BKT transition. The Haldane-to-CSB transition is somewhat exotic, because the Haldane phase maps to a high-temperature disordered phase in a 2D classical model [93], and in the absence of long-range interactions, the CSB phase exists in 2D only at zero temperature [2] and is unlikely to undergo a phase transition directly to a high-temperature disordered phase. We also argue that the CSB-to-Haldane transition is not described by a 1+1D CFT, as supported by our numerical calculations shown in Fig. 6(b), where ceff changes smoothly (at least for finite chains) from a value larger than 1 to 0 during the CSB-to-Haldane transition.
The CSB-to-AFM phase transition is very likely to be first order, similar to the transition between the large-D and AFM phases studied in Refs. [66] and [75], despite the existence of quantum fluctuations in both phases. As shown in Fig. 6, we observe a sharp peak in ceff at small as when Jz is varied, indicating a first order transition [67], with further evidence that includes jumps in sublattice magnetization and spin-spin correlation across the CSB-to-AFM transition (not shown).
V. EXPERIMENTAL DETECTION
It was theoretically proposed in Refs. [54] and [55] that the Hamiltonian we consider can be simulated (for widely tunable Jz and 0 < α < 3) by using microwave field gradients or optical dipole forces to induce spin-spin interactions in a chain of trapped ions. The simulation of Eq. (1) with Jxy = 1 and Jz = 0 was experimentally demonstrated for a few ions with α tuned around 1 [56], where the ground state was adiabatically prepared by slowly ramping down an extra single-ion anisotropy term , with D(t) > 0. As the system size increases, the energy gap separating the ground state from the rest of the spectrum will become progressively smaller near the point where a phase transition between the “large-D” phase and the XY/Haldane/FM/AFM phase occurs in the thermodynamic limit [75]. To avoid a slow ground state preparation process, we can adiabatically ramp down a staggered magnetic field in the z direction, , with h(t) > 0 [54,55]. By preparing an initial state that is the highest excited state of the staggered field Hamiltonian, the same adiabatic ramping process will lead us to the ground state of the Hamiltonian Eq. (1) with the opposite sign of both Jxy and Jz. As discussed in Ref. [55], the spin correlation functions and the string-order correlation can be measured for any i and j, since one can obtain the complete statistics of all spins’ magnetization using spatially resolved measurements. Together with arbitrary single-spin rotations performed with microwave or optical Raman transitions, we can measure these correlations along any direction. Near-future experiments will most likely be limited to a few tens of spins. Although this limitation makes it difficult to probe continuous phase transitions, one can nevertheless observe important signatures of all five phases discussed in the manuscript by tuning Jz/Jxy and α deep into each phase. These signatures are summarized below and shown in Fig. 7.
FIG. 7.
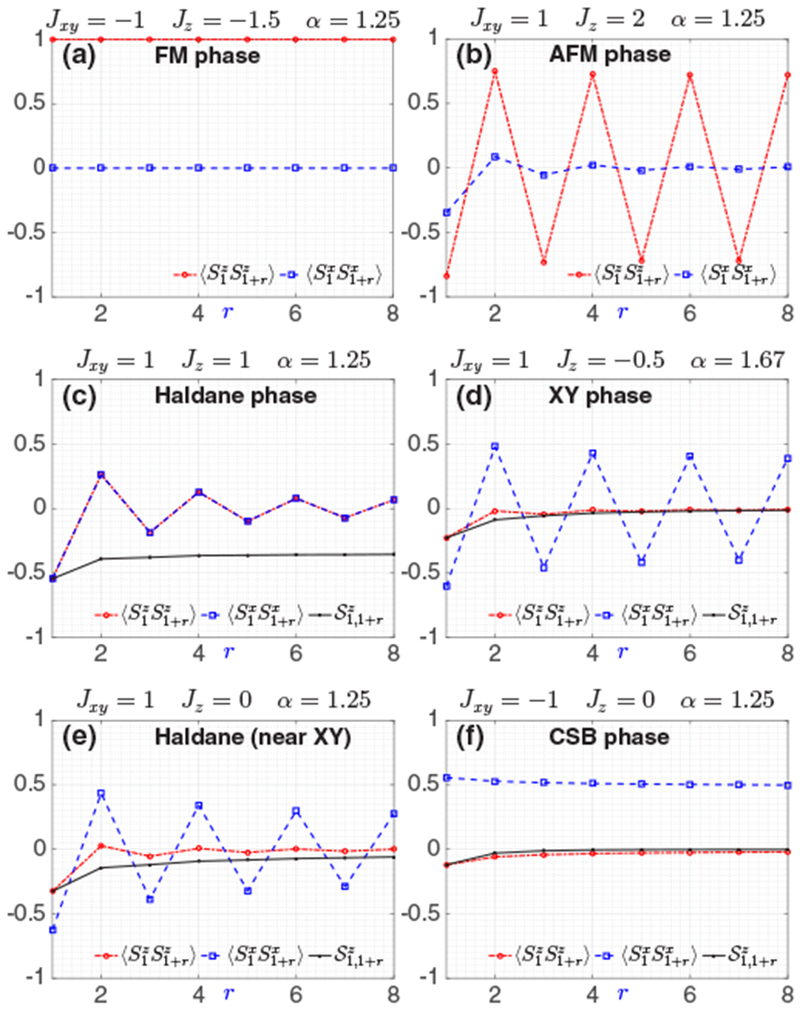
Signatures of all five phases for a N = 16 spin chain. Except for (e), we tune Jxy, Jz, and α to set the ground state deep into each phase. Each phase is distinguished from the other phases by different behaviors in various spin-spin correlation functions.
FM phase [Fig. 7(a)]: Within the FM phase, and for any i and j, thus confirming perfect alignment of spins along the z direction.
AFM phase [Fig. 7(b)]: For sufficiently large Jz > 0, we have , showing a near perfect antialignment of spins along the z direction. In contrast, vanishes over a separation of just a few sites.
Haldane phase [Fig. 7(c)]: converges quickly to a nonzero constant as |i − j| increases. In contrast, and vanish over a separation of just a few sites.
XYphase [Fig. 7(d)]: We consider the XY phase for Jxy = 1 since the XY phase hardly exist for α < 3 and Jxy = −1. and both decay quickly to zero as |i − j| increases. oscillates and its amplitude decays very slowly (the slow decay reflects a relatively small value of the critical exponent associated with the correlation function decay).
CSB phase [Fig. 7(f)]: As in the XY phase, both and decay quickly to zero. However, converges quickly to approximately 0.5 at large |i − j|, showing a near perfect ordering of spins in the x − y plane. Note that we are not explicitly breaking U(1) symmetry here, so . This is done because it is desirable for the experiment to operate within the subspace, where magnetic field noise and unwanted phonon couplings are suppressed [55,56].
Finally, we point out that, even in the experimental setup already demonstrated in Ref. [56], for which Jz = 0, one can still explore the two most interesting phases studied in this paper: the Haldane phase and the CSB phase. Note that, for Jxy = 1, Jz = 0 lies close to the Haldane-to-XY phase boundary, and thus one observes signatures of both phases, as in Fig. 7(e). Here the Haldane phase is identified via bulk correlations, but one can alternatively confirm the existence the Haldane phase by preparing edge excited states and measure edge excitation amplitudes [57].
VI. CONCLUSION AND OUTLOOK
By tuning the anisotropy Jz/|Jxy| and the power-law exponent α, we have explored a rich variety of quantum phases—and the transitions between them—in a long-range interacting spin-1 XXZ chain. For Jxy = −1, long-range interactions give rise to a rather unusual phase diagram due to the emergence of a continuous symmetry breaking phase in one spatial dimension. Because the CSB phase cannot happen in a short-range interacting 1D spin-system, the nature of the phase transitions into and out of it is rather interesting; an in-depth study of the universality class of the CSB-to-XY transition was carried out in a separate work [83], where a similar transition in a long-range interacting spin-1/2 XXZ chain is analyzed. On the other hand, the CSB-to-Haldane transition, absent in spin-1/2 chains, requires further study to be understood thoroughly. The CSB-Haldane-AFM tricritical point is reminiscent of the tricritical point at the intersection of the large-D, Haldane and AFM phases, which has been related to the integrable Takhtajan-Babujian model described by an SU(2)2 Wess-Zumino-Witten (WZW) model with central charge c = 3/2 [67,103–106]. Additional numerical calculations are needed to accurately determine the central charge at the CSB-Haldane-AFM tricritical point. Generalizations of our model to include single-ion anisotropy and a magnetic field are readily achievable in current trapped-ion experiments [55,56]. Understanding these exotic quantum phase transitions—induced by long-range interactions that are highly tunable in current experiments—requires the confrontation of numerous theoretical and numerical challenges, and motivates experimental quantum simulation of the model using AMO systems.
ACKNOWLEDGMENTS
We thank G. Pupillo, D. Vodola, L. Lepori, A. Turner, J. Pixley, M. Wall, P. Hess, A. Lee, J. Smith, A. Retzker and I. Cohen for helpful discussions. This work was supported by the ARO, the AFOSR, NSF PIF, NSF PFC at the JQI, and the ARL. M.F.-F. thanks the NRC for support.
APPENDIX: NUMERICAL TREATMENT OF LONG-RANGE INTERACTIONS
In our infinite-size and finite-size DMRG code [85], the 1/rα long-range interactions are represented as a matrix product operator by fitting the power law to a sum of exponentials [51]. Specifically, we fit fr = 1/rα to for r = 1,2, ⋯ L. For a given L, we numerically find the minimum number of exponentials K that satisfy , with ϵf denoting the residual tolerance. The maximal range L is set to the chain length in our finite-size DMRG calculations, and to 5000 in our infinite-size DMRG calculations (much larger than the 500 site separation of correlations calculated in Fig. 3). ϵf is set to 10−12 in our finite-size DMRG calculations, and 10−10 in our infinite-size DMRG calculations. For all the calculations shown in the main text, we find no distinguishable differences within the resolution of our plots if we further increase L or decrease ϵf.
As an example, we show in Fig. 8 relative differences of (for Jxy = 1, α = 2) and (for Jxy = −1, α = 2) caused by increasing L from 5000 to 104 and by decreasing ϵf from 10−10 to 10−11. In all cases, the relative differences in the calculated observables are below 10−3.
FIG. 8.
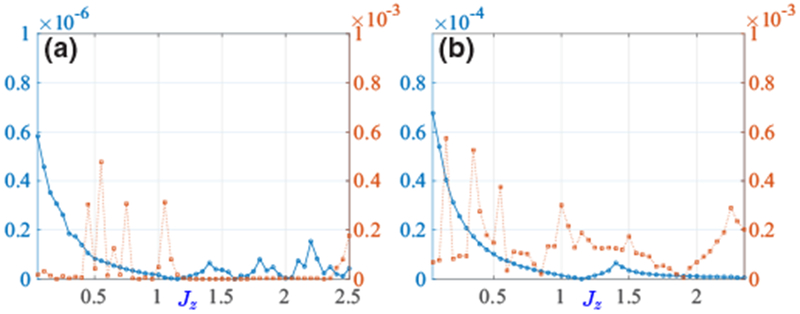
Relative differences of (blue) calculated for Jxy = 1, α = 2 and (red) calculated for Jxy = −1, α = 2 caused by (a) increasing L from 5000 to 104 (with K increasing from 9 to 10) and (b) decreasing ϵf from 10−10 to 10−11 (with K increasing from 9 to 10).
We have avoided the use of DMRG results if α < 1.5 and interactions are unfrustrated in one or more directions (Jxy = −1 or Jz < 0 or both), because of the slow convergence of with L as α → 1. Nevertheless, we do not expect new phase transitions in these situations based on Fig. 1, and we can instead infer the phases of the system there from the presented calculations.
References
- [1].Sachdev S, Quantum phase transitions, 2nd ed. (Cambridge University Press, Cambridge, 2011). [Google Scholar]
- [2].Mermin ND and Wagner H, Phys. Rev. Lett 17, 1133 (1966). [Google Scholar]
- [3].Haldane FDM, Phys. Lett. A 93, 464 (1983). [Google Scholar]
- [4].Haldane FDM, Phys. Rev. Lett 50, 1153 (1983). [Google Scholar]
- [5].Pollmann F, Berg E, Turner AM, and Oshikawa M, Phys. Rev. B 85, 075125 (2012). [Google Scholar]
- [6].Chen X, Gu Z-C, Liu Z-X, and Wen X-G, Phys. Rev. B 87, 155114 (2013). [Google Scholar]
- [7].Di Francesco P, Mathieu P, and Sénéchal D, Conformal Field Theory, Graduate texts in contemporary physics (Springer, New York, 1997). [Google Scholar]
- [8].Bloch I, Dalibard J, and Zwerger W, Rev. Mod. Phys 80, 885 (2008). [Google Scholar]
- [9].Kim K, Chang M-S, Korenblit S, Islam R, Edwards EE, Freericks JK, Lin G-D, Duan L-M, and Monroe C, Nature (London) 465, 590 (2010). [DOI] [PubMed] [Google Scholar]
- [10].Bloch I, Dalibard J, and Nascimbène S, Nat. Phys 8, 267 (2012). [Google Scholar]
- [11].Britton JW, Sawyer BC, Keith AC, Wang C-CJ, Freericks JK, Uys H, Biercuk MJ, and Bollinger JJ, Nature (London) 484, 489 (2012). [DOI] [PubMed] [Google Scholar]
- [12].Yan B, Moses SA, Gadway B, Covey JP, Hazzard KRA, Rey AM, Jin DS, and Ye J, Nature (London) 501, 521 (2013). [DOI] [PubMed] [Google Scholar]
- [13].Peter D, Müller S, Wessel S, and Büchler HP, Phys. Rev. Lett 109, 025303 (2012). [DOI] [PubMed] [Google Scholar]
- [14].Douglas JS, Habibian H, Hung C-L, Gorshkov AV, Kimble HJ, and Chang DE, Nat. Photon 9, 326 (2015). [Google Scholar]
- [15].Jurcevic P, Lanyon BP, Hauke P, Hempel C, Zoller P, Blatt R, and Roos CF, Nature (London) 511, 202 (2014). [DOI] [PubMed] [Google Scholar]
- [16].Hazzard KRA, Gadway B, Foss-Feig M, Yan B, Moses SA, Covey JP, Yao NY, Lukin MD, Ye J, Jin DS, and Rey AM, Phys. Rev. Lett. 113, 195302 (2014). [DOI] [PubMed] [Google Scholar]
- [17].de Paz A, Sharma A, Chotia A, Marechal E, Huckans JH, Pedri P, Santos L, Gorceix O, Vernac L, and Laburthe-Tolra B, Phys. Rev. Lett 111, 185305 (2013). [DOI] [PubMed] [Google Scholar]
- [18].Richerme P, Gong Z-X, Lee A, Senko C, Smith J, Foss-Feig M, Michalakis S, Gorshkov AV, and Monroe C, Nature (London) 511, 198 (2014). [DOI] [PubMed] [Google Scholar]
- [19].Schauß P, Cheneau M, Endres M, Fukuhara T, Hild S, Omran A, Pohl T, Gross C, Kuhr S, and Bloch I, Nature (London) 491, 87 (2012). [DOI] [PubMed] [Google Scholar]
- [20].Manmana SR, Stoudenmire EM, Hazzard KRA, Rey AM, and Gorshkov AV, Phys. Rev. B 87, 081106 (2013). [Google Scholar]
- [21].Yao NY, Laumann CR, Gorshkov AV, Bennett SD, Demler E, Zoller P, and Lukin MD, Phys. Rev. Lett 109, 266804 (2012). [DOI] [PubMed] [Google Scholar]
- [22].Yao NY, Gorshkov AV, Laumann CR, Lauchli AM, Ye J, and Lukin MD, Phys. Rev. Lett 110, 185302 (2013). [DOI] [PubMed] [Google Scholar]
- [23].Dalla Torre EG, Berg E, and Altman E, Phys. Rev. Lett 97, 260401 (2006). [DOI] [PubMed] [Google Scholar]
- [24].Fisher ME, Ma S.-k., and Nickel BG, Phys. Rev. Lett 29, 917 (1972). [Google Scholar]
- [25].Cannas SA and Tamarit FA, Phys. Rev. B 54, R12661 (1996). [DOI] [PubMed] [Google Scholar]
- [26].Luijten E and Blote HWJ, Phys. Rev. B 56, 8945 (1997). [Google Scholar]
- [27].Katzgraber HG and Young AP, Phys. Rev. B 72, 184416 (2005). [Google Scholar]
- [28].Campa A, Dauxois T, and Ruffo S, Phys. Rep 480, 57 (2009). [Google Scholar]
- [29].Koffel T, Lewenstein M, and Tagliacozzo L, Phys. Rev. Lett 109, 267203 (2012). [DOI] [PubMed] [Google Scholar]
- [30].Bachelard R and Kastner M, Phys. Rev. Lett 110, 170603 (2013). [DOI] [PubMed] [Google Scholar]
- [31].Eisert J, van den Worm M, Manmana SR, and Kastner M, Phys. Rev. Lett 111, 260401 (2013). [DOI] [PubMed] [Google Scholar]
- [32].Gong Z-X, Foss-Feig M, Michalakis S, and Gorshkov AV, Phys. Rev. Lett 113, 030602 (2014). [DOI] [PubMed] [Google Scholar]
- [33].Vodola D, Lepori L, Ercolessi E, Gorshkov AV, and Pupillo G, Phys. Rev. Lett 113, 156402 (2014). [DOI] [PubMed] [Google Scholar]
- [34].Foss-Feig M, Gong Z-X, Clark CW, and Gorshkov AV, Phys. Rev. Lett 114, 157201 (2015). [DOI] [PubMed] [Google Scholar]
- [35].Vodola D, Lepori L, Ercolessi E, and Pupillo G, New J. Phys. 18, 015001 (2016). [Google Scholar]
- [36].Nezhadhaghighi MG and Rajabpour MA, Phys. Rev. B 88, 045426 (2013). [Google Scholar]
- [37].Nezhadhaghighi MG and Rajabpour MA, EPL 100, 60011 (2012). [Google Scholar]
- [38].Haldane FDM, Phys. Rev. Lett 60, 635 (1988). [DOI] [PubMed] [Google Scholar]
- [39].Shastry BS, Phys. Rev. Lett 60, 639 (1988). [DOI] [PubMed] [Google Scholar]
- [40].Finkel F and Gonzalez-Lopez A, J. Stat. Mech.: Theor. Exp (2014) P12014. [Google Scholar]
- [41].Choudhury AG and Chowdhury AR, J. Phys. A: Math. Gen. 28, 4015 (1995). [Google Scholar]
- [42].Maghrebi MF, Gong Z-X, Foss-Feig M, and Gorshkov AV, Phys. Rev. B 93, 125128 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Rajabpour MA and Sotiriadis S, Phys. Rev. B 91, 045131 (2015). [Google Scholar]
- [44].Yusuf E, Joshi A, and Yang K, Phys. Rev. B 69, 144412 (2004). [Google Scholar]
- [45].Nakano H and Takahashi M, J. Phys. Soc. Jpn 63,926 (1994). [Google Scholar]
- [46].Sandvik AW, Phys. Rev. Lett 104, 137204 (2010). [DOI] [PubMed] [Google Scholar]
- [47].Sacramento PD and Vieira VR, J. Phys. Condens. Matter 9, 10687 (1997). [DOI] [PubMed] [Google Scholar]
- [48].Sacramento PD and Vieira VR, Z. Phys. B 103, 231 (1996). [Google Scholar]
- [49].Sacramento PD and Vieira VR, Z. Phys. B 101, 441 (1997). [Google Scholar]
- [50].Hastings MB and Koma T, Commun. Math. Phys 265, 781 (2006). [Google Scholar]
- [51].Crosswhite GM, Doherty AC, and Vidal G, Phys. Rev. B 78, 035116 (2008). [Google Scholar]
- [52].Laflorencie N, Affleck I, and Berciu M, J. Stat. Mech (2005) P12001. [Google Scholar]
- [53].Blanchard T, Picco M, and Rajabpour MA, EPL 101, 56003 (2013). [Google Scholar]
- [54].Cohen I and Retzker A, Phys. Rev. Lett 112, 040503 (2014). [DOI] [PubMed] [Google Scholar]
- [55].Cohen I, Richerme P, Gong Z-X, Monroe C, and Retzker A, Phys. Rev. A 92, 012334 (2015). [Google Scholar]
- [56].Senko C, Richerme P, Smith J, Lee A, Cohen I, Retzker A, and Monroe C, Phys. Rev. X 5, 021026 (2015). [Google Scholar]
- [57].Gong Z-X, Maghrebi MF, Hu A, Wall ML, Foss-Feig M, and Gorshkov AV, Phys. Rev. B 93, 041102(R) (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Kac M, Uhlenbeck GE, and Hemmer PC, J. Math. Phys 4, 216 (1963). [Google Scholar]
- [59].For an infinite system, the energy renormalization may change the system from gapped to gapless.
- [60].Kennedy T and Tasaki H, Comm. Math. Phys 147, 431 (1992). [Google Scholar]
- [61].Kitazawa A, Nomura K, and Okamoto K, Phys. Rev. Lett 76, 4038 (1996). [DOI] [PubMed] [Google Scholar]
- [62].Tsukano M and Nomura K, Phys. Rev. B 57, R8087 (1998). [Google Scholar]
- [63].Nomura K, Phys. Rev. B 40, 9142 (1989). [DOI] [PubMed] [Google Scholar]
- [64].Sakai T and Takahashi M, J. Phys. Soc. Jpn 59, 2688 (1990). [Google Scholar]
- [65].Su YH, Young Cho S, Li B, Wang H-L, and Zhou H-Q, J. Phys. Soc. Jpn 81, 074003 (2012). [Google Scholar]
- [66].Liu G-H, Li W, You W-L, Su G, and Tian G-S, Phys. B 443, 63 (2014). [Google Scholar]
- [67].Ejima S and Fehske H, Phys. Rev. B 91, 045121 (2015). [Google Scholar]
- [68].Schulz HJ, Phys. Rev. B 34, 6372 (1986). [DOI] [PubMed] [Google Scholar]
- [69].Alcaraz FC and Moreo A, Phys. Rev. B 46, 2896 (1992). [DOI] [PubMed] [Google Scholar]
- [70].Nomura K, J. Phys. A 28, 5451 (1995). [Google Scholar]
- [71].Nomura K and Kitazawa A, J. Phys. A 31, 7341 (1998). [Google Scholar]
- [72].Kitazawa A, Hijii K, and Nomura K, J. Phys. A: Math. Gen. 36, L351 (2003). [Google Scholar]
- [73].Botet R and Jullien R, Phys. Rev. B 27, 613 (1983). [Google Scholar]
- [74].Ueda H, Nakano H, and Kusakabe K, Phys. Rev. B 78, 224402 (2008). [Google Scholar]
- [75].Chen W, Hida K, and Sanctuary BC, Phys. Rev. B 67, 104401 (2003). [Google Scholar]
- [76].Murashima T, Hijii K, Nomura K, and Tonegawa T, J. Phys. Soc. Jpn 74, 1544 (2005). [Google Scholar]
- [77].Hikihara T, Kaburagi M, Kawamura H, and Tonegawa T, J. Phys. Soc. Jpn 69, 259 (2000). [Google Scholar]
- [78].Hikihara T, Kaburagi M, and Kawamura H, Phys. Rev. B 63, 174430 (2001). [Google Scholar]
- [79].Kolezhuk AK and Schollwöck U, Phys. Rev. B 65, 100401(R) (2002). [Google Scholar]
- [80].Bruno P, Phys. Rev. Lett 87, 137203 (2001). [DOI] [PubMed] [Google Scholar]
- [81].Lobos AM, Tezuka M, and García-García AM, Phys. Rev. B 88, 134506 (2013). [Google Scholar]
- [82].Tezuka M, Garcia-Garcia AM, and Cazalilla MA, Phys. Rev. A 90, 053618 (2014). [Google Scholar]
- [83].Maghrebi MF, Gong Z-X, and Gorshkov AV, arXiv:1510.01325.
- [84].McCulloch IP, arXiv:0804.2509.
- [85].Our MPS code is largely based on the open source MPS project at http://sourceforge.net/projects/openmps/.
- [86].Malvezzi AL and Alcaraz FC, J. Phys. Soc. Jpn 64, 4485 (1995). [Google Scholar]
- [87].Singh RRP and Gelfand MP, Phys. Rev. Lett 61, 2133 (1988). [DOI] [PubMed] [Google Scholar]
- [88].Alcaraz FC and Hatsugai Y, Phys. Rev. B 46, 13914 (1992). [DOI] [PubMed] [Google Scholar]
- [89].Schollwock U, Ann. Phys 326, 96 (2011). [Google Scholar]
- [90].Calabrese P and Cardy J, J. Stat. Mech (2004) P06002. [Google Scholar]
- [91].Affleck I, Phys. Rev. Lett 54, 966 (1985). [DOI] [PubMed] [Google Scholar]
- [92].Here the expressions are for noninteger α. For integer α, the expressions are slightly different but cause no important changes to the discussion below.
- [93].Fradkin E, Field Theories of Condensed Matter Physics, 2nd ed. (Cambridge University Press, Cambridge, 2013). [Google Scholar]
- [94].Brézin E and Zinn-Justin J (eds.), Fields, Strings and Critical Phenomena: Les Houches, sessionXLIX, 1988 (North-Holland, Netherland, 1990). [Google Scholar]
- [95].Sørensen ES and Affleck I, Phys. Rev. B 49, 15771 (1994). [DOI] [PubMed] [Google Scholar]
- [96].Sorensen ES and Affleck I, Phys. Rev. B 49, 13235 (1994). [DOI] [PubMed] [Google Scholar]
- [97].White SR, Phys. Rev. Lett 69, 2863 (1992). [DOI] [PubMed] [Google Scholar]
- [98].White SR and Huse DA, Phys. Rev. B 48, 3844 (1993). [DOI] [PubMed] [Google Scholar]
- [99].Note that gapped phases with sufficiently long-ranged interactions can violate entanglement area law [29,33,35], but this has not been observed in our model.
- [100].Auerbach A, Interacting Electrons and Quantum Magnetism, Graduate texts in contemporary physics (Springer-Verlag, New York, 1994). [Google Scholar]
- [101].For α ⪅ 3, a standard numerical integration of Eq. (14) will fail to converge due to the 1/q(α−1)/2 singularity. To solve this problem, we use Eq. (15) to analytically carry out the integral for , and numerically calculate the rest of the integral.
- [102].Note that in the Haldane phase, there exist edge excited states. The absolute ground state for any chain with an even number of spins has total Sz = 0, and the edge spins are strongly entangled. Here we are interested in the entanglement properties in the bulk, so we instead calculate the ground state in the total Sz = 1 subspace to avoid this edge-spin entanglement [57].
- [103].Tsvelik AM, Phys. Rev. B 42, 10499 (1990). [DOI] [PubMed] [Google Scholar]
- [104].Kitazawa A and Nomura K, Phys. Rev. B 59, 11358 (1999). [Google Scholar]
- [105].Degli Esposti Boschi C, Ercolessi E, Ortolani F, and Roncaglia M, EPJ B 35, 465 (2003). [Google Scholar]
- [106].Pixley JH, Shashi A, and Nevidomskyy AH, Phys. Rev. B 90, 214426 (2014). [Google Scholar]


