Topological phases with long-range interactions

Abstract

Topological phases of matter are primarily studied in systems with short-range interactions. In nature, however, nonrelativistic quantum systems often exhibit long-range interactions. Under what conditions topological phases survive such interactions, and how they are modified when they do, is largely unknown. By studying the symmetry-protected topological phase of an antiferromagnetic spin-1 chain with 1/r^α interactions, we show that two very different outcomes are possible, depending on whether or not the interactions are frustrated. While unfrustrated long-range interactions can destroy the topological phase for α ≲ 3, the topological phase survives frustrated interactions for all α > 0. Our conclusions are based on strikingly consistent results from large-scale matrix-product-state simulations and effective-field-theory calculations, and we expect them to hold for more general interacting spin systems. The models we study can be naturally realized in trapped-ion quantum simulators, opening the prospect for experimental investigation of the issues confronted here.

Since the discovery of topological insulators [1–3], there has been tremendous interest in exploring various topological phases of matter, both theoretically [4,5] and experimentally [6–8]. Topological phases are generally associated with—and derive much of their presumed utility from stability against local perturbations. But precisely what constitutes “local” in this context is a subtle issue; power-law decaying (1/r^α) interactions, which are present in many experimental systems, do not necessarily qualify [9–11]. Recent theoretical advances have begun to elucidate the conditions under which long-range interacting systems maintain some degree of locality [12,13], potentially providing some insight into effects of long-range interactions on topological phases of matter. And recently, explicit theoretical evidence of topological order has been found in a variety of long-range interacting systems, including dipolar spins [14] or bosons [15], fermions with long-range pairing [16] and hopping [ 17,18], and electrons with Coulomb interactions [19]. These results notwithstanding, a complete understanding of how topological phases respond to the addition of long-range interactions is still lacking.

The stability of topological phases to small local perturbations is intimately connected to the existence of a bulk excitation gap [20,21], and the introduction of long-range interactions to a short-range Hamiltonian supporting a topological phase poses several potential challenges to this connection. First, even if the gap remains finite, long-range interactions can change the ground-state correlation decay from exponential to power law [16,18,22,23]. Thus topological phases with local interactions are, at the very least, subject to qualitative changes in their long-distance correlations. Second, the gap can in principle close in the presence of long-range interactions, even when they decay fast enough that the total interaction energy remains extensive [20,24]. Third, long-range interactions have the ability to change the effective dimensionality of the system [25,26], and thus might change the topological properties even if the gap does not close [16,18]. We emphasize that the understanding of these issues is not of strictly theoretical interest. Many of the promising experimental systems for exploring or exploiting topological phases of matter, e.g., dipolar molecules [27–29], magnetic [30] or Rydberg atoms [31], trapped ions [32–37], and atoms coupled to multimode cavities [38], are accurately described as quantum lattice models with power-law decaying interactions. The unique controllability and measurement precision afforded by these systems hold great promise to improve our understanding of topological phases [39–42], but first we must reliably determine when—despite their long-range interactions—they can be expected to harbor the topological phases that have been theoretically explored for short-range interacting systems.

To address these general questions, in this Rapid Communication we study a spin-1 chain with antiferromagnetic Heisenberg interactions, which is a paradigmatic model exhibiting a symmetry-protected topological (SPT) phase [43,44]. Specifically, we consider two extensions of the short-range version of this model by including long-range interactions that decay either as ${\mathcal{J}}_{\alpha }(r)=1∕r^{\alpha }$ or as ${\mathcal{J}}_{\alpha }^{\prime }(r)={(-1)}^{r-1}∕r^{\alpha }$, which could be simulated in trapped-ion based experiments for 0 < α < 3 [45,46]. Based on a combination of large-scale variational matrix-product-state (MPS) simulations and field-theory calculations, we establish and explain a number of important and potentially general consequences of long-range interactions. The ${\mathcal{J}}_{\alpha }^{\prime }(r)$ interactions are unfrustrated, being antiferromagnetic (ferromagnetic) between spins on the opposite (same) sublattice. In this case, numerics and field-theoretic arguments suggest the destruction of the topological phase for α ≲ 3, accompanied by a closing of the bulk excitation gap and spontaneous breaking of a continuous symmetry in one dimension (1D), consistent with other recent findings on the relevance of long-range interactions for α < D + 2 in D-dimensional quantum systems [47,48]. The ${\mathcal{J}}_{\alpha }(r)$ interactions are frustrated, and, remarkably, do not close the bulk excitation gap for any α > 0. In addition, two key properties of the SPT phase, a doubly degenerate entanglement spectrum [49] and a nonvanishing string-ordered correlation [50], are both preserved. However, because of the long-range interactions, spin-spin correlations and the edge-excitation amplitudes only decay exponentially within some intermediate distance scale, after which they decay algebraically. We expect these qualitative changes to be quite general, occurring in other long-range interacting systems in which the topological phase survives.

Model.

We consider a spin-1 chain with either frustrated or unfrustrated long-range Heisenberg interactions:

$$H_{\alpha }=\sum _{j,r>0}{\mathcal{J}}_{\alpha }(r){\mathit{S}}_j\cdot {\mathit{S}}_{j+r},H_{\alpha }^{\prime }=\sum _{j,r>0}{\mathcal{J}}_{\alpha }^{\prime }(r){\mathit{S}}_j\cdot {\mathit{S}}_{j+r}.$$ (1)

With only nearest-neighbor interactions (α → ∞), $H_{\infty }=H_{\infty }^{\prime }$ is usually called the Haldane chain, which has been extensively studied theoretically [51–53], numerically [54–58], and experimentally [59,60]. The low-lying states of the Haldane chain are shown in Fig. 1(a) for an open boundary chain with even size L. The unique ground state has total spin S = 0. The first set of excited states has S = 1 (ℏ = 1), contains spin excitations only near the edge of the chain, and is separated from the ground state by an energy gap (edge gap) that is exponentially small in L and topologically protected. Consequently, these excited states belong to a degenerate ground-state subspace in the thermodynamic (L → ∞) limit. The second set of excited states all have S = 2, contain spin excitations in the bulk of the chain, and have an energy gap (bulk gap) that converges to a finite value when L → ∞. The entanglement structure of the four ground states is close to that of the Affleck-Kennedy-Lieb-Tasaki (AKLT) states [61] shown at the bottom of Fig. 1(a), where each spin-1 is decomposed into two spin-1/2’s, pairs of spin-½’s on neighboring sites form singlets, and the system is finally projected back onto the spin-1’s. The four quasidegenerate ground states correspond to the four states formed by the two unpaired spin-½’s at the edge.

FIG. 1.

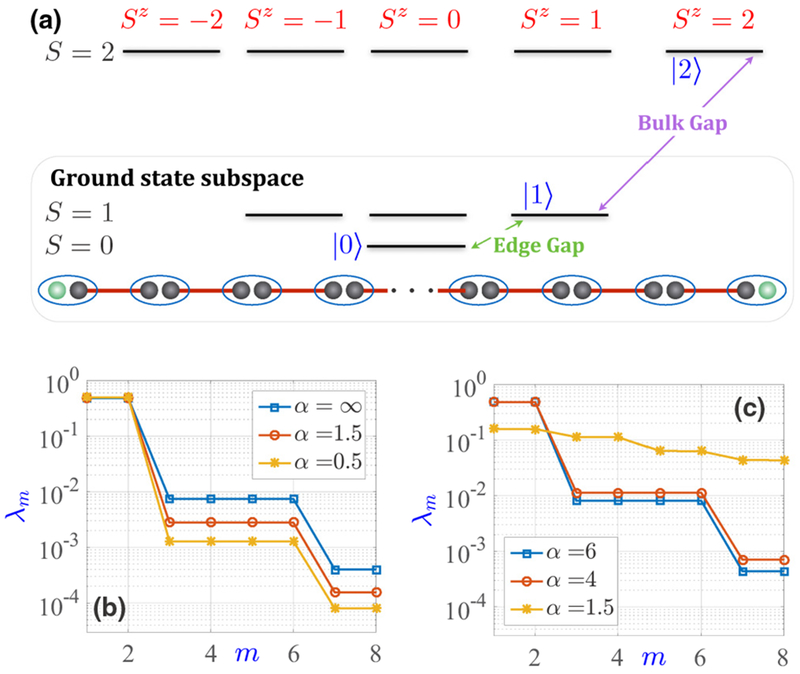
(a) Low-lying energy levels of the Haldane chain for even L. The entanglement structure of ground states is shown at the bottom. The ground states in the total S^z = 0, 1, 2 subspace are named |0〉, |1〉, |2〉 and have energies E₀, E₁, E₂. (b), (c) The mth largest value λ_m (m = 1, 2, …, 8) of the ground-state entanglement spectrum for H_α (b) and $H_{\alpha }^{\prime }$ (c) using finite-size MPS calculations with L = 200. We choose the |1〉 state to avoid extra entanglement between edge spins. For $H_{\alpha }^{\prime }$, the entanglement spectrum for 1.5 ⩽ α ⩽ 4 will exhibit a smooth crossover between the α = 1.5 and α = 4 cases due to the finite system size, but we expect a sharp transition at some α ≲ 3 in the thermodynamic limit. The exact pair degeneracies in {λ_m} are a result of the spatial-inversion symmetry protecting the topological phase [44,49].

We use variational MPS calculations [62–65] to determine the ground-state entanglement structure of H_α and $H_{\alpha }^{\prime }$ in Figs. 1(b) and 1(c). For α > 0 (α > 3), the ground-state entanglement spectrum of $H_{\alpha }(H_{\alpha }^{\prime })$, defined as the eigenvalues of the left/right half chain’s reduced density matrix, is dominated by the two largest degenerate eigenvalues λ₁ = λ₂ ≈ 0.5. This can be understood heuristically as the result of cutting a spin-½ singlet in the AKLT state, and suggests the survival of the topological Haldane phase. For $H_{\alpha }^{\prime }$ with α ≲ 3, the entanglement spectrum has an entirely different structure, and we will study the related ground-state properties below.

Effective field theory.

The low-energy physics of the Haldane chain can be understood via field-theoretic analysis due to Haldane [52] and Affleck [66]; here, we build on their work to provide a field-theoretic treatment of the long-range interacting model. We begin by decomposing the spin operators into staggered and uniform fields, $\mathit{n}(2i+\frac{1}{2})=({\mathit{S}}_{2i}-{\mathit{S}}_{2i+1})∕2$ and $\mathit{l}(2i+\frac{1}{2})=({\mathit{S}}_{2i}+{\mathit{S}}_{2i+1})∕2$. The intuition behind this decomposition is that the classical ground state of both H_α and $H_{\alpha }^{\prime }$ is Néel ordered for any α > 0, with n²(x) = 1 and l(x) = 0. We therefore expect that in the quantum ground state n²(x) ≈ 1, while l(x) ≈ 0 represents small quantum fluctuations in the direction of n(x). Importantly, we expect that only long-wavelength fluctuations of n(x) and l(x) will be important at low energy. In momentum space, we can write H_α ≈ ∫ dq[ω(q)|n(q)|² + Ω(q)|l(q)|²] and $H_{\alpha }^{\prime }\approx \int \mathit{dq}[\Omega (q){\mid \mathit{n}(q)\mid }^2+\omega (q){\mid \mathit{l}(q)\mid }^2]$ [67], with

$$\omega (q)=2\sum _{r=1}^{\infty }{\mathcal{J}}_{\alpha }^{\prime }(r)\cos \mathit{qr},\Omega (q)=2\sum _{r=1}^{\infty }{\mathcal{J}}_{\alpha }(r)\cos \mathit{qr}.$$ (2)

For any α > 0, ω(q) is analytic at small q and can be expanded as ω₀ + ω₂q² + O(q⁴), whereas Ω(q)is nonanalytic at small q with an expansion Ω₀ + Ω₂q² + λ|q|^α−1 + O(q⁴). The coefficients ω_0,2, Ω_0,2, and λ depend on α, but their exact values are not important for the following analysis. Physically, the analyticity (nonanalyticity) of the spectrum arises because the long-range interactions interfere destructively (constructively) for the staggered field. Keeping only the lowest nontrivial order in q for the dispersion of both n(q) and l(q) turns out to be sufficient for obtaining qualitatively correct behavior of the excitation gap. Therefore, we keep only the 0th-order term in the dispersion of l(q), and the next-leading term in the dispersion of n(q) [for n(q), the 0th-order term only adds a constant to the Hamiltonian due to the constraint n²(x) = 1]. Thus for α > 0 (α > 3) the Hamiltonian $H_{\alpha }(H_{\alpha }^{\prime })$ is approximately given by (ignoring the order-unity coefficients) $H_{\alpha }~H_{\alpha }^{\prime }~\int \mathit{dq}[q^2{\mid \mathit{n}(q)\mid }^2+{\mid \mathit{l}(q)\mid }^2]$. When the zero-temperature partition function is expressed as a coherent-spin-state path integral, the action is quadratic in the field l and it can be integrated out [68,69]. The remaining path integral over the staggered field n is a (1 + 1)D O(3) nonlinear sigma model, with Lagrangian density [nonlinear constraint n²(x) = 1 implied]

$$\mathcal{L}(x)\approx \frac{1}{g}({\mid \partial \mathit{n}∕\partial t\mid }^2-v_s^2{\mid \partial \mathit{n}∕\partial x\mid }^2).$$ (3)

Here, g is an effective (α- and short-distance-cutoff-dependent) coupling strength, and the spin-wave velocity v_s is also α dependent. This model is gapped and disordered [51].

To investigate the ground-state properties of Eq. (3), we can remove the constraint n²(x) = 1, while phenomenologically introducing a mass gap Δ_α and a renormalized spin-wave velocity v_α (the parameters ${\Delta }_{\alpha }^{\prime }$ and $v_{\alpha }^{\prime }$ will be used to describe the Lagrangian for $H_{\alpha }^{\prime }$) [57,58]. Transforming to momentum space, we thereby arrive at a free-field Lagrangian density

$$\mathcal{L}(q)\propto {(\partial \mathit{n}∕\partial t)}^2-({\Delta }_{\alpha }^2+v_{\alpha }^2{q}^2){\mid \mathit{n}(q)\mid }^2.$$ (4)

This Lagrangian leads to ground-state correlations ${\mathcal{C}}_{\mathit{ij}}={\langle S_i^z{S}_j^z\rangle }_0$ [where ⟨⋯⟩_m denotes the expectation value in the state |m⟩ defined in Fig. 1(a)] that decays as

$${\mathcal{C}}_{\mathit{ij}}\propto {(-1)}^r\int \frac{e^{\mathit{iqr}}\mathit{dq}}{\sqrt{{\Delta }_{\alpha }^2+v_{\alpha }^2{q}^2}}\propto {(-1)}^r{K}_0(r∕{\xi }_{\alpha }).$$ (5)

Here, ξ_α ≡ v_α/Δ_α (or ${\xi }_{\alpha }^{\prime }\equiv v_{\alpha }^{\prime }∕{\Delta }_{\alpha }^{\prime }$ for $H_{\alpha }^{\prime }$) defines the correlation length, and K₀(x) is a modified Bessel function, which behaves as $K_0(x)~\exp (-x)∕\sqrt{x}$ for large x.

For α < 3, the nonanalytic |q|^α−1 term in $H_{\alpha }^{\prime }$ dominates the dispersion of n(q) at small q, and Eqs. (3) and (4) are not valid. To analyze this case, we write down the renormalization group (RG) flow equation for the coupling strength g under the scaling transformation x → xe^−l to one-loop order [68,70],

$$\frac{\mathit{dg}}{\mathit{dl}}=\frac{\alpha -3}{2}g+\frac{g^2}{4\pi }.$$ (6)

For α < 3, an unstable fixed point appears at g* = 2π(3 − α), and for a bare coupling g < g* the RG flow is towards a weak-coupling ordered state at g = 0 [68]. The bare coupling, and therefore the value of α at which this phase transition occurs, is difficult to determine a priori. But we nevertheless expect (and confirm numerically) that for α < α_c, with 2 < α_c < 3, the gap will close as the system spontaneously breaks the continuous SU(2) symmetry of $H_{\alpha }^{\prime }$ [48,71].

Comparison with numerics.

Using finite-size MPS calculations, we have obtained the bulk excitation gap E₂ − E₁ and the correlation length [fitted using Eq. (5)] for both H_α and $H_{\alpha }^{\prime }$. As shown in Figs. 2(a) and 2(b), we see consistent results with the field-theory predictions. For H_α, the gap remains open for all α > 0, and the correlation length decreases together with α due to both an increase of the bulk gap, and a decrease of the spin-wave velocity (as a result of a weakened Néel order for longer-range interactions). To the contrary, for $H_{\alpha }^{\prime }$, the gap decreases quickly as the interactions become longer ranged, and the correlation length diverges when α decreases to around 3, suggesting the disappearance of the topological phase at α ≲ 3 [72]. Calculation of the string-ordered correlation ${\mathcal{S}}_{\mathit{ij}}\equiv {\langle S_i^z{S}_j^z{\Pi }_{i<k<j}{(-1)}^{S_k^z}\rangle }_0$ of both H_α and $H_{\alpha }^{\prime }$ at α = 1.5 [Fig. 2(c)] provides further evidence that the topological phase survives for H_α, but not for $H_{\alpha }^{\prime }$, for 0 < α ≲ 3.

FIG. 2.

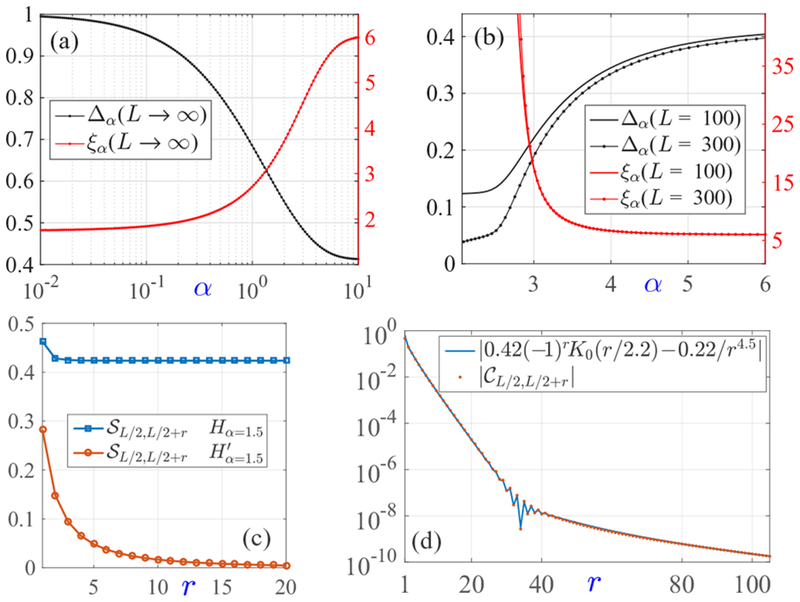
(a) Bulk gap Δ_α and ground-state correlation length ξ_α in the L → ∞ limit, obtained by finite-size scaling for 200 ⩽ L ⩽ 500. (b) Bulk gap ${\Delta }_{\alpha }^{\prime }$ and ${\xi }_{\alpha }^{\prime }$ with L = 100 and L = 300. (c) Ground-state string-ordered correlation function ${\mathcal{S}}_{\mathit{ij}}$ for H_α and $H_{\alpha }^{\prime }$ with α = 1.5 and L = 300. For various α and 200 ⩽ L ⩽ 500, we consistently find that ${\mathcal{S}}_{\mathit{ij}}$ quickly saturates to a finite value for H_α at all α > 0, but vanishes at large distance for $H_{\alpha }^{\prime }$ at α ≲ 3. (d) Ground-state spin-spin correlation ${\mathcal{C}}_{\mathit{ij}}$ for α = 0.5 and L = 500. This choice of α = 0.5 is arbitrary, but assists in a clear presentation of the coexisting exponential and 1/r^α+4 power-law decays.

We now analyze the effects of terms beyond leading order in q that have been ignored in our field-theory treatment. Including the higher-order analytic terms, such as the O(q⁴) term, will result in negligible corrections to the correlation functions that decay in distance faster than Eq. (5) [57]. However, even for α > 3, inclusion of the nonanalytic O(|q|^α−1) term will add a power-law tail to the correlation functions, which will dominate over Eq. (5) at long distance. In the Supplemental Material, we show by a more involved field-theory calculation that, for H_α, ${\mathcal{C}}_{\mathit{ij}}$ decays as 1/r^α+4 at large r. Our MPS calculations using L = 500 spins [Fig. 2(d)] show remarkable agreement with the field-theory predictions, even capturing the oscillations in $\mid {\mathcal{C}}_{\mathit{ij}}\mid$ occurring at intermediate distance where the short-range and long-range contributions to the correlation functions are of comparable magnitude and interfere. A power-law tail in ${\mathcal{C}}_{\mathit{ij}}$ should also exist for $H_{\alpha }^{\prime }$, but the increased correlation length prevents us from observing its existence clearly for α > 3.

Edge-excited states.

We expect the influence of long-range interactions on the edge- and bulk-excited states to be strong at small α; because the topological phase of $H_{\alpha }^{\prime }$ does not survive for α ≲ 3, we will focus on H_α from now on. Edges can be introduced into the field theory by replacing the two end spin-1’s with spin-1/2’s, represented by τ_L (τ_R) for the left (right) edge, resulting in an edge-bulk coupling Hamiltonian $H_c={\Sigma }_{i=2}^{L-1}{\mathit{S}}_i\cdot [{\tau }_L∕{(i-1)}^{\alpha }+{\tau }_R∕{(L-i)}^{\alpha }]$ [57]. For the edge-excited state |1⟩ [Fig. 1(a)], τ_L,R are polarized in the +z direction, and we expect $\langle S_i^z\rangle$ to decay away from the ends. Solving the free theory defined by Eq. (4) and treating H_c using standard first-order perturbation theory [57], we find that ${\langle n^z(x)\rangle }_1\propto \int \mathit{dq}\{\exp [\mathit{iq}(L-x)]-\exp [\mathit{iq}(x-1)]\}∕({\Delta }_{\alpha }^2+v_{\alpha }^2{q}^2)\propto \exp [-(L-x)∕{\xi }_{\alpha }]-\exp [-(x-1)∕{\xi }_{\alpha }]$ for even L. In addition, ⟨l^z (x)⟩₁ contributes a power-law correction 1/(x − 1)^α+2 + 1/(L − x)^α+2 for x far away from both ends [73]. Our numerical calculation of ⟨S^z(x)⟩₁, shown in Fig. 3(a), agrees well with a sum of these two contributions, clearly exhibiting an exponential followed by 1/r^α+2 decay.

FIG. 3.

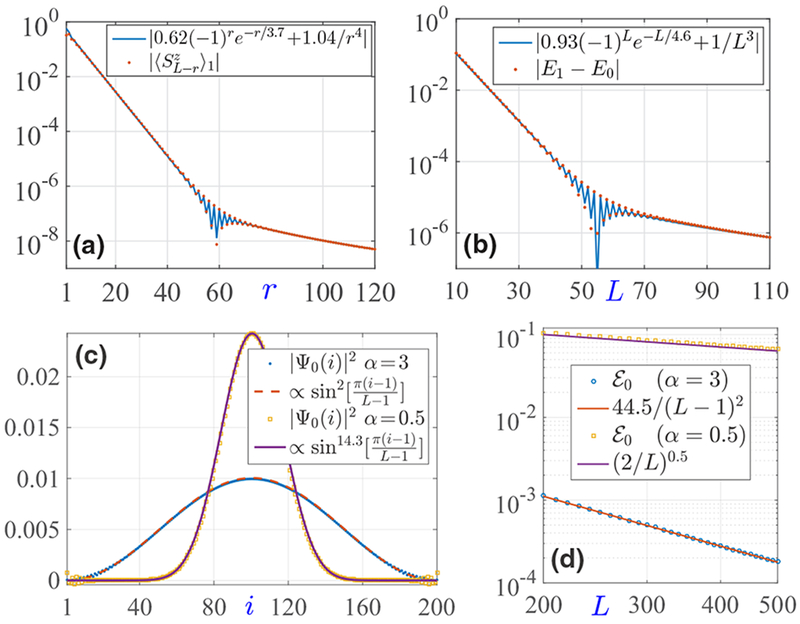
(a) Distribution of an edge excitation in state |1〉 for L = 500 and α = 2. (b) Edge gap |E₁ − E₀| as a function of the chain size L for α = 3. (c) Lowest-energy magnon probability density distribution for L = 200 and α = 3.0, 0.5. (d) The finite-size correction to the lowest magnon excitation energy [see Eq. (7)]. For α = 3, we obtain v_α = 2.18 and v_α/Δ_α ≈ 4.51, in good agreement with the ξ_α ≈ 4.55 obtained in Fig. 2.

The edge gap |E₁ − E₀| can be obtained by using a path integral to integrate out the n> field [57], resulting in an effective edge-edge Hamiltonian ∝ (−1)^L exp(−L/ξ_α)τ_L · τ_R. This scaling is confirmed, at relatively small L, by the numerical results in Fig. 3(b). However, the numerics also reveal that at large L the edge gap receives a long-range correction given by 1/L^α. This remarkably simple result, including the unity prefactor, can be understood as follows. The edge-excited states behave differently from the bulk-excited states due to correlations between the orientations of τ₁ and τ₂, and therefore ⟨S_i · S_j)₁ − ⟨S_i · S_j⟩₀ is very small unless i and j are very close to 0 and L, respectively. Thus we have E₁ − E₀ ≈ L^−α ∑_i<j(⟨S_i · S_j⟩₁ − ⟨S_i · S_j⟩₀⟩) = 1/L^α, where the last equality is a sum rule following from the total spin of the ground (S = 0) and edge-excited (S = 1) states.

Bulk-excited states.

As in the short-range Haldane chain, the elementary bulk excitations of H_α are spin-1 magnons [55–57]. Physically, the magnon represents fluctuations in the staggered magnetization, and, from Eq. (4), these fluctuations have a dispersion relation ${ϵ}_{\alpha }(q)=\sqrt{{\Delta }_{\alpha }^2+{(v_{\alpha }q)}^2}\approx {\Delta }_{\alpha }+q^2{v}_{\alpha }^2∕(2{\Delta }_{\alpha })$ (valid at small q). The lowest-energy magnon wave function Ψ₀(x) can be extracted from the numerics using the relation ${\mid {\Psi }_0(i)\mid }^2\approx \mid {\langle S_i^z\rangle }_2-{\langle S_i^z\rangle }_1\mid$. The presence of long-range interactions gives the magnon an additional potential energy due to the edge-bulk coupling Hamiltonian H_c, and Ψ(x) can be approximately described by the following Schrödinger equation (with Dirichlet boundary condition at x = 1, L),

$$\frac{v_{\alpha }^2}{2{\Delta }_{\alpha }}\frac{{\partial }^2\Psi (x)}{\partial x^2}+\frac{1}{2}\left[\frac{1}{{(x-1)}^{\alpha }}+\frac{1}{{(L-x)}^{\alpha }}\right]\Psi (x)=\mathcal{E}\Psi (x).$$ (7)

The kinetic (potential) energy always scales as 1/L² (1/L^α); therefore, for α > 2 and large L, the potential energy can be ignored. The ground-state energy ${\mathcal{E}}_0\approx v_{\alpha }^2{\pi }^2∕(2{\Delta }_{\alpha }{L}^2)$ and probability density |Ψ₀(x)|² ≈ (2/L)sin²(πx/L) are then identical to those of a particle in a box, as confirmed numerically in Figs. 3(c) and 3(d). The relation $E_2-E_1\approx {\Delta }_{\alpha }+v_{\alpha }^2{\pi }^2∕(2{\Delta }_{\alpha }{L}^2)$ allows us to obtain both v_α and Δ_α through finite-size scaling [Fig. 2(b)], and we confirm that the correlation length determined by ξ_α = v_α/Δ_α agrees with that obtained by fitting ${\mathcal{C}}_{\mathit{ij}}$ using Eq. (5). For α < 2, the potential energy dominates the kinetic energy for large L, and the potential can be approximated as harmonic around x = L/2. Thus |Ψ₀(x)|² resembles a Gaussian [Fig. 3(c)], and a simple scaling analysis predicts a width γ ∝ L^1−α/2. In the large-L limit, |Ψ₀(x)|² becomes sharply peaked at x = L/2 and, from Eq. (7), we expect the bulk gap to scale as Δ_α + (2/L)^α, which is clearly observed in Fig. 3(d). Since E₂ − E₁ = 2 when α = 0, it follows that Δ_α→₀ = 1, consistent with Fig. 2(a).

Outlook.

The stability of the topological Haldane phase to 1/r^α interactions for all α > 0 is favorable for trapped-ion based experiments, as stronger couplings can be achieved for smaller α [36,37]. Moreover, because the correlation length shrinks for longer-range interactions, a relatively small number of ions will suffice to suppress finite-size effects. Probing the topological phase by measuring both ${\mathcal{C}}_{\mathit{ij}}$ and ${\mathcal{S}}_{\mathit{ij}}$ with single-site resolution is nearly impossible in typical condensed-matter systems, but is quite straightforward in ion traps [74]. Based on the generality of our field-theory analysis, we speculate that for generic lattice models, the tails in the power-law interactions can possibly destroy the topological phase only when long-range interactions are unfrustrated and α < D + 2. Experimentally, unfrustrated long-range interactions can be easily implemented by generating a 1/r^α ferromagnetic interaction [71]. We hope that our work can serve as a springboard for future studies on how distinct topological phases behave in the presence of long-range interactions.