Transformation of a Spatial Map across the Hippocampal-Lateral Septal Circuit

SUMMARY

The hippocampus constructs a map of the environment. How this “cognitive map” is utilized by other brain regions to guide behavior remains unexplored. To examine how neuronal firing patterns in the hippocampus are transmitted and transformed, we recorded neurons in its principal subcortical target, the lateral septum (LS). We observed that LS neurons carry reliable spatial information in the phase of action potentials, relative to hippocampal theta oscillations, while the firing rates of LS neurons remained uninformative. Furthermore, this spatial phase code had an anatomical microstructure within the LS and was bound to the hippocampal spatial code by synchronous gamma frequency cell assemblies. Using a data-driven model, we show that rate-independent spatial tuning arises through the dynamic weighting of CA1 and CA3 cell assemblies. Our findings demonstrate that transformation of the hippocampal spatial map depends on higher-order theta-dependent neuronal sequences.

In Brief

How abstract representations are translated into action is unknown. Tingley and Buzsá ki describe how the hippocampal cognitive map is “read out” by a target region. The transformation relies on population coordination referenced to theta oscillations rather than the tuning of individual neurons.

INTRODUCTION

Computation performed by machines or the brain is, in general, referred to as “information processing.” However, the informative content of any computation is not inherent but requires interpretation by an observer/actuator mechanism (Chiel and Beer, 1997; Buzsáki, 2010). Accordingly, the utility of a correlation between the outside world and neuronal activity observed by an experimenter must be tested against the impact of that activity on downstream targets. While environmental-neuronal correlations have been extensively studied through the history of neuroscience (Adrian and Zotterman, 1926; Hubel and Wiesel, 1962), the internal effect of environmentally correlated neuronal activity on other brain regions remains largely unexplored. Thus, we set out to investigate how a well-studied neuronal activity pattern, the hippocampal spatial code, is transformed at the hippocampal-lateral septal interface.

A prominent computation attributed to the hippocampus (HPC) and its partner structures is the evaluation of the animal’s position relative to environmental landmarks, known as the cognitive map (O’Keefe and Nadel, 1978). Individual hippocampal neurons, known as place cells (O’Keefe and Dostrovsky, 1971), fire selectively at particular positions of the animal’s path. While the animal traverses through space, the firing rate of a given place cell waxes and wanes, forming its place field. This correlation between position and firing rate is often referred to as “rate coding.” The activity of place cell populations is coordinated by the hippocampal theta oscillation such that assemblies of place cells representing the past, present, and upcoming positions form ordered sequences of spiking within each theta cycle (Skaggs et al., 1996; Dragoi and Buzsáki, 2006; Foster and Wilson, 2007; Gupta et al., 2012). Progressive movement through an environment results in a systematic phase shift of spikes from single place cells across successive theta cycles. This spike-phase precession phenomenon (O’Keefe and Recce, 1993) is referred to as “phase or temporal coding.”

How these hypothesized rate or phase-coding mechanisms of the abstract cognitive map are read out by downstream partners and help the animal to choose appropriate paths have remained unexplored. One possibility is that place cells in the CA1 and subicular regions of the HPC transfer the map content to the neocortex via entorhinal or retrosplenial cortical outputs where further processing takes place to eventually influence locomotion (Alexander and Nitz, 2015; Rothschild et al., 2017). Another option is the lateral septum (LS), the main subcortical target of CA3, CA1, and subicular pyramidal neurons (Swanson and Cowan, 1979; Risold and Swanson, 1997). Convergence of hippocampal efferents onto LS neurons is orders of magnitude more dense (20–800 times; Figure S3) than any of its cortical targets. Optogenetic activation or silencing of hippocampal efferents in the LS effectively biases ambulatory patterns of the animal (Bender et al., 2015), possibly mediated by its hypothalamic, thalamic, mammillary body, and brainstem targets (Swanson and Cowan, 1979; Risold and Swanson, 1997). These structures are known to be involved in translating motivational values into motor outputs (Grastyán et al., 1965; Valenstein et al., 1970; Sheehan et al., 2004).

Using large-scale simultaneous recording of neuronal activity in the HPC and LS, we found a reliable correlation between the animal’s position in the maze and the spike timing of LS neurons in relation to the hippocampal theta oscillation phase. In contrast, firing rates of LS neurons contained little spatial information. These rate-independent theta “phase fields” of LS neurons covered virtually the entire length of the maze. Using a data-driven model of the HPC-LS circuit, we were able to account for this conversion of spatial encoding formats. The dynamic weighting of convergent synaptic inputs from CA1 and CA3 place cell assemblies, combined with the spatiotemporal theta oscillation phase map across hippocampal subregions, results in a rate-independent encoding of spatial position in LS neurons. These findings suggest that the HPC-LS pathway is a potential route for the transformation of the cognitive map into action.

RESULTS

To explore how hippocampal spiking output affects neuronal firing in the LS during spatial traversal, we simultaneously recorded neurons from the HPC and its target LS (N = 5 animals). First, we examined the firing patterns of 1,587 place fields of 2,297 isolated CA1 units and 224 place fields of 654 CA3 units, while rats traversed one of three different linear tracks (Figure S1). Place cells reliably fired at specific locations on the track, and their spikes displayed systematic advancement relative to the phase of theta oscillation while the animal ran though the place field (O’Keefe and Dovstrovsky, 1971; O’Keefe and Recce, 1993; Figures 1A–1C). Using an information theoretic approach that quantifies the uniqueness and reliability of a signal (Olypher et al., 2003), we quantified the maximum information rate for individual hippocampal place fields at spatial smoothing scales ranging from ~3 to ~100 cm. We found that peak information rates occurred at stereotyped spatial scales across the population (Figures 1D–1F). The mean peak information rate occurred at consistently smaller spatial scales for phase “coding” compared to discharge frequency coding (Figure 1E; N = 1,820; two-sample t test; p < 10⁻⁴⁰). For smoothing windows less than 6 cm, corresponding to approximately one theta cycle at average running speed, the phase code carried significantly (two sample t test; p < 0.00001; N = 1,820 place fields) more spatial information than the firing rate code (Figure 1G), whereas at spatial scales larger than 10 cm the firing rate code was more informative.

Figure 1. Hippocampal Place Cells Carry Precise Rate and Phase Codes for Position.

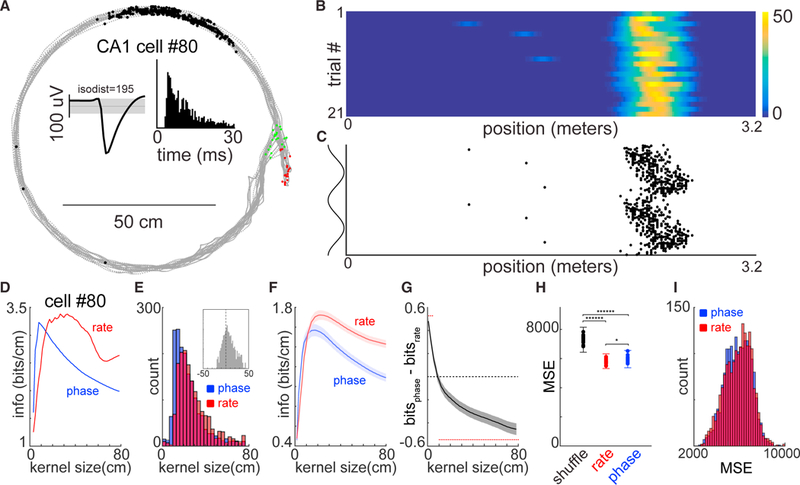
(A) Gray dots indicate the animals head position through out each maze traversal. Green and red dots indicate the starts and stops, respectively (N = 21 trials). Black dots reflect the animals’ position when action potentials were emitted by a single CA1 pyramidal neuron. Insets: black waveform shows the average action potential shape for that neuron (1 Hz to 20 kHz), and the grayed area indicates the third SD in mean voltage throughout the recording. Histogram is the auto-correlogram of spikes for the same neuron.

(B) Linearized firing rate maps. The y axis represents the number of trials (N = 21), and the x axis represents the linearized position of the animal on the maze.

(C) Linearized firing phase maps. Each dot corresponds to a single action potential, with reference to the CA1 pyramidal layer theta phase(y axis; shown twice for visibility) and the linearized position of the animal on the maze (x axis).

(D) Peak spatial information rates for the example neuron in (A)–(C) with different smoothing kernel widths. Red indicates the information rate obtained by using spike rate (1B), and blue indicates the information rate using spike phase (1C).

(E) Histograms represent the smoothing kernels with the maximum peak information rate (peaks of red/blue lines in (D) for phase (blue) and rate (red) codes for a total of 1,820 CA1 and CA3 place fields. Median phase peak information rate was 15 spatial bins, and median discharge frequency peak information rate was 29 spatial bins (two-sample t test p < 10⁻⁴⁰). Inset histogram shows the distribution when smoothing kernel widths with peak information rates are subtracted for phase and rate.

(F) Average peak information rates for 1,820 place fields for all smoothing kernel sizes. Bounds are ±3 SEM.

(G) Average of subtraction of phase and rate information scores for all 1,820 place fields and smoothing kernel sizes. Bounds are ±3 SEM. Red dots indicate bins with significantly different rate and phase information (two sample KS test; p < 0.01).

(H) Mean squared error (MSE) values when using the example cell in (A)–(C) to predict the animal’s position. Blue dots are models that used the neurons firing phase as a predictor, red dots are models that used the firing rate as a predictor, and black dots are MSE values for shuffled data (N = 10 iterations; Monte Carlo cross-validation).

(I) Histogram of mean squared error (MSE) values for all place fields using firing rates (red) or firing phase (blue) to predict the animal’s position.

See also Figures S1 and S2.

To directly compare and cross-validate these two forms of tuning, we followed a predictive modeling approach where the spike-rate or spike-phase relationships of single neurons was used to predict the current position of the animal (20 bin smoothing; ~30 cm; Figure 1H). Across the population of recorded hippocampal place fields, we found that the distributions of mean squared errors for these two forms of encoding were statistically equivalent at a spatial smoothing scale that incorporated both peak information rates (Figure 1I; two-way Kolmogorov-Smirnov [KS] test; N = 1,820 place fields comparison p = 0.19; N = 45 sessions; p = 0.61). While peak information rates (Figures 1D–1G) demonstrate that the spatial smoothing scale largely determines which coding regime confers more spatial information per individual position bin (~1.5 cm), the predictive modeling approach (Figures 1H and 1I) quantifies how much predictive power overall spatial bins a single neuron carries. Taken together, these analyses demonstrate that from the perspective of an ideal observer, such as the experimenter, prediction of the animal’s position is equivalent whether using rate-position or theta phase-position correlations at slower timescales (30 cm, ~500 ms). Yet, at the scale of single theta cycles (corresponding to ~6 cm), phase coding offers more information than firing rates.

However, the significant encoding of an external variable from the perspective of the experimenter does not demonstrate that the brain utilizes this information (Buzsáki, 2010; Brette, 2018). To explore whether and how downstream “readers” may interpret these potential coding regimes, we examined firing patterns of neurons in the LS, the major subcortical target of CA3 and CA1 hippocampal regions (Risold and Swanson, 1997; Witter, 2007; Figures S1A, S1C, and S3).

We recorded a total of 1,647 LS neurons from five animals, of which 840 surpassed a minimum threshold of at least 1.5 action potentials per trial on average (~.33 Hz). In agreement with previous studies, we found that LS neurons carry a degraded firing rate code for position when compared with the HPC (Leutgeb and Mizumori, 2002; Takamura et al., 2006; Figures 2B and 3C). LS action potential ratemaps had significantly lower peak information rates than hippocampal place field maps (average of 0.4 bits/cm versus 1.7 bits/cm; two-sample t test p < 10⁻¹⁰⁰), and only 5.3% (232/4,393) of LS ratemaps showed place fields, using the same criteria we applied to hippocampal units where 31.7% (1,820/5,735) of ratemaps displayed a place field. Those few LS ratemaps that did qualify as having a “place field” were significantly less stable across trials than CA1/CA3 place fields (median coefficient of variance = 41.5 for LS versus 10 for CA1/CA3 place fields; two sample t test; p < 10⁻²⁰). In contrast, the majority of LS neurons showed a form of position encoding in their spike timing relative to the phase of theta oscillations recorded from the CA1 pyramidal layer (751/840,89%; two sample t test; p < 0.01) when compared to shuffled data, in at least one of the behavioral conditions (Figure 2C). Importantly, theta phase coding was often independent from any significant correlation between the animal’s position and firing rates (Figure 2D). Across the population of LS neurons, we observed significantly stronger spike-phase coding when compared with models that utilized spike rate information (Figure 2E; two sample t tests; N = 4,393 conditions, p < 10⁻¹⁰⁰; N = 62 sessions, p < 10⁻¹⁰). Spike-phase-based decoding outperformed firing rate-based decoding of the rat’s position on the tracks (Figures 2F and 2G) whether we made the comparison at the level of LS neurons (N = 786/840; two-sample t test; p < 0.01), conditions (N = 3,046/4,393), or recording sessions (N = 62/62). Thus, the precise timing of action potentials relative to hippocampal theta oscillations is the dominant form of allocentric spatial encoding for single LS neurons, rather than the rate at which action potentials occur at any given location (Figures 3, S4, and S6). Notably, when there is no preselection for subpopulations of neurons (i.e., place fields), the lateral septal phase encoding of position is more reliable than either the rate or phase codes of the HPC (Figures 3A and 3C). Furthermore, the firing phases of ensembles of simultaneously recorded LS neurons (range: 1–53) provided a better readout of spatial position than either the firing phases or rates of an equivalent number of HPC neurons (Figure S7; two-sample t test; p < 0.001 at ensemble sizes of 15–25 neurons).

Figure 2. Lateral Septum Neurons Display a Rate-Independent Spatial Phase Code.

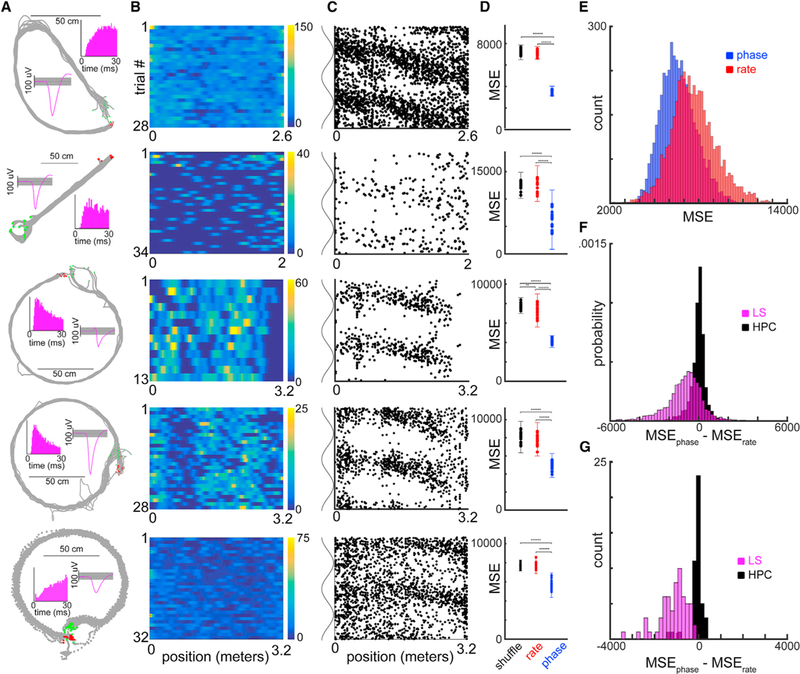
(A) Behavioral tracking data for five different sessions. Same layout as in Figure 1A.

(B) Linearized firing rate maps for each of the five example neurons. For each heatmap, they axis represents the number of trials recorded in the condition for that recording (N = 28, 34, 13, 28, and 32), and the x axis represents the linearized position of the animal on the maze (meters).

(C) Spike theta phase-position scatterplots for each of the five example neurons.

(D) Mean squared error (MSE) values for models using shuffled data (black), firing rates (red), or firing phase (blue) to predict the animal’s position (N = 10 iterations).

(E) Histograms of average MSE values (blue/phase, red/rate) for all recorded LS neurons, across all conditions (N = 4,393).

(F) Histogram of average MSE_phase-MSE_rate values for all conditions for lateral septum (LS) cells (magenta; N = 4,393, mean = − 1,000) and hippocampal place fields (black; N = 1,820, mean = − 33).

(G) Histogram of average MSE_phase-MSE_rate values for all recordings in the hippocampus (HPC) (black; N = 45 sessions, mean = − 25) and lateral septum (magenta; N = 62 sessions, mean = − 1,024).

See also Figures S1–S3.

Figure 3. Rate and Phase Population Correlation Matrices.

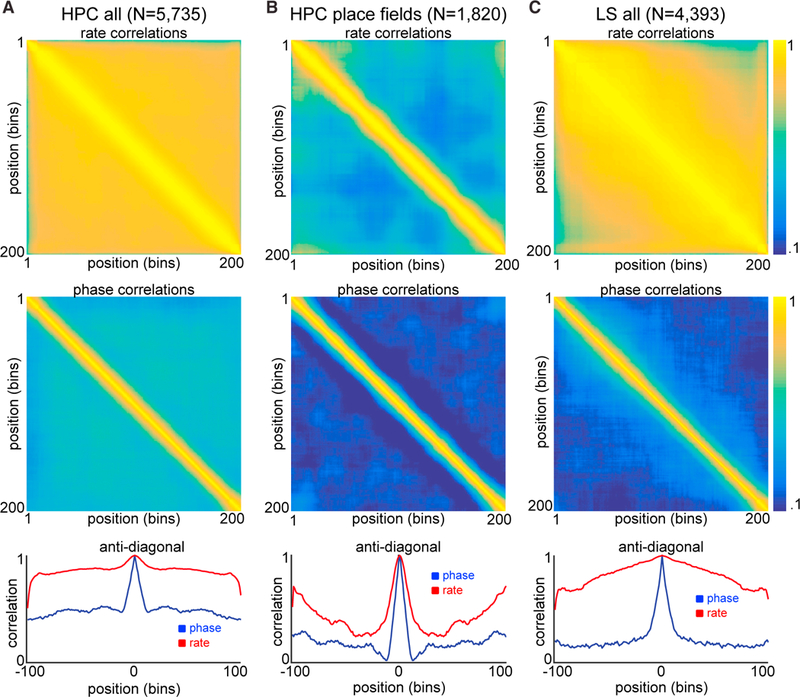
(A–C) Top row: correlation matrix (Pearson’s) across all positions for all 5,735 hippocampal conditions (N = 2,951 units, A), 1,820 hippocampal place fields (N = 711 units, B), and for all 4,393 LS ratemaps (N = 840 units, C) using firing rates. Middle row: correlation matrices (circular) across all positions for all hippocampal conditions (A), hippocampal place fields (B), and LS conditions (C) using theta phase of firing. All color axes are 0.1–1. Bottom row: anti-diagonal lines from each correlation matrix are plotted for phase (blue) and rate (red) mappings. See also Figures S4 and S6.

We also examined the effect of running speed on LS phase coding. Only 125 of 4,393 LS conditions (2.8%) had significant correlations between running speed and the rate of phase precession (two sample t test; p < 0.01) compared to a trial shuffled control distribution. Furthermore, only 10.7% of firing rate maps in LS were significantly modulated by running speed, a value similar to the ~15% reported in HPC and entorhinal cortex (McNaughton et al., 1983; Kropff et al., 2015). In contrast, 89% of LS neurons displayed significant phase precession. Thus, phase coding of LS neurons seems to be independent from the running speed of the animal.

The different electrode locations across animals covered a large volume of the LS, allowing us to examine the anatomical microstructure of this phase code. The multiple site silicon probes and the systematic mapping of LS across days by moving the probe shanks revealed a precise topography for the magnitude of theta phase coding within the LS. Within single recording sessions in individual rats (Figures 4A and 4B) and across all animals (Figures 4C and 4D) the strength of phase coding, relative to rate coding, reliably increased as a function of recording depth within LS. Furthermore, the starting phase for these “phase fields” varied systematically along the medial-lateral axis across animals (Figure 4E). In three of the animals where at least 1 mm of the dorsoventral axis of LS was recorded across multiple sessions, the phase onset for precession varied systematically and significantly with recording depth (DT5 r = 0.38, DT9 r = 0.25, DT2 r = 0.27; circular/linear correlation; p < 0.001). Considering the known anatomical mapping of hippocampal projection patterns (Risold and Swanson, 1997), these data provide evidence that the hippocampal theta oscillation, which is a traveling wave along both the septotemporal and transverse axes of the HPC (Lubenov and Siapas, 2009; Patel et al., 2012), entrains the spiking output of the LS in a manner that is also a traveling wave of spiking activity that propagates in both the medial-to-lateral and dorsal-to-ventral directions.

Figure 4. Microstructure of the Theta Phase Code in the LS.

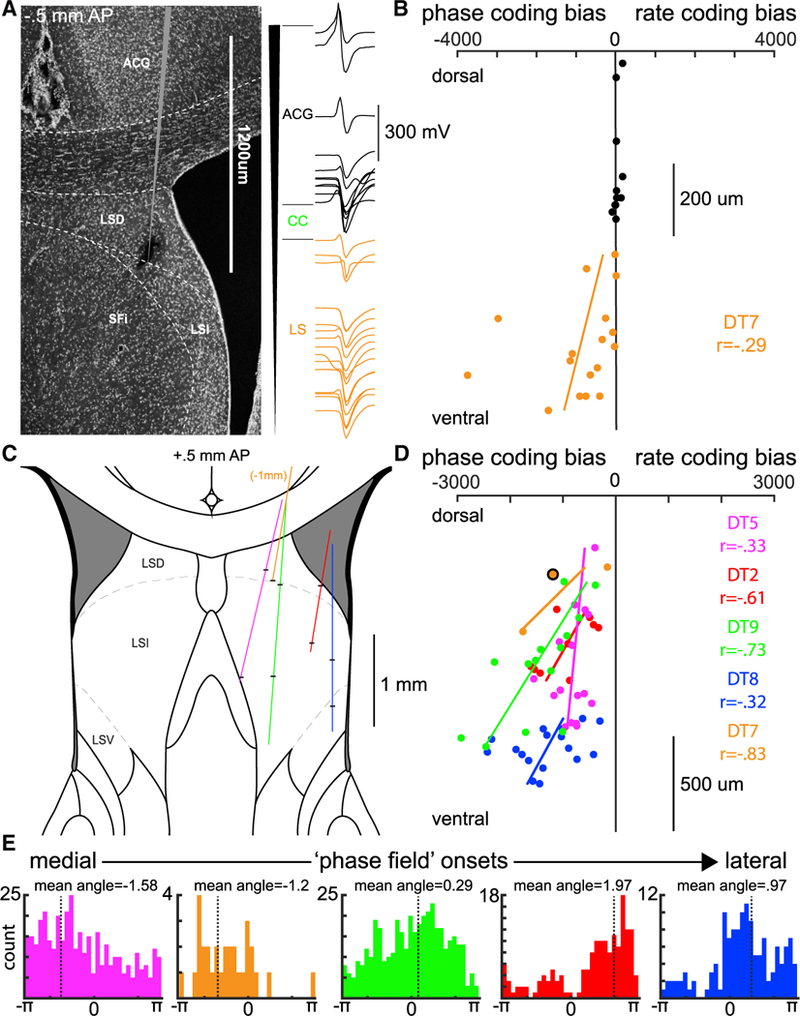
(A) Left: histology for a recording with a single-shank silicon probe (64 channels spanning 1,275 μm). Right: single units were simultaneously isolated from recording sites in the anterior cingulate cortex (ACG; black) and dorsal lateral septum (LSD; orange). Waveforms are positioned to match the recording site along the shank with the largest amplitude waveform. LSI, intermediate lateral septum; SFi, septofimbrial nucleus.

(B) Location of the neuron’s cell body in the LS varies systematically with the strength of phase coding. Each dot indicates the electrode site with the maximum waveform amplitude (0–1,275 μm; y axis) and the relative strength of phase coding (x axis) for a single neuron (MSE_phase-MSE_rate).

(C) Reconstructed recording tracks for all five animals (magenta, orange, green, red, and blue; see also Figure S1). Black horizontal bars indicate the approximate first and last recording site for each animal.

(D) Group data for 5 rats. Each dot is a session mean MSE determined by all recorded neurons in that session (range: 8–53). The orange circle outlined in black corresponds to the session shown in (B). Spacing and estimated depth locations were determined with a combination of histology (Figure S1), electrophysiological markers, and micro-drive turn records.

(E) For every phase precessing LS neuron, the mean phase angle, relative to CA1 theta, for the first 15 bins of its phase field is shown. Each colored histogram shows the mean phase angles for neurons recorded from a single animal.

Colored dots, lines, and histograms in (C)–(E) correspond to the same animal.

Next, we addressed the potential mechanisms by which the hippocampal population output is transformed into firing patterns of LS neurons. We reasoned that such a transformation should involve quantifiable functional coupling between these regions that may be captured at the level of cross-region neuron pairs. To test this hypothesis, we examined cross-correlograms between spikes of hippocampal neurons and simultaneously recorded LS neurons (Figures 5A–5C). Synchronous peaks in the cross-correlograms were often observed within ±25 ms (Figure 5C). To quantify this, we utilized a peer prediction method that has been used to identify cell assemblies within single brain structures (Harris et al., 2003; Tingley et al., 2015; Figure S5). By using simultaneously recorded spike trains to predict the firing of a single neuron, the temporal scale at which a neuron’s peers best predict its firing can be assessed. Across 18.5% (2,087/11,264) of hippocampal-LS cell pairs examined, spike trains of hippocampal neurons reliably predicted the firing of action potentials in LS neurons with a strongly skewed distribution of assembly strengths (Figures 5D and 5E). Across all predictive cell pairs, the median optimal timescale for peer prediction was 25 ms (Figure 5F), corresponding to the slow gamma oscillation generated mainly by the hippocampal CA3 region (Csicsvari et al., 2003; Colgin et al., 2009; Fernández-Ruiz et al., 2017). Notably, theta phase locking magnitudes did not significantly correlate with either the strength or timescale of cell assemblies (Figures S5B–S5E). Furthermore, LS neurons that participated in at least one predictive cell assembly were found to carry a more robust spatial phase code compared to neurons that were not part of a predictive assembly (Figure 5G; two sample t test; p < 10⁻²⁰).

Figure 5. Gamma Timescale Cell Assemblies Bind Hippocampal and Lateral Septal Spatial Phase Codes.

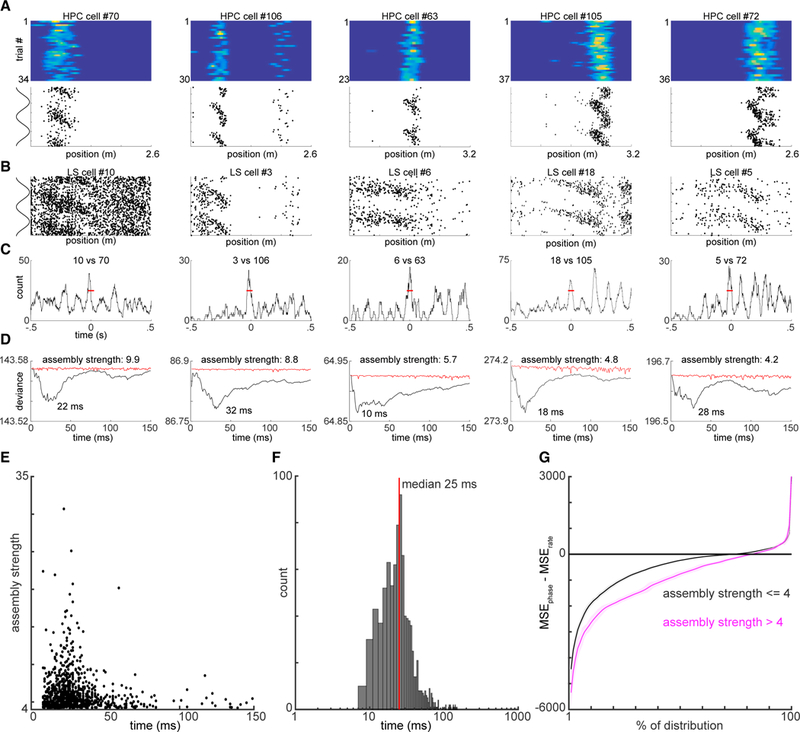
(A) Five example hippocampal (HPC) place fields. Upper: firing rate maps for each example neuron. Y axis is the number of trials; x axis is the linearized position on the track. Color axis is 0 to max rate. Lower: firing phase maps for each example hippocampal neuron. y axis represents the CA1 theta phase; x axis represents the linearized position of the animal.

(B) Firing phase maps for five example LS neurons, simultaneously recorded with the hippocampal neurons shown above.

(C) Cross-correlograms between each example cell pair(one HPC and one LS neuron), smoothed over 20 ms. Red horizontal lines indicatea50-mstimewindow, within which each pair of neurons reliably fires together.

(D) Generalized linear model (GLM) approach to quantify assembly strength of simultaneously recorded HPC-LS neuron pairs. x axis represents the smoothing kernel size (1–150 ms) of spike rate; y axis represents the deviation from fit for each model. Black line shows values for actual data; red lines indicate the average deviation values expected after shuffling trial order.

(E) Scatterplot of smoothing kernel windows versus assembly strength values. For each HPC-LS “assembly” pair, the smoothing kernel with optimal fit (x axis) is plotted against the relative strength of the assembly (y axis).

(F) Histogram of optimal fit windows. Red line indicates the median of 25 ms.

(G) LS neurons that participated in at least one highly predictive HPC-LS assembly pair (threshold ≥4) were observed to carry a significantly stronger spatial phase-coding bias (two-way KS test; p < 10⁻²⁰). x axis represents the percentile of the cumulative distribution (0%–100%) of LS neurons, and y axis represents the sorted MSE value associated with that percentile. Magenta and black lines correspond to MSE_phase-MSE_rate values expected from LS neurons that do or do not participate in at least one gamma assembly with simultaneously recorded hippocampal neurons, respectively. Bounds are ±3 SDs. See also Figure S5.

Unfortunately, the presence of a reliable phase-position correlation in LS neurons (Figures 2, 3, and S4) and their temporal coupling, via gamma assemblies, with hippocampal neurons (Figure 5) does not give mechanistic insight into how LS neurons read out spatial information from the HPC. Possibilities include reading out rate, phase, or population synchrony patterns from upstream hippocampal neurons. Because CA1 and CA3 place cells tend to fire on the opposite phases of the theta cycle (Dragoi and Buzsáki, 2006), we hypothesized that differential coupling to these hippocampal regions could be involved in the phase precession of LS neurons.

To examine whether such a potential mechanism was supported by the data, we split the hippocampal recordings into those in which LS neurons were recorded simultaneously with either CA1 neurons (N = 63 sessions; black) or CA3 neurons (N = 19 sessions; red; Figure 6A). A subset of recordings had electrodes positioned in both CA1 and CA3 regions, allowing for simultaneous local field potential (LFP) recording from all three structures (N = 14 sessions; Figure 6B). LFP theta phase coherence between LS and CA1 pyramidal layer sites was relatively flat during the entire span of the tracks. In contrast, theta phase coherence between LS and CA3 pyramidal layer increased significantly from the beginning to the end of run (Figure 6C). A similar relationship was observed when cross-frequency coupling strength (Bragin et al., 1995) between CA1 or CA3 theta phase and LS gamma oscillation amplitudes were examined. Although the strength of coupling increased in both cases, it was significantly stronger for CA3-LS than for CA1-LS comparisons (Figure 6D). To exclude the potential contribution of volume-conduction for the LFP signals, we also examined assembly strength changes as a function of position. The functional coupling between CA1 place cells and LS neurons decreased somewhat (r = −0.11; p = 0.079; N = 260 pairs), while coupling between CA3 place cells and LS neurons significantly increased (r = 0.34; p = 0.006; N = 72 pairs) as the animal progressed from the start toward the goal location (Figure 6E). The functional coupling of CA1-LS pairs was significantly anti-correlated with CA3-LS pairs (r = − 0.88; p = 2.6e-64; N = 200 spatial bins). Thus, all functional coupling metrics examined −LFP/LFP and spike/spike– provide support for a dynamic weighting model.

Figure 6. Lateral Septal Phase Precession Is a Readout of Dynamic Weighting of CA1 and CA3 Inputs.

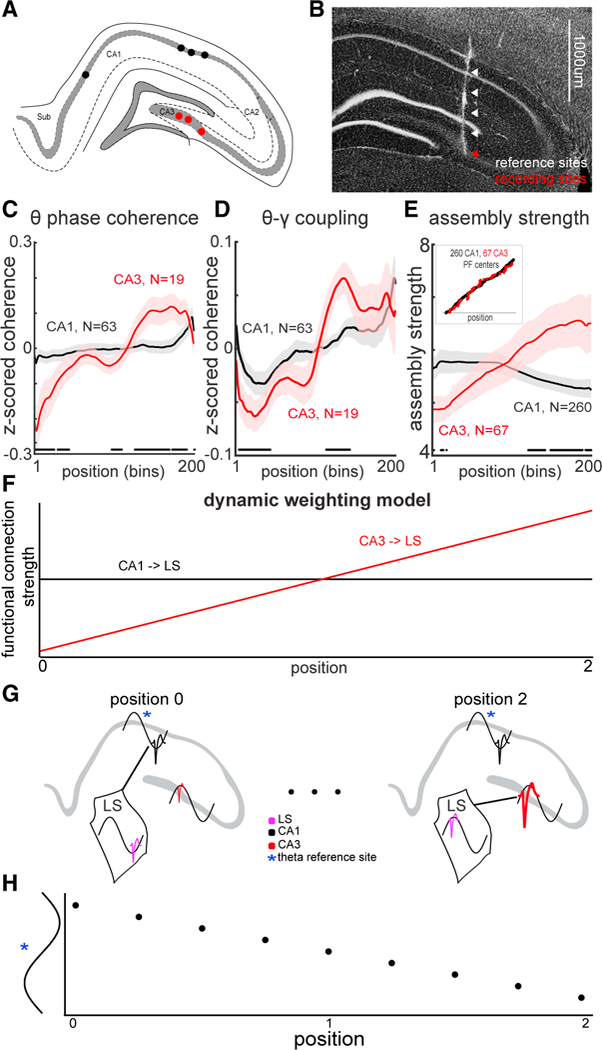
(A) Representative schematic of histological results showing the hippocampal recording locations in four animals (four CA1 and three CA3 sites).

(B) Representative histological results from simultaneous CA1 and CA3 recording of LFP with reference sites that spanned 1 mm above probe recording tip.

(C) Theta phase coherence between CA1 (black), or CA3 (red), recording sites and LS.

(D) Hippocampal theta-septal gamma coherence between CA1 (black), or CA3 (red) sites and LS.

(E) CA3 place fields form progressively stronger gamma assemblies with LS as the animal traverses through space, while CA1 place fields decrease their coupling strength. Bounds are ±1 SEM. Black dots indicate bins that are significantly different between CA1 and CA3 (two-sample KS test; p < 0.05). Inset shows that both CA1 and CA3 place cells tiled the entire track.

(F) Diagram of hypothetical coupling strengths between CA1/LS (black) and CA3/LS (red) as a function of spatial position of the animal.

(G) Conceptual model of how dynamic weighting interacts with theta phase delays across CA1–CA3 regions. LS output neuron is entrained to the phase of theta oscillation reflecting the most strongly coupled input.

(H) Spiking output from a LS “reader” neuron demonstrates phase precession relative to theta recorded at a fixed hippocampal site, in the CA3–CA1 axis, across three different spatial positions

These results suggest that the ratio of input strengths from the hippocampal CA1 and CA3 regions to LS dynamically shift over the course of the track (Figure 6F). When combined with the theta phase shift between these regions, the relative strength of the momentarily active CA1 and CA3 ensembles may determine the phase of spiking output in the LS reader neuron (Figure 6G), causing it to precess relative to the phase of the LFP theta recorded in either upstream region (Figure 6H). Thus, the target LS neuron encodes position along the entire track with the phase of spiking.

To test the feasibility of the dynamic weighting model, we created a spiking neural network of Hodgkin-Huxley model neurons (Carnevale and Hines, 2006) that mimicked the output properties of a single lamella of pyramidal neurons in the hippocampal formation and its projections to a single LS neuron (Figure 7A). The modeled network was designed to recapitulate the following observed phenomena: (1) populations of CA1 and CA3 neurons send convergent projections to the LS (Figures 7A and S3; Risold and Swanson, 1997), (2) place fields uniformly tile a space (Figure 6E, inset; Figure 7B; O’Keefe and Dovstrovsky, 1971), (3) place cells phase-precess relative to an 8-Hz theta oscillation (Figure 7C; O’Keefe and Recce, 1993), (4) theta (H) Spiking output from a LS “reader” neuron demonstrates phase precession relative to theta recorded at a fixed hippocampal site, in the CA3–CA1 axis, across three different spatial positions sequences occur within single trials (Figure 7D; Dragoi and Buzsáki, 2006; Foster and Wilson, 2007; Gupta et al., 2012), and (5) CA3 theta is phase offset from CA1 by 180 degrees (Figures 7C and 7D; Buzsáki et al., 1983; Dragoi and Buzsáki, 2006).

Figure 7. Theta Oscillation-Coordinated Hippocampal Assemblies Are Required for Spike-Phase Precession of LS Neurons.

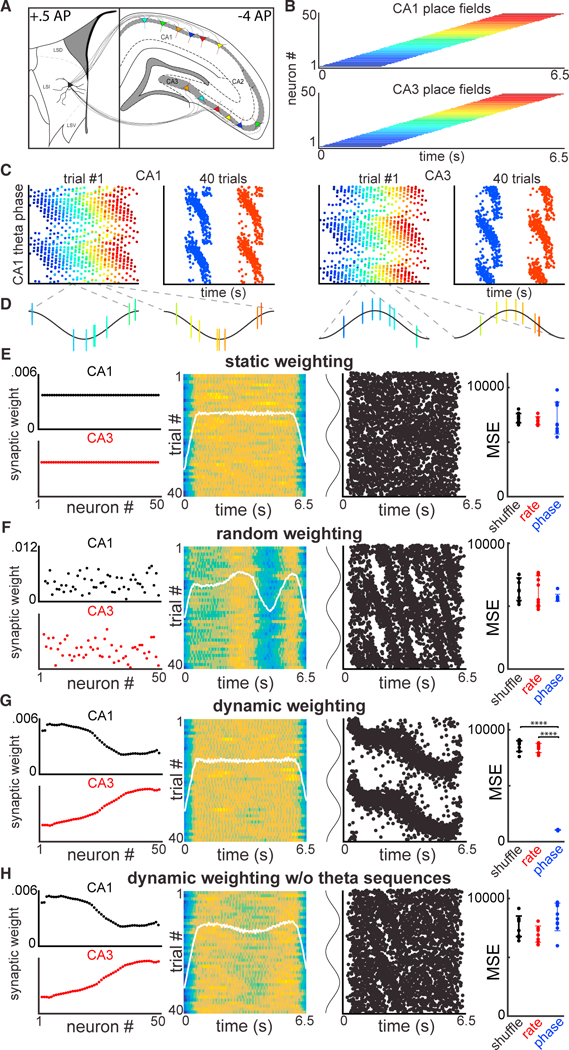
(A) Biophysical model of CA1/CA3 place field populations that provide convergent input to a LS neuron.

(B) CA1/CA3 place fields tile a segment of space (shown as time, assuming constant velocity). Each colored bar indicates the firing field for a single idealized neuron in CA1 (upper) or CA3 (lower).

(C) Left columns: spike-phase maps for 50 simulated CA1 place cells that phase precess over a single trial. Right columns: spike-phase maps for neurons 10 and 40, showing reliable phase precession across 40 trials. Note that CA3 place cells maintain the same dynamics but with a 180° phase offset from CA1 theta.

(D) CA1/CA3 populations form theta sequences within single trials.

(E) Column one: Static synaptic weight matrices for CA1 (black) and CA3 (red). Neuron order is sorted to match the order of place field location in (B). Column two: firing rate maps for the modeled LS neuron across 40 trials. White line is the mean firing rate across trials. Column three: firing phase maps for the modeled LS neuron across 40 trials, relative to CA1 theta phase. Column four: mean squared error values using the same decoder as in (H) and (D) for shuffled data (black), firing rates (red), or firing phases (blue) of the modeled LS neuron.

(F) Same as in (E) but with a random synaptic weight matrix.

(G) Same as in (E) but with a synaptic weight matrix taken directly from the gamma assembly analysis in Figure 6E. Dynamic weighting of synaptic matrix produces a robust spatial phase code.

(H) Same as in (G) but without the presence of population theta sequences. This is achieved by injecting different theta rhythms into individual CA1/CA3 neurons.

Having created this model of hippocampal activity and its output to LS, we asked how different synaptic weight matrices influence the transmission, or transformation, of spatial information through this simulated circuit (Figures 7E–7H). Using a static weighting regime, where all synaptic connections have equal strength, we observed no or highly variable spatial information in the downstream neuron (Figure 7E). This is due to the interference of spatial and temporal offsets of CA1 and CA3 cell firing. Using random weight matrices, where each synaptic weight is drawn from a normal distribution, we observed weak predictions of spatial position that rarely exceeded chance for both firing rates and firing phases (Figure 7F). The next synaptic weight matrix we examined was one derived from the data examining assembly strengths between HPC and LS (Figure 6E). Using a connectivity matrix that matched the experimentally measured negative correlation between CA1 and CA3 populations (r = − 0.88; Figure 7G, left column), we observed that the downstream LS neuron carried a highly reliable phase code, in a manner that is independent of firing rate information (Figure 7G). By injecting uncoordinated theta oscillations into individual CA1 and CA3 neurons, we obtained identical place fields and phase precession clouds but without the presence of coordinated theta sequences within single trials. As a result of this manipulation, the reliability of the phase-position relationship in the model LS neuron was severely degraded (Figure 7H). Thus, by dynamically weighting the outputs of CA3 and CA1 place fields at different positions, the assembly firing of the hippocampal output is transformed into a rate-independent phase code of that space in the LS, consistent with our experimental observations (Figures 2, 3, and S4).

DISCUSSION

We examined the encoding of space in neuronal activity of the HPC and its major subcortical output region, the LS. While firing rate and theta phase of spiking of single place cells correlated similarly with the rat’s spatial position in the HPC, the correlation between firing rate and position was exceptionally rare for LS neurons. Instead, the timing of spikes within the hippocampal theta cycle (i.e., phase) carried a high level of spatial information. Unlike the spatially restricted spike-phase precession of hippocampal place cells, LS phase fields could cover virtually the entire length of the maze (~3.2 m). The strength of this phase coding had an anatomical microstructure within the LS, increasing along the dorsoventral axis. By examining theta coherence, theta-gamma cross-frequency coupling, and cell pair correlations between the HPC and LS, we found that LS neurons compare the relative strengths of the activity of their upstream CA1 and CA3 partner place cell assemblies. The dynamically changing ratio of these strengths within the theta cycle may be responsible for the timing of action potentials in LS neurons. The biophysical model we implemented to examine this hypothesis demonstrates that rate-independent spatial encoding in LS can arise through the hypothesized dynamic weighting of CA1 and CA3 synaptic inputs, which converge on target reader neurons in the LS. Our findings define a transformation rule between the cognitive map of the HPC and its action-executing target, the LS.

Spatial Correlates of Firing Patterns in the Hippocampus and Lateral Septum

Numerous experiments have described that both firing rates and theta phase of place cell spikes in the HPC correlate with the spatial position of the animal (O’Keefe and Nadel, 1978; O’Keefe and Recce, 1993; Jensen and Lisman, 2000; Dragoi and Buzsáki, 2006). Our findings confirm that rate coding of the animal’s position is reliable when long time windows are used for calculating rate (>10 cm, Figure 1). Yet, firing rate is an inherently ambiguous code for spatial position because it waxes and wanes within the place field, and, thus, the same instantaneous rate may refer to two distinct positions. Firing rate also varies as a function of speed of the animal (McNaughton et al., 1983) so at different speeds the same instantaneous rate may refer to different positions. In agreement with the above reasoning, we found that when rate coding of single place cells is examined at high spatial resolution, e.g., at 6 cm or less, which corresponds to approximately a single theta cycle at average running speed, spike-theta phase more reliably correlates with position than spike rate (Figure 1). Therefore, the hippocampal phase code operates at a speed that may be more amenable to the timescales for synaptic integration (Losonczy and Magee, 2006), synaptic plasticity (Bi and Poo, 1998), and perception (Thorpe et al., 1996).

In the LS, bona fide place fields, determined by classical firing rate criteria, were rare and reflected only a degraded and unstable version of hippocampal place fields (Zhou et al., 1999; Leutgeb and Mizumori, 2002; Takamura et al., 2006). In contrast, the magnitude of correlation between spike theta phase and position was comparable between neuronal populations recorded from the LS and HPC (Figures 3 and S7). Thus, theta phase precession appears to be the predominant coding mechanism for position in LS neurons, anchored to either local or distal cues (Figure S6; Knierim, 2002)

Theta phase precession has also been reported in the prefrontal cortex (Jones and Wilson, 2005), ventral striatum (van der Meer and Redish, 2011), and basal forebrain (Tingley et al., 2017). However, in the ventral striatum, neurons show an anticipatory ramping of spiking activity up to the reward sites, while in the prefrontal cortex and basal forebrain firing rates are tuned to specific behavioral task phases, dissociated from spatial cues (van der Meer and Redish, 2011; Tingley et al., 2014). In contrast, LS firing rates lacked reliable tuning to spatial features of the task.

Phase-coding bias for position systematically increased from dorsal-to-ventral regions of the LS (Figure 4), demonstrating a topographical microstructure for spatial encoding within the LS. Additionally, the starting phase for precession (i.e., “onset”) varied along both dorsal-to-ventral and medial-to-lateral axes (Figure 4). Together, this would suggest that a similar computation is being carried out across subregions of the LS, whose spiking output is organized as a “traveling wave,” which reflects theta phase shifted inputs from different regions and septotemporal positions of the HPC (Lubenov and Siapas, 2009; Patel et al., 2012). In addition, we were able to demonstrate that hippocampal-LS spike-spike coupling, coherence of theta oscillations, and theta-gamma cross-frequency coupling could explain several aspects of LS neuron phase precession. Overall, these findings demonstrate that position information can be as reliably “decoded” from the lateral septum as from the HPC, although the format of neuronal signaling that provides such information is different in these structures. We would like to add a cautionary note though that hitherto unexplored multi-synaptic, multi-structure mechanisms may allow for an alternative mechanism of spike-phase coding of position in the LS.

Transmission and Utilization of the Hippocampal Spatial Map by LS Neurons

Ample evidence supports the view that the HPC and its partner structures generate a map of the environment, but less is known about the mechanisms by which this abstract code is read out by downstream partners and utilized for action. Our findings suggest that the LS is a potential decoder of hippocampal output by comparing the ratio of inputs from CA1 and CA3 pyramidal cells within each cycle of the theta oscillation and transforming this ratio into precise spike times.

The correlation between position and theta phase spiking in LS has several potential explanations. First, an argument can be made that the phase shift refects running speed variation. However, only a small fraction of LS neurons were modulated by locomotion speed, and we observed no relationship between the magnitude of speed-rate correlation and the magnitude of phase precession. A second potential explanation of spike theta phase shift is due to reward goals, as in the ventral striatum (van der Meer and Redish, 2011) or path length traveled. These options are less likely because theta phase precession of many LS neurons retained their relation to distant room cues after the rotation of the maze, suggesting that the spike-phase shift is a spatial “code” (Figure S6). A third explanation is that LS neurons inherited their spiking activity directly from ventral hippocampal place cells with large place fields (Kjelstrup et al., 2008; Royer et al., 2010). While we cannot reject this hypothesis, it seems unlikely given several aspects of the currently available data.

If phase precession is simply inherited directly from single hippocampal neurons or coherent place field assemblies, one should expect that concomitant firing rate changes of the upstream neurons should also be transferred to LS neurons. Specifically, we should have also found copies of small place fields with firing rates and phase precession reminiscent of dorsal hippocampal place cells. Because we surveyed a large extent of the LS, it is unlikely that we systematically missed the target zone of dorsal CA1 and CA3 pyramidal neurons. Moreover, previous anatomical mapping studies (Risold and Swanson, 1997; Oh et al., 2014), our own tracing experiments (Figure S3), and the shifting phase “onsets” of precession (Figure 4) show that our LS recordings spanned areas that receive both dorsal and ventral CA1 and CA3 outputs. For an inheritance model of LS phase precession, we would also expect the spatial scaling of hippocampal inputs (Kjelstrup etal., 2008; Royer et al., 2010) to be refected in the firing patterns of LS neurons, yet we observed comparable spatial scaling between the dorsal hippocampal and LS populations (Figures 3B and 3C).

A recently proposed set of “dual-input” models explains phase precession of CA1 pyramidal neurons by the varying strengths of CA3 and layer 3 entorhinal cortical neuron inputs (Hasselmo et al., 2002; Colgin et al., 2009; Chance, 2012; Lasztóczi and Klausberger, 2016; Fernández-Ruiz et al., 2017). Entorhinal drive initiates place cell activity but short-term depression of these afferents reduces the efficacy of this input, while, in the outgoing part of the place field, the CA3 input is the major source of excitation of CA1 place cells (Fernández-Ruiz et al., 2017). In all these experiments and models, firing rates determine the place field, associated with theta phase precession. In contrast, the form of theta phase advancement we observed in LS occurred without the presence of discrete place fields or reliable changes in firing rate (Figures 2 and S2), and at a temporal scale (~6 s) slower than that observed for short-term synaptic plasticity (Stevens and Wang, 1995; Fernández-Ruiz et al., 2017). Importantly, phase precession of LS neurons extended to virtually the entire path length, suggesting that the spike phase relates to the current position, whereas the slope of the phase precession simultaneously predicts a large part or the entire length of the journey.

Our findings allowed for the formulation of an alternative mechanism for theta phase precession in LS neurons. We hypothesize that the changing relative strength of the CA3 and CA1 assemblies (i.e., the ratio of CA1 versus CA3 inputs) is responsible for the spike rate-independent slow phase precession of LS neurons. The computational model we built, using the measured spike data from the HPC, demonstrated that the dynamic weighting of inputs in the model LS neurons can replicate our experimental findings. Using static or random weight matrices, the hippocampal inputs failed to replicate the experimental observations. Selectively removing population “theta sequences” also rendered the circuit incapable of transforming spatial information. Thus, information transference through the hippocampal-LS circuit does not rely on the firing rate or spike-phase codes of single hippocampal neurons. Rather, it requires theta phase coordination across CA1 and CA3 populations, in addition to spatial encoding in single neurons. Theta oscillations gradually shift their phase from the septal to the ventral pole of the HPC (Lubenov and Siapas, 2009; Patel et al., 2012), which was reflected by the mediolateral phase shift of the starting phase of LS neurons. Thus, our model can be generalized to any two anatomical locations in the septotemporal axis of the HPC to provide the necessary theta phase offset inputs for such a ratio-weighing model.

An obvious task for the future is to examine whether and how targets of LS utilize this phase code. One possibility is that the LS phase code that we have shown is a simple byproduct not used for any computation. Intuition would suggest that any decoder of phase-locked spiking requires input from the HPC in order to determine theta phase. However, this information is simultaneously encoded across the LS in lock step with the hippocampal traveling theta wave (Figure 4). This would allow for a similar dynamic weighting decoder mechanism downstream of only convergent LS input. Such a phase code may be useful in selectively addressing only those downstream neurons of LS that receive convergent input or simultaneous hippocampal theta signals. This may explain why neurons in lateral hypothalamic and several brain stem nuclei display theta oscillations (Sławińska and Kasicki, 1995; Vertes and Kocsis, 1997). This hypothetical mechanism, perhaps using the same decoding strategy as LS neurons, would allow for the isolation of single channels within multiplexed signals across distributed and highly interconnected brain networks.

Implications

As external observers, we often make simplifying assumptions as to the nature of neural encoding. However, the lack of “tuning” in a given experiment may simply mean we failed to identify the right coding scheme. The current findings demonstrate a firing rate-independent encoding of positional information, which critically depends upon the spatiotemporal structure across input populations (theta sequences) rather than on the first-order dynamics of single-input neurons (place tuning of rate and phase precession). Our model supports the perspective that the hippocampal cognitive map is embedded within a spatiotemporal phase map across its anatomical subregions, and that LS rate-independent spatial encoding is undetectable to the outside observer, without reference to these inputs. Selective manipulations of this spatiotemporal organization (Robbe et al., 2006; Lenck-Santini and Holmes, 2008; Wang et al., 2015; Newman et al., 2017; Kao et al., 2017), along with our current observations, demonstrate that spatial information in the HPC can only be properly read out when the spatiotemporal phase map is intact and the downstream neural observers have the necessary synaptic architecture with which to decipher upstream information.

STAR★METHODS

KEY RESOURCES TABLE

Resource	Source	Identifier/Location	Description
Antibodies
Red retrobeads IX	Lumafluor	https://lumafluor.com
DAPI antibody	Sigma-Aldrich	Cat#: D8417 SIGMA
Experimental Models: Organisms/Strains
Rat: Long-Evans	Charles River	Cat#: Crl:LE 006	2 female, 3 male; adults
Software and Algorithms
Analysis tools	Buzsáki Lab	https://github.com/buzsakilab/buzcode	Analysis tools used throughout the paper
Data visualization scripts	David Tingley	https://github.com/DavidTingley/papers	Example MATLAB scripts that recreate each main figure
HPC/LS recording data	David Tingley	CRCNS (will be uploaded upon publication)
Projection density data	Allen Brain Institute	http://connectivity.brain-map.org/
Klustaviewa	Rossant et al., 2016	https://github.com/klusta-team/klustaviewa
Spikedetekt2	Cortical Processing Laboratory (UCL)	https://github.com/klusta-team/spikedetekt2
Klustakwik2	Kadir et al., 2014	https://github.com/klusta-team/klustakwik/
Position decoder	Meyers, 2013	http://www.readout.info/
MATLAB	MathWorks	https://www.mathworks.com/
pyNN	Davison et al., 2008	http://neuralensemble.org/PyNN/
Other
Silicon probe (5×12, 6×10, 8×8, and 4×8)	Neuronexus	https://neuronexus.com/
Silicon probe (1×64)	Cambridge Neurotech	https://www.cambridgeneurotech.com/
Intan RHD2000	Intan technologies	http://intantech.com/RHD2000_evaluation_system.html
Motive tracking system	Optitrack	http://optitrack.com/	6 Flex3 camera system

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and datasets should be directed to and will be fulfilled by Gyorgy Buzsáki (gyorgy.buzsaki@nyumc.org).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Animal handling and behavioral training

Five adult Long-Evans rats, 3 male and 2 female, were used in this study. Each animal was handled for 2–3 weeks daily prior to experimental training. After handling, animals were exposed to each maze for several days and trained to alternate, without stopping, between paths through the maze. Because the circular maze was symmetric along the 0 and 90 degree axes, animals were shaped such that alternation took place relative to a cued (tapping prior to trial blocks) start/stop location (one of four possible). Dynamic re-cueing during the behavioral session could then be used to change the animal’s trajectory through space, without changing the allocentric cues in the room or rotating the maze. On the linear maze, animals were trained to continuously alternate between the two ends. All stop locations were rewarded with 1/3 piece of Honey Nut Cheerio if animals completed a successful trial without stopping or alternating the incorrect direction. All experiments were approved by the Institutional Animal Care and Use Committee at New York University Medical Center.

METHOD DETAILS

Surgical procedures

Rats were anesthetized with isofurane and implanted with silicon probes (NeuroNexus and Cambridge NeuroTech) mounted on custom built microdrives. Each animal was implanted with two probes in the right hemisphere, one targeting LS and one targeting dorsal CA1 (Paxinos and Watson, 2013). Coordinates and probe specifications for each animal can be found in Figure S1A. During surgery implants were placed dorsal to target regions, allowing for movement into target regions after recovery from surgery. Craniotomies were sealed with sterile wax. To provide electrical shielding and mechanical protection, copper mesh was shaped around the probes and filled with dental cement. Two stainless steel screws implanted above the cerebellum were used for grounding.

Retrobead injections

Rats were anesthetized with isofurane and injected with 20–150 μL of red retrobeads into the LS at one to three depths, spaced 200 μm apart. After waiting two weeks, hippocampal slices were prepared and examined for localization of beads. In all cases where LS injections were correctly targeted, and no leakage into the ventricle was observed, CA1 and CA3 neurons could reliably be found that were filled retrogradely.

Analysis of Allen Brain Institute connectivity data

55 experiments were downloaded from the Allen Brian Atlas (http://connectivity.brain-map.org/) where CA1 and/or CA3 of the HPC had been injected (AAV-EGFP) without virus leakage into cortex orsubiculum. For each injection, 9 target regions were selected (LS, subiculum, entorhinal, retrosplenial, orbitofrontal, prelimbic, infralimbic, posterior parietal, and primary visual cortices). For each target region, the normalized fluorescence intensity was calculated as the summed fluorescence intensity divided by the injection volume and number of voxels per target region (I_sum/(Vol_inject*Vox_sum).

Recording/Data processing

Recordings were conducted using the Intan RHD2000 interface board, sampled at 20 kHz. Amplification and digitization were done on the head stage. Waveform extraction and initial clustering was conducted using SpikeDetekt and Klustakwik. Example parameters for these algorithms can be found in the GitHub repository (https://github.com/DavidTingley/papers). Manual waveform discrimination was then conducted using the Klustaviewa software suite. Waveform amplitude was utilized during this stage to assess unit stability. Any waveforms that changed significantly throughout the duration of the recording were discarded. Waveform isolation quality was quantified using the isolation distance metric (https://github.com/buzsakilab/buzcode) and the waveform amplitude (Figures S1B–S1E).

For one animal, position within the environment was tracked with two head mounted LED’s (1 blue, 1 red) and an overhead camera (Basler, 30 Hz). For the other four animals, position was tracked with the OptiTrack camera system. IR reflective markers were mounted in unique positions on each animals’ head stage and imaged simultaneously by six cameras (Flex 3) placed above the behavioral apparatus. Calibration across cameras allowed for the three dimensional reconstruction of the animals’ head position, and head orientation, to within 1 mm (avg. displacement error = 0.70 mm ± 1.5 mm) at 120 Hz.

Position data was analyzed and segmented using a custom MATLAB software suite. Only ballistic trials, without stopping or deviation from the trained trajectory, were extracted for further analysis. These trials made up ~90%–95% of all trials attempted for any given recording. Quantification of the different behavioral paradigms and their dynamics can be found in Figures S1F–S1I.

Histology

Animals were placed under anesthesia and electrolytic marker lesions were conducted (4 μA for 4 s). Animals were perfused with 4% paraformaldehyde under deep anesthesia. Brains were removed and sliced in 80 μm slices using a vibratome (Leica VT1000S). For implanted animals, a DAPI stain was used to localize probe tracks. The deepest point of lesion, combined with the record of turn depths, was used to estimate the location of each recording. Initial recordings in more dorsal structures (anterior cingulate, corpus callosum, or the ventricle) were also used to verify depth coordinates in the LS for each animal.

QUANTIFICATION AND STATISTICAL ANALYSIS

Spatial information analysis

To compare phase and rate variables, data was discretized to an equal number of bins (N = 7 phase or rate bins). The metric chosen (Olypheret al., 2003) assigns positional bins information scores that refect the uniqueness of the data at that position relative to other positions, and the reliability of the data across trials at that position. P_k is the probability of observing spike rate (or phase) $k.P_{k|x_i}$ is the conditional probability of observing spike rate (or phase) k in position x_i.

$$I_{pos}\left(x_i\right)=\sum _{K\ge 0}{P}_{k|x_i}\log \frac{P_{k|x_i}}{P_k}$$

Spiking rates (or phases) were smoothed using a box filter over progressively larger sets of position bins (1–50 bins which corresponds to ~1.5–80 cm). The box filter implemented for neural data returned the mean value for a set of bins surrounding each position bin. To apply this to the spike phase data, the circular mean was taken.

Instantaneous firing rate and firing phase independence

When examining the correlation between two signals, it is important to account for inherent structure in both of the individual signals. For two time series, the appropriate null distribution is to circularly shift one time series, relative to the other, by random offsets; thus preserving the autocorrelation structure of both signals while removing any cross-correlation structure. For two rhythmic signals this is especially important, as randomly permuting one time series (thus removing autocorrelation structure) often leads to an inadequate null distribution.

To examine the relationship between instantaneous firing rate and instantaneous firing phase, this circular shifting approach was used to generate a satisfactory null distribution. The instantaneous firing rate (IFR) for each action potential was calculated as one divided by the mean of the previous and following inter-spike intervals (Harris et al., 2003). The instantaneous firing phase was taken as the phase of CA1 theta at which each action potential occurred. As both of these signals (IFR and LFP theta) are rhythmic around ~8Hz, is it very common to find spuriously high circular/linear correlations (.4 – 0.8) that do not differ significantly from those expected after circular shifting Figure S2.

LFP theta phase coherence

A 3^rd order Butterworth bandpass filter (4–12 Hz) was applied to the raw LFP, after which the angle of the Hilbert transform was taken to extract just the phase component of the signal. Theta phase coherence was then measured across 150 ms windows that were moved through time at 50 ms steps using multi-taper estimation.

LFP cross-frequency coupling

Theta-gamma cross frequency coupling was assessed as the circular-linear correlation between CA1 LFP theta phase and LS LFP gamma power. CA1 LFP was bandpass filtered (Butterworth; 4–12 Hz; order = 3), and the angle of the Hilbert transform was taken as the phase angle. LS LFP gamma power was assessed as the root-mean squared (window = 50 ms) power of the bandpass filtered signal (Butterworth; 40–200 Hz; order = 3).

Position prediction analysis

Action potential times were extracted for each successful trial and mapped onto at linearized position vector such that firing rates and firing phases were associated with particular positions, rather than times. Estimates of firing rate or firing phase (relative to dCA1 theta) were calculated for each position bin and smoothed across 20 bins using a box filter (~30 cm). All results were qualitatively similar when smoothing over smaller or larger scales (10–50 cm). A maximum correlation coefficient classifier was then produced where the estimated firing rate, or firing phase, was used as a predictor; and the animals’ position as the response variable. 60% of the data (entire block of trials in the same condition) was randomly selected to train the model, and the remaining 40% of the data was used to test the model, generating a mean squared error (MSE). The classifier operates by building a template from the training data by averaging across different observations at each position. For each test sample it then selects a prediction based on which position bin from the template correlates most strongly with the test sample. When using this method with single features (i.e., neurons), it is equivalent to taking the minimum squared deviation between the training template and test sample. XTr is the template created from training data (average firing rate or phase for all positions). XTe_i is the test sample for position i.

$$Pos{(i)}_{pred}=\underset{{}_i}{argmin}\left({\left(XT{r}_i-XT{e}_i\right)}^2\right)$$

10-fold cross validation was performed with different 60/40 randomly selected splits, generating a distribution of mean squared errors for each model type (rate, phase, and shuffle). The iterations did not serve to obtain ten independent tests but to achieve a more reliable estimate of predictive strength (or mean squared error) than could be obtained with just one cross-validation. Data was shuffled by randomly permuting the vector of phases or rates associated with the vector of positions. Significance was then determined by a two sample t test when comparing these distributions of MSE values. Neurons were required to fire a minimum of 1.5 spikes per trial on average to be considered for this analysis (Ex. > = 30 spikes across 20 trials). All results were qualitatively similar using Bayesian decoding (see Figure S7) and generalized linear modeling approaches.

Ensemble position prediction analysis

The method for predicting animal position from ensemble activity was a naive Bayes decoding method. Populations of simultaneously recorded hippocampal (range: 1–83) or lateral septal (range: 1–53) neuron firing rates, or firing phases, were discretized into 20 bins. Prior to binning, these data were smoothed using the same method as all single neuron decoding (box filter, 20 bins). The data were then split into 60% training and 40% testing partitions. 10-fold cross validation of this splitting procedure was used and mean squared error values were averaged across all iterations. Training data was used to calculate the mean values for each neuron and position. To quantify the relationship between rate (or phase) and position, the log likelihood function is calculated using these discretized mean rates (or phases) as parameters for Poisson distributions for each neuron. The probability of observing a given discretized firing rate (or firing phase) for each neuron is then calculated for each position. These probabilities are then multiplied across all neurons (assuming independence) to give an overall likelihood value for each position. The position with the highest likelihood value is chosen as the predicted position.

Peer prediction analysis

The method for detecting and quantifying gamma cell assemblies between LS and HPC builds off of methods previously developed to assess within region assemblies (Harris et al., 2003; Tingley et al., 2015). The approach uses a generalized linear model with the spike train of one neuron as a ‘predictor’ and a simultaneously recorded peer as a ‘response’. By temporally smoothing the predictor spike train with different windows (1–150 ms), each model will have a different goodness of fit with the response spike train. The model with the best fit, and accompanying temporal smoothing window, are then assessed for significance by comparing the deviation of fit with that expected from shuffled versions of the same data. For shuffling, the trial order between predictor and response variables is shuffled such that two spike trains from different trials are used as the predictor/response variables, rather than two spike trains from the same trial. This shuffling is carried out 10 times to create a distribution of deviation of fits. The ‘assembly strength’ value quantifies the ratio between the actual deviance and the best possible deviance taken from the null distribution. Thus, an assembly strength score of 8 reflects a reduction in ‘deviance of fit’ that is 8 times larger than the best observed reduction taken from the shuffled dataset. The decision for what is, or is not, an assembly (threshold is 4 throughout the paper) was chosen to reflect when cross correlograms clearly showed a visible peak at the expected timescale. When examining the data with assembly strength thresholds ranging from 1.5–8, all results were qualitatively similar.

Each neuron pair has a single assembly strength value, determined by all spikes that occur during a single block of trials. For Figure 6E (position dependence of assembly strengths), these values were then cross-referenced with cells that had significant place fields, thus only firing in a restricted set of positions. The center of mass for each place field was taken as the ‘position’ for these LS-HPC (place cell) pairs. HPC cells that participated in an assembly but did not have a place field were not included in this analysis.

To ensure that co-tuning to theta phase or behavioral correlates did not spuriously lead to assembly detection, the CA1 theta phase (sin, cosine and raw phase angles), the animal’s position, and the animal’s velocity were provided to all GLM’s as additional predictors to regress out such co-variation (Figure S5).

Reference frame analysis

To assess which frame of reference LS phase precessing neurons were locked to, maze rotations were conducted within single recording sessions. This allowed for the dissociation of different frames of reference (egocentric, maze/reward-centric, and allocentric). A multivariate modeling approach was taken using the same maximum correlation decoder as for the position prediction analysis. Egocentric, maze-centric, and allocentric information were provided as predictors to the model, and the firing phase of LS neurons was provided as the response variable. A total of 23 variables were examined, 6 allocentric (x, y, z, pitch, yaw, and roll), 4 route-centric (maze orientation and direction of motion), 1 reward/goal-centric (distance to current reward location), and 12 egocentric (1^st and 2^nd derivatives of position variables for velocity and acceleration). Null distributions were created by circularly shuffling each variable by a random amount and re-running the decoder. Models were trained on a random subset of available data (60%) and evaluated on the remaining data (mean squared error; 40%).

Place field definition

The set of heuristics used to identify a ‘place field’ were the following 1) Minimum peak firing rate of 2 Hz, 2) Minimum field width of 8 cm, 3) Maximum field width of 120 cm, 4) Minimum of 1.5 spikes per trial on average, and 5) at least 10 trials with consistent behavior. Given these criteria, 711 of 1,425 HPC neurons had at least one place field with a mean of 1.27 ± 1.76 fields per neuron. There was no limit set on the number of place fields single neurons could have. The median peak in-field firing rate was 8.5 ± 12 Hz, and the median field width was 38 ± 16 spatial bins (~57 cm). The start and stop position for each field were taken as the spatial bins where the firing rate drops below 20% of the peak firing rate. The center of mass for each field was calculated only for bins between the start/stop bins. As this definition excludes potentially informative spikes outside of the place field of a cell, it was only used to identify and cross reference with other analyses. All rate/phase correlations, peer prediction, and position prediction modeling was carried out using all action potentials recorded during the behavioral trials.

Spiking model

The spiking model was developed in the python programming language with pyNN serving as the frontend and the NEURON simulator as the backend (Davison et al., 2008; Carnevale and Hines 2006). The model consists of 50 CA1, and 50 CA3, ‘place cells’ which all send convergent input to a single LS neuron. Each hippocampal neuron is a Hodgkin-Huxley spiking model that receives two inputs, a subthreshold theta oscillation and a ramp current at a particular time as the model runs. The combination of these two inputs creates a firing output that is localized in time and shifted in theta phase. CA3 neurons receive a 180-degree phase delayed theta oscillation.

When the population of hippocampal neurons receive a single theta input, the population of neurons is coordinated into ‘theta sequences’. Injecting different (phase offset) theta rhythms into individual neurons creates the same firing field and phase precession clouds for single neurons across trials, but without the presence of ‘theta sequences’ on single trials. For all synaptic weight matrices (dynamic, static, random), the weight matrix is scaled such that that LS target neuron receives the same net excitation.

Highlights.

• LS neurons carry a rate-independent phase code for position

• The LS spatial phase code is as reliable as the hippocampal rate or phase codes

• LS phase code is a transformation of the distributed CA1/CA3 cognitive map

• The Hippocampus-LS circuit may be the conduit for translating representation to action