Regulation of axon growth by myosin II–dependent mechanocatalysis of cofilin activity

Synergism between myosin II contractility and cofilin activity modulates serotonin-dependent axon growth. Normally, cofilin-dependent decreases in actin density are compensated by increases in point contact density and traction force; however, myosin hyperactivation leads to catastrophic decreases in actin network density and neurite retraction.

Abstract

Serotonin (5-HT) is known to increase the rate of growth cone advance via cofilin-dependent increases in retrograde actin network flow and nonmuscle myosin II activity. We report that myosin II activity is regulated by PKC during 5-HT responses and that PKC activity is necessary for increases in traction force normally associated with these growth responses. 5-HT simultaneously induces cofilin-dependent decreases in actin network density and PKC-dependent increases in point contact density. These reciprocal effects facilitate increases in traction force production in domains exhibiting decreased actin network density. Interestingly, when PKC activity was up-regulated, 5-HT treatments resulted in myosin II hyperactivation accompanied by catastrophic cofilin-dependent decreases in actin filament density, sudden decreases in traction force, and neurite retraction. These results reveal a synergistic relationship between cofilin and myosin II that is spatiotemporally regulated in the growth cone via mechanocatalytic effects to modulate neurite growth.

Introduction

Serotonin, also referred to as 5-hydroxytryptamine (5-HT) activates G(q) subtype G protein–coupled receptors (GPCRs) in Aplysia californica neurons, leading to phospholipase C activation (Li et al., 1995) and inositol 1,4,5-triphosphate–dependent release of Ca from ER stores. Ca elevation leads to calcineurin (CN)-dependent activation of cofilin activity that increases retrograde actin network flow rates in the growth cone lamellipodium (peripheral domain [P domain]) that promotes increases of threefold or more in neurite outgrowth rates (Zhang et al., 2012). 5-HT–stimulated growth requires coactivation of nonmuscle myosin II; however, the reason for this dependence is not well understood and perhaps paradoxical given the key role Rho/Rho kinase (ROCK) modulation of myosin II activity plays in neuronal chemorepulsion and neurodegenerative responses (Fujita and Yamashita, 2014; Newell-Litwa et al., 2015). For example, in Huntington’s disease, ROCK activity is increased (Narayanan et al., 2016), and in studies of progressive supranuclear palsy and corticobasal degeneration, ROCK has been identified as a therapeutic target to prevent tau accumulation (Gentry et al., 2016). Preclinical studies of Parkinson's and Alzheimer's disease have also identified ROCK as a potential drug target for further translational research (Koch et al., 2018). PKC has emerged as another key signaling agent in neurodegenerative disease and neuronal regeneration research. PKC activation has been implicated in repulsive guidance responses (Hasegawa et al., 2004) and inhibition of axon regeneration (Sivasankaran et al., 2004); however, cytoskeletal mechanisms underlying these effects are not well understood. Conventional PKCs are of obvious relevance to the 5-HT responses we have been studying, given they are activated by Ca and DAG downstream of G(q) subtype GPCR activation (Larsson, 2006; Rosse et al., 2010). In a related study (Yang et al., 2013), we found that direct activation of PKC leads to increased nonmuscle myosin II regulatory light chain (RLC) phosphorylation and contraction of actin–myosin II arc and central actin bundle structures (Schaefer et al., 2002; Zhang et al., 2003) in Aplysia growth cones. These effects appear to be mediated by PKC-dependent activation of CPI-17, a myosin II RLC phosphatase inhibitor (Kitazawa et al., 1999; Watanabe et al., 2001; Eto et al., 2002) with actions similar to ROCK. These findings motivated us to investigate a potential role for PKC activity in 5-HT–mediated neurite growth responses.

In previous reports, including our own, increases in rates of neurite outgrowth have been correlated with reduced retrograde actin network flow in the growth cone (Lin and Forscher, 1995; Suter et al., 1998; Nichol et al., 2016). These results have been interpreted in the context of the “molecular clutch hypothesis” (Lin et al., 1994; Lin and Forscher, 1995) that has been widely adapted to explain traction force generation during haptotactic growth responses in motile cells (Bachir et al., 2017) and neurons (Short et al., 2016). This hypothesis posits that cell adhesion molecules and associated intracellular components create a variable physical linkage, or molecular clutch, situated between extracellular growth substrate and actin networks moving with retrograde flow which serve as the motive force generator. Molecular clutches have been modeled as variable slip, load and fail, or visco-elastic coupling layers (Chan and Odde, 2008; Mejean et al., 2013; Craig et al., 2015), where clutch engagement strengthens actin filament-to-substrate linkages and thereby increases traction force transmission (compare Fig. 10 D). Given the above, it was somewhat surprising to find that increases in growth cone advance rates after 5-HT treatment were accompanied by ∼25% increases in retrograde F-actin flow that were sustained during extended (≥6 h) periods of outgrowth (Zhang et al., 2012). These studies raised the question of how growth cone traction forces were behaving before and after 5-HT treatments.

Figure 10.

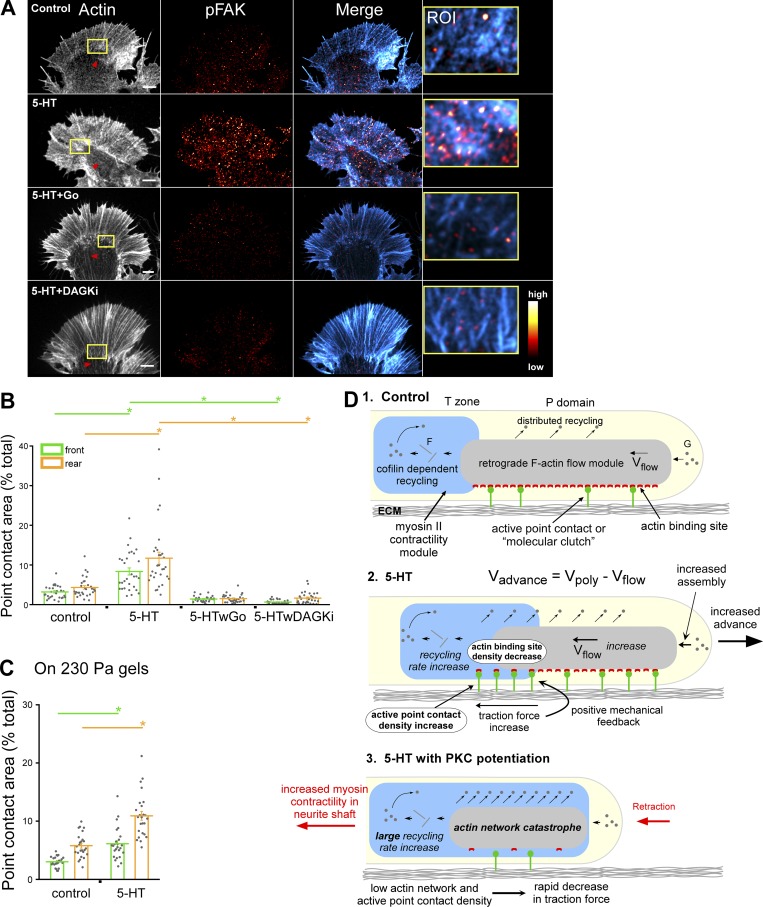
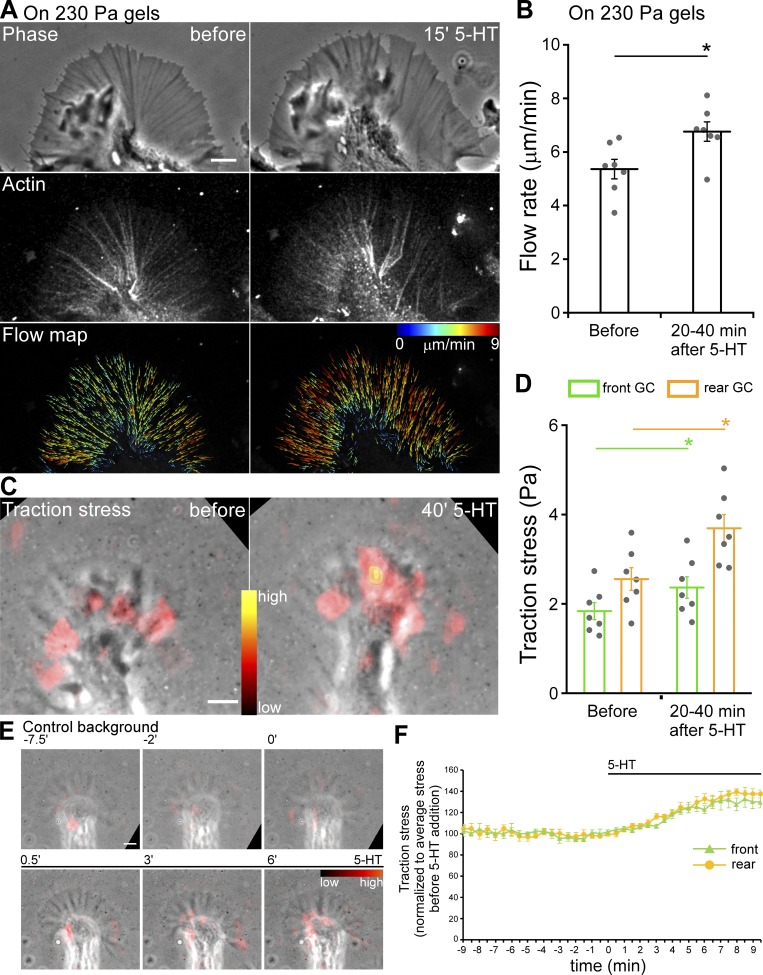
5-HT–evoked increases in active point contact density are PKC dependent. (A) F-Actin (left), pFAK (middle), overlay of F-actin and pFAK (right), and high-magnification overlays of ROI (yellow box) in actin panel. Red arrowheads, contractile central actin bundle system. Row 1, control; row 2, 5-HT (10 µM, 30 min); row 3, 5-HT with PKC inhibition (Go 5 µM, 15-min pretreatment followed by 10 µM 5-HT in the continued presence of Go for 30 min); row 4, 5-HT with PKC potentiation (DAGKi 5 µM, 15-min pretreatment followed by 10 µM 5-HT in the continued presence of DAGKi for 30 min). F-Actin labeled with phalloidin. Immunolabeling performed with anti-FAK pY397 antibody after normal fixation. pFAK levels encoded in a linear pseudocolor lookup table (color bar). Scale bars, 5 µm. (B) Point contact quantification under conditions in A. Region demarcations are illustrated in Fig. S2 A. Data are mean areas (% of total) ± SEM. For each condition, 30 growth cones pooled from three independent experiments were measured. P = 1.31 × 10⁻²¹ (front) and P = 3.36 × 10⁻¹⁶ (rear) with single-factor ANOVA. *, Significant difference using Tukey’s HSD post hoc analysis. (C) Quantification of point contact areas in control versus 5-HT (10 µM, 30 min) on soft PA gels (230 Pa); see Fig. S4 K for the corresponding F-actin and pFAK images. Region demarcations are illustrated in Fig. S2 A. Data are mean (% total) ± SEM. For each condition, 25 growth cones pooled from three independent experiments were measured. *, P < 0.0001 with two-tailed unpaired t test. (D) Graphical summary: see related text in Discussion.

The 5-HT–dependent increases in retrograde flow alluded to above are cofilin dependent. ADF/cofilin activity has been widely implicated in regulation of axon growth (Sarmiere and Bamburg, 2004; Marsick et al., 2010; Flynn et al., 2012; Omotade et al., 2017) and development (Ohashi, 2015). Cofilin is known to both sever actin filaments and promote their depolymerization (Wioland et al., 2017). Every cofilin-severing event also exposes a new barbed end, leading to rapid increases in actin local assembly; in addition, the rate of G-actin subunit dissociation from actin filaments can be modulated by factors such as AIP1 (Condeelis, 2001; Oser and Condeelis, 2009; Bravo-Cordero et al., 2013; Carlier and Shekhar, 2017; Shekhar and Carlier, 2017). Thus, whether cofilin activation results in net increases or decreases in local actin filament density depends on the relative activity of regulatory factors that cap exposed barbed ends and/or accelerate filament disassembly. Cellular cofilin activity is inactivated by phosphorylation of Serine3 by Lim kinase and activated by cofilin phosphatases such as slingshot (Arber et al., 1998; Niwa et al., 2002). In addition, CN has been reported to activate slingshot, providing a mechanism for increasing cofilin activity in response to changes in intracellular Ca (Wang et al., 2005; Zhao et al., 2012), as we observed during 5-HT treatments (Zhang et al., 2012).

In another line of investigation, biophysical studies provide evidence that cofilin activity can be biomechanically regulated. Specifically, actin filament strain tends to promote cofilin severing activity (De La Cruz and Gardel, 2015; Schramm et al., 2017), and torsional stress on actin filament networks increases cofilin severing rates (Wioland et al., 2019). Given our previous findings that myosin II contractile activity induces actin bundle strain and F-actin turnover in parallel in growth cones (Medeiros et al., 2006), we were interested if this could be affecting cofilin activity during 5-HT–stimulated growth responses.

Here we report that PKC-dependent activation of nonmuscle myosin II is indeed necessary for 5-HT–evoked neurite growth. Moreover, the level of PKC activation can modulate the polarity of 5-HT responses. We provide evidence that this occurs via mechanocatalysis of cofilin activity that leads to threshold effects on actin network stability.

Results

5-HT response polarity can be modulated by PKC effects on nonmuscle myosin II activity

To investigate potential PKC effects on 5-HT–dependent neurite growth, long-term time-lapse videos were made before and after 5-HT treatment under control physiological conditions or in backgrounds of varying PKC activity (Fig. S1 and Video 1). Long-term treatment with 5-HT under control conditions resulted in sustained approximately threefold increases in neurite outgrowth rates (Fig. S1, A and B; Zhang et al., 2012). 5-HT–evoked growth was completely blocked in the presence of conventional PKC inhibitors such as Go6976 (Go; Fig. S1, C, D, and K), which have been previously characterized in this system (Kabir et al., 2001; Nakhost et al., 2002; Yang et al., 2013). Note that PKC inhibitor treatment alone had little effect on neurite outgrowth (Fig. S1, C and D, before 5-HT). Similar effects were observed using bisindolylmaleimide-1 (Bis), a structurally distinct PKC inhibitor (Fig. S1 K; Wu-Zhang and Newton, 2013).

We hypothesized that native PKC activity could be potentiated by slowing metabolic conversion of DAG to phosphatidic acid by DAG kinase (compare Fig. 1 A; Baldanzi, 2014). To this end, the pharmacological DAG kinase inhibitor R59022 (DAGKi; Mérida et al., 2008; Sato et al., 2013) was used. Treatment with DAGKi alone had no discernable effect on baseline neurite outgrowth (Fig. S1, E and F, before 5-HT); however, 5-HT responses switched polarity from long-term growth to retraction after DAG kinase inhibition (Fig. S1, E, F, and K; and Video 1). In contrast, 5-HT–evoked retractions in DAGKi backgrounds were absent after PKC inhibition, and growth cones remained quiescent after 5-HT exposure (Fig. S1, G, H, and K). Given that direct activation of PKC results in nonmuscle myosin II activation and growth cone retraction in this system (Yang et al., 2013), we investigated the effects of myosin II inhibition. 5-HT–evoked retractions seen with PKC potentiation were completely suppressed, and growth cones remained quiescent over several hours in 5-HT in the presence of the myosin light chain kinase inhibitor (ML-7; Saitoh et al., 1987; Zhang et al., 2003; Yang et al., 2013; Fig. S1, I, J, and K). Taken together, these results suggest that PKC activity levels can modulate the polarity of 5-HT responses and implicate myosin II as a PKC effector in these modulatory effects.

Figure 1.

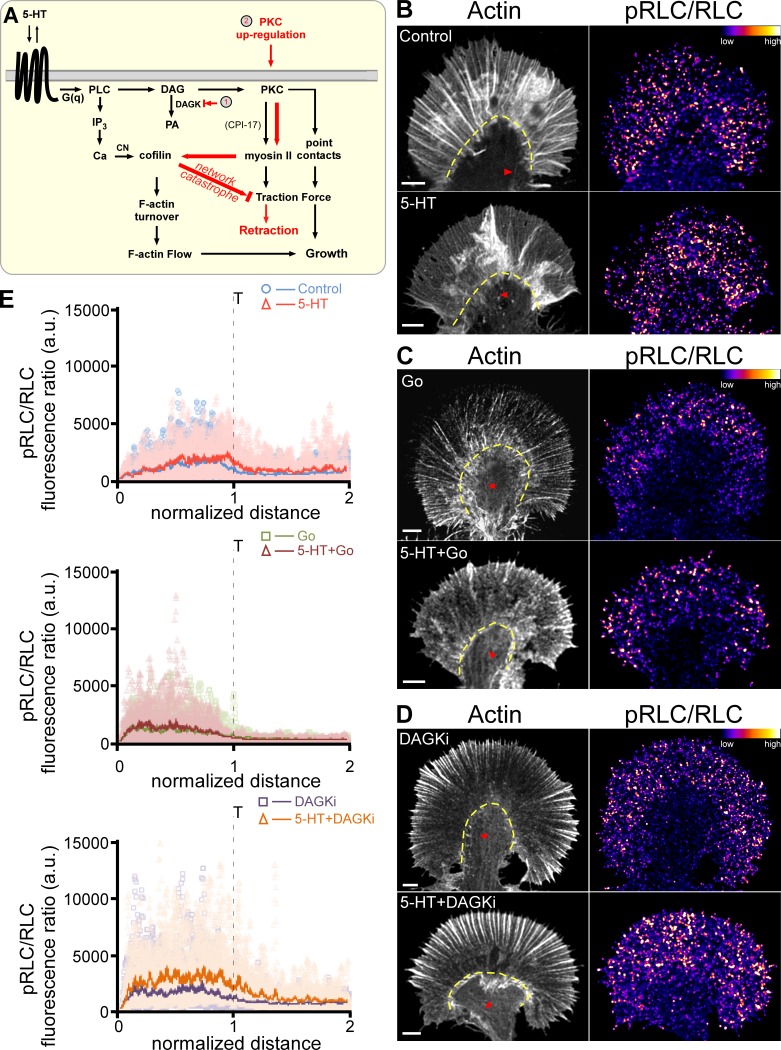
PKC and myosin II activation levels are positively correlated. (A) Signaling cascades in this study. (B) F-Actin (left, red arrowheads point to contractile central actin bundles, yellow dashed line demarcates T zone) and ratio images of pRLC versus total RLC (right) of growth cones showing 5-HT–dependent (10 µM, 30 min) myosin II activation under control conditions. (C) PKC inhibition with Go alone (5 µM, 45 min) versus 5-HT+Go (Go 5 µM, 15-min pretreatment followed by 10 µM 5-HT in the continued presence of Go for 30 min). (D) PKC potentiation with DAGKi (5 µM, 45 min) versus 5-HT+DAGKi (DAGKi 5 µM, 15 min pretreatment followed by 10 µM 5-HT in the continued presence of DAGKi for 30 min). F-Actin visualized with phalloidin. Immunolabeling with pRLC antibody and total Aplysia RLC antibody after normal fixation. Ratio of pRLC versus total RLC after background subtraction, encoded in a linear pseudocolor lookup table (color bar). Scale bars: 5 µm. (E) Line scan analysis of the ratio of pRLC versus total RLC fluorescence in growth cones showing myosin II activation profiles in control versus 5-HT with PKC inhibition (Go) or potentiation (DAGKi) as in B–D above. Line scans (width = 50 pixels and length = 2× the P domain) sampled from front to rear of the growth cone. Two to four line scans were performed depending on the size of the growth cone. Light-colored points are raw data; solid lines are the population average. Number of growth cones sampled: nine control and eight 5-HT (top), seven Go and seven 5-HT+Go (middle), seven DAGKi and eight 5-HT+DAGKi (bottom). 27 measurements performed per condition, and data pooled across three independent experiments.

PKC activates nonmuscle myosin II preferentially in the transition zone (T zone) during 5-HT exposure

To determine if PKC is actually activating myosin II, we quantified cellular myosin II activity by ratio imaging of phosphorylated RLC (pRLC) levels, normalized by total RLC to correct for path length (cell volume) differences, in fixed neurons under the various conditions described above. Under control conditions, 5-HT treatment did not significantly alter myosin II activity in the distal P domain; however, a modest but statistically significant increase in active myosin II was observed in the more proximal T zone region (Fig. 1, B and E, top panel; and Fig. S2, A and B). PKC inhibition with Go alone did not alter myosin II activity in the distal P domain and significantly reduced myosin II activity in the T zone, indicating the presence of basal PKC activity (Fig. S2 B). 5-HT treatment in the presence of Go did not alter the myosin II activity profile relative to what was observed with Go alone (Fig. 1, C and E, middle panel; and Fig. S2 B).

We next looked at the effect of potentiating PKC action with DAG kinase inhibition (Fig. 1, D and E, bottom panel; and Fig. S2 B). Treatment with DAGKi alone did not affect myosin activity in the T zone area and resulted in a modest increase in myosin II activity near the leading edge. In contrast, myosin II activity was significantly increased in both the P domain and T zone after 5-HT treatment in the presence of DAGKi. These results suggest that under normal physiological conditions, 5-HT treatments are associated with relatively modest PKC-dependent increases in myosin II activity that are restricted to the T zone region; however, conditions that potentiate PKC action result in significant increases in myosin II activity throughout the growth cone.

Modulation of PKC action does not affect 5-HT–induced increases in retrograde actin flow

5-HT growth responses are characterized by ∼25% increases in retrograde actin network flow that depend on Ca-CN activation of cofilin and are independent of myosin II activity (Zhang et al., 2012). Given the evidence for PKC regulation of myosin II activity above, we investigated how modulation of PKC action might affect actin filament dynamics during 5-HT responses. To this end, we used fluorescent speckle microscopy (FSM; Danuser and Waterman-Storer, 2006) and automated particle tracking (Burnette et al., 2007) to quantitatively assess retrograde actin flow rates under various conditions.

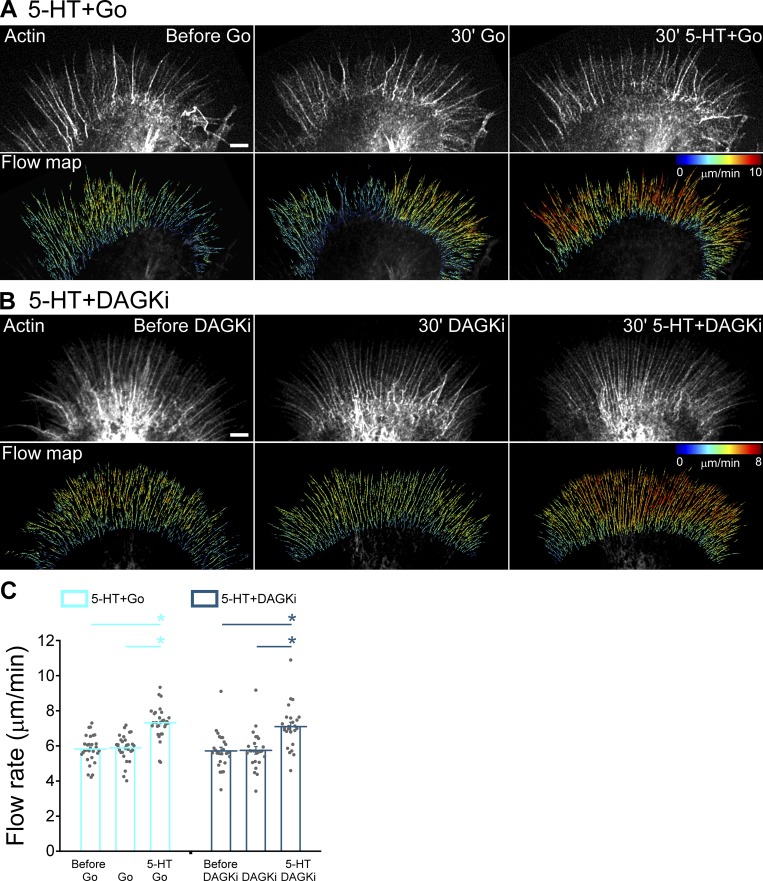
PKC inhibition with Go alone did not affect retrograde flow rates; in contrast, 5-HT treatment in the presence of Go resulted in ∼25% increases in retrograde flow rates indicating that changes in actin dynamics do not depend on PKC activity per se (Fig. 2, A and C). These results mimic responses to 5-HT treatment observed after myosin II inhibition (Zhang et al., 2012). Similar results were obtained using Bis as a PKC inhibitor (Fig. S2, C–E). In other experiments, we investigated the effect of potentiating PKC action by DAG kinase inhibition. Again, no changes in baseline retrograde flow rates were observed, and ∼25% increases in flow were seen after 5-HT exposure in the presence of DAGKi (Fig. 2, B and C). Together, these results show that during 5-HT exposure, retrograde actin flow rates are regulated by a mechanism that is independent of PKC activity.

Figure 2.

Modulation of PKC action does not affect 5-HT–induced increase in retrograde F-actin flow rates. (A and B) Alexa Fluor 594–phalloidin FSM (top) and corresponding flow vector map (bottom) of growth cones showing 5-HT–induced increase in F-actin flow under various conditions. (A) Left: Control. Middle: PKC inhibition with Go (5 µM, 30 min). Right: 5-HT+Go (10 µM in continued presence of Go for 30 min). (B) Left: Control. Middle: PKC potentiation with DAGKi (5 µM, 30 min). Right: 5-HT+DAGKi (10 µM in continued presence of DAGKi for 30 min). Images acquired every 5 s for 2 min to generate vector maps. Vector map colors encode speed (see scale bars), zoom in to view vector details. Scale bars, 5 µm. (C) Summary of P-domain retrograde flow rates in response to 5-HT in Go or DAGKi backgrounds: Go (5 µM, 20–40 min); 5-HT+Go (10 µM, 20–40 min, in the continued presence of Go); DAGKi (5 µM, 20–40 min); 5-HT+DAGKi (10 µM, 20–40 min, in the continued presence of DAGKi). Data are mean (μm/min) ± SEM. Number of growth cones evaluated: 29 for 5-HT+Go and 25 for 5-HT+DAGKi, each pooled from four independent experiments. *, P < 0.001 with two-tailed paired t test.

PKC effects on actin network density

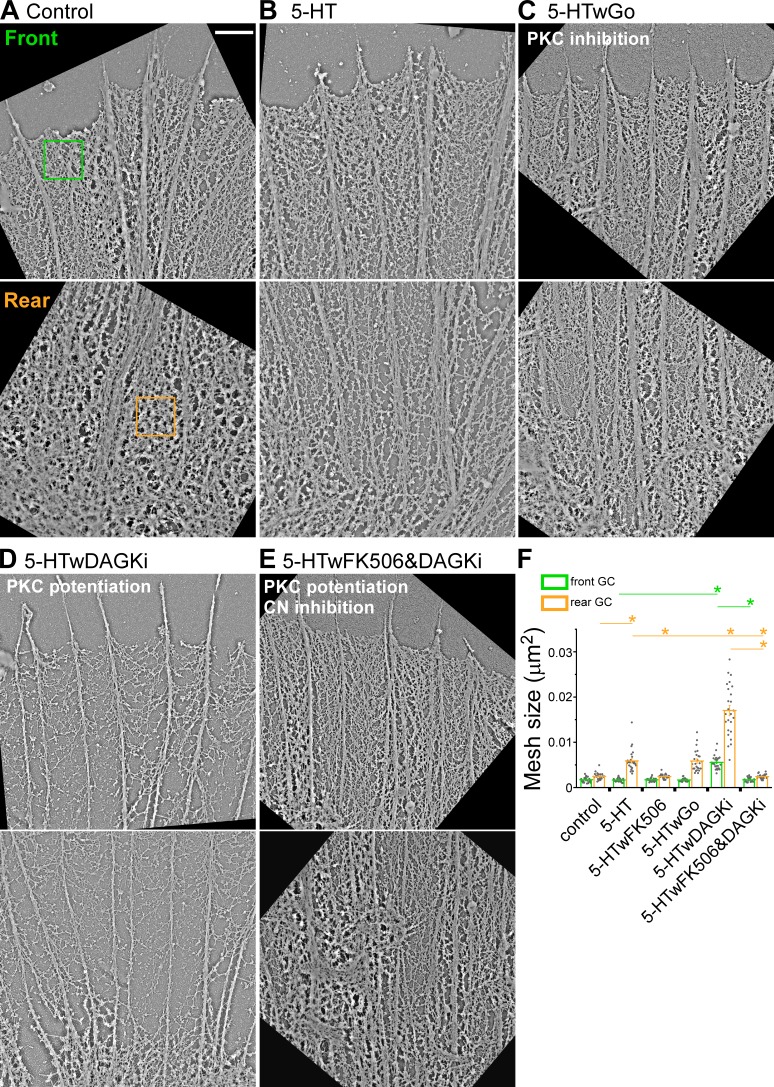
We next investigated the effects of varying PKC activity during 5-HT responses on actin network ultrastructure by platinum replica transmission EM (Schaefer et al., 2002; Figs. 3 and S3). The P domain of Aplysia growth cones is characterized by two main types of actin filament structure: (a) filopodia comprising polarized (barbed end distal) actin filament bundles in radial arrays and (b) actin veils comprising a mixture of branched and unbranched actin filaments that occupy the space between filopodia. These two structures move coherently to generate retrograde actin network flow (Schaefer et al., 2002). We quantified actin filament network structure in representative regions of interest (ROIs) near the growth cone leading edge (front) and in the T zone (rear) under various conditions. 5-HT treatment resulted in significant network thinning, reflected by increases in average mesh size (see Platinum/palladium replica EM for details) in the rear, but had little or no effect on actin network density near the front of the growth cone (Fig. 3, A, B, and F). PKC inhibition did not affect thinning of actin networks in the growth cone rear after 5-HT (Fig. 3, C and F). In contrast, when PKC action was up-regulated by DAGKi, 5-HT treatment resulted in a dramatic thinning of actin networks in both front and rear growth cone domains (Fig. 3, D and F).

Figure 3.

Potentiation of PKC action promotes cofilin-dependent thinning of actin networks during 5-HT responses. Platinum replica transmission electron micrographs illustrating typical actin network ultrastructure in front and rear growth cone domains. (A) Control conditions. (B) 5-HT (10 µM, 30 min). (C) PKC inhibition: 5-HT+Go (Go 5 µM, 15-min pretreatment followed by 10 µM 5-HT for 30 min, in the continued presence of Go). (D) PKC potentiation: 5-HT+DAGKi (DAGKi 5 µM, 15-min pretreatment followed by 10 µM 5-HT for 30 min, in the continued presence of DAGKi). (E) CN→cofilin inhibition: 5-HT+FK-506+DAGKi (2.5 µM FK-506 and 5 µM DAGKi, 15-min pretreatment followed by 10 µM 5-HT for 30 min, in continued presence of FK-506 and DAGKi). 1× 1-µm² regions similar to green and orange boxes were sampled for actin veil morphometry. Scale bar, 1 µm. See Fig. S3 (A–E) for comparative whole growth cone micrographs. (F) Quantification of actin veil mesh size (μm²) under conditions A–E and 5-HT+FK-506 (compare Fig. S3 F). Data are mean (μm²) ± SEM. For each condition, 25 regions from the front and the rear of five growth cones were measured. Experiments were repeated three times. P = 1.96 × 10⁻⁴⁹ (front) and P = 8.12 × 10⁻⁴⁷ (rear) with single-factor ANOVA. *, Significant difference using Tukey’s HSD post hoc analysis.

How can these PKC effects on actin network density be explained? During normal 5-HT responses, increased rates of actin network turnover and retrograde flow rely on CN-dependent cofilin activation (Zhang et al., 2012) in line with the actin network thinning observed in the T zone with 5-HT treatments (Fig. 3, A, B, and F). In contrast, when neurons were pretreated with the CN inhibitor FK506, decreases in actin network density (mesh size increases) in response to 5-HT in the rear were absent (Figs. 3 F and S3 F). Importantly, FK506 pretreatment also completely suppressed the dramatic decreases in actin network structure in the growth cone front and rear evoked by 5-HT treatment after PKC up-regulation with DAGKi (Fig. 3, E and F). Fig. S3 shows lower-magnification transmission EM images of growth cones under the same conditions and two other morphometric analyses (mesh count and mesh area) that complement the data shown in Fig. 3. Taken together, these results show that during physiological 5-HT responses, PKC activation has little effect on cofilin activity; however, when PKC is hyperactivated (after DAGKi), the significant decreases in actin network density observed throughout the growth cone depend on activation of the CN-cofilin pathway (Fig. 3 F and Fig. S3, G and H). These results suggested that PKC-dependent myosin II contractility was having synergistic biomechanical effects on cofilin activity.

Coassessing actin and cofilin dynamics by quantitative FSM (qFSM)

To address possible biomechanical effects on cofilin, a method for dynamically assessing cofilin activity and actin dynamics while varying PKC or myosin II activity was needed. Active dephosphocofilin has much higher affinity for actin filaments than inactive phosphocofilin (Blanchoin and Pollard, 1999), and cofilin is released upon filament severing or monomer dissociation from actin filament pointed ends (Pollard and Borisy, 2003; Kanellos and Frame, 2016). Accordingly, we hypothesized that qFSM (Danuser and Waterman-Storer, 2006; Mendoza et al., 2012) could be used to assess cofilin activity by monitoring binding and unbinding of cofilin to actin filaments moving with retrograde flow. Specifically, bound cofilin molecules should appear as quasistationary speckles given they would move ≤30 nm by F-actin flow (flow rate being 100 nm/s) during typical 200–300-ms image acquisition times. Measured cofilin speckle association and dissociation event densities should reflect local rates of actin filament turnover, since cofilin disassociation occurs mainly after actin filament severing or minus end disassembly (Blanchoin and Pollard, 1998, 1999; Bamburg and Bernstein, 2010; Reymann et al., 2011).

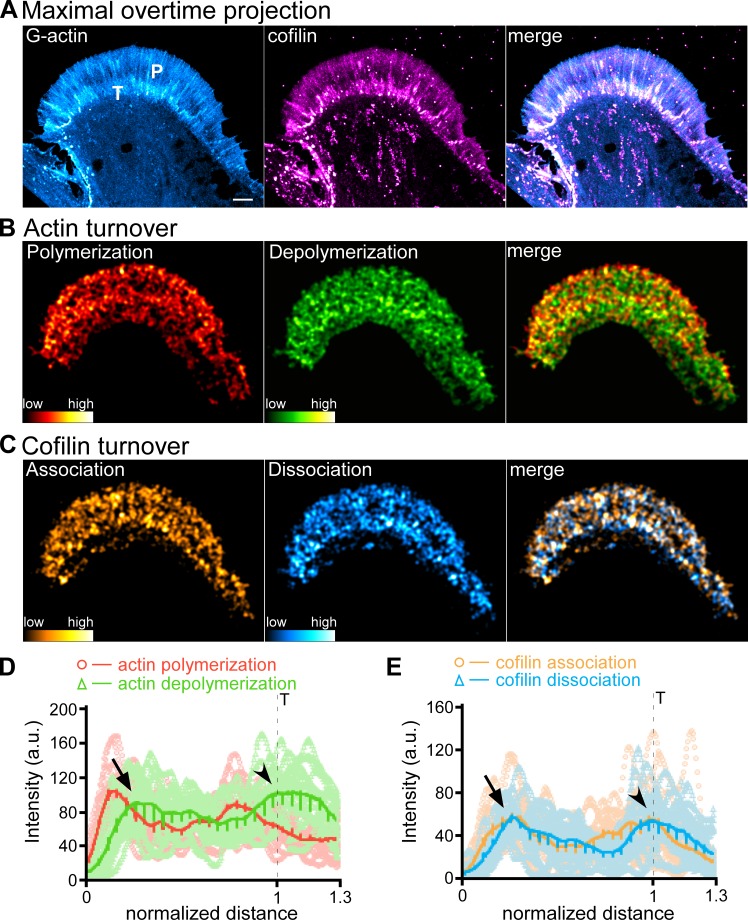
To assess the validity of this method, we coinjected neurons with trace levels of fluorescently tagged G-actin and cofilin and monitored their behaviors by qFSM (Fig. 4 and Video 2). When we compared actin turnover versus cofilin dynamics, integrated actin polymerization intensity peaked near the leading edge, decayed across the P domain, and dropped precipitously near the T zone–C domain boundary (Fig. 4 D). Actin depolymerization intensity was offset to the right of association and plateaued behind the actin polymerization peak (Fig. 4 D, arrow). Cofilin association trends were to the left of dissociation trends in space as expected (Fig. 4, C and E) near the leading edge. Cofilin association and dissociation both peaked near the same position that actin depolymerization plateaued (Fig. 4 E, arrow). Cofilin association–dissociation and actin depolymerization all increased markedly in the T zone (Fig. 4, D and E, arrowheads), where we have previously reported myosin II–assisted severing and recycling of filopodial actin bundles (Medeiros et al., 2006).

Figure 4.

qFSM evaluation of actin turnover and cofilin dynamics. (A) Maximal overtime projections of G-actin (left), cofilin (middle) speckles, and overlay of G-actin and cofilin (merge, right); see also Video 2. P, P domain; T, T zone. (B) Actin turnover: polymerization (left), depolymerization (middle), and overlay of polymerization and depolymerization (right). (C) Cofilin dynamics: association (left), dissociation (middle), and overlay of association and dissociation (right). Alexa Fluor 488–G-actin and Alexa Fluor 568–cofilin were injected into cells sequentially. Actin (B) and cofilin (C) turnover maps were generated by integration of speckle appearance and disappearance events over 225-s sampling periods with images acquired every 5 s. Relative actin polymerization/depolymerization and cofilin association/dissociation frequencies indicated by color bars. Scale bar, 5 µm. (D and E) Line scans of actin polymerization (red)/depolymerization (green) events (D) and cofilin association (orange)/dissociation (cyan) events (E). Dashed lines indicates T zone. Line scans (width = 30 pixels, length = 1.3× the P domain) were sampled from the front to the rear of the growth cone. Five to seven line scans were performed depending on the size of the growth cone. Raw data are shown in lighter colors. Solid lines are the population average. Number of growth cones measured: three, pooled from three independent experiments. 19 measurements were performed. Arrowhead, T zone; arrow, peaks of actin filament depolymerization and cofilin association near the leading edge.

Myosin II contractility catalyzes cofilin activity and increases actin network turnover

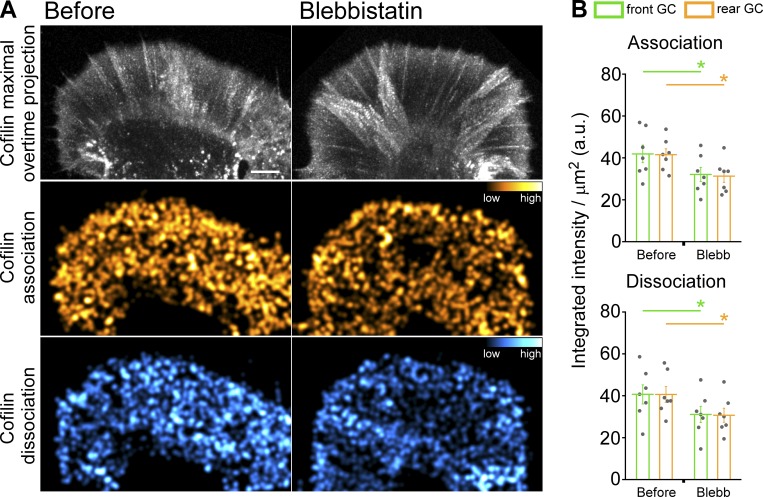
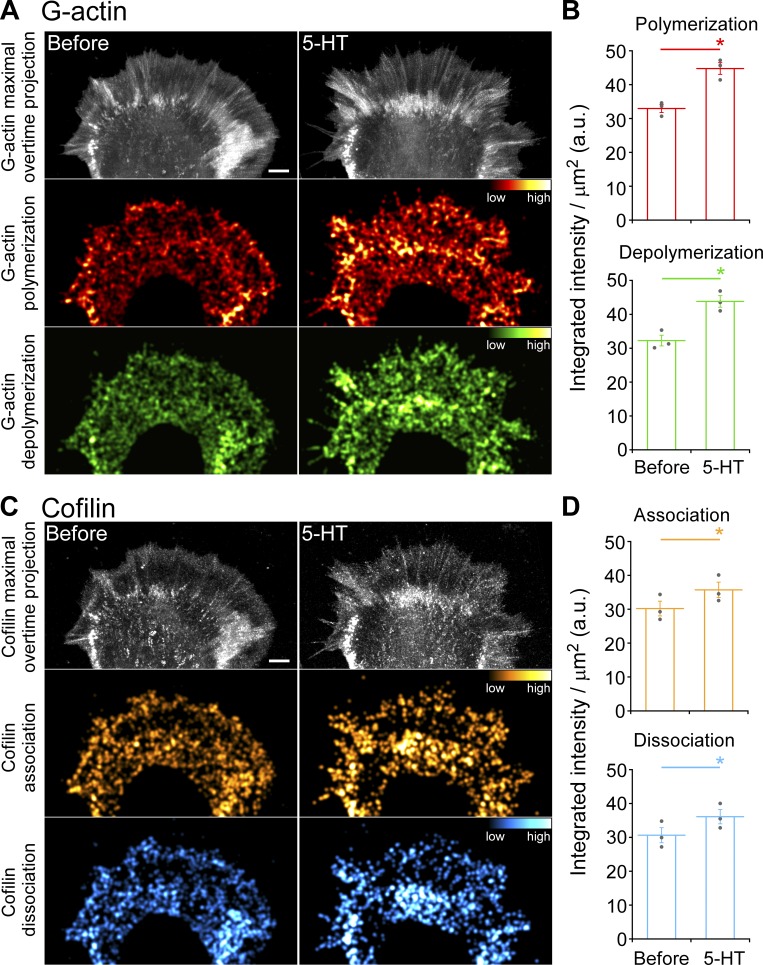
Given evidence that myosin II contractility can promote actin filament recycling and network treadmilling (Medeiros et al., 2006; Wilson et al., 2010), we investigated whether changes in myosin II activity alone could affect cofilin association–dissociation dynamics. When growth cones were treated with blebbistatin at levels known to suppress nonmuscle myosin II activity (Medeiros et al., 2006), significant decreases in integrated cofilin association–dissociation events were observed in front and rear growth cone regions (Fig. 5 and Video 3). Next, we investigated cofilin versus actin dynamics during 5-HT treatments (Fig. 6 and Video 4). We found that during 5-HT treatments, actin polymerization and depolymerization dynamics increased throughout the growth cone (Fig. 6, A and B), and cofilin association and dissociation dynamics increased in parallel (Fig. 6, C and D). These findings in live neurons are in line with previous results using activity-specific antibodies to assess cofilin activity profiles before and after 5-HT treatments in fixed growth cones (Zhang et al., 2012).

Figure 5.

Myosin II inhibition decreases cofilin dynamics. (A) Cofilin dynamics: maximal overtime projection of cofilin speckles (top), cofilin association (middle), and cofilin dissociation (bottom) before (left) and during (right) blebbistatin treatment (66.6 µM, 40 min). Alexa Fluor 568–cofilin was injected into cells; cofilin association and dissociation summation maps generated from 150-s sampling periods with 5-s image acquisition intervals. Colors indicate relative cofilin association/dissociation rates (compare color bars). Scale bar, 5 µm. See also Video 3. (B) Quantification of cofilin association (top) and dissociation (bottom) in front and rear growth cone regions: blebbistatin (66.6 µM, 30–50 min) treatment decreases cofilin dynamics. Region demarcation protocol as in Fig. S2 A. Data are mean (a.u.) ± SEM. Number of growth cones evaluated: seven, pooled from three independent experiments. *, P < 0.001 with two-tailed paired t test.

Figure 6.

5-HT treatment increases actin turnover and cofilin dynamics. (A) Actin turnover: maximal overtime projections of G-actin speckles (top), actin polymerization (middle), and depolymerization (bottom) before (left) and during (right) 5-HT treatment (10 µM, 20 min). (B) Summary of actin polymerization (top) and depolymerization (bottom) before and during 5-HT treatment (10 µM, 20 min). (C) Cofilin dynamics: maximal overtime projections of cofilin speckles (top), cofilin association (middle), and cofilin dissociation (bottom) before (left) and after (right) 5-HT (10 µM, 20 min). (D) Summary of cofilin association (top) and dissociation (bottom) before and after 5-HT (10 µM, 20 min); Alexa Fluor 488–G-actin and Alexa Fluor 568–cofilin were injected sequentially. Actin turnover and cofilin dynamics (A and C) maps generated as in Fig. 5. Colors in A and C indicate relative actin polymerization/depolymerization and cofilin association/dissociation rates, respectively (compare color bars). Scale bar, 5 µm. For B and D, data are mean (a.u.) ± SEM. Number of growth cones evaluated: three, pooled from three independent experiments. *, P < 0.01 with two-tailed paired t test. See also Video 4.

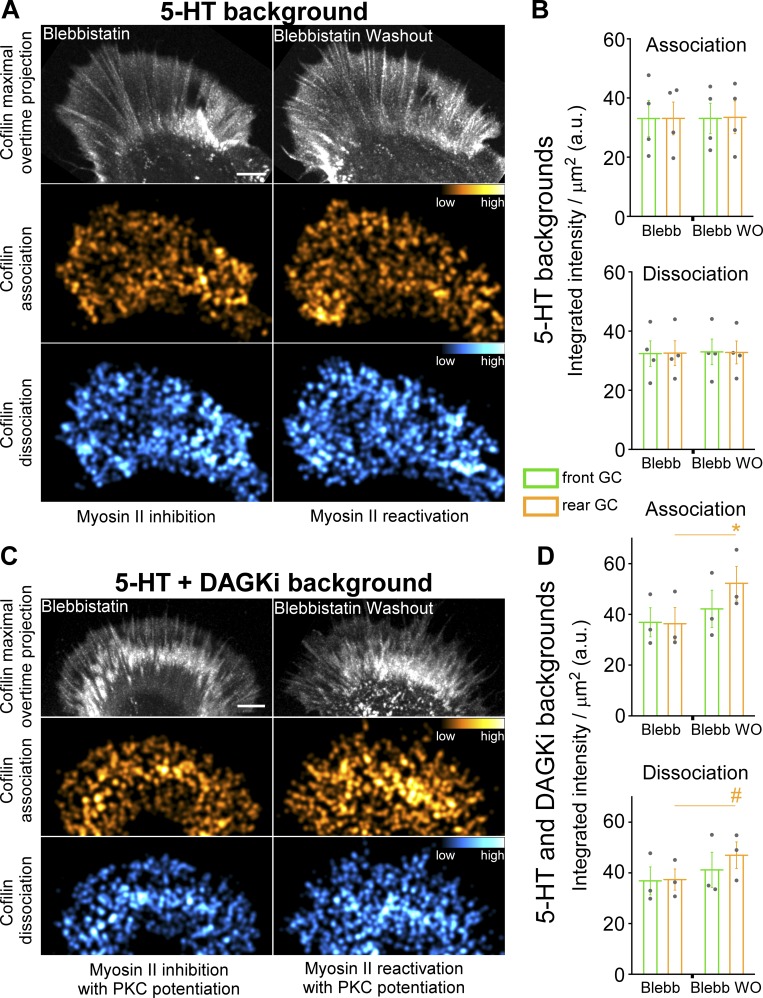
To investigate the relationship between cofilin dynamics and myosin II activity during 5-HT responses, we pretreated growth cones with blebbistatin to inhibit myosin II in a 5-HT background. Then, myosin II activity was reactivated by blebbistatin washout in the continued presence of 5-HT to assess myosin II effects on cofilin activity. Under these conditions, cofilin association and dissociation dynamics were not significantly affected upon myosin II reactivation (Fig. 7, A and B; and Video 5, top). In contrast, when PKC action was potentiated by pretreatment with DAGKi, myosin II reactivation resulted in a significant increase in integrated cofilin association and dissociation intensities in the growth cone rear (Fig. 7, C and D; and Video 5, bottom). These results are consistent with higher levels of PKC activity facilitating the large decreases in actin filament network density observed in the growth cone rear (Fig. 3, D–F), where myosin II activity levels are also highest. These observations also suggest a mechanism by which PKC modulation of myosin II contractility could control 5-HT response polarity, which is considered further below.

Figure 7.

Potentiation of PKC action increases cofilin dynamics during 5-HT responses. (A and B) Cofilin dynamics during myosin II reactivation in 5-HT backgrounds. Cells were pretreated with blebbistatin (30 µM, 15 min) followed by addition of 5-HT (10 µM, 20 min; Myosin II inhibition, A and B, left columns). Blebbistatin was washed out in the continued presence of 5-HT for 15 min (Myosin II reactivation, A and B, right columns). (A) Maximal overtime projections of cofilin (top), cofilin association (middle), and dissociation (bottom). (B) Quantification of cofilin association (top) and dissociation (bottom) in front and rear growth cone regions showing that cofilin dynamics are independent of myosin II activity in 5-HT backgrounds under normal conditions. Data are mean (a.u.) ± SEM. Number of growth cones evaluated: four, pooled from four independent experiments. (C and D) Cofilin dynamics with PKC potentiation. Cells were pretreated with blebbistatin (30 µM) and DAGKi (5 µM) for 15 min, and then 5-HT (10 µM) was added for 20 min (C and D, left columns). Blebbistatin was washed out in the continued presence of 5-HT and DAGKi for 15 min (C and D, right columns). (D) When PKC action is potentiated, myosin II reactivation enhances cofilin dynamics during 5-HT responses. Data are mean (a.u.) ± SEM. Number of growth cones evaluated: three, pooled from three independent experiments. *, P < 0.001 with two-tailed paired t test; ^#, P < 0.05 with two-tailed paired t test; Alexa Fluor 568–cofilin was injected into cells. Cofilin association and dissociation maps (A and C) generated as in Fig. 5. Scale bars, 5 µm. For B and D, regions were demarcated as in Fig. S2 A. See also Video 5.

Actin network turnover rates and traction force both increase during 5-HT–evoked growth

5-HT–evoked responses depend on laminin–integrin interactions; however, unlike classic adhesion responses in which rates of advance have been correlated with decreased rates of retrograde actin flow (Lin and Forscher, 1995; Suter and Forscher, 2000; Nichol et al., 2016; Short et al., 2016), retrograde flow rates increase during periods of 5-HT–evoked growth (Zhang et al., 2012). The above observations prompted us to investigate traction force behavior during 5-HT responses.

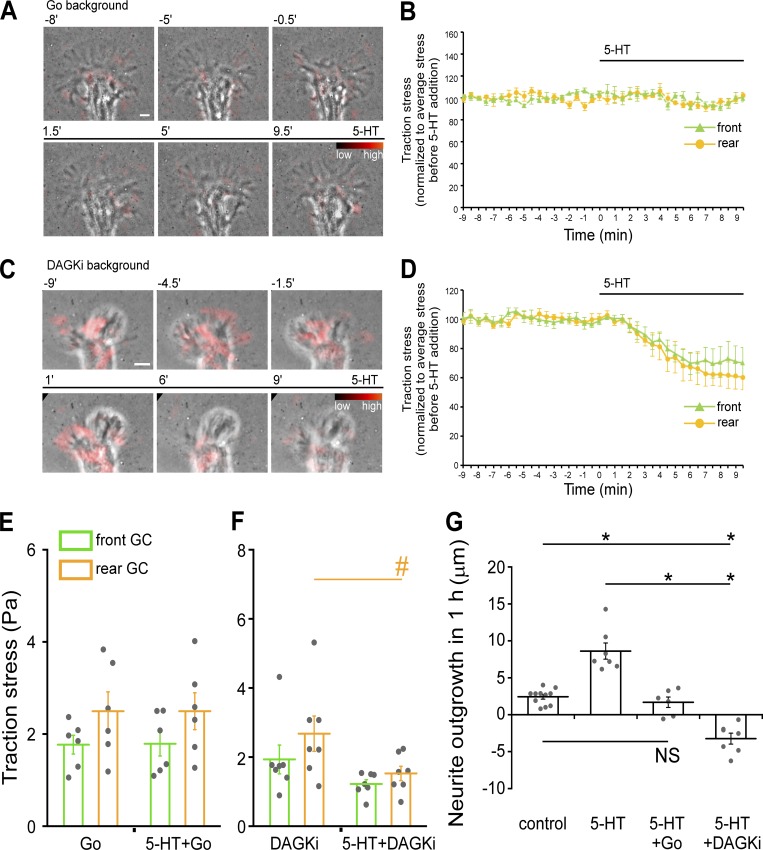
Neuronal growth cones typically exhibit traction stresses that are one to two orders of magnitude less than those generated by epithelial cells (Betz et al., 2011; Koch et al., 2012; Hyland et al., 2014). Accordingly, we plated Aplysia neurons on soft (230- or 430-Pa) elastic substrates embedded with fluorescent fiducial markers for measuring traction stresses. We then used traction force microscopy (Dembo and Wang, 1999) to measure stresses exerted by growth cones on their substrates (Fig. S4, A–G; and Video 6) under control conditions and during 5-HT exposure (Fig. 8). As a control, we first measured retrograde actin flow rates and neurite outgrowth rates when on soft polyacrylamide (PA) substrates and found that 5-HT exposure led to typical increases in retrograde actin flow rates accompanied by sustained increases in neurite outgrowth rates (Fig. 8, A and B; Fig. 9 G; and Video 7). We then assessed corresponding traction forces and found that traction stresses fluctuated over time and tended to be of greatest amplitude in the growth cone rear near the T zone under control conditions (Hyland et al., 2014). 5-HT exposure resulted in significant stress increases in both front and rear growth cone domains, with the largest stress increases observed in the rear during periods of sustained growth (Fig. 8, C–F; Fig. S4 J, right panel; Video 8; and Video 9, right). When PKC was inhibited, traction stress levels and neurite outgrowth rates did not change after 5-HT exposure (Fig. 9, A, B, E, and G; and Video 10, left). In contrast, after PKC potentiation, 5-HT exposure resulted in rapid decreases in traction force (Fig. 9, C, D, and F; and Video 10, right), and growth cones eventually retracted (Fig. 9 G). In experiments to control for possible fluid shear force effects, no change in traction stress was observed during vehicle solution changes (Fig. S4, H, I, and J, left panel; and Video 9, left). Taken together, these results suggest that PKC activation is a prerequisite for the increases in growth cone traction force normally associated with 5-HT–stimulated growth. In contrast, when PKC activity is potentiated, 5-HT treatments lead to rapid decreases in traction force and actin filament density in the growth cone and eventual growth cone retraction.

Figure 8.

5-HT treatment results in increased traction stress and retrograde F-actin flow rates. (A) Phase image (top), Alexa Fluor 594–phalloidin FSM (middle) and corresponding F-actin flow maps (bottom) before (left) and after (right) 5-HT (10 µM, 15 min) on PA soft gels (230 Pa). Images acquired every 5 s with 2.5-min elapsed recording time. Flow map colors encode speed (see scale bar), and arrows indicate flow direction. Scale bars, 5 µm. See also Video 7. (B) Summary of P-domain retrograde flow rates in response to 5-HT (10 µM, 20–40 min) on PA soft gels (230 Pa); data are mean (μm/min) ± SEM. Number of growth cones evaluated: seven, pooled from three independent experiments. *, P < 0.001 with two-tailed paired t test. (C) Overlay of traction stress maps and phase images of a growth cone (GC) before (left) and after (right) 5-HT (10 µM, 40 min). Images acquired every 30 s with 3-min elapsed recording time for each condition. Color shows relative traction stress magnitude (see color bar). Scale bar, 5 µm. See also Video 8. (D) Summary of mean traction stresses measured in front versus rear growth cone regions (compare Fig. S4 A) before and after 5-HT (10 µM, 20–40 min). Data are mean (Pa) ± SEM. Number of growth cones evaluated: seven, pooled from four independent experiments. *, P < 0.001 with two-tailed paired t test. (E) Overlay of traction stress map and phase image of a growth cone before and after 5-HT (10 µM) addition. Images acquired every 30 s with 18.5-min elapsed recording time. Elapsed time shown at the top of time lapse montage in min. Color indicates traction stress magnitude (see color bar). Scale bar, 5 µm. See also Video 9, right. (F) Time course of mean traction stresses assessed in front and rear growth cone regions before and after 5-HT (10 µM) addition (compare Fig. S4 A). Traction stress normalized to average stress before 5-HT addition. Data are mean (%) ± SEM. Number of growth cones evaluated: five, pooled from five independent experiments. Black bars indicate 5-HT addition. See also Video 9, right.

Figure 9.

PKC modulates traction stress and 5-HT response polarity. (A) PKC inhibition: traction stress maps in Go background (Go 5 µM, 30-min pretreatment) overlaid on phase image before and after 5-HT (10 µM) addition in the continued presence of Go. Images acquired every 30 s with 18.5-min elapsed recording time. Elapsed time (in minutes) shown at the top. Color indicates traction stress magnitude (see color bar). See also Video 10, left. (B) Mean traction stress in front and rear of growth cone regions (as defined in Fig. S4 A) before and after 5-HT (10 µM) addition with PKC inhibition (Go 5 µM, 30-min pretreatment and continued presence after 5-HT addition). Traction stress normalized to average stress before 5-HT addition. Data are mean (%) ± SEM. Number of growth cones evaluated: four, pooled from four independent experiments. Black bars indicate 5-HT addition. See also Video 10, left. (C) PKC potentiation: overlay of traction stress map and phase image of a growth cone before and after 5-HT (10 µM) addition in the continued presence of DAGKi (5 µM, 30-min pretreatment). Image acquisition as in A. See also Video 10, right. (D) Summary of mean traction stress in the front and rear of growth cones before and after 5-HT (10 µM) addition in DAGKi backgrounds (DAGKi 5 µM, 30-min pretreatment and continued after 5-HT addition). Traction stress normalized to average stress before 5-HT addition. Data are mean (%) ± SEM. Number of growth cones evaluated: five, pooled from five independent experiments. Black bars indicate 5-HT addition. See also Video 10, right. (E) Mean traction stresses before and after 5-HT (10 µM, 30–60 min) with PKC inhibition. Cells were pretreated with Go (5 µM) for 30 min; Go was present during 5-HT treatment. Traction stresses are average value of mean stresses measured under each condition. Data are mean (Pa) ± SEM. Number of growth cones evaluated: six, pooled from four independent experiments. (F) Mean traction stress in the front and rear of growth cones before and after 5-HT (10 µM, 30–60 min) with PKC potentiation. Cells were pretreated with DAGKi (5 µM) for 30 min; DAGKi was present during 5-HT treatment. Stress data are mean (Pa) ± SEM. Number of growth cones evaluated: seven, pooled from five independent experiments. ^#, P < 0.05 with two-tailed paired t test. (G) Neurite outgrowth data sampled for 1-h periods on soft PA gels (230 Pa) under control conditions, 5-HT (10 µM); PKC inhibition, Go (5 µM) 30-min pretreatment followed by 5-HT (10 µM) addition in continued Go; or PKC potentiation, DAGKi (5 µM) 30-min pretreatment followed by 5-HT (10 µM) addition in continued DAGKi. Data are mean (μm) ± SEM. Number of neurites evaluated: 11, 7, 6, and 7 for control, 5-HT, 5HT+Go, and 5-HT+DAGKi, pooled from four, three, three, and three independent experiments, respectively. P = 1.25 × 10⁻¹⁰ with single-factor ANOVA. *, Significant difference using Tukey’s HSD post hoc analysis. Scale bar, 5 µm.

5-HT effects are accompanied by increases in active point contact density

Decreases in actin filament density in regions of increased traction force production observed during normal 5-HT responses seemed paradoxical. Given that PKC can also regulate integrin signaling (Disatnik and Rando, 1999; Milner and Campbell, 2002; Larsson, 2006), we investigated whether a change in adhesion function could be compensating for decreases in actin filament density. To assess cell adhesion function, we quantified active point contact density (Short et al., 2016) by phospho-FAK (Burridge and Chrzanowska-Wodnicka, 1996; Wang et al., 2001) labeling before and after 5-HT treatments. We discovered that point contact density increased significantly throughout the growth cone P domain with 5-HT treatments on glass and 230-Pa elastic substrates (Fig. 10, A–C; and Fig. S4 K). Stimulated increases in point contact density were absent after PKC inhibition (Fig. 10, A [row 3] and B). Interestingly, after PKC potentiation, 5-HT treatment did not increase point contact density (Fig. 10, A [row 4] and B), suggesting that actin network catastrophe conditions do not support point contact activation and/or maturation. Together, these observations suggest that when the density of available binding sites in the F-actin flow module decreases, there is a compensatory increase in point contact density that facilitates increases in traction force. To our knowledge, increased retrograde actin flow in parallel with reciprocal changes in actin network and molecular clutch density is a unique mechanism for traction force regulation. Given the remarkable dynamicity point contacts typically display (Woo and Gomez, 2006), how their stochastic behavior influences traction force production in various chemotropic growth scenarios will be of future interest.

Discussion

Biochemical signaling pathways involved in regulation of axonal growth have been extensively characterized (Tessier-Lavigne, 1994; Tamariz and Varela-Echavarría, 2015); in contrast, how these signals control the biophysical events that underlie traction force generation is less well understood. To address this question, we developed a simple quantitative model system where signaling could be correlated with underlying ultrastructural changes, cytoskeletal protein dynamics, and biomechanical output assessed during GPCR-mediated responses to 5-HT (Zhang and Forscher, 2009; Yang et al., 2012; Zhang et al., 2012). Our previous findings suggest these results may be generalizable to other Gq GPCR responses, since direct activation of phospholipase C resulted in effects indistinguishable from those observed after 5-HT treatment (Zhang et al., 2012). Under normal conditions (Fig. 1 A, black lines), 5-HT exposure leads to an approximately threefold increase in the rate of neurite growth that depends on Ca-CN–dependent cofilin activation (Zhang et al., 2012) and a PKC-dependent increase of myosin II activity in the growth cone rear. A likely PKC effector is C kinase–potentiated protein phosphatase-1 inhibitor (CPI-17), which inhibits myosin phosphatase when phosphorylated by PKC (Kitazawa et al., 1999; Watanabe et al., 2001; Eto et al., 2002) and is known to potentiate myosin II contractile activity in Aplysia growth cones (Yang et al., 2013). ROCK is not a likely effector of myosin II activity here, as normal 5-HT–evoked growth responses persisted after ROCK inhibition with H-1152P (Fig. S1 K), a potent ROCK inhibitor (Ikenoya et al., 2002; Wen et al., 2012). The current study also revealed functional crosstalk between PKC-dependent myosin II contractility and cofilin activity (Fig. 1 A) that will be discussed in the context of the model shown in Fig. 10 D.

Myosin II contractility facilitates cofilin activity

We previously found that inhibition of myosin II activity had no effect on Ca-CN-cofilin–dependent increases in retrograde actin flow after 5-HT exposure; however, the presence of myosin II activity was necessary for 5-HT–dependent increases in neurite growth (Zhang et al., 2012). We report that, similar to myosin II inhibition, PKC inhibition suppressed 5-HT–evoked neurite outgrowth (Fig. S1) without affecting cofilin-dependent changes in actin dynamics (Fig. 2, A and C, left panel; and Fig. S2, D and E). These results suggest that independent pathways are present for controlling actin turnover and contractility in the growth cone, through regulation of cofilin and myosin II activities, respectively (Fig. 1 A). They also implicated PKC as a possible agent for controlling myosin II activity during 5-HT responses. In agreement, we found that 5-HT exposure resulted in modest, but significant, PKC-dependent increases in myosin II activity in the growth cone T zone (Figs. 1 and S2, A and B). Interestingly, after potentiation of PKC action via DAG kinase inhibition, 5-HT growth responses were converted to retractions (Figs. S1 and 1 A, red lines) accompanied by dramatic decreases in actin filament density throughout the growth cone, and with strongest effects in the T zone (Fig. 3). These decreases in actin filament density, which we refer to as actin “network catastrophes,” were completely suppressed by the CN inhibitor, FK506 (Fig. 3, E and F; and Fig. S3), which is known to inhibit cofilin activation (Zhang et al., 2012) in response to Ca release from ER stores in this system (Zhang and Forscher, 2009). Taken together, these results are consistent with increased myosin II–dependent actin network strain increasing cofilin severing and actin filament turnover. In agreement, we found that direct inhibition of nonmuscle myosin II alone decreased cofilin activity, assessed by speckle association and dissociation dynamics, throughout the growth cone (Fig. 5) and suppressed the PKC-dependent component of cofilin activity during 5-HT responses (Fig. 7).

Mechanical facilitation of actin filament severing is supported by previous evidence that filopodial actin bundle severing in the growth cone T zone depends on nonmuscle myosin II contractility (Medeiros et al., 2006). Myosin II activity could enhance cofilin function by four distinct mechanisms. First, myosin contractility can strain filaments and filament bundles, which promotes filament severing by localizing elastic energy at boundaries between bare (mechanically stiff) and cofilin-decorated (mechanically compliant) segments (McCullough et al., 2008; De La Cruz, 2009; Elam et al., 2013, 2017; Kang et al., 2014; De La Cruz and Gardel, 2015; De La Cruz et al., 2015; Schramm et al., 2017). Second, myosin binding can competitively displace cofilin from decorated filament segments, which introduces additional cofilin-decorated/undecorated boundaries (Elam et al., 2013) where severing preferentially occurs (De La Cruz, 2009; Suarez et al., 2011), thereby accelerating the overall macroscopic severing activity. Third, cofilin can mechanically destabilize filaments and filament bundles by introducing a buckling instability (Schramm et al., 2017). Fourth, simple myosin II tethering can enhance severing (Pavlov et al., 2007; Elam et al., 2013; Wioland et al., 2019). Taken together, our results suggest that myosin II–dependent mechanical stress can enhance the rate of cofilin-dependent turnover of treadmilling actin filament arrays found in the growth cone P domain as well as the T zone (Medeiros et al., 2006). In addition, there appears to be a threshold level of network stress above which rates of cofilin-dependent turnover exceed rates of polymerization, leading to catastrophic decreases in actin network density. The functional implications of actin network catastrophe are considered below.

Implications of cofilin mechanocatalysis for traction force production and growth regulation

Traction stresses in neuronal growth cones are typically one to two orders of magnitude lower than those measured in epithelial and other motile cells (Chan and Odde, 2008; Betz et al., 2011) and can vary between neuronal cell types (Koch et al., 2012). When we assessed traction forces in Aplysia growth cones extending on soft laminin-coated PA substrates under control conditions, we found that traction stresses fluctuated over time and tended to be greatest in the T zone region, as previously reported (Hyland et al., 2014). After 5-HT treatment, increases in neurite outgrowth rates were accompanied by significant traction force increases throughout the growth cone, with the most pronounced changes occurring in the T zone (Fig. 8, C and D, rear GC), where active myosin II levels are also typically highest (Medeiros et al., 2006).

Growth cones and motile cells generate traction forces by functional coupling of rearward-moving intracellular actin networks to underlying extracellular growth substrates (Fig. 10 D1). Molecular clutch models predict traction force transmission for conditions where adhesion protein clutch complexes functionally couple moving intracellular actin filaments to the extracellular matrix (Mitchison and Kirschner, 1988; Chan and Odde, 2008; Bangasser and Odde, 2013; Bangasser et al., 2013; Abe et al., 2018; Minegishi et al., 2018). In some cases, retrograde flow rates scale inversely with molecular clutch engagement as predicted by the original molecular clutch concept (Suter and Forscher, 2001; Nichol et al., 2016); however, other studies suggest that traction stresses correlate biphasically with retrograde F-actin flow speed in a cellular domain–dependent manner. Specifically, traction force and F-actin speed are inversely related in the leading edge lamellipodium where F-actin network velocity is high and myosin II independent, whereas there is a direct relationship between F-actin speed and traction stress in the more central lamellum domain where F-actin flow speed is low and depends on myosin II activity (Gardel et al., 2008). In a similar vein, when Aplysia bag cell neurons are maintained on laminin substrates, retrograde actin flow in the P domain is only weakly myosin II dependent and can be maintained by actin treadmilling (assembly and turnover) alone in the absence of myosin II (Zhang et al., 2012) or PKC activity (Figs. 2 and S2). Traction forces oscillate in time and space in both the P domain and T zone in growth cones (Betz et al., 2011; Koch et al., 2012; Hyland et al., 2014; Jiang et al., 2015). During 5-HT treatments, traction forces increased in both the P domain and T zone; however, stress increases were larger and more sustained in the T zone, where significant increases in myosin II activity were also observed (Figs. 1 E and S2 B). Given that the T zone is where myosin II– and PKC-dependent contractile actin arcs form and morph into central actin bundles (Fig. 1, B–D; and Fig. 10, A [red arrowheads] and D [blue modules]) and that traction force production is PKC dependent, these structures (Schaefer et al., 2002; Zhang et al., 2003; Medeiros et al., 2006; Yang et al., 2013) are likely the main traction force effectors during 5-HT responses. Our observations are consistent with the presence of an oscillating population of nascent point contacts in the P domain and myosin II–dependent point contact maturation and force transduction occurring in the more central T zone, similar to what has been described in fibroblasts (Wu et al., 2017). Although it is clear that fast retrograde flow in the P domain increases in parallel with modest increases in traction force, an outstanding question for future studies will be addressing how actin arcs and/or central actin bundle dynamics are affected during 5-HT–mediated growth.

When we analyzed effects of 5-HT treatments on actin network ultrastructure, we noted a significant decrease in actin filament density (increase in mesh area) in the growth cone rear, and, this effect depended on cofilin activity (Fig. 3, B and F; and Fig. S3 F). Thus, traction forces were paradoxically increasing in regions where actin networks were actually becoming more sparse (Fig. 3, A, B, and F). When we investigated active point contacts by assessing phosphorylated FAK (pFAK) distributions, we found that active point contact densities increased with 5-HT treatments, and these increases were PKC dependent (Fig. 10, A and B; and Fig. S4 K), consistent with longstanding evidence that PKC can potentiate integrin function (Disatnik and Rando, 1999; Larsson, 2006). Taken together, these findings suggest that PKC-dependent increases in molecular clutch density compensate for cofilin-dependent decreases in F-actin binding site density, thereby facilitating the observed increases in traction force (Fig. 10 D2). Given the classic role myosin II activity plays in focal adhesion maturation (Chrzanowska-Wodnicka and Burridge, 1996), the increases in myosin II activity we observe in the T zone are predicted to create a positive mechanical feedback loop that promotes traction force increases (Fig. 10 D2). Further investigation of the relationship between point contact dynamics, actin dynamics, and traction force generation in this system will be an intriguing line of future investigation.

Functional consequences of actin network catastrophe

Interestingly, potentiation of PKC action flipped 5-HT response polarity from growth to retraction (Figs. S1 and 9 G). In related traction force experiments, we expected to see a sudden increase in traction force upon 5-HT exposure, given the higher myosin II activation levels throughout the growth cone under these conditions (Fig. 1). Instead, we observed sudden decreases in traction force (Fig. 9, C, D, and F) and eventual growth cone retraction (Fig. 9 G). We suggest that mechanocatalysis of cofilin activity can explain these effects. Specifically, coincidence of (a) higher than normal myosin II activity and network stress due to PKC potentiation and (b) Ca-CN–dependent cofilin activation could push peripheral actin networks above the catastrophe threshold. The resulting drastic reduction in actin network density would limit traction force–generating capability in the P domain and T zone and break the positive mechanical feedback loop for adhesion reinforcement we suggest is present in the T zone (Fig. 10 D2). In agreement, we see a rapid loss of traction force (Fig. 9, D–F) and a significant decrease in active point contact density under these conditions (Fig. 10, A [bottom row] and B). Independent evidence suggests that contractile actin–myosin II bundles are protected from cofilin-dependent severing due to mutually exclusive myosin and cofilin binding to actin filaments (Tojkander et al., 2015; Ngo et al., 2016). We suspect that the contractile actin arcs and central actin bundles that comprise the myosin II contractility module in growth cones (Zhang et al., 2003; Yang et al., 2013; Fig. 10, A and D1) and the neurite shaft (Ahmad et al., 2000) are similar structures that could sustain neurite retraction despite elevated cofilin activity (Fig. 10 D3). These findings are likely to have far-reaching mechanistic implications for understanding regulation of axon growth by GPCR signaling, spinal cord degeneration (Sivasankaran et al., 2004), and cell migration, all of which depend on coordinated crosstalk between actin network dynamics, nonmuscle myosin II contractility, and cell adhesion.

Materials and methods

Cell culture and chemicals

Primary culture of Aplysia bag cell neurons was as previously described (Forscher et al., 1987). Coverslips were pretreated with 20 µg/ml poly-l-lysine (Sigma-Aldrich) for 15 min, and then incubated in a 50-µg/ml laminin (Sigma-Aldrich) solution for 2 h and rinsed in L15–artificial seawater (ASW). 5-HT was obtained from Sigma-Aldrich. Go, Bis, H-1152P, blebbistatin, ML-7, DAGKi (also called R59022), and FK-560 were obtained from Calbiochem. Alexa Fluor 488–rabbit skeletal muscle G-actin (Alexa Fluor 488–G-actin) and Alexa Fluor 594 phalloidin were purchased from Invitrogen. Alexa Fluor 568 yeast cofilin was prepared as described previously (Suarez et al., 2011). Mouse anti-FAK pY397 was obtained from BD Biosciences (611722). Carboxylated red fluorescent FluoSphere beads (580/605 nm excitation/emission), at 0.2-µm diameter (Thermo Fisher Scientific; F8810), were used as markers in TFM substrates.

Solutions

ASW contained 400 mM NaCl, 10 mM KCl, 15 mM Hepes, 10 mM CaCl₂, and 55 mM MgCl₂ at pH 7.8. ASW was supplemented with 3 mg/ml BSA, 0.5 mM vitamin E, and 1 mg/ml carnosine before experiments. Live-cell extraction buffer (LE) contained 100 mM Pipes, pH 6.9, 10 mM KCl, 100 mM NaCl, 5 mM EGTA, 5 mM MgCl₂, 4% polyethylene glycol, average molecular weight 35,000, and 20% sucrose at ∼1,000 mOsm/liter and was supplemented with 1% Triton X-100, 10 µM phalloidin, 10 µM Taxol, and 10 mg/ml 1,2-bis(o-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid immediately before use. Washing buffer for live-cell extraction (WLE) contained 80 mM Pipes, pH 6.9, 5 mM EDTA, and 5 mM MgCl₂. Block solution for antibody labeling was 5% BSA and 10% goat serum in PBS containing 0.1% Triton X-100 (PBS-T). Mowiol (Calbiochem) for cell mounting in immunocytochemistry was prepared following the manufacturer’s protocol with 10% Mowiol, 25% glycerol, 0.2 M Tris, pH 8.5, and 20 mM n-propylgalate.

Microinjection

The microinjection protocol was as described previously (Lin and Forscher, 1995). For actin dynamics, neurons were injected with Alexa Fluor 594–phalloidin (needle concentration, 20 µM). For cofilin dynamics, neurons were injected with Alexa Fluor 568–cofilin (needle concentration, 21 µM). For simultaneous imaging of actin and cofilin dynamics, neurons were first injected with Alexa Fluor 488–G-actin (needle concentration, 0.5 mg/ml) and 30 min later were injected with Alexa Fluor 568–cofilin (needle concentration, 21 µM). Reagent injections were typically ∼10% of cell volume. After microinjection, cells were incubated in ASW for 1 h before imaging.

Confocal microscopy

Images were acquired using a Revolution XD spinning disk confocal system (Andor) with a CSU-X1 confocal head (Yokogawa) and mounted on a TE 2000E inverted microscope with Perfect Focus (Nikon). Confocal images were acquired using an Andor iXonEM+ 888 electron-multiplying charge-coupled device camera. Transillumination was provided by a halogen lamp and controlled by a SmartShutter (Sutter Instrument). Confocal excitation was provided by an Andor Laser Combiner with three laser lines at 488, 561, and 647 nm. Emission wavelength was controlled using a Sutter LB10W-2800 filter wheel outfitted with bandpass filters from Chroma Technology. Image acquisition and all other peripherals were controlled by Micro-Manager (https://micro-manager.org/). A Nikon CFI Plan Apo 100×/1.4-NA objective was used. Experiments were performed at room temperature using ASW as imaging medium unless stated otherwise.

Quantification of actin retrograde flow rates and actin turnover by qFSM

Two methods were used to visualize F-actin for FSM: (a) fluorescently labeled G-actin incorporated into actin filaments and (b) low levels of fluorescent phalloidin, which specifically binds F-actin but not G-actin. Images were acquired using 300- to 600-ms integration times with 5-s intervals. Kymography (Zhang et al., 2003) and automated speckle tracking using the qFSM Matlab algorithms (Mendoza et al., 2012) from Gaudenz Danuser’s group (https://github.com/DanuserLab/QFSM) were used to assess rates of actin filament movement. Kymographs were generated along the direction of actin network translocation in the P domain and T zone of growth cones from actin FSM images using the ImageJ multiple kymograph plug-in. Slopes of lines parallel to speckle movement over time in kymographs were converted to flow rates based on imaging interval and pixel scale. To generate actin flow vector fields, an adaptive multiframe correlation algorithm (Ji and Danuser, 2005) was used to determine the average flow over five frame intervals. This information was used to initialize a single-particle tracking algorithm (Ponti et al., 2003, 2005; Thomann et al., 2003), which was run on every frame in the video. Single-particle tracking results were used to generate time-integrated actin polymerization–depolymerization kinetic maps (Ponti et al., 2003, 2004, 2005). Actin polymerization–depolymerization activities were expressed as integrated intensity per square micrometer.

Quantification of cofilin activity in growth cones by qFSM

When a trace amount of Alexa Fluor 568–cofilin is injected, a speckle is observed whenever an active Alexa Fluor 568–cofilin molecule binds to an actin filament. Thus, cofilin speckle appearances represent cofilin association events, while speckle disappearances represent cofilin dissociation events. Time-lapse recordings of cofilin speckle dynamics were acquired using 200- to 500-ms frame integration times and 5-s acquisition intervals. Cofilin speckle tracking was performed as described above for actin. Cofilin association–dissociation maps were generated by integration of signal captured during the entire sampling interval, and their respective activities were expressed as integrated intensity per square micrometer. When a cell was coinjected with Alexa Fluor 488–G-actin and Alex Fluor 568–cofilin, the integrated intensity levels per square micrometer from actin polymerization–depolymerization maps and cofilin association–dissociation maps were used to correlate actin turnover versus cofilin activities. To compare the spatial distribution profiles of actin turnover and cofilin activities, five to seven 30-pixel-wide lines were drawn from the leading edge to 1.3× P-domain width in actin polymerization–depolymerization maps and cofilin association–dissociation maps. The intensity was measured with the plot profile function in ImageJ, and the data were exported to Excel (Microsoft). Intensity was plotted versus normalized distance for population analysis of line scans. Normalized distance was specified by setting the beginning (left end) of the lines scan at the leading edge and letting the position 0.77 be the peripheral–central domain interface.

Immunocytochemistry

Cells were fixed with 4% formaldehyde and 400 mM sucrose in ASW and permeabilized with 1% Triton X-100 (Forscher and Smith, 1988). Actin filaments were labeled with 0.66 µM Alexa Fluor 594–phalloidin stock in PBS-T. For myosin II labeling, cells were blocked for 20 min with the blocking solution, incubated with 1:100 of anti-pSer19 of RLC mouse monoclonal antibody (P24844; Cell Signaling Technology) and 1:2,000 of rabbit anti–Aplysia myosin II RLC sera (Yang et al., 2013) for 30 min, washed three times with blocking solution, and incubated for 15 min with 10 µg/ml secondary antibody. For pFAK labeling, cells were blocked for 30 min with the blocking solution, incubated with 1:100 of mouse anti-FAK pY397 for 30 min, washed three times with blocking solution, and incubated for 15 min with 10 µg/ml secondary antibody. For pFAK labeling on PA soft gels, 230-Pa gels without fluorescent beads were used (see Preparation of traction force substrates for gel making). Cells were then washed three times in PBS-T and mounted in Mowiol.

Quantification of myosin II activity

Line scans of ratio images of background-corrected intensity values of phosphorylated myosin II RLC divided by total myosin II RLC were used to analyze the spatial intensity distribution of phosphorylated (active) relative to total myosin II RLC. Two to four 50-pixel-wide lines were drawn from the leading edge to 2× P-domain width. Average intensity was measured with the plot profile function in ImageJ, and the data were exported to Excel. Intensity was plotted versus normalized distance for population analysis of line scans. Normalized distance was specified by setting the beginning (left end) of the lines scan at the leading edge and letting the middle position be the peripheral–central domain interface. Alternatively, to compare phosphorylated myosin II RLC normalized to total myosin II RLC in growth cones under different conditions, the growth cone was divided into two parts: front, two-thirds sectors of P domain in the front, and rear, one-third sector of P domain in the rear plus T zone, as illustrated in Fig. S2 A. Average intensities in the front and rear of growth cones were calculated and compared between different conditions.

Quantification of pFAK in growth cones

Fluorescent images were subjected to background subtraction before quantitative intensity analysis. Image processing was performed in ImageJ. All images were acquired and scaled using the same parameters and a linear lookup table. To quantify pFAK area density, the growth cone was divided into two parts: front, two-thirds sectors of P domain in the front, and rear, one-third sector of P domain in the rear plus T zone, as illustrated in Fig. S2 A. Images were subjected to an intensity threshold process until all pFAK point contact labeling was highlighted. Area density was then quantified using the analyze particle function in ImageJ. The size minimum was set to 0.1 µm² to exclude noise in the selected regions. The area density is defined as

$$\text{area}\hspace{0.17em}(\%)=\frac{\text{sum of area covered by particles}}{\text{total area of the specified region}}.$$

Neurite outgrowth analysis

Long-term time-lapse experiments were performed on a Nikon TE300 inverted microscope equipped with a CoolSNAP HQ cooled charge-coupled device camera (Photometrics) and a variable-zoom lens (0.9–2.25). Transillumination was with a halogen lamp and controlled by a Uniblitz Shutter (Vincent Associates). Images were captured with a phase-contrast objective (10× Achrostigmat/NA 0.25). Cell positions were registered using a custom Matlab function developed by Paul Forscher Hardware, and image acquisitions were controlled with the open-source μ-Manager device adapter library through a custom Java user interface. After cells were incubated with different inhibitors for 20–30 min, time-lapse recordings were performed at 3-min intervals for 2 h, and after 5-HT exposure, recordings were resumed overnight. Recordings were performed at room temperature using ASW as imaging medium. Time-lapse images were converted to a kymograph by drawing a 9-pixel-wide line along the presumed growth axis using the ImageJ multiple kymograph plug-in. The persistent displacement of the growth cone’s leading edge over time was used to calculate neurite outgrowth.

Platinum/palladium replica EM

Cells were live extracted and fixed as described, followed by treatment with 3.25% glutaraldehyde in water and 0.2% tannic acid for 20 min each with water washes in between (Svitkina and Borisy, 1999). Samples were dehydrated with a graded series of ethanol concentrations before critical point drying. Critical point drying was performed using Leica EM CPD300 (Yale Medical School electron microscopy facility). Specimens were rotary shadowed with platinum/palladium at a 45° angle to a thickness of 2 nm, followed by carbon coating (Edwards Auto 306 Evaporator). Replicas were mounted on carbon/Formvar-coated EM grids and observed by transmission EM (Jeol JEM-1230) at 80 kV. To quantify actin veil network density, electron micrographs at 20,000× magnification were used to assess 1 × 1-μm² ROIs near the growth cone leading edge and the T zone (e.g., Fig. 3 A, green and yellow box). ROIs were subjected to an intensity threshold process until all the negative spaces bounded by actin filaments were selected, thereby defining the properties of the actin mesh. Thus mesh size is related to the amount of free space bounded by actin filaments and is a measure of the network density. Mesh images were then quantified using the analyze particle function in ImageJ. For each condition, 25 regions from both the front and the rear of five growth cones were analyzed. Regions containing filopodial bundles or intrapodia were excluded.

Image processing

Fluorescence images were subjected to background subtraction before quantitative intensity analysis. The only exception was automated speckle tracking, which was performed on raw image data. For ratio calculations, background-subtracted images were divided pixel by pixel and multiplied by 1,000 to prevent the loss of numerical precision, then subjected to Gaussian blur with a radius of 2 pixels to obtain a smooth contour followed by an unsharp mask. For display only, fluorescence images were convolved with a Gaussian kernel, processed with an unsharp mask, and scaled according to a linear lookup table. For display of ratio images, areas outside of the growth cones were cleared with a mask. EM images were inverted and processed with pseudo flat field to eliminate artifacts of uneven illumination, followed by an unsharp mask. Image processing was performed in ImageJ. All images of the same fluorescence label from each experiment were acquired and scaled using the same parameters (excitation intensity, exposure time, and gain) and a linear lookup table.

Preparation of traction force substrates

Compliant PA substrates with rigidities of 230 and 430 Pa were prepared as follows (Aratyn-Schaus and Gardel, 2010). Briefly, a mixture consisting of final concentration of 3% acrylamide and 0.06% bisacrylamide or final concentration of 5% acrylamide and 0.05% bisacrylamide was added to 0.75 µl of tetramethylethenedamine (Thermo Fisher Scientific; 17919) and 2.5 µl of final concentration of 0.05% ammonium persulfate (APS; Thermo Fisher Scientific; 17874) to create the substrates (Fischer et al., 2012). Carboxylated beads (200-nm diameter) were added to the solution to enable stress deformations by the cells. 12 µl of this final solution was sandwiched between an activated coverslip (treated with 2% silane and 1% glutaraldehyde) and a silanized glass slide resulting in an ∼60-µm-thick gel with a stiffness of 230 and 430 Pa, respectively. The substrate thickness was verified using confocal z-stack imaging of the beads embedded in the gel. Rigidity measurements were verified by measuring indentation (δ) in z direction and the radius of contact (r) of a 250-µm (R) polystyrene bead placed on top of the gel (Chan and Odde, 2008). The resulting gel rigidity estimates were based on the following calculations:

$$\delta =R-\sqrt{R^2-r^2},$$

$$E=\frac{3\left(1-{\nu }^2\right)f}{4R^{1/2}{\delta }^{1/2}},$$

where f is the buoyancy corrected force of the sphere and ν is the estimated Poisson ratio of the hydrogel (ν = 0.3). Measured elastic moduli were 230 ± 20 and 430 ± 20 Pa for three independent samples, respectively. PA gels were activated using 200 µl of sulfoSANPAH (Sigma-Aldrich; 803332) at a 1-mg/ml concentration (Wang and Pelham, 1998). The samples were exposed to UV light for 5 min followed by several washes under DI water to remove excess sulfoSANPAH. Activated gels were inverted on 100 µl of poly-D-lysine (Millipore; A-003-E) at 1 mg/ml and left overnight at 4°C. Gels were then rinsed under deionized water and inverted on a 100-µl drop of 50 µg/ml laminin (Sigma-Aldrich; L2020) for 2 h at room temperature, washed 3×, and stored at 4°C in 1× PBS until ready for use.

Traction force microscopy

Images were acquired on the confocal microscope with a phase-contrast Plan Apo 100×/1.45-NA objective. Two-channel images were acquired using the time-channel-slice acquisition setting. Specifically, images were focused on the growth cone’s P domain, and 1-μm depth at a z-step size of 0.25 µm was set up for acquiring fluorescent beads. The paired images were recorded using 100–250-ms integration times for fluorescent beads and 300–400-ms for phase contrast images with 30-s intervals. Recordings were performed at room temperature using culture medium as imaging medium. The growth cone was centered in the field of view such that bead displacements would be expected to decrease to zero at the edges. For all traction force microscopy experiments, an unstressed reference image was required to calculate absolute stress magnitudes. Accordingly, after the experiment, chambers were perfused with 1% Triton X-100 in ASW to dissolve cells and relax the stress exerted by the cells on the substrate. A confocal z-stack of the beads at a z-step size of 0.25 µm and a phase-contrast image were then acquired for every field of interest. For each time point and the unstressed reference beads image, the 3D bead stack was projected to an average 2D image using ImageJ Z projection function. Then, each 2D image was combined into a time-lapse stack with the reference beads image as the last frame. Phase time-lapse images were also combined with the reference phase image. The resulting bead and phase stacks were drift-corrected using ImageJ register virtual stack slices plug-in. Cellular forces were measured by traction force microscopy as described (Sabass et al., 2008). Force-dependent strain calculations are based on the Fourier transform traction cytometry with an ∼10-µm grid size. Specifically, traction stresses were measured in the front and the rear of the growth cone as defined in Fig. S4 A, with the front being two-thirds of the front P domain and the rear being one-third of the rear P domain plus central domain. Background stresses were calculated in an area of 16–25 µm² close to the field edge for each time point, and the average background stress was used to correct traction stress in the growth cone.

Statistical analysis

Statistical analysis was performed in Excel using two-tailed paired or unpaired t test or single-factor ANOVA followed by Tukey’s honestly significant difference (HSD) post hoc analysis, with significance established at P < 0.05. Data are presented as mean ± SEM of measurement, unless otherwise specified. Data distribution was assumed to be normal, but this was not formally tested.

Online supplemental material

Fig. S1 shows that growth cone 5-HT response polarity is modulated by PKC via effects on myosin II activity. Fig. S2 shows that 5-HT activates nonmuscle myosin II preferentially in the T zone in a PKC-dependent manner, while 5-HT regulation of peripheral retrograde F-actin flow is independent of PKC activity. Fig. S3 shows that PKC up-regulation results in cofilin-dependent depletion of actin veils in response to 5-HT. Fig. S4 shows that 5-HT treatment results in increased traction stress and pFAK area density. Video 1 (related to Fig. S1) shows that 5-HT evokes different growth cone responses under different backgrounds. Video 2 (related to Fig. 4) shows FSM evaluation of actin turnover and cofilin dynamics in tandem. Video 3 (related to Fig. 5) shows that myosin II inhibition results in decrease in cofilin dynamics. Video 4 (related to Fig. 6) shows that 5-HT treatment increases actin turnover and cofilin dynamics in growth cones. Video 5 (related to Fig. 7) shows that up-regulation of PKC activation leads to myosin II–assisted cofilin hyperactivation in response to 5-HT. Video 6 (related to Fig. S4, A–G) shows quantification of traction stress of growth cones. Video 7 (related to Fig. 8 A) shows that 5-HT increases peripheral F-actin retrograde flow rates on PA soft gels (230 Pa). Video 8 (related to Fig. 8 C) shows that 5-HT evokes traction stress increase in growth cones. Video 9 (related to Figs. S4 H and 8 E) shows comparison traction stresses in growth cones during medium exchange versus 5-HT addition. Video 10 (related to Fig. 9, A and C) shows comparison of 5-HT–evoked traction stress changes in growth cones under Go versus DAGKi background.