Novel Combinations of Experimental and Computational Analysis Tested on the Binding of Metalloprotoporphyrins to Albumin.

Abstract

The evidence that Human Serum Albumin (HSA) binds metal ions and organometallic compounds has generated interest in its physiological role as a metalloprotein and as a vehicle for synthetic biology applications (e.g., synthetic blood and solar energy conversion). HSA has been shown to bind metallo-porphyrins, however, the structural details of such interactions are available only for the HSA:heme complex. A typical challenge for studying the interaction of proteins with metalloporphyrins is the poor solubility of the ligands that affect the characterization the complexes. The manuscript shows that a combination of dialysis and centrifugation yields aqueous solutions that contain > 90% HSA:porphyrin complexes and virtually eliminate aggregated ligands. The removal of aggregates increases the quality of the optical spectroscopy data which, in turn, yield more accurate binding constants (~ 0.1 and 2.1 × 10⁶ M⁻¹) and reveal FRET between Trp214 and the porphyrins. The Trp-porphyrin distance was estimated to be within the 28–34Å range and was used to guide the search of binding sites through a novel feedback approach with docking simulations. Results suggest while some protoporphyrins (metal-free, Fe(III)PPIX and Mg(II)PPIX) bind HSA at the heme site, others (Zn(II)PPIX, Mn(III)PPIX and Sn(IV)PPIX) are more likely to bind the Cys34.

1. Introduction

Metalloproteins form a class of polypeptides that share the ability to coordinate metal co-factors. Their functions span from metal ions storage to highly coordinated enzymatic processes [1–4]. Human Serum Albumin (HSA) was recently suggested to share common characteristics with this class of proteins because, among other functions, it binds and transports metal ions either directly [5] or by coordination to organic molecules [6]. HSA is known as the most abundant carrier protein in human plasma and is involved in the solubilization and transportation of endogenous and exogenous molecules [5, 7, 8]. The metalloprotein nature of the HSA has been suggested by the discovery of multiple sites that can coordinate metals [6] such as: i.) an ATCUN motif which involves His3 [9], ii.) a site that coordinates metals between the nitrogens of His67, Asn99, His247 and Asp249 [10] and iii.) a site that coordinates metals through the thiol of the only free Cys residue (Cys34) [5]. An additional site was identified for the binding of heme (or hemin) [11] which renders HSA a de facto heme protein [12] This site coordinates the central metal through two Tyr residues (Tyr 138 and Tyr 161) [11] instead of a pair of His residues as it is common for heme proteins [13, 14]. The presence of multiple metal binding locations has prompted much interest in their physiological activity [6] as well as their potential role in synthetic biology. In particular, the formation of complexes of HSA (or other albumins) with metalloprotoporphyrins (MePP) has been investigated for diverse non-native applications that range from the development of artificial blood [6] to the creation of photosensitized fuel cells [15].

Despite the interest for these structures, the complexes of HSA with metals have proven difficult to characterize. For instance, while the structure of HSA with hemin has been resolved experimentally, the evidence of whether other PPs dock to HSA [15, 16] at the same location has not been directly provided [17]. Considering the potential physiological and non-physiological roles of these complexes a more complete understanding of the interaction between MePPs and HSA must be obtained.

One of the major challenges to the study the assembly of proteins and MePPs has been the tendency of the latter to aggregate in aqueous solutions [18, 19]. While aggregates do not appear to directly interact with proteins they do interfere with experimental techniques[20, 21]. Recently, however, we have discovered a protocol that enables the separation and recovery of the HSA:MePP complexes from the aggregated MePPs [17]. As a result the experiments revealed details (such as the possibility to extract the molar extinction coefficient of the bound PP) that were previously unavailable [22]. In this study we investigated the spectroscopic properties of a series of MePPs bound to HSA. The elimination of MePP aggregates enabled us to improve the estimate of binding parameters and, more importantly, revealed the evidence of the occurrence of Förster Resonance Energy Transfer (FRET) between the lone tryptophan residue (Trp214) of HSA and the bound MePP. Access to this distance yielded a more precise characterization of the location of the MePP binding sites because it was used to guide the search for the most likely docking location through computational simulations. Combination of spectroscopic and computational docking methods have been employed in the past with HSA [8, 23], but we introduced a novel approach to further improve the ability to identify the binding location, whereby docking simulations data were used to refine the dipole orientation factor (κ) in FRET analysis. [24] The refined value subsequently enabled us to retrieve a better estimate of the distance between Trp214 and the MePP ligand. The “double-feedback” approach (between docking simulations and FRET) was carried out to seek the best agreement between the experimental data and the computational results in order to identify the binding location of each MePP.

Through this methodology we established that the heme binding site is energetically favored over other locations and is consistent with the experimental data for most MePPs. However, the data also suggest that Mn(III)PPIX, Zn(II)PPIX and Sn(IV)PPIX bind at a different location. Unfortunately, we were unable to investigate the ATCUN motif because the available HSA structures for computational analysis lack the N terminal amino acid residues that form this metal binding site. Nevertheless, the data provided in this work may facilitate future investigations of the use of HSA:MePP complexes for synthetic biology and/or physiological applications.

2. Experimental

2.1. Chemicals.

Human Serum Albumin (HSA), dimethylsulfoxide (DMSO), protoporphyrin IX (PPIX) and hemin (Fe(III)PPIX(Cl)) were purchased from Sigma-Aldrich (St. Louis, MO). Zn(II)PPIX, Mg(II)PPIX, Mn(III)PPIX, and Sn(IV)PPIX were purchased from Frontier Scientific Inc. (Logan, UT).

2.2. Sample preparation.

Millimolar stocks of metal and metal-free PPIX were prepared by dissolving an aliquot of the solid PP in ~ 1 ml of DMSO. Each stock was kept in the dark at room temperature for at least 48 hours prior to use, in order to ensure equilibration of monomeric PPs in solution. An aliquot (< 20 μL) of such stock was then dissolved in 2 ml of deionized water (DI) to form an aqueous stock where the PPs were in the 50–100 μM range and the concentration of DMSO was < 1% in volume. Under these conditions, most PPs tend to form inhomogeneous aggregates that can be detected spectroscopically (see below).

2.3. Elimination of aggregated porphyrins.

The detailed description of the procedure to decrease or eliminate aggregated PPs can be found in a previous manuscript [17]. Briefly, the protocol included the addition of HSA to the aqueous stock of the PPs at varying molar ratios. Under these conditions the DMSO content is reduced further so that undesired interactions with HSA can be ruled out. After equilibration in the dark for 1 hour at room temperature, the solutions were dialyzed for 48 hrs using a 12 kDa cut-off pore size kit (Sigma-Aldrich, St. Louis, MO) and subsequently centrifuged for 5 minutes at 11.5 g, using an Eppendorf MiniSpin Plus centrifuge (Hauppauge, NY). After centrifugation ~ 2 ml of the supernatant were collected in a 1 cm optical path quartz cuvette for spectroscopic measurements. This protocol yields solutions with optical density (OD) between 0.1–0.5 for both the maximum of the absorption of the porphyrins (370–420 nm) and that of the aromatic amino acids of HSA (~ 278 nm). The actual values of the absorption maxima were used to determine the concentration of HSA and monomerized porphyrins in the remaining samples (see below).

2.4. UV-Vis Absorption Spectroscopy.

Absorption spectra of the solutions were recorded with a Cary-100 UV-Vis spectrophotometer (Agilent Technologies Inc., Santa Clara, CA) at a speed of 300 nm/min and spectral resolution of 1 nm. Typical absorption spectra were carried out in 1 cm quartz cells (FireflySci, Brooklyn, NY) and recorded between 250 and 700 nm in order to include the region of the aromatic amino acids of HAS (250–310 nm), as well as the Soret band (350–450 nm) and the region of the Q-bands bands (420–700 nm) of the PPs. All measurements were baseline corrected with the appropriate reference solutions.

2.5. Steady-State Fluorescence Spectroscopy.

Fluorescence spectra were collected using a Perkin-Elmer LS-55 fluorimeter (Perkin Elmer, Waltham, MA). Spectra were recorded in a 1 cm, four-clear side quartz cuvette (FireflySci, Brooklyn, NY) at 1.5 nm/sec with bandwidth of 4 nm both in excitation and emission. Emission of HSA was recorded in the 305–450 nm range upon excitation at 294 nm. This excitation wavelength predominantly excites the lone Trp214 residue of HSA, located at the bottom of the central cleft [25]. In order to ensure a linear response of the instrument and avoid artifacts, the concentration of the samples used for fluorescence experiments was adjusted to ensure an optical density (OD) at the excitation wavelength < 0.15. All fluorescence spectra were corrected and normalized as explained in the Supplemental Information (Section S.1) using the corrections (e.g., inner filter effects) suggested in recent seminal reviews [26, 27].

2.6. Fluorescence Quenching.

The quenching produced by the PPs on the fluorescence of HSA (i.e., Trp214) was investigated by preparing samples with increasing concentrations of PP to a solution containing ~ 10 μM HSA prior to dialysis and centrifugation. Although the process does not allow to precisely set the final concentration of the bound PP, it does produce samples of HSA:MePP complexes with an increasing concentration of PP and almost identical concentration of the protein. The emission spectrum of HSA was recorded for each sample as explained above and the emission intensity was analyzed using the Stern-Volmer equation [24]

$$\frac{F_0}{F}=1+K_{SV}\left[Q\right]$$ (1)

where F₀ and F are the fluorescence intensities (corrected according to equation S1, Supplemental Information) in the absence and presence of a concentration [Q] of quencher (i.e., PPs) and K_SV is the Stern-Volmer constant. This concentration was obtained from the optical density of the maximum of the Soret band using Beer-Lambert law (see below).

2.7. Time-resolved fluorescence lifetime.

Fluorescence lifetime experiments were recorded with a time correlated single photon counting (TCSPC) system (5000U, Horiba JobinYvon, Edison,NJ) which uses a pulsed source with a fixed repetition rate of 1 MHz and pulse width of ~ 700 ps (NanoLED 294, Horiba Sci., Edison, NJ ) that preferentially excites Trp214 at 294 nm. The emission decay was recorded at 334 ± 8 nm corresponding to the region of the maximum of HSA fluorescence. The decay data were analyzed using the deconvolution software DAS 6.2 (IBH, Glasgow, U.K.), which yields the value of the fluorescence lifetimes (τ_i) and their fractional amplitude (α_i) through a re-convolution algorithm between the time profile of the pulsed source, whose principles were explained in detail elsewhere [28]. The quality of the fitting is judged by i.) the value of the reduced χ² (target ~1.0–1.5), ii.) the visual inspection of the residuals, and iii.) the value of the Durbin-Watson parameter (target ~1.8–2.0) [29]. Data analysis is typically carried out with one, two or three lifetime components according to the assumption of a multi-exponential decay (equation 2):

$$I\left(t\right)={\sum }_i{\alpha }_i{e}^{\frac{-t}{{\tau }_i}}$$ (2)

The best fitting (based on the criteria above) that uses the fewest decay components was selected. From the individual components (α_i, τ_i), the average decay lifetime was calculated as [24]

$$\langle \tau \rangle ={\sum }_i{\alpha }_i{\tau }_i$$ (3)

2.8. Förster Resonance Energy Transfer (FRET).

Energy transfer occurs as a result of long range dipole–dipole interactions between and energy donor and an energy acceptor chromophore [30, 31]. A common application of FRET is the measurement of the distance between donor and acceptor [32, 33]. In the case of our experiments evidence was collected that demonstrates the occurrence of FRET between the Trp214 residue (donor) of HSA and the MePP ligands (acceptor). According to Förster’s theory one can define a standard distance (i.e., Förster’s radius) between donor and acceptor by calculating the integral J(λ) which quantifies the spectral overlap between emission of the donor and absorption of the acceptor (Figure S1, Supplementary Information). This integral is then used to estimate the Förster’s distance R₀ (in Å) according to [24]:

$$R_0=\sqrt[6]{8.8\cdot {10}^{-5}{k}^2{n}^{-4}{\varphi }_{D}J\left(\lambda \right)}$$ (4)

where n is the refractive index of the medium (in this case the estimated average refractive index of proteins, ~ 1.38 [34]), φ_D is the emission quantum yield of the donor (~ 0.13 for Trp214 [35]) and k² is a factor that accounts for the relative orientation of the transition dipole moments of the donor and the acceptor [36] (Section S.2.3, Supplemental Information). Typically, this last term is taken as the isotropic average which yields $k^2=\frac{2}{3}$. However, we will discuss in the next section that this value should be corrected when considering amino acid residues and protein ligands that have sterically restricted orientations. Once the value of R₀ is obtained, the estimate of the distance, r, between the donor and acceptor is retrieved using the following two expressions:

$$E=1-\frac{\langle {\tau }_{DA}\rangle }{\langle {\tau }_D\rangle }$$ (5)

$$r^6=R_0^6\frac{1-E}{E}$$ (6)

where E is the transfer efficiency, while ⟨τ_DA⟩, and ⟨τ_D⟩ are the average fluorescence decay lifetime of Trp214 in the presence and in the absence of the PPs [24]. However, a correction of equation 5 is required when using molecules that are interacting non-covalently, whereby a fraction of the HSA molecules (donor) in solution is bound to a PP molecule (acceptor). The correction is provided by the use of fractional labeling [24], $f_A=\frac{\left[boundHSA\right]}{\left[totalHSA\right]}$, which represents the ratio between the concentration of the HSA/PP complex and the total concentration of HSA. is applied to equation 5 to yield [24]

$$E=\left(1-\frac{\langle {\tau }_{DA}\rangle }{\langle {\tau }_D\rangle }\right)\frac{1}{f_A}$$ (7)

which provides the corrected FRET efficiency. The value of f_A was extrapolated from the UV-Vis spectra of the HSA/PP complex as described in the Supplemental Information (SectionS.2.2).

2.8.1. Orientation factor.

As anticipated above, a major variable in determining R₀ (equation 4) is the factor κ² which accounts for the relative orientation between the transition dipole moments of the donor and the acceptor. The value of κ² is defined as the average [36]

$$k^2=\langle {\left[cos\left(\alpha \right)-3cos\left(\beta \right)cos\left(\gamma \right)\right]}^2\rangle$$ (8)

where the angles are represented in Figure S2 (Supplemental Information). The assumption that $k^2=\frac{2}{3}$, is correct only when α, β and γ have equal probability of varying between 0 and 4π [36]. However, when FRET occurs between an aromatic amino acid (especially one relatively buried like Trp214) and a non-covalent ligand, it is likely that neither the donor nor the acceptor molecules are free to rotate with respect to each other over the 4π range because of steric restriction of their motion. Such restriction can have a dramatic effect on the value of κ² [24]. Such large variability can introduce significant uncertainty on R₀ and, in turn, on r (see section S 2.3 in Supplemental Information). In order to reduce such uncertainty, we introduced an approach whereby computational docking simulations (see section 2.6) were carried out to extract a more precise range of angles and derive a more accurate estimate of κ² for equation 8. A detailed description of how the angles were calculated from the docked conformation can be found in section S.2.3 of the Supplemental Information. The new values of κ² (Table S2, Supplemental Information) were then used to recalculate R₀ and obtain a more precise estimate of the donor-acceptor distance.

2.9. Computational Docking Simulation.

In order to predict more accurate binding configurations between HSA and the various MePPs we performed docking simulations with AutoDock 4.2.6 [37] and used the experimental data to guide the choice of the most likely docked structures. The Protein Data Bank file ID 1N5U was used for the coordinates of the atoms in HSA. Hemin and the myristic acid ligands [38] were removed from the coordinate file using AutoDockTools 1.5.6. The ground-state structure and parametrization of each PP was created using Spartan 10 (Wavefunction Inc., Irvine, CA). The PP macrocycle was built using the appropriate orbital hybridization structure for C, N, H and O. Thereafter, the metal atom e.g., Zn, Fe, etc., were inserted by selecting the element with corresponding atomic hybrid and bond type from the inorganic model kit. The structure of the ground state of the PP ligand was retrieved by the global energy-minimization obtained using the PM3 semi-empirical model of Spartan 10. The structure that yielded the lowest global energy was chosen and the coordinates of all the atoms and the parametrization of the bonds and partial charges were used as the starting structure for the docking simulations.

The preparation of HSA and PP molecules as well as the settings for the docking simulations were described in a previous manuscript [39]. Conversely, the position of the center of the simulation box and the starting position of the PP were modified to probe three of the hypothesized metal-binding locations: i.) between Tyr138 and Tyr161, ii.) at the coordinates of the sulfur atom of Cys 34 or iii.) between the nitrogens of His67 and His247 (Table S3, Supplemental Information). For the docking simulations we utilized the Lamarckian Genetic search algorithm executed over 15 runs with a population size of 200, a maximum number of evaluations of 3 × 10⁷, and a maximum number of generations of 4 × 10⁷. Autodock uses a grid map with precalculated interactions for each atom type which treats the protein as rigid. For the PP ligands, the aromatic bonds are also treated as rigid while the dihedrals can be rotated. The best docked configurations were selected using the total binding energy (as estimated by Autodock) corrected for the internal energy of the ligand (also estimated by Autodock) to include the energy penalty of the ligand created by the imposed rigidity of the aromatic bonds in the porphyrin macrocycle. For each run the 10 best docking configuration were retained and clustered based on the position of center of mass of the porphyrin (i.e., to be considered part of a cluster, the center of mass of the porphyrin had to be within 4Å which is the estimated “radius” of the porphyrin macrocycle if treated as a disk [40]).

2.10. Analytical Ultracentrifugation (AUC).

We have recently reported a method used to analyze the effectiveness of the protocol described in section 2.3 for the recovery of HSA:MePP complexes from the solutions containing PP aggregates and described how AUC can be used to determine the molar extinction coefficient of the bound MePP. [22] This was an important breakthrough since, until then, the independent estimate of the molar extinction coefficient of the bound ligand could not be obtained. The details of the AUC experiments are described in that manuscript. Succinctly, experiments were performed on a Beckman Proteomelab XLI at the Center for Analytical Ultracentrifugation of Macromolecular Assemblies (CAUMA) at UT Health San Antonio. The experiments measured the sedimentation velocity by recording the optical density of the samples at 280 nm and 410 nm (368 nm for HSA:MnPPIX) in separate runs, using epon 2 channel centerpieces fitted with quartz windows, while centrifuging the sample at 45,000 rpm and 20 °C until pelleted. Data analysis was performed with UltraScan release 2130 [41] which utilizes the Lonestar-5 system at the Texas Advanced Computing Center (TACC). The sedimentation velocity data were initially fitted with the two-dimensional spectrum analysis [42, 43] to remove time- and radially invariant noise from the raw data, and to fit the meniscus position. Subsequently, the data were analyzed with the parametrically constrained spectrum analysis using straight-line parametrization [44] (see Figure 2), and the enhanced van Holde – Weischet method [45]. This approach provides diffusion-corrected, model-independent sedimentation distributions (see Figures S4 and S5, Supplemental Information). Buffer density and viscosity were estimated with UltraScan based on buffer composition and all hydrodynamic values were corrected for standard conditions (20°C and water). All sedimentation coefficients are represented in Svedberg units of 10⁻¹³ s.

Figure 2.

(A) Sedimentation coefficient distributions of sample measured at 280 nm. Red: Zn(II)PPIX/has; green: Fe(III)PPIX ; blue: Mg(II)PPIX/HSA; black: Mn(III)PPIX; magenta: Sn(IV)PPIX. (B) Distribution of sedimentation coefficients of sample with detection at the peak of the Soret band. Red: Zn(II)PPIX/has (402 nm); green: Fe(III)PPIX (405 nm); blue: Mg(II)PPIX/has (388 nm). (C) Sedimentation of HSA alone under the same condition of the samples in A and B, but measured at 280 nm

3. Results and Discussion.

3.1. Elimination of Aggregates of Protoporphyrins in Aqueous Solution.

One of the major challenges presented by working with aqueous solutions of PPs is their tendency to form aggregates at neutral pH and physiological ionic strength [18, 19, 46, 47]. PPs aggregates can be identified spectroscopically by the presence of broad absorption spectra with multiple peaks and shoulders in the 350–450 nm region. These features strongly interfere with optical experiments and hinder the ability to quantify the binding parameters [21, 47]. As mentioned above, we have recently reported a protocol whereby a sequence of dialysis and centrifugation was used to remove the organic solvent (i.e., DMSO) and recover aqueous solutions that contain (virtually) only free HSA and HSA:MePP complexes without the presence of porphyrin aggregates. Notably, this preparation yields the complexes without introducing factors that would limit the spectroscopic experiments (such as organic solvents or extremely alkaline pH) [17, 22]. The crucial breakthrough of the protocol is that solutions containing the complexes without interference from aggregated MePPs enables the quantification of key parameters and improves the structural model and understanding of the binding in an aqueous environment.

3.1.2. UV-Vis Spectroscopy.

3.1.2.1. Hemin (Fe(III)PPIX(Cl)).

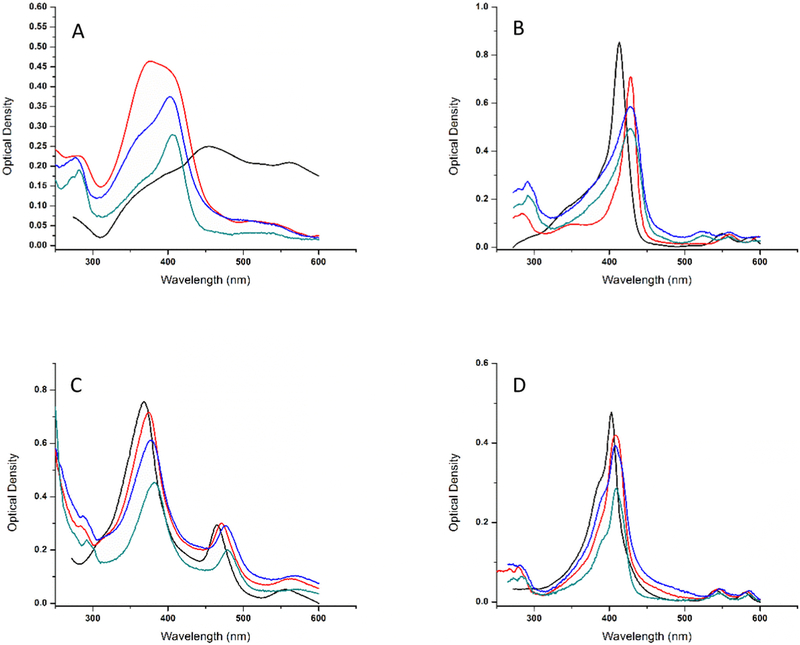
When transferred from the concentrated stock in DMSO to water, Fe(III)PPIX(Cl) shows a nearly featureless spectrum with broad peaks indicative of the prevalence of polydispersed aggregates (Figure 1A). The same figure shows that addition of HSA produces broad bands in the 368 – 600 nm range which indicates that large aggregates still dominate the sample. After dialysis for 48 hours, an absorption peak at 402 nm emerges accompanied by a shoulder near 352 nm. After centrifugation, the main peak at 402 nm remains while the contribution of the absorbance typically seen for aggregates (352 nm) reduces. The effect is similar to what we observed with metal-free and Zn(II)PPIX [17] and leads to the same interpretation: after addition of HSA, dialysis and centrifugation most of the aggregated forms of hemin have been eliminated, leaving a prevalent population of HSA:Fe(III)PPIX complexes.

Figure 1.

Representative UV-Vis spectra of (A) Fe(III)PPIX(Cl); (B) Mg(II)PPIX; (C) Mn(III)PPIX; (D) Sn(IV)PPIX as a function of the preparations steps used to eliminate the contribution of porphyrin aggregates. Initial PP concentrations were 2.6 μM (A), 4.6 μM (B), 4.1 μM (C) and 1.4 μM (D). For each PP the following spectra are represented: PP in aqueous solution (black); PP in the presence of HSA before dialysis: {HSA concentration = 6.8 μM (A), 8.8 μM (B), 10 μM (C) and 2.9 μM (D)} (red); the same sample after 60 hours dialysis (blue) and the dialyzed sample after 5 minutes centrifugation (green).

3.1.2.2. Mg(II)PPIX.

The absorption spectrum of Mg(II)PPIX in aqueous solution is already characterized by a very distinguishable Soret band at 413 nm (Figure 1B) consistent with better monomerization of the PP. The shoulder at ~ 350 nm is indicative of the residual presence of aggregates. Addition of HSA causes the spectrum to undergo a bathochromic shift (Figure 1B) (to 428 nm) and a narrowing of the Soret band. This effect indicates binding to HSA. Since the Soret band is already so well defined, dialysis and centrifugation do not provide improvement of the spectrum. indicating that the HSA:Mg(II)PPIX complex may already be efficiently formed without the interference from aggregates even before any other steps in the protocol.

3.1.2.3. Mn(III)PPIX.

Compared to other porphyrins, the absorption spectrum of Mn(III)PPIX shows a Soret band that is substantially blue-shifted (Figure 1C) and is in agreement with results obtained by other groups [48]. The peak undergoes a small bathochromic shift after each preparation step (368 → 373 nm after addition of HSA, 373 → 378 nm after dialysis, 378 → 382 nm after centrifugation). The absorption spectra also decrease in optical density after each step without changing the ratio (~ 8:3:1) between the three peaks (Figure 1C). A peak near 700 nm becomes more prominent after centrifugation. The bathochromic shift of the spectrum in the Soret band region suggests that our protocol is able to separate the aggregated Mn(III)PPIX from the HSA:Mn(III)PPIX complex consistent with the spectrum of Figure 1C [48].

3.1.2.4. Sn(IV)PPIX.

The spectra of Sn(IV)PPIX and HSA mixtures show a similarity to the spectra observed for Mg(II)PPIX and HSA. Addition of HSA to the PP in aqueous solution causes a bathochromic shift from 403 nm to 408 nm of the Soret band which is not affected in position by dialysis or centrifugation. A shoulder at the shorter wavelength (~ 390 nm) becomes more distinctive after the last two steps. The interpretation is that the contribution of aggregated Sn(IV)PPIX is already small in aqueous solution and the bathochromic shift indicates the almost exclusive presence of the HSA:Sn(IV)PPIX complex.

A common feature across the various PPs is the decrease in optical density after each preparation step, which can be explained by the overall loss of material (i.e., aggregated PP, HSA and HSA:PP complexes) that may remain attached to the membrane or the tubes in the dialysis or may be incompletely recovered after centrifugation.

All of the spectra after centrifugation (Figure 1) provide simultaneously the intensity of the peak of the Soret band of the monomeric PPs bound to HSA as well as the peak of the absorption of the aromatic amino acids (278 nm). The values of these two peaks yielded the total concentration of HSA as well as the bound monomeric PPs by use of the Beer-Lambert equation. For the Beer-Lambert equation we used molar extinction coefficients of 3.4 × 10⁴ at 278 nm for HSA (as an approximate average value over several dozens cited in the literature[49]) and the values reported in Table S1 (Supplemental Information) for the PPs. The concentrations then enabled us to obtain the value of (Section S.2.2 of the Supplemental Information) in equation 7.

Overall, the UV-vis data suggest that in analogy with metal-free and Zn(II)PPIX [17], the dialysis and centrifugation protocols nearly eliminate aggregated PPs (indicated by the disappearance of featureless spectra and the appearance of well-defined Soret bands) and yield solutions that contain almost exclusively HSA:PP complexes (indicated by the significant bathochromic shifts), together with free HSA. Formation of HSA:Mg(II)PPIX, HSA:Mn(III)PPIX and HSA:Sn(IV)PPIX complexes are evident even before dialysis and centrifugation. Conversely, the isolation of the HSA:Fe(II)PPIX complex requires the elimination of large aggregates through dialysis and centrifugation. Although qualitatively significant, the UV-Vis data alone do not provide definitive proof that aggregated PPs have been eliminated from the solution. Therefore, we carried out AUC experiments in order to better quantify the amount of aggregated PPs present in solution.

3.1.3. Analytical Ultracentrifugation (AUC).

AUC experiments provide direct information about the size distributions of the species in solution, and can separate components based on mass, anisotropy and density. As the absorption spectra show (Figure 1) PP aggregates absorb strongly in the violet region of the spectrum where HSA does not absorb (i.e., > 300 nm). Thus, by following the sedimentation pattern at 280 nm (where HSA absorption is dominant) and at 410 nm (where only the PP contribute), one can distinguish the HSA:MePP complexes from the free as well as aggregated PP. Sedimentation coefficient distributions, derived from the enhanced van Holde-Weischet method, were used to quantify the amount of aggregated, free and bound PP and HSA.

3.1.3.1. Zn(II)PPIX, hemin and Mg(II)PPIX.

With detection at 280 nm the chromatogram-like boundary fraction shows only one plateau boundary line of the sedimentation coefficient with comparable values for all four PP (Figure S3, Supplemental Information). The histogram of the g(s) distribution plot (Figure 2A) consistently shows a major peak centered at sedimentation coefficients 4.2 × 10⁻¹³ s (HSA:Zn(II)PPIX), 4.3 × 10⁻¹³ s (HSA:hemin) and 4.4 × 10⁻¹³ s (HSA:Mg(II)PPIX) as well as smaller peaks at lower and higher values of g(s). The measurements in Figure 2A were taken at 280 nm where HSA is the only significant contributor to absorption. In comparison with the same histogram obtained from apo-HSA (Figure 2C) at the same detection wavelength, one can infer that the major peak is consistent with the sedimentation of HSA (which is slightly larger in the complex compared to the free protein). The minor peaks at smaller and larger values of sedimentation are likely due, respectively, to fragmented apo-HSA (which might be present in the original sample) and small amounts of aggregated protein [50]. The same samples with detection at 410 nm show chromatograms and distribution plots (Figure 2B) that are virtually identical to the ones shown by the 280 nm detection. Since at 410 nm the only contribution to the optical absorption can be safely assumed to be generated by the PPs, the evidence indicates that HSA:Zn(II)PPIX, HSA:hemin and HSA:Mg(II)PPIX sediment with nearly the same coefficient as monomeric apo-HSA. The data reveal that after dialysis and centrifugation one retrieves samples containing predominantly the HSA:PP complexes with <15% apo-HSA. The plots of Figure 2B also show a small peak near 1 × 10⁻¹³ s which we interpret being due to some remaining monomeric or oligomeric PPs. The substantial elimination of PP aggregates is also supported by the integral distribution plots (Figure 2) which show the presence of significant amounts of aggregates before dialysis and centrifugation but virtually no aggregates after the procedure. Integration of the peaks enabled us to estimate that in all three cases HSA:MePP form > 90% of the solution (from < 20% before the procedure) and we thus assumed that interference from the aggregated MePP became negligible for spectroscopic measurements.

3.1.3.2. Mn(III)PPIX and Sn(IV)PPIX.

The experiments with detection at 280 nm shows results comparable with the ones obtained for the other porphyrins (single boundary and single-peak g(s) distribution) at values (4.5 ± 0.3 ×10⁻¹³ s) identical for both porphyrins (Figure 2A, Figure S3 and S4, Supplemental Information). Once again this is in agreement with the sedimentation of monomeric HSA. The detection at 410 nm, however, presents some important differences with the other porphyrins. The peaks are clustered around the same 4.5 × 10⁻¹³ s value (Figure 2C), however there appear to be more prominent peaks near this region which might be an indication of aggregation of the protein. More important, in both cases, the boundary fraction is bimodal and translates into the presence of a second prominent peak near 1.4 ± 0.2 × 10⁻¹³ s (Figure 2C). The presence of the peaks near 4 s are evidence that both PPs are bound to HSA, whereas the first peak indicates the presence of a much smaller species in solution which we attributed to monomeric and/or oligomeric PPs since it is only apparent at 410 nm where the porphyrins absorb. The integration of the peaks estimated that in these cases (as well as in the case of metal-free PPIX [22]) HSA:MePP form > 95% of the solution making any contribution from aggregated porphyrins to the spectroscopic measurements negligible.

The AUC data therefore validate the interpretation of the UV-vis spectra. The protocol we adopted virtually eliminates the large aggregates of metal-free PP and MePPs. In fact, after dialysis and centrifugation samples appeared to be made for at least 90% of HSA:MePP complexes and the remaining contribution being from apo-HAS and only traces of aggregates. In the case of the assembly of HSA with Mn(III)PPIX and Sn(IV)PPIX the absorption spectra suggested that these molecules are substantially monodispersed (narrow Soret band in Figure 1) even before the addition of apo-HSA or the subsequent sample preparation. AUC validates this interpretation through the presence of an abundantly populated species with low sedimentation coefficient (< 1.5 × 10⁻¹³ s). In both porphyrins this peak decreases in intensity with the addition of the protein and subsequent dialysis and centrifugation, therefore validating that these two PPs are more soluble in aqueous solution but still bind as monomers to HSA (Figure 2C). In fact, in agreement with the UV-Vis absorption these samples showed > 95% presence of the complex even before centrifugation. The comparison of the position of the smaller peaks in the sedimentation coefficient distributions offers further insights. The sample containing apo-HSA (Figure 2C) at conditions identical to the ones containing the PPs, shows only two small peaks at ~ 2 × 10⁻¹³ s and ~ 6.5 × 10⁻¹³ s which have values within the experimental noise. Since the ~ 6.5 × 10⁻¹³ s peak appears in nearly all the AUC plots combined with the fact that its intensity is close to experimental noise may indicate that this peak may be originated by the instrument.

3.2. Fluorescence Quenching.

Binding can often be validated and quantified using the quenching caused by a ligand, which changes the emission of the protein. [51, 52] In the case of the PPs investigated here, there are some common aspects to the quenching results. As expected, the addition of the PP creates an increase in the optical density of the Soret band (350–420 nm), however, more relevant to the quenching experiments is the UV-vis spectrum in the region < 310 nm given that HSA fluorescence is prompted by the excitation of the Trp214 residue at 294 nm. In the UV region of the spectrum there are two contributions with opposite trends: the decrease of the optical density of the aromatic amino acids of HSA (caused by the dilution produced by the addition of the PP aliquots), and the increasing residual absorption (i.e., the low-wavelength tail of the Soret band) caused by the addition of PPs. One must, therefore, separate the contribution of the Trp residue and the porphyrin ligand in order to properly normalize and analyze the emission of HSA. In addition, contributions from the emission spectra of the porphyrins can be ignored since these molecules emit > 550 nm (thus beyond the region analyzed for quenching of HSA) as shown in section S7 of the Supplemental Information. The separation of the contributions is explained in detail in section S.1 of the Supplemental Information.

The emission spectra show that the addition of the PPs produces a marked quenching of the fluorescence of HSA and induces a small (~ 2–3 nm) hypochromic shift (Figure 3). The latter effect can be explained either by a change of the environment of the Trp214 residue or to a relative increase of the contribution of Tyr residue to the emission. A better understanding of this effect will be gained later through the discussion of the behavior of the fluorescence decay of HSA.

Figure 3.

Emission spectra of HSA (λ_ex294nm) as a function of the PP (A) Fe(III)PPIX(Cl) [0–7.8 μM]; (B) Mg(II)PPIX [0 – 4.8 μM]; (C) Mn(III)PPIX [0 – 4.7 μM]; (D) Sn(IV)PPIX [0 – 1.3 μM]. The intensity of the spectra decrease with increasing the concentration of the PPs and is accompanied by a hypsochromic shift of the emission maximum.

The corrected emission spectra of HSA (section S.1 in Supplemental Information) yields linear S-V plots (Figure 4). Compared to other porphyrins, the quenching produced by Fe(III)PPIX and by Mn(IV)PPIX show a slightly more scattered plots and a slight deviation from linearity. Because of this evidence we also carried out a non-linear fitting according to established procedures [24], however as discussed in section S6 of the Supplemental Information, the fitting yielded unphysical values for the quenching constants. In both cases we suspect that the effect is due the fact that our method may underestimate the contribution to the absorption of these two PPs at 294 nm (section S.1, Supplemental Information). From the plots one can retrieve quenching constants that are summarized in Table 1. One observes that the quenching rate of Fe(III)PPIX and Mn(III)PPIX are the largest. They are 2–20 - fold larger than for the other PPs. The magnitude of the quenching constant, does not seem to correlate with either the size or the coordination number of the metal (Table 1). Fe and Mn have the same oxidation number, yet the correlation with the quenching rate does not appear to be sufficiently strong since the rate decreases for both smaller oxidation state (Zn and Mg) and the larger oxidation state metal (Sn). This evidence suggest that quenching efficiency is related to other effects as will be discussed below.

Figure 4.

Stern-Volmer plots for the quenching of HSA emission by the PPs. (■) PPIX; (●) Zn(II)PPIX; (▲) Fe(III)PPIX(Cl); (♦) Mg(II)PPIX; () Mn(III)PPIX; () Sn(IV)PPIX. HAS concentration was ~ 5.5 μM; λ_ex = 294 nm.

Table 1.

Stern-Volmer constant for the quenching of HSA by various PP. Under the assumption of static quenching these constants are identical to the apparent binding constant.

Quencher	KS-V [Kb]	Atomic radius/ Coordination number
PPIX	0.85 ± 0.08 × 106 M−1	0
ZnPPIX	0.11 ± 0.05 × 106 M−1	1.31/4
FePPIX	1.55 ± 0.09 × 106 M−1	1.25/6 or 4
MgPPIX	0.60 ± 0.06 × 106 M−1	1.30/6
MnPPIX	2.13 ± 0.07 × 106 M−1	1.39/6
SnPPIX	0.43 ± 0.07 × 106 M−1	1.45/4

The linearity of the S-V plots carries the intrinsic ambiguity between collisional and static quenching mechanisms [24]. However, we have previously demonstrated [39, 53] that under similar conditions of temperature and concentrations, collisional quenching would require a diffusion constant of HSA and/or of the PPs that is 2 order of magnitude larger than what has been experimentally established [54, 55]. Therefore, we conclude that the quenching is produced by the formation of HSA:PP complexes (in agreement with the UV-vis absorption data) at a location that decreases the fluorescence of Trp214.

So far, the observation of the changes in the UV-Vis spectra of the PPs in the presence of HSA as well as the quenching experiments, support the evidence of binding between monomeric PPs and the protein. However, other details of the binding must be refined using other techniques as discussed in the following sections.

3.3. Docking Simulations.

Docking simulations are often used to investigate possible binding pockets of small ligands on proteins. Non-docked simulations (i.e., simulations in which the ligands are not placed already at the binding site) however, often provide non-unique solutions whereby multiple potential binding sites are retrieved and ranked. Different strategies have been employed to determine the most likely binding configurations out of these multiple outcomes. Often, these approaches are based on additional refined simulations or statistical analysis of the large number of binding conformations. [56–58]. We employed a different approach whereby we used experimental fluorescence data to interpret the ranked docked conformation and identify the most likely binding site for each PP [59]. This method also allowed us to estimate the average orientation of the PP transition dipole moment relative to that of Trp214 and use this information to refine the calculation of κ² (section 3.4 and S2.3 in the Supplemental Information) in FRET analysis. With this method one uses a double feedback approach between computational and experimental data to obtain the most likely location of the bound PPs ligands.

As explained in section 2.7, we limited the search for docking conformations to regions postulated to coordinate metals, with the exception of the ATCUN for the reasons explained before. Also, we were unable to characterize the docking of Sn(IV)PPIX because the proper parametrization of Sn for the simulations could not be established.

The docking simulations showed that, energetically (Table 2), the most favorable docking configuration places all PPs at the site attributed to hemin (Figure 5 and Figures S4 and S5) [38]. In this conformation, the porphyrin ring is virtually parallel to the phenyls of the two Tyr residues. Approximately 80% of the docking configurations retrieved for this site are clustered at this position (Figure S6 through S8, Supplemental Information). The simulations suggest that, besides the coordination with Tyr138 and Tyr161, the binding is stabilized by contacts of the vinyl groups of the PPs with the Phe134, Leu115, Leu135 and Ile142 residues inside the pocket. In addition, at the opening of the pocket the carboxyl tails of the PPs interact with three positively charged residues (Arg114, Arg186 and Lys190). All these favorable interactions produce binding energies that are 8–10 kcal/mol more favorable than the other metal-coordinating sites (Table 2) such as Cys34 or the His67/His247 pair. The less favorable energy for these sites appears to be produced by the lack of additional favorable electrostatic contacts between the PPs and other residues. In addition, docking simulations at Cys34 and His67/His247 sites returned < 60% of clustered conformations which indicates a lower consensus on the binding prediction.

Table 2.

Docking binding energy for the three different metal binding site as obtained from Autodock simulations.

Ligand	Binding Energy Tyr138-Tyr161 (kcal/mol)	Binding Energy Cys34 (kcal/mol)	Binding Energy His67-His247 (kcal/mol)
PPIX	− 15.2 ± 1.2	− 5.5 ± 0.5	− 4.0 ± 0.8
Zn(II)PPIX	− 16.7 ± 0.7	− 7.5 ± 0.7	− 7.5 ± 0.6
Fe(III)PPIX	−17.5 ± 0.5	− 6.5 ± 0.5	− 5.6 ± 0.7
Mg(II)PPIX	− 17.4 ± 0.2	− 7.9 ± 0.5	− 8.6 ± 0.7
Mn(III)PPIX	−17.9 ± 0.5	− 6.0 ± 0.4	− 5.2 ± 0.6
Sn(IV)PPIX	N/A	N/A	N/A

Figure 5.

Representative lowest energy binding configuration for Mg(II)PPIX and HSA at the heme binding site. Panel (A) shows the interaction between the PP and several amino acid residues that contribute to the energy minimization. Aromatic amino acids (Tyr138, Tyr161 and Phe134) are in green, aliphatic amino acids (Leu115, Leu135 and Ile142) are in orange and cationic residues (Arg114, Arg186 and Lys190) are in blue. Panel (B) shows the porphyrin ring sandwiched between Tyr138 and Tyr161 (in green). Panel (C) shows the general location of the binding site within the HSA.

One can summarize the findings by observing that the heme-binding site yields by far the most energetically favorable energy configuration for all PPs. Nevertheless, as will be discussed in the next section, such location does not always match the experimental data we obtained. It is therefore possible that the energy of binding is underestimated for certain sites because the docking simulations do not include a proper metal coordination term (as it only considers the electrostatic contribution due to the metal ion).

As discussed earlier, the results of the docking simulations were also used to refine the value of κ² for FRET calculations (Equation 4). For each binding site that was explored, we used the clustered conformations (for example Figure S7, Supplemental Information) to calculate the average relative orientation between Trp214 (energy donor) and the PP ligands (energy acceptor). The average was then used, as explained in section S2.3 (Supplemental Information), to retrieve a more realistic estimate of the value of κ² (see section 3.4).

3.4. Fluorescence Lifetime and FRET.

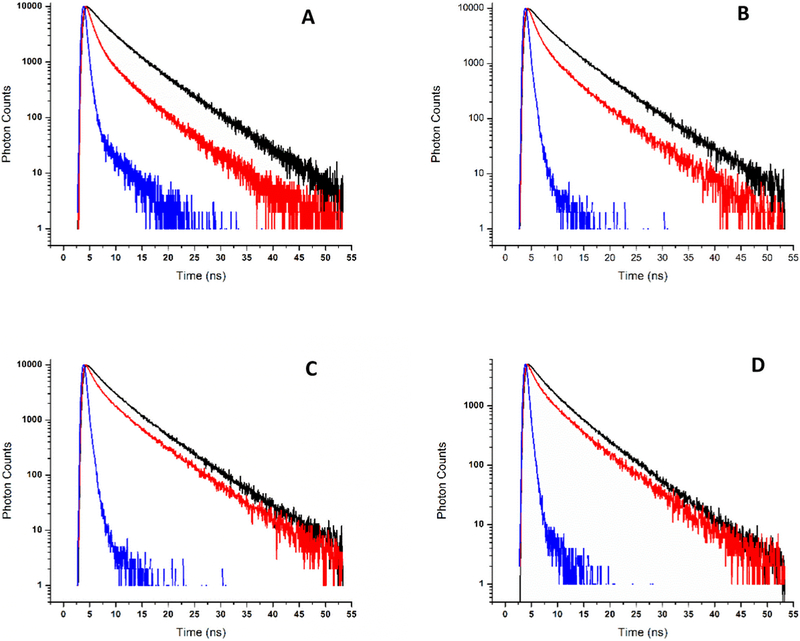
The decay lifetime of HSA was best fitted with 3 exponential components (Equation 2) which included a short (τ₁ < 1ns), an intermediate (τ₂ 2.8ns) and a longer-lived (τ₃ 6.5 ns) contribution. Using the parameters from the three components (equation 3) one obtains an average decay lifetime, ⟨τ⟩ = 5.2 ± 0.2ns for free HSA which is in agreement with previous results [51, 60]. The addition of the PPs causes a faster fluorescence decay (Figure 6) and a smaller value of ⟨τ⟩ (Table 3 and Table 4). Upon closer inspection of Table 3 one notices that the effects are distributed among the components of the decay. All three lifetime components decrease, however, since τ₁ is at the limit of the temporal resolution of the instrument, the change of τ₁ is within experimental uncertainty. As the lifetimes decrease, a change in their relative contributions is apparent, characterized by a large (typically > 5-fold) increase in the value of α₁, which causes a decrease in α₂ and α₃ (since α₁ + α₂ + α₃ = 1). The increase of α₁ is largely due to the decrease in the overall emission intensity of HSA which causes the relative increase in detection of photons generated by Rayleigh scattering, as discussed in a previous manuscript [39].

Figure 6.

Fluorescence decay of HSA [~ 5.5 μM; λ_ex = 294 nm] upon addition of PP. (A) Fe(III)PPIX(Cl) [7.8 μM]; (B) Mg(II)PPIX [4.8 μM]; (C) Mn(III)PPIX [4.7 μM]; (D) Sn(IV)PPIX [1.3 μM].

Table 3.

Fluorescence decay parameters (Equation 2) of HSA (i.e., Trp214) in the absence and in the presence of the maximum amount of each PP.

	α1	α2	α3	τ1 (ns)	τ2 (ns)	τ3 (ns)	Ave Lifetime <τ> (ns)
HSA	0.04	0.33	0.62	0.54	3.01	6.66	5.17
HSA-Hemin	0.25	0.35	0.40	0.43	1.47	5.70	2.67
HSA-Zn(II)PPIX
HSA-Mg(II)PPIX	0.15	0.39	0.46	0.29	1.33	5.49	3.08
HSA-Mn(III)PPIX	0.13	0.28	0.59	0.24	1.75	6.19	4.19
HSA-Sn(IV)PPIX	0.12	0.25	0.63	0.17	1.61	5.93	4.16

Table 4.

Fluorescence lifetime and corrected efficiency for FRET between Trp214 and each PP ligand^a.

Sample	⟨τD⟩ (ns)	⟨τDA⟩ (ns)	fA	Ec(%)
HSA-PPIX	4.80	3.58	0.59 ± 0.08	0.43 ± 0.10
HSA-ZnPPIX	“	4.10	0.37± 0.16	0.39 ± 0.05
HSA-Hemin	“	3.06	0.53± 0.12	0.68 ± 0.16
HSA-Mg(II)PPIX	“	3.38	0.70 ± 0.14	0.42 ± 0.10
HSA-Mn(III)PPIX	“	4.10	0.50 ± 0.12	0.29 ± 0.04
HSA-Sn(IV)PPIX	“	3.88	0.96 ± 0.10	0.20 ± 0.03

^aThe table reports the amplitude-weighted average lifetime of HSA (τ_D) and HSA-Fe(III)PPIX(Cl)/ Mg(II)PPIX/ Mn(III)PPIX/ Sn(IV)PPIX (τ_DA), the calculated values of energy transfer efficiency (E), the fractional labeling factor (f_A), the corrected energy transfer efficiency ^[47].

The decrease of emission decay at increasing porphyrin concentration could be an indication of possible collisional quenching between the PPs and HSA [24]. However, as discussed above, under the condition of our experiments (i.e., μM concentrations) the possibility of a “collision” between a PP molecule and HSA during the fluorescence lifetime of the Trp214 residue (⟨τ⟩ ~ 5.0ns) is negligible. If the quenching is not collisional one can hypothesize a static mechanism [24]. However, when purely static quenching occurs, changes in the decay would be limited to the τ₁ component, due to the increased relative contribution of scattering [39]. Thus, the fact that the values of τ₂ and τ₃ also change, is very significant because when binding of the quencher causes a decrease in fluorescence lifetime, it strongly suggests the occurrence of FRET between the protein chromophore (i.e., Trp214) and the quencher (i.e., PPs bound to HSA) [24]. This also explains the lack of correlation between the values of K_SV and the properties of the metal ions since FRET depends on other parameters (e.g., the value of J and κ² of equation 4). From equations 4 (and S2, Supplemental Information) one can use the spectral overlap (Figure S1, Supplemental Information) to calculate the Förster radius (R₀) for each Trp-PP donor-acceptor pair. A typical challenge for this calculation is the choice of molar extinction coefficient, ε, for the bound PPs [17]. This value is required to calculate the overlap integral, J (equation S2). Recently we were able to obtain the value of ε for two protoporphyrins bound to HSA [59] Although the exact value of was only obtained for bound Zn(II)PPIX and Sn(IV)PPIX, the similarities between the results suggest that they can be used to estimate J for other porphyrins. In fact, even though these values would be strictly correct only for estimating J for these two porphyrins, the dependence of the magnitude of the R₀ to $\sqrt[6]{J}$, translates into small effects of ε on the estimated magnitude of R₀ (Table S2, Supplemental Information).

Another refinement introduced by our method is the improved analysis of the value of κ² (equation 4). Initial values of R₀ that were obtained using the average value $k^2=\frac{2}{3}$ are summarized in Table 4. One notices that they vary in a small range between 29.7 and 35.9 Å, as one might expect given the similarity of the photophysical properties among various PPs. From the values of R₀ and the values of $\langle {\tau }_D\rangle$ and $\langle {\tau }_{DA}\rangle$ (Table 4) one estimates the FRET efficiency E (equation 5). After correction for the fractional labeling factor, f_A (Table 4, section S.2.2 (Supplemental Information)) in equation 7 one retrieves a more appropriate value of FRET efficiency, E_c (Table 4). The corrected efficiency yields (equation 6) a more accurate estimate of the distance, r, between the Trp214 residue and the bound PPs (Table 5). By inspecting the data in the table one observes that, when using the value $k^2=\frac{2}{3}$ one obtains values of r that are a poor fit in comparison with the distances evaluated by inspecting the HSA structure. In fact, in the case of Mn(III) and Sn(IV) the value of r exceeds the distance between the Trp214 residue and the furthest point on the surface of the protein, which was estimated using the Visual Molecular Dynamic (VMD) software [61] to be ~ 40 Å in the 1N5U.pdb file. As discussed earlier, the typical estimate of $k^2=\frac{2}{3}$ is strictly appropriate only if both donor and acceptor (i.e., their transition dipole moments) are isotropically oriented in space. However, the docking simulations show clustered conformations where the orientation of the plane of the PP macrocycle is virtually fixed in space (Figure S7 in Supplemental Information). Thus, the simulation results enable us to estimate a more realistic value of κ² whose effect is explained in detail in Section S.2.3 (Supplemental Information). The corrected values of κ² (for each PP) were then applied to equation 4 in order to produce a more accurate estimate of R₀. From this value we obtained a more accurate estimate of the distance and an increased confidence in our interpretation of the location of the PP ligands. The cluster of docked conformation at the Tyr161 position (i.e., heme site) yielded different values of κ² from the conformation at the Cys34 site or the His67. The values of obtained with the re-calculated κ² for each site are summarized in Table 5. This approach was also used to refine previous estimates for the HSA:PPIX (metal-free) and HSA:Zn(II)PPIX complexes [15]. The analysis of the data in Table 5 lead to several considerations. The comparison between the values of estimated by corrected FRET analysis and the ones estimated from the pdb structure of HSA (last row in Table 5) show that HSA:PPIX, HSA:Fe(III)PPIX and HSA:Mg(II)PPIX yield data that is consistent with a binding location at the Tyr138/Tyr161 site (heme binding site). FRET data for HSA:Zn(II)PPIX consistently returns an estimated distance > 32 Å which is closer in distance to the His67 site. On the other hand the Cys34 and His67 sites appear to be better fits for the FRET data of HSA:Mn(III)PPIX. The docking simulations at this site yield poorly clustered solutions. In fact < 30% of the docking conformations can be considered “clustered” (i.e., having an RMSD < 5 Å). The clustered conformations at this site show that the ring of Mn(III)PPIX makes contact with Cys34 as well as Pro35 and Phe36 while one of the propionyl tails makes contact with the same Arg114 that participates at the entrance of the heme binding site (Figure 7). Therefore at this location the driving elements of the interactions appear to be aromatic interactions of the porphyrin with the Phe and Pro rings as well as Coulomb interaction between the negatively charged propionyl tails and the positively charged Arg114. As we mentioned earlier the lack of parametrization prevented us from refining the FRET data for HSA:Sn(IV)PPIX which, in the absence of corrections yield a distance of 40 Å, much larger than the distance estimated to any of the three sites considered.

Table 5.

Corrected and uncorrected Foster radii and Trp214 ⋯ PP distance.

Sample	R0 (Å)	r (Å)	R0 (Å) [Heme Site]	r (Å) (Heme Site)	R0 (Å) [Cys 34 site]	r (Å) [Cys 34 site]	R0 (Å) [His 67 site]	R (Å) [His 67 site]
HSA-PPIX	33.3	34.5	28.8 (± 2.6)	27.0 (± 2.7)	28.1 (± 2.2)	29.2 (± 2.2)	32.0 (± 2.7)	32.6 (± 0.7)
HSA-Zn(II)PPIX	35.1	37.1	30.5 (± 3.6)	32.3 (± 3.3)	32.3 (± 2.3)	34.2 (± 2.4)	30.5 (± 2.5)	32.3 (± 2.6)
HSA-Fe(III)PPIX	31.5	28.7	35.6 (± 1.6)	28.0 (± 1.3)	28.1 (± 1.8)	25.6 (± 1.7)	30.1 (± 1.3)	27.4 (± 1.2)
HSA-Mg(II)PPIX	29.7	30.9	26.8 (± 4.8)	27.9 (± 4.9)	27.1 (± 2.8)	28.2 (± 2.9)	25.7 (± 2.0)	26.7 (± 2.1)
HSA-Mn(III)PPIX	35.9	40.1	30.1 (± 5.4)	33.7 (± 6.1)	34.5 (± 2.3)	38.6 (± 2.5)	28.5 (± 1.1)	31.9 (± 2.2)
HSA-Sn(IV)PPIX	33.6	40	N/A		N/A
Estimated Distance from Trp214 to the center of each binding site				29.7		37.3		31.0

Figure 7.

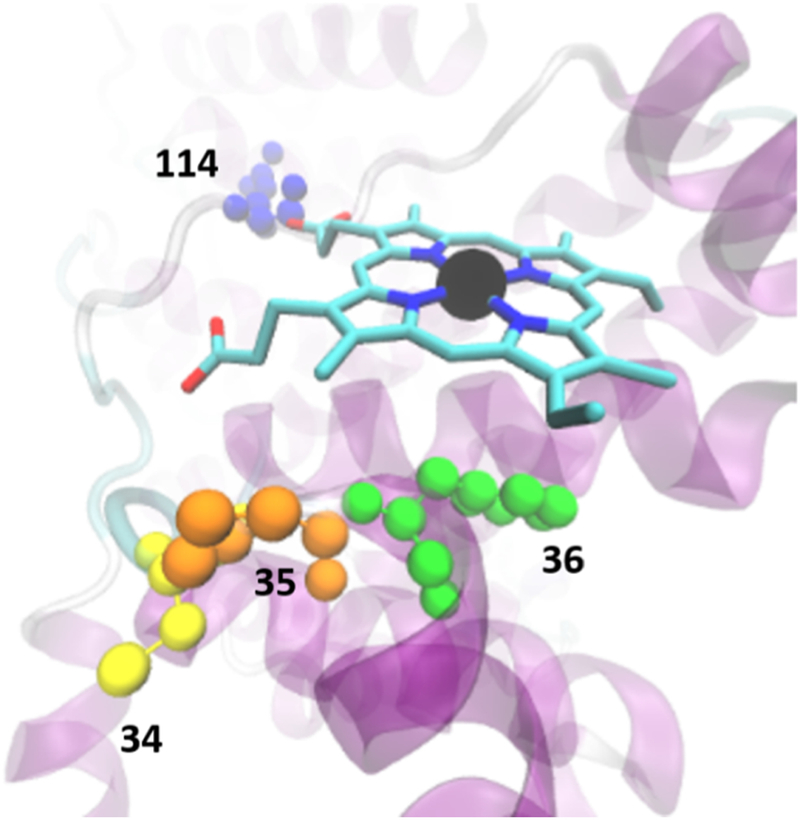
Representative lowest energy binding configuration for Mn(III)PPIX and HSA at the Cys34 (yellow) location. The figure shows the contacts of the porphyrins with Pro35 (orange) and Arg114 (blue) as well as the aromatic interaction with Phe36 (green).

The discrepancy between experimental results (that suggest Mn(III)PPIX and Sn(IV)PPIX located at a location different from the heme site) and the simulations (that suggest much less favorable interaction energy at the Cys43 and His67 sites) can be attributed at least to three potentially important factors:

1. the code used in the docking simulations is not optimized for metal coordination (neither coordination number nor geometry) and favors electrostatic interactions between the metals and oxygen atoms [62],

2. the residues in the proteins are kept rigid thus preventing sampling of more relaxed structures where the ligand may have more favorable energy conformations,

3. binding to the ATCUN location which could also lead to more energetically favorable conformation.

The first limitation cannot be resolved at the moment in the absence of a modification of the docking algorithm that would improve the simulation of metal coordination. Indeed such an updated application is available but only for the Zn ion. We did not employ this version since it could only be applied to Zn(II)PPIX but also because it is optimized for a free Zn ion which has a different coordination number and geometry than the one already coordinated with the porphyrin ring.

For the second limitation we are in the process of running simulations with limited residue mobility around the ligand as well as molecular dynamic simulations that use the CHARMM force field (instead of the Amber force field used by Autodock). Since Sn(IV)PPIX could not be properly parametrized, it was not recognized by the force field. We hope to be able to reach the correct parametrization of this metal in the future.

The third limitation will be overcome by properly patching the current pdb structure of HSA with the correct N-terminal residues to reproduce the binding motif.

4. Conclusions.

From the results obtained from experiments and the simulations and the ensuing discussion, several conclusions can be drawn.

4.1. Protocol to Eliminate Aggregated Protoporphyrins and Protein Binding.

We demonstrated that the protocol that was used to eliminate aggregated metal-free PPIX and Zn(II)PPIX [17], successfully applies to other metal PPs and removes large aggregates of the protoporphyrins. The removal of the aggregates enables a more accurate investigation of the interaction of the monomeric dyes with HSA.

4.2. Resonance Energy Transfer and Location of the Binding Site.

Crucially, the removal of aggregates provides evidence of the occurrence of FRET between the Trp214 monomer and the bound PPs which can be used to estimate the distance between the two and provide key information to identify the most likely binding site. We improved this estimate, compared to previous reports, by mitigating the limitation caused by the incorrect approximation of the κ² orientation coefficient in the calculation of the Förster distance. The corrected value of κ² was used to refine the FRET calculation for each PP and identify with higher confidence the location of the binding. We therefore conclude that metal-free, as well as HSA:Fe(III)PPIX and HSA:Mg(II)PPIX yield sets of experimental and computational data that are consistent with binding at the heme site (Tyr/138Tyr161). On the other hand, HSA:Mn(III) and HSA:Zn(II)PPIX show data consistent with binding at the His67/His247 location. Uncertainty remains regarding the HSA:Sn(IV)PPIX binding.

In conclusion, our study indicates that different porphyrins may bind HSA at different locations. The discrepancy between the binding energy retrieved through docking simulations and the location estimated through FRET indicates that the metal coordination at the site plays a crucial role in stabilizing the interaction. Properties of this different docking preference will be investigated in future studies, however the different binding locations suggest potentially different properties both for physiological activity and for potential applications in synthetic biology.