Reproducibility and Generalizability in Radiomics Modeling: Possible Strategies in Radiologic and Statistical Perspectives

Abstract

Radiomics, which involves the use of high-dimensional quantitative imaging features for predictive purposes, is a powerful tool for developing and testing medical hypotheses. Radiologic and statistical challenges in radiomics include those related to the reproducibility of imaging data, control of overfitting due to high dimensionality, and the generalizability of modeling. The aims of this review article are to clarify the distinctions between radiomics features and other omics and imaging data, to describe the challenges and potential strategies in reproducibility and feature selection, and to reveal the epidemiological background of modeling, thereby facilitating and promoting more reproducible and generalizable radiomics research.

INTRODUCTION

Radiomics is a research field in which models are built based on high-dimensional feature space and tested using new datasets (1,2). After the features are extracted, they eventually become variables for the construction of diagnostic, prognostic, and/or predictive models, and the sophisticated use of bioinformatics tools reduces the number of dimensions and selects variables for a model. This model is subsequently validated using an independent validation set to test its real-world performance. By dealing with both imaging and numerical data, radiomics poses unique challenges, requiring in-depth knowledge in both radiology and statistics to build an informative model.

The field of radiomics has adopted multiple ‘-omics’ terms that represent generation of complex high-dimensional data from single objects (3) and were first used to link genomic data with noninvasive imaging surrogates of liver and brain tumors (4,5). In contrast to other high-dimensional omics data, including those from genomics, transcriptomics, and metabolomics, radiomics shows unique characteristics, in that there is no direct biological relationship, and feature stability is greatly dependent on imaging itself. Since radiomics features are extracted by multiple processes, including imaging acquisition, segmentation, and feature extraction, reproducibility is dependent on each process. Because data mining after feature extraction require statistical knowledge of dimensionality reduction and modeling, different methods of dimensionality reduction and feature selection may alter the results. Radiomics models developed for predictive purposes require validation by testing with a new dataset. Thus, although both reproducibility and generalizability are important for radiomics analysis, both of them complicate the clinical use of radiomics.

Several excellent review articles have discussed the reproducibility of imaging data in radiomics and the approach for performing phantom studies (1,6,7,8,9). However, acquiring new data is often very difficult and strategies to improve reproducibility by using retrospective data have been insufficient. Few studies have assessed statistical perspectives in radiomics modeling to control for abundant imaging data and to build a more generalizable model (9,10). In this review article, we will describe the possible strategies to acquire reproducible radiomics features and to build generalizable models controlling for high dimensionality from the perspectives of both radiologists and statisticians. This review also includes carefully chosen examples in published radiomics research, which may guide beginners in radiomics research to assess the adequacy of these methods. Finally, the purposes of this review are to describe a reproducible and generalizable model that can promote radiomics modeling in scientific research and facilitate the incorporation of radiomics models into future clinical practice.

Characteristics of Radiomics Features

Data Reproducibility Can Be Easily Challenged

Radiomics features contain characteristics of both imaging and numeric features. Radiomics features generally refer to “agnostic” quantitative measurements that are mathematically extracted (1) and differ from “semantic” features such as those covered by radiological lexicons (11). Four main radiomics phenotypes have been used to capture tissue heterogeneity: 1) volume and shape; 2) first-order statistics to assess voxel distributions without considering their spatial relationship; 3) second-order statistics (texture analysis) to study spatial relationships among voxels; and 4) transformed features (1,2,9,10,12).

Similar to common imaging biomarkers, the reproducibility of radiomics features can be questioned due to the nature of the imaging data itself. For example, intra-individual test-retest repeatability, image-acquisition technique, multi-machine reproducibility, and image reconstruction parameters all contribute in challenging reproducible research in radiomics. Another major challenge is imposed by the variations among the different techniques to process the images into analyzable quantitative data. One can obtain widely different results from the same radiomics data by using different transformation or feature-selection methods. With all these variations in image acquisition and processing in radiomics, it seems a daunting task to obtain a stable, generalizable result that can be consistently reproduced. Therefore, the reproducibility of radiomics features and modeling can be easily challenged, and great effort should be made to reduce variations.

High Dimensionality and Small n-to-p Data

In addition to having high dimensionality, radiomics yields “large-predictors (p) and small-number of patients (n)” or “small n-to-p” data, in which the number of measurements is far greater than the number of independent samples (13,14). For example, non-radiomics analysis of apparent diffusion coefficient (ADC) results can yield parameters such as median, mean, or several histogram parameters of ADC. Using a radiomics approach, however, the number of extracted features can range from hundreds to thousands while the number of patients remains small. This introduces problems related to high dimensionality: 1) One drawback of dimensionality is that the volume of the data space increases exponentially with the attribute dimensions, resulting in sparsity of the data (15,16). This implies that high-dimensional feature spaces require a large number of patients to achieve statistical significance. Moreover, this phenomenon causes overfitting in high-dimension and low-sample size situations. 2) The large number of features requires intensive computational resources. 3) The multiplicity of data can result in a high probability of a false-positive rate (14,17).

Highly Correlated and Clustered Data

Radiomics features are highly correlated and are likely to be clustered. As large numbers of features can be generated by performing replicative first-order and second-order statistics on the transformed images, the radiomics features are inherently correlated with each other. For example, “number of runs” in the gray-level run-length matrix features and “run percentage” are correlated since the run percentage is calculated by the number of runs divided by the number of voxels.

Radiomics data can be clustered following multi-region analysis within the same patient. When assessing tumors, ragions of interest (ROIs) are drawn on subregions of the tumor, including areas of contrast-enhancing lesions, necrosis, and non-enhancing peritumoral regions. Then, all subregions are subsequently included in the model. This method results in multiple observations per individual, indicating a clustering of observations within each patient. Clustered data violates the independence assumption that is the basis for a majority of traditional statistical tests. Clustered data can bias estimates of sensitivity and specificity with a misleadingly small estimated standard error (18). To date, however, no strategy has been demonstrated for radiomics.

No Direct Biological Relationship

Genomics and radiomics data differ, in that there is no direct relationship between radiomics and biology, whereas genes are associated with biological changes. Pixel-wise assessments of pathology and the texture features of ADC showed that increases in ADC correlated positively with extracellular spaces and nuclear sizes (19), but negatively with nuclear counts, suggesting that radiomics has macroscopic biological associations (7). The radiomics features reflect spatial heterogeneity, but currently no direct biologic validation is available. A strict lesion-by-lesion analysis between surgical sites on stereotactic biopsy and three-dimensional (3D) imaging will be helpful in increasing knowledge regarding the biological associations of radiomics (1,20). A recent study suggested that a mouse xenograft model can be used for biologic validation (21), and further adaptation to clinical magnetic resonance scanners is needed.

Although radiomics holds great potential for clinical use, the current limitations of radiomics application can be explained on the basis of the abovementioned characteristics. First, radiomics features show challenges related to feature reproducibility, and strategies to improve reproducibility need to be applied. Second, the features are numeric variables calculated from the averaged ROI, which can be highly correlated and clustered in terms of data shape. Third, biological validation with pathologic data is difficult, especially when demonstrating spatial heterogeneity. Further issues and strategies related to radiomics research will be discussed.

Reproducibility and Generalizability of Radiomics Research

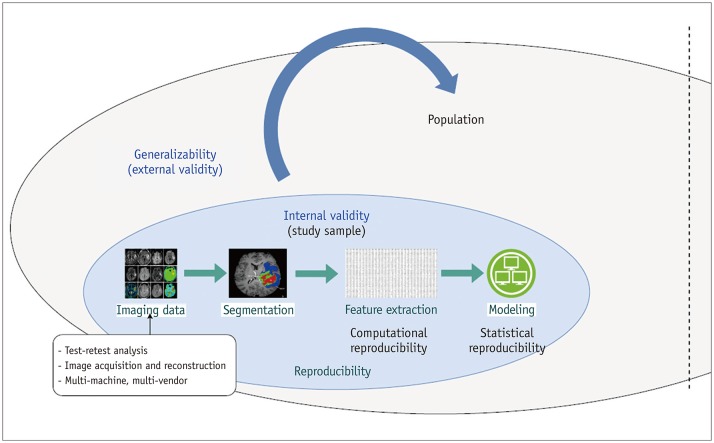
Figure 1 demonstrates the relationship between reproducibility, internal validity, and external validity of radiomics analysis. Internal validity refers to how well an experiment is done, especially whether it avoids confounding and explains relationships between variables (22). External validity indicates the ability of the study to allow for generalization of the study results to the target population and is associated with the term “generalizability” (23,24).

Fig. 1. Relationships among reproducibility, internal validity, and generalizability of radiomics features.

Reproducible radiomics features contribute internal validity wherein features are associated with outcome without noise or error. Generalizability refers to external validity, i.e., whether model can be transported and adopted to different populations.

Internally valid radiomics features are free from noise or errors, and the relationship between predictors and outcome is explainable in the study participants. Reproducibility in radiomics features belong to internal validity that maintains the integrity of a radiomics study. On the other hand, generalizability refers to whether the results of the study (radiomics model) can be applied in different settings or different populations, and will be used in an epidemiologic background.

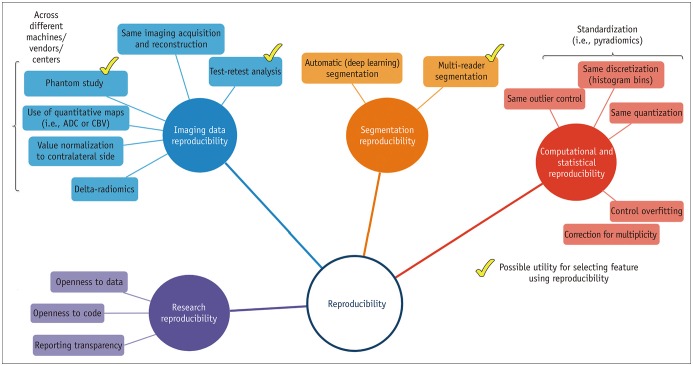
Figure 2 demonstrates different aspects of reproducibility. Reproducibility in radiomics analysis can be determined by assessing imaging data reproducibility, segmentation reproducibility, computational/statistical reproducibility, and research reproducibility. Imaging data reproducibility consists of both repeatability and reproducibility of imaging data. Repeatability is defined as repeated measurements of the same or similar parameters under identical/near-identical conditions, using the same procedures, operators, measuring system, conditions, and physical location over a short period of time (25,26). Reproducibility is defined as repeat measurements in different settings, including at different locations, or with different operators or scanners (25,26). Segmentation reproducibility is unique for radiomics, since radiomics analysis is based on ROI. Computational reproducibility is provided when a standardized algorithm is pursued while statistical reproducibility is achieved with control of overfitting and correction for multiplicity. Then, reproducible research is achieved through open-source code and data and transparency of reporting (27,28). Since research reproducibility is beyond the scope of this review, we recommend further reading for reviews regarding research reproducibility (27,28).

Fig. 2. Reproducibility in radiomics research.

Reproducibility in radiomics analysis can be obtained by pursuing imaging data reproducibility, segmentation reproducibility, computational or statistical reproducibility, and research reproducibility. ADC = apparent diffusion coefficient, CBV = cerebral blood volume

Radiomics features will be discussed with regard to imaging reproducibility, segmentation reproducibility, and computational/statistical reproducibility. By achieving internal validity, the radiomics study will be robust when transferred to different population and setting, thus achieving generalizability or external validity.

Reproducibility of Radiomics Features

Imaging Data Reproducibility

We tried to avoid the term “stability” since the terms “repeatability” and “reproducibility” are recommended by Radiologic Society of North America-Quantitative Imaging Biomarkers Alliance. Repeatability and reproducibility of radiomics features have been investigated using computed tomography (CT), magnetic resonance imaging (MRI), and positron emission tomography (PET). The study methodology differs for 1) intra-individual test-retest repeatability (29,30,31,32,33,34,35,36,37,38), 2) multi-machine reproducibility (33,39,40,41), and 3) image-acquisition (33,41,42) and reconstruction parameters (42,43,44).

Intra-Individual Repeatability Study

A test-retest analysis for 40 rectal cancer patients using CT (40) found that only 9 of 542 features had a concordance correlation coefficient (CCC) > 0.85. In contrast, a test-retest analysis of CT in 40 patients with lung cancer found that 446 of 542 features had a CCC > 0.85. In assessments of test-retest repeatability, features may be affected by differences in patient variables, such as positioning, respiration phase, and contrast enhancement, as well as by differences in acquisition and processing parameters. Respiration was found to strongly affect the feature reproducibility of test-retest CT image pairs in lung cancer patients (33). A test-retest analysis of phantoms showed better results, with 91%, 93.2%, and 96% of the features having CCCs > 0.95, > 0.9, and > 0.85, respectively (41).

To date, only one MRI study has performed a test-retest analysis for three acquisitions (45). Only 386 (37.0%) of the 1043 extracted radiomics features were found to be reproducible with CCCs > 0.8.

Multi-Machine Reproducibility Study

CT radiomics features were tested in five different scanners using the same CT parameters with phantoms made of rubber, plaster, polyurethane, polymethyl methacrylate, cork, wood, P20, P40, and P50 (41). The study found differences in reproducibility, with reproducible features ranging from 15.8% for polyurethane to 85.3% for wood, based on a coefficient of variation > 15% (41).

Image Acquisition and Reconstruction Reproducibility Study

When applying different acquisition modes and image reconstructions on CT, most features were redundant in that only 30.14% of the features were found to be reproducible with CCC ≥ 0.90 across the test-retest and acceptable dynamic range (31). Using a phantom with 177 features, 76–151 (43.1–89.3%) were found to be reproducible when the pitch factor and reconstruction kernel were modified (41). When different reconstruction parameters were assessed in texture features by using fluorodeoxyglucose-PET (42), the features with a small variability (range 5%) were entropy (first-order feature), energy, maximal correlation coefficient (second-order feature), and low-gray-level run emphasis (high-order feature). The features with small variations may serve as better candidates for reproducible auto-segmentation.

Segmentation Reproducibility

Segmentation is regarded as the most “critical, challenging, and contentious component” for radiomics analysis (1). Oncology research is based on identification of tissue volumes, and robust segmentation imposes a great challenge in radiomics. Semiautomatic segmentation has shown greater reproducibility in feature extraction (intra-correlation coefficient [ICC], 0.85 ± 0.15) than manual segmentation (ICC, 0.77 ± 0.17) (46). Even using semiautomatic segmentation, however, the reproducibility of radiomics features is less than ideal, and automatic segmentation needs to be pursued.

Segmentation reproducibility can differ according to tumor types. In a study regarding the delineation of tumor ROIs by three different readers on CT scans of patients with head and neck cancer, pleural mesothelioma, and non-small cell lung cancer (47), investigators found that the ROIs and radiomics features showed the highest reproducibility in lung cancer, followed by head and neck cancer and pleural mesothelioma.

Computational Reproducibility

During feature extraction, outlier control, setting ranges of intensity, and the number of bins can significantly influence the radiomics features. The effect of gray-level discretization was assessed on CT (48), MRI (49), and PET (50). Bin sizes strongly affected reproducibility on perfusion CT, whereas a quantitatively similar but less severe impact was seen on PET (48,50,51). The discrete intensity values (discretization or quantification) varied across 2ⁿ bins, with n usually ranging from 3 to 8 (6): the rationale for the upper limit is to reduce intensive computation. In addition, a clinical PET study showed that resampling values over 64 (2⁶) bins did not provide additional prognostic information using gray-level co-occurrence matrix (GLCM)-entropy (52).

An MRI study tested different 33 combinations of variations (49) using different voxel sizes, four gray-level discretizations (32, 64, 128, and 256), and three quantization methods (uniform quantization, the equal-probability quantization, and the Lloyd-Max quantization). Surprisingly, the study found that no feature showed an overall CCC more than 0.85 across different combinations.

Possible Strategies to Build More Reproducible Radiomics Features

Table 1 summarizes the strategies for reproducible radiomics features. High reproducibility and/or repeatability can be pursued by enhancing intra-individual repeatability/reproducibility, multi-machine and multi-center reproducibility, multi-reader reproducibility, and imaging reconstruction and processing methods. Intra-individual test-retest studies using phantoms or patients on CT, MRI, and PET will enhance repeatability. In addition, selecting features based on ICC and CCC cutoff values can remove redundant features. Among the different imaging modalities, MRI has non-standardized pixel values and large variations in signal intensities, making its assessment of the repeatability and reproducibility of radiomics features particularly challenging. The signal intensities on MRI result from a complex interplay of tissue relaxation time and imaging acquisition (9), with information on MRI not based solely on tissue properties. Thus, test-retest studies in patients may be helpful in designing MRI-based radiomics studies that involve highly reproducible and non-redundant features.

Table 1. Strategies for Reproducible Radiomics Features.

Aspects	Strategy	Purpose	Utility for Feature Selection
Imaging data	Test-retest study with short time interval	Intra-individual repeatability	Yes
	Use of same reconstruction methods on CT, MRI, and PET	Imaging data reproducibility	No
	Phantom or patient study	Multi-machine/center reproducibility	Yes
	Quantitative* maps of ADC or CBV	Multi-machine/center reproducibility	No
	Normalization* to contralateral side	Multi-machine/center reproducibility	No
		Patient-specific radiomics
	Delta-radiomics*	Longitudinal data	No
		Patient-specific radiomics
Segmentation	Multi-reader segmentation	Segmentation reproducibility	Yes
	Automated segmentation (possible deep learning)	Segmentation reproducibility	No
Feature extraction	Use of same discretization and quantization methods across studies (standardization): Pyradiomics	Quantification reproducibility	No
Feature processing	Correction of batch effect from different machine andprotocols: Combat function	Quantification reproducibility	No

^*Potential, published strategies to improve reproducibility. ADC = apparent diffusion coefficient, CBV = cerebral blood volume, PET = positron emission tomography

Reproducibility across machines and centers is important for the external validity of radiomics methods. Ideally, patients should undergo imaging by different scanners at different centers, allowing the selection of highly reproducible features for subsequent modeling. However, CT and PET involve the use of ionizing radiation, making repeated examinations of the same patients problematic. In addition, MRI is expensive, making multiple MRI examinations problematic.

Although there is no golden rule for achieving multi-center reproducibility, several ideas have been tested in clinical studies. Several multi-center studies have indicated that quantitative imaging maps of ADC or cerebral blood volume may show better comparability than conventional T1-weighted, T2-weighted, and FLAIR MRI although this was not explicitly studied using phantoms or in patients (53,54). Using The Cancer Genome Atlas/The Cancer Imaging Archive (TCGA/TCIA) public data, radiomics features of tumor ROIs were normalized relative to ROIs for the contralateral normal-appearing white matter (21). Even though the TCGA/TCIA data varied in magnet strength, repetition time, echo time, and slice thickness, variations among patients were reduced after feature normalization. This method can be regarded as “patient-specific” radiomics.

In “delta (Δ)-radiomics,” longitudinal data obtained from individuals can be used to assess intra-individual reproducibility at different times of imaging acquisition. The radiomics features are calculated as the differences between two time points, divided by the features at the first time point (55). Several studies have utilized Δ-radiomics (56,57,58,59) to assess relative differences between pre- and post-treatment radiomics features and to predict outcomes and treatment responses. Δ-radiomics can also be regarded as “patient-specific” radiomics.

Multiple segmentations by physicians, algorithms, and software have been recommended to limit the extent of bias and to improve radiomics quality (60). Selecting stable features across different segments can reduce the dimensionality of radiomics features. Alternatively, automatic segmentation may maintain robustness across studies. According to a PET study regarding auto-segmentation thresholds (45–60% of the maximum standard uptake value) for metabolic tumor volume, to determine the precision of PET-based radiomics texture quantification (61), alteration of image segmentation thresholds had little effect on the quantification, suggesting that the metabolic tumor volume may be precisely defined by thresholding.

Since computational tumor segmentation may reduce significant variations among individuals, several automatic algorithms have been developed. In a Multimodal Brain Tumor Image Segmentation Benchmark challenge, a fully automatic brain tumor segmentation method based on deep neural networks showed high performance (62) and an over 30-fold faster speed than other machine learning-based algorithms (63). This method indicated that robust features can be obtained using computer vision, reducing the dependency on individual readers.

Use of the same features with the same discretization and quantification methods may enhance reproducibility across studies. The reproducibility and generalizability of results may be enhanced by using a standardized and open-source platform. One of the most commonly used automatic feature extraction platforms is PyRadiomics (64), on which source code, documentation, and examples are publicly available (www.radiomics.io). Feature extraction is supported for both 2D and 3D segmentations, and five feature class-shaped, first-order, texture GLCMs, texture gray-level run length matrix (GLRLM), and gray-level size zone matrices are available. A comparison of reproducibility from different segmentations using PyRadiomics found high reproducibility for first-order, Laplacian, and Gaussian-filtered features, as well as texture features, but low reproducibility for shape and wavelet features (64). This finding may yield reproducible results in quantitative imaging research.

Recently, a compensation approach was suggested, which enables a protocol-specific transformation to express all the data in a common space that are devoid of protocol effects. This is a data-driven, post-processing method called the ComBat function (ComBat function in R or https://github.com/Jfortin1/ComBatHarmonization) (65) and was originally proposed to explain batch effects across different laboratories in microarray expression data. This compensation method has shown potential to be effective in PET (66) and CT (67), without altering the biologic information.

In summary, increased reproducibility of radiomics features, including imaging data, segmentation, and numeric data, is desirable. Test-retest and phantom studies can improve reproducibility and also can be utilized for feature selection using ICC or CCC cutoff values. When the above objectives are not achievable, potential strategies in assessing retrospective data include the use of quantitative MRI maps, normalization to the contralateral side in the brain, and Δ-radiomics. However, these strategies may not reduce the number of dimensions. The process of feature extraction may be enhanced by a more robust strategy of automatic segmentation and standardization of the feature extraction algorithm.

How to Reduce Dimensionality and Select Features in Radiomics Analysis

The performance of a radiomics model depends on the inter-relationships among sample size, data dimensionality, model complexity, and outcome (14,15). Therefore, no single rule can be applied to maximize model performance. In particular, the radiomics data is so called “large-p, small-n” data, or “wide type” data, which is known to have issues such as multiplicity, dimensionality-related problems, and computational burden. Two possible strategies are available for radiomics analysis of data from a small-sized sample (68): 1) the use of ensemble feature-selection approaches by combining different feature-selection methods, 2) adequate evaluation criteria using proper internal validation. Possible ensemble examples for radiomics research are summarized in Table 2.

Table 2. No Golden Rule, but Possible Ensemble of Feature-Selection Methods for Radiomics Studies.

Strategy	Details
Based on reproducibility
Test-retest analysis	1. Sample size calculation
	2. Two or three imaging acquisitions for repeatability
	3. Feature selection with high repeatability
Segmentation reproducibility	1. Segmentation by two or three readers
	2. Feature selection with high reproducibility
Based on univariate test
Filter methods such as t test, univariate logistic regression, correlation	Screen one feature at time based on strength of association with outcome
Based on multivariable models
LASSO	Automatic feature selection
	Selects one feature among correlated features
Elastic Net	Automatic feature selection
	Selects all features that are correlated each other, or takes them out altogether
SVM, ridge regression	Use magnitude of estimated beta coefficients to select features
Deep learning, random forest	More appropriate when sample size is huge

LASSO = least absolute shrinkage and selection operator, SVM = support vector machine

Feature Selection Based on Reproducibility

As discussed previously, several strategies to improve feature reproducibility can be utilized for dimension reduction. For example, application of a step-wise procedure can be used to select the most reproducible, informative, and non-redundant features (31). Test-retest analysis was performed on CT scans, and non-redundant features were selected based on CCC, dynamic range, and coefficient of determination. Along with test-retest analysis, multi-reader segmentation and changes in image reconstruction and processing methods can be adopted to reduce dimensions. In an MRI study, voxel sizes of 1, 2, and 3 mm for first-order features, three quantization methods, and four different discretization methods (32, 64, 128, and 256) were calculated to reduce dimensions by selecting robust features across parameters (49). Although no radiomics features showed robustness across 36 combinations of settings, this study showed the potential of feature selection using feature reproducibility (49).

Univariate Feature-Selection Method

Filter-type methods including correlation, univariate regression, t test, and analysis of variance (ANOVA) can be applied to each feature, one by one, as screening in the feature space. However, multiple testing issues can arise in high-dimensional data. For example, when the 1000 variables are tested with univariate regression in 50 patients, performing 1000 tests creates an accumulated type I error rate and increases the false discovery rate. That is, although the type I error rate of each test can be controlled to be 0.05, the probability of making a type I error in any of those 1000 tests becomes much larger than 0.05 if such a test is repeated on 1000 features. Adjustment of the p value with Bonferroni corrections is conservative and limits the power of the test (69). The false discovery rate provides an alternative way to correct such multiplicity (69,70,71,72). Use of the filter-type feature-selection method with p value adjusted for the false discovery rate provides reasonable screening of radiomics features.

Feature-Selection Methods Using Multivariable Classification Models

After a subset of features are screened, one can consider investigating the screened features as a whole using multivariable models, to further narrow down the features strongly associated with the outcome. Because of the high-dimension, low-sample size aspect of the radiomics data, caution needs to be taken when building the multivariable model on these data. There have been considerable advances in classification methods that are suitable for high-dimension, low-sample size situations that traditional statistical methods were not able to handle. Examples include support vector machine (SVM), least absolute shrinkage and selection operator (LASSO), and Elastic Net. A key aspect of these methods is regularization, which “shrinks” the beta coefficients of the classifier to reduce variance and thus avoid overfitting. This results in a more generalizable, stable classifier that is robust against the idiosyncrasies of the training data.

LASSO and Elastic Net make some of the beta coefficients of the classifier (sometimes called decision functions, linear predictors, or separating hyperplanes) as zero, which effectively removes some features from the fitted model. Thus, one can consider the features with non-zero beta coefficients were “selected,” since these remain in the model due to their strong association with the outcome of interest. When a group of features is correlated with each other, LASSO tends to choose only one of them, while Elastic Net takes either all of them in or out of the model altogether. The level of shrinkage, that is, the number of features to be selected, is determined by a tuning parameter. Careful choice of the tuning parameter is critical to achieve a good fit and to avoid overfitting, and is usually done by cross-validation.

Standard SVM or logistic regression with a ridge penalty term also shrinks beta coefficients towards zero to avoid overfitting. However, they do not generate a set of beta coefficients that are absolutely zero like LASSO or Elastic Net does. The approach to use these methods to select features has been suggested in the literature (68). Instead, the magnitude of beta coefficients can be used for feature selection since the beta coefficient of each feature reflects the impact that feature makes on the outcome: feature selection is performed using a cutoff based on beta coefficients or their absolute values.

With the advent of the big data era, tree-based methods such as classification and regression tree (CART) or Random Forests, or deep learning are attracting attention. These methods show better performance with “tall” data that has a considerably big sample size (number of patients) than with “wide” data. To avoid overfitting, one should use these methods with caution when applying them to radiomics data with high dimensionality and low sample size.

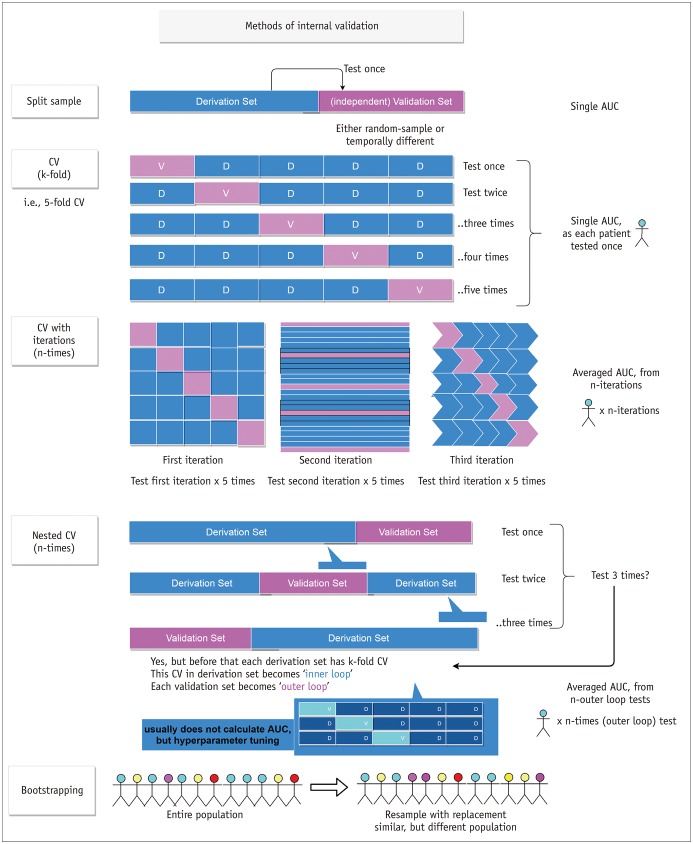
Internal Validation of the Selected Features

To gain confidence in the robustness of the findings and improve generalizability, the selected features or any models that were built based on those selected features should be carefully validated. Internal validation methods are shown in Figure 3. The most straightforward method is a split-sample validation. The data are divided into the derivation and validation sets according to time sequence or randomly. Feature selection and/or model development are performed using the derivation set, after which the resulting features and/or model are tested on the validation set. This method is intuitive and easy to understand, but the drawback is that the result heavily depends on the manner in which the derivation and validation sets are divided. Cross-validation is a method that overcomes this issue by repeating the process similar to split-sample validation. In cross-validation, the data are randomly divided into k parts. The first part of the data is used as the validation set, and the rest of the data are labeled as the training set and used for feature selection and model building. Then, the resulting features or models are tested on the validation set. This process is repeated k times, holding each of the k data parts as the validation set, one at a time, so that every patient in the data gets to belong to the validation set exactly once. This whole process can be iterated for hundreds of times, because one iteration of cross-validation depends on the random division of the data into k parts. Another validation method is a nested cross-validation, which has been used in recent studies for models that require cross-validation during the model-building step. One example is a situation where one wants to perform feature selection using LASSO and validate the result using cross-validation. This approach is the same as standard cross-validation in some degree because the feature selection is done in the training set and the selected features are validated on the test set. The difference is that the feature selection on the training set involves another “inner” cross-validation within the training set, because the optimal value of the LASSO tuning parameter needs to be selected using cross-validation. Another useful internal validation method is bootstrapping. It refers to drawing of random samples from the original data with replacement and is usually used for estimating accuracy of sample estimates. For model validation purpose, bootstrap samples can be used to estimate the “optimism” of apparent validation (73).

Fig. 3. Various internal validation methods.

Split-sample, CV, CV with iterations, and nested CV methods can be applicable. Bootstrapping method can be combined to other internal validation methods. Note that CV has single AUC since each patient is tested once. AUC = area under receiver operating characteristic curve, CV = cross-validation

Generalizability of the Radiomics Predictive Models and Epidemiological Considerations

Statistical models can be classified into three main categories: predictive, explanatory, and descriptive models (74). Predictive models are designed to accurately predict outcomes from a set of predictors. Explanatory models aim to explain differences in outcomes based on differences in explanatory variables. Descriptive models assess associations between independent and dependent variables. For example, studies attempting to identify radiomics features that can distinguish between cancer patients and those with benign conditions are descriptive in nature. In contrast, studies applying these identified radiomics features to diagnose cancer in a new set of patients are predictive in nature. The purpose of most radiomics analyses is not limited to descriptive analytics but can include predictive analytics.

Predictive models, however, should be preceded by determinations of the incidence or prevalence of the targeted disease. A higher prevalence leads to an increase in the positive predictive value when using the test than that with a lower prevalence does (75). If there is a radiomics-based screening tool, applying this in a population for a relatively infrequent disease may yield few previously undetected cases. On the other hand, a radiomics-based screening tool will become productive and efficient in the setting of a high-risk target population. Differing prevalence does not affect the diagnostic performance such as area under the receiver operating characteristics curve, sensitivity, and specificity, but it does affect positive and negative predictive values (76,77). This factor will be important in making disease-positive and disease-negative decisions based on a radiomics analysis (76).

The second consideration is an external validation. A predictive model is not limited to the same population of patients, but targets the general population. Although a best model can be constructed using data collected from individuals who visited a few selective major hospitals, this model may not be applicable to the general population. Therefore, validation in other populations is especially important for radiomics models. Because of the feasibility issue, considerable internal data must be validated using the following methods: split-sample validation, crossvalidation, nested cross-validation, and bootstrapping. Regardless of data resampling, the data collection process cannot be altered because these data were previously collected by an unknown process that cannot be reproduced. Since the purpose of a prediction model is to forecast outcomes in future populations, not to classify previously described characteristics, the robustness of the model is critical. Regardless of the size and heterogeneity of the data, even after they are divided internally, the selection issue resulting from the collection process cannot be overcome. Although internal validation guarantees the specific findings of the study, these findings are limited to the studied population. Generalizing these results to the general population requires external viability or the validity of applying the conclusions of a scientific study outside the context of that study. Thus, external validation of radiomics features is required.

For external validation, the first step should be data standardization as it is critical for presenting data in a common format that allows for collaborative research, large-scale analytics, and sharing of sophisticated tools and methodologies. Various efforts in the field of radiology have been attempted in the Common Data Model (CDM; https://www.ohdsi.org/data-standardization/), allowing systematic analysis of disparate observational big and realistic databases. Although various radiologic examinations are performed solely to provide information to the radiologist or patient, allowing an “informed choice,” additional evidence from high-quality randomized controlled trials is needed to determine whether radiomics is effective in reducing mortality and morbidity rates in various clinical scenarios.

CONCLUSION

Predictive radiomics models require reproducibility and generalizability of radiomics features. Several strategies such as test-retest, phantom studies, robust segmentation, and standardization can be applied for obtaining reproducible features. When constructing a model, overfitting should be controlled by selecting more reproducible features, by screening and determining of false discovery rates, and by determining a feature-selection algorithm suitable for small n-to-p data. Generalizability must be emphasized in radiomics research as validation in a new dataset is a key to applicability of the model. The population used to develop the radiomics model must be considered, and multi-center CDMs must be constructed in designing more valid clinical tools.