Engineering entropy for the inverse design of colloidal crystals from hard shapes

We design particles to self-assemble into colloidal crystals by directly engineering the emergent crystal entropy.

Abstract

Throughout the physical sciences, entropy stands out as a pivotal but enigmatic concept that, in materials design, typically takes a backseat to energy. Here, we demonstrate how to precisely engineer entropy to achieve desired colloidal crystals via particle shapes that, importantly, can be made in the laboratory. We demonstrate the inverse design of symmetric hard particles that assemble six different target colloidal crystals due solely to entropy maximization. Our approach efficiently samples 10⁸ particle shapes from 92- and 188-dimensional design spaces to discover thermodynamically optimal shapes. We design particle shapes that self-assemble into known crystals with optimized symmetry and thermodynamic stability, as well as new crystal structures with no known atomic or other equivalent.

INTRODUCTION

Our understanding of entropy has undergone three revolutions since its association with lost heat by Clausius in the 1800s (1). The first is the discovery by Boltzmann (2) and Gibbs (3) of entropy’s central role in statistical mechanics and its colloquial association with disorder. The second is the discovery by Shannon of entropy’s central role in information theory as a quantifier of statistical ignorance (4). The third is the discovery by Onsager (5) in the late 1940s and then by Kirkwood and collaborators (6, 7) in the late 1950s of entropy’s seemingly paradoxical implication in ordering hard particles. The systematic study via simulation of entropic ordering was pioneered by Frenkel and collaborators in the 1980s [see, e.g., (8, 9)], leading to recent discoveries of an unexpectedly large number of possible structurally ordered phases from hard, anisotropically shaped particles (10–13). In those works, simulation studies begin with a volume of identical hard particles of fixed shape, and the entropy of the system is maximized to find thermodynamic equilibrium phases. In 2015, van Anders et al. (14) introduced a method to start not with a given particle shape, but instead with a target colloidal crystal structure, and, via entropy maximization, find a shape within a limited family of shapes that maximizes entropy for that structure at the selected density. That inverse design approach—“digital alchemy”—flips the usual idea of entropy optimization in hard particle systems on its head.

In this paper, we seek not only to optimize entropy starting from a target structure but also to engineer it so as to inversely design shapes that will self-assemble into the target structure and have a good chance of being synthesizable. Engineering entropy is both conceptually and technically difficult because entropy is a globally defined, purely statistical concept. This means that no direct, quantitative link exists between the macroscopic order that emerges from entropy maximization and the microscopic, designable details of a system’s components. Moreover, the range of designable attributes of component particle shapes has exploded due to advances in colloidal synthesis, e.g., (15–25), and now go well beyond what can be designed by trial and error. In contrast to the design of particle shapes, pairwise interaction potentials (force fields) between atoms or nanoparticles are now routinely designed for simple target structures, and realized in experiment, in cases where potential energy, rather than entropy, dominates (26–32).

Here, we generalize “digital alchemy” (14), an extended ensemble approach that treats particle shape parameters as thermodynamic variables, to sample hundreds of millions of different shapes with no restrictions other than convexity of the particle shape. Whereas an extended ensemble approach was previously applied to ensembles that were extended in one or two design dimensions (14, 33), here we add hundreds of design dimensions, providing a general approach for quantitatively engineering entropy for structure. We perform alchemical Monte Carlo (Alch-MC) simulations and engineer optimal particle shapes for the assembly of six target structures known to self-assemble in simulations of hard particles. In each case, we then identify key symmetry characteristics of the particle shape necessary for that target structure, symmetrize the optimal particle shape, and, by rerunning Alch-MC on the symmetrized particle with symmetry restrictions, find an even better (higher entropy) shape that, because of its high symmetry, has the potential to actually be made in the laboratory. Further, we propose an additional, as-yet-unknown structure and engineer a symmetrized particle shape that forms that structure in simulation. Our approach demonstrates a general quantitative paradigm for engineering entropy in large design spaces that reflect the diversity of colloids and nanoparticles that can be synthesized using current techniques (15–25). Moreover, it opens the possibility of quantitatively engineering entropy for other novel structures or behaviors, allows for the discovery of important features determining structural outcomes in self-assembly (34), and can be generalized to systems with enthalpic interactions.

RESULTS

Our approach proceeds in two steps (see Fig. 1A). The first step begins with randomly generated, arbitrarily shaped convex polyhedra composed of either 32 or 64 vertices whose shape evolves during an MC simulation by randomly moving vertices, thereby sampling from an extended, “alchemical” (here, shape) ensemble (14). Unlike a traditional molecular MC simulation in which a system of fixed particle shapes samples configurational states in phase space, in an alchemical MC (Alch-MC) simulation, particles sample not only positions and orientations but also shapes consistent with the target structure, finding thermodynamically optimal shapes. Alch-MC simulations for polyhedra with n vertices explore a D = 3n − 4 dimensional parameter space accounting for fixed particle volume and rotational invariance and produce mathematically irregular but well-defined convex particle shapes that (i) maximize the entropy of the target structure and (ii) successfully self-assemble the target structure in an MC simulation starting from a disordered fluid. The second step in our approach symmetrizes the designed particles to obtain shapes that still easily assemble the target structure but, because of their symmetry, can potentially be made today using existing synthesis methods (16, 22, 25, 35). Depending on the target crystal structure, we symmetrized particle shapes through truncation or vertex augmentation; this choice tunes features that can be controlled experimentally, e.g., via ligand attachment. Full simulation details and mathematical descriptions of all optimal particle shapes are reported in Materials and Methods and the Supplementary Materials.

Fig. 1. Two-step inverse design process.

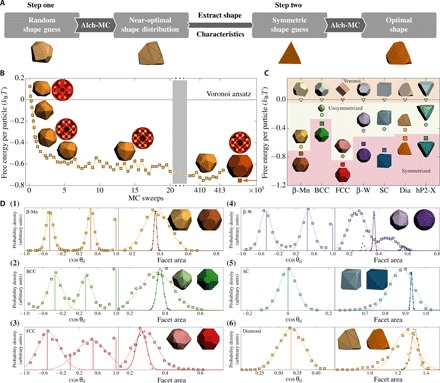
(A) Schematic diagram illustrating the process. In step one, Alch-MC starts from a random convex shape and then finds an unsymmetrized optimal shape for the target structure (here, diamond). Cosine of dihedral angle distribution and PMFT isosurface of the unsymmetrized optimal shape reveals that it has tetrahedral characteristics. In the second step, fluctuating particle shape Alch-MC simulation starts from a tetrahedron and finds an optimal symmetrized shape for the diamond structure. (B) Alch-MC for the inverse design of an unsymmetrized thermodynamically optimal hard particle shape to form a target structure (here, β-Mn). The structure is imposed by an auxiliary design criterion, and detailed balance drives particles to take on shapes (selected shapes are displayed in light yellow) that are favorable for the target structure (indicated by selected bond order diagrams). Directly computed free energy confirms that Alch-MC simulation over ≳10⁵ distinct shapes converges to shapes that have lower free energy (by ≈0.7 k_BT per particle; numerical errors are smaller than markers) than shapes chosen by Voronoi construction. Desired shape features can be inferred from the equilibrium particle shape distribution and used to create a symmetry-restricted ansatz, which yields a thermodynamically optimal synthesizable shape (shown in dark yellow). (C) Direct free energy comparison of our entropic engineering strategy for seven target structures: β-Mn, BCC, FCC, β-W, SC, diamond, and hP2-X. For each structure, we calculated the free energy of the target crystal for a shape formed from a geometric ansatz based on the Voronoi decomposition of the structure (triangles). Compared with the Voronoi ansatz, we find that Alch-MC simulation over arbitrary convex polyhedra in step one produces shapes (circles) that spontaneously self-assemble the target structures with higher entropy. Symmetry-restricted polyhedra (squares) (truncated polyhedra for β-Mn, BCC, and FCC; truncated and vertex-augmented polyhedra for β-W, SC, diamond, and hP2-X) inferred from shapes in step one produce putatively thermodynamically optimal particle shapes by maximizing entropy. (D) Two-step shape Alch-MC entropic particle shape optimization for six target structures: β-Mn, BCC, FCC, β-W, SC, and diamond. For each target structure, an initial Alch-MC simulation over 92- or 188-dimensional spaces of convex polyhedra in step one converged to highly faceted modifications of identifiable Platonic, Archimedean, or Catalan solids, obtained by calculation of the equilibrium distribution of the cosine of dihedral angles cosθ_d (left, light color, squares) and facet areas (right, light color, squares) (Gaussian distributions are plotted with solid lines for comparison). We show the mean of the cosine of dihedral angle distributions in table S1. In step two, Alch-MC simulation over symmetry-restricted families of shapes determined a thermodynamically optimal and synthesizable shape (shown in dark color). For each target structure, we calculate the equilibrium distribution of the cosine of dihedral angles cosθ_d (left, dark color, vertical line) and facet areas for symmetrized optimal shapes (right, dark color points, with Gaussian distribution fitting). The distributions are in arbitrary units. In all cases, representative shapes spontaneously self-assembled target structures in NVT simulations, with periodic boundary condition satisfied.

We targeted six structures—simple cubic (SC), body-centered cubic (BCC), face-centered cubic (FCC), diamond, β-W, and β-Mn. For β-Mn, FCC, and BCC, symmetrized, truncated shapes in step two produced lower free energy crystal structures than sampled unsymmetrized polyhedra found in step one. We give detailed results here for the most complex case, β-Mn. For β-Mn, the equilibrium distribution of convex polyhedra shapes resulting from our Alch-MC simulations at packing density η = 0.6 in step one yields a family of shapes with characteristic dodecahedral facet angles [distribution peaks at ≈ −0.447 and 0.448, see Fig. 1D, (1), versus the perfect dodecahedron ≈ ± 0.447]. Consistent with particle faceting, the potential of mean force and torque (PMFT) calculations (36) for a particle selected from the peak of the shape distribution (Fig. 2A) produced isosurfaces with dodecahedral entropic valence (37). Alch-MC simulation of symmetrized shapes restricted to a one-parameter family of truncated dodecahedra (see fig. S1B) in step two yielded an optimal truncated shape with a facet area of 0.36 [Fig. 1D, (1)]; the peak in the facet area differs by less than 3% from the peak observed for the unrestricted shapes (0.37). We confirmed using regular MC that shapes generated by Alch-MC simulation spontaneously self-assemble the target structure for both the arbitrary convex polyhedron case (depicted in movie S1) and the symmetry-restricted case. To further validate that the particle shape with manifest dodecahedral symmetry is the putative optimal shape, we directly compared the free energy of the target colloidal crystal with the optimal truncated shape and a shape from the peak of the angle distribution of arbitrary convex shapes (Fig. 1C) and found that the symmetric-shape crystal has lower free energy. This result is consistent with our expectation that the free energy landscape of the high-dimensional parameter space of shapes is rough with nearly degenerate minima. For comparison, we also computed the free energy for a packing-based estimate, the Voronoi shape (38). There are two Voronoi cells in β-Mn, one of which can self-assemble the structure without enthalpic interactions (11). We computed the free energy for the target structure with the Voronoi shape and found that our approach produced shapes with lower free energy than the Voronoi shape (Fig. 1C). Figure 1B shows that Alch-MC converged rapidly to shapes that have lower free energy than the Voronoi ansatz by ≈0.7k_BT per particle and implies the existence of a large space of shapes that are all better than the geometric ansatz. The simulation trajectory shown in Fig. 1B explores ≳10⁶ shapes that have lower free energy in the target structure than the geometric ansatz. We follow standard conventions and express all (free) energies in units of the thermal energy (k_BT). Consistent results were found for BCC [Fig. 1D, (2)] and FCC [Fig. 1D, (3)] target structures (details in the Supplementary Materials). The connection between faceting and the emergence of entropic valence with local structural order is robust (BCC, Fig. 2B; FCC, Fig. 2C). In the second step, we repeat the procedure using symmetric truncated shapes suggested by the shapes observed in the first step. In all cases, we obtained lower free energy shapes than the geometric ansatz (β-Mn, −0.753 ± 0.001 k_BT; FCC, −0.907 ± 0.001 k_BT; BCC, −0.334 ± 0.001 k_BT) (see Fig. 1C).

Fig. 2. Structure and PMFT isosurfaces for optimal shapes in six target structures: β-Mn, BCC, FCC, β-W, SC, and diamond.

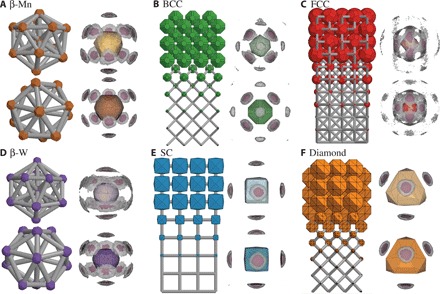
(A to F) Structural coordination (global: BCC, FCC, SC, diamond; local: β-Mn, β-W) and PMFT isosurfaces at free energy values of 1.4 k_BT (light gray) and 0.7 k_BT (pink) above the minimum value for an optimal but unsymmetrized convex polyhedron (top) and for an optimal symmetry-restricted polyhedron (bottom). PMFT isosurfaces indicate that the emergence of particle faceting corresponds with entropic valence localized at particle facets that preferentially align along crystal lattice directions. PMFT isosurfaces for symmetry-restricted polyhedra retain valence-lattice correspondence.

For β-W, SC, and diamond, we found that unsymmetrized polyhedra had lower free energy than symmetrized truncated polyhedra. For these crystals, we implemented step two using symmetrized, truncated, and vertex-augmented polyhedra. We give detailed results here for the most complex case, β-W. For β-W, Alch-MC simulation of unsymmetrized shapes in step one yielded an equilibrium distribution of convex polyhedra with facet angle distribution peaks at ±0.458 [Fig. 1D, (4)]. Like for β-Mn, this falls near the peaks for dodecahedra, but for β-W, the facet area distribution is bimodal, indicating, and confirmed by visual inspection, the existence of two large parallel facets. Faceting is again consistent with emergent entropic valence (Fig. 2D) evident in isosurfaces of PMFT measurements (36). Free energy calculations (Fig. 1C) confirm that a geometric ansatz shape has 0.433 ± 0.006 k_BT more free energy per particle in the target crystal than a shape at the peak of the distribution of convex shapes. We also confirmed that peak shapes self-assemble the target structure with regular MC (see fig. S2). In contrast to the case 1 structures, Alch-MC of symmetrized shapes restricted to a two-parameter family of truncated dodecahedra (see fig. S1E, top) in step two yielded shapes with lower free energy in the target β-W structure than the geometric ansatz but higher free energy than for shapes at the peak of the angle distribution of arbitrary convex polyhedra. This finding indicates that the restriction to truncation alone is too severe for β-W. Alch-MC simulation of a refined truncated dodecahedron with vertex-augmented faces (see fig. S1E, bottom) converged to a shape with 0.620 ± 0.001 k_BT lower free energy per particle than the geometric ansatz. Truncated and augmented free energy minimizing shapes were also found for SC and diamond (SC, −0.704 ± 0.006 k_BT; diamond, −0.54 ± 0.01 k_BT) (Fig. 1C), which again preserve the connection between faceting and entropic valence (SC, Fig. 2E; diamond, Fig. 2F). Because this facet–valence connection persists, the facet area distributions for SC [Fig. 1D, (5)] and diamond structures [Fig. 1D, (6)] are unimodal because of the simpler local structural motif in those structures compared to β-W, where the facet area distribution is bimodal [Fig. 1D, (4)].

Last, we targeted the self-assembly of a hypothetical structure with no known atomic or other equivalent. The structure is a modified version of the hexagonally close packed (HCP) structure with distorted lattice spacing (see Fig. 3A) so that particles have eight nearest neighbors, whereas HCP has 12. We denote this structure as hP2-X. Alch-MC simulations of convex polyhedra with 116 vertex parameters in step one yielded the faceted shape shown in Fig. 3B (left). A symmetrized free energy minimizing shape was then found in step two (Fig. 3B, right). We tested that both the unsymmetrized and symmetrized optimal shapes spontaneously self-assembled the target structure from a disordered fluid, with the resulting structure shown in Fig. 3C. This demonstrates the inverse design of a colloidal particle shape to entropically self-assemble a previously unknown target structure using only digital alchemy (14).

Fig. 3. Alch-MC design and self-assembly of a previously unreported novel crystal structure with no known atomic equivalent.

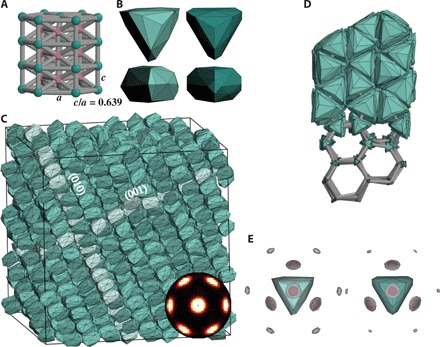
(A) The structure hP2-X is a distorted version of HCP with 8 rather than 12 nearest neighbors. (B) Alch-MC simulation produces a particle that (C) spontaneously self-assembles the target structure in simulation (inset, bond order diagram of the structure). (D) Particle organization relative to lattice directions. (E) PMFT isosurface for optimal shapes.

DISCUSSION

Particle shape has, in principle, an infinite-dimensional parameter space. Here, for tractability, and motivated by shapes that can be realized using current nanoparticle synthesis techniques, we searched for optimal particle shapes over 92- and 188-dimensional parameter spaces of convex shapes, using a precisely defined entropic design criterion. Our method yields not only thermodynamically optimal particle shapes but also distributions of candidate shapes that provide insight into the sensitivity of target structures to shape features (Fig. 1D). More details of shape sensitivity will be reported elsewhere. Emergent entropic valence that is commensurate with the emergence of faceting in an ensemble of arbitrary convex polyhedra, both of which, in turn, commensurate with local structural coordination, is a strong indication in favor of the hypothesized connection between faceting, emergent directional entropic forces, and structural order (36, 37). By furthering the connection between the emergence of faceting and entropic valence, our results suggest that future work could assume this connection and either skip our intermediate step of facet characterization by reading particle faceting directly from PMFT measurements, and/or rather than working agnostically, start the Alch-MC shape evolution from, e.g., a Voronoi cell shape (38).

MATERIALS AND METHODS

Alchemical Monte Carlo

We used the entropic design strategy (summarized in Fig. 1A) that begins with the extended partition function (14)

$$Z={\displaystyle \sum _{\mathrm{\sigma }}}{e}^{-\mathrm{\beta }(H-{\displaystyle \sum _i}{\mathrm{\mu }}_{i}N{\mathrm{\alpha }}_i-\mathrm{\lambda }\mathrm{\Lambda })}$$ (1)

where β is the inverse temperature, μ_i are so-called alchemical potentials that are thermodynamically conjugate to the particle attribute parameters α_i that describe particle shape, N is the number of particles in the system, Λ is the external field that forces the particles to sit in an Einstein crystal with spring constant λ, and the summation is over particle coordinates and orientations and over the space of particle shapes, as in (14). The combination of λΛ serves as the design term. When λ is positive, the system is driven toward particle shape parameters α_i that favor increasing Λ, which allows one to design toward a target structure encoded in Λ. To design purely entropic systems, we modeled particles with purely hard interactions so that the partition function is a sum over all non-overlapping particle configurations, and the phase space part of the Hamiltonian reduces to kinetic terms, which we can integrate analytically. Hereafter, and following (14), we set μ_i = 0 to sample shapes without bias. Unbiased shape sampling, coupled with detailed balance, drives randomly chosen initial shapes to converge toward shapes that are thermodynamically optimal (maximizing entropy) for the target structure at a given temperature and density. Our method differs with the original version of digital alchemy (14) in that here we extended the algorithm to hundreds of design dimensions. We used the HPMC plugin (39) for HOOMD-blue (40) in an NVTμ ensemble at μ = 0. We placed no fewer than 100 particles in a periodic simulation box. The exact number was chosen to be a multiple of the number of particles in the unit cell of the target structure. Particle shapes were initialized randomly with 32 or 64 vertices (in the arbitrary convex polyhedron case) or with each shape parameter taken as either 0 or 1 as convenient (in the symmetry-restricted case). MC sweeps involve particle translations, rotations, and collective shape moves for all particles in the system. For each shape move, we (i) either moved a vertex (arbitrary convex polyhedron case) or generated a trial change in shape parameters (symmetry-restricted case), (ii) resized the trial shape to unit volume, (iii) checked if the move induced any particle overlaps, and then (iv) accepted the move based on the Boltzmann factor as described in (14). Translation and rotation moves followed standard procedures [see, e.g., (10–12, 36, 37, 41, 42)]. We compressed the system to packing fraction η = 0.6, with the spring constant λ fixed to 1000 (where energy is specified in units of k_BT, and length units are given in terms of the particle volume). After we reached the target packing fraction, we logarithmically relaxed the spring constant to zero. We then relaxed the system for 1 × 10⁶ (BCC, FCC, SC, diamond) or 8 × 10⁶ (β-W) or 3.6 × 10⁷ (β-Mn) MC sweeps. For each target crystal structure and each case, we performed 20 independent simulations and analyzed the shapes in the final 1.5 × 10⁵ sweeps. For validation, we directly computed the free energy (43) of the thermally sampled particle shapes as a function of Alch-MC time (Fig. 1B) (step one) and verified that, after starting from random initial particle shapes, our simulations converged to shapes comprising systems of lower free energy for a given target structure (β-Mn is depicted) than for a geometric ansatz that is a hard, space-filling particle in the shape of Voronoi cells of the target structure and gives a possible candidate to assemble its target structure (38). Movie S1 shows an example of Alch-MC shape optimization, followed by melting upon decompression and subsequent spontaneous self-assembly of a shape designed for β-Mn, a complex structure with 20 particles in the unit cell.

Cosine of dihedral angles and facet areas

Unsymmetrized shapes have 32 or 64 vertices. Facets with area $a_{\mathrm{f}}>a_{\mathrm{f}}^{*}$ (we used $a_{\mathrm{f}}^{*}=0.03$, but our results are not sensitive to changes in $a_{\mathrm{f}}^{*}$) were clustered by their normal vector using the DBSCAN (44) scikit-learn module (45) for Python. Clustered facets are represented by area-weighted average normals. We computed aggregate facet areas and the cosine of the angle between all average normals in a polyhedron, which, for adjacent facets, is just the dihedral angle.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/7/eaaw0514/DC1

Symmetric shape constructions

Demonstration of successful self-assembly

Direct free energy computation

Table S1. Mean of cosine of dihedral angle distribution.

Table S2. Optimal geometric parameters.

Fig. S1. Symmetric shape families.

Fig. S2. Successful self-assembly from disordered fluid.

Movie S1. Alch-MC and regular MC for the β-Mn structure.

References (46–48)