Summarizing the solution space in tumor phylogeny inference by multiple consensus trees

Abstract

Motivation

Cancer phylogenies are key to studying tumorigenesis and have clinical implications. Due to the heterogeneous nature of cancer and limitations in current sequencing technology, current cancer phylogeny inference methods identify a large solution space of plausible phylogenies. To facilitate further downstream analyses, methods that accurately summarize such a set $\mathcal{T}$ of cancer phylogenies are imperative. However, current summary methods are limited to a single consensus tree or graph and may miss important topological features that are present in different subsets of candidate trees.

Results

We introduce the Multiple Consensus Tree (MCT) problem to simultaneously cluster $\mathcal{T}$ and infer a consensus tree for each cluster. We show that MCT is NP-hard, and present an exact algorithm based on mixed integer linear programming (MILP). In addition, we introduce a heuristic algorithm that efficiently identifies high-quality consensus trees, recovering all optimal solutions identified by the MILP in simulated data at a fraction of the time. We demonstrate the applicability of our methods on both simulated and real data, showing that our approach selects the number of clusters depending on the complexity of the solution space $\mathcal{T}$.

Availability and implementation

https://github.com/elkebir-group/MCT.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

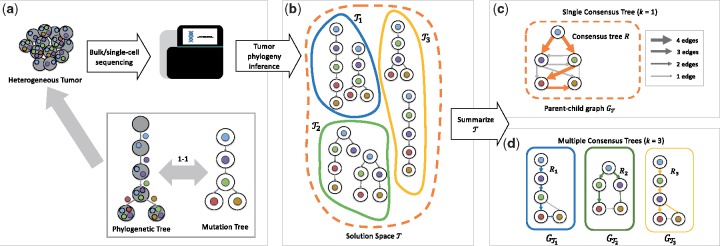
Cancer results from an evolutionary process, during which somatic mutations accumulate in a population of cells (Nowell, 1976), resulting in the formation of multiple tumor clones with distinct sets of mutations (Fig. 1a). A phylogenetic tree, or phylogeny, is a model that represents this process. Mathematically, a phylogenetic tree for a tumor is a rooted tree T, whose leaves correspond to extant cells and whose internal vertices correspond to ancestral cells. The root of T is a normal cell, containing no somatic mutations. In classic phylogenetics, we aim to infer T given the leaf set L(T) under an appropriate evolutionary model. However, due to extensive uncertainty in single-cell DNA sequencing data (Navin, 2014) and the presence of mixed cellular populations in bulk DNA sequencing data (El-Kebir et al., 2015), we do not observe the leaves of T. Rather, our data consist of individually-sequenced cells that may contain errors that must be corrected, or cell populations that have been sequenced in bulk, resulting in mutation frequencies. As a consequence of this ambiguity, tumor phylogeny inference methods for both data types typically infer multiple phylogenetic trees $\mathcal{T}=\{T_1,\dots ,T_n\}$ with distinct topologies and distinct leaf sets that represent alternative evolutionary histories (Fig. 1b).

Fig. 1.

(a) Tumors are heterogeneous, composed of multiple clones with different sets of somatic mutations. This heterogeneity is the result of an evolutionary process, as modeled by a phylogenetic tree. Under the commonly used infinite sites model of evolution, where each mutation is acquired once and never lost, a phylogenetic tree may be equivalently represented by a mutation tree. (b) Due to ambiguities in bulk and single-cell sequencing data of tumors, current methods infer a large solution space of plausible mutation trees $\mathcal{T}$. For further downstream analyses of tumorigenesis, this solution space needs to be summarized. (c) Current summary methods either construct the parent-child graph G_T or identify a single consensus tree R, failing to adequately summarize solution spaces comprised of clusters of trees with distinct topological features. (d) Here, we introduce the Multiple Consensus Tree problem to simultaneously cluster mutation trees and construct a consensus tree of each cluster

The majority of current methods in cancer phylogenetics make the infinite sites assumption, which states that a mutation is gained only once and never subsequently lost (Dang et al., 2017; Deshwar et al., 2015; Donmez et al., 2016; El-Kebir et al., 2015, 2016; Jahn et al., 2016; Jiang et al., 2016; Jiao et al., 2014; Malikic et al., 2015; Popic et al., 2015; Ross and Markowetz, 2016; Strino et al., 2013; Yuan et al., 2015). Under this assumption, we may represent a phylogenetic tree T by a mutation tree$T\prime$ (El-Kebir et al., 2016; Jahn et al., 2016). More specifically, we contract unlabeled edges of T to obtain $T\prime$, whose vertices we label by the mutations that were introduced on the incoming edges (Fig. 1a). Tumor phylogenies that adhere to the infinite sites assumption have been used to identify mutations that drive cancer progression (Jamal-Hanjani et al., 2017; McGranahan et al., 2015), assess the interplay between the immune system and the clonal architecture of a tumor (Łuksza et al., 2017; Zhang et al., 2018) and identify common evolutionary patterns in tumorigenesis and metastasis (Turajlic et al., 2018a, b). These downstream analyses critically rely on the accuracy of the input phylogenetic tree. Thus, methods to accurately summarize the solution space $\mathcal{T}$ are essential, so as to remove inference errors and identify common dependencies between mutations in the input trees.

A common approach employed in several studies (Deshwar et al., 2015; El-Kebir et al., 2015; Jiao et al., 2014) summarizes the solution space $\mathcal{T}$ by constructing the parent-child graph$G_{\mathcal{T}}$, which is a directed, edge-weighted graph that represents the union of all trees in $\mathcal{T}$. That is, each edge (u, v) of this graph corresponds to an edge in a tree T in the solution space $\mathcal{T}$ and is weighted by the number of occurrences in $\mathcal{T}$ (Fig. 1c). A key deficiency of the parent-child graph is that it does not accurately represent topological features of the solution space, i.e. patterns of co-occurrence and mutual exclusivity among edges in individual trees in the solution space. Moreover, downstream analyses require a single phylogenetic tree as input and are unable to operate directly on the parent-child graph.

To overcome the latter limitation, Govek et al. (2018) introduced the Single Consensus Tree problem, which aims at constructing a consensus tree that best represents the solution space $\mathcal{T}$. To quantify similarity or distance between two trees, one needs a distance function. Recently, Karpov et al. (2018) introduced a tree edit distance measure that can be efficiently computed using dynamic programming. Using a distance function that directly measures edge similarity, Govek et al. (2018) seek a consensus tree with minimum total distance to the trees in $\mathcal{T}$. The main drawback to summarizing $\mathcal{T}$ by a single tree is that important topological features may be missed, which is especially the case when $\mathcal{T}$ contains multiple clusters of distinctive trees. We note that there is a large body of work for consensus tree problems in classic phylogenetics (cf. Warnow, 2017). These methods are often based on bipartitions of a fixed leaf set. However, as mentioned above, the leaf set is typically unknown a priori in cancer phylogenetics due to the nature of the input data, preventing the direct application of consensus tree methods that rely on fixed leaf sets.

In this paper, we introduce the Multiple Consensus Tree (MCT) problem of simultaneously grouping trees $\mathcal{T}$ into k clusters and reconstructing a consensus tree for each cluster with minimum total distance. The MCT approach better summarizes solution spaces $\mathcal{T}$ with distinct topological features, overcoming limitations of current approaches (Fig. 1d). We prove that MCT is NP-hard, and give an exact approach based on mixed integer linear programming (MILP) that is able to efficiently solve small instances to optimality. In addition, we introduce a heuristic based on coordinate ascent that scales to large input instances. We benchmark our methods on simulated data, showing that the heuristic approach yields solution of quality comparable to that of the MILP approach at only a fraction of the time. We demonstrate the applicability of the MCT problem on recent lung cancer data. Our methods enable one to draw informed conclusions in downstream phylogenetic analyses of tumors.

2 Problem statement

The key object in this paper is a mutation tree, which is a defined as follows.

Definition 1

A mutation tree T is a rooted tree whose m nodes are uniquely labeled by mutations $[m]=\{1,\dots ,m\}$.

We obtain a mutation tree $T=(V,E)$ from a phylogenetic tree $T\prime =(V\prime ,E\prime )$ that satisfies the infinite sites assumption by first contracting its unlabeled edges, and then labeling the resulting vertices by the mutations present on their incoming edges (Fig. 1a). To summarize a set $\mathcal{T}$ of mutation trees (Fig. 1b), we consider the following distance function, which was shown to be a distance metric by Govek et al. (2018).

Definition 2

Let $T=(V,E)$ and $T\prime =(V,E\prime )$ be two rooted trees on the same vertex set V. The parent-child distance$d(T,T\prime )$ is the number of edges unique to either tree, i.e.

$$d(T,T\prime )=|E\setminus E\prime |+|E\prime \setminus E|.$$ (1)

Mathematically, the parent-child distance $d(T,T\prime )$ of two rooted trees $T=(V,E)$ and $T\prime =(V,E\prime )$ is the size of the symmetric difference between E and $E\prime$. This distance has been used extensively in the tumor phylogeny inference literature to compare inferred trees to simulated trees (El-Kebir et al., 2015; Malikic et al., 2015; Popic et al., 2015). Govek et al. (2018) used the parent-child distance to define a consensus tree for a set input trees $\mathcal{T}$ as follows.

Definition 3

A consensus tree for rooted trees $\mathcal{T}=\{T_1,\dots ,T_n\}$ with the same vertex set V is a rooted tree R with vertex set V.

Subsequently, Govek et al. (2018) introduced the Single Consensus Tree problem, which given a set $\mathcal{T}=\{T_1,\dots ,T_n\}$ of input trees seeks a consensus tree R with minimum total distance $d(\mathcal{T},R)={\sum }_{i=1}^{n}d(T_i,R)$.

Problem 1

(Single Consensus Tree (SCT)) Given distinct rooted trees $\mathcal{T}=\{T_1,\dots ,T_n\}$ with the same vertex set, find a consensus tree R such that $d(\mathcal{T},R)={\sum }_{i=1}^{n}d(T_i,R)$ is minimum.

To better account for extensive ambiguity in the topology of solution trees, we introduce the Multiple Consensus Tree problem, which generalizes the Single Consensus Tree to k clusters.

Problem 2

(Multiple Consensus Tree (MCT)) Given distinct rooted trees $\mathcal{T}=\{T_1,\dots ,T_n\}$ and integer $1\le k\le n$, find a clustering $\sigma :[n]\to [k]$ and consensus trees $\mathcal{R}=\{R_1,\dots ,R_k\}$ such that (i) no cluster $s\in [k]$ is empty, i.e. σ is surjective, and (ii) $d(\mathcal{T},\mathcal{R},\sigma )={\sum }_{i=1}^{n}d(T_i,R_{\sigma (i)})$ is minimum.

3 Combinatorial structure and complexity

Section 3.1 characterizes the solution space of the MCT problem. Section 3.2 shows that this problem is NP-hard. Proofs are in the supplement due to space constraints.

3.1 Combinatorial characterization of optimal solutions

To characterize the space of solutions to the MCT, we start by reviewing results for the SCT problem (Govek et al., 2018). Given input trees $\mathcal{T}$, Govek et al. (2018) defined the parent-child graph $G_{\mathcal{T}}$ as follows.

Definition 4

(Govek et al. (2018)) The parent-child graph$G_{\mathcal{T}}$ of a set $\mathcal{T}=\{T_1,\dots ,T_n\}$ of trees is a weighted directed graph $G_{\mathcal{T}}=(V,E)$ with the same vertex set V as each input tree, an edge $(u,v)\in E$ if and only if there exists an input tree $T_i=(V,E_i)\in \mathcal{T}$ where $(u,v)\in E_i$, and weight $\ell (u,v)$ equal to the number of input trees with edge (u, v), i.e.

$$\ell (u,v)=\left|\right\{T_i=(V,E_i)\in \mathcal{T}|(u,v)\in E_i\}|.$$ (2)

Subsequently, the authors showed that solutions to an SCT instance $\mathcal{T}$ are maximum weight spanning arborescences in the parent-child graph $G_{\mathcal{T}}$. We note that maximum weight spanning arborescences and branchings (with multiple root vertices) have frequent applications in computational biology (e.g. Desper et al., 1999).

Theorem 1

(Govek et al., 2018) Given input trees $\mathcal{T}=\{T_1,\dots ,T_n\}$, there exists a consensus tree R with minimum distance $d(\mathcal{T},R)={\sum }_{i=1}^{n}d(T_i,R)$ that is a maximum weight spanning arborescence in the parent-child graph $G_{\mathcal{T}}$.

We have the following two lemmas that follow from the above theorem.

Lemma 1

There exists an optimal consensus tree R to SCT instance $\mathcal{T}$ where each edge (u, v) of R occurs in an input tree.

Lemma 2

There exists an optimal consensus tree R to SCT instance $\mathcal{T}$ where if an edge (u, v) is present in all trees $\mathcal{T}$ then (u, v) is an edge of the consensus tree R.

Let $m=\left|V\right|$ be the size of the vertex set V of a set $\mathcal{T}$ of input trees. We prove the following relationship between the weight $\ell (R)=\sum _{(u,v)\in E(R)}\ell (u,v)$ of any spanning arborescence R in $G_{\mathcal{T}}$ and its distance $d(\mathcal{T},R)$ to input trees $\mathcal{T}$.

Lemma 3

The total distance $d(\mathcal{T},R)=\sum _{i=1}d(T_i,R)$ of any spanning arborescence $R=(V,E_R)$ of parent-child graph $G_{\mathcal{T}}$ to input trees $\mathcal{T}=\{T_1,\dots ,T_n\}$ equals $2[n(m-1)-\ell (R)]$.

We have the following important proposition.

Proposition 1

Given a clustering $\sigma :[n]\to [k]$, the MCT problem decomposes into k independent SCT problems.

From the above proposition and Theorem 1, we obtain the following corollaries that are generalizations of Lemmas 1, 2 and 3.

Corollary 1 There exists an optimal solution $(\mathcal{R},\sigma )$ to MCT instance $(\mathcal{T},k)$ where each edge of each consensus tree $R_s\in \mathcal{R}$ occurs in an input tree in the set ${\mathcal{T}}_s$ of trees assigned to cluster s.

Corollary 2 There exists an optimal solution $(\mathcal{R},\sigma )$ to MCT instance $(\mathcal{T},k)$ where if an edge (u, v) is present in all trees ${\mathcal{T}}_s$ assigned to cluster s then (u, v) is an edge of the consensus tree R_s.

Corollary 3 There exists an optimal solution $(\mathcal{R},\sigma )$ to MCT instance $(\mathcal{T},k)$ with total distance

$$d(\mathcal{T},\mathcal{R},\sigma )=n(m-1)-\sum _{s=1}^k\ell (R_s),$$ (3)

where $\ell (R_s)$ is the weight of a maximum weight spanning arborescence R_s of the parent-child graph $G_{{\mathcal{T}}_s}$ obtained from ${\mathcal{T}}_s$.

As the number of k of clusters increases the minimum total distance will decrease, as shown by the following proposition.

Proposition 2

The minimum total distance of an MCT instance $(\mathcal{T},k)$ is monotonically decreasing with increasing number k of clusters.

3.2 Complexity

Theorem 2 Multiple Consensus Tree (MCT) is NP-hard.

We give a polynomial-time reduction from the Clique problem, a known NP-complete problem (Garey and Johnson, 1979).

Problem 3

(Clique) Given an undirected, simple graph H with vertex set V(H), edge set E(H) and a positive integer $c\le |V(H)|$, decide whether G contains a clique of size c.

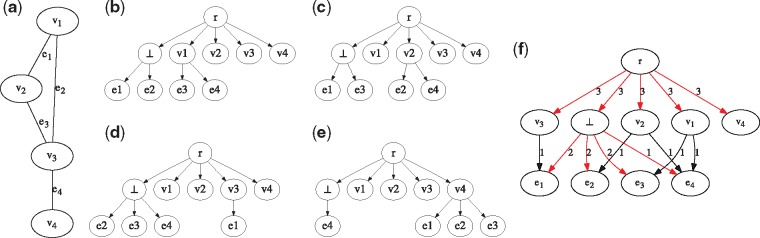
To reduce a Clique instance (H, c) to an MCT instance $(\mathcal{T},k)$, we introduce the notation $\delta (v)$ to indicate the subset of edges that are incident to v, i.e. $\delta (v)=\{(u,w)\in E(H)|u=v \hspace{0.17em}\text{or}\hspace{0.17em} w=v\}$. For each vertex v_i of H, we construct a tree $T_i=(U,A_i)$. The vertex set U of T_i is defined as $\{r,\perp \}\cup V(H)\cup E(H)$ and the edge set A_i contains directed edges $\{(r,\perp )\},\hspace{0.17em}\{(r,v_i)|v_i\in V(H)\},\hspace{0.17em}\{(\perp ,e)|e\in \delta (v)\}$ and $\{(v_i,e)|e\in E(H)\setminus \delta (v)\}$. We set $k=n-c+1$. Since all the input trees $\mathcal{T}=\{T_1,\dots ,T_n\}$ are on the same vertex set U and $1\le k\le n$, it holds that $(\mathcal{T},k)$ is an instance of MCT problem. Clearly, this construction can be performed in time polynomial in n and m. Figure 2 shows an example of reduction.

Fig. 2.

An example reduction from the Clique problem to MCT. (a) An undirected graph H with $|E(H)|=4$ edges and $n=|V(H)|=4$ vertices, containing a clique of size 3. (b–e) The n = 4 input trees $\mathcal{T}=\{T_1,T_2,T_3,T_4\}$ to the MCT problem obtained from H. The problem instance of determining whether H contains a clique of size c = 3 reduces to the MCT instance $(\mathcal{T},k)$ where $k=n-c+1=2$. An optimal clustering σ for $(\mathcal{T},2)$ yields ${\mathcal{T}}_1=\{T_1,T_2,T_3\}$ and ${\mathcal{T}}_2=\left\{T_4\right\}$. (f) The parent-child graph $G_{{\mathcal{T}}_1}$, with the optimal consensus tree R₁ for input trees ${\mathcal{T}}_1$ indicated in red. The parent-child graph of ${\mathcal{T}}_2$ is identical to T₄ with edge weights $\ell (u,v)=1$ for each edge (u, v) such that the corresponding optimal consensus tree R₂ equals T₄. As such, the total distance equals $2[(c-1)·|E(H)|-\left(\begin{array}{c}c\\ 2\end{array}\right)]=10$. By Lemma 6, H contains a clique of size c = 3

Defining the cost as the total distance $d(\mathcal{T},\mathcal{R},\sigma )$, we have the following two lemmas that provide lower bounds on the cost of any feasible solution $(\mathcal{R},\sigma )$ to $(\mathcal{T},k)$ obtained from a Clique instance (H, c).

Lemma 4

The cost of a clustering $\sigma :[n]\to [k]$ that partitions $\mathcal{T}$ into parts of sizes $n_1,\dots ,n_k$ is at least $2[(c-1)·|E(H)|-{\sum }_{s=1}^k\left(\begin{array}{c}{n}_s\\ 2\end{array}\right)]$. This bound is tight if and only if the input trees ${\mathcal{T}}_s$ assigned to each cluster s encode a clique in the undirected graph H.

Lemma 5

The cost of any clustering $\sigma :[n]\to k$ of $(\mathcal{T},k)$ is at least $2[(c-1)·|E(H)|-\left(\begin{array}{c}c\\ 2\end{array}\right)]$. This bound is tight if and only if σ contains k – 1 singleton clusters and one cluster with c trees that encode the vertices of a clique in the undirected graph H.

Finally, we use the above two lemmas to prove the following lemma, from which the theorem follows.

Lemma 6

There is a clique of size c in the undirected graph H if and only if the corresponding MCT instance $(\mathcal{T},k)$ has an optimal solution with cost $2[(c-1)·|E(H)|-\left(\begin{array}{c}c\\ 2\end{array}\right)]$.

4 Material and methods

This section introduces three algorithms for Multiple Consensus Tree that exploit the combinatorial structure identified in the previous section. Section 4.4 describes a procedure for selecting the number k of clusters, balancing the decrease in distance and the additional complexity with increasing k.

4.1 Brute force algorithm

By Proposition 1, each MCT instance $(\mathcal{T},k)$ decomposes into k SCT instances when given the clustering σ. Thus, one can identify optimal solutions $(\mathcal{R},\sigma )$ to $(\mathcal{T},k)$ by exhaustively generating all clusterings σ, retaining clusterings that have minimum total distance. The number of clusterings is given by the Stirling number of the second kind (Knuth, 1997), which is bounded by kⁿ. Given σ, we must solve k maximum weight spanning arborescence problems on sets $\{{\mathcal{T}}_1,\dots {\mathcal{T}}_k\}$ of trees. Gabow et al. (1986) give an algorithm that identifies a maximum (minimum) weight spanning r-arborescence rooted at a given vertex r of a weighted directed graph $G=(V,E)$ in $O(|E|+|V|\hspace{0.17em}\text{log}\hspace{0.17em}|V|)$ time. For simplicity, we bound the number $|E(G_{{\mathcal{T}}_s})|$ of edges in each parent-child graph $G_{{\mathcal{T}}_s}$ by $O(|V(G_{{\mathcal{T}}_s}){|}^2)=O(m^2)$. As such, the complexity of identifying an optimal consensus tree of a set of trees is $O(m[m^2+m\hspace{0.17em}\text{log}\hspace{0.17em}m])=O(m^3)$. It follows that the time of identifying the optimal set of consensus trees is bounded by $O(k{m}^3)$ Therefore the complexity of the brute force algorithm is $O(k^n·k{m}^3)=O(k^{n+1}{m}^3)$.

4.2 Mixed integer linear program

We introduce a mixed integer linear program (MILP) that models the feasible solution space of an MCT instance $(\mathcal{T}=\{T_1,\dots ,T_n\},k)$. To do so, we model (i) the surjective clustering function $\sigma :[n]\to [k]$, (ii) the consensus trees $\{R_1,\dots ,R_k\}$ as spanning arborescences, (iii) the weight $\ell (R_s)$ of each consensus tree R_s and (iv) additional cuts to improve performance. Let m be the number of vertices in the shared vertex set of input trees $\mathcal{T}$.

4.2.1 Clustering

We introduce binary variables $\mathbf{x}\in {\{0,1\}}^{n\times k}$ to model clustering $\sigma :[n]\to [k]$. More specifically, we require $x_{i,s}=1$ if $\sigma (i)=s$ and $x_{i,s}=0$ if $\sigma (i)\ne s$ for each cluster s and input tree i. To that end, we introduce the following constraints.

$$\sum _{s=1}^k{x}_{i,s}=1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall i\in [n]$$ (4)

$$x_{i,s}\in \{0,1\}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i\in [n],s\in [k]$$ (5)

In addition, we require σ to be surjective. That is, each cluster s contains at least one tree, which we model as follows.

$$\sum _{i=1}^n{x}_{i,s}\ge 1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall s\in [k]$$ (6)

4.2.2 Consensus trees

By Proposition 1, the MCT problem decomposes into k instances of the SCT problem. By Theorem 1, we know that each SCT instance is a maximum weight spanning arborescence problem with unknown root. Consider the subproblem of a cluster $s\in [k]$. To model the edges of the consensus tree R_s, we introduce variables $y_{s,p,q}$ for each ordered pair $(p,q)\in [m]\times [m]$ of vertices such that $y_{s,p,q}=1$ if consensus tree R_s contains the edge (p, q) and $y_{s,p,q}=0$ otherwise. We require that R_s is a spanning arborescence of the vertex set $[m]$, i.e. R_s contains a single vertex p that does not have a parent. To indicate the root vertex, we introduce variables $z_{s,p}$ for each vertex p such that $z_{s,p}=1$ if p is the root of R_s and $z_{s,p}=0$ otherwise. We have the following constraints that model a single root vertex and the presence of a unique parent of each non-root vertex.

$$\sum _{p=1}^m{z}_{s,p}=1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall s\in [k]$$ (7)

$$\sum _{p=1}^m{y}_{s,p,q}=1-z_{s,q}\hspace{1em}\hspace{1em}\hspace{1em}\forall s\in [k],q\in [m]$$ (8)

$$y_{s,p,q}\ge 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall s\in [k],p,q\in [m]$$ (9)

$$z_{s,p}\ge 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall s\in [k],p\in [m]$$ (10)

For each order pair $(p,q)\in [m]\times [m]$, let $b_{p,q}=1$ if there exists an input tree $T_i\in \mathcal{T}$ containing the edge (p, q) and $b_{p,q}=0$ otherwise. By Corollary 1, we have that each edge (p, q) of R_s must occur in at least one input tree $T_i\in \mathcal{T}$. As such, we have the following constraint:

$$y_{s,p,q}\le b_{p,q}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall s\in [k],p,q\in [m]$$ (11)

Next, we need to model connectivity, i.e. from the root vertex p of R_s every other vertex $q\ne m$ must be reachable. In other words, we need to prevent that R_s has cycles. For a subset $U\subseteq [m]$ of vertices, let ${\delta }^{-}(U)$ be the subset of directed edges (p, q) occurring in the input trees $\mathcal{T}$ where $p\cancel{\in }U$ and $q\in U$. More formally, ${\delta }^{-}(U)=\{(p,q)\in [m]\times [m]|p\in [m]\setminus U,q\in U,b_{p,q}=1\}$. For any cut set $U\subseteq [m]$, it must hold that U contains either the root vertex or there must be at least one incoming edge to U. This is captured by the following constraint.

$$\sum _{(p,q)\in {\delta }^{-}(U)}{y}_{s,p,q}+\sum _{p\in U}{z}_{s,p}\ge 1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall s\in [k],U\subseteq [m]$$ (12)

The spanning arborescence polytope defined by constraints (7)–(12) has integral vertices (Schrijver, 2003). In other words, we do not require variables y and z to be binary.

4.2.3 Parent-child distance

For each ordered pair $(p,q)\in [m]\times [m]$, let $a_{i,p,q}=1$ if input tree T_i contains the edge (p, q) and $a_{i,p,q}=0$ otherwise. To model the distance $d(T_i,R_{\sigma (i)})$ of input tree $T_i\in \mathcal{T}$ to its corresponding consensus tree $R_{\sigma (i)}$, we introduce the variable $w_{i,s,p,q}$ which indicates that trees T_i and R_s contain the edge (p, q) and T_i is assigned to cluster s. In other words, $w_{i,s,p,q}$ is the product of $a_{i,p,q},\hspace{0.17em}{y}_{s,p,q}$ and $x_{i,s}$. We thus have

$$d(T_i,R_{\sigma (i)})=\sum _{s=1}^k\sum _{p=1}^m\sum _{q=1}^m{w}_{i,s,p,q}.$$ (13)

Using Corollary 3, we obtain the following objective function.

$$\min n(m-1)-\sum _{i=1}^n\sum _{s=1}^k\sum _{p=1}^m\sum _{q=1}^m{w}_{i,s,p,q}.$$ (14)

We model $w_{i,s,p,q}=a_{i,p,q}·y_{s,p,q}·x_{i,s}$ using the following constraints, which force $w_{i,s,p,q}$ to 0 if one of $\{a_{i,p,q},y_{s,p,q},x_{i,s}\}$ is 0.

$$w_{i,s,p,q}\le a_{i,p,q}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i\in [n],s\in [k],p,q\in [m]$$ (15)

$$w_{i,s,p,q}\le y_{s,p,q}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i\in [n],s\in [k],p,q\in [m]$$ (16)

$$w_{i,s,p,q}\le x_{i,s}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i\in [n],s\in [k],p,q\in [m]$$ (17)

$$w_{i,s,p,q}\ge 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i\in [n],s\in [k],p,q\in [m]$$ (18)

By integrality of x and y, we do not require w to be binary variables. Moreover, by the direction of the objective function, we do not need to force $w_{i,s,p,q}$ to 1 if $a_{i,p,q}=y_{s,p,q}=x_{i,s}=1$.

4.2.4 Additional cuts

To improve performance of the ILP, we use Corollary 1 to require that R_s contains the edge (p, q) only if there exists a tree $T_i\in {\mathcal{T}}_s$ containing the edge (p, q). To that end, we introduce the following constraint.

$$y_{s,p,q}\le \sum _{i=1}^n{a}_{i,p,q}{x}_{i,s}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall s\in [k],p,q\in [m]$$ (19)

By Corollary 2, if all input trees $T_i\in {\mathcal{T}}_s$ contain the edge (p, q) then there exists an optimal solution in which consensus tree R_s contains (p, q) as well. This is captured by the following constraint.

$$y_{s,p,q}\ge \sum _{i=1}^n{a}_{i,p,q}{x}_{i,s}-\sum _{i=1}^n{x}_{i,s}+1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall s\in [k],p,q\in [m]$$ (20)

Finally, we introduce the following symmetry breaking constraints that impose an ordering on σ such that $\left|{\mathcal{T}}_1\right|\ge \left|{\mathcal{T}}_2\right|\ge \dots \ge \left|{\mathcal{T}}_k\right|$.

$$\sum _{i=1}^n{x}_{i,s}\ge \sum _{i=1}^n{x}_{i,s+1}+1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall s\in [k-1]$$ (21)

4.2.5 Cut separation

The number of constraints (12) grows exponentially in m. Therefore, we do not include these constraints in our formulation. Following a standard approach (Wolsey, 1998), we separate these constraints during the branch-and-bound procedure by identifying a minimum cut in a directed graph. Excluding constraints (12), our formulation has $O(\mathit{nk}{m}^2)$ variables and constraints. Supplementary Figure S1 contains the full MILP.

Algorithm 1:

CoordinateAscent($\mathcal{T}$, k)

Input: Trees $\mathcal{T}=\{T_1,\dots ,T_n\}$ and number k > 0 of clusters

Output: Consensus trees $\mathcal{R}=\{R_1,\dots ,R_k\}$ and clustering σ 1 $\sigma \leftarrow$ random clustering

2 $L,\Delta \leftarrow \infty$

3 whileΔ > 0do

4 for$s\leftarrow 1$tokdo

5    Let $G_{{\mathcal{T}}_s}$ be the parent-child graph of input trees ${\mathcal{T}}_s$ with edge weights $\ell :E(G_{{\mathcal{T}}_s})\to \mathbb{N}$

6    Compute max weight spanning arborescence R_s of $G_{{\mathcal{T}}_s}$

7  for$i\leftarrow 1$tondo

8    σ(i)←argmin_sϵ[k]d(T_i,R_s)

9  $L\prime \leftarrow d(\mathcal{T},\mathcal{R},\sigma )$

10  $\Delta \leftarrow L\prime -L$

11  $L\leftarrow L\prime$

12  return($\mathcal{R}$, σ)

4.3 Coordinate ascent heuristic

We use coordinate ascent to solve the Multiple Consensus Tree heuristically. The idea is to identify consensus trees and clusterings alternatingly, starting from a random clustering σ. Then, for each cluster $s\in [k]$, we construct the parent-child graph $G_{{\mathcal{T}}_s}$ from the set ${\mathcal{T}}_s$ of input trees in cluster s. From $G_{{\mathcal{T}}_s}$, we obtain the consensus tree R_s by computing the maximum weight spanning arborescence of the graph. Finally, we update the clustering σ by reassigning each $T_i\in \mathcal{T}$ to a cluster $s\in [k]$ such that $d(T_i,R_s)$ is minimized. These steps are repeated until convergence is achieved (Algorithm 1). To avoid getting stuck in local optima, we allow the user to specify the number of restarts, initializing each restart with a new randomly-generated clustering. Alternatively, we allow the user to specify a time limit, restarting the algorithm until the running time exceeds the time limit.

4.4 Model selection for the number k of clusters

Given input trees $n=\left|\mathcal{T}\right|$ with m vertices, the number k of clusters ranges from 1 to n. To decide which number k of clusters to use, we apply the Bayesian Information Criterion (BIC). Note that this criterion requires a likelihood of the data given the model. In our case, the model corresponds to a solution $(\mathcal{R},\sigma )$ to MCT instance $(\mathcal{T},k)$. We need to define a likelihood function that is proportional to the probability $\mathrm{Pr}(\mathcal{T}|\mathcal{R},\sigma )$ of generating the data $\mathcal{T}$ given solution $(\mathcal{R},\sigma )$. To do so, we define the normalized distance$\overline{d}(T,T\prime )$ between two trees T and $T\prime$ as

$$\overline{d}(T,T\prime )=\frac{d(T,T\prime )}{2(m-1)}.$$ (22)

Therefore, the mean normalized distance$\overline{d}(\mathcal{T},\mathcal{R},\sigma )$ of a set $\mathcal{T}$ of n trees and a solution $(\mathcal{R},\sigma )$ equals

$$\overline{d}(\mathcal{T},\mathcal{R},\sigma )=\frac{{\sum }_{i=1}^{n}d(T_i,S_{\sigma (i)})}{2n(m-1)}.$$ (23)

We assume that the probability $\mathrm{Pr}(T|\mathcal{R},\sigma )$ of generating a tree T in $\mathcal{T}$ by a model $(\mathcal{R},\sigma )$ is proportional to the mean normalized similarity$h(\mathcal{T},\mathcal{R},\sigma )$ defined as

$$h(\mathcal{T},\mathcal{R},\sigma )=1-\overline{d}(\mathcal{T},\mathcal{R},\sigma )=1-\frac{{\sum }_{i=1}^{n}d(T_i,R_{\sigma (i)})}{2n(m-1)}.$$ (24)

Note that as k increases, the sum of the distances of the optimal solutions to a set $\mathcal{T}$ of trees is strictly decreasing by Proposition 2. Therefore, as k increases, the likelihood $h(\mathcal{T},\mathcal{R},\sigma )$ of optimal solutions $(\mathcal{R},\sigma )$ is increasing. Assuming independence in generating each input tree, the probability $\mathrm{Pr}(\mathcal{T}|\mathcal{R},\sigma )$ of the model generating a set $\mathcal{T}$ of n trees is $\mathrm{Pr}{(T|\mathcal{R},\sigma )}^n$, which is proportional to $h{(\mathcal{T},\mathcal{R},\sigma )}^n$.

However, as k increases, the complexity of the model, i.e. the number of parameters in solution $(\mathcal{R},\sigma )$, is also increasing. Using Proposition 1, optimal consensus trees $\mathcal{R}$ are determined by the clustering σ. The clustering σ contains k clusters, amounting to the following Bayesian Information Criterion (BIC).

$$\frac{k}{2}\ln n-2\hspace{0.17em}\ln \hspace{0.17em}(h{(\mathcal{T},\mathcal{R},\sigma )}^n)$$ (25)

$$=\frac{k}{2}\hspace{0.17em}\ln \hspace{0.17em}n-2n\hspace{0.17em}\ln \hspace{0.17em}\left[1-\frac{{\sum }_{i=1}^{n}d(T_i,S_{\sigma (i)})}{2n(m-1)}\right]$$ (26)

The factor of 1/2 ensures that the two terms are of similar scale. The task is now to choose k such that the above equation is minimized.

5 Results

We implemented the three algorithms (BF, MILP and CA) in C++ using the LEMON graph library (http://lemon.cs.elte.hu). We implemented MILP using CPLEX v12.8 (https://www.ibm.com/analytics/cplex-optimizer). In this section, we illustrate the application of our methods to simulated and real data. Specifically, Section 5.1 provides results of our algorithms on simulated data, whereas Section 5.2 applies our methods to recent lung cancer data (Jamal-Hanjani et al., 2017).

5.1 Simulations

To evaluate our methods, we simulate bulk DNA sequencing data of tumors using a previously published tumor simulator (El-Kebir et al., 2018). We generate a total of 45 instances, composed of either five or ten bulk samples per instance and $m\in \{9,11,13\}$ mutation clusters (Supplementary Table S1). Subsequently, we run the SPRUCE algorithm (El-Kebir et al., 2015) to enumerate the set $\mathcal{T}$ of mutation trees for each instance. The mean number of trees is 47 (Supplementary Table S1). We group the 45 simulated instances by the number of mutation trees into three classes, resulting in 16 ‘small’ instances with 6-10 trees, 15 ‘medium’ instances with 11–39 trees and 14 ‘large’ instances with 40-352 trees (Fig. 3a).

Fig. 3.

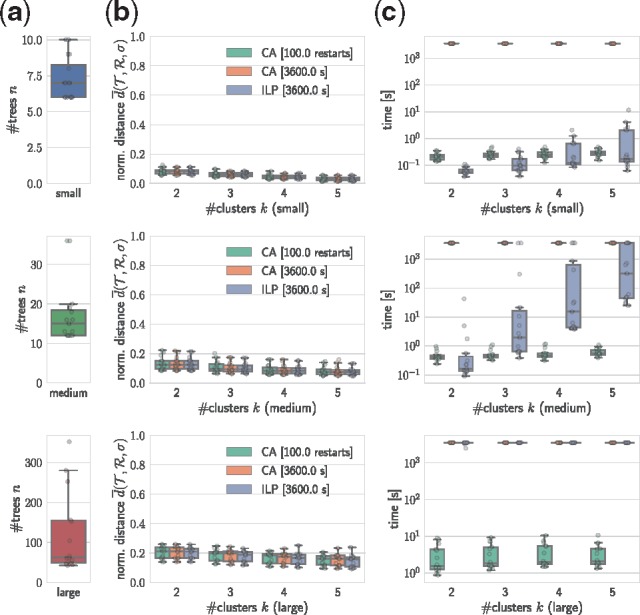
Coordinate ascent (CA) algorithm computes consensus trees with similar mean distance as the MILP algorithm in only a fraction of the time. (a) Number of trees for each class of simulated instances. (b) Mean normalized distance for solutions for each method. (c) Running time in seconds for each method (logarithmic scale)

For each class of instances (small, medium or large) and number $k\in \{2,\dots ,5\}$ of clusters, we run the mixed integer linear program (MILP) and the brute force algorithm (BF) restricted to a running time of 1 h. In addition, we run the coordinate ascent (CA) algorithm in two modes: (i) using a time limit of 1 h, and (ii) restricted to 100 restarts. We run each algorithm in single-threaded mode on a computer with two Intel Xeon CPUs at 2.6 GHz (32 cores) and 512 GB of RAM.

Supplementary Table S2 shows the number of instances solved to optimality by MILP and BF. We find that MILP outperforms the BF algorithm, solving 65% of instances to optimality versus 45.6% for BF. All small instances were solved to optimality by MILP, whereas BF failed to solved two small instances with k = 5 clusters within the time limit. In particular, performance of BF decreases with increasing number k of clusters and number n of input trees, reflecting the exponential increase in the number kⁿ of enumerated clusterings with increasing number n of trees. Similarly, MILP performance decreases with increasing n and k (Supplementary Fig. S1). The instances that were solved to optimality by MILP include all instances solved to optimality by BF. For these reasons, we exclude BF from further analyses and focus on MILP and CA.

To investigate the behavior of CA versus the MILP algorithm, we compute the mean normalized distance $\overline{d}(\mathcal{T},\mathcal{R},\sigma )$ for each simulated instance $\mathcal{T}$ and output $(\mathcal{R},\sigma )$. This distance is defined in Section 4.4. We find that CA using only 100 restarts identifies solutions with similar mean normalized distance as CA and MILP using a time limit of 1 h (Fig. 3b). These 100 restarts were completed in seconds (Fig. 3c). Thus, CA with a small number of restarts computes high-quality consensus trees at only a fraction of the time required by MILP. Moreover, the CA algorithm with 100 restarts recovers all optimal solutions computed by MILP (Supplementary Table S2).

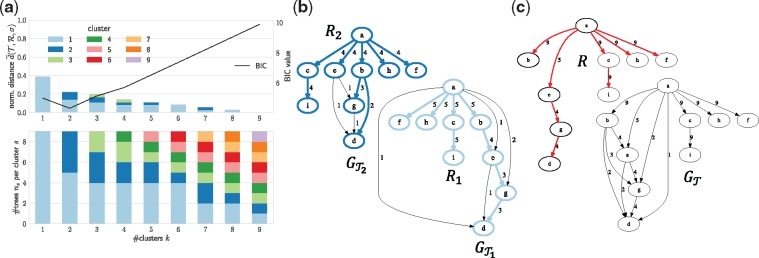
Finally, we consider one simulated instance to illustrate the advantages of the Multiple Consensus Tree over previous approaches, and to illustrate the model selection step for choosing the number k of clusters. The instance we consider has n = 9 trees and m = 9 mutation clusters (Supplementary Fig. S2). Thus, the maximum number k of clusters equals n = 9. We use CA with 100 restarts to compute consensus trees $\mathcal{R}=\{R_1,\dots ,R_k\}$ and clusterings $\sigma :[n]\to [k]$ for each number $k\in \{1,\dots ,9\}$ of clusters. In line with Proposition 2, Figure 4a shows that the mean normalized distance $\overline{d}(\mathcal{T},\mathcal{R},\sigma )$ decreases with increasing number k of clusters. In particular, $\overline{d}(\mathcal{T},\mathcal{R},\sigma )=0$ for k = 9 clusters, each containing a single input tree.

Fig. 4.

Adequate representation of the solution space $\mathcal{T}$ requires k = 2 consensus trees. This simulated instance contains $n=\left|\mathcal{T}\right|=9$ input trees. (a) Top plot shows the mean normalized distance inferred by the coordinate ascent algorithm as a function of the number k of clusters. Bottom plot shows the number of trees per cluster. Using the BIC criterion, we summarize $\mathcal{T}$ with k = 2 clusters. (b) Parent-child graphs $G_{{\mathcal{T}}_1},G_{{\mathcal{T}}_2}$ and consensus trees R₁, R₂ (colored edges) of computed clustering. (c) Parent-child graph $G_{\mathcal{T}}$ (bottom) and corresponding consensus tree R (top) do not adequately represent the topological features in input trees $\mathcal{T}$. That is, edge (b, e) does not co-occur with edges (b, d) or (b, g) in $\mathcal{T}$, which cannot be concluded from $G_{\mathcal{T}}$. Moreover, consensus tree R does not contain the edge (b, e), which occurs in 4 out of 9 input trees. Hence, R is an incomplete summary of $\mathcal{T}$

Applying the Bayesian Information Criterion (BIC), we select the solution with k = 2 clusters (Fig. 4a). The two resulting consensus trees R₁ and R₂ contain $\left|{\mathcal{T}}_1\right|=5$ and $\left|{\mathcal{T}}_2\right|=4$ input trees, respectively (Fig. 4a). Figure 4b and c show the parent-child graphs $G_{{\mathcal{T}}_1}$ and $G_{{\mathcal{T}}_2}$, with colored edges indicating the two corresponding consensus trees. In these figures, we see that the two consensus trees R₁ and R₂ differ in vertices d, e and g. Input trees ${\mathcal{T}}_1$ include the edge (b, e) whereas input trees ${\mathcal{T}}_2$ include the edge (a, e). In addition, trees in ${\mathcal{T}}_1$ include a branch composed of edges (e, g) and (g, d), whereas trees ${\mathcal{T}}_2$ contain d and g as siblings of parent b. Importantly, these topological features are not apparent when summarizing $\mathcal{T}$ by the parent-child graph $G_{\mathcal{T}}$ or by constructing a single consensus tree from $G_{\mathcal{T}}$. That is, the parent-child graph $G_{\mathcal{T}}$ does not show patterns of co-occurrence and mutual exclusivity among edges. For instance, edge (b, e) does not co-occur with edges (b, d) or (b, g) in $\mathcal{T}$, which cannot be concluded from $G_{\mathcal{T}}$ (Fig. 4c). Furthermore, the unique optimal consensus tree R obtained from $G_{\mathcal{T}}$ does not contain the edge (b, e) (Fig. 4c), which occurs in 4 out of 9 input trees (Supplementary Fig. S2). Hence, R is an incomplete summary of $\mathcal{T}$. Only by summarizing $\mathcal{T}$ using multiple consensus trees do these topological features become apparent. Supplementary Figure S3 shows the distribution of the identified number k of clusters for each class of instances, showing that the number k of clusters selected by BIC increases with the number n of trees.

5.2 Real data

We consider a lung cancer cohort of 100 patients (Jamal-Hanjani et al., 2017), composed of tumors that have undergone multi-region bulk DNA sequencing. Jamal-Hanjani et al. (2017) used PyClone (Roth et al., 2014) to cluster mutations with similar cancer cell fractions and ran CITUP (Malikic et al., 2015) to compute solution spaces $\mathcal{T}$ for each tumor, identifying multiple trees for 25 patients. We focus our analysis on patients CRUK0013 and CRUK0037, the only two patients with more than four reported trees. Jamal-Hanjani et al. (2017) identified 8 trees for patient CRUK0013 (Supplementary Fig. S4) and 17 trees for patient CRUK0037 (Supplementary Fig. S5). To summarize these trees, we run CA coupled with the model selection procedure for the number k of clusters.

First, we consider patient CRUK0013, which has m = 9 vertices/mutation clusters. Figure 5a shows the relationship between the number k of clusters and the mean normalized distance $\overline{d}(\mathcal{T},\mathcal{R},\sigma )$ computed by the CA method. The decrease in distance from k = 1 to k = 2 is modest. Consequently, the BIC prefers the k = 1 solution. Inspection of the parent-child graph $G_{\mathcal{T}}$ and consensus tree R reveals that the consensus tree R covers 55 out 64 edges in $\mathcal{T}$, where the 9 uncovered edges are incoming to v₈ and v₉. In particular, there are no patterns of co-occurrence or mutual exclusivity among the edges leading to v₈ and v₉ in individual trees in $\mathcal{T}$ (Fig. 5c), justifying the choice for k = 1 cluster. This example, in addition to our simulated data results (Supplementary Fig. S3), show that our method does not overfit the input data when there are no clear topological features in the solution space.

Fig. 5.

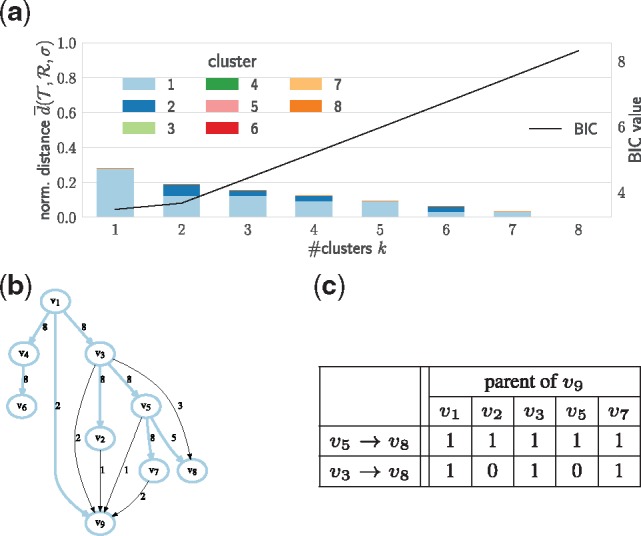
Lung cancer patient CRUK0013 with n = 8 trees is accurately summarized by a single consensus tree. (a) The mean normalized distance inferred by the coordinate ascent algorithm as a function of the number k of clusters, and the BIC. (b) The parent-child graph and consensus tree. (c) The number of input trees supporting each possible combination of topological features

By contrast, for patient CRUK0037, with m = 10 vertices (mutations clusters) and n = 17 trees, our method infers k = 2 clusters (Fig. 6a). Inspection of the n = 17 input trees reveals that there is variation in the placement of five vertices, as shown by the parent-child graph (Fig. 6b). We focus our attention on vertices v₅, v₇ and v₁₀, each with two possible parents. Figure 6c shows the contingency table of all combinations of these three clusters, enabling us to observe that $v_1\to v_7$ and $v_4\to v_{10}$ are mutually exclusive. This pattern of mutual exclusivity is not apparent in the parent-child graph obtained from all trees (Fig. 6b). Furthermore, the placement of the three mutation clusters in the k = 1 consensus tree obtained from this graph is supported by only 2 out of 17 input trees. Thus, with k = 1, neither the parent-child graph nor the consensus tree provide an adequate summary of the solution space of this patient.

Fig. 6.

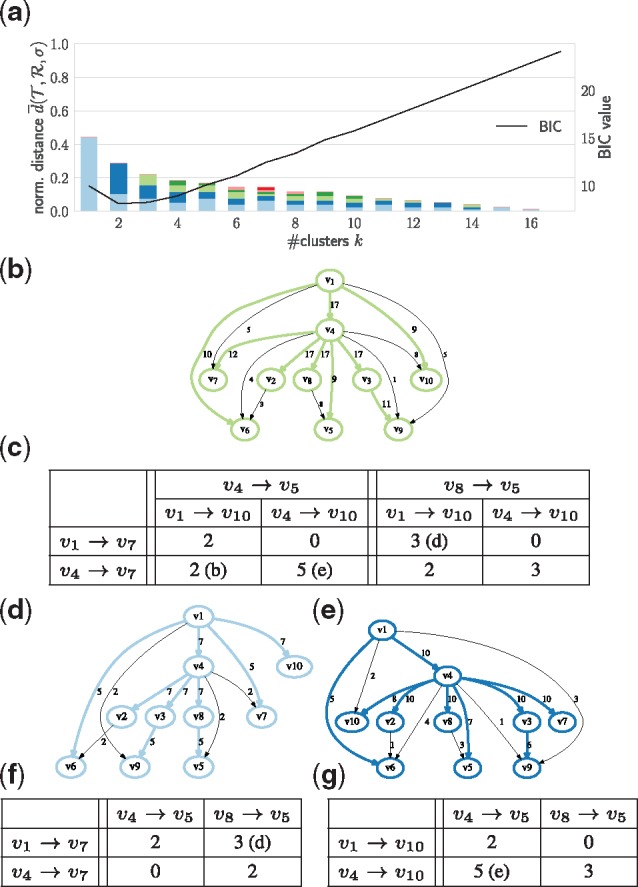
Lung cancer patient CRUK0037 with n = 17 trees is accurately summarized by k = 2 consensus trees. (a) The mean normalized distance inferred by the coordinate ascent algorithm as a function of the number k of clusters, and the BIC. (b) The parent-graph and the consensus tree for k = 1. (c) The number of input trees supporting each possible combination of topological features. (d, e) The two parent-child graphs and consensus trees for k = 2. (f, g) The number of input trees in each cluster supporting each possible combination of topological features.

Our method partitions the input trees into k = 2 clusters: one cluster with seven input trees (Fig. 6d) and the other cluster with the remaining ten trees (Fig. 6e). This partition identifies patterns of co-occurrence and mutual exclusivity that are unique to each cluster. All seven trees in the first cluster contain the edge $v_1\to v_{10}$, whereas the remaining ten trees in the second cluster contain the edge $v_4\to v_7$. On the other hand, the trees in the first cluster exhibit mutual exclusivity between $v_4\to v_5$ and $v_4\to v_7$, whereas these two edges are present in 7/10 trees in the second cluster. Similarly, edges $v_1\to v_{10}$ and $v_8\to v_5$ are mutually exclusivity in all ten trees in the second cluster, whereas these two edges are present in 5/7 trees in the first cluster. Thus, our method partitions the solution space of 17 trees into two clusters with distinct topological features. In addition, our method infers a consensus tree for each of the two clusters. The placement of v₅, v₇ and v₁₀ in the consensus tree of the first cluster is supported by 3/7 trees assigned to this cluster, being the dominant topological feature among these seven trees (Fig. 6f). Similarly, the consensus tree of the second cluster highlights the most representative placement of these three vertices (supported by 5/10 trees, see Fig. 6g).

The first consensus tree contains the branch $v_1\to v_{10}$, whereas the second consensus tree contains the branch $v_1\to v_4\to v_{10}$. Vertex v₁₀ contains the driver mutation HOOK3, whose placement may alter conclusions in downstream analyses, including those that assess tumor fitness to immunotherapy (Łuksza et al., 2017) or identify repeated evolutionary trajectories among driver mutations (Turajlic et al., 2018b). To avoid incorrect conclusions both consensus trees must be considered in these analyses. Our method facilitates such more robust downstream analyses, by simultaneously clustering input trees according to shared topological features, identifying the right number of clusters depending on the degree of differences among solution trees.

6 Discussion

We introduced the Multiple Consensus Tree (MCT) problem that enables one to accurately summarize a solution set $\mathcal{T}$ composed of tumor phylogenies with distinct topological features using multiple consensus trees, overcoming limitations of current approaches. Current approaches that summarize $\mathcal{T}$ by constructing a graph that is the union of all edges in $\mathcal{T}$ fail to account for mutual exclusivity or co-occurence of edges in individual trees (Deshwar et al., 2015; El-Kebir et al., 2016; Jiao et al., 2014). In a similar vein, summarizing $\mathcal{T}$ by constructing a single consensus tree as described by Govek et al. (2018) may fail to represent topological features that are specific to a subset of trees in $\mathcal{T}$.

Mathematically, MCT is a generalization of the Single Consensus Tree to k consensus trees. That is, given input trees $\mathcal{T}$ and integer k > 0, we aim to simultaneously partition $\mathcal{T}$ into k disjoint, non-empty clusters and reconstruct a consensus tree for each cluster with minimum total distance. We proved that MCT is NP-hard. In addition, we presented two exact approaches based on mixed integer linear programming (MILP) and exhaustive enumeration. Using simulated data, we showed that the MILP efficiently solves small instances to optimality. In addition, we introduced a heuristic based on coordinate ascent that scales to large input instances. By benchmarking our methods on simulated data, we showed that the heuristic approach recovered all optimal solutions identified by the MILP at only a fraction of the time. We demonstrated the applicability of the MCT problem on lung cancer data, illustrating that our model selection step selects the right number k of clusters depending on the degree of differences among solution trees.

There are a couple of avenues for future research. First, we used the parent-child distance in this manuscript. One could consider alternative distance functions, such as the tree distance function recently introduced by Karpov et al. (2018). Second, the complexity of the MCT given fixed number k of clusters remains open. As we have seen in our analysis of real and simulated data, it is often the case that $k\ll n$. Thus, an algorithm that is fixed parameter tractable in k would have immediate practical applications. Third, there may be multiple optimal solutions to MCT. More specifically, for a fixed clustering there might be multiple optimal consensus trees, and there might be multiple clusterings with the same total distance. Similarly to the original problem, it will be an interesting direction to identify common patterns and differences among such optimal solutions. Fourth, the mutation trees $\mathcal{T}$ considered in this manuscript adhere to the infinite sites assumption. Recent works in cancer phylogenetics have considered other evolutionary models, such as the infinite alleles model (El-Kebir et al., 2016), the Dollo parsimony model (Bonizzoni et al., 2017; El-Kebir, 2018) or the finite sites model (Zafar et al., 2017). It will be an interesting question to adapt the methodology and problem to trees that employ these alternative models of evolution. Finally, a characterization of the distribution of trees in the solution space $\mathcal{T}$ and their topological features under an error model of single-cell or bulk DNA sequencing has not been attempted yet. Akin to the work by Steel and Penny (1993) in classic phylogenetics, such work would provide much needed theoretical guidance on the larger issue of non-uniqueness of solutions in cancer phylogenetics.

Funding

This work was supported by UIUC Center for Computational Biotechnology and Genomic Medicine (grant: CSN 1624790) and the National Science Foundation (grant: 1850502).

Conflict of Interest: none declared.