GkmExplain: fast and accurate interpretation of nonlinear gapped k-mer SVMs

Abstract

Summary

Support Vector Machines with gapped k-mer kernels (gkm-SVMs) have been used to learn predictive models of regulatory DNA sequence. However, interpreting predictive sequence patterns learned by gkm-SVMs can be challenging. Existing interpretation methods such as deltaSVM, in-silico mutagenesis (ISM) or SHAP either do not scale well or make limiting assumptions about the model that can produce misleading results when the gkm kernel is combined with nonlinear kernels. Here, we propose GkmExplain: a computationally efficient feature attribution method for interpreting predictive sequence patterns from gkm-SVM models that has theoretical connections to the method of Integrated Gradients. Using simulated regulatory DNA sequences, we show that GkmExplain identifies predictive patterns with high accuracy while avoiding pitfalls of deltaSVM and ISM and being orders of magnitude more computationally efficient than SHAP. By applying GkmExplain and a recently developed motif discovery method called TF-MoDISco to gkm-SVM models trained on in vivo transcription factor (TF) binding data, we recover consolidated, non-redundant TF motifs. Mutation impact scores derived using GkmExplain consistently outperform deltaSVM and ISM at identifying regulatory genetic variants from gkm-SVM models of chromatin accessibility in lymphoblastoid cell-lines.

Availability and implementation

Code and example notebooks to reproduce results are at https://github.com/kundajelab/gkmexplain.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Deciphering the combinatorial regulatory DNA sequence patterns that determine transcription factor (TF) binding and chromatin state is critical to understand gene regulation and interpret the molecular impact of regulatory genetic variation. High-throughput in vivo and in vitro functional genomics experiments provide large datasets to train predictive models using machine learning approaches that can learn the relationship between regulatory DNA sequences and their associated molecular phenotypes. A Support Vector Machine (SVM) is a popular type of supervised classification model that learns an optimal linear separating hyperplane in a high-dimensional feature space. SVMs rely on a function called a kernel that measures the similarity between all pairs of datapoints in the high-dimensional feature space. SVMs are appealing because they are stable to train and, when used with an appropriate kernel, can model complex input-output relationships. The gapped k-mer (gkm) string kernel (Ghandi et al., 2014; Leslie and Kuang, 2004) was developed to enable training SVMs on string inputs such as DNA or protein sequences. The gkm kernel computes a similarity between pairs of sequences based on the biologically motivated notion of shared approximate occurrences of short subsequences allowing for gaps and mismatches. The gkm kernel can be further combined with other nonlinear kernels such as the radial basis function (RBF) kernel to capture complex nonlinear relationships between the input string features. Gapped k-mer SVMs and their extensions have been successfully applied to several prediction tasks in regulatory genomics such as TF binding and chromatin accessibility prediction (Ghandi et al., 2014; Lee, 2016; Lee et al., 2015). Interpretation of these trained SVMs is important to decipher the patterns such as TF binding motifs present in input DNA sequences that are predictive of their associated molecular labels. Moreover, these models can be used to predict the impacts of genetic variants in regulatory DNA sequences (Lee et al., 2015). Unfortunately, interpretation of gkm-SVMs can be challenging. DeltaSVM (Lee et al., 2015), a popular tool that estimates the effects of variants using a trained gkm-SVM, does not give improvements in variant scoring when applied to SVMs trained with nonlinear versions of the gkm kernel, even though these nonlinear kernels perform better at regulatory sequence classification (suggesting that deltaSVM is not fully leveraging the advantages of the nonlinear kernel) (Lee, 2016). In-silico mutagenesis (ISM) (Bromberg and Rost, 2008), an interpretation approach that involves measuring the impact of exhaustive perturbations of every nucleotide in an input sequence on the output label, can be computationally inefficient and can fail to reveal the presence of motifs when nonlinear saturation effects are present (Shrikumar et al., 2017). SHAP (Lundberg and Lee, 2017), a method based on estimating Shapely values, can address the nonlinearity issues faced by deltaSVM and ISM but is even less computationally efficient than ISM. As such, there is a need for fast interpretation of gapped k-mer Support Vector Machines that works reliably in the presence of nonlinear effects.

2 Our contributions

Here we present GkmExplain, a computationally efficient method for explaining the predictions of both linear and nonlinear versions of gapped k-mer SVMs. Specifically, GkmExplain is a feature attribution method that efficiently computes the predictive contribution or importance of every nucleotide in an input DNA sequence to its associated output label through the lens of a gkm-SVM model. GkmExplain works by decomposing the output of the gapped k-mer string kernel into the contributions of matching positions within the k-mers. It has theoretical connections to Integrated Gradients, a feature attribution method originally developed to interpret deep learning models (Sundararajan et al., 2017). On simulated regulatory DNA sequences, where the ground truth predictive motifs are known, we find that GkmExplain substantially outperforms deltaSVM and ISM at identifying predictive motifs and also outperforms SHAP while being multiple orders of magnitude more computationally efficient. We further show that by supplying GkmExplain contribution score profiles to the recently-developed importance score clustering and aggregation tool TF-MoDISco (Shrikumar et al., 2018), we can recover motifs of TFs from gkm-SVM models trained on in vivo TF binding data. The resulting motifs are more consolidated, less redundant and better matches to known canonical TF motifs when compared to those produced by the method of Ghandi et al. (2014) as well as those produced by the traditional motif discovery approaches MEME and HOMER. Finally, using non-linear gkmSVM models trained to identify regulatory DNA sequences associated with accessible chromatin, we show that mutation impact scores derived through GkmExplain outperform deltaSVM and ISM at identifying DNase-I hypersensitive quantitative trait loci (dsQTLs) in lymphoblastoid cell-lines (LCLs).

3 Background

3.1 Gapped k-mers

A full k-mer refers to a letter subsequence of length k—for example, AAGT is a full 4-mer. By contrast, a gapped k-mer refers to a subsequence containing k letters and some number of gaps—for example, A*AG*T is a gapped 4-mer containing 2 gaps (* is used to denote a gap). In the gkm-SVM implementation, the parameter l denotes the full length of the subsequences considered (including gaps), while k denotes the number of non-gap positions—for example, the l-mer ACG (where l = 3) contains the gapped k-mers AC*, A*G and *CG (where k = 2). The parameter l is also called the ‘word length’. The number of possible gapped k-mers can be calculated using the formula $\left(\begin{array}{c}l\\ k\end{array}\right)4^k$. A higher value of l allows the gkm-SVM to learn wider patterns, while a higher value of the number of gaps (l – k) increases the flexibility of the learned patterns.

3.2 Support vector machines and gapped k-mer kernels

Let x be an input to a Support Vector Machine (SVM), m be the total number of support vectors, Zⁱ be the ith support vector, yⁱ be the label (+1 or -1) associated with the ith support vector, α_i be the weight associated with the ith support vector, b be a constant bias term and K be a kernel function that is used to compute a similarity score between Zⁱ and x. SVMs produce an output of the form:

$$F(X)=b+\sum _{i=1}^m{\alpha }_i{y}^{i}K(Z^i,\mathbf{x})$$ (1)

Kernel functions can be thought of as implicitly mapping their inputs to vectors in some feature space and then computing a dot product. For example, the gapped k-mer kernel implicitly maps its DNA sequence inputs to feature vectors representing the normalized counts of distinct gapped k-mers. Formally, it can be written as:

$$\begin{array}{cc}{K}_{\text{gkm}}(S_1,S_2)\hfill & =\langle \frac{f_{\text{gkm}}^{S_1}}{\Vert f_{\text{gkm}}^{S_1}\Vert },\frac{f_{\text{gkm}}^{S_2}}{\Vert f_{\text{gkm}}^{S_2}\Vert }\rangle =\frac{\langle f_{\text{gkm}}^{S_1},f_{\text{gkm}}^{S_2}\rangle }{\sqrt{\langle f_{\text{gkm}}^{S_1},f_{\text{gkm}}^{S_1}\rangle }\sqrt{\langle f_{\text{gkm}}^{S_2},f_{\text{gkm}}^{S_2}\rangle }}\hfill \end{array}$$ (2)

where $f_{\text{gkm}}^{S_1}$ and $f_{\text{gkm}}^{S_2}$ are feature vectors representing the counts of distinct gapped k-mers in sequences S₁ and S₂ respectively. As the feature space corresponding to gapped k-mer counts can be large, for computationally efficiency the gkm kernel (Ghandi et al., 2014; Leslie and Kuang, 2004) computes the dot product $\langle f_{\text{gkm}}^{S_1},f_{\text{gkm}}^{S_2}\rangle$ without explicitly computing $f_{\text{gkm}}^{S_1}$ or $f_{\text{gkm}}^{S_2}$. Let $u_i^{S_x}$ represent the identity of the l-mer at position i in sequence S_x, and let $f_m(u_i^{S_1},u_j^{S_2})$ be a function that returns the number of mismatching positions between the l-mers $u_i^{S_1}$ and $u_j^{S_2}$. The gkm kernel leverages the fact that:

$$\langle f_{\text{gkm}}^{S_1},f_{\text{gkm}}^{S_2}\rangle =\sum _i\sum _{j}h\left(f_m(u_i^{S_1},u_j^{S_2})\right)$$ (3)

where the indexes i and j sum over all l-mers in S₁ and S₂ respectively, and h(m) is a function that returns the contribution of an l-mer pair with m mismatches to the dot product $\langle f^{S_1},f^{S_2}\rangle$. For example, if $u_i^{S_1}$ and $u_j^{S_2}$ are a pair of l-mers with m mismatches between them, then the number of gapped k-mers they share is $\left(\begin{array}{c}l-m\\ k\end{array}\right)$. Thus, in the case of the traditional gapped k-mer kernel, $h(m)=\left(\begin{array}{c}l-m\\ k\end{array}\right)$. Ghandi et al. (2014) additionally proposed variants of the gapped k-mer kernel such as the truncated gkm-filter that differ in the function h(m), but otherwise have an identical formulation.

For computational efficiency, the gkm-SVM implementation contains a parameter d that sets h(m) = 0 for all m > d (regardless of the values of l and k). This is efficient because it limits the number of l-mer pairs that need to be considered to those where $m\le d$. In the documentation, d is referred to as the maximum number of allowed mismatches.

3.3 Extensions of the gkm kernel

Lee (2016) proposed variants of the gapped k-mer kernel. We describe these variants below.

3.3.1 The wgkm kernel

In regulatory DNA sequence, motifs often exhibit a positional preferences—for example, they may tend to occur close to the summit of peaks in ChIP-seq data. The weighted gkm (wgkm) kernel leverages this property by giving l-mers weights according to the position at which they occur. These weights are pre-defined by the user, and the lsgkm implementation supports weights that decay exponentially with distance from the center of the sequence. A dot product in the feature space of weighted gapped k-mers can be expressed as:

$$\langle f_{\text{wgkm}}^{S_1},f_{\text{wgkm}}^{S_2}\rangle =\sum _i\sum _{j}h\left(f_m(u_i^{S_1},u_j^{S_2})\right)w_i{w}_j$$ (4)

where w_i and w_j are the weights associated with l-mers at positions i and j respectively. Analogous to Eqn. 2, the wgkm kernel can be written as:

$$\begin{array}{cc}{K}_{\text{wgkm}}(S_1,S_2)\hfill & =\langle \frac{f_{\text{wgkm}}^{S_1}}{\Vert f_{\text{wgkm}}^{S_1}\Vert },\frac{f_{\text{wgkm}}^{S_2}}{\Vert f_{\text{wgkm}}^{S_2}\Vert }\rangle =\frac{\langle f_{\text{wgkm}}^{S_1},f_{\text{wgkm}}^{S_2}\rangle }{\sqrt{\langle f_{\text{wgkm}}^{S_1},f_{\text{wgkm}}^{S_1}\rangle }\sqrt{\langle f_{\text{wgkm}}^{S_2},f_{\text{wgkm}}^{S_2}\rangle }}\hfill \end{array}$$ (5)

The gkm kernel is a special case of the wgkm kernel with w_i=1 for all i.

3.3.2 The gkmrbf kernel

The RBF kernel is useful for modeling complex nonlinear interactions between input features. It is defined as $K_{\text{RBF}}(\mathbf{x},\mathbf{y})=\text{exp}\hspace{0.17em}\left(-\frac{{\Vert \mathbf{x}-\mathbf{y}\Vert }^2}{2{\sigma }^2}\right)$ (where x and y are vectors). Recall that the gkm kernel can be thought of as mapping the input sequences to a feature space of normalized gapped k-mer counts. The gkmrbf kernel maps sequences to the same feature space as the gkm kernel, but then applies the RBF kernel to the vectors rather than the dot product. For efficient computation, this equality is leveraged:

$${\Vert \mathbf{x}-\mathbf{y}\Vert }^2=\langle \mathbf{x}-\mathbf{y},\mathbf{x}-\mathbf{y}\rangle =\langle \mathbf{x},\mathbf{x}\rangle +\langle \mathbf{y},\mathbf{y}\rangle -2\langle \mathbf{x},\mathbf{y}\rangle$$

As gkm feature vectors are always unit normalized, $\langle \mathbf{x},\mathbf{x}\rangle =\langle \mathbf{y},\mathbf{y}\rangle =1$. If we let $\gamma =\frac{1}{{\sigma }^2}$, we get:

$$K_{\text{gkmrbf}}(S_x,S_y)=\text{exp}\hspace{0.17em}\left(\gamma (K_{\text{gkm}}(S_x,S_y)-1)\right)$$ (6)

3.3.3 The wgkmrbf kernel

Analogous to Eqn. 6, the wgkmrbf kernel is a combination of the wgkm kernel and the RBF kernel:

$$K_{\text{wgkmrbf}}(S_x,S_y)=\text{exp}\hspace{0.17em}\left(\gamma (K_{\text{wgkm}}(S_x,S_y)-1)\right)$$ (7)

4 Previous work

4.1 DeltaSVM

DeltaSVM (Lee et al., 2015) is a popular tool developed by the authors of gkm-SVM to estimate the in-silico effects of genetic variants. DeltaSVM precomputes a score for each l-mer as the output when the gkm-SVM is supplied only that l-mer as input. It then estimates the impact of a mutation as the total change in the scores of all l-mers overlapping the mutation. Because the scores of individual l-mers are precomputed, calculating the impact of a single mutation is computationally efficient. However, this formulation does not consider non-additive relationships between l-mers that can be learned by the gkmrbf or wgkmrbf kernels, such as those illustrated in Figure 1. It also does not consider the influence of positional weights that are present in the wgkm or wgkmrbf kernels. Consistent with this, Lee (Lee, 2016) observed that deltaSVM used in conjunction with the gkmrbf, wgkm or wgkmrbf kernels did not produce improvements in variant scoring relative to the gkm kernel, even when predictive models trained with the former kernels performed better.

Fig. 1.

Toy example illustrating drawback of ISM. Presented is a gkmrbf model exhibiting ‘AND’-type logic: at least one instance of ‘TATA’ and one instance of ‘CCGG’ must be present for the model to give a high positive prediction. The model has a single positively-weighted support vector containing one TATA and one CCGG. It has two negatively-weighted support vectors consisting exclusively of TATA and CCGG. Importance scores on a sequence containing two instances of TATA (blue boxes) and one instance of CCGG (violet box) are shown. The sequence has a positive prediction. Although the TATA instances are relevant for the positive prediction, ISM does not clearly highlight them. This is because perturbing any single TATA instance does not tend to decrease the prediction, as high similarity with the positively-weighted support vector can be achieved with only one TATA instance

4.2 In-silico mutagenesis (ISM)

An alternative to deltaSVM for estimating the impact of individual mutations is to directly compute the change in the output of the SVM when the mutation is introduced into the input sequence. This approach is called in-silico mutagenesis (ISM) (Bromberg and Rost, 2008), and it has been successfully applied to interpret complex machine learning models (Zhou and Troyanskaya, 2015). However, repeatedly rerunning the model to compute the impact of every possible mutation in an input sequence can become computationally inefficient. Further, when ISM is applied to a model that has learned nonlinear saturating effects, it can fail to reveal the presence of motifs in a sequence (Shrikumar et al., 2017). Such nonlinear effects can be learned by the gkmrbf or wgkmrbf kernels (Section 3.3), both of which were found to produce improvements in performance relative to the gkm kernel (Lee, 2016). An example is provided in Figure 1.

4.3 SHAP

SHAP (Lundberg and Lee, 2017) is a general-purpose model interpretation algorithm that addresses the saturation issue of ISM by sampling several combinations of input perturbations and looking at the change in the output for all the sets of perturbations. Perturbations are performed by replacing the perturbed features with the values that those features have in a user-supplied ‘background’. For example, in the case of DNA sequence, if the original input sequence is AAA and the background is TTT, and positions 1 and 3 are sampled for perturbation, then the corresponding perturbed sequence would be TAT. In scenarios where there is no single background input, but rather there is a collection of potential background inputs (as is often the case for DNA sequence), SHAP computes the model output when each background input is used individually for substitution and takes the average. For example, if the original input sequence is AAA, and there are three background sequences of TTT, CCC and GGG, then when computing the output when positions 1 and 3 are sampled for perturbation, SHAP would compute the average of the model output over TAT, CAC and GAG. The runtime of SHAP thus depends on the product of the number of sampled perturbations and the number of background sequences.

Although SHAP has been shown to have good theoretical guarantees, it is far less computationally efficient than ISM because the number of sampled perturbations needed to get accurate importance estimates can be quite large. For example, the authors of SHAP used 50 000 sampled perturbations to obtain stable estimates of feature importance on a single example from the MNIST digit recognition dataset (each MNIST digit is a 28 × 28 image, and only one background—consisting of the all-zeros image—was used). In our experiments with simulated DNA sequences of length 200 bp, we ran SHAP with both 2000 and 20 000 sampled perturbations per input and 20 background sequences per input, where the background sequences were generated for each input sequence by performing a dinucleotide-preserving shuffle. We found that increasing the number of background sequences from 20 to 200 did not appear to substantially change the results (Fig. 2). At 20 000 perturbations per input and 20 background sequences, the number of model evaluations needed per sequence was $20\hspace{0.17em}000\times 20=400\hspace{0.17em}000$. Despite this hefty computational requirement, we still found that GkmExplain outperformed SHAP (Figs 2 and 4 and Supplementary Fig. SA.1).

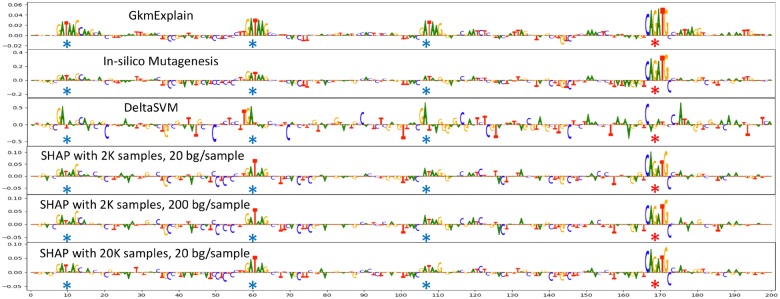
Fig. 2.

Comparison of GkmExplain, ISM, deltaSVM and SHAP on an individual simulated sequence. An SVM with a gkmrbf kernel with l = 6, k = 5 and d = 1 was used to distinguish sequences containing both TAL1 and GATA1 motifs from sequences containing only one kind of motif or neither kind of motif. The locations of embedded GATA1 motifs are indicated by blue stars, and the location of the embedded TAL1 motif is indicated by a red star. The relatively poor performance of ISM and deltaSVM is due to the nonlinear nature of the RBF kernel

4.4 SVM motif discovery method of Ghandi et al. (2014)

Although there exist a variety of unsupervised motif discovery methods such as MEME (Bailey et al., 2009) and HOMER (Heinz et al., 2010), we sometimes wish to understand the motifs that are specifically learned de-novo by a supervised machine learning model. For example, when debugging our models, we may wish to know which patterns the supervised model has failed to pick up. In cases where the supervised model can represent more complex motifs, we may be curious whether the supervised model has learned motifs that the unsupervised model did not identify. To our knowledge, the only method in the literature that attempts to reveal the motifs specifically learned by a gapped k-mer SVM is the method presented by Gandhi et al. (2014) in the gkm-SVM paper (Ghandi et al., 2014). Their strategy was based on first scoring all possible 10-mers using the gkm-SVM and then finding motifs within the top 1% of 10-mers that received the highest scores using an iterative greedy algorithm. In our experiments, we found that by supplying the importance scores produced by GkmExplain to the importance score clustering and aggregation tool TF-MoDISco (Shrikumar et al., 2018), we recovered more consolidated, non-redundant motifs with better matches to known canonical motifs than those produced by the method of Ghandi et al. (2014) (see Figs 5 and 6).

Fig. 5.

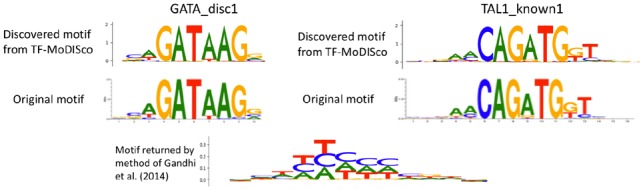
Motifs extracted by running TF-MoDISco on GkmExplain importance scores successfully recovers ground-truth simulated motifs. Letter heights are proportional to the information content of the probabilities across the different bases at that position. The single motif returned by the method of Gandhi et al. on this dataset is also shown

5 Materials and methods

5.1 GkmExplain importance scores

We will begin by presenting a method for explaining the wgkm kernel output between a sequence S_x and a support vector S_z in terms of the contributions of individual basepairs in sequence S_x. Once we have a method for explaining the kernel output, it will be straightforward to extend this to explain the final SVM output. Recall that the gkm kernel is a special case of the wgkm kernel where the weights are uniformly set to 1, and that the gkmrbf and wgkmrbf kernels build on the gkm and wgkm kernels respectively. Thus, explaining the wgkm kernel is an essential step to explaining the gkmrbf and wgkmrbf kernels as well.

As a reminder, the weighted gapped k-mer kernel between sequences S_x and S_z, denoted as $K_{\text{wgkm}}(S_x,S_z)$, can be understood as the dot product between unit-normalized feature vectors $f_{\text{wgkm}}^{S_x}$ and $f_{\text{wgkm}}^{S_z}$, where $f_{\text{wgkm}}^{S_x}$ denotes a vector of the position-weighted gapped k-mer counts in S_x. Also recall that, for computational efficiency, rather than explicitly computing the feature vectors $f_{\text{wgkm}}^{S_x}$ and $f_{\text{wgkm}}^{S_z}$, we can instead compute the dot product $\langle f_{\text{wgkm}}^{S_x},f_{\text{wgkm}}^{S_z}\rangle$ in terms of the number of mismatches between the l-mers in S_x and S_z. Formally, if we let ${\mu }_j^{S_x}$ denote the l-mer at position j in S_x, ${\mu }_k^{S_z}$ denote the l-mer at position k in S_z, we had in Eqn. 3 that the contribution of the l-mer pair $({\mu }_j^{S_x},{\mu }_k^{S_z})$ to $\langle f_{\text{wgkm}}^{S_x},f_{\text{wgkm}}^{S_z}\rangle$ is $w_j{w}_{k}h(f_m({\mu }_j^{S_x},{\mu }_k^{S_z}))$, where f_m is a function that returns the number of mismatches and h is a function that depends on the specific variant of the kernel used. For notational convenience, we will denote $f_m({\mu }_j^{S_x},{\mu }_k^{S_z})$ as m here.

How should we distribute the quantity $w_j{w}_{k}h(m)$ over the bases in S_x? Consider a position i in sequence S_x that overlaps the l-mer ${\mu }_j^{S_x}$. Let us denote the base at position i as $B_x=S_x^i$, and the corresponding base within the other l-mer ${\mu }_k^{S_z}$ (from position k in support vector S_z) as $B_z=S_z^{k+(i-j)}$ (‘corresponding’ means that the offset of B_x relative to the start of ${\mu }_j^{S_x}$ is the same as the offset of B_z relative to the start of ${\mu }_k^{S_z}$). If we evenly distribute $w_j{w}_{k}h(m)$ among the $(l-m)$ matching positions between l-mers ${\mu }_i^{S_x}$ and ${\mu }_j^{S_z}$, then position i would inherit an importance of $\frac{w_j{w}_{k}h(m)}{l-m}$ if B_x = B_z, and would inherit an importance of 0 if $B_x\ne B_z$. Leaving out the weights $w_j{w}_k$ (which don’t depend on m, B_x or B_z), we can encapsulate the core logic in the function $\text{eff}(m,B_x,B_z)$, defined as:

$$\text{eff}(m,B_x,B_z)::=\{\begin{array}{cc}\frac{h(m)}{l-m}\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}{\mathrm{B}}_x{=\mathrm{B}}_z\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (8)

Using this function, we write the weighted contribution to $\langle f_{\text{wgkm}}^{S_x},f_{\text{wgkm}}^{S_z}\rangle$ inherited by position i from the l-mer pair $({\mu }_j^{S_x},{\mu }_k^{S_z})$ as:

$$\text{imp}(i,j,k,S_x,S_z)::=w_j{w}_k\text{eff}(f_m({\mu }_j^{S_x},{\mu }_k^{S_z}),S_x^i,S_z^{k+(i-j)})$$ (9)

If we sum this quantity over all possible l-mer pairs where ${\mu }_j^{S_x}$ overlaps position i—that is, we sum over the range $j=\max (i-(l-1),0)$ to $j=\min (i,\text{len}(S_x)-l)$—and normalize by the total wgkm feature vector lengths $\Vert f_{\text{wgkm}}^{S_x}\Vert \Vert f_{\text{wgkm}}^{S_z}\Vert$ (as is done in the wgkm kernel), we arrive at the total contribution of position i in S_x to $K_{\text{wgkm}}(S_x,S_z)$, which we denote as ${\varphi }_{i,S_x,S_z}^{\text{wgkm}}$:

$${\varphi }_{i,S_x,S_z}^{\text{wgkm}}::=\sum _{j=\max (i-(l-1),0)}^{\min (i,\text{len}(S_x)-l)}\sum _k\left(\frac{\text{imp}(i,j,k,S_x,S_z)}{\Vert f_{\text{wgkm}}^{S_x}\Vert \Vert f_{\text{wgkm}}^{S_z}\Vert }\right)$$ (10)

$\Vert f_{\text{wgkm}}^{S_x}\Vert =\sqrt{K_{\text{wgkm}}(S_x,S_x)}$ is efficiently computed using the kernel function. Now that we have defined the contribution of base i to the wgkm kernel output $K_{\text{wgkm}}(S_x,S_x)$, we can define the final contribution of base i to the output of the wgkm-SVM as simply being the weighted sum of ${\varphi }_{i,S_x,S_{z^j}}^{\text{wgkm}}$ over all support vectors $S_{z^j}$, where the weights are ${\alpha }_j{y}^j$ (as per Eqn. 1). We denote this quantity as ${\varphi }_{i,S_x}^{\text{wgkmsvm}}$

$${\varphi }_{i,S_x}^{\text{wgkmsvm}}=\sum _{j=1}^m{\alpha }_j{y}^j{\varphi }_{i,S_x,S_{z^j}}^{\text{wgkm}}$$ (11)

How can we compute a similar quantity for per-base attributions with the wkgmrbf kernel? We first note that when $\langle f_{\text{wgkm}}^{S_x},f_{\text{wgkm}}^{S_z}\rangle$ is 0, the output of $K_{\text{wgkmrbf}}(S_x,S_z)$ is $\text{exp}(-\gamma )$ as per Eqn. 7. If we pretend that a hypothetical ‘baseline’ input S_x is one that produces $\langle f_{\text{wgkm}}^{S_x},f_{\text{wgkm}}^{S_z}\rangle =0$ for any support vector S_z, then $K_{\text{wgkmrbf}}(S_x,S_z)-\text{exp}(-\gamma )$ is the ‘difference from baseline’. How can we explain this ‘difference from baseline’ in terms of the contributions from individual bases in S_x? Given that we already have a way to compute ${\varphi }_{i,S_x,S_z}^{\text{wgkm}}$, we can simply distribute the ‘difference from baseline’ proportionally to ${\varphi }_{i,S_x,S_z}^{\text{wgkm}}$. Because $\sum _i{\varphi }_{i,S_x,S_z}^{\text{wgkm}}=K_{\text{wgkm}}(S_x,S_z)$ by design, this gives us:

$${\varphi }_{i,S_x,S_z}^{\text{wgkmrbf}}=\frac{{\varphi }_{i,S_x,S_z}^{\text{wgkm}}}{K_{\text{wgkm}}(S_x,S_z)}(K_{\text{wgkmrbf}}(S_x,S_z)-\text{exp}(-\gamma ))$$ (12)

Thus, by design, we again have the property that $\sum _i{\varphi }_{i,S_x,S_z}^{\text{wgkmrbf}}=K_{\text{wgkmrbf}}(S_x,S_z)-\text{exp}(-\gamma )$. This is what allows GkmExplain to address the saturation issue faced by ISM in Figure 1: even in situations where perturbing any individual base locally produces a near-zero change in the kernel $K_{\text{wgkmrbf}}(S_x,S_z)$, the GkmExplain importance scores are not saturated as they cover the entire difference $K_{\text{wgkmrbf}}(S_x,S_z)-\text{exp}(-\gamma )$. Specifically, in the case of the toy example in Figure 1, GkmExplain recognizes that the similarity with the positively-weighted support vector is well above its baseline value, and therefore grants positive importance to gapped k-mer matches between the input sequence this support vector—even though similarity with the support vector is locally insensitive to specific individual perturbations. The fact that importance scores sum to the ‘difference from baseline’ is related to a theoretical connection between GkmExplain and the method of Integrated Gradients, which we discuss in Supplementary Appendix SA.2.

Once we have the contribution of base i to the wgkmrbf kernel output $K_{\text{wgkmrbf}}(S_x,S_z)$, we can find the contribution of base i to the wgkmrbf-SVM output by simply taking the weighted sum of ${\varphi }_{i,S_x,S_{z^j}}^{\text{wgkmrbf}}$ over all support vectors $S_{z^j}$, analogous to what we did in Eqn. 11, giving:

$${\varphi }_{i,S_x}^{\text{wgkmrbfsvm}}=\sum _{j=1}^m{\alpha }_j{y}^j{\varphi }_{i,S_x,S_{z^j}}^{\text{wgkmrbf}}$$ (13)

In terms of implementation, GkmExplain importance scores can be computed efficiently by modifying the k-mer tree depth-first search originally used to compute the output of the gkm-SVM (our implementation is at https://github.com/kundajelab/lsgkm).

5.2 Mutation impact scores

An intuitive approach to estimating the impact of individual mutations is in-silico mutagenesis (ISM) (Zhou and Troyanskaya, 2015). In ISM, a mutation is introduced in the sequence and the change in the predicted output is computed. However, as illustrated in Figures 1 and 2, ISM can overlook motifs if the response of the model has saturated in the presence of the motif (as can happen when RBF variants of the gkm kernel are used). For these reasons, it can be beneficial to estimate the effects of mutations using a different quantity that we call the GkmExplain Mutation Impact Scores, which we describe in detail below.

Consider a pair of l-mers ${\mu }_j^{S_x}$ and ${\mu }_k^{S_z}$, and a mutation that changes base B_x in ${\mu }_j^{S_x}$ to $B^{*}$. Let B_z denote the base in ${\mu }_k^{S_z}$ that has the same relative position within the l-mer as B_x has in ${\mu }_j^{S_x}$. As before, let m denote the number of mismatches between ${\mu }_j^{S_x}$ and ${\mu }_k^{S_z}$. If the mutation from B_x to $B^{*}$ decreased the number of mismatches between ${\mu }_j^{S_x}$ and ${\mu }_k^{S_z}$ (that is, $B_z\ne B_x$ and $B_z=B^{*}$), then the contribution of the l-mer pair to the dot product between $\langle f_{\text{wgkm}}^{S_x},f_{\text{wgkm}}^{S_z}\rangle$ would change by $w_j{w}_k(h(m-1)-h(m))$. Let us set aside the weights $w_j{w}_k$ for now, and focus the term $(h(m-1)-h(m))$. Let us call this term $\text{meff}$, for ‘mutation effect’—analogous to $\text{eff}$ in Eqn. 8. If the mutation from B_x to $B^{*}$ increased the number of mismatches (that is, B_z = B_x and $B_z\ne B^{*}$), then $\text{meff}$ would be $h(m+1)-h(m)$. If the mutation did not change the number of mismatches, then $\text{meff}$ would be 0. To summarize:

$$\text{meff}(m,B_x,B_z,B^{*})::=\{\begin{array}{cc}h(m-1)-h(m)\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}{\mathrm{B}}_x\ne {\mathrm{B}}_z\hspace{0.17em}\text{and}\hspace{0.17em}{\mathrm{B}}_z{=\mathrm{B}}^{*}\hfill \\ h(m+1)-h(m)\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}{\mathrm{B}}_x{=\mathrm{B}}_z\hspace{0.17em}\text{and}\hspace{0.17em}{\mathrm{B}}_z\ne {\mathrm{B}}^{*}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (14)

By analogy to Eqn. 9, we can now include the l-mer weights w_j and w_k to get the impact of mutating the ith base in S_x to $B^{*}$, mediated by the l-mer pair $({\mu }_j^{S_x},{\mu }_k^{S_z})$, on $\langle f_{\text{wgkm}}^{S_x},f_{\text{wgkm}}^{S_z}\rangle$:

$$\text{mimp}(i,j,k,B^{*},S_x,S_z)::=w_j{w}_k\text{meff}(f_m({\mu }_j^{S_x},{\mu }_k^{S_z}),S_x^i,S_z^{k+(i-j)},B^{*})$$ (15)

By analogy to Eqn. 10, we replace $\text{imp}(\dots )$ with $\text{mimp}(\dots )$ to get the a score for the impact on $K_{\text{wgkm}}(S_x,S_z)$ of mutating the base at position i in S_x to $B^{*}$:

$${\varphi }_{i,B^{*},S_x,S_z}^{\text{mwgkm}}::=\sum _{j=\text{max}(i-(l-1),0)}^{\text{min}(i,\text{len}(S_x)-l)}\sum _k\left(\frac{\text{mimp}(i,j,k,B^{*},S_x,S_z)}{\Vert f_{\text{wgkm}}^{S_x}\Vert \Vert f_{\text{wgkm}}^{S_z}\Vert }\right)$$ (16)

Formulas for ${\varphi }_{i,B^{*},S_x}^{\text{mwgkmsvm}}$ and ${\varphi }_{i,B^{*},S_x}^{\text{mwgkmrbfsvm}}$ can then be obtained by replacing ${\varphi }_{i,S_x,S_z}^{\text{wgkm}}$ with ${\varphi }_{i,B^{*},S_x,S_z}^{\text{mwgkm}}$ in Eqns. 11 and 13 respectively. As before, these quantities can be efficiently computed by modifying the k-mer tree depth-first search originally used to compute the output of the gkm-SVM. While the original implementation only performs recursion on l-mer pairs for which no more than d mismatches have been encountered so far, we perform recursion on l-mer pairs for which up to d + 1 mismatches have been encountered (because a mutation can flip a mismatching position to a match).

5.3 Hypothetical importance scores

For motif discovery with TF-MoDISco (Shrikumar et al., 2018), it is useful to have hypothetical importance scores in addition to the true importance scores. The hypothetical importance score of base B at position i estimates the preference of the classifier for seeing base B at position i instead of the base that is actually present at position i. If base B is the same as the base that is actually present in the sequence at position i, the hypothetical importance score is defined to be the same as the actual importance score. As an example, suppose a particular TF has high affinity to the sequences GATAAT and GATTAT and a low affinity to the sequences GATCAT and GATGAT. If the sequence GATAAT is presented to a classifier trained to predict binding sites of the TF, the hypothetical importance assigned to base T in the 4th position would be high, as would be the (actual) importance assigned to base A in the 4th position. By contrast, the hypothetical importance scores assigned to C and G in the 4th position would be low and likely negative. These hypothetical importance scores are useful for motif discovery with TF-MoDISco because different instances of a motif that have slight variations in their underlying sequence may nonetheless have similar hypothetical importance scores, because the hypothetical importance scores impute the importance on all possible bases that could be present (and not just the bases that happen to be present in the specific instance of the motif). Although it may seem that the Mutation Impact Scores defined in Section 5.2 could serve this purpose, this is not the case because the mutation impact scores for the bases that are actually present in the sequence are always 0 (as mutating them to be themselves does not change the output).

To motivate our formula for the hypothetical importance scores, recall from Eqn. 8 that when an l-mer ${\mu }_j^{S_x}$ in input sequence S_x has m mismatches with an l-mer ${\mu }_k^{S_z}$ in support vector S_z, each matching position in ${\mu }_j^{S_x}$ can be thought of as contributing $\frac{w_j{w}_{k}h(m)}{l-m}$ through the l-mer pair $({\mu }_j^{S_x},{\mu }_k^{S_z})$ to the dot product $\langle f_{\text{wgkm}}^{S_x},f_{\text{wgkm}}^{S_z}\rangle$. Let us set aside the weights $w_j{w}_k$ for now and focus on how the term $\frac{h(m)}{l-m}$ changes as different bases are substituted in S_x. Call this term $\text{heff}$, for ‘hypothetical effect’—analogous to $\text{eff}$ in Eqn. 8. Let B_x denote a base in ${\mu }_j^{S_x},\hspace{0.17em}{B}^{*}$ denote the ‘hypothetical’ alternative to B_x, and B_z denote the base in ${\mu }_k^{S_z}$ that has the same relative position within the l-mer as B_x has in ${\mu }_j^{S_x}$. We define $\text{heff}$ to be the value that $\text{eff}$ would have if we were to substitute $B^{*}$ for B_x. If $B_x=B^{*}$ and B_x = B_z (that is, if the ‘hypothetical’ base we are looking at is the same as the base that is actually present, and it is a match), we’d have, by definition, that $\text{heff}=\text{eff}=\frac{h(m)}{l-m}$. If, instead, we had $B_x\ne B^{*}$ and $B^{*}=B_z$ (that is, substituting $B^{*}$ for B_x would flip a mismatch to a match), then we’d decrease the number of mismatches m by one to get $\text{heff}=\frac{h(m-1)}{l-(m-1)}$. Finally, if we had $B^{*}\ne B_z$—that is, $B^{*}$ is a mismatch to B_z—then $B^{*}$ would not be viewed as contributing through the l-mer pair, and we would have $\text{heff}=0$. To summarize:

$$\text{heff}(m,B_x,B_z,B^{*})::=\{\begin{array}{cc}\frac{h(m)}{l-m}\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}{\mathrm{B}}_x{=\mathrm{B}}_z\hspace{0.17em}\text{and}\hspace{0.17em}{\mathrm{B}}_z{=\mathrm{B}}^{*}\hfill \\ \frac{h(m-1)}{l-(m-1)}\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}{\mathrm{B}}_x\ne {\mathrm{B}}_z\hspace{0.17em}\text{and}\hspace{0.17em}{\mathrm{B}}_z{=\mathrm{B}}^{*}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (17)

By replacing $\text{meff}(m,B_x,B_z,B^{*})$ with $\text{heff}(m,B_x,B_z,B^{*})$ everywhere in the Mutation Impact Score formulas defined in Section 5.2, we get the corresponding formulas for the hypothetical importance scores ${\varphi }_{i,B^{*},S_x}^{\text{hwgkmsvm}}$ and ${\varphi }_{i,B^{*},S_x}^{\text{hwgkmrbfsvm}}$. As before, these hypothetical importance scores can be efficiently computed by modifying the k-mer tree depth-first search originally used to compute the output of the gkm-SVM. While the original implementation only performs recursion on l-mer pairs for which no more than d mismatches have been encountered so far, in order to get the most accurate hypothetical importance scores we should perform recursion on l-mer pairs for which up to d + 1 mismatches have been encountered, because a mutation can flip a mismatching position to a match. However, the additional layer of recursion can increase runtime substantially. In practice, we found that hypothetical importance scores derived by only considering recursions on l-mer pairs with up to d mismatches work well, and that is what we used in this paper.

6 Results

6.1 Recovery of predictive motifs from SVM models of simulated regulatory DNA sequences

To evaluate the performance of different explanation methods, we used the simulated genomics dataset from Shrikumar et al. (2017). Briefly, 8000 200 bp-long sequences were generated by randomly sampling the letters A, C, G, T with background probabilities of 0.3, 0.2, 0.2 and 0.3 respectively. 0-3 instances of TAL1_known1 (a known motif for TAL1) and GATA1_disc1 (a motif for GATA1 discovered from GATA1 ChIP-seq data) from Kheradpour and Kellis (2014) were then embedded into non-overlapping positions in each sequence. 25% of sequences contained both embedded TAL1 motifs and embedded GATA1 motifs and were labeled + 1. The remaining sequences contained either embedded GATA1 motifs only, embedded TAL1 motifs only or did not contain either of the two motifs, and were labeled -1. 10% of sequences were reserved for a testing set, while the remaining were used for training. An SVM with a gkmrbf kernel and parameters l = 6, k = 5 and d = 1 was trained to distinguish the positive set from the negative set (due to the non-additive nature of the interaction between the TAL1 and GATA1 motif, a regular gkm kernel does not perform well on this task). As shown in Figure 5, the core TAL1 and GATA1 motifs are 6 bp long, hence the choice of l = 6. The gkmrbf-SVM attained 90% auROC.

Figure 2 illustrates the behavior of different algorithms on a sequence containing three GATA1 motifs and one TAL1 motif. For deltaSVM and ISM, the importance of a position was computed as the negative of the mean impact of all 3 possible mutations at that position (positions that produce negative deltas when mutated will therefore receive positive importance). SHAP was run with the following different settings: 2000 samples per example sequence with 20 dinuc-shuffled backgrounds each (for a total of 40 000 model evaluations per sequence), 2000 samples per example sequence with 200 dinuc-shuffled backgrounds each (for a total of 400 000 model evaluations per sequence), and 20 000 samples per example sequence with 20 dinuc-shuffled backgrounds each (for a total of 400 000 model evaluations per sequence). See Section 4.3 for more details on the SHAP algorithm. We found that GkmExplain successfully highlights all GATA1 and TAL1 motifs present in the sequence. DeltaSVM performs very poorly, likely due to the nonlinear nature of the gkmrbf decision function (the nonlinearity is needed to learn the logic that both GATA1 and TAL1 must be present in the sequence for the output to be positive). ISM fails to clearly highlight some individual GATA1 motifs in this sequence, likely because the presence of multiple GATA1 motifs has a saturating effect on the nonlinear decision function. SHAP shows promise at highlighting the relevant motifs, but only when many perturbation samples are used. Unfortunately, at 40 000+ model evaluations per sequence, SHAP has a very slow runtime compared to the other methods (Fig. 3). To confirm this was not an isolated example, we compared the ability of GkmExplain, ISM and SHAP to identify the embedded motifs across all examples in the test set, and found that GkmExplain does indeed perform better (Fig. 4 and Supplementary Fig. SA.1).

Fig. 3.

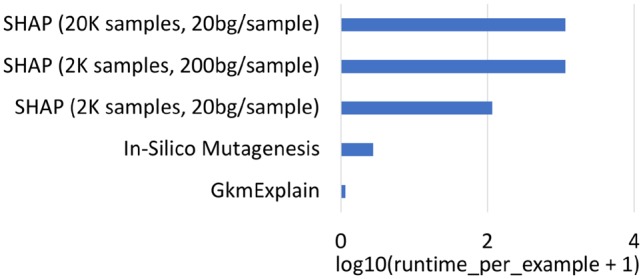
Time taken to compute importance on a single sequence for various algorithms (log scale). Evaluation was done on model and data described in Section 6.1. Runtime estimates for ISM and SHAP are optimistic, as they were calculated by estimating the time required for evaluating the model on a single example and multiplying by the min. number of model evaluations required by each method (i.e. any computational overhead required by the algorithm to synthesize the results of the model evaluations was excluded). For example, ISM requires a min. of 601 model evaluations for a sequence of length 200 (one for the original sequence, and 600 for all three possible mutations at every position). SHAP with 2 K samples per sequence and 20 backgrounds requires a minimum of 40 K model evaluations (see Section 4.3 for more details on the SHAP algorithm)

Fig. 4.

GkmExplain outperforms ISM at identifying GATA1 motifs. A gkmrbf SVM was trained as described in Section 6.1. The 400 positives in the held-out test set were scanned using 10 bp windows (the length of the GATA_disc1 motif). Windows containing a complete embedded GATA_disc1 motif were labeled positive. Windows containing no portion of any embedded motif were labeled negative. All other windows were excluded from analysis. Windows were ranked according to the total importance score produced by the importance scoring method in question, and auROC and auPRC were computed. The GkmExplain method outperforms ISM and SHAP on both metrics. The dashed black line shows the performance of a random classifier. See text for more details

As further confirmation that GkmExplain was able to detect the embedded TAL1 and GATA1 motifs, we supplied GkmExplain-derived importance score profiles across all sequences in the positive set to the recently-developed importance score clustering and aggregation tool TF-MoDISco (Shrikumar et al., 2018). Briefly, TF-MoDISco identifies subsequences (termed ‘seqlets’) of high importance in all the input sequences, builds an affinity (similarity) matrix between seqlets using a cross-correlation-like metric, clusters the seqlets using the affinity matrix, and then aggregates aligned seqlets in each cluster to form consolidated motifs. TF-MoDISco accepts both importance score profiles as well as ‘hypothetical’ importance score profiles of multiple sequences. Hypothetical importance scores can be intuitively thought of as revealing the preference of the classifier for seeing alternative bases at any given position in a sequence (see Section 5.3). We also normalized the scores as described in Supplementary Appendix SA.3, as we found this improved the results. For comparison, we also ran the motif discovery method of Ghandi et al. (2014) with default settings. The resulting motifs are shown in Figure 5. We find that, in contrast to the method of Gandhi et al., TF-MoDISco is able to learn motifs that closely match the true embedded motifs. This is likely because the method of Gandhi et al. works by scoring k-mers individually and then merging the most predictive k-mers, but in this particular simulation, the dependency between the TAL1 and GATA1 motifs causes the scores of k-mers calculated in isolation to be unreliable. This is similar to the reason why deltaSVM also produces poor results in this scenario.

6.2 Motif discovery from SVM models of in vivo transcription factor binding

We used GkmExplain to interpret a gkm-SVM trained on ChIP-seq data for the Nanog transcription factor in H1-hESCs. The positive set consisted of 200 bp sequences around the summits of 5647 reproducible Nanog ChIP-seq peaks (we used ‘conservative’ IDR peaks) (ENCODE Project Consortium, 2012). The negative set consisted of 200 bp sequences around the summits of ENCODE DNase-seq peaks in H1-hESCs that were not within 1 kb of reproducible Nanog ChIP-seq peaks (we used the union of ‘optimal’ and ‘conservative’ IDR peaks here) in H1-hESCs. To achieve a roughly balanced dataset for training the gkm-SVM, the negative set was subsampled by a factor of 20 to produce 5981 negatives. The held-out test set consisted of regions on chromosomes 1 and 2. The SVM was trained with the gkm kernel using the lsgkm package (Lee, 2016). Other parameters were set to their default values (l = 11, k = 7 and d = 3). The model achieved an auROC of 83%.

GkmExplain was run on the 960 positives in the test set, and the importance scores were supplied to TF-MoDISco. For comparison, we ran HOMER (Heinz et al., 2010) and MEME in discriminative mode (Bailey et al., 2009) with default settings to find motifs enriched in the full set of 5647 positives relative to the 5981 negatives. We also ran the SVM motif discovery method of Ghandi et al. (2014) using 11-mers rather than 10-mers (the default setting involving 10-mers failed to produce motifs, likely because our model was trained with 11-mers). The results for motif discovery are shown in Figure 6. Scores on a few example sequences are shown in Figure 7. TF-MODISCO+gkmExplain found motifs matching canonical Zic3, Sox2 and Oct4-Sox2-Nanog motifs. Gandhi et al. and MEME missed the SOX2 motif. Gandi et al. motifs were also far noisier when compared to canonical known motifs. HOMER found multiple partially redundant and often truncated versions for the three motifs.

Fig. 6.

Nanog motifs in H1-hESCs derived using TF-MoDISco with GkmExplain scores, HOMER, MEME and the method of Gandhi et al. Letter heights are proportional to the information content of the probabilities across the different bases at each position in the motif. ‘Seqlets’ are subsequences of high importance that are used by TF-MoDISco to create motifs (Shrikumar et al., 2018). The number of seqlets contained within each TF-MoDISco motif is indicated. The TF-MoDISco motifs were derived using only importance scores from the test set, while HOMER and MEME used the full set of training and test sequences. We find that TF-MoDISco run on GkmExplain importance scores tends to produce consolidated motifs that have a strong resemblance to the canonical motifs. Note that the underlying GkmExplain model used 11-mers, which might be why the Oct4-Sox2-Nanog motif, which is wider than 11 bp, is learned as two separate motifs by TF-MoDISco. Also note that the Sox2 motif, while present in the MEME results, did not meet the E-value threshold for significance and was 9th in the list of 10 motifs, ranking below several non-significant motifs that had very few supporting instances

Fig. 7.

Normalized GkmExplain importance scores on three example sequences that were strongly predicted as being bound by Nanog. The underlying model was trained to distinguish 200 bp sequences centered around the summits of H1-hESC Nanog ChIP-seq peaks from sequences that were accessible in H1-hESCs but were not bound by Nanog. The model used the standard (unweighted) gkm kernel and achieved an auROC of 83%

6.3 Predicting regulatory genetic variants affecting chromatin accessibility

We trained models using the lsgkm package (Lee, 2016) on a DNase-seq dataset in the GM12878 lymphoblastoid cell-line obtained from the deltaSVM website [www.beerlab.org/deltasvm/. http://www.beerlab.org/deltasvm/ (Accessed on 10/26/2018)]. It consists of a single positive set containing 22 384 300  bp sequences that overlapped DNase hypersensitive peaks, and five independently-generated negative sets that each matched the size, length distribution, GC-content and repeat-fraction of the positive set. One gkm-SVM and one gkmrbf-SVM were trained for each choice of negative set. For the gkm-SVM and gkmrbf-SVM, we used the parameter settings l = 10, k = 6 and d = 3, consistent with the deltaSVM paper. For the gkmrbf-SVM, we further set the regularization parameter c to 10 and the gamma value g to 2, as suggested by the lsgkm documentation. Remaining values were left to the lsgkm defaults.

To assess whether GkmExplain could be used to quantify the functional impact of regulatory genetic variants, we used the same benchmarking dataset of DNase I-sensitivity quantitative trait loci (dsQTLs) in lymphomablastoid cell lines (LCLs) that was used in the deltaSVM paper (Degner et al., 2012; Lee et al., 2015), consisting of 579 dsQTL SNPs and 28 950 control SNPs. The dsQTL SNPs were each located within their associated 100 bp DNase hypersensitive peak and had an association P-value below ${10}^{-5}$, while the control SNPs each had minor allele frequency above 5% and were randomly sampled from the top 5% of DNase hypersensitive sites.

We used 4 methods to score dsQTLs and control SNPs: deltaSVM applied to the gkm-SVM, deltaSVM applied to the gkmrbf-SVM, in-silico mutagenesis (ISM) applied to the gkmrbf-SVM, and GkmExplain mutation impact scores (Section 5.2) applied to the gkmrbf-SVM. For ISM and GkmExplain, a window of 51 bp centered on the SNP was used as context. Although we attempted to use SHAP, we found the runtime to be prohibitively large (at a context size of 51 bp, 20 backgrounds per sequence, and 510 samples per sequence, SHAP was taking over 8 min per example; note that these models were substantially larger than the ones used to profile runtimes in Figure 3). Results are shown in Figure 8, and GkmExplain scores on example dsQTLs are visualized in Figure 9. Across the models trained on the 5 independent negative sequence sets, GkmExplain consistently produced the best auPRC (binomial P-value = ${0.5}^5=0.03125$). Interestingly, we found that deltaSVM applied to the gkmrbf-SVM consistently produced better auRPC than deltaSVM applied to the gkm-SVM, even though Lee (2016) found that deltaSVM did not produce improvements when used with the gkmrbf kernel (Lee, 2016), possibly due to differences in the dataset and parameter settings. Results for auROC are in Supplementary Appendix SA.4.

Fig. 8.

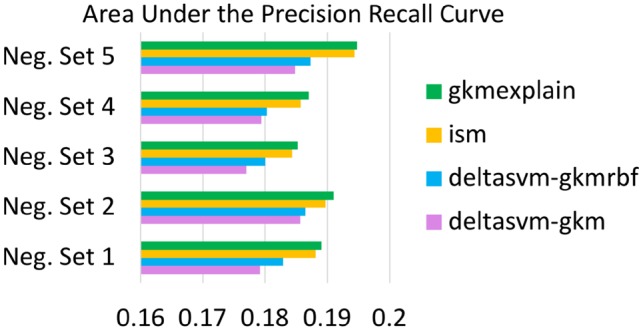
GkmExplain Mutation Impact Scores Outperform deltaSVM and ISM at identifying dsQTLs. For each choice of negative set provided in the deltaSVM paper, we trained a gkm-SVM and gkmrbf-SVM. LCL dsQTLs and control SNPs were then scored using four methods: deltaSVM on the gkm-SVM, deltaSVM on the gkmrbf-SVM, ISM on the gkmrbf-SVM and GkmExplain Mutation Impact Scores (Section 5.2) on the gkmrbf-SVM. For ISM and GkmExplain, a 51 bp window centered around the SNP was used as context. The GkmExplain mutation impact scores consistently produce the best auPRC across all 5 choices of the negative set (binomial P-value = ${0.5}^5=0.03125$). SHAP was excluded from the comparison due to a prohibitively large runtime

Fig. 9.

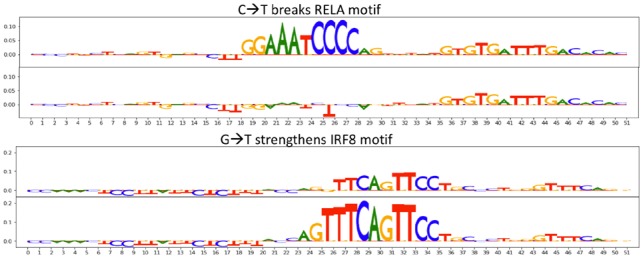
GkmExplain scores around significant dsQTLs. Pictured are GkmExplain scores around dsQTLs that were identified by GkmExplain at precision levels >75%. The dsQTLs are present at the centers of the sequences, with 25  bp flanks on either side. GkmExplain scores on the sequences with the major and minor alleles are shown in pairs. In the top example, a mutation from C to T disrupts a RELA motif. In the bottom example, a mutation from G to T strengthens an IRF8 motif. The corresponding precision level of deltaSVM for these variants was more than 5% lower than the precision level achieved by GkmExplain

7 Conclusion

We presented GkmExplain, an algorithm with theoretical connections to Integrated Gradients that can explain the predictions of an SVM trained with various gapped k-mer string kernels. On simulated data, GkmExplain outperforms ISM and deltaSVM when used with a nonlinear gapper k-mer kernel such as the gkmrbf kernel (Figs 2 and 4 and Supplementary Fig. SA.1), while being far more computationally efficient than ISM or SHAP (Fig. 3). Importance scores derived through GkmExplain can be supplied to TF-MoDISco (Shrikumar et al., 2018) to perform motif discovery (Figs 5 and 6), resulting in improved recovery of consolidated, non-redundant motifs as compared to previous motif discovery approaches for gkmSVMs (Ghandi et al., 2014). Mutation Impact Scores derived from GkmExplain outperform ISM and deltaSVM for identifying regulatory genetic variants (dsQTLs) affecting chromatin accessibility in LCLs. (Fig. 8). Our approach is not limited to SVM models of genomic sequences and can be generalized to other data modalities, as illustrated in Supplementary Appendix SA.5.

Funding

AS was funded by HHMI International Student Research and Bio-X Bowes fellowships. AK was funded by National Institute of Health grants 1DP2GM123485, 1U01HG009431 and 1R01HG00967401.

Conflict of Interest: none declared.