TADA: phylogenetic augmentation of microbiome samples enhances phenotype classification

Abstract

Motivation

Learning associations of traits with the microbial composition of a set of samples is a fundamental goal in microbiome studies. Recently, machine learning methods have been explored for this goal, with some promise. However, in comparison to other fields, microbiome data are high-dimensional and not abundant; leading to a high-dimensional low-sample-size under-determined system. Moreover, microbiome data are often unbalanced and biased. Given such training data, machine learning methods often fail to perform a classification task with sufficient accuracy. Lack of signal is especially problematic when classes are represented in an unbalanced way in the training data; with some classes under-represented. The presence of inter-correlations among subsets of observations further compounds these issues. As a result, machine learning methods have had only limited success in predicting many traits from microbiome. Data augmentation consists of building synthetic samples and adding them to the training data and is a technique that has proved helpful for many machine learning tasks.

Results

In this paper, we propose a new data augmentation technique for classifying phenotypes based on the microbiome. Our algorithm, called TADA, uses available data and a statistical generative model to create new samples augmenting existing ones, addressing issues of low-sample-size. In generating new samples, TADA takes into account phylogenetic relationships between microbial species. On two real datasets, we show that adding these synthetic samples to the training set improves the accuracy of downstream classification, especially when the training data have an unbalanced representation of classes.

Availability and implementation

TADA is available at https://github.com/tada-alg/TADA.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Understanding the impact of the composition of the microbiome on clinically-relevant traits is a major promise of microbiome profiling National Research Council (US) Committee on Metagenomics: Challenges and Functional Applications, 2007] using both 16S (Gill et al., 2006) and metagenomic sampling (Venter et al., 2004). The goal is to understand how the composition of species, or genes, in a microbial community such as human gut impacts phenotypes of interest such as obesity (e.g. Turnbaugh et al., 2007). The relationship between microbial composition and traits, however, is complex and hugely variable, from person to person (Dave et al., 2012) and from one time to another (Caporaso et al., 2011; Flores et al., 2014). As a result, microbial communities have been hard to model (Waldor et al., 2015) using traditional sample differentiation methods (Langille et al., 2013; Paulson et al., 2013).

Machine learning (ML) methods have proved capable of capturing complex relationships in many fields, such as vision and speech recognition. As a result, researchers have pointed out the potential of ML models to capture complexities of the microbiome (Knights et al., 2011). Many researchers (e.g. Saulnier et al., 2011; Statnikov et al., 2013) have formulated understanding microbiome as a classification task: given is a set of samples, each consisting of a set of sequences from various microorganisms, and each sample is labeled by a trait of interest (e.g. lean or obese); a model is learned to predict these labels and classify unlabeled (new) samples. Some studies have shown promise in achieving an accurate classification of clinically-relevant traits using microbiome (e.g. Aagaard et al., 2012; Beck and Foster, 2014; Feng et al., 2015).

The number of samples available for training an ML algorithm has tremendous effects on the accuracy of the model. Tuning a large number of parameters of a classifier or regression method using a small dataset can lead to overfitting and poor generalization to new samples. Impacts of overfitting are particularly severe when we have an unbalanced distribution of class labels or hidden confounding factors in training datasets (e.g. Chawla et al., 2002, 2010; Kubat and Matwin, 1997).

The number of microbiome samples, compared to applications like vision and speech recognition, is relatively small. For example, ImageNet Large-Scale Visual Recognition Challenge (ILSVRC-2010) involved the classification of 1.2 million high-resolution images into 1000 different classes (Russakovsky et al., 2015), whereas, one of the largest microbiome datasets, the American Gut Project (AGP) (McDonald et al., 2018), includes 14 794 samples, has only self-reported labels, and is heterogeneous (e.g. only 1942 samples are omnivores of age between 20 and 80 with no self-reported disease or antibiotic usage). For classifying specific traits, AGP has even fewer samples [e.g. only 262 samples report having inflammatory bowel disease (IBD)]. Moreover, the representation of traits of interest is often not balanced, and the distribution of the labels often is not even close to the larger population (e.g. targeted datasets are often over-represented in the diseased state and short on healthy samples). Biases are further compounded by the natural variability of microbiome and auto-correlation between labels due to hidden or nuisance variables, which abound. These difficulties have led to diminished hope for the generalization of methods (Sze and Schloss, 2016).

Perhaps the ultimate goal should be gathering more (and less biased) labeled samples for training, a task that will progress only slowly, especially given difficulties of combining datasets gathered with various lab protocols (Leek et al., 2010; Weiss et al., 2014). An alternative that has been explored extensively in recent years by the ML community is data augmentation. The idea is to create artificial labeled samples algorithmically and add them to the training data. For example, two widely-used methods, SMOTE (Chawla et al., 2002) and ADASYN (He et al., 2008) seek to reduce biases introduced by unbalanced distributions of labels using a k-NN clustering of samples and combining points in the same cluster. Beyond these generic methods, which do not seek to capture domain knowledge, augmentation has the potential to combine the power of black-box ML models and biologically-motivated generative statistical models.

In this paper, we propose a new data augmentation technique for microbiome data, called Tree-based Associative Data Augmentation (TADA). The main ideas behind TADA are 2-fold. (i) Each observed sample captures the underlying microbiome only imperfectly, and hence, a variation of the sample could have easily been observed, (ii) such variations are constrained by the phylogenetic relationships between species (Matsen, 2015), which underlie the sequence similarity and microbial diversity (O’Dwyer et al., 2012; von Mering et al., 2007). Thus, TADA generates new samples while considering the evolutionary relationships between organisms. Furthermore, we do not stop at just increasing the number of samples. As we will show, it is crucial to deal with unbalances and biases in the training data. In deciding what samples to add, TADA can also remove unbalances in the data with respect to both observed and hidden variables (which we seek to approximate using clustering). We test TADA on two datasets with various biases added to the training dataset. We show that two leading ML models (random forests and neural networks) fail to perform well on unbalanced and biased samples. We also show that data augmentation improves the accuracy, marginally but meaningfully for balanced datasets and dramatically in the presence of unbalanced training sets.

2 The TADA method

2.1 Background and notations

The training data used in microbiome classification is an operational-taxonomic-unit (OTU) table X. The rows of the table correspond to a set of m samples, often one per individual, $\mathcal{S}=\{s_1,s_2,\dots ,s_m\}$ and the columns correspond to features. Features can be defined in various ways, but for simplicity, we focus on a specific form. Our features are a set of n OTUs (e.g. representing species)$\{o_1,o_2,\dots ,o_n\}$. Each cell of the matrix gives the number of times an OTU is observed in a sample. The counts in each row can also be normalized so that they add up to one. In addition to the OTU table, we need a class label y_i for each sample s_i. The class labels correspond to phenotypes (e.g. healthy versus diseased or lean versus obese) that we seek to classify using the microbiome.

The OTUs have a corresponding sequence, for example from the marker genes like 16S rRNA. These sequences may be obtained using a number of approaches, including the traditional OTU picking methods (Edgar, 2010; Schloss and Handelsman, 2005) or sub-operational-taxonomic-unit methods (Amir et al., 2017; Callahan et al., 2016; Edgar, 2016). Depending on the method, the exact meaning of OTUs changes; however, they always correspond (at least in approximation) to microorganisms that constitute the sample.

2.2 Generative model used in TADA

Data augmentation seeks to add to the training set new samples that could have been seen but are not seen. TADA achieves this using a generative model to create synthetic samples distributed around existing samples. TADA models two types of variations.

• True variation (TV). From one individual to another, even among those with the same phenotype, the true proportions of different OTUs in the microbiome change. These variations may be due to confounding factors (i.e. hidden variables) or natural biological variation among people. Moreover, the microbial composition for each person may also change through time. Thus, samples have true biological variation.

• Sampling variation (SV). Environmental sequencing takes a random (but not necessarily uniformly random) subsample of the true diversity, creating additional variation around the true proportions. Moreover, sequencing adds errors and ambiguity that further increase variation.

Of the two forms of variation, true variation is much harder to model statistically. Confounding factors are mostly unknown as are the source of natural or temporal variations. However, a major source of inter-correlation, the phylogenetic structure, can be inferred and modeled.

Phylogenetic structure. Microorganisms that make up a sample are all descendants from a common ancestor, as captured by their phylogenetic tree. The shared evolutionary history creates a dependence between OTUs, and a phylogenetic tree can represent the relationships (in its topology) as well as the distance between the species. Close phylogenetic relationships between OTUs corresponds to closeness in the sequence space and perhaps also in functional roles. Both forms of variation are likely influenced by the phylogeny. True variation can be phylogenetic because phylogenetically similar organisms may interchange easily, though we note that this is far from a universal rule; strain-variation may have a large impact on the function. Sampling variation is impacted because algorithms for creating OTU tables are prone to merge or confuse OTUs that are close phylogenetically.

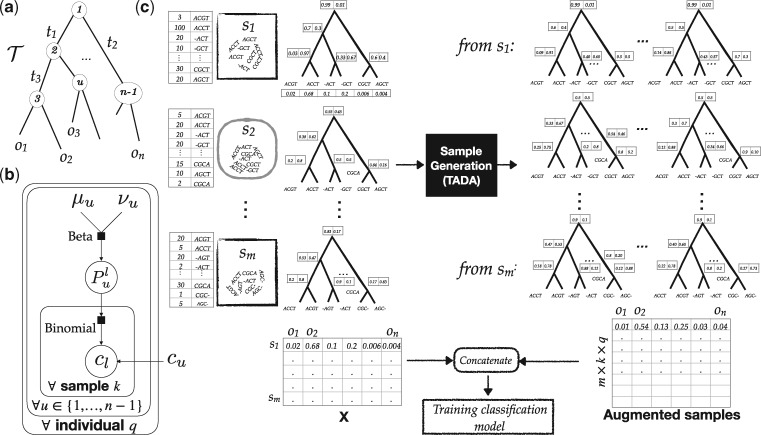
TADA uses an inferred binary phylogenetic tree (details are given in Section 3.4), called$\mathcal{ }\mathcal{T}$, with leaves labeled by OTUs $o_1\dots o_n$ (Fig. 1a). We index internal nodes of $\mathcal{T}$ from 1 (for the root) to n − 1 and refer to the length of the edge above node u by t_u. Using a simple O(n) algorithm (Supplementary Algorithm S1), we compute d_u: the average length of the path from each leaf under the left child of u to each leaf under the right child of u.

Fig. 1.

(a) A phylogeny $\mathcal{T}$ with branch lengths (t_u), OTUs at leaves (o_i) and internal node indices. (b) The hierarchical graphical model used to generate new samples. (c) The augmentation procedure. First, each sample is mapped to the phylogeny, then we estimate parameters of the model for each sample s_i (or a collection of samples; see Supplementary Fig. S2), and then generate new samples using the generative model. The augmented samples are concatenated with the original samples for training the classifier (e.g. RF or NN)

2.2.1 Generative model: the base model

We design a hierarchical generative model to capture both sources of variation and the phylogenetic auto-correlation. The model has three sets of parameters: (i) the phylogeny, $\mathcal{T}$, and its branch lengths (and, thus, d_u’s), with the two nodes below each node u arbitrarily labeled as left (l) and right (r), (ii) a set$\mathcal{ }\mathcal{M}=\{{\mathrm{\mu }}_1\dots {\mathrm{\mu }}_{n-1}\},0<{\mathrm{\mu }}_u<1$, each corresponding to an internal node of the phylogenetic tree, (iii) the total sequence count N. In addition to these parameters, we define for each node, a value ${\nu }_u=f\left(d_u\right)$ where f can be any monotonically increasing function.

Our generative hierarchical model (Fig. 1b) is defined recursively, starting at the root and traversing the tree top–down. Algorithm 1 shows this model generates q individuals and k new samples for each individual (k × q in total), each with N sequences. The true variation is modeled using a Beta distribution and the sample variation using a Binomial distribution. We use the μ,ν parameterization of the Beta distribution (as opposed to the standard α, β parameterization). For each node u, we have the parameter μ_u, which gives the population-wide portion of sequences under the node u that fall under the left subtree of u. A draw from the Beta distribution gives us$\mathrm{ }{p}_u^l$: the true portion of sequences that go to the left subtree in the underlying microbiome. Then, a draw from the Binomial distribution gives the actual observed count and models the variation due to sampling (sequencing) around the true proportion $p_u^l$.

In this model, the true variance is inversely proportional to the square root of phylogenetic distance. In the parameterization of the Beta distribution used here, the mean is μ and the variance is$\mathrm{ }\frac{\mathrm{\mu }(1-\mathrm{\mu })}{\mathrm{\nu }+1}$. By setting the ν parameter of Beta to a monotonically increasing function of d_u, we make sure that the variance increases closer to the tips of the tree (where d_u is small), and decreases toward the root (where d_u is high). The choice of the exact function f (see Section 3.4) is arbitrary. However, the fact that variance should be higher closer to tips has a biological justification. Closer to the leaves of the tree, microbial organisms become more similar and therefore more likely to be able to replace each other in an environment or be confused with each other. Conversely, the microbial composition becomes more stable close to the root of the tree.

Algorithm 1.

TADA sample generation procedure

1: for individual $1\le i\le q$do

2:   for node u in preorder traversal of $\mathcal{T}$do

3:    Draw $p_u^l\sim \mathrm{Beta}({\mathrm{\mu }}_u,{\mathrm{\nu }}_u)$

4:   for$1\le j\le k$do

5:    $c_1\leftarrow N$ % Index 1 refers to the root node

6:    for internal node u with children l and r in preorder traversal do

7:     Draw $c_l\sim \mathrm{Binomial}(p_u^l,c_u)$

8:     $c_r\leftarrow c_u-c_l$

9:    Output $c_{o_1},\dots ,c_{o_n}$ as a new sample and normalize if needed.

2.2.2 Generative model: mixtures

The model described above is limited in a fundamental way: it assumes all samples are generated from the same underlying distribution. Therefore, it completely ignores the fact that individuals belong to several classes (the identification of which is the goal) and that within each class, confounding factors may create further structure among samples. For example, we may have healthy and diseased samples for our main classes, and for each of those, samples may be further differentiated based on age, gender, weight or other factors (which, may not be known). Thus, the phenotype structure of samples is not modeled.

To capture the phenotype structure, we use a mixture model. The population is assumed to be divided into clusters, each with its own $\mathcal{M}$ parameters, but all sharing the same phylogeny. Clusters can correspond to class labels, confounding factors or a mixture of the two. In the generative process, each sample is first assigned to a cluster, according to cluster probabilities, and then the procedure described above is followed.

2.3 Data augmentation procedure

Assuming the training data come from our generative model, we can design parameter estimators and use the estimated parameters to generate new data. In fact, a model-based approach (coupled with the mixture model), in principle can also infer the class labels. However, on typical microbiome training datasets, the total number of mixture components is likely large, and the model has a large number of parameters. Thus, parameter estimation using these complex models will be underpowered. Moreover, despite a large number of parameters, the model does not come close to capturing all the biological complexity of microbiome. Thus, instead of using the generative model for inference, we use it only as a tool for data augmentation for training ML models.

Based on the hierarchical model, we design two versions of TADA, which vary in their ambition, ranging from capturing only sampling variation to capturing both sources of variation and confounding factors. The more ambitious versions include more parameters, and this reliance on more parameters makes them vulnerable when applied to limited datasets.

TADA-SV. This version only captures sampling variation and has a single user setting: a number k. For each training sample s_i, we first estimate $p_u^l$ in our training set independently from other samples (assuming samples are unlinked). Then, for each sample, k new samples are generated and added to the training set using the fixed $p_u^l$ following Algorithm 1 (setting q = 1 and starting in line 5). Thus, this method is only drawing from the Binomial component of our Hierarchical model and ignores the rest. To estimate $p_u^l$ from a single sample s_i, we use the total count of sequences that fall to the left of the node u in s_i, normalized by the total count of sequences below u. As proved in the Supplementary Lemma S1, this estimator gives the joint ML estimate for all $p_u^l$ values (treated as parameters of the binomial) over the entire tree.

TADA-TVSV-C. This version captures both sampling and true variation and optionally also confounding factors. The method has three user settings: k, q and C. We first cluster samples $s_1\dots s_m$ into C groups per classification label based on the training data X using any clustering method of choice (see our default choice in Section 3.4). These clusters correspond to components of the mixture model we described before; note that instead of using a complex parameter-rich model-based inference of mixture components, we use a clustering method to approximate the components. The hope is that the clustering based on X captures the hidden phenotype structure, at least partially. The choice of C controls the level of complexity and therefore the number of parameters. For example, acknowledging the difficulty of finding the phenotype structure, we explore the extreme setting of C = m where each sample in our training set belongs to its cluster and therefore is unlinked from others, just like SV. We also explore other settings of C, including C = 1.

After clustering, we first estimate $\mathcal{M}$ parameters per each cluster using a method of moments. The estimator, as shown in Supplementary Lemma S2, simplifies to computing the sum of counts on the left child of each node u across all samples of the cluster, normalized by the sum of the counts under the node u. Then, for each cluster, we generate q new individuals and k new samples per individual (thus, k × q in total). To do so, we follow the generative procedure given in Algorithm 1.

2.4 Balancing

So far, we have generated a fixed number of new samples per input training sample. However, by generating a different number of samples per input sample, we can use augmentation for balancing (or otherwise adjusting) our input training set in terms of the distribution of labels. As we will show, the lack of balance between representations from different phenotype classes (e.g. the training labels) can degrade the accuracy of ML methods. TADA, therefore, can also be run with balancing (Supplementary Fig. S2). In this mode, training data are first divided into several groups; these groups can be based on classification labels, the result of clustering training points or a combination. We then choose the number of extra samples generated per sample (e.g. k and q) such that all groups have the same number of samples after augmentation. We will test two modes.

• TADA-Balance adds exactly as many new samples as necessary (and not any more) so that all groups have the same total number of samples.

• TADA-Balance++ not only makes all groups balanced in size but also increases the total number of samples for all groups, so that the largest group has q times more samples than before augmentation.

3 Experimental setup

3.1 Datasets

We use two datasets, both based on 16S profiling of gut microbiome.

Gevers. As our main dataset, we use a dataset by Gevers et al. (2014) [publicly available on Qiita (Gonzalez et al., 2018); study ID 1939], which the authors put together to study the impact of the microbiome on the IBD. This study has 1359 samples, has been gathered in a clinical setting, is carefully curated, and has reliable class labels. We filtered out samples from people on antibiotics, or with <10 000 16S sequences. Before running our experiment, we also removed 9 outliers and any OTUs with total counts across all samples below 3. This leaves us with 647 diseased samples and 243 healthy samples, gathered using either biopsy or stool. Gevers et al. (2014) were able to find a clear indication that IBD changes the microbiome composition, and thus, ML methods should be able to achieve reasonable classification accuracy on this dataset.

BMI. In addition, we use the AGP (McDonald et al., 2018). This dataset has only self-reported labels and is gathered by crowdsourcing instead of a clinical setting. Thus, it is less curated than the Gevers dataset, though authors have taken several quality control steps. With an understanding of the shortcomings, we use the AGP data to test our method on a phenotype other than IBD. We classified the self-reported body mass index (BMI) phenotype categorized into 1360 lean versus 582 overweight samples (cutoff at BMI: 25). Similar to Gevers dataset, we further filtered this dataset to control for many factors that might affect microbiome composition. These factors include diet (we keep omnivore samples), ethnicity (Caucasian), country (USA), disease (healthy), antibiotics (no antibiotic usage in the past year) and age (between 20 and 70). We also filtered samples with <1000 de-noised reads, one outlier and we removed OTUs with total counts across all samples below 4.

3.2 Experiments

E1. On both Gevers and AGP datasets, we compare TADA, in its two settings, against ADASYN and SMOTE, and the baseline approach where no augmentation is performed. In this experiment, we use all the data for training and testing in a cross-validation setting (see Section 3.3) performed using the held-out original samples.

E2. We next test the impact of balancing by generating unbalanced training data. We created datasets such that 1/10, 1/5 or 1/3 of both the training and testing data are from healthy/overweight individuals. We created two versions of this unbalanced dataset. In the first version (E2-fix), we used a fixed number (243 for IBD and 582 for BMI) training samples for all three ratios to test the impact of the ratio without changing the training size. Here, the testing sets are chosen to match the ratio in the training set but have a larger total sum (the maximum possible in each case). We also created a version (E2-max) only for the IBD dataset with the maximum possible training size for each ratio. To do this, we removed the minimum possible number of samples from healthy (for 1/10 and 1/5 ratios) or diseased (for 1/3) so that we obtain the desired ratios; this leaves us with 574 training samples for 1/10, 646 for 1/5 and 587 for 1/3. Once again, the testing sets are chosen to match the training set in ratio. E2-max enables us to make sure results on E2-fix hold if training datasets are as large as possible. Here, in addition to no augmentation, we compare TADA-Balance(++) to ADASYN, SMOTE and a simple balancing strategy that reduces the number of diseased samples to match the healthy count by random down-sampling.

E3. While E2 is to test lack of balance, E3 is concerned with biases in the composition of classification labels in the training dataset. In E3, we use the 1/5 dataset of E2-fix for training, but for the testing set, we choose samples such that 1/5, 1/2 or 4/5 are healthy (achieved by randomly removing diseased cases until the desired ratio is achieved). Thus, the last two cases have a different composition of labels between training and testing datasets.

3.3 Evaluation procedure

For measuring classification accuracy, we rely on the area under curve (AUC) of receiver operating characteristic. The AUC measure is computed by exploring different cutoffs for the threshold used internally in each classification method, hence exploring the tradeoff between precision and recall. AUC is the standard method used for measuring the accuracy of ML classification because it does not depend on arbitrary sensitivity/specificity tradeoffs.

All of our tests are based on a cross-validation strategy, repeated several times to get a total of 20 evaluations of AUC. We report the mean and standard error of AUC across the 20 replicates. In E1 and E2-max, we use 5-fold cross-validation, repeated four times. In E2-fix and E3, we use 3-fold validation for the 1/3 setting, 5-fold validation for 1/5 and 10-fold validation for 1/10, each repeated enough to get 20 replicates. The augmented samples are only added to the training data, and testing is done using the held-out samples from the original datasets.

3.4 Method details

OTU and phylogeny. We use Deblur (Amir et al., 2017) to extract error-corrected (de-noised) sequences from each sample and take each resulting sequence as an OTU. We then use SEPP (Janssen et al., 2018; Mirarab et al., 2012) to insert OTUs onto a backbone phylogeny of GreenGenes (DeSantis et al., 2006); removing the backbone sequences and randomly resolving the remaining polytomies gives us a binary tree on the OTUs observed in the samples. We use this tree as$\mathcal{ }\mathcal{T}$.

TADA. We implemented TADA in Python using DendroPy (Sukumaran and Holder, 2010) for manipulating phylogenies, biom-format (McDonald et al., 2012) for processing OTU tables, scikit-learn (Pedregosa et al., 2011) for ML methods, and scikit-bio for computing distances between microbiome samples. In all the analyses, we use$f\left(d_u\right)=100\sqrt{d_u}$. The choice of the square root is arbitrary but is motivated by wanting a slower than linear reduction in variance closer to the tips (where d_u < 1); the constant 100 ensures the variance of Beta is not extremely high and had little impact on results in our initial tests on a different dataset. To cluster samples, we use the k-means method (Arthur and Vassilvitskii, 2007) applied to the Bray–Curtis (McMurdie and Holmes, 2014) distances between samples computed from the normalized matrix X. In all analyses, unless specified, we set k = 5 for TADA-SV and k = 1, q = 5 for TADA-TVSV-C (our initial experiments showed marginal improvements with increased k or q; see Supplementary Fig. S3). For TADA-Balance++, we set k = 50 for TADA-SV and k = 1 and q = 50 for TADA-TVSV-C. For TVSV, we will explore five settings of C, the number of clusters: 1, 4, 8, 40 and m. In order to avoid zero counts, we add the pseudocount 5/n to the count of all OTUs for all samples (n ≈ 10⁴ for IBD and ≈ 2 × 10⁴ for BMI).

ADASYN/SMOTE. We use ADASYN and SMOTE implemented in the imbalanced-learn package (ver. 0.4.3) (Lemaître et al., 2017). We use the normalized counts of OTUs (so that values in each row of X add up to 1) as inputs. We use k = 5 (default value) for the k-nearest neighbor clustering step of these methods. Both methods allow us to set the number of samples we want to generate from each class.

ML. We use two ML methods: random forests (RF) (Breiman, 2001) and neural networks (NN), both as implemented in the scikit-learn package (Pedregosa et al., 2011) (ver. 0.20). We use RF because of its superior performance on previous studies of microbiome (e.g. Statnikov et al., 2013). We set the number of trees for RF to 2000 and use default options otherwise. For NN, we use Multi-layer Perceptron classifier (MLPC). Our MLPC had two layers with dimensions 2000 and 1000, respectively, with an early stopping rule. For the other parameters of MLPC, we used the default options. We use the normalized counts of OTUs as input features.

4 Results

4.1 E1: complete datasets

We start with the E1 experiment where all the data are used (Fig. 2).

Fig. 2.

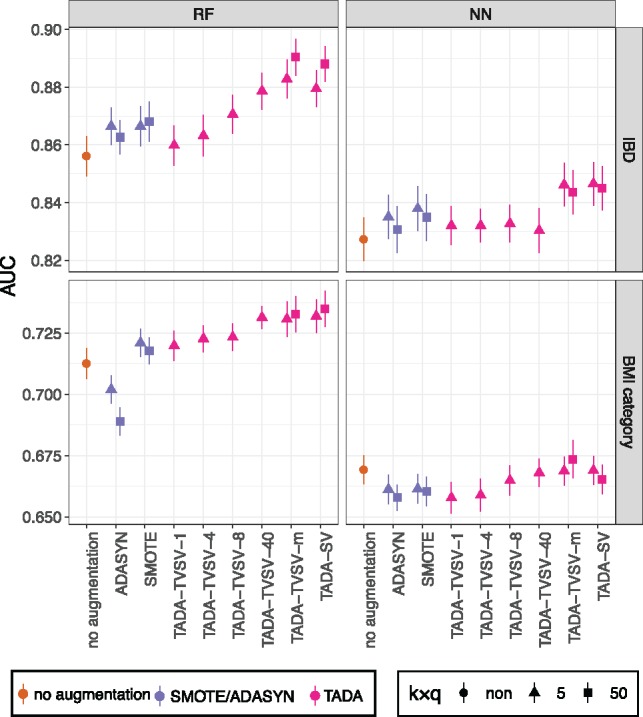
Results on E1. Area under curve (AUC) is shown for both neural networks (NN) and random forest (RF) classifiers and on both Gevers IBD dataset and AGP BMI dataset. We compare training on original dataset with no augmentation, SMOTE, ADASYN and using both SV and TVSV versions of TADA. For TVSV-C, we set the number of clusters, C, to 1, 4, 8, 40 or m (number of samples). We used ADASYN and SMOTE with their default settings. We show mean (dots) and standard error over 20 replicates. For TADA-SV, we show both k = 5 and k = 50, and for TADA-TVSV-m, we show both q = 5 and q = 50 with k = 1; see Supplementary Figure S3 for other q and k

On the Gevers IBD dataset, the accuracy of ML methods, as measured by AUC, is reasonably high (mean AUC > 0.8, both for NN and RF) even without augmentation. Nevertheless, TADA is able to increase the mean accuracy for both NN and RF. For example, for RF, the AUC improves from 0.857 to 0.890 with TADA-TVSV-m (q = 50) and the difference is statistically significant according to a paired t-test ($\mathit{P}\ll {10}^{-5}$). This improvement, while not large in magnitude, corresponds to a 23% reduction in the gap compared to the ideal AUC = 1 and therefore is substantial. In contrast, ADASYN and SMOTE result in much smaller improvements (mean AUC < 0.87); these improvements are not statistically significant for ADASYN (P = 0.15) but are significant for SMOTE (P = 0.0003).

For BMI classification using the AGP dataset, the AUC was generally low in the absence of augmentation (mean <0.72 for both methods), perhaps reflecting the heterogeneous nature of the AGP dataset or the difficulty of classifying BMI into two categories based on the microbiome. Data augmentation using TADA-TVSV increases the accuracy for RF; for example, the AUC is increased to 0.73 using TADA-TVSV-m, and this improvement is statistically significant ($\mathit{P}\hspace{0.33em}\ll \hspace{0.33em}{10}^{-5}$). Here, ADASYN reduces accuracy while SMOTE helps accuracy insignificantly (P = 0.18) and not as much as TADA. Unlike RF, NN is not helped by TADA-SV, and TADA-TVSV-m gives only a statistically insignificant improvement (P = 0.35). Both ADASYN and SMOTE reduce the accuracy.

Comparing different numbers of clusters (C) for TVSV-C, we observe an interesting pattern. Increasing the number of clusters improves AUC consistently, and the trend is especially apparent for RF. The highest accuracy is obtained by either TVSV-40 or TVSV-m where a single sample (for m) or a handful of samples (for 40) constitute a cluster. Based on these results, we focus only on TVSV-m for E2 and E3. Interestingly, the accuracy of the simpler model, SV, is very close to TVSV, except perhaps on the BMI dataset with NN. Finally, increasing k or q and also using k = q = 5 tends to improve accuracy, albeit marginally (Supplementary Fig. S3).

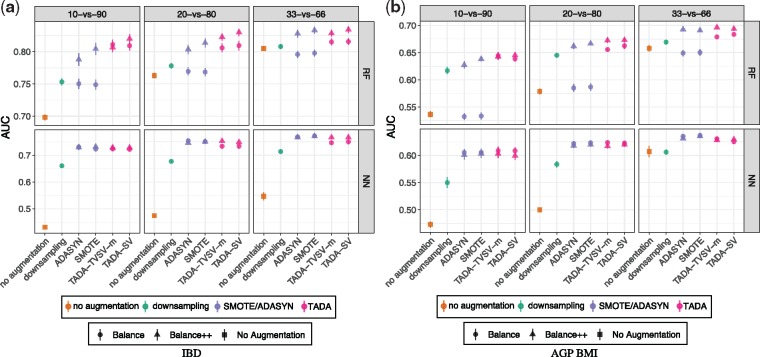
4.2 E2: unbalanced class labels

The power of TADA becomes evident when the classes have an unbalanced representation (Fig. 3). By making the representation of the two labels unbalanced, we observe that the accuracy of ML methods degrades quickly. In E2-fix, we see a sharp drop in AUC of both ML methods as the level of unbalance increases (Fig. 3). For example, on the IBD dataset, RF with no augmentation goes from AUC = 0.8 with 1/3 healthy samples to AUC = 0.7 when 1/10 are healthy. Similarly, on BMI, AUC goes down from 0.66 in the 1/3 case to AUC = 0.54 when 1/10 are overweight. Simply down-sampling the number of over-represented class to match the other label by random removals increases AUC despite training from a smaller dataset. This improved accuracy further underscores the detrimental impact of a lack of balance.

Fig. 3.

Results on the E2-fix dataset. Training dataset is randomly subsampled to create unbalance: healthy (for IBD) and overweight (for BMI) samples constitute 1/10 (10-versus-90), 1/5 (20-versus-80) or 1/3 (33-versus-66) of the samples for both the training and testing sets. We compare AUC on the original training set (no augmentation); the over-represented class down-sampled to match the number of under-represented class (down-sampling); and, augmentation using SMOTE, ADASYN and TADA. Methods are run in two ways: TADA-Balance just adds samples to the healthy class to balance labels; TADA-Balance++ adds both healthy and unhealthy samples to make them balanced and to increase the total number of samples by 50×

Large improvements in AUC are obtained when we use TADA to balance the representation from the two groups. For example, on the IBD dataset, the AUC of RF with TADA-SV-Balance is >0.8 even when the original training data (i.e. before augmentation) has only 1/10 healthy individuals. Similar levels of improvement are observed for BMI. Across both datasets, improvements in accuracy can be as large as 0.11 points for RF and 0.29 points for NN. Thus, TADA-Balance can largely erase the negative impacts of unbalance in the original training dataset. Like E1, here, TADA-SV and TVSV-m perform similarly.

More interestingly, using TADA-Balance++ results in additional improvements beyond TADA-Balance. For example, for IBD, the AUC in the 1/5 healthy case goes from 0.81 with TADA-SV-Balance to 0.83 with TADA-SV-Balance++ with RF (statistically significant: P = 0.00004). The improvements of Balance++ over Balance are consistent with improvements of TADA over no augmentation observed in E1.

The two standard methods, SMOTE and ADASYN, have mixed performance. We start with RF on the IBD dataset. With the Balance version, both methods improve AUC substantially only for the 1/10 healthy case but they fail to outperform down-sampling. In the 1/5 healthy case, they result in small improvements and in the 1/3 healthy case they reduce AUC compared to no augmentation. The Balance++ versions of both methods, however, consistently improve AUC. Nevertheless, with 1/10 or 1/5 healthy, TADA-SV outperforms both methods (P < 0.007 in all four comparisons) whereas with 1/3, TADA-SV and both methods are statistically indistinguishable (P > 0.16 in both comparisons). Similar patterns are observed for BMI with RF. With NN (which has much lower AUC than RF) SMOTE, ADASYN and TADA have similar accuracy in all conditions.

The positive impact of balancing on E2-fix is not merely due to its small training set. On E2-max, which has roughly double the training set size of E2-fix, TADA continues to improve accuracy over no augmentation and other methods, especially for 1/10 and 1/5 levels of unbalance (Fig. 4). Compared to E2-fix, AUC is improved for all methods in E2-max, as expected due to the larger training set. Here, down-sampling and SMOTE/ADASYN-Balance stop increasing accuracy for RF.

Fig. 4.

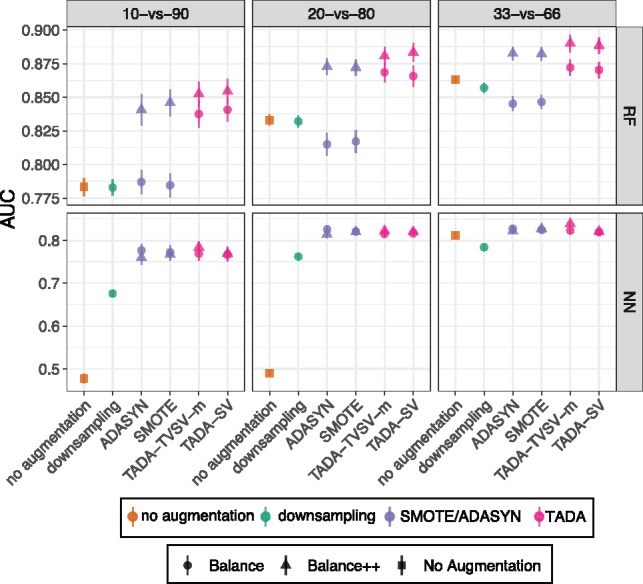
Results on the E2-max dataset. Settings similar to Figure 3

Note that before augmentation, the composition of class labels in the testing set matches that of the training set. Thus, the reductions in accuracy for unbalanced data without augmentation are not due to a biased distribution of labels in the training set. In fact, after balancing using TADA, the distribution of labels between training and testing data will not match, making the high accuracy of balanced results even more noteworthy.

4.3 E3: biased class labels

Focusing on the IBD data, we next test the impact of not just unbalanced but also biased sampling by fixing training set to have 1/5 healthy (for IBD) but changing the relative representation in testing data. Interestingly, including bias does not further reduce the accuracy in substantial ways (Fig. 5). However, in the biased scenario, we continue to see dramatic improvements obtained by TADA compared to no augmentation, down-sampling, and to less extent, SMOTE and ADASYN. Thus, for unbalanced training data, augmentation can improve the accuracy regardless of whether the testing data have the same label distribution.

Fig. 5.

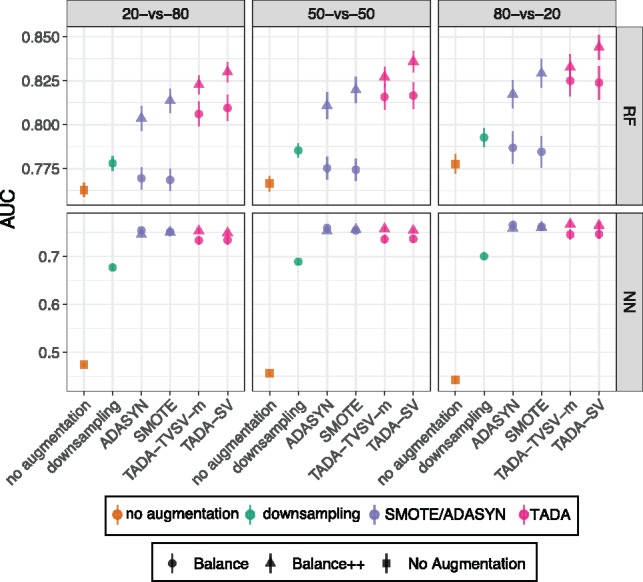
Results for E3. The training set includes 1/5 healthy out of a total of 243 samples. The testing set has 1/5 (20-versus-80), 1/2 (50-versus-50) or 4/5 (80-versus-20) of samples coming from healthy individuals on the IBD dataset. Methods labeled identically to Figure 3

5 Discussions and conclusions

We described a new data augmentation method to generate artificial samples for augmenting the training set of ML methods for phenotype classification from microbiome samples. Our method, TADA, combines the power of statistical generative models that incorporate phylogenetic knowledge with the flexibility of black-box ML methods. We tested our method for two phenotypes (IBD and BMI) and using one type of microbiome data, namely 16S. Our results showed that TADA improved the classification accuracy and the improvements were dramatic when the samples were unbalanced in terms of the distribution of class labels.

We emphasize that the unbalance in training data is not a corner case; in microbiome data, unbalance is the rule, not the exception. Often, microbiome datasets gathered in clinical settings are short on control (i.e. healthy) cases, especially when compared to the larger population. Our results clearly demonstrate that ML methods fail to train well on unbalanced data. While we focused on AUC, it is instructive also to examine the percentage of times a method makes the correct classification call. With 1/10 or 1/5 unbalance levels, the trained ML model is mostly useless because it classifies all testing samples as diseased, achieving artificially high levels of correct classification (Fig. 6) despite low AUC (Fig. 3); i.e. here, ML models just match a no-skill classifier and are, thus, grossly overfit. Balancing augmentation helps to alleviate this issue, as evident in increased AUC values. Nevertheless, balancing changes the prevalence of labels and needs to be done with care. Overall, our results provide a cautionary note on applying ML methods for unbalanced labels and are a reminder that clinical applications of ML to microbiome are fraught with dangers and can benefit from further improvements in the methodology.

Fig. 6.

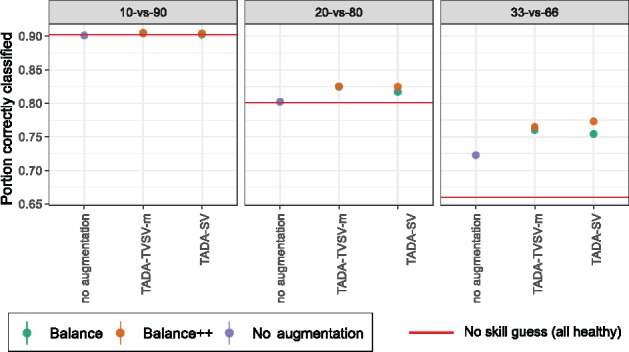
Percentage of correct classification on the E2-fix IBD dataset. Figure settings are similar to Figure 3 but we show percentage of correct classifications instead of AUC. Red line shows the accuracy achieved by simply guessing the healthy label each time

Our results did not show a consistent difference between SV and TVSV generative models across all dataset. The more complex model, TVSV, was slightly more accurate on the BMI dataset but did not manage to outperform SV on IBD. TVSV seeks to capture variability due to biological sources and adds more variance than SV. The failure of TVSV to provide a substantial improvement over SV only on the IBD dataset may indicate that for some datasets (perhaps more carefully curated) the biological variance is already sufficiently captured. But it could also indicate that the variance generated using our hierarchical Beta model, fails to emulate biological variance in a meaningful way. Beta is a powerful model to capture the distribution of proportions, especially when distributed around a center (or the two extremes) but biological distributions may not fit Beta. Moreover, we make conditional independence assumptions on the phylogenetic tree, which may not match the biology (e.g. due to horizontal gene transfer).

Our results indicated that clustering samples and using the mixture model could reduce accuracy if the clusters are big and is neutral or only slightly beneficial when clusters are small (Fig. 2). Thus, sample augmentation was most effective when applied to individual samples or small clusters. It may be that with the small sample sizes that we have and large numbers of confounding factors, samples are so varied that only one or a handful of data points are available per component of the mixture model. Thus, it is possible that as the size of the training datasets increase, the mixture model starts to outperform the TVSV-m consistently. Thus, for existing small datasets, using TVSV-m is a safe choice, but in the future, as more data become available, this question needs to be revisited.

The framework we described for combining generative models and ML methods can be extended beyond the exact generative models we used. Our specific generative model combines a Binomial and a Beta distribution, with one learned parameter (μ) and one parameter fixed based on the phylogeny (ν). The method we used to choose the fixed ν (inversely related to the variance) relies on the phylogenetic knowledge, incorporated as the mean divergence below each node (similar to the F_ST measure). We selected a particular function f, but note that our choice is without strong theoretical underpinnings. Future work should explore more principled choices, deriving the function f as a result of a dispersion process running along the branches of the phylogeny (e.g. a Poisson model). These future attempts could also explore the Balding and Nichols (1995) model, which also is based on a similar Beta model and the F_ST measure.

A natural extension of our generative model is to let ν be learned from the data instead of using the phylogeny. In fact, we have derived the necessary parameter estimators for such a model using the method of moments (see Appendix A.2). However, using this model will double the number of parameters and will rely less on the known phylogenetic knowledge. Our initial tests (Supplementary Fig. S4) indicate this more parameter-rich model fails to perform well on our two test datasets. However, if substantially larger training sets are available in the future, this method should be revisited. Another natural extension is to use Dirichlet+Multinomial instead of Beta+Binomial to allow multifurcating trees. Finally, instead of assuming all μ_u and ν_u parameters are separate parameters, they can be considered random variables drawn from another distribution with appropriate hyperparameters.

We observed that RF had somewhat higher accuracy than NN in our experiments. This observation is in line with some previous studies (e.g. Statnikov et al., 2013), which have demonstrated similar results. However, we note that with augmentation, NN comes much closer to the accuracy of RF. We also note that we have not fine-tuned the NN models. Thus, it is possible that NN, perhaps in the form of smaller networks or conversely deeper networks along with regularization techniques could outperform RF. In particular, deep learning requires large training samples. It is conceivable that deep learning methods paired with augmented data can in the future outperform ensemble methods such as NN in the future.

Other steps of TADA could also be changed. For example, for the phylogenetic inference, instead of placement on a common backbone tree, a de novo inference may be feasible using scalable phylogenetic inference methods. Clustering of samples can also be done using more complex methods designed for microbiome, such as phylogeny-based methods like weighted/unweighted Unifrac distances (Lozupone et al., 2007; Lozupone and Knight, 2005) and compositional methods like Aitchison’s distance (Aitchison, 1982; Aitchison et al., 2000). Finally, as features for the ML training, we used OTUs as obtained using the Deblur algorithm (i.e. de-noised sequences). However, extracting features can also follow more complex methods, perhaps using those that include the phylogenetic knowledge (e.g. Albanese et al., 2015; Morton et al., 2017).

Our studies show potential for improving the generalization of ML methods. We tested only two datasets, each with only two categories. Future work should explore applications of TADA to more phenotypes, including multi-labeled ones. Also, nothing in the method limits it to gut or human microbiome; the same method should be explored on other types of environments. Future experiments should also explore training models on a dataset and testing on a separate dataset produced by a different lab; perhaps augmentation can also help reduce batch effects, which are notoriously difficult to deal with in microbiome modeling. Finally, we focused on 16S profiling. However, phylogenetic placement methods for shotgun metagenomic samples also exist [e.g. TIPP (Nguyen et al., 2014)]; future work should explore the application of TADA to metagenomic data.