Identifying and ranking potential driver genes of Alzheimer’s disease using multiview evidence aggregation

Abstract

Motivation

Late onset Alzheimer’s disease is currently a disease with no known effective treatment options. To better understand disease, new multi-omic data-sets have recently been generated with the goal of identifying molecular causes of disease. However, most analytic studies using these datasets focus on uni-modal analysis of the data. Here, we propose a data driven approach to integrate multiple data types and analytic outcomes to aggregate evidences to support the hypothesis that a gene is a genetic driver of the disease. The main algorithmic contributions of our article are: (i) a general machine learning framework to learn the key characteristics of a few known driver genes from multiple feature sets and identifying other potential driver genes which have similar feature representations, and (ii) A flexible ranking scheme with the ability to integrate external validation in the form of Genome Wide Association Study summary statistics. While we currently focus on demonstrating the effectiveness of the approach using different analytic outcomes from RNA-Seq studies, this method is easily generalizable to other data modalities and analysis types.

Results

We demonstrate the utility of our machine learning algorithm on two benchmark multiview datasets by significantly outperforming the baseline approaches in predicting missing labels. We then use the algorithm to predict and rank potential drivers of Alzheimer’s. We show that our ranked genes show a significant enrichment for single nucleotide polymorphisms associated with Alzheimer’s and are enriched in pathways that have been previously associated with the disease.

Availability and implementation

Source code and link to all feature sets is available at https://github.com/Sage-Bionetworks/EvidenceAggregatedDriverRanking.

1 Introduction

Late onset Alzheimer’s disease (LOAD) is a debilitating illness with no known disease modifying treatment (Alzheimer’s, 2015; Frozza et al., 2018). To address this, there have been a recent surge in the generation of multi-modality data (Hodes and Buckholtz, 2016; Mueller et al., 2005) to understand the biology of the disease and potential drivers that causally regulate it. Identification new genetic drivers of LOAD will be key to the development of effective disease modifying therapeutics. To prioritize experimental evaluation of LOAD drivers, we present a data driven approach to rank genes based on the probability that they drive LOAD using transcriptional (RNA-seq) data collected from postmortem brain tissue in patient cohorts.

While there exists some prior work on driver gene ranking (Grechkin et al., 2016; Hou and Ma, 2014; Liu et al., 2015; Mukherjee et al., 2018; Zhang et al., 2013), these approaches have several limitations that make them unsuitable for all feature types. Many of these approaches work only with somatic mutation data from patients tumor samples, ranking genes by comparing the mutation rates of somatic variants in patients for different genes to an appropriate null model to identify cancer driver genes (Tian et al., 2014). While some other approaches use ensemble approaches to rank genes using predictions from other tools that use genomic data (Liu et al., 2015). Unfortunately, these approaches are highly specialized to the type of data and cannot be easily generalized to a broader class of feature sets. Furthermore, while in cancer driver genes are defined based on somatic genetic variation, in complex diseases such as Alzheimer’s disease we define driver genes as those that are causally affecting risk of disease via germline genetic variation. While there exist approaches such as DawnRank (Hou and Ma, 2014) which utilize RNA-Seq data in addition to genomic data for each patient, these too have strong modeling assumptions leading to lack of generalizability. Furthermore, most of these previous approaches are designed for detecting driver genes that are driven by somatic mutation events aside from the Key Driver analysis of Zhang and Zhu (2013). Alternatively, we are interested in identifying signatures of driverness from somatic tissue that are indicative of germline risk for LOAD. Here, we propose a highly generalizable machine learning approach to learn signatures of germline genetic risk within summaries of transcriptomic expression of somatic postmortem brain tissue driver ranking and demonstrate it’s effectiveness on RNA-Seq derived feature sets.

Our driver ranking approach serves as an evidence aggregation framework, and currently uses differential expression, undirected gene networks inferred with an ensemble co-expression network inference method and co-expression module summaries (Logsdon et al., 2019) generated using transcriptional data collected from postmortem brain tissue across three studies (ROSMAP, Mayo RNAseq, MSBB) in AMP-AD. We assume that each analytic summary (while originating from the same RNA-seq data-sets) contains independently predictive information that can be used to identify genes with a burden of germline AD risk variants. We process these independent analytic summaries into the following feature sets (see Table 1) to be used for machine learning: (i) genes that are differentially expressed between AD cases and controls in specific brain regions, (ii) global un-directed network topological features for specific brain regions and (iii) module specific network topological features for 42 tissue specific co-expression modules.

Table 1.

Description of various feature sets used for multiview evidence aggregation

Feature set	SynapseID	No. features	Type	Descriptions
Differential expression	syn18097426	250	Binary	Membership based on differential expression in different brain regions and patient subgroups (such as males/females)
Global network	syn18097427	42	Numeric	Features derived from graph structure in different brain regions
Module network	syn18097424	66	Numeric	Features derived from graph structure in important co-expression modules from different brain regions

Here, we divide the task of ranking potential driver genes into two sub-tasks: (i) training machine learning models to identify probabilities of genes being driver genes using each feature set, (ii) aggregation of predictions of models for each feature set along with independent Genome Wide Association Study (GWAS) statistics to rank potential driver genes (Fig. 1). The primary goal of the first task is to learn the unique characteristics of 27 previously known drivers of AD identified from published LOAD GWAS studies (Kunkle et al., 2019; Lambert et al., 2013) and use it to identify potential novel drivers of the disease. These AD drivers were defined as loci that were genome-wide significant in one study (P < 5 × 10⁻⁸), with significant replication P-value (P < 0.05) in a second study. The technical challenges associated with the first task include finding an appropriate approach to identify the driver probabilities and finding a way to learn from sparsely labeled data (only 27 genes have labels, while others may or may not be driver genes). To tackle this, here we propose a novel multiview classification (Xu et al., 2013) approach, which includes iterative update of labels to infer additional candidate driver genes. For the latter task the primary challenge is to define an appropriate scoring system to rank genes. Here, we propose a flexible scoring system that not only utilizes model predictions for each feature set but also independent LOAD GWAS statistics.

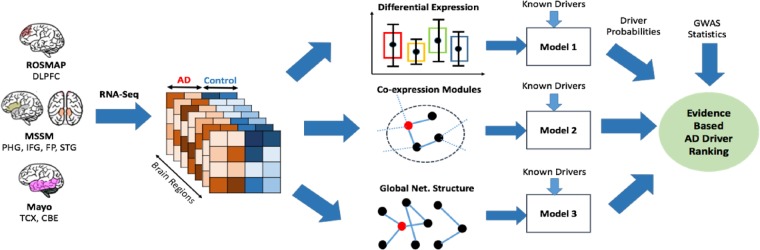
Fig. 1.

RNA-Seq data for AD patients and controls were derived for seven different brain regions from three centers. Differential expression, co-expression module and global network features were derived from all brain regions. Each feature and known drivers were used to build predictive models for driver genes. These driver probabilities and GWAS statistics were used for an evidence-based driver ranking

We demonstrate our multiview classification algorithm achieves substantially higher performance compared with models trained for individual feature sets on standardized multiview datasets. We then demonstrate that similar performance benefits hold when applied to LOAD postmortem brain tissue RNA-seq using qualitative metrics. We observe that global network topological features from inferred sparse co-expression networks—such as node degree—are predictive of LOAD driver genes as identified in GWAS, and more so than differential expression features. Finally, we show that our ranking methodology identifies several previously known LOAD loci implicated in other studies (Jonsson et al., 2013; Ki et al., 2002; Kiyota et al., 2015; Mukherjee et al., 2017) as well potentially new LOAD risk loci. These findings may lead to new mechanistic hypotheses regarding the genetic drivers of LOAD. Furthermore, a Gene Ontology (Chen et al., 2013) pathway analysis of the highly ranked predicted driver genes identifies multiple pathways previously implicated in LOAD disease etiology.

2 Materials and methods

2.1 Study description

In brief, all feature sets are derived from analyses of RNA-seq data on 2114 samples from 1100 patients from seven distinct brain regions (Temporal Cortex, Cerebellum, Frontal Pole, Inferior Frontal Gyrus, Superior Temporal Gyrus, Parahippocampal Gyrus and Dorsolateral prefrontal cortex) and three studies—the Mount Sinai Brain Bank study (Wang et al., 2018), the Mayo RNA-seq study (Allen et al., 2016) and the ROSMAP study (A Bennett et al., 2012). A full description of the data and the RNA-seq processing pipeline that was used to generate analytic outputs is described in Logsdon et al. (2019).

2.2 Deriving usable features for meta-analysis

Features were inferred from specific statistical analyses that were run on RNA-seq datasets within each of the seven tissue types. These analyses included set membership features from differential expression analysis (e.g. test of changes in mean expression between AD cases/controls and subgroups such as males and females), global network features from a sparse ensemble co-expression network inference method described in further detail in Logsdon et al. (2019), and network topological features for communities of genes identified from the networks described in the same paper. The sparse network inference approach applies 17 distinct co-expression network inference algorithms (including ARACNe, Genie3, Tigress, Aparrow, Lasso, Ridge, c3net and WGCNA) to data derived from each tissue type, and averages across the edge strength rankings from each method to determine an ensemble sparse representation of co-expression relationships (see Logsdon et al., 2019) for details). In all network type features we extract standard network topological characteristics such degree, authority score, betweeness centraility, pagerank and closeness.

2.3 Iterative multiview classification for driver prediction

Here, we pose the driver gene prediction as a binary classification problem using corrupted labels (Frénay and Verleysen, 2014). Formally, given a feature vector $X_i\in {\mathbf{R}}^d$ for a gene denoted by the index i, we wish to predict a class label from {0, 1} where 1 would indicate that the gene is a driver gene and 0 if it’s not. Additionally, we also desire to predict the conditional probability for of a gene being a driver, given the feature information, i.e. $\mathbb{P}({\widehat{Y}}_i=1|X=X_i)$. This problem is solved by a broad class of binary classification problems such as logistic regression, support vector machines etc. in the presence of a training dataset with input features and output class labels. However, here we are only provided a list of a small subset of drivers (from existing literature), whereas all other genes may or may not be a driver. Mathematically, this is akin to learning from noisy labels $\tilde{Y}$ instead of the actual labels Y where $\mathbb{P}(Y=1|\tilde{Y}=1)=1$ but $\mathbb{P}(Y=0|\tilde{Y}=0)\ne 1$. While there are many general strategies for learning from noisy labels such as removing bad data points, active learning etc. (Frénay and Verleysen, 2014), they generally don’t account for this specific type of label noise or make assumptions about rates of mis-labeling in each class. Hence, here we focus on a simple existing approach for such problems (Iterative Classification) and propose a variant of it utilizing the fact that we have features from multiple views for the same genes.

2.3.1 Iterative classifier

Iterative classification is a simple approach where the general idea is to update the labels samples where $\tilde{Y}\ne 1$ to that of the predicted class $\widehat{Y}$ after each iteration of model training (Liu et al., 2003). This can be written in algorithmic terms as in Algorithm 1. While this algorithm is general and can be used for different classifiers, here we demonstrate it on a L2-penalized logistic regression. Here, ll denotes the maximum likelihood loss for logistic regression and thresh is a constant in $[0,1]$, typically chosen to be greater than 0.5. The higher the threshold, the more conservative the iterative updates are, acting as a trade-off between specificity and sensitivity.

Algorithm 1.

Iterative classification with L2-penalized logistic regression

function IC($X,\tilde{Y},\mathit{maxiters},\mathit{thresh},\lambda$)

 $y\leftarrow \tilde{Y}$

 for$\mathit{iter}\leftarrow \mathrm{1\dots }m\mathit{axiters}$do

  $\widehat{w}={\text{argmin}}_{w}1/N{\sum }_{k=1}^N-ll(y_k|X_k,w)+\lambda |\left|w\right|{|}_2^2$

  for$j\leftarrow \mathrm{1\dots }N$ s.t. ${\tilde{Y}}_j\ne 1$do

   $p_j\leftarrow \mathbb{P}(y_j=1|X_j,\widehat{w})$

   $y_j\leftarrow 1(\mathbb{P}(y_j=1|X_j,\widehat{w})\ge \mathit{thresh})$

  end for

 end for

 returnp, y

end function

In the presence of data from multiple views from the same samples ${\left\{X^i\right\}}_{i=1}^K$, the algorithm is run for each view separately and an average of the predicted probabilities of all models is considered while evaluating the final multiview predictions (we shall refer to this as ’consensus’ for short in later text and figures).

2.3.2 Iterative classifier with co-training

While the previous algorithm solves the problem of noisy labels and integrates information from multiple views, it does so by training models for each individual view independently. However, as seen in Figure 1, the features for different views are generated from the same underlying source, i.e. the RNA-Seq data from brain samples of patients and controls. Hence, the different views can be seen as functional transformations of the same underlying data, corrupted with different noise sources and should encode the same classification information.

In the case of original multiview classification problems, it is common to enforce view similarity which requires predictions made by different views to be similar to each other, through co-training or co-regularization (Xu et al., 2013). Here, the problem is more difficult to the noise in the labels. Hence, we develop a method which integrates the iterative updating scheme developed previously with co-training. Formally, we pose the problem of iteratively learning labels with co-training as the following optimization problem:

$$\underset{{\left\{w^k\right\}}_{k=1}^K,{\left\{y_i^k\right\}}_{k=1}^K}{\text{argmin}}-\frac{1}{N}\sum _{k=1}^K\hspace{0.17em}[\sum _{i=1}^{N}ll(y^k|X_i^k,w^k)+{\lambda }^k\left|\right|w^k\left|{|}_2^2\right]$$

$$+\frac{\rho }{4}\sum _{k=1}^K\sum _{k\prime =1}^K||y^k-y^{k\prime }|{|}_2^2$$

subject to:

$$\hspace{1em}{y}^k\in {\{0,1\}}^N,\hspace{1em}{y}_i^k=1,\hspace{1em}\forall \hspace{1em}{\tilde{Y}}_i=1$$

It can be seen that this is a mixed-integer optimization problem, which is a particularly hard class of optimization problems to solve. However, for fixed ${\left\{y^k\right\}}_{k=1}^K$, the optimization problem is convex in ${\left\{w^k\right\}}_{k=1}^K$ and is simply logistic regression for the different views. Hence, a locally optimal solution to the optimization problem is via alternative minimization on ${\left\{y^k\right\}}_{k=1}^K$ and ${\left\{w^k\right\}}_{k=1}^K$ starting with ${\left\{{\tilde{Y}}^k\right\}}_{k=1}^K$. Unfortunately, the problem of optimizing over ${\left\{y^k\right\}}_{k=1}^K$ is a constrained binary quadratic programming problem, which does not have exact solutions or efficient exact solvers (Kochenberger et al., 2014). However, upon relaxing the binary constraint to a linear constraint ($\{0,1\}\to$ [0, 1]), the optimization problem becomes a tractable convex optimization problem:

$$\underset{{\left\{y^k\right\}}_{k=1}^K}{\text{argmin}}-\frac{1}{N}\sum _{k=1}^K\hspace{0.17em}[\sum _{i=1}^N{y}_i^k\hspace{0.17em}\text{log}(\frac{P(y_i^k=1|X_i^{\mathrm{kT}},w^k)}{P(y_i^k=0|X_i^{\mathrm{kT}},w^k)})+$$

$$\frac{\rho }{4}\sum _{k=1}^K\sum _{k\prime =1}^K||y^k-y^{k\prime }|{|}_2^2]$$

subject to:

$$\hspace{1em}0\le y^k\le 1,\hspace{1em}{y}_i^k=1\hspace{1em}\forall \hspace{1em}{\tilde{Y}}_i=1$$

Here, we note that $\text{log}(O{R}_i^k)=\text{log}\left(\frac{P(y_i^k=1|X_i^{\mathrm{kT}},w^k)}{P(y_i^k=0|X_i^{\mathrm{kT}},w^k)}\right)$. We note that this optimization problem is independent in each i and can be solved independently. Next we demonstrate that the previously posed linear relaxation which can be solved using the co-ordinate descent methodology using a closed form update rule for each $y_i^k$.

Claim 1: A co-ordinate descent strategy leads to an optimal solution to the previously stated optimization problem.

Proof:

It is sufficient to show that the optimization problem is convex. Since the inequality constraints are linear in $y_i^k$’s, to demonstrate convexity of the optimization problem, we simply need to demonstrate that the cost function is convex. This can be shown by re-parameterizing the problem for the ith variable in terms of a new variable $x_i=[y_i^1,\mathrm{..},y_i^K]$.

$$\begin{array}{c}J(x_i)=\frac{\rho }{4}\sum _{j=1}^K\sum _{k=1}^K|\left|A_j^k{x}_i\right|{|}_2^2+b^T{x}_i\hspace{0.17em}\\ \text{Where},{({\mathrm{A}}_{\mathrm{j}}^{\mathrm{k}})}_{\text{pq}}=\{\begin{array}{c}1,\hspace{0.17em}\text{for}\hspace{0.17em}\mathrm{p}=\mathrm{j},\mathrm{q}=\mathrm{k}\hfill \\ -1,\hspace{0.17em}\text{for}\hspace{0.17em}\mathrm{p}=\mathrm{k},\mathrm{q}=\mathrm{j}\hfill \\ 0,\hspace{0.17em}\text{Otherwise}\hfill \end{array}\end{array}$$

$$\hspace{0.17em}\text{And},{\mathrm{b}}^{\mathrm{T}}=\frac{1}{\mathrm{N}}[\hspace{0.17em}{\text{log}}_{10}({\text{OR}}_{\mathrm{i}}^1),\mathrm{..},\hspace{0.17em}{\text{log}}_{10}({\text{OR}}_{\mathrm{i}}^{\mathrm{K}})]$$

Next, we calculate the second derivative of $J(x_i)$:

$${\nabla }^{2}J(x_i)=\frac{\rho }{4}\sum _{j=1}^K\sum _{k=1}^K{(A_j^k)}^T{A}_j^k$$

We see that, since this is a sum of positive semi-definite matrices, ${\nabla }^{2}J(x_i)\succcurlyeq 0$ for all x_i, which is a sufficient condition for convexity (Q.E.D.).

Claim 2: The previously stated optimization problem has a closed form co-ordinate descent rule given by:

$$y_i^k=\max \{0,\min \{\frac{1}{K-1}\sum _{j\ne k}{y}_i^j+\frac{1}{N\rho }\text{log}(O{R}_i^k),1\left\}\right\}$$

$$\hspace{1em}\forall i\in \{1,\mathrm{..},N\}\hspace{1em}s.t.\hspace{1em}{\tilde{Y}}_i\ne 1,\hspace{1em}\forall k\in \{1,\mathrm{..},K\}$$

Proof

: The loss function for each $y_i^k$ can be written as:

$$J(y_i^k)=-\frac{1}{N}{y}_i^k\hspace{0.17em}\text{log}(O{R}_i^k)+\frac{\rho }{2}\sum _{k\prime \ne k}{(y_i^k-y_i^{k^{\prime }})}^2$$ (1)

It is easy to see that this is a parabola of the form $y=a{(x-b)}^2+c$. For a parabola of this form, the minima (if a > 0) or maxima (if a < 0) occurs at x = b. For our cost function, we see that $a=\frac{(K-1)\rho }{2}>0$ and $b=\frac{1}{K-1}\sum _{j\ne k}{y}_i^j+\frac{1}{N\rho }\text{log}(O{R}_i^k)$. Hence, $\frac{\delta J(y_i^k)}{\delta y_i^k}<0$ if $y_i^k<b,\hspace{0.17em}\frac{\delta J(y_i^k)}{\delta y_i^k}=0$ if $y_i^k=b$ and $\frac{\delta J(y_i^k)}{\delta y_i^k}>0$ if $y_i^k>b$. We now look at three possible locations of $y_i^k=b$ with respect to the interval $y_i^k\in [0,1]$ and the constrained minima in each case:

Case I ( $b\in [0,1]$ ): Here, the constrained minima is the same as the global minima.

Case II (b < 0): Here, $\frac{\delta J(y_i^k)}{\delta y_i^k}>0$ in $[0,1]$. Hence, the constrained minima occurs at $y_i^k=0$.

Case III (b > 0): Here, $\frac{\delta J(y_i^k)}{\delta y_i^k}<0$ in $[0,1]$. Hence, the constrained minima occurs at $y_i^k=1$.

Now, compiling the closed form solutions in the three cases, we can re-write the co-ordinate descent rule as $y_i^j=\max \{0,\min \{\frac{1}{K-1}\sum _{j\ne k}{y}_i^j+\frac{1}{N\rho }\text{log}(O{R}_i^k),1\left\}\right\}$ (Q.E.D.).

Algorithm 2.

Iterative classifier with co-training

function ICCT(${\left\{X^i\right\}}_{i=1}^K,\tilde{Y},\mathit{maxiters},\mathit{thresh},\lambda ,\rho$)

 $y^k\leftarrow \tilde{Y}\hspace{1em}\forall k\in \{1,\mathrm{..},K\}$

 for$\mathit{iter}\leftarrow \mathrm{1\dots }m\mathit{axiters}$do

  for$k\leftarrow \mathrm{1\dots }K$do

   ${\widehat{w}}^{\mathit{k}}={\text{argmin}}_{w^k}1/N{\sum }_{l=1}^N-ll(y_l|X_l^k,w^k)+\lambda |\left|w^k\right|{|}_2^2$

  end for

  for$j\leftarrow \mathrm{1\dots }N$ s.t. ${\tilde{Y}}_j\ne 1$do

   for$k\leftarrow \mathrm{1\dots }K$do

    $p_j^k\leftarrow \mathbb{P}(y_j=1|X_k,{\widehat{w}}^{\mathit{k}})$

    $y_j^k\leftarrow 1(y_j^{k,\mathit{LR}}\ge \mathit{thresh})$

   end for

  end for

 end for

 return${\left\{p^i\right\}}_{i=1}^K,{\left\{y^i\right\}}_{i=1}^K$

end function

The solutions can then be binarized by selecting an appropriate threshold like in the previous algorithm. An interesting observation is that the update rule for any y^k is simply an average of all the other y’s and an additional term which is solely dependent on the odds ratio of the kth view. This can be implemented as seen in Algorithm 2.

Similar to the separately trained approach, consensus is taken to obtain final multiview predictions.

2.3.3 Implementation and hyperparameter tuning

Both multiview iterative learning schemes were built using the Logistic regression in the sci-kit learn package of Python. A generalizable implementation of the code can be found at the link mentioned in the abstract. Values of λ for each feature set were chosen using a 10-fold cross-validation approach using the original labels using the LogisticRegressionCV function in sci-kit learn. The value of ρ was chosen to be $1/N$ for analysis of the RNA-Seq dataset based on performance on the benchmark datasets.

2.4 Evidence aggregated ranking

The goal of the evidence aggregated ranking scheme is to aggregate the predictions of the models trained using different feature sets and also (optionally) integrate unrelated external information from large sample GWAS studies. Here, we develop a flexible scoring system that achieves the above stated goal:

$$\mathit{Score}(\mathit{Gen}{e}_i)=\frac{\alpha }{K}\sum _{j=1}^K{\hspace{0.17em}\text{log}\hspace{0.17em}}_{10}(O{R}_i^j)$$

$$-\frac{1-\alpha }{|\mathit{SNP}(\mathit{Gen}{e}_i)|}\sum _{k\in \mathit{SNP}(\mathit{Gen}{e}_i)}{\hspace{0.17em}\text{log}\hspace{0.17em}}_{10}{(\mathrm{p}-\text{value})}_k$$

Here, $\alpha \in (0,1]$ is a user specified weighting parameter which controls the relative importance given to the external GWAS evidence vis-a-vis the model predictions using our feature sets, and $|\mathit{SNP}(\mathit{Gen}{e}_i)|$ refers to the number of single nucleotide polymorphisms (SNPs) in a pre-specified window around Gene_i. The models themselves are weighed equally relative to each other. For the purposes of this paper we chose the $\alpha =0.5$, thereby assigning equal weight to our model predictions and external GWAS evidence. The average of log transformed SNP P-value is chosen instead of the minimum P-value (MP) in order to capture the composite effect of all SNPs in a gene.

3 Results

3.1 Comparison of learning approaches on benchmark datasets

To first test quantitatively test the relative efficiency of the two learning approaches, we first test them on some standard benchmark datasets obtained from https://github.com/yeqinglee/mvdata [used in Li et al. (2015)]:

Handwritten digits: This is a dataset containing handwritten digits (0 through 9) originally from UCI’s Machine Learning repository. It consists of 2000 data points. We use three of the published features namely: 240 pixel averages in 2 × 3 windows, 76 Fourier coefficients of the character shapes and 216 profile correlations.

Caltech-101: This is a dataset comprising of seven classes of images amount to a total of 1474 images (Dueck and Frey, 2007). We use three of the published features namely: 48 Gabor features, 254 CENTRIST features and 40 features derived from Wavelet moments.

For each dataset, we performed binary classification with different algorithms on each class separately, after corrupting the labels by randomly deleting 50% of the ’true’ class labels to simulate the driver identification problem. The training was performed on corrupted labels while testing was performed on the actual labels. Algorithms were compared by their mean accuracy across all the class labels on the actual class labels. The algorithms compared were: (i) Iterative classifiers (ICs) trained on each feature type separately, (ii) ICs trained on each feature type separately followed by consensus among the learned models (using simple majority), (iii) IC trained on a ‘stacked’ feature set (all feature sets were horizontally stacked into one) and (iv) IC with co-training.

As seen in Figure 2, we see that IC with co-training outperforms other algorithms on both standard datasets by a large margin, while IC with consensus does not always lead to improvements over the best single view iteratively trained model. The stacked model tends to perform better than the best single view model but not as well as iterative classifier with co-training (ICCT) in either dataset. This is perhaps because the difference in information content between the different views can sometimes make taking consensus ineffective.

Fig. 2.

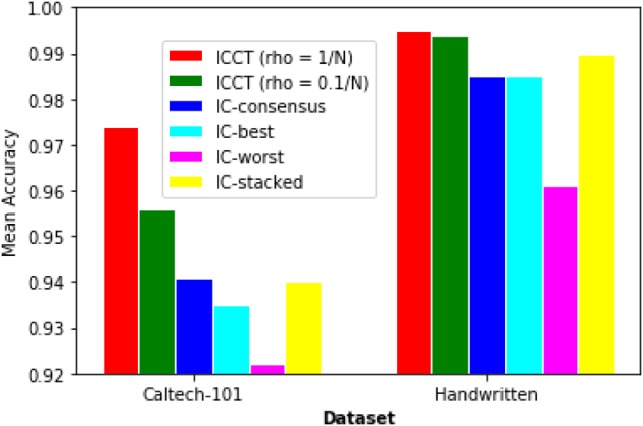
Comparison of various classification algorithms trained on corrupted class labels and tested on actual labels

3.2 Validation of driver prediction using independent GWAS datasets

To validate our multiview data aggregation schemes and generate a biologically meaningful ranking, we first generated gene-wise summary statistics from two separate GWAS datasets, namely IGAP (Lambert et al., 2013) and Jansen (Jansen et al., 2019). The IGAP study has a sample size of 74 046 (25 580 cases and 48 466 controls) from individuals of European ancestry with over 7 million total SNPs. The Jansen study has a sample size of 455 258 (71 880 cases, 383 378 controls) also from European ancestry. This study contains in the addition to the data used in the IGAP study in addition to 3 complementary studies: Alzheimer’s Disease Sequencing Project (ADSP), Psychiatric Genomics Consortium (PGC-ALZ) and UK Biobank studies.

For each of these GWAS datasets, we generated two gene-wise summary statistics, namely: (i) mean of log P-value of SNPs (MLP) and (ii) MP of SNPs. This was done by mapping each SNPs to a 10 kb window around known protein coding gene locations in a reference genome (hg38) and then computing the two summary statistics of interest per gene. The mapping of SNPs to genes was performed using the MAGMA software package (de Leeuw et al., 2015).

Similar to the benchmark datasets, we trained both IC and ICCT models on the three previously mentioned feature sets to obtain probabilities of all genes being driver genes for AD. We first performed a validation using a leave-one-out approach where we trained models excluding one driver gene each time and compared the predicted probability for the held out gene for ICCT and IC approaches. We find a stark improvement in the performance at predicting the driver probability by ICCT (mean = 0.47, median = 0.59, standard deviation = 0.36) when compared with IC (mean = 0.24, median = 0.09, standard deviation = 0.29). In the absence of true labels for validation, we adopt a qualitative metric to further test the model accuracies using external GWAS data. This was done by performing a Mann–Whitney U test between the distributions of MP/MLP values of predicted driver genes and genes not predicted to be drivers. A significant difference between the distributions would suggest that predicted driver genes contain more genes significant to AD than non-driver genes. Using this metric, we find that the ICCT-consensus model shows the strongest difference between the distributions (measured using the Mann–Whitney U test P-value), followed by models trained on the network topological features trained as a part of the ICCT algorithm (Fig. 3). It is seen in both datasets, that even some feature set specific predictions of the ICCT algorithm outperforms the basic iterative learning approach (IC), demonstrating the utility of co-training. Interestingly, the high relative performance of the network topological features when compared with the differential expression features implies that local and global network structure plays a strong role in determining which genes have causal effects on Alzheimers.

Fig. 3.

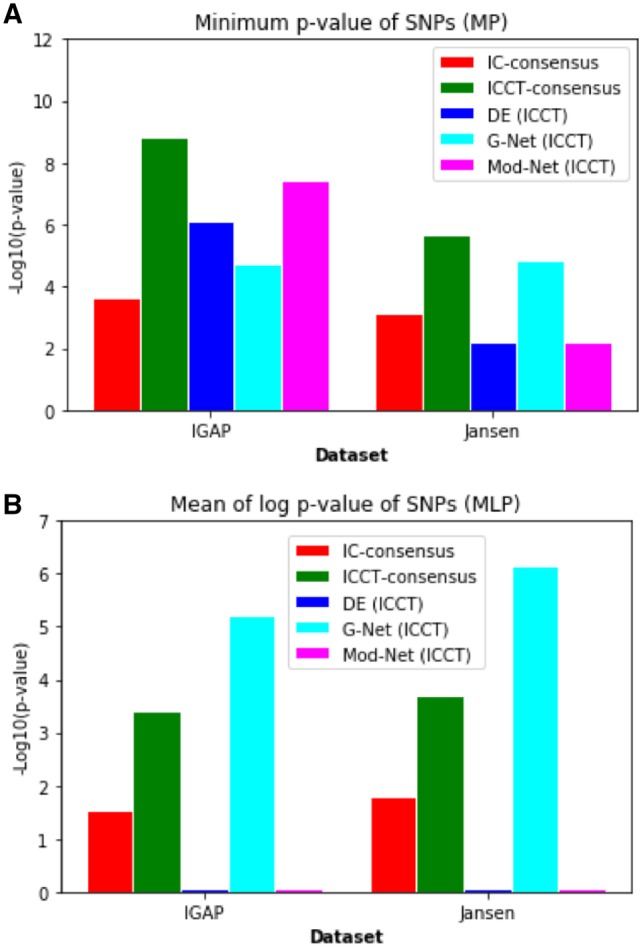
(A) Results of the Mann–Whitney U test performed on IGAP and Jansen MP distributions for predicted driver versus non-driver genes. (B) Results of the t-test performed on IGAP and Jansen MLP distributions for predicted driver versus non-driver genes

3.3 Biological analysis of predicted drivers

Having demonstrated the statistical significance of the predicted driver genes, we ranked them using our ranking schema. The top 20 ranked genes can be seen in Table 2, which contains several genes strongly linked with AD such as APOE, APOC1, CD74, TREM2, SLC7A7 (Jonsson et al., 2013; Ki et al., 2002; Kiyota et al., 2015; Mukherjee et al., 2017) etc. Table 2 also contains the minimum SNP P-values for each of these genes according to the IGAP and Jansen studies. It can be seen that while our models are not trained on any SNP information, the results strongly align with additional validation GWAS data.

Table 2.

Top 20 ranked genes along with their associated driver score and minimum P-value from IGAP (Lambert et al., 2013) and Jansen (Jansen et al., 2019) GWAS datasets

Genes	Driver score	Jansen P-value	IGAP P-value
APOC1	42.92	<1E−308	<1E−308
APOE	41.75	<1E−308	<1E−308
BCAM	5.88	1.60E−143	4.66E−69
CD74	4.92	1.93E−02	1.20E−01
TREM2	4.65	2.95E−15	1.07E−03
CLPTM1	4.58	7.07E−50	2.80E−21
DEF6	4.28	5.94E−03	3.52E−02
SLC7A7	4.05	2.29E−03	2.36E−02
DOCK2	3.72	9.14E−04	4.82E−03
SPI1	3.62	1.06E−06	1.99E−06
STEAP3	3.61	3.63E−05	2.21E−02
PICALM	3.56	2.19E−18	1.91E−12
HMOX1	3.56	1.16E−02	1.43E−01
CLU	3.55	2.61E−19	2.48E−17
MS4A6A	3.55	1.55E−15	6.64E−11
IRF5	3.45	1.21E−02	1.48E−02
TYROBP	3.44	1.34E−02	5.40E−02
PARVG	3.42	1.44E−02	1.05E−03
ITGAL	3.41	1.92E−04	4.36E−03
PTPRC	3.33	2.12E−03	7.24E−03

To further validate the results we performed gene set enrichment analyses with the top-500 ranked potential driver genes using Enrichr (Chen et al., 2013), a web based gene set enrichment tool. The top 20 significant processes and functions ranked according to their adjusted P-values can be seen in Table 3. Several of the processes such as immune response, amyloid processing, amyloid catablism, amyloid clearance and apoptotic processes, and functions such as low-density lipoprotein binding and activity are already known to significantly altered in AD, whereas several other interesting ones such as endocytosis, scavenger receptor activity and peptidase activity can lead to potential new insights into AD disease mechanisms.

Table 3.

Top 20 enriched genesets for biological process and function along with their associated adjusted P-values obtained from Enrichr (Chen et al., 2013)

GO biological process	Adjusted P-value	GO molecular function	Adjusted P-value
Neutrophil mediated immunity	3.03E−12	MHC Class II receptor activity	7.67E−03
Neutrophil activation involved in immune response	3.03E−12	Activin binding	7.67E−03
Neutrophil degranulation	4.62E−12	MHC Class II protein complex binding	7.67E−03
Interferon-gamma-mediated signaling pathway	4.62E−12	MHC protein complex binding	7.67E−03
Cytokine-mediated signaling pathway	9.91E−11	Transforming growth factor beta binding	7.67E−03
Cellular response to interferon-gamma	5.79E−10	Phosphotyrosine residue binding	7.67E−03
Negative regulation of amyloid precursor protein catabolic process	7.71E−05	Transforming growth factor beta receptor binding	7.67E−03
Regulation of amyloid-beta formation	7.94E−05	Amyloid-beta binding	7.67E−03
Positive regulation of intracellular signal transduction	1.62E−04	Scavenger receptor activity	1.04E−02
Positive regulation of actin nucleation	1.68E−04	Protein phosphorylated amino acid binding	1.09E−02
Endocytosis	2.26E−04	Low-density lipoprotein receptor activity	1.42E−02
Regulation of mast cell degranulation	3.07E−04	Phosphatidylinositol bisphosphate binding	1.42E−02
Regulation of apoptotic process	3.07E−04	Protein kinase binding	1.42E−02
Extracellular matrix organization	3.07E−04	Clathrin heavy chain binding	1.91E−02
Negative regulation of amyloid-beta formation	4.01E−04	Lipoprotein particle receptor activity	1.95E−02
Antigen receptor-mediated signaling pathway	4.01E−04	GTPase regulator activity	2.02E−02
Negative regulation of extrinsic apoptotic signaling pathway	5.26E−04	Actin binding	2.23E−02
Regulation of amyloid-beta clearance	5.77E−04	Type II transforming growth factor beta receptor binding	2.30E−02
T cell receptor signaling pathway	5.77E−04	Low-density lipoprotein particle binding	2.30E−02
Cellular response to transforming growth factor beta stimulus	1.09E−03	Peptidase activity, acting on L-amino acid peptides	2.30E−02

3.4 Analysis of top features for driver prediction models

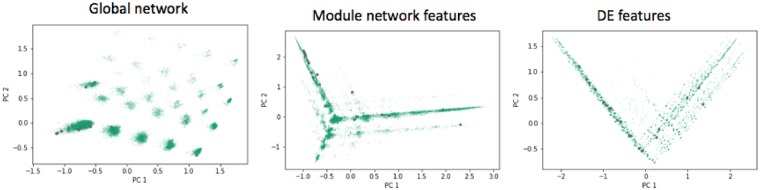
Having noted that the network topological features provide are more predictive of the driver ranking of genes, we evaluate the most predictive features of each of the network feature sets in Table 4. We calculated the Spearman’s rank correlation for each feature with the model predictions for their feature set, to evaluate their relative predictive power. Interestingly, we find several highly correlated features from both feature sets. Upon closer look at the top 10 highly correlated features from the Module-Network feature set all are negatively correlated, with all the features derived from with DLPFC (Dorsolateral Prefrontal Cortex) and TCX (Temporal Cortex) brain regions. This is intriguing because the sample size in DLPFC is largest (n = 630), and the signal to noise ratio in TCX is highest (it is a highly affected brain region, and the median depth of sequencing for that study was 60 million reads compared with 35 million for the other studies). The same trend cannot be observed in the Global-Network feature set, where the top 10 features are associated with STG (Superior Temporal Gyrus), PHG (Parahippocampal Gyrus) and DLPFC brain regions and all the correlations are positive. However, in this case, the top features are all associated with high connectivity of genes, which agrees with the popular notion that driver genes are also typically hub genes (Liu et al., 2012, 2011; Mukherjee et al., 2018). This can also be seen in Figure 4, where we note that most of the known drivers lie in one of the islands of genes (in the principle component plot) which corresponds to genes with very high degrees (or hubs).

Table 4.

Spearman rank correlation (with model predictions) for the top 10 features of network topological feature sets

Module net	ρs	Global net	ρs
TCXbrownTCXauthority	−0.36	STGcloseness	0.58
TCXbrownTCXdegree	−0.36	STGdegree	0.57
TCXbrownTCXeccentricity	−0.36	STGauthority	0.57
DLPFCredDLPFCauthority	−0.34	PHGauthority	0.54
DLPFCredDLPFCeccentricity	−0.34	STGpagerank	0.53
TCXbrownTCXcloseness	−0.34	PHGdegree	0.53
DLPFCredDLPFCdegree	−0.34	PHGcloseness	0.52
TCXbrownTCXpagerank	−0.34	DLPFCauthority	0.52
DLPFCredDLPFCcloseness	−0.33	STGcentr_betw	0.50
DLPFCredDLPFCpagerank	−0.33	DLPFCdegree	0.50

Fig. 4.

Known driver genes (colored in gray) and all other genes highlighted on the top two principal components for each of the three feature sets

4 Conclusion

Here, we provide a generalizable framework for integration of diverse systems biology outputs to rank and identify new transcriptomic and genetic drivers of Alzheimer’s disease. This provides evidence that integration of multiple systems biology resources can provide insights into new Alzheimer’s disease loci, which can help researchers prioritize future experimental studies focusing on specific genes and pathways that are driving disease etiology. While not all genes in genomic neighborhoods implicated by GWAS may actually be causal drivers of disease, we expect genes implicated in GWAS to be highly enriched for disease specific drivers. Our approach takes these genes implicated from GWAS analyses and finds common patterns from expression data that are predictive of these genes. We do not expect the predictions from our model to be devoid of false positives, but we do expect genes that are in fact genetic drivers to be ranked higher by our model—which we see evidence of when looking at the (Jansen et al., 2019) summary statistics.

We currently demonstrate the utility of the approach on three RNA-Seq derived feature sets, providing strong qualitative agreement with known biology as well as previously published GWAS studies. Furthermore, we show the approach for driver gene prediction itself is a broadly application machine learning approach by demonstrating quantitative performance improvement over baseline models.

While the current work has focused on engineering and using RNA-Seq feature sets, future work will focus on integrating other -omics datasets from the AMP-AD study to further improve the evidence driven ranking of driver genes. Another direction of future work will focus on identifying the relevance and agreement of different feature views. While the current approach equally weighs the predictions from different feature views, this may be unadvisable if a feature view has limited information about the driverness of genes.