Abstract
Motivation
Genome rearrangements drastically change gene order along great stretches of a chromosome. There has been initial evidence that these apparently non-local events in the 1D sense may have breakpoints that are close in the 3D sense. We harness the power of the Double Cut and Join model of genome rearrangement, along with Hi-C chromosome conformation capture data to test this hypothesis between human and mouse.
Results
We devise novel statistical tests that show that indeed, rearrangement scenarios that transform the human into the mouse gene order are enriched for pairs of breakpoints that have frequent chromosome interactions. This is observed for both intra-chromosomal breakpoint pairs, as well as for inter-chromosomal pairs. For intra-chromosomal rearrangements, the enrichment exists from close (<20 Mb) to very distant (100 Mb) pairs. Further, the pattern exists across multiple cell lines in Hi-C data produced by different laboratories and at different stages of the cell cycle. We show that similarities in the contact frequencies between these many experiments contribute to the enrichment. We conclude that either (i) rearrangements usually involve breakpoints that are spatially close or (ii) there is selection against rearrangements that act on spatially distant breakpoints.
Availability and implementation
Our pipeline is freely available at https://bitbucket.org/thekswenson/locality.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Large-scale rearrangements drastically change linear genome organization. Hundreds of large rearrangements between human and mouse have moved once close loci far from each other. These moves are significant since proximity on the linear genome is linked to gene co-expression and co-regulation in many species across the tree of life (Dai et al., 2014; Hurst et al., 2004), including in human (Li et al., 2006; Sémon and Duret, 2006; Singer et al., 2005; Thévenin et al., 2014). Further, rearrangements inhibit subsequent crossover and are thus thought to increase genetic variability (Lu et al., 2003; Navarro and Barton, 2003; Sequencing and Consortium, 2005), and are a mechanism for enforcing reproductive isolation between individuals possessing, or not, a particular rearrangement (Liu et al., 2012; Noor et al., 2001; Rieseberg, 2001). Thus, the primary mechanisms and constraints governing the advent and fixation of rearrangements in a population are of high interest.
For eukaryotes, the effect of rearrangements on gene function and coexpression seems contradictory: on one hand genes tend to group into functional and coexpressed clusters according to their linear gene order, on the other hand genes with similar expression profiles in different species show little conservation in terms of gene order (Weber and Hurst, 2011), and adjacent coexpressed and functionally coordinated genes are actually more likely to be separated by rearrangement (Al-Shahrour et al., 2010; Liao and Zhang, 2008). One potential reconciling explanation is that the functionally coordinated genes stay co-localized in 3D space, rather than 1D sequential order, after rearrangement (Dai et al., 2014; Thévenin et al., 2014). Indeed, there is increasing evidence showing that high order chromatin structure (lamina association, replication timing and inter-locus contact preference) is partially conserved between human and mouse (Chambers et al., 2013).
There are multiple proposed mechanisms for rearrangement. The mechanisms can roughly be grouped into two categories: (i) those that result from repair of double-stranded breaks (DSBs) and (ii) those that are replication based. Non-allelic homologous recombination (NAHR) (Stankiewicz and Lupski, 2002) and non-homologous end joining (Moore and Haber, 1996) belong to the former, while fork stalling and template switching (FoSTeS), microhomology-mediated break-induced replication (MMBIR) and serial replication slippage (SRS) belong to the latter (Liu et al., 2012). Both mechanisms depend on a confusion of spatially close, but linearly distant pieces of DNA. The replication based mechanism also depends on synchronous replication of spatially close DNA during S-phase of mitosis, a condition that appears to hold on an evolutionary scale between mouse and human (Ryba et al., 2010; Yaffe et al., 2010).
A clean and simple picture of genotype evolution is consistent with the hypothesis that rearrangements happened between pairs of breakpoints that were generally close in 3D space; normal cell function would not have been greatly disturbed, and known mechanisms explain these seemingly large-scale changes. Disease-causing somatic rearrangements seem to support this hypothesis (Berger et al., 2011; Branco and Pombo, 2006; Hakim et al., 2012; Meaburn et al., 2007; Nikiforova et al., 2000; Spielmann et al., 2018; Wijchers and de Laat, 2011; Zhang et al., 2012). The advent of Hi-C methods for chromosome capture (Dixon et al., 2012; Lieberman-Aiden et al., 2009; Sexton et al., 2012) has opened the door to similar studies on an evolutionary scale. Yaffe et al. (2010) showed that rearrangement breakpoint pairs between human and mouse are concentrated around replicating domains, and occur at locations with similar time-of-replication. They also showed that some subset of 55 interchromosomal breakpoint pairs existing in human (with respect to mouse) correlate with interaction frequency obtained from Hi-C experiments. Véron et al. (2011) took this result further by studying more of the breakpoint pairs between human and mouse. They found a significant correlation between 3D proximity and intrachromosomal breakpoint pairs, but they found no such correlation for interchromosomal pairs.
These studies do not use a model of genome rearrangement, so only consider breakpoints that can be repaired by a single rearrangement, and that have undergone little or no re-use. This represents a major limitation due to the known bias of breakpoints to be re-used along one or between multiple lineages (Alekseyev and Pevzner, 2010; Berthelot et al., 2015; González et al., 2007; Hinsch and HannenhalLi, 2006). Specifically, Veron et al. categorized breakpoint pairs into groups that they called ‘reciprocal’ and ‘non-reciprocal’; the reciprocal pairs are those that participated in an isolated rearrangement with no breakpoint re-use, while the non-reciprocal pairs have a single breakpoint that has undergone re-use. They acknowledge that ‘The evolutionary origin of most non-reciprocal breakpoint pairs remained elusive, highlighting the loss of evolutionary signal due to re-use’. Consequently, out of the 18 046 possible double-stranded break induced rearrangements that move the current human gene order one step closer to that of the mouse, Veron et al. study under 300, while Yaffe et al. study 55. Furthermore, many ancient rearrangements are likely left out of the analyses of Veron et al. due to their limited ability to handle re-use, the reason being that ancient breakpoints have had more time to be re-used than recent ones. Since breakpoints driven by 3D physical proximity are those that are the most likely to be re-used, excluding or under-representing breakpoint re-use may lead to a severe underestimation of the role of 3D chromosome organization on genome rearrangements.
Yet rearrangements can be view as a process transforming one gene order into another, allowing for the proper handling of re-used breakpoints. The sequence of rearrangements is called a scenario. There exist algorithmic tools and models for rigorous investigation of the many possible scenarios transforming one gene order into another. The Double Cut and Join (DCJ) model of rearrangement neatly includes chromosome rearrangements such an inversion, translocation, fission and fusion, while being simple enough to be computationally tractable (Bergeron et al., 2006; Yancopoulos et al., 2005). We have started using these tools to indirectly show the link between chromosome conformation and chromosome rearrangement (Pulicani et al., 2017; Simonaitis and Swenson, 2018). However, our methodology is convoluted, in that it requires a clustering of the breakpoints by spatial proximity, followed by the application of algorithms that compute scenarios that minimize the number of between-cluster rearrangements.
In this article, we attack the question directly by using DCJ to consider 10 000 randomly sampled parsimonious scenarios of rearrangements; the scenarios are composed of 2 914 417 unique rearrangements acting on potentially ancient breakpoints that are not observed in human or mouse. By harnessing algorithmic results based on over 20 years of study (Bader et al., 2001; Bergeron et al., 2006; Day and Sankoff, 1987; Hannenhalli and Pevzner, 1995; Sankoff, 1992; Swenson et al., 2010; Tannier et al., 2007; Yancopoulos et al., 2005), we uncover a strong correlation between breakpoint pairs and Hi-C interaction frequencies in human chromatin. The pattern exists for both intrachromosomal and interchromosomal pairs and is largely consistent over Hi-C experiments from multiple labs on six different cell types, as well as for cells in interphase and metaphase.
This observation, which holds across different cell lines could suggest at least a couple of possibilities:
the rearrangement mechanism depends on breakpoints being spatially close or
there is negative selection against rearrangements that are distant in 3D space in any one of the differentiated cell types.
Since the heritable rearrangements are those that occur in the zygote, and not in any of the cell lines studied in existing Hi-C experiments, the first case describes a situation where differentiated cell lines have conserved important contact frequencies after differentiation. If they had not have, we could not observe the correlation. Alternatively, the second case describes a situation where germ line rearrangements are negatively selected against in a differentiated cell, when the breakpoints are distant in 3D space.
Our results show that intrachromosomal rearrangements are likely to occur between spatially co-located breakpoint pairs, on an evolutionary scale. The pattern exists despite the fact that we use only the present-day Hi-C interaction frequency data from human to assess spatial proximity over entire scenarios between mouse and human. This suggests that chromosome conformation is fairly conserved over the evolutionary distance between human and mouse, as previously reported by Véron et al. (2011) and Dixon et al. (2012).
In Section 2.2, we show that this result is true for intrachromosomal rearrangements from short (1 Mb) to long (100 Mb). In Section 2.3, we show that the amount of formaldehyde used in the Hi-C protocol can affect our analyses. In Section 2.4, we show that rearrangements are likely to happen between spatially co-located breakpoint pairs occurring in different cell types.
2 Results
Our work is motivated by the hypothesis that rearrangement breakpoint pairs are enriched among physically interacting genomic regions. Throughout the rest of the article, we call this correlation the contact/rearrangement link. We tested this hypothesis by considering DCJ rearrangement scenarios between the human and mouse gene orders. The most parsimonious DCJ scenarios between human and mouse require 588 rearrangements, each operating on a pair of breakpoints. Since parsimonious scenarios are not unique, we generated a set of 10 000 parsimonious scenarios and studied the physical relation between the loci from 2 914 417 unique breakpoints pairs.
An initial hint suggesting the contact/rearrangement link comes from a simple inspection of these sampled scenarios. Rearrangements with two breakpoints correspond to two genomic coordinates, whose interaction frequency corresponds to an entry in a Hi-C interaction frequency matrix. Figure 1 shows the normalized intrachromosomal matrix for the Naumova et al. (2013) HeLaS3-G1 experiment, for chromosome 3 and the normalized interchromosomal matrix for chromosomes 1 and 3. Blue marks show breakpoint pairs used in scenarios between human and mouse. The more scenarios a breakpoint pair is used in, the lighter blue the mark is. Visual inspection of Figure 1 shows a tendency for blue marks to occur in areas of higher contact frequency, even when the area is far from the diagonal or even across chromosome arms. For interchromosomal matrices, a similar pattern is observed.
Fig. 1.
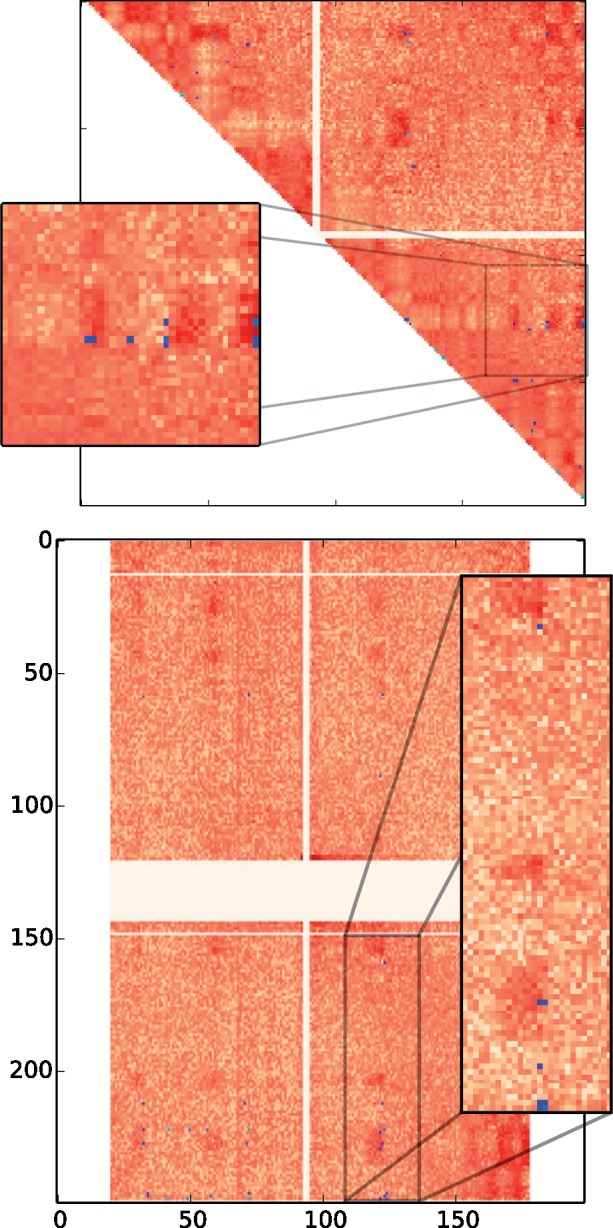
Interaction frequency matrices for chromosome 3 (top) and for chromosome 3 against chromosome 1 (bottom). The darker red an entry (i, j) is, the more enriched for 3D contacts the pair of chromosome coordinates (i, j) is. Blue marks correspond to rearrangements from 10 000 DCJ scenarios. The lighter the blue, the higher the number of occurrences of the rearrangement. Square panels are blow-ups of regions from their respective matrices
To formally explore this apparent correlation, we devised the following experiment, which we call the canonical experiment. Our principle technique compares two distributions over Hi-C interaction frequency values: one derived from the true breakpoint locations for proposed rearrangements and the other derived from randomized locations for the same rearrangements, controlling for breakpoint region size and linear genomic distance between breakpoints (for intrachromosomal rearrangements). Depending on the question of interest, we perform the canonical experiment on different interaction frequency matrices.
The following is a rough description of our canonical experiment (full details are found in Section 3.3). We sampled 10 000 parsimonious scenarios using the theory of Double Cut and Join (see Section 3.2 for a description of DCJ). Moves were scored for contact frequency as described in Section 3.3, so that the average 3D interaction frequency for each scenario was computed. Distributions for these values appear as light bars in the charts of Figures 2 and 3. Scenarios with randomized locations were then computed and scored, represented by the dark distributions in Figures 2 and 3.
Fig. 2.
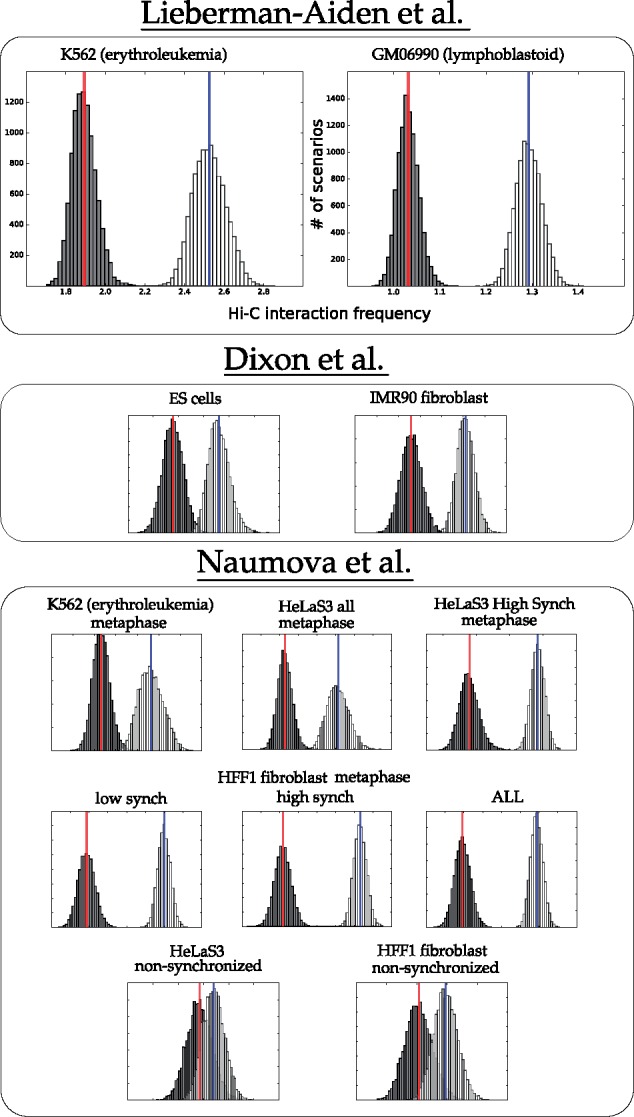
Distribution of mean interaction frequency values for intra-chromosomal rearrangements from parsimonious DCJ scenarios between human and mouse (white, with mean in blue) and randomized scenarios (black, with mean in red)
Fig. 3.
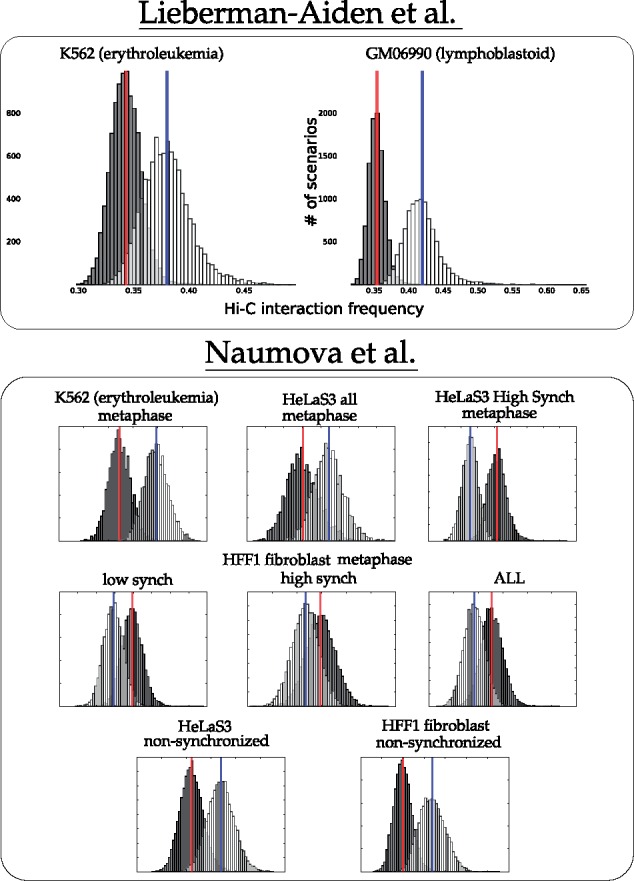
Distribution of mean interaction frequency values for inter-chromosomal rearrangements from parsimonious DCJ scenarios between human and mouse (white, with mean in blue) and randomized scenarios (black, with mean in red)
2.1 Sampled scenarios are spatially closer than expected
Visual inspection of the interaction matrices in Figure 1 seems to show a correlation between high contact frequency and rearrangement breakpoints. We tested this hypothesis by applying our canonical experiment to matrices normalized for linear genomic distance (normalization described in Supplementary Section S1).
Figure 2 shows the actual distribution against the randomized distribution for intrachromosomal rearrangements. For most of the cell lines, the actual breakpoint locations have many more contacts than expected by chance. For the non-synchronized cell lines, the unknown state of the cell seems to contribute to a weaker signal.
For interchromosomal rearrangement breakpoint pairs, Figure 3 shows that contacts are enriched in more than half of the datasets. Exceptions are the HFF metaphase and HeLaS3 high synchrony cell lines.
We also performed a one-sample t-test that compares the mean of a single scenario against many randomized versions of that scenario. We computed P-values for the null-hypothesis that the score h(s) for a single scenario s is drawn from the same distribution as average scores for a sample R of randomized versions of that scenario (as described in Supplementary Section S6). Table 1 summarizes the results of this test. They agree with the results reported in Figures 2 and 3. Oddities in the G1 HeLaS3 cell lines reported in Table 1 are discussed in detail in Section 2.3.
Table 1.
The percentage of scenarios for which the scenario test (see Supplementary Section S6) yields a P-value <10–4
| Intra | Inter | |
|---|---|---|
| Lieberman-Aiden et al. | ||
| K562 | 100% + | 95.6% + |
| GM06990 | 100% + | 99.8% + |
| Dixon et al. | ||
| hESC | 100% + | Na |
| IMR90 | 100% + | Na |
| Naumova et al. | ||
| Metaphase | ||
| K562 | 100% + | 99.7% + |
| HeLaS3 all | 100% + | 91.5% + |
| HeLaS3 hi-sync | 100% + | 99.7% – |
| HFF1 low-sync | 100% + | 94.3% – |
| HFF1 hi-sync | 100% + | 75.5% – |
| HFF1 all | 100% + | 90.8% – |
| Non-synchronized | ||
| HeLaS3 | 84.7% + | 97.9% + |
| HFF1 | 98.5% + | 99.1% + |
| G1 | ||
| HeLaS3 all | 79.6% + | 99.8% + |
| HeLaS3 1% | 72.7% + | 99.5% + |
| HeLaS3 0.25% | 100% + | 57.6% + |
Note: Columns are labeled with ‘+’ if actual rearrangements are closer than expected at random and ‘–’ if they are farther.
We performed a variety of control experiments to ensure that: (i) the mean score for the scenarios are not dominated by few rearrangements that occur in many of the scenarios and (ii) the differences between the distributions in Figures 2 and 3 are not observed by chance. See Supplementary Sections S2 and S3.
2.2 Spatial proximity over varying breakpoint distances
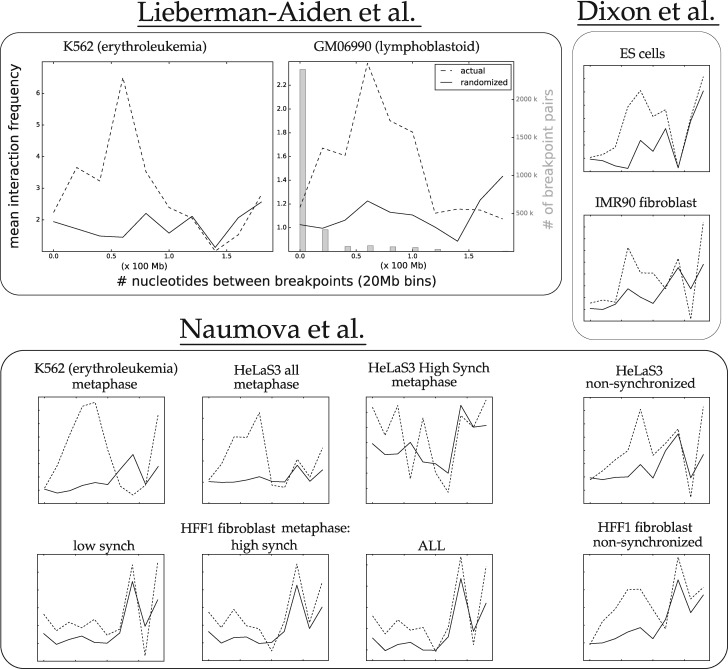
Figure 2 shows that a scenario transforming the human to mouse gene order contains rearrangements that, on an average, have more 3D interactions than expected by chance. In this section, we show that this result holds for rearrangements with breakpoints having vastly different 1D distances in Human. Indeed, the patterns of Figure 2 would be of less interest if, for example, all the differences were due only to breakpoint pairs that have close genomic coordinates.
To this end, we binned the intrachromosomal DCJs based on the linear genomic distance between their breakpoints. Figure 4 shows the 3D proximity as a function of linear genomic distance. See also Supplementary Figure S5. Notice that the majority of the plots show a higher average proximity score for actual breakpoints even for rearrangements that span 100 Mb, while many continue to show that trend up to 140 Mb. The datasets from Figure 2 that show less separation between the randomized and actual distributions (e.g. the non-synchronized datasets) show less separation for the smallest distance ranges, where the curves actually cross. As we will see in the next section, this effect is correlated with the amount of formaldehyde used in the Hi-C protocol.
Fig. 4.
The average Hi-C interaction frequency of human-mouse DCJ breakpoint pairs as a function of linear genomic distance between rearrangement breakpoints in Human (20-Mb bins). Dashed lines show mean interaction frequency for rearrangements with breakpoints binned for a given 1D distance (in Human), while solid lines show the randomized interaction for those rearrangements. The GM06990 plot also shows (in gray) the quantity of breakpoint pairs binned for each distance
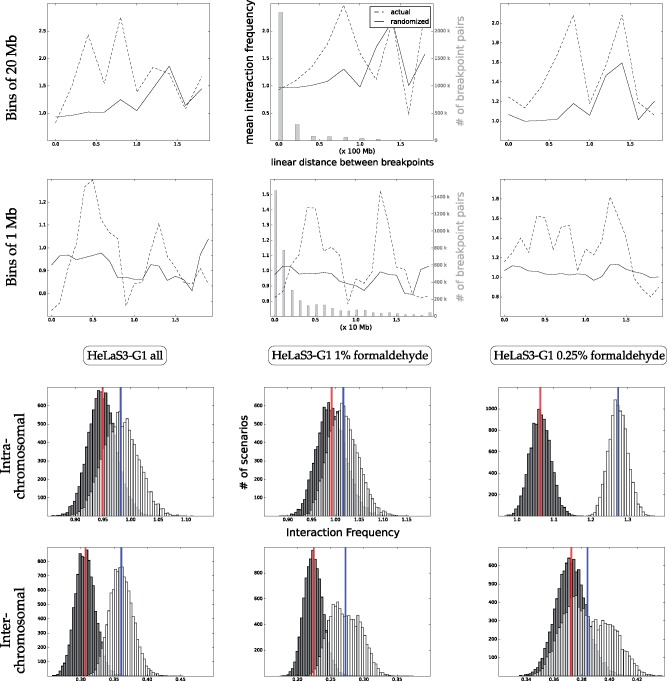
2.3 Formaldehyde concentrations
The work of Naumova et al. (2013) contains a suite of control experiments done on the HeLaS3 cell line, where three Hi-C experiments are performed with varying concentrations of the fixating agent formaldehyde. Figure 5 shows that as formaldehyde concentrations increase (from right to left in the figure), the separation between the intrachromosomal observed and randomized distributions disappears. The second row of the figure shows that the gap between the randomized scores and actual scores is increased for short rearrangements (those shorter than 20 Mb), as the quantity of formaldehyde increases. This pattern suggests that greater formaldehyde contents create links between pairs that are too distant in 3D space to have an influence on a rearrangement. The pattern appears to be inverted for interchromosomal interaction matrices; more formaldehyde accentuates the signal. This may be caused by the fact that those contacts are known to be weaker, possibly requiring more formaldehyde to be captured.
Fig. 5.
Increased formaldehyde concentrations in the HeLaS3 cell line obscure intrachromosomal signal. Top two rows: mean proximity between breakpoints binned by 1D distance. The middle plots also show (in gray) the quantity of breakpoint pairs binned for each distance. Third row: intrachromosomal normalized contacts for scenarios. Bottom row: interchromosomal normalized contacts for scenarios. As the quantity of formaldehyde is decreased, the signal for intra-chromosomal matrices becomes clearer. The top row shows that this decrease is due to the change in signal between closer breakpoints, particularly those breakpoints 2 Mb or fewer apart. The inverse is true for the inter-chromosomal signal
2.4 Similarities across cell lines
It was surprising to see a correlation between contact frequency and rearrangement scenarios through so many diverse conditions; cell lines that have differentiated to perform diverse functions, and cells in different states of their cycle often display a similar pattern. This raised the natural question of whether or not two different cell lines exhibit the contact/rearrangement link for a shared set of rearrangements. In this section, we address the following questions:
Is the contact/rearrangement link displayed in two different cell lines due to the same subset of breakpoint pairs?
Are there cell lines that differ significantly for a subset of breakpoint pairs?
We explored these questions by running our canonical experiment on specially prepared Hi-C matrices.
Denote a matrix as M, and a particular entry at row i and column j of M as Mij. Then an intersection matrix is defined from normalized matrices A and B (corresponding to the same pair of chromosomes) as follows:
Consider the set of intersection matrix entries associated with a particular rearrangement scenario. An entry in I will have a high value if and only if the value is high in both A and B. We ran the canonical experiment on the intersection matrices and found a separation between distributions resulting from breakpoint pairs that have many contacts in both pairs of cell lines.
The results are reported in Figure 6. For both intra- and inter-chromosomal contacts, we observe that the intersection matrices correlate well with rearrangements, as compared to randomized rearrangements. The interchromosomal intersection matrices often yield correlations stronger than the individual matrices themselves.
Fig. 6.
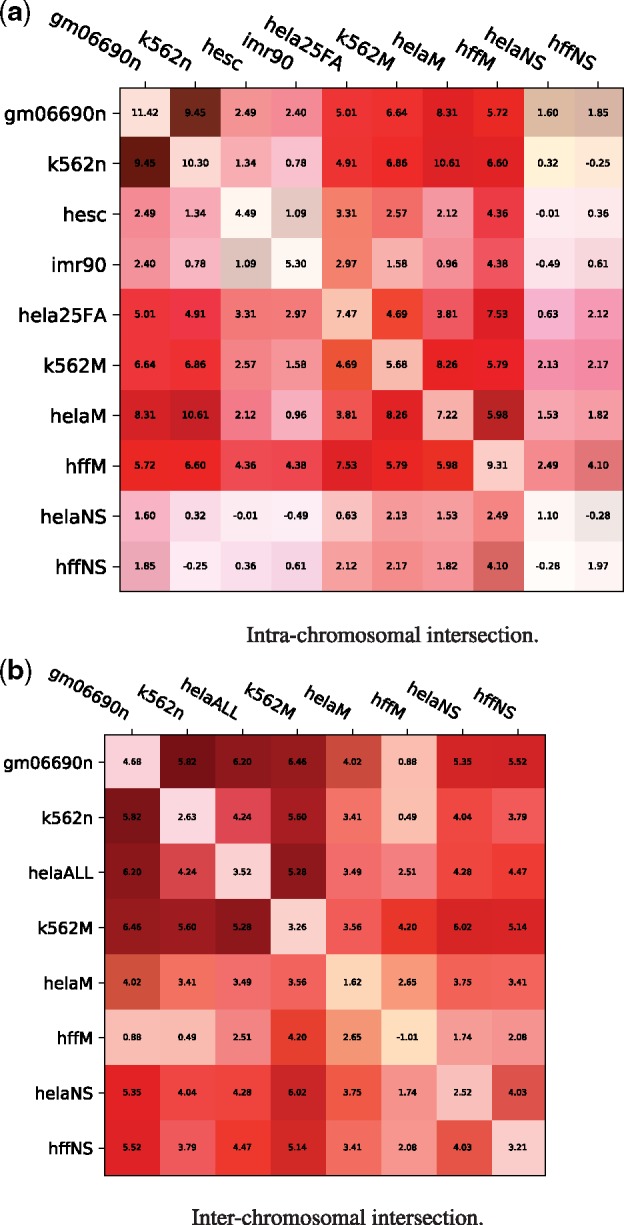
Similarities between intrachromosomal Hi-C matrices for different cell lines generally coincide with rearrangement scenarios. Each entry shows the distribution distance, indicating the distance between the randomized and actual distributions computed in the canonical experiment: where is the mean over all actual scenarios and are the mean and SD over all randomized scenarios. The values on the diagonal represent the distribution differences on the original normalized matrices (the distributions in Figures 2 and 3). Each entry has a green bar corresponding to the balance of values chosen for that pair of matrices (if the intersection matrix was composed of values all from one dataset, the entire box edge facing that dataset would be green, a perfectly balanced intersection would have no green bar). (a) Intra-chromosomal intersection. (b) Inter-chromosomal intersection
A control was conducted to ensure that the sampled breakpoint pairs were not getting their score from only one of the two cell lines (e.g. if matrix A has a smaller value for every position corresponding to the sampled rearrangements, then the canonical experiment run on the intersection matrix will reflect only the information from A). The green bar in the corner of each square indicates the balance of values in that intersection matrix. We conclude that no single matrix is accounting for the observed similarities between cell lines.
3 Materials and Methods
3.1 Genome representation
Following the approach of Lemaitre et al. (2008), we represent genomes by a sequence of genes on chromosomes where each chromosome ends at a telomere marker. The subset of genes labeled as one-to-one orthologs by Ensembl were downloaded from Biomart. Thus, each ortholog occurs once in each genome and regions between these orthologs were potential locations for breakpoints in rearrangements.
Note that more complex methods for syntenic block creation, of which many exist, were avoided in order to avoid potential introduction of bias.
3.2 DCJ scenarios
We use the standard DCJ model for chromosomes with a single copy of each gene (Bergeron et al., 2006; Yancopoulos et al., 2005). In short, a DCJ rearrangement operation transforms one set of genomic adjacencies into another. A single DCJ cuts one or two adjacencies, and glues the resulting ends back together according to the following rules:
if a single adjacency is cut, then add new telomeres to the resulting ends (resulting in two new telomeric adjacencies),
if two adjacencies are cut, then glue the adjacencies back in one of two new ways.
Application of a single DCJ can model diverse genomic operations such as inversions, chromosome fissions and fusions, as well as transpositions. A sequence of DCJs transforming one genome into another is called a rearrangement scenario.
We assign to each adjacency a genomic interval. When a DCJ is performed on two adjacencies, the intervals associated to these adjacencies are associated to the two new adjacencies in one of the two possible ways.
Rearrangement scenarios are sampled by, at each step, choosing uniformly at random a DCJ that moves human closer to mouse. Supplementary Section S4 describes this process in detail.
3.3 The canonical experiment
We developed novel experiments to test the contact/rearrangement link. Many results are based on a single canonical experiment that evaluates a set of rearrangement scenarios S on a set of normalized interaction frequency matrices. Each is inferred by sampling, using the DCJ model of genome rearrangement (see Section 3.2 and Supplementary Section S4). The null hypothesis is that spatial proximity is unrelated to the scenario s. Thus, the goal is to compare proximity for the scenarios in S to that of a set R of randomized scenarios, where the breakpoints of the rearrangements in the scenarios of R have the same properties as those in S, but do not correspond to the actual genome coordinates of the rearrangements in S.
The scenarios in R are constructed through a randomization procedure on the breakpoint pairs in the scenarios of S. Consider a scenario . Each intrachromosomal rearrangement in s that has two breakpoint intervals b1 and b2 with lengths l1 and l2 has a linear genomic distance d between them (see Fig. 7). An intrachromosomal rearrangement in s is randomized by choosing uniformly at random a new location for the two intervals such that l1, l2 and d remain unchanged. This is equivalent to sampling a random box at distance d from the main diagonal. An interchromosomal move chooses a random location such that l1 and l2 remain unchanged.
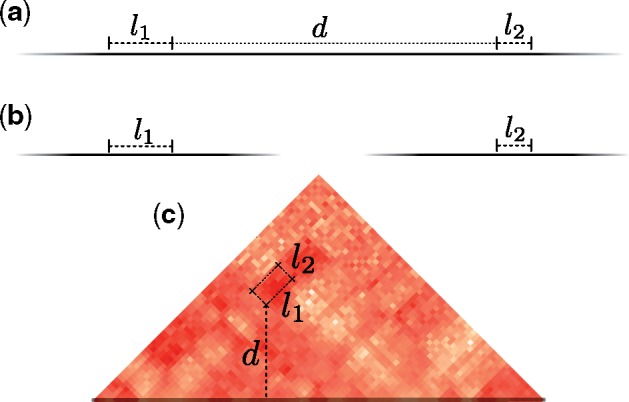
Fig. 7. Two breakpoints that participate in a rearrangement and their position in the matrix. Solid black lines that fade out represent chromosomes. (a) Two intrachromosomal breakpoints that participate in an inversion of linear length d. (b) Two interchromosomal breakpoints that participate in a translocation have infinite linear genomic distance. (c) The position of the breakpoints in the matrix for the inversion depicted in (a)
Take Σ to be the set of all possible scenarios, with associated genomic intervals, from human to mouse. We score a scenario with a function defined as follows:
For a rearrangement with breakpoints b1 and b2, take the mean interaction matrix value inside the box defined by intervals b1 and b2 (see Fig. 7).
h(s) is the mean score over its intra or inter-chromosomal rearrangements.
For a set of scenarios S, we compute the distribution of the mean interaction over all moves in a scenario (using the median gave similar results). This is done by binning the value h(s) for all 10 000 scenarios, yielding a distribution of mean interaction values. Our canonical experiment compares the distribution for the scenarios S to the distribution for the randomized scenarios R.
The expectation is that this test, run on matrices that are unassociated to rearrangements, will on an average yield distributions with similar properties for S and for R. This is true, but subject to some amount of variability. The next section describes how we tested against this variability.
Different tests can be done using different matrices. Section 2.1 describes the application of our methods to normalized matrices. Section 2.4 describes the application of our methods to combinations of these matrices.
3.4 Control via permuted matrices
The null hypothesis is that interaction frequency is unrelated to the location of rearrangement breakpoints. We controlled our canonical experiment against this hypothesis by randomly permuting the original interaction matrices; a matrix is permuted by taking pairs of entries uniformly at random and swapping their values (Note that we call the process done on matrices ‘permuting’, while ‘randomizing’ is a process we do on scenarios as described in Section 3.3). To compute this control, the canonical experiment was performed using the permuted matrices as input. We expect to have distributions for normal scenarios and randomized scenarios that are identical. The methodology is further explained in the Supplementary Section S3.
While for most cases the canonical experiment run on permuted matrices yields two indistinguishable distributions, there was some variability; the same set of scenarios produced slightly different distributions on different permuted matrices. This variability is much less pronounced, however, than the differences seen with the original unpermuted matrices. To quantify this difference, we produced 100 permuted matrices and calculated the difference between the mean of the actual scenario distribution and the randomized scenario distribution. We also computed the same difference on the unpermuted matrices and performed a t-test against the differences from the permuted matrices. The P-value is lower than 10–12 for all experiments. See Supplementary Section S3 for more details.
3.5 Reproducibility of the experiments
All results from this article can be reproduced by downloading the Hi-C data and running Snakemake (Köster and Rahmann, 2012) as described at https://bitbucket.org/thekswenson/mammal_rearrange_interactions.
4 Conclusion
Rearrangements that acted on breakpoints which are not currently apparent in human or mouse are completely ignored in previous work. These constitute a very large fraction of all rearrangements. This is due to methodological constraints that disqualified breakpoint pairs that were both re-used. Thus, the question of whether the contact/rearrangement link holds for more than just the most recent rearrangements was unanswered.
We devised a novel experiment to study the 3D interaction frequency between breakpoints implicated in genomic rearrangements transforming the human gene order into the mouse (called the contact/rearrangement link). By sampling scenarios, we are able to (i) exclude breakpoint pairs that probably do not participate in rearrangements and (ii) study rearrangements that are not immediate apparent in the current state of human and mouse gene orders.
Our experiments show that the contact/rearrangement link exists for interchromosomal and intrachromosomal rearrangements. We conjecture two reasons for this: (i) rearrangement events happen between spatially close breakpoints and (ii) rearrangements that act on spatially distant breakpoints may perturb 3D conformation, causing a negative selective pressure against them.
Little was known about the interplay between rearrangements and the 3D conformation of chromatin in differentiated cells. We showed that the results hold between human and mouse over multiple cell lines from multiple labs. By studying the intersection for pairs of interaction frequency matrices, we show that there are shared rearrangements that contribute to the contact/rearrangement link across pairs of cell lines.
Finally, we studied the effect of formaldehyde content when conducting a Hi-C experiment. Our results suggest that quantities of formaldehyde play in important role when studying rearrangements, but conjecture that this understudied aspect of the Hi-C experiment can have downstream effects in other bioinformatics analyses.
Our work has impact on multiple areas. First, it provides a strong foundational basis for the study of how selective pressure acts on 3D genomes and their rearrangements, for example, opening the possibility for the identification of highly conserved 3D contacts that may be of critical functional relevance. Huynh and Hormozdiari (2018) and Fudenberg and Pollard (2019) have indeed shown that there is negative selection against deletions at TAD boundaries; our work could facilitate the extension of this type of study to a broader range of contacts. Implications on cancer genomics are also important, by providing a means to better predict the phenotypic consequences of rearrangements.
Our pipeline is fully-automated, freely available and can be easily reused as new fully assembled genomes data become available. Pertinent targets of study would be the primates (e.g. gibbon, macaque and orangutan) (Catacchio et al., 2018; Kronenberg et al., 2018; Lazar et al., 2018) and mouse (Zhang et al., 2012). Study of within species variation could soon be possible with the work of the Human Genome Structural Variation Consortium, where more and more individuals are being characterized (see Chaisson et al., 2018 for an example).
In this article, we used Hi-C data from a single species. While large-scale 3D structures between species appears to be conserved (Dixon et al., 2012), we expect that there do exists differences. It is possible that some of the rearrangements between human and mouse correspond to close contacts that we do not observe, due to their relationship to the chromatin conformation in the mouse. Thus, we expect the pattern that we see in our canonical experiment to be weaker than it should be.
Several future challenges exist. One obvious challenge is to incorporate Hi-C data from multiple species or cell lines into the study of genome rearrangement. Another challenge is that it is currently difficult to study breakpoint re-use directly. Since all parsimonious DCJ scenarios are considered equally likely, breakpoints on the same connected component of the Adjacency Graph share the same properties of breakpoint re-use with other breakpoints on that component; the problem is under-constrained. By adding biological constraints to scenario inference, we may, one day, be able to study breakpoint re-use in detail. It would also be interesting to consider sampling scenarios from a probabilistic model (e.g. through MCMC) rather than from the set of parsimonious scenarios, although this would be unlikely to substantially alter our conclusions. A final challenge is to infer rearrangement scenario using the contact/rearrangement link. We have made progress in this area by developing methods to choose a scenario based on the contacts given by Hi-C data (Pulicani et al., 2017; Simonaitis and Swenson, 2018; Swenson et al., 2016).
Supplementary Material
Acknowledgements
K.M.S. would like to thank Anne Bergeron for her helpful comments on the experiments and Fabio Pardi and Laurent Brehelin for their consultation on statistical matters.
Funding
This work was supported by the Labex NUMEV flagship project GEM and the CNRS project Osez l’Interdisciplinarité for K.M.S. and the NSERC Discovery grant for M.B.
Conflict of Interest: none declared.
References
- Al-Shahrour F. et al. (2010) Selection upon genome architecture: conservation of functional neighborhoods with changing genes. PLoS Comput. Biol., 6, e1000953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alekseyev M.A., Pevzner P.A. (2010) Comparative genomics reveals birth and death of fragile regions in mammalian evolution. Genome Biol., 11, R117.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader D.A. et al. (2001) A linear-time algorithm for computing inversion distance between signed permutations with an experimental study. J. Comput. Biol., 8, 483–491. [DOI] [PubMed] [Google Scholar]
- Berger M.F. et al. (2011) The genomic complexity of primary human prostate cancer. Nature, 470, 214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergeron A. et al. (2006) A unifying view of genome rearrangements. Algorithms Bioinformatics, 4175, 163–173. [Google Scholar]
- Berthelot C. et al. (2015) The 3D organization of chromatin explains evolutionary fragile genomic regions. Cell Rep., 10, 1913–1924. [DOI] [PubMed] [Google Scholar]
- Branco M.R., Pombo A. (2006) Intermingling of chromosome territories in interphase suggests role in translocations and transcription-dependent associations. PLoS Biol., 4, e138.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catacchio C.R. et al. (2018) Inversion variants in human and primate genomes. Genome Res., 28, 910–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaisson M.J. et al. (2018) Multi-platform discovery of haplotype-resolved structural variation in human genomes. Nat. Commun., 10. [DOI] [PMC free article] [PubMed]
- Chambers E.V. et al. (2013) Divergence of mammalian higher order chromatin structure is associated with developmental loci. PLoS Comput. Biol., 9, e1003017.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai Z. et al. (2014) Neighboring genes show interchromosomal colocalization after their separation. Mol. Biol. Evol., 31, 1166–1172. [DOI] [PubMed] [Google Scholar]
- Day W.H., Sankoff D. (1987) Computational complexity of inferring phylogenies from chromosome inversion data. J. Theor. Biol., 124, 213–218. [DOI] [PubMed] [Google Scholar]
- Dixon J.R. et al. (2012) Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature, 485, 376–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fudenberg G., Pollard K.S. (2019) Chromatin features constrain structural variation across evolutionary timescales. Proc. Natl. Acad. Sci. USA, 116, 2175–2180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- González J. et al. (2007) Testing chromosomal phylogenies and inversion breakpoint reuse in Drosophila. Genetics, 175, 167–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hakim O. et al. (2012) DNA damage defines sites of recurrent chromosomal translocations in B lymphocytes. Nature, 484, 69–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hannenhalli S., Pevzner P.A. (1995) Transforming men into mice (polynomial algorithm for genomic distance problem). In: Proceedings of 36th Annual Symposium on Foundations of Computer Science, Milwaukee, WI, USA, pp. 581–592.
- Hinsch H., Hannenhalli S. (2006) Recurring genomic breaks in independent lineages support genomic fragility. BMC Evol. Biol., 6, 90.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurst L.D. et al. (2004) The evolutionary dynamics of eukaryotic gene order. Nat. Rev. Genet., 5, 299–310. [DOI] [PubMed] [Google Scholar]
- Huynh L., Hormozdiari F. (2018) Contribution of structural variation to genome structure: TAD fusion discovery and ranking. In: Research in Computational Molecular Biology – 22nd Annual International Conference, RECOMB 2018, Paris, France, April 21–24, 2018. Proceedings, Vol. 10812. pp. 259–260. Springer.
- Köster J., Rahmann S. (2012) Snakemake – a scalable bioinformatics workflow engine. Bioinformatics, 28, 2520–2522. [DOI] [PubMed] [Google Scholar]
- Kronenberg Z.N. et al. (2018) High-resolution comparative analysis of great ape genomes. Science, 360, eaar6343.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazar N.H. et al. (2018) Epigenetic maintenance of topological domains in the highly rearranged gibbon genome. Genome Res., 28, 983–997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemaitre C. et al. (2008) Precise detection of rearrangement breakpoints in mammalian chromosomes. BMC Bioinformatics, 9, 286.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y.-Y. et al. (2006) Systematic analysis of head-to-head gene organization: evolutionary conservation and potential biological relevance. PLoS Comput. Biol., 2, e74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao B.-Y., Zhang J. (2008) Coexpression of linked genes in mammalian genomes is generally disadvantageous. Mol. Biol. Evol., 25, 1555–1565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman-Aiden E. et al. (2009) Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science, 326, 289–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu P. et al. (2012) Mechanisms for recurrent and complex human genomic rearrangements. Curr. Opin. Genet. Dev., 22, 211–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu J. et al. (2003) Comment on “chromosomal speciation and molecular divergence-accelerated evolution in rearranged chromosomes”. Science, 302, 988.. [DOI] [PubMed] [Google Scholar]
- Meaburn K.J. et al. (2007) Spatial genome organization in the formation of chromosomal translocations. Semin Cancer Biol., 17, 80–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore J.K., Haber J.E. (1996) Cell cycle and genetic requirements of two pathways of nonhomologous end-joining repair of double-strand breaks in Saccharomyces cerevisiae. Mol. Cell Biol., 16, 2164–2173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naumova N. et al. (2013) Organization of the mitotic chromosome. Science, 342, 948–953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Navarro A., Barton N.H. (2003) Chromosomal speciation and molecular divergence – accelerated evolution in rearranged chromosomes. Science, 300, 321–324. [DOI] [PubMed] [Google Scholar]
- Nikiforova M.N. et al. (2000) Proximity of chromosomal loci that participate in radiation-induced rearrangements in human cells. Science, 290, 138–141. [DOI] [PubMed] [Google Scholar]
- Noor M.A. et al. (2001) Chromosomal inversions and the reproductive isolation of species. Proc. Natl. Acad. Sci. USA, 98, 12084–12088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pulicani S. et al. (2017) Rearrangement scenarios guided by chromatin structure In: RECOMB International Workshop on Comparative Genomics, pp. 141–155. Springer, Cham. [Google Scholar]
- Rieseberg L.H. (2001) Chromosomal rearrangements and speciation. Trends Ecol. Evol., 16, 351–358. [DOI] [PubMed] [Google Scholar]
- Ryba T. et al. (2010) Evolutionarily conserved replication timing profiles predict long-range chromatin interactions and distinguish closely related cell types. Genome Res., 20, 761–770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sankoff D. (1992) Edit distance for genome comparison based on non-local operations In: Combinatorial Pattern Matching, pp. 121–135. Springer, Cham. [Google Scholar]
- Sémon M., Duret L. (2006) Evolutionary origin and maintenance of coexpressed gene clusters in mammals. Mol. Biol. Evol., 23, 1715–1723. [DOI] [PubMed] [Google Scholar]
- Sequencing C., Consortium A. (2005) Initial sequence of the chimpanzee genome and comparison with the human genome. Nature, 437, 69–87. [DOI] [PubMed] [Google Scholar]
- Sexton T. et al. (2012) Three-dimensional folding and functional organization principles of the Drosophila genome. Cell, 148, 458–472. [DOI] [PubMed] [Google Scholar]
- Simonaitis P., Swenson K.M. (2018) Finding local genome rearrangements. Algorithms Mol. Biol, 13, 9.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer G.A.C. et al. (2005) Clusters of co-expressed genes in mammalian genomes are conserved by natural selection. Mol. Biol. Evol., 22, 767–775. [DOI] [PubMed] [Google Scholar]
- Spielmann M. et al. (2018) Structural variation in the 3D genome. Nat. Rev. Genet., 19, 453–467. [DOI] [PubMed] [Google Scholar]
- Stankiewicz P., Lupski J.R. (2002) Genome architecture, rearrangements and genomic disorders. Trends Genet., 18, 74–82. [DOI] [PubMed] [Google Scholar]
- Swenson K.M. et al. (2010) Sorting signed permutations by inversions in o (n log n) time. J. Comput. Biol., 17, 489–501. [DOI] [PubMed] [Google Scholar]
- Swenson K.M. et al. (2016) Models and algorithms for genome rearrangement with positional constraints. Algorithms Mol. Biol., 11, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tannier E. et al. (2007) Advances on sorting by reversals. Discrete Appl. Math., 155, 881–888. [Google Scholar]
- Thévenin A. et al. (2014) Functional gene groups are concentrated within chromosomes, among chromosomes and in the nuclear space of the human genome. Nucleic Acids Res., 42, 9854–9861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Véron A.S. et al. (2011) Close 3D proximity of evolutionary breakpoints argues for the notion of spatial synteny. BMC Genomics, 12, 303.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber C.C., Hurst L.D. (2011) Support for multiple classes of local expression clusters in Drosophila melanogaster, but no evidence for gene order conservation. Genome Biol., 12, R23.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wijchers P.J., de Laat W. (2011) Genome organization influences partner selection for chromosomal rearrangements. Trends Genet., 27, 63–71. [DOI] [PubMed] [Google Scholar]
- Yaffe E. et al. (2010) Comparative analysis of DNA replication timing reveals conserved large-scale chromosomal architecture. PLoS Genet., 6, e1001011.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yancopoulos S. et al. (2005) Efficient sorting of genomic permutations by translocation, inversion and block interchange. Bioinformatics, 21, 3340–3346. [DOI] [PubMed] [Google Scholar]
- Zhang Y. et al. (2012) Spatial organization of the mouse genome and its role in recurrent chromosomal translocations. Cell, 148, 908–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.