Abstract
Motivation
The prediction of protein–protein interaction (PPI) sites is a key to mutation design, catalytic reaction and the reconstruction of PPI networks. It is a challenging task considering the significant abundant sequences and the imbalance issue in samples.
Results
A new ensemble learning-based method, Ensemble Learning of synthetic minority oversampling technique (SMOTE) for Unbalancing samples and RF algorithm (EL-SMURF), was proposed for PPI sites prediction in this study. The sequence profile feature and the residue evolution rates were combined for feature extraction of neighboring residues using a sliding window, and the SMOTE was applied to oversample interface residues in the feature space for the imbalance problem. The Multi-dimensional Scaling feature selection method was implemented to reduce feature redundancy and subset selection. Finally, the Random Forest classifiers were applied to build the ensemble learning model, and the optimal feature vectors were inserted into EL-SMURF to predict PPI sites. The performance validation of EL-SMURF on two independent validation datasets showed 77.1% and 77.7% accuracy, which were 6.2–15.7% and 6.1–18.9% higher than the other existing tools, respectively.
Availability and implementation
The source codes and data used in this study are publicly available at http://github.com/QUST-AIBBDRC/EL-SMURF/.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Protein–protein interaction (PPI) is the basis for cells to carry out activities and the key to the realization of cell functions. It plays a vital role in biocatalysts, organism immunity, cell regulatory network construction, etc. (Gavin et al., 2002; Han et al., 2004). Since it is not realistic to carry out wet-lab experiments for PPI identification (Ezkurdia et al., 2009; Giot et al., 2003; Hamp and Rost, 2015), the computational prediction of PPI has become one of the primary goals in bioinformatics and biomedical studies (Aumentado-Armstrong et al., 2015; Northey et al., 2018).
The computational PPI prediction methods were developed mainly based on the (i) diverse genomic information, (ii) evolutionary information and (iii) protein structure information. The diverse genomic information-based methods include, but not limited to, (i–1) the phylogenetic profiling method, which annotates functional proteins by identifying the relationship between the adjacent genes and is suitable for the early evolutionary structure of simple organisms (Pellegrini et al., 1999); (i–2) the gene neighborhood method, which refers to the functional identification of gene products through the adjacency gene relationships (Dandekar et al., 1998; Overbeek et al., 1999; Tamames et al., 1997) and (i–3) the gene fusion method, which was used in metabolic proteins but lack of the ability to determine whether the fusion proteins directly exposed (Enright et al., 1999; Marcotte et al., 1999). The mirror tree algorithm is one representative method based on evolutionary information, which identifies the common evolutionary characteristics among functional proteins. Specifically, Goh et al. (2000) introduced a linear correlation coefficient to quantify the similarity of trees, and Pazos and Valencia (2001) used the same method to successfully predict 2742 pairs of proteins from a population of 67 000 Escherichia coli protein pairs. The protein structure information-based methods were first proposed by Sprinzak and Margalit that using sequence domain signals to reduce the experimental search space for PPI identification (Sprinzak and Margalit, 2001). Gomez et al. (2003) constructed an interaction attraction model by linking PPI to the protein domain interactions.
A PPI site is the position where proteins interact with neighbor residues that are the remaining structures of peptide bonds other than amino acids. The identification of PPI sites is the premise of PPI prediction, contributes to the extensive clinical and industrial applications and promote the identification of pharmacological targets and the drug design. The selection of different features based on the diversity of protein biochemical properties affects the prediction accuracy of PPI sites. Li et al. (2012) and Liu et al. (2010) identified residues using the random forest (RF) method based on sequence structural information. Zhou and Shan (2001) used the Position-Specific Score Matrix (PSSM) and solvent accessible surface area to extract features. Fariselli (2002) used the Homology-derived Secondary Structure of Proteins (HSSP) for feature vector extractions and Yan et al. (2004) extracted the feature of 19 adjacent residues to predict interfacial residues, leading to the sequence information-based PPI sites prediction.
The rapid development of machine learning provided unprecedented opportunities for the computational analysis and prediction of PPI sites (Krüger and Gohlke, 2010). Multiple classifiers have been applied to the prediction of PPI sites, such as neural networks (Gomez et al., 2001;Ofran and Rost, 2003,2007), Markov model (Friedrich et al., 2006), Naïve Bayes (NB) (Lin and Chen, 2013; Neuvirth et al., 2004), support vector machine (SVM) (Li et al., 2008; Porollo and Meller, 2007; Sriwastava et al., 2015), RF (Hou et al., 2017), ensemble learning (Lei et al., 2009; Porollo and Meller, 2007; Yan et al., 2004), conditional random field (Li et al., 2007) and minimum covariance determinant (Qiu et al., 2017). Ofran proposed a neural network-based classifier for PPI sites prediction and found most of the interface residues in continuous sequences (Ofran and Rost, 2003,2007). Other tools, e.g. cons-PPISP (Chen and Zhou, 2005) and meta-PPISP (Qin and Zhou, 2007), were developed based on the same neural network strategy. Porollo and Meller proposed the SPPIDER server to identify residues involved in PPI and improved the accuracy by integrating SVM and neural network (Porollo and Meller, 2007). Neuvirth et al. (2004) used the NB classifier to predict the interface residues and achieved a better classifier performance, and Murakami and Mizuguchi improved the performance by training the NB classifier with the kernel density estimation (Murakami and Mizuguchi, 2010). Chen and Liu (2005) proposed a new method based on protein domain prediction, which can explore all possible domain interactions. Considering the effect of neighboring residues on target residues, Mihel et al. (Mihel et al., 2008) combined a sliding window and RFs to identify interaction sites which get better precision and F-measure. Hou et al. (2017) evaluated the importance of various features using RF and included a new feature backbone flexibility predicted from sequences to further optimize PPI sites prediction. As new classifiers have springing up in recent years, Dhole’s team developed Sequence-based predictor of PRotein–protein InteractING Sites (SPRINGS) (Singh et al., 2014) and L1-regularized LOgistic Regression-based PPI Sites predictor (LORIS) (Dhole et al., 2014) through integrating the neural network and L1-regularized logistic regression. Friedrich et al. (2006) used the Markov model, Li et al. (2007) utilized conditional random fields and Qiu et al. (2017) used minimum covariance determinant and machine learning in the identification of PPI sites.
Although the existing methods for PPI sites prediction have achieved good prediction performance, the sample imbalance issue can decrease the performance of traditional learning algorithms (Japkowicz and Stephen, 2002; Kim et al., 2015; Yu et al., 2013,2014) and deflect predictions towards the non-interface residues in most classifiers. We proposed a new PPI sites prediction algorithm, Ensemble Learning of synthetic minority oversampling technique (SMOTE) for Unbalancing samples and RF algorithm (EL-SMURF), which integrated the SMOTE and the RF methods to oversample interfacial residues in the feature space through generating new data from two types of sample data (Blagus and Lusa, 2013; Chawla et al., 2002; Díez-Pastor et al., 2015; Ma and Fan, 2017). For the first time, the fusion of sequence profile feature in PSSM (PSSM-SPF) and residue evolution rate (RER) was applied for feature extraction of neighboring residues with a sliding window. SMOTE was then applied to oversample interface residues in the feature space to deal with the imbalance problem. In addition, we optimized the parameters of RFs and selected a different number of decision trees for different classifications by the leave-one-out cross-validation. Meanwhile, we used the Multi-dimensional Scaling (MDS) feature selection method to reduce the feature redundancy and improved the classification performance. Finally, the ensemble learning model was obtained by integrating the above optimized RF classifier. One training dataset (Dset186) and two independent validation datasets (Dtestset72 and PDBtestset164) were used to perform the leave-one-out cross-validation, and EL-SMURF showed the highest accuracies of 79.1%, 77.1% and 77.7% on the three datasets, respectively. The experimental results demonstrated that EL-SMURF can improve the state-of-the-art accuracy of PPI sites prediction.
2 Materials and methods
2.1 Datasets
Three datasets, namely Dset186, Dtestset72 (Murakami and Mizuguchi, 2010) and PDBtestset164 (Singh et al., 2014), were used to validate the effectiveness of EL-SMURF in this study. Dset186 consists 186 protein sequences extracted from 108 heterodimeric protein complexes in the PDB database (Berman et al., 2000), used as the training dataset, with sequence homology less than 25% and solved by X-ray crystallography with the resolution less than 3.0 Å. To generate Dset186, protein complexes were filtered by six steps: (i) remove protein complexes with missing residues ratio higher than 30%, (ii) remove complexes with two chains assigned by the same UniProt (Boutet et al., 2007) accessions or the same SCOP Concise Classification Strings (Murzin et al., 1995), (iii) remove transmembrane proteins listed in PDBTM (Tusnády et al., 2004), (iv) remove proteins with structure included a large structures found in other PDB entries by scanning against the BLAST PDB database with threshold greater than 95%, (v) remove protein complexes with interface buries surface accessibility of ≤500 Å2 or ≥Å2 and interface polarity less than 25% and (vi) cluster the remaining sequences and keep those with over 90% of pair-wise sequence identity. The two independent datasets, Dtestset72 and PDBtestset164, were constructed following the same process of Dset186 generation but using different annotated proteins, giving rise to 72 and 164 protein sequences, respectively.
On the other hand, we defined a residue to be interfacial if its absolute solvent accessibility is less than 1 Å2, before and after the binding of protein in the binding form; otherwise, non-interfacial (Aloy and Russell, 2002; Jones and Thornton, 1997). By using Protein Structure and Interaction Analyzer (Mihel et al., 2008), the number of interfacial residues was identified. As a result, 15.2% (5517/36 219), 10.6% (1923/18 140) and 18.1% (6096/33 681) of the residues in Dtestset72, Dset186 and PDBtestset164, respectively, are interfacial, indicating that sample imbalance issues exist among all the three datasets.
2.2 PSSM-SPF and RER features
The PSSM-SPF and RER were used to obtain protein sequence features. The SPF recorded in PSSM is a sequence characteristic table constructed by the entire information of the multiple sequence alignment results, which describes the substitution, insertion and deletion of each residue (Zhou and Zhou, 2004). It can be used as a feature of protein by the multiple alignments of homologous sequences. Moreover, PSSM-SPF is constructed by all members of the homologous family, thus, can adequately reflect the long-distance homology. The other protein sequence feature, RER, can be used to describe the evolutionary information based on the statistical knowledge in estimating the position of amino acids by conservatism scores. Since RER differs at various locations, the phylogenetic relationship between sequences and their random evolutionary processes can be determined. The RER method was designed based on the hypothesis that more interaction of proteins with other macromolecules, such as proteins, ligands and DNA molecules, can lower the evolutionary rate of the surface residues (Armon et al., 2003; Landgraf et al., 1999; Lichtarge et al., 1996). The ConSurf method (Armon et al., 2003) constructed by the Matching Pursuit algorithm was used to extract evolutionary rate of target residues and their neighboring residues of the three datasets, giving rise to an 11-dimensional RER feature.
2.3 SMOTE
SMOTE was used to solve the imbalance problem that leads biased classifications to the non-interfacial due to a large amount of non-interfacial residues in the three datasets (Blagus and Lusa, 2013; Chawla et al., 2002; Díez-Pastor et al., 2015; Ma and Fan, 2017). Specifically, it generated new data from two types of sample data to oversample a small number of sample sets. The synthesis strategy is to find the K-nearest neighbor of the sample from the samples of the interface residue, denoted by . Then, a sample and a random number of 0 to 1 were generated from the K-nearest neighbor, and a new sample was synthesized: .
| (1) |
Repeat the above procedure times until we got new samples: .
2.4 EL-SMURF
Ensemble learning has been frequently applied to the field of machine learning due to its ‘fault-tolerant rate’ (Afolabi et al., 2018; Jia et al., 2015) which shows better classification prediction results compared with individual classifiers. To improve the prediction accuracy of PPI sites, an EL-SMURF model was constructed following the three steps below (Fig. 1). The framework of EL-SMURF has been implemented in MATLAB 2014 b and R3.4.2 on a PC with system configuration Inter (R) Xeon (R) E5-2650 V3 CPU @2.30 GHz 2.30 GHz. Intel (R) Xeon (TM) CPU E5-2650 @ 2.30 GHz 2.30 GHz with 32.0 GB of RAM.
Fig. 1.
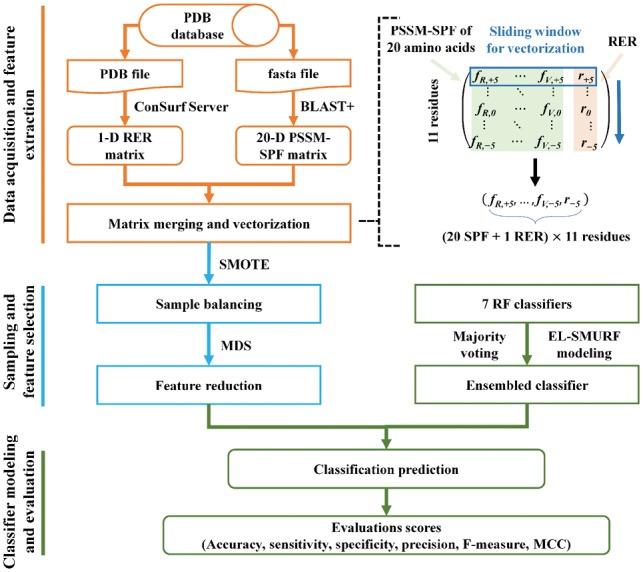
The flowchart of EL-SMURF with three steps: (A) Data acquisition and feature extraction. The PDB file and the FASTA file are downloaded from the PDB database, and the feature subsets of protein sequences are obtained by the combination of RER features and PSSM-SPF where a 231-D subset can be obtained by the sliding window. (B) Sampling and feature selection. A small number of samples (interface residues) were oversampled by SMOTE algorithm to get the balanced samples, and the MDS was used to reduce the feature redundancy and improve the classification performance. (C) Classifier modeling and classification. Using the optimal feature subset as the input vector, the majority voting method is used as the ensemble learning strategy to integrate the RF classifier and construct the integrated learning model EL-SMURF. The comparison of Acc, Se, Sp, Pr, F-Measure and MCC was carried out among several classifiers and prediction methods
Step 1 —
Data acquisition and feature extraction. For a known PDB ID, we downloaded its FASTA sequence from the PDB database. For a query protein sequence, we used BLAST+ to search the NCBI non-redundant database for three times with (Wei et al., 2016) as the cutoff for multiple sequence alignment against the query sequence (Camacho et al., 2009). Then we got an n-by-20 matrix with each row representing a 20-dimensional vector of the position of an amino acid, and each element in a vector representing the frequency at which 20 amino acids appear. This matrix is so-called a PSSM, and the corresponding feature is named as PSSM-SPF. Considering the effect of neighboring residues on the target residues, we fused the RER features and PSSM-SPF in each residue, giving rise to a 21-dimensional feature vector. Residues are not only determined by the target residues but also closely related to the properties of the residues adjacent to the target residues (Wei et al., 2016). Hence, we set a sliding window of 11 (Dohkan et al., 2004) which includes the target residue at the center and 10 neighbor residues to extract the PSSM-SPF and the RER features. Then a 231-dimensional feature vector (21 x 11) was created to predict the PPI sites as the input feature of the following two steps.
Step 2 —
Sampling and feature selection. To solve the imbalance problem of sample classes, we used the SMOTE algorithm to sample a small number of class samples of three datasets and form balanced samples with the same number of positive and negative samples. Then we used MDS to reduce the feature redundancy and got the new feature subset as the input of the next step. (Supplementary Fig. S1).
Step 3 —
Classifier modeling and classification. RF was used as an individual classifier to the ensemble, and the integration strategy is the expert system voting method,
(2) where, is the final result of the EL-SMURF, is the normal sign function, equals +1 or –1 indicating the predicted result of each RF, indicates the number of ensemble RF. The balanced samples were integrated into the EL-SMURF model the prediction results can be generated by formula (2).
Sensitivity (Se), Specificity (Sp), Accuracy (Acc), Precision (Pr), F-measure and Matthews correlation coefficient (MCC) were used for evaluation. Se (3) and Sp (4) reflect the performance of classifier interface residues; Acc (5) reflects the prediction ability of classifier for the test set; MCC (6) demonstrates the correlation between prediction results and real data; Pr (7) describes the random error; F-measure (8) indicates the harmonic mean of Se and Pr. The formula of six indexes are shown as follows (Wei et al., 2016):
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
where TP is the number of correctly classified interface residues, FP is the number of incorrectly classified non-interface residues, TN is the number of correctly classified non-interface residues and FN is the number of wrongly classified interface residues. Also, the ROC curve was used to check the generalization performance of the construction model. The higher value of the area under the ROC curve (AUC) indicates a more robust and generalized model.
3 Results
Dset186, Dtestset72 and Dtestset164 contain far more non-interface residues than interface residues. The performances of traditional learning algorithms will decrease naturally, and the classification results are mostly biased to the non-interface residues. The classifier parameters, feature extraction methods, classifier performance and comparison with other methods were performed on the balanced samples.
3.1 Parameter optimization for the RF model
In an RF algorithm, the number of decision trees has a significant influence on the accuracy of the model and the running speed of the model (Chung and Chen, 2012). The training data Dset186 was transferred to balanced dataset after the SMOTE step. The parameter was chosen from 100 to 1000, with tolerance at 100, for achieving the best accuracy value (Supplementary Table S1 and Supplementary Fig. S2). The Acc index achieved the highest value when equals to 300. Hence, we set equals 300 in this study.
3.2 Determination of the number of integrating RFs on Dset186
In EL-SMURF, the majority voting method was used to integrate the RF classifier. The number of the individual RF classifier used for integration was decided by the balanced sample treated by SMOTE. As shown in Table 1 , a different number of RF classifiers were chosen for optimizing the prediction accuracy in the training dataset Dset186. Overall, the seven RF classifier integration showed better performance than the other two options, especially in Acc, Sp and Pr. On the other hand, the running time of EL-SMURF increased along with the increase of the RF number, and it may take days for an RF number larger than seven. Considering the efficiency and the maximization of model accuracy, we used seven RF classifiers to construct the EL-SMURF model.
Table 1.
Influence of different number of RFs on Dset186
| RF number | Acc (%) | Se (%) | Sp (%) | Pr (%) | F-Measure | MCC |
|---|---|---|---|---|---|---|
| 3 | 72.0 | 96.3 | 47.7 | 64.8 | 0.775 | 0.503 |
| 5 | 71.8 | 96.4 | 47.2 | 64.6 | 0.773 | 0.501 |
| 7 | 73.1 | 91.7 | 54.5 | 66.8 | 0.773 | 0.498 |
Note: Bold numbers in the table indicate the highest Acc result.
3.3 Comparison of feature extraction methods
A protein sequence and its RER were commonly used as the feature attributes to empower a classifier, which was used to study the feature extraction degree of the protein sequence information. Meanwhile, the feature fusion of PSSM-SPF and RER, and each of the two features, were used to extract the features of the protein sequence. After SMOTE, the extracted feature vectors were classified and predicted by the EL-SMURF model, in support of the comparison of the feature extraction effects of two individual feature attributes and the effect of feature fusion on the prediction performance. The effects of different feature extraction methods on EL-SMURF classification were shown in Table 2 .
Table 2.
Influence of different features extraction methods on Dset186
| Features | Acc (%) | Se (%) | Sp (%) | Pr (%) | F-Measure | MCC |
|---|---|---|---|---|---|---|
| SPF | 71.3 | 96.4 | 46.2 | 75.4 | 0.770 | 0.491 |
| RER | 68.9 | 96.7 | 41.1 | 62.1 | 0.756 | 0.454 |
| Feature fusion | 73.1 | 91.7 | 54.5 | 66.8 | 0.773 | 0.498 |
Note: Bold numbers in the table indicate the highest Acc result.
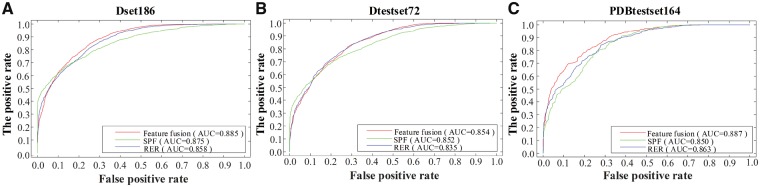
As shown in Table 2, the feature extraction methods of feature fusion reached the maximum Acc, Sp, Pr, F-measure and MCC. This indicated that feature extraction based on feature fusion plays a vital role in accurately identifying PPI sites. To compare the effect of the three feature extraction methods on the performance of the classifier, the ROC curves of the three methods on three datasets were showcased in Figure 2.
Fig. 2.
Comparison of feature fusion, PSSM-SPF and RER methods on three datasets. (A) The ROC curves on Dset186. (B) The ROC curves on Dtestset72. (C) The ROC curves on PDBtestset164
Based on the ROC curves in Figure 2, the algorithms utilizing the feature fusion of RER and SPF had the highest AUC values across the three datasets. For all three datasets, the fusion of SPF and RER yielded the higher AUC value of 0.885, 0.854 and 0.887, respectively, than individual SPF and RER methods. As a result, the feature fusion extraction method has the better extraction effect and the feature vectors extracted from feature fusion can be more comprehensive to reflect the sequence information of protein than the feature vectors obtained from the single feature extraction method. By comparing the effects of different feature extraction methods on the results, the robustness of feature extraction algorithms was derived from the ROC curve and the feature fusion was determined as the best feature extraction method in this study.
3.4 Effect of feature selection algorithm on results
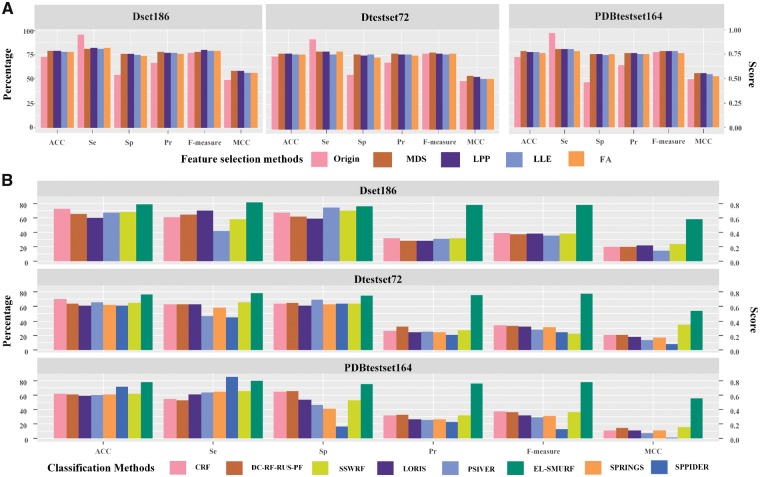
To reduce the computational complexity and feature redundancy, we carried out feature selection among features extracted in Section 3.3, using MDS (Taguchi and Oono, 2005), Locality Preserving Projection (LPP) (Heidari et al., 2018), Locally Linear Embedding (LLE) and Factor Analysis (FA) (Salas‐Gonzalez et al., 2010). First, we used the maximum likelihood estimator for estimating essential dimensions. The feature was reduced to 20 on Dset186, 19 on Dataset72 and 18 on PDBtestset164. The parament k in LLE and LPP was set to 12 to discover the 12 nearest neighbor points for each sample point. The comparison of different feature selection methods on three datasets is shown as Figure 3 A. We also use other feature selection methods such as Linear Discriminant Analysis (Wang and Yue, 2018), Neighborhood Preserving Embedding (Lee et al., 2015) and Auto-encoder (Deng et al., 2017), with more details in Supplementary Table S2.
Fig. 3.
Comparison of the feature selection and classification methods on Dset186, Dtestset72 and PDBtestset164. (A) Performance of MDS, LPP, LLE and FA feature selection methods with the original method. (B) Comparison of eight classification methods on the three datasets. SPINGS and SPPIDER were not included for Dset186 due to the unavailability of their source code
As shown in Figure 3A, feature selection has a significant improvement on the classification performance. The ACC achieved 79.1% with the MDS method on Dset186, which increased by 6% compared with the original method. Feature selection methods also achieved an improvement on F-Measure and MCC, which is an increase by 1.1% and 6.8%, respectively, from 0.773 and 0.498 of the original method to 0.784 and 0.584 of MDS on Dset186. The ACC achieved 77.1% and 77.7% with the MDS method on Dtestset72 and PDBtestset164, which increases by 4% and 5.7% respectively compared with the original method. The F-measure and MCC also achieved the highest values with the MDS method on the independent test sets. In conclusion, MDS, as a global algorithm that utilizes the similarity between pairs of samples, is more reliable than local feature selection methods, since it had the most significant effect on the three datasets. The purpose is to use this information to construct a suitable low-dimensional space so that the distance between the samples in this space and the similarity between the samples in the high-dimensional space are as consistent as possible. The result showcased that the importance of feature selection in reducing the computational complexity and feature redundancy and improving the prediction performance.
3.5 Performance comparisons with other methods
To evaluate the prediction performance of the EL-SMURF method, its results were compared with NB (Supplementary Method Illustration Si 1), SVM (Supplementary Method Illustration Si 2) and RF (Supplementary Method Illustration Si 3) on the three datasets (Supplementary Tables S3–S5). To compare the robustness of the prediction model under different classifiers, the ROC curve of NB, SVM, RF classifiers was plotted on the three datasets (Supplementary Figs S3–S5). We also planned to compare our classification method with seven others such as SPRINGS (Singh et al., 2014), PSIVER (Murakami and Mizuguchi, 2010), SPPIDER (Porollo and Meller, 2007), CRF (Wei et al., 2015), DC-RF-RUS-RF (Liu et al., 2016), LORIS (Dhole et al., 2014) and SSWRF (Wei et al., 2016), which have solved the imbalance problem in different evolution index. Due to the unavailability of the source code of SPRINGS and SPPIDER were and the evolution index on Dset186 are not offered, the comparison was only carried among the rest six methods on Dset186 (Fig. 3B).
The results performance (Fig. 3B) demonstrated that EL-SMURF performed the best for almost all the indexes among three datasets only except the Se which was slightly lower than the performance of SPPIDER in PDBtestset164. Specifically, on Dset186, the ACC index of EL-SMURF reached the maximum 79.1%, which is much higher than the other five methods. Meanwhile, Sp, Se, Pr, F-measure and MCC also reached the highest by the EL-SMURF on this dataset. On the independent validation Dtestset72, the ACC index of EL-SMURF achieved 77.1%, which is 6.2% higher than the second highest CRF method with 70.6%. Compared with the other seven methods in F-measure and MCC, EL-SMURF achieved 0.775 and 0.542, which means the F-measure and MCC have been significantly improved 33.5–53.4% and 19.1–46.5%, respectively. For the independent validation dataset PDBtestset164, every index has a noticeable improvement by EL-SMURF. The ACC index had an increase of 6.1%% from 71.6% of SPPIDER to 77.7% of EL-SMURF. F-measure and MCC achieved the highest, respectively, 0.782 and 0.554 by EL-SMURF. Detailed results can be found in Supplementary Tables S6–S8.
According to the classification effect of the above three datasets, the proposed EL-SMURF method achieved better prediction accuracy than other methods in the training dataset Dset186, and the two independent validation sets Dtestset72 and PDBtestset164. The above results fully demonstrated that the prediction model constructed in this study can significantly improve the accuracy of PPI sites prediction, with satisfactory prediction results.
4 Conclusion
With a large number of protein sequences in the public domain, the traditional biological experiments are difficult to meet the demands in the PPI research field. The critical challenge of bioinformatics is to develop computational methods for efficiently and accurately determining the structures and functions of proteins (Afolabi et al., 2018; Lei et al., 2016,2018; Song et al., 2017; Wang et al., 2017; Yu et al., 2018). In this study, we presented a machine learning method EL-SMURF to predict the PPI sites from protein sequences, whose prediction accuracies achieve 79.1%, 77.1% and 77.7%, respectively, on the datasets Dest186, Dtestset72 and PDBtestset164. Compared with other existing methods, the results showed that EL-SMURF can effectively improve the prediction accuracy of PPI sites. We expect this method to be a powerful tool for researchers in bioinformatics, proteomics and molecular biology. Although EL-SMURF improved the accuracy of PPI sites prediction to a certain extent, there is still a big room for improvement of prediction accuracy and algorithm efficiency. In the future, we will try more feature selection methods to improve the performance of EL-SMOTE and implement deep learning for the PPI sites identification.
Supplementary Material
Acknowledgement
The authors thank anonymous reviewers for valuable suggestions and comments.
Funding
This work was supported by the National Nature Science Foundation of China (No. 61863010, 11771188), the Natural Science Foundation of Shandong Province of China (No. ZR2018MC007) and the Project of Shandong Province Higher Educational Science and Technology Program (No. J17KA159). This work was also supported by an R01 award #1R01GM131399-01 from the National Institute of General Medical Sciences of the National Institutes of Health. B.L.’s work was supported by the National Nature Science Foundation of China (NSFC) [61772313 and 61432010 to B.L.] and Young Scholars Program of Shandong University (YSPSDU, 2015WLJH19).
Conflict of Interest: none declared.
References
- Afolabi L.T., et al. (2018) Ensemble learning method for the prediction of new bioactive molecules. PLoS One, 13, e0189538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aloy P., Russell R.B. (2002) Interrogating protein interaction networks through structural biology. P. Natl. Acad. Sci. USA, 99, 5896–5901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armon A., et al. (2003) ConSurf: an algorithmic tool for the identification of functional regions in proteins by surface mapping of phylogenetic information. Bioinformatics, 307, 447–463. [DOI] [PubMed] [Google Scholar]
- Aumentado-Armstrong T.T., et al. (2015) Algorithmic approaches to protein–protein interaction site prediction. Algorithm. Mol. Biol., 10, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H.M., et al. (2000) The protein data bank. Nucleic Acids Res., 28, 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blagus R., Lusa L. (2013) SMOTE for high-dimensional class-imbalanced data. BMC Bioinformatics, 14, 106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boutet E., et al. (2007) Uniprotkb/swiss-prot. Plant Bioinformatics, 406, 89–112. [Google Scholar]
- Camacho C., et al. (2009) BLAST+: architecture and applications. BMC Bioinformatics, 10, 421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chawla N.V., et al. (2002) SMOTE: synthetic minority over-sampling technique. J. Artif. Intell. Res., 16, 321–357. [Google Scholar]
- Chen H., Zhou H.X. (2005) Prediction of interface residues in protein–protein complexes by a consensus neural network method: test against NMR data. Proteins, 61, 21–35. [DOI] [PubMed] [Google Scholar]
- Chen X.W., Liu M. (2005) Prediction of protein–protein interactions using random decision forest framework. Bioinformatics, 21, 4394–4400. [DOI] [PubMed] [Google Scholar]
- Chung R.H., Chen Y.E. (2012) A two-stage random forest-based pathway analysis method. PLoS One, 7, e36662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dandekar T., et al. (1998) Conservation of gene order: a fingerprint of proteins that physically interact. Trends Biochem. Sci., 23, 324–328. [DOI] [PubMed] [Google Scholar]
- Deng L., et al. (2017) A sparse autoencoder-based deep neural network for protein solvent accessibility and contact number prediction. BMC Bioinformatics, 18, 569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhole K., et al. (2014) Sequence-based prediction of protein–protein interaction sites with L1-logreg classifier. J. Theor. Biol., 348, 47–54. [DOI] [PubMed] [Google Scholar]
- Díez-Pastor J.F., et al. (2015) Random balance: ensembles of variable priors classifiers for imbalanced data. Knowl. Based Syst., 85, 96–111. [Google Scholar]
- Dohkan S., et al. (2004) Prediction of protein–protein interactions using support vector machines. IEEE BIBE 2014, 576. [Google Scholar]
- Enright A.J., et al. (1999) Protein interaction maps for complete genomes based on gene fusion events. Nature, 402, 86–90. [DOI] [PubMed] [Google Scholar]
- Ezkurdia I., et al. (2009) Progress and challenges in predicting protein–protein interaction sites. Brief. Bioinform., 10, 233–246. [DOI] [PubMed] [Google Scholar]
- Fariselli P., et al. (2002) Prediction of protein–protein interaction sites in heterocomplexes with neural networks. FEBS J., 269, 1356–1361. [DOI] [PubMed] [Google Scholar]
- Friedrich T., et al. (2006) Modelling interaction sites in protein domains with interaction profile hidden Markov models. Bioinformatics, 22, 2851–2857. [DOI] [PubMed] [Google Scholar]
- Gavin A.C., et al. (2002) Functional organization of the yeast proteome by systematic analysis of protein complexes. J. Econ. Surv., 415, 141–147. [DOI] [PubMed] [Google Scholar]
- Giot L., et al. (2003) A protein interaction map of Drosophila melanogaster. Science, 302, 1727–1736. [DOI] [PubMed] [Google Scholar]
- Goh C.S., et al. (2000) Co-evolution of proteins with their interaction partners. J. Mol. Biol., 299, 283–293. [DOI] [PubMed] [Google Scholar]
- Gomez S.M., et al. (2001) Probabilistic prediction of unknown metabolic and signal-transduction networks. Genetics, 159, 1291–1298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomez S.M., et al. (2003) Learning to predict protein–protein interactions from protein sequences. Bioinformatics, 19, 1875–1881. [DOI] [PubMed] [Google Scholar]
- Han J.D.J., et al. (2004) Evidence for dynamically organized modularity in the yeast protein–protein interaction network. Nature, 430, 88–93. [DOI] [PubMed] [Google Scholar]
- Hamp T., Rost B. (2015) More challenges for machine-learning protein interactions. Bioinformatics, 31, 1521–1525. [DOI] [PubMed] [Google Scholar]
- Heidari M., et al. (2018) Prediction of breast cancer risk using a machine learning approach embedded with a locality preserving projection algorithm. Phys. Med. Biol., 63, 035020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou Q., et al. (2017) Seeing the trees through the forest: sequence-based homo- and heteromeric protein–protein interaction sites prediction using random forest. Bioinformatics, 33, 1479–1487. [DOI] [PubMed] [Google Scholar]
- Japkowicz N., Stephen S. (2002) The class imbalance problem: a systematic study. Intell. Data Anal., 6, 429–449. [Google Scholar]
- Jia J., et al. (2015) iPPI-Esml: an ensemble classifier for identifying the interactions of proteins by incorporating their physicochemical properties and wavelet transforms into PseAAC. J. Theor. Biol., 377, 47–56. [DOI] [PubMed] [Google Scholar]
- Jones S., Thornton J.M. (1997) Analysis of protein–protein interaction sites using surface patches. J. Theor. Biol., 272, 121–132. [DOI] [PubMed] [Google Scholar]
- Kim M.J., et al. (2015) Geometric mean based boosting algorithm with over-sampling to resolve data imbalance problem for bankruptcy prediction. Expert Syst. Appl., 42, 1074–1082. [Google Scholar]
- Krüger D.M., Gohlke H. (2010) DrugScorePPI webserver: fast and accurate in silico alanine scanning for scoring protein–protein interactions. Nucleic Acids Res., 38, 480–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landgraf R., et al. (1999) Analysis of heregulin symmetry by weighted evolutionary tracing. Protein Eng., 12, 943–951. [DOI] [PubMed] [Google Scholar]
- Lee S., et al. (2015) Exploring supervised neighborhood preserving embedding (SNPE) as a nonlinear feature extraction method for vibrational spectroscopic discrimination of agricultural samples according to geographical origins. Talanta, 144, 960–968. [DOI] [PubMed] [Google Scholar]
- Lei D., et al. (2009) Prediction of protein–protein interaction sites using an ensemble method. BMC Bioinformatics, 10, 426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lei X., et al. (2016) Identification of dynamic protein complexes based on fruit fly optimization algorithm. Knowl. Based Syst., 105, 270–277. [Google Scholar]
- Lei X., et al. (2018) Predicting essential proteins based on rna-seq, subcellular localization and GO annotation datasets. Knowl. Based Syst., 151, 136–148. [Google Scholar]
- Li B.Q., et al. (2012) Prediction of protein–protein interaction sites by random forest algorithm with mRMR and IFS. PLoS One, 7, e43927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M.H., et al. (2007) Protein–protein interaction site prediction based on conditional random fields. Bioinformatics, 23, 597–604. [DOI] [PubMed] [Google Scholar]
- Li N., et al. (2008) Prediction of protein–protein binding site by using core interface residue and support vector machine. BMC Bioinformatics, 9, 553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lichtarge O., et al. (1996) An evolutionary trace method defines binding surfaces common to protein families. J. Mol. Biol., 257, 342–358. [DOI] [PubMed] [Google Scholar]
- Lin X., Chen X.W. (2013) Heterogeneous data integration by tree-augmented naive Bayes for protein–protein interactions prediction. Proteomics, 13, 261–268. [DOI] [PubMed] [Google Scholar]
- Liu G.H., et al. (2016) Prediction of protein–protein interaction sites with machine-learning-based data-cleaning and post-filtering procedures. J. Membrane Biol., 249, 141–153. [DOI] [PubMed] [Google Scholar]
- Liu Z.P., et al. (2010) Prediction of protein-RNA binding sites by a random forest method with combined features. Bioinformatics, 26, 1616–1622. [DOI] [PubMed] [Google Scholar]
- Ma L., Fan S. (2017) CURE-SMOTE algorithm and hybrid algorithm for feature selection and parameter optimization based on random forests. BMC Bioinformatics, 18, 169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcotte E.M., et al. (1999) Detecting protein function and protein–protein interactions from genome sequences. Science, 285, 751–753. [DOI] [PubMed] [Google Scholar]
- Mihel J., et al. (2008) PSAIA–protein structure and interaction analyzer. BMC Struct. Biol., 8, 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murakami Y., Mizuguchi K. (2010) Applying the Naïve Bayes classifier with kernel density estimation to the prediction of protein–protein interaction sites. Bioinformatics, 26, 1841–1848. [DOI] [PubMed] [Google Scholar]
- Murzin A.G., et al. (1995) SCOP: a structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol., 247, 536–540. [DOI] [PubMed] [Google Scholar]
- Neuvirth H., et al. (2004) ProMate: a structure based prediction program to identify the location of protein–protein binding sites. J. Mol. Biol., 338, 181–199. [DOI] [PubMed] [Google Scholar]
- Northey T., et al. (2018) IntPred: a structure-based predictor of protein–protein interaction sites. Bioinformatics, 34, 223–229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ofran Y., Rost B. (2003) Predicted protein–protein interaction sites from local sequence information. FEBS Lett., 544, 236–239. [DOI] [PubMed] [Google Scholar]
- Ofran Y., Rost B. (2007) ISIS: interaction sites identified from sequence. Bioinformatics, 23, 13–16. [DOI] [PubMed] [Google Scholar]
- Overbeek R., et al. (1999) Use of contiguity on the chromosome to predict functional coupling. Silico Biol., 1, 93–108. [PubMed] [Google Scholar]
- Pazos F., Valencia A. (2001) Similarity of phylogenetic trees as indicator of protein–protein interaction. Protein Eng., 14, 609–614. [DOI] [PubMed] [Google Scholar]
- Pellegrini M., et al. (1999) Assigning protein functions by comparative genome analysis: protein phylogenetic profiles. P. Natl. Acad. Sci. USA, 96, 4285–4288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porollo A., Meller J. (2007) Prediction-based fingerprints of protein–protein interactions. Proteins, 66, 630–645. [DOI] [PubMed] [Google Scholar]
- Qin S., Zhou H.X. (2007) Meta-PPISP: a meta web server for protein–protein interaction site prediction. Bioinformatics, 23, 3386–3387. [DOI] [PubMed] [Google Scholar]
- Qiu Z., et al. (2017) Protein–protein interaction site predictions with minimum covariance determinant and Mahalanobis distance. J. Theor. Biol., 433, 57–63. [DOI] [PubMed] [Google Scholar]
- Salas‐Gonzalez D., et al. (2010) Feature selection using factor analysis for Alzheimer’s diagnosis using 18F-FDG PET images. Med. Phys., 37, 6084–6095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh G., et al. (2014) SPRINGS: prediction of protein–protein interaction sites using artificial neural networks. J. Proteom. Comput. Biol., 1, 7. [Google Scholar]
- Song Q., et al. (2017) Combination of minimum enclosing balls classifier with SVM in coal-rock recognition. PLoS One, 12, e0184834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprinzak E., Margalit H. (2001) Correlated sequence-signatures as markers of protein–protein interaction 1. J. Mol. Biol., 311, 681–692. [DOI] [PubMed] [Google Scholar]
- Sriwastava B.K., et al. (2015) Protein–Protein interaction site prediction in Homo sapiens and E. coli using an interaction-affinity based membership function in fuzzy SVM. J. Biosci., 40, 809–818. [DOI] [PubMed] [Google Scholar]
- Taguchi Y.H., Oono Y. (2005) Relational patterns of gene expression via non-metric multidimensional scaling analysis. Bioinformatics, 21, 730–740. [DOI] [PubMed] [Google Scholar]
- Tamames J., et al. (1997) Conserved clusters of functionally related genes in two bacterial genomes. J. Mol. Evol., 44, 66–73. [DOI] [PubMed] [Google Scholar]
- Tusnády G.E., et al. (2004) Transmembrane proteins in the Protein Data Bank: identification and classification. Bioinformatics, 20, 2964–2972. [DOI] [PubMed] [Google Scholar]
- Wang S., Yue Y. (2018) Protein subnuclear localization based on a new effective representation and intelligent kernel linear discriminant analysis by dichotomous greedy genetic algorithm. PLoS One, 13, e0195636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y., et al. (2017) Protein secondary structure prediction by using deep learning method. Knowl. Based Syst., 118, 115–123. [Google Scholar]
- Wei Z.S., et al. (2015) A cascade random forests algorithm for predicting protein–protein interaction sites. IEEE T. Nanobiosci., 14, 746–760. [DOI] [PubMed] [Google Scholar]
- Wei Z.S., et al. (2016) Protein–protein interaction sites prediction by ensembling SVM and sample-weighted random forests. Neurocomputing, 193, 201–212. [Google Scholar]
- Yan C., et al. (2004) A two-stage classifier for identification of protein–protein interface residues. Bioinformatics, 20, 371–378. [DOI] [PubMed] [Google Scholar]
- Yu B., et al. (2018) Prediction of subcellular location of apoptosis proteins by incorporating PsePSSM and DCCA coefficient based on LFDA dimensionality reduction. BMC Genomics, 19, 478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu D.J., et al. (2013) Improving protein-ATP binding residues prediction by boosting SVMs with random under-sampling. Neurocomputing, 104, 180–190. [Google Scholar]
- Yu D.J., et al. (2014) Enhancing protein-vitamin binding residues prediction by multiple heterogeneous subspace SVMs ensemble. BMC Bioinformatics, 15, 297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H., Shan Y. (2001) Prediction of protein interaction sites from sequence profile and residue neighbor list. Proteins, 44, 336–343. [DOI] [PubMed] [Google Scholar]
- Zhou H., Zhou Y. (2004) Single‐body residue‐level knowledge‐based energy score combined with sequence‐profile and secondary structure information for fold recognition. Proteins, 55, 1005–1013. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.