Abstract
Motivation
How predictable is the evolution of cancer? This fundamental question is of immense relevance for the diagnosis, prognosis and treatment of cancer. Evolutionary biologists have approached the question of predictability based on the underlying fitness landscape. However, empirical fitness landscapes of tumor cells are impossible to determine in vivo. Thus, in order to quantify the predictability of cancer evolution, alternative approaches are required that circumvent the need for fitness landscapes.
Results
We developed a computational method based on conjunctive Bayesian networks (CBNs) to quantify the predictability of cancer evolution directly from mutational data, without the need for measuring or estimating fitness. Using simulated data derived from >200 different fitness landscapes, we show that our CBN-based notion of evolutionary predictability strongly correlates with the classical notion of predictability based on fitness landscapes under the strong selection weak mutation assumption. The statistical framework enables robust and scalable quantification of evolutionary predictability. We applied our approach to driver mutation data from the TCGA and the MSK-IMPACT clinical cohorts to systematically compare the predictability of 15 different cancer types. We found that cancer evolution is remarkably predictable as only a small fraction of evolutionary trajectories are feasible during cancer progression.
Availability and implementation
https://github.com/cbg-ethz/predictability\_of\_cancer\_evolution
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Dissecting the relative contribution of stochastic versus deterministic forces in shaping the outcome of evolutionary processes is a long-standing question of both experimental and theoretical research in evolutionary biology (Blount et al., 2018; Gould, 1990; Lobkovsky and Koonin, 2012; Orgogozo, 2015). While stochastic forces (e.g. genetic drift) allow evolution to take place in an undirected manner, deterministic forces (e.g. natural selection) can impose constraints on the potential evolutionary trajectories. Stephen Jay Gould highlighted the problem of chance and necessity by devising the metaphor of ‘replaying the tape of life’. He concluded that the outcome of evolution at large is not likely to be repeatable, because many equally likely evolutionary trajectories may exist (Gould, 1990).
However, recent technological advancements in experimental evolution, high-throughput sequencing and modeling of complex biological systems have revealed some repeatable features in diverse evolutionary processes and pervasive evolutionary constraints in various biological systems (Achaz, 2014; Blount et al., 2018; Ferretti et al., 2018; Hosseini and Wagner, 2017; Lieberman et al., 2011; Miles et al., 2011; Poelwijk et al., 2007; Salverda et al., 2011; Toprak et al., 2012; Weinreich et al., 2006). These repeatable patterns and regularities suggest a predictive theory of evolution, which has been pioneered by studies attempting to predict the future of evolution in various biological systems (Barton et al., 2016; Bull and Molineux, 2008; Cowperthwaite et al., 2008; Luksza and Lässig, 2014; Neher et al., 2014; Nyerges et al., 2018). Thus, beyond reconstructing evolutionary history of the past, the task of predicting future outcomes of evolutionary processes has emerged in computational evolutionary biology (Lässig et al., 2017).
Predictability is tightly linked with controllability (Fischer et al., 2015; Lässig et al., 2017). Once we can predict the outcome of evolution, we will be able to design specific intervention strategies and manipulate biological systems towards our desired goals. This is where fundamental principles of evolutionary biology come into play in biomedical research, particularly in the diagnosis and treatment of diseases with evolutionary nature such as cancer. Cancer progression can be regarded as an evolutionary process, which is caused by step-wise accumulation of selectively advantageous mutations (Beerenwinkel et al., 2016; Nowell, 1976).
Like all evolutionary processes, cancer progression is the outcome of events driven by a mixture of both stochastic and deterministic forces. On the one hand, because of the extensive inter- and intra-patient heterogeneity of cancer-associated mutations, the genetic progression of cancer seems to be an unpredictable evolutionary process (Burrell et al., 2013; Lipinski et al., 2016; Marusyk and Polyak, 2010). On the other hand, a growing body of evidence attests to the predictability of cancer evolution. For example, only a minor fraction of mutations, called drivers, contributes to the malignancy of cancer, while most are passenger mutations with no phenotypic effects (Vogelstein et al., 2013), such that, typically, only a handful of genes are frequently mutated among patients with a given cancer type (Lawrence et al., 2013; Vogelstein et al., 2013). Moreover, the pervasive constraints in the temporal ordering of tumorigenic mutations (Bagcchi, 2015; Fisher et al., 2014; Kent and Green, 2017; Martins et al., 2012; Ortmann et al., 2015), and the repeatability of evolutionary trajectories during cancer progression (Caravagna et al., 2018) suggest the predictability of cancer evolution. Nevertheless, these anecdotal examples and sporadic reports on heterogeneity or repeatability are not sufficient for a systematic insight into the extent of evolutionary predictability of different cancer types. Instead, a rigorous quantitative framework is needed for this purpose (Linnen, 2018).
Various attempts using different approaches have been made to gain quantitative insights into the predictability of evolution in general (de Visser and Krug, 2014). Whereas experimentally, evolutionary predictability is assessed as the fraction of identical outcomes in replicate evolutionary experiments (Blount et al., 2018; Tenaillon et al., 2012; Woods et al., 2006), theoretical studies of predictability analyze the probabilities of mutational pathways on a given fitness landscape (de Visser and Krug, 2014). A common model is the strong selection and weak mutation rate (SSWM) assumption (Gillespie, 1983; Orr, 2005), which implies successive clonal expansions driven by selectively advantageous mutations. The SSWM assumption allows for computing mutational pathway probabilities based on the fixation probabilities of the mutations (Weinreich et al., 2006). It is widely used for analyzing fitness landscapes (de Visser and Krug, 2014; Weinreich et al., 2005) and its validity has been confirmed by experimental evolution studies (Poelwijk et al., 2007; Weinreich et al., 2006).
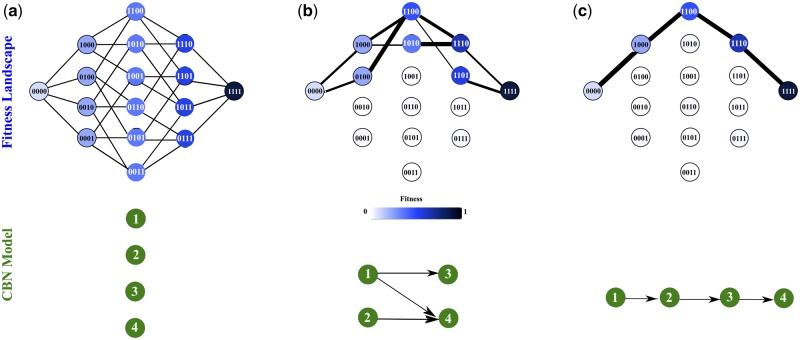
The predictability of evolution is minimal if all mutational pathways are all equally likely (Fig. 1a). In contrast, non-uniform distributions of mutation trajectories bias evolution towards specific directions and increase the predictability of evolution (Fig. 1b and c). The extent of the non-uniformity can be quantified by the entropy of the pathway probability distribution (Szendro et al., 2013).
Fig. 1.
Fitness landscapes and CBN. Upper panels show schematic representations of three different fitness landscapes each including four mutations. Each vertex corresponds to a genotype, which is represented as a binary string and is color-coded according to its fitness. Each fitness landscape is arranged in five columns and each column contains all genotypes with the same number of mutations. The leftmost and the rightmost columns correspond, respectively, to the wild-type and the fully mutated genotype. There is an edge between a pair of genotypes if they differ in exactly one fitness-increasing mutation. A mutational pathway is comprised of a set of edges that connect the wild-type to the genotype with the highest fitness (i.e. the fully mutated one). In panel (a), all genotypes belonging to the same column have the same fitness and fitness increases monotonically from left to right. In this fitness landscape, all 4!=24 potential pathways are accessible with equal probability (minimum predictability). In panel (b), not all genotypes belonging to the same column have the same fitness, such that evolutionary trajectories are restricted: only five pathways are accessible with different probability (shown as different edge thickness) (intermediate predictability). In panel (c), only a single mutational pathway is accessible and predictability is maximal. Each network on the bottom (with green vertices and labeled by the mutation) represents a CBN, whose DAG encodes the order constraints. An edge in the DAG means that mutation a must occur prior to mutation b. The graphs on the top are exactly the genotype lattices of the corresponding CBN models on the bottom
In practice, however, defining evolutionary predictability based on empirical fitness landscapes is usually unfeasible, because of the high costs associated with experimentally determining the fitness of all possible genotypes (de Visser and Krug, 2014). Moreover, measuring fitness landscapes in vivo is impossible and in vitro systems have their own limitations. Furthermore, inferring fitness landscapes from genomic data, especially for cancer is also extremely challenging. Although in other systems, such as, e.g. HIV under the strong assumption of equilibrium distribution of the quasispecies model, systematic inference of fitness landscapes has become possible (Seifert et al., 2015), for cancer similar attempts are so far limited to small-scale studies, such as estimating the fitness effects of single mutations (e.g. BCR-ABL in chronic myeloid leukemia) (Traulsen et al., 2010). Therefore, for quantifying evolutionary predictability of cancer, it is necessary to define an alternative framework, which operates independently of fitness landscapes, and is based solely on cross-sectional mutational patterns, which are abundant.
Here, we assess whether cancer progression models, such as conjunctive Bayesian network (CBN) (Beerenwinkel and Sullivant, 2009; Gerstung et al., 2009), CAncer PRogression Inference (CAPRI) (Ramazzotti et al., 2015) or Oncogenetic Tree (OT) (Szabo and Boucher, 2008), which are probabilistic graphical models used for describing the constraints in the ordering of mutation accumulation events, can be used to quantify the predictability of cancer evolution. Among cancer progression models, CBNs are particularly appropriate for this purpose, because they allow for inferring both elements of predictability directly from mutational data, namely (i) the constraints on evolutionary trajectories encoded in the inferred network structure and (ii) the distribution of pathway probabilities derived from the local probability distributions of the CBN model (Beerenwinkel and Sullivant, 2009). Therefore, we employ CBNs in this study for estimating mutational pathway probabilities.
In order to systematically assess the validity of the CBN model for quantifying the predictability of cancer evolution, it is essential to establish that the CBN-based constraints on the ordering of mutations approximate well those based on the underlying fitness landscape and the SSWM assumption (Fig. 1). Leveraging the simulated data of previous work (Diaz-Uriarte, 2018), which has made a connection between CBNs and fitness landscapes, here we quantify the predictability of cancer progression (i) based on fitness landscapes under the SSWM assumption (as the ground truth) and (ii) by applying the CBN model directly to simulated genotypes (our novel CBN-based framework). We show that the collections of feasible evolutionary pathways derived by the two approaches correlate strongly, implying that CBNs can be used to approximate the SSWM- and fitness landscape-based notion of evolutionary predictability, thus offering an alternative way to quantify the predictability of cancer progression that does not require any knowledge of the fitness landscape. Using our robust and scalable CBN-based framework, we systematically compare the predictability of up to 15 different cancer types using TCGA (Cancer Genome Atlas Research Network et al., 2013) and MSK-IMPACT (Zehir et al., 2017) data.
2 Materials and methods
2.1 Conjunctive Bayesian networks
CBNs are probabilistic graphical models that describe constraints on the ordering of mutations, which occur during mutation accumulation processes such as tumorigenesis (Beerenwinkel et al., 2007). A CBN is defined by a set of n mutational events and a partial order ‘’ on . For , we write if and . We represent the partially ordered set, or poset, by its Hasse diagram, the directed acyclic graph (DAG) with vertices and edges (i, j) for all relations , such that no exists with (Fig. 1, bottom). The genotype lattice is the set of all genotypes compatible with the partial order on (Beerenwinkel et al., 2006). It is defined as the set of order ideals, i.e. the subsets for which and implies . We identify a genotype with the binary string indicating the occurrences of all mutations in g, e.g. for n = 5, corresponds to 01101. The genotype lattice is represented by the DAG with vertices and edges for all with (Fig. 1, top). It defines the state space of the evolutionary process and is a subset of the genotype universe, the n-dimensional hypercube .
In continuous-time CBNs (CT-CBNs), the waiting time for mutation to occur is the random variable Ti, defined recursively as
| (1) |
where denotes the set of parents of i in the Hasse diagram and are independent exponentially distributed random variables with rates (Beerenwinkel and Sullivant, 2009). Equation (1) reflects the order constraints of : mutation i can occur only after all parent mutations have occurred. The occurrence times of mutations are unknown and instead genotypes G are observed after a certain random sampling time . Mutation i is then observed if Ti < Ts. The CT-CBN model is the model for G defined as the marginalization with respect to the waiting times T1, …, Tn, Ts. The hidden CBN (H-CBN) extends the CT-CBN by additionally allowing observation errors with probability ε independently for each mutation, such that the true genotypes become hidden random variables.
We performed maximum likelihood inference of the poset structure and the parameters λ and ε of the H-CBN based on simulated annealing and expectation maximization as described previously (Gerstung et al., 2009). For simulated annealing, we used temperature T = 1, and as initial poset the DAG inferred for the CT-CBN model with fixed error rate of 0.05 (Beerenwinkel and Sullivant, 2009). We varied the number of simulated annealing steps depending on the number (n) of mutations (i.e. for , 100 steps, for n = 5, 1000 steps and for , 10 000 steps).
2.2 Mutational pathways
A mutational pathway in of length n is a permutation , such that mutation π1 occurs first, π2 second, etc. Equivalently, the mutational pathway π is given by the ordered list of n + 1 genotypes , where , i.e. the genotypes successively accumulating the mutations in π. For a poset with genotype lattice , the mutational pathways in are exactly the linear extensions of the poset, i.e. the total mutation orders that respect the partial order. For example, in Figure 1b, defines a mutational pathway compatible with the order constraints. It is equivalently represented by the ordered genotypes (0000, 0100, 1100, 1101, 1111).
Let Π be a collection of mutational pathways in U. The exit set of a genotype g is the set of all genotypes that can be reached from g by acquiring one additional mutation along any of the pathways in Π,
| (2) |
For example, the CBN model in Figure 1b defines the mutational pathways and . Each mutational pathway, at each step, realizes exactly one of the options recorded in the exit set.
Let P(π) be a probability distribution over a set of mutational pathways Π. As in Szendro et al. (2013), its entropy is
| (3) |
We define the predictability of an evolutionary process described by the pathway distribution as
| (4) |
where the maximal entropy is attained when all pathways have the same probability. We have with indicating no predictability (all mutational pathways have the same probability) and ϕΠ = 1 indicating maximal predictability (one pathway is taken with probability 1).
2.3 Evolutionary predictability in the fitness landscape-based SSWM model
A fitness landscape is a mapping that assigns to each genotype g its fitness wg. For a mutational pathway π, we define the selective coefficient of mutation πi as the fitness difference
| (5) |
that it causes along the mutational pathway.
In the SSWM regime (Gillespie, 1983; Orr, 2005), mutations are fixed sequentially in a population, resulting in a multi-step evolutionary process along mutational pathways. The probability of a mutational pathway is the product of the fixation probabilities of mutations in each of the n steps, where the fixation probability of each beneficial mutation is proportional to its selective coefficient (Kimura, 1962). Under the SSWM assumption, a mutational pathway is accessible if the fitness of its genotypes is monotonically increasing along the pathway.
Thus, we define the set of all accessible pathways as
| (6) |
With , the probability of a mutational pathway is
| (7) |
if and zero otherwise (Weinreich et al., 2006), where C is the normalizing constant defined as follows:
| (8) |
The evolutionary predictability in the fitness landscape-based SSWM model is then (Equations (4) and (3)), with P(π) given by Equation (7).
2.4 Evolutionary predictability in the CBN model
We now derive another notion of evolutionary predictability that does not require a fitness landscape, but is based only on genotype data. We assume that a CBN model with genotype lattice and waiting time parameters λ has been learned from genotype data (Section 2.1).
The feasible mutational pathways in are the linear extensions of the poset,
| (9) |
To compute the probability of a pathway π, we consider the waiting time process (Equation (1)). At each step i, all possible one-step extensions of g(π)i are recorded in its exit set. Thus, the pathway probability is given by the product of competing exponentials,
| (10) |
if and zero otherwise. For each step i, has cardinality 1 and consists of the possible additional mutation. We have used the abbreviation . Note that the above equation does not need to be normalized, because the following equality always holds:
| (11) |
The evolutionary predictability in the CBN model is (Equation (4)). The above procedure, however, requires modification to be widely applicable: for large numbers n of mutations it becomes increasingly difficult to estimate the CBN model both statistically and computationally. Although the uncertainty in the genotype lattice may be high in this situation, this need not necessarily be the case for the evolutionary predictability. For large n, we fix a smaller number , such that CBN learning is feasible on mutations, and approximate the evolutionary predictability by averaging over all subsets of mutations of size ,
| (12) |
2.5 Simulated data
We leveraged the simulated data of a previous study (Diaz-Uriarte, 2018) both for generating random fitness landscapes and for producing genotypes from evolutionary simulations.
For the fitness landscape-based approach (Section 2.3), we used 100 representable and 111 non-representable fitness landscapes, where a landscape is called representable if its support is the genotype lattice of a CBN. Both types of fitness landscapes are derived from an initial DAG of restrictions, and the genotypes are binary vectors of length 7, defined based on the presence or absence of beneficial mutations in seven genes, resulting in 128 distinct genotypes. The fitness to each genotype is assigned based on the restrictions imposed by the DAG and the fitness effects of each individual mutation. If a genotype is not accessible according to the given DAG, its fitness will be zero; otherwise its fitness will be determined based on the set of mutations it contains. In any given fitness landscape, the fitness of the wild-type genotype is 1 and the fitness of accessible genotypes with a single mutation is 1 + s, where s is the fitness effect of the mutation and is chosen from a uniform distribution between 0.1 and 0.7. More generally, the fitness of accessible genotypes with multiple mutations is , where si is the fitness effect (i.e. selection coefficient) of the ith mutation and j is the total number of mutated genes in the given genotype. This way of fitness assignment, which is implemented in the representable fitness landscapes, ensures that there will be no reciprocal sign epistasis in the landscape. To introduce reciprocal sign epistasis, in the second type of fitness landscapes (non-representable ones), synthetic lethals or holes are introduced into the landscape by assigning a randomly chosen subset of (accessible) genotypes with two or more mutations to 0.2, which makes the accessibility of the chosen genotypes very unlikely. Using this approach, in the previous study 100 representable and 200 non-representable fitness landscapes has been constructed (Diaz-Uriarte, 2018). Because our analyses are based on the SSWM assumption, and we assume cancer progression as a mutational pathway from the wild-type genotype towards the fully mutated one, we required the fitness landscapes to assign the highest fitness to the fully mutated genotype (as the sole global peak). Moreover, we required that the genotype with the highest fitness to be connected to the wild-type genotype by at least one accessible mutational pathway. All 100 representable and 111 out of the 200 non-representable fitness landscapes fulfilled these requirements, so we used them in this study. Note that in the non-representable fitness landscapes, the fully mutated genotype is the genotype with highest fitness, but it is still possible to see multiple local fitness peaks, which accounts for the ruggedness of the fitness landscape.
Moreover, in the previous study (Diaz-Uriarte, 2018) based on an evolutionary model (McFarland et al., 2013) implemented in the OncoSimulR package (Diaz-Uriarte, 2017), from each fitness landscape, under different mutation rates (high: 10–5 and low: 10–6) and detection regimes (slow and fast), 20 000 genotypes were generated (Diaz-Uriarte, 2018), which we used for our CBN-based predictability estimation (Section 2.4 and Supplementary Text S1).
2.6 Real data
We used cancer genomic data from two distinct sources, referred to as TCGA and MSK-IMPACT, which were collected differently. Whereas TCGA includes samples from primary tumors of untreated patients (Cancer Genome Atlas Research Network et al., 2013), MSK-IMPACT is comprised of sequence data from patients with metastatic cancer under treatment at Memorial Sloan Kettering Cancer Center, 43% of which were obtained from metastatic sites, most commonly liver, lymph node and bone (Zehir et al., 2017). We gained access to these datasets through the cBioPortal platform (Gao et al., 2013).
We used 15 distinct cancer types in our analyses. The number of samples varies based on cancer type and data source from 186 to 836 in TCGA and from 93 to 1357 in MSK-IMPACT (Supplementary Table S1). We determined the genotype of each tumor using a given number of most frequently mutated driver genes (Supplementary Table S2) predicted by Mutsig2CV v3.1, which is a significantly mutated gene-based method that adjusts for known covariates of mutation rates (Lawrence et al., 2013). We exclusively focused on 15 cancer types that are (i) frequent enough in both datasets and (ii) are included in the Broad Institute TCGA GDAC Firehose (http://gdac.broadinstitute.org/), where we obtained the driver gene information.
3 Results
3.1 Evolutionary predictability: fitness landscape-based SSWM model versus CBN-based model
We first compared the predictability of evolution as quantified either by a fitness landscape w using the SSWM assumption or by a CBN model learned from genotype data collected during evolution on the landscape w. That is, we asked whether . We used four different simulation conditions (two different mutation rates and two different detection regimes), in 100 representable and 111 non-representable fitness landscapes. For each fitness landscape and each condition, we computed ϕw and learned a CBN model from 20 000 simulated genotypes to compute . Each genotype is a binary vector of length seven indicating the occurrence of seven different mutations (see Section 2 for more details).
We found a strong correlation between and ϕw in both types of fitness landscapes under low mutation rate and slow detection regime (Fig. 2; Pearson’s R=0.92, P < 10–43 in representable fitness landscapes and R = 0.86, P < 10–33 in non-representable ones). Thus, the congruence between the two methods is not limited to representable fitness landscapes, but it also holds for non-representable ones, where pervasive reciprocal sign epistasis causes the fitness landscape to be rugged. However, under high mutation rates (10–5) or fast detection regimes, where the SSWM assumption is only weakly respected, starts to deviate from ϕw (Supplementary Fig. S1).
Fig. 2.
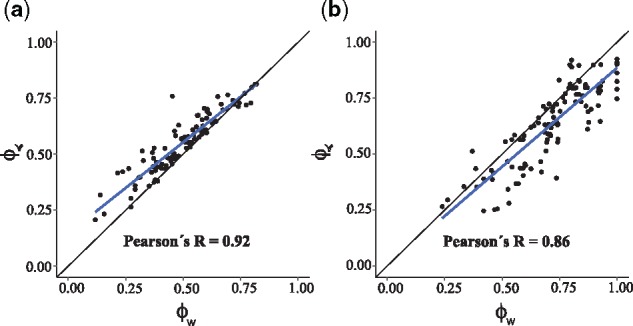
Strong correlation between CBN-based and fitness landscape-based quantification of evolutionary predictability. Panels (a) and (b), respectively, correspond to representable and non-representable fitness landscapes. Each point corresponds to a fitness landscape. The black lines are the identity lines, and the blue lines are the linear regression models surrounded by a shaded confidence interval region. The used genotypes are the outcomes of evolutionary simulations with slow detection and low mutation rate
Next, we compared the pathway probability distributions as estimated from the CBN, (Equation (10)), to those computed from the fitness landscape directly under the SSWM assumption, (Equation (7)). Figure 3 shows that the Jensen–Shannon divergence between the two distributions is smaller than 0.25 for most fitness landscapes (with median 0.045 in representable and 0.146 in non-representable ones), which is strikingly smaller than that of the baseline comparisons to the empty CBN, which assumes independence of mutations (with median 0.318 in representable and 0.432 in non-representable ones) and to the uniform distribution of pathways (with median 0.433 in representable and 0.487 in non-representable ones). These observations highlight the importance of the inferred DAG of restrictions by the CBN model. We also found that departure from the SSWM assumption, e.g. in simulation conditions with fast detection and high mutation rates, increases the divergence between the two distributions (Supplementary Fig. S2). Additional analyses using different metrics further confirmed the similarity between the two approaches (Supplementary Text S2 and Figs S3–S7). Thus, under the SSWM assumption, the CBN-based approach reliably quantifies the predictability of evolution directly from genotypic data alone.
Fig. 3.
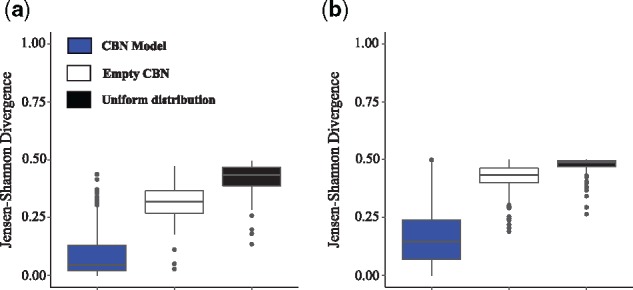
Similarity of the CBN model-based and fitness landscape-based pathway probability distributions. Displayed is the Jensen–Shannon divergence (where a value of 0 denotes the distributions are identical and a value of 1 that distributions do not overlap) between the pathway probability distributions of the fitness landscape approach, P(πw) (Equation (7)), and that of the CBN-based approach, (Equation (10)), (blue boxes), the empty CBN model (white boxes) and the uniform pathway probability distribution (black boxes) in (a) 100 representable and (b) 111 non-representable fitness landscapes in the slow detection and low mutation rate condition. Boxes span the two middle quartiles, and whiskers indicate maxima and minima
3.2 Scalability and robustness
In order to apply our framework to real cancer genomics data, we next explore the scalability and robustness of estimating . In our simulations, we had fixed number of genes to n = 7, which resulted in 27 = 128 possible genotypes and 7! = 5040 mutational pathways. However, the number of driver genes, which are frequently mutated among cancer patients can reach up to 20 resulting in more than a million genotypes and 1018 distinct mutational pathways, which renders the quantification of unfeasible. Moreover, in our simulations, we had a large sample size of N = 20 000 genotypes, which could mask the potential variability in the estimation of , as current real datasets are often on the order of 100 to 1000 genotypes. Since the structure learning of CBNs relies on simulated annealing, by increasing the number of genes, n, the search space grows exponentially in n, which can lead to increased variability in the estimation of . We confirmed this by a bootstrap analysis (see Supplementary Text S3 and Fig. S8).
To address the challenges of both scalability and robustness, we consider the approximation of in Equation (12) obtained from averaging over all mutation subsets of fixed size . The idea is to choose such that CBN inference becomes reliable for the given amount of data. Rather than trying to assemble the subnetworks into a global model, a common strategy in network inference, we aggregate on the level of predictability motivated by the multiplicative structure of the pathway probabilities (Equation (10)).
If all consecutive waiting time rates λi differ by the same factor, i.e. is constant for all i, then the approximation (Equation (12)) is almost exactly the same as (Supplementary Text S4 and Figs S9 and S10). This approximation is indeed also valid for the simulated data to a great extent (Supplementary Text S5 and Fig. S11). Moreover, in real data including 15 cancer types from TCGA and MSK-IMPACT, where the sample size is substantially smaller than in the simulated data, this approximation still holds strongly (Supplementary Text S6 and Figs S12 and S13). Based on a bootstrap analysis of the real data, we showed that the approximate formula considerably reduces the variability of the estimated predictability (Supplementary Text S7 and Fig. S14), and thus it facilitates not only a scalable but also a robust quantification of predictability.
3.3 Cancer progression is remarkably predictable
We employed our framework of evolutionary predictability and used Equation (12) to estimate from two real cancer genomics datasets, namely TCGA and MSK-IMPACT (Section 2.6), in order to address our central question on the predictability of cancer evolution and to systematically compare its extent in different cancer types.
As is robust w.r.t. (Supplementary Fig. S13), we kept it constant at , but systematically varied n from 4 to 20 to assess how varies as a function of the number of (predicted) driver genes in different cancer types. We observed that although from n = 4 to n = 10, different cancer types show different trends, from n = 10 upwards, levels off and remains almost constant in all cancer types and datasets (Supplementary Fig. S15). Indeed, the absolute difference between of consecutive n, , for , becomes negligible in both datasets (Supplementary Fig. S16). Moreover, based on a leave-one-out sensitivity analysis, we found that for n = 10, is robust to removal of any driver gene (Supplementary Text S8 and Fig. S17), such that undetected drivers are unlikely to confound the analysis. We fixed n = 10 for all subsequent analyses.
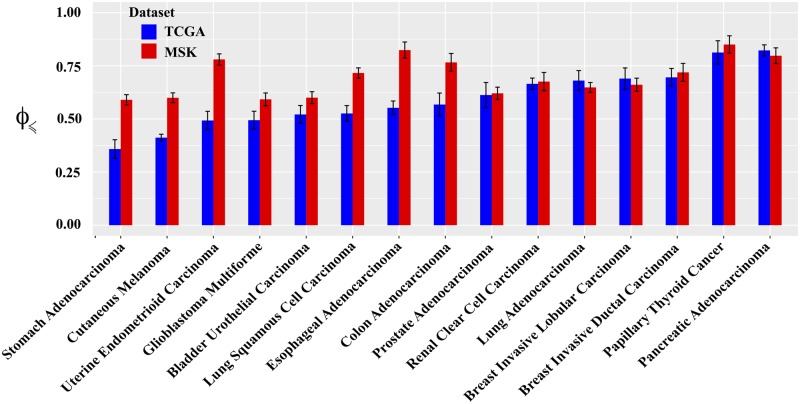
Comparing across cancer types in TCGA, we found that predictability of cancer evolution is generally high, but varies considerably, from 0.36 in stomach adenocarcinoma to 0.82 in pancreatic adenocarcinoma (Fig. 4). To further illustrate the extent of predictability and its diversity across cancer types, we use the fact that is approximately proportional, on a logarithmic scale, to the fraction α of feasible, i.e. non-zero probability, pathways (Supplementary Text S9 and Fig. S18). Indeed, only a tiny fraction of mutational pathways is feasible. Even in the least predictable cancer type with , only of the pathways are accessible, while for pancreatic adenocarcinoma, , which is 1000 times smaller than for stomach adenocarcinoma. Furthermore, we observe that for the MSK-IMPACT data, which was collected from patients with metastatic tumors, is on average higher than for TCGA (P=0.032, Mann–Whitney U test). Whereas in seven cancer types, is almost the same in both MSK-IMPACT and TCGA datasets, for eight other cancer types, particularly for cancer types with lower in the TCGA data, the evolutionary predictability is substantially higher in MSK-IMPACT as compared to TCGA (Fig. 4).
Fig. 4.
Comparison of evolutionary predictability among different cancer types. The vertical axis shows the CBN-based predictability , computed based on Equation (12) for each given cancer type. The error bars indicate the standard deviation of calculated from 100 bootstrap samples of equal size as the original genotype data. The genotypes for each cancer type are defined based on the mutational data of the corresponding n=10 most frequently mutated driver genes from TCGA (blue bars) or MSK-IMPACT (red bars). The cancer types are arranged from left to right in ascending order of their quantified based on TCGA data
3.4 Predictability, mutation frequency and intra-tumor heterogeneity
Next, we compared the evolutionary predictability of cancer types with other observable evolutionary traces, namely mutational load and intra-tumor genetic heterogeneity. Both of these parameters indicate lack of predictability and hence are expected to correlate negatively with .
We found that evolutionary predictability of cancer types in TCGA is indeed significantly anti-correlated with the average mutation rate measured by analyzing >3000 samples (Fig. 5a) (Lawrence et al., 2013). Similarly, our analysis revealed a significant negative correlation between predictability and intra-tumor heterogeneity based on a recent comprehensive pan-cancer inference of intra-tumor genetic heterogeneity (Raynaud et al., 2018) (Fig. 5b). The results of this study further corroborated our expectation that the average number of clonal and sub-clonal mutations is significantly anti-correlated with the corresponding measure of evolutionary predictability (Fig. 5c and d). These negative correlations, albeit to a lesser extent, are also observed for MSK-IMPACT (Supplementary Fig. S19).
Fig. 5.
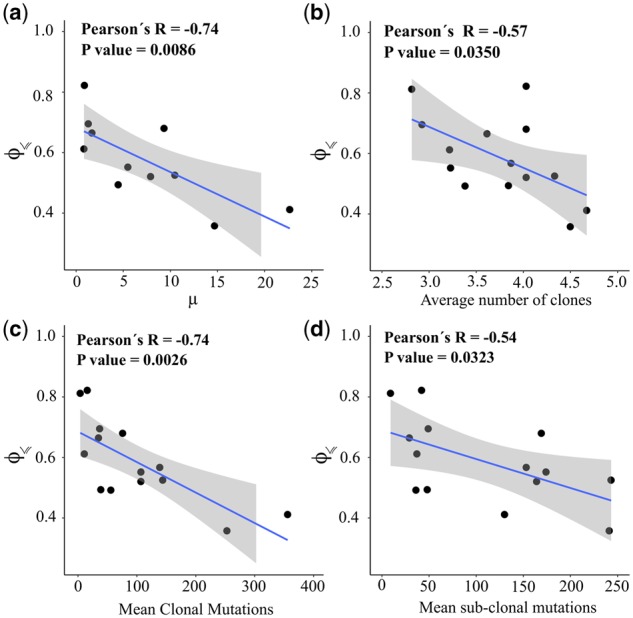
Predictability, mutation rate and intra-tumor heterogeneity. In all panels, each point corresponds to a given cancer type and the vertical axis indicates the estimated predictability . The horizontal axis shows (a) the average mutation frequency per mega base-pairs [from Lawrence et al. (2013)], (b) the average number of clones per tumor, (c) the mean number of clonal mutations and (d) the mean number of sub-clonal mutations according to Raynaud et al. (2018). The blue lines are the linear regression models surrounded by a shaded confidence interval region. Evolutionary predictability is approximated using Equation (12), with n=10 and for the TCGA data. Note that in panel (a) only 11 cancer types are included in this analysis, because Lawrence et al. (2013) covered only 11 of the 15 cancer types
4 Discussion
In this study, we have established a statistical framework based on CBNs to rigorously quantify the predictability of cancer progression directly from cross-sectional genomic data. In particular, our approach does not require measuring or estimating the fitness effects of mutations, which is common practice in evolutionary biology, where the dominating paradigm for studying the predictability of evolution relies on the concept of fitness landscapes.
We systematically analyzed the validity of our approach by leveraging the simulated data of a previous study (Diaz-Uriarte, 2018), which has made a connection between CBNs and fitness landscapes. We have shown that CBN-based approach strongly agrees with the fitness landscape approach under the SSWM model in estimating the evolutionary predictability, not only in representable but also in non-representable fitness landscapes, which are deliberately designed to be rugged by having an elevated level of reciprocal sign epistasis and hence are not consistent with the DAG assumption of CBNs.
Our results revealed that CBN models, by inferring a maximum likelihood DAG of restrictions, are able to identify similar collections of feasible evolutionary trajectories as the SSWM-based model, although with a tendency of CBN models to allow more evolutionary pathways than the SSWM-based model (Supplementary Text S2). Our comparison of the maximum likelihood CBN model with the empty CBN, in which mutations are assumed to occur independently, further highlighted the fact that the power of the CBN model lies in its ability to capture dependencies among mutations in the inferred DAG, rather than only their marginal frequencies. In fact, a pure frequency-based method (i.e. the empty CBN) distinguishes between mutational pathways almost as poorly as the uniform pathway distribution (Fig. 3) and therefore considerably underestimates the predictability of cancer evolution (Supplementary Text S10 and Fig. S20). Furthermore, it is important to note that CBNs estimate the joint probability distribution of all genes, including more complex forms of epistasis. Hence, higher order epistasis, which is beyond pairwise epistasis, is captured by the CBN model and implicitly taken into account the final estimate of the predictability of cancer evolution.
That being said, we acknowledge that the validity of our approach depends on the accuracy of the SSWM assumption. We do not know to what extent the SSWM assumption is valid for cancer evolution, as we cannot measure the in vivo fitness effect of mutations, but departure from the SSWM assumption might be conceivable at least for hyper-mutated tumors with elevated chromosomal instability. Nevertheless, the SSWM assumption with all its potential pitfalls is broadly applied in studying the predictability of evolution in general (de Visser and Krug, 2014; Weinreich et al., 2005) and it is well-supported by experimental evidence (Poelwijk et al., 2007; Weinreich et al., 2006).
In order to address scalability and robustness of our framework for analyzing high-dimensional real genomic data, we developed a subsetting scheme (Equation (12)), which aggregates the results of smaller mutation subsets. We have shown that this approximation works well for both simulated and real data. It enabled us to cope with the high-dimensionality of the data and ensured robust estimation of the predictability (see Supplementary Text S7 and Fig. S14) by drastically reducing the network space in the structure learning step of the CBN model. In other words, while evolutionary constraints may be difficult to learn (Diaz-Uriarte, 2018), this does not necessarily imply that predictability cannot be estimated reliably (which is a simpler task addressed and well approximated by the subsetting scheme). The robust estimation conferred by our subsetting scheme partly explains the different conclusion of our study as compared to the previous one (Diaz-Uriarte and Vasallo, 2018), which reports that cancer evolution can be unpredictable for many datasets. In addition, the former study uses the ‘Lines of Descent’ (Szendro et al., 2013), instead of the SSWM assumption employed here, such that different evolutionary regimes are analyzed.
We observed that cancer evolution is remarkably constrained, as only a tiny fraction of mutational pathways (between 0.4% and 0.0004% depending on cancer type in TCGA data for n=10 driver mutations) are feasible during the process of tumorigenesis. Furthermore, the analysis of the MSK-IMPACT dataset showed that tumor samples from metastatic sites display an even higher level of predictability, perhaps because in metastatic samples longer tumorigenic pathways have already been traversed or the evolution of metastatic potential is more convergent. This high level of constrained evolution can open a new avenue for further analysis of the feasible mutational pathways towards predictive modeling of cancer progression and calls for further research in the direction of pan-cancer identification of repeatable evolutionary trajectories (Caravagna et al., 2018).
Proving the usability of our framework for the ambitious goal of predictive modeling of cancer progression, however, would necessitate a rigorous benchmarking with longitudinal data, single-cell or multi-region samples, which is beyond the scope of our current study and calls for future research. However, our present work is still well-supported by empirical data. In line with our expectations, we have observed significant anti-correlation between estimated predictability of cancer types and alternative observable evolutionary traces such as mutational load and intra-tumor heterogeneity.
A major limitation of our present study is that mutations used in the CBN model have been restricted to single nucleotide variants and incorporating copy number variations (CNVs) into our framework still remains as an unmet challenge. The reason is that the CBN model estimates the co-occurrence of mutations, but for CNVs, a more sophisticated model is necessary, which accounts for CNVs of varying sizes affecting simultaneously different sets of physically proximate genes. Thus, integration of CNV data in our framework for future applications requires the CBN model to be adapted for such physically correlated mutations.
Moreover, it is important to note that our analyses of the real genomic data are based exclusively on frequent driver genes, which probably provide a strong selective advantage, and we have not taken into account rare drivers, which likely provide only a small selective advantage. Including weak drivers may or may not affect the predictability of cancer evolution, depending on how strong they depend on other mutations. In future work, the impact of weak drivers on the predictability of cancer evolution should be further explored.
Furthermore, in our study, genotypes were defined exclusively on the level of ‘genes’. It is potentially interesting to estimate the predictability of cancer evolution alternatively on a higher level (e.g. on the level of ‘functional pathways’). A previous study (Gerstung et al., 2011) has found stronger evidence for pathway order constraints than for gene order constraints, which indicates that temporal ordering results from selective pressure acting on the pathway level. Therefore, if we estimate predictability of cancer evolution on the level of functional pathways, rather than genes, it is very likely that the predictability of cancer evolution is even higher on the pathway level. Also, a model has been presented for estimating groups of mutually exclusive genes and their dependency structure at the same time (Cristea et al., 2017). Using this version of a CBN model, one might arrive at pathway-level estimates of the predictability of evolution. We will explore this approach in future work.
On the other hand, we might need to define genotypes on a lower level, e.g. on the level of individual mutations, because different non-silent mutations in a given gene can exert different phenotypic effects. Some mutations in a driver gene may not be driver mutations and some genes may harbor both loss and gain of function mutations. Therefore, another open question, which calls for further research, is how genotypes defined on the level of driver mutations rather than driver genes affects the predictability of cancer evolution.
In summary, the key insight of our analyses of real genomic data on the level of driver genes is that cancer evolution is remarkably predictable, and hence there is high potential for systematic discovery of phenotype-determining repeatable evolutionary trajectories, which are of increasing importance in personalized medicine. Whether the relatively high level of predictability we found is driven mostly by known gene–gene interactions or whether many novel interactions contribute to it remains to be analyzed in future studies that likely require larger sample sizes.
Supplementary Material
Acknowledgement
S.R.H. would like to thank Lisa Lamberti and Sumana Srivatsa for helpful discussions.
Funding
Part of this work was supported by the ERC Synergy grant 609883 (http://erc.europa.eu/) and by SystemsX.ch RTD grant 2013/150 (http://www.systemsx.ch/). R.D.U. partially supported by the Spanish Ministry of Economy, MINECO/FEDER grant BFU2015-67302-R (MINECO/FEDER, EU). This work was further supported by BBSRC grant BB/R006563/1 and Cancer Research UK grant C14303/A17197.
Conflict of Interest: none declared.
References
- Achaz G. (2014) The reproducibility of adaptation in the light of experimental evolution with whole genome sequencing. Adv. Exp. Med. Biol., 781, 211–231. [DOI] [PubMed] [Google Scholar]
- Bagcchi S. (2015) Gene mutation order affects cancer behaviour. Lancet Oncol., 16, e112.. [DOI] [PubMed] [Google Scholar]
- Barton J.P. et al. (2016) Relative rate and location of intra-host HIV evolution to evade cellular immunity are predictable. Nat. Commun., 7, 11660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beerenwinkel N., Sullivant S. (2009) Markov models for accumulating mutations. Biometrika, 96, 645–661. [Google Scholar]
- Beerenwinkel N. et al. (2006) Evolution on distributive lattices. J. Theor. Biol., 242, 409–420. [DOI] [PubMed] [Google Scholar]
- Beerenwinkel N. et al. (2007) Conjunctive Bayesian networks. Bernoulli, 13, 893–909. [Google Scholar]
- Beerenwinkel N. et al. (2016) Computational cancer biology: an evolutionary perspective. PLoS Comput. Biol., 12, e1004717.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blount Z.D. et al. (2018) Contingency and determinism in evolution: replaying life’s tape. Science, 362, eaam5979.. [DOI] [PubMed] [Google Scholar]
- Bull J.J., Molineux I.J. (2008) Predicting evolution from genomics: experimental evolution of bacteriophage T7. Heredity, 100, 453–463. [DOI] [PubMed] [Google Scholar]
- Burrell R.A. et al. (2013) The causes and consequences of genetic heterogeneity in cancer evolution. Nature, 501, 338–345. [DOI] [PubMed] [Google Scholar]
- Cancer Genome Atlas Research Network et al. (2013) The Cancer Genome Atlas Pan-Cancer analysis project. Nat. Genet., 45, 1113–1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caravagna G. et al. (2018) Detecting repeated cancer evolution from multi-region tumor sequencing data. Nat. Methods, 15, 707–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowperthwaite M.C. et al. (2008) The ascent of the abundant: how mutational networks constrain evolution. PLoS Comput. Biol., 4, e1000110.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cristea S. et al. (2017) pathTiMEx: joint inference of mutually exclusive cancer pathways and their progression dynamics. J. Comput. Biol., 24, 603–615. [DOI] [PubMed] [Google Scholar]
- de Visser J.A.G., Krug J. (2014) Empirical fitness landscapes and the predictability of evolution. Nat. Rev. Genet., 15, 480–490. [DOI] [PubMed] [Google Scholar]
- Diaz-Uriarte R. (2017) OncoSimulR: genetic simulation with arbitrary epistasis and mutator genes in asexual populations. Bioinformatics, 33, 1898–1899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diaz-Uriarte R. (2018) Cancer progression models and fitness landscapes: a many-to-many relationship. Bioinformatics, 34, 836–844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diaz-Uriarte R., Vasallo C. (2018). Every which way? On predicting tumor evolution using cancer progression models. bioRxiv, 371039. [DOI] [PMC free article] [PubMed]
- Ferretti L. et al. (2018) Evolutionary constraints in fitness landscapes. Heredity, 1121, 466–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer A. et al. (2015) The value of monitoring to control evolving populations. Proc. Natl. Acad. Sci. USA, 112, 1007–1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher R. et al. (2014) Development of synchronous VHL syndrome tumors reveals contingencies and constraints to tumor evolution. Genome Biol., 15, 433.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao J. et al. (2013) Integrative analysis of complex cancer genomics and clinical profiles using the cBioPortal. Sci. Signal., 6, pl1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstung M. et al. (2009) Quantifying cancer progression with conjunctive Bayesian networks. Bioinformatics, 25, 2809–2815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstung M. et al. (2011) The temporal order of genetic and pathway alterations in tumorigenesis. PLoS One, 6, e27136.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie J.H. (1983) A simple stochastic gene substitution model. Theor. Pop. Biol., 23, 202–215. [DOI] [PubMed] [Google Scholar]
- Gould S.J. (1990). Wonderful Life: The Burgess Shale and the Nature of History. W. W. Norton & Company, NY. [Google Scholar]
- Hosseini S.-R., Wagner A. (2017) Constraint and contingency pervade the emergence of novel phenotypes in complex metabolic systems. Biophys. J., 113, 690–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent D.G., Green A.R. (2017) Order matters: the order of somatic mutations influences cancer evolution. Cold Spring Harb. Perspect. Med., 7, a027060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M. (1962) On the probability of fixation of mutant genes in a population. Genetics, 47, 713–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lässig M. et al. (2017) Predicting evolution. Nat. Ecol. Evol., 1, 77. [DOI] [PubMed] [Google Scholar]
- Lawrence M.S. et al. (2013) Mutational heterogeneity in cancer and the search for new cancer-associated genes. Nature, 499, 214–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman T.D. et al. (2011) Parallel bacterial evolution within multiple patients identifies candidate pathogenicity genes. Nat. Genet., 43, 1275–1280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linnen C.R. (2018) Predicting evolutionary predictability. Mol. Ecol., 27, 2647–2650. [DOI] [PubMed] [Google Scholar]
- Lipinski K.A. et al. (2016) Cancer evolution and the limits of predictability in precision cancer medicine. Trends Cancer, 2, 49–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lobkovsky A.E., Koonin E.V. (2012) Replaying the tape of life: quantification of the predictability of evolution. Front. Genet., 3, 246.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luksza M., Lässig M. (2014) A predictive fitness model for influenza. Nature, 507, 57–61. [DOI] [PubMed] [Google Scholar]
- Martins F.C. et al. (2012) Evolutionary pathways in BRCA1-associated breast tumors. Cancer Disc., 2, 503–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marusyk A., Polyak K. (2010) Tumor heterogeneity: causes and consequences. Biochim. Biophys. Acta, 1805, 105–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McFarland C.D. et al. (2013) Impact of deleterious passenger mutations on cancer progression. Proc. Natl. Acad. Sci. USA, 110, 2910–2915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miles J.J. et al. (2011) Bias in the αβ T-cell repertoire: implications for disease pathogenesis and vaccination. Immunol. Cell Biol., 89, 375–387. [DOI] [PubMed] [Google Scholar]
- Neher R.A. et al. (2014) Predicting evolution from the shape of genealogical trees. eLife, 3, e03568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowell P.C. (1976) The clonal evolution of tumor cell populations. Science, 194, 23–28. [DOI] [PubMed] [Google Scholar]
- Nyerges k. et al. (2018) Directed evolution of multiple genomic loci allows the prediction of antibiotic resistance. Proc. Natl. Acad. Sci. USA, 115, E5726–E5735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orgogozo V. (2015) Replaying the tape of life in the twenty-first century. Interface Focus, 5, 20150057.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr H.A. (2005) The genetic theory of adaptation: a brief history. Nat. Rev. Genet., 6, 119–127. [DOI] [PubMed] [Google Scholar]
- Ortmann C.A. et al. (2015) Effect of mutation order on myeloproliferative neoplasms. N E J. Med., 372, 1865–1866. [DOI] [PubMed] [Google Scholar]
- Poelwijk F.J. et al. (2007) Empirical fitness landscapes reveal accessible evolutionary paths. Nature, 445, 383–386. [DOI] [PubMed] [Google Scholar]
- Ramazzotti D. et al. (2015) CAPRI: efficient inference of cancer progression models from cross-sectional data. Bioinformatics, 31, 3016–3026. [DOI] [PubMed] [Google Scholar]
- Raynaud F. et al. (2018) Pan-cancer inference of intra-tumor heterogeneity reveals associations with different forms of genomic instability. PLoS Genet., 14, e1007669.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salverda M.L.M. et al. (2011) Initial mutations direct alternative pathways of protein evolution. PLoS Genet., 7, e1001321.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seifert D. et al. (2015) A framework for inferring fitness landscapes of patient-derived viruses using quasispecies theory. Genetics, 199, 191–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szabo A., Boucher K. (2008). Oncogenetic trees In: Tan W.-Y., Hanin L. (eds.), Handbook of Cancer Models with Applications. World Scientific, Singapore. [Google Scholar]
- Szendro I.G. et al. (2013) Predictability of evolution depends nonmonotonically on population size. Proc. Natl. Acad. Sci. USA, 110, 571–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenaillon O. et al. (2012) The molecular diversity of adaptive convergence. Science, 335, 457–461. [DOI] [PubMed] [Google Scholar]
- Toprak E. et al. (2012) Evolutionary paths to antibiotic resistance under dynamically sustained drug selection. Nat. Genet., 44, 101–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traulsen A. et al. (2010) Reproductive fitness advantage of BCR-ABL expressing leukemia cells. Cancer Lett., 294, 43–48. [DOI] [PubMed] [Google Scholar]
- Vogelstein B. et al. (2013) Cancer genome landscapes. Science, 339, 1546–1558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinreich D.M. et al. (2005) Perspective: sign epistasis and genetic constraint on evolutionary trajectories. Int. J. Org. Evol., 59, 1165–1174. [PubMed] [Google Scholar]
- Weinreich D.M. et al. (2006) Darwinian evolution can follow only very few mutational paths to fitter proteins. Science, 312, 111–114. [DOI] [PubMed] [Google Scholar]
- Woods R. et al. (2006) Tests of parallel molecular evolution in a long-term experiment with Escherichia coli. Proc. Natl. Acad. Sci. USA, 103, 9107–9112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zehir A. et al. (2017) Mutational landscape of metastatic cancer revealed from prospective clinical sequencing of 10,000 patients. Nat. Med., 23, 703–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.