Robust network inference using response logic

Abstract

Motivation

A major challenge in molecular and cellular biology is to map out the regulatory networks of cells. As regulatory interactions can typically not be directly observed experimentally, various computational methods have been proposed to disentangling direct and indirect effects. Most of these rely on assumptions that are rarely met or cannot be adapted to a given context.

Results

We present a network inference method that is based on a simple response logic with minimal presumptions. It requires that we can experimentally observe whether or not some of the system’s components respond to perturbations of some other components, and then identifies the directed networks that most accurately account for the observed propagation of the signal. To cope with the intractable number of possible networks, we developed a logic programming approach that can infer networks of hundreds of nodes, while being robust to noisy, heterogeneous or missing data. This allows to directly integrate prior network knowledge and additional constraints such as sparsity. We systematically benchmark our method on KEGG pathways, and show that it outperforms existing approaches in DREAM3 and DREAM4 challenges. Applied to a novel perturbation dataset on PI3K and MAPK pathways in isogenic models of a colon cancer cell line, it generates plausible network hypotheses that explain distinct sensitivities toward various targeted inhibitors due to different PI3K mutants.

Availability and implementation

A Python/Answer Set Programming implementation can be accessed at github.com/GrossTor/response-logic. Data and analysis scripts are available at github.com/GrossTor/response-logic-projects.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Complex molecular networks control virtually all aspects of cellular physiology as they transduce signals and regulate the expression and activity of genes. Understanding those molecular networks requires an appropriate simplification of the stupefying complexity that we find in cells. A very successful and common abstraction in molecular cell biology is to define effective modules and map out their interactions (Ideker and Nussinov, 2017). But even though new experimental techniques can reveal and quantify countless cellular components in ever increasing level of detail, they typically cannot identify the relationships between them. This is why for more than two decades various methods were developed to infer gene regulatory networks, signalling pathways and genotype–phenotype maps (De Smet and Marchal, 2010). These methods vary widely in their notion of network (e.g. directed versus undirected, weighted versus unweighted links), their mathematical methodology (e.g. statistical measures versus model-based parameter fits) or their goals (e.g. interaction discovery versus network property characterization versus perturbation response prediction) (Basso et al., 2005; de la Fuente et al., 2004; Ghanbari et al., 2015; Kholodenko et al., 2002; Klamt et al., 2006; Molinelli et al., 2013; Natale et al., 2017). Not surprisingly, different methods produce radically different results on same datasets (Marbach et al., 2010; Meisig and Blüthgen, 2018). This makes for an intricate choice of method and guarantees a certain degree of arbitrariness in interpreting the inferred networks.

One major goal of network inference for signalling and regulatory networks is to derive directed networks, that is, to infer information about causal relations within the studied system. This differs profoundly from the inference of undirected associations between node pairs, such as by correlation, as it requires to trace the flow of information through the network. A popular approach is to use time-series data, for which methods like convergent cross mapping (Čenys et al., 1991; Sugihara et al., 2012) or Granger causality (Granger, 1969) can distinguish correlation from causation, given sufficiently dense samples. But most often, experimental protocols or excessive expenditures preclude the observation of suitable temporal trajectories for many contexts in molecular biology. Thus, a complementary approach is to observe the system’s responses, for instance the steady-state response, to a set of localized perturbations (Bruggeman et al., 2002; Sachs et al., 2005; Wagner, 2001a). Depending on the specific system, these perturbations could, for example, be gene knockouts or kinase inhibitions. However, existing methods for such data rely on context-specific assumptions whose validity is hard or impossible to assess in practice, which makes it very difficult to interpret their results. Facing this challenge, we asked whether we could derive a more generally applicable scheme for the inference of directed networks—a method that is based on a principle which is accurate enough for most contexts while also sufficiently simple to allow for an intuitive understanding of how the network structure was resolved. Furthermore, we noticed that even though most network inference problems are embedded within very well-studied contexts, the vast majority of reverse-engineering methods predicts networks de novo. Therefore, we additionally aimed for a method that could readily incorporate prior knowledge about presence or absence of certain links or about other known network properties. This resulted in what we call the response logic approach.

In the following, we describe the response logic approach in more detail and then benchmark it by (i) assessing the performance using synthetic data derived from KEGG pathways (Kanehisa et al., 2017), and (ii) comparing its performance to competing methods using community-wide inference challenges (Dialogue for Reverse Engineering Assessments and Methods, DREAM) (Stolovitzky et al., 2007). Finally, we use the approach to study RAS/MAPK/PI3K signalling in a colon cancer cell line, and predict differences in the signalling network topology due to different PI3K mutants, that manifests in differential sensitivity of a colon cancer cell to various targeted drugs.

2 Materials and Methods

We developed a method to infer directed network structures from perturbation data that we term response logic (see Fig. 1). As an input, this method requires binary information about which nodes in the network respond to which perturbation, together with a rank of confidence of each data point. We refer to this set of experimental observations as the response pattern. Given this information, the response logic approach infers networks that agree to the following simple rule: a perturbation at a node is propagated along all outgoing edges to the set of connected nodes, and these responding nodes will in turn propagate the signal and so forth. Consequently, a perturbation of a node causes a response at all nodes to which it is connected by a path, and no response at all others. The information about which node can be reached from which other nodes is known as the network’s transitive closure. Thus, the central assumption of our response logic approach is that experimentally observed responses are in agreement with the transitive closure. This assumption then leads to the inverse problem of identifying the networks whose transitive closure actually matches the response pattern.

Fig. 1.

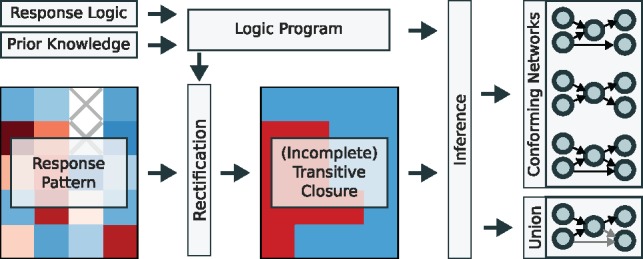
The steps of the response logic approach. The response logic and all additional prior network knowledge are formulated as a logic program. It is first used to rectify the experimentally determined response pattern, and second, takes the resulting (potentially incomplete) transitive closure as input to infer either all individual conforming networks or the union thereof

The algorithm to infer these networks consists of two main steps. Using a logic programming approach, it first modifies the experimental response pattern to match a transitive closure (rectification step) and then infers either all individual networks that comply to the given data or the union over all those conforming networks. We will describe the different steps in the following sections.

2.1 Rectifying the response pattern

The response logic approach interprets the measured response pattern as a noisy, incomplete transitive closure. But because of misclassification, a response pattern might not match any actual (incomplete) transitive closure. Consider for example a three-node network in which all nodes are observed to respond to a perturbation at node one. This implies two paths, from nodes one to two and nodes one to three. Therefore, if a perturbation at node two causes a response at node one, node three is expected to respond as well. But assume that this response at node three was not observed (misclassification). Then, there is no directed network with a transitive closure that would match this response pattern. We expect that such misclassification occurs rather often when working with experimental data because of experimental noise or because the system under consideration does not fully comply with the assumptions of the response logic. Thus, it is necessary to identify the most relevant subset of the response pattern that forms an (incomplete) transitive closure which can then be used to infer networks.

Our rectification algorithm requires to rank the observations of the response pattern from most to least confident. Typically, such confidence levels are readily available since the response pattern is often derived from a binarization of continuous experimental readouts, in which case a confidence score could be the distance to the binarization threshold, or a score of statistical significance. The algorithm then iterates the elements of the response pattern from high to low confidence, and at each step, determines whether the so far collected elements form a transitive closure and also conform with additional constraints from prior knowledge. This is done using a logic program (see below), which determines if there is any network that is compatible with these elements of a transitive closure. If the new element is compatible, it is added to the collection of conforming data and otherwise discarded. The more data points enter the collection the more restrictions apply to the remaining elements of the response pattern. As high confidence observations are taken into account first they are thus less likely to be discarded, ensuring that we extract the most relevant subset of the response pattern that indeed forms an incomplete transitive closure that is in line with additional constraints. If confidence levels of different data points cannot be easily distinguished, it is recommendable to repeat the response logic analysis for alternative rankings and inspect how this impacts the set of compatible networks.

Figure 2 demonstrates this scheme for a toy network of five nodes, for which we assume that four nodes were perturbed (indicated as flashes in Fig. 2A, top). The resulting response pattern then consists of a five-by-four matrix, and we assume that two data points are missing, and two elements of the response pattern do not match the transitive closure (compare heat maps in Fig. 2A). In Figure 2B, we exemplify how the response pattern is iteratively rectified. We assume that we know that a link from node two to node three exists and that there is no link between node one to node three (green stars). Given this prior knowledge, already the first (highest confidence) data point (yellow star in the leftmost panel) additionally implies that node three also responds to a perturbation of node one. Any subsequent data point that is in conflict with this information will be discarded. The middle panels of Figure 2B show that the five most trusted data points constrain five other elements of the rectified response pattern. Among them are the two misclassified, as well as the two missing data points. Therefore, in this toy example, the high confidence data points automatically correct these false or missing pieces of information. The bottom panel of Figure 2B shows how adding data points increasingly constrains the network structure. Once all data are considered, most of the links (but not all, as discussed later on) are known to be either present or absent from the network. Note, however, that the rectification process does not require to compute the shown union of conforming networks, but only requires to determine if for any network at all, all constraints are satisfiable, which is computationally far less expensive.

Fig. 2.

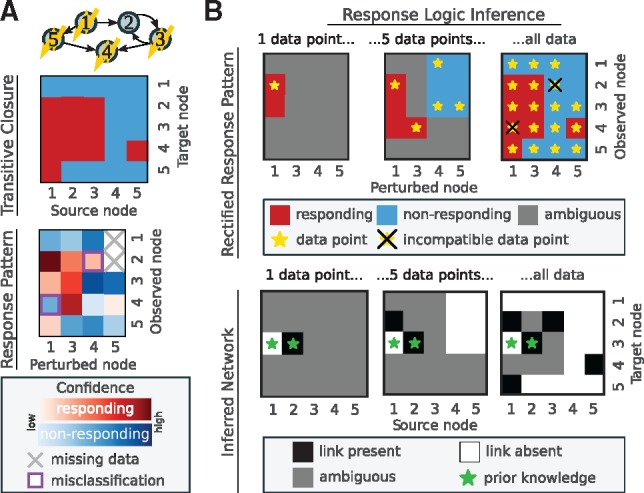
Response logic inference of a toy network. (A) From top to bottom: an example network of five nodes, where flashes indicate which nodes were perturbed; the full transitive closure; the response pattern that captures parts of the network’s transitive closure, with missing or misclassified data and confidence scores. (B) Three instants during data rectification: data points are added sequentially from high to low confidence (stars in top row), and increasingly constrain the inferred network and the (rectified) response pattern (red and blue fields in top row). Bottom row shows the inferred network at the given instant during rectification

2.2 Finding conforming networks with logic programming

Mapping the response pattern to its corresponding set of conforming networks is a substantial computational challenge, as there are $2^{N·N}$ possible directed networks (with N being the number of nodes), making it infeasible to enumerate all networks even for small sizes. We therefore solve the search problem with a logic programming approach, which is a form of declarative programming where the problem is represented via a set of logical rules. We chose to use the logic modelling language Answer Set Programming (ASP) (Baral, 2003), as implemented in the Potsdam Answer Set Solving Collection (Gebser et al., 2011). For ASP solving, we apply the clingo (Gebser et al., 2014) system.

ASPs generate-define-test pattern (Lifschitz, 2002) allows for a convenient encoding of the response logic, which is detailed in Supplementary Material S1. In short, we generate the collection of answer sets, consisting of all possible network structures, then define auxiliary predicates, in our case the networks’ transitive closure, and then test whether this transitive closure agrees with the data and also whether the tested network complies to all other heuristic constraints. Then the ASP solver, clingo, allows to enumerate all conforming networks. Note that the computational effort needed to identify a conforming network heavily depends on network size and the provided heuristic constraints. But overall, the logic programming approach infers networks of up to 100 nodes within seconds, without any parallelization.

The previously discussed data rectification sequentially checks the satisfiability of every data point and could therefore become a performance bottleneck for large systems. However, because this process only requires to decide whether any network at all is in agreement with the latest data, instead of having to provide the entire set of conforming networks, we can solve a much simpler logic program, which is detailed in Supplementary Material S1. It drastically improves performance because it does not require to define an answer set for each possible network structure.

2.3 Identifiability and heuristic constraints

While every directed network has a single transitive closure, a transitive closure can often be mapped to many different networks, even more so if the transitive closure is only partially known. Thus, we can usually not infer a unique directed network from a rectified response pattern alone. For example, any feedback loop creates a strongly connected network component, that is, a set of nodes for which any pair is connected by a path. Therefore the response pattern is independent on how exactly the nodes are connected to each other. Similarly, the response pattern does not change with any additional feed-forward loops that cuts short an existing path. To resolve such structures we need to resort to additional constraints that are derived from contextual knowledge about the studied system. A crucial advantage of the response logic approach is that it can easily integrate various kinds of such constraints. Here, we want to exemplify this and introduce those constraints that are used in the applications shown further below.

Rarely will we analyze networks that have never been studied before. Therefore one can use prior knowledge to constrain networks, such as by requiring the presence of well-established links in the network, or by excluding links that are physically not feasible (such as interactions between molecules located in different compartments). This information can directly be integrated into the logic program by defining the presence or absence of links as additional constraints. In addition, the logic program can also accommodate more subtle constraints, such as to enforce bounds on the numbers of incoming and outgoing edges of (groups of) nodes, see the implementation in Supplementary Material S1. This allows, for example, to encode the information that a module of nodes signals to other parts of the network without having to explicitly state which of the module’s nodes has the outward link. The same idea holds for a module that is known to receive at least one input to any subset of its components. Note that these types of constraints directly limit the space of possible networks and in turn that of the transitive closures. They will thus influence how the response pattern can be rectified and must be taken into consideration during the process.

But even these additional constraint might not sufficiently limit the number of conforming networks to consider them individually. Alternatively, an extension of the logic program, described in Supplementary Material S1, allows to efficiently find the union of all answer sets. This union reveals which links (or missing links) appear in all solutions and which are ambiguous. The latter is particularly informative to either guide the choice of additional perturbation experiments or to reveal effective strategies on how to further filter the set of solutions.

One widely used strategy in this regard is to require an overall sparse architecture (Wagner, 2001b). We would thus want to identify the conforming networks with the fewest links. However, naïvely parsing all network solutions will be infeasible when the set of solutions is large. To overcome this problem we developed an algorithm that sequentially removes as many ambiguous links as possible, without violating any constraint. To do so, after every link removal the pruned network is tested for satisfiability. If it complies to the given constraints, the link remains removed and the procedure continues. Otherwise the link is considered necessary and the procedure continues without the removal of the link. This leads to what will be referred to as the sparsified network. Yet, such scheme is only reasonable if the order by which links are removed, reflects to some extent a knowledge about which links are more likely to be absent in the underlying network, and should therefore be tested for removal first. However if such information is not available, one can use yet another approach to filter for sparse networks, termed the parsimony constraint. This constraint asks whether a link from a conforming network can be removed without it changing the network’s transitive closure. If that is the case, the network is considered non-sparse and is removed from the solution set. The specific encoding is found in Supplementary Material S1. While this procedure does not generally single out a unique solution as before (multiple networks can be parsimonious), it was nevertheless observed to drastically reduce the solution space.

Taken together, a response pattern will typically be compatible with a large number of network topologies, but various types of prior network information can be incorporated into the response logic approach to reveal a finer network structure than what would have been possible from the response pattern alone. At the same time, the approach states explicitly whether or not the presence or absence of a link can be inferred from the given data and constraints.

2.4 Implementation and data acquisition

The response logic approach is implemented in Python 3.6 as a package available at github.com/GrossTor/response-logic. Numerical computations, data handling and plotting was done using the SciPy libraries (Jones et al., 2001) and seaborn. Additional functions were taken from the networkx package (Hagberg et al., 2008). Clingo’s python API (version 5.2.2) (Gebser et al., 2014) is used to ground and solve the Answer Set Programs.

The repository contains all Answer Set Programs, which are accessed by the main response.py module. It includes the prepare_ASP_program function to set up a logic program according to the provided data and additional constraints, the conform_response_pattern function that rectifies the response pattern, as well as various functions to solve a logic program. Additionally, a projects repository available at github.com/GrossTor/response-logic-projects includes all scripts and data that were used to obtain the results from the following sections.

KEGG data (Kanehisa et al., 2017) was retrieved via the KEGG package within the biopython library. The KEGG pathway maps database was parsed for human pathways and the retrieved KGML files were used to build network representations based on their ‘relation elements’.

The data and evaluation scripts for the DREAM3 and DREAM4 challenge was retrieved with the official DREAMTools python package (Cokelaer et al., 2016). Leaderboards were taken from Cokelaer and Costello (2015) and Figure 3 from Marbach et al. (2010).

Fig. 3.

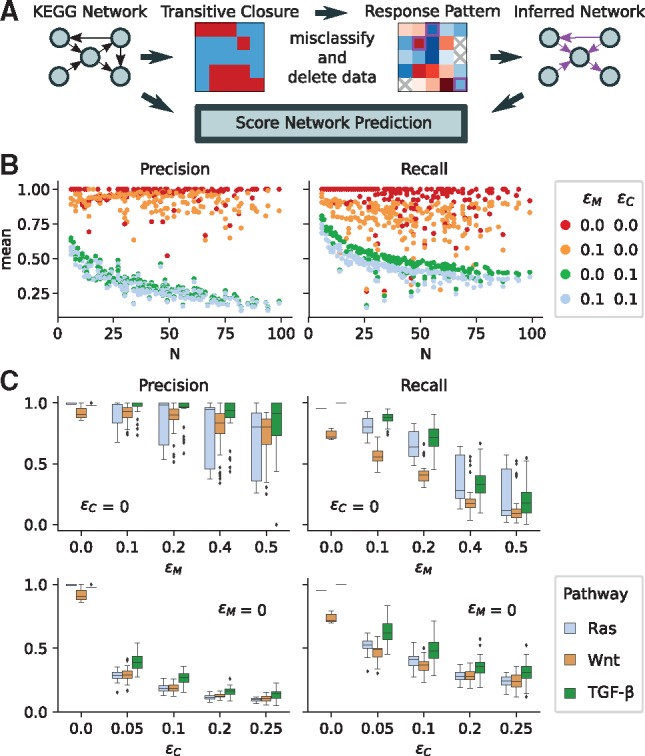
The performance of the response logic approach on synthetic data generated from 270 human KEGG pathways (Kanehisa et al., 2017). N denotes network size, ϵ_M quantifies the fraction of missing and ϵ_C the fraction of misclassified data points. (A) Data generation and scoring scheme. (B) Each dot per colour represents a different pathway, colours represent different parameters for misclassification (ϵ_C) and missing data (ϵ_M). (C) Precision and recall for three particular signalling pathways as a function of the fraction of misclassified or missing data

The SW-48 perturbation data were generated using a SW-48 cell line, and two derived clones with mutations in PI3K. Cell lines were obtained from Horizon Discovery. All lines were maintained in RPMI (Invitrogen) with 10% FBS (Invitrogen). Cell growth was assessed using the Cell Titer 96 Aqueous One Solution Cell Proliferation Assay (Promega). Cells were treated with compound 24 h after plating and grown for 72 h. The cell growth was determined by correcting for the cell count at time zero (time of treatment) and plotting data as percent growth relative to vehicle (DMSO)-treated cells. Reverse-phase protein array (RPPA): cells were treated 24 h after plating and incubated with inhibitor (GDC0973, GDC0068, Erlotinib) or solvent control (DMSO) for 1 h, and then stimulated either with EGF, HGF and IGF or with control (BSA) for 30 min. Cells were lysed in T-PER (Thermo), 300 mM NaCl, cOmplete^® protease inhibitor (Roche) and Phosphotase Inhibitor Cocktails 2, 3. RPPA measurements were carried out by Theranostics Health. All data can be accessed from the according data folder in the projects repository (response-logic-projects/SW-48_analysis/data/).

3 Results

3.1 Performance assessment on KEGG pathways

We first set out to systematically quantify how misclassification and missing data in the experimentally determined response pattern impacts the quality of the predicted network structure. To this end, we inferred network structures from synthetic datasets. As a relevant and representative collection of test networks, we extracted all 270 human gene regulation and signal transduction networks (maximally containing 100 nodes) from the KEGG pathway database (Kanehisa et al., 2017). For each of these network structures we generated its transitive closure, which we considered as the immaculate response pattern. Then, we repeatedly generated a random confidence pattern, C, where each entry is drawn from a uniform distribution between 0 and 1. To evaluate the effect of missing data, we remove a fraction ϵ_M of data points from the perfect response pattern and to evaluate the effect of measurement error, we also misclassify a fraction ϵ_C of the remaining data points. Missing or misclassified data points were chosen with a probability that was proportional to their confidence score C_ij. We then used the resulting response and confidence patterns to infer the sparsified network, as defined in the previous section, via the response logic approach and, comparing it to the original KEGG network, computed precision and recall as performance scores, see Figure 3A.

For each of the 270 KEGG networks the procedure was repeated 50 times for different choices of ϵ_M and ϵ_C, and the mean of the scores is shown in Figure 3B. In the absence of misclassifications (ϵ_C = 0, red and orange dots in Fig. 3B), prediction errors stem exclusively from the previously discussed multitude of conforming network structures. Interestingly, for a vast set of biological pathways the resulting inference errors are rather mild, and highly accurate predictions can be made independent of network size. However, once misclassifications are present, the predictivity is markedly reduced. Interestingly, this effect increases with growing network size.

We next examined the dependency on missing data and misclassification rates in more detail for the three signalling pathways: RAS, Wnt and TGF-β. We chose to scan the parameters from 0.0 to 0.5 and 0.0 to 0.25 for ϵ_M and ϵ_C, respectively, as a complete loss of information would either occur when all data were missing, ϵ_M = 1, or half of the entries were misclassified, ϵ_C = 0.5 (ϵ_C = 1 would produce an inversion of the response pattern). For all pathways, we found that recall is more affected by missing data than precision (see Fig. 3C). That is, with less data the predicted links remain rather accurate but fewer of them are predicted. We also confirmed our previous finding that misclassification reduces prediction scores much stronger than missing data. Interestingly, even when half the data were discarded, in many instances precision remained still close to one. This suggests that discarding low-confidence data points rather than risking to accept many misclassified data points might be a good strategy to improve predictions. We will re-examine this idea by the end of the next section.

3.2 Response logic approach outperforms competing methods in DREAM challenges

The DREAM (Stolovitzky et al., 2007) provides community-wide reverse-engineering challenges that foster the development of new systems biology models. Particularly, the DREAM3 and DREAM4 in-silico challenges (Greenfield et al., 2010; Marbach et al., 2010) assessed the performance of various gene network-inference methods and have since become a standard benchmark to which we can compare the response logic approach. In these two challenges various biologically plausible in-silico gene networks of different sizes were simulated under stochastic conditions to emulate realistic transcription dynamics resulting from knockdowns and knockouts of each single gene. Participants were given the resulting time courses, the steady states and the wild-type level of each gene and asked to infer the directed network structure from them. A ranked list of predicted gene pair interactions was then compared against the gold standard from which the area under the precision–recall (PR) and the area under the receiver operating characteristic curve (ROC) are computed, see Supplementary Figures S1 and S2. Comparing these to a null model provides P-values for each of the given five networks per network size that then get combined into a single overall score (Stolovitzky et al., 2009).

To infer the DREAM networks with the response logic approach, we generated response patterns from the in-silico knockout experiments of these challenges only (not considering knockdown or time-series data). These were computed as follows. When K_ij denotes the level of gene i after knockout of gene j, and the wild-type levels are w, we defined the normalized global response matrix, R, as

$$R_{\mathit{ij}}=\frac{|K_{\mathit{ij}}-w_i|}{s_i},$$

with s_i being the standard deviation of the knockout levels of gene i (row i of K). We then defined gene i to be responding to a knockout of gene j if R_ij > 1. The entries of the associated confidence matrix were defined as a normalized distance of knockout levels to this threshold, see Supplementary Material S2. We then applied our response logic approach to these matrices to infer sparsified networks, as defined earlier. The goal of the DREAM challenge is to provide a list of gene pairs that is ranked by their predicted likelihood to be interacting. We generated it by first listing the predicted interacting and then the non-interacting gene pairs, where within each group, the pair list was ordered according to the associated entries in the global response matrix (interaction $i\to j$ was ranked higher than $k\to l$ if R_ij > R_kl). As comparison, we also created a ranked list by simply ranking gene pairs in the order of the global response matrix, without the grouping that was introduced by the response logic, which we termed ‘naïve approach’.

These ranked lists were then scored using the official DREAMTools package (Cokelaer et al., 2016) (with a minor modification for one network score at DREAM3 N = 100, see Supplementary Material S2). Figure 4A shows the results of our method and that of the naïve approach in comparison to the 10 best performing participants at each network size and challenge that were provided with the full (knockout, knockdown, time-course) datasets. Except for the small networks with N = 10, where the response logic approach ranks second and third, it outperforms all 29 competitors participating in DREAM3 (Marbach et al., 2010), as well all 29 competitors participating in DREAM4 (Cokelaer and Costello, 2015). Note that the best performers for the small networks (N = 10) that scored higher than the response logic (Küffner et al., 2010; Yip et al., 2010) also used the provided time-course data, which we did not use in our response logic approach.

Fig. 4.

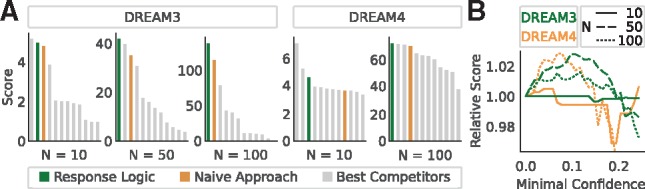
(A) Performance of the response logic approach for the gene-network reverse engineering challenges DREAM3 and DREAM4 (Greenfield et al., 2010; Marbach et al., 2010) (green bars), compared with a ‘naïve’ scoring approach (orange bars) and the 10 best approaches that took part in the respective challenges (grey bars). Scores are calculated as in the original challenge, with higher scores indicating better performance. (B) Relative changes in performance when excluding data points with confidence below a certain threshold. N: network size

We also observed that the response logic always outperformed the naïve approach, confirming that non-trivial additional knowledge is gained when applying the response logic. Notably however, already the naïve approach scores comparatively well, which let the challenge’s organizers to conclude that ‘sophisticated methods that would in theory be expected to perform better than the naïve approach described above, were more strongly affected by inaccurate prior assumptions in practice’ (Marbach et al., 2010). This observation affirms our initial motivation to design an approach with minimal assumptions on the data.

Finally, the DREAM data also allowed us to test if disregarding low-confidence data points, as suggested by the KEGG pathway analysis, improves predictions. Thus, considering the confidence matrix with scaled entries between 0 and 1 (Supplementary Material S2), we removed data points with confidence scores below a threshold and re-engineered the networks from those smaller datasets. The resulting scores relative to the original scores, which were obtained from the full response patterns, are shown in Figure 4B. With the exception of the N = 10 networks, these numerical experiments confirmed that removing low-confidence data effectively improved network inference. Peak performance is reached when approximately 5% of the data are discarded.

In summary, our benchmarks using the DREAM in-silico challenges provide a strong indication that the response logic approach is capable of reverse-engineering biological networks. Its simplicity not only makes its results comprehensible but the DREAM challenge showed that they are also more accurate than those of existing methods.

3.3 Reverse engineering MAPK and PI3K signalling in a colon cancer cell line

Having benchmarked the response logic formalism, we next used it to investigate signalling networks in cancer cells. In a first step, we decided to reverse engineer the Ras-mediated signalling network including MAPK and PI3K/AKT signalling in SW-48 colon cancer cells. We performed multiple perturbation experiments using either ligands or inhibitors that targeted EGFR, PDFR, ERK and AKT, and measured changes in phosphorylation using a reverse-phase protein assay (RPPA) platform. Ten of the antibody-based readouts passed a quality control and were relevant to the considered pathways, see details in Supplementary Material S3. Using replicate measurements of both unperturbed and perturbed conditions, we constructed the response pattern as well as the according confidence scores, which are shown in Figure 5A (see Supplementary Material S3 for details).

Fig. 5.

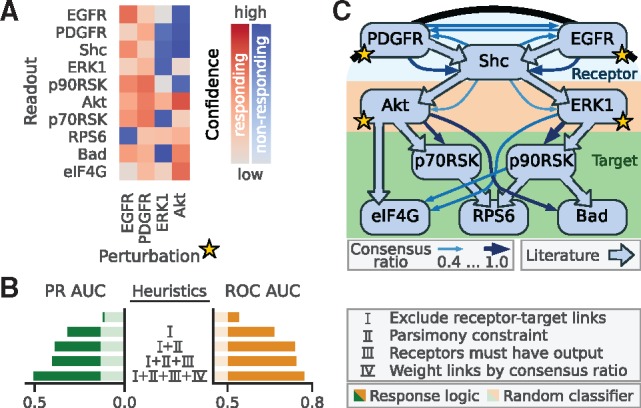
(A) Response pattern of the SW-48 cell line of selected phospho-proteins after perturbations affecting EGFR, PDGFR, ERK1 and AKT. (B) Performance of response logic network inference under various (combinations of) heuristics, as explained in text, compared to a random classifier (shaded colours). (C) Literature network (filled arrows) and final network prediction (finer arrows, only links with consensus ratio ≥0.4 are shown)

The RAS signalling network has been well studied, which allowed us to compile a literature network shown in Figure 5C that can be used as a gold standard to measure prediction performance. We then applied our response logic framework to the response pattern, and evaluated predictions by means of the areas under the ROC-, as well as PR curves, as shown in Figure 5B, see Supplementary Material S3 for details. As it was computationally impossible to enumerate all networks, we determined the union of all conforming networks, as described earlier, and scored links based on whether they are found in all, in some and in no conforming networks. Doing so led to PR and ROC curves that were only marginally better than random (top row in Fig. 5B). The apparent challenge concerning the network inference for this network is the substantial disparity between 10 readouts to only 4 perturbations, making the reverse engineering problem strongly underdetermined. A crucial benefit of the response logic analysis is that it allows for the incorporation of various additional insights about the structure of signalling networks to reduce the space of solutions. We therefore investigated how the inclusion of generic and indirect network knowledge rendered the analysis more meaningful. First, we enforced a hierarchy in the network (heuristic I). Signalling networks typically process signals received on the receptor level through a chain of intermediate kinases, before they are passed on to a set of targets. We therefore disallowed any direct connections between the receptor and the target level (according to the allocation shown in Fig. 5C) (these ruled-out links were obviously not taken into account for the scoring procedure, which explains the different areas under the PR curve for the random classifier in Fig. 5B). Furthermore, kinase interactions are highly specific, resulting in sparse signalling networks. Therefore, we found it reasonable to rid the network of redundant links and apply the parsimony constraint, as defined earlier (heuristic II). Lastly, we required that any node at receptor level must have at least one outgoing link (heuristic III).

Adding these three heuristics, I–III in Figure 5B, considerably improved the performance and reduced the solution space to 666 conforming networks. This makes it possible to enumerate them all and compute for each possible link the fraction of how many times it was present in all conforming networks (consensus ratio). We reasoned that a higher consensus ratio also implies a higher relevance, which we found confirmed when using the consensus ratio, rather than the union of networks to score the predictions (heuristic IV). From these results, we conclude that the response logic is indeed a valid assumption for the MAPK and PI3K pathway activity in the SW-48 cell line and that rather apparent additional information can effectively compensate for the small number of perturbations.

3.4 Modelling the effects of PI3K mutations in a colon cancer cell line

Having verified the validity of the response logic approach on the SW-48 cell data, we next used it to investigate how different mutations in the PI3K change signalling. To investigate this, we used clones of SW-48, in which two mutations that are commonly found in tumours were integrated, namely PIK3CA^H1047R and PIK3CA^E545K. We generated data using the same scheme as before, by perturbing the cells with ligands and inhibitors, and measuring the response using RPPA. Considering that the MAPK and PI3K pathways are very well studied, we assumed that the literature network depicted in Figure 5C is valid for all three cell lines, except for those links that could be affected by the different PI3K mutations. Because PI3K is not among the readouts, we model PI3K mutations to potentially affect links from and to its next downstream target, which is AKT. Furthermore, the literature network does not include context-dependent feedbacks in the MAPK pathway (Lake et al., 2016). As we observed mutant-dependent upregulation of EGFR as well as SHC upon MEK inhibition, see Supplementary Figure S4, we considered this option in the inference as well. Therefore, to model the different mutant response patterns shown in Figure 6A, we used a heavily constrained response logic approach in which the presence or absence of network links is governed by the literature network, except for those links going in and out of AKT and those links going into EGFR. Not only did these constraints compensate for the few perturbations but also connect differences in the data to plausible alterations of the network. Furthermore, as the parsimony constraint has proven beneficial in the response logic validation on the parental cell line data, Figure 5, it is used as well (with the constrained literature network, previous heuristics I and III no longer apply, and IV is not relevant as shown next).

Fig. 6.

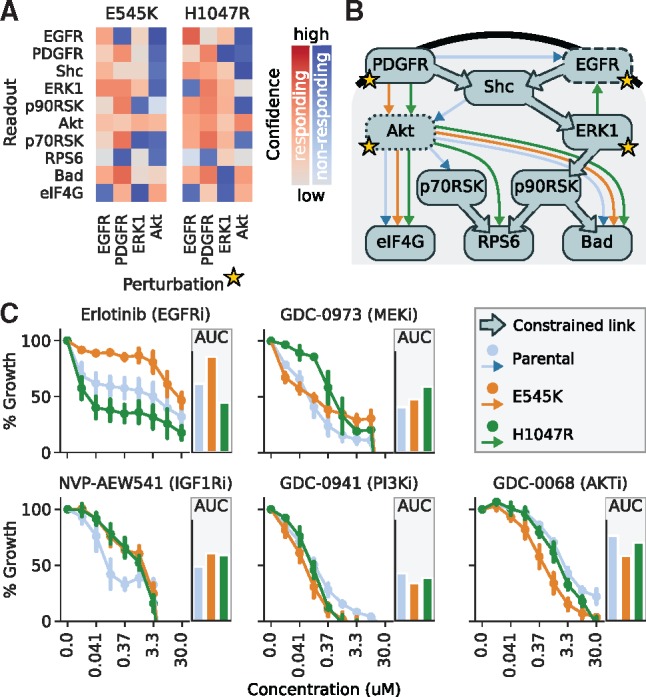
(A) Response pattern for two PI3K-mutant cell lines derived from SW-48, carrying either the E545K or H1047R mutations in PIK3CA, as in Figure 5. (B) Mutant-specific networks derived from the response data arrows in blue (parental cell line), orange and green (two mutant cell lines), with links constrained due to literature knowledge shown with large arrows. (C) Dose–response curves for different inhibitors targeting the inferred networks in the parental cell line (blue) and the two clones with PI3K mutations (orange and green), and the area under the curve displayed as bar graphs

This approach resulted in four, one and two conforming networks for the parental, the E545K and the H1047R cell line, respectively. For the two ambiguous cell lines, we decided to isolate the single, biologically most plausible network hypothesis. In the case of the parental cell line, the four conforming networks consist of the combined options of whether or not SHC feeds back to EGFR and whether EGFR signals directly to AKT or via SHC. SHC has been found to be an adapter protein that is recruited to the activated EGFR (but does not activate it) and is essential for the receptor’s signal relay (Ravichandran, 2001). We thus chose the parental network hypothesis that excludes the SHC to EGFR and the EGFR to AKT link. The two H1047R networks only differed in whether a feedback to EGFR originates from p90RSK or from ERK. Since the ERK to EGFR feedback is well described in the literature (Lake et al., 2016), we decided for that option. With this, we could compare the mutant-specific network hypotheses, as shown in Figure 6B, which led to two main observations. First, in contrast to the parental cell line, the mutant cell lines do not have a link from the EGFR receptor to the PI3K pathway. And second, the H1047R cell line is the only one bearing a feedback from ERK (or any node) to EGFR.

We next aimed to explore if these different network topologies might explain phenotypic differences between these cell lines. We therefore evaluated the drug response of these cells for different targeted drugs, as shown in Figure 6C. Some differences in drug response can be understood directly from the mutations that have been added to the cell lines: the PI3K and AKT inhibitors seem to be slightly more effective in the PI3K-mutant cell lines, which is not surprising as these cells have constitutively active PI3K signalling. Similarly, inhibition of IGFR was more effective in the wild-type cells, as the mutant cells are more self-sufficient in PI3K signalling and therefore potentially require less IGFR activity. The drug responses to the EGFR inhibitor, and the MEK inhibitor are more complex and can only be interpreted when considering the network rewiring. The PI3K^H1047 mutant cell line is rather resistant to the MEK inhibitor. This can be understood by the presence of the negative feedback from ERK to EGFR in this cell line, which is known to cause resistance by re-activating ERK and amplifying AKT signalling upon MEK inhibition (Klinger et al., 2013). EGFR inhibition effects the cell line with the E545K mutant less, and the cell line with the H1047R mutant more strongly compared to the parental cell line. Both mutants decouple the EGF-receptor to the AKT pathway, so one would expect that they also show a less pronounced effect upon its inhibition. However, in the H1047R cell line there is a strong ERK-EGFR feedback that generally reduces the MAPK pathway activity, and one can speculate that additional EGFR inhibition can push the MAPK pathway activity to sub-critical levels.

Taken together, the response logic modelling allows to reconstruct networks from complex perturbation data and provides network information that can be interpreted and linked to phenotypic behaviour. This example demonstrates how this approach allows to integrate noisy response data, prior network knowledge and generic signalling constraints to identify hypothesis on changes in networks due to mutations that can subsequently be studied experimentally.

4 Discussion

We developed the response logic approach as a method to infer directed networks from perturbation data. Its central idea is to assume that a perturbation of a node is propagated along the edges and thus causes a response at all nodes to which there is a directed path, starting from the perturbed node. This simple hypothesis is integrated in a logic program that allows to identify the networks whose transitive closure most closely matches that of the experimental data. The power of logic programming, and more generally declarative programming, has enabled its use in a wide range of topics in computational biology (Backofen and Gilbert, 2001; Becker et al., 2018; Bockmayr and Courtois, 2002; Dunn et al., 2014; Videla et al., 2015; Yordanov et al., 2016). In our approach, logic programming provides a way to efficiently scan the vast search space of all directed networks and to easily express and incorporate additional information and prior knowledge about the network.

Many reverse-engineering methods involve tunable parameters, which can drastically affect the results. However, it is often far from obvious how these parameters should be set in a specific context. In contrast, our response logic approach is parameter free and strictly infers the networks that follow from the provided response pattern and any additional constraints provided.

At first glance, it might seem wasteful to reduce the data to a binary information of responding versus non-responding, when many experimental techniques allow to quantify the magnitude of response of the observed components. However, data binarization renders inference more general and robust, and in many settings, technical issues such as measurement error, heterogeneous data sources or various normalization steps, make the interpretation of magnitudes difficult.

The idea to map an experimentally observable response pattern onto a transitive closure has been proposed before. It was hypothesized that the sparsest directed acyclic graph whose transitive closure matches the observed response pattern describes the direct regulatory interactions in gene networks (Wagner, 2001a). Such a graph is also known as the transitive reduction and can be computed efficiently (Aho et al., 1972). This approach was heuristically expanded to also allow for some cycles, and to refine the inferred network by incorporating double mutant perturbations and information about up- and downregulation (Tringe et al., 2004). Yet, this procedure has several shortcomings: it cannot incorporate existing domain knowledge, it cannot handle missing data points, but simply considers an unknown or uncertain response behaviour as non-responding and it only finds a single, most parsimonious, network, which might not necessarily represent the underlying structure.

This last point is a strategy to compensate for the fact that network inference is an inherently underdetermined problem, because the number of independent measurements generally falls short on the number of possible interactions (De Smet and Marchal, 2010). The response logic approach explicitly addresses this problem as it considers the entire ensemble of conforming networks rather than to single out a particular one, based on some fixed and potentially inaccurate assumption. It thereby reveals which parts of the network cannot be inferred from the information provided so far. This important insight can then be used to either guide additional experiments or to systematically reduce the solution space by adding constraints that are most warranted in the given context. We consider this as a crucial advantage over existing approaches, whose inferred networks can generally not be intuitively traced back to the data and thus tend to disguise if and how the inferred network is justified by the data.

But while the response logic is based on a simple and intuitive concept, such simplicity comes at a price. As with any other assumption, it might not actually be representative of the studied system. Major problems might occur due to robustness, or saturation effects, all of which disrupt the presumed flow of signal but are an essential part of various biological systems (Fritsche-Guenther et al., 2011). Also, from a Boolean perspective, the response logic treats nodes exclusively as OR gates, whereas certain systems require a more involved logic (Razzaq et al., 2018). But again, the declarative nature of the ASP encoding allows to account for such effects. One could, for example, rather easily implement a maximal path length over which a perturbation gets attenuated, or explicitly state a Boolean function that governs the signal propagation of a certain node. Another important shortcoming for many questions is that it does not neither assign any weights nor signs to the inferred links. Yet, the inferred network can serve as an input for methods that are devised to quantify link strengths on a given input network (Dorel et al., 2018).

On the other hand, the response logic’s simplicity makes it suitable for various different fields of research. Because it is based on a formalization of an intuitive network behaviour, it can infer ecological, infection, or even social or transportation networks. Such generality would even permit to use the response logic to ask the inverse question: given a certain network structure and the observed perturbation responses, can I infer where a perturbation hit the network? This question could be particularly interesting in the analysis of man-made networks, for which the structure is typically known, but not the location of the perturbation. The inverted logic program would then identify where an electric connection malfunctioned, an intruder attacked or a disease originated from. All these possibilities show that the simplicity of the response logic does not limit its applicability.