Building large updatable colored de Bruijn graphs via merging

Abstract

Motivation

There exist several large genomic and metagenomic data collection efforts, including GenomeTrakr and MetaSub, which are routinely updated with new data. To analyze such datasets, memory-efficient methods to construct and store the colored de Bruijn graph were developed. Yet, a problem that has not been considered is constructing the colored de Bruijn graph in a scalable manner that allows new data to be added without reconstruction. This problem is important for large public datasets as scalability is needed but also the ability to update the construction is also needed.

Results

We create a method for constructing the colored de Bruijn graph for large datasets that is based on partitioning the data into smaller datasets, building the colored de Bruijn graph using a FM-index based representation, and succinctly merging these representations to build a single graph. The last step, merging succinctly, is the algorithmic challenge which we solve in this article. We refer to the resulting method as $\text{VariMerge}$. This construction method also allows the graph to be updated with new data. We validate our approach and show it produces a three-fold reduction in working space when constructing a colored de Bruijn graph for 8000 strains. Lastly, we compare $\text{VariMerge}$ to other competing methods—including $\text{Vari}$, Rainbowfish, Mantis, Bloom Filter Trie, the method of Almodaresi et al. and Multi-BRWT—and illustrate that $\text{VariMerge}$ is the only method that is capable of building the colored de Bruijn graph for 16 000 strains in a manner that allows it to be updated. Competing methods either did not scale to this large of a dataset or do not allow for additions without reconstruction.

Availability and implementation

VariMerge is available at https://github.com/cosmo-team/cosmo/tree/VARI-merge under GPLv3 license.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The money and time needed to sequence a genome have decreased remarkably in the past decade. With this decrease has come an increase in the number and rate at which sequence data are collected for public sequencing projects. This led to the existence of GenomeTrakr, which is a large public effort to use genome sequencing for surveillance and detection of outbreaks of foodborne illnesses. This effort includes over 50 000 samples, spanning several species available through this initiative—a number that continues to rise as datasets are continually added (Stevens et al., 2017). Another example is illustrated by the sequencing of the human genome. The 1000 Genomes Project Consortium (2015) was announced in 2008 and completed in 2015, and now the 100 000 Genomes Project is well underway (Turnbull et al., 2018). Unfortunately, methods to analyze these and other large public datasets are limited due to their size.

Iqbal et al. (2012) presented one method for analysis of sequence data from large populations (such as the ones described above) which focuses on the construction of the colored de Bruijn graph. To define the colored de Bruijn graph, we first define the traditional de Bruijn graph and then show how it can be extended. Formally, a de Bruijn graph constructed for a set of strings (e.g. sequence reads) has a distinct vertex v for every unique $(k-1)$-mer (substring of length $k-1$) present in the strings, and a directed edge (u, v) for every observed k-mer in the strings with $(k-1)$-mer prefix u and $(k-1)$-mer suffix v. In the colored de Bruijn graph, the edge structure is the same as the classic structure, but now to each node ($(k-1)$-mer) and edge (k-mer) is associated a list of colors corresponding to the samples in which the node or edge label exists. More specifically, given a set of n samples, there exists a set $\mathcal{C}$ of n colors $c_1,c_2,\mathrm{..},c_n$ where c_i corresponds to sample i and all k-mers and $(k-1)$-mers that are contained in sample i are colored with c_i. A bubble in this graph corresponds to an undirected cycle and is shown to be indicative of biological variation. Iqbal et al. (2012) show after constructing a colored de Bruijn graph, they can recover all genetic variants in the underlying population by traversing the graph, and finding paths with bubbles (‘bubble finding’).

A bottleneck in applying Cortex (Iqbal et al., 2012) to large datasets lies in the amount of memory and CPU time required to build and store the colored de Bruijn graph. Thus, $\text{Vari}$ (Muggli et al., 2017), Rainbowfish (Almodaresi et al., 2017), Mantis (Almodaresi et al., 2019), the method of Karasikov et al. (2019), as well as others, sought to overcome this limitation by building and/or storing the colored de Bruijn graphs in a space- and time-efficient manner. $\text{Vari}$ was one of the first methods to build the colored de Bruijn graph in a memory efficient manner. It extends the de Bruijn graph construction of Bowe et al. (2012). Rainbowfish (Almodaresi et al., 2017) was later developed. It uses $\text{Vari}$ to build the colored de Bruijn graph, which it further compresses by storing identical rows in the $\text{Vari}$ color matrix as a single row. Cortex, $\text{Vari}$ and Rainbowfish have bubble-calling methods that allow genetic variation between the datasets to be detected.

Mantis (Pandey et al., 2018) improves on $\text{Vari}$ and Rainbowfish by constructing a different data structure which is not reliant on $\text{Vari}$. Most recently, the method of Almodaresi et al. (2019) was presented, which is referred to as an minimum spanning tree-based color-class representation. This method first uses Mantis to build the colored de Bruijn graph, which it then compresses by building minimum spanning trees of the underlying graph and storing only deltas between similar vectors. Both Mantis and the method of Almodaresi et al. (2019) do not have bubble-calling procedures. We note there exists more colored de Bruijn graph construction algorithms, and give a comprehensive review in the next section.

Unfortunately, there does not exist a method to build the colored de Bruijn graph in a manner that is scalable to large datasets and allows for the addition of new data. This is important since one of the original purposes of the colored de Bruijn graph was to analyze population-level datasets—such as GenomeTrakr and 100 000 Genomes Project—which continually grow in size due to the addition of new data. Existing colored de Bruijn graph methods either cannot scale well enough to construct their data structure for large datasets or cannot update the data structure without complete reconstruction. For example, $\text{Vari}$ (Muggli et al., 2017), Rainbowfish (Almodaresi et al., 2017), Mantis (Pandey et al., 2018) and the method of Almodaresi et al. (2019) are efficient with respect to memory and time but cannot be updated without reconstructing the entire colored de Bruijn graph. Bloom Filter Trie (Holley et al., 2016) and the method of Karasikov et al. (2019) allow for the addition of new data but cannot scale to large datasets, as we show in this article. Crawford et al. (2018) build a de Bruijn graph that can be updated but restrict interest to the traditional (non-colored) de Bruijn graph.

Here, we focus on scalable construction of the colored de Bruijn graph in a manner that allows new data to be added without reconstruction. One way to achieve this construction is to devise a divide-and-conquer approach which will divide the dataset into smaller sets, construct a succinct colored de Bruijn graph for each smaller set, and merge these succinct colored de Bruijn graphs into progressively larger graphs until a single one remains. The problem of merging succinct colored de Bruijn graphs efficiently is a challenging problem but necessary to solve since it avoids memory, disk and time overhead. This divide-and-conquer approach also allows the graph to be updated. Given an additional dataset, a compressed colored de Bruijn graph can be constructed for it, and then merged into the existing (larger) compressed colored de Bruijn graph.

1.2 Our contributions

We present $\text{VariMerge}$ which constructs a colored de Bruijn graph for large datasets in a manner that allows new data to be added efficiently. As suggested earlier, $\text{VariMerge}$ builds through a process of dividing the data into smaller sets, building the colored de Bruijn graph in a RAM-efficient manner for each smaller set and merging the resulting colored de Bruijn graphs. Each of the colored de Bruijn graphs is stored using the FM-index in the same manner as $\text{Vari}$ (Muggli et al., 2017). Thus, the algorithmic challenge that we tackle is merging the graphs in a manner that keeps them in their compressed format throughout the merging process—rather than decompressing, merging and compressing, which would be impractical with respect to disk and memory usage.

We verify the correctness of our approach and the accompanied bubble-calling algorithm by showing the colored de Bruijn graph built via merging is bit-for-bit identical to standard construction, and successfully identifies all bubbles in the merged graph. Next, we demonstrate that $\text{VariMerge}$ improves construction scalability over $\text{Vari}$, reducing the running time by a third and the working space three-fold by comparing the peak disk and memory required to build the colored de Bruijn graph for 8000 Salmonella strains using $\text{Vari}$ and $\text{VariMerge}$.

Next, we use $\text{VariMerge}$ to build a colored de Bruijn graph for 16 000 strains of Salmonella. This construction required 254 GB of RAM, 2.34 TB of external memory, and ∼140 h of CPU time. To contextualize these results, we compare the construction of $\text{VariMerge}$ with those of state-of-the-art methods, including $\text{Vari}$ (Muggli et al., 2017)/Rainbowfish (Almodaresi et al., 2017), Bloom Filter Trie (Holley et al., 2016), Mantis (Pandey et al., 2018)/the method of Almodaresi et al. (2019) and the method of Karasikov et al. (2019), on datasets consisting of 4000, 8000 and 16 000 strains. Further, we demonstrate the ability of the graph to be updated efficiently through $\text{VariMerge}$ by showing a Salmonella strain can be added to the graph in an order of magnitude faster than its initial construction. These results demonstrate that $\text{VariMerge}$ is the only method that is capable of building the colored de Bruijn graph for 16 000 strains in a manner where new data can be added. Mantis was the only other method that was capable of building the colored de Bruijn graph for 16 000 strains, yet it is unable to update the graph without reconstruction. Although the authors suggest a dynamic update strategy in future work, no implementation is available. In addition, we note that $\text{VariMerge}$ has several practical advantages over Mantis—it has a bubble-calling implementation which allows variants to be detected from the graph and is capable of constructing the graph for any value of k up to 64. All other methods were not scalable to 16 000 and thus, were unable to complete construction in 150 h and using at most 4 TB of disk space and 750 GB of memory.

2 Related works

2.1 Efficient de Bruijn graphs

Space-efficient representations of de Bruijn graphs have been heavily researched in recent years. One of the first approaches was introduced with the creation of the ABySS assembler, which stores the graph as a distributed hash table (Simpson et al., 2009). Conway and Bromage (2011) reduced these space requirements by using a sparse bit vector representation, which is due Okanohara and Sadakane (2007), to represent the edges in the graph, and using rank and select operations (to be described shortly) to traverse the edges. Minia (Chikhi and Rizk, 2013) use a Bloom filter to store the edges, which requires the graph to be traversed by generating all possible outgoing edges at each node and testing their membership in the Bloom filter. Bowe et al. (2012) develop a succinct data structure based on the Burrows–Wheeler transform (BWT). This data structure is combined with ideas from IDBA-UD (Peng et al., 2012) in order to create MEGAHIT (Li et al., 2015). Chikhi et al. (2014) describe a space-efficient data structure that combines the use of the FM-index and minimizers.

2.2 Efficient colored de Bruijn graphs

As previously mentioned, $\text{Vari}$ (Muggli et al., 2017) and Rainbowfish (Almodaresi et al., 2017) are both space-efficient data structures for storing the colored de Bruijn graph which each use the structure of (Bowe et al., 2012). Muggli et al. (2017) build the compressed color matrix by compressing each row using Elias-Fano encoding. Rainbowfish (Almodaresi et al., 2017) takes as input the color matrix of $\text{Vari}$ and compress it by decomposing the matrix into ‘color sets’ based on an equivalence relation and compresses each color set individually. Thus, this method relies on the construction of $\text{Vari}$ prior to building the sets of compatible colors. Holley et al. (2016) introduced the Bloom Filter Trie, which is another succinct data structure for the colored de Bruijn graph. It encodes frequently occurring sets of colors separate from the graph and stores a reference to the set if the reference takes fewer bits than the set itself. This data structure allows incremental updates of the underlying graph. More recently, Mantis (Pandey et al., 2018) and its extension (Almodaresi et al., 2019) improve upon $\text{Vari}$ and Rainbowfish. They build a compressed colored de Bruijn graph by building sets of compatible colors (similar to Rainbowfish) but construct the compressed graph directly rather than constructing it from $\text{Vari}$. Lastly, the most recent method of Almodaresi et al. (2019) constructs the colored de Bruijn graph using Mantis, which it further compresses by careful reconstruction and compression of the color matrix.

Lastly, there are a couple of methods that construct the color matrix in a manner that is both compressed and dynamic, which include the method of Mustafa et al. (2019) and Multi-BRWT (Karasikov et al., 2019). These methods use a simple representation of a de Bruijn graph where each edge (the k-mer) is stored in a hash table. This graph representation allows it to be updated along with the color matrix—thus, the main contribution is not the data structure used to store the graph but that used to store the color matrix.

2.3 Other related compressed data structures

Some related compressed data structures are SeqOthello (Yu et al., 2018), SBT (Solomon and Kingsford, 2016), Split-SBT (Solomon and Kingsford, 2018) and Allsome-SBT (Sun et al., 2017). These methods index all k-mers or variants of k-mer indexes but do not provide graph information. For this reason, they are frequently applied to querying large collections of RNA-seq data but not genome assembly. Another indexing method is BIGSI (Bradley et al., 2017), which provides graph features and can be viewed as a probabilistic colored de Bruijn graph.

Two other approaches are worthy of note because they merge the BWT of a set of strings. BWT-Merge (Sirén, 2016) is related to our work since the data structure we construct and store is similar to BWT. BWT-Merge merges two strings stored using BWT by using a reverse trie of one BWT to generate queries that are then located in the other BWT using FM-index backward search. The reverse trie allows the common suffixes across multiple merge elements to share the results of a single backward search step. Thus, BWT-Merge finds the final rank of each full suffix completely, one suffix at a time. Finally, MSBWT (Holt and McMillan, 2014) is a method which merges the BWTs of multiple strings in a method similar to our own except applied to strings instead of graphs. Lastly, Egidi et al. (2019) recently improved upon the algorithm in this article. Their algorithm has the same asymptotic cost as the method presented here but is more space-efficient.

In Section 5, we compared the performance of $\text{VariMerge}$ against $\text{Vari}$ (Muggli et al., 2017)/Rainbowfish (Almodaresi et al., 2017), Bloom Filter Trie (Holley et al., 2016), Multi-BRWT (Karasikov et al., 2019) and Mantis (Pandey et al., 2018)/the method of Almodaresi et al. (2019). Among all mentioned methods in this section, we chose these tools based on the following criteria: the method should be both graph-based and non-probabilistic (exact) for a fair comparison.

3 Preliminaries

As previously mentioned, $\text{Vari}$ (Muggli et al., 2017) represents the colored de Bruijn graph using BWT and $\text{VariMerge}$ efficiently merges de Bruijn graphs that are represented in this manner. Here, we first define some basic notation and definitions concerning BWT, then show how the colored de Bruijn graph can be stored using BWT.

3.1 Basic definitions and terminology

Here, we begin with some basic definitions related to our representation. Throughout we consider a string $X=X[\mathrm{1..}n]=X[1]X[2]\dots X[n]$ of $\left|X\right|=n$ symbols drawn from the alphabet $[\mathrm{0..}\sigma -1]$. For $i=1,\dots ,n$ we write $X[i\mathrm{..}n]$ to denote the suffix of $X$ length $n-i+1$, that is $X[i\mathrm{..}n]=X[i]X[i+1]\dots X[n]$. Similarly, we write $X[\mathrm{1..}i]$ to denote the prefix of $X$ length i. $X[i\mathrm{..}j]$ is the substring$X[i]X[i+1]\dots X[j]$ of $X$ that starts at position i and ends at j.

The suffix array $S{A}_X$ of input text $X$ is an array $\mathit{SA}[\mathrm{1..}n]$ of length n that contains a permutation of the integers $[\mathrm{1..}n]$, where $X[\mathit{SA}[1]\mathrm{..}n]\prec X[\mathit{SA}[2]\mathrm{..}n]\prec \cdots \prec X[\mathit{SA}[n]\mathrm{..}n]$ and $\prec$ denotes lexicographic precedence. Next, for a string $Y$, we refer to the $Y$-interval in the suffix array $S{A}_X$ as the interval $\mathit{SA}[s\mathrm{..}e]$ that contains all suffixes having $Y$ as a prefix. For a character c and a string $Y$, the computation of $\mathit{cY}$-interval from $Y$-interval is called the left extension.

3.1.1 BWT and FM-index

For a string $Y$, we denote $A$ as the list of $Y$’s characters sorted lexicographically by the suffixes starting at those characters. Further, we denote $B$ be the list of $Y$’s characters sorted lexicographically by the suffixes starting immediately after those characters. Thus, if $Y[i]=Y[j]$ then $Y[i]$ and $Y[j]$ have the same relative order in both lists. This implies that if $Y[i]$ is in position p in $B$ then in $A$ it is in position

$$\left|\right\{h : Y[h]\prec Y[i]\left\}\right|+\left|\right\{h : L[h]=Y[i],\hspace{0.17em}h\le p\left\}\right|-1 .$$

We note that the last character in $Y$ always appears first in $B$. It follows that we can recover $Y$ from $B$, which is the principle of BWT (Burrows and Wheeler, 1994).

Ferragina and Manzini (2005) showed BWT can be used for indexing as follows. Here, we denote $\mathit{BWT}(Y)$ as the BWT array computed for $Y$. Hence, if we know the range $\mathit{BWT}(Y)[i\mathrm{..}j]$ occupied by characters immediately preceding occurrences of a pattern P in $Y$, then we can compute the range $\mathit{BWT}(Y)[i\prime \mathrm{..}j\prime ]$ occupied by characters immediately preceding occurrences of $\mathit{cP}$ in $Y$, for any character c, since

$$\begin{array}{c}i\prime =\left|\right\{h : A[h]\prec c\left\}\right|+\left|\right\{h : B[h]=c,h<i\left\}\right|\\ j\prime =\left|\right\{h : A[h]\prec c\left\}\right|+\left|\right\{h : B[h]=c,h\le j\left\}\right|-1 .\end{array}$$

As can be seen above: $j\prime -i\prime +1$ is the number of occurrences of $\mathit{cP}$. To recap, the FM-index for $Y$ requires: (i) an array that stores $\left|\right\{h : Y[h]\prec c\left\}\right|$ for each character c and (ii) a (rank) data structure for $\mathit{BWT}(Y)$ that returns how many times a given character occurs up to a specific position. The latter data structure is used in backward search in order to compute the left extension of a given string.

3.2 Storage of de Bruijn graphs using the BWT

We now give a brief explanation of the data structure behind $\text{Vari}$. An example of this representation is shown in Supplementary Figure S2 in Section 7. We refer the reader to Muggli et al. (2017) for a full explanation.

Given a de Bruijn graph $G=(V,E)$, we assume each edge $e\in E$ has a k-mer corresponding to it. We define the co-lexicographic (colex) ordering of V as the lexicographic order of their reversed $(k-1)$-mers. We let $F$ be the edges in E in colex order by their ending nodes, where ties are broken by their starting nodes, and let $L$ be the edges in E sorted colex by their starting nodes, with ties broken by their ending nodes. We define $\mathit{label}(e)$ as a function that takes in an edge $e\in E$ and returns the final symbol of the k-mer corresponding to it.

If we are given two edges e and $e\prime$ that have the same label then they have the same relative order in both $F$ and $L$; otherwise, their relative order in $F$ is the same as their labels’ lexicographic order. This means that if e is in position p in $L$, then in $F$ it is in position

$$\begin{array}{cc}\left|\right\{d:\hfill & d\in E,\hspace{0.17em}\mathit{label}(d)\prec \mathit{label}(e)\left\}\right|+\left|\right\{h:\mathit{label}(L[h])\hfill \\ \hfill & =\mathit{label}(e),\hspace{0.17em}h\le p\left\}\right|-1. \hfill \end{array}$$

We let $\mathit{Edge}-\mathit{BWT}(G)$ be the sequence of edge labels given the ordering of the edges in $L$. Thus, we let $\mathit{label}(L[h])$ be equal to $\mathit{Edge}-\mathit{BWT}(G)[h]$ for all h. We let $B_F$ be the bit vector with a 1 marking the position in $F$ of the last incoming edge of each node, and let $B_L$ be the bit vector with a 1 marking the position in $L$ of the last outgoing edge of each node. Therefore, given a character c and the index of a node v (we note that there is no explicit stored set of nodes. Hence, we refer to the “node index” as the position among all nodes if sorted in colex order), we can use $B_L$ to find the interval in $L$ containing v’s outgoing edges and search in $\mathit{Edge}-\mathit{BWT}(G)$ to find the position of edge e labeled c. Similarly, we can find all incoming edges of a node v using their position in $F$ and $B_F$.

We annotate each bit of $B_F$ to the corresponding symbols in $\mathit{Edge}-\mathit{BWT}(G)$. We let $\mathit{flags}$ be a bit array of such annotation bits. In practice, we store $\mathit{Edge}-\mathit{BWT}(G),\hspace{0.17em}{B}_L$ and $\mathit{flags}$ (rather than $B_F$) to store the de Bruijn graph but limit our discussion to the construction that uses $B_F$ for ease of explanation. We refer the reader to Bowe et al. (2012) for a full explanation of $\mathit{flags}$.

We note that an important aspect of this succinct representation of the graph is that the $(k-1)$-mers (nodes) and k-mers (edges) of the de Bruijn graph G are not explicitly stored in the above representation—rather they than can be computed from this representation. We can efficiently traverse the graph in a forward or reverse manner and recover incoming and outgoing edges of a given node v. Therefore, given a node v identified by its index, we can recover the $(k-1)$-mer corresponding to v by traversing the graph in a backward direction $(k-1)$ times starting from v. See Supplementary Section 8 for more details. This also illustrates the necessity of adding extra nodes and edges to the graph, which we refer to as dummy nodes and edges. In order to ensure there is a directed path of length at least $k-1$ to each original node, we augment the graph with additional nodes (and edges) so that each new node has a $(k-1)$-mer that is prefixed by one or more copies of a special symbol $\$$ not in the alphabet and lexicographically strictly less than all others. When new nodes are added, we are assured that the node corresponding to ${\$}^{k-1}$ is always first in colex order and has no incoming edges. Lastly, we augment the graph in a similar manner by adding extra outgoing edges, whose $k$-mer ends in $\$$, doing so for each original node with no outgoing edge.

3.2.1 Storage of colors

Given a multiset $\mathcal{G}=\{G_1,\dots ,G_t\}$ of individual de Bruijn graphs, we set G to be the union of those individual graphs and build the previously-described representation for G. We also build and store a 2D binary array $C$ in which $C[i,j]$ indicates whether the ith edge in G is present in the jth individual de Bruijn graph.

4 Methods

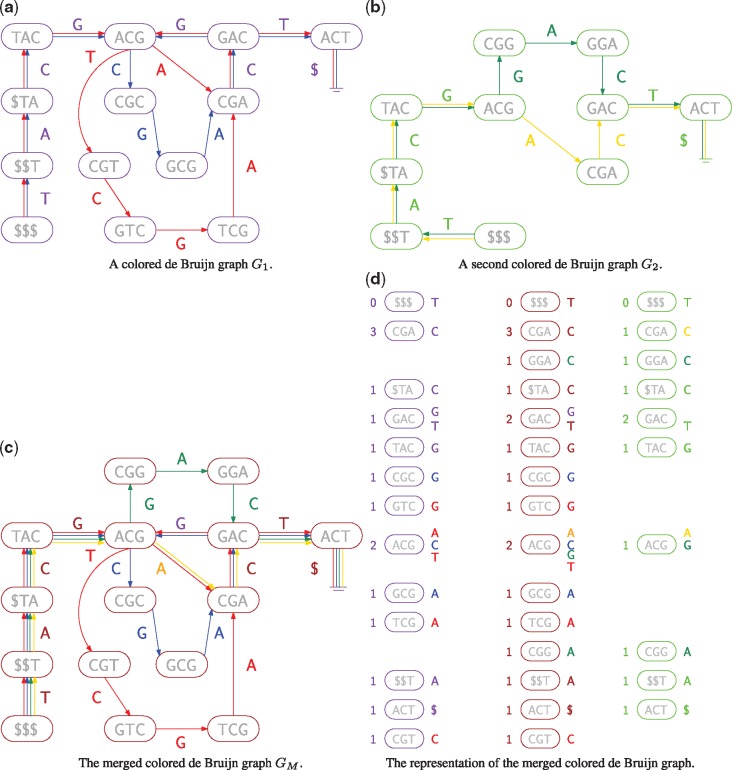
In this section, we begin by describing a naive merge algorithm, which will motivate the necessity of the succinct algorithm. In the description of both algorithms, we describe how to merge two-colored de Bruijn graphs but note that it generalizes to an arbitrary number of graphs. Hence, we assume that we have two de Bruijn graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ as input, which are stored as $\mathit{Edge}-\mathit{BWT}(G_1),\hspace{0.17em}{B}_{L1},\hspace{0.17em}{B}_{F1}$, and $C_1$ as well as $\mathit{Edge}-\mathit{BWT}(G_2),\hspace{0.17em}{B}_{L2},\hspace{0.17em}{B}_{F2}$, and $C_2$, respectively. And we output the merged graph $G_M=(V_M,E_M)$ as $\mathit{Edge}-\mathit{BWT}{(G)}_M,\hspace{0.17em}{B}_{\mathit{LM}},\hspace{0.17em}{B}_{\mathit{FM}}$, and $C_M$. An illustration of G₁, G₂, G_M and the corresponding data structures is given in Figure 1.

Fig. 1.

(a) A colored de Bruijn graph consisting of two individual graphs, whose edges are shown in red and blue. The nodes are shown in purple because they can occur in either graph. (b) A second colored de Bruijn graph, whose edges are green and yellow. Again, the nodes are shown in lime because they can occur in either graph. (c) A colored de Bruijn graph merged from the two-colored de Bruijn graphs. (d) The nodes for all three graphs arranged in columns (red and blue, merged, green and yellow). Each column is sorted into co-lexicographic order, with each node’s number of incoming edges shown on its left and the labels of its outgoing edges shown on its right. Vertical alignment illustrates how the merged components (center) are copied from either the left, the right or both

4.1 A naive merge algorithm

We recall from Section 3 that the edges (k-mers) of G₁ and G₂ can be computed from the succinct representation. We denote these k-mers for G₁, G₂ as $L_1$ and $L_2$, respectively. For example, if we want to reconstruct the k-mer AGAGAGTTA contained in G₁ which is stored as A in $\mathit{Edge}-\mathit{BWT}(G_1)$, we need to backward navigate in G₁ from the edge labeled A through k – 1 predecessor edges (T, T, G,…), and concatenate the abbreviated characters encountered during this backward navigation in reverse order. Thus, a naive merging algorithm would reconstruct $L_1$ and $L_2$ then merge them, which can be trivially given they are in sorted (colex) order. This algorithm requires explicitly building $L_1,\hspace{0.17em}{L}_2$, and the merged list. Thus, it has a significant memory footprint. See Supplementary Algorithm S3 in Section 9 for the details of this naive merge algorithm.

4.2 The succinct merge algorithm

Before we give a detailed explanation of our succinct merge algorithm, we consider the problem of merging two sorted lists of strings with the constraint that we can only examine a single character from each string at a time. We can solve this problem with a divide and conquer approach. First, we group all the strings in each list by their first character. This partially solves the problem, as we know all the strings in the first group from each list must occur in the output before all the strings in the second group in each list and so on. Thus, the problem is now reduced to merging the strings in the first group, followed by merging the strings in the second group and so on. Each of these merges can be addressed by again grouping the elements (i.e. subgroups of the initial groups) by examining the second character of each string. We can apply this step recursively until all characters of each string have been examined. We now draw the reader’s attention to the fact that our succinct colored de Bruijn graph representation is a space-efficient representation of the list of sorted k-mers.

4.2.1 Overview of the algorithm

We now return to the problem of merging succinct colored de Bruijn graphs. The algorithm consists of two steps: (i) a planning step which plans the merge and (ii) an executing step which executes the merge. Thus, the planning step outputs a merge plan, which consists of lists of non-overlapping intervals for $L_1$ and $L_2$. These lists detail how to construct the data structure for the merged graph from the succinct data structures for G₁ and G₂.

We refer to $\mathit{Edge}-\mathit{BWT}$ and $C$ as the primary components of the data structure and $B_F$ and B_L as secondary components. We describe how to merge the primary components, and leave the details of how to merge the secondary components to Supplementary Section 12.

4.2.2 The planning step

Formally, we denote the merge plan as $P_1=\{[0,p_1^1],\dots ,[p_i^1,\left|L_1\right|-1]\}$, where each $p_1^1,\dots ,p_i^1$ is an index in $L_1$, and $P_2=\{[0,p_1^2],\dots ,[p_i^2,\left|L_2\right|-1]\}$, where each $p_1^2,\dots ,p_i^2$ is an index in $L_2$. An overview of the planning step is given in Algorithm 1. We first initialize P₁ and P₂ to be single intervals covering $L_1$ and $L_2$, respectively (e.g. $P_1=\{[0,\left|L_1\right|-1]\}$ and $P_2=\{[0,\left|L_2\right|-1]\}$). Next, we revise P₁ and P₂ in an iterative manner k times (where k corresponds to the k-mer value). At each iteration of the algorithm, a single character of the strings in $L_1$ and $L_2$ is processed, and the merge plan is revised. Thus, in order to fully describe the planning stage, we define (i) how the characters of $L_1$ and $L_2$ are computed, and (ii) how P₁ and P₂ are revised based on these characters. An illustration of the merge plans is given in the Supplementary Figure S3 in Section 10.

Algorithm 1 . The planning step to merge G₁ and G₂.

$P_1\leftarrow ([1,\left|\mathit{EBWT}{(G)}_1\right|])$

$P_2\leftarrow ([1,\left|\mathit{EBWT}{(G)}_2\right|])$

$\mathit{Co}{l}_1\leftarrow []$

$\mathit{Co}{l}_2\leftarrow []$

% Iterate through ‘edge label matrix’ columns in sort precedence order

for all $i\in \left\{\mathrm{1..}k\right\}$ do

  $\mathit{Co}{l}_1\leftarrow \mathit{GetCol}(i,\mathit{Co}{l}_1,G_1)$

  $\mathit{Co}{l}_2\leftarrow \mathit{GetCol}(i,\mathit{Co}{l}_2,G_2)$

  % RefinePlan is given in Algorithm 2.

  $(P_1^{\prime },P_2^{\prime })\leftarrow \mathit{RefinePlan}(P_1,P_2,\mathit{Co}{l}_1,\mathit{Co}{l}_2,i)$

  $(P_1,P_2)\leftarrow (P_1^{\prime },P_2^{\prime })$

end for

Computing the next character of L₁ and L₂. Let i denote the current iteration of our revision of P₁ and P₂, where $1\le i<k$. We compute the next character of $L_1$ and $L_2$ using two temporary character vectors $\mathit{Co}{l}_1^i$ and $\mathit{Co}{l}_2^i$, which are of length $\left|L_1\right|$ and $\left|L_2\right|$, respectively. We note that the ‘next’ character is the preceding character in the k-mer since $\mathit{Edge}-\mathit{BWT}(G_1)$ and $\mathit{Edge}-\mathit{BWT}(G_2)$ only store the last character of $L_1$ and $L_2$. Thus, we process the characters of $L_1$ and $L_2$ from right to left. Conceptually, we define these vectors as follows: $\mathit{Co}{l}_1^i[j]=L_1[j][k-i]$ if i < k and otherwise $\mathit{Co}{l}_1^i[j]=L_1[j][k]$, and $\mathit{Co}{l}_2^i[j]=L_2[j][k-i]$ if j < k; and otherwise $\mathit{Co}{l}_2^i[j]=L_2[j][k]$. Yet, since we do not explicitly build or store $L_1$ and $L_2$, we must compute $\mathit{Co}{l}_1^i$ and $\mathit{Co}{l}_2^i$.

We define the computation of $\mathit{Co}{l}_1^i$ by describing the following three cases. When $1<i<k$, we compute $\mathit{Co}{l}_1^i$ by traversing G₁ in a forward direction from the first incoming edge of every node and copying the character found at the $(q+1)$-th position of that incoming edge (again, stored in $\mathit{Co}{l}_1^{i-1}$) into q-th position of all outgoing edges of that node. When i = 1, the $(q+1)$-th position corresponds to $\mathit{Edge}-\mathit{BWT}(G_1)$, so $\mathit{Edge}-\mathit{BWT}(G_1)$ is used in place of $\mathit{Co}{l}_1^{i-1}$ but is otherwise identical to the previous case. Lastly, when i = k, we let $\mathit{Co}{l}_1^i$ equal $\mathit{Edge}-\mathit{BWT}(G_1)$. We compute $\mathit{Co}{l}_2^i$ in an analogous manner. An illustration of how to compute the next column of $L_1$ and $L_2$ is given in the Supplementary Section 11. Moreover, the pseudocode for GetCol is shown in Supplementary Algorithm S11.

Revising P₁ and P₂. We revise P₁ and P₂ based on $\mathit{Co}{l}_1^i$ and $\mathit{Co}{l}_2^i$ at iteration i by considering each pair of intervals in P₁ and P₂, i.e., $P_1[n]$ and $P_2[n]$ for $n=1,\dots ,\left|P_1\right|$, and partitioning each interval into at most five sub-intervals. We store the list of sub-intervals of P₁ and P₂ as SubP₁ and SubP₂. Intuitively, we create SubP₁ in order to divide $P_1[n]$ based on continuous ranges in $\mathit{Co}{l}_1^i$ that have the same character, e.g. each continuous range of A’s, C’s, G’s, T’s or $’s. Similarly, SubP₂ is used to divide $P_2[n]$. We divide P₁ by first computing the subvector of $\mathit{Co}{l}_1^i$ that is covered by $P_1[n]$, which we denote as $\mathit{Co}{l}_1^i(P_1[n])$, and computing the subvector of $\mathit{Co}{l}_2^i$ that is covered by $P_2[n]$, which we denote as $\mathit{Co}{l}_2^i(P_2[n])$. Next, given character c, we populate $\mathit{Sub}{P}_1[c]$ and $\mathit{Sub}{P}_2[c]$ based on $\mathit{Co}{l}_1^i(P_1[n])$and$\mathit{Co}{l}_2^i(P_2[n])$ as follows: (i) we check whether c exists in either $\mathit{Co}{l}_1^i(P_1[n])$ or $\mathit{Co}{l}_2^i(P_1[n])$; (ii) if so, we add an interval to $\mathit{Sub}{P}_1[c]$ covering the contiguous range of c in $\mathit{Co}{l}_1^i(P_1[n])$ (or add an empty interval if $\mathit{Co}{l}_1^i(P_1[n])$ lacks any instances of c), and add an interval to $\mathit{Sub}{P}_2[c]$ covering the contiguous range of c in $\mathit{Co}{l}_2^i(P_1[n])$ (or, likewise, add an empty interval if $\mathit{Co}{l}_2^i(P_1[n])$ lacks any instances of c) (we are guaranteed by the definition of our data structure that any instances of c in $\mathit{Co}{l}_1^i(P_1[n])$ will be in a contiguous range, and likewise, any instances of c in $\mathit{Co}{l}_2^i(P_1[n])$ will also be in a contiguous range). Finally, we concatenate all the lists in SubP₁ and SubP₂ to form the revised plan $P_1^{\prime }$ and $P_2^{\prime }$. This revised plan $P_1^{\prime }$ and $P_2^{\prime }$ becomes the input P₁ and P₂ for the next refinement step. Supplementary Figure S3 shows three-merged plans, including two refined ones (green and blue). The pseudocode for this step is given in Algorithm 2.

We crafted the method above to maintain the property described in the following observation.

Observation 1 Let P₁ be a (partial) merge plan, and$P_1^{\prime }$its refinement by our merge algorithm, where${\ell }_1,\mathrm{..},{\ell }_n$are the elements in$L_1$that are covered by interval$p_i\in P_1$and$m_1,\dots ,m_o$are the elements of$L_2$covered by interval$q_j\in P_2$. The following conditions hold: (1)$\left|P_1\right|=\left|P_2\right|$and$\left|P_1^{\prime }\right|=\left|P_2^{\prime }\right|$; (2) given any pair of elements where${\ell }_a\in p_i,\hspace{0.17em}{\ell }_b\in p_j$and$p_i\cap p_j=\phi$there exists intervals$p_i^{\prime }$and$p_j^{\prime }$in$P_1^{\prime }$such that$p_i^{\prime }\cap p_j^{\prime }=\phi$and${\ell }_a\in p_i^{\prime },\hspace{0.17em}{\ell }_b\in p_j^{\prime }$; and lastly, (3) given an interval p_i in P₁ and the subsets of the alphabet used${\sigma }_1\in {\ell }_1,\mathrm{..},{\ell }_n$and${\sigma }_2\in m_1,\dots ,m_o$, then p_i will be partitioned into$\left|\mathit{Sub}{P}_1\right|=|{\sigma }_1\cup {\sigma }_2|$subintervals in$P_1^{\prime }$.

We defined this observation for P₁ but note that an analogous observation exists for P₂.

Algorithm 2. Revising P₁ and P₂

procedure Partition(W₁, W₂)

  $\Sigma \prime \leftarrow \mathit{AlphabetUsed}(W_1,W_2)$

  $\mathit{Sub}{P}_1\leftarrow ()$

  $\mathit{Sub}{P}_2\leftarrow ()$

  for all$c\in \Sigma \prime$do

    $\mathit{Sub}{P}_1.\mathit{Append}(\mathit{IntervalOccupied}(c,W_1))$

    $\mathit{Sub}{P}_2.\mathit{Append}(\mathit{IntervalOccupied}(c,W_2))$

  end for

  return (SubP₁, SubP₂)

end procedure

 

 

procedure RefinePlan(P₁, P₂, Col₁, Col₂, i)

  $P_1^{\prime }\leftarrow ()$

  $P_2^{\prime }\leftarrow ()$

  % For each interval in P₁ (and P₂)

  for all$j\in \left\{\mathrm{1..}\right|P_1\left|\right\}$do

   %…extract a window from each column covered by the interval…

    $W_1\leftarrow \mathit{CoveredSymbols}(\mathit{Co}{l}_1,P_1[j])$

    $W_2\leftarrow \mathit{CoveredSymbols}(\mathit{Co}{l}_2,P_2[j])$

    %…and partitioning that window on its character runs, forming sub-intervals.

    $(\mathit{Sub}{P}_1,\mathit{Sub}{P}_2)\leftarrow \mathit{Partition}(W_1,W_2)$

    $P_1^{\prime }.\mathit{Concatenate}(\mathit{Sub}{P}_1)$

    $P_2^{\prime }.\mathit{Concatenate}(\mathit{Sub}{P}_2)$

  end for

  if$i\in \{1,k-1,k-2\}$then

    $S_i\leftarrow (P_1^{\prime },P_2^{\prime })$

  end if

  return$(P_1^{\prime },P_2^{\prime })$

end procedure

4.2.3 The execution step

We execute the merge plan by combining the elements of $\mathit{Edge}-\mathit{BWT}(G_1)$ that are covered by an interval in P₁ with the elements of $\mathit{Edge}-\mathit{BWT}(G_2)$ that are covered by the same interval in P₂ into a single element in $\mathit{Edge}-\mathit{BWT}(G_M)$. We note that when all characters of each k-mer in $L_1$ and $L_2$ have been computed and accounted for, each interval in P₁ (and P₂) will cover either 0 or 1 element of $L_1$ (and $L_2$) and the number of intervals in P₁ (equivalently P₂) will be equal to $|\mathit{Edge}-\mathit{BWT}(G_M)|$. Thus, we consider and merge each pair of intervals of P₁ and P₂ in an iterative manner. We let $(p_i^1,p_i^2)$ as the i-th pair of intervals. We concatenate the next character of $\mathit{Edge}-\mathit{BWT}(G_1)$ onto the end of $\mathit{Edge}-\mathit{BWT}(G_M)$ if $\left|p_i^1\right|=1$. If $\left|p_i^2\right|=1$ then we dismiss the next character of $\mathit{Edge}-\mathit{BWT}(G_2)$ since it corresponds to the edge that was just added. Lastly, if $\left|p_i^1\right|=0$ and $\left|p_i^2\right|=1$, we copy the next character from $\mathit{Edge}-\mathit{BWT}(G_2)$ onto the end of $\mathit{Edge}-\mathit{BWT}(G_M)$.

We merge the color matrices in an identical manner by copying elements of $C_1$ and $C_2$ to $C_M$. Again, we iterate through the plan by considering each pair of intervals. If $\left|p_i^1\right|=1$ and $\left|p_i^2\right|=1$ then we concatenate the corresponding rows of $C_1$ and $C_2$ to form a new row that is added to $C_M$. If only one of $p_i^1$ or $p_i^2$ is non-zero then the corresponding row of $C_1$ or $C_2$ is copied to $C_M$ with the other elements of the new row set to 0. Lastly, we note that we discussed the planning and execution steps of merging the primary components. As previously mentioned, details about merging the secondary components are given in the Supplementary Section 12.

The following theorem demonstrates the efficiency of our approach. The proof of the following theorem is found in the Supplementary Section 13.

Theorem 1. Given two colored de Bruijn graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ constructed for k, where $\left|E_1\right|\ge \left|E_2\right|$. It follows that our merge algorithm constructs the merged colored de Bruijn graph G_M in $O(|E_1|·\max (k,t))$-time, where t is the number of colors in G_M.

5 Results

In this section, we show the correctness of our method, the reduction in the resources used to build a colored de Bruijn graph by merging, and the comparison between state-of-the-art methods for building colored de Bruijn graphs. We ran all performance experiments on a machine with two Xeon E5-2640 v4 chips, each having 10 2.4 GHz cores. The system contains 755 GB of RAM and two ZFS RAID pools of nine disk each for storage. We report wall clock time and maximum resident set size from Linux.

5.1 Validation on Escherichia coli

In order to validate the correctness of our approach, we generated two succinct colored de Bruijn graphs with two sets of three Escherichia coli (E.coli) incomplete assemblies each, merged them to a single six-color graph, and verified its equivalence to a six-color graph built from scratch using $\text{Vari}$. We obtained the six sub-strains of E.coli K-12 from NCBI. Each of the genomes contained approximately 4.6 million base pairs and had a median GC content of 49.9%. This experiment tests that the merged colored de Bruijn graph built by $\text{VariMerge}$ is equivalent to that produced by building the graph without merging (i.e. with $\text{Vari}$ alone) even in the presence of any redundant dummy edges. We tested equivalence by running a bubble-calling algorithm on both six-color graphs and found the identical set of bubbles between them. Further, we found $\text{VariMerge}$ produced files on disk that were bit-for-bit identical to those generated by $\text{Vari}$ when consuming complete assemblies, demonstrating the merge algorithm perfectly merges the succinct source graphs. We leave additional details of this validation to the Supplementary (see Supplementary Table S4).

5.2 Demonstration of large-scale construction and incremental updates

We downloaded the sequence data from for 16 000 Salmonella strains (NCBI BioProject PRJNA18384), assembled them individually with IDBA, then divided them into four sets of 4000 strains, which we label 4A, 4B, 4C and 4D. From these datasets we construct a colored de Bruijn graph for 8000 strains, to demonstrate the efficiency of the merge process, and 16 000 strains, to demonstrate scalability. The exact accessions for each dataset are available in our repository.

In order to measure the effectiveness of $\text{VariMerge}$ for the proposed divide-and-conquer method of building large graphs, we constructed the colored de Bruijn graph using $\text{Vari}$ for a set of 4000 salmonella assemblies (4A). This took 8 h 46 min, 1 TB of external memory and 136 GB of RAM to build the graph for 4000 strains. We then built a graph for a second set of 4000 assemblies (4B) using 10 h 40 min, 1.5 TB of external memory and 137 GB of RAM. We merged these two 4000 sample graphs (i.e. 8AB) using our proposed algorithm in 2 h 1 min, no external memory and 10 GB of RAM. ‘0’ is shown in the external memory column of Table 1 for merge since no external memory is ever used for merging. Thus the $\text{VariMerge}$ method required a combined 137 GB of RAM, 26 h 30 min of runtime to produce the graph for 8000 strains. We denote this graph with 8000 strains as 8AB. In contrast, running $\text{Vari}$ on the same 8000 strains required 37 h 27 min, 4.6 TB of external memory and 271 GB of RAM. Thus $\text{VariMerge}$ reduced runtime by 11 h, reducing RAM requirements to 134 GB and reducing external memory requirements by 3.1 TB.

Table 1.

Breakdown of the memory, disk and time usage of $\text{VariMerge}$ to build the colored de Bruijn graph for 8000 strains

	Input stats		de Bruijn graph			Color matrix			Combined requirements
Program and dataset	k-mers	Colors	RAM (GB)	Time	Size (GB)	RAM (GB)	Time	Size (GB)	RAM (GB)	External memory (TB)	Time	Size (GB)
$\text{Vari}$(4A)	1.1 B	4000	136	8 h 46 min	0.31	52	1 h 39 min	51.2	136	1	10 h 25 min	51
$\text{Vari}$(4B)	1.5 B	4000	137	10 h 40 min	0.52	54	2 h 22 min	52.5	137	1.5	13 h 2 min	53
$\text{Merge}$(4A, 4B)	2.4 B	8000	10	2 h 1 min	0.63	117	1 h 2 min	106	117	0	3 h 3 min	106
$\text{VariMerge}$	2.4	8000	137	21 h 27 min	0.63	117	5 h 3 min	117	137	1.5	26 h 30 min	106

Note: The $\text{VariMerge}$ method consists of running $\text{Vari}$ on subsets of the population (4A and 4B) and then merging the results with our proposed merge algorithm (denoted $\text{Merge}$ here). We list the resources used for both individual runs of $\text{Vari}$, the $\text{Merge}$ required and the combined resources. The combined resources consist of the total time and maximum space used across all three components of $\text{VariMerge}$ used in this dataset. No external memory is needed for merging itself so ‘0’ is in the external memory column for $\text{Merge}$.

We further used this facility to merge two more 4000 color graphs (i.e. 4C + 4D) (Table 2). We denote the resulting graph as 8CD. We then merged this 8000 sample graph with the aforementioned 8000 color graph to produce a succinct colored de Bruijn graph of 16 000 samples (i.e. 8AB + 8CD).

Table 2.

Breakdown of the peak memory, peak disk and time required by $\text{VariMerge}$ to build the colored de Bruijn graph for 16 000 strains of Salmonella

	Input stats		de Bruijn graph			Color matrix			Combined requirements
Program and dataset	k-mers (B)	Colors	RAM (GB)	Time	Size (GB)	RAM (GB)	Time	Size (GB)	RAM (GB)	External memory (TB)	Time	Size (GB)
$\text{Vari}$(4C)	1.7 B	4000	135	10 h 53 min	0.46	53	2 h 34 min	51.8	135	1.6	13 h 27 min	52
$\text{Vari}$(4D)	2.4 B	4000	137	14 h 35 min	0.67	59	3 h 37 min	57.9	137	2.34	18 h 12 min	59
$\text{Merge}$(4C, 4D)	3.8 B	8000	17	2 h 59 min	1.00	118	57 min	107	118	0	3 h 56 min	108
$\text{Merge}$(8AB, 8CD)	5.8 B	16 000	25	4 h 53 min	1.60	254	2 h 10 min	232	254	0	7 h 3 min	233
$\text{VariMerge}$	5.8 B	16 000	137	54 h 47 min	1.60	254	14 h 21 min	232	254	2.34	69 h 8 min	233

Note: We note $\text{VariMerge}$ includes the resources required of the two 4000 runs of $\text{Vari}$ (i.e. $\text{Vari}$(4A) and $\text{Vari}$(4B)) and the merge run (i.e. $\text{Merge}$(4A, 4B)) from Table 1. No extra external memory is needed for merging so ‘0’ is in the external memory column for $\text{Merge}$.

In order to measure the effectiveness of $\text{VariMerge}$ for incremental additions to a graph that holds a growing population of genomes, we started with the colored de Bruijn graph of 16 000 salmonella assemblies. We then constructed a second graph for a singleton set of just one additional assembly. Next, we ran our proposed merge algorithm on these two graphs. $\text{VariMerge}$ took 69 h 8 min, 2.34 TB of external memory and 254 GB of RAM to build the graph for 16 000 strains. To build a single colored de Bruijn graph for an additional strain, $\text{Vari}$ took 7 s, 460 MB of external memory and 2.3 GB of RAM. Our proposed merge algorithm took 7 h 9 min, no external memory and 254 GB of RAM to merge the 16 000 color graph with the one color graph. This is an order of magnitude faster than the almost 70 h it would take to build the same 16 001 color graph from scratch.

This experiment also reveals that increasing the number of divisions (below a reasonable threshold) will lower the time, memory and external memory—with the tradeoff being the practical challenge of dividing and merging the data. Nonetheless, this is one of the benefits of $\text{VariMerge}$, as smaller and smaller memory and external memory could be used by making further divisions of the data.

5.3 Comparison to existing methods

We compare our method to the existing space- and memory-efficient colored de Bruijn graphs. To accomplish this, we ran Bloom Filter Trie (Holley et al., 2016), $\text{Vari}$ (Muggli et al., 2017)/Rainbowfish (Almodaresi et al., 2017), Mantis (Pandey et al., 2018)/the method of Almodaresi et al. (2019) and Multi-BRWT (Karasikov et al., 2019). The peak RAM use and running time required by the methods to construct a colored de Bruijn graph for 4000, 8000 and 16 000 strains is shown in Table 3. In addition, Table 3 illustrates the output size of all the methods. We note that all methods were run with default parameters and k = 32, except from Bloom Filter Trie which can only work with k values which are multiples of 9, hence we ran it with k = 27. We ran Mantis with their ‘log-slot’ parameter set to 33 and 36 for the experiments using 4000 and 8000 strains, and 16 000 strains, respectively. All methods are exact, colored de Bruijn graph construction methods. Since Rainbowfish first runs $\text{Vari}$ and then compresses, the peak RAM, peak disk usage, and time will be at least that of $\text{Vari}$ for construction; this is why they are shown together in Table 3. Similarly, we report peak RAM, peak disk usage and time of Mantis together with that of the method of Almodaresi et al. (2019) because the latter method first runs Mantis and then compresses the output of Mantis. These points are also discussed in the related work. Again, because we are interested in construction (not exclusively compression) we are interested in peak RAM and external memory usage.

Table 3.

Comparison between space-efficient colored de Bruijn graph construction methods for 4000, 8000 and 16 000 Salmonella strains using $\text{VariMerge}$ versus competing methods

Dataset	No. of k-mers (Billion)	Program	Output size (GB)	Time	RAM (GB)
4000	1.1	$\text{Vari}$/Rainbowfish	51	10 h 25 min	136
		Bloom Filter Trie	99	51 h 42 min	120
		Multi-BRWT	1.3 TB	42 h 23 min	156
		Mantis/Method of Almodaresi et al.	36	5 h 58 min	313
		$\text{VariMerge}$	51	10 h 25 min	136
8000	2.4	$\text{Vari}$/Rainbowfish	114	37 h 27 min	271
		Bloom Filter Trie	N/A	N/A	N/A
		Multi-BRWT	N/A	N/A	N/A
		Mantis/Method of Almodaresi et al.	38	13 h 37 min	370
		$\text{VariMerge}$	106	26 h 30 min	137
16 000	5.8	$\text{Vari}$/Rainbowfish	N/A	N/A	N/A
		Bloom Filter Trie	N/A	N/A	N/A
		Multi-BRWT	N/A	N/A	N/A
		Mantis/method of Almodaresi et al.	256	36 h 12 min	316
		$\text{VariMerge}$	233	69 h 8 min	254

Note: We report N/A for any method that exceeded 140 CPU hours, 4 TB of disk space and 750 GB of memory. We anticipate add-on methods to compress better but will still consume the resources shown for their base method because they reuse base the method’s output. We measured RAM as max resident set size. Mantis authors noted their use of memory mapped I/O means this reveals opportunistic consumption and not necessarily requirement for their program. To the best of our knowledge, no extra external memory is needed for Bloom Filter Trie, Multi-BRWT, Mantis and the method of Almodaresi et al., so it is omitted from the table.

We report N/A in Table 3 for any method that exceeded 140 h, and/or our RAM and external memory quota. We had 4 TB of disk space for each method (20 TB in total) and 750 GB of RAM. All methods performed reasonably well on 4000 strains. Bloom Filter Trie required the most time, and Multi-BRWT required the most space. This was unsurprising as Multi-BRWT focuses on compression of the color matrix and not the graph (see Related Work). Mantis (and its successor (Almodaresi et al., 2019)) required the largest peak memory (313 GB). With 8000 strains Bloom Filter Trie and Multi-BRWT required more than 140 h, Vari and Rainbowfish were able to run within the given constraints but had the longest running time (over 37 h). Mantis was more efficient with respect to final output (38 GB versus 106 GB) and $\text{VariMerge}$ was more efficient with respect to RAM consumed (137 GB versus 370 GB). Lastly, only Mantis and $\text{VariMerge}$ were capable of building the colored de Bruijn graph with 16 000 strains. For 16 000 strains our method had improved output size and RAM usage and Mantis had improved running time. Yet, as shown in the previous section, $\text{VariMerge}$ allows the graph to be updated with new data via merging. Mantis (as well as $\text{Vari}$ and Rainbowfish) provide no option to update the graph without reconstruction.

Lastly, $\text{VariMerge}$ has several practical advantages over competing methods. It allows large values of k, i.e. $k\le 64$, and allows for efficient queries of the form: given a color c, return all k-mers that have that color. Competing methods cannot perform such queries without the input files or cannot scale to large datasets. We discuss this more in the conclusions.

6 Conclusion

In this article, we develop a method to build the colored de Bruijn graph by merging smaller graphs in a resource-efficient manner. This allows the colored de Bruijn graph to be constructed for large datasets and provides an efficient means to update it. As previously mentioned, resource use can be optimized by partitioning the data into smaller, carefully selected datasets. We leave how to optimize the construction via data partitioning size as future work.

Lastly, we mention that the underlying graph data structure of $\text{VariMerge}$ has some advantages over competing methods. First, $\text{VariMerge}$ allows arbitrary k up to 64 while other tools are more restricted; BFT requires k to be multiples of 9 and Mantis only supports values of k up to 32. Second, the node labels can be recovered from the index alone, allowing the following queries to be performed: given a particular color c, what k-mers have color c. These queries can be accomplished by $\text{VariMerge}$ scanning a particular column of the color matrix and can be used for comparing samples, i.e. which k-mers are shared and which differ between sample x and sample y. While the Mantis authors have suggested an approach to supporting this query, it is unimplemented and requires the input files, increasing the size of the data structure.

Funding

This work was supported by the National Science Foundation (NSF) IIS [Grant No. 1618814 to C.B.] and National Institute of Allergy and Infectious Diseases Institute of the National Institutes of Health [Grant No. R01AI141810-01 to C.B.].

Conflict of Interest: none declared.