Topology on a new facet of bismuth

Significance

We uncover the presence of a new topological crystalline insulator (TCI) state in bismuth, which is protected by a twofold rotational symmetry. In contrast to the recently discovered higher-order topological phase in bismuth, the present TCI phase hosts unpinned Dirac cone surface states that could be accessed directly through photoemission experiments. Our study provides a comprehensive understanding of the rich topological electronic structure of bismuth.

Abstract

Bismuth-based materials have been instrumental in the development of topological physics, even though bulk bismuth itself has been long thought to be topologically trivial. A recent study has, however, shown that bismuth is in fact a higher-order topological insulator featuring one-dimensional (1D) topological hinge states protected by threefold rotational and inversion symmetries. In this paper, we uncover another hidden facet of the band topology of bismuth by showing that bismuth is also a first-order topological crystalline insulator protected by a twofold rotational symmetry. As a result, its $\left(1\overline{1}0\right)$ surface exhibits a pair of gapless Dirac surface states. Remarkably, these surface Dirac cones are “unpinned” in the sense that they are not restricted to locate at specific $k$ points in the $\left(1\overline{1}0\right)$ surface Brillouin zone. These unpinned 2D Dirac surface states could be probed directly via various spectroscopic techniques. Our analysis also reveals the presence of a distinct, previously uncharacterized set of 1D topological hinge states protected by the twofold rotational symmetry. Our study thus provides a comprehensive understanding of the topological band structure of bismuth.

Bismuth is well known for its peculiar physical properties. It was long considered to be the stable element with the highest atomic mass, but relatively recent experiments have shown that bismuth is in fact weakly radioactive (1). It is a semimetal with a vanishingly small carrier density ($10^{17}$ cm⁻³) but an exceptionally high electron mobility ($10^6\hspace{0.17em}{\mathrm{c}\mathrm{m}}^2\cdot$s⁻¹⋅V⁻¹) (2–5). As a result, the ultraquantum regime is reached in bismuth at a magnetic field as small as 9 T, beyond which a number of correlated electron states have been observed (4–7). Because of bismuth’s large spin–orbit coupling, bismuth-based materials have also played a fundamental role in topological physics (8, 9). A bismuth–antimony alloy (Bi_1−xSb_x) was the first experimental realization of a 3D topological insulator (TI) (10). The ${\mathrm{B}\mathrm{i}}_2{\mathrm{X}}_3$ family supports the prototypical TI state with a single surface Dirac cone (11–14). Doped ${\mathrm{B}\mathrm{i}}_2{\mathrm{X}}_3$ gives rise to the quantum anomalous Hall effect (15) and unconventional nematic superconductivity (16, 17). ${\mathrm{N}\mathrm{a}}_3$Bi is a 3D Dirac semimetal (18, 19). Despite being a crucially important chemical component in many topological materials, pure bismuth has long been thought to be topologically trivial. However, distinct from an atomic band insulator, bismuth does have an even number of band inversions (10, 20). The existence of these band inversions implies that bismuth cannot be smoothly connected to an atomic band insulator without undergoing closing of its band gap. This suggests that the band topology of bismuth must be far from being trivial (8, 9, 20–22).

Theoretical advances on topological crystalline insulators (TCIs) (21) have greatly expanded the topological classification of band insulators beyond the ${\mathbb{Z}}_2$ TIs (8, 9). After the success of theoretical prediction and experimental realization of the mirror-symmetry–protected TCIs (20–35), two novel TCI phases, rotational-symmetry–protected TCIs (36) and higher-order TIs (37–43), have been theoretically proposed recently. Rotational-symmetry–protected TCIs are predicted to harbor “unpinned” Dirac surface states in that the surface normal to an $N$-fold rotational axis ($N=\mathrm{2,4,6}$) can host $N$ Dirac cones whose Dirac points appear at generic $k$ points in the surface Brillouin zone. In contrast, higher-order TIs are generated through the consideration of higher-order bulk-boundary correspondence. For instance, a 3D second-order TI supports 1D topological hinge states in a rotational symmetry-preserving rod. It is important to note that the first-order and higher-order topologies are not mutually exclusive. In particular, a TCI could support both topological 2D surface states and 1D hinge states. Thus, strictly speaking, a pure higher-order TI should refer to the TCIs that do not show the presence of topological surface states. Beyond these new TCI phases, another important theoretical advance is the development of methods to systematically diagnose topological invariants in terms of the symmetry eigenvalues of the electronic states (44–51). In this connection, Song et al. (47) and Khalaf et al. (48) found that, when certain additional symmetry $Y$ is present, topological invariants of TCIs protected by symmetry $X$ can be inferred from the $Y$-related symmetry eigenvalues of the energy bands. Such proposals of symmetry indicators and topological quantum chemistry have facilitated first-principles studies of new topological materials (52–58).

Building upon these theoretical advances, a recent work (41) showed that pure bismuth hosts a second-order band topology that is protected by threefold rotational and inversion symmetries. As a result, it supports 1D topological hinge states in a crystal whose shape preserves the threefold rotational and inversion symmetries. Here we show that the band topology of bismuth is even richer in that it also hides a first-order TCI state, which is protected by its twofold rotational symmetries, resulting in a pair of unpinned topological Dirac surface states on its $\left(1\overline{1}0\right)$ surface. We also reveal the presence of a distinct, previously uncharacterized set of 1D topological hinge states protected by twofold rotational symmetry.

Results

First-principles calculations were carried out using the VASP package (59, 60). An ultrasoft pseudopotential and the generalized-gradient approximation were applied in the self-consistency process. The experimental crystal structure of Bi was used (61) in the calculations. A Wannier-basis–based tight-binding model, where the $s$ and $p$ orbitals of Bi were included, was obtained via the Wannier90 package (62).

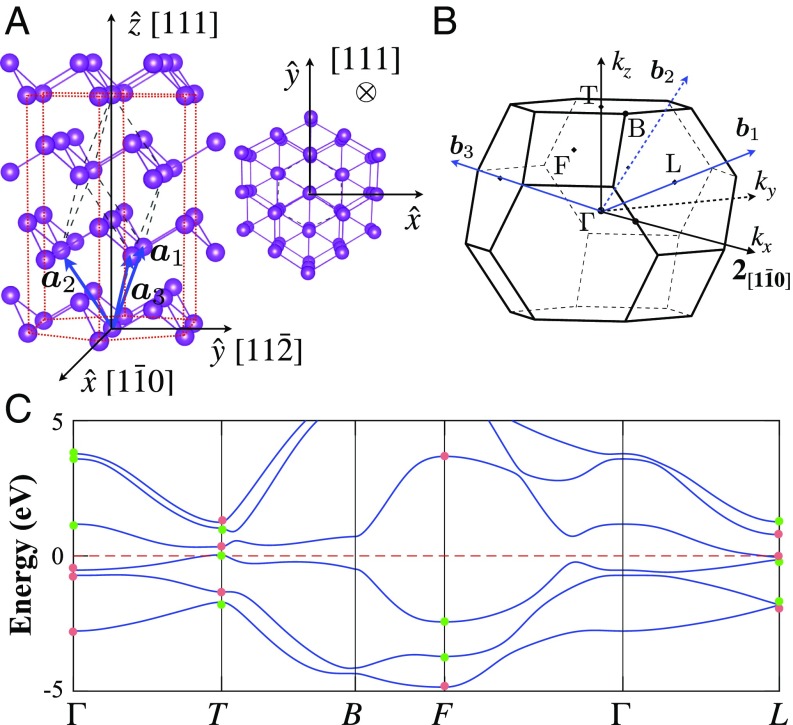
Bismuth crystalizes in a rhombohedral structure (61). Its space group and point group are R-3m ($\#166$) and $D_{3d}$, respectively. Each layer in this structure forms a buckled honeycomb lattice. The three principle lattice vectors (${\overrightarrow{a}}_{i=\mathrm{1,2,3}}$) are tilted with respect to the Cartesian directions (Fig. 1A). In this construction, the out-of-plane $\widehat{z}$ direction is [111], and the $\left[1\overline{1}0\right]$, $\left[10\overline{1}\right]$, and $\left[01\overline{1}\right]$ directions lie in plane. Key point-group symmetries of bismuth are space inversion $\mathcal{I}$; out-of-plane threefold rotation axis $3_{\left[111\right]}$; in-plane twofold rotational axes $2_{\left[1\overline{1}0\right]}$, $2_{\left[10\overline{1}\right]}$, and $2_{\left[01\overline{1}\right]}$; and mirror planes ${\mathcal{M}}_{\left[1\overline{1}0\right]}$, ${\mathcal{M}}_{\left[10\overline{1}\right]}$, and ${\mathcal{M}}_{\left[01\overline{1}\right]}$. The bulk Brillouin zone (BZ) has the shape of a truncated octahedron (Fig. 1B). The time-reversal invariant momentum (TRIM) points include one $\mathrm{\Gamma }$, one $T$, three $L$, and three $F$ symmetry points. Our band structure (Fig. 1C) confirms that bismuth is a compensated semimetal with a continuous band gap. To unfold the nature of band inversions in bismuth, we calculated the parity eigenvalues at the TRIM points, and with the exception of the $\mathrm{\Gamma }$ point, the lowest three valence bands at all of the TRIM points were found to have one state with positive parity and two states with negative parity. In contrast, at $\mathrm{\Gamma }$, all three valence bands have positive parity eigenvalues, so that bismuth has two band inversions at the $\mathrm{\Gamma }$ point.

Fig. 1.

(A) Crystal structure of bulk bismuth. The principle lattice vectors ${\overrightarrow{a}}_1=\left(\frac{-1}{2},\frac{-1}{2\sqrt{3}},\frac{1}{3}\right)$, ${\overrightarrow{a}}_2=\left(\frac{1}{2},\frac{-1}{2\sqrt{3}},\frac{1}{3}\right)$, and ${\overrightarrow{a}}_3=\left(0,\frac{1}{\sqrt{3}},\frac{1}{3}\right)$ are expressed in the Cartesian coordinates. (B) The bulk Brillouin zone. The principle reciprocal space vectors (${\overrightarrow{b}}_1$, ${\overrightarrow{b}}_2$, and ${\overrightarrow{b}}_3$) and high-symmetry points are noted. (C) Band structure of bismuth including spin–orbit coupling. The red and green circles represent positive and negative parity eigenvalues, respectively.

We turn next to discuss the symmetry-based indicators. As shown in refs. 47 and 48, crystals in the space group $\#166$ are characterized by four symmetry indicators, three ${\mathbb{Z}}_2$ invariants and one ${\mathbb{Z}}_4$ invariant (${\mathbb{Z}}_{\mathrm{2,2,2,4}}$). By enumerating the symmetry eigenvalues of the electronic states at high-symmetry points, we obtain ${\mathbb{Z}}_{\mathrm{2,2,2,4}}=\left\{\mathrm{0,0,0,2}\right\}$. Table 1 shows the corresponding topological states and the associated topological invariants. Importantly, the specific symmetry indicators (${\mathbb{Z}}_{\mathrm{2,2,2,4}}=\left\{\mathrm{0,0,0,2}\right\}$) point to two possible topological states, one being a purely rotational-symmetry–protected TCI with $n_{2_{\left[1\overline{1}0\right]}}=1$, while the other is a purely mirror-symmetry–protected TCI with $n_{{\mathcal{M}}_{\left[1\overline{1}0\right]}}=2$. To uniquely determine the topological state of bismuth, we have further calculated the mirror Chern number $n_{{\mathcal{M}}_{\left[1\overline{1}0\right]}}$ and found $n_{{\mathcal{M}}_{\left[1\overline{1}0\right]}}=0$ for bismuth; see SI Appendix, section 1 for details. Our analysis thus reveals that bismuth is a purely rotational-symmetry–protected TCI with $n_{2_{\left[1\overline{1}0\right]}}=1$. Note that there are three twofold rotational axes ($2_{\left[1\overline{1}0\right]}$, $2_{\left[10\overline{1}\right]}$, and $2_{\left[01\overline{1}\right]}$) involved here, which are related by the out-of-plane threefold rotation $3_{\left[111\right]}$. We elaborate on the nontrivial topology protected by $2_{\left[1\overline{1}0\right]}$. The other two twofold rotational axes are associated with the same nontrivial topology, so that the associated surfaces can also be expected to host a pair of unpinned Dirac surface states. Moreover, the symmetry indicators point to a nontrivial topological invariant associated with space-inversion symmetry ($n_{\mathcal{I}}=1$). This guarantees 1D topological hinge states protected by inversion symmetry, which is consistent with previous findings based on the additional $C_{3\left[111\right]}$ constraint (41). We emphasize that the high-order TI predicted in ref. 41 does not support first-order surface states (36, 47, 48) because there are no topological invariants associated with $C_{3\left[111\right]}$ alone.

Table 1.

Two possible topological states for the symmetry indicator ${\mathbb{Z}}_{\mathrm{2,2,2,4}}=\left\{\mathrm{0,0,0,2}\right\}$ (47)

$\left({\nu }_0;{\nu }_1{\nu }_2{\nu }_3\right)$	$n_{2_{\left[1\overline{1}0\right]}}$	$n_{{\mathcal{M}}_{\left[1\overline{1}0\right]}}$	$n_{\mathcal{I}}$
(0;000)	1	0	1
(0;000)	0	2	1

$\left({\nu }_0;{\nu }_1{\nu }_2{\nu }_3\right)$ are the ${\mathbb{Z}}_2$ invariants for 3D ${\mathbb{Z}}_2$ TIs. $n_{2_{\left[1\overline{1}0\right]}}$ is a ${\mathbb{Z}}_2$ invariant for the twofold rotational symmetry $2_{\left[1\overline{1}0\right]}$. $n_{2_{\left[1\overline{1}0\right]}}=1$ corresponds to a rotational-symmetry–protected TCI, which features two unpinned Dirac surface states on the $\left(1\overline{1}0\right)$ surface. $n_{{\mathcal{M}}_{\left[1\overline{1}0\right]}}$ is the mirror Chern number for mirror plane ${\mathcal{M}}_{\left[1\overline{1}0\right]}$ and is a ${\mathbb{Z}}_N$ invariant. $n_{{\mathcal{M}}_{\left[1\overline{1}0\right]}}=N$ features N Dirac surface states. Finally, $n_{\mathcal{I}}$ is the ${\mathbb{Z}}_2$ classified inversion ($\mathcal{I}$) protected TCI index. $n_{\mathcal{I}}=1$ features the hinge state in a 3D finite geometry preserving $\mathcal{I}$.

To obtain a deeper understanding of ${\mathbb{Z}}_4=2$, we provide an intuitive physical picture that connects the band inversion property to the rotational-symmetry–protected topology along the lines of the physics discussed in ref. 41. Recall that a single band inversion at $\mathrm{\Gamma }$ can lead to a strong TI state. Therefore, the double band inversions in bismuth can be viewed as representing two sets of strong TI band structures, where each strong TI contributes a surface Dirac cone at $\overline{\mathrm{\Gamma }}$ (Fig. 2C). The nontrivial topology protected by the twofold rotation $2_{\left[1\overline{1}0\right]}$ then yields the double Dirac cones, which remain gapless on the $\left(1\overline{1}0\right)$ surface. To further connect the above intuitive picture to the symmetry indicators, we provide a more detailed analysis of the representations at the TRIM points. For this purpose, it is helpful to rearrange the Fu–Kane formula (63) (Eq. 1) as

$${\left(-1\right)}^{{\nu }_0}={\left(-1\right)}^{\frac{1}{2}{\sum }_{k\in \mathrm{T}\mathrm{R}\mathrm{I}\mathrm{M}\mathrm{s}}{n}_k^{-}}$$ [1]

$$={\left(-1\right)}^{\frac{1}{2}{\sum }_{k\in \mathrm{T}\mathrm{R}\mathrm{I}\mathrm{M}\mathrm{s}}{\mathcal{C}}_{2+,k}^{-}+\frac{1}{2}{\sum }_{k\in \mathrm{T}\mathrm{R}\mathrm{I}\mathrm{M}\mathrm{s}}{\mathcal{C}}_{2-,k}^{-}}$$ [2]

$$={\left(-1\right)}^{\left({\nu }^{\left(+\right)}+{\nu }^{\left(-\right)}\right)},$$ [3]

where ${\nu }_0$ is the strong TI (STI) index, and $n_k^{-}$ is the number of occupied bands with negative parity eigenvalue. For space group $\#$166, only TRIMs $\left\{\mathrm{\Gamma },T,L_1,F_1\right\}$ are invariant under one of the three ${\mathcal{C}}_2^{i\left(i=\mathrm{1,2,3}\right)}$ axes. However, states at the other pairs of $\left\{L_2,L_3\right\}$ and $\left\{F_2,F_3\right\}$ can be linearly combined into states invariant under ${\mathcal{C}}_2^{i=1}$. Thus, the occupied bands can be separated into two subspaces according to their respective ${\mathcal{C}}_2$ eigenvalues ($\pm$), which are $\left\{{\mathcal{C}}_{2+}^{-}\right\}$ and $\left\{{\mathcal{C}}_{2-}^{-}\right\}$ (Eq. 2). This rearrangement may lead to new topology beyond the ${\mathbb{Z}}_2$ TI state, but it can be made only when the system is ${\mathbb{Z}}_2$ trivial (${\nu }_0=0$). From Eq. 3, we see that ${\nu }^{\left(+\right)/\left(-\right)}$ plays a role similar to that of ${\nu }_0$ within each of the ${\mathcal{C}}_2$ subspaces. ${\nu }^{\left(\pm \right)}$ can be directly obtained from the symmetry indicator ${\mathbb{Z}}_4$ (37, 46–48), using

$${\mathbb{Z}}_4=\sum _{k\in \mathrm{T}\mathrm{R}\mathrm{I}\mathrm{M}\mathrm{s}}{C}_{2+,k}^{-}\hspace{0.17em}\mathrm{mod}\hspace{0.17em}4.$$ [4]

Eq. 4 shows that ${\mathbb{Z}}_4=2$ corresponds to ${\nu }^{\left(+\right)}={\nu }^{\left(-\right)}=1$. In other words, the band structure in each ${\mathcal{C}}_2$ subspace can be viewed as a strong TI. The hybridization between the two strong TI surface states in the presence of the $2_{\left[1\overline{1}0\right]}$ rotational symmetry thus leads to the pair of unpinned Dirac surface states on the $\left(1\overline{1}0\right)$ surface.

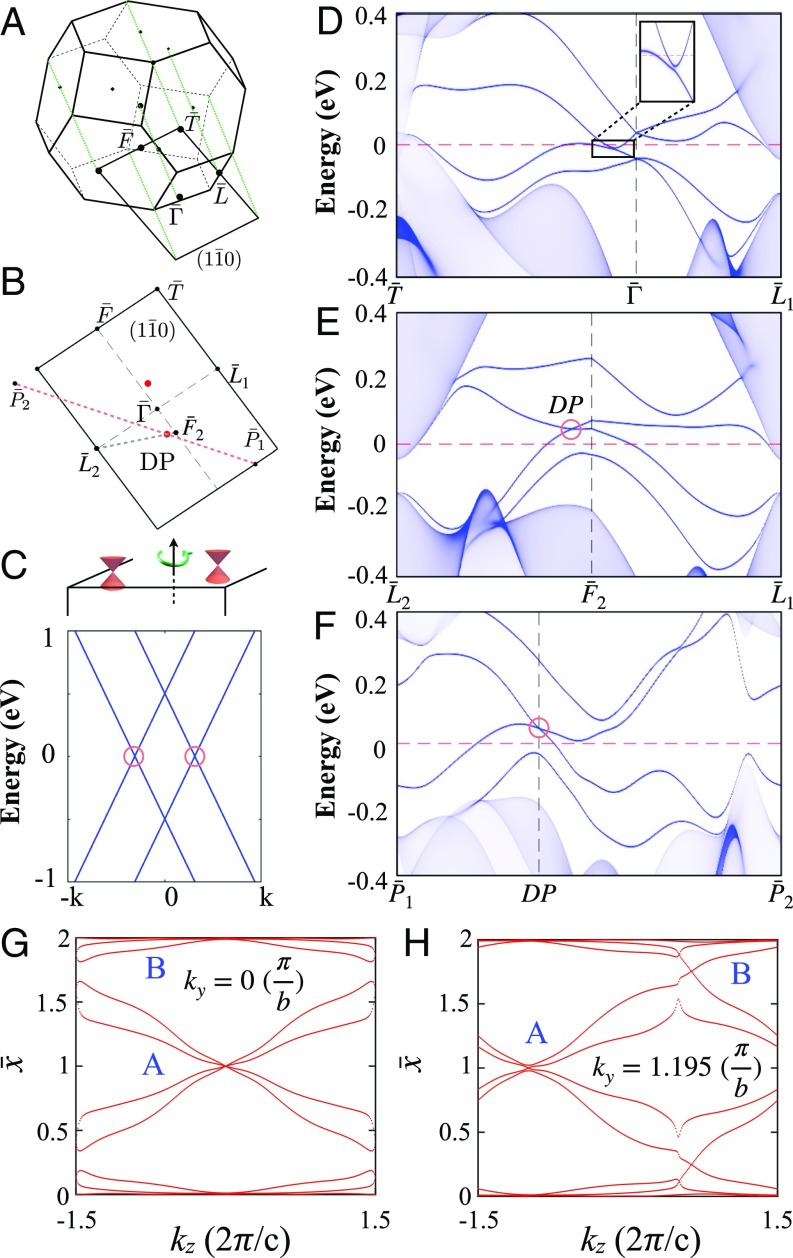
Fig. 2.

(A and B) The projected ($1\overline{1}0$) surface Brillouin zone on which several $k$ points, $k$ paths, and the predicted positions of the unpinned surface DPs are detailed. (C) The schematic shows the unpinned surface DPs on the surface preserving ${\mathcal{C}}_2$. (D) Surface band spectrum along the high-symmetry $k$ path, $\overline{T}-\overline{\mathrm{\Gamma }}-\overline{L}$. Inset shows that the surface states are gapped along this path. (E and F) Surface band spectrum along the $k$ paths containing the DP (see the trajectories in B). The spectrum in F shows that the surface Dirac fermion is type II: The Dirac cone is strongly tilted so that the velocities of the two bands that cross have the same sign. (G and H) WCCs of the loop integrated around $\left[1\overline{1}0\right]$ ($k_x$) at (G) $k_y=0\hspace{0.17em}\pi /b$ and (H) $k_y=1.195\hspace{0.17em}\pi /b$ with respect to $k_z$, where A and B indicate two WCC sheets that connect only at generic ($k_y,k_z$).

With the preceding discussion in mind, we computed the surface band structure throughout the $\left(1\overline{1}0\right)$ surface BZ (Fig. 2). As expected, we found two sets of surface Dirac cones, whose Dirac points are located at ($\pm 0.01\hspace{0.17em}\pi ,\mp 0.269\hspace{0.17em}\pi$) of ($k_y,k_z$) axes indicated in Fig. 1B. These are generic $k$ points, which are related only by the twofold rotational symmetry $2_{\left[1\overline{1}0\right]}$. The calculated surface states along the $k$ paths passing through the Dirac points (DPs) (Fig. 2 E and F) directly show the presence of gapless Dirac surface states. Interestingly, these unpinned Dirac fermions are of type II (64) in that the velocities of the two surface bands that cross possess the same sign. By contrast, along the path $\overline{T}-\overline{\mathrm{\Gamma }}-{\overline{L}}_1$ that does not go through the DP, the surface states are gapped (Fig. 2D). To further confirm the nontrivial nature of these states, we studied the Wannier charge centers (WCCs) (65–67) ${\overline{x}}_n\left(k_y,k_z\right)=⟨W_{n0}\left|\widehat{x}\right|W_{n0}⟩$ on the $\left(1\overline{1}0\right)$ surface, where $\left|W_{n0}\right.⟩$ is the $n$th Wannier state in the unit cell of $R_x$ = 0 and $\widehat{x}$ is the position operator (68). Two dominant WCC sheets, marked by A and B in Fig. 2 G and H, are seen to be disjointed in the whole surface Brillouin zone, except at $\left(k_y,k_z\right)=\left(1.195\hspace{0.17em}\frac{\pi }{b},1.28\hspace{0.17em}\frac{\pi }{c}\right)$ (Fig. 2H). These results unambiguously demonstrate the presence of unpinned Dirac surface states associated with the twofold rotational-symmetry–protected topology.

We now demonstrate the 1D topological hinge states protected by $2_{\left[1\overline{1}0\right]}$. For this purpose, we constructed two types of bismuth rods (Fig. 3 A and B), which are periodic along the $\left[1\overline{1}0\right]$ axis but finite sized within the plane that is perpendicular to $\left[1\overline{1}0\right]$. In the first rod, the side surfaces are the (111) and $\left(11\overline{2}\right)$ surfaces and the cross-section is rectangular (Fig. 3A). In the second rod, the side surfaces are (001) and (111) and the cross-section is a parallelogram (Fig. 3B). Both rods are invariant under the twofold rotation $2_{\left[1\overline{1}0\right]}$. The calculated band structures for rods 1 and 2 are shown in Fig. 3 C and D, from which we can clearly identify the existence of 1D helical edge states lying inside the bulk band gap. We also investigated the real-space distribution of the wave function of these 1D helical edge states. Fig. 3 E and F shows that these helical states are localized on the edges shared by adjacent side surfaces, further confirming that these are topological hinge states.

Fig. 3.

(A and B) Two types of 1D bismuth rods that preserve the twofold rotation symmetry $2_{\left[1\overline{1}0\right]}$. These rods are periodic along the $\left[1\overline{1}0\right]$ axis but finite sized within the plane that is perpendicular to $\left[1\overline{1}0\right]$. In the first rod (A), the side surfaces are the (111) and $\left(11\overline{2}\right)$ surfaces and the cross-section is a rectangle. (C and D) Energy dispersions of rods 1 and 2. The topological hinge states are marked by red lines. (E and F) Real-space distributions of the hinge states of rods 1 and 2.

Finally, we show that the $2_{\left[1\overline{1}0\right]}$ rotational-symmetry–protected topology sheds light on the large Rashba surface states observed on the (111) and (001) surfaces (2, 3). The double bulk band inversion at $\mathrm{\Gamma }$ also leads to a pair of surface Dirac cones on the (111) and (001) surfaces. However, as (111) and (001) surfaces do not respect $2_{\left[1\overline{1}0\right]}$, these Dirac cones are gapped, which naturally gives rise to the Rashba surface bands (Fig. 4). Note that since the Rashba surface states are nontopological, they can be created or removed by adjusting the surface potential (69). Our analysis gives insight into the origin of Rashba bands on bismuth’s (111) and (001) surfaces, which have been observed experimentally (2, 3, 69), in terms of the underlying symmetries and the double band inversions in the band topology of bismuth.

Fig. 4.

(A and B) The projected (111) and (001) surface Brillouin zones (SBZs) on which some of the high-symmetry k points are indicated. (C) Schematic illustration of the gapped surface states due to the double band inversions without the ${\mathcal{C}}_2$ protection as discussed in the text. (D and E) Band spectrum for (111) and (001) surfaces, respectively. The green dotted lines show the Rashba bands due to the double band inversions.

In summary, we have investigated topological properties of the bulk and surface band structures of bismuth. We show that bismuth is a TCI with multiple nontrivial topological invariants. In the first order, bismuth features unpinned Dirac surface states on the $\left(1\overline{1}0\right)$, $\left(01\overline{1}\right)$, and $\left(\overline{1}01\right)$ surfaces that are protected by their twofold rotational symmetries. These unpinned Dirac surface states would be amenable to direct imaging via photoemission spectroscopy. In the second order, bismuth features two sets of independent topological helical hinge states. The first set is protected by the twofold rotational symmetries whereas the second set is protected by space inversion symmetry. Our study thus provides a comprehensive picture of the rich band topology of bismuth, which is arguably the most important element involved in the field of topological materials.

Note Added in Proof.

After we completed our study, we became aware of refs. 54 and 55, which also propose bismuth as a potential TCI. Our analysis, however, uniquely identifies bismuth as a rotational-symmetry–protected TCI.