Abstract
Working memory is fundamental to cognition, allowing one to hold information ‘in mind’. A defining characteristic of working memory is its flexibility: we can hold anything in mind. However, typical models of working memory rely on finely tuned, content-specific, attractors to persistently maintain neural activity and therefore do not allow for the flexibility observed in behavior. Here we present a flexible model of working memory that maintains representations through random recurrent connections between two layers of neurons: a structured ‘sensory’ layer and a randomly connected, unstructured, layer. As the interactions are untuned with respect to the content being stored, the network maintains any arbitrary input. However, in our model this flexibility comes at a cost: the random connections overlap, leading to interference between representations and limiting the memory capacity of the network. Additionally, our model captures several other key behavioral and neurophysiological characteristics of working memory.
Keywords: working memory, cognitive flexibility, capacity limitations, cognitive control, E/I balance, mixed selectivity, computational model
eTOC Blurb :
Working memory is highly flexible; one can hold anything ‘in mind’. Bouchacourt and Buschman present a model of working memory that uses random connections to flexibly maintain any input. Many behavioral and neurophysiological characteristics of working memory are also captured.
1. Introduction
Working memory is the ability to hold information ‘in mind’. It acts as a workspace on which information can be held, manipulated, and then used to guide behavior. In this way, it plays a critical role in cognition, decoupling behavior from the immediate sensory world. However, the circuit mechanisms that support working memory remain unclear. In particular, existing models fail to capture key behavioral and neural characteristics of working memory.
Working memory has two defining behavioral characteristics. First, it is highly flexible: one can hold anything in mind and can do it from the first experience. This provides cognition with its versatility, allowing us to think and learn about anything. Second, working memory has a severely limited capacity. Humans and monkeys are able to maintain only 3-4 objects at once (Luck and Vogel, 1997; Cowan, 2010; Buschman et al., 2011). In other words, although one can hold anything in mind, one can only hold a few of them at a time.
In addition to these behavioral characteristics, previous work has identified several neural characteristics of working memory. First, the contents of working memory are thought to be represented in both the persistent activity of neurons (Funahashi et al., 1989; Fuster, 1999; Romo et al., 2002) and in the dynamic evolution of neural activity over time (Murray et al., 2016; Stokes, 2015). Second, working memory representations are distributed across the brain: they have been observed in prefrontal, parietal, and sensory cortex (for review, see Christophel et al. (2017)). Third, increasing the number of items held in working memory (the ‘memory load’), increases the overall activity in these brain regions (up to an individual capacity limit; (Curtis and D’Esposito, 2003; Ma et al., 2014)). However, increasing memory load also reduces the selectivity of individual neurons in a divisive-normalization-like manner; the firing rate of neurons selective for one item is decreased with the addition of other items. This normalization is thought to lead to the reduced memory performance and accuracy at high memory loads (Buschman et al., 2011; Sprague et al., 2014).
Theoretical models have captured some, but not all, of these characteristics. The dominant model of working memory is that recurrent network interactions, either within or between brain regions, give rise to persistent neural activity (Wang, 2001; Barak and Tsodyks, 2014). These models have a limited capacity, as lateral inhibition limits the number of simultaneous patterns of activity that can be maintained (Edin et al., 2009; Swan and Wyble, 2014). However, these models are inflexible. They rely on fine tuning of connections to embed stable fixed points in the network dynamics specific to the content being stored. These connections must be hardwired or learned for each type of information, and so the network cannot flexibly represent novel, unexpected, stimuli. Indeed, networks of this type in the brain seem to encode ecologically relevant information, such as heading direction (Kim et al., 2017).
Models that represent working memory as a result of transient dynamics in neural activity are similarly inflexible. They require learning to embed the dynamics, to decode the temporally evolving representations, or to ensure the dynamics are orthogonal to mnemonic representations (Vogels et al., 2005; Druckmann and Chklovskii, 2012; Jaeger, 2002).
Other models capture the flexibility of working memory, such as those that hypothesize working memory representations are encoded in short-term synaptic plasticity or changes in single-cell biophysics (Loewenstein and Sompolinsky, 2003; Hasselmo and Stem, 2006; Mongillo et al., 2008). However, these models do not directly explain the limited capacity of working memory and do not capture many of the neurophysiological characteristics of working memory, such as the coexistence of persistent and dynamic representations seen in neural data.
Here we propose a flexible model of working memory that relies on random reciprocal connections to generate persistent activity. As the connections are random, they are inherently untuned with respect to the content being stored and do not need to be learned, allowing the network to maintain any representation. However, this flexibility comes at a cost - when multiple memories are stored in the network, they begin to interfere, resulting in a divisive-normalization-like reduction of responses and imposing a capacity limit on the network. Thus, our model provides a mechanistic explanation for the limited capacity of working memory; it is a necessary trade-off for its flexibility.
2. Results
2.1. A flexible model of working memory
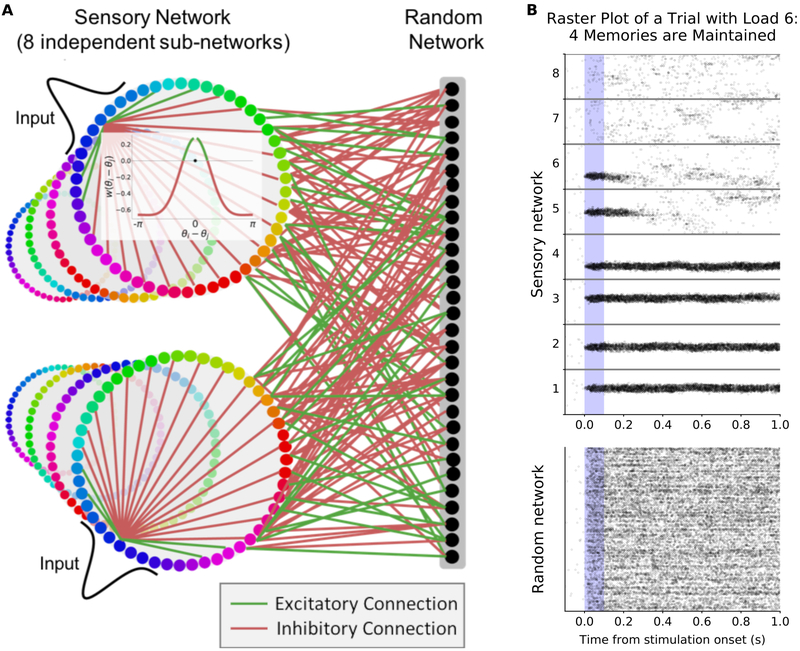
We model a simplified two-layer network of Poisson spiking neurons (Fig. 1A; see Methods for a detailed description). The first layer is the ‘sensory network’ and consists of 8 independent ring-like sub-networks (each with 512 neurons). These sub-networks mimic simplified sensory networks and can be thought of as encoding the identity of independent stimuli at different locations in space. Therefore, we can vary working memory load by varying the number of sensory sub-networks receiving inputs.
Figure 1: Flexible working memory through interactions between a structured network and a random network.
(A) Model layout. The sensory network is composed of 8 ring-like sub-networks (although other architectures can be used, Figs. 8, S4F, and S8). The inset shows center-surround connectivity within a sensory sub-network (excitatory connections in green, inhibitory in red). The connections to the random network are randomly assigned and balanced. (B) Raster plot of an example trial with 8 sensory sub-networks (512 neurons each) randomly connected to the same random network (1024 neurons). Six sensory sub-networks (1-6) receive a Gaussian input for 0.1 seconds during the ‘stimulus presentation’ period (shaded blue region). Representations are maintained (without external drive) for four of the inputs. See also Fig. S1A.
Neurons within each sensory sub-network are arranged topographically according to selectivity. Position around the ring corresponds to specific values of an encoded feature, such as color or orientation. Consistent with biological observations, connections within a sensory sub-network have a center-surround structure: neurons with similar selectivity share excitatory connections while inhibition is broader (Fig. 1A, inset, (Kiyonaga and Egner, 2016; Kim et al., 2017)). However, recurrent excitation within each sub-network is too low to maintain memories alone. For simplicity, we first consider a network without connections between sensory sub-networks, although this constraint is relaxed in later models.
The second layer is the ‘random network’ (1024 neurons, a four-fold compression from the sensory network). Neurons in this layer are randomly and reciprocally connected to neurons in the sensory network. Each neuron in the random network has bi-directional excitatory connections with a random subset of neurons in the sensory network (with likelihood γ here, 0.35). Importantly, all sensory neurons converge onto the same random network. The connections between the sensory and random networks are balanced, such that individual neurons receive an equal amount of excitatory and inhibitory drive (i.e. the summed input weight to each neuron from the other network is zero). To achieve this, all pairs of random and sensory neurons without excitatory connections have direct, weak, inhibitory connections (see Methods for details). Such excitation-inhibition balance is consistent with neurophysiological findings (Vogels et al., 2011; Vogels and Abbott, 2005; Mariño et al., 2005).
Despite this simple architecture, the network is able to maintain stimulus inputs over extended memory delays (Fig. 1B). This is due to the bi-directional and reciprocal connections between the sensory and random networks. Activity in the sensory network feeds-forward into the random network, activating a random subset of neurons (Fig. 1B, bottom). In turn, neurons from the random network feedback into the sensory network, maintaining activity after the stimulus input is removed (Fig. 1B, top, sensory sub-networks 1-4). The reciprocal nature of the connections ensures the synaptic drive fed back into a sensory sub-network from the random network closely matches its own representation (Fig. S1A). In this way, the network can flexibly maintain the representation of any input into the sensory network.
Neurons from the random network project back to multiple sensory sub-networks. However, activity in the random network does not lead to spuriously sustained representations in other, unstimulated, sensory sub-networks (Fig. 1B, sub-networks 7 and 8). As feedback connections are random and balanced, they destructively interfere at other locations. In other words, the feedback input from the random network to other sensory sub-networks is orthogonal to their encoding space.
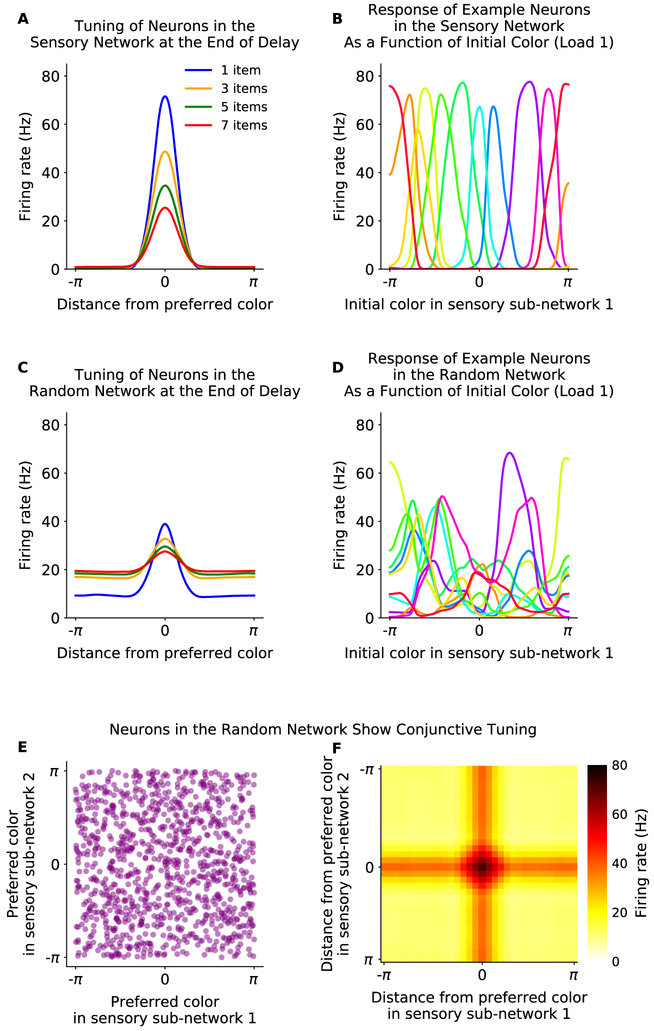
Neurons in the sensory network show physiologically realistic tuning curves, due to their center-surround architecture (Fig. 2A,B). This tuning is effectively inherited by the random network, although with greater complexity (Fig. 2C,D), matching neurophysiological findings (Funahashi et al., 1989; Zaksas and Pasternak, 2006; Mendoza-Halliday et al., 2014). However, as connectivity is random, the tuning of neurons in the random network is not consistent across inputs to different sensory networks (Fig. 2E). This leads to neurons in the random network showing ‘linear conjunctive’ coding (Fig. 2F), preferring different input values for different sensory sub-networks (e.g. different colors at different locations) and responding to unique combinations of inputs into multiple sensory sub-networks. Such linear conjunctive representations are consistent with experimental observations in prefrontal cortex (Fusi et al., 2016; Lindsay et al., 2017).
Figure 2: Tuning in the sensory and random networks.
(A) Neurons in the sensory sub-networks have physiologically realistic tuning curves. Average response of neurons (y-axis) is shown at the end of the delay period, relative to each neuron’s preferred stimulus input (x-axis). Tuning decreases with increased working memory load (colored lines). (B) Example tuning curves in the sensory network. (C) Neurons in the random network show physiologically realistic tuning, inherited from the sensory network. Tuning decreases with memory load (colored lines). (D) Example tuning curves of a subset of neurons in the random network. (E and F) Neurons in the random network show conjunctive tuning. (E) Neurons respond to the conjunction of stimulus identity and location. The preferred stimulus of neurons in the random network is uncorrelated between sensory sub-networks, due to the randomness of projections (shown here as preferred input for sensory sub-network 1, x-axis, and subnetwork 2, y-axis). (F) Neurons in the random network preferentially respond to a conjunction of stimulus inputs across sensory networks. This is shown here by the two-dimensional tuning curve of neurons from the random network to inputs to sensory sub-network 1 and 2. The firing rate (color axis) is aligned on the x-axis to the preferred input for sensory sub-network 1, and on the y-axis to the preferred input for sensory sub-network 2, revealing a peaked response at the conjunction of the two stimuli.
2.2. Interference between memory representations imposes a capacity limit
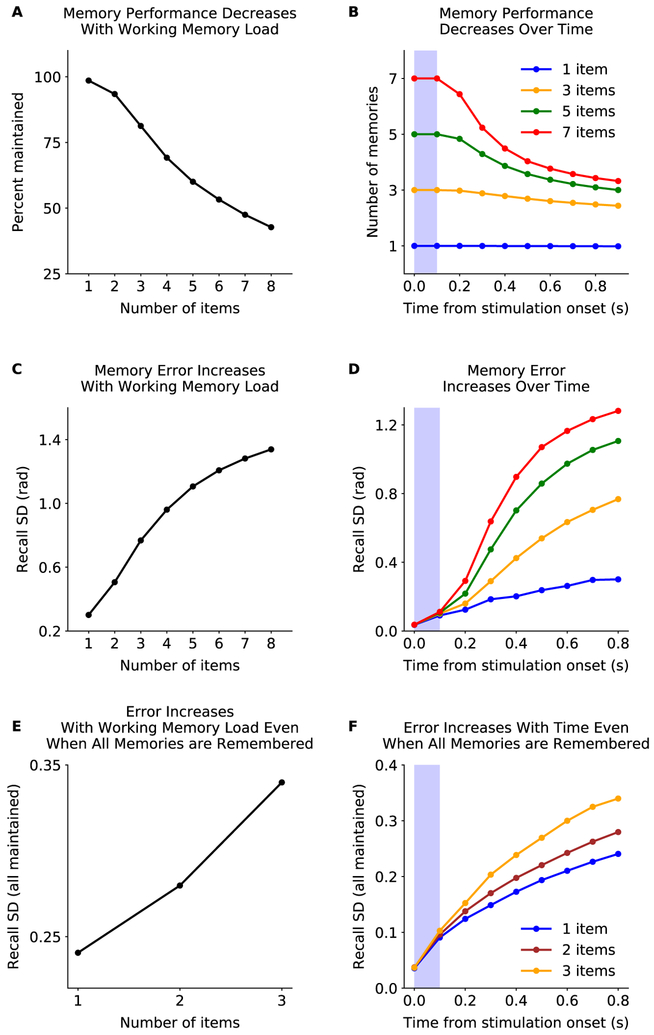
Multiple memories can be stored in the network simultaneously (Fig. 1B). For a few items (typically 3), memories do not significantly interfere - there is sufficient space in the high-dimensional random network for maintaining multiple patterns. However, as the number of sensory inputs is increased, interference in the random network also increases, eventually causing memory failures (Fig. 1B, sub-networks 5 and 6). Figure 3 A shows the percentage of correct memories at the end of the delay period, as a function of load (i.e. number of items presented; see Methods for details). This closely matches behavioral results in both humans and monkeys (Buschman et al., 2011; Cowan, 2010). Indeed, the decrease in performance with working memory load in the model was highly correlated with experiments (r = 0.97, p = 0.0054, to experimental data from (Luck and Vogel, 1997); see Methods for details). Also consistent with behavior, the speed of forgetting during the delay period increased with load (Fig. 3B). As with all of our results, this is not due to tuning of network parameters; parameters were set to maximize the total number of items remembered across all loads, not to match any behavioral or electrophysiological results (see Methods).
Figure 3: Memory performance decreases with working memory load.
(A) The network has a limited memory capacity. The percentage of memories maintained decreases with memory load (‘number of items’; see Methods for details). (B) Forgetting during the delay period is faster for higher memory loads. (C) Memory precision decreases with working memory load. The precision was measured as the standard deviation of the circular error computed from the maximum likelihood estimate of the memory from the sensory network (decoded from 0.8s to 0.9s after the stimulus onset). See also Fig. S1B. (D) Memory precision decreases over time and with load. Decoding time window is 0.1s forward from the time point referenced. (E-F) The decrease in memory precision with memory load is not simply due to forgetting. Same as in C-D, respectively, but only considering simulations where all memories are maintained.
Errors in working memory increased with the number of items held in memory (Fig. 3C and S1B). Errors also accumulated more quickly at higher loads (Fig. 3D). The increase in error was not just due to forgetting of inputs – even when an input was successfully maintained, memory error increased with memory load (Fig. 3E,F). This is consistent with behavioral studies that have shown increases in memory error, even below working memory capacity limits (Rademaker et al. (2018); Bays et al. (2009); Adam et al. (2017); but see Pertzov et al. (2017)). Indeed, the load-dependent decrease in memory accuracy was highly correlated between the model and experiments (r = 0.997, p = 0.00205, experimental data from Ma et al. (2014)). Together, these results show how our model bridges the gap between ‘discrete’ models where memories are completely forgotten and ‘continuous’ models where interference between memories decreases their accuracy. To directly test the model’s ability to generalize across these results, we fit the model parameters to match either memory performance or memory accuracy (see Methods for details). Models fit on one dataset generalized to capture the other dataset (Fig. S1D,E; note this is the only model fit directly to experimental data).
Our model provides a simple mechanistic explanation for the limited capacity of working memory: it is due to interference in neural representations in the shared random network. This is a natural consequence of the convergent, random connectivity between the two non-linear networks; as multiple inputs are presented to the sensory networks, their representations interfere in the random network, disrupting maintenance. This is an unavoidable consequence of the convergence and does not depend on network parameters (as we show below). In this way, our model suggests capacity limits are a necessary tradeoff for the flexibility of working memory.
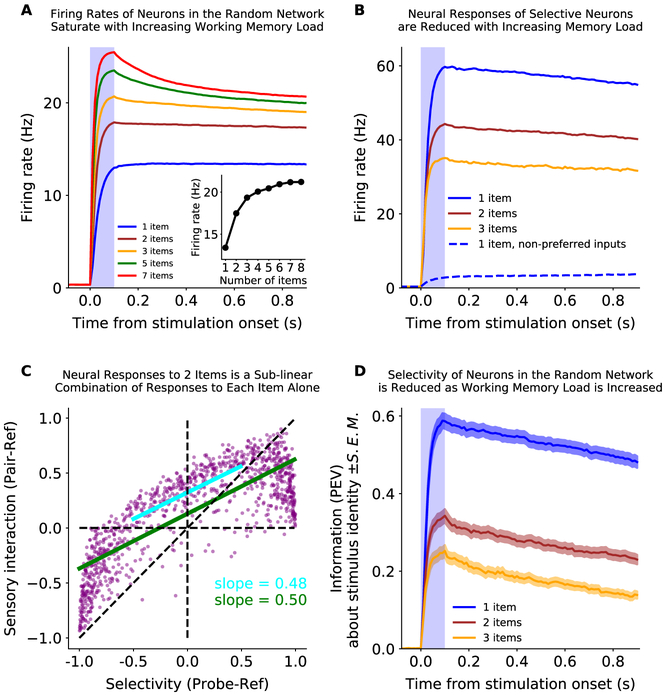
The model makes specific predictions about how neural activity should change as more items are held in working memory. First, increasing the number of stimulus inputs increases the overall average firing rate in the random network, saturating at the capacity limit of the network (~ 3-4 items; Fig. 4A). This is consistent with experimental observations of gross activity levels in prefrontal and parietal cortex; both BOLD and evoked potentials increase with working memory load, saturating at an individual’s capacity limit (Curtis and D’Esposito, 2003; Ma et al., 2014). Again, the model was highly correlated with experiments (r = 0.998, p = 1.97·10−6. experimental data from Ma et al. (2014)).
Figure 4: The effect of working memory load on neural responses.
(A) The average overall firing rate of neurons in the random network increases with memory load and saturates at the capacity limit of the network. Inset: The mean firing rate during the second half of the delay period as a function of initial load (‘number of items’). (B) The firing rate of selective neurons in the random network is reduced when inputs are added to other sub-networks. Selective neurons (N=71, 6.9% of the random network) were classified as having a greater response to a preferred input than to other, non-preferred, inputs into other sensory networks (preferred is blue, solid; non-preferred is blue, dashed; see Methods for details). The response to a preferred stimulus (blue) is reduced when it is presented with one or two items in other sub-networks (brown and yellow, respectively). (C) Divisive-normalization-like regularization of neural response is observed across the entire random network. The response of neurons in the random network to two inputs in two sub-networks is shown as a function of the response to one input alone. The x-axis is the ‘selectivity’ of the neurons, measured as the response to the ‘probe’ input into sub-network 2 relative to the ‘reference’ input into sub-network 1. The y-axis is the ‘sensory interaction’ of the neurons, measured as the response to the ‘pair’ of both the ‘probe’ and the ‘ref’ inputs, relative to the ‘ref’ alone. A linear fit to the full distribution (green) or the central tendency (blue) shows a positive y-intercept (0.13 and 0.32 for full and central portion) and a slope of 0.5, indicating the response to the pair of inputs is an even mixture of the two stimulus inputs alone. (D) The information about the identity of a memory decreases with memory load. Information was measured as the percent of variance in the firing rate of neurons in the random network explained by input identity (see Methods for details). Shaded region is S.E.M.
Second, the model predicts maintaining multiple memories will reduce the response of selective neurons in the random network (Fig. 4B). This is consistent with experimental observations, which have shown divisive-normalization-like regularization of mnemonic responses in single neurons and across the population (Buschman et al., 2011; Sprague et al., 2014). Our model provides a potential circuit mechanism for such divisive-normalization-like regularization, suggesting it is the result of balanced excitation/inhibition between networks. The low fraction of connectivity (γ) and balanced excitation/inhibition means that a neuron in the random network that is selective for one stimulus is more likely to be inhibited than excited by a second stimulus (see Methods). Thus, the response of selective neurons is reduced as items are added to memory (Fig. 4B).
This effect can be seen across the population. Figure 4C shows the relative response of neurons in the random network to two stimuli either presented separately (x-axis) or together (y-axis). As noted above, the overall average response increases when two stimuli are presented. However, the response to the pair of stimuli was not a summation of the response to each stimulus alone; rather it was a sublinear mixture (slope is ~ 0.50). This is consistent with electrophysiological results during perception (Reynolds et al., 1999) and with divisive normalization models that predict the response to two stimuli should be the average of the response to each stimulus alone (resulting in a slope of 0.5). Divisive normalization has been observed in many cognitive domains (Carandini and Heeger, 1994, 2012). Indeed, in working memory, divisive-normalization-like regularization may explain the observed decrease in stimulus information with memory load: it reduces selectivity, which reduces information (Fig. 4D, Buschman et al. (2011); Sprague et al. (2014)). More broadly, our model suggests excitation/inhibition balance within a convergent, non-linear, network could be a circuit mechanism for implementing divisive normalization.
Interference between memory representations also provides a simple mechanistic explanation for the reduced memory precision at higher memory loads (Ma et al., 2014; Bays and Husain, 2008). In our model, memory representations drift over time, due to the accumulation of noise from Poisson variability in neural spiking (Burak and Fiete, 2012). The increased interference in the random network at higher memory loads leads to weaker feedback, reducing the representation in the sensory network. This reduction both allows noise to have a greater impact, causing an increase in drift (Fig. 3C-F), and impairs decoding of memory representations (Bays, 2014, 2015).
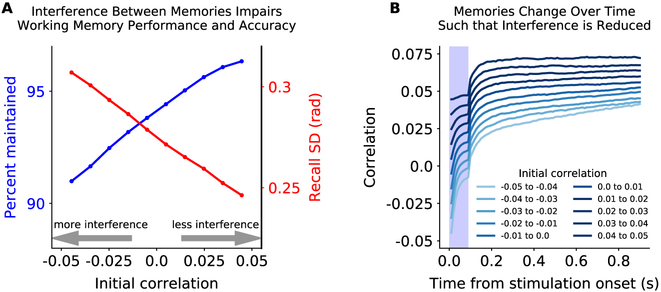
Given the model’s prediction that interference impairs memory performance, then reducing interference between memories should improve working memory performance and accuracy. Indeed, how much two stimulus representations overlapped in the random network strongly determined the ability to accurately maintain both memories. Figure 5A shows memory performance was impaired when two memories were less correlated, reflecting greater interference between the memories in the random network (see also S1C). Conversely, more correlated memories were better remembered. Surprisingly, errors in memory accumulated over time in a way that reduced interference between memories (Fig. 5B). Both of these predictions are testable hypotheses that could be addressed with future electrophysiology or imaging experiments.
Figure 5: Interference between inputs reduces performance and accuracy.
(A) Percent of memories maintained (blue, as in Fig. 3A) and memory accuracy (red, as in Fig. 3E) increased when two inputs into two sensory sub-networks are more correlated in the random network. Correlation was measured as the dot product of the vector of random network responses to each input (see Methods for details). So, an increase in correlation reflects increasing overlap of each memory’s excitatory/inhibitory projections into the random network, reducing interference. (B) Memory representations change over time in a way that increases correlation and, thus, reduces interference.
2.3. Stable and dynamic encoding of memories
The model captures several more key electrophysiological findings related to working memory. First, we observe persistent mnemonic activity, consistent with electrophysiological results in both monkeys and humans (Funahashi et al., 1989; Fuster, 1973; Vogel and Machizawa, 2004). This is true, even on the first trial of being exposed to a stimulus, as observed in monkeys (Constantinidis and Klingberg, 2016). Second, working memory activity is distributed across multiple networks, reflecting the distributed nature of working memory representations in the brain (Christophel et al., 2017). Third, as noted above, the random nature of connections in our model yields high-dimensional, mixed-selective, representations in the random network; as has been seen in prefrontal cortex (Fusi et al., 2016). Finally, as we show next, our model shows the same combination of stable and dynamic representations seen in neural data (Murray et al., 2016; Stokes, 2015).
Recent work has highlighted the dynamic nature of working memory representations. In particular, neural representations early in the trial are not well correlated with representations later in the trial (e.g. stimulus presentation vs. memory delay, (Stokes et al., 2013)). This argues against the classic view of a static mnemonic representation. In contrast, Murray et al (2016) found these dynamics are orthogonal to the space in which memories are represented, such that although neural responses are dynamic, their encoding is stable (see also (Spaak et al., 2017)).
Our model can capture both effects with two simple, biologically-motivated, additions: 1) a direct projection from the input into the random network and 2) weak recurrent connections within the random network (see Methods). These changes did not disrupt memory performance (Fig. S2A) but did increase dynamics within the random network. These dynamics can be seen in the low crosscorrelation of neural representations across time (Fig. 6A). Consistent with experimental observations, representations early in the trial are not well correlated with later representations but representations within the memory delay are relatively more stable (Fig. 6B).
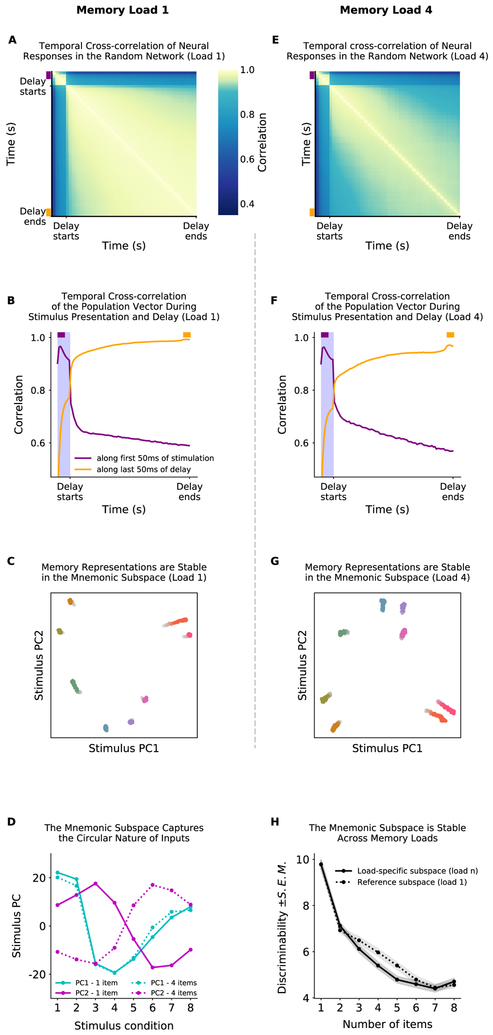
Figure 6: Neural dynamics are orthogonal to the mnemonic subspace.
Simulations use a network with weak direct sensory input into the random network and weak recurrence within the random network (see Methods for details). (A) Temporal cross-correlation of neural activity in the random network. Correlation (color axis) is measured between the vector of firing rates in the random network across time (x and y axes). Correlation was low between the stimulation and delay time periods and within the delay period, reflecting dynamic changes in the representation of memory. This was not due to forgetting: all memories are maintained in these simulations. Note non-linear color axis to highlight difference between stimulation and delay periods. (B) Slices of the matrix represented in A: correlation of population state from the first 50ms of the stimulus period (purple) and the last 50ms of the delay period (orange) against all other times. (C) Neural activity is dynamic, but memory encoding is stable. Here the response of the random network population is projected onto the mnemonic subspace (see Methods for details). Each trace corresponds to the response to a different input into sensory sub-network 1, shown over time (from lighter to darker colors). (D) Mnemonic subspace is defined by two orthogonal, quasi-sinusoidal representations of inputs, capturing the circular nature of sensory sub-networks. (E-G) Same as A-C but for a load of 4. Only uses simulations where the memory in sensory sub-network 1 was maintained (other three might be forgotten). (H) The mnemonic subspace is stable across working memory load. Decodability of memory was measured as discriminability between inputs (d’; mean ± S.E.M., see Methods for details). Decodability was similar for mnemonic subspaces defined for a single input (dashed line) and for each load (solid line); no significant difference for load 2, 3, 7 and 8 (p = 0.69, p = 0.081, p = 0.21, and p = 0.54, respectively) but the single input subspace was better for loads 4-6 (p = 0.0012, p < 10−1 and p = 0.044 respectively, all by two-sample Wald test). In general, as expected, decodability is reduced with load (p < 0.001). See also Figs. S2, S3.
However, despite these dynamics, the subspace in which a memory is represented is stable. Following the approach from Murray et al. (2016), we estimated the ‘mnemonic subspace’ of the random network by finding the first two dimensions that explained the most variance of the time-averaged response to eight different stimulus inputs (Fig. S2C, see Methods). Projecting the response of the random network over time into this subspace showed stable representations (Fig. 6C; note the subspace is not designed to minimize temporal variability). Furthermore, despite the randomness of connections, the representational subspace of the stimuli was a mixture of two orthogonal sinusoids, consistent with a Fourier decomposition of the circular inputs into the sensory network (Fig. 6D, solid lines; see Fig. S3H for higher modes). Remarkably, this matches the stable subspace found in prefrontal cortex (Murray et al., 2016). These results show the low (two) dimensional space of each sensory network is embedded in the higher dimensional space of the random network.
Previous experimental work has focused on the representation of single items in working memory. Our model makes several predictions for how representations should change when the memory load is increased. First, we found increasing working memory load decreased the cross-correlation over time (Fig. 6E,F). Second, we found representations drifted more in the mnemonic subspace (Fig. 6G). Only simulations where the memory was maintained are included, therefore these changes do not reflect drift toward an inactive ‘null’ state. Instead, the increased dynamics reflect the weakening of memory representations due to interference and the related increase in drift, as discussed above. This reduces the discriminability of memories (Fig. 6H, solid line), impairing working memory performance. Eventually, if activity is reduced enough, memories fall to the null state and are forgotten (Fig. S3F,G).
The mnemonic subspace for decoding the memory from a given sub-network did not change with memory load. The subspace for the first item, when remembered with 3 other items, was still a combination of two orthogonal sinusoids (Fig. 6D, dashed lines; Fig. S3H). Importantly, because the subspace was stable across memory loads, one could use the decoding subspace for when an item was remembered alone to decode that same item when it was remembered with other stimuli (Fig. 6H and S2D). This is critical for using the representations within the random network – as the subspace doesn’t change, any learning done at one memory load will generalize to other loads.
These results highlight how the mnemonic subspaces for each sensory network are nearly orthogonal to one another when projected into the high-dimensional space of the random network. This also explains how dynamics in the random network do not impact memory representations – if the dynamics are orthogonal to the mnemonic subspace of the sensory network, then they will not alter memories.
2.4. The network is robust to changes in parameters and connectivity
For all of our simulations, network parameters were set to maximize the total number of remembered stimuli and minimize the number of spurious memories, across all loads (see Methods). Next, we show that network performance is robust to changes in these parameters.
Maintenance of working memory representations in our model relies on sufficient recurrent activity between the sensory and random networks. This constrains the feedforward and feedback weights between the sensory and random networks such that a single action potential in the sensory network leads to roughly one action potential in the random network on average (and vice versa). However, this can be relaxed without loss of functionality. First, what matters is the product of feedforward and feedback weights. Many feedforward/feedback weights give nearly identical network performance as an increased feedforward weight can be offset by a decreased feedback weight (or vice versa, Fig. 7A, inset). Second, the product can be changed up to ~ 5% without significant loss of function (Fig. 7A). Beyond this range, there is either insufficient drive to sustain memories (Fig. 7A, below −5%, weights are too low) or there is unchecked amplification of activity, leading to spurious representations across the network (Fig. 7A, above +5%, weights are too high).
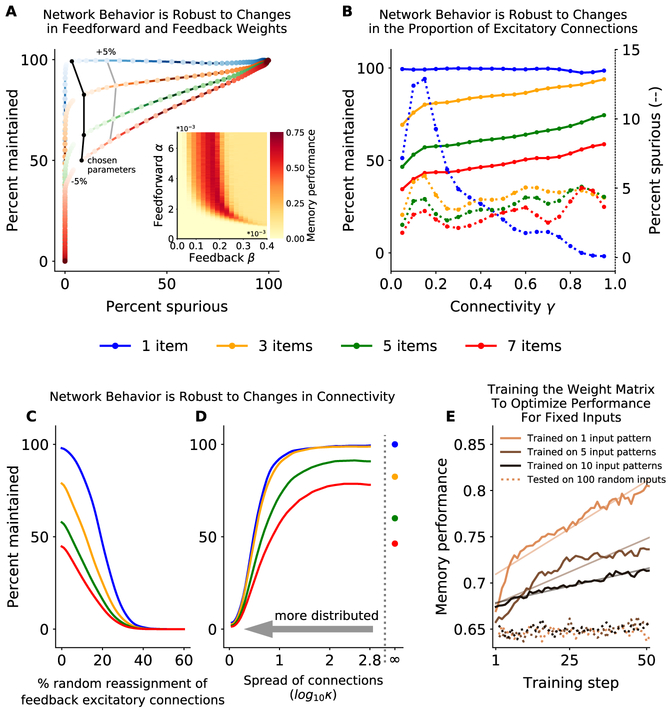
Figure 7: The network is robust to changes in parameters.
(A) Network performance is robust to changing feedforward/feedback weights. The probability of correctly maintaining a memory (y-axis) and the probability of a spurious memory in non-stimulated sensory sub-networks (x-axis) varies with the product of feedforward and feedback weights (darker colors move away from optimal value). Isolines show network performance across memory load when the product of weights is changed by ±5%. Performance decreases with memory load (colored lines) for all parameter values. Inset: Memory performance of the network (color axis; see Methods for details) as a function of feedforward and feedback weights. Here γ = 0.35. (B) Optimal feedforward and feedback weights can be found for a broad range of γ values that maximize the percent of inputs maintained (solid lines) and minimize the number of spurious memories (dashed line). Memory performance is decreased with load (colored lines), for all parameters. (C and D) Network behavior is robust to changes in connectivity. The percent of remembered inputs (y-axis) for different memory loads (colored lines) decreases as connections between random and sensory networks are either (C) randomly re-assigned (breaking symmetry) or (D) locally redistributed in the sensory network. See Methods for details and Fig. S4E for examples of redistribution for different values of κ. Bit depth constrained calculations to log10κ < 2.8; ∞ indicates no redistribution (i.e. the original random network). (E) Training random network connections improves memory performance for trained inputs but does not generalize. Networks were trained to maximize memory performance for 1, 5 or 10 inputs patterns (solid lines, see Methods for details). Learning was slower when the number of inputs to be simultaneously optimized was increased, reflected in a reduced slope of learning (linear fit). Memory performance did not improve for 100 random, untrained, input patterns, across all loads (dashed lines), showing training did not generalize. See also Fig. S7.
Similarly, the network is robust to changes in connectivity within the sensory sub-networks; weights can be scaled by up to ~ 4% without loss of functionality (Fig. S4A,B). However, the network can be robust to greater changes in the strength of connections within the sub-network if the feedforward/feedback weights are also changed (Fig. S4C).
The network is also robust to changes in the connectivity between the sensory and random networks. The fraction of connectivity between neurons in the random network and the sensory network (γ) can be changed without any qualitative change in network behavior (Fig. 7B, assuming the connection weights are adjusted). We chose γ = 0.35 to maximize maintenance, minimize spurious memories, and minimize connections (thereby minimizing structural costs).
The network is also robust to changes in the relative size of the sensory and random networks. Increasing (decreasing) the size of the random network, relative to the sensory network, increased (decreased) the capacity of the network to maintain multiple inputs (Fig. S5). However, this increase was not absolute; all network sizes had a capacity limit.
The final constraint on connectivity is that the neurons between the sensory and the random networks are reciprocally connected. This is consistent with wiring in the brain – neurons are more likely to be reciprocally connected than expected by chance (see below for biological mechanisms, (Ko et al., 2011; Song et al., 2005; Holmgren et al., 2003)). However, as with the other parameters in the model, the reciprocal nature of connections can be relaxed significantly without degrading network performance. To demonstrate this, we randomly reassigned a proportion of the feedback excitatory connections from one sensory neuron to another (all other model parameters were left unchanged). The model was robust to ~ 10% of excitatory connections being switched with a random inhibitory connection (Fig. 7C). However, biological connection errors are more likely to be spatially localized and so we tested whether the network is also robust to distributing excitatory feedback connections to nearby neurons within a sensory sub-network. The network was surprisingly robust to these changes. Performance was constant, even when half of the connection weight was distributed over more than 45° away from its initial position in the sensory sub-network (i.e. κ ≥1, Fig. 7D and S4D,E). In fact, distributing connections over a small range of nearby neurons (κ ~ 2) improved performance of the network over baseline, as smoothing feedback connections reduced the impact of stochasticity in neural activity. This suggests the local distribution of connections observed in the brain may be advantageous.
Finally, adding lateral connections between sensory sub-networks did not change overall network performance, but did allow memories to interact (Fig. S6A-D). Lateral interactions between memories in neighboring sub-networks stabilized memories, increasing memory performance. However, memories also drifted towards one another, decreasing memory accuracy. This is consistent with experimental work which has shown increased stability and attractive drift when subjects held two similar items in working memory (Kiyonaga et al., 2017; Lin and Luck, 2009).
2.5. Learning can optimize performance for trained memories but does not generalize to other memories
Memory performance in our network is limited by interference in the random network (Fig. 5). Theoretical work has suggested that random networks maximize information capacity and minimize interference when the structure of inputs are unknown (Maass et al., 2002; Jaeger and Haas, 2004; Sussillo and Abbott, 2009). However, to directly test whether connections could be optimized to maintain memories in our network structure, we trained a network to maximize memory performance for a small subset of inputs (see Methods for details). Training improved performance of the network for the trained inputs (Fig. 7E and Fig. S7A-B). This improvement was largely due to increased correlations between the representations in the random network of the trained inputs (Fig. S7C). However, learning was significantly slower when more patterns were trained (slope of performance across all loads was m = 0.021 for 1 input pattern; 0.0014 for 5 input patterns, and 0.00075 for 10 input patterns; p < 10−4 for all comparisons; see Methods for details). Furthermore, learning did not generalize beyond the trained inputs: untrained inputs showed little to no improvement with training (Fig. 7E, dashed lines; m = 10−6, p = 0.87; m = 10−4, p < 10−4; and m = 10−4, p = 0.026 for 1, 5, and 10 trained input patterns, respectively, tested against zero). In fact, memory performance and accuracy for non-trained inputs was reduced when they were paired with trained inputs (Fig. S7D,E). Together, these results suggest training of working memory performance does not generalize to new inputs, consistent with experimental results that training on specific working memory tasks does not generalize to other types of information (Melby-Lervåg and Hulme, 2013).
2.6. The network can maintain memories across a variety of sensory architectures
Our model demonstrates how random connections can support the flexible maintenance of memories. To highlight the flexibility of the model with respect to the architecture of sensory inputs, we developed three alternative models. First, we replaced four of the ring-like sensory sub-networks with line networks, modeling a one-dimensional psychometric spaces such as brightness or spatial frequency (Fig. S4F). Without changing any parameters, the network was able to maintain inputs into both circular and linear spaces (Fig. S4G).
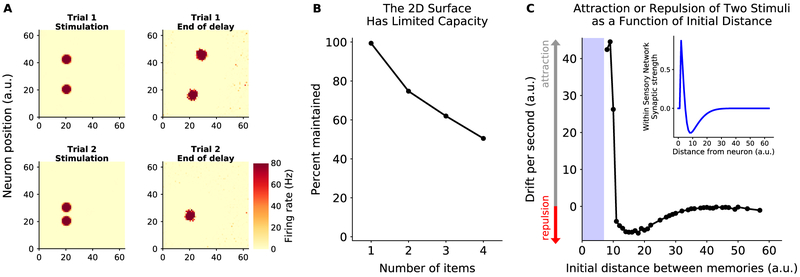
Second, we completely changed the architecture of the sensory network, replacing it with a 2D surface of neurons (Fig. 8). As in the ID rings, neurons were connected with neighbors in a center-surround manner, with local excitation and distal inhibition (see Methods for details). All other model parameters were the same as for the original model, except for slightly different optimal feedforward/feedback weights. In general, the network behavior was as before: any input could be maintained (Fig. 8A) but the network showed a limited capacity to maintain multiple memories (Fig. 8B). Interestingly, because sensory inputs existed in the same sensory network, memories interacted with one another: nearby memories were pulled together, eventually merging, while more separated memories repulsed one another (Fig. 8C). These interactions were due to the center-surround structure in the sensory network and are consistent with previous theoretical and experimental observations (Kiyonaga et al., 2017; Almeida et al., 2015; Nassar et al., 2018).
Figure 8: Memories can be maintained in different sensory architectures.
(A) Example trials of two memories maintained in a 2D sensory network. Firing rate during stimulation (left) and at the end of delay (right) for trials with two initial inputs. Memories interact such that distant memories are repulsed from one another (top) while nearby memories are attracted to one another and can merge (bottom). (B) Memories interfere in the random network, limiting the network’s capacity. (C) Plot of the speed of attraction/repulsion of memories (y-axis) as a function of the initial distance d between memories (x-axis). Attraction and repulsion were defined relative to the initial vector between inputs (see Methods for details). Note that for d < 10. the two initial inputs cannot be distinguished from each other (shaded blue region), and thus movement cannot be computed. (Inset) Connection weights within the sensory network, as a function of distance. The center-surround structure in the 2D sensory network explains the observed attraction/repulsion of memories.
Third, we replaced the sensory network with a Hopfield-like network (see Methods). As for the other architectures, arbitrary inputs could be maintained (if they matched a pattern embedded in the Hopfield network) but the network had a limited capacity (Fig. S8).
Altogether, these results demonstrate that our network is robust to changes in parameters, connectivity, and architecture. Importantly, for all parameters and structures tested the network was flexible and had a limited capacity.
3. Discussion
We present a model of working memory that relies on random and recurrent connectivity between a structured sensory network and an unstructured random network. Despite its simplicity, the model captures several key behavioral and neural findings. Foremost, the model is flexible. Such flexibility is critical for cognition, allowing working memory to act as a workspace on which anything can be held, manipulated and used to guide behavior. However, our model’s flexibility comes at the cost of a limited capacity. Interference between multiple memories leads to divisive-normalization-like regularization of responses which, in turn, leads to an increase in memory error and, eventually, to a failure to maintain some memories (forgetting). Additionally, the model explains 1) observations that working memory is distributed across cortex; 2) conjunctive stimulus tuning in associative (e.g. prefrontal) cortex; 3) the general increase in neural activity with working memory load; 4) how working memory representations can be both static and dynamic; and 5) interactions between memory representations.
3.1. Biological plausibility
Our model maintains memories through the interaction of two networks: a sensory network and a random network. The sensory network is intended to capture two key aspects of generic sensory cortex. First, neurons receive tuned inputs, giving rise to selectivity in their responses. Second, there is a center-surround architecture with respect to tuning. Pyramidal neurons with similar selectivity are more likely to be connected to one another (Song et al., 2005; Holmgren et al., 2003; Harris and Mrsic-Flogel, 2013) while inhibitory interneurons spread inhibition across the population (likely through parvalbumin-positive inhibitory interneurons (Atallah et al., 2012; Packer and Yuste, 2011; Wilson et al., 2012)). Such structure is thought to emerge through unsupervised learning mechanisms, such as Hebbian plasticity. In this way, the structure of sensory networks reflects the statistics of the world; embedding knowledge about how stimuli relate to one another. As we discuss below, this is critical to our model, as it constrains the activity in the random network to a biologically meaningful subspace, allowing it to be easily interpreted for behavior.
In contrast to the sensory network, the random network in our model is unstructured. Similar to reservoir pool computing approaches in machine learning (Maass et al., 2002; Jaeger and Haas, 2004), the random connections to the random network create a high dimensional space where any type of information can be represented. The random connections also create conjunctive representations, which could support learning contextually-specific associations (e.g. responding to a green input in sub-network 1 only in the context of a red input into sub-network 2, Fusi et al., 2016). Experimental results suggest associative regions, such as prefrontal cortex or the hippocampus, may have such highdimensional, conjunctive, representations (Rigotti et al., 2013; McKenzie et al., 2014) and therefore could act as our ‘random network’. In particular, prefrontal cortex has strong bi-directional connections throughout sensory cortex, making it particularly well-suited to play the functional role of the random network (Miller and Cohen, 2001). Indeed, lesioning prefrontal cortex severely impairs working memory performance (Petrides, 1995). Similarly, the size of prefrontal cortex is correlated with working memory performance (Haier et al., 2004; Klingberg, 2006; Nissim et al., 2017), consistent with the positive correlation we observed between the random network size and memory capacity.
One molecular mechanism that could support reciprocal random connectivity are protocadherins, a subclass of cell adhesion molecules. Protocadherins undergo a recombination process such that each neuron expresses a unique, random, set of these cell adhesion molecules (De Wit and Ghosh, 2016). Neurons with overlapping expression profiles of protocadherins are more likely to make synaptic connections (Kostadinov and Sanes, 2015). Thus, the randomness of protocadherins could help randomly initialize the connections between neurons. This is important for the functioning of neural networks: randomization of initial connections is critical for efficient learning in artificial neural networks. Here, we propose that this randomization forms a reservoir pool in the random network, providing the architecture for the flexibility of working memory. The slow developmental timecourse and slow learning rates seen in prefrontal cortex may help to maintain this randomness through development and learning (Kiorpes, 2015; Haier et al., 2004; He et al., 2015; Pasupathy and Miller, 2005).
Our network uses balanced excitation and inhibition to constrain neural activity to a stable regime. This is consistent with recent experimental work that has found excitation and inhibition are tightly balanced within the cortex (Vogels et al., 2011; Vogels and Abbott, 2005; Mariño et al., 2005). Although long-range connections, such as those modeled between the sensory and random networks, are largely excitatory in the brain, feedforward inhibition within the target region can ensure these projections are effectively excitation/inhibition balanced.
Although the model is biologically plausible, it is intentionally simple. Several simplifying assumptions were made: neurons send both excitatory and inhibitory projections and there are no cell types. Here, our goal was to demonstrate the explanatory power of the simplest network. This highlights the computational power of random, convergent, connections, showing how they can account for the flexibility of working memory, as well as its limited capacity.
It is important to note that a few aspects of working memory representations remain unexplained by our model. For example, recent results suggest working memory relies, at least in part, on short-term synaptic changes (Mongillo et al., 2008; Postle, 2017; Stokes, 2015) or oscillations (Lundqvist et al., 2016; Salazar et al., 2012). The simplified biophysics of our neurons do not capture these effects; future work will investigate whether extending the model can explain these additional findings.
3.2. Model predictions
In addition to capturing existing behavioral and electrophysiological results, the model makes several testable hypotheses. First, the model predicts that memory performance should be a function of how strongly neural representations interfere with one another. As we show above, interference between two items can be estimated from the correlation between representations when each item is presented alone. Our model predicts increasing interference should reduce behavioral performance. Furthermore, it suggests that as memories degrade, they should do so in a way that reduces interference between memories.
Second, the model predicts that disrupting random connectivity in the cortex should disrupt working memory performance. Indeed, mice with reduced diversity in protocadherins have impairments in sensory integration and short-term memory (Yamagishi et al., 2018). At the single neuron level, the model predicts reducing protocadherin diversity will reduce the variety of conjunctive representations in associative cortex.
Finally, the model predicts that maintaining a stimulus presented at one location should increase neural activity in other locations in sensory cortex. This activity should be consistent from trial to trial, but unstructured with respect to the content held in memory (although, lateral connections between sensory sub-networks may provide some structure to this noise, as in Fig. S6).
3.3. The trade-off between flexibility and stability
The random architecture of our model supports its flexibility but leads to interference between memories, limiting capacity. One way to reduce interference would be to construct specialized, independent networks for each type of information one wants to maintain in working memory. There is evidence for such network specialization in the brain. For example, heading direction is represented in specialized ring attractors (Kim et al., 2017; Seelig and Jayaraman, 2015). However, these specialized networks are inflexible, unable to represent information outside of their domain. This trade-off between flexibility and stability was seen in our model: when we trained the network to improve memory performance for specific inputs, it reduced performance for untrained inputs.
This tradeoff is not limited to working memory. Well-learned behaviors (e.g. walking or chewing gum) are thought to be represented in specialized networks of neurons. Such independent representations are robust to noise and reduce interference between behaviors. However, they require extended periods of learning (either across evolution or during an organism’s lifetime). In contrast, our network architecture provides the structure needed for generalized behavior. Indeed, the flexible representations found in our model are reminiscent of the selectivity seen in prefrontal cortex and as predicted by adaptive models of cognitive control (Miller and Cohen, 2001; Duncan, 2001). While these complex, adaptive representations are ideal for representing the complexity of all possible behaviors (Fusi et al., 2016), it is unclear how they can act on other brain regions in a meaningful, behaviorally-relevant, manner. Our results may provide an answer: recurrent interactions with structured networks constrains activity to behaviorally-relevant manifolds.
3.4. Local structure constrains complex top-down projections
In our model, the random network inherits its selectivity from the structured sensory network. The center-surround structure of the sensory network ensures similar stimulus inputs result in similar patterns in the random network. In this way, the lower-dimensional representation in the sensory network is embedded within the high dimensional space of the random network. Importantly, because recurrent projections are random and E/I balanced, if representations in the random network move outside of this lower dimensional manifold it does not impact activity in the sensory sub-network (i.e. irrelevant information has no net impact, Fig. S1A).
In this way, complex, multi-faceted, representations in the higher-dimensional random network will be effectively filtered by the structure of the sensory sub-networks. This could allow the complex representations observed in higher-order brain regions (e.g. PFC) to influence activity in lower-order, sensory regions in a meaningful manner. While our model shows how these interactions can be used to hold items in working memory, this same concept can apply to other forms of top-down control, such as cognitive control or attention.
Finally, filtering by structure in lower cortical regions may also facilitate learning of top-down control signals. Learning in high-dimensional spaces is an unavoidably difficult problem; our results suggest only the relevant components will impact behavior, limiting the effective dimensionality in which the control signal must be learned.
8. STAR METHODS
8.1. CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to Tim Buschman (tbuschma@princeton.edu).
8.2. METHOD DETAILS
8.2.1. Computational model
We consider a two-layer network of Poisson spiking neurons. Model parameters were adapted from (Burak and Fiete, 2012). Each neuron i generates Poisson spikes based on its time-varying firing rate ri(t). The firing rate of neuron i is a non-linear function of the weighted sum of all pre-synaptic inputs:
| (1) |
| (2) |
where Wij is the synaptic strength from pre-synaptic neuron j to post-synaptic neuron i; sj(t) is the synaptic activation of pre-synaptic neuron j: and Φ is a baseline-shifted hyperbolic tangent: τΦ (g) = 0.4(1 + tanh (0.4g − 3)). As in the brain, the rate of a neuron is strictly positive and saturates at an upper bound (which also constrains runaway excitation and stabilizes the network). The synaptic activation produced by neuron j is computed by convolving its spike train with an exponential function:
| (3) |
where are the spike times of neuron j. For simplicity, we choose the synaptic time constant τ = 10ms to be equal for all synapses. As noted in the main text, we are using a simplified model of neural activity; neglecting cell-types, the existence of refractory periods, and bursts of neural activity.
Previous work has shown the variability in spiking activity plays a significant role in the diffusion of memories over time ((Burak and Fiete, 2012)), which motivated our choice of using spiking neurons instead of a rate model. All variability in spiking arises from the inhomogeneous Poisson process used to generate spike events (i.e. no noise was added).
The model consists of two interacting layers of neurons: a ‘sensory’ network and a ‘random’ network (Fig. 1A). The sensory network consists of 8 independent ring-like sub-networks. These sub-networks are each composed of Nsensory =512 neurons and mimic simplified sensory networks, with neurons around the ring corresponding to specific values of a continuously encoded feature, such as shape, orientation, or color (here graphically represented as color). Every neuron i has an associated angle θi = 2πi / Nsensory. Consistent with biological observations (Funahashi et al., 1989; Kuffler, 1953; Kiyonaga and Egner, 2016), connections within each sensory sub-network have a center-surround structure (Fig. 1A, inset). The synaptic weight between any pair of neurons is rotationally invariant, with nearby excitation and surround inhibition. The synaptic weight between any pair of neurons i, j within a sensory sub-network depends only on θ = θi – θj through:
| (4) |
where k1 = 1 is the inverse width of the excitation kernel, k2 = 0.25 is the inverse width of the suppression kernel, A = 2 is the amplitude and λ = 0.28 is the baseline. Self-excitation is set to 0 (w(0) = 0). To test the robustness of the network to changes in recurrent connectivity within the sensory sub-networks, the strength of all recurrent connections () was scaled by a constant factor (Fig. S4A).
Different sub-networks reflect independent sensory inputs (either stimuli at different locations in space or different sensory features or modalities). In most of the models presented, the sensory sub-networks are independent (unconnected). However, the network was robust to relatively strong lateral excitatory connections between sensory sub-networks (Fig. S6). Similarly, adding weak inhibition between sub-networks did not qualitatively change our results (not shown).
The random network is composed of Nrand = 1024 neurons randomly connected to each of the 8 simulated sensory sub-networks. Such convergence is consistent with the convergence observed along the cortical hierarchy (Man et al., 2013). Here we use a four-fold convergence, although this ratio can be varied without dramatically impacting our results (Fig. S5). As there is a single random network, all sensory sub-networks converge onto it through a random feedforward connectivity matrix (WFF). Each neuron in the random network then feeds back into the same random subset of neurons in the sensory network that provided excitatory inputs. In other words, the connections were bi-directional and therefore, the feedback connectivity matrix (WFB) from the random network to the sensory network is the transpose of the feedforward connectivity matrix, with distinct weight values (i.e. WFB ~ WFFT). The likelihood of an excitatory connection between any pair of neurons across the sensory and random networks was defined by γ (default is 0.35). Therefore, the number of internetwork excitatory connections (Nexc) for any given neuron followed a binomial distribution (with p = γ The strength of the excitatory feedforward and feedback connections were defined by the parameters α and β, respectively (how these were chosen is detailed below).
Connection weights between the sensory and random networks were balanced in two ways. First, in order to balance the total excitatory drive across neurons, feedforward (or feedback) weights were scaled by Nexc. Second, the connections between the sensory and random networks were balanced such that individual neurons receive an equal amount of excitatory and inhibitory drive (i.e. ). To achieve this, an equal inhibitory weight was applied to all inputs for each neuron (). This method of balancing is intended to reflect broad inhibition in the target network due to local inhibitory interneurons.
Thus, after balancing, excitatory feedforward connections from the sensory to random network neuron i had weight while inhibitory feedforward connections had weight . Similarly, neuron j in the sensory network will receive excitatory feedback connections with weight and inhibitory feedback connections with weight .
8.2.2. Presentation of stimuli to the sensory network
Sensory stimuli were provided as synaptic drive (sext) to the sensory sub-networks:
| (5) |
All inputs were presented for 100 ms, indicated by the blue shaded region in all figures. Inputs were Gaussian, with the center of the input (μ) chosen randomly for each sensory sub-network. The width of the input (σ) was defined as a fraction of the total number of neurons in the sensory sub-network, , which was 16 neurons for the presented network. Inputs beyond three σ were set to 0.
Therefore, the sensory input to neuron i was
| (6) |
where Sext was the strength of external sensory input (here, Sext = 10).
8.2.3. Sensory inputs and recurrence in the random network
The baseline model used for most analyses is intentionally simple. The activity of neurons in the sensory network was given by Equation 5 and the activity of neurons in the random network was:
| (7) |
However, to investigate the dynamics of activity within the network, two biologically-motivated connections were added (only for results presented in Figs. 6, S2 and S3). First, inputs were projected directly into the random network (in addition to inputs into the sensory network). A random weight matrix, defined the feedforward connectivity of sensory inputs into the random network. Similar to the weight matrix from the sensory network, the likelihood of an excitatory connection from any given input was γext (default is 0.2) with weight proportional to αext. As with other connections in the network, inhibitory connections were added to all neurons in the random network in order to balance excitation and inhibition.
Second, recurrence within the random network was added. Again, a random weight matrix was constructed () with a likelihood of excitatory connection defined by γrec (default 0.2) and with weight proportional to αrec. As with feedforward and feedback connections, these connections were balanced such that overall excitatory drive was constant across neurons and excitation and inhibition were balanced within a neuron.
Therefore, in the network used to investigate dynamics (Fig. 6, S2 and S3), the activity of neurons in the random network was:
| (8) |
8.2.4. Lateral connections between sensory sub-networks
Lateral connections are a prominent feature of connectivity within cortex. To study how these may influence memory performance in our model, we added reciprocal connections between neighboring sensory sub-networks. This resulted in a chain of connections from sub-network 1 through 8 (e.g. 1 to 2, 2 to 3, etc, but no connection from 8 back to 1). These connections are direct excitatory connections between the same feature-selective neurons in each sensory sub-network (i.e. neuron 0 in sensory subnetwork 1 is connected to neuron 0 in sensory sub-network 2, itself connected to neuron 0 in sensory sub-network 3, etc; Fig. S6A). We manipulated both the percentage of neurons in each sub-network with these lateral connections and the strength of the connections (all connections were equal strength). As seen in Figure S6B, moderately strong lateral connections do not disrupt network performance. However, if strong enough, these connections can lead to spurious memories. Lateral connections allowed memories in nearby sensory sub-networks to interact. This caused nearby memories to drift towards one another (Fig. S6C), decreasing memory accuracy. However, interactions also stabilized memories, reducing the likelihood a memory would be forgotten (Fig. S6D). As noted in the main text, these results are consistent with experimental observations (Kiyonaga et al., 2017; Lin and Luck, 2009).
8.2.5. Testing overlap in the random network
To study the impact of overlapping connections between the sensory and random networks, we varied the similarity in projections to the random network from sensory sub-networks 1 and 2. In other words, if neuron 0 in sensory sub-network 1 is connected to neuron n in the random network by an excitatory connection, the ‘percent difference’ in Fig. S6F,G is the probability that neuron 0 in sensory sub-network 2 is also connected to neuron n in the random network by an excitatory connection. For a percent difference of 0, both weight matrices were completely identical, thus projections overlapped 100% (as schematized in Fig. S6E). For a percent difference of 100, a neuron in sensory sub-network 1 and its featural homolog in sensory sub-network 2 are excluded from sending an excitatory connection to the same neuron in the random network and, thus, the overlap is 0%. In our baseline model, projections are random and the connectivity rate was γ = 0.35. Therefore, the percent difference for our baseline model was 65%. The weight matrix from the other sensory sub-networks, and all the other parameters remained unchanged. As seen in Figure S6F,G, memory performance suffers if projections are completely different (100% difference). As the difference in projections is reduced, then the representations in the random network begin to overlap, allowing memories to support one another. However, if the overlap in projections is too great, then a single input into one sensory sub-network can induce a spurious memory in the other sub-network.
8.2.6. 2D surface sensory network
To determine the robustness of the network to new sensory architectures, we tested the model with a continuous 2D surface for the sensory network. All network parameters remained the same (e.g. the overall network size and the fraction of connectivity between neurons in the random network and the sensory networks, γ). Similarly, all the network equations remained the same, except for changes in connectivity within the sensory network and the nature of the input. The 2D surface was modeled with N = 4096 neurons, arranged in a 64×64 neuron square. The synaptic weight between any pair of neurons i, j within the 2D surface depended only on their Euclidean distance dij:
| (9) |
where Aexc = 1.7, Ainh = 0.5, σexc = 3 and σinh = 10. Weights are set to 0 for all d < 1.2 (i.e. w(d < 1.2) = 0; this includes the center neuron itself and the 4 nearest neighbors).
One to four 2D Gaussian inputs were presented during the first 100 ms of each trial. Each input was centered on a specific neuron i, and the strength of stimulation to neuron j depended on the distance to the center d ij through:
| (10) |
with Sext,2D =1000 and σ2D = 2.
The results of simulations with the 2D surface are displayed in Figure 8.
8.2.7. Hopfield-like sensory network
To test an architecture without center-surround connectivity, we replaced the sensory network with a Hopfield-like network. As for the 2D surface, most model parameters remained the same, such as network size and the fraction of connectivity between the random and sensory networks (γ). All network equations remained the same, with the exception for changes in connectivity within the sensory network and the nature of the input. N p = 8 Hopfield-like patterns were embedded in the sensory network. Each pattern μ is a vector pμ of length N = 4096, including 100 positive value (), the rest being null (). The exact identity of the neurons involved in a pattern does not matter, so we clustered them together for illustration purpose (Fig. S8A). In the first instantiation of the model the patterns were exclusive (i.e. non-overlapping; although we relaxed this constraint later). Similar to the original Hopfield model, the patterns were embedded in the weight matrix:
| (11) |
with
| (12) |
Note the major difference from the classic Hopfield network is that neurons that are both not active in a given pattern inhibit one another (as supposed to exciting one another in the classic Hopfield network). This change was to accomodate the fact that our neurons do not have negative firing rates and our patterns are not balanced (with non zero expected value).
Memories could be maintained in the Hopfield sensory network alone if weights were strong (λ = 600 and below, Fig. S8B). To disrupt this maintenance, but keep the structure of the network, weights were reduced (λ = 800, Fig. S8C). Although the Hopfield network could no longer maintain memories alone, interactions with a random network recovered the ability to sustain memories (Fig. S8D).
Inputs were taken as the sum of NL pattern vectors, depending on the load chosen (L). All active input neurons received the stimulus drive as previous models (Sext = 10).
To systematically investigate how overlap in the sensory network representations impacted memory performance, we changed one pattern such that a proportion of its active neurons overlapped with another pattern (Fig. S8A, example for 20%). By varying the percentage of overlap, we could quantify the impact of overlap on memory performance, as seen in Figure S8F,G. If two embedded memories were partially overlapping, then memory performance for one was improved as the structure of the other embedded pattern helped stabilize the active pattern (even when it was not active; Fig. S8G). However, if embedded patterns overlapped significantly (>~ 16%), an input matching one pattern tended to spuriously activate the other, overlapping, pattern. It is important to note that overlap also induces spurious memories in typical Hopfield networks; this is a consequence of the recurrent connections within the Hopfield network and not the recurrent connections with the random network. As noted above, similar effects were seen when two sensory inputs had overlapping projections on the random network (Fig. S6E,F,G). Together, these results suggest that while some correlation in the random network improves working memory performance (Fig. 5), too much correlation can lead to spurious activation of memories.
8.3. QUANTIFICATION AND STATISTICAL ANALYSIS
8.3.1. Performance of the network
For all model variants, ‘memory performance’ was quantified as the percent of memories maintained minus the percent of spurious memories. This statistic is used in Figures 7, S5. ‘Percent maintained’ was defined as proportion of successfully maintained memories with respect to the number of initial inputs to sensory sub-networks. This statistic is used in Figures 3, 5, 7, 8, S1, S2, S4, S5, S6, S7, S8. Similarly, the ‘percent spurious’ statistic was defined as the proportion of spurious memories created, relative to the maximum number of spurious memories possible (the maximum inputs tested minus the number of inputs provided). This statistic is used in Figures 7, S4, S5, S6, S7, S8.
For the ring-like sensory sub-networks, a memory was ‘maintained’ if the norm of the activity vector for a given sub-network exceeded 3Hz. We did not choose a similarity metric with the initial representation of inputs, because that would not allowed for taking memory drift into account. Similarly, a sub-network carried a ‘spurious’ memory if it did not receive any input during stimulation but had activity that exceeded the same threshold.
For the 2D surface sensory network, active memories were identified by looking for clusters of activity (¿20Hz) in the 2D surface. The clustering algorithm was taking from the scipy.ndimage.measurements toolbox. Tracking the clusters over time allowed us to estimate the drift of memories over time. A cluster was taken to be lost if its peak activity dropped below 20Hz. Spurious memories were clusters that appeared without a driving input.
For the Hopfield-like sensory network, we determined what memories were represented in the network by comparing the firing rate at the end of the delay to the set of all possible pattern combinations. The pattern combination with minimum difference was taken as the set of memories active in the network. Pattern difference was defined as the squared difference between the final firing rate and the firing rate that the combination would have created with perfect encoding, summed across all neurons. If all neurons in the Hopfield network were active, all memories were taken as lost and spurious (i.e. 100% spurious).
8.3.2. Fitting feedforward and feedback connection weights
The only constraint on network sizes is the fact that the random network is convergent (Nrand < 8*Nsensory). Here we use a four-fold convergence. Changing this ratio did not qualitatively change network behavior, other than the observation that larger random networks had greater capacity (Fig. S5).
Feedforward and feedback connection weights (α and β. respectively) were set using a grid search that optimized memory performance over hundreds of simulated trials. As described in the Results, the exact values of network parameters can be relaxed without changing network behavior. The parameters were fit to optimize two constraints: 1) maximize the number of inputs that were maintained throughout the stimulation and the delay periods and 2) minimize the number of spurious memories. We chose these criteria as they satisfied the minimal requirements for working memory: maintaining items without hallucinating. The performance of a set of parameters was evaluated as the sum of network performance (defined above) across all loads from 1 to 8. Parameters that created spurious memories on greater than 10% of trials were discarded. Despite attempting to optimize for overall network performance, no parameters were found that escaped the capacity limitation, even when the size of the random network was increased (Fig. S5).
We found parameter sets (α, β) that maintain stimulus inputs and minimize spurious memories for a broad range of γ (Fig. 7B). We set γ to 0.35 as it roughly maximized the number of maintained stimuli, minimized the number of spurious memories, and minimized the number of connections. The corresponding best fit for feedforward and feedback connections was α = 2100 and β = 200. This resulted in an average excitatory feedforward connection weight of 0.95 and an average excitatory feedback connection weight of 0.36. From the balance, we compute the inhibitory feedforward connection weight as −0.51 and the inhibitory feedback weight as −0.20.
For the model that included direct sensory inputs into the random network and recurrence within the random network (Fig. 6), αext and αrec were fit using a coarse grid search. As for α and β, parameters were chosen to maximize network performance (i.e. maximizing maintenance of memories while minimizing spurious memories). In addition, parameters were constrained to be positive in order to ensure transient dynamics in neural activity. The best fit parameters were αext = 100 and αrec = 250. Figure S2A shows that the addition of these connections does not qualitatively change the model behavior.
For the 2D surface model, feedforward and feedback weights were fit as before, optimizing the memory performance of the network. However, to avoid crowding in the sensory network, the maximum number of inputs was limited to 4. A grid search found the optimal parameters were α = 2800 and β = 150. This resulted in an average excitatory feedforward connection weight of 1.3 and an average excitatory feedback connection weight of 0.27. From the balance, we can compute that the inhibitory feedforward connection weight is −0.68 and the inhibitory feedback weight is −0.15.
For the Hopfield-like sensory network, feedforward and feedback weights were fit to maximize memory performance across memory loads from 1 to 8. A grid-search found the optimal parameters were α = 5700 and β = 100. This resulted in an average excitatory feedforward connection weight of 2.6 and an average excitatory feedback connection weight of 0.18. From the balance, we can compute that the inhibitory feedforward connection weight is −1.4 and the inhibitory feedback weight is −0.098.
Note that, for all parameters and architectures tested, interference between inputs into the random network limits memory maintenance and accuracy – the capacity of the network is unavoidable.
8.3.3. Estimating memory accuracy
Building on (Pouget et al., 2000; Bays, 2014), memories were decoded from the sensory sub-networks using a maximum likelihood decoder on spiking activity in a 100 ms time window (shortening the decoding interval to 50 ms or 10 ms did not qualitatively change the results). In Figure 3C,D, and Figure S1B, all simulations were taken into account, even when the memories were forgotten. In Figure 3E,F, only the simulations where all the memories were maintained were taken into account.
8.3.4. Correlation of memories in the random network
In Figures 5, S1C, and S7C, we show how memory performance increases as the correlation between memories in the random network is increased (i.e. there is a reduction in interference). The correlation between memories was computed as the dot product of the sensory inputs projected into the random network. This projection was done by multiplying the sensory input by the feedforward connection matrix (sext*WFF). When calculating the correlation over time, we used the maximum likelihood decoded representation as our representation in the sensory network.
8.3.5. Divisive-normalization-like regularization
Neural responses are reduced with an increase in load, both in the sensory domain (Heeger, 1992; Heeger et al., 1996; Carandini and Heeger, 1994, 2012) and in working memory (Buschman et al., 2011; Sprague et al., 2014). We tested whether similar divisive-normalization-like regularization was seen in our network model.
First, we tested whether the response of’selective’ neurons was reduced as memory load was increased. To this end, we simulated trials where each of three different sensory sub-networks received an input (s1, s2, or s3 into the first, second, or third sub-network, respectively). This can be conceptualized as presenting a stimulus at one of three different locations. Neurons in the random network were classified as ‘selective’ if their response to any individual input (the ‘preferred’ input) was greater than the other two inputs (‘non-preferred’ inputs). This follows the procedure typically used for electrophysiology experiments. Requiring a difference of at least 40 Hz resulted in 71 selective cells (6.9%). The response of selective neurons was then computed when the preferred input was presented alone (load 1), with either of the other two non-preferred inputs (load 2), or with all three inputs (load 3). We considered only the simulations where all inputs were maintained over the delay period. As seen in Fig. 4B, increasing memory load reduced the activity of selective neurons. Similar results were observed with selectivity thresholds of 50 Hz or 60 Hz.
As noted in the main text, our model shows how divisive-normalization-like regularization can arise from balanced excitation/inhibition between networks. The balanced excitation/inhibition means that a neuron in the random network that is selective for one stimulus is more likely to be inhibited than excited by a second stimulus (with a ratio of , as connections are random and independent across sensory networks). This results in the overall reduction in the response of selective neurons as items are added to memory (Fig. 4B).
To quantify the impact of memory load on all neurons, we adapted the statistic from (Reynolds et al., 1999) to measure the response of a neuron to a pair of stimuli, relative to the response to each stimulus alone (Fig. 4C). The response of all neurons in the random network were calculated for three conditions: a single input to sensory sub-network 1 (s1), a single input to sensory sub-network 2 (s2), and inputs to both sensory sub-network 1 and 2 simultaneously (s1,2). As in (Reynolds et al., 1999), responses were normalized by the maximum response for each neuron (max(s1,s2,s1,2)). Figure 4C shows the relative change in response to the two single stimuli (x-axis, s2 – s1) against the pair of stimuli (y-axis, s1,2, – s1). A linear fit was used to estimate the slope of the response. The resulting slope of 0.5 indicates the response to a pair of stimuli (s1,2) is a mixture of the two stimuli presented alone, as in (Reynolds et al., 1999).
Finally, we quantified whether increasing memory load reduced the selectivity of neurons. To this end, we calculated the response of neurons in the random network to two different inputs into the first sensory sub-network ( and ). The two sensory inputs were evenly separated (offset by 180°). As above, neurons were classified as selective if their response to the two inputs differed by at least 40 Hz (). This resulted in 67 selective neurons in the random network (6.5%). The response of these selective neurons was then calculated when each input ( and ) was presented with a second (or third) input into sub-network 2 (or 3), reflecting an increasing memory load. Again, we considered only the simulations where all inputs were maintained over the delay period. Following (Buschman et al., 2011), we computed the information these selective neurons carried about the identity of the stimulus in sensory sub-network 1 using the percentage of explained variance (PEV) statistic. Specifically, we computed for each selective neuron and for each time step, where is the total squared error across trials (t) and where and are the average response to sensory input and , respectively. Figure 4D shows η2 decreases with increasing memory load, as seen experimentally (Buschman et al., 2011). Similar results were seen with a threshold of 50 or 60 Hz.
8.3.6. Quantifying fit to experimental data
Data from published results were extracted using the Gimp image editor software, by measuring pixel positions relative to the scale on the y-axis of each figure. The effect of working memory load on human memory performance was taken from Fig. 1A of (Luck and Vogel, 1997). The effect of load on memory accuracy was taken from Fig. 1C of (Ma et al., 2014). The effect of load on overall neural activity was estimated by using the increase in BOLD activity with working memory, as shown in Fig. 3B of (Ma et al., 2014). As described in the main text, these values were compared to model behavior (Figures 3A, 3C, and 4A, respectively). However, we face two issues when trying to compare our model statistics with experimental data. First, our model does not include many critical components of cognition that may affect behavioral performance (e.g. encoding, decision making and motor responses). Second, the statistics extracted from the model may be different from the experimental observations (e.g. population firing rate versus BOLD). Therefore, to compare model performance and experimental observations, we used the Pearson correlation statistic as a marker of similarity (using the scipy.stats.pearsonr function). All statistical tests were against the null hypothesis of no correlation.
8.3.7. Direct fit to experimental data
Next, we tested whether models could be directly fit to experimental data. To this end, models were directly fit to behavioral estimates of either memory performance or memory accuracy. The size of the random network was set to Nrand = 2048 to match an overall higher performance (following Fig. S5), and the feedforward and feedback weights α and β were fit from a grid search in order to minimize the least-squares error between model performance and experimental observations.
For memory performance (Fig. 1A from (Luck and Vogel, 1997)), the optimal parameters were α = 2400, and β = 200. Note that, as the behavioral data from (Luck and Vogel, 1997) used a change detection task, memory performance was adjusted to account for a guess rate of 50%. Similarly, the optimal parameters for memory accuracy (Fig. 1C from (Ma et al., 2014)) were α = 2300, and β = 200. As seen in Figure S1D,E, our model can capture both datasets. Furthermore, fitting the model to one dataset generalized well to the other, withheld dataset. This suggests our single model can capture both effects.
8.3.8. Subspace Analysis
Analysis of the stable mnemonic space (Figs. 6 as well as S2 and S3) followed the methods of (Murray et al., 2016). To understand the subspace used for encoding, we calculated the response of the network to 8 different inputs into the first sensory sub-network (). The number of stimulus conditions was chosen to match (Murray et al., 2016), corresponding to 8 angular locations evenly separated within the sub-network (i.e. spaced by 45°). For each input condition, 500 independent trials were simulated for the same network.
We assessed temporal dynamics of neural activity by computing the cross-correlation of responses across trials with the same input. Correlations were then averaged across input conditions, yielding the cross-correlation matrix in Fig. 6A. Slices of the cross-correlation are displayed in Fig. 6B to match recent findings (Murray et al., 2016; Stokes et al., 2013).
Next, we defined the mnemonic and temporal subspaces as in (Murray et al., 2016). First, we averaged the activity of each neuron over trials. This resulted in a high-dimensional state space defined by the firing rate of Nrand neurons, over time T, for each of 8 input conditions (i.e. a Nrand × T ×8 matrix). Then, we defined the mnemonic subspace by estimating the principal components of the time-averaged response (which would now be a Nrand ×1 ×8 matrix). The first four PCs explained 77% and 82% of the variance in the data for load 1 and load 4 respectively. Projecting the original full timecourse of neural activity onto the first two principal components defined the mnemonic subspace in Figure 6C, showing the 8 clusters of time-varying activity for the 8 stimulus inputs. Figure S3C,D,E,H,I,J shows the projection of neural activity onto the subspace composed by the third and fourth components. In Figure 6, we only used simulations for which the memory in the first sensory sub-network is maintained. Figures S3A,B,F,G shows the evolution of activity for both maintained and forgotten memories.
In order to analyze how memory load impacted the mnemonic subspace (Fig. 6H and Fig. S2D), we repeated this process for memory loads 2 through 8. Memory load was manipulated by providing a random input into sensory sub-networks 2 through 8, in addition to the parametrically varying input to sub-network 1. We took into account only the simulations for which the memory in the first sensory sub-network was maintained, although the memories in the other sensory sub-networks could have been forgotten. This provided new mnemonic subspaces for each load.
Discriminability was computed as the distance between the neural response to different input conditions, normalized by the standard deviation of responses (d'). Neural responses were calculated as the average response over the delay period. The response for each trial was then projected into either the mnemonic subspace defined for a stimulus presented alone (the reference subspace, load = 1) or the mnemonic subspace optimized for each memory load, d' was calculated for each pair of inputs, along the vector connecting each cluster’s barycenter. The overall discriminability was then taken as the average d' across all pairs of inputs. Standard error was estimated by bootstrapping (1000 draws). Discriminability was computed within the reference (load 1) subspace and within the subspace optimized for each load. As seen in Fig. 6H, decodability was nearly equal across subspaces. For completeness, we also built a nearest centroid classifier as in (Murray et al., 2016). Decoder accuracy was estimated by testing cross-validation performance on withheld trials, for both the reference (load 1) subspace and the subspaces optimized for each load (Fig. S2D). Standard error was estimated by bootstrapping (1000 draws). This second analysis also shows that decodability was nearly equal across subspaces.
As noted above, all subspace analyses used the model with direct sensory input into the random network and recurrence within the random network (as described in section ‘Sensory inputs and recurrence in the random network’).
8.3.9. Estimating the interactions between memories
To understand how memories interact with one another, we estimated the drift of a memory relative to a second, simultaneously active memory. For models involving ring-like sensory sub-networks (e.g. Fig. S6), two inputs (A and B) were provided to sensory sub-networks 1 and 2. The drift of each memory was calculated as the distance between the initial input value and the decoded value at the end of the memory delay. As above, decoding was done with a maximum-likelihood decoder. Next, we compared the sign of the angle between the initial and final memories. If the sign of the drift was equal to the sign of the initial angle between A and B, then the drift was classified as an attraction (defined here as a positive bias). Otherwise, the signs were different and the drift was classified as a repulsion (defined here as a negative bias). This procedure was done for both memories, generating two bias values for each trial.
A similar process was used when using the 2D-surface as a sensory network (Fig. 8). Drift was taken as movement of the memory through the 2D surface, where the location of each memory was estimated with a clustering algorithm (see above). The vector of the drift from the initial to final positions of a memory (A-A’) was compared to the vector between the initial positions of two memories (A-B). If the dot product between A-A’ and A-B was positive, then the drift was classified as attractive (positive bias). If the dot product was negative, then the drift was classified as repulsive (negative bias). Attracted memories often merged in the 2D surface and so we measured the speed of attraction or repulsion by dividing the magnitude of absolute drift by the time for which both memories existed (which ended after the memory delay, with memories merging, or with memories being lost).
8.3.10. Training the random connections
Theoretical work has suggested that random projections are particularly useful when the structure of inputs is unknown (Jaeger, 2002; Maass et al., 2002; Jaeger and Haas, 2004; Sussillo and Abbott, 2009). To test whether this was true in our model, we trained the weights between the sensory network and the random network to maximize memory performance. The performance of the network was evaluated as before (the proportion of memories maintained minus the proportion of spurious memories across all loads). As this is not differentiable with respect to the weights between the sensory and the random networks, we used a random walk procedure to optimize the weights for a set of’trained’ inputs:
100 new networks were generated from the current ‘best’ network at each step n by rearranging 1% of bi-directional excitatory connections (swapping them with inhibitory connections). All connections were balanced after rearrangement.
The performance of each new network on the trained inputs was tested by running 1000 simulations per trained input.
The network with the best performance was then selected as the best network for step n +1.
Initially, the network was trained to optimize performance for one, five or ten input pattern(s). Each of these ‘trained’ input patterns consisted of one randomly chosen input for each sub-network (i.e. they were an 8 element vector with random numbers drawn from 1..Nsensory). Memory load was varied by selecting a random subset of sub-networks to receive an input. Therefore, the number of possible inputs across the entire sensory network was much higher than 1, 5, or 10. For example, if each sub-network was trained on a single input pattern, there were 255 different inputs possible across the entire sensory network (across all loads, ). For five and ten trained input patterns, there were 1,275 and 2,550 different inputs possible, respectively.
To test whether training generalized to other inputs, the performance of the ‘best’ network at each training step was tested on a set of 100 random input patterns (50 simulations each, across all loads). The set of 100 random inputs were fixed across training steps to facilitate comparison (Fig. 7E and Fig. S7A-B). Note that computational time at each training step increased as we increased the number of trained patterns. This limited the total number of training iterations possible for higher numbers of inputs (notably 10 input patterns). Therefore, to quantify the speed of learning across training steps we used the statsmodels toolbox to fit a line to each training curve (Fig. 7E). The line was fit to the first 50 training steps for 1, 5 and 10 input patterns. To test for significant differences in the learning rate as a function of the number of input patterns, we built a generalized linear model, adding a categorical variable for the number of inputs. Thus, significant differences would manifest as a significant interaction term (p-value included in the main text).
Finally, we tested whether training interfered with maintenance of other memories. For simplicity, only the networks trained to optimize one input vector were used. To systematically test the impact of training on memory, we varied the input to sub-network 1 (SN1), relative to the trained input. For higher loads all other sub-networks received their trained input. As seen in Figure S7D,E, training improved memory performance and accuracy for the trained input but at the cost of impaired memory for dissimilar inputs.
8.4. DATA AND SOFTWARE AVAILABILITY
All simulations were done with Python 3 (using numpy and scipy) and the Brian2 simulator (Stimberg et al., 2013; Goodman et al., 2014), using exact integration with time-step dt = 0.1ms. For PCA and the nearest centroid classifier, we used the scikit-learn package (Pedregosa et al., 2011). The script of the model is available at https://github.com/buschman-lab/FlexibleWorkingMemory or by contacting TJB.
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Software and Algorithms | ||
| The Brian 2 simulator |
Stimberg et al., 2013; Goodman et al., 2014 |
https://brian2.readthedocs.io/en/stable/ |
| Scikit-Learn | Pedregosa et al., 2011 | https://scikit-learn.org |
| Programming Language Python 3.6 | www.python.org | |
| Script of the Flexible Working Memory model | This paper | https://github.com/buschman-lab/FlexibleWorkingMemory |
Highlights :
Random recurrent connections can support flexible working memory.
Overlap of connections causes interference between memories, limiting capacity.
Model captures many behavioral and physiological characteristics of working memory.
Structured sensory networks can constrain high-dimensional random representations.
4. Acknowledgements
The authors are grateful to Sarah Henrickson, Adam Charles, Alex Libby, Camden MacDowell, Sebastian Musslick, and Matt Panichello for discussions and feedback on the manuscript. This work was supported by NIMH R56MH115042 and ONR N000141410681 to TJB.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests
The authors declare no competing interests.
References
- Adam KC, Vogel EK, Awh E, 2017. Clear evidence for item limits in visual working memory. Cognitive Psychology 97, 79–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almeida R, Barbosa J, Compte A, 2015. Neural circuit basis of visuo-spatial working memory precision: a computational and behavioral study. American Journal of Physiology-Heart and Circulatory Physiology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atallah BV, Bruns W, Carandini M, Scanziani M, 2012. Parvalbumin-expressing interneurons linearly transform cortical responses to visual stimuli. Neuron. Neuron 73, 159–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barak O, Tsodyks M, 2014. Working models of working memory. Current opinion in neurobiology 25, 20–24. [DOI] [PubMed] [Google Scholar]
- Bays PM, 2014. Noise in neural populations accounts for errors in working memory. Journal of Neuroscience 34, 3632–3645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bays PM, 2015. Spikes not slots: noise in neural populations limits working memory. Trends in cognitive sciences 19, 431–438. [DOI] [PubMed] [Google Scholar]
- Bays PM, Catalao RF, Husain M, 2009. The precision of visual working memory is set by allocation of a shared resource. Journal of vision 9, 7–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bays PM, Husain M, 2008. Dynamic shifts of limited working memory resources in human vision. Science 321, 851–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burak Y, Fiete IR, 2012. Fundamental limits on persistent activity in networks of noisy neurons. Proceedings of the National Academy of Sciences 109, 17645–17650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buschman TJ, Siegel M, Roy JE, Miller EK, 2011. Neural substrates of cognitive capacity limitations. Proceedings of the National Academy of Sciences 108, 11252–11255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carandini M, Heeger DJ, 1994. Summation and division by neurons in primate visual cortex. Science 264, 1333–1336. [DOI] [PubMed] [Google Scholar]
- Carandini M, Heeger DJ, 2012. Normalization as a canonical neural computation. Nature Reviews Neuroscience 13, 51–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christophel TB, Klink PC, Spitzer B, Roelfsema PR, Haynes JD, 2017. The distributed nature of working memory. Trends in Cognitive Sciences 21,111–124. [DOI] [PubMed] [Google Scholar]
- Constantinidis C, Klingberg T, 2016. The neuroscience of working memory capacity and training. Nature Reviews Neuroscience 17, 438–449. [DOI] [PubMed] [Google Scholar]
- Cowan N, 2010. The magical mystery four: How is working memory capacity limited, and why? Current directions in psychological science 19, 51–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curtis CE, D’Esposito M, 2003. Persistent activity in the prefrontal cortex during working memory. Trends in cognitive sciences 7, 415–423. [DOI] [PubMed] [Google Scholar]
- De Wit J, Ghosh A, 2016. Specification of synaptic connectivity by cell surface interactions. Nature Reviews Neuroscience 17, 4. [DOI] [PubMed] [Google Scholar]
- Druckmann S, Chklovskii DB, 2012. Neuronal circuits underlying persistent representations despite time varying activity. Current Biology 22, 2095–2103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan J, 2001. An adaptive coding model of neural function in prefrontal cortex. Nature Reviews Neuroscience 2. [DOI] [PubMed] [Google Scholar]
- Edin F, Klingberg T, Johansson P, McNab F, Tegnér J, Compte A, 2009. Mechanism for top-down control of working memory capacity. Proceedings of the National Academy of Sciences 106, 6802–6807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funahashi S, Bruce CJ, Goldman-Rakic PS, 1989. Mnemonic coding of visual space in the monkey9s dorsolateral prefrontal cortex. Journal of neurophysiology 61, 331–349. [DOI] [PubMed] [Google Scholar]
- Fusi S, Miller EK, Rigotti M, 2016. Why neurons mix: high dimensionality for higher cognition. Current opinion in neurobiology 37, 66–74. [DOI] [PubMed] [Google Scholar]
- Fuster JM, 1973. Unit activity in prefrontal cortex during delayed-response performance: neuronal correlates of transient memory. Journal of Neurophysiology. [DOI] [PubMed] [Google Scholar]
- Fuster JM, 1999. Memory in the cerebral cortex: An empirical approach to neural networks in the human and nonhuman primate. MIT press. [Google Scholar]
- Goodman DF, Stimberg M, Yger P, Brette R, 2014. Brian 2: neural simulations on a variety of computational hardware. BMC Neuroscience 15, PI99. [Google Scholar]
- Haier RJ, Jung RE, Yeo RA, Head K, Alkire MT, 2004. Structural brain variation and general intelligence. Neuroimage 23, 425–433. [DOI] [PubMed] [Google Scholar]
- Harris KD, Mrsic-Flogel TD, 2013. Cortical connectivity and sensory coding. Nature 503, 51. [DOI] [PubMed] [Google Scholar]
- Hasselmo ME, Stern CE, 2006. Mechanisms underlying working memory for novel information. Trends in cognitive sciences 10, 487–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He K, Huertas M, Hong SZ, Tie X, Hell JW, Shouval H, Kirkwood A, 2015. Distinct eligibility traces for ltp and ltd in cortical synapses. Neuron 88, 528–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heeger DJ, 1992. Normalization of cell responses in cat striate cortex. Visual neuroscience 9, 181–197. [DOI] [PubMed] [Google Scholar]
- Heeger DJ, Simoncelli EP, Movshon JA, 1996. Computational models of cortical visual processing. Proceedings of the National Academy of Sciences 93, 623–627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmgren C, Harkany T, Svennenfors B, Zilberter Y, 2003. Pyramidal cell communication within local networks in layer 2/3 of rat neocortex. The Journal of physiology 551, 139–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaeger H, 2002. Short term memory in echo state networks. gmd-report 152, in: GMD-German National Research Institute for Computer Science (2002), http://www.faculty.jacobs-university.de/hjaeger/pubs/STMEchoStatesTechRep.pdf, Citeseer. [Google Scholar]
- Jaeger H, Haas H, 2004. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. science 304, 78–80. [DOI] [PubMed] [Google Scholar]
- Kim SS, Rouault H, Druckmann S, Jayaraman V, 2017. Ring attractor dynamics in the drosophila central brain. Science 356, 849–853. [DOI] [PubMed] [Google Scholar]
- Kiorpes L, 2015. Visual development in primates: neural mechanisms and critical periods. Developmental neurobiology 75, 1080–1090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiyonaga A, Egner T, 2016. Center-surround inhibition in working memory. Current Biology 26, 64–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiyonaga A, Scimeca JM, Bliss DP, Whitney D, 2017. Serial dependence across perception, attention, and memory. Trends in Cognitive Sciences 21, 493–497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klingberg T, 2006. Development of a superior frontal–intraparietal network for visuo-spatial working memory. Neuropsychologia 44, 2171–2177. [DOI] [PubMed] [Google Scholar]
- Ko H, Hofer SB, Pichler B, Buchanan KA, Sjöström PJ, Mrsic-Flogel TD, 2011. Functional specificity of local synaptic connections in neocortical networks. Nature 473, 87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kostadinov D, Sanes JR, 2015. Protocadherin-dependent dendritic self-avoidance regulates neural connectivity and circuit function. Elife 4, e08964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuffler SW, 1953. Discharge patterns and functional organization of mammalian retina. Journal of neurophysiology 16, 37–68. [DOI] [PubMed] [Google Scholar]
- Lin PH, Luck SJ, 2009. The influence of similarity on visual working memory representations. Visual Cognition 17, 356–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindsay GW, Rigotti M, Warden MR, Miller EK, Fusi S, 2017. Hebbian learning in a random network captures selectivity properties of the prefrontal cortex. Journal of Neuroscience 37, 11021–11036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loewenstein Y, Sompolinsky H, 2003. Temporal integration by calcium dynamics in a model neuron. Nature neuroscience 6, 961–967. [DOI] [PubMed] [Google Scholar]
- Luck SJ, Vogel EK, 1997. The capacity of visual working memory for features and conjunctions. Nature 390, 279–281. [DOI] [PubMed] [Google Scholar]
- Lundqvist M, Rose J, Herman P, Brincat SL, Buschman TJ, Miller EK, 2016. Gamma and beta bursts underlie working memory. Neuron 90, 152–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma WJ, Husain M, Bays PM, 2014. Changing concepts of working memory. Nature neuroscience 17, 347–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maass W, Natschläger T, Markram H, 2002. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural computation 14, 2531–2560. [DOI] [PubMed] [Google Scholar]
- Man K, Kaplan J, Damasio H, Damasio A, 2013. Neural convergence and divergence in the mammalian cerebral cortex: from experimental neuroanatomy to functional neuroimaging. Journal of Comparative Neurology 521, 4097–4111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mariño J, Schummers J, Lyon DC, Schwabe L, Beck O, Wiesing P, Obermayer K, Sur M, 2005. Invariant computations in local cortical networks with balanced excitation and inhibition. Nature neuroscience 8, 194. [DOI] [PubMed] [Google Scholar]
- McKenzie S, Frank AJ, Kinsky NR, Porter B, Rivière PD, Eichenbaum H, 2014. Hippocampal representation of related and opposing memories develop within distinct, hierarchically organized neural schemas. Neuron 83, 202–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melby-Lervåg M, Hulme C, 2013. Is working memory training effective? a meta-analytic review. Developmental psychology 49, 270. [DOI] [PubMed] [Google Scholar]
- Mendoza-Halliday D, Torres S, Martinez-Trujillo JC, 2014. Sharp emergence of feature-selective sustained activity along the dorsal visual pathway. Nature neuroscience 17, 1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EK, Cohen JD, 2001. An integrative theory of prefrontal cortex function. Annual review of neuroscience 24, 167–202. [DOI] [PubMed] [Google Scholar]
- Mongillo G, Barak O, Tsodyks M, 2008. Synaptic theory of working memory. Science 319, 1543–1546. [DOI] [PubMed] [Google Scholar]
- Murray JD, Bernacchia A, Roy NA, Constantinidis C, Romo R, Wang XJ, 2016. Stable population coding for working memory coexists with heterogeneous neural dynamics in prefrontal cortex. Proceedings of the National Academy of Sciences, 201619449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassar MR, Helmers JC, Frank MJ, 2018. Chunking as a rational strategy for lossy data compression in visual working memory. Psychological review 125, 486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nissim NR, O’Shea AM, Bryant V, Porges EC, Cohen R, Woods AJ, 2017. Frontal structural neural correlates of working memory performance in older adults. Frontiers in aging neuroscience 8, 328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Packer AM, Yuste R, 2011. Dense, unspecific connectivity of neocortical parvalbumin-positive interneurons: a canonical microcircuit for inhibition? Journal of Neuroscience 31, 13260–13271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasupathy A, Miller EK, 2005. Different time courses of learning-related activity in the prefrontal cortex and striatum. Nature 433, 873. [DOI] [PubMed] [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. , 2011. Scikit-learn: Machine learning in python. Journal of machine learning research 12, 2825–2830. [Google Scholar]
- Pertzov Y, Manohar S, Husain M, 2017. Rapid forgetting results from competition over time between items in visual working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition 43, 528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrides M, 1995. Impairments on nonspatial self-ordered and externally ordered working memory tasks after lesions of the mid-dorsal part of the lateral frontal cortex in the monkey. Journal of Neuroscience 15, 359–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Postle BR, 2017. Working memory functions of the prefrontal cortex, in: The Prefrontal Cortex as an Executive, Emotional, and Social Brain. Springer, pp. 39–48. [Google Scholar]
- Pouget A, Dayan P, Zemel R, 2000. Information processing with population codes. Nature Reviews Neuroscience 1, 125. [DOI] [PubMed] [Google Scholar]
- Rademaker RL, Park YE, Sack AT, Tong F, 2018. Evidence of gradual loss of precision for simple features and complex objects in visual working memory. Journal of Experimental Psychology: Human Perception and Performance. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds JH, Chelazzi L, Desimone R, 1999. Competitive mechanisms subserve attention in macaque areas v2 and v4. Journal of Neuroscience 19, 1736–1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigotti M, Barak O, Warden MR, Wang XJ, Daw ND, Miller EK, Fusi S, 2013. The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romo R, Hernández A, Zainos A, Lemus L, Brody CD, 2002. Neuronal correlates of decision-making in secondary somatosensory cortex. Nature neuroscience 5, 1217–1225. [DOI] [PubMed] [Google Scholar]
- Salazar R, Dotson N, Bressler S, Gray C, 2012. Content-specific fronto-parietal synchronization during visual working memory. Science 338, 1097–1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seelig JD, Jayaraman V, 2015. Neural dynamics for landmark orientation and angular path integration. Nature 521, 186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song S, Sjöström PJ, Reigl M, Nelson S, Chklovskii DB, 2005. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS biology 3, e68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spaak E, Watanabe K, Funahashi S, Stokes MG, 2017. Stable and dynamic coding for working memory in primate prefrontal cortex. Journal of Neuroscience 37, 6503–6516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprague TC, Ester EF, Serences JT, 2014. Reconstructions of information in visual spatial working memory degrade with memory load. Current Biology 24, 2174–2180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stimberg M, Goodman DF, Benichoux V, Brette R, 2013. Brian 2-the second coming: spiking neural network simulation in python with code generation. BMC Neuroscience 14, P38. [Google Scholar]
- Stokes MG, 2015. ‘activity-silent’ working memory in prefrontal cortex: a dynamic coding framework. Trends in cognitive sciences 19, 394–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes MG, Kusunoki M, Sigala N, Nili H, Gaffan D, Duncan J, 2013. Dynamic coding for cognitive control in prefrontal cortex. Neuron 78, 364–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sussillo D, Abbott LF, 2009. Generating coherent patterns of activity from chaotic neural networks. Neuron 63, 544–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swan G, Wyble B, 2014. The binding pool: A model of shared neural resources for distinct items in visual working memory. Attention, Perception, & Psychophysics 76, 2136–2157. [DOI] [PubMed] [Google Scholar]
- Vogel EK, Machizawa MG, 2004. Neural activity predicts individual differences in visual working memory capacity. Nature 428, 748. [DOI] [PubMed] [Google Scholar]
- Vogels TP, Abbott LF, 2005. Signal propagation and logic gating in networks of integrate-and-fire neurons. Journal of neuroscience 25, 10786–10795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogels TP, Rajan K, Abbott LF, 2005. Neural network dynamics. Annu. Rev. Neurosci. 28, 357–376. [DOI] [PubMed] [Google Scholar]
- Vogels TP, Sprekeler H, Zenke F, Clopath C, Gerstner W, 2011. Inhibitory plasticity balances excitation and inhibition in sensory pathways and memory networks. Science 334, 1569–1573. [DOI] [PubMed] [Google Scholar]
- Wang XJ, 2001. Synaptic reverberation underlying mnemonic persistent activity. Trends in neurosciences 24, 455–463. [DOI] [PubMed] [Google Scholar]
- Wilson NR, Runyan CA, Wang FF, Sur M, 2012. Division and subtraction by distinct cortical inhibitory networks in vivo. Nature 488, 343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamagishi T, Yoshitake K, Kamatani D, Watanabe K, Tsukano H, Hishida R, Takahashi K, Takahashi S, Horii A, Yagi T, et al. , 2018. Molecular diversity of clustered protocadherin-α required for sensory integration and short-term memory in mice. Scientific reports 8, 9616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaksas D, Pasternak T, 2006. Directional signals in the prefrontal cortex and in area mt during a working memory for visual motion task. Journal of Neuroscience 26, 11726–11742. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All simulations were done with Python 3 (using numpy and scipy) and the Brian2 simulator (Stimberg et al., 2013; Goodman et al., 2014), using exact integration with time-step dt = 0.1ms. For PCA and the nearest centroid classifier, we used the scikit-learn package (Pedregosa et al., 2011). The script of the model is available at https://github.com/buschman-lab/FlexibleWorkingMemory or by contacting TJB.