SUMMARY
In the ocean, the crab, Cancer borealis, is subject to daily and seasonal temperature changes. Previous work, done in the presence of descending modulatory inputs, had shown that the pyloric rhythm of the crab increases in frequency as temperature increases, but maintains its characteristic phase relationships until it “crashes” at extreme high temperatures. To study the interaction between neuromodulators and temperature perturbations, we studied the effects of temperature on preparations from which the descending modulatory inputs were removed. Under these conditions the pyloric rhythm was destabilized. We then studied the effects of temperature on preparations in the presence of oxotremorine, proctolin, and serotonin. Oxotremorine and proctolin enhanced the robustness of the pyloric rhythm, while serotonin made the rhythm less robust. These experiments reveal considerable animal-to-animal diversity in their crash stability, consistent with the interpretation that cryptic differences in many cell and network parameters are revealed by extreme perturbations.
Keywords: stomatogastric ganglion, crustaceans, temperature, serotonin, proctolin, pyloric rhythm, neuronal oscillators, central pattern generator
INTRODUCTION
Most animals must function in a variety of environments. Consequently, most neuronal circuits must be sufficiently flexible to allow for behavioral adaptation in response to environmental fluctuations. In the case of poikilothermic animals, environmental temperature fluctuations can be a strong evolutionary pressure that gives rise to robust mechanisms of temperature preference (Beverly et al., 2011; Dell et al., 2011; Hamada et al., 2008) that cause animals to physically translocate in their habitats to maintain relatively constant body temperature. Nonetheless, many animals, such as the North Atlantic crab, Cancer borealis, used in this study, experience substantial temperature fluctuations daily and seasonally (Donahue et al., 2009; Haeffner, 1977; Krediet and Donahue, 2009; Stehlik et al., 1991), even as they also move between deeper and shallower waters in search of their preferred temperatures.
Because temperature influences all biological processes to a different extent, it presents an extraordinary challenge to maintaining relatively stereotyped performance (Caplan et al., 2014; O’Leary and Marder, 2016; Rinberg et al., 2013; Robertson and Money, 2012; Roemschied et al., 2014; Schleimer and Schreiber, 2016; Tang et al., 2010; Tang et al., 2012). This is easily understood if one thinks of multiple membrane currents that contribute to some physiological process, each with a different temperature dependence (Partridge and Connor, 1978). Consequently, even modest temperature changes could cause significant changes or disruptions to that physiological system (Caplan et al., 2014; O’Leary and Marder, 2016). Nonetheless, there are examples of neurons and circuits that are well temperature compensated, although their individual membrane currents show appreciable temperature dependencies (Partridge and Connor, 1978; Roemschied et al., 2014).
Almost perfect temperature compensation is likely the exception, not the rule, and many poikilothermic animals show significant alterations in motor patterns and behavior as ambient temperature fluctuates (Lenz et al., 2005; Long and Fee, 2008; Long et al., 2016; Neumeister et al., 2000; Robertson and Money, 2012; Shoemaker and Robertson, 1998; Soofi et al., 2014; Stevenson and Josephson, 1990; Tang et al., 2010; Tang et al., 2012; Tyler, 1970). Moreover, because all individuals of the same specie vary in the synaptic strengths and conductance densities found in individual neurons and networks (Goaillard et al., 2009; Golowasch et al., 1999; Lane et al., 2016; Norris et al., 2011; Roffman et al., 2012; Schulz et al., 2006; Schulz et al., 2007; Temporal et al., 2014; Wenning et al., 2014), it is not surprising that the population may show substantial variance in their sensitivity to temperature. In this paper, we use temperature as a perturbation of the activity of the crustacean stomatogastric ganglion (STG) to ask whether neuromodulation can stabilize network output in response to changes in temperature. To do so, we characterize state changes in network performance in response to temperature changes under a variety of modulatory conditions. The significant animal-to-animal variability revealed in the absence of strong modulatory drive impelled us to design new methods of analyzing this variability.
RESULTS
The stomatogastric nervous system (STNS) has led to numerous insights into the basic mechanisms of the generation of rhythmic movements and their modulation (Marder, 2012; Marder and Bucher, 2007; Marder and Calabrese, 1996) because the circuit neurons and many neuromodulatory inputs are identified and characterized. The C. borealis STG contains 26–27 neurons (Kilman and Marder, 1996). There are about 20–25 pairs of descending modulatory neurons (Coleman et al., 1992) that contain a large number of peptide and small molecule cotransmitters (Nusbaum and Beenhakker, 2002; Nusbaum et al., 2017; Nusbaum et al., 2001) and project into the STG from the anterior oesophageal ganglion (OG) and the paired commissural ganglia (CoGs). The STG contains the essential circuitry for the generation of the relatively fast triphasic pyloric rhythm while the slower gastric mill rhythm depends on the descending inputs (Blitz and Nusbaum, 1997; Blitz and Nusbaum, 2011). When impulse traffic in the stomatogastric nerve that brings the modulatory inputs to the STG is blocked, the gastric mill rhythm stops and the pyloric rhythm markedly slows (Hamood et al., 2015; Hamood and Marder, 2015; Russell, 1979). In turn, exogenous application of a number of excitatory neuromodulators, such as the neuropeptide proctolin and muscarinic agonists such as oxotremorine, strongly activates the pyloric rhythm (Bal et al., 1994; Hooper and Marder, 1987; Marder and Eisen, 1984).
In previous work the effects of temperature were characterized on the pyloric rhythm when the descending modulatory inputs were left intact (Soofi et al., 2014; Tang et al., 2010; Tang et al., 2012). Here we first study the effects of temperature on the pyloric rhythm in the absence of neuromodulation, and then in the presence of exogenously applied neuromodulators.
STG preparations were “decentralized”, that is the action of descending modulatory inputs from anterior ganglia were removed by cutting the stomatogastric nerve (stn). Figure 1A shows the recording configuration used and the placement of the extracellular electrodes on the motor nerves used to monitor the activity of the neurons that are active in the pyloric and gastric mill rhythms. Previous work (Hamood et al., 2015) quantified the effects of the removal of the descending modulatory inputs on large populations of STGs and demonstrated a range of network outputs when STGs were decentralized. Some preparations continued to generate normal but slow pyloric rhythms, while others lost activity entirely or became arrhythmic (Fig. 1B 11 °C).
Figure 1.
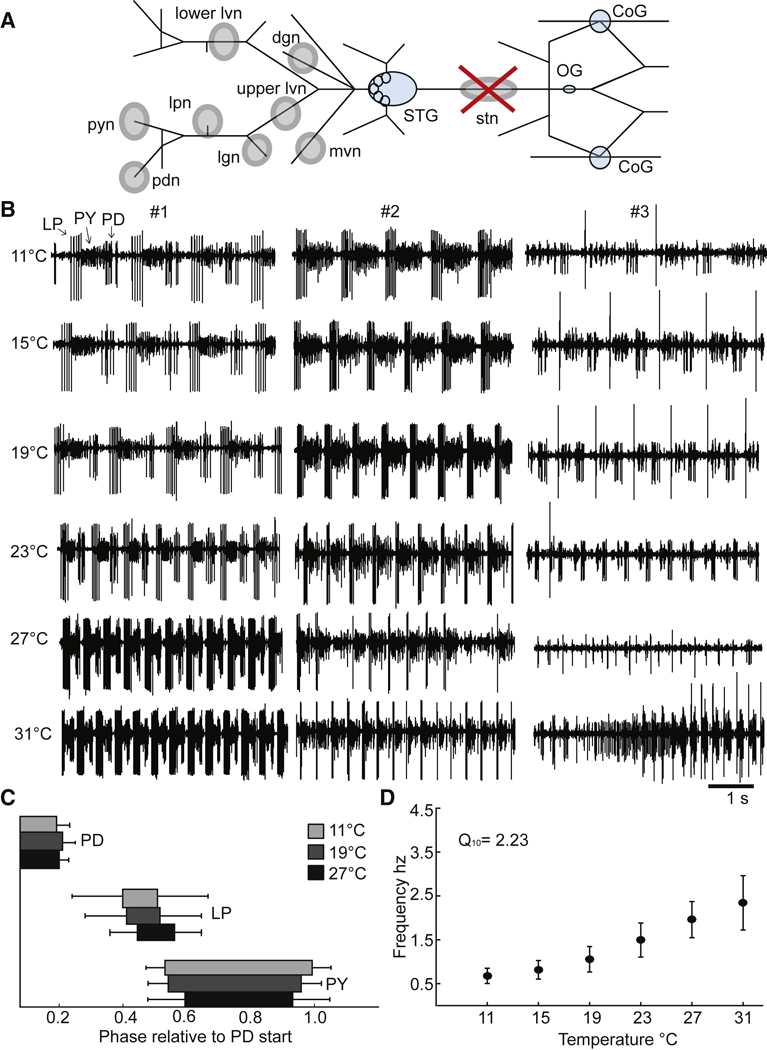
Recording configuration and control data from decentralized preparations. A. Simplified diagram of the STNS as it would appear dissected and pinned out onto a Sylgard coated petri dish. The Stomatogastric Ganglion (STG), Commissural Ganglia (CoGs) and Esophageal Ganglion (OG) are colored light blue. Grey circles indicate where Vaseline wells are made around nerves of interest for extracellular recordings. The stn (stomatogastric nerve) well with the large red ‘X” indicates where the stn is cut for decentralization after the well surrounding the stn had been filled with TTX and sucrose to silence the nerve. All the other wells, which fall posterior (left on diagram) to the STG, indicate the nerves where extracellular recordings were made. B. Five seconds of raw extracellular traces from the lvn from three different decentralized preparations (#1, #2, #3), at 11°C, 15°C, 19°C, 23°C, 27°C and 31°C. The activity shown from these preparations represents the variety of activity seen in the decentralized condition across temperature. C. The average phase relationships of the neurons that generate the triphasic rhythm for three temperatures, 11°C (light grey), 19°C (dark grey) and 27°C (black). The phase is calculated relative to the start of the PD burst per cycle. The bars represent the standard deviation of the data. Only preparations with a triphasic rhythm are included in these plots. (N@11=24, @15=24, @19=25, @23=23, @27=18, @31=11). D. The mean frequency of the rhythm calculated from the activity of the PD neurons, across temperature. The bars represent the standard deviation of the data. Only preparations with rhythmic PD bursts are included in this plot. (N@11=24, @15=24, @19=25, @23=24, @27=19, @31=14).
The effects of temperature on the decentralized pyloric rhythm.
We first characterize the effects of temperature on 40 decentralized preparations, as these data constitute baseline measurements for the effects of exogenously applied neuromodulators. Figure 1B shows examples of the triphasic pyloric rhythm as a function of temperature in preparations from three different animals. In preparation #1, we see a characteristic and classic pyloric rhythm (activity of LP, PY, and PD) at all temperatures from 11 °C to 31 °C. Over this temperature range the pyloric rhythm frequency increased from 0.8 Hz to 2.4 Hz. Preparation #2 also displayed a classical pyloric rhythm from 11 °C to about 23 °C, but when the temperature was further increased, the rhythm became less regular, and showed intermittent changes in activity. Preparation #3 shows an example of a weaker pyloric rhythm at 11 °C, characterized by a single LP spike/burst. As the temperature was increased, LP activity first dropped out, and eventually the rhythm became highly irregular. These three examples show the ranges of activity routinely seen at 11 °C under these conditions (Hamood et al., 2015; Hamood and Marder, 2015).
Figure 1C shows the normalized phase relationships for the activity of the LP, PY and PD neurons at different temperatures, for those stretches of data that maintained a regular pyloric rhythm. Note that these phase relationships are relatively temperature invariant, as had been reported for data from preparations with modulatory inputs intact (Tang et al., 2010). Figure 1D shows the effects of temperature on the frequency of the triphasic rhythm for those stretches of data when it was triphasic. Similar to what was seen with the modulatory inputs intact (Tang et al., 2010), the apparent Q10 of the frequency was 2.23.
Characterization of different activity patterns
The raw data shown in Figure 1B illustrate that at high temperatures it is common to see disturbances or “crashes” in the activity patterns produced by neurons of the pyloric circuit (Tang et al., 2012). We wanted to display both the kinds of activity patterns displayed by different preparations and to characterize the potential effects of modulators on these. Because the recordings are often not stationary, but individual stretches of data show transitions between qualitatively different states of activity, we classified the raw data into eight different activity states, as defined in Figure 2. The GLR (lavender) (Gastric-like Rhythm) state has a robust pyloric rhythm with bursts of activity in the gastric LG neuron (pink traces) and DG neuron (not shown). The NTf (Normal triphasic fast) (dark blue) state is a normal triphasic rhythm with a frequency greater than 0.8 Hz. The NTs (Normal triphasic slow) (yellow) state is a triphasic rhythm slower than 0.8 Hz, with a concomitant change in phase (Hamood et al., 2015).
Figure 2.
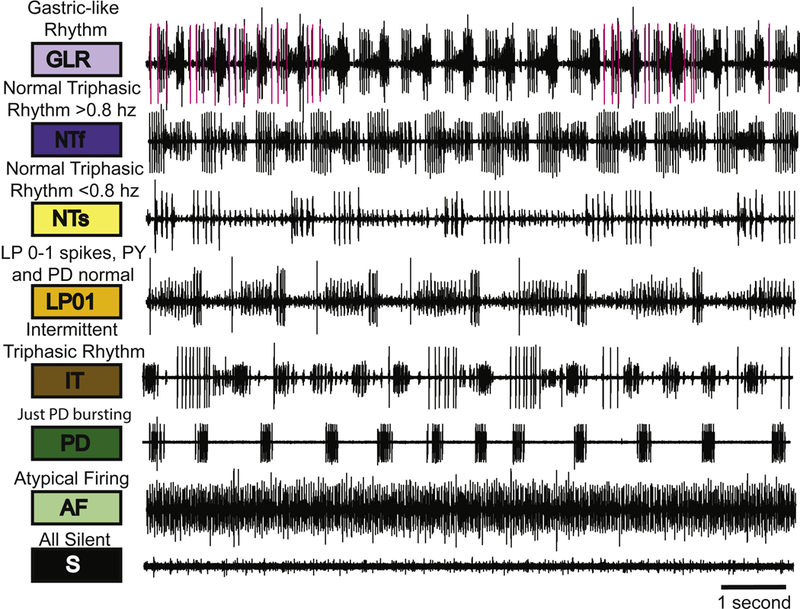
The categorization system. The eight categories are illustrated with sample raw traces that represent each category used in this analysis. The colored boxes designate the color that represents that particular category. Above each box is the descriptive name of each category and the abbreviation for each category is indicated within the colored box.
The LP01 (LP, 0 or 1 spike/burst) (orange) rhythm has normal PD, PY alternation with either 0 or 1 LP spike/burst. The IT (Intermittent Triphasic) (brown) rhythm is an intermittent triphasic rhythm (Fig. 2) with short periods of triphasic activity with interruptions. The PD (just PD bursting) (dark green) traces are associated with activity only in the PD neurons. The AF (Atypical Firing) (light green) state is atypical firing. The S (All silent) (black) state is all units silent (Fig. 2).
Temperature-Dependent State Transitions
Using the classifications defined in Figure 2, we classified 150 seconds of data into state blocks, with each block at least 1 second long (Methods). This allows each stretch of data to show as many as 149 state transitions. Figure 3A shows the three preparations from Figure 1B analyzed from 11 °C to 31 °C in this way. Preparation #1 was slow triphasic (NTs) at the two lowest temperatures and NTf at the four higher temperatures. Preparation #2 also went from NTs to NTf at lower temperatures, but made a variety of other state transitions at higher temperatures. Preparation #3 was LP01 at lower temperatures and again showed state transitions at higher temperatures.
Figure 3.
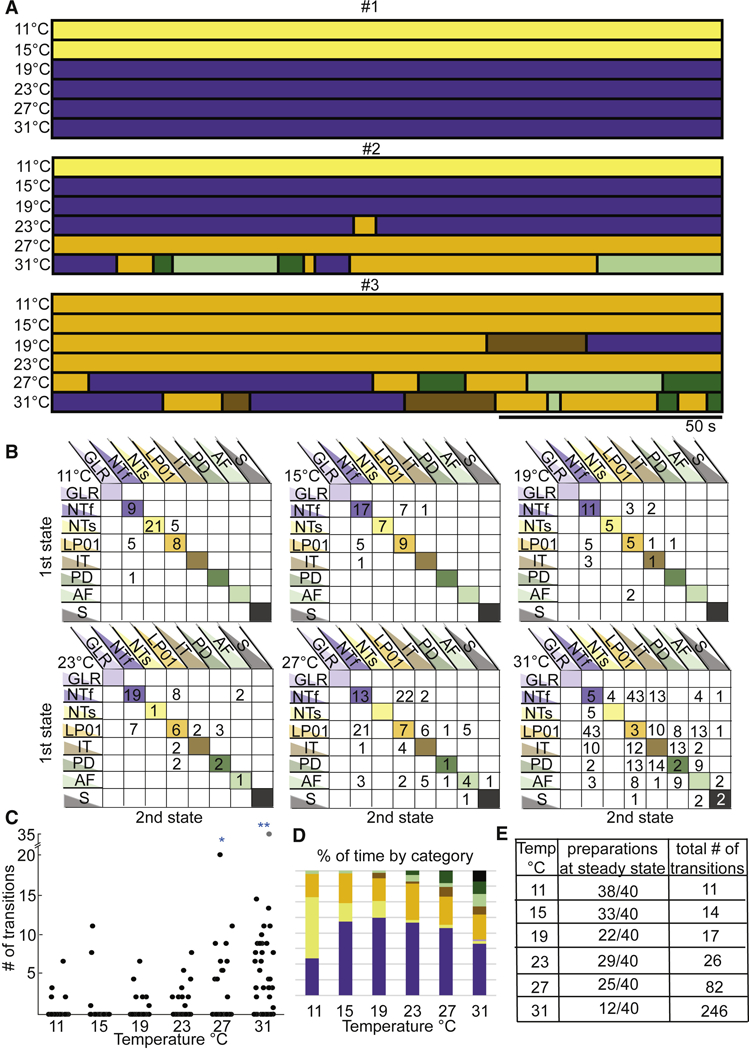
Transitions seen in decentralized preparations. A. Same preparations shown in Figure 1 (#1, #2, #3) with activity patterns of each preparation at each of the 6 temperatures, categorized as described in Figure 2. Each horizontal bar represents one data file of recordings 150s long, during which the preparation is at a stable temperature, indicated to the left. B. These matrices contain the cumulative data of transitions and stable activity patterns, for all the decentralized preparations (N=40) at each temperature. The y-axis indicates the starting activity state and the x-axis indicates the state to which the transition occurs. The diagonal lists the number of preparations that were at that particular state for an entire temperature/file, meaning they did not transition across states for that 150 s. C. Cumulative data showing the number of transitions counted per preparation (each black dot is a single preparation) as a function of temperature. The number of transitions is significantly higher at 27°C and 31°C than the other temperatures (*p<0.01 for 27°C and **p<0.001 for 31°C calculated with a one-way ANOVA adjusted for multiple comparisons). D. Each bar represents the 100% of time of all the preparations as a function of temperature. This shows that more types of activity patterns appear as the temperature is increased and more of the less stable activity patterns are present. E. The tabulated counts of preparations at one state for an entire file (steady state) and the number of transitions counted across all preparations at each temperature.
The state transitions seen at higher temperatures in Figure 3 have highly variable durations. To determine whether there are specific patterns of state transitions within a given preparation, we plotted the specific transitions shown across temperatures. There are 6 plots shown in Figure 3B, one for each temperature (indicated in the top left of each plot). The y axis shows the state of the preparation before a transition, and the x axis shows the state of the preparation after a transition. The numbers in the colored diagonals are the numbers of preparations that made no transitions. That is to say at 11 °C, 9 preparations showed NTf throughout the entire recording time, while 21 preparations were NTs throughout and 8 were LP01 throughout. The numbers in the white boxes not on the diagonals are the number of those specific transitions across all 40 preparations. That is, there were 5 LP01 transitions to NTf, and 5 NTs to LP01.
As the temperature was increased, the number of preparations on the diagonal generally decreased, and the number of transitions between other states increased. At 31 °C, there were only 12 preparations left on the diagonal and there were 246 transitions. Additionally, the destabilizing effects of temperature can be seen by the fact that the number of transitions in the lower portions of the plots increased at higher temperatures.
Figure 3C shows a plot of the total number of transitions for each preparation (each preparation is represented by a single point) at each temperature. A one-way ANOVA adjusted for multiple comparisons shows that the number of transitions at 27 °C and 31 °C were statistically different from all other temperatures. Figure 3D displays the total amount of time these preparations spent in each category, and again illustrates that temperature increases the frequency of the pyloric rhythm (the dark blue bars) but eventually at high temperatures less and less time is spent in a characteristic triphasic rhythm. Figure 3E summarizes the number of preparations that maintained steady-state activity as a function of temperature and the total number of transitions from all 40 preparations at each temperature.
Oxotremorine and proctolin stabilize the pyloric rhythm to temperature.
Muscarinic agonists and the neuropeptide proctolin have been long known to strongly activate the pyloric rhythm (Elson and Selverston, 1992; Hooper and Marder, 1987; Marder and Eisen, 1984; Marder and Paupardin-Tritsch, 1978; Nagy and Dickinson, 1983; Nusbaum and Marder, 1989a; Nusbaum and Marder, 1989b), by activating a voltage-dependent inward current, now called IMI (Golowasch and Marder, 1992b; Swensen and Marder, 2000). Interestingly, although oxotremorine and proctolin have somewhat different neuronal targets in the STG, they converge on the same final membrane current, and this is associated with increases in the amplitude of the slow wave bursts that govern the pacemaker activity of the STG networks (Golowasch and Marder, 1992b; Sharp et al., 1993; Swensen and Marder, 2000, 2001).
The raw data shown in Figure 4A,B show that both 10−5 M oxotremorine and 10−6 M proctolin stabilize the pyloric rhythm against temperature disruption. Preparations #4 and #5 are shown in oxotremorine, and preparations #6 and #7 are seen in proctolin. In these cases, the frequency of the pyloric rhythm increased as the temperature was increased, and the triphasic nature of the rhythm was maintained, even at 31 °C. The stability of the rhythms is seen in the relative lack of transitions in all 4 preparations at all temperatures (Fig. 4C,D). This is independent of the fact that in modulator the starting frequencies were quite different. Figures 5A and 5B show the effect of temperature on the phase of each of the neurons in the triphasic rhythm in both oxotremorine and proctolin. All of the preparations remained triphasic in oxotremorine (n = 10) and proctolin (n = 10) at all temperatures. Figures 5C and 5D show the effect of temperature on the pyloric rhythm frequency in oxotremorine and proctolin. Note that the oxotremorine preparations increased in frequency far more than did the proctolin preparations. The apparent Q10 of the pyloric rhythm frequency in the oxotremorine condition is 2.07. The apparent Q10 of the pyloric rhythm frequency in proctolin is 1.79. Figures 5E,F show that the number of transitions counted (per individual) in the modulator conditions (red) were significantly different in comparison to the decentralized controls (black) at 27 °C and 31 °C. Figures 5G,H show that the preparations spent all of the recorded time in one of two stable conditions across the range of temperatures, whereas the same preparations, in the absence of modulators, displayed a range of activity patterns, with progressively less stable conditions present as temperature increases.
Figure 4.
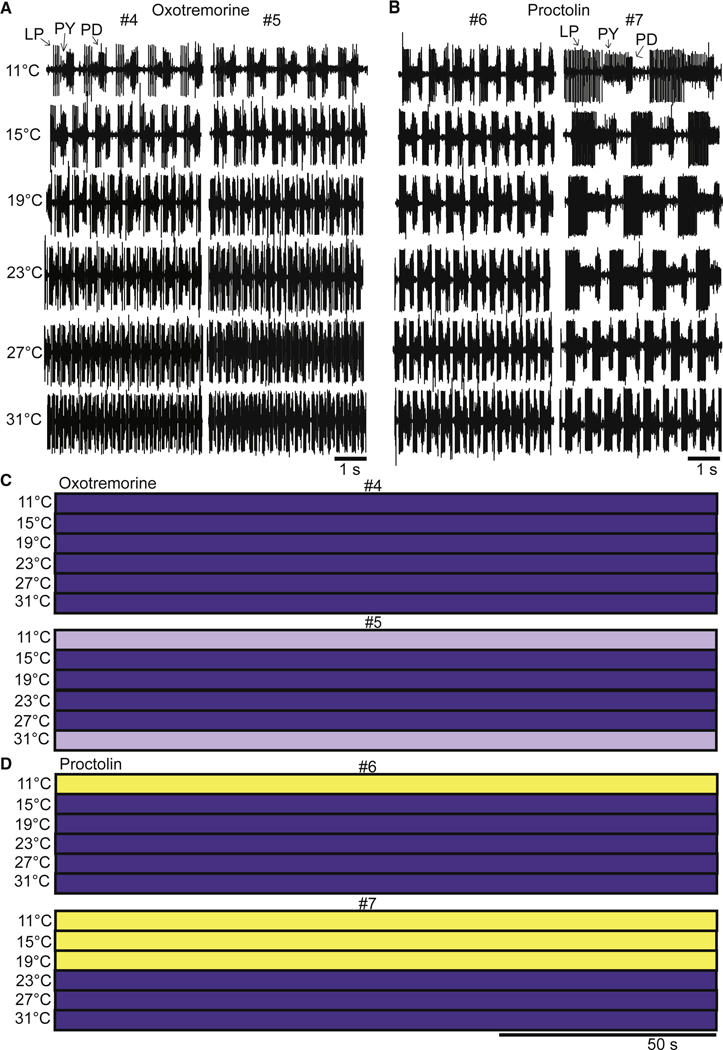
The effects of oxotremorine and proctolin as a function of temperature. A. Example raw traces from two different preparations (#4 and #5) in 10−5 M oxotremorine at each temperature. B. Example raw traces from two different preparations (#6 and #7) in 10−6 M proctolin at each temperature. C. The activity of the same preparations (#4 and #5) from panel A across the entire 150 s file as a function of temperature. D. The activity of the same preparations (#6 and #7) from panel B across the entire 150 s file as a function of temperature.
Figure 5.
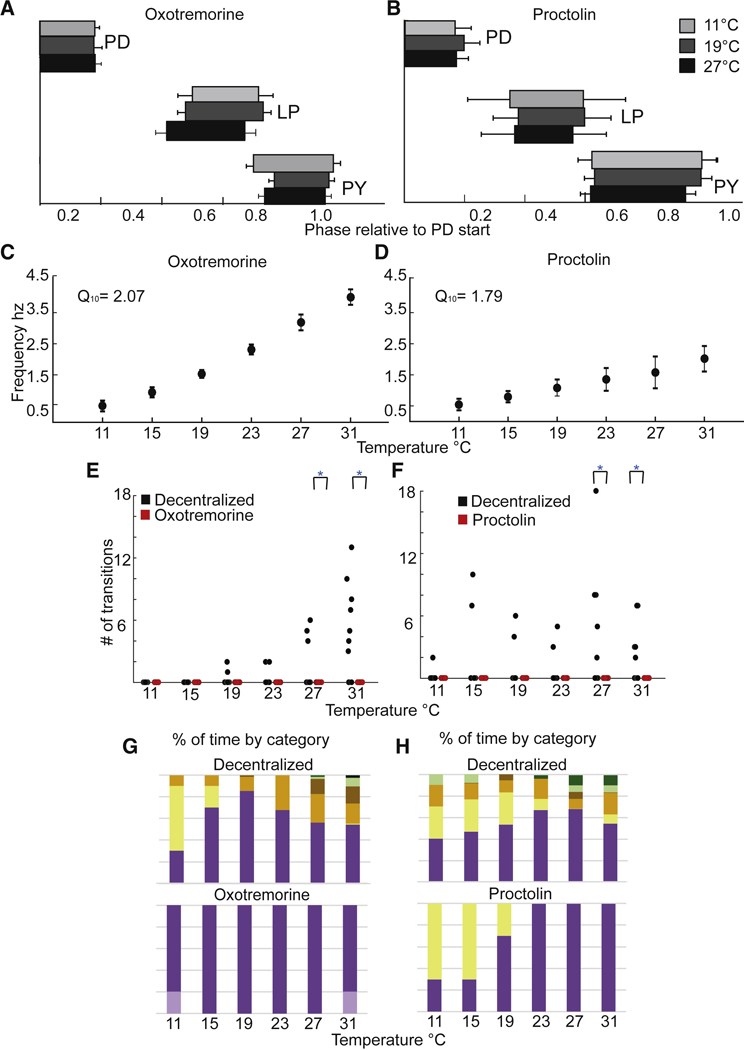
The effects of proctolin and oxotremorine on STG motor patterns as a function of temperature. A B. The average phase relationships (means with S.D.) of the neurons that generate the triphasic rhythm for three temperatures, 11°C (light grey), 19°C (dark grey) and 27°C (black) in 10−5 M oxotremorine (A) (N=10) and in 10−6 M proctolin (B) (N=10). C.D. The mean (with S.D.) frequency of the rhythm calculated from the activity of the PD neurons, across temperature in 10−5 M oxotremorine (C) (N=10) and in 10−6 M proctolin (N=10) (D). E.F. The number of transitions/preparation in the decentralized condition (black circles) and in the presence of 10−5 M oxotremorine and 10−6 M proctolin (red circles) at each temperature (N=10 for each). Decentralized and oxotremorine and proctolin conditions are significantly different at 27°C and 31°s (*p<0.01; paired t-test). G. Each bar represents the cumulative sums of the conditions for all preparations as a function of temperature where the top bar graph is the sum of the decentralized condition and the lower bar graph is the sum of activity patterns in the oxotremorine condition. This shows that more types of activity patterns appear as the temperature is increased in the decentralized condition and more of the less stable activity patterns are present. In oxotremorine all preparations maintain stable activity in one of 2 robust states. H. As (G) for proctolin.
Serotonin destabilizes the pyloric rhythm to temperature
Serotonin is liberated from the Gastropyloric Receptor Neurons (GPR) (Katz et al., 1989; Katz and Harris-Warrick, 1989), and modulates a large number of different currents in STG neurons by activating several 5-HT receptors (Clark et al., 2004; Kiehn and Harris-Warrick, 1992a, b; Zhang and Harris-Warrick, 1994). Moreover, serotonin applications can result in highly variable changes in activity across individuals (Spitzer et al., 2008).
The across-animal variability is readily observed in the raw traces seen in Figure 6A. This figure includes raw data from 5 different preparations, to illustrate the range of activity seen in the presence of 10−5 M serotonin, first at 11 °C, and then as a function of increased temperature. Preparations #8 and #12 were triphasic at low temperature, but lost this behavior as a function of increased temperature. Preparations #9 and #11 had gastric-like behavior at low temperatures and then lost this activity at higher temperatures. The raw traces in Figure 6A and the state-blocks in Figure 6B show that in all cases, the activity patterns seen at higher temperatures were disorganized, with a variety of different non-triphasic patterns observed.
Figure 6.
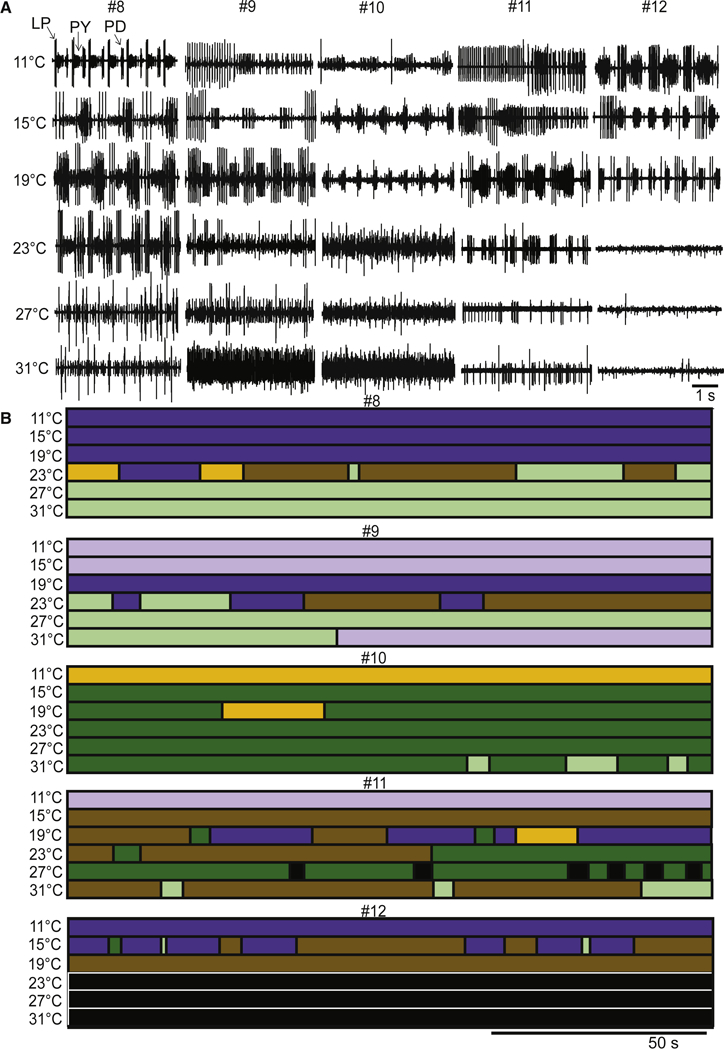
The effects of serotonin as a function of temperature. A. Example raw traces from five different preparations (#8, #9, #10, #11 and #12) in 10−5 M serotonin at each temperature. B. The activity of the same preparations (#8, #9, #10, #11 and #12) from panel A across the entire 150 s file as a function of temperature, using the color codes as previously described.
Figure 7A presents the state-transitions seen in serotonin for data pooled for all animals. Interestingly, all preparations are in a steady state at 11 °C (all individuals are accounted for in the diagonal blocks of the diagram). The largest number of transitions appears at 19 ºC when the preparations are beginning to become unstable. These preparations are significantly more temperature sensitive in the presence of serotonin than in the absence of modulation. This can be seen in Figure 7B, as the number of transitions per individual is significantly different by 19 °C and 23 °C. The number of transitions decreases again at higher temperatures in the presence of serotonin as preparations maintain a particular form of disrupted pyloric activity. Figure 7C shows that by 27 °C and 31°C preparations show almost no triphasic activity. Figure 7D shows the number of preparations at steady state and the total numbers of transitions present in the data in serotonin at all temperatures. The paucity of triphasic rhythms in these data sets across temperature makes it difficult to meaningfully plot and analyze either pyloric rhythm frequency or phase across temperature in serotonin.
Figure 7.
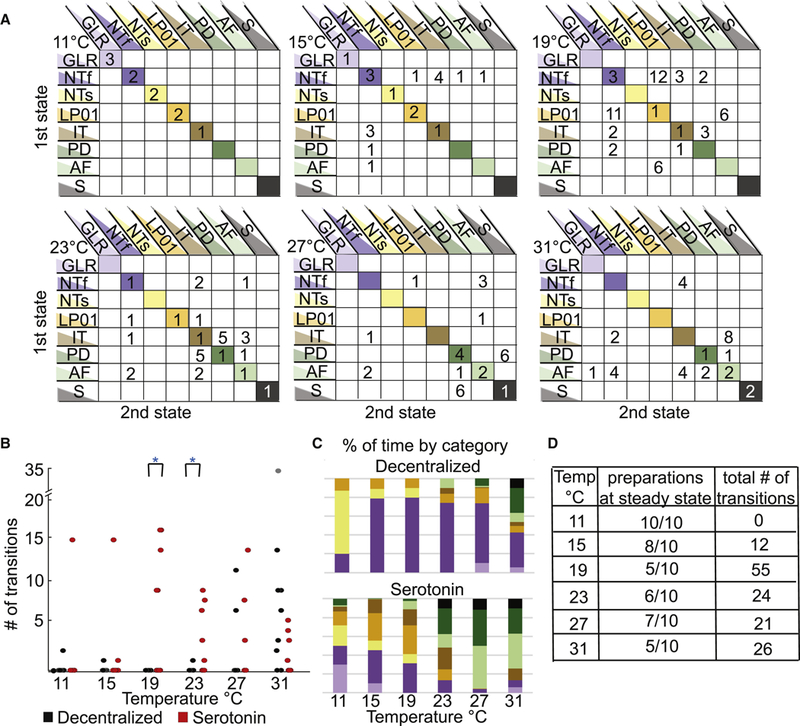
Quantification of transitions seen in serotonin across temperature. A. Matrices of the cumulative data of transitions and stable activity patterns, for all the decentralized preparations (N=10) at each temperature. The y-axis rows indicate the first activity state the preparation is in, while the x-axis columns indicate the state transitioned to. The diagonal lists the number of preparations that were at that particular state for an entire temperature/file, meaning they did not transition across states for that 150 s. B. The number of transitions per preparation in the decentralized condition (black circles) and in the presence of 10−5 M serotonin (red circles) at each temperature (N=10). The number of transitions per preparation in the decentralized and serotonin conditions, when each preparation is compared in a pairwise t-test the number of transitions are significantly different at 19°C and 23°s (*p<0.01). C. Each bar represents the cumulative sums of the conditions that all the preparations were in as a function of temperature where the top bar graph is the sum of the decentralized condition and the lower bar graph is the sum of activity patterns in present in the serotonin condition. This shows that more types of activity patterns appear at lower temperatures in serotonin and as temperature is increased, more of the less stable activity patterns are present in both conditions. D. The tabulated counts of preparations at one state for an entire file (steady state) and the number of transitions counted across all preparations at each temperature in the serotonin condition.
DISCUSSION
A fundamental question in neuroscience is understanding how reliable and robust circuit outputs can result from variable components. This has been illuminated by the finding in both theoretical and experimental work that there can be multiple and degenerate solutions to the production of similar outputs (Britton et al., 2013; Goaillard et al., 2009; Gutierrez et al., 2013; Muszkiewicz et al., 2016; Prinz et al., 2004). Therefore, in principle, one would expect to find that individuals of the same specie could show considerable variability in the parameters that govern intrinsic excitability, synaptic strength, and the details of neuronal structure across animals. In fact, across animals there appears to be a 2–6 fold range in synaptic strengths, conductance densities, and ion channel mRNA expression (Golowasch et al., 1999; Roffman et al., 2012; Schulz et al., 2006; Schulz et al., 2007). Moreover, the same identified neuron or neurons in different animals can show variable branching structures (Bucher et al., 2007; Hay et al., 2013; Otopalik et al., 2017).
This is further complicated by the ability of neuronal circuits to maintain robust output in environments with fluctuating conditions. Even if individual animals show similar motor patterns, to the extent that they do so with different sets of membrane and synaptic conductances and when in a permissible range of environmental conditions, one would expect that extreme perturbations will reveal the consequences of those differences. In previous work we used temperature as a perturbation to probe the animal-to animal differences in conductance densities (Rinberg et al., 2013; Tang et al., 2010; Tang et al., 2012), and showed that the pyloric rhythm and its isolated pacemaker neurons from individual animals maintained robust output across a permissible range of temperatures but outside of this range “crashed” with individual dynamics. These experiments were done with the descending modulatory inputs from the CoGs and OG left intact, which means that the recorded pyloric rhythms were enhanced by the release of endogenous neuromodulatory substances. In the absence of these substances, the pyloric rhythm is less robust, slows or stops, and becomes less regular (Hamood et al., 2015; Hamood and Marder, 2015), and one might expect that these preparations would be more sensitive to extreme temperatures. In this paper we confirm that decentralized preparations, in which the modulatory inputs are removed, are variable at 11 °C, and become even more so at higher temperatures. Thus, in the absence of modulatory inputs, temperature perturbation effectively reveals the consequence of underlying differences in network parameters across animals.
Classification of Network States
Tang et al (2012) attempted to design a measure of the extent to which a given set of recordings become disorganized or crashed, and developed a robustness index. The robustness index was only partially successful in capturing the essence of the fluctuating and intermittent patterns of activity that are seen in the raw data (e.g. Fig. 1). We experimented with a variety of other quantitative data analysis methods, but ran into several problems. A) Once the preparation reached a temperature at which it starts to become disrupted, it goes through patterns of state transitions of widely different durations and characteristics. This means that collapsing the data via spectral analyses or other common ways of analyzing rhythmic data, fail to capture some of the qualitatively interesting and significant features of the data. B) These are long experiments with many conditions (multiple series of temperature steps in the presence and absence of modulator). Therefore, we were restricted in the amount of time we were able to record each condition, and settled on analyses of 150 seconds after the preparation had reached a given temperature. Given the period of the pyloric rhythm, and the durations and numbers of qualitatively different states in the raw data, this is not enough data with which to use many machine learning or other automated methods of data classification. This problem is exacerbated by the lack of obvious stationarity shown at any given temperature.
After unsatisfactory attempts to analyze these data in a way that preserves its qualitatively rich properties, we settled on using the best pattern classifier we know for these sorts of data: the human observer. Subsequently, we have encountered numerous other investigators with similar problems in which an experienced human observer can classify data using multiple features without a struggle, even in relatively small data sets. In this paper we defined 8 qualitatively different network states after looking at large amounts of raw data. This is a balance between using very broad classifications that might lead to fewer states or narrower classifications that might lead to the identification of many more states. Again, these decisions were made on the basis of experience with the stomatogastric motor patterns and experience-dependent evaluation of what is likely to be important for this network. We would argue that accrued knowledge by investigators is not necessarily a bad way to design a classification scheme, as long as this is done transparently, and not hidden in decisions about algorithm choices.
Unfortunately, because each stretch of data was relatively short, we are unable to determine whether there are specific sets of preferred transitions among states, and whether the statistics of preferred transitions might differ across animals and across modulatory condition. To address this question in the future would require collecting longer sets of data while holding the preparations at an appropriate high temperature, without damaging it.
Modulators as Stabilizers or Destabilizers
Decentralization, which removes the effects of most of the neuromodulatory substances that routinely reach the STG, destabilizes the pyloric rhythm and produces state-transitions between a variety of outputs. This argues that the modulatory inputs to the STG may be protecting the pyloric rhythm from the deleterious effects of high temperatures. Consistent with this idea are previous studies on lobster neuromuscular junctions that showed that dopamine (Thuma et al., 2013) and serotonin (Hamilton et al., 2007) extend the temperature range of functional muscle and neuromuscular junction performance. In a fascinating study, Zhurov and Brezina (2005) showed that while increased temperature decreased transmitter release at an Aplysia neuromuscular junction, the modulators themselves enhanced muscle contractility that compensated for this decrease, and maintained muscle activity at high temperatures (Zhurov and Brezina, 2005). A similar conclusion was suggested by a modest increase by modulators in the temperatures over which the gastric mill rhythm is active (Stadele et al., 2015). Moreover, work in C. elegans argues that neuromodulation is important in allowing animals to maintain appropriate thermosensory behaviors (Beverly et al., 2011). Therefore, we were curious to see whether specific neuromodulatory substances would alter the effective operating range of the pyloric rhythm in response to extreme temperature perturbation.
The stabilizing action of modulators that activate IMI
Proctolin and oxotemorine activate a current called IMI which is a voltage-dependent inward current that is blocked by extracellular Ca2+ (Golowasch and Marder, 1992b; Gray et al., 2017; Gray and Golowasch, 2016; Swensen and Marder, 2000, 2001). IMI ‘s voltage-dependence makes it ideally suited to enhance oscillations (Sharp et al., 1993) because it provides an additional inward current at more depolarized membrane potentials and is blocked at the trough of the oscillation. Consequently, agonists that activate IMI characteristically strongly enhance oscillatory properties of pyloric network neurons (Hooper and Marder, 1987; Sharp et al., 1993; Swensen and Marder, 2000). Thus, our expectation was that both oxotremorine and proctolin might counteract some of the decrease in membrane resistance that commonly occurs with increased temperature (Stadele et al., 2015; Tang et al., 2010), and stretch the operating range of the pyloric rhythm by enhancing the neurons’ ability to burst.
Other cell intrinsic and network characteristics can also contribute to network stabilization by these modulators. The pyloric circuit contains multiple instances of reciprocal inhibitory connections, and rebound from inhibition is an important determinant of when the follower neurons will fire (Goaillard et al., 2010; Harris-Warrick et al., 1995; Hartline, 1979). The rebound from inhibition depends both on the strength and time course of the inhibition and the rebound membrane currents that contribute, to the rebound (Sharp et al., 1996). A number of modulators that target IMI, including proctolin (Oh et al., 2012; Zhao et al., 2011) and RPCH (Thirumalai et al., 2006) enhance synaptic strength in pyloric neurons, and therefore will enhance the reciprocal inhibitory connections that promote rhythmic activity in the pyloric rhythm.
Additionally, the increase in the number of spikes/ burst and enhancement of the amplitude of slow wave oscillation of a presynaptic neuron, characteristic of IMI activation (Hooper and Marder, 1987; Sharp et al., 1993), can further increase the inhibitory input onto its postsynaptic targets, because the chemical synapses within the STG function through graded synaptic transmission (Graubard, 1978; Graubard et al., 1980; Manor et al., 1997). The neurons that generate the pyloric rhythm have hyperpolarization-activated rebound currents (Ih and ICaL)(Golowasch and Marder, 1992a; Kiehn and Harris-Warrick, 1992a). An increase in inhibitory input increases the activation of post-inhibitory rebound currents and the rebound burst in the follower neuron. These features of network structure have been shown in experimental and computational modeling work to confer robustness on circuit activity (Angstadt and Calabrese, 1991; Dethier et al., 2015). Therefore, the activation of IMI on any pyloric neuron can enhance the robustness of bursting activity of multiple neurons within the network.
It is possible that the increased robustness of rhythmic circuit output, observed by the activation of a current like IMI, is a common solution found in many organisms. The I-V curve of IMI is similar to that of the NMDA-activated current which can activate and regularize the rhythmic oscillations of motor neurons in the lamprey spinal cord (Sigvardt et al., 1985). This suggests that the NMDA receptor may contribute to stabilizing rhythmic oscillations when lampreys or other cold-blooded vertebrates encounter temperature changes.
Serotonin as a Circuit Destabilizer
Serotonin acts on numerous receptors to modulate a variety of voltage-dependent currents in STG and other crustacean neurons (Clark et al., 2004; Kiehn and Harris-Warrick, 1992a, b; Sosa et al., 2004; Spitzer et al., 2008; Zhang and Harris-Warrick, 1994). The variability of serotonin’s actions on the decentralized C. borealis rhythm is shown in the 11 °C data on Figure 6. Notice, that even at low temperatures the preparation to preparation variability of the decentralized preparations is higher in serotonin than in controls. In each of the 10 decentralized preparations we examined, the application of serotonin elicited a unique constellation of features, making the recorded activity visually distinctive for each individual. We hypothesize that this occurs because serotonin modulates so many different currents, that it is likely that the starting set of conductances in each individual will lead to considerable variation in serotonin’s actions at 11 °C. This individual variability seen in serotonin is then amplified when the temperature is changed. In this context, it is interesting that serotonin enhances individual variability of zebra fish behavior (Pantoja et al., 2016).
Under the conditions used here, serotonin was a destabilizing factor, and therefore was a useful probe to reveal cryptic animal-to-animal differences in underlying intrinsic and synaptic parameters. It is quite striking that serotonin reveals the animal-to-animal differences profoundly, considerably more so than is seen in the controls of other modulators. But in the animal, serotonin is both a circulating hormone (Kravitz et al., 1980), and therefore presumably acting at low concentrations, as well as a cotransmitter released from the Gastro-Pyloric (GPR) sensory neurons (Katz et al., 1989; Katz and Harris-Warrick, 1989). A considerable body of work on dopamine in the lobster, Panulirus interruptus shows that low concentrations of tonic dopamine can alter the effects of higher phasic dopamine applications (Krenz et al., 2013; Krenz et al., 2014; Rodgers et al., 2013). In a similar way, it is possible that low hormonal concentrations of serotonin in vivo, acting in a richer modulatory environment, might have different effects on circuit stability than seen here. Moreover, serotonin enhances the operating range of the heart neuromuscular junctions in response to temperature fluctuations (Hamilton et al., 2007) in Homarus americanus, as does dopamine for stomach muscles in Panulirus interruptus (Thuma et al., 2013).
One of the puzzling features of the stomatogastric ganglion is that it is modulated by more than 30 different substances (Marder, 2012; Marder and Bucher, 2007; Marder et al., 2014). Early work on STG modulation focused on the potential of these modulators to promote behavioral flexibility (Harris-Warrick and Marder, 1991; Hooper and Marder, 1984; Marder and Bucher, 2007). Nonetheless, it is likely that much of the modulation of the STG may be physiologically necessary to maintain stable function to counteract environmental perturbations such as temperature changes. As crabs and lobsters must deal with a variety of environmental perturbations such as alterations in O2 tension (Clemens et al., 1999; Clemens et al., 1998; Clemens et al., 2001), pH, salinity, etc. in addition to temperature, it is possible that different subsets of modulators are called into play in response to each of these potential stressors. As some of these environmental changes are potentially linked as pH and O2 tension change as a function of temperature, it will be interesting to determine how multiple modulators may coordinately regulate the central pattern generating circuits of the stomatogastric nervous system to maintain the animal’s feeding behavior over a large range of environmental circumstances.
STAR Methods
Animals
Adult male Jonah Crabs, Cancer borealis, were purchased from Commercial Lobster (Boston, MA). Animals were housed in tanks containing artificial saline maintained at 11°C until used. Animals used in these experiments obtained between February 2013 and January 2017.
Solutions
C. borealis physiological saline was composed of (in mM): NaCl, 440; KCl, 13; CaCl2, 26; MgCl2, 11; Trizma base, 11; maleic acid, 5, pH 7.4–7.5 at room temperature. Microelectrode solution was composed of (in mM): Na2SO4, 15; NaCl, 20; MgCl2, 10; K gluconate, 400 (Hooper et al., 2015). All chemicals were obtained from Sigma Aldrich.
Modulators
Proctolin 10−6 M (Abbiotech), oxotremorine 10−5 M (Sigma Aldrich) and serotonin 10−5 M (Sigma Aldrich) were dissolved in physiological saline and applied through a continuously flowing superfusion system running at approximately 500 ml/hour.
Electrophysiology
Stomatogastric nervous systems were dissected from crab stomachs and pinned out onto Sylgard coated petri dishes. Electrically isolating Vaseline wells were constructed around nerves of interest for extracellular recordings. For most preparations, these nerves were the upper LVN, the lower LVN, PDN, PYN, LPN, DGN, LGN and MVN. Another well was built around the STN to later be filled with TTX to block impulse traffic in the STN. The recordings were made with stainless steel pin electrodes and A-M systems amplifiers. The amplifiers were connected to a DigiData 1440A which was further connected directly to a computer. The data were recorded using pClamp software (Axon instruments). Each file collected 150s of data.
The superfused physiological saline was passed through a peltier device (Warner Instruments) which maintained temperature at 11°, 15°, 19°, 23°, 27° or 31°C during temperature steps. While recording was continuous throughout the entire duration of the experiment, the data analyzed in this paper were taken when the temperature was stable (within +/−0.3 degrees Celsius) at one of the previous listed temperatures. The temperature was measured continuously with a miniature thermistor placed within the saline stream within a few millimeters of the STG. Each preparation was subjected to three sequences of temperature steps. The duration of each series of steps was ~45 minutes long. The first series of temperature steps was with the descending modulatory inputs intact. In the second series, the descending nerves were first silenced by TTX 10−7 M (Tocris) being added to a well surrounding the stomatogastric nerve which was then cut. The preparation was left at 11°C for 30–45 minutes before the subsequent series of temperature steps. In the third series, one of the previous listed modulators (oxotremorine, proctolin or serotonin) was added to the superfused saline. The modulator temperature series was started after ~5 minutes (for oxotremorine and proctolin) or ~15–25 minutes (for serotonin) after the saline containing the modulator was circulating through the peltier, to make sure the bath saline was completely replaced with the modulator saline and physiological effects of the modulator were seen.
Analysis
Data were analyzed using Spike2 v 7.0 (Cambridge Electronic Design) and MATLAB v R2012b (Mathworks). MATLAB and SigmaPlot v 11.0 (Jandel Scientific) were used for statistical analyses. After visual inspection of long stretches of data from many conditions, we described the states of activity as 1 of 8 categories. Each data set was then manually scored, across time, temperature and modulatory condition, with the behavior of one of these categories. Transitions from one category to another shorter than one second, were not noted. Subsequently, transition data sets were counted for number of transitions, pair-wise transitions present and their frequency and how long preparations exhibited the denoted behavior.
Categorization Method.
Recordings from the isolated nerves of the three pyloric motor neurons, LP, PY and PD, and the recording from the upper and lower lvn (which contain the signals of all three of these neurons together and the LG neuron which indicates the presence of gastric activity) were simultaneously evaluated each second so that the activity of each neuron and their activity in the network were clear for categorization. If the LG neuron and the DG neuron were firing alternating bursts of action potentials rhythmically, then that second of data was designated as Gastric-like rhythm (GLR, lavender). If all three neurons were firing bursts of action potentials in the correct order for the pyloric rhythm sequentially and the frequency of the rhythm was above 0.8 Hz then this second was denoted as Normal Triphasic rhythm, fast (NTf, dark purple). If all three neurons were firing bursts of action potentials sequentially and the frequency of the rhythm was less than or equal to 0.8 Hz then this second was denoted as Normal Triphasic rhythm, slow (NTs, pale yellow). If the LP neuron fired one action potential rhythmically at the start of each cycle of the rhythm or none and the PY neurons and PD neurons fired bursts of action potentials rhythmically and in order then this second was denoted as LP 0–1 spike, PY and PD normal (LP01, light orange). As temperature is increased, the frequency of the rhythm often exceeds 1 Hz, which means that more than one cycle of the triphasic rhythm is present per second. If, within one second, there is a full cycle of normal triphasic activity (LP-PY-PD bursting) and additional activity that does not fall into the category off normal triphasic activity, then this second is denoted as Intermittent triphasic rhythm (IT, brown). If the PD neurons are bursting rhythmically but there was no activity from the LP or PY neurons, than this second is denoted as Just PD bursting (PD, dark green). If there is no rhythmic activity, neurons are firing out of order or firing tonically, this second was denoted as Atypical firing (AF, pale green). If there is no activity present from LP, PY or PD then this second was denoted as Silent (S, black).
Validation of classification system.
To test the reliability of the classification system used in this paper, an independent observer was given 12 sets of data that represent different temperature and modulatory conditions. The individual was given the set of instructions used to classify the data and the raw data traces, without information on the temperature and modulatory conditions pertaining to each file. Figure S1-A shows how Individuals 1 and 2 classified the 12 sets of data (a-l). All of the data that contribute to the findings described in the main text of the paper come from recordings made while the temperature was stable within +/− 0.3 ºC throughout the 150s file. To test the system on the most ‘difficult’ data to classify, 2 of the 12 files chosen (a,b) were taken from recordings made as the temperature was being increased between two stable points and in the presence of serotonin, where activity is most variable and unstable. To quantify how similar the classification of the data sets was between the two individuals we first looked at how many transitions each individual marked per file and how much of each file each individual marked being in which state (Figure S1-B,C). To compare how often the two individuals’ classification of the data sets was due to true concordance, taking into account the possibility of random agreement, we calculated the Cohen’s kappa coefficient (Table S1) (Cohen, 1960). Each data set was discretized into one second bins, starting from 0 to 150s (i.e. 0–1, 1–2, 2–3 etc). The bin was then marked as being classified as one of the possible states detected across the 12 data sets (i.e. NTf) or as a bin that contained one of the possible transitions present in the data sets (i.e. NTf to LP01). Therefore, each file provided 150 data points of 25 possible categories. The kappa values calculated from a matrix containing all the data (a-l) and those from individual data sets (a, b, j respectively) are above 0.81, which as defined by Landis and Koch (1977), represents near perfect agreement. These values actually underrepresent the agreement between the two individuals for at least two reasons: 1) The 1 second time bins are treated as independent events and therefore this calculation does not acknowledge the consistency in sequential categorizations across the two individuals along time. 2) Each individual was given the possibility of marking the data into 1 of 8 activity states so the number of possible categories two individuals could choose from is underrepresented.
Statistics.
Paired T-tests were used to calculate significance (p<0.01*, p<0.001**) on the number of transitions counted for each preparation, at each temperature in the decentralized vs. modulator conditions. Kruskal-Wallis one-way ANOVA, adjusted for multiple comparisons, was used to calculate significance in the number of transitions counted for each preparation across the 6 temperatures in the decentralized condition. Matlab was used to perform these calculations.
STAR METHODS KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Bacterial and Virus Strains | ||
| Biological Samples | ||
| Chemicals, Peptides, and Recombinant Proteins | ||
| Serotonin (Serotonin Creatinine Sulfate Monohydrate) | Sigma Aldrich | Catalog #: H7752, CAS#: 61–47-2, PubChem: 24895804 |
| Oxotremorine (Oxotremorine sesquifumarate salt) | Sigma Aldrich | Catalog #: O9126, CAS #: 17360–35-9, PubChem: 24278614 |
| Tetrodotoxin (TTX, tetrodotoxin citrate) | Tocris | Catalog #: 1069, CAS #: 18660–81-6, PubChem: 16759596 |
| Proctolin Peptide | Abbiotec | Catalog #: 350353, Accession #: P67859 |
| Critical Commercial Assays | ||
| Deposited Data | ||
| Experimental Models: Cell Lines | ||
| Experimental Models: Organisms/Strains | ||
| Cancer borealis (Jonah crab), Adult male | Commercial lobster, Boston, MA, USA | NCBI:txid39395 |
| Oligonucleotides | ||
| Recombinant DNA | ||
| Software and Algorithms | ||
| Spike 2 software | Cambridge Electronic Design | RRID: SCR_000903 |
| pClamp software | Molecular Devices | RRID: SCR_011323 |
| Matlab software | Mathworks | RRID: SCR_001622 |
| Sigmaplot software | Sigmaplot | RRID: SCR_003210 |
| Other | ||
Supplementary Material
Acknowledgments:
Research Supported by R01 NS017813, R01 NS081013 and R35 NS097343. We thank Drs. Michael P. Nusbaum and Farzan Nadim for comments on the manuscript.
Footnotes
Declaration of Interests: Neither author has any competing interests to declare.
REFERENCES
- Angstadt JD, and Calabrese RL (1991). Calcium currents and graded synaptic transmission between heart Interneurons of the leech. J Neurosi 11, 746–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bal T, Nagy F, and Moulins M (1994). Muscarinic modulation of a pattern-generating network: control of neuronal properties. J Neurosci 14, 3019–3035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beverly M, Anbil S, and Sengupta P (2011). Degeneracy and neuromodulation among thermosensory neurons contribute to robust thermosensory behaviors in Caenorhabditis elegans. J Neurosci 31, 11718–11727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blitz DM, and Nusbaum MP (1997). Motor pattern selection via inhibition of parallel pathways. J Neurosci 17, 4965–4975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blitz DM, and Nusbaum MP (2011). Neural circuit flexibility in a small sensorimotor system. Curr Opin Neurobiol. 21: 544–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Britton OJ, Bueno-Orovio A, Van Ammel K, Lu HR, Towart R, Gallacher DJ, and Rodriguez B (2013). Experimentally calibrated population of models predicts and explains intersubject variability in cardiac cellular electrophysiology. Proc Natl Acad Sci U S A 110, E2098–2105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bucher D, Johnson CD, and Marder E (2007). Neuronal morphology and neuropil structure in the stomatogastric ganglion of the lobster, Homarus americanus. J Comp Neurol 501, 185–205. [DOI] [PubMed] [Google Scholar]
- Caplan JS, Williams AH, and Marder E (2014). Many parameter sets in a multicompartment model oscillator are robust to temperature perturbations. J Neurosci 34, 4963–4975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark MC, Dever TE, Dever JJ, Xu P, Rehder V, Sosa MA, and Baro DJ (2004). Arthropod 5-HT2 receptors: a neurohormonal receptor in decapod crustaceans that displays agonist independent activity resulting from an evolutionary alteration to the DRY motif. J Neurosci 24, 3421–3435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clemens S, Massabuau J-C, Meyrand P, and Simmers J (1999). Changes in motor network expression related to moulting behaviour in lobster: role of moult-induced deep hypoxia. J Exp Biol 202, 817–827. [DOI] [PubMed] [Google Scholar]
- Clemens S, Massabuau JC, Legeay A, Meyrand P, and Simmers J (1998). In vivo modulation of interacting central pattern generators in lobster stomatogastric ganglion: influence of feeding and partial pressure of oxygen. J Neurosci 18, 2788–2799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clemens S, Massabuau JC, Meyrand P, and Simmers J (2001). A modulatory role for oxygen in shaping rhythmic motor output patterns of neuronal networks. Respir Physiol 128, 299–315. [DOI] [PubMed] [Google Scholar]
- Coleman MJ, Nusbaum MP, Cournil I, and Claiborne BJ (1992). Distribution of modulatory inputs to the stomatogastric ganglion of the crab, Cancer borealis. J Comp Neurol 325, 581–594. [DOI] [PubMed] [Google Scholar]
- Dell AI, Pawar S, and Savage VM (2011). Systematic variation in the temperature dependence of physiological and ecological traits. Proc Natl Acad Sci U S A 108, 10591–10596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dethier J, Drion G, Franci A, and Sepulchre R (2015). A positive feedback at the cellular level promotes robustness and modulation at the circuit level. J Neurophysiol, 114: 2472–2484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donahue MJ, Nichols A, Santamaria CA, League-Pike PE, Krediet CJ, Perez KO, and Shulman MJ (2009). Predation risk, prey abundance, and the vertical distribution of three brachyuran crabs on Gulf of Maine shores. Journal of Crustacean Biology 29, 523–531. [Google Scholar]
- Elson RC, and Selverston AI (1992). Mechanisms of gastric rhythm generation in the isolated stomatogastric ganglion of spiny lobsters: bursting pacemaker potentials, synaptic interactions, and muscarinic modulation. J Neurophysiol 68, 890–907. [DOI] [PubMed] [Google Scholar]
- Goaillard JM, Taylor AL, Pulver SR, and Marder E (2010). Slow and persistent postinhibitory rebound acts as an intrinsic short-term memory mechanism. J Neurosci 30, 4687–4692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goaillard JM, Taylor AL, Schulz DJ, and Marder E (2009). Functional consequences of animal-to-animal variation in circuit parameters. Nat Neurosci 12, 1424–1430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Abbott LF, and Marder E (1999). Activity-dependent regulation of potassium currents in an identified neuron of the stomatogastric ganglion of the crab Cancer borealis. J Neurosci 19, RC33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, and Marder E (1992a). Ionic currents of the lateral pyloric neuron of the stomatogastric ganglion of the crab. J Neurophysiol 67, 318–331. [DOI] [PubMed] [Google Scholar]
- Golowasch J, and Marder E (1992b). Proctolin activates an inward current whose voltage dependence is modified by extracellular Ca2+. J Neurosci 12, 810–817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graubard K (1978). Synaptic transmission without action potentials: input-output properties of a non-spiking presynaptic neuron. J Neurophysiol 41, 1014–1025. [DOI] [PubMed] [Google Scholar]
- Graubard K, Raper JA, and Hartline DK (1980). Graded synaptic transmission between spiking neurons. Proc Natl Acad Sci U S A 77, 3733–3735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray M, Daudelin DH, and Golowasch J (2017). Activation mechanism of a neuromodulator-gated pacemaker ionic current. J Neurophysiol 118, 595–609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray M, and Golowasch J (2016). Voltage dependence of a neuromodulator-activated ionic current. eNeuro 3, 0038–0016.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutierrez GJ, O’Leary T, and Marder E (2013). Multiple mechanisms switch an electrically coupled, synaptically inhibited neuron between competing rhythmic oscillators. Neuron 77, 845–858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haeffner PA (1977). Aspects of the biology of the Jonah crab, Cancer borealis Stimpson, 1859 in the mid Atlantic Bight. J Nat Hist 11, 303–320. [Google Scholar]
- Hamada FN, Rosenzweig M, Kang K, Pulver SR, Ghezzi A, Jegla TJ, and Garrity PA (2008). An internal thermal sensor controlling temperature preference in Drosophila. Nature 454, 217–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton JL, Edwards CR, Holt SR, and Worden MK (2007). Temperature dependent modulation of lobster neuromuscular properties by serotonin. J Exp Biol 210, 1025–1035. [DOI] [PubMed] [Google Scholar]
- Hamood AW, Haddad SA, Otopalik AG, Rosenbaum P, and Marder E (2015). Quantitative reevaluation of the effects of short- and long-term removal of descending modulatory inputs on the pyloric rhythm of the crab, Cancer borealis. eNeuro 2, 0058–0014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamood AW, and Marder E (2015). Consequences of acute and long-term removal of neuromodulatory input on the episodic gastric rhythm of the crab Cancer borealis. J Neurophysiol 114, 1677–1692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris-Warrick RM, Coniglio LM, Levini RM, Gueron S, and Guckenheimer J (1995). Dopamine modulation of two subthreshold currents produces phase shifts in activity of an identified motoneuron. J Neurophysiol 74, 1404–1420. [DOI] [PubMed] [Google Scholar]
- Harris-Warrick RM, and Marder E (1991). Modulation of neural networks for behavior. Annu Rev Neurosci 14, 39–57. [DOI] [PubMed] [Google Scholar]
- Hartline DK (1979). Pattern generation in the lobster (Panulirus) stomatogastric ganglion. II. Pyloric network simulation. Biol Cybern 33, 223–236. [DOI] [PubMed] [Google Scholar]
- Hay E, Schurmann F, Markram H, and Segev I (2013). Preserving axosomatic spiking features despite diverse dendritic morphology. J Neurophysiol 109, 2972–2981. [DOI] [PubMed] [Google Scholar]
- Hooper SL, and Marder E (1984). Modulation of a central pattern generator by two neuropeptides, proctolin and FMRFamide. Brain Res 305, 186–191. [DOI] [PubMed] [Google Scholar]
- Hooper SL, and Marder E (1987). Modulation of the lobster pyloric rhythm by the peptide proctolin. J Neurosci 7, 2097–2112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hooper SL, Thuma JB, Guschlbauer C, Schmidt J, and Buschges A (2015). Cell dialysis by sharp electrodes can cause nonphysiological changes in neuron properties. J Neurophysiol 114, 1255–1271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katz PS, Eigg MH, and Harris-Warrick RM (1989). Serotonergic/cholinergic muscle receptor cells in the crab stomatogastric nervous system. I. Identification and characterization of the gastropyloric receptor cells. J Neurophysiol 62, 558–570. [DOI] [PubMed] [Google Scholar]
- Katz PS, and Harris-Warrick RM (1989). Serotonergic/cholinergic muscle receptor cells in the crab stomatogastric nervous system. II. Rapid nicotinic and prolonged modulatory effects on neurons in the stomatogastric ganglion. J Neurophysiol 62, 571–581. [DOI] [PubMed] [Google Scholar]
- Kiehn O, and Harris-Warrick RM (1992a). 5-HT modulation of hyperpolarization-activated inward current and calcium-dependent outward current in a crustacean motor neuron. J Neurophysiol 68, 496–508. [DOI] [PubMed] [Google Scholar]
- Kiehn O, and Harris-Warrick RM (1992b). Serotonergic stretch receptors induce plateau properties in a crustacean motor neuron by a dual-conductance mechanism. J Neurophysiol 68, 485–495. [DOI] [PubMed] [Google Scholar]
- Kilman VL, and Marder E (1996). Ultrastructure of the stomatogastric ganglion neuropil of the crab, Cancer borealis. J Comp Neurol 374, 362–375. [DOI] [PubMed] [Google Scholar]
- Kravitz EA, Glusman S, Harris-Warrick RM, Livingstone MS, Schwarz T, and Goy MF (1980). Amines and a peptide as neurohormones in lobsters: actions on neuromuscular preparations and preliminary behavioural studies. J Exp Biol 89, 159–175. [DOI] [PubMed] [Google Scholar]
- Krediet CJ, and Donahue MJ (2009). Growth-mortality trade-offs along a depth gradient in Cancer borealis. Journal of Experimental Marine Biology and Ecology 373, 133–139. [Google Scholar]
- Krenz WD, Hooper RM, Parker AR, Prinz AA, and Baro DJ (2013). Activation of high and low affinity dopamine receptors generates a closed loop that maintains a conductance ratio and its activity correlate. Frontiers in neural circuits 7, DOI: 10.3389/fncir.2013.00169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krenz WD, Parker AR, Rodgers EW, and Baro DJ (2014). Dopaminergic tone persistently regulates voltage-gated ion current densities through the D1R-PKA axis, RNA polymerase II transcription, RNAi, mTORC1, and translation. Front Cell Neurosci 8, 39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lane BJ, Samarth P, Ransdell JL, Nair SS, and Schulz DJ (2016). Synergistic plasticity of intrinsic conductance and electrical coupling restores synchrony in an intact motor network. elife 5, 16879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenz PH, Hower AE, and Hartline DK (2005). Temperature compensation in the escape response of a marine copepod, Calanus finmarchicus (Crustacea). Biol Bull 209, 75–85. [DOI] [PubMed] [Google Scholar]
- Long MA, and Fee MS (2008). Using temperature to analyse temporal dynamics in the songbird motor pathway. Nature 456, 189–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long MA, Katlowitz KA, Svirsky MA, Clary RC, Byun TM, Majaj N, Oya H, Howard MA 3rd, and Greenlee JDW (2016). Functional segregation of cortical regions underlying speech timing and articulation. Neuron 89, 1187–1193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manor Y, Nadim F, Abbott LF, and Marder E (1997). Temporal dynamics of graded synaptic transmission in the lobster stomatogastric ganglion. J Neurosci 17, 5610–5621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E (2012). Neuromodulation of neuronal circuits: back to the future. Neuron 76, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, and Bucher D (2007). Understanding circuit dynamics using the stomatogastric nervous system of lobsters and crabs. Annu Rev Physiol 69, 291–316. [DOI] [PubMed] [Google Scholar]
- Marder E, and Calabrese RL (1996). Principles of rhythmic motor pattern generation. Physiol Rev 76, 687–717. [DOI] [PubMed] [Google Scholar]
- Marder E, and Eisen JS (1984). Electrically coupled pacemaker neurons respond differently to same physiological inputs and neurotransmitters. J Neurophysiol 51, 1362–1374. [DOI] [PubMed] [Google Scholar]
- Marder E, O’Leary T, and Shruti S (2014). Neuromodulation of circuits with variable parameters: single neurons and small circuits reveal principles of state-dependent and robust neuromodulation. Annu Rev Neurosci 37, 329–346. [DOI] [PubMed] [Google Scholar]
- Marder E, and Paupardin-Tritsch D (1978). The pharmacological properties of some crustacean neuronal acetylcholine, gamma-aminobutyric acid, and L-glutamate responses. J Physiol 280, 213–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muszkiewicz A, Britton OJ, Gemmell P, Passini E, Sanchez C, Zhou X, Carusi A, Quinn TA, Burrage K, Bueno-Orovio A, et al. (2016). Variability in cardiac electrophysiology: Using experimentally-calibrated populations of models to move beyond the single virtual physiological human paradigm. Prog Biophys Mol Biol 120, 115–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagy F, and Dickinson PS (1983). Control of a central pattern generator by an identified modulatory interneurone in crustacea. I. Modulation of the pyloric motor output. J Exp Biol 105, 33–58. [DOI] [PubMed] [Google Scholar]
- Neumeister H, Ripley B, Preuss T, and Gilly WF (2000). Effects of temperature on escape jetting in the squid Loligo opalescens. J Exp Biol 203, 547–557. [DOI] [PubMed] [Google Scholar]
- Norris BJ, Wenning A, Wright TM, and Calabrese RL (2011). Constancy and variability in the output of a central pattern generator. J Neurosci 31, 4663–4674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusbaum MP, and Beenhakker MP (2002). A small-systems approach to motor pattern generation. Nature 417, 343–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusbaum MP, Blitz DM, and Marder E (2017). Functional consequences of neuropeptide and small-molecule co-transmission. Nat Rev Neurosci. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusbaum MP, Blitz DM, Swensen AM, Wood D, and Marder E (2001). The roles of co-transmission in neural network modulation. Trends Neurosci 24, 146–154. [DOI] [PubMed] [Google Scholar]
- Nusbaum MP, and Marder E (1989a). A modulatory proctolin-containing neuron (MPN). I. Identification and characterization. J Neurosci 9, 1591–1599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusbaum MP, and Marder E (1989b). A modulatory proctolin-containing neuron (MPN). II. State-dependent modulation of rhythmic motor activity. J Neurosci 9, 1600–1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Leary T, and Marder E (2016). Temperature-robust neural function from activity-dependent ion channel regulation. Current Biology 26, 2935–2941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh M, Zhao S, Matveev V, and Nadim F (2012). Neuromodulatory changes in short-term synaptic dynamics may be mediated by two distinct mechanisms of presynaptic calcium entry. J Comput Neurosci 33, 573–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otopalik AG, Goeritz ML, Sutton AC, Brookings T, Guerini C, and Marder E (2017). Sloppy morphological tuning in identified neurons of the crustacean stomatogastric ganglion. Elife 6, DOI: 10.7554/eLife.22352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pantoja C, Hoagland A, Carroll EC, Karalis V, Conner A, and Isacoff EY (2016). Neuromodulatory regulation of behavioral individuality in zebrafish. Neuron 91, 587–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Partridge LD, and Connor JA (1978). A mechanism for minimizing temperature effects on repetitive firing frequency. The American journal of physiology 234, C155–161. [DOI] [PubMed] [Google Scholar]
- Prinz AA, Bucher D, and Marder E (2004). Similar network activity from disparate circuit parameters. Nat Neurosci 7, 1345–1352. [DOI] [PubMed] [Google Scholar]
- Rinberg A, Taylor AL, and Marder E (2013). The effects of temperature on the stability of a neuronal oscillator. PLoS Comput Biol 9, e1002857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson RM, and Money TG (2012). Temperature and neuronal circuit function: compensation, tuning and tolerance. Curr Opin Neurobiol 22, 724–734. [DOI] [PubMed] [Google Scholar]
- Rodgers EW, Krenz WD, Jiang X, Li L, and Baro DJ (2013). Dopaminergic tone regulates transient potassium current maximal conductance through a translational mechanism requiring D1Rs, cAMP/PKA, Erk and mTOR. BMC Neurosci 14, 143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roemschied FA, Eberhard MJ, Schleimer JH, Ronacher B, and Schreiber S (2014). Cell-intrinsic mechanisms of temperature compensation in a grasshopper sensory receptor neuron. Elife 3, e02078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roffman RC, Norris BJ, and Calabrese RL (2012). Animal-to-animal variability of connection strength in the leech heartbeat central pattern generator. J Neurophysiol 107, 1681–1693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell DF (1979). CNS control of pattern generators in the lobster stomatogastric ganglion. Brain Res 177, 598–602. [DOI] [PubMed] [Google Scholar]
- Schleimer JH, and Schreiber S (2016). Homeostasis: how neurons achieve temperature invariance. Current Biology 26, R1141–R1143. [DOI] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard JM, and Marder E (2006). Variable channel expression in identified single and electrically coupled neurons in different animals. Nat Neurosci 9, 356–362. [DOI] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard JM, and Marder EE (2007). Quantitative expression profiling of identified neurons reveals cell-specific constraints on highly variable levels of gene expression. Proc Natl Acad Sci U S A 104, 13187–13191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp AA, O’Neil MB, Abbott LF, and Marder E (1993). The dynamic clamp: artificial conductances in biological neurons. Trends Neurosci 16, 389–394. [DOI] [PubMed] [Google Scholar]
- Sharp AA, Skinner FK, and Marder E (1996). Mechanisms of oscillation in dynamic clamp constructed two-cell half-center circuits. J Neurophysiol 76, 867–883. [DOI] [PubMed] [Google Scholar]
- Shoemaker KL, and Robertson RM (1998). Flight motor patterns of locusts responding to thermal stimuli. Journal of Comparative Physiology a- Sensory Neural and Behavioral Physiology 183, 477–488. [Google Scholar]
- Sigvardt KA, Grillner S, Wallen P, and Van Dongen PA (1985). Activation of NMDA receptors elicits fictive locomotion and bistable membrane properties in the lamprey spinal cord. Brain Res 336, 390–395. [DOI] [PubMed] [Google Scholar]
- Soofi W, Goeritz ML, Kispersky TJ, Prinz AA, Marder E, and Stein W (2014). Phase maintenance in a rhythmic motor pattern during temperature changes in vivo. J Neurophysiol 111, 2603–2613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sosa MA, Spitzer N, Edwards DH, and Baro DJ (2004). A crustacean serotonin receptor: cloning and distribution in the thoracic ganglia of crayfish and freshwater prawn. J Comp Neurol 473, 526–537. [DOI] [PubMed] [Google Scholar]
- Spitzer N, Cymbalyuk G, Zhang H, Edwards DH, and Baro DJ (2008). Serotonin transduction cascades mediate variable changes in pyloric network cycle frequency in response to the same modulatory challenge. J Neurophysiol 99, 2844–2863. [DOI] [PubMed] [Google Scholar]
- Stadele C, Heigele S, and Stein W (2015). Neuromodulation to the Rescue: Compensation of Temperature-Induced Breakdown of Rhythmic Motor Patterns via Extrinsic Neuromodulatory Input. PLoS Biol 13, e1002265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stehlik LL, MacKenzie CL, and Morse WW (1991). Distribution and abundance of four brachyuran crabs on the northwest Atlantic shelf. Fish Bull, U S 89, 473–492. [Google Scholar]
- Stevenson RD, and Josephson RK (1990). Effects of operating frequency and temperature on mechanical power output from moth flight-muscle. Journal of Experimental Biology 149, 61–78. [Google Scholar]
- Swensen AM, and Marder E (2000). Multiple peptides converge to activate the same voltage-dependent current in a central pattern-generating circuit. J Neurosci 20, 6752–6759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swensen AM, and Marder E (2001). Modulators with convergent cellular actions elicit distinct circuit outputs. J Neurosci 21, 4050–4058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang LS, Goeritz ML, Caplan JS, Taylor AL, Fisek M, and Marder E (2010). Precise temperature compensation of phase in a rhythmic motor pattern. PLoS Biol 8, e1000469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang LS, Taylor AL, Rinberg A, and Marder E (2012). Robustness of a rhythmic circuit to short- and long-term temperature changes. J Neurosci 32, 10075–10085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Temporal S, Lett KM, and Schulz DJ (2014). Activity-dependent feedback regulates correlated ion channel mRNA levels in single identified motor neurons. Curr Biol 24, 1899–1904. [DOI] [PubMed] [Google Scholar]
- Thirumalai V, Prinz AA, Johnson CD, and Marder E (2006). Red pigment concentrating hormone strongly enhances the strength of the feedback to the pyloric rhythm oscillator but has little effect on pyloric rhythm period. J Neurophysiol 95, 1762–1770. [DOI] [PubMed] [Google Scholar]
- Thuma JB, Hobbs KH, Burstein HJ, Seiter NS, and Hooper SL (2013). Temperature sensitivity of the pyloric neuromuscular system and its modulation by dopamine. PLoS ONE 8, e67930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyler AV (1970). Rates of gastric emptying in young cod. J of fisheries research board of canada. [Google Scholar]
- Wenning A, Norris BJ, Doloc-Mihu A, and Calabrese RL (2014). Variation in motor output and motor performance in a centrally generated motor pattern. J Neurophysiol 112, 95–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B, and Harris-Warrick RM (1994). Multiple receptors mediate the modulatory effects of serotonergic neurons in a small neural network. J Exp Biol 190, 55–77. [DOI] [PubMed] [Google Scholar]
- Zhao S, Sheibanie AF, Oh M, Rabbah P, and Nadim F (2011). Peptide neuromodulation of synaptic dynamics in an oscillatory network. J Neurosci 31, 13991–14004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhurov Y, and Brezina V (2005). Temperature compensation of neuromuscular modulation in Aplysia. J Neurophysiol 94, 3259–3277. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


