Cognitive Effort Drives Workspace Configuration of Human Brain Functional Networks

Abstract

Effortful cognitive performance is theoretically expected to depend on the formation of a global neuronal workspace. We tested specific predictions of workspace theory, using graph theoretical measures of network topology and physical distance of synchronization, in magnetoencephalographic data recorded from healthy adult volunteers (N = 13) during performance of a working memory task at several levels of difficulty. We found that greater cognitive effort caused emergence of a more globally efficient, less clustered, and less modular network configuration, with more long-distance synchronization between brain regions. This pattern of task-related workspace configuration was more salient in the β-band (16–32 Hz) and γ-band (32–63 Hz) networks, compared with both lower (α-band; 8–16 Hz) and higher (high γ-band; 63–125 Hz) frequency intervals. Workspace configuration of β-band networks was also greater in faster performing participants (with correct response latency less than the sample median) compared with slower performing participants. Processes of workspace formation and relaxation in relation to time-varying demands for cognitive effort could be visualized occurring in the course of task trials lasting <2 s. These experimental results provide support for workspace theory in terms of complex network metrics and directly demonstrate how cognitive effort breaks modularity to make human brain functional networks transiently adopt a more efficient but less economical configuration.

Introduction

How are human brain networks configured to support higher cognitive functions, such as working memory, that demand conscious effort for successful performance? According to global workspace theory (Baars, 1988, 2002; Dehaene and Naccache, 2001; Shanahan, 2010), conscious mental states depend on integrated activity of many elements of the nervous system. Phase synchronization of neuronal oscillations, especially in the γ and β frequency intervals, has been identified as a mechanism for coordination of information processing among a set of anatomically distributed neurons (Gross et al., 2004; Fries, 2005; Melloni et al., 2007; Womelsdorf et al., 2007; Gaillard et al., 2009). A dynamic model of workspace formation has been proposed whereby a community structure of locally synchronized, modular subsystems for unconscious processing can be suddenly replaced by the ignition of a globally synchronized system representing the consciously attended stimulus (Dehaene and Changeux, 2005). Such dynamic transitions from modular to global synchronization have been demonstrated in computational models based on the anatomical connectivity of the cat's brain (Gómez-Gardeñes et al., 2010).

These predictions of workspace theory can now be tested directly in humans using the mathematical concepts and tools of complex systems science (Albert and Barabási, 2002) to measure the organization of brain networks experimentally (Bullmore and Sporns, 2009; He and Evans, 2010; Sporns, 2010; Bullmore and Bassett, 2011). It has been shown that nervous systems generally have the small-world property of high local clustering or cliquishness of connections, as well as short path length between any pair of neuronal or regional nodes (Watts and Strogatz, 1998; Latora and Marchiori, 2001; Sporns et al., 2004; Achard et al., 2006; Achard and Bullmore, 2007). Short path length confers high global efficiency of parallel information transfer in brain networks and these metrics have been negatively and positively correlated, respectively, with accuracy of executive task performance and general intelligence, (van den Heuvel et al., 2009; Li et al., 2009). Nervous systems also have the complementary topological property of modularity, meaning that the network is nearly decomposable (Simon, 1962) into a set of modules comprising nodes that are densely connected to each other and sparsely connected to nodes in other modules (Newman, 2006; Chen et al., 2008; Fair et al., 2009; Meunier et al., 2009, 2010; Pan et al., 2010).

The convergence of workspace theory and complex systems science generates the following testable hypotheses: performance of cognitively effortful tasks will be associated with more integration of processing, topologically measurable in brain networks by increased global efficiency or reduced minimum path length; and less segregation of processing, measurable by reduced clustering or modularity. Additionally, it is expected that these topological shifts from local to global network organization will be accompanied by synchronization over longer physical distances, especially in functional networks oscillating at γ and β frequency intervals.

We tested these hypotheses in healthy human participants using magnetoencephalography (MEG) to measure changes in the brain's magnetic field during performance of a verbal working memory (N-back) task at several levels of difficulty (zero-, one-, and two-back). We estimated phase synchronization between each pair of sensors in each of the following frequency intervals (Kitzbichler et al., 2009): α, 8–16 Hz; β, 16–32 Hz; γ, 32–63 Hz; and high γ, 63–125 Hz. From the resulting synchronization matrices, we constructed weighted, undirected graphs that represented the most synchronized connections between sensors as edges between nodes of a brain functional network. We measured four key hypothesis-driven topological and physical properties of these networks and investigated changes in network configuration related to experimentally controlled variation of task difficulty and to individual differences in speed of accurate task performance.

Materials and Methods

Sample.

Sixteen neurologically healthy, young adult volunteers (mean age = 29.5 years, SD = 7.9 years; 10 male) were recruited as part of a larger project approved by a local ethics committee (LREC 07/H0306/120) and were compensated for their time. The MEG and/or behavioral datasets from three participants did not pass quality criteria (see below) and had to be discarded, leaving 13 datasets available for analysis.

Working memory task.

The N-back task is a test of working memory. In the version used here, it requires a continual working memory response from the participant during continual presentation of incoming stimuli (for more details, see Winterer et al., 2004). In brief, participants performed a series of brief trials: in each trial, one of the numbers 1, 2, 3, or 4 was visually displayed and the participant's task was to indicate, by pressing one of four different buttons, the integer that was currently displayed (zero-back), the integer displayed in the previous trial (one-back), or the integer displayed in the trial before the previous trial (two-back). Stimuli were presented for 200 ms with an interstimulus interval of 1800 ms. There were six blocks of 14 trials for each level of difficulty, with each block separated by 5 s during which instructions for the next block were presented. The whole task lasted for ∼9 min.

Only data from correctly performed trials were included in subsequent analysis. The number of correct trials was constrained to be identical for each participant at all levels of difficulty by subsampling the larger number of correct trials at zero- and one-back to match the number of correct trials at the two-back level (resulting in 38 trials per level of difficulty for each participant on average).

MEG data acquisition and preprocessing.

The MEG data were recorded from a 306-channel Vectorview system (Elekta Neuromag) at the Medical Research Council Cognition and Brain Sciences Unit, Cambridge, which combines two orthogonal, planar gradiometers and one magnetometer at each of 102 sensors within a hemispherical array situated in a magnetically shielded room. The data were recorded at 1 kHz using a bandpass filter of 0.03–330 Hz. The position of the head, relative to the sensor array, was monitored continuously by four or five head-position indicator (HPI) coils attached to the scalp.

The gradiometric data in two orthogonal directions were combined into an overall amplitude, A = ∂_xB_z² + ∂_yB_z², equivalent to the electric flux |J_xy|² ∝ A in the plane of the cortex (assuming B_x = B_y = 0). The electric flux strength is assumed to be a measure of the firing intensity of an ensemble of neurons in the cortex immediately beneath the sensor location and thus the local cortical activity.

Before the experiment, the four to five HPI coils were attached to each participant (one on each mastoid, two on the forehead, and the fifth, when present, on the crown of the head). Two bipolar electrodes were attached above and below the left eye to record vertical electro-oculogram (EOG), two bipolar electrodes were attached at the outer canthi of each eye to record horizontal EOG, and one electrode was attached to the lower cheek (ground). The location of each of the HPI coils was defined using a 3D digitizer (Fastrak Polhemus) with respect to three anatomical (fiducial) locations: the nasion and the left and right preauricular points.

External noise was removed from the MEG data using the temporal extension of Signal-Space Separation (tSSS) (Taulu and Kajola, 2005) as implemented with the MaxFilter software (version 2.0, Elekta-Neuromag). The data were subsequently adjusted for head movement every 200 ms, notch-filtered to remove mains (50 Hz and harmonics), downsampled to 250 Hz, and transformed into a common space by aligning the origin and axes as defined by the fiducials with those defined by the MEG helmet. A handful of poor quality channels were detected by visual inspection or automated methods within MaxFilter and their data were recreated using tSSS. The data were then read into the SPM5 software package (http://www.fil.ion.ucl.ac.uk/spm/), implemented in Matlab (MathWorks). Independent component analysis, as implemented in EEGLAB (http://sccn.ucsd.edu/eeglab/), was applied to the data; components that correlated highly with the recorded electro-oculogram were projected out of the data.

Before further analysis, 15 of 102 gradiometer pairs located in the lower posterior hemisphere of the skull (in the vicinity of neck muscles) were excluded because they contributed only very low-amplitude but highly synchronized signals, likely to be muscular rather than neuronal in origin.

Time series analysis.

The time series analysis was based on estimating the instantaneous phase synchronization of all pairs of sensors during each trial by each participant. These data were then averaged or stacked over all trials of the same task and either averaged over time to estimate the stationary synchronization between sensors over the course of the whole trial or smoothed with a sliding window to generate a time series of changing levels of synchronization between each pair of sensors over the course of the trial.

To characterize the time series and network statistics under the null hypothesis of coherence between random processes, we also used a phase-scrambling algorithm (Davison and Hinkley, 1997) to generate 10 independent sets of surrogate time series for each sensor and then we estimated synchronization between each pair of surrogate time series using exactly the same methods (described below) as were applied to the experimental data.

The standard phase-scrambling algorithm is comprised of the following steps: (1) input the original data into an array: x[t], t = 1, 2, …, N; (2) compute the discrete Fourier transform (DFT): z[f] = DFT(x[t]), which is generally complex, i.e., has real and imaginary components; (3) randomize the phases z′[f] = z[f] · e^iϕ[f] with ϕ[f] uniformly distributed in [0, 2π]; (4) to obtain a real inverse Fourier transform, symmetrize the phases such that ℜ (z′[f]) = ℜ (z′[f] + z′[N + 1 − f])/2 and ℑ (z′[f]) = ℑ (z′[f] − z′[N + 1 − f])/2, where ℜ and ℑ are the real and imaginary parts of a complex number, respectively; and (5) invert the DFT: x′[t] = DFT⁻¹(z′[f]).

The resulting time series x′[t] is the surrogate data. This algorithm maintains the linear covariance structure of the data, but it may not emulate nonlinear, non-normal, or nonstationary properties correctly. We thus also explored an alternative way of generating surrogate data by simply shuffling trials arbitrarily between task conditions. The results are not presented here in detail but were essentially very similar to the surrogate data generated by the Fourier phase-scrambling algorithm.

Hilbert wavelet transform.

Wavelet-based techniques have the advantage over classical Fourier-based spectral measures in that they are more adapted to nonstationary time series that commonly occur in biological systems (Bullmore et al., 2004; Whitcher et al., 2005). Additionally, compared with more traditional measures of association, like correlation, wavelet synchronization has the benefit of being sensitive to different frequency bands or wavelet scales, which were chosen here to approximately match conventional frequency intervals, i.e., α, β, γ, and high-γ bands in EEG/MEG. However, there were insufficient data points available within the course of each 1.8 s trial to provide precise estimates of synchronization at frequencies lower than the α band.

Synchronization was measured as phase coherence between the wavelet transforms of two time series. This can be expressed as the phase difference between their instantaneous complex phase vectors, as follows:

Here, W_k denotes the kth scale of a Hilbert wavelet transform, † denotes the complex conjugate, and ϕ_i(t) is the instantaneous phase of signal F_i(t).

To estimate nonstationary or dynamic synchronization changes over time, we used a sliding window technique, as follows:

This corresponds to averaging 〈〉_Δt over the interval [t, t + Δt] with Δt = L_win × 2^k × 4 ms (sampling frequency f = 250 Hz, 1/f = 4 ms). The window size L_win expressed in units of wavelet scale determines the number of cycles over which the average is taken and was chosen as L_win = 16 (Kitzbichler et al., 2009).

For both stationary and nonstationary (sliding window) analysis, phase synchronization data were stacked or collapsed over multiple trials of the same task by averaging the modulus squared of the synchronization measure C̄_ij(t) over all the individual synchronization time series for each correctly performed trial, locked to the time of trial onset, to estimate one group mean synchronization time series for each level of task difficulty.

We chose not to average over the complex phase vector but over its modulus instead because, in the case of nonstationary synchronization, it cannot be assumed that the coherence is simultaneously phase and time accurate between two trials. Since typical phase differences for the frequency ranges considered here correspond to time delays of 10 ms, averaging of the phase vector could lead to doubt about whether one should align the trials in time, indexed by stimulus presentation, or button press response. It is true that, in the analysis of stationary synchronization, where the time dimension is collapsed and there is only one coherence vector per trial, a complex average would have probably increased sensitivity due to better noise cancellation (Siegel et al., 2009). However, we did not want to use different methods for analysis of stationary and nonstationary synchronization, so we preferred to average the modulus of the coherence consistently in both cases.

Sensor space and volume conduction.

It has been shown that functional networks based on synchronization of MEG sensors are qualitatively similar to networks calculated from the same data after reconstruction of sources in anatomical space (S. Palva et al., 2010), even though the latter approach may be more sensitive to frequency dependence. Yet it has also been noted that MEG and other available techniques for whole human brain electrophysiological recording will severely undersample electrical activity at a neuronal level. Therefore, the topology of a network derived from surface field recordings will not inevitably reflect the topology of the underlying network of neuronal sources (Antiqueira et al., 2010) or the network of anatomical connections between them (Ponten et al., 2010). Source reconstruction promises greater anatomical resolution of electrical activity but multisource MEG reconstruction is a challenging area of active methodological development and at least some reconstruction algorithms can severely perturb patterns of synchronization or covariance in the sensor data (Bullmore and Bassett, 2011). Given this background context and our theoretical emphasis on a relativistic analysis of brain functional networks recorded under different experimental conditions, we decided that the promise of greater anatomical resolution was outweighed by the possibility of biasing the covariance structure of the sensor data by source reconstruction. Networks were therefore constructed from sensor data rather than from anatomically reconstructed sources.

However, to mitigate volume conduction effects and to emphasize neurophysiological rather than instrumental sources of synchronization between sensors, we recentered the synchronization distribution of each pair of sensors around zero by subtracting the average synchronization from each synchronization time series. This correction assumes that synchronization between neighboring sensors attributable to volume conduction will be stationary or unchanging over time. We also assumed that synchronization between sensors due to volume conduction will always have zero (or π) phase lag (field retardation due to the finite speed of light being obviously negligible at all frequencies below several gigahertz) to further refine the method by only correcting for the real part of the phase vector, as previously described (Stam et al., 2007). Explicitly, this correction for volume conduction was applied to the modulus squared of the phase vector in the form C′² = C² − ℜ²(V), where ℜ denotes the real part of a complex number and is applied to the average synchronization V approximating volume conduction.

Network analysis overview.

From static or time-resolved synchronization matrices, we constructed weighted and undirected graphs by applying a threshold so that only the most highly synchronized pairs of sensors had a line or edge drawn between the corresponding nodes of the graph. The topological and physical properties of these networks were then measured by the following metrics: average physical (geodesic) distance (Bassett et al., 2006), topological global efficiency, local efficiency (Latora and Marchiori, 2001), and modularity (Newman and Girvan, 2004). All metrics in the MEG networks were normalized by their median values in 10 random networks matched for degree distribution (Bullmore and Bassett, 2011).

Thresholding and weighting of networks.

Each matrix of 87 × 87 instantaneous synchronization time series was converted into an adjacency matrix A by applying an arbitrary threshold such that the number of edges in the adjacency matrix was fixed according to a predefined connection density (or topological cost). This was required to allow a comparison of network properties at different times, frequency bands or wavelet scales, and levels of cognitive load, while controlling for effects of connection density on network topology.

Values above the threshold were preserved and carried through the subsequent steps of the analysis as edge weights. Formally, this corresponds to

where sup{x, 0} = x if x > 0 and sup{x, 0} = 0 if x ≤ 0. For each synchronization matrix, the threshold C_τ was adjusted to define the proportion of nonzero elements, or connection density, in the corresponding adjacency matrix: $p=\frac{{\displaystyle \sum \left[\text{A}>C_{\tau }\right]}}{n\left(n-1\right)}$. Initially, we fixed connection density at 10% based on the Erdös-Rényi model (Erdös and Rényi, 1961) of random graphs, G(n, p), having n nodes, which predicts that almost all G(n, p) are fully connected if the connection density p ≥ 2lnn/n, giving p ∼ 0.1 for 87 nodes. However, we also constructed networks over a wider range of connection densities, from 2% to 20% of maximum connection density. On this basis, we were able to plot key topological and other metrics for each task-related network and for the surrogate networks as a function of topological cost or connection density.

Physical distance and sensor location mapping in 2D.

The intrinsic sensor locations in 3D were mapped into a planar coordinate system using an azimuthal equidistant projection and approximating the skull as a sphere. In this plane, cartesian distances from the center correspond to geodesic distances on the surface of the skull, which are assumed to be rough estimates of the physical distances between neuronal groups represented by different sensors. The physical distance measure reported for each network is simply the mean cartesian distance of all edges in the graph.

We accept that geodesic distance on the scalp surface is an approximate measure of connection distance in MEG networks. But we consider that it is nonetheless useful as a first approximation for measuring the distances between synchronized sensors on a relatively coarse spatial scale compared with the finer-grained convolutions of underlying cortical anatomy. Future work can be expected to validate new and more sophisticated measures of connection distance in space, or conduction delay in time, for pairs of functionally coherent sensors or sources in electrophysiological data.

Global and local efficiencies.

The average global efficiency of information transfer in graph 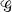having n nodes can be calculated from the inverse of the edge distances, d_ij:

The topological distance, d_ij, between nodes i and j is the minimum number of edges one has to traverse to get from one node to the other, or, in the case of a weighted network, the sum over the weights of the minimum path.

Whereas the quantity above is a measure of the global efficiency of information transfer for the whole graph 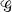, there is also a local efficiency for each node i measuring how efficiently its neighbors can communicate when node i is removed. If the subgraph of all neighbors of i is denoted by 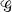_i, then its local efficiency E(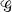_i) is approximately equivalent to the clustering coefficient (Achard and Bullmore, 2007).

To show that results for global efficiency and local efficiency are analogous to the equivalent results obtained using classical small-world metrics of path length and clustering, respectively, we also estimated path length and clustering in these data (Watts and Strogatz, 1998) (Table 1).

Table 1.

Effects of task difficulty (zero-back, one-back, or two-back), frequency band (α, β, γ or high γ), and task × frequency interaction, on brain functional network metrics.

	Sum of squares	SSError	df	F	P	Pτ
Synchronization threshold
Task difficulty	0.000101	8.74 × 10−5	2, 24	13.9	0.000	0.000
Frequency band	0.333	0.000754	3, 36	5.3 × 103	0.000	0.000
Task × frequency	2.14 × 10−5	0.000134	6, 72	1.91	0.090	0.082
Path length
Task difficulty	0.00912	0.0115	2, 24	9.52	0.001	0.006
Frequency band	0.0961	0.0239	3, 36	48.3	0.000	0.000
Task × frequency	0.00369	0.0192	6, 72	2.3	0.043	0.090
Clustering
Task difficulty	1.22	1.01	2, 24	14.4	0.000	0.000
Frequency band	6.59	1.02	3, 36	77.8	0.000	0.000
Task × frequency	0.289	1.23	6, 72	2.84	0.016	0.012
Global efficiency
Task difficulty	0.00568	0.00643	2, 24	10.6	0.001	0.004
Frequency band	0.03	0.00768	3, 36	46.8	0.000	0.000
Task × frequency	0.000949	0.012	6, 72	0.947	0.467	0.039
Local efficiency
Task difficulty	1.47	1.16	2, 24	15.2	0.000	0.000
Frequency band	8.26	1.34	3, 36	73.9	0.000	0.000
Task × frequency	0.353	1.39	6, 72	3.03	0.011	0.035
Physical distance
Task difficulty	0.084	0.0809	2, 24	12.4	0.000	0.001
Frequency band	2.01	0.129	3, 36	188	0.000	0.000
Task × frequency	0.0462	0.101	6, 72	5.5	0.000	0.003
Modularity
Task difficulty	0.185	0.263	2, 24	8.47	0.002	0.053
Frequency band	5.52	0.622	3, 36	107	0.000	0.000
Task × frequency	0.047	0.536	6, 72	1.05	0.399	0.667

Detailed ANOVA statistics are presented for two-way mixed effect models estimated with the connection density held constant across all conditions at 10% of maximum connection density. For comparison, the P_τ values are given for the same analyses repeated for networks with the synchronization threshold C_τ held constant across conditions, allowing some variation of connection density around 10%.

Modularity.

A modularity measure of graph 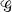with n nodes, N edges, and nodal degrees k_i can be defined on the basis of its adjacency matrix A, as follows (Newman, 2006):

where c_i is the module to which node i belongs and δ is the Kronecker delta. This function was maximized by a computationally expedient greedy algorithm (Meunier et al., 2010). The maximum value of Q is essentially a measure of the fraction of edges that fall within the given modules minus the expected fraction if edges were distributed randomly, preserving nodal degrees. An extension to the weighted case follows naturally by using a weighted adjacency matrix A and nodal weights instead of degrees (where correct normalization instead of the canonical 1/2N has to be ensured).

Statistical methods: factorial analysis and resampling.

We used repeated-measures ANOVA models for statistical analysis of the synchronization threshold C_τ and each of the key network parameters considered separately as the dependent variable, with frequency band, task difficulty, and task-by-frequency as within-subject fixed effects, and participant as a random effect (Table 1). We also tested dynamic effects on network parameters within the course of each trial by splitting the trials into first (response generation) and second (working memory) halves and using paired t tests to identify significant task-related differences in metrics measured in each half of the trials.

We used surrogate data to compare the distributions of synchronization and key network metrics in experimental MEG data to an appropriate null distribution. MEG segments comparable to single trials in the experimental data were resampled using a Fourier-based algorithm (Davison and Hinkley, 1997), which preserves the amplitude distribution and autocorrelation function of each time series but disrupts the phase synchronization between pairs of time series. This therefore provides an appropriate point of reference to evaluate coherence estimates in experimental multivariate time series compared with the null hypothesis of random multivariate (1/f) noise (Achard et al., 2008), while controlling for any possible estimation bias attributable to autocorrelation or amplitude changes in the observed time series. An alternative approach to the same statistical issues has been to construct an innovative estimator of pairwise phase consistency (Vinck et al., 2010) that is an analytically unbiased and consistent estimator of population parameters of oscillations, but does not address the problem of amplitude-related bias.

Although the sample of participants and trials available was relatively small (and future studies might profitably consider larger samples), by normalizing with matched random networks and comparing to surrogate datasets, we found statistically significant changes in brain network organization as a function of cognitive demand (see below).

Results

Behavioral measures of task performance

The relative difficulty of the tasks is indicated by the mean accuracy of performance: for zero-back, 97.3 ± 2.9%; one-back, 75.8 ± 18.4%; and two-back, 54.3 ± 22.6% (chance = 25%). Most participants who responded correctly to presentation of a target letter did so within the first half of the trial: mean latency for correct (all) trials was 719 ms (718 ms) for zero-back, 688 ms (739 ms) for one-back, and 661 ms (766 ms) for two-back. We inferred that cognitive effort in the first half of each trial was probably dedicated to motor response generation processes, which were similar between all versions of the task. In the second half of each trial, however, the cognitive differences between tasks were more marked. The zero-back task is relatively effortless after the button press has been executed, whereas in the one- and two-back tasks, active short-term memory processes must be engaged to update the identity of the numbers presented in previous trials, one of which becomes the new target number for the next trial. The second half, or working memory phase, of each trial is therefore considerably more effortful for the one- and two-back versions than the zero-back version of the task.

Task-related effects on functional network organization

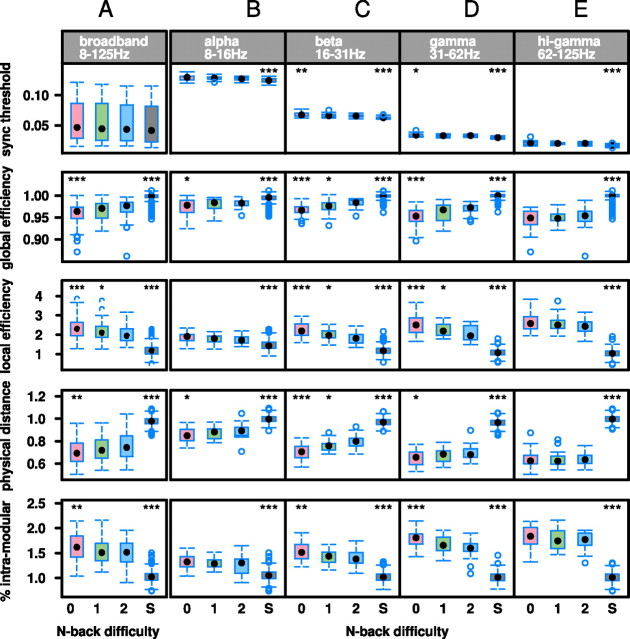
We found that greater cognitive effort, i.e., the progression from zero-back to one- and two-back versions of the working memory task, was associated with highly significant effects on global network topology and geometry. Global efficiency of parallel information transfer was increased, indicating a more integrated, isotropic, or random network architecture, whereas local efficiency or clustering was decreased (Fig. 1; Table 1). These task-related changes in network topology were associated with the emergence of more long-distance synchronization between anatomically separated sensors. Greater task difficulty was also associated with a less modular community structure of the networks (Figs. 1, 2; Table 1). Significant task-related differences in topology and synchronization distance were also evident at a nodal level of analysis. Increased degree and physical distance of synchronization, and reduced proportion of intramodular edges, were seen mainly in central and anterior sensors during performance of the two-back task compared with the zero-back task (Fig. 1).

Figure 1.

Brain functional network changes associated with differently effortful cognitive tasks (zero-, one-, and two-back working memory trials) in the β-band frequency interval (16–32 Hz). A, Thresholded synchronization matrices can be represented graphically as a network in anatomical space (F, front; L, left, R, right): each node represents an MEG sensor and there is a line or edge drawn between nodes if β-band oscillations are highly synchronized between sensors. The diameter of each node indicates its degree; nodes are colored to indicate their membership of topological modules. B, Node size indicates local efficiency or clustering coefficient, a measure of segregated network topology. C, Long-distance connections, at least as long as the 95th percentile of the distance distribution in the two-back network, are highlighted as black edges. D, Modularity is represented by color-coding the connections between nodes: intermodular connections are red and intramodular connections are gray. Right column, Statistical significance of task-related differences in local (nodal) network properties are shown for local efficiency (B), physical distance (C), and proportion of intramodular edges (D). In these panels, the size of each node corresponds to the log P value for a t test of the null hypothesis that the task-related difference in network metrics is zero. The most effortful two-back task is associated with less clustering, longer-distance synchronization, and a larger proportion of intermodular connections compared with the least effortful zero-back task.

Figure 2.

Effects of task difficulty on synchronization and workspace configuration of brain functional networks operating at different frequency intervals. A, Over all frequencies in the broadband interval 8–125 Hz, there are significant differences in organization of zero-back (red box), one-back (green box), and two-back (blue box) brain networks compared with the equivalent metrics estimated in comparable surrogate (S) data representing fully randomized networks (gray box). B–E, Considering four narrowband frequency intervals separately, task-related network differences indicating workspace configuration are most salient in β- and γ-bands. ***p < 0.001, **p < 0.01, and *p < 0.05 for the null hypothesis that two-back brain network organization is identical to network organization in other task conditions or in surrogate networks.

We will refer to this theoretically predicted pattern of task-related changes in key network parameters as workspace configuration. It could also be described as a shift of network architecture to a more random configuration at higher levels of task difficulty. However, brain network topology was never completely randomized or dominated by random noise. This is evident by the comparison between network metrics estimated in experimental MEG data and the same metrics estimated in surrogate data generated by random resampling of the observed time series (Fig. 2). These results show that, although higher levels of task difficulty are indeed associated with a trend toward more random network organization, there are significant differences between surrogate data and experimental MEG data in all metrics at all levels of difficulty in the β and γ frequency bands. These results strongly suggest that the emergence of workspace configuration in networks during performance of more demanding cognitive tasks is not simply attributable to random noise predominating in the data acquired during more effortful tasks.

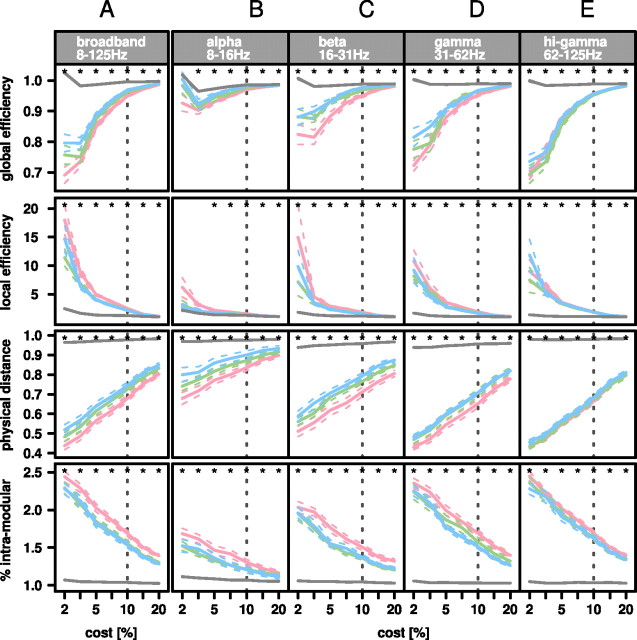
The task-related changes in brain network organization described so far were estimated on the basis of networks thresholded at a particular, fairly sparse connection density (10%). To test the robustness of these results to a reasonable degree of variation in connection density, we estimated all key metrics for each task-related network and for the surrogate networks over a range of thresholds corresponding to connection densities in the range of 2–20% (Fig. 3). These results show that the key findings at 10% connection density are broadly conserved: greater cognitive effort was typically associated with greater workspace configuration of brain networks; and under all task conditions, brain networks remained somewhat less than fully randomized by comparison to surrogate networks. As connection density was increased and more edges representing less strongly synchronized pairs of sensors were added to the graphs brain network metrics naturally tended to converge on their limiting values in the surrogate networks; this process of convergence was most evident in the lowest frequency α-band networks.

Figure 3.

Effects of task difficulty on workspace configuration of brain functional networks at different frequency intervals over a range of network connection densities. A–E, Over all frequencies (A) and in each frequency interval (B–E), mean brain network metrics with 95% confidence interval (dotted lines) for zero-back (red line), one-back (green line), and two-back (blue line) tasks tend to converge on their values in surrogate networks (gray line) as connection density is increased from 2% to 20% of possible edges. The vertical dotted lines indicates the connection density of 10% chosen for ANOVA modeling. Asterisks denote significant difference at p < 0.05 between two-back and surrogate networks.

Workspace configuration of thresholded network topology was accompanied by some changes in magnitude of the synchronization threshold between sensors (Table 1). However, task-related differences in synchronization strength were relatively small in degree and synchronization was significantly greater in experimental data recorded under the two-back condition than in the surrogate data (Fig. 2). This indicates that the relatively low level of synchronization in data recorded during the most difficult (two-back) task does not represent the substitution of neurophysiological signals by random multivariate noise. To further test this null hypothesis, we repeated the analysis of task difficulty effects on network topology by applying the same threshold value of synchronization to generate graphs from the task-specific synchronization matrices. This approach ensures that all edges in each graph represent at least the same minimum strength of synchronization, although it allows a minor degree of variation in the number of edges between graphs. However, the results of this graph analysis controlling for task-related variability in synchronization strength were very similar to the previously reported results of analysis controlling for connection density of the thresholded graphs (Table 1). This indicates that variation in synchronization strength between levels of task difficulty is not sufficient to account for the observed differences in network topology.

Task-related network effects at different frequencies

Task-related workspace configuration was evident to some extent in networks oscillating at all frequency intervals; it is illustrated graphically for the β-band network in Figure 1; but similar results were obtained for all other frequency intervals. The main effect of task difficulty (regardless of frequency band) on all four key network parameters was in the theoretically expected direction and statistically significant (Fig. 2; Table 1). Thus, there was some evidence for scale invariance of task-related reconfiguration of brain functional networks (Bassett et al., 2006) over the range of frequencies or wavelet scales considered.

However, there were also some significant differences between networks at different frequencies. Regardless of variation in task difficulty, the main effect of frequency was significant for all four network parameters; lower frequency networks, e.g., α-band, had greater global efficiency, longer physical connection distance, lower clustering, and lower modularity than higher frequency networks, e.g., γ-band. Additionally, there were significant differences between networks oscillating at different frequencies in how markedly they demonstrated topological changes in configuration as a function of increasing task difficulty. For example, there was a significant task-by-frequency interaction for most of the network parameters (Table 1) and, considering each frequency band separately in a post hoc analysis, task-related differences in workspace configuration were identified more clearly in the intermediate frequency range of β- and γ-band networks than in networks oscillating at lower (α) or higher (high γ) frequencies (Fig. 2).

Workspace configuration and cognitive performance

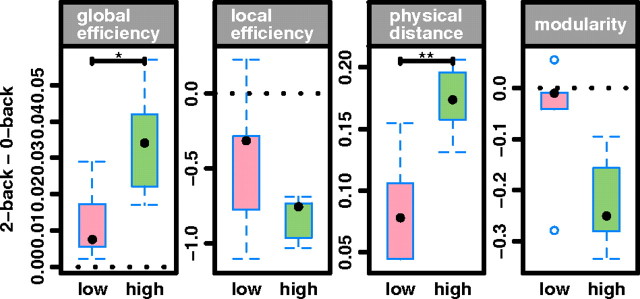
To test our prediction that superior individual performance on effortful cognitive tests would be associated with stronger emergence of workspace configurations, we split the sample into fast- and slow-performing subgroups (defined by individual mean latency of accurate response greater or less than the sample median latency) and compared task-related change in network parameters between the differently performing subgroups. We found that fast-performing participants showed clearer evidence for workspace configuration of β-band networks under conditions of increased task difficulty. Specifically, fast-performing participants, compared with slow-performing participants, demonstrated significantly greater difficulty-related increase in physical distance, and greater difficulty-related decrease in clustering (Fig. 4).

Figure 4.

Cognitive load effects on β-band network properties in two groups of fast- and slow-performing participants. Both fast- and slow-performing subgroups of participants demonstrate workspace configuration of networks at higher cognitive load, but this task-related effect on efficiency and physical distance is greater in the fast-performing group (high) than in the slow-performing group (low). The dotted lines indicate zero difference in network metrics between different levels of task difficulty. *p < 0.05 and **p < 0.01 for the null hypothesis that task-related change in network metrics is not different between fast- and slow-performing subgroups. Box sizes represent first and third quartile; whiskers show extent of distribution; black dot is the median and blue dots are outliers.

Dynamic network changes within a single trial

The results presented so far have confirmed that, on average over the 1800 ms duration of each trial, human brain networks are differentially configured as workspaces during performance of tasks demanding different degrees of cognitive effort, and that faster-performing individuals tend to show clearer evidence of task-related workspace configuration. This supports the workspace theory but provides a rather static picture of network differences that are expected to emerge dynamically in response to momentarily changing experimental (or environmental) demands for processing. To further test the hypothesis that workspace reconfiguration is dynamically related to cognitive effort, we measured network properties in overlapping time windows running consecutively from the start to the end of each trial. This allowed us to track time-related changes in network properties during performance of the zero- and two-back tasks, and to relate these changes to the different degrees of cognitive effort entailed by the tasks over the course of a single trial.

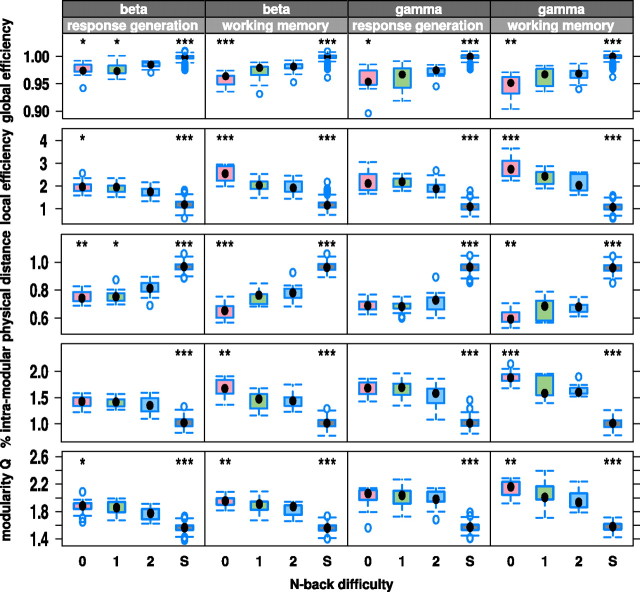
We found that during the first 900 ms of each trial, both zero- and two-back brain networks demonstrated high global efficiency, long physical connection distance, low clustering, and low modularity. However, during the second half of each trial, while the two-back network maintained workspace configuration, presumably in support of ongoing working memory processes, the zero-back network rapidly adopted a more crystallized configuration, indicated by relatively low global efficiency, short physical connection distance, higher clustering, and modularity (Fig. 5). This time-related change in network configuration under different task conditions was further represented by significant differences between zero-, one-, and two-back networks in the β- and γ-band frequencies during the second half (working memory phase) of the trial but not during the first half (response generation phase) (Fig. 6). The observation that the most significant differences between task-related networks were found in the second, working memory phase of the trials discounts the possible contribution of stimulus-evoked responses (which will be greatest during the response generation phase) to the pattern of task-related change in network organization.

Figure 5.

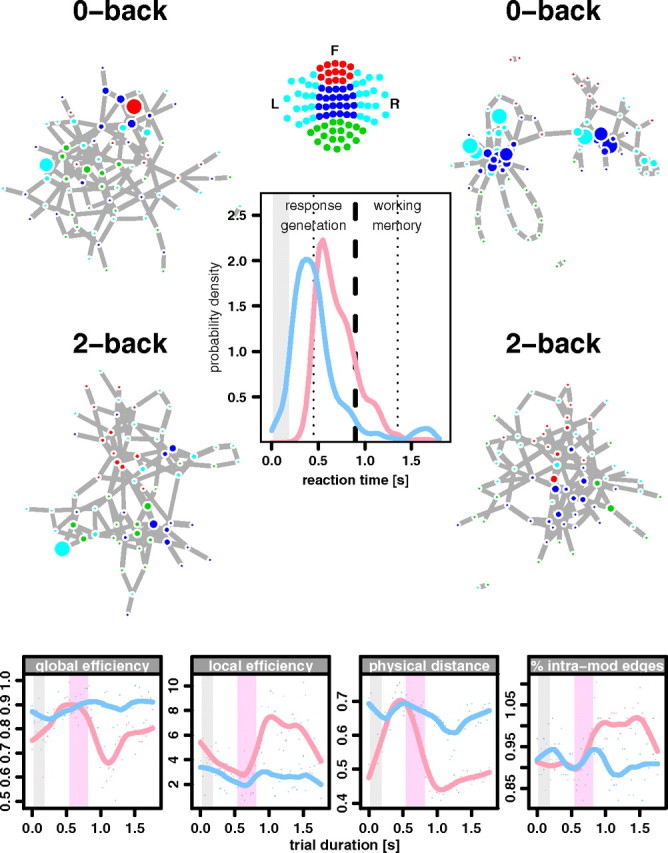
Dynamic changes in workspace configuration of β-band networks related to changing levels of cognitive effort in the course of a single (1800 ms) trial. Center, Period of visual stimulus presentation (gray bar) and the frequency distributions of latency of button press response in the zero-back (red line) and two-back (blue line) tasks. Note that most participants executed a motor response by the end of the first half of the trial (thick dashed line). Left, Zero-back (top) and two-back (bottom) networks measured at time ∼500 ms. During this response generation phase of the trials, both tasks elicited workspace configuration of brain networks. This is represented by low clustering (small diameter of most nodes) and topological proximity of nodes from anatomically different regions [node colors code anatomical location of sensors (top center)]. Right, Zero-back (top) and two-back (bottom) networks measured at time ∼1350 ms in the working memory phase of the task demonstrate different topologies: the two-back network maintained a workspace configuration whereas the zero-back network relaxed to a more locally clustered configuration. This is represented by the greater clustering (node diameter) of many nodes and greater topological proximity of nodes from the same anatomical regions in the zero-back network. Bottom row, Changes in key workspace parameters as a function of trial duration for zero-back (red lines) and two-back (blue lines) versions of the task: from left to right, global efficiency, local efficiency or clustering, physical distance, and proportion of intramodular edges. Red bar, Interquartile range of response latencies. L, Left; R, right; F, front.

Figure 6.

Time-resolved changes in β- and γ-band network topology during zero- and two-back tasks. Networks oscillating at β- and γ-band frequencies demonstrate significant task-related differences in network metrics during the second half (working memory phase) of each trial but not during the first half (response generation phase). ***p < 0.001, **p < 0.01, and *p < 0.05 for the null hypothesis that metrics are not different in the zero-back (red box), one-back (green box), or surrogate (S; gray box) networks compared with the two-back networks (blue box). Box sizes represent first and third quartile; whiskers show extent of distribution; black dot is the median and blue dots are outliers.

Discussion

These results provide new evidence in support of the predictions of global neuronal workspace theory and demonstrate how the mathematical tools of complex network analysis can be used to demonstrate rapid, task-related changes in functional networks derived from human MEG data.

Complex networks and workspace theory

We have shown that greater cognitive effort was associated with the emergence of a more efficient, less modular, and less clustered network topology. This topological workspace configuration was associated with greater long-distance synchronization between some pairs of anatomically separated sensors. Anatomically extensive coactivation of multiple cortical regions and long-range interareal synchronization between cortical areas have been frequently reported as neurophysiological correlates of conscious or effortful states elicited by a wide range of experimental paradigms (for review, see Baars, 2002). For example, greater synchronization of left prefrontal, right posterior parietal, and temporal areas was reported in the context of the attentional blink paradigm, specifically when a second target stimulus was correctly identified 292 ms after presentation of a first target stimulus, but not when the stimulus onset asynchrony between stimuli was reduced (to 146 ms) and the second target was not identified (Gross et al., 2004). Long-range synchronization has also been reported in the context of working memory task performance (J. M. Palva et al., 2010) and during conscious perception of unmasked words compared with unconscious processing of masked words (Gaillard et al., 2009).

The new insight provided by our results in this context is that the innovative use of graph analysis has allowed us to see more clearly how task-related changes in long-range synchronization are related to the overall topological organization of brain networks. As cognitive effort increases, emergent long-range synchronization provides topological short-cuts between cortical areas that are relatively segregated from each other in the more modular configuration of the network under cognitively undemanding conditions, and so increases the global efficiency of the network for parallel information transfer.

A special role for β-band oscillations in workspace reconfiguration?

Phase synchronization between rhythmic oscillations in anatomically distributed neuronal populations has been widely accepted as a key neurophysiological mechanism to coordinate information processing between components of large-scale brain functional networks (Varela et al., 2001; Fries, 2005; Buzsáki, 2006). Our results demonstrate that workspace formation is a fairly broadband or scale-invariant phenomenon: there is some evidence for task-related increases in global efficiency and physical distance, as well as task-related decreases in clustering and modularity, across all frequency intervals considered (collectively encompassing the range of 8–120 Hz). This is compatible with various prior reports highlighting the significance of α-, β-, and γ-band synchronization as mechanisms for communication between distributed neuronal groups (Rodriguez et al., 1999; Doesburg et al., 2009; S. Palva et al., 2010).

However, our results also suggest that synchronization in the β-band specifically plays a crucial role in workspace formation. This claim is supported by greater statistical significance of task-related effects in the β-band on average over the whole duration of each 1800 ms trial (Fig. 2); more significant task-by-time interaction, indicating that rapid workspace relaxation, specifically during the second half of the zero-back trial, is especially marked in β-band networks (Fig. 6); as well as evidence that variability in individual performance is most clearly related to parameters of workspace configuration in β-band networks (Fig. 4).

The special significance of β-band oscillations for long range synchronization is also supported by several lines of prior evidence. For example, biophysical models have demonstrated that the longer period length of β-band oscillations, compared with γ, is more appropriate for synchronization over greater physical distances, which impart appreciable conduction delay (Kopell et al., 2000). Coherence and Granger causal interactions between components of a large-scale motor control network were also strongest in the β frequency interval (Brovelli et al., 2004). The topological cost efficiency (Latora and Marchiori, 2001) of brain functional networks oscillating at β-band frequencies was shown to be more strongly correlated with variability of performance on a working memory task than the cost efficiency of networks operating at other frequencies (Bassett et al., 2009). Working memory task-related changes in synchronization likelihood and small-worldness of MEG networks were most salient in β- and γ-bands (Micheloyannis et al., 2009). Together, it seems that β-band synchronization is very likely a key mechanism in the task-related workspace configuration of large-scale brain functional networks.

Dynamic workspace reconfiguration: critical and economical

Topological analysis of structural and functional brain networks, in many species and in all modalities of neuroimaging data, has previously demonstrated that brain networks generally have the property of small-worldness (Bassett et al., 2006; Bullmore and Sporns, 2009). This has long seemed theoretically attractive for understanding how brain networks support cognitive function because small-world architecture is potentially able to deliver both segregated or local processing as well as distributed or global processing (Sporns et al., 2004). Our analysis of time-resolved changes in topology over the course of a single cognitive trial lasting <2 s shows how quickly brain functional networks can shift from a relatively random configuration when the demand for distributed processing is high to a more crystalline configuration when cognitive demands are reduced. This process of workspace relaxation occurred over an interval of 10–100 ms after completion of the response generation phase of the least demanding zero-back task and was not seen in the second (working memory) phase of the two-back trials (Fig. 5). Clearly, functional networks can vary rapidly on a small-world spectrum of possible topologies rather than being located persistently at a single fixed point between lattice and random architectures. Many of the task-related changes in network organization predicted by workspace theory can be topologically described as a shift toward randomization, but the surrogate data show that brain networks typically remain more modular than randomly synchronized networks, even under conditions of greatest cognitive effort.

This rapidity of network reconfiguration in response to changing environmental demands is compatible with theory and data suggesting that neuronal dynamics exist in a critical state, i.e., a physical state close to the point of a phase transition (Chialvo, 2004; Roa et al., 2007; Beggs, 2008). Electrophysiological studies have found that neuronal firing in cortical slices (Beggs and Plenz, 2003), local field potentials in awake monkey cortex (Petermann et al., 2009), and phase synchronization in resting-state MEG data (Kitzbichler et al., 2009) all demonstrate power law scaling behavior compatible with criticality. Dynamically critical systems have the capacity to change configuration spontaneously, as well as rapidly in response to external perturbation, and computational and animal models have demonstrated that critical networks are optimal for information processing and storage (Shew et al., 2009). Specifically in relation to workspace theory, it has already been suggested that the moment of ignition, when locally modular processing of some stimulus becomes generalized by formation of a global workspace, is a phase transition, and that cortical systems can be driven to this critical point by increasing levels of ascending neuromodulatory input from brainstem nuclei (Dehaene and Changeux, 2005). More generally, it may be that the self-organized criticality of spontaneous cortical dynamics favors rapid transitions between different states of the system, supporting the adaptive emergence and disappearance of global workspaces in response to changing demands, without tuning of an external driving parameter such as ascending neuromodulatory input.

If criticality provides a possible answer to the question of how brain workspaces can rapidly reconfigure in response to external perturbation, what about the question of why release of cognitive effort should be associated with such a rapid lattice crystallization, or relaxation of workspace architecture? One hypothetically plausible driver could be an economical principle. The small-world topology of spatially embedded networks like brains tends to be associated with economical if not minimal wiring costs (Bassett et al., 2010). Brain regions or neurons that have clustered interconnectivity tend to be spatial as well as topological neighbors. So high clustering of brain networks is associated with low wiring cost and we can infer that conservation of wiring cost may have been an important selection factor in the evolution of nervous systems (Chen et al., 2006). However, it is known that although brain wiring costs are low, they are not minimal, as they would be if the brain was topologically arranged as a lattice (Kaiser and Hilgetag, 2006). The existence of relatively few long distance connections between anatomically separate and otherwise topologically remote regions reduces path length at the expense of more than minimal wiring cost. Thus, the physical instantiation of small-world topology can be regarded as the outcome of selection by competitive criteria: minimization of wiring cost versus maximization of efficiency of information transfer (Bassett et al., 2006; Bullmore and Sporns, 2009; Sporns, 2010; Fornito et al., 2011).

It is conceivable that workspace formation and relaxation represents the same economy/efficiency trade-off in operation dynamically. The metabolic costs of the brain are generally large (∼20%) in proportion to the total energy budget of the body, and the largest single cost is that of ATP-dependent active transport systems required to restore neuronal membrane potentials after depolarization (Niven and Laughlin, 2008). Thus, metabolic demands would be expected to increase with longer-range communication, such that the capacity to rapidly attenuate long distance connectivity when it is no longer functionally required would be advantageous. So, assuming that the metabolic costs of synchronized oscillations scale with the physical distance between synchronized regions, we can say that the human brain breaks modularity (Dehaene and Naccache, 2001) to adopt a more efficient workspace configuration when necessary in response to cognitive demands, but it wastes little time in reverting to a more economical and modular state when the demand for cognitive effort is reduced.

Notes

Supplemental material for this article is available at http://sms.cam.ac.uk/media/1587355: a movie of dynamic network changes during performance of zero- and two-back working memory tasks. This material has not been peer reviewed.