Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2011 Aug 10;31(32):11692–11696. doi: 10.1523/JNEUROSCI.0237-11.2011

Neural Development of Binaural Tuning through Hebbian Learning Predicts Frequency-Dependent Best Delays

Bertrand Fontaine 1,2, Romain Brette 1,2,✉
PMCID: PMC6623129  PMID: 21832198

Abstract

Birds use microsecond differences in the arrival times of the sounds at the two ears to infer the location of a sound source in the horizontal plane. These interaural time differences (ITDs) are encoded by binaural neurons which fire more when the ITD matches their “best delay.” In the textbook model of sound localization, the best delays of binaural neurons reflect the differences in axonal delays of their monaural inputs, but recent observations have cast doubts on this classical view because best delays were found to depend on preferred frequency. Here, we show that these observations are in fact consistent with the notion that best delays are created by differences in axonal delays, provided ITD tuning is created during development through spike-timing-dependent plasticity: basilar membrane filtering results in correlations between inputs to binaural neurons, which impact the selection of synapses during development, leading to the observed distribution of best delays.

Introduction

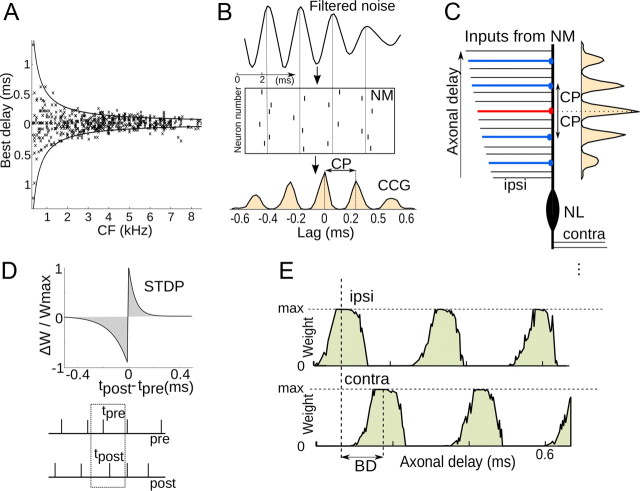
In many species, interaural time difference (ITD) is the main cue to sound localization in the horizontal plane (Yin, 2002; Konishi, 2003). Binaural neurons in the nucleus laminaris (NL) of birds and in the medial superior olive of mammals are sensitive to ITD: they fire maximally at a preferred interaural delay, called the “best delay” (BD). They also have a preferred frequency (characteristic frequency, CF), which is inherited from their monaural inputs in the nucleus magnocellularis (NM, for birds) or cochlear nucleus (for mammals). In birds, physiological observations are in general accordance with the Jeffress model (Jeffress, 1948): in each frequency band, binaural neurons have heterogeneous BDs, resulting from differences in axonal delays of their inputs, and the ITD of the sound source is signaled by the BD of the maximally activated neuron (Carr and Konishi, 1990). One notable disagreement is that, instead of covering the full physiological range of ITDs (±250 μs in the barn owl) (von Campenhausen and Wagner, 2006), BDs rarely exceed half the characteristic period of the neuron (Wagner et al., 2007; Köppl and Carr, 2008; Carr et al., 2009), an approximate constraint called the “π-limit.” Figure 1A shows the BD and CF of 625 cells in the core of central nucleus of the inferior colliculus (ICCc) of the barn owl (data provided by H. Wagner (Rheinisch-Westfälische Technische Hochschule, Aachen, Germany) and previously shown in Wagner et al., 2007): high-frequency cells tend to have smaller BDs than low-frequency cells, and 85% of all BDs fall within the π-limit (i.e., BD < 1/(2CF), solid curves). From a functional point of view, this is not a strong constraint because BDs with the same phase relative to the CF are mostly redundant. Yet, how this π-limit arises is puzzling and questions the validity of the Jeffress model: if BDs reflect the difference in axonal delays of ipsilateral and contralateral inputs, how could they depend on CF, which is a property of monaural neurons? An alternative model of ITD processing, the stereausis model (Shamma et al., 1989), postulates that BDs arise not from differences in axonal delays, but from inputs to binaural neurons coming from slightly different places along the cochlea. This would result in a frequency-dependent distribution of BDs (Joris et al., 2006). However, in the barn owl, the inputs to binaural neurons have no or small interaural CFs mismatches, which are not correlated with the best ITD (Peña et al., 2001; Fischer and Peña, 2009; Singheiser et al., 2010). Therefore, there is currently no satisfactory explanation of the frequency dependence of BDs in birds.

Figure 1.

Figure 1.

Open in a new tab

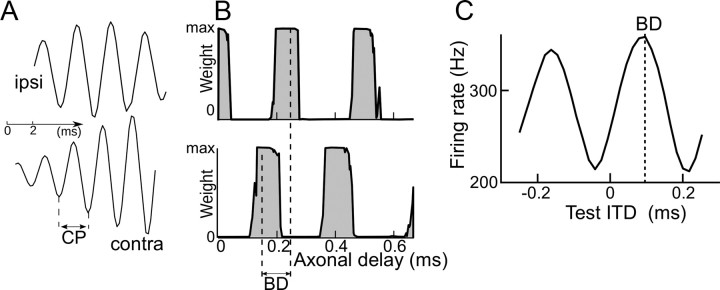
Principle of the model. A, BD versus CF for 625 cells of the barn owl ICCc (Wagner et al., 2007): 85% of all BDs are within the π-limit (solid curves). B, Top, The sound is bandpass filtered by the basilar membrane around a characteristic frequency (vertical units are arbitrary). Middle, Neurons in the NM encode the filtered sound in spike trains, with a temporal structure that reflects the filtering. Bottom, As a result, two NM neurons with the same CF show correlated firing, and the periodicity in the cross-correlogram corresponds to the characteristic period (CP = 1/CF). C, NM neurons project to binaural neurons in the NL, with different axonal delays (the correspondence between dendritic location and axonal delay is only an illustration choice). The periodicity in the cross-correlogram of input spike trains results in firing correlations at synapses with delays related by a integer multiple of the CP: firing at the synapse in red is correlated with firing at synapses in blue. D, Synaptic weights are modified depending on the relative timing of presynaptic (tpre) and postsynaptic spikes (tpost), for all pairs of spikes, with an asymmetrical function typical of excitatory synapses (Bi and Poo, 1998; Tzounopoulos et al., 2004). E, Correlated firing results in correlated synaptic weight modifications, so that stabilized synaptic weights are periodic with respect to their corresponding axonal delay, the period being the CP. It follows that the BD cannot be greater than the CP.

Modeling studies have shown that Hebbian spike-timing-dependent plasticity (STDP) can account for the development of ITD selectivity (Gerstner et al., 1996) and the formation of an ITD map (Leibold et al., 2001; Leibold and van Hemmen, 2005). Since the frequency selectivity of binaural neurons is inherited from their monaural inputs, it is natural to hypothesize that the frequency dependence of BDs may be a consequence of exposure to sounds during a critical development period. Therefore, we investigated the impact of frequency filtering on the selection of synapses during development.

Materials and Methods

All models were simulated with the Brian simulator (Goodman and Brette, 2009), with 5 μs timestep. The longest simulation took 12 d (see Fig. 5B). Basilar membrane filtering is modeled by fourth-order gammatone bandpass filters (Patterson, 1994), followed by half-wave rectification and compression by a 1/3 power law. These filtered sounds are encoded into spike trains by NM neurons, modeled as noisy integrate-and-fire neurons, as described in Goodman and Brette, 2010 (membrane time constant, τm = 2 ms; reset potential, Vr = −60 mV; resting potential, V0 = −52 mV; threshold, Vt = −50 mV; refractory period, trefrac = 1.7 ms; noise, σ = 0.2 mV). Each NL neuron, modeled in the same way (except τm = 0.1 ms; V0 = −60 mV; trefrac = 1 ms), receives synapses from 250 NM neurons on each side, with random axonal delays between 0 and 667 μs. Synaptic weights are initially random between 0 mV and wmax = 1 mV, except in Figure 5 where they are randomly initialized on each side within a Gaussian envelope with mean chosen at random between 0 and 667 μs and SD 220 μs (providing a mild initial ITD selectivity with a random BD).

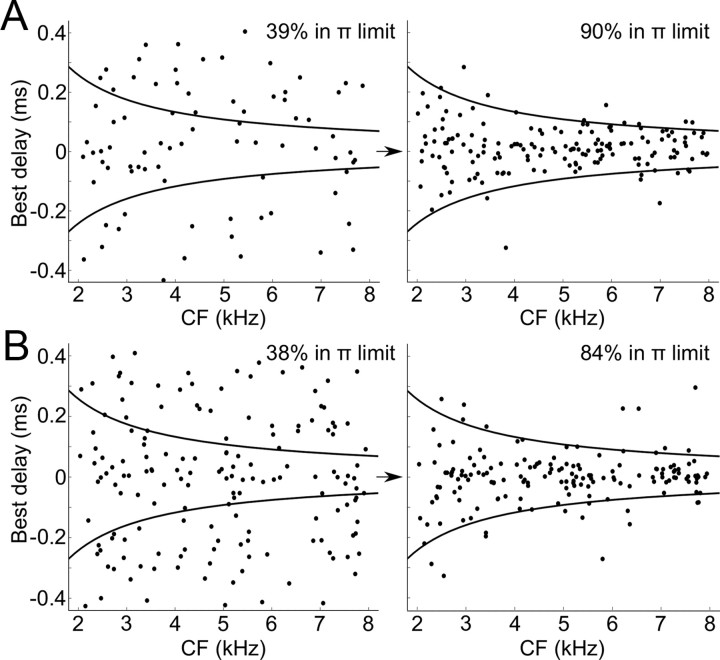
Figure 5.

Figure 5.

Open in a new tab

Distribution of best delays versus characteristic frequency. A, The best delays of binaural neurons with various CFs are initially random, with only ∼40% within the π-limit. After a long exposure to uncorrelated binaural noise, most stabilized best delays lie within the π-limit. B, The same phenomenon occurs when uncorrelated noise is replaced by stereo recordings of a natural environment (forest).

Synapses are subsequently potentiated or depressed, according to a standard asymmetrical STDP rule typical of excitatory synapses (Markram et al., 1997; Bi and Poo, 1998, 2001; Caporale and Dan, 2008), as shown in Figure 1D (maximum potentiation: 1% of wmax, time constant 50 μs; maximum depression: 2.1%, time constant 125 μs). The contributions of all spike pairs are summed. Plasticity time constants are short compared with values measured in the cortex, but neurons in the auditory brainstem (specifically in the ITD-processing pathway) are known for their specialized cellular and synaptic mechanisms that minimize integration time and preserve precise timing information (Trussell, 1997; Trussell, 1999).

Sounds were either binaural white noise (uncorrelated or interaurally delayed) or commercial stereo recordings of natural environments. After development, ITD selectivity was tested using binaurally delayed white noise (measuring best delays as the difference of latencies in response to monaural clicks did not yield significant changes).

Results

The principle is demonstrated in Figure 1. Monaural neurons in the NM inherit their frequency selectivity from hair cells in the basilar membrane, which filters sounds around the CF. Neurons preferentially fire at certain phases of their auditory nerve input, so that the input periodicity appears in the cross-correlogram of any two neurons with the same CF (Fig. 1B). A binaural neuron in the NL receives inputs from the NM with different delays. Any two inputs with delays related by an integer multiple of the characteristic period are then correlated (Fig. 1C). If synaptic weights evolve according to some Hebbian mechanism, i.e., synapses are strengthened when input and output are coactive, then these input correlations should translate into correlated synaptic modifications. Since we are interested in the development of delay selectivity at a submillisecond timescale, the basis of such a Hebbian mechanism must be the timing of presynaptic and postsynaptic spikes, that is, STDP. This mechanism has been demonstrated in vitro in many preparations (Markram et al., 1997; Bi and Poo, 1998, 2001; Caporale and Dan, 2008), in particular in the auditory system (Tzounopoulos et al., 2004), and has been the subject of many modeling studies (Kempter et al., 1999; Song et al., 2000; van Rossum et al., 2000), including in the context of ITD selectivity (Gerstner et al., 1996; Kempter et al., 2001; Leibold et al., 2001; Leibold and van Hemmen, 2005). Specifically, we consider a plasticity rule where synaptic modification is determined by the difference in timing of postsynaptic and presynaptic spikes, at each synapse (Fig. 1D): the synapse is potentiated when the postsynaptic spike occurs shortly after the presynaptic spike and depressed in the reversed order (this asymmetry is typical of excitatory synapses) (Markram et al., 1997; Bi and Poo, 1998; Tzounopoulos et al., 2004). Because of input correlations, at the end of the development period, the synaptic weights for each side (ipsilateral and contralateral) should be periodic with respect to their corresponding delay, the period being that of the cross-correlogram of inputs, which is the characteristic period of the neuron (Fig. 1E). Therefore, the best delay, as assessed from the delay shift in synaptic weights between the ipsilateral and contralateral sides, could not exceed the characteristic period.

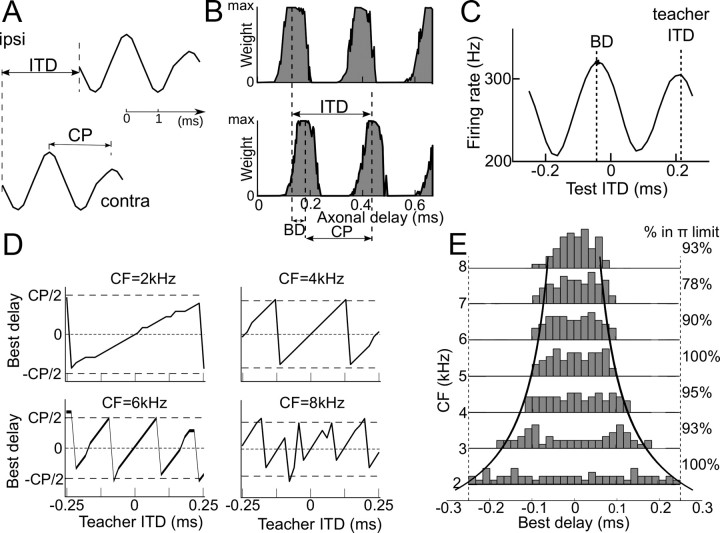
To test this principle, we simulated the development of ITD selectivity in models of binaural neurons stimulated by binaural sounds. Initially, the neuron receives synaptic inputs from monaural neurons on both sides, with monaural delays varying between 0 and 667 μs [several times larger than the maximal ITD experienced by a barn owl (Moiseff, 1989); as in Gerstner et al., 1996; Kempter et al., 2001; Leibold et al., 2001; Leibold and van Hemmen, 2005; using a larger range (0–1250 μs) did not affect the results], and the synaptic weights evolve according to STDP. We first tested the development of ITD selectivity when the binaural neuron is stimulated by a binaurally delayed white noise, band-passed filtered around its CF (Fig. 2A). The ITD is held constant during the entire development period. Monaural sounds are first transformed into spike trains by a set of NM neurons with the same CF, which are modeled as noisy integrate-and-fire neurons (typical responses shown in Fig. 1B). These neurons project to a binaural NL neuron with various transmission delays. After a long simulation time, the firing rate of the NL neuron stabilizes, and the synaptic weights converge (Fig. 2B). The resulting weights are then periodic with respect to axonal delay, the period being the characteristic period. The response of the NL neuron to delayed noises is then modulated by ITD, with peaks at the “teacher” ITD (that of the stimulus during the development period) and at ITDs shifted by multiples of the characteristic period, but the highest peak is at the smallest such ITD (Fig. 2C). We repeated the same numerical experiment with teacher ITDs varying in the natural range experienced by owls (±250 μs) and for various CFs between 2 and 8 kHz, which cover the behaviorally relevant frequency range for sound localization in owls, with all other model parameters unchanged. Figure 2D shows the BD after development for four different CFs, as a function of teacher ITD: for small ITDs, the BD essentially follows the teacher ITD, but when the π-limit is exceeded, a discontinuity occurs so that the BD remains approximately within the π-limit. As a result, in most cases, the resulting BD is in the π-limit, even though for high frequencies most presented ITDs exceed it (Fig. 2E). ITDs may be larger in low frequencies, because of the interaural canal (Calford and Piddington, 1988) and possibly because of reflections in complex acoustical environments. Therefore, we checked that the BD in low frequencies remained approximately within the π-limit when the ITD range was doubled (Fig. 3).

Figure 2.

Figure 2.

Open in a new tab

Development of best delays with fixed ITDs. A, The model is presented with binaurally delayed white noise, bandpass filtered at the CF, with a fixed “teacher” ITD. Here, the ITD is larger than the CP. B, Synaptic weights are modified by activity through STDP (Fig. 1C). At the end of the development period, synaptic weights are periodic with respect to their axonal delay so that contralateral and ipsilateral weights differ by a delay shift that is smaller than the characteristic period. C, As a result, the ITD curve of the neuron, measured with delayed white noise, peaks at the smallest value that has the same phase as the teacher ITD, i.e., within the π-limit. D, Best delay after development versus teacher ITD for CF = 2, 4, 6, and 8 kHz. The BD remains within the π-limit. E, Histograms of BDs for all tested CFs (2–8 kHz), where teacher ITD was varied within the physiological range (−250 to 250 μs). The two curves represent the π-limit.

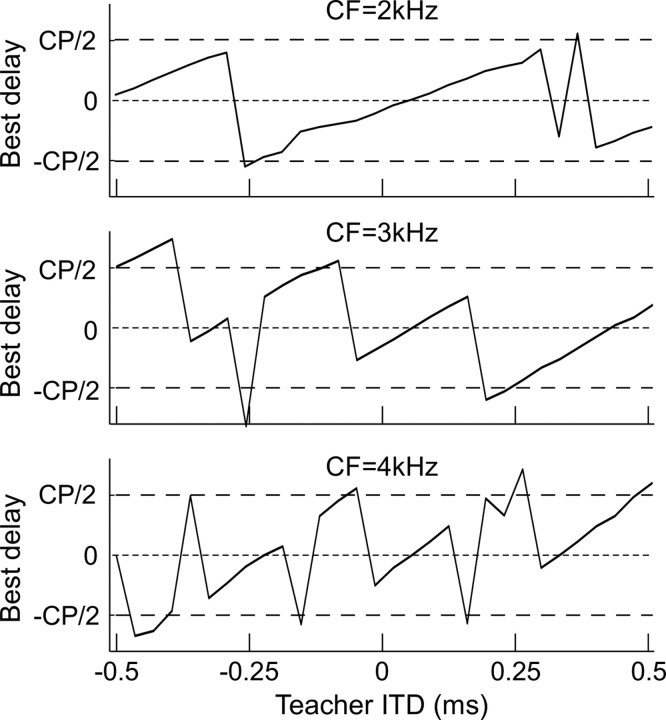
Figure 3.

Figure 3.

Open in a new tab

Best delay after development versus teacher ITD for CF = 2, 3, and 4 kHz, for a larger range of ITDs (−500 to 500 μs).

This first scenario corresponds to the situation when the bird hears a single sound source in a nonreverberant environment. Although it provides useful insight about the development of the π-limit, this is probably not a very realistic representation of the natural acoustical environment of a barn owl. A more realistic scenario would include multiple sound sources with echoes, reverberation, and noise (e.g., wind, moving leaves, vocalizations, etc.). However, our explanation does not rely on exposure to spatialized sounds but on the frequency content of auditory nerve inputs to the monaural NM neurons. We simulated the exact same model but with uncorrelated white noise at both ears, instead of delayed noise (Fig. 4). This type of acoustic stimulation is presumably closer to complex reverberant environments than binaurally delayed sounds. The inputs to the monaural neurons on both sides are uncorrelated, but they still oscillate around the CF (Fig. 4A). As a result, the synaptic weights after development are periodic with respect to axonal delay (Fig. 4B), as in the case of delayed binaural noise (Fig. 2), the only notable difference being that the phase is random. Thus, the binaural NL neuron is ITD-selective, with a random BD approximately within the π-limit (Fig. 4C).

Figure 4.

Figure 4.

Open in a new tab

Development of best delays with uncorrelated binaural noise. A, The model is presented with uncorrelated binaural noise, bandpass filtered at the CF. B, Because of correlations between monaural inputs from the same side, stabilized synaptic weights are a periodic function of axonal delay, as in Figure 2. C, As a result, the best delay lies within the π-limit.

We then simulated the development of ITD selectivity in a population of neurons with various CFs between 2 and 8 kHz, stimulated by uncorrelated broadband noise (Fig. 5A). It appears that the resulting BDs are approximately uniformly distributed within the π-limit. In this scenario, the range of BDs is unrelated to the natural range of ITDs of single sources. Instead, it is determined by the frequency selectivity of monaural neurons. Although this might seem surprising if the neurons are to represent the ITDs of natural sounds, it has the advantage that it provides a complete representation of all possible interaural phases at all frequencies, even if the size of the head changes after the development period. Finally, we repeated the same simulation of the neural population but using stereo recordings of a forest instead of uncorrelated noise. The results in terms of ITD selectivity are very similar, with almost all BDs within the π-limit (Fig. 5B), the main difference being that the stabilization of synaptic weights takes more time. In both scenarios, we note that the π-limit constraint is only approximately satisfied: 10–15% of all BDs lie beyond this limit. This is consistent with experimental observations in birds, where BDs can also exceed this limit (e.g., 15% in Fig. 1A), especially in high frequency.

Discussion

In the classical description of ITD processing in birds, essentially based on the Jeffress model, ITD selectivity comes from the convergence of monaural inputs with different axonal delays onto binaural neurons. This seems at odds with the observation that binaural best delays are smaller than the characteristic period, because it seems unlikely that axonal delays can be so precisely related with characteristic frequency. We propose that this is not initially the case but that it arises through activity-dependent synapse selection, because of the frequency content of monaural inputs to binaural neurons. Our explanation relies on a minimal number of assumptions. First, we assume that binaural neurons receive monaural inputs with the same frequency selectivity. In the barn owl, reverse correlation studies have shown that this is a reasonable assumption (Peña et al., 2001; Fischer and Peña, 2009; Singheiser et al., 2010). Second, we hypothesized that ITD selectivity arises from activity-dependent synaptic plasticity. Although this is more speculative because it has not been directly observed in the NL yet, such plasticity mechanisms have been observed to underlie the development of sensory receptive fields in many areas of the nervous system (Meliza and Dan, 2006; Mu and Poo, 2006; Keuroghlian and Knudsen, 2007; Richards et al., 2010). In barn owls raised with a monaural occlusion (which changes both the timing and level of sounds), the ITD tuning of neurons of the optic tectum is shifted, consistently with changes in acoustical cues (Mogdans and Knudsen, 1992). Since this adaptation is frequency-specific, it must occur at an early stage in the auditory pathway: it has indeed been identified in the lateral shell and external nucleus of the inferior colliculus (Gold and Knudsen, 1999, 2000). Previous modeling studies have also shown that STDP is a viable mechanism for the development of ITD selectivity (Gerstner et al., 1996; Kempter et al., 2001; Leibold et al., 2001; Leibold and van Hemmen, 2005). Thus, these two assumptions are plausible and are sufficient to account for the frequency dependence of BDs. In addition, while previous studies showed that ITD selectivity could develop with binaurally delayed noise, we have shown that this is not a requirement for either ITD selectivity or the emergence of the π-limit, since we obtained similar results with uncorrelated binaural noise. This is an important point because the natural acoustical environment of a bird includes multiple sources, reverberation and noise, which is very different from a single source with no reverberation.

Alternative hypotheses have been proposed to explain the frequency dependence of BDs. A frequency selectivity mismatch between the ipsilateral and contralateral sides could in principle result in frequency-dependent BDs (Joris et al., 2006). However, at least in the barn owl, this does not seem to be the case (Peña et al., 2001; Fischer and Peña, 2009; Singheiser et al., 2010). Another possibility is that delays are not axonal but due to intrinsic voltage-dependent ionic channels in the dendrites, for example, K+ channels. Indeed, tonotopic variations in intrinsic neuronal properties have been observed [e.g., shorter time constants for higher frequencies in the chicken (Fukui and Ohmori, 2004; Kuba et al., 2005)]. However, these delays would still need to be adjusted in a frequency-dependent way (e.g., with CF-dependent channel density). While this does not seem impossible, it poses the same fine-tuning problem as with axonal delays. Therefore, it seems likely that the frequency dependence of BDs must be accounted for by an activity-dependent plasticity mechanism, whether it affects synapses or intrinsic channels.

Although we have focused on ITD processing in birds, BDs are also CF-dependent in mammals (McAlpine et al., 2001; Thompson et al., 2006; Joris and Yin, 2007). In principle, our proposition could apply equally well to mammals, but some aspects of the distribution of BDs are not predicted by Hebbian learning alone. Specifically, BDs near 0 μs are rare in small mammals (gerbils and guinea pigs), while corresponding ITDs are present in natural acoustical environments. As this is not seen in birds with similar head size and preferred frequencies (Köppl and Carr, 2008), a different or additional mechanism must explain this aspect of delay distributions in mammals. It has been proposed that the source of internal delays in mammals is fast contralateral inhibition rather than axonal delay (Grothe, 2003) (this inhibitory mechanism is not present in birds). However, it does not explain by itself the frequency dependence of BDs, because inhibitory strength would still need to be fine-tuned as a function of CF.

In conclusion, our results suggest that the frequency dependence of BDs may simply be a by-product of the way ITD tuning develops in binaural neurons. It does not impair the ability of these neurons to represent the azimuth of sound sources, because BDs that differ by an integer number of characteristic periods are mostly redundant. Perhaps more interestingly, it also provides a complete representation of ITDs which is functional in any acoustical environment, even if the head of the animal continues to grow after the critical development period. This suggests that the distribution of BDs does not simply mirror the statistics of binaural sounds during development but instead provides a robust representation of changing environments.

Notes

Supplemental material for this article is available at http://audition.ens.fr/brette/papers/pilimit.html. Supplementary movies. This material has not been peer reviewed.

Footnotes

This work was supported by the European Research Council (ERC StG 240132). We thank Hermann Wagner for providing physiological measurements of best delays in the barn owl.

References

  1. Bi G, Poo M. Synaptic modification by correlated activity: Hebb's postulate revisited. Annu Rev Neurosci. 2001;24:139–166. doi: 10.1146/annurev.neuro.24.1.139. [DOI] [PubMed] [Google Scholar]
  2. Bi GQ, Poo MM. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell Type. J Neurosci. 1998;18:10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Calford MB, Piddington RW. Avian interaural canal enhances interaural delay. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1988;162:503–510. [Google Scholar]
  4. Caporale N, Dan Y. Spike timing-dependent plasticity: a Hebbian learning rule. Annu Rev Neurosci. 2008;31:25–46. doi: 10.1146/annurev.neuro.31.060407.125639. [DOI] [PubMed] [Google Scholar]
  5. Carr CE, Konishi M. A circuit for detection of interaural time differences in the brain stem of the barn owl. J Neurosci. 1990;10:3227–3246. doi: 10.1523/JNEUROSCI.10-10-03227.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Carr CE, Soares D, Smolders J, Simon JZ. Detection of interaural time differences in the alligator. J Neurosci. 2009;29:7978–7990. doi: 10.1523/JNEUROSCI.6154-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Fischer BJ, Peña JL. Bilateral matching of frequency tuning in neural cross-correlators of the owl. Biol Cybern. 2009;100:521–531. doi: 10.1007/s00422-009-0312-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Fukui I, Ohmori H. Tonotopic gradients of membrane and synaptic properties for neurons of the chicken nucleus magnocellularis. J Neurosci. 2004;24:7514–7523. doi: 10.1523/JNEUROSCI.0566-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Gerstner W, Kempter R, van Hemmen JL, Wagner H. A neuronal learning rule for sub-millisecond temporal coding. Nature. 1996;383:76–81. doi: 10.1038/383076a0. [DOI] [PubMed] [Google Scholar]
  10. Gold JI, Knudsen EI. Hearing impairment induces frequency-specific adjustments in auditory spatial tuning in the optic tectum of young owls. J Neurophysiol. 1999;82:2197–2209. doi: 10.1152/jn.1999.82.5.2197. [DOI] [PubMed] [Google Scholar]
  11. Gold JI, Knudsen EI. A site of auditory experience-dependent plasticity in the neural representation of auditory space in the barn owl's inferior colliculus. J Neurosci. 2000;20:3469–3486. doi: 10.1523/JNEUROSCI.20-09-03469.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Goodman DF, Brette R. The brian simulator. Front Neurosci. 2009;3:192–197. doi: 10.3389/neuro.01.026.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Goodman DF, Brette R. Spike-timing-based computation in sound localization. PLoS Compute Biol. 2010;6:e1000850. doi: 10.1371/journal.pcbi.1000993. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Grothe B. New roles for synaptic inhibition in sound localization. Nat Rev Neurosci. 2003;4:540–550. doi: 10.1038/nrn1136. [DOI] [PubMed] [Google Scholar]
  15. Jeffress LA. A place theory of sound localization. J Comp Physiol Psychol. 1948;41:35–39. doi: 10.1037/h0061495. [DOI] [PubMed] [Google Scholar]
  16. Joris P, Yin TC. A matter of time: internal delays in binaural processing. Trends Neurosci. 2007;30:70–78. doi: 10.1016/j.tins.2006.12.004. [DOI] [PubMed] [Google Scholar]
  17. Joris PX, Van de Sande B, Louage DH, van der Heijden M. Binaural and cochlear disparities. Proc Natl Acad Sci U S A. 2006;103:12917–12922. doi: 10.1073/pnas.0601396103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kempter R, Gerstner W, van Hemmen JL. Hebbian learning and spiking neurons. Phys Rev E. 1999;59:4498–4514. [Google Scholar]
  19. Kempter R, Leibold C, Wagner H, van Hemmen JL. Formation of temporal-feature maps by axonal propagation of synaptic learning. Proc Natl Acad Sci U S A. 2001;98:4166–4171. doi: 10.1073/pnas.061369698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Keuroghlian AS, Knudsen EI. Adaptive auditory plasticity in developing and adult animals. Prog Neurobiol. 2007;82:109–121. doi: 10.1016/j.pneurobio.2007.03.005. [DOI] [PubMed] [Google Scholar]
  21. Konishi M. Coding of auditory space. Annu Rev Neurosci. 2003;26:31–55. doi: 10.1146/annurev.neuro.26.041002.131123. [DOI] [PubMed] [Google Scholar]
  22. Köppl C, Carr CE. Maps of interaural time difference in the chicken's brainstem nucleus laminaris. Biol Cybern. 2008;98:541–559. doi: 10.1007/s00422-008-0220-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kuba H, Yamada R, Fukui I, Ohmori H. Tonotopic specialization of auditory coincidence detection in nucleus laminaris of the chick. J Neurosci. 2005;25:1924–1934. doi: 10.1523/JNEUROSCI.4428-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Leibold C, van Hemmen JL. Spiking neurons learning phase delays: how mammals may develop auditory time-difference sensitivity. Phys Rev Lett. 2005;94:168102. doi: 10.1103/PhysRevLett.94.168102. [DOI] [PubMed] [Google Scholar]
  25. Leibold C, Kempter R, van Hemmen JL. Temporal map formation in the barn owl's brain. Phys Rev Lett. 2001;87:248101. doi: 10.1103/PhysRevLett.87.248101. [DOI] [PubMed] [Google Scholar]
  26. Markram H, Lübke J, Frotscher M, Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science. 1997;275:213–215. doi: 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
  27. McAlpine D, Jiang D, Palmer AR. A neural code for low-frequency sound localization in mammals. Nat Neurosci. 2001;4:396–401. doi: 10.1038/86049. [DOI] [PubMed] [Google Scholar]
  28. Meliza CD, Dan Y. Receptive-field modification in rat visual cortex induced by paired visual stimulation and single-cell spiking. Neuron. 2006;49:183–189. doi: 10.1016/j.neuron.2005.12.009. [DOI] [PubMed] [Google Scholar]
  29. Mogdans J, Knudsen EI. Adaptive adjustment of unit tuning to sound localization cues in response to monaural occlusion in developing owl optic tectum. J Neurosci. 1992;12:3473–3484. doi: 10.1523/JNEUROSCI.12-09-03473.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Moiseff A. Binaural disparity cues available to the barn owl for sound localization. J Comp Physiol A. 1989;164:629–636. doi: 10.1007/BF00614505. [DOI] [PubMed] [Google Scholar]
  31. Mu Y, Poo MM. Spike timing-dependent LTP/LTD mediates visual experience-dependent plasticity in a developing retinotectal system. Neuron. 2006;50:115–125. doi: 10.1016/j.neuron.2006.03.009. [DOI] [PubMed] [Google Scholar]
  32. Patterson RD. The sound of a sinusoid: spectral models. J Acoust Soc Am. 1994;96:1409–1418. [Google Scholar]
  33. Peña JL, Viete S, Funabiki K, Saberi K, Konishi M. Cochlear and neural delays for coincidence detection in owls. J Neurosci. 2001;21:9455–9459. doi: 10.1523/JNEUROSCI.21-23-09455.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Richards BA, Voss OP, Akerman CJ. GABAergic circuits control stimulus-instructed receptive field development in the optic tectum. Nat Neurosci. 2010;13:1098–1106. doi: 10.1038/nn.2612. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Shamma SA, Shen NM, Gopalaswamy P. Stereausis: binaural processing without neural delays. J Acoust Soc Am. 1989;86:989–1006. doi: 10.1121/1.398734. [DOI] [PubMed] [Google Scholar]
  36. Singheiser M, Fischer BJ, Wagner H. Estimated cochlear delays in low best-frequency neurons in the barn owl cannot explain coding of interaural time difference. J Neurophysiol: 2010;104:1946–1954. doi: 10.1152/jn.00501.2010. [DOI] [PubMed] [Google Scholar]
  37. Song S, Miller KD, Abbott LF. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat Neurosci. 2000;3:919–926. doi: 10.1038/78829. [DOI] [PubMed] [Google Scholar]
  38. Thompson SK, von Kriegstein K, Deane-Pratt A, Marquardt T, Deichmann R, Griffiths TD, McAlpine D. Representation of interaural time delay in the human auditory midbrain. Nat Neurosci. 2006;9:1096–1098. doi: 10.1038/nn1755. [DOI] [PubMed] [Google Scholar]
  39. Trussell LO. Cellular mechanisms for preservation of timing in central auditory pathways. Curr Opin Neurobiol. 1997;7:487–492. doi: 10.1016/s0959-4388(97)80027-x. [DOI] [PubMed] [Google Scholar]
  40. Trussell LO. Synaptic mechanisms for coding timing in auditory neurons. Annu Rev Physiol. 1999;61:477–496. doi: 10.1146/annurev.physiol.61.1.477. [DOI] [PubMed] [Google Scholar]
  41. Tzounopoulos T, Kim Y, Oertel D, Trussell LO. Cell-specific, spike timing-dependent plasticities in the dorsal cochlear nucleus. Nat Neurosci. 2004;7:719–725. doi: 10.1038/nn1272. [DOI] [PubMed] [Google Scholar]
  42. van Rossum MC, Bi GQ, Turrigiano GG. Stable Hebbian learning from spike timing-dependent plasticity. J Neurosci. 2000;20:8812–8821. doi: 10.1523/JNEUROSCI.20-23-08812.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. von Campenhausen M, Wagner H. Influence of the facial ruff on the sound-receiving characteristics of the barn owl's ears. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2006;192:1073–1082. doi: 10.1007/s00359-006-0139-0. [DOI] [PubMed] [Google Scholar]
  44. Wagner H, Asadollahi A, Bremen P, Endler F, Vonderschen K, von Campenhausen M. Distribution of interaural time difference in the barn owl's inferior colliculus in the low- and high-frequency ranges. J Neurosci. 2007;27:4191–4200. doi: 10.1523/JNEUROSCI.5250-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Yin TCT. Neural mechanisms of encoding binaural localization cues in the auditory brainstem. In: Fay RR, Popper AN, editors. Integrative functions in the mammalian auditory pathway. New York: Springer; 2002. pp. 99–159. [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES