Resurgence as Choice: Implications for Promoting Durable Behavior Change

Abstract

Resurgence is an increase in a previously suppressed behavior resulting from a worsening in reinforcement conditions for current behavior. Resurgence is often observed following successful treatment of problem behavior with differential reinforcement when reinforcement for an alternative behavior is subsequently omitted or reduced. The efficacy of differential reinforcement has long been conceptualized in terms of quantitative models of choice between concurrent operants (i.e., the matching law). Here, we provide an overview of a novel quantitative model of resurgence called Resurgence as Choice (RaC), which suggests that resurgence results from these same basic choice processes. We review the failures of the only other quantitative model of resurgence (i.e., Behavioral Momentum Theory) and discuss its shortcomings with respect to the limited range of circumstances about which it makes predictions in applied settings. Finally, we describe how RaC overcomes these shortcomings and discuss implications of the model for promoting durable behavior change.

The notion that effective behavior change can be transient is neither novel nor particularly surprising. In fact, early pioneers in applied behavior analysis clearly recognized this transience. Baer, Wolf, and Risley (1968) noted, “A behavioral change may be said to have generality if it proves durable over time, if it appears in a wide variety of possible environments, or if it spreads to a wide variety of related behaviors” (p. 96). Baer et al. went on to say that generality is not an automatic feature of behavior change and that generality “should be examined explicitly” (p. 96).

Recently, researchers have begun to distinguish between behavior that has generality over time (i.e., maintenance) and behavior that maintains in the face of environmental challenge (Nevin & Wacker, 2013; Wacker et al., 2011). An example of the importance of this distinction can be seen in the results of a study by Wacker et al. (2011). Wacker et al. showed that problem behavior for seven of eight participants remained low or decreased across successive applications of functional communication training (FCT), which spanned an average of 14 months (range, 9 to 17 months per participant). These persistent treatment effects exemplify the generality of effective behavior change over time (i.e., maintenance). However, when therapists temporarily discontinued FCT during periodic extinction challenges throughout this same period, problem behavior for five of the eight participants recurred. Such findings highlight the inadequacy of examining maintenance of effective behavior change in the traditional sense (i.e., over time but under training conditions) and suggest that applied behavior analysts must evaluate the durability of effective behavior change when treatment is challenged. That is, treatments must be effective enough that their effects persist in the absence of treatment implementation. This is indeed a radical departure from traditional wisdom.

Resurgence Following Differential Reinforcement

Given the importance of developing treatments that are durable, recent translational research on the durability of common interventions for problem behavior has generated some troubling findings. Despite their widespread use (Petscher, Rey, & Bailey, 2009; Tiger, Hanley, & Bruzek, 2008) and robust efficacy while in effect (Greer, Fisher, Saini, Owen, & Jones, 2016; Hagopian, Fisher, Sullivan, Acquisto, & LeBlanc, 1998; Kurtz, Boelter, Jarmolowicz, Chin, & Hagopian, 2011; Petscher et al., 2009; Rooker, Jessel, Kurtz, & Hagopian, 2013), differential-reinforcement-based interventions for socially reinforced problem behavior are prone to relapse when differential reinforcement is suspended (Fisher et al., 2019; Fisher, Greer, Fuhrman, Saini, & Simmons, 2018; Fuhrman, Fisher, & Greer, 2016; Harding, Wacker, Berg, Lee, & Dolezal, 2009; Lichtblau, Greer, & Fisher, under review; Mace et al., 2010; Nevin et al., 2016; Volkert, Lerman, Call, & Trosclair-Lasserre, 2009; Wacker et al., 2011). These increases in problem behavior with the suspension of differential reinforcement are examples of resurgence. Resurgence has typically been defined as an increase in previously extinguished target behavior when a more recently reinforced alternative behavior is also subsequently extinguished (e.g., Cleland, Guerin, Foster, & Temple, 2001; Epstein, 1985).

Recent research by Briggs, Fisher, Greer, and Kimball (2018) examined the prevalence of resurgence of problem behavior when thinning reinforcement schedules during functional communication training (a common differential-reinforcement-based intervention) and found that resurgence occurred in 76% (or 19 of 25) schedule-thinning applications. These results are noteworthy because they show that differential reinforcement need not be suspended completely for problem behavior to resurge (e.g., Volkert et al., 2009). Indeed, the fact that resurgence occurs under conditions that do not involve a complete suspension of alternative reinforcement (e.g., during differential reinforcement thinning) has led to calls to return to a broader definition of the phenomenon (i.e., Epstein, 1985) in terms of a worsening of reinforcement conditions (e.g., Lattal et al., 2017; Lattal & Wacker, 2015; see also Shahan & Craig, 2017). Within the context of such a definition, a previously eliminated target behavior might be expected to show resurgence anytime the reinforcement conditions for a current alternative behavior worsen.

The most common way to study resurgence experimentally is with a progression of three phases (see Lattal & St. Peter Pipkin, 2009, for an overview). In Phase 1, a target (e.g., problem) behavior produces reinforcement on some schedule. Phase 2 consists of reinforcing an alternative, incompatible, or undefined “other” (i.e., differential reinforcement of other behavior) behavior, while reinforcement is suspended for the target behavior. Phase 3 begins once rates of the target behavior have decreased considerably from baseline and typically, but not always, consists of discontinuing all reinforcer deliveries (i.e., extinction). The worsening in reinforcement conditions that occurs upon transitioning from Phase 2 to Phase 3 often produces the recurrence of target responding (i.e., resurgence).

Given the high likelihood that caregivers often do not implement interventions consistently or as designed (e.g., Mitteer, Greer, Fisher, Briggs, & Wacker, 2018), resurgence is a serious concern in applied settings. In such settings, the transition from Phase 1 to Phase 2 parallels the transition from baseline, in which problem behavior produces the reinforcer responsible for its occurrence (as demonstrated via functional analysis; Iwata, Dorsey, Slifer, Bauman, & Richman, 1982/1994), to treatment, in which the same reinforcer often becomes available for another response. In turn, the transition from Phase 2 to Phase 3 parallels the transition from treatment, which has now had sufficient time to both suppress problem behavior and to establish the alternative response, to a condition that is likely to challenge those treatment effects. Complete suspension of reinforcement in Phase 3 is common when evaluating resurgence of problem behavior (e.g., Briggs et al., 2018; Fisher, Greer, Fuhrman, et al., 2018; Fisher et al., 2019; Fuhrman et al., 2016; Harding et al., 2009; Lichtblau et al., under review; Mace et al., 2010; Nevin et al., 2016; Volkert et al., 2009; Wacker et al., 2011); however, as noted above, resurgence can occur even when reinforcement is not completely suspended in Phase 3 (e.g., Briggs et al., 2018; Volkert et al., 2009). In practice, natural downshifts in the reinforcement schedule maintaining an alternative to problem behavior are likely to coincide with times in which caregivers are preoccupied or otherwise unable to deliver the reinforcer (e.g., when busy changing an infant sibling). Furthermore, when resurgence does occur with such changes in reinforcement, there is an increased risk of the caregiver mistakenly reinforcing problem behavior, which may cause rapid reacquisition (e.g., Bouton, 2014) or response-dependent reinstatement (e.g., Podlesnik & Shahan, 2009) of problem behavior. Applied and translational research has generally shown such errors of commission to be more detrimental to treatment efficacy than simple errors of omission (i.e., not reinforcing the alternative response; Leon, Wilder, Majdalany, Myers, & Saini, 2014; St. Peter Pipkin, Vollmer, & Sloman, 2010) Thus, resurgence appears to pose a serious threat to the durability of effective behavior change in applied settings.

Fortunately, basic scientists have long been interested in the phenomenon of resurgence (e.g., Carey, 1951; 1953; Epstein, 1983; 1985; Leitenberg, Rawson, & Bath, 1970; Leitenberg, Rawson, & Mulick, 1975; Rawson, Leitenberg, Mulick, & Lefebvre, 1977). This extensive history of research on resurgence with nonhuman animals has generated a wealth of data on variables affecting the likelihood and magnitude of resurgence (see Doughty & Oken, 2008; Lattal & St. Peter Pipkin, 2009; Shahan & Craig, 2017; St. Peter, 2015, for reviews). Furthermore, there have been recent attempts to develop comprehensive quantitative models of resurgence (Shahan & Craig, 2017; Shahan & Sweeney, 2011). The overall goal of this paper is to explore the implications of the most recent and promising quantitative model of resurgence (i.e., Resurgence as Choice; RaC) for promoting durable behavior change in applied settings. To do so, we first provide an overview of the utility of quantitative models for applied behavior analysts and then describe the shortcomings of the only other quantitative model of resurgence (Behavioral Momentum Theory; BMT).

Quantitative Models and Their Utility

An applied behavior analyst might reasonably ask what they stand to gain from the effort required to understand a quantitative model of resurgence. A comprehensive tutorial and discussion of what quantitative models have to offer in general for translational and applied behavior analysts can be found in Critchfield and Reed (2009). In addition, McDowell (1988) provides a particularly relevant discussion of how a quantitative model of choice might provide important insights for applied behavior analysts. Quantitative models are useful in science and application because they provide a means to succinctly summarize large amounts of data and to formalize current understanding of the processes thought to be involved in some phenomenon. The overall goal of such a model is to describe and summarize the functional relations between environment and behavior. Thus, the equations (i.e., functions) describe how exposure to a broad range of environmental conditions impacts behavior. In addition to summarizing, the equations can convey relations that are difficult to describe in words. Once the insights provided by an equation are understood, it can open up new and more fertile ways of thinking about a phenomenon. It is here that spending some time to understand a quantitative model can pay dividends for an applied behavior analyst. An understanding of the theory can lead you to see the situation in a different light, and thus, the actions you take or the interventions you consider might be entirely different—even if you never fit an equation to your data. The insights provided by a quantitative theory hold the promise of inspiring innovative and durable behavioral interventions. Theories are like lenses through which we view the world, and they guide us to what the theory identifies as the relevant processes. This is true of implicit and/or narrative theories as well as explicit quantitative theories, although we often do not recognize how implicit theories are guiding our interpretation of the phenomenon. With a formal theory, the assumptions and relevant processes are explicitly and precisely formalized so that they are easily recognized and can be evaluated for their accuracy and utility.

Resurgence of a target behavior after extinction is an interesting example of how our informal ways of thinking about behavior can lead us astray. Resurgence can be a perplexing phenomenon to many behavior analysts when they first encounter it. Looking at the phenomenon from a traditional behavior-analytic perspective, it seems strange that a behavior that has been extinguished might suddenly reappear. The reason is that if extinction eliminates the strength of the target behavior, how is it that in the absence of any further reinforcement for the target behavior, it can suddenly display a large increase in response strength? Thinking about the target behavior in terms of increases and decreases in response strength is an implicit narrative theory of behavior (see Shahan, 2017, for discussion). In introducing many behavior analysts to resurgence for the first time, we have noticed that this implicit way of thinking about behavior leads them to suggest an account of resurgence that seems to escape this apparent difficulty. The account goes like this: perhaps resurgence occurs because the availability of reinforcement for an alternative behavior during extinction of a target behavior leads that behavior to compete with and prevent the target behavior from occurring, and therefore, from undergoing extinction. Thus, when the reinforcer for the alternative behavior is removed, so too is a source of competition for the target behavior, and the target behavior increases because its strength was never extinguished in the first place. This potential account of resurgence has a long history and is known in the literature as the response-prevention hypothesis (e.g., Leitenberg et al., 1970; Rawson et al., 1977). Although this sounds reasonable enough, it turns out to be wrong. There are many sources of contradictory evidence (see Shahan & Sweeney, 2011, for a review), but the most important is that even if the target behavior is thoroughly extinguished prior to the introduction of reinforcement for the alternative behavior, resurgence still occurs when the alternative reinforcer is subsequently removed (e.g., Cleland, Foster, & Temple, 2000; Epstein, 1983; Lieving & Lattal, 2003). If this account of resurgence is wrong, what should a behavior analyst see when they encounter a situation in which resurgence is occurring? It might seem mysterious that an extinguished response can reappear without any change in the reinforcement conditions for that response, but it only seems that way because of an implicit theory of extinction as a process of eliminating response strength or reversing prior learning. Other ways of thinking about the phenomenon provided by an alternative theory might encourage a more effective approach to understanding resurgence and lead to better interventions that prevent it.

The ways of thinking about phenomena provided by quantitative models are explicit and formalized theories. As opposed to implicit, qualitative, or narrative theories, quantitative theories are more constrained by the formal structure of the equations and the processes that those equations represent. Thus, quantitative models serve to hold a scientist’s feet to the fire with respect to the processes hypothesized to be at work (Mazur, 2006). Most importantly, a quantitative model can serve to rule out particular ways of thinking about a phenomenon based on existing and incoming data. This ability to rule out explanations requires the scientist to sometimes accept that their current understanding is flawed and that they must correct the equations of the theory or consider entirely new interpretations of the phenomenon (below, we will consider the behavioral momentum-based theory of resurgence as an example of this process). Because of a lack of formal structure, qualitative, narrative, and implicit theories simply allow too much flexibility in terms of explaining data. Thus, it can be difficult or sometimes impossible to generate data that disagree with the theory, and thus, it is difficult for the scientist to learn how their thinking about the phenomenon might be flawed.

As an example of the shortcomings of a narrative theory, briefly consider the Context Theory of resurgence (e.g., Bouton, Winterbauer, & Todd, 2012; Trask, Schepers, & Bouton, 2015). As described by Bouton and Todd (2014), this theory asserts that resurgence results from a change in context from where the target behavior was extinguished. The extinction context for the target behavior is said to be provided by the stimulus effects of reinforcement of the alternative behavior in Phase 2 of a typical resurgence experiment. The account suggests that extinction is not the elimination of old learning, but instead it is the result of new inhibitory learning (i.e., an inhibitory association between the target behavior and reinforcement). Further, this inhibitory association is highly specific to the stimulus context in which it is learned, and thus, when there is a change in context, that learning does not generalize, and thus, target behavior recurs. Specifically, in a resurgence procedure when the alternative behavior is extinguished in Phase 3, the absence of the alternative reinforcer now serves as a new context, the inhibitory association for the target behavior learned in Phase 2 does not generalize, and the target behavior increases. Detailed concerns with this theory can be found in Craig and Shahan (2016) and Shahan and Craig (2017). In short, the difficulty is that the lack of formal specification of the processes involved leads to so much explanatory flexibility that it is nearly impossible to imagine data that could contradict the theory. For example, the concept of a “context” is so broad that it can and has included explicit stimuli, reinforcer deliveries, the absence of reinforcer deliveries, rates of reinforcement, internal states, the passage of time, etc. (see Bouton, 2010; Urcelay & Miller, 2014, for additional examples). Further, anytime resurgence is observed, one would infer that there was a change in context, and anytime resurgence is expected but does not occur, then one could infer that the change in context was not sufficiently discriminable. Thus, there is no obvious way to provide a contradictory outcome and no way to learn that this way of thinking about resurgence might be wrong. So, how does one ever gain novel insights about the underlying processes at work if the current account cannot reasonably be challenged?

The point above about Context Theory is not that it is wrong. All theories are wrong, some just perform better than others and are more useful in encouraging progress in our understanding. A good theory summarizes as much as possible, as parsimoniously as possible, as precisely as possible, and does so in a way that is amenable to disconfirming evidence. Clearly, as suggested by Context Theory, organisms can discriminate a wide variety of events including reinforcer deliveries or their rates of occurrence, and clearly such processes could be involved in resurgence. Nevertheless, the point is that the nature of a narrative theory and its associated lack of precision, coupled with its excessive flexibility, allows one to wield these hypothesized processes in such a way that it can be nearly impossible to disconfirm them. Alternatively, as an example of how a quantitative theory can be useful for a while, inform clinical practice, but ultimately be shown to be flawed and then inspire a search for novel ways of thinking, consider the behavioral momentum-based theory of resurgence (Shahan & Sweeney, 2011).

Behavioral Momentum Theory of Resurgence

BMT is a quantitative model of behavior that invokes the metaphor of the momentum of moving objects to help explain the behavior of organisms. Just as added mass increases the momentum of a moving object, BMT suggests that reinforcers delivered in a given stimulus context will strengthen responding in that context, increasing its persistence if later disrupted (see Nevin & Grace, 2000; Nevin, Mandell, & Atak, 1983, for reviews). BMT also has been extended to provide a quantitative theoretical account of resurgence (Shahan & Sweeney, 2011). Indeed, when it comes to the resurgence of operant behavior, no model has received more attention from translational and applied researchers than BMT (for reviews of BMT in application and its extension to resurgence, see Dube, Ahearn, Lionello-DeNolf, & McIlvane, 2009; Greer, Fisher, Romani, & Saini, 2016; Nevin & Wacker, 2013; Pritchard, Hoerger, & Mace, 2014). Given existing reviews and tutorials describing the quantitative details of BMT and its extension to resurgence for applied behavior analysts (e.g., Greer, Fisher, Romani, & Saini, 2016; Nevin & Shahan, 2011), we will not reiterate those details here. Rather, we will simply summarize the theoretical account and the difficulties it has encountered (detailed accounts of the quantitative difficulties can be found in Craig & Shahan, 2016; Nevin et al., 2017; Shahan & Craig, 2017).

Like Context Theory, BMT also suggests that the decreases in responding resulting from extinction are not due to an elimination of previous learning (see Nevin & Shahan, 2011, for a conceptual and quantitative overview of BMT). Unlike Context Theory, BMT does not hypothesize new inhibitory learning, but rather it suggests that responding decreases because of the disruptive impact of extinction. The theory suggests that the disruptive effects of extinction grow with time and are due specifically to breaking the contingency between responses and reinforcers and to the generalization decrement associated with the removal of reinforcers from the context (Nevin, McLean, & Grace, 2001). Further, the theory suggests that the impact of the pre-extinction history of reinforcement is not reduced or eliminated by extinction, but rather it is carried forward in time unchanged as behavioral mass (Nevin & Grace, 2000). According to the equations, behavioral mass is a direct function of the reinforcement rates previously experienced in the discriminative-stimulus context (compare Equations 1 and 2 in Nevin & Shahan, 2011). Thus, contexts previously associated with higher rates of reinforcement have greater mass, and therefore, are more resistant to the disruptive effects of extinction.

The extension of this theory of extinction to resurgence (Shahan & Sweeney, 2011) suggests that resurgence is the result of removing the disruptive impact of alternative reinforcement. More specifically, reinforcers delivered for target (e.g., problem) behavior in Phase 1 enhance the behavioral mass (i.e., response strength) of the target response, which is responsible for its persistence when alternative reinforcement begins in Phase 2. Although alternative reinforcement also serves as an added source of disruption and helps to suppress target responding in Phase 2 (along with the disruptive effects of extinction), reinforcers delivered for the alternative (e.g., socially appropriate, communicative) response also contribute to the behavioral mass of the target response, increasing the likelihood of the target response resurging in the event that alternative reinforcement is later suspended or reduced. When the disruptive impact of alternative reinforcement on target responding is suspended or reduced in Phase 3, the behavioral mass of the target response is responsible for whether, and the degree to which, resurgence occurs. In fact, BMT predicts treatments based on alternative reinforcement (e.g., differential reinforcement, alternative reinforcement) that better suppress target responding by programming dense schedules of alternative reinforcement are more likely to produce resurgence than are similar, yet less-efficacious, treatments that rely on leaner schedules of alternative reinforcement (Greer, Fisher, Romani, & Saini, 2016).

At the time it was introduced, the BMT of resurgence did a good job describing existing data in the basic literature (see Shahan & Sweeney, 2011, for a review). Furthermore, the theory inspired considerable basic, translational, and applied research examining its predictions. For example, a handful of recent translational studies on the resurgence of problem behavior have used this framework to test whether resurgence of problem behavior can be mitigated by modifying treatment procedures accordingly (Fisher, Greer, Fuhrman, et al., 2018; Fisher et al., 2019; Fuhrman et al., 2016; Lichtblau et al., under review; see also Fisher, Greer, Craig, et al., 2018). The study by Fisher, Greer, Fuhrman, et al. exemplifies a translational evaluation of BMT. These researchers treated the problem behavior of four participants by arranging two conditions—one which approximated standard of care (called dense-short) and another which was informed by quantitative predictions of BMT (called lean-long). In the dense-short condition, the researchers delivered a dense schedule of reinforcement for both problem behavior in baseline and for the alternative response in treatment, and treatment with extinction was in place for a short period of time. In the lean-long condition, the researchers delivered a lean schedule of reinforcement for both problem behavior in baseline and for the alternative response in treatment, and treatment with extinction was in place for a longer period of time (i.e., three times the number of sessions as the dense-short condition). After experiencing baseline and treatment in both conditions using a multiple schedule (i.e., multielement design), an extinction challenge began in which reinforcement for the alternative response ceased, and a lean schedule of response-independent reinforcement (i.e., variable-time 200 s) began. Levels of resurgence expressed as a proportion of baseline response rate were lower for each of the four participants in the lean-long condition than in the dense-short condition, as predicted by BMT. Thus, Fisher, Greer, Fuhrman, et al. showed that BMT, and quantitative models of resurgence more generally, have the ability improve standard of care when it comes to treating problem behavior. Additional translational research by Fisher et al. (2019), Fuhrman et al. (2016), and Lichtblau et al. (under review) supported similar predictions of BMT when treating problem behavior.

Despite these and other promising findings resulting from applying BMT to the development of more durable treatments for problem behavior, some of the basic research inspired by the theory has challenged its core underlying assumptions and predictions of the equations (e.g., Craig & Shahan, 2016; Nevin et al., 2017; Sweeney & Shahan, 2013). First, the BMT equation suggests that differential reinforcement (and alternative reinforcement more broadly) in Phase 2 must always disrupt target responding. The results of two studies (Craig & Shahan, 2016; Sweeney & Shahan, 2013) clearly show that alternative reinforcement delivered at a relatively low rate in Phase 2 can produce more target responding than a condition with no alternative reinforcement available (i.e., extinction alone). These findings represent a critical failure of the BMT equation describing resurgence and a core underlying assumption of the theory—alternative reinforcement serves as an additional source of disruption of target responding in Phase 2, and it is the removal of this added disruption that causes resurgence. This assumption as formalized in the equation is clearly false.

Second, the behavioral momentum model of resurgence (Shahan & Sweeney, 2011) assumes that reinforcers delivered in Phases 1 and 2 are additive. That is, the strengthening effects of reinforcement on the target response in Phases 1 and 2 are calculated as the sum of all reinforcers delivered across phases. This assumption is rooted in the basic behavioral momentum model of extinction, which assumes that the reinforcement rate experienced in baseline is carried forward unchanged as behavioral mass across all of extinction (Nevin & Grace, 2000). But, as discussed by Craig and Shahan (2016) and by Shahan and Craig (2017), this assumption generates bizarre predictions under many circumstances when applied to resurgence. For example, transitioning from Phase 1 to Phase 2 under the same reinforcement schedule (but now arranged for the alternative response rather than the target response) would suggest a doubling of the behavioral mass of the target response, even though the overall rate of reinforcement has not changed. This problem is further compounded across conditions with changing reinforcement rates during treatment. For example, during schedule thinning, the model suggests that each of the reduced reinforcement rates experienced across thinning steps further increases the strength of target behavior, even though the ongoing rate of reinforcement for the target behavior is decreasing. In short, the model assumes that every reinforcement rate experienced in the past continues to add to response strength forever, and it has no way to accommodate the likely decreasing effects of reinforcers experienced in the more remote behavioral history. As a result of this shortcoming, the model has no way to make meaningful or accurate predictions about how schedule thinning should impact resurgence of target behavior.

Third, BMT predicts that in Phase 3, when reinforcement has ceased for both the target and the alternative response, target responding should be highest in the first session of Phase 3 and, thereafter, should decrease across all subsequent sessions. However, Podlesnik and Kelley (2015) noted that resurgence of target responding during Phase 3 often takes on more of a bitonic function, initially increasing across the first few sessions in Phase 3 before then decreasing across sessions. BMT has no way to account for this common finding.

Fourth, BMT makes no predictions about how a number of variables relevant in applied settings might be likely to impact the efficacy of differential-reinforcement-based treatments and the likelihood of resurgence. For example, the BMT-based theory of resurgence makes no predictions about how differences in response effort or reinforcement quality for target and alternative behaviors might be expected to impact resurgence.

Thus, despite the promise that BMT has shown when translational researchers have applied its predictions to inform the development of more durable treatments for problem behavior, recent basic research suggests that fundamental problems exist with the BMT account of resurgence. Nevertheless, the theory has done its job. It formalized a way of thinking about resurgence and inspired experiments to evaluate this way of thinking. It turns out that the core assumptions of the theory as formalized in its equations were not sustainable in the face of new data. In addition, the theory inspired translation and application. Although the translations of BMT into applied settings have been reasonably successful, the conditions to which it has been applied remain fairly restricted. The failures of the theory with key variables in basic research suggest that the conditions under which it can be further successfully translated are relatively limited, and more troubling, it is likely to lead to predictions in applied settings that are incorrect and possibly countertherapeutic. Finally, the range of conditions to which the theory can be applied are even more limited by the fact that the theory does not make predictions about additional variables that are likely to be critically important in applied settings. It was these seemingly insurmountable difficulties with BMT that inspired a new theory of resurgence.

Resurgence as Choice

Simply stated, RaC suggests that resurgence can be understood as a natural outcome of the same basic processes that govern choice between concurrent operants. In its most general form, RaC is merely an extension of Herrnstein’s (1961) matching law. The matching law suggests that the proportion of behavior allocated to two response options is equal to or “matches” the proportion of reinforcers obtained from those options (Herrnstein, 1961). Quantitatively, that is,

$$\frac{B_1}{B_1+B_2}=\frac{R_1}{R_1+R_2}$$ (1)

where B₁ and B₂ are response rates for two options and R₁ and R₂ are the rates of reinforcement obtained from those options. Although Equation 1 describes the allocation of behavior as varying with relative reinforcement rates, behavior might also produce reinforcers that vary on any number of other dimensions (e.g., magnitude, immediacy, quality). An extension of Equation 1 known as the concatenated matching law (Baum & Rachlin, 1969) suggests that the allocation of behavior to two options matches the relative value of the consequences obtained by those options, where value is defined as the combined effects of the relevant reinforcement dimensions, for example,

$$\frac{B_1}{B_1+B_2}=\frac{R_1{A}_1{I}_1}{R_1{A}_1{I}_1+R_2{A}_2{I}_2}=\frac{V_1}{V_1+V_2}$$ (2),

where A₁ and A₂ are the amounts, I₁ and I₂ are the immediacies, and V₁ and V₂ are the values of the two options. The concatenated matching law in one form or another has been enormously influential in behavior analysis. It has served as the conceptual foundation of behavior-analytic theories of a wide variety of phenomena including self-control/delay discounting (e.g., Mazur, 1987; Rachlin & Green, 1972) and conditioned reinforcement (e.g., Fantino, 1969; Grace, 1994; Mazur, 2001), and it has been extended to a wide variety of applied and naturalistic settings (e.g., Fisher & Mazur, 1997; McDowell, 1988; Vollmer & Bourret, 2000).

Most importantly for present purposes, differential-reinforcement-based interventions have long been conceptualized in terms of choice, concurrent operants, relative value, and the matching law (e.g., Carr, 1988; Fisher et al., 1993; Fisher & Mazur, 1997; Horner & Day, 1991; Mace & Roberts, 1993; McDowell, 1981; Piazza et al., 1997). For example, Piazza et al. (1997) showed that severe problem behavior of children was reduced when compliance was reinforced with combinations of a break, tangibles, and attention, even though problem behavior also continued to be reinforced with a break. In interpreting these results, Piazza et al. suggested that “One potential explanation of these findings is that the relative rates of compliance and problem behavior were a function of the relative value of the reinforcement produced by each response” (p. 280). This interpretation is, of course, just a restatement of the concatenated matching law (i.e., Equation 2).

Given that RaC is also a version of the concatenated matching law, it suggests that the allocation of responding to a target (e.g., problem behavior) versus an alternative behavior (e.g., compliance) is a function of the relative values of the consequences generated by those behaviors. Thus,

$$\frac{B_T}{B_T+B_{Alt}}=\frac{V_T}{V_T+V_{Alt}}$$ (3),

where B_T and B_Alt refer to rates of the target and alternative behaviors, and V_T and V_Alt refer to the relative values of the consequences of those behaviors. Because the term on the left side of the equation represents the proportion of responses occurring that are B_T, it can also be interpreted as a conditional probability and can be written as,

$$pT=\frac{V_T}{V_T+V_{Alt}}$$ (4),

where pT represents the probability that the target response occurs given that one of the responses occurs.

To understand Equation 4, consider for example the probability of compliance versus problem behavior in the Piazza et al. (1997) study. Prior to implementation of explicit reinforcement of compliance, the children likely received little reinforcement for compliance (i.e., V_Alt was low) and more reinforcement for problem behavior (i.e., V_T was high), and as a result, the probability of problem behavior (i.e., pT) was likely quite high. But, even though problem behavior continued to produce the same reinforcement (i.e., V_T remained the same), an increase in the value of compliance (i.e., V_Alt) with the onset of explicit reinforcement for compliance would be expected to decrease the probability of problem behavior (i.e., pT). Using arbitrary units for value as an example, if V_T=20 and V_Alt= 5 prior to explicit reinforcement of compliance, then pT=20/(20+5)=0.8. That is, problem behavior would be expected 80% of the time when responding occurred, and because the probability of the alternative behavior is the complement of the target behavior, compliance would be expected only 20% of the time. If when explicit reinforcement is introduced for compliance V_Alt increases to 140, then pT=20/(20+140)=0.125, and problem behavior would be expected only 12.5% of the time when responding occurred and compliance 87.5% of the time. The larger the increase in V_Alt, the larger the reduction in the probability of problem behavior. Hence, it makes perfect sense to try to increase the value of the reinforcers for alternative behavior as much as possible, and it is indeed very common to arrange immediate, high-quality reinforcers for the alternative behavior at a very high rate in order to decrease problem behavior as much as possible (e.g., Horner & Day, 1991). Alternatively, it also makes perfect sense to try to reduce the value of the reinforcers for the problem behavior (i.e., decrease V_T), which would also be expected to decrease the probability of the problem behavior with no change in V_Alt. The best way to reduce the value of the reinforcer for the problem behavior is to remove it completely, and, as discussed above, it is very common for differential-reinforcement-based interventions to arrange for extinction of the target behavior while simultaneously reinforcing alternative behavior (e.g., as is common with FCT; e.g., Fisher, Greer, & Bouxsein, in press).

Thus, at a broad conceptual level, the beneficial effects of placing the target behavior on extinction while also explicitly reinforcing an alternative behavior seem clear in terms of Equation 4. But, extinction actually introduces a serious quantitative problem for the matching law more generally, and for Equation 4 specifically. If the reinforcer for target behavior is removed entirely, its rate of occurrence is zero (i.e., R=0). Thus, if value is calculated as the combined effects of different reinforcement parameters as suggested by Equation 2, V_T would always be zero once extinction begins for the target behavior. If V_T in Equation 4 is zero, then pT is always zero, and the target behavior is predicted to never occur again once extinction has begun. Unfortunately, this is not how extinction works. Target behavior often persists for quite some time after extinction is started. In addition, even if the target behavior is reduced to a zero rate of occurrence, phenomena such as resurgence demonstrate that it can easily reappear in the future, even though extinction remains in effect. Note that in a typical demonstration of resurgence, both the target behavior and the alternative behavior are under extinction during a Phase 3 resurgence test when alternative reinforcement is suspended. Without some way to calculate values based on the previous histories of reinforcement, Equation 4 returns only zeros. So, although differential-reinforcement-based interventions seem to make conceptual sense when considered from the perspective of the concatenated matching law, the formal structure collapses as soon as extinction is introduced. This is the problem that RaC was designed to address.

How does one calculate the value of a response option that was once reinforced but is no longer reinforced? It seems uncontroversial to suggest that the effects of a history of reinforcement are carried forward in time somehow such that they can continue to impact behavior even after extinction is implemented. Indeed, BMT does just this using the construct of behavioral mass. Unfortunately, some of the failings of BMT result from the fact that it assumes that reinforcement history is carried forward as mass across time unchanged (Nevin & Grace, 2000). How then should one quantify the residual effects of a changing history of reinforcement across time such that a number can be placed in the value terms in Equation 4? In what follows, we will provide a description of how RaC accomplishes this. In doing so, we will be glossing over some of the more complex quantitative details about how the effects of a history of reinforcement are calculated. To understand the implications of RaC for durable behavior change in applied settings, it is not necessary to understand every quantitative detail—although understanding those details could certainly improve one’s ability to gain insights from RaC. Thus, in the body of the text below, we will use mainly graphs and qualitative descriptions to show how RaC quantifies a history of reinforcement. More detailed quantitative descriptions can be found in the Supporting Information and in the original Shahan and Craig (2017) paper.

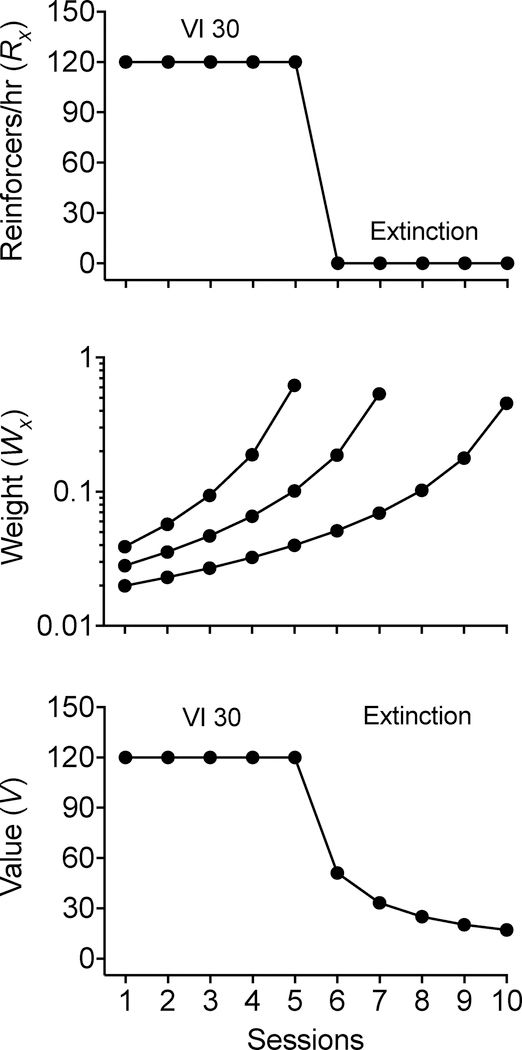
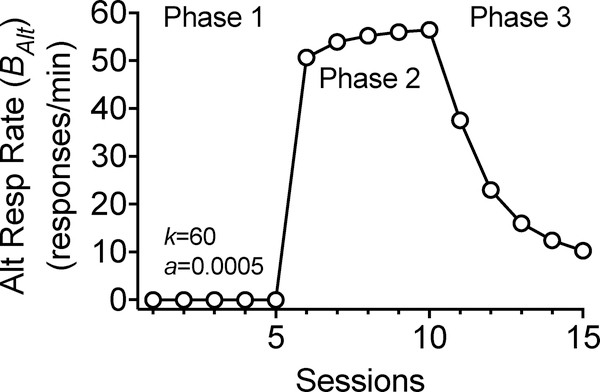
To formally quantify the effects of a history of reinforcement on the value of a response option, it is first necessary to have a record of the objective history of reinforcement. An example of such a record is presented in the top panel of Figure 1. The figure shows the reinforcement rates (i.e., R_x in reinforcers/hr) experienced for a single response across 10 sessions. For the first 5 sessions, the response was reinforced on a variable-interval (VI) 30-s schedule (i.e., 120 reinforcers/hr). For the following 5 sessions, the response was placed on extinction, and thus, produced zero reinforcers per hr. It is important to note that behavior is not represented in this panel—it simply presents a record of the reinforcement rates experienced. If the numbers represented in the top panel were used in Equation 4, the equation would suggest that this response has zero value and should never occur again once extinction begins at Session 6.

Figure 1.

A record of reinforcement rates across baseline (i.e., VI 30 s) and extinction conditions (top panel), examples of weighting functions generated by the Temporal Weighting Rule for Sessions 5, 7, and 10 (middle panel), and the value of the response obtained by applying weighting functions, like those in the middle panel, to the reinforcement rates across sessions in the top panel.

In order to turn a history of reinforcement like that in the top panel of Figure 1 into value, RaC uses a slight modification of an approach borrowed from the animal-foraging literature called the Temporal Weighting Rule (TWR; see Devenport & Devenport, 1994; Mazur, 1996, for reviews). Simply put, the TWR suggests that recent experiences (i.e., experiences of reinforcement rates in this case) are more heavily weighted (i.e., have a greater impact on value) than experiences from the more distant past. But, even though the impact of experiences from the more distant past are reduced, they nevertheless continue to influence behavior for a long time. The TWR generates weightings that are applied to a record of a reinforcement history like that presented in the top panel of Figure 1. In this case, the reinforcement rate experienced in each session starting with the most recent session and going back to the first in the record is simply multiplied by the weighting provided by the TWR for each session. By performing this calculation, we are quantifying a history of reinforcement by determining the value of past experiences as a function of what happened in the past (i.e., rates of reinforcement experienced) and how heavily each past experience is weighted.

The middle panel of Figure 1 shows examples of weighting functions for Sessions 5, 7, and 10 generated by the TWR. Each curve in that panel is a weighting function for a particular session and shows how the weightings (i.e., W_x) decrease as sessions recede into the past (i.e., the curves decrease as you move from right to left). A brief description of the quantitative details for generating these weighting functions is provided in the Supporting Information. Note that every session would have its own weighting function but plotting them all would make it difficult to see any particular function. Also note that when interpreting the weighting function for any given session, only that function is relevant. That is, a single function describes the weightings for the current session and for each session in the past, relative to the current point in time (i.e., the current session). There are a few additional important things to notice about the weighting functions. First, the weights in every function always sum to 1. Thus, each W_x tells you the proportion of total weight that a particular session in the past gets. Second, for each weighting function, sessions that happened longer ago get less weight (i.e., smaller W_x), and more recent sessions get more weight (larger W_x). Take for example the function for Session 10 (only the curve on the far right). The most recent session (i.e., the data point for Session 10 on the curve on the right) receives approximately 0.46 (i.e., 46%) of the total weight, but Session 5 on this same function receives only about 0.04 (i.e., 4%) of the total weight. Finally, the weighting functions decrease quickly at first, but more slowly for sessions in the more distant past (i.e., further to the left on the function). Specifically, the weighting functions generated by the TWR and displayed in the middle panel are hyperbolic (note that the y-axis is logarithmic). Thus, reinforcers experienced in more recent sessions have a relatively large impact, but the effects of the more distant reinforcement history linger for a very long time.

To calculate the value of a response option, RaC simply multiplies the reinforcement rate (i.e., R_x) experienced in each session in the top panel of Figure 1 by the corresponding weighting (i.e., W_x) for that session in the middle panel, and then sums up the weighted reinforcement rates across those sessions. The bottom panel shows the value (i.e., V) of the response option calculated this way for each of the same 10 sessions as depicted in the other two panels. Note that value declines quickly at first when extinction is implemented but declines more slowly as extinction sessions progress. To demonstrate how to calculate the values in the bottom panel, we will present a couple of examples. In calculating the value for Session 5, the reinforcement rate for each session starting at Session 5 and moving back to Session 1 would first be multiplied by the weights for those sessions. The weighting function for Session 5 (the function on the left in the middle panel of Figure 1) provides the following W_x values 0.039, 0.057, 0.094, 0.189, and 0.621 for Sessions 1, 2, 3, 4, and 5 respectively. The reinforcement rates in those sessions were 120, 120, 120, 120, and 120. Thus, the value (i.e., V) of the response for Session 5 is (0.039*120)+(0.057*120)+(0.094*120)+(0.189*120)+(0.621*120)=120. Next, to see how extinction impacts value, consider Session 7. The weighting function for Session 7 is the middle curve in the middle panel of Figure 1 and provides the following Wx values 0.028, 0.035, 0.048, 0.066, 0.101, 0.187, and 0.535 for Sessions 1, 2, 3, 4, 5, 6, and 7, respectively. The reinforcement rates for those same sessions were 120, 120, 120, 120, 120, 0, 0. Thus, the value (i.e., V) of the response for Session 7 is (0.028*120)+(0.035*120)+(0.048*120)+(0.066*120)+(0.101*120)+(0.187*0)+(0.535*0) =33.29. Value is calculated similarly for all the other sessions based on the weighting function for each session in order to construct the bottom panel.

By providing a way to calculate value, the TWR allows RaC to use Equation 4 to make predictions about situations in which either the target behavior, the alternative behavior, or both are on extinction. This allows the concatenated matching law to be formally applicable to differential-reinforcement-based interventions involving extinction, and most importantly for present purposes, it permits RaC to account for resurgence. The example in Figure 1 showed how to apply the TWR to a single response option. When there are two responses under consideration (i.e., a target and an alternative response), the process is exactly the same. Weighting functions generated by the TWR are applied to the record of the reinforcement history for each response separately, and value is calculated for each response separately.

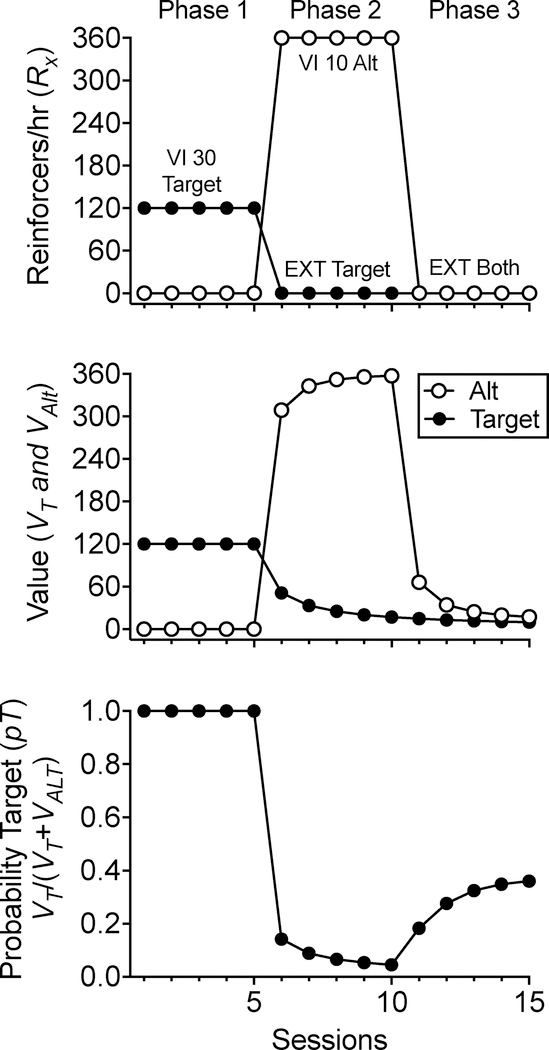
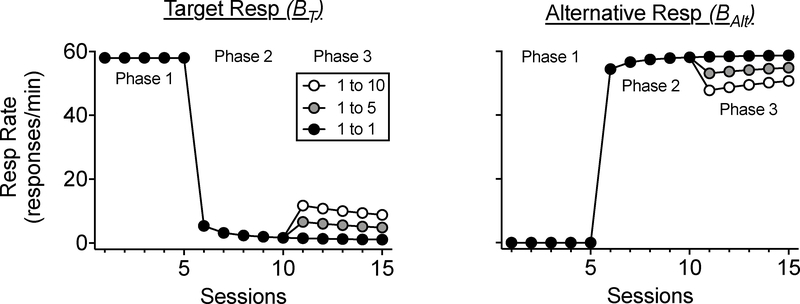
The top panel of Figure 2 shows a record of the reinforcement histories for a target and an alternative response across the typical three phases of a resurgence experiment. In Phase 1, the target behavior was reinforced on a VI 30-s schedule. In Phase 2, the target behavior was extinguished, and the alternative behavior was reinforced on a VI 10-s schedule. In Phase 3, reinforcement for the alternative behavior was also omitted (i.e., it was placed on extinction). The middle panel of Figure 2 shows value of the target (i.e., V_T) and alternative behavior (i.e., V_Alt). Value for both options was calculated in the same way as described for Figure 1 using the relevant weighting functions for each option (see Supporting Information). Note that the value function for the target behavior is exactly the same as in Figure 1, but it has been extended out to 15 sessions (i.e., 10 sessions of extinction). Also note that although value of the target behavior gets quite low by the time Phase 3 begins (i.e., at Session 11), it is not zero. Its precise value is 9.74. When Phase 3 begins and the alternative behavior is also placed on extinction, the value of the alternative behavior drops precipitously at first and then more slowly as sessions progress.

Figure 2.

Changes in value (middle panel) and response probability (bottom panel) as a function of changes in reinforcement rate (top panel) of target and alternative responding across three phases of a resurgence sequence. Increases in the probability of target responding when transitioning from Phase 2 to Phase 3 drive the resurgence effect.

The bottom panel of Figure 2 shows the probability of the target behavior obtained by plugging the V_T and V_Alt values across sessions in the middle panel into Equation 4 [i.e., pT = V_T/(V_T+V_Alt)]. Note that when only the target behavior is reinforced in Phase 1, the probability of the target behavior is 1 (i.e., only the target behavior occurs). When the target behavior is placed on extinction and high-rate reinforcement of the alternative behavior is introduced in Phase 2, the probability of the target behavior decreases rapidly. Finally, when reinforcement is omitted for the alternative behavior in Phase 3, the precipitous decrease in value of the alternative behavior generates an increase in the probability of the target behavior. This increase in the probability of the target behavior suggests that when responding occurs in Phase 3, whether it be target or alternative responding, there is an increased likelihood that, relative to Phase 2, responding will take the form of target behavior. This increased probability of the target is what we see as resurgence. Note that this increase in the probability of the target occurs even though the absolute value of the target has not changed and remains low. What has changed is that the relative value of the target has increased because of the decrease in V_Alt in Equation 4. In short, RaC suggests that resurgence results from an increase in the allocation of responding to the target as a result of a decrease in the value of the alternative behavior.

As we hope is clear at this point, RaC is a formalization of the broader definition of resurgence noted above in terms of a “worsening of conditions” (e.g., Epstein, 1985; Lattal & Wacker, 2015). In the matching-law-based approach provided by RaC, a “worsening of conditions” is quantified as decreases in the value of the alternative behavior. In the examples above, we have shown how RaC uses the TWR to provide a quantitative description of how value decreases with exposure to extinction. But, in a broader sense, RaC can be applied to any conditions that affect the relative value of the target behavior. Decreases in the value of an alternative resulting from other operations would also be expected to generate resurgence. For example, decreases in the rate of alternative reinforcement to non-zero values would be expected to generate resurgence, and as is clear from the discussion above about reinforcement thinning, such decreases do generate resurgence (e.g., Briggs et al., 2018). Further, decreases in the magnitude of alternative reinforcement would be expected to induce resurgence of an extinguished target behavior, and in fact, they do (Craig, Browning, Nall, Marshall, & Shahan, 2017). Similarly, punishment of an alternative behavior would be expected to precipitate resurgence of an extinguished behavior, and it does (Fontes, Todorov, & Shahan, 2018; see also Wilson & Hayes, 1996). Although there has been no research on other forms of devaluation of the alternative behavior, RaC suggests that decreases in immediacy, quality, motivation, or increases in the effort required for alternative reinforcement should also induce resurgence. Indeed, in its most general conceptual sense, RaC suggests that a target behavior that is suppressed by any means might resurge as a result of any operation that produces an increase in the relative value of the target behavior. A target behavior might be suppressed by extinction, punishment, decreases in motivation, or by any other means, and resurgence might be induced by anything that decreases the value of an alternative behavior or that increases the value of the target behavior.

The broad conceptual approach to resurgence provided by RaC and summarized above might be sufficient for many applied behavior analysts. The approach provides a way to think about resurgence that is consistent with existing conceptual approaches to differential-reinforcement-based interventions in terms of concurrent operants and the matching law. Further, the approach provides general guidelines about when resurgence might be expected and what sorts of conditions one might avoid in order to prevent resurgence. In a general sense, to benefit from such insights provided by RaC, it is probably not necessary, or in many cases not possible, to have an accurate record of the reinforcement history for a particular problem behavior that would permit an explicit calculation of value. It most cases, it is a fairly reasonable assumption that there is a reinforcement history for problem behavior once a functional reinforcer has been identified. As a result, the general conceptual approach to resurgence provided by RaC would still provide insights about the sorts of conditions that might lead one to expect resurgence. In many cases, this is probably enough. But, because RaC provides a way to more specifically quantify the processes thought to be at work, the theory makes explicit predictions about how a variety of variables might affect resurgence. In what follows, we will explore some of those predictions that might be most relevant to applied behavior analysts. In order to do that, it is first necessary to describe how RaC generates predictions about the usual dependent measure employed in applied behavior analysis.

Equation 4 describes resurgence in terms of the probability of a target behavior. Although this is useful in a general sense for contemplating when resurgence might be expected, most behavior analysts do not measure the relative rate or probability of behavior—they measure the absolute rate of behavior (e.g., responses/min). Thus, in order to make predictions about the most relevant dependent variable, RaC needs to make predictions in terms of absolute response rates. Fortunately, because RaC is based on the matching law, it is fairly straightforward to generate a version of the theory that predicts absolute response rates.

Herrnstein (1970) proposed an absolute response rate version of the matching law, suggesting that when two response options are available, the absolute rate of one of those responses is,

$$B_1=\frac{{kR}_1}{R_1+R_2+R_e}$$ (5),

where B₁ is the absolute rate (i.e., response/min) of the target behavior, R₁ is the rate of reinforcement for that behavior (i.e., reinforcers/hr), R₂ is the rate of reinforcement for the other behavior, k is a parameter representing the asymptotic rate of B₁ in that situation, and R_e is a parameter representing extraneous sources of reinforcement in the environment produced by unmeasured other behavior (see McDowell, 1988, for a tutorial). This equation suggests that the rate of the target behavior (i.e., B₁) increases with increases in the rate of reinforcement for that behavior (i.e., R₁) and decreases with increases in reinforcement for the other behavior (i.e., R₂). The parameter R_e determines how quickly rates of the target behavior approach the asymptotic level (i.e., k) with increases in R₁ and is assumed to remain constant in a given situation.

RaC uses a slightly modified version of Equation 5 to generate absolute response rates. First, RaC replaces reinforcement rates for the two responses with the values for the target (i.e., V_T) and alternative (i.e., V_Alt) behaviors. Second, as will be discussed in more detail below, RaC replaces R_e with the invigorating (i.e., arousing) effects of reinforcement (i.e., A; see Killeen, 1994). Thus, the absolute response rate version of RaC is,

$$B_T=\frac{k{V}_T}{V_T+V_{Alt}+\frac{1}{A}}A=a(V_T+V_{Alt})$$ (6),

where B_T is the rate of the target behavior, k is the asymptotic rate of B_T, and all other terms are as described above. Thus, RaC suggests that the absolute rate of a target behavior increases with increases in the value of the outcomes produced by that option (i.e., V_T) and decreases with increases in the value of the outcomes produced by an alternative behavior (i.e., V_Alt). Because 1/A is in the denominator of the equation, as A increases (i.e., more invigoration), B_T tends to increase, and as A decreases, B_T tends to decrease. RaC uses 1/A instead of R_e from Herrnstein’s Equation because (a) the assumption that R_e should remain constant, even during extinction of both the target and alternative behaviors, turns out to be untenable when accounting for resurgence data (see Shahan & Craig, 2017, for elaboration), and (b) the switch to the invigorating effects of reinforcement (i.e., A) allows the model to more naturally incorporate the effects of motivation. As shown in the right-hand portion of Equation 6, the degree to which target behavior is invigorated (i.e., A) is assumed to depend on the sum of the values of the two options. The parameter a determines how much of an impact the current values of the options have on invigoration and can be thought of as representing the strength of the motivating operations in effect for the relevant reinforcers (e.g., Laraway, Snycerski, Michael, & Poling, 2003). Higher values of parameter a (i.e., an establishing operation) mean that the current values of the available options produce more vigorous behavior. For an organism satiated on the relevant reinforcers (i.e., an abolishing operation), the prospect of even nominally highly valuable reinforcers (e.g., high rate, magnitude, immediacy, etc.), is not likely to produce much vigor (i.e., lower values of parameter a), and thus, not much responding. Most importantly, in a typical resurgence test, both target and alternative responding are on extinction. The longer extinction is in effect for both responses, the lower V_T + V_Alt becomes as all reinforcement drifts into the past, and A becomes smaller and behavior less invigorated.

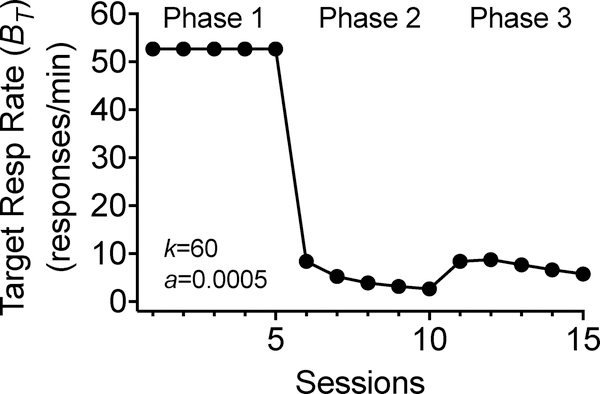
Figure 3 shows target response rates calculated using Equation 6 for the same example shown previously in Figure 2. For this simulation, the V_T and V_Alt values for each session as shown in the middle panel of Figure 2 were plugged into Equation 6 using parameter values comparable to those used in previous applications of RaC to existing animal data (i.e., k=60, a=0.0005; Shahan & Craig, 2017). As shown in Figure 3, RaC can produce the usual pattern of behavior obtained in resurgence experiments. Rates of the target behavior are higher in Phase 1 when only the target is reinforced. In Phase 2 when the target behavior is placed on extinction and the alternative behavior is reinforced at a high rate, target response rates decrease to low levels. Finally, in Phase 3 when the alternative behavior is also extinguished, the target behavior increases (i.e., shows resurgence) and then gradually decreases across continued extinction sessions.

Figure 3.

Target response rate across three phases of a resurgence sequence in which reinforcers are provided for target responding in Phase 1, an alternative response in Phase 2, and neither response in Phase 3. Increases in target responding when transitioning from Phase 2 to Phase 3 constitute resurgence.

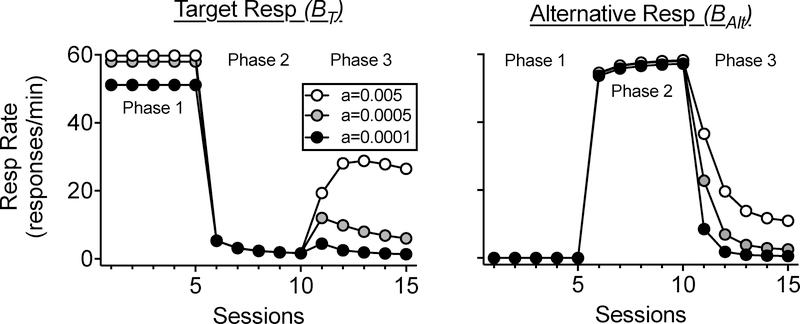
At this point, it is important to briefly consider what happens with response rates (i.e., B_T) in Figure 3 during Phase 3 and what happens with the probability of the target (i.e., pT) in Phase 3 in the bottom panel of Figure 2. Note that in Figure 2, the probability of the target response increases across Phase 3. What this means specifically is that given that one of the behaviors occurs (either target or alternative), how likely is it that the behavior that occurs is the target behavior? Thus, what Figure 2 shows is that as extinction of both behaviors continues in Phase 3, it becomes increasingly likely that when a behavior does occur, it is the target behavior. On the other hand, response rates in Phase 3 as shown in Figure 3 tend to decrease across sessions as both responses continue to be on extinction for a longer period of time. This decrease is the result of decreases in invigoration (i.e., A) in Equation 6, as extinction continues, and all reinforcer deliveries drift into the past (i.e., V_T and V_Alt continue to decrease). Thus, although the target response is becoming more likely when a behavior actually occurs (Figure 2), behavior is occurring less often (Figure 3) because of the increasing exposure to extinction. Importantly, as noted in the section on shortcomings of BMT above, resurgence data also show sometimes that when reinforcement is omitted for both the target and the alternative behavior, target behavior initially increases across the first few sessions in Phase 3 before then beginning to decrease across sessions (see Podlesnik & Kelley, 2015, for discussion). Interestingly, Equation 6 can naturally describe such a pattern with variations in the motivation-related parameter (i.e., a). As parameter a increases, the pattern of response rates across Phase 3 becomes more bitonic (see Figure 9 below for simulations). Thus, according to RaC, the pattern of responding across continued extinction sessions during a resurgence test is influenced by motivating operations—with greater motivation likely to result in increases in target responding across the first few sessions in which the alternative behavior is also extinguished.

Figure 9.

Target (left panel) and alternative (right panel) response rates under various conditions of motivation (i.e., the a parameter). Lighter data points simulate greater motivation.

In applied settings, it is usually not just the target behavior that is of interest. For example, although FCT might be used to decrease problem behavior, the alternative behavior is a desirable, functional communication response. So, although a clinician might justifiably be interested in how much the target problem behavior decreases during treatment and whether it resurges, they are also likely to be keenly interested in how often the communication response occurs. Because RaC is a choice-based approach, it naturally also provides an account of the alternative behavior. All that is required for such an account is to rearrange Equation 6 so that it is stated in terms of the alternative behavior rather than the target behavior. Thus,

$$B_{Alt}=\frac{k{V}_{Alt}}{{V_T+V}_{Alt}+\frac{1}{A}}A=a(V_T+V_{Alt})$$ (7),

where B_Alt is the rate of the alternative behavior, and all other terms are as in Equation 6. Note that in Equation 7, V_Alt has simply replaced V_T in the numerator. Figure 4 shows rates of the alternative behavior (i.e., B_Alt) across the same phases as presented for the target behavior in Figure 3 using the same parameter values (i.e., k=60, a=0.0005). Note that the alternative behavior does not occur in Phase 1 (i.e., prior to the introduction of reinforcement for that behavior) and occurs at a high rate in Phase 2 after the introduction of high-rate reinforcement for that behavior. In Phase 3, when the alternative behavior is placed on extinction, it declines across sessions. It is important to note, however, that if the target and alternative behaviors are topographically different (which is almost surely the case in applied settings), the asymptotic rate of the target behavior might be different than that of the alternative behavior (e.g., saying, “Play please” can happen many more times per minute than elopement). In these circumstances, a different value of the k parameter might be required to make reasonable predictions about the rates of the two behaviors.

Figure 4.

Alternative response rate across three phases of a resurgence sequence in which reinforcers are provided for target responding in Phase 1, an alternative response in Phase 2, and neither response in Phase 3.

Implications of Resurgence as Choice for Promoting Durable Treatments

RaC suggests a number of ways in which applied behavior analysts may mitigate the resurgence of problem behavior, and in so doing, promote treatment durability. In the sections below, we provide simulations of key predictions of RaC that may be especially relevant when treating problem behavior.

Value Manipulations

A core prediction of RaC is that any procedure that keeps the value of the alternative response (V_alt) high relative to the value of the target response (V_t) will mitigate resurgence of target behavior. To help illustrate this prediction, we simulated various situations in which differences in value affect treatment efficacy, resurgence of target responding, and rates of alternative responding following treatment with differential reinforcement. For these and all subsequent simulations we set k=60, a=0.0005, and λ=0.006 (see Supporting Information for discussion of λ).

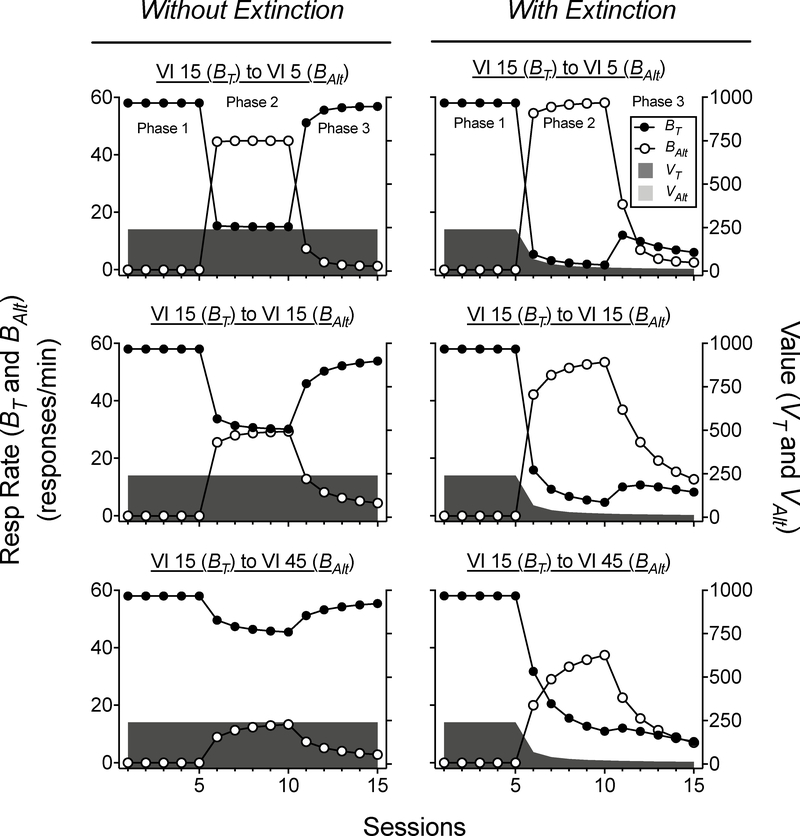
All simulations in Figure 5 begin with a VI 15-s schedule of reinforcement for the target response in Phase 1. Panels in the left column show target and alternative response rates (and associated values of each response) without extinction programmed for target responding in Phase 2. Panels in the right column show these same measures but under conditions in which extinction was programmed for target responding in Phase 2. In all panels, extinction was then arranged for alternative behavior in Phase 3. The top panels show simulations in which the rate of alternative reinforcement (i.e., VI 5 s) in Phase 2 was denser than that programmed in Phase 1 for target responding. The middle panels depict simulations in which the rate of alternative reinforcement (i.e., VI 15 s) in Phase 2 was identical to that programmed in Phase 1 for target responding. Finally, the bottom panels depict simulations in which the rate of alternative reinforcement (i.e., VI 45 s) in Phase 2 was leaner than that programmed in Phase 1 for target responding.

Figure 5.

Target and alternative response rates across three phases. Shaded areas correspond to values of the target and the alternative responses. Panels in the left column simulate different reinforcement schedules in Phase 2 for the alternative response when extinction is not programmed for target responding, whereas panels in the right column simulate these same conditions in Phase 2 when extinction is programmed for target responding (i.e., a typical resurgence sequence).

Given that RaC is based on the matching law (Equation 1), the model suggests that the effects of alternative reinforcement on suppression of target responding in Phase 2 are consistent with existing conceptualizations of differential reinforcement in terms of relative reinforcement value (e.g., Fisher & Mazur, 1997; Piazza et al., 1997). Specifically, suppression of target responding in Phase 2 is highly influenced by the rate of alternative reinforcement arranged in Phase 2, even if there is no change in reinforcement arranged for the target behavior. The left panels in Figure 5 clearly show this relation. When target responding continues to produce reinforcement across the three phases and alternative reinforcement is arranged only in Phase 2, target response rates decrease in Phase 2, with the magnitude of the reduction being greater with higher rates of alternative reinforcement (moving up panels in the left column). Whether response allocation favors the alternative in Phase 2 depends on the relative rates of reinforcement produced by each alternative in that phase. In Phase 2 of the top, left panel of Figure 5, a schedule of alternative reinforcement that is three times denser than that arranged for target responding produces three times the amount of alternative responding relative to the target response. In Phase 2 of the middle, left panel of Figure 5, equal reinforcement schedules arranged for target and alternative responding produce equal response allocation. Finally, in Phase 2 of the bottom, left panel of Figure 5, a schedule of alternative reinforcement that is three times leaner than that arranged for target responding produces a third of the amount of alternative responding relative to the target response. When alternative reinforcement is removed in Phase 3, target responding increases to its previous level, and alternative responding decreases. In each situation, transitions from Phases 1 to 2 and from Phases 2 to 3 produce relatively rapid transitions in response allocation toward the relatively denser of the two options. These rapid transitions are not immediate because, as discussed above and in the Supporting Information, RaC incorporates the TWR, which describes how a history of experiences (e.g., reinforcement for the target response) affects current behavior. It is this history of experiences that linger and continue to affect response allocation upon changes in reinforcement schedules.

When extinction is programmed for target responding in Phase 2 (right-hand panels of Figure 5), the impact of alternative reinforcement tends to be increased. When compared to corresponding panels to the left, target behavior is reduced more by the availability of alternative reinforcement when target behavior is simultaneously placed on extinction. This outcome is consistent with the well-known effects of combining extinction with differential reinforcement of alternative behavior (Fisher, Thompson, Hagopian, Bowman, & Krug, 2000; Hagopian et al., 1998; Petscher et al., 2009; Shirley, Iwata, Kahng, Mazaleski, & Lerman, 1997). As with the panels on the left in which target responding was not placed on extinction, the degree to which target responding is suppressed in Phase 2 is dependent upon the density of reinforcement arranged for the alternative response relative to that arranged for the target response. Relatively denser schedules of alternative reinforcement in Phase 2 help to better suppress target responding and promote acquisition of the alternative response. However, RaC suggests that even though target responding is suppressed more by higher rates of alternative reinforcement in Phase 2, greater resurgence can be expected as a result when alternative reinforcement is removed in Phase 3. This can be seen when comparing response rates in the final session of Phase 2 (Session 10) to those in the first session of Phase 3 (Session 11) across the three panels in the right column of Figure 5. In all three cases, removal of alternative reinforcement produces some increase in target responding, with the magnitude of the increase being larger for alternative behavior previously maintained by a higher rate of reinforcement. Such effects have been demonstrated in basic research with both non-humans and humans (e.g., Craig & Shahan, 2016; Smith, Smith, Shahan, Madden, & Twohig, 2017) and in applied settings (e.g., Fisher, Greer, Fuhrman, et al., 2018; Garner, Neef, & Gardner, 2018).

The simulations in Figure 5 demonstrate an important aspect of RaC. Exactly the same processes are implemented in exactly the same way by the model to generate the simulations in the panels on the left in which target behavior was not placed on extinction and those on the right in which it was placed on extinction. Thus, the increases observed when alternative reinforcement is removed in both cases are due to exactly the same thing—the removal of alternative reinforcement and the resulting change in the relative value of the target behavior. In the left-hand panels, this is easily and traditionally understood as being governed by the matching law. In the right-hand panels, a similar increase after extinction of the target behavior has seemed to require a special explanation, and it has been given a special name (i.e., resurgence). But, RaC suggests that there is nothing different or special about resurgence. Resurgence is a natural result of the matching law and changing relative values of target and alternative behaviors across time. It is important to note that like the matching law in general, and unlike the response-prevention hypothesis (see above), RaC suggests that it is the changes in relative value themselves, rather than the accompanying changes in the rates of alternative behavior that produce these effects (see Catania, 1963, and Rachlin & Baum, 1972, for data and discussions).

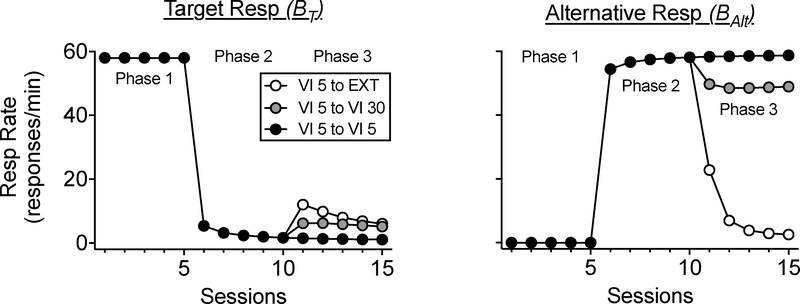
The fact that RaC characterizes resurgence as resulting from changes in the relative values of the target and alternative behaviors allows it to predict the effects of reducing, but not necessarily eliminating, alternative reinforcement (i.e., reinforcement schedule thinning). As an example of how RaC predicts changes in target and alternative behavior as a result of reinforcement schedule thinning, consider a situation in which following a phase of treatment, the schedule of alternative reinforcement (a) remains intact and unchanged, (b) remains intact but decreases, or (c) is suspended entirely. Figure 6 simulates these three situations. In these and all subsequent simulations, a VI 15-s schedule is assumed for the target behavior during Phase 1, and target behavior is extinguished in Phase 2 while an alternative behavior is reinforced on a VI 5-s schedule. In Figure 6, black data points simulate no reinforcement schedule thinning (i.e., VI 5-s schedule for the alternative response remains constant across Phases 2 and 3), grey data points simulate a thinning of the schedule of alternative reinforcement from a VI 5-s schedule in Phase 2 to a VI 30-s schedule in Phase 3, and white data points simulate the complete suspension of alternative reinforcement (i.e., VI 5-s schedule in Phase 2 to extinction in Phase 3). Larger downshifts in the rate of alternative reinforcement (and the associated value of the alternative response) are predicted to produce larger magnitudes of resurgence, as can be seen in the relatively large increases in target responding when transitioning from Phases 2 to 3 when Phase 3 arranges a leaner schedule of alternative reinforcement. The right panel in Figure 6 shows how these changes in rate of alternative reinforcement affect alternative responding in Phase 3. As one might expect, leaner schedules of alternative reinforcement are predicted to maintain less alternative responding. If one were to use these predictions of RaC to inform clinical practice, a reasonable progression of steps to accomplish reinforcement schedule thinning would entail making only incremental reductions in the rate of alternative reinforcement across successive steps. Increases in the rate of problem behavior upon any given transition would suggest too large of a decrease in the rate of alternative reinforcement (i.e., an increase in the relative value of problem behavior), which would further suggest more gradual reductions in the rate of alternative reinforcement in future steps.

Figure 6.

Target (left panel) and alternative (right panel) response rates when Phase 3 constitutes a downshift in the rate of alternative reinforcement programmed in Phase 2. Lighter data points simulate greater downshifts in rate of alternative reinforcement.

Although we have limited the simulations above to changes in the relative value of a target response produced by changes in reinforcement rate, RaC provides a broader quantitative framework (see Shahan & Craig, 2017), describing how changes in relative value resulting from a wide range of manipulations might impact resurgence (e.g., changes in reinforcer magnitude, punishment). In the most general sense, RaC suggests that any intervention that can help to keep the value of the target behavior low relative to that of the alternative behavior should help to mitigate resurgence. Conversely, any change that might be reasonably expected to increase the relative value of the target behavior, whether via decreases in the value of alternative behavior or increases in the value of the target behavior itself, might be expected to increase the likelihood and magnitude of resurgence.

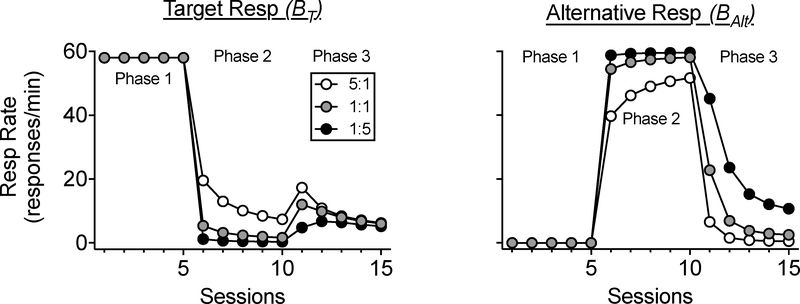
Asymmetrical Choice Situations

Although the effects of differential-reinforcement-based interventions on problem behavior have been conceptualized in terms of the matching law, it has long been noted that there is a disconnect between basic research and clinical practice in this area (see Fisher & Mazur, 1997; Mace & Roberts, 1993, for reviews). As was the case in Herrnstein (1961), most research with animals has examined “symmetrical” situations with choices between two topographically similar responses (e.g., two keys) leading to the same reinforcer type (e.g., food). But, most applications of differential reinforcement to the treatment of problem behavior involve “asymmetrical” choices between topographically dissimilar behaviors (e.g., aggression and a communicative response), often leading to qualitatively different reinforcers (e.g., higher quality for the alternative). As noted above, the BMT of resurgence had no means to easily incorporate and make predictions about such asymmetrical choice situations. But, because RaC is based on the matching law, it can incorporate such asymmetries and describe their impact on the efficacy of treatment and the likelihood of resurgence.

To incorporate asymmetries between response options in a choice situation, the matching law uses the concept of bias (Baum, 1974). In the context of the matching law, bias refers to preference for one option over the other due to unaccounted-for factors (e.g., Baum, 1974; see McDowell, 1989, for a tutorial). Thus, even when the values of the reinforcers arranged for two behaviors are nominally equivalent (i.e., the same rates, magnitudes, and immediacies), organisms may still show a preference for one of the options. Indeed, clients in applied settings can show an unaccounted-for bias for problem behavior over appropriate behavior (e.g., DeLeon, Fisher, Herman, & Crosland, 2000) or a bias for one appropriate behavior over another (e.g., Ringdahl et al., 2018) under identical reinforcement conditions. Bias can also be used to quantify asymmetries in choice. For example, the concept of bias allows one to quantify the qualitative differences in effort of two topographically different responses (e.g., engaging in aggression versus saying, “Play please”). Similarly, the concept of bias allows one to quantify differences in reinforcer quality (e.g., 15-s access to a tablet computer versus escape from demands).

RaC incorporates bias into its absolute response-rate equations (i.e., Equations 6 & 7) in a manner suggested by McDowell (2005) for Herrnstein’s original equation (i.e., Equation 5). Specifically, for the target behavior RaC suggests,

$$B_T=\frac{k{V}_T}{V_T+\frac{V_{Alt}}{b}+\frac{1}{A}}$$ (8),

and for the alternative behavior,

$$B_{Alt}=\frac{k\frac{V_{Alt}}{b}}{V_T+\frac{V_{Alt}}{b}+\frac{1}{A}}$$ (9),

where all terms are as above, and b represents the bias term. Note that value of the alternative behavior (i.e., V_Alt) is simply divided by the bias term. When b is equal to 1, there is no bias, and Equations 8 and 9 are identical to Equations 6 and 7. When b is greater than 1, there is a bias in favor of the target because value of the alternative behavior is being reduced, and Equation 8 predicts that target response rates will be higher than when b is less than or equal to 1. When b is less than 1, there is a bias in favor of the alternative behavior because the value of the alternative is being increased (i.e., dividing V_Alt by a number less than 1 increases it), and Equation 8 predicts that target response rates will be lower as a result.

As an example of how bias can influence resurgence, consider the case of two responses requiring different effort. For this example, assume that the two responses produce exactly the same reinforcer at the same rate and with the same immediacy. Thus, value of the two responses might be expected to be the same. But, one response requires less effort than the other (e.g., saying, “Please?” versus saying, “May I please stop working and play now?”). If a child were given free choice between these two responses such that either produces the reinforcer, perhaps the child emits the less-effortful response 5 times more often than the more-effortful response. In this case, the bias term (i.e., b) would be 5. Specifically, the bias term in RaC represents the ratio by which the target behavior is preferred over the alternative behavior if all else is equal. Thus, the effect of the differential effort requirements is being measured by the degree to which those differential requirements shift preference. In terms of finding out what the bias term should be in Equation 8, the most straightforward approach would be to do a preference assessment under conditions where all else is equal to obtain the preference ratio (and thus b). Similarly, the bias term can be used in exactly the same way to account for the effects of qualitatively different reinforcers if all else is equal. Finally, if the responses differ in terms of both effort and in terms of qualitative differences in the reinforcers they produce, then the bias term would measure the combined effects of those differences in effort and quality.

Incorporation of the bias term in Equations 8 and 9 allows RaC to make predictions about how differences in unaccounted-for bias (e.g., DeLeon et al., 2000; Ringdahl et al., 2018), effort, or reinforcement quality might be expected to affect resurgence in the asymmetrical choice situations typical of applied settings. For example, a general finding in the clinic is that differential reinforcement is more effective at reducing problem behavior when the alternative response is less effortful and when the alternative response produces a higher-quality reinforcer (e.g., Horner & Day, 1991; Piazza et al., 1997). As such, applied behavior analysts are encouraged to select an alternative response that is of low effort and that produces a high-quality reinforcer when initiating FCT (Tiger et al., 2008). RaC actually predicts these same therapeutic effects when initiating treatments using differential reinforcement (e.g., FCT). RaC further suggests that any manipulation increasing bias toward the alternative response over the target response (e.g., less effort, higher-quality reinforcer) will promote acquisition of the alternative response while in treatment, and importantly, will better mitigate resurgence if and when treatment is later disrupted.

Figure 7 simulates three different situations in which changes in bias affect target-response suppression and alternative-response acquisition in treatment (Phase 2), as well as resurgence of target responding and persistence of the alternative response when treatment is suspended (Phase 3). For Figure 7, we set the bias term (i.e., b) to 5 (a five-fold bias for the target response; white data points), 1 (no bias; grey data points), or 0.20 (a five-fold bias for the alternative response; black data points). As the figure shows, RaC predicts better suppression of target responding and higher rates of alternative responding in Phases 2 and 3 when biased responding favors the alternative over the target. An equal, yet opposite, bias for the target response is predicted to minimize treatment efficacy in Phase 2 and to interfere with treatment maintenance in Phase 3.

Figure 7.

Target (left panel) and alternative (right panel) response rates when responding is biased toward the target (white data points), the alternative (black data points), or neither response (grey data points).

RaC further suggests that a change in bias might also induce resurgence. For example, in addition to initially selecting an alternative response that is simple and low effort, it is also typically desirable to increase the complexity and effort of the alternative response (Ghaemmaghami, Hanley, Jessel, & Landa, 2018). RaC suggests that such an increase in effort of the alternative behavior might be expected to produce resurgence of problem behavior, even if the reinforcement conditions have not otherwise changed. Figure 8 shows simulations of the effects of different increases in effort of alternative behavior. In Phases 1 and 2, the conditions are the same for all three simulations. In Phase 3, the effects of no change in effort of the alternative behavior (i.e., 1 to 1, black data points), a five-fold increase in effort (i.e., 1 to 5, grey data points), and a 10-fold increase in effort (i.e., 1 to 10, white data points). The left panel shows that larger increases in effort of the alternative behavior are predicted to produce more resurgence of target behavior, and the right panels show that larger increases in effort of the alternative behavior are also expected to produce larger decreases in the rates of alternative behavior. There is existing evidence consistent with this prediction of RaC that increases in alternative-response effort can produce resurgence of problem behavior (see Ghaemmaghami et al., 2018). In addition, Ghaemmaghami et al. showed that such resurgence might be reduced by employing a gradual shaping process in which progressively complex and effortful alternative responses are reinforced at a high rate. Although it is difficult to precisely quantify such a procedure with RaC at this point, the outcome of the procedure is at least conceptually consistent with RaC in terms of establishing and increasing the value of approximations to the terminal response relative to problem behavior.

Figure 8.

Target (left panel) and alternative (right panel) response rates when there is no shift (black data points), an intermediate shift (grey data points), or a large shift (white data points) in bias toward the target behavior in Phase 3 (e.g., an increase in effort of the alternative behavior).

Finally, although our description of Figure 8 focused on increases in the effort of the alternative behavior, the figure displays what would be expected with increases in bias for the target behavior resulting from any number of manipulations. For example, decreases in the quality of reinforcement for the alternative behavior or even increases in the quality of reinforcer for the problem behavior would be expected to have a similar effect. Further, a switch from an alternative behavior for which a client has an unaccounted-for bias to an alternative for which they have a bias against (e.g., differentially preferred mands as in Ringdahl et al., 2018) would also be expected to produce resurgence, the magnitude of which would depend on the strength of the bias.

Motivation Manipulations

As discussed above, parameter a first introduced above in Equation 6 of RaC can be thought of as representing the current state of motivation, with higher values of a indicating more vigorous behavior. Motivation to obtain reinforcement (i.e., a) persists in Phase 3 even though the values associated with each response (i.e., V_T and V_Alt) decline when extinction is programmed for both responses. Thus, the specific value of parameter a is predicted to impact the magnitude and persistence of the resurgence effect according to RaC. The a parameter of RaC might be influenced by a wide range of events, including biological events (Carr, Smith, Giacin, Whelan, & Pancari, 2003); deprivation of social-positive reinforcers (e.g., Sy & Borrero, 2009; Vollmer & Iwata, 1991); as well as task novelty, rate of task presentation, and session duration (e.g., Smith, Iwata, Goh, & Shore, 1995). Gradations of parameter a represent the continuum of motivation (see Kelley, Shillingsburg, & Bowen, 2017), with smaller values of a indicating lower motivation and larger values of a indicating higher motivation.

Figure 9 shows three simulations in which motivation for the reinforcer maintaining problem behavior ranges from relatively low (i.e., a small value of parameter a; black data points) to relatively high (i.e., a large value of parameter a; white data points). Grey data points in Figure 9 simulate moderate motivation (i.e., a moderate value of parameter a, which is the value used in all other simulations above). At lower values of parameter a, resurgence of target responding is smaller and less persistent than when parameter a takes on a higher value. At higher values of parameter a, resurgence of target responding is larger and more persistent. As might be expected, higher values of parameter a are predicted to result in more persistent alternative responding than when the value of parameter a is lower. Figure 9 further suggests that any improvement in the persistence of alternative responding afforded by increased values of parameter a is heavily offset by large increases in target responding in Phase 3.

The simulations in Figure 9 suggest that motivating operations might play an important role in the magnitude and persistence of the resurgence effect. RaC suggests that applied behavior analysts looking to mitigate the resurgence of problem behavior when treatments are likely to be challenged might consider minimizing motivation for the functional reinforcer.

Conclusions

RaC is a novel, quantitative model of resurgence that combines the predictive utility of the matching law with the ability to quantify the effects of a history of reinforcement over time, including a history of extinction for one or more responses. In summary, RaC suggests that resurgence might be expected anytime there is a decrease in the value of a more recently reinforced alternative behavior relative to the value of a problem behavior. In addition, RaC suggests that resurgence might be reduced by manipulations that minimize the effects of such changes in value. As is the case with any novel theory, many of the predictions of RaC must be validated experimentally before we will fully know the pragmatic utility of RaC for treating problem behavior.

We simulated some predictions of RaC that may be especially relevant when using differential-reinforcement-based approaches to treating problem behavior (e.g., FCT). The simulations we chose to provide in this paper are far from exhaustive. RaC makes predictions about how a wide range of variables might be expected to impact treatment efficacy and resurgence. We encourage interested readers and researchers alike to explore these and other predictions of RaC by conducting their own simulations using Microsoft Excel or within the R software environment using code specifically designed to simulate RaC by Craig & Shahan (2017).

Inevitably, even the most efficacious treatments for problem behavior are likely to be disrupted when implemented outside of the clinic and by caregivers. Durable treatment effects are those that not only stand the test of time but produce continued therapeutic changes in behavior even when those treatment procedures supporting behavior change are disrupted. We encourage applied behavior analysts to take this broader view of treatment maintenance, as others have suggested (e.g., Nevin & Wacker, 2013; Wacker et al., 2011). With this broader view in mind, we hope that applied behavior analysts might find the implications of RaC described herein useful when attempting to design more durable treatments for problem behavior.