Network Accelerated Motion Estimation and Reduction (NAMER): Convolutional neural network guided retrospective motion correction using a separable motion model

Abstract

Purpose:

We introduce and validate a scalable retrospective motion correction technique for brain imaging that incorporates a machine learning component into a model-based motion minimization.

Methods:

A convolutional neural network (CNN) trained to remove motion artifacts from 2D T₂-weighted RARE images is introduced into a model-based data-consistency optimization to jointly search for 2D motion parameters and the uncorrupted image. Our separable motion model allows for efficient intra-shot (line-by-line) motion correction of highly corrupted shots, as opposed to previous methods which do not scale well with this refinement of the motion model. Final image generation incorporates the motion parameters within a model-based image reconstruction. The method is tested in simulations and in vivo motion experiments of in-plane motion corruption.

Results:

While the CNN alone provides some motion mitigation (at the expense of introduced blurring), allowing it to guide the iterative joint-optimization both improves the search convergence and renders the joint-optimization separable. This enables rapid mitigation within shots in addition to between shots. For 2D in-plane motion correction experiments, the result is a significant reduction of both image space RMSE in simulations, and a reduction of motion artifacts in the in vivo motion tests.

Conclusion:

The separability and convergence improvements afforded by the combined CNN+model-based method show the potential for meaningful post-acquisition motion mitigation in clinical MRI.

Introduction

Since its inception MRI has been hindered by artifacts due to patient motion, which are both common and costly [1]. Many techniques attempt to track or otherwise account and correct for motion during MRI data acquisition [2], [3], yet few are currently used clinically due to workflow challenges or sequence disturbances. While prospective motion correction methods measure patient motion and update the acquisition coordinates on the fly, they often require sequence modifications (insertion of navigators [4], [5]) or external hardware tracking systems [6], [7]. On the other hand, retrospective methods correct the data after the acquisition, possibly incorporating information from navigators [8] or trackers. Data-driven retrospective approaches operating without tracker or navigator input are attractive because they minimally impact the clinical workflow [9]–[13]. These algorithms estimate the motion parameters providing the best parallel imaging model agreement [14] through the addition of motion operators in the encoding [15]. Unfortunately, this approach typically leads to a poorly conditioned, nonconvex optimization problem. In addition to potentially finding a deficient local minimum, the reconstructions often require prohibitive compute times using standard vendor hardware, limiting the widespread use of the methods.

Machine learning (ML) techniques provide a potential avenue for dramatically reducing the computation time and improving the convergence of retrospective motion correction methods. Recent work has demonstrated how ML can be used to detect, localize, and quantify motion artifacts [16] and deep networks have been trained to reduce motion artifacts [17]–[20]. While the reliance on an ML approach alone shows promise, issues remain with the degree of artifact removal and the robustness of the process to the introduction of blurring or non-physical features. In this work, we attempt to harness the power of a CNN within a controlled model-based reconstruction. We demonstrate how ML can be effectively incorporated into retrospective motion correction approaches based on data consistency error minimization. Other works have balanced data consistency error with ML generated image priors (created using variational networks) to dramatically reduce reconstruction times and improve image quality for highly accelerated acquisitions [21]–[25]. Here, we demonstrate the effective use of ML to guide each step in an iterative model-based retrospective motion correction.

Specifically, we show how a CNN trained to remove motion artifacts from images can improve a model-based motion estimation. During each pass of the iterative process, a CNN image estimate is used as an image prior for the motion parameter search. This motion estimate is then used to create an improved image which can be propagated as input to the CNN to initialize the next pass of the algorithm. The quality of this image estimate can significantly improve the conditioning and convergence of the nonconvex motion parameter optimization. In addition, we demonstrate that with this high quality CNN image estimate, the motion optimization becomes separable. The separability of the motion model allows for small sub-problems to be optimized in a highly parallel fashion. This allows for a scalable extension of the model-based approach to include intra-shot (line-by-line) motion as well as the inter-shot motion in the RARE acquisition. The increased computation speed also facilitates implementation on standard vendor computation hardware.

Methods

An overview of the Network Accelerated Motion Estimation and Reduction (NAMER) method is shown in Fig. 1. The method is initialized with a SENSE [26] reconstruction of the raw k-space data. The motion correction algorithm is divided into three processes that are iteratively performed: (1) an artifact detecting CNN (Fig. 2) is applied to identify motion artifacts that are subsequently removed, (2) based upon the CNN output, a non-linear optimization estimates the associated motion parameters that minimize the data-consistency error of the forward model, and (3) a model-based reconstruction is performed to generate an updated image based on the motion parameters found in step (2). These steps are then repeated using the updated model-based reconstruction to further reduce the data consistency error and related motion artifacts. Example NAMER code can be found at https://github.com/mwhaskell/namer_mri.

Figure 1. NAMER method overview.

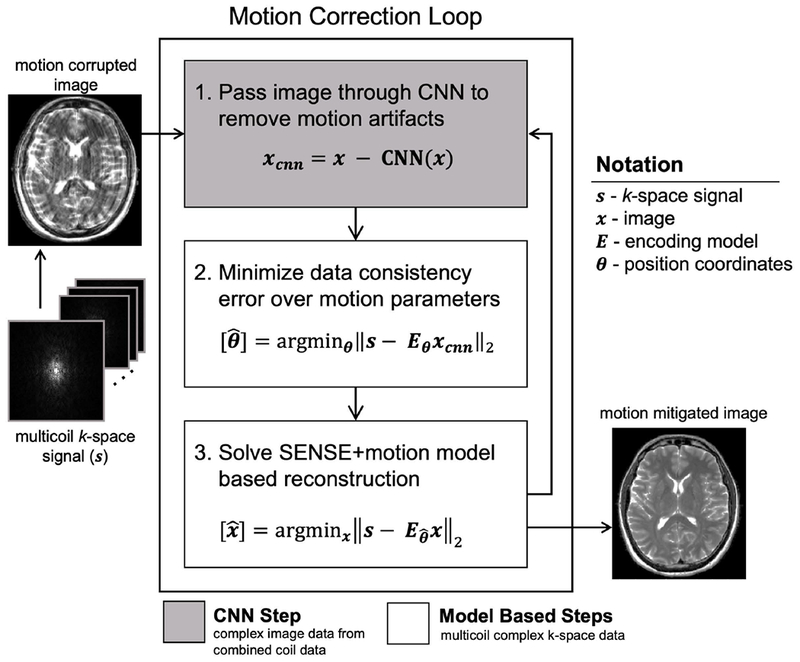
First, a motion corrupted image is reconstructed from the multicoil data, assuming no motion occurred. Next, motion mitigation is performed by looping through three steps: (1) remove motion artifacts in image space by passing the 2-channel complex image (1 channel for the real component and one channel for the imaginary component) through the motion detecting CNN, (2) search for the motion parameters by minimizing the multicoil data consistency error of a motion-inclusive forward model, using complex voxel values from the CNN image, and (3) reconstruct the full image volume using the motion-inclusive multicoil forward model and position coordinates from step (2).

Figure 2. Convolutional neural network for motion artifact detection.

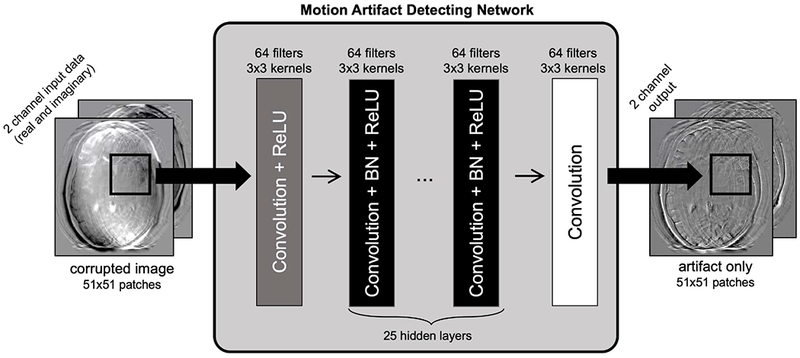
A motion corrupted image is input as two channels (corresponding to the real and imaginary components) to a 27-layer patch-based CNN consisting of convolutional layers, batch normalization, and ReLU nonlinearities. The network outputs the image artifacts, which can be subtracted from the input image to arrive at a motion mitigated image.

MRI Acquisition

T2-weighted RARE/TSE/FSE [27] data were acquired on 3T MAGNETOM Skyra and Prisma scanners (Siemens Healthcare, Erlangen, Germany) using the product 32-channel head array coil and default clinical protocols. The imaging parameters are: TR/TE=6.1s/103ms, in-plane FOV=220×220mm², 4mm slices, 448×448×35 matrix size, 80% phase resolution, R=2 uniform undersampling, and echo train length (ETL)=11. A 12s FLASH [28] scan provides motion robust auto-calibration data that is used to generate coil sensitivity maps (calculated using ESPRiT [29] from the BART toolbox [30]). In this work data from six healthy subjects were acquired in compliance with institutional practice. Data from four of the subjects were utilized to train the CNN, and the data from the two other subjects were used to evaluate the performance of our method through simulations and supervised motion experiments.

Training Data Generation

Training data for the CNN were created by manipulating raw k-space data (free of motion contamination) using the forward model described in [13] to simulate the effects of realistic patient motion trajectories. Motion trajectories were created using augmentation (shifting and scaling) of timeseries registration information from fMRI scans of patients with Alzheimer’s disease (see Supplementary Figure S1). The residual learning CNN attempts to identify the motion artifacts using an L₂-norm loss function against the motion corrupted input image minus the ground truth image. Ten evenly spaced slices from the four healthy subjects were used, and each slice was corrupted by 10 different motion trajectories. Thus, there were 400 motion examples available to choose from in order to create the training data.

The training data was refined through the exclusion of motion corrupted images with RMSE (compared to ground truth) that was greater than 0.50 or less than 0.12. Images with RMSE greater than 0.50 were excluded because they contained severe motion corruption artifacts that could bias the training (due to the large error). Images with RMSE less than 0.12 were excluded because they contained so few motion artifacts which were not productive toward training the CNN to detect artifacts. Overall 76 of the 400 examples were excluded, 61 for RMSE < 0.12 and 15 for RMSE > 0.50, leaving 324 remaining. To reduce the memory and computational footprint, 24 random cases were dropped to limit the training size to 300 motion cases. These 300 images were divided into patches of size 51×51 with a stride size of 10 (resulting in an overlap region of 41 voxels), which produced 1600 patches per motion corrupted image. For each image, 1250 out of 1600 patches were randomly selected to bring the total number of motion corrupted patches to 375k. From this set of patches, 300k were used for training and 75k used for validation (80/20 training/validation split).

Motion Artifact Detecting Convolutional Neural Network

Fig. 2 shows the 27 layer network topology, which follows previous work [31] and is implemented in Keras [32]. The network isolates the image artifacts within the two-channel (real and imaginary) motion corrupted input patch. The initial layer is a convolutional layer followed by a ReLU activation. The next 25 layers consist of a convolutional layer with batch normalization and ReLU activation, and the final layer is a convolution layer. The number of hidden layers was chosen because the loss function did not improve using more than 25 layers. Additional layers were not added to avoid potential problems with overfitting. Each convolutional layer uses 3×3 kernels with 64 filters. The network was trained using the Adam optimizer [33], with learning rate = 1e-4 and a mean squared error loss function.

Before being passed through the CNN, the images are scaled to range in magnitude from 0 to 1. Patches are then created, with size 51×51 (as in the training data) and a stride size of 8, which generated 2500 patches per image. After patches were passed through the CNN, they were combined and normalized by the number of patches overlapping at each pixel. No image padding was used for the examples in this paper since the FOV was not tight on the anatomy. The updated artifact free image, x_cnn, can be described mathematically as:

$${\mathit{x}}_{\mathit{cnn}}=\mathit{x}-\mathrm{CNN}(\mathit{x})$$

where CNN(x) is an image containing the detected motion artifacts within the input image x.

Motion Parameter Optimization

The vector containing the motion parameters, θ, is estimated from x_cnn through a non-linear optimization to minimize the data consistency error between the acquired data and the forward model described by the encoding matrix. The encoding includes the effect of the motion trajectory as well as the Fourier encoding and undersampling. The encoding matrix, E_θ, for the motion parameters θ, is described mathematically as:

$${\mathit{E}}_{\theta }={\mathit{UFCT}}_{\theta }{\mathit{R}}_{\theta }$$ (1)

where R_θ is the rotation operator, T_θ is the translation operator, C applies coil sensitivities, F is Fourier encoding, and U is the sampling operator. The motion parameters are found by minimizing the data consistency error between the acquired k-space data, s, and the k-space data generated by applying the motion forward model E_θ to the CNN image:

$$[\widehat{\theta }]={\mathrm{argmin}}_{\theta }{\parallel \mathit{s}-{\mathit{E}}_{\theta }{\mathit{x}}_{\mathit{cnn}}\parallel }_2$$ (2)

The minimization is performed using a quasi-Newton search available with the built in fminunc function in MATLAB (Mathworks, Natick, MA).

As discussed in prior work [11], [13], the underlying image and motion parameters are tightly coupled which prohibits the separation of the optimization variables into orthogonal subsets. This directly limits the performance of alternating methods to only 1 or 2 productive steps during each alternating pass. However, we will demonstrate that the application of the CNN allows for the efficient decomposition of the optimization. Specifically, the motion parameters, θ, which are typically optimized in a single cost function as shown in (2), can be separated to create a set of much smaller optimization problems, where we can independently estimate θ for each shot of the RARE sequence (11 k-space lines in our case). The motion parameters can then be indexed by the shot number; θ = [θ₁, θ₂, … θ_N] where N is the total number of shots, and each vector θ_n contains the six rigid body motion parameters for a given shot. The motion forward model, E_θ, is reduced to only generate the subset of k-space associated with shot n, and is denoted as E_θn. Similarly, the acquired data for a single shot is denoted as s_n and the cost function for a single shot is:

$$[{\widehat{\theta }}_n]={\mathrm{argmin}}_{{\theta }_n}{\parallel {\mathit{s}}_n-{\mathit{E}}_{{\theta }_n}{\mathit{x}}_{\mathit{cnn}}\parallel }_2$$ (3)

By using (3) instead of (2), the number of unknowns for any optimization is decreased by a factor of N (the total number of shots). These separate minimizations can be done in parallel, which greatly improves the computational scalability of the retrospective motion correction approach.

This computational efficiency allows us to consider further refinement of the optimization variables. Namely, we extend cost function (3) to consider motion within the RARE shots (intra-shot motion) by assigning additional motion parameters to the individual lines of k-space within a shot. Thus θ_n is expanded from size 6×1 to size (6*ETL)x1, and can be written as θ_n = [θ_n,1, θ_n,2, … θ_n,L] where L is the number of lines per shot (the ETL of the RARE sequence) and θ_n,l contains the six rigid body motion parameters for shot n, line l. The forward model is further reduced to E_θn,l to generate the k-space data only for line l of shot n, and the signal for that line is written as s_n,l. To find the optimal motion parameters for an individual line, the cost function becomes:

$$[{\widehat{\theta }}_{n,l}]={\mathrm{argmin}}_{{\theta }_{n,l}}{\parallel {\mathit{s}}_{n,l}-{\mathit{E}}_{{\theta }_{n,l}}{\mathit{x}}_{\mathit{cnn}}\parallel }_2$$ (4)

The ability to selectively refine the optimization variables is extremely valuable as only small portions of the acquisition are likely to suffer from significant intra-shot motion. These shots show significant data consistency error and are often considered as outliers to be discarded [12]. However, with the separable model approach we can expand the model dynamically. The parallel optimizations in Eqn. (3) can be performed for each shot, and then shots that had large data inconsistency after this first pass can then be improved upon using Eqn. (4) (see Supplementary Figure S2). By using this multiscale optimization for the motion parameters, the length of θ can vary depending on how many shots require intra-shot correction, with the minimum length being 6N and a maximum length of 6NL. Similar to Eqn. (2), a quasi-Newton search using MATLAB’s fminunc is performed for equations (3) and (4).

Model-based Image Reconstruction

Using the raw k-space data, s, and the current estimate for the motion trajectory, $\widehat{\theta }$, the linear least squares image reconstruction problem is solved using the conjugate gradient method to find the image, x:

$$[\widehat{\mathit{x}}]={\mathrm{argmin}}_{\mathit{x}}{\parallel \mathit{s}-{\mathit{E}}_{\widehat{\theta }}\mathit{x}\parallel }_2$$ (5)

The model-based reconstruction, $\widehat{\mathit{x}}$, can then be fed back through the CNN to identify remaining artifacts. The three steps (apply CNN, motion search, solve for image) are repeated until a stopping criterion is met (either a maximum number of iterations or the change in $\widehat{\mathit{x}}$ is below a given threshold). In all cases, the final image returned by NAMER is the model-based reconstruction from Eqn. (5).

Simulation Experiments

The performance of the motion detecting CNN was tested using simulated motion corrupted data. For an unseen subject, each slice was motion corrupted and passed through the CNN. Image space RMSE was calculated for all the motion corrupted slices. Next, a single slice was chosen from the imaging volume and NAMER was performed using both a single cost function (Eqn. (2)), and a separable cost function (Eqn. (3) for all shots). Motion correction using an alternating minimization (only the 2^nd and 3^rd steps of the NAMER loop) was also performed with both a single and separable cost function, in order to compare to previous methods [11]. No intra-shot motion corruption or correction was used for the comparison experiment. We performed 20 total iterations for all four methods, and the algorithm convergence and final images are compared. Additionally, a simulation using NAMER with the separable cost function was performed in a case with intra-shot motion corrupted data.

We also investigate the potential of combining NAMER with previously developed reduced modeling strategies [13] using simulations. During the third step of NAMER (update of the voxel values), we only updated a strip of voxels that corresponded to the width of a single patch (51 voxels), and then passed the partially updated image through the CNN at the next step. We then evaluated the total number of voxel updates required using a full volume solve versus a targeted voxel update during step 3 of NAMER.

In Vivo Experiments

NAMER was applied to a single brain volume from a healthy subject who was instructed to move during the scan. The subject was asked to shake their head in a “no” pattern for a few seconds, approximately halfway through the 2-minute scan. This motion pattern was used in order to restrict motion artifacts to those caused by within slice motion. Here, a 2D implementation of NAMER, correcting for in-plane translations and rotations, was employed. First, eight iterations of NAMER were performed for each slice, assuming motion only occurred between the shots. Next, one iteration of line-by-line motion correction was performed for the three shots that occurred during the middle of the scan (shots 10, 11, and 12 out of 17 total) and had larger data consistency error.

Results

We present results demonstrating the motion mitigation capabilities of NAMER in simulations and a supervised motion experiment. First, we show that the CNN removes motion artifacts and decreases image space RMSE in all slices of an unseen subject with simulated motion corruption. Next, we show in simulations that NAMER removes more motion artifacts than an alternating minimization for both a single cost function (Eqn. 2) and a separable cost function (Eqn. 3). Unlike the alternating method, the performance of NAMER does not suffer when using a separable cost function. Finally, NAMER removes inter-shot and intra-shot motion artifacts from an in vivo motion experiment where the subject was instructed to move during the scan.

Performance of convolutional neural network

Fig. 3 shows the artifact removal performance of the CNN when applied to simulated motion corruption of data from a subject not included in the training data. Significant ringing artifacts are removed for all slices. When compared to the ground truth images, the simulated motion resulted in an average RMSE of 20% across the slices. The average error was reduced to 16.1% through the application of the CNN. As can be seen in Fig. 3-C, the network removes a significant portion of the motion artifacts, but some residual ringing and blurring are present.

Figure 3. CNN artifact mitigation across whole brain.

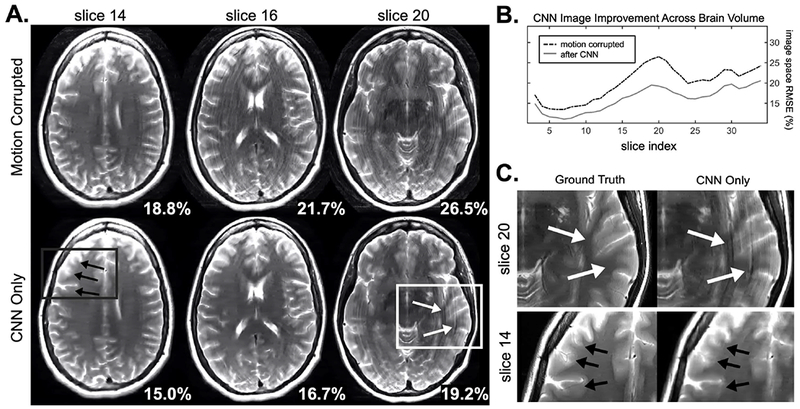
A. Representative slices of CNN motion artifact mitigation across the brain volume for a simulated motion example. Bottom right shows the image space RMSE compared to the ground truth image. B. For all slices in the brain volume, the image space RMSE decreased after the CNN, with an average improvement of 3.9%. C. Despite large reductions in artifacts shown in A., compared to the ground truth ringing and blurring artifacts still remain.

Simulated motion correction using NAMER

Fig. 4 shows the performance of NAMER motion correction compared to an alternating method. Each approach was applied to simulated motion corruption which produced a 43.8% image space RMSE (compared to the ground truth). The final images returned by NAMER for the single cost function (Eqn. 2) and separable cost function (Eqn. 3) formulations show negligible remaining artifacts and the image space RMSE decreased to 12.7% and 11.7% respectively. For the alternating method, significant artifacts remain after the 20 optimization steps. The lack of separability of the alternating optimization is observed as the single cost function outperformed the separable cost function. In that case, the single cost function produced cleaner images with a lower final RMSE (28.2% compared to 31.2%).

Figure 4. NAMER compared to alternating method in simulated motion data.

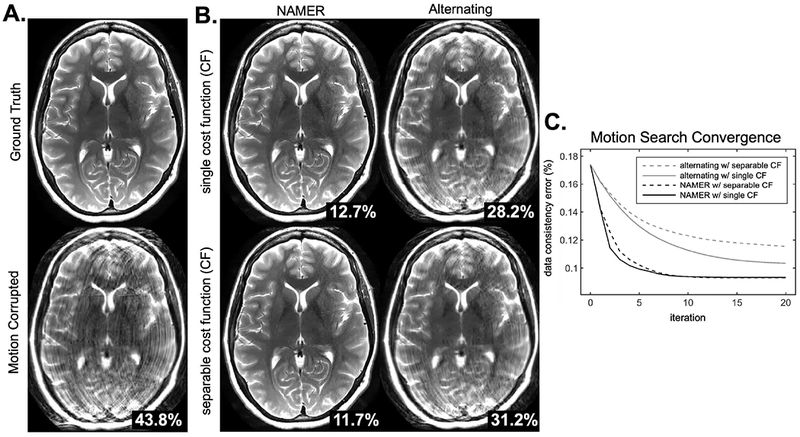
A. Original ground truth image and simulated motion corrupted image. B. Image results after 20 iterations of NAMER or an alternating motion correction method. The white numbers in the bottom right are image space RMSE compared to the ground truth image. Top row shows the reconstruction results when using a single cost function for the motion minimization (Eqn. 2), bottom row shows results from a separable cost function for the motion minimization (Eqn. 3). C. Convergence of the four methods displayed in B are shown. Both of the NAMER implementations converge more quickly, and to a lower final data consistency error.

The convergence rates of the NAMER and alternating optimizations can be seen in Fig 4-C. The initial data consistency error of the motion corrupted image was 17.4% (corresponding to 43.8% image space RMSE), compared to a data consistency error of 9.4% when using the ground truth motion. With NAMER motion correction, the data consistency error was reduced to the ground truth level of 9.4% after 9 iterations for both the single cost function (Eqn. 2) and separable cost functions (Eqn. 3). After 20 iterations, the alternating method was only able to achieve data consistency errors of 10.4% for the single cost function, and 11.6% for the separable cost function.

For the simulated motion corruption example shown in Figure 4, using a reduced model [13] for image reconstruction (instead of a full volume solve at each NAMER iteration) requires 33% fewer voxels updates. Additionally, NAMER simulations of intra-shot motion correction also produced an artifact mitigated image (Supplementary Figure S3).

NAMER motion correction applied to supervised in vivo motion experiment

NAMER motion correction was applied across the full 3D brain volume to correct artifacts produced by the subject shaking their head “no” during the acquisition. Slice 14 from the 35 slice stack is shown in Fig. 5. The image without any motion correction contains substantial ringing artifacts. Using only between shot NAMER correction with a separable cost function (Eqn. 3) resulted in residual ringing. By refining the model to optimize individual lines within the shots that contain the largest data consistency error (Eqn. 4), the ringing artifacts are significantly reduced. The data consistency RMSE (shown in bottom right of the images in Fig. 5) decreased for all slices within the volume. For slices within the brain region there was an average reduction of 0.2% between the no correction reconstruction and the within shot motion correction. Similar qualitative improvements in image quality were observed for the slices not shown in Fig. 5, and two additional slices are presented in Supplementary Figure S4.

Figure 5. NAMER in vivo inter- and intra-shot motion correction.

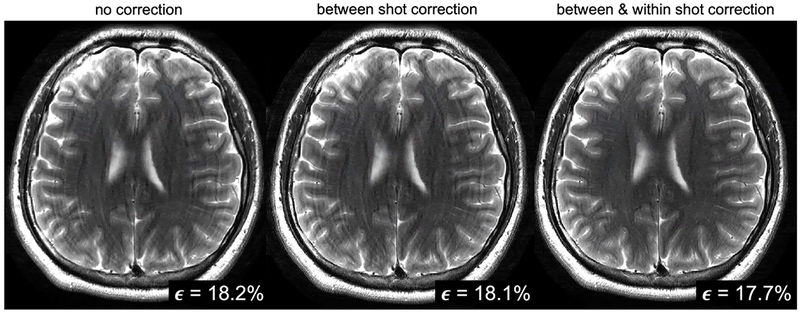
Reconstructed images assuming no motion occurred, correcting for motion between shots (inter-shot correction), and correction results after allowing fine-tuning of the motion parameters for each line of k-space at highly corrupted shots (intra-shot correction). Motion artifacts are significantly reduced by allowing the motion parameters to vary across the lines within a shot, as shown in the right column. Data consistency error values are shown in the bottom right of each image.

For a single slice of real motion corrupted data (subject 2 in Supplementary Figure S2), the first step of NAMER (CNN evaluation) took on average (averaged across the iterations) 10s on a 12GB NVIDIA Tesla P100. The I/O time to interface the CNN to MATLAB required an additional 40s. The second step of NAMER (motion optimization) took on average 2.7 minutes, and the final step of NAMER (full image solve with motion parameters included) took on average 3.6 minutes.

Discussion

In this work we introduce a scalable retrospective motion correction method that effectively integrates a motion artifact detecting CNN within a model-based motion estimation framework. The image estimates provided by the CNN allow for separation of the motion parameter search into either individual shots (containing 11 k-space lines in our case) or individual k-space lines. The small optimization problems can be efficiently computed in an embarrassingly parallel fashion. This results in a highly scalable algorithm that has the potential for clinical acceptance. In addition, the separability of the motion optimization facilitates efficient refinement of the model to consider motion disturbances that can occur within a shot. These specific shots can be clearly identified due to their large data consistency error and line-by-line motion correction can be applied. The separability afforded by our method allows us to focus on further improving these limited number of troubled regions without incurring a substantial computational burden. The benefits of this model refinement can be clearly observed (e.g. Fig. 5).

The model-based reconstruction presented here also relaxes concerns about the accuracy, robustness, and predictability of the CNN. As can be seen in Fig. 3, the CNN is able to reduce motion artifacts across all slices from a previously unobserved data set. But, following our expectations, the CNN is not able to completely remove all of the artifacts (see Fig. 3, slice 20) and it can introduce undesirable blurring to the images (see Fig. 3, slice 14). However, the CNN output is accurate enough to both improve the convergence of the reconstruction and promote the separability of the motion parameter optimization. Through the inclusion of more diverse and larger training data sets we expect these benefits to grow. In addition, the NAMER method presented in this work utilizes a standard convolution network. Further improvement might be achieved with more sophisticated networks or loss functions [34]. The topology used here could benefit from further optimization of design parameters, where a sensitivity analysis across network attributes could be performed (i.e. patch size, number of hidden layers). It is important to note that the optimal network may not necessarily be the one which has the lowest validation loss during network training, but instead will be the network that best aids in advancing the motion optimization (step 2 of NAMER).

The NAMER motion mitigation method was assessed through both simulations and supervised in vivo motion experiments. These include testing the CNN artifact removal capabilities on simulated 2D motion corrupted data, simulations to show convergence of the method toward a ground truth, and the supervised head shaking experiment where 2D motion occurred parallel to the imaging planes. The reconstruction framework presented here does generalize to 3D motion trajectories and we think similar benefits can be achieved with adequate training of the CNN, although these remain to be demonstrated. For 3D motion correction with NAMER, the 2D CNN developed here can still be used to mitigate some motion artifacts. However, we think training data that incorporates through plane motion effects will increase the performance of the CNN in general patient motion situations. Due to the limited range of rigid body brain motion, we anticipate that a CNN could be trained on small stacks of slices, where the objective is to remove artifacts from the interior voxels in the stack. The challenges we anticipate in extending NAMER to 3D are present in both the CNN step and the model-based motion optimization. First, the performance of the CNN on data corrupted by through-plane motion that includes spin history effects (which are currently not in the simulated training data model) would need to be evaluated. Second, previous model-based motion optimizations [12], [13] did not include spin history effects into their motion models, and this could hinder NAMER’s performance even if the CNN was able to filter out many of these effects.

The NAMER framework can also accommodate state-of-the-art model reduction and data re-weighting strategies. Prior works have also shown that outlier rejection or soft gating can be beneficial for the mitigation of through plane motion artifacts [12], [35], and we see those prior works as complementary to the NAMER method. The outlier rejection strategy from those works could be used to determine which shots need to have intra-shot motion correction (shown in Fig 5). Further, the data interpolation step in [12] could instead be replaced with our motion mitigating CNN, similar to the cascading network approach in [36]. This could potentially relax the requirement of 2× oversampling used in [12] to achieve robust through plane motion correction. NAMER could also be combined with prior work shown in [13] that performed reduced modelling in image space, and preliminary simulation results presented here demonstrate the potential of the approach, with 33% fewer voxel updates required. Replacing the third step of the NAMER algorithm (see Fig 1) with a reduced model image reconstruction could improve algorithm efficiency and in this case the CNN would only need to evaluate the patches that contain updated voxel values.

Supplementary Material

Supp figS1-4

Supplementary Figure S1. Motion trajectories used for CNN training. These are the rigid body parameters used to create motion corrupted images for CNN training, which were generated by registering fMRI timeseries data of Alzheimer’s disease subjects. There were 10 subjects with 2-3 experiments per subject, leading to a total of 27 trajectories. Since the trajectories are 120 frames long and we need only 17 for a single image, we had 189 unique motion trajectories, which were augmented with shifting and scaling to produce 400 motion trajectories total.

Supplementary Figure S2. How to determine if intra-shot correction is needed. A. Two different subject were imaged and asked to shake their heads in a “no” pattern to generate in-plane motion artifacts. B. NAMER was performed on both subjects, only correcting for between shot motion (i.e. assuming no motion during the echo train readout). C. The data consistency errors were evaluated after inter-shot correction, and if high data consistency shots were present, intra-shot correction was performed. If not, the image from between shot correction is returned. D. Final NAMER image for subject 1 and subject 2.

Supplementary Figure S3. Simulated intra-shot motion correction. A. Motion artifacts were simulated from a ground truth image, using a motion case which contained motion during the readout of the echo train (see dotted lines in B.). NAMER motion correction was applied first between shots (inter-shot correction), and then applied allowing there to be motion during three shots of the readout (shots 10, 11, and 12, which start at lines 110, 111, and 122 respectively). When intra-shot motion occurs, only within shot motion correction fully removes for the artifacts, in this case signal dropouts and hyperintensities, as noted with the red arrows. B. The output motion trajectories from NAMER compared to the ground truth motion parameter are shown. (Left) motion parameters from the inter-shot correction (Right) motion parameters from intra-shot correction.

Supplementary Figure S4. Full volume NAMER motion correction. A. NAMER motion correction results for three slices corrupted by subject motion during the acquisition. Left column shows the reconstruction with no motion correction, middle shows the results of NAMER motion correction when only correcting for between shot motion (i.e. assuming no motion during the readout), and the right column shows the results after allowing fine-tuning of the motion parameters for each line of k-space at highly corrupted shots. Bottom rights shows data consistency error. B. Zoomed in portions of images from part A. Ringing is reduced in slices 14 and 18, and in slice 29 blurring is reduced using NAMER. All other shots in the volume achieved similar levels of motion correction.