Restoring universality to the pinch-off of a bubble

Significance

We observe the formation of bubbles and drops on a daily basis, from dripping faucets to raindrops entraining bubbles on the surface of a lake. The ubiquity of the phenomenon masks the fascinating underlying nonlinear dynamics that is such an important aspect of modern physics. Here, we report on the surprising observation that confinement makes the pinch-off of a bubble a universal process, as opposed to the unconfined case, where pinch-off is sensitive to the details of the experimental setting. We explain how the motion of the contact line, where the liquid, gas, and solid phases meet, leads to self-similar dynamics that effectively erase the memory of the system. Our observations have implications for immiscible flow phenomena from microfluidics to geophysical flows, where confinement, together with fluid–solid physicochemical interactions, play a key role.

Abstract

The pinch-off of a bubble is an example of the formation of a singularity, exhibiting a characteristic separation of length and time scales. Because of this scale separation, one expects universal dynamics that collapse into self-similar behavior determined by the relative importance of viscous, inertial, and capillary forces. Surprisingly, however, the pinch-off of a bubble in a large tank of viscous liquid is known to be nonuniversal. Here, we show that the pinch-off dynamics of a bubble confined in a capillary tube undergo a sequence of two distinct self-similar regimes, even though the entire evolution is controlled by a balance between viscous and capillary forces. We demonstrate that the early-time self-similar regime restores universality to bubble pinch-off by erasing the system’s memory of the initial conditions. Our findings have important implications for bubble/drop generation in microfluidic devices, with applications in inkjet printing, medical imaging, and synthesis of particulate materials.

From dripping faucets to children blowing soap bubbles, we observe the formation of drops and bubbles on a daily basis. This seemingly simple phenomenon, however, has long puzzled and attracted scientists, from the early descriptions of da Vinci, Savart, Plateau, and Rayleigh (1–3) to advanced experimental techniques that yield precise observations of the interface evolution leading to pinch-off (4–9). Most previous studies of singularities during bubble or drop formation have focused on unbounded fluid domains (10–17). Many natural phenomena and industrial processes, however, often involve flows under confinement (18–23), where the dimensionality of the confined geometry is known to strongly influence the pinch-off (24–28). These studies have assumed that a continuous liquid phase coats all of the bounding surfaces. In many situations, however, one encounters partially wetting liquids, which naturally lead to the presence of contact lines, where a fluid–fluid interface meets the solid surface (29).

Here, we study the pinch-off of a bubble in confinement in the partial wetting regime. We show that the moving contact line singularity (30, 31) dominates the viscous dissipation at early times, leading to an axially dominated flow and the emergence of an early-time self-similar regime, which then crosses over to a late-time regime, where the flow is mainly radial and the viscous dissipation is dominated by the pinch-off singularity. While the observation of different self-similar regimes is expected when the balance of forces between inertia, viscosity, and capillarity changes (11, 32, 33), here we show that in our system, the cross-over between self-similar regimes occurs even though the entire evolution is controlled by a balance between viscous and capillary forces.

The separation of length and time scales in the vicinity of a singularity suggests that the local balance of forces should become independent of the details of the initial or boundary conditions, making the dynamics of the pinch-off universal (10). Surprisingly, in the case of the pinch-off of an inviscid bubble in an unbounded ambient viscous liquid, the local structure of the singularity is sensitive to the details of the experimental conditions, rendering the pinch-off nonuniversal (13, 34–36). Here, we show that the presence of the early-time regime in a confined geometry establishes the tube diameter as the only length scale in the problem and erases the system’s memory of the experimental details and initial conditions, leading to the universality of the bubble pinch-off.

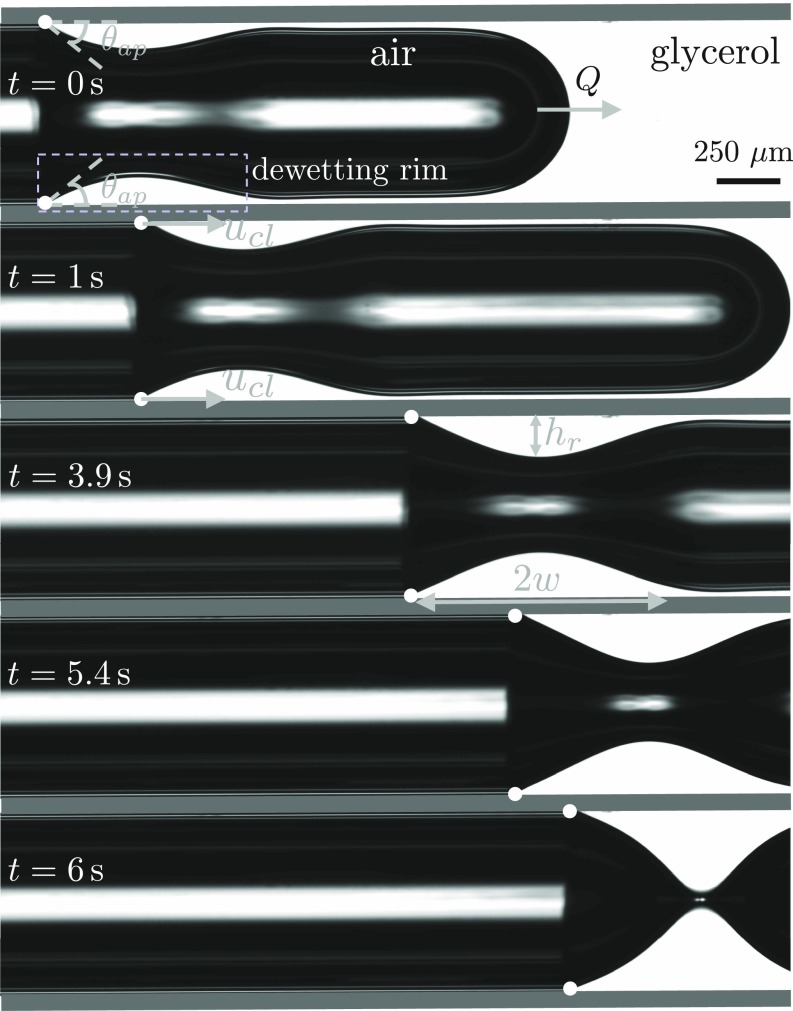
We study the bubble generation process in a microcapillary tube (diameter $d=\mathrm{280,750}\hspace{0.17em}\mu \mathrm{m}$). The tube is connected to a syringe pump on one end and is open to the atmosphere on the other end (Fig. 1). We first fill the tube with a water–glycerol mixture (viscosity $\mu =0.2$ or $1.4\hspace{0.17em}\mathrm{P}\mathrm{a}.\mathrm{s}$ depending on composition, and surface tension $\gamma =65\hspace{0.17em}\mathrm{m}\mathrm{N}/\mathrm{m}$) that is partially wetting to the tube (${\theta }_{eq}\approx 65^{○}$) and then start withdrawing the liquid using the pump at a specified flow rate $Q$. At low flow rates, the meniscus deforms slightly and moves downstream at a constant velocity $U=4Q/\left(\pi d^2\right)$. When the imposed flow rate is higher than a critical value, however, a wetting transition occurs: the meniscus loses its quasi-static geometry and air starts invading the tube in the form of an extending axial finger, leaving a film of the viscous liquid on the walls (37). Fig. 1 shows that the entrained liquid film immediately starts to dewet along the tube walls. As the contact line recedes, the rim ahead of it grows and the bubble neck shrinks until it finally pinches off and forms a bubble (Movie S1).

Fig. 1.

Displacement of a partially wetting liquid from a microcapillary tube. As the glycerol (white) is withdrawn from the right end of the tube with a constant flow rate $Q$, air (black) invades the tube from the left end at atmospheric pressure and entrains a thin film of the glycerol on the tube walls (the white stripe in the middle of the tube is due to light refraction; SI Appendix, section 1). The entrained liquid film then starts receding along the tube axis with a velocity $U_{\mathrm{c}\mathrm{l}}$, forming a growing dewetting rim ahead of the contact line, where the liquid, solid, and air meet at a nonzero apparent contact angle ${\theta }_{ap}$. As the liquid rim grows, the bubble neck diameter shrinks and ultimately leads to pinch-off and the formation of a bubble.

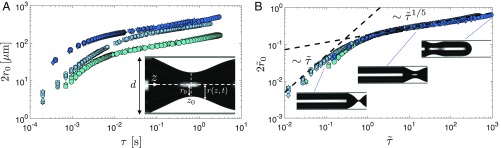
In the case of bubble formation in a large quiescent tank, the balance of radial viscous flow and surface tension causes the bubble neck diameter to shrink linearly in time (35, 38). In contrast, here, during the process of bubble pinch-off in a microcapillary tube, the evolution of the diameter of the bubble neck indicates the presence of two distinct self-similar regimes (Fig. 2A), as illustrated with the results from 12 different experiments: the bubble neck diameter initially follows a ${\tau }^{1/5}$ scaling before transitioning to the familiar linear scaling regime, where $\tau =\left(t_0-t\right)$ is the time to the singularity with $t_0$ as the pinch-off time (Fig. 2B). The Reynolds number is defined as $\mathrm{R}\mathrm{e}=\rho Ul/\mu$, where $\rho$ is the liquid density, and $U$ and $l$ are the characteristic velocity and length scales. At early times, the characteristic velocity and length scales are set by the moving contact line and the tube diameter, leading to $U\sim U_{cl}\sim \left(\gamma /\mu \right){\theta }_{eq}^3$ and $l\approx h_r^2/w$, where $h_r$ and $w$ represent the height and width of the dewetting rim, respectively (Fig. 1). At late times, in the vicinity of the pinch-off, the bubble neck can be idealized as a cylindrical thread of radius $r_0$ that is shrinking in time, leading to $U\sim d{r}_0/d\tau$ and $l\sim r_0$. During the entire evolution, $\mathrm{R}\mathrm{e}\ll 1$ and inertia can be neglected.

Fig. 2.

Evolution of the neck diameter versus time $\tau =\left(t_0-t\right)$ to pinch-off at $t_0$. (A) Data from 12 different experiments are shown: light blue symbols correspond to $d=750\hspace{0.17em}\mu \mathrm{m}$ and $\mu =1.4\hspace{0.17em}\mathrm{P}\mathrm{a}.\mathrm{s}$; the cyan symbols correspond to $d=280\hspace{0.17em}\mu \mathrm{m}$ and $\mu =1.4\hspace{0.17em}\mathrm{P}\mathrm{a}.\mathrm{s}$; the dark blue symbols correspond to $d=750\hspace{0.17em}\mu \mathrm{m}$ and $\mu =0.2\hspace{0.17em}\mathrm{P}\mathrm{a}.\mathrm{s}$. Each color represents data corresponding to four different flow rates with $\mathrm{C}\mathrm{a}=\mu U/\gamma \in \left[0.008,0.02\right]$, where $U=4Q/\left(\pi d^2\right)$ and $Q$ is the liquid flow rate. While changing the flow rate does not influence the evolution of the bubble neck diameter ($2r_0$), changing $\mu$ or $d$ shifts the curves. (B) When time and length scales are nondimensionalized with the visco-capillary time scale $t*=\mu d/\gamma$ and the tube diameter $d$, respectively, the data corresponding to all 12 experiments collapse onto a single curve ($\tilde{\tau }=\tau /t*=\gamma \tau /\left(\mu d\right)$, and ${\tilde{r}}_0=r_0/d$). Here, two self-similar regimes can be observed: an early-time regime, which follows a $1/5$ power-law scaling in time, and a late-time regime very close to the point of pinch-off, which follows a linear scaling in time.

To gain an understanding of this early-time self-similar regime for the time evolution of the bubble radius, we consider the dynamics of the growing dewetting rim (Fig. 1). This can be analyzed using a long-wave approximation (37), which assumes that the flow is mainly parallel to the tube axis. Near the point of pinch-off, we postulate that the shape of the profile becomes self-similar: $\tilde{R}\left(\xi \right)=\tilde{r}\left(\tilde{z},\tilde{\tau }\right)/{\tilde{\tau }}^{\alpha }$, and $\xi =\left(\tilde{z}-{\tilde{z}}_0\right)/{\tilde{\tau }}^{\beta }$ with $\alpha$ and $\beta$ as constants (Fig. 2A, Inset); here, all of the length scales are nondimensionalized by the tube diameter $d$, and the dimensionless time to the singularity is defined as $\tilde{\tau }=\tau /t^{*}$, where $t^{*}=\mu d/\gamma$ is the visco-capillary time scale. Unlike the inertia-viscocapillary regime, where fluid properties introduce an intrinsic length scale into the problem $l_{\nu }={\mu }^2/\gamma \rho$ (10), the visco-capillary regime discussed here requires an external length scale—the tube diameter $d$. Using this ansatz, we arrive at an ordinary differential equation for the neck profile (SI Appendix, section 2):

$$\begin{array}{ll}\hfill & \left(-\alpha \tilde{R}+\beta \xi {\tilde{R}}^{\prime }\right){\tilde{\tau }}^{\alpha -1}\hfill \\ \hfill & =\frac{1}{{\left(16\right)}^2}\frac{1}{\tilde{R}}\left(\left[-\frac{2}{{\tilde{R}}^3}{\tilde{R}}^{\prime 2}+\frac{1}{{\tilde{R}}^2}{\tilde{R}}^{″}\right]{\tilde{\tau }}^{-2\left(\alpha +\beta \right)}+{\tilde{R}″}^{″}{\tilde{\tau }}^{-4\beta }\right),\hfill \end{array}$$ [1]

where primes indicate differentiation with respect to $\xi$. The left-hand side of Eq. 1 represents the viscous forces, and the right-hand side represents the capillary forces: the first two terms represent the out-of-plane curvature and the last term represents the in-plane curvature. The only way for all of the terms to balance in time is to have $\alpha =\beta =1/5$, leading to $\tilde{R}\left(\xi \right)=\tilde{r}\left(\tilde{z},\tilde{\tau }\right)/{\tilde{\tau }}^{1/5}$, and $\xi =\left(\tilde{z}-{\tilde{z}}_0\right)/{\tilde{\tau }}^{1/5}$. This result is consistent with the experimentally observed scaling of the neck diameter as a function of time to pinch-off in the early-time self-similar regime shown in Fig. 2B. The self-similar ordinary differential equation governing the neck profile in the early-time regime therefore has the following form:

$$\left(-\tilde{R}+\xi {\tilde{R}}^{\prime }\right)=\frac{5}{{\left(16\right)}^2}\frac{1}{\tilde{R}}\left(\left[-\frac{2}{{\tilde{R}}^3}{\tilde{R}}^{\prime 2}+\frac{1}{{\tilde{R}}^2}{\tilde{R}}^{″}\right]+{\tilde{R}″}^{″}\right).$$ [2]

The early-time self-similar regime is an example of self-similarity of the first kind, in which the scaling exponents can be uniquely determined based on dimensional analysis (39), as outlined above. The cross-over to the late-time self-similar regime, however, hints at the breakdown of the long-wave model very close to the point of pinch-off.

An important point here is that the long-wave approximation is developed for the dewetting rim, and not for the bubble neck. The relevant length scales are therefore the height ($h_r$) and width ($2w$) of the dewetting rim (Fig. 1), the ratio of which determines the apparent contact angle as ${\theta }_{ap}=2h_r/w\approx 30^{○}$, which is small enough for the long-wave approximation to be valid (40, 41). This observation is further confirmed in our earlier work, showing an excellent match between the experimentally observed profiles and the theoretical prediction (37). Of course, the long-wave approximation ultimately breaks down as the slope of the meniscus near the point of singularity diverges, leading to a cross-over to the late-time self-similar regime. While both regimes are governed by a balance of capillary and viscous forces, the cross-over occurs due to a change in the nature of the viscous flow in the dewetting film from axially dominated to radially dominated, as the dominant dissipative process changes from the moving contact line singularity to the pinch-off singularity (Movie S2).

To estimate the cross-over time between the two regimes, we compare their corresponding radial velocities. In the early-time regime, the growth rate of the dewetting rim is proportional to the velocity of the receding contact line, i.e., $d{r}_0/d\tau \sim U_{\mathrm{c}\mathrm{l}}\sim \left(\gamma /\mu \right){\theta }_{eq}^3$, which is nearly constant for a given wettability (37, 41). In the late-time regime, the thin bubble neck close to the point of singularity can be approximated as an axisymmetric cylinder, and the flow in the outer viscous fluid can be approximated as purely radial. The normal viscous stress generated by the radial flow is balanced by surface tension, leading to $d{r}_0/d\tau \sim \left(\gamma /\mu \right)e^{{-\tau /t}^{*}}$ as an estimate for the radial velocity in the late-time regime (SI Appendix, section 3). Note that very close to the point of pinch-off (${\tau /t}^{*}\ll 1$), we recover the familiar linear scaling in time (13, 38). Equating the two radial velocities corresponding to the early- and late-time regimes, we obtain an estimate of the cross-over time ${\tau }_c\sim t^{*}=\mu d/\gamma$, indicating that the visco-capillary time scale sets the point of transition between the two regimes. Fig. 2B shows that, indeed, using the visco-capillary time scale and the tube diameter as the characteristic time and length scales leads to the collapse of all data corresponding to 12 different experiments with different tube diameters ($d=\mathrm{280,750}\hspace{0.17em}\mu \mathrm{m}$), liquid viscosities ($\mu =0.2,1.4\hspace{0.17em}\mathrm{P}\mathrm{a}.\mathrm{s}$), and flow rates ($\mathrm{C}\mathrm{a}=\mu U/\gamma \in \left[0.008,0.02\right]$).

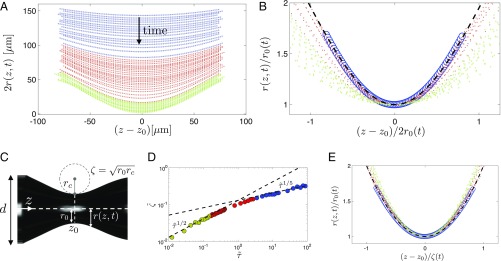
To test the self-similarity of the bubble neck profile, we probe its evolution in time in Fig. 3A (for the experiment with $d=750\hspace{0.17em}\mu \mathrm{m}$, $\mu =1.4\hspace{0.17em}\mathrm{P}\mathrm{a}.\mathrm{s}$, and $\mathrm{C}\mathrm{a}=0.008$), where the blue and green symbols correspond to the early- and late-time regimes, respectively, and red corresponds to the transition between the two regimes. The long-wave model predicts that the bubble neck diameter and also its axial extent both scale as ${\tilde{\tau }}^{1/5}$. In Fig. 3B, we show that, indeed, scaling both the neck diameter and axial dimension with the the minimum neck diameter collapses the profiles in the early-time regime (blue symbols). The self-similar solution of the long-wave model Eq. 2 (black dashed line) fits the data in this regime. This observation further confirms the validity of the long-wave model in the early-time self-similar regime. The data in the late-time regime (green symbols), however, deviate from the predictions of the long-wave theory.

Fig. 3.

Self-similarity of the neck profile. (A) The evolution of the bubble neck profile in time (data corresponding to $d=750\hspace{0.17em}\mu \mathrm{m}$, $\mu =1.4\hspace{0.17em}\mathrm{P}\mathrm{a}.\mathrm{s}$, and $\mathrm{C}\mathrm{a}=0.008$); blue and green symbols represent the data corresponding to the early and late-time self-similar regimes, and red symbols represent the transition between the two. (B) Scaling the neck profile with the minimum neck diameter collapses the data corresponding to the early-time self-similar regime, where $\tilde{R}\left(\xi \right)=\tilde{r}\left(\tilde{z},\tilde{\tau }\right)/{\tilde{\tau }}^{1/5}$ and $\xi =\left(\tilde{z}-{\tilde{z}}_0\right)/{\tilde{\tau }}^{1/5}$. The dashed line, overlaying the blue symbols corresponding to the early-time self-similar regime, represents the self-similar solution of the long-wave model (SI Appendix, section 2). The data corresponding to the late-time self-similar regime, however, deviate from the predictions of the long-wave model. (C) The definition of parameters used to characterize the bubble neck profile. (D) The evolution of the axial length scale defined as $\tilde{\zeta }=\sqrt{{\tilde{r}}_0{\tilde{r}}_c}$ versus time to pinch-off. In the early-time regime, $\tilde{\zeta }=\sqrt{{\tilde{r}}_c{\tilde{r}}_0}\sim {\tilde{\tau }}^{1/5}$, consistent with the predictions of the long-wave model. In the late-time regime, however, ${\tilde{r}}_0\sim \tilde{\tau }$ and $\tilde{\zeta }\sim {\tilde{\tau }}^{1/2}$, which indicates that the axial radius of curvature becomes constant, i.e., the neck profile becomes a parabola that simply translates in time (13, 42). (E) Scaling the axial length scale with the expressions obtained in D leads to the collapse of all bubble neck profiles during the entire pinch-off process (shown in A) onto a single parabolic curve: $r/r_0=1+{\left[\left(z-z_0\right)/\zeta \right]}^2$ (dashed line).

Very close to the point of pinch-off, in the late-time self-similar regime, we can simplify the balance of normal viscous stresses and the surface tension to obtain $\partial r/\partial \tau =\gamma /\left(2\hspace{0.17em}\mu \right)$ (13, 42). Assuming the scale invariance of the dynamics close to the singularity, and using the ansatz $\tilde{R}\left(\xi \right)=\tilde{r}\left(\tilde{z},\tilde{\tau }\right)/{\tilde{\tau }}^{\alpha }$, and $\xi =\left(\tilde{z}-{\tilde{z}}_0\right)/{\tilde{\tau }}^{\beta }$, we obtain:

$$-\alpha {\tilde{\tau }}^{\alpha -1}\tilde{R}+\beta {\tilde{\tau }}^{\alpha -1}\xi {\tilde{R}}^{\prime }=-1,$$ [3]

where the prime indicates differentiation with respect to $\xi$. For all of the terms to balance in time, we need to have $\alpha =1$. The exponent $\beta$, however, remains undetermined; this is one of the hallmarks of self-similarity of the second kind (39). The value of the exponent $\beta$ can be obtained from matching the solution close to the pinch-off to the outer solution and imposing the regularity and stability of the solution (43). This leads to an eigenvalue problem, the solution of which shows that $\beta =1/2$ (SI Appendix, section 4).

In the local neighborhood of the minimum neck radius, we expect the profile to be parabolic: $r\left(z,t\right)=r_0\left(t\right)+{\left(z-z_0\right)}^2/r_c\left(t\right)$, where $r_0$ is the minimum neck radius, and $r_c$ is the axial radius of curvature. Scaling the profile with the radius $r_0\left(t\right)$, we then obtain $r/r_0=1+{\left(z-z_0\right)}^2/{\zeta }^2$, where $\zeta =\sqrt{r_c{r}_0}$ represents the axial extent of the parabola. We fit a parabola to the neck profile in the vicinity of the minimum neck radius to extract the axial length scale $\zeta$. In the early-time self-similar regime, the long-wave model predicted that $\tilde{\zeta }\sim {\tilde{\tau }}^{1/5}$. In the late-time self-similar regime, we further showed that Eq. 3 indicates the axial extent of the profile scales as $\tilde{\zeta }\sim {\tilde{\tau }}^{1/2}$. Both of these detailed predictions are supported by the experimental data in Fig. 3D. Using $\zeta$ as the axial length scale, we can therefore collapse the neck profiles over the entire pinch-off process onto a single parabolic curve (Fig. 3E).

In the early-time self-similar regime, both the neck radius, $r_0\left(\tau \right)$, and the corresponding axial radius of curvature, $r_c\left(\tau \right)$, are time-dependent. However, in the late-time regime, we have ${\tilde{r}}_0\sim \tilde{\tau }$ (Fig. 2B), and the axial scale of the profile scale as $\tilde{\zeta }=\sqrt{{\tilde{r}}_c{\tilde{r}}_0}\sim {\tilde{\tau }}^{1/2}$ (Fig. 3C), indicating that the axial radius of curvature of the neck profile becomes independent of time: $r_{cf}\equiv \underset{\tau \to 0}{lim}{r}_c\left(\tau \right)=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}$. The temporal invariance of the axial radius of curvature of the bubble neck might suggest that the separation of scales is lost and the singularity formation becomes nonuniversal. In other words, the axial extent of the neck profile retains an imprint of the details of the experimental system, and the memory of the initial conditions will persist all of the way to the point of pinch-off (13, 42).

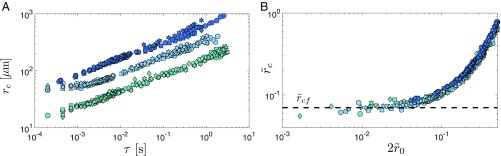
In our system, however, this late-time self-similar regime is preceded by an early-time self-similar regime of the first kind, which sets the axial length scale of the late-time regime at the cross-over between the two regimes. This characterization is captured in Fig. 3D, which shows a cross-over in the scaling of the axial length scale at $\tilde{\tau }\approx 1$ (see also SI Appendix, section 5). In the early-time regime, we have ${\tilde{r}}_0\approx 0.09{\tilde{\tau }}^{1/5}$, and ${\tilde{r}}_c\approx 0.19{\tilde{\tau }}^{1/5}$, leading to $\tilde{\zeta }=\sqrt{{\tilde{r}}_c{\tilde{r}}_0}\approx 0.13{\tilde{\tau }}^{1/5}$ as the scaling of the axial length scale. In the late-time regime, we also have $\tilde{\zeta }=\sqrt{{\tilde{r}}_c{\tilde{r}}_0}\approx 0.5{\tilde{\tau }}^{1/2}\sqrt{{\tilde{r}}_{cf}}$. Therefore, at the point of cross-over, $\tilde{\tau }\approx 1$, the early-time self-similar regime sets the axial length scale of the late-time regime ($\tilde{\zeta }\approx 0.13$), leading to ${\tilde{r}}_{cf}\approx 0.07$. Fig. 4A shows a plot of the axial radius of curvature as a function of time to the pinch-off for each experiment. When nondimensionalized, we observe that, indeed, the data corresponding to all 12 experiments collapse onto a single curve (Fig. 4B), with an asymptotic universal radius of curvature of ${\tilde{r}}_{cf}\approx 0.07$. This observation indicates that the early-time self-similar regime effectively erases the system’s memory of the initial conditions and restores universality to bubble pinch-off in a viscous liquid.

Fig. 4.

Axial radius of curvature versus time. The evolution of the axial radius of curvature $r_c$ versus time to the pinch-off shows that as the point of pinch-off is approached, the curvature asymptotes to a constant value (symbols are the same as in Fig. 2). (A) The time evolution of axial radius of curvature is independent of the flow rate but changes when the liquid viscosity or the tube diameter is varied. (B) The data corresponding to all 12 experiments collapse on a single curve when the nondimensional axial radius of curvature is plotted against the nondimensional minimum neck diameter. The nondimensional late-time axial radius of curvature asymptotes to a universal constant $\underset{\tilde{\tau }\to 0}{lim}{\tilde{r}}_c\left(\tilde{\tau }\right)={\tilde{r}}_{cf}\approx 0.07$.

We therefore conclude that the combined effect of geometric confinement and contact-line motion leads to the emergence of an early-time self-similar regime of the first kind, which at late times crosses over to a regime of self-similarity of the second kind. While the balance between viscous and capillary forces controls the dynamics of interface evolution in both regimes, the cross-over occurs due to a change in the dominant contribution to the viscous dissipation; from the spatially localized moving contact-line singularity at early times to the temporally localized bubble pinch-off singularity at late times. This change in the dominant contributor to the viscous effects is accompanied by a change in the direction of the flow, from axially dominated in the early-time regime to radially dominated in the late-time regime. The late-time regime is also observed in the pinch-off of bubbles in unbounded fluid domains, where the flow is mainly radial and the axial length scale characterizing the bubble neck is sensitive to the details of the experimental system, making the pinch-off nonuniversal (13, 34–36). Here, in the case of bubble pinch-off in confined domains, however, we observe that the axial length scale of the neck region is set by the early-time self-similar regime, effectively erasing the system’s memory of the initial conditions and restoring universality to the pinch-off process.

While we have focused on the case of bubble pinch-off in a viscous liquid, we expect our observation of the universality of the pinch-off process to persist for any other (at least viscously dominated) fluid–fluid displacement process in a confined medium involving moving contact lines. The restoration of universality has important consequences for controlled generation of bubbles, drops, and emulsions in microfluidic devices with a myriad of applications in medicine (44, 45) and material science (46–50), as well as for understanding of multiphase flows in geologic media (22, 51), where geometric confinement and liquid–solid physicochemical interactions play a key role.

Materials and Methods

Materials and Methods are described in SI Appendix.