Combined Adaptiveness of Specific Motor Cortical Ensembles Underlies Learning

Abstract

Learning motor skills entails adaptation of neural computations that can generate or modify associations between sensations and actions. Indeed, humans can use different strategies when adapting to dynamic loads depending on available sensory feedback. Here, we examined how neural activity in motor cortex was modified when monkeys made arm reaches to a visual target and locally adapted to curl force field with or without visual trajectory feedback. We found that firing rates of a large subpopulation of cells were consistently modulated depending on the distance of their preferred direction from the learned movement direction. The newly acquired activity followed a cosine-like function, with maximal increase in directions that opposed the perturbing force and decrease in opposite directions. As a result, the combined neuronal activity generated an adapted population vector. The results suggest that this could be achieved without changing the tuning properties of the cells. This population directional signal was however altered in the absence of visual feedback; while the cosine pattern of modulation was maintained, the population distributions of modulated cells differed across feedback consistent with the different trajectory shapes. Finally, we predicted generalization patterns of force-field learning based on the cosine-like modulation. These conformed to reported features of generalization in humans, suggesting that the generalization function was related to the observed rate modulations in the motor cortex. Overall, the findings suggest that the new combined activation of neuronal ensembles could underlie the change in the internal model of movement dynamics in a way that depends on available sensory feedback and chosen strategy.

Introduction

The beautiful rendering of a symphony entails a modulation of the dynamics of crescendi and decrescendi of note sequences combined to form harmonious chords. During arm-reaching movements, motor cortical cells modulate their firing rates in such harmony to encode a myriad of movement parameters such as direction (Georgopoulos et al., 1982; Schwartz et al., 1988), force (Evarts, 1968; Kalaska et al., 1989; Taira et al., 1996), speed, or amplitude (Schwartz, 1992; Fu et al., 1993; Johnson et al., 1999; Moran and Schwartz, 1999; Reina et al., 2001). However, it has been a formidable challenge to dissociate elegantly between these parameters. Complicating the issue further is that motor cortex and even single units simultaneously encode multiple parameters (Caminiti et al., 1990; Ashe and Georgopoulos, 1994; Fu et al., 1995; Kakei et al., 1999; Paninski et al., 2004; Kurtzer et al., 2005; Aflalo and Graziano, 2006; Hatsopoulos et al., 2007; Stark et al., 2007;). For example, relevant to our study (see supplemental information, available at www.jneurosci.org as supplemental material) is the finding that speed modulates the cell's directional tuning.

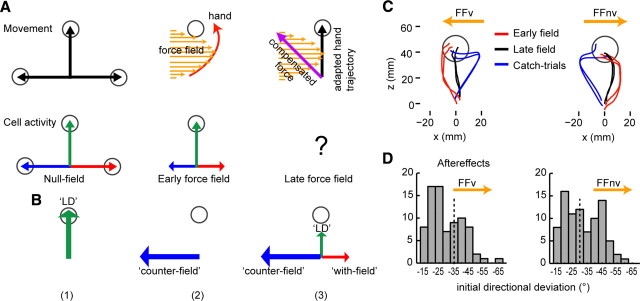
Motor cortex also plays a role in learning (Sanes, 2003; Scott, 2004; Lalazar and Vaadia, 2008). Changes in the neurons' discharge patterns correlate with the new kinematics or dynamics of movement (Wise et al., 1998; Gandolfo et al., 2000; Li et al., 2001; Paz et al., 2003). Yet, what is represented by the learning-related changes remains largely unknown. Here, we examined how motor cortical cells modify their activity to orchestrate new movement strategies as monkeys learn to reach to a single visual target in the presence of viscous curl force fields. In such perturbations, the compensatory direction, which is opposite to the force field and away from the learned direction (LD), yields the adapted hand trajectory when summed vectorially with the force field (Fig. 1A). Specifically, we tested whether the neuronal responses would depend on the distance of the cells' preferred direction (PD) from the LD. The task was designed to test two possibilities concerning which neurons would modify their firing during learning (Fig. 1B): (1) a specific subpopulation of cells with PD near the LD or orthogonal to the LD, and (2) subpopulations of cells with diverse PDs. The first possibility implies that cells would represent either the LD (Fig. 1B1) or the force-field direction (Fig. 1B2). The alternate possibility would imply that cells with wide-ranging PDs would represent the compensatory direction (Fig. 1B3). Depending on which subpopulation of cells was recruited, the population directional signal would point either toward the LD or orthogonal to the LD or toward the direction of compensation.

Figure 1.

Schema of hypothetical activity of different cells to generate adapted movements under force field. A, Left, Trajectories in the absence of force field are straight (upper row, black arrows). Firing rate of cells whose PD corresponds to these directions are marked by the length of the colored arrows (lower row). Center, Trajectory (red, upper row) deviates in the direction of the force field (orange arrows) as nonadapted cells fire as in the null-field (lower row). For simplicity, the viscous curl force field was represented as straight lines whose length varied to reflect the bell-shaped velocity profile. Note that the direction of the force field was always orthogonal to the direction of movement. Right, When monkeys effectively anticipate the force properties (orange) and generate a compensatory direction (purple), the hand takes an approximately straight path (black) when reaching to the target. B, Two possibilities: (1) adaptive changes in one subpopulation of cells in which activity increases for cells with PD near the LD (B1) or those with PD orthogonal to the LD (B2); and (2) adaptive changes in different subpopulations of cells (B3) in which activity increases for cells with PD that counters the force field and decreases with PD along the direction where force field assists movement. C, Behavioral after-effects. Hand paths corresponding to single trials (early and late force field trials and catch trials) from the same recording day for each feedback condition (counterclockwise, FFv; clockwise, FFnv). Deviations of hand paths in catch trials (blue) were mirror images of the deviations early in adaptation (red). D, Histograms of the initial directional deviations of all catch trials. The directional deviations are expressed in angles. Negative values denote directional deviations opposite to the force field direction. Initial directional deviations did not differ with and without VFB (t test, p > 0.10). The mean directional deviations of significant after-effects [i.e., those above 2 SD from the mean directional deviation (dashed vertical lines) of control trials] reflect the compensatory direction (FFv = −45 ± 2° and FFnv = −41 ± 2° for LD at 0° convention).

Following our findings that humans used different strategies when adapting to force fields with or without visual feedback (Arce et al., 2009), we also examined here how sensory feedback might affect the computation of the new motor output. Since the final hand position is dissociated from the compensatory direction, manipulating the visual feedback of trajectory and endpoint could influence what eventually drives adaptation (Scheidt and Ghez, 2007). We tested whether neuronal activity would vary according to the expected sensory outcomes relating to trajectory or endpoint. The findings have been reported previously in abstract form (Arce et al., 2008).

Materials and Methods

Animal care and experimentation were in accord with the U.S. National Institutes of Health Guide for the Care and Use of Laboratory Animals and with the Hebrew University guidelines for the use and care of laboratory animals in research, approved and supervised by the Institutional Animal Care and Use Committee. Before, during, and after experimentation, monkeys were assessed for general well being. When the health of the monkeys so required, the experiment was terminated or appropriate treatment was applied as recommended by the head veterinarian.

Behavioral task and recordings

Two monkeys (Macaca fascicularis, ∼4 kg) were trained to reach visual targets using a lightweight robotic arm (Phantom Premium 1.5 High Force, SensAble Devices). Details of the setup were described previously (Arce et al., 2009). Once the monkeys were fully trained, neural recordings were initiated. Monkey A was implanted with a recording chamber (27 × 27 mm) above the left hemisphere. Signals from 32 moveable microelectrodes were amplified, filtered, online sorted, and sampled at 20 kHz (Alpha-Omega). Penetration sites in the premotor (PM) and primary motor (M1) cortices were verified using combined analyses of magnetic resonance imaging (Biospec 4.7 T, Bruker) and skull endocast, microstimulation (50 ms of 200 μs cathodal pulses at 300 Hz), passive limb movements, and light touch (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). Monkey B was chronically implanted with a 96 microelectrode array (Cyberkinetics Neurotechnology Systems) on the arm region of the left M1. Signals were online sorted and sampled at 30 kHz.

The monkeys completed three blocks of target reaching sequentially: prelearning null-field reaches to eight different targets (160 trials), force-field reaches to one and the same target (144 field trials and 16 interspersed catch trials in one same direction), and postlearning null-field reaches to eight targets (160 trials). Each recording session was either with or without visual feedback (VFB) of the cursor (FFv and FFnv, respectively, where FF is force field), which instantaneously tracked the hand position. In the learning block, the robot's motors generated forces that perturbed the hand perpendicular to the current reach direction and proportional to the hand velocity. To ensure that the monkeys learned anew, the learned target (0°, 45°, 90°, 135°, 180°) and force-field direction (clockwise or counterclockwise) were varied. Moreover, null-field reaches before and after learning assured a washout of the previous learning. Indeed, analysis of success rates across days showed that success rates for the first 20 trials were significantly lower than success rates for the next 20 trials (paired t test, FFv: p = 0.01; FFnv: p = 0.005).

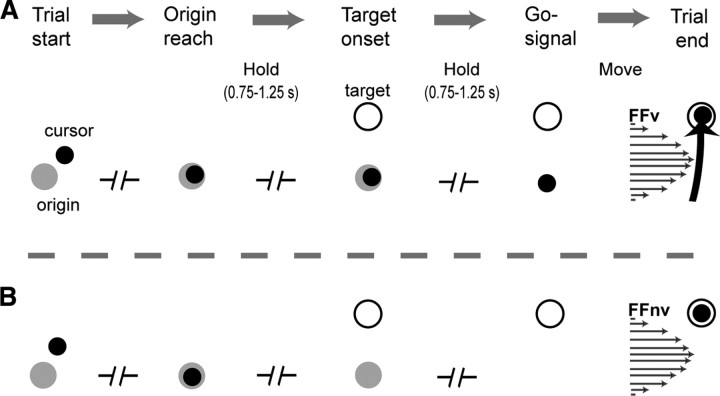
Trials started with the appearance of an origin and a cursor (both 10 mm radius) (Fig. 2A,B). Without VFB, the cursor appeared when near the origin (0–20 mm). Monkeys positioned the cursor at the origin and held it there for a randomized variable period (0.75–1.25 s) until a target (10 mm radius) appeared. [The target distance, 4.24 cm from center points of origin and target (equivalent to >12 cm in humans), required movements of shoulder and elbow joints with minimal postural adjustments of axial (trunk) muscles.] After another randomized variable hold period from target onset (0.75–1.25 s), the origin disappeared (go signal) and the monkeys should have reached the target within 1 s from go signal. With VFB the cursor was visible during the reach movement, while without VFB the cursor disappeared at target onset and appeared only at trial end. Note that since prior adaptation might influence subsequent ones, recording sessions were done separately with or without VFB. Upon reaching the target, monkeys held the position for 0.2 s to get a reward. Trial end was defined by a success or failure event. Successful trials were cued by change of target color and an auditory cue (Notify.wav, Microsoft Windows). In failed trials (i.e., inability to comply with required hold and movement times), monkeys were given a different auditory cue (Pop-up Blocked.wav, Microsoft Windows). An intertrial interval (1.5 s) followed trial end, during which the workspace was blanked. In field trials, the velocity-dependent force field (Arce et al., 2009) was generated with k = 8 N * s/mm and turned off 200 ms after trial end.

Figure 2.

Behavioral task. A, B, Trial flow in force field with visual feedback (FFv) (A) and without (FFnv) (B). A, With VFB, the cursor is seen throughout the movement. B, Without VFB, cursor disappears at target onset and appears only at trial end.

Data analysis

Behavioral analysis.

We examined behavioral performance based upon success rates, initial directional deviation, path curvature, and spatial error and compared differences between the feedback conditions and across the early (first 20 trials) and late phases (trials 61–80) of force-field adaptation using one-way ANOVA. Initial directional deviation was the angular difference between the direction of a vector going from the hand position at movement onset to the target and one from the origin to the hand position 150 ms after movement onset. Path curvature was the mean perpendicular distance along the path to a straight line that connected the origin to the target from movement onset to trial end. Initial deviation and path curvature were also assessed using the perpendicular distance measured at 150 ms and the maximal value along the trajectory. All measures yielded similar results. Spatial error was the perpendicular distance between the target's center and the hand position at trial end. Other behavioral parameters were also evaluated (see supplemental Table 1, available at www.jneurosci.org as supplemental material). For further details, see Arce et al. (2009).

Neuronal analysis.

Cell activity was evaluated from the go signal to 600 ms afterward. The dataset included cells based upon their stable isolation, an average firing rate of >1 Hz, and at least five successful trials per direction in the prelearning and postlearning blocks separately. We constructed separate directional tuning curves for prelearning and postlearning blocks using the target directions and calculated each cell's PD using the vector method (Batschelet, 1981). Only cells with significant directional tuning (bootstrap technique, p < 0.05) were included in this analysis. For each directionally tuned cell, we computed a normalized PD (nPD) as the angular distance between the cell's PD and the learned target direction (LD) and was signed positive or negative (+/−) depending on the direction of the force field. Positive denotes nPDs in the direction of the force field, while negative denotes nPDs in the opposing direction. To pool data across force field directions, we flipped the PD distance for the counterclockwise force field. We then subdivided the population of cells according to their nPDs: (1) near-LD (LD, −45 to 45°), (2) counter-field (CF, −135 to −46°), (3) with-field (WF, 46° to 135°), and (4) far-LD (−136 to −180° and 136 to 180°).

For each cell, we compared the discharge rates during the prelearning, learning (early and late phases), and postlearning reaches to the LD. Differences were assessed using one-way ANOVA with post hoc Tukey–Kramer correction for multiple comparisons (p < 0.05). For cells that showed significant differences in discharge rates between the prelearning null field reaches and force-field reaches (here referred to as “force field-modulated cells”), we calculated a modulation index as follows:

where F_k and N_k are the mean discharge rates of a single-unit k in field trials and null-field trials of the LD, respectively. The index values range between −1 and 1, and positive values denote increased firing in field trials. The average index value corresponds to a geometric mean that is less influenced by large values. The modulation index was calculated separately for the early (first 20 successful trials) and late (successful trials 61 to 80) phases of adaptation.

To test whether the changes in firing rate during adaptation depended on the cells' nPD, we fitted the response of the population of force field-modulated cells to a cosine model. The nPDs were binned into eight ranges (−180 to −136°, −135 to −91°, −90 to −46°, −45 to 0°, 0 to 45°, 46 to 90°, 91 to 135°, 136 to 180°). The population modulation index per nPD range was obtained by averaging across the modulation index values of cells whose nPDs fall within a range. The model relates the population modulation index to the normalized PD as follows:

where PI_(ri,pj) is the population modulation index per nPD range r_i (where i = 1 to 8) and per adaptation phase p_j (where j = 1 to 2), θ_(ri,pj) are the angles corresponding to the center of the nPD range (−157.5, −112.5, −67.5, −22.5, 22.5, 67.5, 112.5, 157.5). PD_pop is the population preferred direction, which indicates the nPD of maximal modulation index, a is the offset, and b is the amplitude. To obtain 95% confidence intervals for the R² of the cosine fit, we used the bootstrap technique (1000 repeats). By taking the population modulation index per nPD range, we considered primarily the variability of the mean responses and not the variability of each neuron with respect to the mean. However, to ensure that the dependence in nPD did not depend on the binning procedure, we also evaluated the cosine fit by taking the modulation index and nPD of each cell instead of the population modulation index per nPD range. We also evaluated whether the cosine model best described this relation. For these, we used stepwise multiple regressions (Matlab built-in software) with higher harmonics as additional regressors. Significance was obtained using F test on the regression analysis.

To compare the tuning curves of prelearning and learning blocks, we estimated the directional tuning curves of cosine-tuned units during the adaptation block. To do this, we obtained the cell's predicted firing rates for field reaches to all eight directions based on the coefficients of the cosine fit on the observed population response during the late phase of adaptation. Here, we made the following assumptions: (1) the single unit is cosine-tuned to the target directions; (2) the prelearning directional tuning curves of single units remain the same during the learning block; and (3) during the late phase of adaptation, the actual hand movement direction approximates the learned target direction. We first calculated the predicted population modulation index for target direction M_i (where i = 1 to 8 and M = 0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°) for each feedback condition. We then calculated the adjusted predicted modulation index Îa_(k,MI) for a single-unit k at target direction M_i by multiplying the predicted population modulation index at target direction M_i (Îp,_Mi) by the ratio between the single-unit's observed modulation index at the LD [I_(k,LD)] and its predicted population modulation index at the LD (Îp_LD). This makes the predicted modulation index of each single-unit to be proportional to its observed response at the LD:

The predicted modulation index indicates the expected magnitude of decrease/increase in the single unit's firing rate. Given the single-unit's firing rates in the prelearning block and its predicted modulation index for force field, we derived the single unit's predicted force-field firing rate F̂_Mi for direction M_i. Equation 4 was algebraically derived from Equation 1:

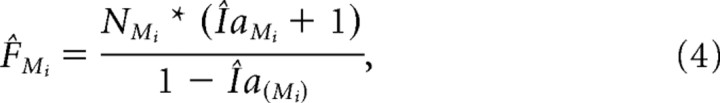where N_Mi is the observed prelearning rate for direction M_i. Finally, we estimated the cell's tuning curve based on the predicted force-field firing rates and compared it to the tuning curve based on the observed prelearning rates.

We calculated the population vector P_t for the trial block t corresponding to prelearning and learning blocks as follows:

where C_k is the normalized preferred direction (a two-dimensional unit vector) of neuron k in the population of cells N in the vision (N = 85 cells) or nonvision (N = 90 cells) conditions, and w_(k,t) is a weighting function calculated as follows:

where d_(k,t) is the neuron's average firing rate for reaches to the learned direction for trial block t, D_k is the neuron's average firing rate across all prelearning null-field trials and target directions, and R_k is the half-range for the eight directions (Georgopoulos et al., 1988). Assuming that the directional tuning of cells did not change, we used the weighting function of the prelearning dataset when calculating the population vector for the learning block. Cells were included in this analysis if: (1) R²_k ≥ 0.70, (2) D_k ≥ 5 Hz, and (3) R_k ≥ 3 Hz. We tested whether the sample population per feedback condition had: (1) symmetrical tuning around the PD, (2) PD distribution that did not show nonuniformity (Raleigh test p > 0.25), and (3) amplitude and offset that were uncorrelated with PD (Pearson's correlation coefficient, p > 0.10). The bootstrap technique (5000 repeat samples) was used to test whether the estimated PV length resulted from random activity and to compare PVs between feedback conditions. Before pooling data for both monkeys together, we performed all analyses separately for each monkey to ensure that results were similar and to verify that differences found when using the pooled data were not due to sampling bias.

EMG recording and analysis.

We obtained 32 samples of surface EMGs (bipolar electrodes, Motion Lab Systems) from the anterior and middle deltoids, biceps brachii, and triceps brachii. The EMG traces were bandpass filtered (0.005–3 kHz) and sampled at 10 kHz. EMG traces were rectified and integrated from 0.25 s before the go signal to 0.75 s after. We compared the change in muscle activation from prelearning to learning blocks by calculating the modulation index as described above. To examine coupling between adaptive modulation and directional tuning, we included only those muscles with significant directional tuning (bootstrap technique, p < 0.01) and whose mean modulation index of the late 40 trials was significantly different from zero (t test, p < 0.05). As in the neuronal analysis, muscles were grouped according to the distance of their PD from the LD. Mean modulation index values were compared between feedback conditions using t test (p < 0.01).

Results

Monkeys did three blocks of reaching movements: prelearning null-field reaches to eight directions, force-field reaches to one direction, and postlearning null-field reaches to eight directions. All reaching movements were either with or without VFB of the cursor, which instantaneously tracked the hand position. With VFB, monkeys always saw the cursor, whereas without VFB, the cursor only provided feedback of the hand position at trial end (Fig. 2).

Behavioral findings

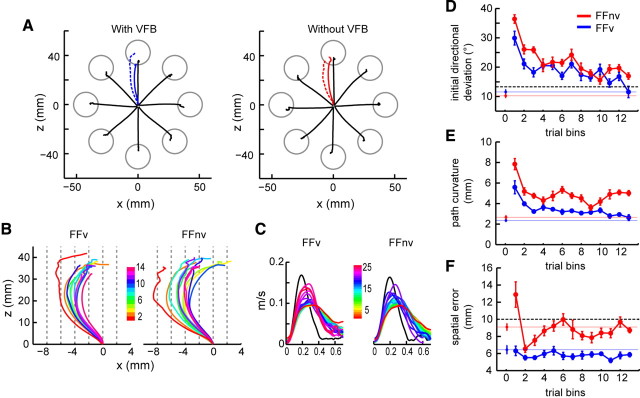
During the first encounter with the velocity-dependent force field, monkeys missed the target as the hand was pushed by the force field. With practice, they learned to compensate for the perturbations (Fig. 1C, red vs black) as indicated by the improved success rates (supplemental Table 1, available at www.jneurosci.org as supplemental material) along with reductions in deviations in trajectory (Fig. 3) (ANOVA p < 0.0001) and endpoint accuracy (FFnv: p < 0.01). As we previously found in humans (Arce et al., 2009), trajectories were significantly more curved without VFB than with it (Fig. 3E) (ANOVA p < 0.001). Nevertheless, the progressive reduction in the initial directional deviation both with and without VFB suggests that adaptation involves feed-forward changes and not merely reliance on online feedback corrections. It further suggests that the monkeys have learned a new motor plan.

Figure 3.

Behavioral performance during adaptations to force field. A, Average hand paths during prelearning null (black) and field reaches with and without VFB [averaged trajectories of the first (dashed line) and last 10 (solid line) field trials]. Data from all recording days. B, Average hand paths across field trials (10 trials/bin). The x-axis is enlarged to show lateral path deviations. C, Velocity profiles of null (black) and field (colored) reaches averaged across trials (five successful trials/bin). D–F, Means and ±1 SE of initial directional deviation (D), path curvature (E), and spatial errors (F) during adaptation (10 trials/bin). Isolated points and colored lines denote baseline values of the same directions used in the learning blocks. Dashed black lines in D and F denote error level that achieves reward. While spatial error was sufficiently reduced to achieve success, trajectory errors were not fully compensated without VFB.

Learning was confirmed by the emergence of behavioral after-effects in both feedback conditions (Fig. 1C,D). After-effects, implicated as a signature of new internal models (Shadmehr and Mussa-Ivaldi, 1994), were apparent in the opposite directional deviations in catch trials, which were the null-field trials that were randomly interspersed throughout the learning block. This implies that predicting the novel forces, the monkeys modified their motor commands in a new intended direction to compensate for the perturbation. The directional after-effects indicated the direction that compensates for the perturbation. Alternatively, monkeys might have used strategies other than a change in the motor command; however, other results showed that this was unlikely (see supplemental information, available at www.jneurosci.org as supplemental material).

Neuronal findings

We analyzed the movement-related activity of 685 cells in PM and M1 cortices. Over 78% of the cells were directionally tuned (bootstrap p < 0.05), with similar proportions across feedback conditions (binomial test p > 0.10, FFv = 284/344, FFnv = 252/341). Tests on non-uniformity of the distribution of PDs in the prelearning block for each feedback condition were found nonsignificant (Raleigh test, p > 0.10).

Movement-related responses of PM and M1 neurons during adaptation to force field were found to be similar, consistent with previous studies (Li et al., 2001; Xiao et al., 2005). Therefore, we pooled together the results from both areas (supplemental Fig. 1 and supplemental Table 2, available at www.jneurosci.org as supplemental material). Of the directionally tuned cells, the following was found: (1) 45% (240/536) showed significant changes in firing during perturbed reaches relative to prelearning null-field reaches to the same direction; (2) 25% changed activity from prelearning to postlearning blocks; and (3) 30% remained unchanged in both learning and postlearning blocks (ANOVA, p < 0.05; post hoc for multiple comparisons, p < 0.05). Modulation of firing rates during adaptation also occurred in nondirectionally tuned cells (28%).

The proportions of cells that modified their discharge during adaptation (i.e., force field-modulated cells) were similar with or without VFB (FFv = 125 (44%), FFnv = 115 (46%), binomial test p > 0.10). Discharge modulation occurred early or late in adaptation (159 and 183 cells, respectively) or persisted throughout the learning block (102 cells). Of the total population of force field modulated cells, 29% retained the adaptive changes in the postlearning null-field block (ANOVA, p < 0.05).

Single neuron's activity depends on PD distance from the learned direction

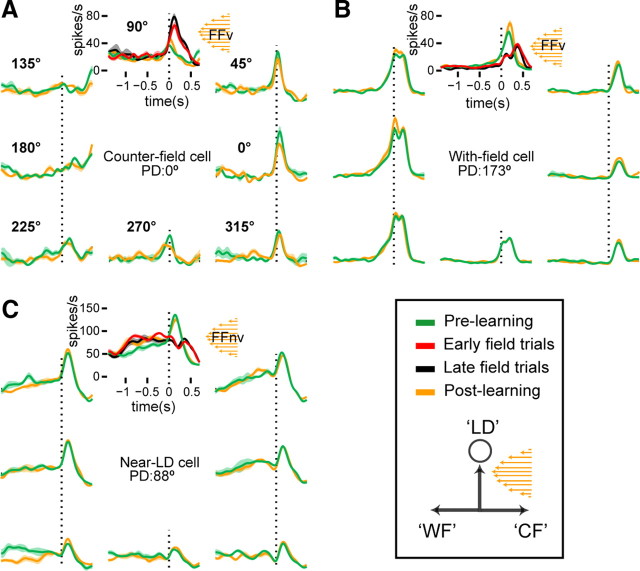
Examples of three classes of directionally tuned cells that showed adaptive modulation are shown in Figure 4. Compared with prelearning reaches to the LD, the movement-related activity of the cell in Figure 4A increased during field reaches (ANOVA, p < 0.001). The cell's PD (0°) was in the direction that countered the perturbation and was orthogonal to the LD at 90°. Thus, the heightened activity of the cell during movement toward LD reflects an increased contribution to the population directional signal (counter-field) (Fig. 1B). During the same recording session, another cell with PD (173°) along the direction of the perturbation (with-field) (Fig. 1B) decreased its activity (Fig. 4B) (ANOVA p < 0.001). Similarly, a cell whose PD was near the LD (88°) decreased its firing during the perturbed reaches (Fig. 4C) (ANOVA p < 0.001). This suggests that the cells in Figure 4, B and C, reduced their contribution to the population directional signal during the perturbation. In the postlearning block, activity of these cells at the LD returned to prelearning level (orange perievent time histogram), suggesting that the modulation in perturbed reaches were force-field specific. As mentioned above, other cells did retain the increased/decreased activity even after the cessation of the perturbation, as monkeys returned to performing null-field reaches.

Figure 4.

Changes of single unit's activity during adaptations to force field. Perievent time histograms (PETH and ±1 SE), smoothed by a 50 ms-Gaussian kernel, show mean discharge of M1 neurons during prelearning (green) and postlearning (orange) reaches to eight directions and during early (red) and late (black) field reaches to 90°. PETHs are aligned at movement onset (dashed vertical line) for counter field (A), with-field (B), and near-LD (C) cells. During adaptation, activity around movement onset increased in the cell shown in A but decreased in the cells shown in B and C. See supplemental Figure 2 (available at www.jneurosci.org as supplemental material) for the raster plots.

To measure the differences between firing rates in null-field and field reaches to the same direction, we calculated an index of modulation for each cell. We then plotted each cell's modulation index as a function of the angular distance of its PD from the LD, referred to as the normalized PD (supplemental Fig. 3A, available at www.jneurosci.org as supplemental material). We found that the firing rates of single cells either increased or decreased depending on the cells' nPD. In both feedback conditions, positive modulations were more frequent in counter-field cells whose nPDs ranged from −46° to −135° (Fig. 5, black circles) (binomial test, p < 0.001). By contrast, negative modulations were associated with with-field cells whose nPDs ranged from 46 to 135° (Fig. 5, gray circles) (p < 0.001).

Figure 5.

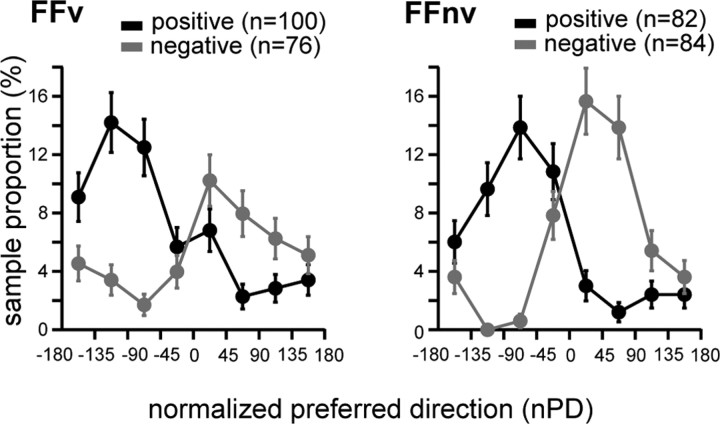
Modulation of neuronal activity depends on the cells' PD distance from the learned direction. Sample proportion of cells (y-axis) according to the cells' normalized PD (x-axis) is shown for each feedback condition. The population was divided into positively (black) and negatively (gray) modulated cells. The nPDs, which indicate the distance of the cells' PD from the LD, were binned into eight ranges. Negative nPDs denote nPDs opposite to the force-field direction. With VFB, cells with positive modulation were more frequent than negative modulation (binomial test; p < 0.05), while without VFB, no such difference was found (p > 0.10).

Modulations of firing rates of the population follow a cosine model

To test whether the changes in firing rates depended on the cells' normalized PDs, the response of the population of force field-modulated cells was fitted to a cosine model. We first binned the nPDs into eight ranges (−180 to −136°, −135 to −91°, −90 to −46°, −45 to 0°, 0 to 45°, …, 136 to 180°). We then obtained the population modulation index per nPD range by averaging across the modulation index values of cells whose nPDs fall within a range. This was done separately for each adaptation phase and feedback condition. Figure 6A relates the nPD to the population modulation index. For all conditions tested, we found a significant fit of the population data to the cosine model (F test p < 0.01); R² values were high (early and late phases were 0.91 ± 0.06 and 0.88 ± 0.09 for FFv, respectively, and 0.93 ± 0.07 and 0.95 ± 0.04 for FFnv, respectively) (Fig. 6A). The cosine model therefore explains the graded adaptive response according to the normalized PDs; the adaptive response is maximal at nPDs that lie on the steepest slope of the tuning curve (±90°) and minimal at nPDs where the tuning curve is flat (∼0°). Note that while the peaks of the fit to cosine depicted in Figure 6A are shifted from 0°, they do not indicate PD shifts of the force field-modulated cells. Rather, they signify that the peak positive modulation during adaptation corresponds to the subpopulation of CF cells. Note also that the peak negative modulation in the subpopulation of WF cells was of comparable magnitude to the modulation of CF cells. Thus, the cosine-like profile indicated that compensation for the perturbing force was not accomplished by counter-field cells alone but involved cells with diverse PDs. Cells whose output countered the force field increased their firing in concert with decreased firing of other cells whose output was in the force-field direction.

Figure 6.

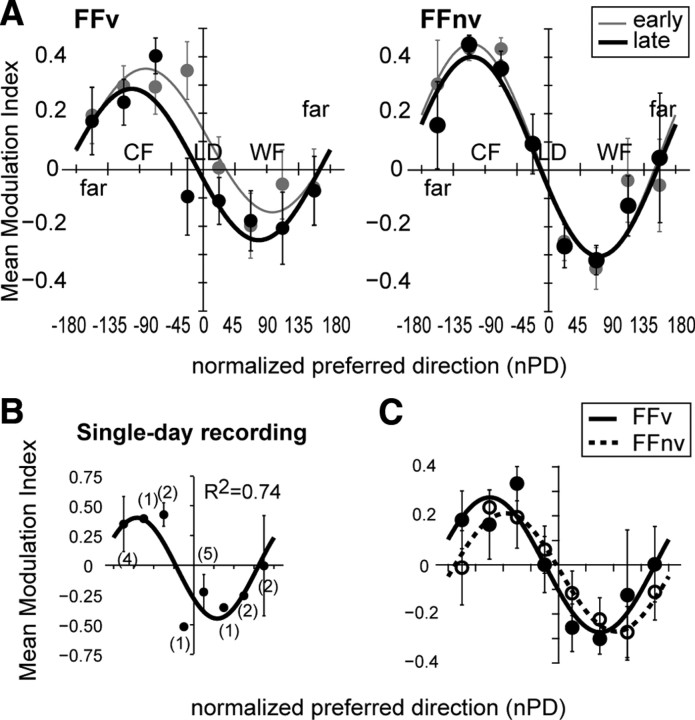
Adaptive modulation follows a cosine. A, Population modulation index (y-axis) as a function of normalized PDs (x-axis) is shown separately for early and late phases of adaptation and for each feedback condition. Each point denotes the mean modulation index across cells within a range of nPDs: near-LD (±45°), counter-field (−46 to −135°), with-field (46 to 135°), and far-LD (136 to 180°, −136 to −180°). Positive values indicate increased firing rates in field reaches. Population modulation index showed a good fit to cosine (R² for early and late phases were = 0.91 ± 0.06 and 0.88 ± 0.09 for FFv, respectively, and 0.93 ± 0.07 and 0.95 ± 0.04 for FFnv, reespectively). Modulation index did not differ between early and late phases (paired Wilcoxon test, p > 0.10) nor between feedback conditions (Mann–Whitney, p < 0.05). The PDs (late phase: FFv = −100°; FFnv = −109°) and the amplitudes (late phase, FFv = 0.28; FFnv = 0.36) of the cosine fit were not significantly different with and without VFB (bootstrap, p > 0.10). Error bars are ±1 SE. B, As in A, but for a single-day recording where 15–20 cells modulated by force field were simultaneously recorded. C, Population modulation indexes corresponding to neural activity from 300 ms before movement onset to 200 ms after. Shown for late force field trials of each feedback condition. The population modulation index fit the cosine model well (R² for FFv = 0.97; R² FFnv = 0.88).

This adaptive modulation profile was even observed at the level of single recording days that yielded 15–20 simultaneously recorded cells that were modulated by force field (Fig. 6B). We also found that R² values were comparable under both feedback conditions (bootstrap, p > 0.10), suggesting that the rate modulation was not feedback driven. In addition, we examined the early epoch of the trial and obtained similar modulation profiles when neural activity was examined 300 ms before movement onset to 200 ms after it and before reaching peak velocity (early and late phases were 0.72 and 0.97, respectively, for FFv and 0.75 and 0.88, respectively, for FFnv) (Fig. 6C). As this time window is unaffected by sensory feedback, this suggests that the observed rate modulation is most likely feed forward.

When the same analysis was done without binning the nPDs, we obtained lower R² data compared with the binned data due to intercell variability (R² values for early and late phases were 0.21 and 0.27 for FFv, respectively, and 0.47 and 0.42 for FFnv, respectively). Nevertheless, these latter R² values were all significant (bootstrap, p < 0.001). To assess whether the cosine model best describes this relation, we performed stepwise regression using higher harmonics as regression terms. For early adaptation, results were significant only for the first harmonic (p < 0.00001). For late adaptation, regression was significant for the first harmonic (p < 0.00001) and was only improved by the fifth harmonic from R² of 0.42 to 0.45 for FFnv (root mean square error from 0.314 to 0.307) and R² of 0.27 to 0.31 for FFv (root mean square error from 0.33 to 0.32). Overall, the results indicate that the cosine model accounts for the largest portion of the variability in the data whether the normalized PDs are binned or not.

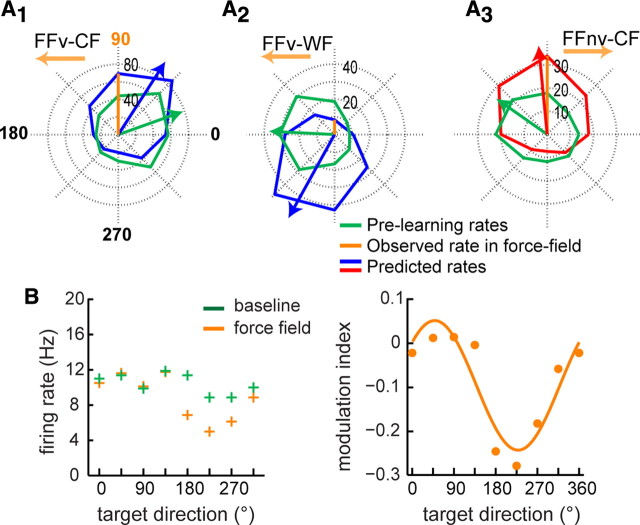
Since the adaptive modulation of the population fits well to a cosine, a cosine-tuned cell might exhibit a similar response profile. Using the parameters of the cosine fit on the population's response, we predicted a single unit's adaptive response for the untested directions (see Materials and Methods). Figure 7A illustrates the observed prelearning firing rates and the predicted firing rates in force field for three representative cells. The predicted discharges showed graded increase/decrease from prelearning activity across all eight directions. For example, in Figure 7A₁ the discharges of the CF cell were predicted to increase in the directions near the LD (i.e., 45, 135, and 180°) and to decrease in the remaining directions. Since this procedure was analogous to an eight-target learning, we verified our predictions against the reported findings during force field learning in eight directions (Gandolfo et al., 2000; Li et al., 2001). We found that the changes in firing rates of a cell described by Gandolfo et al. (2000) also followed a cosine model (Fig. 7B). We then computed the PD of the cells based on the predicted discharges and found that the new PDs were shifted in the direction of the force field (Fig. 7A, compare green vs blue arrows), consistent to that reported by Li et al., (2001). Thus, our findings suggest that PD-dependent adaptive modulation explains how the prelearning PDs of single units shifted in the direction of the force field during adaptation.

Figure 7.

Predicted firing rates in force field based upon the cosine model. A, Polar plots of single neurons' prelearning firing rates (green) and predicted force-field firing rates (red/blue) for FFv counter-field (A₁), FFv with-field (A₂), and FFnv counter-field (A₃). Observed force-field firing rate at the LD (90° in all cases) is also shown (orange). Note that the PDs of the predicted rates (red/blue arrows) are significantly shifted from the PD in prelearning (green arrows) in the direction of the force field (orange arrow). That is, PD shifts clockwise for clockwise force field (A₁ and A₂) and counterclockwise for counterclockwise force field (A₃). B, Left, A single cell's average firing rates in baseline (green) versus force field (orange) learned in all eight directions. Reproduced from Gandolfo et al. (2000), their Fig. 3b. (Copyright © 2000 National Academy of Sciences, U.S.A.). Right, Modulation index calculated for each direction show a good cosine fit (R² = 0.85), consistent with our model predictions.

Reorganization of cells depended on available sensory feedback

While the cosine-like adaptive modulation was comparable with and without VFB, the population distribution of modulated cells differed between feedback conditions. Figure 8A shows that the peaks of the two distributions were different; although the proportion of counter-field cells was significantly greater with VFB (binomial test, p = 0.01), near-LD cells were significantly greater without VFB (p = 0.015). This suggests different reorganization of cells in these two conditions; when VFB was available and trajectory errors could be used to drive adaptation, more counter-field cells were modulated. By contrast, more near-LD cells were modulated when visual inputs provided only the final hand position (no VFB), and mainly endpoint errors could drive adaptation.

Figure 8.

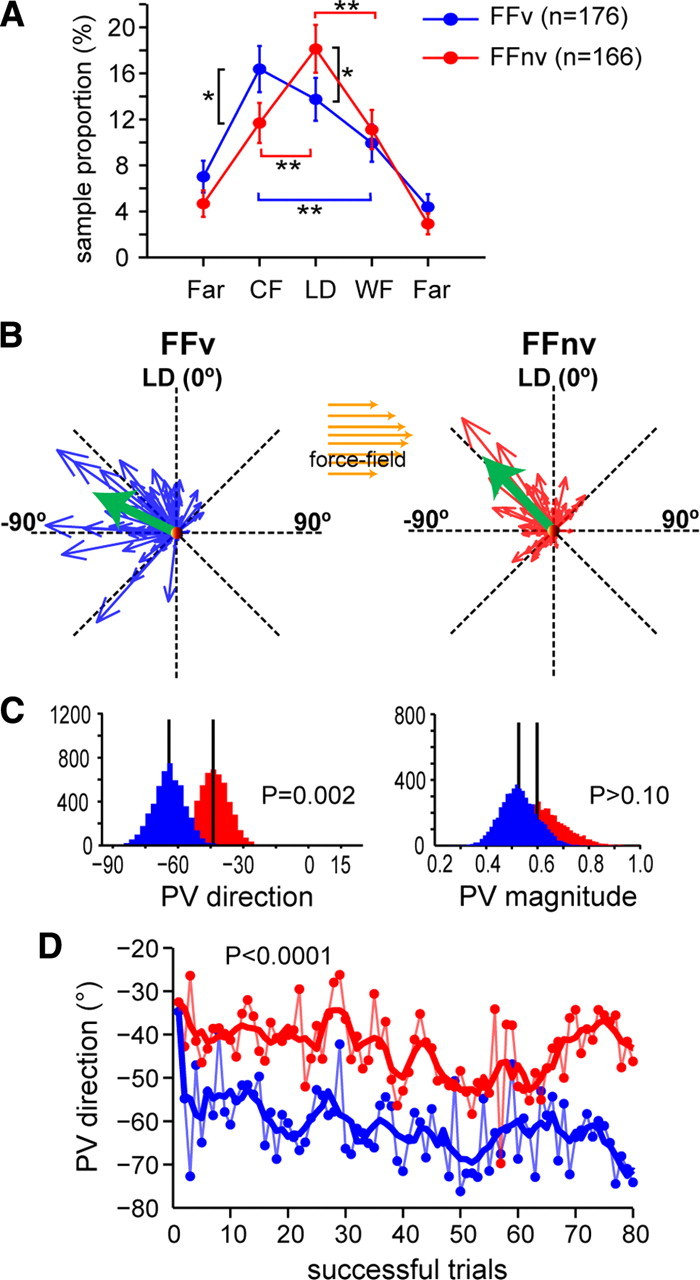
Population distributions of modulated cells differ between feedback contexts. A, Population distribution of cells (n = 342) according to their nPDs and feedback condition. The FFv distribution is negatively skewed relative to the LD (−0.07), while the FFnv distribution was positively skewed (0.07). Skewness was calculated as follows: S = E(x − μ)³/σ³ where μ is the mean of x, σ is the standard deviation of x, and E(t) is the expected value of t. Error bars are ±1 SE. Brackets correspond to significant comparisons between nPD ranges within (colored) and between feedback (black) conditions (*p = 0.01; **p < 0.001). B, Population vectors during force-field adaptations (green) did not point to the hand movement direction. In both feedback conditions, they pointed toward the compensatory direction [FFv = −64.2° (−65.3°, −63.2°); FFnv = −43.6° (−44.5°, −42.8°)]. Similar results were obtained when PVs were calculated separately for each monkey (a, FFv = −51.7°; FFnv = −33.3°; bootstrap, p = 0.03; B, FFv = −72.0°; FFnv = −46.0°; bootstrap, p = 0.003). PVs were calculated using mean firing rates of late force-field trials (41–80). C, Histograms of the direction and magnitude of PVs shown in B, obtained from resampling using the bootstrap technique, show significant differences in direction but not in magnitude. D, PV direction calculated trial-by-trial (dotted line, raw data; solid line, smoothed data) during adaptations to force fields with and without VFB.

We then examined how the different population distributions affected the population directional signal. We thus calculated the predicted population vector (PV) during force field based on the prelearning null-field tuning curves of cells, assuming that cells' directional tuning did not change. For this analysis, the number of cells that were included, based upon the set criteria (see Materials and Methods), were as follows: with-VFB, 85 cells, of which 61% were modulated; without-VFB, 90 cells, of which 62% were modulated. Unlike the PVs in unloaded reaches [PV and 95% confidence intervals: with VFB, 1.6° (1.1°, 2.1°); without VFB, 5° (4°, 6°)], the PVs in force field no longer pointed in the direction of hand movement but were instead deviated away from the LD and were opposite the force field direction [FFv: −64° (−65°, −63°); FFnv, −43.6° (−44.5°, −42.8°); bootstrap, p < 0.0001] (Fig. 8B). The PVs mirrored the directional after-effects observed in the catch trials, suggesting that PVs pointed toward the intended direction that compensated for the perturbing force. Thus, the vector sum of PV plus force field yielded the hand motion toward the LD. This was true for both feedback conditions. However, the PV was found significantly more deviated in the counter-force direction with VFB than without VFB (bootstrap, p = 0.002) (Fig. 8C). Furthermore, separate PV analyses on force field-modulated cells showed significant differences across feedback (bootstrap, p < 0.001). By contrast, the PVs did not deviate significantly from the LD for the subpopulation that did not modify their firing rates (bootstrap, p = 0.08). The results may explain the different trajectory shapes found with and without VFB. To further verify that the difference was not due to sampling bias (see “Neuronal analysis” in Materials and Methods), we compared the cosine-fit parameters of single cells in vision versus nonvision and found that they were not significantly different (amplitude: t-Test, p > 0.10; base: t test, p > 0.10; PD: Wheeler's Test, p > 0.10).

Since PVs may differ between M1 and PM areas (Schwartz et al., 2004), we calculated the PVs excluding the PM cells (FFv = 21 cells; FFnv = 9 cells). Similar results were obtained, indicating that directional signals from the PM did not account for the difference [FFv = −63° (−64°, −62°); FFnv = −45° (−48°, −42°); bootstrap, p = 0.01]. This suggests that the different reorganization of force field-modulated cells underlies the different population directional signals generated with or without visual feedback. Indeed, PVs calculated trial-by-trial showed that PVs evolved in time to point to the direction that compensates for the force field. However, PVs differed significantly between feedback conditions and throughout the learning block (t test on PV differences, p < 0.0001) (Fig. 8D).

To verify the PV analyses, we determined the target directions that best explained the firing rates of a population of cells using maximum likelihood estimation (Chase et al., 2009). We performed this analysis for each recording session separately using all directionally tuned cells. We obtained consistent results; the population directional signal generally pointed away from the LD and opposite to the force-field direction (−43.1° ± 5.6°). Lastly, we tested whether the change in the population directional signal might happen in the absence of force field (150 ms from target onset to 600 ms after) and found that it did not deviate from the LD (−8.3° ± 4.5°).

Muscle activity during force field adaptation

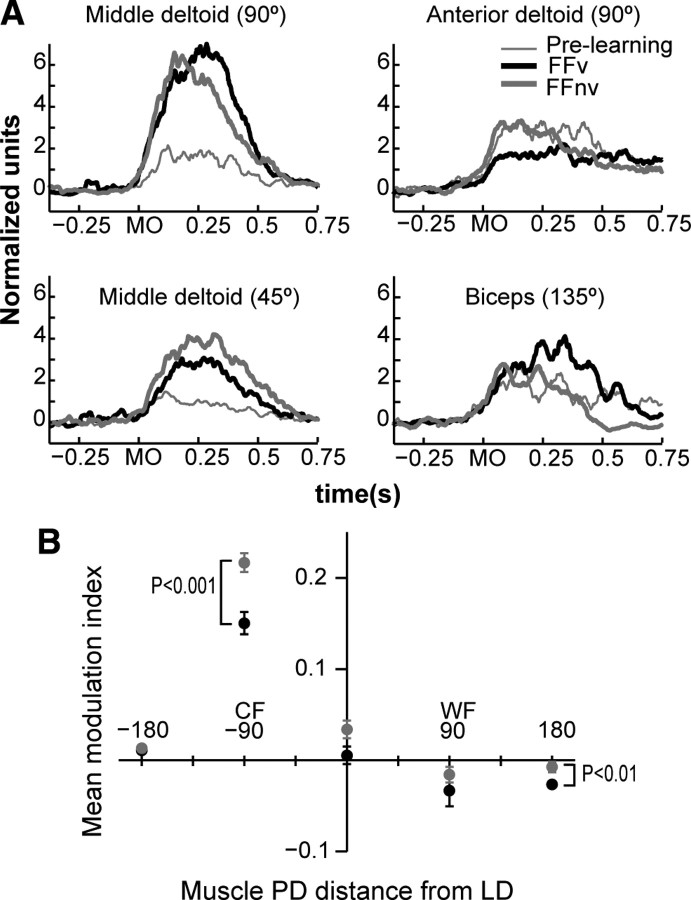
Muscle EMG activity in field reaches generally increased relative to that in unperturbed reaches to the same target direction (Fig. 9A). The modulation of EMG activity also depended on the distance from the PD to the LD (Fig. 9B). Increased activation was mainly observed in muscles with counter-field PD, while all other muscles did not show significant modulation (although with R² = 0.79 for both feedback conditions). This result indicated that changes in the muscles' activity were evoked mainly in the muscles that can contribute to the direction of force compensation. This differed from the neuronal responses that showed comparable magnitudes in the positive and negative modulation of CF and WF cells, respectively (Fig. 6A). While the direction of PV points to a new direction away from the LD, the final activation of muscles together with the perturbing force yields the hand motion toward the target. Therefore, the results cannot support a simple relation between the population neuronal modulation and muscle activity.

Figure 9.

Forelimb EMG responses to force field. A, Average normalized EMG activity of representative shoulder and elbow muscles that showed significant change of activity from prelearning to late field reaches to specified targets. Activity was aligned at movement onset (MO). These muscles also showed significantly different activities between feedback conditions. B, Mean modulation index of EMG activity as a function of the distance of muscle PD from LD and cosine fit for each feedback condition. Error bars: ±1 SE, p values are shown for significant comparisons between feedback conditions.

We also found that force field responses of the same muscles significantly differed between feedback conditions. For example, activation of the middle deltoid in perturbed reaches to 90° was significantly higher with VFB than without (t test, p < 0.01) (Fig. 9A). Simultaneously, the activity of the anterior deltoid decreased, thereby enhancing the compensation by the middle deltoid. This occurred with VFB but not without it (t test, p = 0.02). While the relationships between muscle activity to endpoint force, and endpoint force to hand motion are not trivial, the differences may partly explain the different trajectories found with and without VFB.

Discussion

Like humans (Arce et al., 2009), monkeys adopted different strategies when coping with force fields under different feedback contexts. Along with the observed changes in behavioral performance, we found that motor cortical cells rapidly modulated their firing rates to predict the novel force properties and generated a coherent population directional signal that incorporated the feedback context. This new pattern of neuronal activity, encompassing cell ensembles with wide-ranging PDs, depended on the cells' contribution to a new computation of movement direction that compensated for the perturbation. Sensory feedback influenced the profile of the population of cells recruited for the task, but not the combined activity pattern. Finally, the emergence of directional after-effects during catch trials suggests that the combined adaptive activation of cell ensembles underlie the generation of new internal models with which monkeys anticipate the force field and modify the motor commands.

Combined adaptive modulation of cell ensembles

Cell ensembles with diverse PDs modulated their firing rates depending on the distance of the PD from the LD to generate a compensatory directional signal. Thus, cells with PD along the direction that counters the perturbation increase their contribution to the PV. Meanwhile, other cell subpopulations reduce their contribution to the PV when the PD lies near the LD or where the dynamic load assists the movement. Our results differed from previous studies that reported changes in activity occurring mostly along the cells' PD during loaded-reaching (Kalaska et al., 1989; Gribble and Scott, 2002) or in cells with PD near the learned movement direction during visuospatial perturbations (Paz et al., 2003).

The underlying computations at the population and single-unit levels consistently followed a simple rule: the modulations of firing rates follow a cosine model. Furthermore, the predictions derived from the cosine-like adaptive modulation provided an explanation for the PD shifts reported during eight target adaptation to force field (Li et al., 2001). The PD shifts result from the rate modulations that signal a change in the intended movement direction under force field and may not necessarily reflect changes in the cells' directional tuning properties during adaptation. These findings were made evident when learning was local, allowing evaluation of cells' activity depending on PD. Such relation could not be assessed when load was applied for all directions (Kalaska and Crammond, 1992; Gandolfo et al., 2000; Li et al., 2001; Gribble and Scott, 2002). Since reach errors experienced in one trial affected errors in successive trials to other directions (Thoroughman and Shadmehr, 2000; Donchin et al., 2003), neurons might change their activity for more than one direction.

The combined modulation of cell ensembles suggests formation of a representation of a novel compensatory strategy during adaptation. Indeed, their combined activation yielded a new population directional signal that was dissociated from the actual hand movement direction and mirrored the directional after-effects (Fig. 1D). Alternatively, the rate modulation may reflect control signals of multiple movement features by single units or distinct subpopulations; the activity of cells that are cosine tuned to both movement and force might change to some intermediate value that is also cosine tuned. In any case, neurons modified their activity to accommodate the changing dynamics of the environment.

How do neurons carry out the computations of desired motor output?

The directional after-effects in catch-trials (Fig. 1,C,D) signify that the computation of reaches to the targets has changed, generating a new mapping of limb states to external forces. We suggest that the PD-dependent modulation of firing rates underlies the change in the internal model of the movement dynamics. What does this modulation represent? One possibility is that the intended reach direction remains to be the LD, and changes in neuronal activity could reflect changes of an inverse dynamics model. This would represent changes in muscular activation patterns that accommodate the dynamics of force changes inherent in viscous force fields. Another possibility is that the neuronal population computes a new intended reach direction away from the LD without detailed computation of real-time dynamics of the hand. Predicting the hand's displacement by the force field, the neuronal population specifies a new intended target direction such that with the force field, the hand reaches the LD. Thus, the rate modulation could reflect reaiming, as suggested for visuomotor rotation (Jarosiewicz et al., 2008). Indeed, the population directional signal in field reaches pointed away from the LD (Fig. 8B) and reflected the intended compensatory direction. This was the sum of the weighted activity of the directionally tuned cells that were modulated by force field and those that were not. Although we cannot conclusively determine which aspect of the internal model has changed, reaiming may provide the neuronal population a simpler computation of the desired motor output.

A neuronal basis for generalization patterns in force-field learning

The notion of basis function was first proposed to underlie object recognition in the visual cortex (Poggio, 1990) and spatial transformations in the parietal cortex (Pouget and Snyder, 2000; Pouget et al., 2000; Deneve and Pouget, 2003). It was later proposed to underlie sensorimotor adaptations and generalization patterns in the motor cortex (Poggio and Bizzi, 2004; Paz et al., 2004). Here, we suggest that the same principle holds for the directionally tuned cells when computing the motor output during force-field adaptation as a linear combination of their weighted activities. Thus, these neurons may serve as “upper motor neuronal primitives” that activate the spinal motor primitives to generate muscle synergies. A similar principle of vector summation was found in the spinal cord as simultaneous stimulation of two sites led to a linear combination of the endpoint forces generated by each site separately (Bizzi et al., 1991; Mussa-Ivaldi et al., 1994). We also found PD-dependent responses of muscles here, suggesting that the population directional signal could be translated downstream into specific muscle activation patterns using the same principle. Although this is a clear parallel between neuronal and muscle activities, important differences were also found. Furthermore, the activity of >50% of the directionally tuned cells did not correlate with changes in the muscle activity.

Human psychophysical studies have sought to infer the neuronal computations involved in force-field adaptation from the patterns of generalization. Thus, it has been suggested that the neural elements that underlie such learning have wide tuning curves that encode hand velocity bimodally and are found in the cerebellum (Shadmehr et al., 2005). However, evidence is yet to be found. Besides, more recent findings (Pasalar et al., 2006) do not give support to the cerebellum as the site for inverse dynamics of the arm as suggested previously (Kawato, 1999). Our findings suggest that for the motor cortex, the shape of the generalization function arises from the cosine-tuned modulation of different subpopulations of directionally tuned neurons. The generalization patterns that we predict for force-field learning (see supplemental Discussion, available at www.jneurosci.org as supplemental material) conform to the reported features of generalization in humans (Gandolfo et al., 1996; Shadmehr and Brashers-Krug, 1997; Shadmehr and Moussavi, 2000; Malfait et al., 2002; Donchin et al., 2003; Criscimagna-Hemminger et al., 2003; Caithness et al., 2004; Mattar and Ostry, 2007). Taken together, the findings suggest that the new activity pattern of the same basis functions could underlie learning and generalization. This further implies that cells' directional tuning properties do not necessarily change during adaptation, in contrast to previous reports (Li et al., 2001).

Integration of sensory feedback in the motor output

Understanding how feedback signals affect the motor output has important consequences for motor control (Jordan and Rumelhart, 1992; Ghez et al., 1995; Todorov, 2004), and in particular for the development of brain-machine interfaces (Suminski et al., 2009). We have previously suggested that humans use different adaptive strategies depending on the available sensory feedback (Arce et al., 2009). Here, the monkeys behaved similarly, yielding different trajectory shapes with and without VFB. While feedback did not influence pattern of combined activity of cell ensembles, it affected the profile of the population of cells recruited for the task. This is consistent with the notion that sensory stimuli do not determine the firing patterns but rather modulate them (Llinas and Pare, 1991). The peaks in the population profiles of force field-modulated cells varied according to the expected sensory outcomes relating to either trajectory or final hand position. When trajectory could be assessed easily with VFB, counter-field cells outnumbered all other cell ensembles. Without VFB, near-LD cells were recruited the most, suggesting a shift to the final hand position as the relevant parameter that drove adaptation. Such different reorganization underlies the different population directional signals generated with or without VFB, consistent with the differing trajectory shapes (straight vs curved). Thus, without changing how the new activity pattern is computed, the population signal can be fine tuned by the profile of the recruited cells. This shows how the computation of the motor output incorporates sensory feedback and as such may imply representations of sensory state estimates or changes of forward sensory models. Because sensory feedback mediates trajectory corrections on-the-fly as well, adaptive responses of motor cortical neurons may show different temporal dynamics. Thus, our conclusion is limited by the fact that firing rates had to be averaged across a relatively wide time window.

Conclusion

Our findings provide support for changes of population signals produced by the motor cortical neurons during force-field adaptation. We have shown how the motor cortex incorporates sensory feedback in the generation of the desired directional signal. The combination of the adapted activations of neuronal ensembles, while keeping their directional tuning properties, may reflect a general principle of how the computation of motor output is accomplished in the motor cortex.