Crunch: integrated processing and modeling of ChIP-seq data in terms of regulatory motifs

Abstract

Although ChIP-seq has become a routine experimental approach for quantitatively characterizing the genome-wide binding of transcription factors (TFs), computational analysis procedures remain far from standardized, making it difficult to compare ChIP-seq results across experiments. In addition, although genome-wide binding patterns must ultimately be determined by local constellations of DNA-binding sites, current analysis is typically limited to identifying enriched motifs in ChIP-seq peaks. Here we present Crunch, a completely automated computational method that performs all ChIP-seq analysis from quality control through read mapping and peak detecting and that integrates comprehensive modeling of the ChIP signal in terms of known and novel binding motifs, quantifying the contribution of each motif and annotating which combinations of motifs explain each binding peak. By applying Crunch to 128 data sets from the ENCODE Project, we show that Crunch outperforms current peak finders and find that TFs naturally separate into “solitary TFs,” for which a single motif explains the ChIP-peaks, and “cobinding TFs,” for which multiple motifs co-occur within peaks. Moreover, for most data sets, the motifs that Crunch identified de novo outperform known motifs, and both the set of cobinding motifs and the top motif of solitary TFs are consistent across experiments and cell lines. Crunch is implemented as a web server, enabling standardized analysis of any collection of ChIP-seq data sets by simply uploading raw sequencing data. Results are provided both in a graphical web interface and as downloadable files.

The advent of high-throughput sequencing technologies and the associated reduction of cost for sequencing have led to a spectacular increase in the use of a variety of methods, including RNA-seq, ChIP-seq, DNase-seq, ATAC-seq, and CLIP-seq, that combine high-throughput sequencing with other molecular biology techniques to quantitatively characterize internal states of cells on a genome-wide scale (Buenrostro et al. 2013; Soon et al. 2013). As one of the most prominent of these technologies, ChIP-seq (Johnson et al. 2007) combines chromatin immunoprecipitation with high-throughput sequencing to quantify the genome-wide binding patterns of any molecule that associates with the DNA. Apart from large-scale efforts, such as the ENCODE Project in which ChIP-seq was used to systematically map the binding patterns of many transcription factors (TFs) (The ENCODE Project Consortium 2012), many individual laboratories are now using ChIP-seq to characterize the binding patterns of particular DNA-binding proteins in their specific system of interest, for example, particular tissues or specific biological conditions.

The result of a ChIP-seq experiment is a collection of short DNA sequence reads, that is, typically tens of million reads that are a few tens of base pairs long each. Like for other high-throughput experimental techniques, extracting meaningful biological information from such large data sets is a nontrivial computational task that involves a significant number of separate steps, including read quality control and preprocessing; mapping the reads to the genome; estimating the typical length of the DNA fragments from which the reads derive; identifying binding peaks, that is, identifying genomic regions that are statistically significantly enriched for immunoprecipitated fragments; and downstream analyses such as identification of sequence motifs enriched within the peak sequences. Over the last decade, a large number of bioinformatic tools have been developed to perform each of these tasks (e.g., for a review of read mapping tools, see Schbath et al. 2012; for a review of methods for detecting binding peaks, see Wilbanks and Facciotti 2010; for an overview of algorithms for finding sequence motifs overrepresented among a set of short sequence segments, see Das and Dai 2007). A number of tools have also been presented that allow researchers to combine individual tools into a workflow, namely, by allowing users to manually execute one tool after another or by constructing a pipeline that runs the tools automatically. These include commercial solutions such as Avadis NGS (https://www.strand-ngs.com/avadis-platform), Chipster (Kallio et al. 2011), CLCbio Genomics Workbench (https://www.qiagenbioinformatics.com/), Genomatix Mining Station (https://www.genomatix.de/solutions/genomatix-mining-station.html), and Partek Genomics Suite (http://www.partek.com/partek-genomics-suite/), as well as free-to-use solutions such as HOMER (Heinz et al. 2010), CisGenome (Ji et al. 2008), seqMINER (Ye et al. 2011), ChIPseeqer (Giannopoulou and Elemento 2011), GeneProf (Halbritter et al. 2013), and Galaxy/Cistrome (Liu et al. 2011).

However, current ChIP-seq analysis methods are highly unsatisfactory in a number of respects. First, although the ENCODE Projects have developed basic practices and guidelines for ChIP-seq data (Landt et al. 2012), there is still little consensus on what tools are most appropriate for each step in the ChIP-seq analysis, let alone regarding details of their parameters and implementation. Consequently, there is large variability in the way ChIP-seq data are currently analyzed. The main challenge, especially for experimental researchers that wish to perform ChIP-seq analysis but lack computational biology expertise, is that there are no standardized pipelines that are widely accepted to give satisfactory performance. A private survey that we performed among colleagues suggests that every group with expertise in processing ChIP-seq data uses a different combination of tools that they have individually customized to deal with various issues that are not addressed by the publicly available versions. A consequence of this situation is that it is extremely difficult to compare results of ChIP-seq data from different experiments. That is, in order to compare one's own results with those of other ChIP-seq experiments, it is necessary to reanalyze the raw data from these experiments using one's own customized analysis pipeline.

Another unsatisfactory aspect of current analysis practices is that popular peak finders, for example, MACS (Zhang et al. 2008), assume statistical models for the fluctuations in ChIP-seq read densities that do not match those that are observed in the data. Consequently, the interpretation of the enrichment statistics (i.e., P-values) that such methods provide is problematic, and other methods, such as the analysis of the reproducibility of peaks across replicates (Landt et al. 2012), are necessary to determine cutoffs on the statistical significance of peaks.

Probably the most unsatisfactory aspect of current ChIP-seq analysis practices concerns the analysis of DNA sequence motifs. Although the entire genome-wide ChIP signal should ultimately be determined by local constellations of binding sites for DNA-binding factors, current ChIP-seq analyses do not attempt to directly model the observed ChIP signal in terms of the underlying DNA sequence. Instead, downstream sequence analysis is typically limited to simply running standard motif–finding algorithms on the sequences of the top binding peaks.

To address all these issues, we here present Crunch, a completely automated procedure that performs all steps of the ChIP-seq analysis and integrates comprehensive modeling of the genome-wide ChIP signal in terms of binding sites for both known and novel motifs, which Crunch identifies de novo. Crunch is implemented as a web server at crunch.unibas.ch and only requires the upload of the raw sequencing reads, allowing any researcher to perform comprehensive ChIP-seq analysis of any number of data sets in a completely standardized manner. Besides flat files for download, all results of Crunch's analysis are available through an easily navigable graphical web interface.

Results

In a typical ChIP-seq experiment, the protein that is immunoprecipitated is a DNA-binding protein or a protein that forms complexes with DNA-binding proteins, and the aims of the experiment include identifying the genomic loci where the protein is binding (either directly or indirectly) and the genes that are potentially regulated by these binding events. For DNA-binding proteins that bind DNA in a sequence-specific manner, additional aims are to characterize the sequence specificity of the protein and to identify other DNA-binding proteins that are colocalizing with the immunoprecipitated factor, possibly through direct interactions. Crunch provides answers to all of these questions and makes its analysis results accessible through an interactive graphical web interface and downloadable files.

The web server at crunch.unibas.ch only requires the user to provide raw ChIP-seq data in the form of FASTQ or FASTA files and to indicate the organism from which the data derived (currently human, mouse, and Drosophila have been implemented). Although a single immunoprecipitation data set suffices, users are advised to also upload “background” samples, that is, input DNA, whenever these are available. Multiple replicate data sets can be analyzed either separately or jointly. Optionally, more advanced users can choose to edit a number of options (see Methods), including the possibility to upload BED files of already mapped data instead of raw sequence data. Users can specify an e-mail address to get an automatic notification with a link to the results when the analysis has finished.

We applied Crunch to a large set of ChIP-seq experiments from the ENCODE Consortium (The ENCODE Project Consortium 2012), including all experiments performed on the cell line GM12878 and all experiments that were performed on the HeLa S3 cell line by the laboratory of Michael Snyder at Stanford University. In total, we analyzed 128 experiments in which 93 different TFs were immunoprecipitated. The full reports that result from submitting the raw FASTQ data of all these ChIP-seq data sets to Crunch are available at crunch.unibas.ch/ENCODE_REPORTS. Below we will first use one data set to illustrate all parts of the Crunch analysis and results.

Analysis overview and quality control summary

To illustrate Crunch's results, we chose the ENCODE experiment in which the BRCA1 protein was immunoprecipitated from GM12878 cells. Two replicate foreground (immunoprecipitation) samples and two replicate background (input DNA) samples were jointly analyzed.

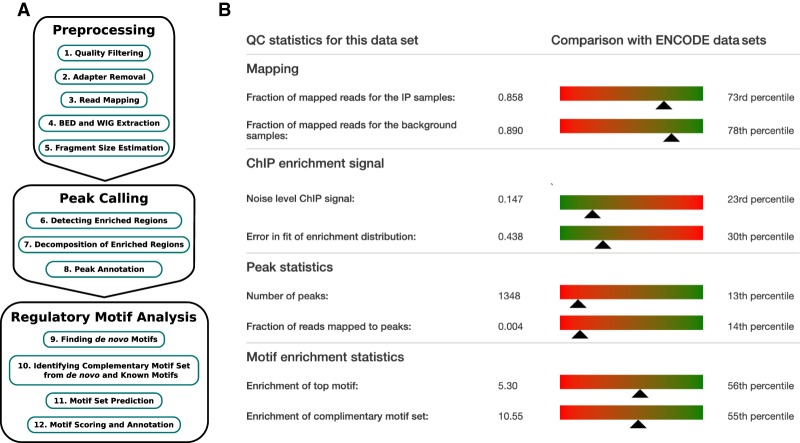
Crunch's analysis is structured into three parts, as shown in Figure 1A, and the analysis report is structured accordingly. In the preprocessing part, reads are filtered for quality and mapped to the genome, and the average size of the DNA fragments in the sample is estimated. Depending on the size of the input data, this preprocessing stage typically takes 2–6 h for the ENCODE data sets analyzed here (Supplemental Fig. S1A). In the second part, peaks are identified and annotated. This stage typically takes between 2.5 and 4 h (Supplemental Fig. S1B). In the third “motif analysis” part, novel binding motifs are inferred de novo, and the peak sequences are then modeled in terms of these novel and a library of known regulatory motifs. In particular, a set of complementary motifs is identified that jointly best explains the peak sequences. This stage takes <3 h for most data sets, but can take >12 h in rare cases (Supplemental Fig. S1D). Thus, the overall processing time of a typical data set is 10–14 h on the current version of our server.

Figure 1.

Analysis overview and quality-control (QC) summary. (A) Overview of the steps in Crunch's ChIP-seq analysis, which divides into three parts: preprocessing of the data, identification of the binding peaks, and regulatory motif analysis. (B) QC summary statistics for the BRCA1 data set. Statistics are separated into those associated with the mapping, the modeling of the ChIP signal, peak calling, and motif enrichment. For each statistic, a color gradient bar and indicator show how the statistic for this data set compares with those across the full set of ENCODE data sets, with green indicating relatively high quality and red relatively low quality.

To provide users a summary of the quality of the results on their data set, Crunch's report starts with a quality-control summary that lists a number of key statistics and indicates how these statistics compare with the full reference set of ENCODE data sets (Fig. 1B). For the mapping part, the fraction of all sequencing reads that passed quality control and were successfully mapped to the genome is reported. For the analysis of the ChIP signal, an overall measure of the noise level and the error in the fit to a reference distribution are reported. For the peak calling, the total number of peaks and the fraction of reads mapping to peaks are reported. And finally, for the motif finding, the enrichment of the top motif and the enrichment of the full set of complementary motifs are reported. To the right of each statistic is a bar plot that shows how this statistic compares with all data sets. For example, 85.8% of all reads in the immunoprecipitated sample passed QC and were successfully mapped, and this corresponds to the 73rd percentile; that is, for 73% of all ENCODE data sets we analyzed, a smaller fraction of reads was mapped. The bar runs from green to red to give an immediate visual indication whether these statistics are in a relatively high-quality regime (green) or low-quality regime (red).

Sequence quality control, mapping, and fragment size estimation

The raw read quality control, mapping, and estimation of the DNA fragment lengths are performed separately for each submitted sample and use relatively standard procedures as described in the Methods. An extensive report with detailed statistics regarding the quality control, adapter removal, and mappings is provided as a PDF for download (Supplemental Fig. S2). For each sample, Crunch also provides a BED file with the mappings and a WIG file that allows visualization of the read density along the genome.

In many ChIP-seq protocols, reads are obtained only from either the 5′ or 3′ end of the immunoprecipitated fragments, such that a single binding event on the genome will lead to two peaks in read density on opposite strands, shifted by approximately the average fragment length (Schmid and Bucher 2007; Landt et al. 2012). To correctly infer the locations of binding events, Crunch estimates fragment length from the correlations of read occurrences at opposite strands (Methods; Supplemental Fig. S3).

Binding peak identification and annotation

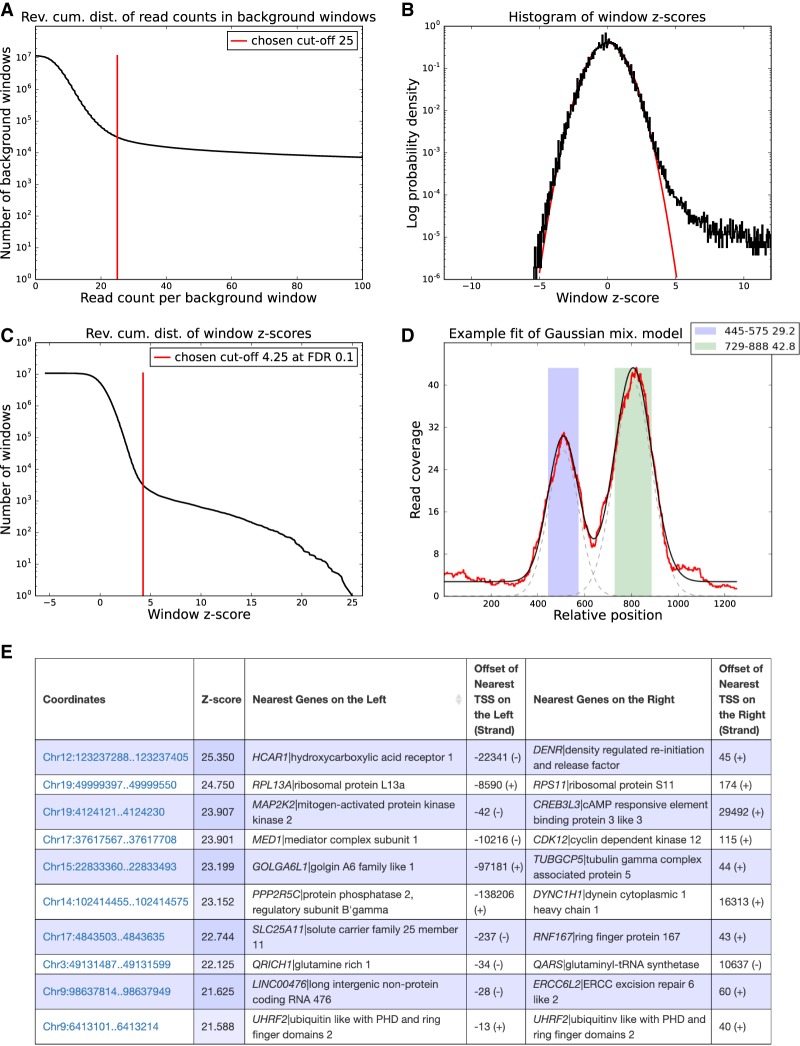
Crunch first calculates the observed read densities in sliding windows along the genome for both the ChIP and background samples. A very small fraction of windows, typically ∼0.1% associated with repeat regions, shows aberrantly high read density in the background (Fig. 2A), and these regions are removed by Crunch because ChIP enrichment cannot be reliably assessed in these regions (see Methods).

Figure 2.

Peak calling results for the BRCA1 data set. (A) Reverse cumulative distribution of the summed read counts from the BRCA1 background samples in genome-wide sliding windows of 2000 bp. Crunch adaptively determines a cutoff (red line), and windows with coverage higher than this cutoff are removed from further analysis. (B) Distribution of the observed z-values from all genome-wide sliding widows (in black) and a reference standard normal distribution (in red). (C) Reverse cumulative distribution of the same z-values (in black), as well as the z-score threshold (in red) corresponding to an FDR of 0.1. Note that the vertical axes in panels A, B, and C are in log-scale. (D) ChIP read-density profile of an individual enriched region (red), together with the fitted mixture model (black). The two gray dashed lines show the Gaussians used in the mixture model of this region. The colored bars show the two individual binding peaks with their locations and amplitudes shown in the legend. (E) Table with the top 10 peaks of the BRCA1 experiment. Each peak is annotated with its coordinates on the genome, its z-value, its nearest upstream and downstream genes, and the distance to the transcription start sites (TSS) of these genes.

Crunch uses a Bayesian mixture model that assumes that the genomic windows derive from a mixture of unenriched and enriched regions, and uses a new statistical model for read-density fluctuations in unenriched regions consisting of a convolution of log-normal and Poisson sampling noise (Balwierz et al. 2009). The parameters of this model are automatically fitted for each data set, resulting in a z-statistic for the enrichment of each genomic window. In the absence of any enriched windows, these z-values follow a standard normal distribution, and Figure 2B shows that for the BRCA1 data set, we indeed observe that the z-statistics of >99.9% of the windows almost perfectly follow a standard normal distribution, and that a small fraction of significantly enriched windows show much higher z-values. Crunch orders all windows by their z-values and by default picks a cutoff corresponding to a false discovery rate (FDR) of 0.1 (Fig. 2C; Supplemental Methods).

Crunch then merges enriched windows that overlap on the genome into enriched genomic regions. To identify individual binding events, Crunch models the observed ChIP profile in each enriched region as a mixture of a constant background and Gaussian peaks (Fig. 2D), with widths that are constrained by the estimated fragment length (Methods; Supplemental Methods). A final z-value is calculated for each individual binding peak, and the peak finding results are summarized as a list with genomic coordinates, z-value, and the locations of the nearest transcription start sites of genes upstream of and downstream from each binding peak (Fig. 2E). The web interface also provides, for each peak, a link to a view of the peak's locus within the SwissRegulon genome browser (Pachkov et al. 2013).

Explaining the observed peak sequences by a complementary set of motifs

Probably the most novel aspect of Crunch is that it aims to explicitly explain the observed peak sequences in terms of sequence motifs that occur within them. To make this notion precise, we use an idealized model of the ChIP-seq experiment in which, given a set of motifs {w}, the probability of immunoprecipitating a sequence s is proportional to the number of binding sites for the motifs {w} in s. As detailed in the Methods, the probability for the observed set of peak sequences given a set of motifs {w} can then be quantified by an enrichment score, E_{w}, that gives the geometric average of the fold enrichment of binding sites for the motifs {w} in peak sequences relative to random sequences of the same length and nucleotide composition.

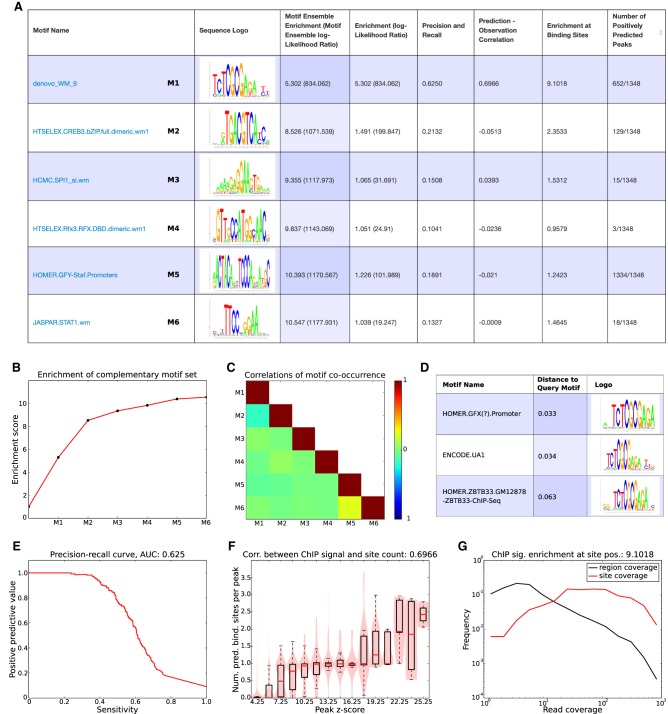
To find an optimal set of motifs {w}, Crunch divides the top peaks into a training and a test set of peaks and then first performs de novo motif finding on the training peaks using the PhyloGibbs (Siddharthan et al. 2005) and MotEvo (Arnold et al. 2012) algorithms previously developed in our laboratories. Both these algorithms are designed to incorporate information from sequence conservation patterns by running on multiple alignments of orthologous genomic regions, and Crunch automatically aligns each peak sequence with orthologous sequences from related organisms. The motifs that were found de novo are then combined with a large collection of more than 2000 position-specific weight matrices (PWMs) that we collected from a number of resources into a motif library, W_lib. From this library, a motif set {w} is iteratively constructed by starting with the single motif w that has the maximal enrichment E_w and adding motifs so as to maximize E_{w} on the test set of peaks. The result is a set of complementary motifs that jointly best explain the observed binding peak sequences (Fig. 3A).

Figure 3.

Motif analysis results for the BRCA1 data set. (A) List of complementary motifs that jointly explain the BRCA1 binding peaks. The motifs are sorted in the order in which they were added to the motif set, and for each motif, its name, sequence logo, and a set of statistics characterizing the performance of the motif are shown. (B) Evolution of the enrichment score of the ensemble of complementary motifs {w} as more motifs are added. (C) Heatmap of pairwise correlations of the occurrence of all motifs in {w} across binding peaks. (D) The top three motifs from the library of known motifs with most similarity to the motif denovo_WM_9. (E) Precision-recall curve for motif denovo_WM_9. The area under the curve (AUC) is 0.625. (F) Correlation between the ChIP signal (peak z-scores) and the number of predicted binding sites for denovo_WM_9 in peaks. The Pearson correlation coefficient is 0.6966. (G) Distributions of ChIP coverage at denovo_WM_9 sites (red curve) and at all positions in peaks (black curve). The coverage at sites is on average 9.1018, as high as at random positions in the peaks. Both axes are shown on a log-scale.

For the BRCA1 peaks, the top motif was a motif found de novo, called denovo_WM_9, with an enrichment score of about 5.3. That is, the peak sequences have on average 5.3 times as many sites for this motif as random sequences of the same nucleotide composition. The other five motifs in the set {w} all have enrichments less than 1.5 when considered individually, but considered jointly, they increase the enrichment, and all six together almost double the enrichment to 10.547 (Fig. 3A,B). Crunch also shows to what extent different motifs in the set tend to either co-occur or avoid co-occurring within the same peak sequences by reporting the correlations in motif occurrence for all pairs of motifs in the set (Fig. 3C).

For each motif in the set {w}, Crunch reports a number of additional pieces of information. Besides showing the motif's sequence logo, each motif is compared with all other motifs in the library of known motifs, and a list of the top matching motifs is reported (Fig. 3D). Crunch's top motif for the BRCA1 data, that is, denovo_WM_9, is very similar to a GFX motif in HOMER, the UA1 motif from ENCODE (which is the top motif for BRCA1 reported by ENCODE), and a motif from HOMER for the TF ZBTB33, also known as KAISO, which is in line with previous analysis of this data set (Wang et al. 2012). Besides the enrichment score, each motif is characterized by a number of additional performance measures. First, the precision-recall curve that would be obtained if peak sequences were classified based on the number of sites for the motif is calculated, and the area under the curve is reported (Fig. 3E). We see that motif denovo_WM_9 can identify ∼40% of the peaks with high precision. Second, Crunch investigates to what extent the number of predicted binding sites in a peak correlates with the significance (z-value) of the peak (Fig. 3F). We see that as soon as the z-value is larger than about eight, peaks are virtually guaranteed to contain at least one site for denovo_WM_9. In addition, peaks with very high z-scores tend to have more than one binding site. Third, if the sites of the motif correspond to the locations where the immunoprecipitated protein associates to the DNA, we would expect that the sites would tend to occur where the ChIP coverage is highest (see Supplemental Fig. S4), and to quantify this, Crunch reports the distribution of coverage at binding sites versus at all positions in the peaks (Fig. 3G). We see that the ChIP coverage at binding sites for denovo_WM_9 is more than nine times higher than at random positions in peaks. Finally, for each motif Crunch also reports the number of peaks for which binding sites are predicted to occur (Fig. 3A). Note that although denovo_WM_9 occurs in ∼50% of all peaks, its occurrence is highly specific, whereas the GFY-Staf motif occurs in almost all peaks but is much less specific. All other motifs in the set occur in only a small subset of the peaks. The Supplemental Text provides a discussion of the biological significance of these motifs, which we hypothesize correspond to direct interaction partners of BRCA1.

All results of the motif analysis are available through an interactive graphical interface that is automatically generated for each data set that is submitted to Crunch, allowing the user to explore the results in detail. For example, a user can decide to select from all binding peaks only those peaks in which sites for a given motif are predicted to occur. In addition, to allow further downstream analysis of the binding site constellations in peaks, flat files are provided that annotate each peak with the precise occurrences of all the motifs from the complementary set {w}. PWM files for all the reported motifs are also provided.

Crunch's noise model accurately reflects fluctuations in ChIP read densities

Because peak callers use a statistical model to distinguish true binding peaks from “random” fluctuations in read density, the accuracy of peak finding relies on the accuracy of the statistical model. In the BRCA1 example above, we saw that the distribution of z-values inferred by our noise model accurately tracked the expected standard normal distribution, supporting that Crunch's noise model correctly captures the statistics of ChIP-seq coverage fluctuations across the genome. We find that this is observed for most of the ENCODE ChIP-seq data sets.

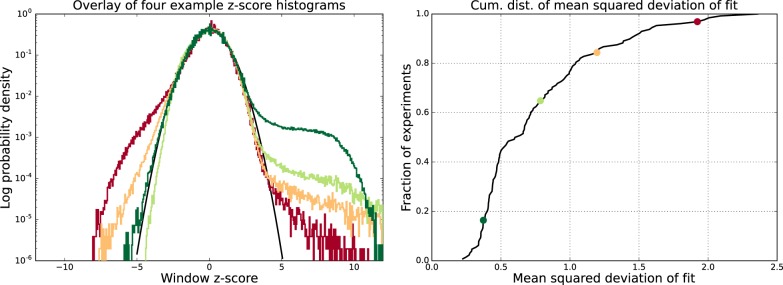
For each data set, we quantified the difference between the expected distribution of z-values and the observed one by the root of the average squared deviation of the observed log-density of z-values and the standard normal log-density, that is, $-z^2/2-\log \left(\sqrt{2\pi }\right)$ over the range z ∈ [ − 5, 3], which covers 99.9% of the distribution. High z-values were excluded because the distribution is expected to deviate from the expected standard normal at high z-values, and very negative z-values were excluded to avoid having the measure be dominated by a few outliers in this regime. We observe a very good match between the expected and observed distribution of z-value for ∼90% of all data sets (Fig. 4). Note that, even for the worst case, the observed distribution follows the standard normal over the range z ∈ [ − 2.5, 2.5] which includes ∼99% of all windows.

Figure 4.

Genome-wide fluctuations in ChIP signal fit Crunch's noise model. (Left) Examples of the z-value distributions of ChIP-enrichments genome-wide for four data sets (colored lines) together with the reference standard Gaussian (black line). The vertical axis is shown on a logarithmic scale. (Right) Cumulative distribution of the mean squared deviation between the observed z-value distribution and the standard Gaussian for the 128 ENCODE data sets. The locations in the cumulative distribution of the four data sets shown in the left panel are shown as correspondingly colored points.

As far as we are aware, Crunch is the only peak finding tool for which the noise model is explicitly supported by the data. In addition, because Crunch provides a figure with the comparison of the observed and expected z-value distribution in its report, users can immediately check whether their data show an aberrant distribution of ChIP signal fluctuations.

Crunch's peak finding outperforms other popular peak finders

We made a version of the Crunch pipeline that replaces Crunch's peak finding with the peak finding of two popular and well-established peak finders—MACS2 (Zhang et al. 2008) and SISSR (Jothi et al. 2008), reran the pipeline for all 128 ENCODE data sets using these two tools, and made an extensive comparison of the quality of the peak predictions (see Supplemental Results). Several different lines of evidence show that Crunch's peak predictions outperform those of MACS2 and SISSR. First, Crunch's peaks show more overlap with those of both MACS2 and SISSR than the peaks of these two tools with each other (Supplemental Fig. S5).

Second, for pairs of data sets in which the same TF was analyzed in different cell lines or by different laboratories, Crunch typically predicts similar peak numbers, whereas MACS2 and SISSR predict peak numbers that vary more than 10-fold or even 100-fold (Fig. 5A, inset). We strongly suspect that the large variability in the number of predicted peaks for MACS2 and SISSR results from the fact that, in contrast to Crunch, these tools do not have a realistic statistical model for the fluctuations in ChIP density along the genome. Third, the predicted peaks on data sets for the same TF have consistently larger overlap for Crunch than for MACS2 and SISSR (Fig. 5A; Supplemental Fig. S6).

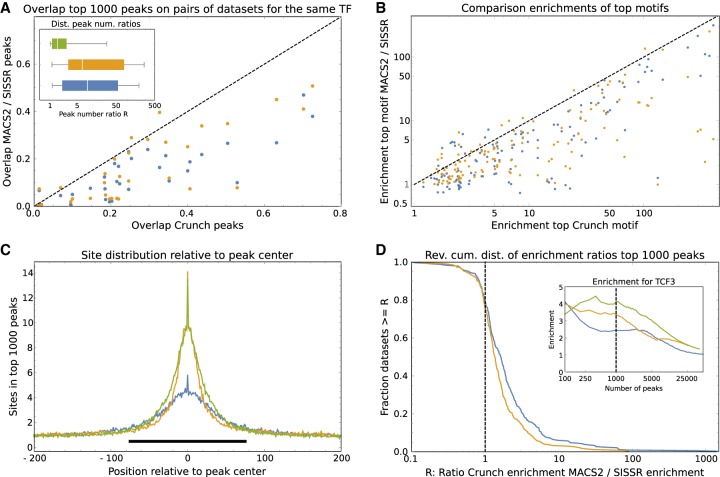
Figure 5.

Comparison of the peak predictions of Crunch, MACS2, and SISSR. (A) For each of the 31 pairs of data sets for the same TF, the overlap of the top 1000 peaks predicted by Crunch on the two data sets is shown on the horizontal axis versus the overlaps of the top 1000 peaks predicted by MACS2 (blue) and SISSR (orange) on the vertical axis. The dotted line shows y = x. The inset shows box-whisker plots of the ratios R of predicted peak numbers for pairs of data sets for the same TF for Crunch (green), MACS2 (blue), and SISSR (orange). (B) Enrichment of the most enriched motif in the top 1000 peaks of Crunch (horizontal axis) versus enrichment of the most enriched motifs in the top 1000 peaks of MACS2 (blue) and SISSR (orange). The dashed line shows the line y = x. (C) Average number of sites for the most enriched motif in the top 1000 peaks of Crunch (green), MACS2 (blue), and SISSR (orange) as a function of position relative to the peak's center. The black bar shows the region [−75, 75]. (D) The inset shows enrichment of Crunch's top motif as a function of the number of top peaks for Crunch (green), MACS2 (blue), and SISSR (orange). The dashed line shows the enrichments for the top 1000 peaks. The main plot shows the reverse cumulative distribution of the ratio of site enrichment in Crunch's top 1000 peaks versus enrichment of the same motif in the top 1000 MACS2 (blue) or SISSR (orange) peaks across all data sets and top motifs for each of the three tools.

Fourth, for the large majority of data sets the top motif found on the Crunch peaks has a higher enrichment score than the most enriched motif found on either the MACS2 or SISSR peaks (Fig. 5B; Supplemental Fig. S7). Finally, because we noted that MACS2 typically predicts wider peaks than Crunch and because we wanted to exclude the possibility that the poorer performance of MACS2 and SISSR results from these differences in peak width, we also performed an in-depth comparison of motif enrichment on regions of the same width for all tools. To investigate what width would be appropriate, we calculated the average number of sites for the most enriched motif in the top 1000 peaks as a function of position relative to the peak center and found that site enrichment is mainly concentrated in a region of roughly a single nucleosome wide, that is, from −75 to +75 around the peak center (Fig. 5C). We thus decided to compare the statistics of site enrichment in regions of 150 bp, centered on each peak's center. Second, because the motif finding on the MACS2 and SISSR peaks might have failed to identify the best motif, we compared the enrichment of the same motif across the top n Crunch, MACS2, and SISSR peaks as a function of the number of peaks n. For example, the inset of Figure 5D shows the enrichment of Crunch's top motif for the TCF3 data set on 150-bp regions centered on the peak centers of Crunch (green), MACS2 (blue), and SISSR (orange) as a function of the number of peaks taken. Crunch's peaks show highest enrichment over almost the entire range of peak numbers, and this is also observed when using the top motifs of MACS2 or SISSR (Supplemental Fig. S8). For the top 1000 peaks (Fig. 5D, inset, dotted line) Crunch's peaks have an enrichment of 3.81; MACS2's peaks, an enrichment of 2.14; and SISSR's peaks, an enrichment of 3.07. Thus, the ratios of enrichments are R = 3.81/2.14 ≈ 1.78 for Crunch versus MACS2 and R = 3.81/3.07 ≈ 1.24 for Crunch versus SISSR. To summarize the enrichments across all data sets, Figure 5D shows the distribution of these ratios R on the top 1000 Crunch peaks versus those of the same motif on the top 1000 MACS2 and SISSR peaks. For 80% of the data sets and motifs, Crunch's top 1000 peaks are more enriched than those of MACS2 and SISSR (Fig. 5D, dotted line), and superior enrichments are observed for all peak numbers ranging from the top 200 to the top 10,000 peaks (Supplemental Fig. S9). Finally, in addition to motif enrichments as defined by Equation 9, we also calculated all these statistics using the often used AUC metric, that is, the area under a receiver operator curve (see Supplemental Results). We find that all our observations also apply when AUC scores are used to measure motif enrichment: For 70%–80% of all data sets and motifs, the Crunch peaks show higher AUCs than the peaks of MACS2 or SISSR (Supplemental Fig. S10).

Crunch's de novo motifs outperform known motifs for the majority of data sets

To assess the importance and quality of the motifs that Crunch found de novo, we compared the enrichment scores of the top de novo and library motifs for each of the ENCODE ChIP-seq data sets (excluding seven data sets for which fewer than 200 peaks were found). Note that for most of the TFs that were immunoprecipitated in these data sets, the library of known motifs already includes several motifs representing these TFs, including all the ENCODE motifs that were previously inferred from these data sets (Wang et al. 2012). We thus expected that for most data sets, one of the many known motifs would outcompete the motifs that Crunch found de novo. In contrast, we find that for the majority of data sets, the top de novo motif outperformed all known motifs (Fig. 6). Because the motif finding was performed on a different set of peaks than used for evaluating motif enrichment, the superior performance cannot be because of overfitting the training peaks. In addition, for cases in which a de novo motif was most enriched and another data set was available for the same TF, we find that the de novo motif still outperforms the best-known motif on this other data set for the large majority of the cases (Supplemental Fig. S11).

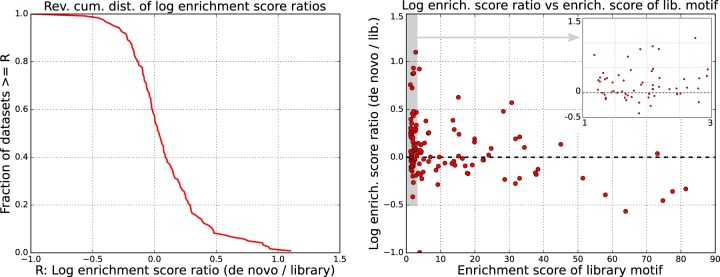
Figure 6.

Comparison of the performance of known and de novo motifs. (Left) The reverse cumulative distribution of the log-ratios R of enrichment of the top motif found de novo by Crunch and the top motif from the library of known motifs across the 121 ENCODE data sets for which at least 200 binding peaks were identified. A positive difference means that Crunch's de novo motif outperformed all library motifs. (Right) Scatter plot of the log-ratio R as a function of the enrichment score of the best-known motif. The inset zooms in on the gray region on the left side of the plot.

For about a quarter of the data sets, the motif enrichment improves by 0.2 or more. Although a difference in log-enrichment of 0.2 may seem modest, because there are typically 500 sequences in our test set, this increase in enrichment corresponds to a likelihood ratio of e^0.2×500 ≈ 2.7 × 10⁴³. Finally, we note that de novo motifs show improved enrichment especially when there was no highly enriched motif in the library of known motifs (Fig. 6, right panel).

The inferred motif sets are highly consistent across replicate experiments

For TFs that specifically bind the DNA, one might expect that the binding peaks should in principle be explainable by just a single motif, that is, the motif representing the sequence specificity of that TF. To quantify to what extent additional motifs are needed to account for the observed peaks, we defined, for each data set, the “additional information” as the log-ratio of enrichments of the entire motif set and of the top motif. The histogram of additional information shows that TFs can be separated into “solitary binding” TFs, for which the binding peaks are explained by a single motif, and “cobinding” TFs, which require a set of multiple motifs to explain (Fig. 7A). Although one might expect that additional information predominantly occurs when the top motif has low information content, we find no correlation between the information content of the top motif and the additional information (Supplemental Fig. S12). In addition, for TFs that were immunoprecipitated in two different cell lines, the additional information is generally very similar in both cell lines (Fig. 7B), supporting that the additional information is an intrinsic property of the TF.

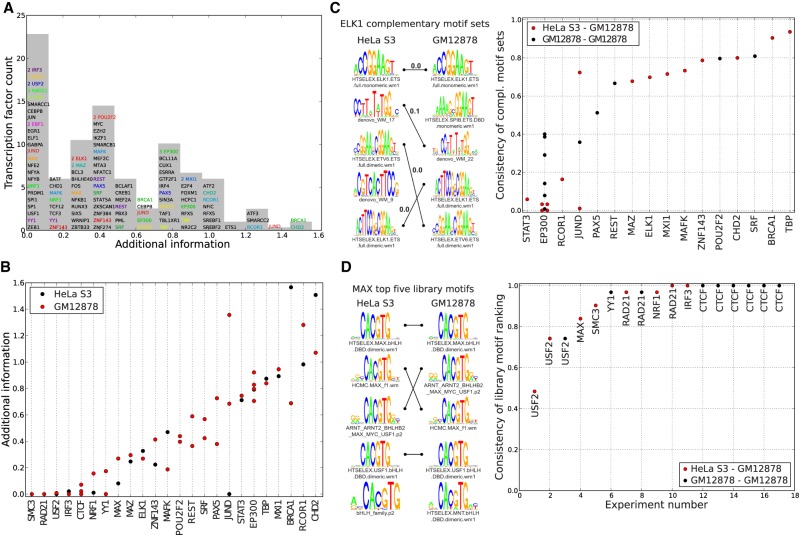
Figure 7.

Consistency of the motif sets across replicate data sets. (A) Histogram of the additional information for all complementary motif sets from the ENCODE data. The height of the bin corresponds to the number of unique TFs in the bin. TFs with multiple experiments are shown in a colored font, and the multiplicity of experiments for one TF within a bin is indicated. (B) Additional information across replicates for the 24 TFs for which multiple experiments were performed. Each dot corresponds to an experiment, with the color indicating the cell line. TFs are sorted by their mean additional information. (C) Consistency scores for all pairs of experiments (dots) with cobinding TFs (columns). The color indicates whether the experiments were performed in the same (black) or different (red) cell lines. As an example, the logos on the left show the complementary motif sets for two ELK1 experiments in different cell lines, with matching motifs connected by lines. The consistency score for these two sets is 0.7 (see Methods). (D) Consistencies of the top five known motifs for all pairs of experiments (columns) with the same solitary binding TF (indicated next to each dot). The color indicates whether the pair of experiments was performed in the same (black) or different (red) cell lines. As an example, we show the top motifs for two experiments with the TF MAX, in two different cell lines. Identical motifs are connected by lines, and the consistency of these two sets of motifs is 0.84.

We next investigated to what extent the inferred motifs were consistent across different experiments with the same TF. We divided the set of TFs into “solitary binders” and “cobinders” depending on whether the average additional information in the complementary motif set was smaller or larger than 0.2. For each pair of experiments performed with the same cobinding TF, we compared the motif sets using a consistency score that runs from zero, when there is no overlap between the motif sets, to one, when the exact same motifs occur in the exact same order (see Methods). With the exception of a few motifs such as STAT3, EP300, and RCOR1, the large majority of cobinding TFs shows highly consistent motif sets across the experiments, including experiments on different cell lines (Fig. 7C). This suggests that, for most cobinding TFs, the complementary motif set is an inherent characteristic of the TF and that Crunch can successfully identify such cobinding motif sets. In addition, when motif sets differ substantially between cell lines, Crunch's predictions can be used as hypotheses for further biological follow-up. For example, for STAT3 Crunch's analysis suggests that STAT3 associated significantly more often with RUNX factors in the GM12878 cell line and with AP-1 factors in the HeLa S3 cell line.

There were eight solitary binding TFs for which multiple experiments were performed, with 22 experiments performed in total with these factors. For each of these experiments, we extracted the top five known motifs with the highest enrichment scores and calculated the consistency of the top five motifs across all pairs of experiments performed with the same TF. Note that the consistency again runs from zero for disjoint sets to one for sets of identical motifs in the exact same order. We find that of the eight TFs tested, only the experiments on USF2 showed disagreement on the order of the top motifs. All others showed very high to perfect consistency, preserving the relative order even of highly similar motifs (Fig. 7D). This suggests that the binding specificity of the TF is independent of the details of the experiment and that, more importantly, Crunch's results can be used to select an optimal motif for solitary binding TFs.

Discussion

We here presented Crunch, a completely automated pipeline that performs all ChIP-seq analysis steps in a standardized manner. Crunch does not require any computational expertise of the user. Raw data can simply be directly uploaded to the Crunch web server, all analysis is performed automatically, and results are provided both through an interactive graphical web interface, as well as through flat files for further downstream analysis. In this way, Crunch allows any user not only to perform ChIP-seq analysis on their own data but also to systematically compare different ChIP-seq data sets.

Beyond providing a standardized pipeline, Crunch also introduces a number of novel features, and we show the power of the method on a large collection of ChIP-seq data sets from the ENCODE Project. In contrast to all peak finding tools that we are aware of, Crunch uses a noise model for fluctuations in ChIP read densities that is automatically fitted to the data and that demonstrably matches the statistics of the fluctuations that are actually observed in the data. In comparison to other well-established peak finders, Crunch's peak predictions are more consistent across data sets for the same TF and are substantially more enriched for the sequence motif associated with the TF. Probably the most important novel feature of Crunch is that a comprehensive regulatory motif analysis is integrated into the pipeline. By capitalizing on motif finding tools previously developed in our laboratory (Siddharthan et al. 2005; Arnold et al. 2012), Crunch uses a combination of de novo motif finding and prediction of binding sites for a large library of known motifs to explain the observed binding peak sequences in terms of the constellations of regulatory motifs that occur within them. In particular, Crunch automatically identifies a minimal set of complementary motifs that jointly best explain the observed peak sequences. Included among Crunch's result are files listing not only all binding peaks, their chromosomal locations, and ChIP signal strength but also annotations of all regulatory motifs occurring within these sequences, as well as statistical analyses of the co-occurrence of all these motifs and their contribution to explaining the peak sequences. These results may be especially valuable for further downstream analysis of how sequence motif constellations determine the genome-wide binding patterns of TFs that are observed in vivo.

We found that the motifs that Crunch identified de novo outcompeted all known motifs for the majority of data sets, supporting the power of Crunch's motif finding procedures. Second, Crunch's analysis showed that immunoprecipitated factors can be naturally divided into “solitary binding TFs,” in which the peak sequences are characterized by a single binding motifs, and “cobinders,” in which the peak sequences contain sites for a combination of complementary motifs. These cobinding motifs most likely correspond to TFs that tend to co-occur in binding regions of the TF in question, but some of them may also correspond to TFs that bind at other genomic loci that form 3D interactions with the binding loci of the TF in question. Both the complementary motif set and the top motifs for solitary binding TFs are highly reproducible across experiments, even when very similar motifs from different collections are available, suggesting that Crunch can be used to identify the optimal in vivo binding motif for a given solitary TF.

Although we here focused on the application of Crunch to data from ChIP-seq experiments with TFs, Crunch can also be applied to other types of data. For example, by using data from DNase-seq experiments, Crunch can be used to identify regions of open chromatin. Similarly, by using data from ChIP-seq experiments for the H3K4me1 or H3K27ac chromatin marks, Crunch can be used to identify the locations of cis-regulatory modules. In this context, we believe that Crunch's comprehensive motif analysis will be especially valuable for downstream analysis of how the genome-wide location of open chromatin and active enhancers is determined by local sequence motifs.

Methods

The Crunch analysis pipeline has been implemented using the Anduril workflow engine (Ovaska et al. 2010). Below we describe the analysis steps in the order in which they occur in the pipeline (see Fig. 1), providing details for novel methods and relegating more standard analysis steps to the Supplemental Methods.

Quality control and adapter removal

Crunch directly takes raw FASTQ files as input. To avoid contaminating downstream analyses with low-quality or erroneous sequences, we perform quality filtering and adapter removal, which includes automated determination of the adapter that was used using a list of known Illumina adapters (see Supplemental Methods; https://support.illumina.com/downloads/illumina-customer-sequence-letter.html).

Mapping

After filtering, Crunch maps the remaining reads to the reference genome using Bowtie version 1.1.1 (for details, see Supplemental Methods; Langmead et al. 2009). Instead of only retaining uniquely mapping reads, which would lead to a systematic loss of binding peaks in regions whose sequences are not unique in the genome, we retain multimapping reads and equally distribute the weight of each read to all mapping locations. To allow visualization of the ChIP profiles in a genome browser, Crunch produces downloadable WIG files of the aligned reads.

Crunch by default uses the older version of Bowtie (Langmead et al. 2009) rather than the newer version Bowtie 2 (Langmead and Salzberg 2012), which runs faster and with less memory for longer reads and can also perform gapped alignment. To compare the performance of Bowtie with that of Bowtie 2, we randomly selected 13 data sets that have a range of sequencing depths and numbers of binding peaks, and replaced Bowtie with Bowtie 2 for the mapping. We find that Bowtie 2 systematically maps fewer reads than Bowtie (Supplemental Fig. S13). This is consistent with the guidelines from the Bowtie developers that Bowtie 2 can have less sensitivity for reads that are <50 bp long. Nonetheless, there is virtually no change to the downstream peak calling (Supplemental Fig. S13).

Fragment size estimation

After shearing and pulling down the DNA, ChIP-seq protocols for sequencing library preparation generally include a step that selects fragments in a certain size range. Because the lengths of the selected fragments are typically significantly longer than the length of the sequencing reads, reads are produced from both ends of each double-stranded fragment. Consequently, the read distribution in the neighborhood of a protein-binding site typically shows two peaks on opposite strands of the DNA, at a distance approximately equal to the typical fragment length (Schmid and Bucher 2007). Crunch uses this fact to estimate the fragment length from the correlations in occurrence of reads on opposite strands as a function of their distance d (see Supplemental Methods; Supplemental Fig. S3).

Peak calling: identifying enriched regions

The first step in Crunch's peak finding consists of calculating, for each length 500 window in the genome, the number of fragments n and m from the ChIP and background samples, respectively, whose centers map to the corresponding window (see Supplemental Methods). Next, Crunch identifies and removes genomic windows with aberrantly high read densities in the background samples (see Supplemental Methods). These regions typically correspond to repetitive regions that align poorly with genomes of closely related species, and we suspect that the fragment counts are aberrantly high in these regions because these repeats are much more abundant in the genome used in the experiment than in the reference assembly, causing reads to pile up in these regions. These regions do not obey the statistics that are observed for the vast majority of the genome, and this leads to a high rate of false prediction of binding peaks in these regions.

To compare the fragment densities in ChIP and background samples, we normalize the fragment counts by the total fragment counts. We first add a pseudocount of 0.5 to the fragment counts n and m for each window and then determine the sums N and M of the fragment counts across all windows in the ChIP and background sample. To detect windows that are significantly enriched in the ChIP sample relative to the background, we need a statistical model for the fluctuations in observed read densities for windows that are not enriched. It is well known that even for identical sequence libraries, the act of sequencing itself introduces Poisson sampling noise in the number of observed reads in a given window. Although many peak finders make the assumption that this Poisson sampling noise is the only source of fluctuations, it is also well recognized that the other steps in the protocol, such as the fragmenting of the DNA and PCR amplification, introduce additional noise. For reasons of mathematical convenience, it has become popular to assume that these additional fluctuations are gamma distributed, leading to an overall negative binomial distribution of read densities across replicates, (see, e.g., Anders and Huber 2010). However, in previous work we have shown that the empirically observed fluctuations in read densities across replicates are well described by a convolution of multiplicative, that is, log-normal, and Poisson sampling noise (Balwierz et al. 2009). In particular, if f is the true fraction of fragments deriving from a certain locus, the probability to obtain n reads at the locus when sequencing N reads in total is approximately given by

$$P(n|f,N)\propto \exp \left(-{\displaystyle \frac{{\left(\log \left({\displaystyle \frac{n}{N}}\right)-\log \left(f\right)\right)}^2}{2\left({\sigma }^2+{\displaystyle \frac{1}{n}}\right)}}\right),$$ 1

where σ² is the variance of the multiplicative noise component, and the term 1/n corresponds to the variance owing to the Poisson sampling noise (for details, see Balwierz et al. 2009). If a given window corresponds to a region of the genome that was unbound, then the true fraction f should be the same in the ChIP and background sample. Consequently, the probability to obtain n out of N fragments in the ChIP sample when m out of M fragments were observed in the background sample is given by

$$\begin{array}{r}{P}_u\left(n\right|N,m,M,\sigma ,\mu )=\\ & {\displaystyle \frac{1}{\sqrt{2\pi \left(2{\sigma }^2+{\displaystyle \frac{1}{n}+{\displaystyle \frac{1}{m}}}\right)}}\exp \left(-{\displaystyle \frac{{\left(\log \left({\displaystyle \frac{n}{N}}\right)-\log \left({\displaystyle \frac{m}{M}}\right)-\mu \right)}^2}{2\left(2{\sigma }^2+{\displaystyle \frac{1}{n}+{\displaystyle \frac{1}{m}}}\right)}}\right)}\end{array}.$$ 2

The term 2σ² is the variance of the multiplicative noise component, and the term 1/n + 1/m constitutes the contribution to the variance from the Poisson noise components of both the foreground and background samples. As a significant fraction of the reads in the foreground sample derives from bound regions, the fragment density in regions without binding is systematically lower in the ChIP sample than in the background sample. The parameter μ corresponds to the resulting overall shift in log-density in the unbound regions.

If a window corresponds to a region that had binding of the immunoprecipitated factor, then the fragment density can be arbitrarily higher in the ChIP sample than in the background sample. Instead of making specific assumptions about this distribution, we will describe the probability P_b(n|N, m, M) to obtain n out of N reads in the ChIP sample, given m out of M in the background sample, by a uniform distribution in the difference δ of log-densities between ChIP and background. That is, let δ = log(n/N) − log(m/M), and let R = δ_max − δ_min correspond to the observed range in δ values across all windows. We then assume that, for a bound region, the δ value can take on any value in this range:

$$P_b(n|N,m,M)={\displaystyle \frac{1}{R}.}$$ 3

To model the joint distribution of both bound and unbound windows, we now assume a mixture model. That is, the overall probability for a window to obtain n out of N fragments in the ChIP sample given that it had m out of M fragments in the background sample is given by

$$\begin{array}{rl}{P}_{\mathrm{mix}}\left(n\right|N,m,M,\sigma ,\mu ,\rho )& =\rho P_u\left(n\right|N,m,M,\sigma ,\mu )\\ & +(1-\rho )P_b\left(n\right|N,m,M),\end{array}$$ 4

where ρ is the fraction of windows that are unbound, and μ and σ are the parameters of the noise model for unbound regions as described above. We then fit the parameters μ, σ, and ρ by maximizing the log-likelihood across all windows using expectation maximization (see Supplemental Methods). Finally, because the Gaussian approximation in Equation 2 becomes inaccurate when the raw fragment counts are only zero or one, we exclude windows in which the ChIP fragment count is below two.

After the parameters μ, σ, and ρ have been fit, we compute a z-value for every window:

$$z={\displaystyle \frac{\log \left({\displaystyle \frac{n}{N}}\right)-\log \left({\displaystyle \frac{m}{M}}\right)-\mu }{\sqrt{2{\sigma }^2+{\displaystyle \frac{1}{n}+{\displaystyle \frac{1}{m}}}}}.}$$ 5

Note that if there was no binding at any of the windows in the genome, the z-values should follow a standard normal distribution. As a final list of bound windows, we select all windows with a z-value over a threshold $z_{\ast }$. We set $z_{\ast }$ by default such that the FDR is 0.1 (Supplemental Methods; Fig. 2C), but this value can also be altered by the user if desired. Finally, because we chose the sliding windows to overlap, we merge overlapping windows that passed the threshold into larger bound regions.

Peak calling: identifying individual binding peaks within enriched regions

The enriched genomic regions that result from the analysis in the previous section are typically 500–1000 bp in length, which is significantly longer than the length of individual protein-binding sites on the DNA. In the second step of peak calling, we search for individual binding events by inspecting the ChIP signal within the regions at single–base pair resolution. For each position in each significantly enriched region, we compute the number of foreground fragments that overlap it. Here fragments are reads that were extended from their 5′ end to fragment size in 3′ direction. The result is a ChIP coverage profile for each significantly enriched region (Fig. 2D). To detect individual binding events, we now fit the coverage profile of each enriched region to a mixture of Gaussian peaks plus a uniform background distribution, in which the widths of the Gaussian peaks are constrained by the estimated fragment length (Supplemental Methods; Supplemental Fig. S14). A z-value is recalculated for each individual binding peak.

Association of binding peaks with genes and promoters

To annotate which genes may be regulated by the regulatory elements within the peak, we use our curated collection of promoters from SwissRegulon (Balwierz et al. 2009; Pachkov et al. 2013) and record the three closest promoters upstream of and downstream from the peak, as well as the genes associated with these promoters. In addition, for each peak we provide a link to the SwissRegulon genome browser, displaying the peak within its genomic context, including annotations of known transcripts, known promoters, and predicted TF binding sites within these promoters.

Regulatory motif analysis

To perform the motif analysis, Crunch first sorts the binding peaks by z-value and collects either all binding peaks, or the top 1000 peaks when there are more than 1000 significant peaks (no motif finding is performed when there are fewer than 200 peaks). The peaks are then randomly divided into two equally sized subsets: a training set {P_training} that Crunch uses to find and optimize motifs, as well as a test set {P_test} that Crunch uses to assess the performance of motif sets.

As detailed in the Supplemental Methods, Crunch then first performs de novo motif finding on the training set {P_training} using the PhyloGibbs (Siddharthan et al. 2005) and MotEvo (Arnold et al. 2012) algorithms previously developed in our laboratory. PhyloGibbs is used to find a set of motifs and MotEvo to refine these motifs. Both these algorithms are designed to incorporate information from sequence conservation patterns by running on multiple alignments of orthologous genomic regions. Crunch automatically aligns each peak sequence in the training set with orthologous sequences from related organisms and runs PhyloGibbs and MotEvo on these multiple alignments (Supplemental Methods). The result is a set of up to 24 candidate de novo motifs of different widths. These de novo motifs are combined with a large collection of more than 2300 PWMs that we collected from a number of resources into a motif library W (see Supplemental Methods).

Crunch then finds a complementary set of regulatory motifs from this library that together optimally explain the observed ChIP-seq data using an idealized model of the chromatin immunoprecipitation process. First, we approximate the genome by a pool of sequences, P, consisting of the observed binding peaks, P_o, together with a very large set of “background” sequences, P_b, that have the same lengths and nucleotide composition but are otherwise random. Second, we assume that when immunoprecipitating with a protein X, the probability of detecting a particular peak sequence, p, as a peak is proportional to the average number, n_p, of copies of X that are bound to the sequence (averaged over many cells). To relate the binding of X to the sequence of peak p, we assume the following model. We assume that there is a set of motifs {w} representing the sequence specificities of both X itself (if X is a sequence-dependent DNA-binding factor), as well as all other DNA-binding factors to which X binds either directly or indirectly, and that the total binding of X to sequence p is proportional to the total number of binding sites in p for the motifs in {w}. That is, we assume that the probability of observing sequence p as a peak sequence is given by

$$P_{\mathrm{IP}}(p|\{w\})\propto n_{p,\left\{w\right\}}+\beta l_p,$$ 6

where n_p,{w} is the total number of binding sites for motifs of the set {w} within p, l_p is the peak's length, and β corresponds to the amount of nonspecific binding per nucleotide. We added a nonspecific binding term to the model because it strongly improves the performance of the model, and it is well-known that TFs associate nonspecifically with the DNA (mostly through electrostatic attraction). Using Equation 6, the probability to observe, that is, immunoprecipitate, all of the observed peaks P_o and none of the backgrounds peaks P_b is then given by

$$P_{\mathrm{IP}}(P_o|\{w\})=\prod _{p\in P_o}\left[{\displaystyle \frac{n_{p,\left\{w\right\}}+\beta l_p}{\sum _{p\mathrm{\prime }\in P}{n}_{p\mathrm{\prime },\left\{w\right\}}+\beta l_{p\mathrm{\prime }}}}\right]=\prod _{p\in P_o}\left[{\displaystyle \frac{n_{p,\left\{w\right\}}+\beta l_p}{N_{\left\{w\right\}}+\beta L}}\right],$$ 7

where N_{w} is the total number of binding sites for the motifs {w} within the large pool P, and L is the total length of all sequences in the pool P. To assess the performance of the set of motifs {w} relative to random expectation, we use the difference between the log-likelihoods of observing the set P_o given motifs {w} and when randomly sampling peak sequences, and we take the limit of assuming the background set P_b much larger than the set of observed peaks P_o. We then find

$$d{L}_{\mathrm{IP}}(P_o|\{w\})=\sum _{p\in P_o}\log \left({\displaystyle \frac{n_{p,\left\{w\right\}}+\beta l_p}{\langle n_{b,\left\{w\right\}}\rangle +\beta \langle l\rangle }}\right),$$ 8

with 〈n_b,{w}〉 denoting the average numbers of sites for motifs {w} per background sequence, and 〈l〉 is the average length of the background sequences. Equation 8 gives the log-likelihood ratio of immunoprecipitating the true peak sequences P_o from a very large pool of sequences of equal nucleotide composition and length, between a model in which sequences are sampled proportional to the number of sites they contain for motifs from {w} and a model in which sequences are sampled randomly. Finally, to give a more intuitive measure, we transform this log-likelihood ratio into an “enrichment” score as follows:

$$E_{\left\{w\right\}}=\exp \left[{\displaystyle \frac{1}{\left|P_o\right|}\sum _{p\in P_o}\log \left({\displaystyle \frac{n_{p,\left\{w\right\}}+\beta l_p}{\langle n_{b,\left\{w\right\}}\rangle +\beta \langle l\rangle }}\right)}\right].$$ 9

The enrichment E_{w} has a simple interpretation: It measures the geometric average of the ratio of the amount of binding to observed peak sequences versus background sequences. As detailed in the Supplemental Methods, for any set of motifs {w}, the enrichment E_{w} is calculated by optimizing the parameters of the motif finding and the nonspecific binding on a training set of peaks and background sequences and then calculating E_{w} on a test set of peaks and background sequences.

Crunch searches for a minimal motif set {w} that maximizes the enrichment E_{w}. As a complete search across all subsets of {W_lib} is computationally infeasible, we use a greedy algorithm that maximizes E_{w} by adding one motif at a time (Fig. 3A). Crunch starts by calculating the enrichment E_w for each individual motif w in the library and sorts all motifs by this score. Because the motif library {W_lib} is highly redundant, we typically find that any high scoring motif w on the list is accompanied by a number of highly similar but lower-scoring motifs further down the list. These motifs are highly unlikely to end up in the final set {w}, and for computational efficiency, we remove these motifs from the list. That is, for any motif on the sorted list, all motifs that are highly similar but lower on the list are removed (for details, see Supplemental Methods). We denote the sorted list of remaining motifs by {W_reduced}. We initiate the motif set {w} with the top motif w_top, that is, the motif with maximal enrichment E_w, and iterate

1. For every motif w left in {W_reduced}, compute E_{w}∪w.

2. Denote the motif w with maximal E_{w}∪w by w_*.

3. If E_{w}∪w* increases E_{w} by >5%, add w_* to {w} and go to step one. Otherwise, terminate the algorithm.

The cutoff of at least a 5% increase for each added motif was chosen so as to allow even motifs that add relatively little to be incorporated while at the same time avoiding adding redundant motifs.

Additional motif statistics

Besides the enrichment score E_w, Crunch calculates a number of additional statistics to characterize the way in which each motif from the set {w} associates with the binding peaks (Fig. 3). First, for each motif, Crunch reports what fraction of the binding peaks contains at least one site for the motif. Second, although Crunch uses the enrichment score E_w to quantify the ability of the motif to explain the observed peaks, it also provides a standard precision-recall curve that shows how well binding peaks can be distinguished from background sequences based on the number of predicted sites (Fig. 3E). That is, by varying a cutoff on the total number of binding sites, T, Crunch calculates what fraction of binding peaks have a number of sites larger than T (sensitivity) and what fraction of all sequences with more than T sites are true binding peaks (precision).

As a third measure, Crunch calculates to what extent the number of predicted binding sites in a peak correlates with the strength of the peak's ChIP signal, that is, whether sequences with more sites lead to more enriched peaks. Crunch both provides a graph showing a box plot of the distribution of the number of predicted sites as a function of ChIP signal strength (Fig. 3F) and calculates the overall Pearson correlation between the number of binding sites, n_p,w, and the peak's z-value. Finally, if binding sites for the motif were directly responsible for the immunoprecipitation of the fragments, then we would expect the positions of the binding sites within the peak region to colocalize with the peak of the ChIP signal. Crunch's results also include a figure that shows the distribution of ChIP signal at predicted binding sites and, for reference, at all positions in the peaks (Fig. 3G). To quantify the enrichment of the ChIP signal at predicted binding sites, we calculate a ChIP signal enrichment:

$$C{E}_w={\displaystyle \frac{{\sum }_i{c}_i{p}_w(i)}{\overline{c}{\sum }_i{p}_w(i)},}$$ 10

where i runs over all positions at which a binding site for motif w is predicted, p_w(i) is the posterior probability (as assigned by MotEvo) for the site at i, c_i is the ChIP signal (fragment coverage) at position i, and $\overline{c}$ is the average ChIP signal in the binding peaks. Only binding sites with posterior p_w(i) > 0.2 are included in this calculation.

Finally, Crunch also reports statistics on the co-occurrence of motifs from the set {w} within binding peaks. For each pair of motifs (w, w′) in {w}, Crunch calculates the Pearson correlation in the number of binding sites n_{p, w} and n_{p, w’} across the binding peaks p. To visualize these correlations, Crunch provides a heat map of between motif correlation over peaks (Fig. 3C).

Consistency of motif sets

To compute the consistency C of two sets of motifs S and S′, we use the following measure, which is an extension of the Dice set similarity measure for ordered sets (Egghe and Michel 2003):

$$C(S,S\mathrm{\prime })={\displaystyle \frac{{\sum }_{i,j}\mathrm{\Theta }(0.2-d(S_i,{S\mathrm{\prime }}_j)){\displaystyle \frac{1}{2^{max(i,j)-1}}}}{{\sum }_i{\displaystyle \frac{1}{2^{i-1}}+{\sum }_j{\displaystyle \frac{1}{2^{j-1}}}}},}$$ 11

where i and j run from one to the number of motifs in S and S′, respectively; Θ(x) is the Heaviside step-function, which is zero if its argument is negative and one otherwise; and $d(S_i,S_j^{\mathrm{\prime }})$ is the distance between motif i in S and motif j in S′ (see Supplemental Methods). That is, if the distance between two motifs is lower than 0.2, the motifs are considered to match (for an example of motif distances among motifs, see Supplemental Fig. S15). Note that the consistency C(S, S′) runs from zero (no matching members) to one (two identical sets in the same order).

Software availability

Crunch is available as a web server at crunch.unibas.ch. For completeness, we also make an archive with all the source code of the current implementation of Crunch available as a Supplemental Code file.