Learning-Associated Gamma-Band Phase-Locking of Action–Outcome Selective Neurons in Orbitofrontal Cortex

Abstract

Gamma oscillations (30–100 Hz) correlate to a variety of neural functions, including sensory processing, attention, and action selection. However, they have barely been studied in relation to emotional processing and valuation of sensory signals and actions. We conducted multineuron and local field potential recordings in the orbitofrontal cortex (OFC) of rats performing a task in which they made go or no-go decisions based on two olfactory stimuli predicting appetitive or aversive outcomes.

Gamma power was strongest during the late phase of odor sampling, just before go/no-go movement, and increased with behavioral learning. Learning speed was correlated to the slope of the gamma power increment. Spikes of OFC neurons were consistently timed to the gamma rhythm during odor sampling, regardless of the associated outcome. However, only a specific subgroup of cells showed consistent phase timing. These cells showed action–outcome selective activity, not during stimulus sampling but during subsequent movement responses. During sampling, this subgroup displayed a suppression in firing rate but a concurrent increment in the consistency of spike timing relative to gamma oscillations.

In addition to gamma rhythm, OFC field potentials were characterized by theta oscillations during odor sampling. Neurons phase-locked to either theta or gamma rhythms but not to both, suggesting that they become associated with separate rhythmic networks involving OFC. Altogether, these results suggest that OFC gamma-band synchronization reflects inhibitory control over a subpopulation of neurons that express information about the emotional valence of actions after a motor decision, which suggests a novel mechanism for response inhibition.

Introduction

Gamma oscillatory activity (30–100 Hz) is manifested in local field potentials (LFPs) recorded from a wide range of brain areas in both human and animals. Gamma activity correlates to a variety of cognitive processes, including sensory processing, attention, working memory, and action selection (Bressler et al., 1993; Murthy and Fetz, 1996; Roelfsema et al., 1997; Tallon-Baudry et al., 1999; Fries et al., 2001; Pesaran et al., 2002; Buzsáki, 2006; Beshel et al., 2007; Pesaran et al., 2008). Synchronization of neural firing activity in the gamma band may enhance the impact on targets as a result of temporal summation of postsynaptic responses (Singer, 1993; Azouz and Gray, 2000; Salinas and Sejnowski, 2000) provided that the phase relationship between areas facilitates interaction (Womelsdorf et al., 2007). Similarly, the timing of joint firing patterns may affect long-term synaptic plasticity in local circuits or target areas via mechanisms of spike-timing-dependent plasticity (Levy and Steward, 1983; Markram et al., 1997; Lisman and Spruston, 2005; Cassenaer and Laurent, 2007). In conjunction with theta rhythmicity, gamma oscillations may temporally structure sensory read-in and episodic memory encoding in the hippocampus (Lisman, 2005; O'Keefe and Burgess, 2005; Montgomery et al., 2008).

In contrast to sensory processing and attention, gamma oscillations have been barely studied in the domain of emotional processing and valuation of sensory signals and actions. Thus, we investigated gamma oscillatory activity in the rat orbitofrontal cortex (OFC), a prefrontal structure implicated in making behavioral adjustments to changing reward contingencies and control over prepotent, impulsive responses to incentive stimuli (Jones and Mishkin, 1972; Chudasama et al., 2003; Winstanley et al., 2004) (but see Chudasama et al., 2007; Man et al., 2009). OFC neurons have been shown to flexibly encode representations of stimulus–outcome and action–outcome associations (Schoenbaum et al., 1998; Tremblay and Schultz, 1999; Wallis and Miller, 2003; Padoa-Schioppa and Assad, 2006; van Duuren et al., 2008, 2009). Although gamma oscillatory activity has been reported previously for human, monkey, and rat OFC (Nishida et al., 2004; Liu et al., 2005; Sun et al., 2006), the question arises whether gamma oscillations exert similar functions in emotional decision-making and valuation as suggested by studies on sensory processing.

Using tetrode arrays, we recorded orbitofrontal neurons and LFPs from rats performing an olfactory discrimination task. Selectively during odor sampling, we observed an increase in LFP gamma oscillations and associated phase-locking of OFC firing patterns that correlated with the speed of behavioral learning. In contrast to visual cortex, gamma-band phase-locking in OFC was primarily accounted for by an outcome-selective subgroup of neurons and was inversely correlated to the instantaneous firing rate of these neurons. In contrast, theta-band oscillatory activity was expressed in the early phase of odor sampling and expressed by a different neuronal subpopulation. These findings reveal a differential role for gamma and theta activity during emotional decision-making and support the hypothesis that OFC gamma activity exerts temporal control over neural representations encoding actions and their associated values.

Materials and Methods

Subjects

For the experiment described here, we used three adult male Wistar rats (Harlan CPB), weighing 370–450 g at the time of surgery. Rats were maintained two to a cage on a reversed light/dark cycle (lights off, 7:00 A.M.; lights on, 7:00 P.M.) with ad libitum food and water during training but housed individually in a transparent cage (40 × 40 × 40 cm) after surgery. They remained in the presence of other rats in the climate-controlled colony room. To induce motivation for the appetitive learning task, we restricted the rat's diet to 5–15 g of food available from >0.5 h after training, depending on the amount of reward collected in the session. The total amount of food available was calibrated to 90% of the free-feeding intake. All experiments were conducted according to the National Guidelines on Animal Experiments and with approval of the Animal Experimentation Committee of the University of Amsterdam.

Behavioral training

Apparatus.

Rats were trained on odor discrimination sessions in an operant chamber (56 × 30 × 40 cm, length × width × height) containing an odor sampling port and trial light on a front panel and a tray for delivery of fluids placed at the opposing wall (Fig. 1). The front panel was slanted at 45° (with respect to ground level) above the odor sampling port to allow unhindered nose poking into the odor port by implanted animals. The rat's interaction with the behavioral apparatus was monitored through photobeam interruptions occurring at the odor port, the fluid well, and during licking in the well. These events were timestamped and stored on a computer dedicated to behavioral data acquisition. During recording sessions, the output of the behavioral cage was routed to the Neuralynx Cheetah system and timestamped there, synchronized with electrophysiological data acquisition. Odors were delivered, mixed 1:1 with clean air, from separate glass vials via a system of electronically operated valves and tubing to avoid mixing. Likewise, quinine and sucrose solutions were delivered to the fluid well via separate fluid lines (van Duuren et al., 2007). Behavioral training and recording sessions were fully automated.

Figure 1.

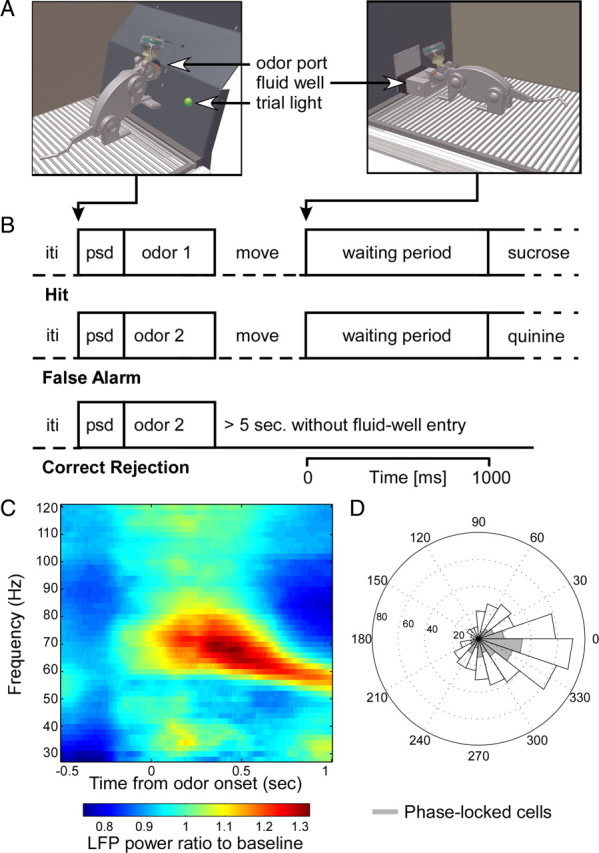
Operant chamber, behavioral task outline, and gamma oscillatory activity. A, Operant chamber; impression of rat making odor poke (left) and fluid poke (right). B, Trial types; sequence of task elements on hit, false-alarm, and correct rejection trials. iti, Intertrial interval; psd, prestimulus delay. C, Baseline-corrected power spectrum, averaged over odor pokes in all sessions. D, Polar histogram of mean phase of spike timing relative to the gamma cycle. Shaded part corresponds to significantly phase-locked units (184 of 525; Rayleigh's test, p < 0.001). Averaged mean phase: −20.55° (95% confidence interval: −28.24 to −12.85°). Distribution of phases deviated significantly from uniformity (p < 10⁻²⁰).

Training procedure.

We trained our rats on a two-odor go/no-go discrimination task (Schoenbaum et al., 1998). After habituation to the chamber and pretraining, rats were confronted with novel odor discrimination problems each day. Each session, one odor (for example, jasmine) was associated with reward (100 μl of 15% sucrose solution) and a second odor (for example, cinnamon) with an aversive outcome (100 μl of 0.01 m quinine solution). The odor set was found previously to contain no intrinsically aversive odorants (van Duuren et al., 2007). After an initial familiarization block of 10 trials exclusively consisting of S+ trials, 5 + 5 pseudorandomly ordered positive (S+) and negative (S−) odor trials occurred per block. Training continued over consecutive blocks until a behavioral criterion was met (scoring >85% hits and correct rejections over a moving block of the preceding 20 trials) or until the rat stopped interacting with the box. Demarcations between blocks were not overtly signaled to the animals. Rats could initiate a trial by poking their snout in the odor sampling port when a trial light was lit. After a 500 ms prestimulus delay, the selected odor/air mixture was released in the odor chamber. A nose poke of sufficient duration in the odor port (wait for odor 500 ms and sample odor for at least 750 ms) was indicated by the trial light turning off. After sampling, the rats could move over to the fluid well. On entering the well, rats were required to make a nose poke for ≥1000 ms before the outcome (sucrose or quinine solution) was delivered. We refer to the 1000 ms delay period as the “waiting” or anticipatory period. When the rats left the fluid well, an intertrial interval (ITI) of 10–15 s was observed before the next trial started. A correct rejection after the odor predicting quinine was accomplished if the rat did not enter the reinforcement tray within the first 5 s after sampling of that odor. Responses during the ITI had no programmed consequences, whereas premature responses (i.e., short pokes) during the odor sampling or waiting period resulted in a slightly aversive outcome, namely an immediate start of a new trial, beginning with another ITI.

Rats were implanted after they reached behavioral criterion and allowed recovery for 1 week. We retrained implanted rats on a familiar odor pair until performance once again reached criterion and started the recording of neural activity in the next session, in which a novel odor pair was introduced. When rats reached criterion performance during the recording sessions, the odor–outcome contingencies were reversed for the remainder of the session. This reversal phase is not further considered in this paper.

Surgical procedures

Animals were anesthetized by intramuscular injection of 0.08 ml/100 g Hypnorm (0.2 mg/ml fentanyl, 10 mg/ml fluanison; VetaPharma Ltd.), followed by 0.04 ml/100 g Dormicum (5 mg/ml midazolam; Roche Nederland B.V.) subcutaneously and mounted in a stereotact. Body temperature was maintained between 35 and 36°C. A microdrive, holding 14 individually moveable electrode drivers, was chronically implanted onto a craniotomy (2 mm diameter) in the left hemisphere dorsal to the OFC at 3.4–3.6 mm anterior and 3.0–3.2 mm lateral to bregma. The drivers were loaded with 12 tetrodes and two reference electrodes, circularly spaced (Gothard et al., 1996; Lansink et al., 2007) with distances between adjacent tetrodes at 300 μm, not taking into account slight offsets in dorsoventral position. Using dental cement, the drive was anchored to six stainless steel screws, one of which was positioned in the left parietal bone and served as ground. Immediately after surgery, all tetrodes and reference electrodes were advanced 0.8 mm into the brain. Next, the animal was allowed to recover for 7 d with ad libitum food and water, during which the 12 recording tetrodes were advanced in daily steps to the upper border of the OFC according to a standardized rat brain atlas (Paxinos and Watson, 2007) (supplemental Fig. S1, available at www.jneurosci.org as supplemental material). The reference electrodes were lowered to a depth of 1.2–2.0 mm and adjusted to minimize spiking activity on the reference channel.

After surgery, saline was injected subcutaneously (2 ml per flank), and pain relief was provided by 0.1 ml/100 g presurgical weight of a 10% Finadyne (50 mg/ml flunixin meglumine; Schering-Plough) solution administered in saline subcutaneously.

Electrophysiology

Using tetrodes (Gray et al., 1995), neural activity was recorded by a 64-channel Cheetah setup (Neuralynx). Signals were passed through a unity-gain preamplifier head stage and a 72-channel commutator (Dragonfly; Ridgeley), amplified 5000×, and bandpass filtered between 600 and 6000 Hz for spike recordings. If a signal on any of the leads of a tetrode crossed a preset threshold, activity on all four leads was sampled at 32 kHz for 1 ms and stored for offline analysis. Local field potentials recorded on all tetrodes were amplified 1000×, continuously sampled at 1874 Hz, and bandpass filtered between 1 and 475 Hz. Events in the behavioral task were coregistered and timestamped by the Cheetah system.

Data analysis

Behavioral correlates of single-unit activity.

Spike trains were sorted to isolate single units using a semiautomated clustering algorithm (BubbleClust), followed by manual refinement using MClust. Automated and manual clustering of spikes was done using the waveform peak amplitude, area, squared amplitude integral, and the first three principal components. Clusters were accepted as single units when having no more than 0.1% of interspike intervals shorter than 2 ms.

Behavioral correlates of firing-rate changes were assessed by constructing perievent time histograms synchronized on task events (i.e., onset and offset of odor sampling, fluid well entry, reward delivery). Firing rates in time bins (100 ms) around the event of interest were each compared against firing rates in five control bins from the ITI on a trial-by-trial basis to exclude within-session drift of firing rate as confounding factor and tested for significance using the nonparametric Wilcoxon's matched-pairs signed-rank test (p < 0.01). Binned firing rates were considered significantly modulated in relation to the task event only if the test bin of interest differed significantly from all five baseline bins (van Duuren et al., 2007). Cells were classified into four categories based on the task period in which they exhibited significant firing-rate changes (for odor sampling: change in relation to odor onset and during odor delivery; for movement: change after odor offset but before fluid poke onset; for waiting: change after fluid poke onset but before outcome; for outcome: change after application of sucrose or quinine solution) (Fig. 1). Cells with multiple behavioral firing-rate correlates were excluded from the analysis in Figure 5. See Table 1 and supplemental Figure S2 (available at www.jneurosci.org as supplemental material) for the distribution of neurons across categories and examples of units in each category. We computed whether cells with similar behavioral correlates clustered in space, i.e., whether “same” correlates were more likely for within-tetrode cell pairs compared with between-tetrode cell pairs. Indeed, our data support anatomical clustering of functionally defined groups of cells (supplemental Fig. S4, available at www.jneurosci.org as supplemental material).

Figure 5.

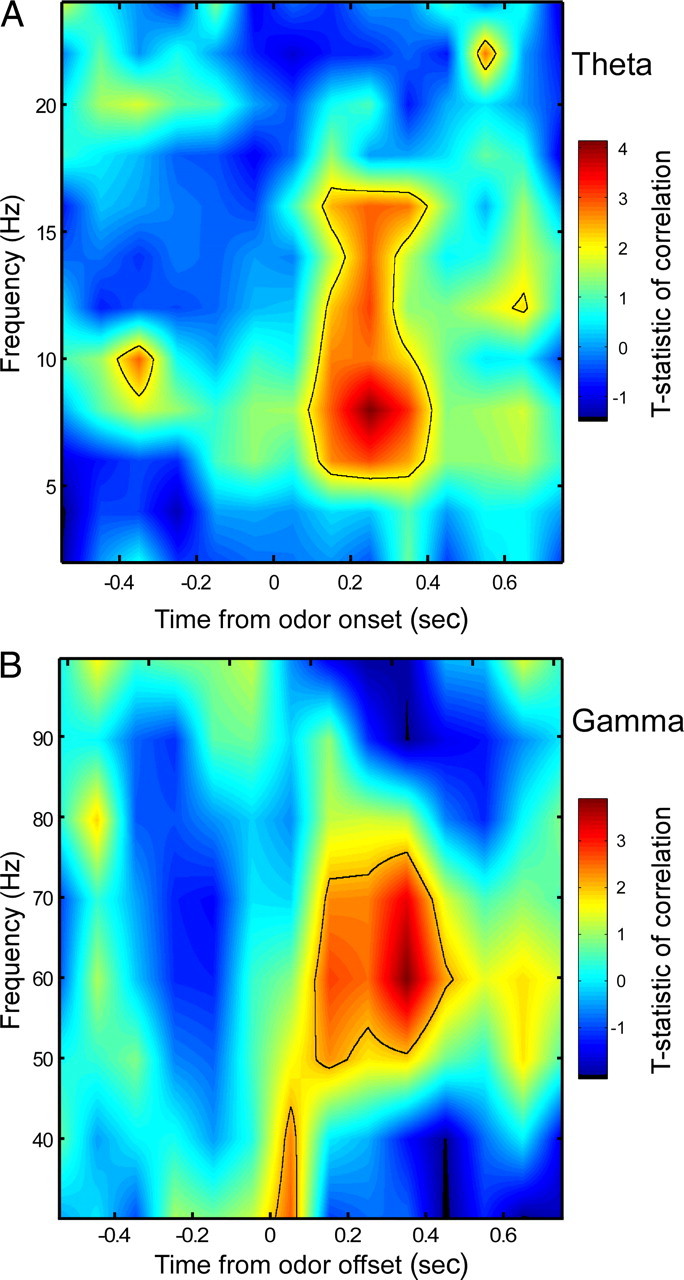
Prediction of firing rates from phase-locking values. A, Time–frequency correlation between theta-band phase-locking values for the odor sampling period and binned, instantaneous firing rates for all cells over trials centered on odor onset. Pseudocolors indicate the interpolated and smoothed value of the T statistic of the observed correlation compared with Student's t distribution. Theta-band phase-locking values best predict firing rates ∼200 ms after odor onset in a spectrally specific manner. Solid line contour encloses time–frequency patches with p < 0.05 (T statistic >1.96). Note that the upper band of predictive correlations extends into the low to medium beta range (12–17 Hz) (cf. Buzsáki, 2006). B, As in A but now for gamma-band phase-locking values for the odor sampling period and binned, instantaneous firing rates for all cells over trials centered on odor offset. Gamma-band phase-locking values best predict firing rates 300–400 ms after odor offset (during the movement period). This predictive relationship was not present for phase-locking values taken from the movement period.

Table 1.

Distribution of behavioral firing-rate correlates across the recorded population of cells

None [324]/0.62	Plus odor sampling	Plus movement period	Plus waiting period	Plus fluid delivery
Odor sampling	43 (26)	14 (6)	9 (7)	10 (8)
[88]/0.17	0.08	0.03	0.02	0.02
Movement period	14 (4)	36 (12)	9 (5)	4 (0)
[72]/0.14	0.03	0.07	0.02	0.01
Waiting period	9 (2)	9 (6)	24 (12)	9 (6)
[64]/0.12	0.02	0.02	0.05	0.02
Fluid delivery	10 (9)	4 (2)	9 (5)	28 (20)
[62]/0.12	0.02	0.01	0.02	0.06
Triple	OD_WT_FD	OD_MV_FD	OD_MV_WT	MV_WT_ FD
	6/0.01	2/0.01	4/0.01	3/0.01

Distribution of 256 significant task-related correlates from a sample of 201 of 525 units. The total number of correlates is larger than the number of cells, because cells can display more than one type of behavioral correlate. Rows show categories of task-related correlates, and columns specify single (on the diagonals) and double correlates in absolute numbers and fractions of total cell number. The numbers in brackets in the leftmost column indicate total number of units with a behavioral correlate in that category (including double and triple correlates), thus amounting to more than 256 correlates. Numbers in parentheses indicate the number of cells in those correlate categories that significantly discriminate between odors or outcomes. OD, Odor sampling; MV, movement period; WT, waiting period; FD, fluid delivery.

Spike–LFP phase-locking.

All analyses were done with Matlab (MathWorks) and using FieldTrip (http://www.ru.nl/fcdonders/fieldtrip/), an open source toolbox for the analysis of neurophysiological data. In all analyses in which pairs of single units and LFPs were used, the unit was recorded on a different tetrode than the LFP to avoid a possible frequency bias when the LFP around a spike was filtered. Briefly, for each spike of a given cell, we cut out a 1.0 s data segment of the LFPs recorded simultaneously on the other tetrodes (such that we never included a spike–LFP pair from the same tetrode). Several methods exist to measure spike–LFP phase consistency (Fries et al., 1997; Jarvis and Mitra, 2001; Pesaran et al., 2002; Womelsdorf et al., 2006). The basis of all of these methods is to determine the phase of a spike or a spike train relative to an LFP trace in a particular frequency band. Here, we multiplied each unfiltered LFP data segment by a Hanning window and Fourier transformed the windowed data segment of length T, so that the spike-triggered LFP frequency (f) spectrum is given as follows:

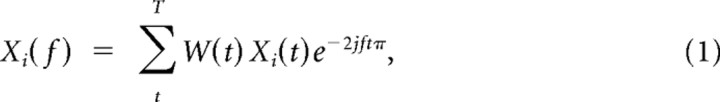where X_i(t) is the LFP time segment around the ith spike (i = 1, 2, …, N) and W(t) the Hanning window. Using a 1.0 s data segment length set the Rayleigh's frequency at 1 Hz, allowing a frequency resolution of 1 Hz. We determined the complex average spike-triggered LFP spectrum across the C different tetrodes as follows

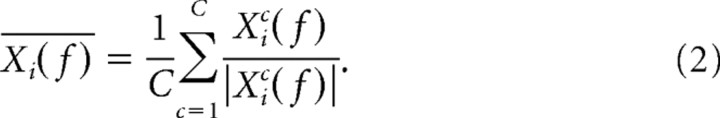Equation 2 ensures that the power of each LFP segment is ignored in the computation of the average spike phase. The spike phase is now simply given by θ_i = arg(X_i(f)). We measured phase consistency by means of the spike–LFP phase-locking value (PLV), which is defined as the resultant vector length across all spikes N,

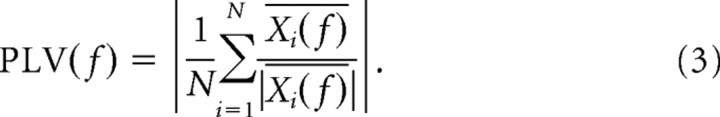The resultant vector length is a real number in the range of 0 (low phase consistency) to 1 (high phase consistency). The more spikes we use to obtain our statistical estimate of the resultant length, the more reliable it is. Spike–LFP phase-locking is a biased measure with respect to the number of spikes that are entered in the computation. In the method used here (Womelsdorf et al., 2008), we controlled for the bias by always entering the same fixed number of spikes (N = 50) into Equation 3 when we compared between samples with a different number of elements. This was the case whenever we compared phase-locking between trial types (see Fig. 3D), different task periods (see Fig. 2B,C), and different cell groups (see Fig. 4). Only in the time-resolved estimate of phase-locking (see Fig. 2A) did we use a lower criterion of N = 40 spikes per cell because here the sliding time windows (500 ms) were half the size of regular LFP windows. We further reduced the statistical variance of the spike–LFP phase-locking estimate by means of a bootstrapping procedure. For every repetition, we drew a fixed number of spikes without replacement from all spikes in the sample. For each sample drawn, we determined the spike–LFP phase-locking value. Subsequently, we averaged these spike–LFP phase-locking values across all bootstrapped samples (N = 5000), producing an unbiased phase-locking value. Nonetheless, the statistical significance of spike–LFP phase-locking can still be assessed across the entire sample of spikes, using the Rayleigh's test (p < 0.001).

Figure 3.

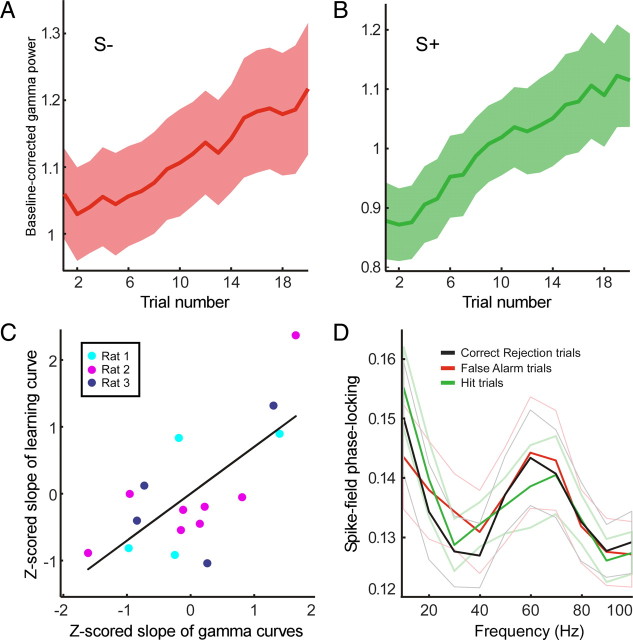
Gamma-band power is correlated with learning. A, Average baseline-corrected gamma-band LFP power during sampling of odors predicting quinine outcome across sessions as a function of the number of trials featuring those odors. Shading indicates 95% confidence interval. B, Same as in A but now for odors predicting sucrose outcome. C, Scatter plot of Z-scored slope parameters of learning and gamma-band power during odor sampling (see Materials and Methods). Solid line indicates slope of linear correlation (p < 0.01). D, Spike-field phase-locking values during odor sampling split according to subsequent behavioral choice by the animals. No significant differences contingent on outcome or action were found. Dimmed lines indicate 95% confidence interval.

Figure 2.

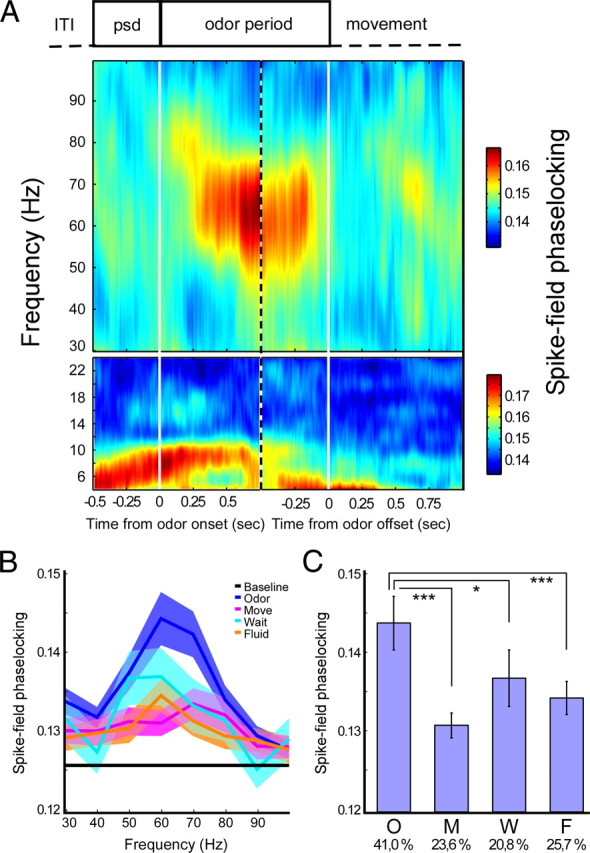
Gamma-band phase-locking as a function of trial time. A, Time course of average (across all cells) phase-locking centered on odor onset (left) and odor offset (right), indicated by solid white lines. Vertical dotted line segregates the independently calculated time courses. Phase-locking was calculated in 400 ms symmetric windows centered on each time point. Top shows gamma-band phase-locking, and bottom shows theta-band phase-locking. B, Gamma-band phase-locking spectrum separated for different behavioral periods. Shading indicates 95% confidence intervals. C, Bar plot of averaged phase-locking values at 50–70 Hz (mean ± SEM) for different task periods. We used N = 144 cells with >50 spikes in every task period. O, Odor delivery period; M, movement period; W, waiting period; F, fluid delivery period. Numbers below abscissa indicate percentages of cells significantly phase-locked [Rayleigh's test p < 0.0167 (0.05/3; Bonferroni's correction for testing at 50, 60, and 70 Hz)]. *p < 0.05, ***p < 0.001, Wilcoxon's matched-pairs signed-rank test.

Figure 4.

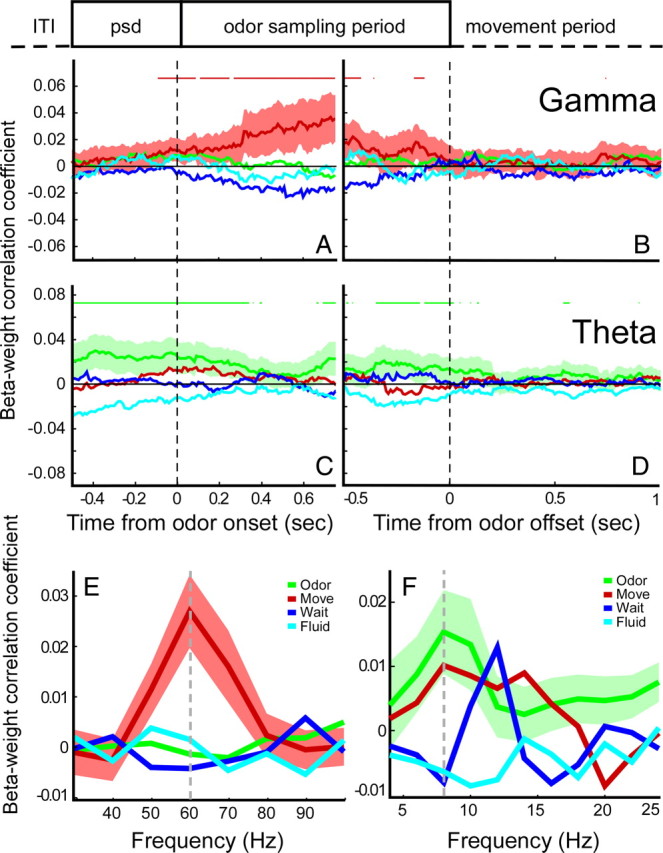
Temporally and spectrally delineated contributions to phase-locking by type of behavioral firing-rate correlate. A, Beta weights of contribution to gamma-band phase-locking (60–70 Hz) calculated in sliding windows, centered on odor onset. Green, Odor-type correlate; red, movement type; blue, waiting type; cyan, fluid type. Shading indicates 95% confidence interval for movement-type. Horizontal red lines indicate time points with significant correlation coefficients for movement-type correlates. B, Same as in A but now centered on odor offset. C, Same as in A but now for beta weights of theta-band phase-locking (6–10 Hz). Shading indicates 95% confidence interval for odor type. Green horizontal lines indicate time points with significant correlation coefficients for odor-type correlates. D, Same as in C but now centered on odor offset. E, Beta weights of contribution to gamma-band phase-locking spectrum during odor sampling by type of behavioral correlate. Shading indicates 95% confidence interval. F, Same as in E but now for the theta-band phase-locking spectrum.

Time-resolved power spectra.

For every tetrode, we isolated LFP data segments in 500 ms windows (setting the Rayleigh's frequency resolution at 2 Hz) centered on the time point of interest, separated by time steps of 10 ms. This yielded a frequency resolution of 2 Hz. Using Equation 1, the LFP power of the ith segment was determined by first computing the windowed Fourier transform as follows

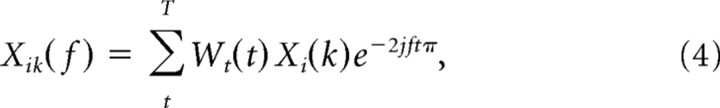and then averaging across the K tapers to obtain the power spectrum by

Here, k = (1, 2, …K) are indices for K orthogonal Slepian tapers, W(t), and X(t) is the LFP time series. We chose K = 7 (Percival and Walden, 1993).

To obtain the baseline-corrected LFP power spectrum, we first determined the LFP power in the intertrial interval in the same way as in the task period. We averaged the baseline LFP power across time segments and trials. We then defined the baseline-corrected trial LFP power by dividing the trial LFP power by the baseline LFP power.

Relationship between learning and gamma-band power.

First, we determined, for every session, the gamma-band power modulation relative to baseline per trial. This was done separately for the odor sampling periods of S+ and S−. Then, we computed the average gamma-band power modulation as a function of trial number across sessions. Trial number was defined relative to the first presentation of the S+ or S− odor. The significance of the relationship between gamma-band power modulation and trial number (over the first 20 trials) was assessed by a Pearson's r correlation.

We next examined, again for every session, the relationship between the speed of learning and gamma-band power modulation. To determine the speed of learning, we first indexed “instantaneous” behavioral performance as the moving average of the rats performance over the preceding 10 trials until the end of the acquisition stage of learning (i.e., excluding reversal stages). Performance was defined as the percentage of correct decisions, including both S+ and S− trials, i.e., hits and correct rejections as opposed to misses and false-alarm responses. For a given session, we then linearly regressed behavioral performance onto trial number, which yielded a Pearson's r correlation coefficient and a beta-regression weight. To determine for a given session whether learning was fast or slow, we Z-scored the Pearson's r correlation coefficients and beta-regression weights for every rat separately. This ensured that the speed of learning was not defined across rats but for every rat separately. This yielded two statistical quantities for what we call the “learning curve.” Similarly, we Z-scored the Pearson's r correlation coefficients and beta-regression weights for gamma-band power and trial number, in which we pooled together the S+ and S− here (i.e., we included all trials to compute the correlation), yielding two statistical quantities for what we call the “gamma-band power curve.” Then we computed the Pearson's r correlation coefficient between the statistics for the learning curve and the gamma-band power curve. This was done as both a correlation between the Z-scored beta-regression weights and the Z-scored Pearson's r correlation coefficients.

Multiple regression analysis

To investigate the contribution of a type of behavioral correlate in firing rate to phase-locking values during a specific trial period, we coded the presence or absence of such a correlate per cell in a binary fashion. Next, we constructed a design matrix with firing-rate correlate presence as dummy independent variables to explain phase-locking values as a dependent variable, separately for each trial period. This resulted in a matrix of beta weights (correlation coefficients) and associated p values. As control predictors, two columns indicating rat identity and whether a neuron was a putative interneuron or pyramidal cell were entered.

Histology

After the final recording session, current (25 μA for 10 s) was passed through one lead per tetrode to mark the endpoint of the tetrode with a small lesion. The animals were deeply anesthetized with Nembutal (sodium pentobarbital, 60 mg/ml, 0.9 ml i.p.; Ceva Sante Animale) and transcardially perfused with a 0.9% NaCl solution, followed by a 4% paraformaldehyde solution, pH 7.4 (phosphate buffered). After immersion fixation, coronal sections of 40 μm were cut using a vibratome and stained with cresyl violet to reconstruct tetrode tracks and localize the endpoints. Histological verification of the tetrode endpoints and recording tracks showed that all recordings were performed between 3.2 and 4.2 mm anterior to bregma and confined to the ventral and lateral aspects of the OFC (supplemental Fig. S1, available at www.jneurosci.org as supplemental material).

Results

Behavior

We trained food-restricted rats (N = 3) on a series of go/no-go discrimination problems, using new, unfamiliar odors as stimuli each session. A total of 17 sessions was analyzed. Rats learned to associate one odor (S+) with the availability of a fluid reward (sucrose solution) and the other odor (S−) with an aversive trial outcome (quinine solution). On sampling one of the odors, rats initially made a “go” response, i.e., they moved from the odor port to the fluid well and waited at the well for 1 s before fluid delivery (Fig. 1A). With learning, they started to withhold the response to the fluid well when the S− was presented (“no-go,” or correct rejection), requiring on average 86 ± 6 (mean ± SEM) trials to reach behavioral criterion, which was defined as 85% correct go/no-go responses over a moving block of 20 trials. Before reaching criterion, rats made on average 16 ± 2 false-alarm responses (i.e., a failure to withhold a response to the odor predicting quinine) (Fig. 1B). During the acquisition phase, the mean reaction time, spanning the period of movement from odor port to fluid well, was negatively correlated with increasing trial number (p < 0.05, Spearman's rank correlation), indicating that learning was expressed in the speed of the behavioral response as well as in the operant choices of the animals.

We recorded 525 well isolated single units from the OFC of three male Wistar rats using tetrode arrays (Gray et al., 1995). LFPs were simultaneously recorded from all tetrodes.

Gamma-band phase-locking of OFC cells

In many parts of the brain, prominent gamma oscillations are evoked by sensory stimuli (Gray and Singer, 1989; Brosch et al., 2002; Bauer et al., 2006; Buzsáki, 2006). In rats, gamma-band synchronization has also been found in several relay stations committed to odor processing (Eeckman and Freeman, 1990; Kay, 2003) and seems to be especially important for fine odor discrimination of chemically similar odorants (Stopfer et al., 1997; Beshel et al., 2007). The OFC is reciprocically connected to early olfactory cortical areas, such as the anterior olfactory nucleus and piriform cortex, which in turn receive direct input from the olfactory bulb (OB) (Carmichael et al., 1994; Carmichael and Price, 1995; Cavada et al., 2000; Illig, 2005). We therefore hypothesized that gamma-band oscillatory activity would be primarily present during the odor sampling period of our task. Indeed, we observed robust gamma oscillations (50–80 Hz) in the LFPs during the odor sampling period (Fig. 1C).

To assess whether the observed gamma-band oscillatory activity is related to spiking activity of OFC neurons, we examined whether single neurons showed consistent phase timing of action potentials relative to LFPs recorded simultaneously from different electrodes. Across all task periods, the mean phases of significantly phase-locked units clustered on the trough of the gamma oscillation (−20.55°; 95% confidence interval, −28.24 to −12.85°; 224 of 525 significantly phase-locked; Rayleigh's test, p < 0.001) (Fig. 1D), indicating a period of decreasing inhibition in the network (cf. Csicsvari et al., 2003; Hasenstaub et al., 2005). OFC lacks a clearly layered structure as found in the hippocampus and could potentially encompass multiple gamma oscillatory sources. However, we found that the vast majority of cells displayed mean gamma phases in a 90° quadrant from −45 to 45° and hardly any in the opposite quadrant, suggesting that the phases of our sample have been determined against the same or multiple zero-lag gamma source(s).

We hypothesized that rhythmic spike–LFP gamma-band synchronization would be most prominent during periods of robust gamma oscillations in the LFP, i.e., the odor sampling period. We investigated the strength of spike–LFP phase-locking (see Materials and Methods) as a function of time and frequency around odor sampling (Fig. 2A). During odor sampling, a spectrally concentrated rise in gamma-band phase-locking occurred (maximum at 60 Hz), reaching its peak at 600–700 ms after odor onset and lasting until the termination of the odor poke (Fig. 2A, top). In contrast, theta-band phase-locking (concentrated at 8–10 Hz) showed a slight enhancement starting with the initiation of an odor poke and peaking around odor release (Fig. 2A, bottom). Odor poke starts at −0.5 s.

A direct comparison of phase-locking spectra over all cells between different task periods showed that the highest values for gamma-band phase-locking were found in the odor sampling period (Fig. 2B). Phase-locking averaged over 50–70 Hz in the odor period was significantly higher than in other periods (Fig. 2C) (p < 0.05 for odor vs waiting period, p < 0.001 for odor vs movement and fluid delivery period, Mann–Whitney U test). Moreover, the odor sampling period showed the highest percentage of neurons phase-locked to gamma oscillations compared with other task periods (Fig. 2C, phase-locked percentages below abscissa) (determined with Rayleigh's test, p < 0.05; Bonferroni's correction for testing significance at 50, 60, and 70 Hz).

Power of gamma-band oscillations is learning dependent but not outcome specific

If the observed gamma-band oscillations are mainly driven by olfactory input, we expect them to be present regardless of the acquisition of stimulus–outcome associations. If, conversely, gamma-band synchronization is also dependent on the association of olfactory input and subsequent action and task outcome, we expect gamma-band oscillations to correlate with operant learning as assessed by the behavioral performance of the animals. In support of the latter hypothesis, we found that, at the onset of the session, gamma-band power in the odor sampling period was comparable with baseline levels but subsequently showed an upward ramp as a function of trial number during task acquisition (Fig. 3A,B), for both S+ and S− trials (Pearson's r = 0.73, p < 0.001; Pearson's r = 0.55, p < 0.05). Note that the first 10 S+ trials constitute the familiarization phase present at the start of each training session. After those 10 S+ trials, intermixed S+ and S− trials were presented to the rats. Therefore, gamma power levels for S− trials 1–10 should be compared with concurrent S+ trials 11–20 that are interleaved with those S− trials. The increases in gamma power between stimuli for these trial ranges do not show significant differences. Trial-to-trial changes in spike-field phase-locking could not be computed because single-trial data did not contain sufficient spike counts for analysis.

It is possible that highly similar learning-related increases in gamma-band power as shown in Figure 3, A and B, for the whole population of LFPs in fact consists of subgroups of LFPs specifically tuned to either the S+ or the S− stimulus. Alternatively, the population activity as probed by the recorded LFPs might be nondiscriminatory toward the S+ and S−. We computed a spectral power activity contrast, [(P_S+) − (P_S−)]/[(P_S+) + (P_S−)], per channel over the 60–80 Hz frequency range for the odor sampling period (supplemental Fig. S4A, available at www.jneurosci.org as supplemental material). We found only N = 5 of 204 channels that showed a significant contrast; therefore, it appears unlikely that the averaged LFP power as reported in Figure 3, A and B, consists of a mix of multiple selective pools of LFPs.

Based on the correlation between gamma-band oscillations and learning, we predicted that, in sessions in which rats demonstrated steeper learning curves, gamma-band oscillations should show a steeper increase as a function of trial number as well. We expressed both the increase in performance and the increase in gamma power as two statistical quantities reflecting the slope of these processes, namely a Pearson's correlation coefficient (PCC) and associated beta-weight of regression. We next examined the correlation between the PCC values for performance and gamma power across all sessions (Fig. 3C). This analysis was repeated for the correlation between the beta weights for performance and gamma power, with comparable results (data not shown). Indeed, in sessions in which a rat learned particularly fast, the gamma-power ramp in that session was particularly steep, as expressed in a significant positive correlation between both the Z-scored beta-regression weights for performance and gamma (Pearson's r = 0.70, p = 0.007) and the Z-scored PCCs for both processes (Pearson's r = 0.54, p = 0.03) (Fig. 3C). This correlation may reflect a role of OFC gamma-band oscillations in the acquisition of current odor–outcome mappings. Importantly, we found no differences in gamma-band spike-field synchronization between the odor sampling periods featuring the odor predicting sucrose versus the odor predicting quinine (Fig. 3D).

Here, as well, two subpopulations of neurons might exist that lock preferentially to either stimulus, which would be compatible with nondiscriminatory phase-locking across the population. Using the same approach as applied to spectral power activity contrast calculation, we computed phase-locking contrasts for S+ versus S−. Of N = 404 cells, we found N = 15 and N = 19 cells with a significant PLV contrast favoring S+ and S−, respectively (p < 0.05 two-tailed against randomization distribution) (supplemental Fig. S4B, available at www.jneurosci.org as supplemental material). Thus, although individual cells do show strong stimulus-specific phase-locking profiles, at the population level, OFC cells do not exhibit discriminatory phase-locking responses (compare with Fig. 3D). This suggests that gamma-band synchronization does in general not signal odor identity or outcome-specific information associated with the olfactory input but is involved in a process that is similarly triggered by sampling of the S− odor and the S+ odor.

Different subgroups of cells phase-lock to gamma and theta oscillations in different behavioral periods

OFC cells are known to exhibit a wide range of firing-rate modulations in relation to task events, such as odor presentation or reward delivery (Schoenbaum et al., 1998; Wallis and Miller, 2003; Padoa-Schioppa and Assad, 2006; van Duuren et al., 2008, 2009). Given the presence of gamma-band synchronization in odor processing stages in primary olfactory cortices, we expected that OFC cells responding with changes in firing rates to odor cues (i.e., showing odor selectivity) would show enhanced gamma-band phase-locking compared with other cell groups. We segmented our sample of neurons in groups with a behavioral firing-rate correlate in the odor period (O-cells), movement period (M-cells), waiting period (W-cells), and fluid delivery period (F-cells), as assessed by comparing binned firing rates around behavioral events with firing rates in the intertrial interval (cf. van Duuren et al., 2007) (supplemental Fig. S2, available at www.jneurosci.org as supplemental material). Often, cells could be classified as belonging to more than one group (Table 2), and cells with similar behavioral correlates were tended to cluster in space (supplemental Fig. S3, available at www.jneurosci.org as supplemental material).

Table 2.

Stability of oscillatory profiles across trial periods

	Odor sampling (FA)	Odor sampling (CREJ)	Odor sampling (hits)	Move	Wait	Fluid delivery: sucrose	Fluid delivery: quinine
Odor sampling (FA) (p = 0.0020)	×	0.56***	0.54***	0.1	0.24*	0.13	0.19
Odor sampling (CREJ) (p = 0.0008)		×	0.6***	0.28***	0.13	0.14*	0.25*
Odor sampling (hits) (p = 0.0028)			×	0.36***	0.13	0.16	0.43***
Move (p = 0.0360)				×	0.20*	0.26***	0.31**
Wait (p = 0.0012)					×	0.23**	0.19
Fluid delivery: sucrose (p = 0.0004)						×	0.15
Fluid delivery: quinine (p = 0.0004)							×

Pairwise correlation coefficients and significance levels for the correlation between oscillatory preference values (i.e. ratio of gamma to theta phase-locking values). First, we determined the ratio of gamma to theta phase-locking per cell per period. Next, we made pairwise comparisons between trial periods across cells. If the ratio of phase-locking is a stable feature of cells, we would expect these ratio values to correlate positively across periods. Values indicate the computed correlation coefficients between periods. p values with in parentheses with each category indicate the significance levels of finding the observed phase-locking ratios in that period compared with a randomized distribution of pairs of theta-band and gamma-band phase-locking values. FA, False alarm; CREJ, correct rejection.

*p < 0.05;

**p < 0.01;

***p < 0.001.

To investigate the relationship between behavioral firing-rate correlates and phase-locking over the course of trials, we computed the relative contribution of these correlate types to the spectrum of gamma- and theta-band phase-locking over time using multiple regression analysis. We defined the frequencies of interest as 60–70 Hz for gamma and 6–10 Hz for theta, because these frequency bands comprised the highest phase-locking values in the time–frequency analysis (Fig. 2A). Next, we assessed the relative contribution by the different groups of correlate types to the observed phase-locking values over time by computing beta weights of a multiple linear regression analysis for all correlate types, separate for theta and gamma frequencies, using a sliding time window approach (see Materials and Methods). The dynamic phase-locking spectrum found when all cells were considered (Fig. 2A) was found to consist of transient bouts of phase-locking carried by functionally delineated groups of cells (Fig. 4A–F). A direct comparison of contribution to phase-locking values by correlate type was performed using the same multiple linear regression model but now applied to predict phase-locking values restricted to the odor sampling period. Strikingly, only the presence of a firing-rate correlate during the movement period (M-type) was a strong and positive predictor of gamma-band phase-locking at 60 Hz (beta-weight regression coefficient ± SE of 0.0269 ± 0.0073; p < 0.001, two-sided t test) (Fig. 4E). This analysis controlled for other possible sources of variation such as rat identity and whether a neuron was a putative interneuron or pyramidal cell (see below) by entering these factors as dummy variables in the multiple regression analysis. In contrast to, for example, gamma-band synchronization in visual cortex (Gray and Singer, 1989), this suggests that gamma-band oscillatory activity during odor sampling is not widespread and is mainly carried by cells that during this trial period show no apparent firing-rate modulation but rather exhibit firing-rate modulations during the subsequent goal-directed movement to the fluid well. Conversely, a firing-rate correlate during the odor sampling period (O-type) was the best positive predictor of phase-locking in the theta band (6–10 Hz) during odor sampling (beta weight ± SE of 0.0154 ± 0.0065 at 8 Hz; p = 0.0194, two-sided t test) (Fig. 4F).

To gain additional insight in the relationship between spike–LFP phase-locking and firing rates, we performed a direct linear correlation analysis between firing rates and the odor sampling gamma-band phase-locking value, across time and frequency and over trials. We binned the firing rates of all cells during and after odor sampling in 100 ms bins until 1 s after odor offset and correlated these binned firing rates on a trial-by-trial basis with phase-locking values observed during the odor sampling period. We found a spectrally specific positive correlation between odor sampling gamma-band phase-locking values and firing rates that was restricted to the first few hundred milliseconds of the goal-directed movement phase over all cells (Fig. 5, within solid-line contours: p < 0.05). In contrast, theta-band phase-locking values predicted firing rates during the odor sampling period, suggesting that two functional assemblies are operating in two different carrier frequency bands.

Strength of gamma-band phase-locking predicts firing rates of outcome-selective cells

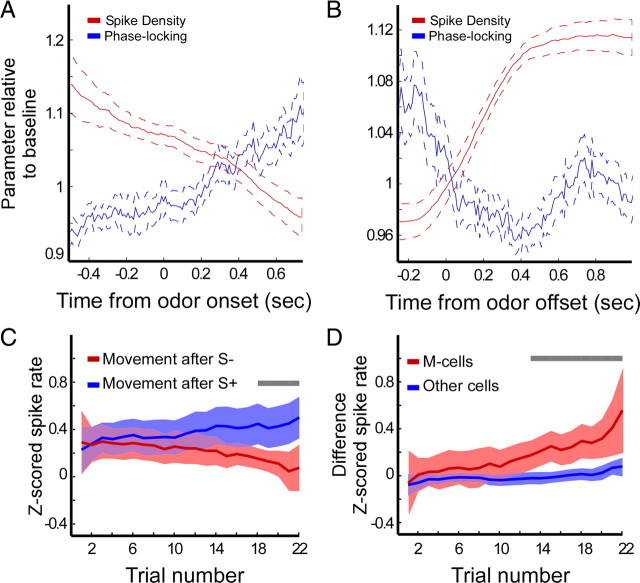
Analysis of the relation between gamma-band phase-locking and firing rates of M-cells revealed that these quantities were negatively correlated over the course of the odor sampling period (Pearson's r = −0.98, p < 0.001) (Fig. 6A) and the subsequent movement period (Pearson's r = −0.65, p < 0.001) (Fig. 6B). Thus, gamma-band rhythmicity during the odor sampling period could reflect an inhibitory control mechanism over the outcome-dependent firing rates of these neurons. The M-cell group, by definition, showed firing-rate modulations during the movement period compared with the intertrial interval. Critically, however, the average firing rate across this cell group differed for movement periods after the sampling of the odor predicting sucrose or quinine. Thus, the firing rate of M-cells does not only correlate with ongoing locomotion but also with predicted trial outcome (van Duuren et al., 2007, 2008). Across all sessions, for the movement periods after sampling of the S+, we found a positive correlation between average firing rate and trial number (Fig. 6C) (Pearson's r = 0.59, p < 10⁻⁵), whereas there was no such relation for movement periods after sampling of S−. After on average 18 presentations of S+ and S−, the average firing rates for the two odors during the subsequent movement period were significantly different (Mann–Whitney U test, p < 0.01). Moreover, the firing-rate responses of the M-cells became more differentiated with increasing trial number. First, as a control for running speed, we performed a multiple linear regression including the time from odor offset to outcome delivery in the design matrix. Running speed did not significantly correlate with M-cell firing rates for the movement periods after either the S+ (hit trials) or S− (false alarms; both p > 0.05) (results not shown). We next computed a difference score per trial by subtracting the responses after the negative odor from the responses after the positive odor. For M-cells, the difference score was positive correlated with trial number (Fig. 6D) (Pearson's r = 0.65, p < 0.01). Compared with the difference score for the group of remaining cells, a significant difference was observed starting after 13 presentations of S+ and S− (Mann–Whitney U test, p < 0.01). Because these M-cells are both strongly phase-locked to gamma oscillations during odor sampling and show outcome-selective firing rates during approach behavior, we propose that these cells are part of a network transforming stimulus input into action–outcome values that are used in guiding goal-directed behavior.

Figure 6.

Firing rate of movement-related (M) cells are outcome selective and anticorrelated to gamma-band phase-locking. A, Baseline-corrected average spike density of M-cells (red) and baseline-corrected average gamma-band phase-locking (blue) as a function of time centered on odor onset. Dotted lines indicate 95% confidence intervals. B, Same as in A but now centered on odor offset. C, Average Z-scored firing rates of M-cells during movement period as a function of trial number. Blue line represents averaged Z-scored firing rates from periods of movement toward the fluid well after sampling the S+ and red after sampling the S−. Shading indicates 95% confidence intervals. Gray bar indicates significant difference (p < 0.01, Mann–Whitney U test). D, Difference in average Z-scored firing rates during movement periods following S+ versus S− for M-cells (red) and other cells (blue) as a function of trial number. Shading indicates 95% confidence intervals. Gray bar indicates significant difference (p < 0.01, Mann–Whitney U test).

Gamma-band and theta-band phase-locking values are independent

Together, these results suggest that we can identify groups of cells by a phase-locking profile that is behavior and frequency specific. This raises the question whether phase-locking of OFC neurons to gamma- and theta-band oscillations are independent quantities or, alternatively, are related by a general propensity for oscillatory entrainment. For example, in hippocampal areas CA1 and CA3, neurons can phase-lock to both theta and gamma oscillations, and phase-locking values of significantly locked pyramidal cells are comparable for the gamma and theta band (Senior et al., 2008). The existence of two functional cell assemblies (i.e., O- and M-cells) locked to different oscillatory frequency ranges (i.e., theta and gamma) during the odor period suggests that very few cells are locking strongly to both gamma- and theta-band oscillations. Indeed, in the odor sampling period (Fig. 7A), we found cells that were highly theta-band and gamma-band phase-locked, but we rarely found cells that were phase-locked strongly to both frequencies, suggesting that theta- and gamma-band phase-locking are independent processes. This pattern was also observed when we included spike phases taken from all task periods together (Fig. 7B) and was not a consequence of the presence of both interneurons and pyramidal cells in our sample (see below).

Figure 7.

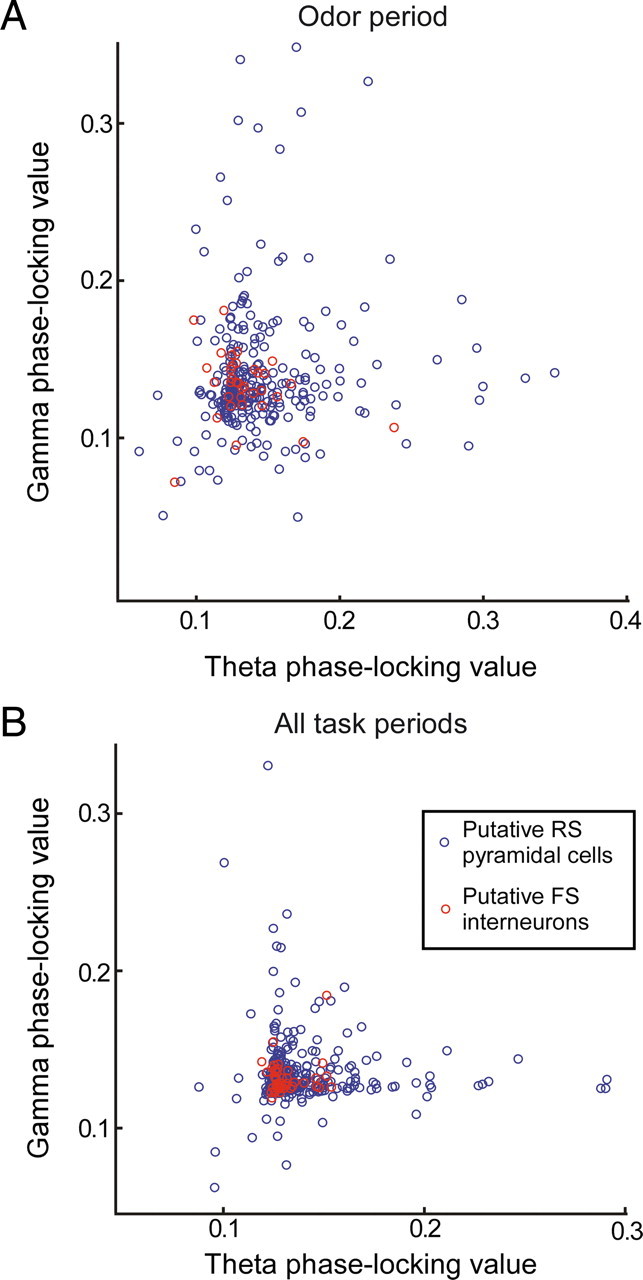
Strength of gamma-band and theta-band phase-locking is independent. A, Scatter plot of gamma-band phase-locking versus theta-band phase-locking per cell for the odor sampling period. Two tails with either high gamma-band or high theta-band phase-locking values are visible. Blue circles, Putative regular-spiking pyramidal cells. Red circles, Putative fast-spiking interneurons. B, As in A but now taking phase-locking values calculated for all trial periods. Cells with high values for gamma-band or theta-band phase-locking are visible but no cells with high phase-locking values for both frequency bands.

If the ratio between gamma-band and theta-band phase-locking is a property of the neuron (and its specific inputs), then we expect it to be stable across task periods. Indeed, as shown in Table 2, oscillatory preference, as expressed by the difference between theta- and gamma-band phase-locking in a given task period, was generally positively correlated across the majority of task period comparisons. This suggests that OFC neurons have a propensity to phase-lock to a specific LFP frequency band, essentially independent of behavioral activity specific to trial phases, presumably as a result of intrinsic resonant properties or specific configurations of synaptic inputs, or both.

Fast-spiking units do not exhibit a consistent oscillatory preference

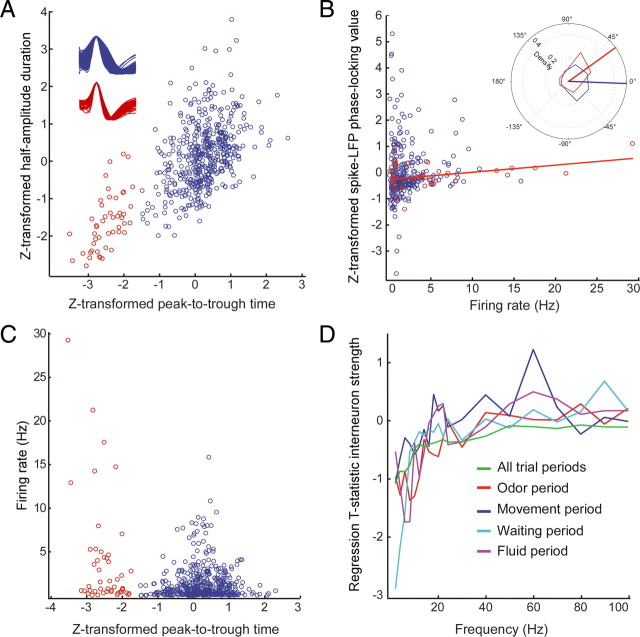
Fast-spiking interneurons (FSIs) and regular spiking pyramidal cells (RSs) in the neocortex and archicortex are thought phase-lock to different phases of the gamma cycle (Csicsvari et al., 2003; Hasenstaub et al., 2005; Senior et al., 2008), and rhythmic inhibition of pyramidal cells by FSIs is thought to contribute to cortical gamma rhythms and sensory gating (Bartos et al., 2007; Tukker et al., 2007; Cardin et al., 2009). We performed a segmentation of our cell sample (N = 525) on the basis of waveform characteristics. To correct for potential differences in waveform characteristics across rats, we first Z-score transformed waveform parameters. As in the study by Barthó et al. (2004), working in the primary somatosensory cortex, a separation using spike duration characteristics “peak-to-trough time” and “half-amplitude time” provided two clusters of cells, yielding 48 (9.1%) fast-spiking units (henceforth called putative FSIs) and 477 (90.9%) regular-spiking units (putative RS pyramidal cells) (Fig. 8A). Mean spike duration (peak-to-trough) was 0.204 ± 0.005 ms for putative FSIs and 0.359 ± 0.002 ms for putative RS cells. Mean firing rates were strongly elevated for putative FSIs (Fig. 8C) (3.96 ± 0.89 vs 1.34 ± 0.09) compared with putative RS cells. For primary visual cortex, neocortex, and hippocampus, it was shown previously that putative interneurons fire at later phases in the gamma cycle and are stronger gamma-band phase-locked than putative pyramidal cells (Csicsvari et al., 2003; Hasenstaub et al., 2005; Womelsdorf et al., 2008). We examined whether the same dissociation holds during odor sampling in OFC as well. To correct for potential phase differences between rats, we first transformed the group distribution of mean spike phases for every rat individually by rotating the group mean phase toward zero. This ensured that, for every rat, the mean spike phase across cells was the same. Consistent with previous reports, putative FSIs fired a few milliseconds later in the gamma cycle than putative RS cells (Fig. 8B, inset) (at 50–70 Hz: circular mean ± 95% confidence range, 36.1 ± 36.3° for putative FSIs and −1.7 ± 14.3° for putative RS cells; circular ANOVA, p < 0.05).

Figure 8.

Waveform characteristics and firing rates of putative FSIs (red circles) and putative RS cells (blue circles). A, Scatter plot of Z-transformed mean half-amplitude duration of spike waveforms versus Z-transformed mean peak-to-trough time per cell. Insets, Overlays of mean waveforms of putative FSIs (N = 48; red) and putative RS cells (N = 477; blue). B, Z-transformed gamma-band phase-locking values over all trial periods as a function of firing rate. Plot conventions as in A. Red line shows slope of correlation (Pearson's r = 0.39; p < 0.05) for putative FSIs. Inset, Mean gamma-phase distribution for putative FSIs (red) and putative RS cells (blue). The two distributions show a significant difference (circular ANOVA, p < 0.05). C, Z-transformed mean peak-to-trough time per cell versus firing rate. Putative FSIs (red circles) have higher firing rates than putative RS cells (blue circles). D, Assessment of the contribution of putative FSIs to observed phase-locking values for different trial periods. Regression T statistic of the specific (interneuron × firing rate; interneuron firing strength) interaction predictor to phase-locking values over frequencies per trial period. Interneuron strength is a negative predictor for low-frequency phase-locking values but adds no significant additional explanatory power to high-frequency phase-locking values for each trial period.

Surprisingly, when only selected on the basis of waveform, putative FSIs were not more gamma-band phase-locked than putative RS cells (Fig. 8B). However, a significant correlation was observed between firing rate and gamma-band PLV (Pearson's r = 0.39, p < 0.05), suggesting that a small subset of cells (with potential widespread influence on the pyramidal network) with interneuron-typical waveform and firing-rate characteristics does fit the classical phase-locking profile. To provide a more sophisticated analysis, we performed a multiple linear regression analysis, taking into account other sources of variation, such as the presence of different firing rate correlates (e.g., an M-cell correlate) and the identity of the rat. Instead of entering a predictive factor denoting the membership to the putative FSI or putative RS cell cluster into our model, we entered the interaction term of FSI membership and firing rate (i.e., zeros for putative RS cells and the firing rate for putative FSIs), which we call “interneuron firing strength.” As shown in Figure 8D, the T statistic for the correlation of interneuron firing strength with phase-locking value rose as a function of frequency (p < 0.05 for movement period, p < 0.001 for all other periods), being negative for a broad range of lower frequencies, i.e., contributing negatively to explaining the variance in low-frequency phase-locking, and converging to neutral values at higher frequencies. In contrast, the reverse term, RS group membership, contributed positively to explaining a significant portion of low-frequency phase-locking values (data not shown), consistent with the low-frequency resonating properties of pyramidal cells (Hasenstaub et al., 2005).

Discussion

In summary, we showed that subgroups of OFC cells with different behavioral firing-rate correlates in an olfactory discrimination task phase-locked selectively to OFC oscillations in the theta- or gamma-frequency band and that the periods of strongest phase-locking occurred in different periods over the course of an olfactory discrimination learning trial. Gamma-band synchronization was strongest in the late phase of odor sampling, and gamma-band power increased with learning. Cells that showed outcome-selective changes in firing rate during subsequent goal-directed movement (M-cells) exhibited strong phase-locking to LFP gamma-band oscillations during later stages of odor sampling. Theta-band phase-locking occurred in an earlier phase of odor sampling, was carried by a different cell group (O-cells), and was decoupled from gamma-band phase-locking.

Gamma-band phase-locking in OFC

The OFC receives highly processed sensory information, in our task specifically in the olfactory modality (Carmichael and Price, 1995; Cavada et al., 2000). Our results showed that the strength of gamma-band spike-field synchronization during odor sampling did not generally carry information on expected outcomes, nor did it distinguish between (subsequent) correct or incorrect behavioral choices (Fig. 3D) and could, on first impression, be considered as merely a consequence of olfactory input patterns in the gamma range.

However, arguing against a purely sensory-processing-related rhythmic activity, we found that gamma power during odor sampling increased over trials for both the odor predicting sucrose and the odor predicting quinine (Fig. 3A,B). Moreover, across sessions, the speed of this increase within a session was correlated with the speed of learning in the same session (Fig. 3C). This suggests that gamma oscillations make a contribution to or facilitate olfactory discrimination learning.

Previous research suggested that the strength of gamma-band synchronization and elevated population firing rates go together, casting the gamma oscillation as a population-wide “activity rhythm” for visual information processing (Gray and Singer, 1989; Womelsdorf et al., 2006). Here, however, we report that only a subset of neurons is phase-locked to OFC gamma oscillations. Approximately 40% of cells significantly phase-locked to gamma oscillations across the whole session, with strongest locking occurring during the odor sampling period. Interestingly, the M-cell group accounts for most of the gamma-band phase-locking found during odor sampling, when the firing rates of these cells are not significantly enhanced from baseline levels. In contrast, O-cells carried most theta-band phase-locking during odor sampling. In theory, cells could have been classified as having both an O-type and an M-type correlate, although only a small number of cells was classified as belonging to more than one category (Table 1). However, theta- and gamma-band phase-locking values per cell were independent (Fig. 7, Table 2), supporting the notion of two functionally separate OFC assemblies that participate selectively in different carrier frequency bands.

It is well established that inhibitory interneurons in hippocampus and sensory neocortex are important for the generation of gamma-band synchronization by imposing rhythmic inhibition on pyramidal cells (Csicsvari et al., 2003; Hasenstaub et al., 2005; Bartos et al., 2007; Cardin et al., 2009). The balance between the strength and timing of excitatory and inhibitory inputs greatly affects the activation levels of pyramidal cells (Pouille and Scanziani, 2001). After receiving visual input, excitation and inhibition in the visual cortex rise in a balanced way, resulting in a positive association between gamma-band oscillations and firing rate (Gray and McCormick, 1996; Haider et al., 2006). However, an increase in stimulus size has a negative impact on primary visual cortex V1 firing rates but a positive impact on gamma-band synchronization, likely reflecting an increase of inhibitory inputs from the surround (Gieselmann and Thiele, 2008; Ray and Maunsell, 2009). In line with these latter findings, we observed a negative correlation between gamma-band synchronization and firing rates of M-cells during odor sampling (Fig. 6A), which likely reflects a net inhibitory effect of gamma-band rhythmicity on M-cells. When M-cell gamma-band synchronization increases during odor sampling, their firing rates concurrently decrease, resulting in increased precision in phase-timing of M-cell action potentials.

Based on a split on waveform characteristics (cf. Barthó et al., 2004), our results indicated that the putative FSIs phase-locked to a significantly later phase of the gamma cycle than putative RS cells (Fig. 8). However, the strength of phase-locking did not differ between these groups.

Altogether, we conclude that gamma-band synchronization correlates with a suppression of M-cell spiking activity that is subsequently released during goal-directed movement and conveys action–outcome selective information.

Comparisons with other studies

Gamma-band synchronization has been extensively studied in the visual and olfactory system and in the hippocampus. The percentage of phase-locked cells that we report (∼40%) here is comparable with recent hippocampal data (Senior et al., 2008). However, in that study, putative pyramidal cells phase-locked with comparable levels with theta and gamma oscillations, whereas we found two distinct clusters of cells that phase-lock significantly to either gamma or theta oscillations, but not both.

Stimulation with odorants evokes gamma (65–100 Hz) oscillations in the OB of behaving rats (Eeckman and Freeman, 1990; Kay, 2003) and fast (20–30 Hz) oscillations in the antennal lobe of locusts and honeybees (Laurent and Davidowitz, 1994; Laurent et al., 2001). Gamma-band oscillations in the OB or antennal lobe seem to be especially important for effortful odor discrimination (Stopfer et al., 1997; Beshel et al., 2007). Comparable with Beshel et al. (2007), who recorded from OB, we found learning-related increases in gamma power. In addition, Martin et al. (2004, 2007) found similar learning-related increases in beta power (centered at 24–27 Hz) in rat OB. In our data, some beta power was also found in the odor sampling period, slightly later than the gamma power increase (results not shown). This timing (500–600 ms after odor onset) corresponds to the time window found by Martin et al., raising the possibility that a gamma-to-beta transition in OFC could reflect a general beta synchronization across odor-processing areas, putatively underlying a switch from local to global interactions (Kopell et al., 2000). Despite the similarities between these studies and our results, we show that OFC gamma-band synchronization, in contrast to LFP power, is not a population-wide phenomenon and specifically relates to the suppression of action–outcome selective activity.

Prominent theta-band oscillations are found in the OB as well, associated with sniffing and odor discrimination and suggested to function as a basic cycle of olfactory sampling (Kepecs et al., 2007; Verhagen et al., 2007). In line with this rhythmic input from early olfactory areas, we found that, in OFC, O-cells that discriminate between odors carry most of the observed theta-band phase-locking (Fig. 4C,D) (supplemental Fig. S2, available at www.jneurosci.org as supplemental material).

Several differences emerged between our results and studies in the primary visual system: we found that gamma-band synchronization in OFC, although elicited concurrently with olfactory input, is generally not stimulus-selective itself (cf. Frien et al., 2000; Siegel and König, 2003; Gail et al., 2004). Furthermore, we found gamma-band synchronization in OFC to be expressed only by a select subgroup of single units, instead of a broad population of single-unit or multiunit activity. Next, gamma-band synchronization in OFC is not associated with increased firing rate but rather with suppression, which may be caused by an altered balance of excitatory and inhibitory inputs to M-cells. Finally, putative FSIs, present in OFC in proportions comparable with other studies (Barthó et al., 2004), were not more gamma-band phase-locked than putative RS cells, a deviation from the classic picture of interneurons as the “drivers” of gamma-band oscillations (Csicsvari et al., 2003; Bartos et al., 2007; Tukker et al., 2007). These findings call for additional research into the local circuit mechanisms underlying OFC gamma-band activity.

Functional implications of orbitofrontal gamma-band synchronization

The OFC is associated with the inhibition of prepotent or premature responses, especially under reversal or incongruent response conditions (Chudasama and Robbins, 2003) (but see Chudasama et al., 2007; Man et al., 2009). OFC cells signal outcome expectations conditional on a behavioral response (van Duuren et al., 2007, 2008; Schoenbaum et al., 2009), which may be particularly important for flexible behavior. They probably play a minor role in assigning values to sensory cues, a function that has been attributed more to the amygdala (Schoenbaum et al., 2003; Paton et al., 2006; Stalnaker et al., 2007), although outcome-dependent odor representations in the piriform cortex are thought to be modulated by orbitofrontal feedback (Roesch et al., 2007; Cohen et al., 2008). Nonetheless, OFC has been widely implicated in affecting behavioral decisions, as verified by lesion studies (Baxter et al., 2000; Winstanley et al., 2004), implying that its activity must be relevant before a decision has been made.

We propose that OFC gamma-band synchronization during odor sampling reflects inhibitory control over M-cells, whose firing activity represents action values after a decision has been made (van Duuren et al., 2008, 2009). This increased inhibitory control occurs when the rat has to withhold its behavioral response. To maintain suppression of premature responses, this inhibitory control has to match the increase in motivational drive associated with the learned significance of the stimulus. Learning will indeed proceed more efficiently if the strength of gamma synchronization can be flexibly adjusted for inhibitory control.