A shared limiting resource leads to competitive exclusion in a cross-feeding system

Summary

Species interactions and coexistence are often dependent upon environmental conditions. When two cross-feeding bacteria exchange essential nutrients, the addition of a cross-fed nutrient to the environment can release one species from its dependence on the other. Previous studies suggest that continued coexistence depends on relative growth rates: coexistence is maintained if the slower-growing species is released from its dependence on the other, but if the faster-growing species is released, the slower-growing species will be lost (a hypothesis that we call “feed the faster grower” or FFG). Using invasion-from-rare experiments with two reciprocally cross-feeding bacteria, genome-scale metabolic modeling, and classical ecological models, we explored the potential for coexistence when one cross-feeder became independent. We found that whether nutrient addition shifted an interaction from mutualism to commensalism or parasitism depended on whether the nutrient that limited total growth was required by one or both species. Parasitism resulted when both species required the growth-limiting resource. Importantly, coexistence was only lost when the interaction became parasitism, and the obligate species had a slower growth rate. Under these restricted conditions, the FFG hypothesis applied. Our results contribute to a mechanistic understanding of how resources can be manipulated to alter interactions and coexistence in microbial communities.

Introduction

Determining how resource availability affects the stability of resource-exchange mutualisms is critical for understanding the dynamics of microbial communities. Many microbial communities are organized into webs of cross-feeding interactions, in which species rely on nutrients excreted by others (Schink 2002, Seth & Taga 2014, Zelezniak et al. 2015). Altering the metabolites that are available in the environment, for example through the addition of prebiotics, is likely to alter the nature of cross-feeding interactions and thereby change community composition and function (Roberfroid et al. 2010). To successfully use metabolites to manage microbial communities, it is essential that we understand how metabolite addition alters cross-feeding interactions. Furthermore, understanding the context dependency of cross-feeding will inform broader ecological theory about the stability of mutualistic interactions (Heath & Tiffin 2007, Egerton-Warburton et al. 2007, Ehinger et al. 2009, Johnson 2010, Lau et al. 2012, Grman & Robinson 2013).

Theoretical and empirical studies with cross-feeding microbes have shown that interactions and community composition can be determined by environmental resource availability (Muller et al. 2014, Hoek et al. 2016, Shantz et al. 2016). If a resource that is typically generated biotically by a cross-feeder becomes available abiotically, a bidirectional cross-feeding mutualism can become unidirectional, which can alter the ability of both species to coexist. In this work, we test a hypothesis inspired by recent studies (Hom & Murray 2014, LaSarre et al. 2016) that suggests that a community of two microbes that engage in a unidirectional cross-feeding interaction will be stable if the faster growing species is limited by the slower growing species, but not if the faster growing species is made independent. We refer to this hypothesis as the “feed the faster grower” (FFG) hypothesis. In both studies, feeding the faster grower its cross-fed resource led to a significantly smaller population size of the slower-growing, obligate species. However, it was not clear whether the slower grower would ultimately be driven to extinction. Furthermore, toxic by-products produced by the faster grower that harmed the slower grower were likely an important cause of the small population size of the slower grower. It is therefore unclear whether FFG is a general expectation that should be used to predict the impact of adding metabolites to a cross-feeding community.

In contrast to FFG, classic ecological theory would suggest that adding cross-fed nutrients to a bi-directional cross-feeding mutualism should benefit both species. The null expectation from a simple model of interaction—the generalized Lotka-Volterra model—is that an obligate species will always benefit from an increase in growth rate of its nutrient provider (Vandermeer & Boucher 1978, Boucher et al. 1982). More recent phenomenological theory that combines the positive effects of cross-feeding with the negative effects of competition suggest that cross-feeding systems can be destabilized by the addition of cross-fed nutrients (Estrela et al. 2012, Momeni et al. 2013, Muller et al. 2014, Hoek et al. 2016). This discrepancy is because in the recent models, the net impact that one species has on the other can switch from positive to negative as the system approaches a shared carrying capacity. Here, in addition to empirical tests, we investigate a mechanistic, resource-explicit cross-feeding model to determine the role of relative growth rate on the stability of a resource-exchange mutualism without toxicity. We also measure the emergent net ecological effects to better interpret observed coexistence patterns and relate our resource-explicit model to existing phenomenological theory.

To empirically test the FFG hypothesis, we examine the stability of an experimental community of two human gut bacteria, Escherichia coli K12, and Salmonella enterica LT2(Fig. 1A). Previously, this system was engineered and experimentally evolved into a metabolic mutualism in which our S. enterica strain secretes methionine in exchange for acetate byproducts from an auxotrophic E. coli (Harcombe 2010). In lactose minimal media the species form an obligate mutualism, but when excess methionine or acetate is added to the media, the species that requires that nutrient becomes independent of the other. To guide our empirical work and hone in on the relevant state variables for our consumer-resource modeling, we use dynamic genome-scale metabolic modeling in ‘seasonal’ batch culture. We used this multi-pronged approach to determine how coexistence is influenced by the physiological characteristics of species (i.e. growth rate and production rate of cross-fed nutrients), and the relative availability of resources.

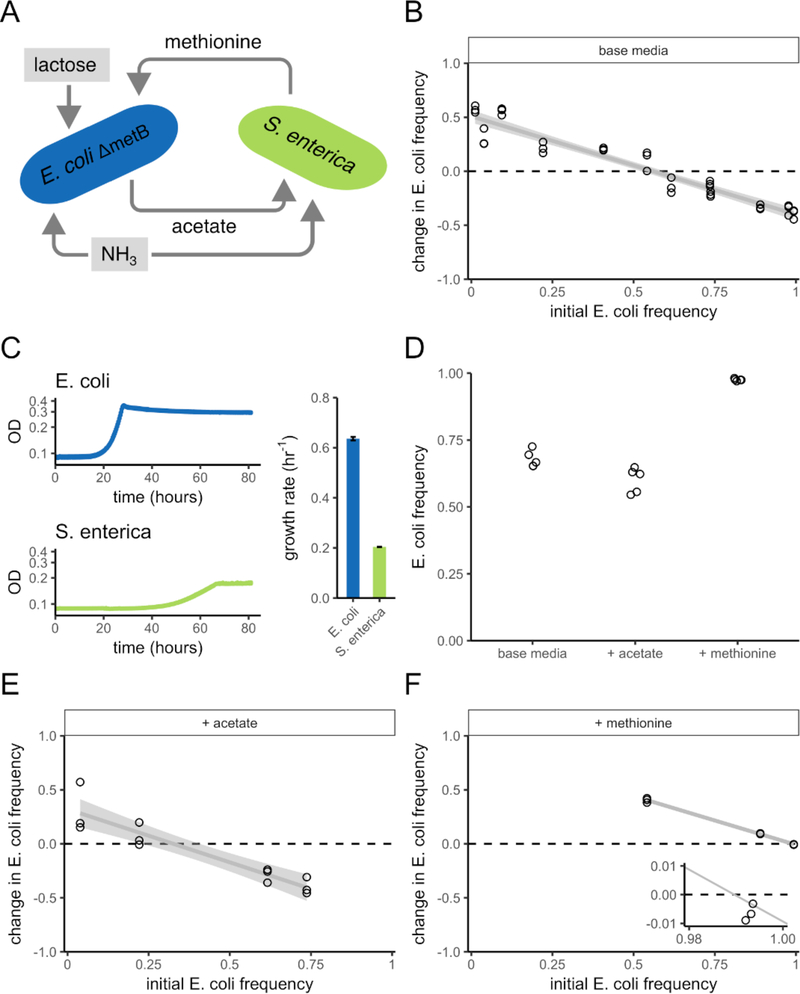
Figure 1: Nutrient additions to an obligate mutualism alter species ratios, but not coexistence.

A) Schematic showing the cross-feeding interaction between E. coli and S. enterica. E. coli consumes lactose, which S. enterica is unable to consume. E. coli excretes acetate as a by product, which S. enterica consumes. S. enterica secretes methionine, required by E. coli. Both species consume ammonia. The resources provided in the base medium, lactose and ammonia, are highlighted in gray. B) The change in frequency of E. coli as a function of the initial E. coli frequency, in base media. Change in frequency is quantified as [E/(E+S)]_final -[E/(E+S)]_initial. Here, E. coli and S. enterica are obligate mutualists and can mutually invade from rare, as indicated by the downwards slope that crosses y = 0. Therefore, they can stably coexist (Chesson 2000). C) Growth curves showing optical density (absorption = 600nm) over four days of growth for E. coli (blue) and S. enterica (green) in onoculture in an environment where their required nutrient (methionine or acetate) is provided. E. coli has a faster growth rate than S. enterica (bar plot, error bars are standard deviations). N = five replicates per treatment. D) The final frequency of E. coli started from 0.5 in base media, or base media with sufficient acetate or methionine addition to release a dependency. The final frequencies upon either nutrient addition differed significantly from the final frequency in base media (see Results). E) The change in frequency of E. coli as a function of the initial E. coli frequency, in base media + acetate. F) The change in frequency of E. coli as a function of the initial E. coli frequency, in base media + methionine. When methionine is supplied, the initial E. coli frequency at which E. coli frequency decreases after four days of growth is much higher than in B or E, but coexistence is maintained, as shown in the inset plot where E. coli’s frequency decreases when started at an initial frequency of 0.997 (in the inset, points are jittered in the x-direction to show all replicates). In B, E, and F, gray lines are linear regressions and shaded gray regions are 95% confidence intervals.

We find that the FFG hypothesis applies only under a restricted set of conditions. The slower growing species is lost upon feeding the faster grower only when the community is strongly limited by a communal nutrient that both species require. It is competition for this shared nutrient that causes exclusion of the slower species, regardless of the magnitude of any concurrent positive interactions. We argue that modeling approaches that incorporate species’ traits like growth rate and resource consumption are best for modeling such interactions and predicting coexistence.

Results

Reducing the dependence ofthe faster growing species on the slower growing species alters species frequencies, but not coexistence

Cross-feeding mutualism tends to promote coexistence (Shou et al. 2007, Harcombe et al. 2014). To confirm that E. coli and S. enterica coexist in our mutualism we used ‘invasion-from-rare’ experiments. Coexistence is indicated in such batch culture experiments if both species are able to increase in frequency when initially rare (increases in the rare species’ density is insufficient—see Experimental Procedures for more detail). We started co-cultures in lactose minimal medium with initial E. coli frequencies ranging from 0.012 (i.e. E. coli rare) to 0.993 (i.e. S. enterica rare). We found that both species, when initially rare, were able to increase in frequency after one growth period (Fig. 1B), indicating the mutualism allows coexistence.

We tested the impact of adding nutrients that released each species from reliance on the other. In our system, E. coli grows faster than S. enterica when grown in monocultures with their necessary metabolites provided (Fig. 1C; one-tailed t-test, df = 4, p-value = 5.5e-9). Therefore, according to the FFG hypothesis, providing acetate to release S. enterica from its dependence on E. coli should not destabilize the community, while adding methionine should lead to the loss of S. enterica. When we added acetate to the lactose media and began co-cultures with equal population sizes of E. coli and S. enterica, we observed a slight decrease in E. coli frequency after saturation of the batch culture, compared to the lactose base media (Fig. 1D; two-tailed t-test, df = 4, p = 2.3e-4). When we added methionine, we observed a large increase in E. coli frequency (two-tailed t-test, df = 4, p-value = 1.3e-4), indicating that the FFG hypothesis may apply.

However, when we conducted invasion-from-rare experiments to assess coexistence, coexistence was maintained in both the acetate addition (Fig. 1E) and the methionine addition (Fig. 1F) environments. Under methionine addition, E. coli dominated the community, but the new species ratio was stable, i.e. S. enterica was still able to invade from rare (Fig. 1F inset; one-tailed t-test, df = 2, p-value = 0.015). This result suggests that feeding the faster growing species alters species ratios, but does not necessarily destroy coexistence.

Exposure of underlying resource competition by limiting a shared nutrient causes the faster growing species to exclude the slower growing species

Classically, two species can compete to the point of competitive exclusion if a single communal resource that both species require limits total growth (Gause 1934, Hardin 1960, Hutchinson 1961). In our mutualistic environment, lactose limited the final community population size, and ammonia, a communal nitrogen resource, was in over-abundance. Therefore, we hypothesized that reducing the concentration of ammonia until it limited system productivity, in addition to feeding methionine to E. coli, could cause exclusion of S. enterica. We examined the effect of growth-limiting ammonia on coexistence when either species was provided with its cross-fed nutrient.

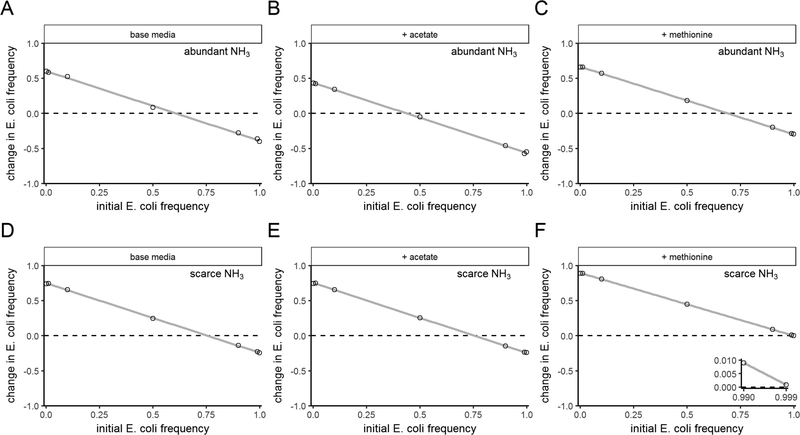
We first generated predictions using dynamic multi-species genome-scale metabolic modeling, which provides a close interface to empirical experiments. Metabolic modeling allows us to set the abundance of every metabolite in the simulated environment, and growth of the species emerges as a function of this environment and their metabolic networks. Using well-curated models of our experimental system (Harcombe et al. 2014, and see Experimental Procedures), we first mimicked the environment in our lab experiments. The species coexisted in a stable mutualism in an environment initiated without acetate or methionine (Fig. 2A). Like in our experiments, both species could invade from rare when acetate (Fig. 2B) or methionine (Fig. 2C) was supplied. We then repeated these simulations with limiting ammonia concentrations (1/20^th of the initial concentration used in experiments), which we hypothesized would change the net interaction to parasitism (also called exploitation): a positive benefit to S. enterica due to production of acetate by E. coli, and a negative effect to E. coli due to ammonia competition. This change switched the limiting nutrient from lactose to ammonia and reduced productivity of the community (data not shown). We still saw coexistence in the absence of nutrient addition (Fig. 2D) and when acetate was supplied (Fig. 2E), but E. coli excluded S. enterica when methionine was supplied (Fig. 2F). This indicates that coexistence is lost when slower-growing S. enterica both depends upon E. coli and competes with it for a limited resource, simultaneously.

Figure 2: Dynamic metabolic modeling predicts that coexistence of an obligate cross-feeder with its nutrient supplier depends on species identity and the abundance of the communal nutrient, ammonia.

Invasion-from-rare experiments using dynamic metabolic models in environments with ammonia concentrations that do not limit (A-C) or strongly limit (D-F) total community growth. Environments in (A, D) contained base media, (B, E) contained acetate added to base media, and (C, F) contained methionine added to base media. The y-axes show the change in frequency E. coli, as a function of the initial E. coli frequency. As in Fig. 1, trends that cross y = 0 with a downwards slope show mutual invasibility and therefore coexistence. The inset in (F) shows that S. enterica could not invade even when simulations began with a very high frequency of E. coli, because the E. coli frequency still increased. Lines are least-squares linear fits.

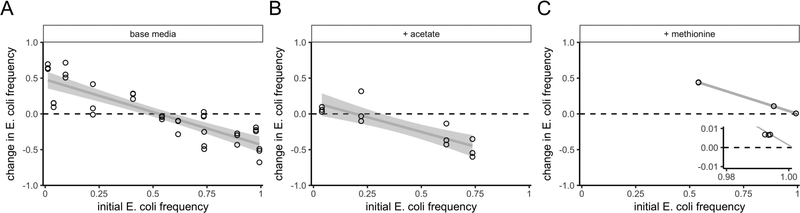
Because the FFG hypothesis was supported by our genome-scale metabolic modeling experiments, we tested the effect of limiting ammonia in our experimental system. Ammonia limitation by itself did not affect coexistence when each species relied on metabolites from the other species (Fig. 3A). Adding acetate to low-ammonia media also did not affect coexistence (Fig. 3B; one-tailed t-test, df = 2, p-value = 0.026). However, when we added methionine to low-ammonia media, E. coli increased in frequency from any starting frequency, showing that S. enterica is unable to persist (Fig. 3C; one-tailed t-test, df = 2, p-value = 2.1e-3; see inset).

Figure 3: In in vitro experiments, ammonia limitation causes competitive exclusionof S. enterica when E. coli is made independent by addition of methionine.

All panels show invasion-from-rare experiments, in vitro, in environments with ammonia concentrations that limited total growth, and acetate or methionine addition. The y-axes show the change in frequency of E. coli, as a function of the initial E. coli frequency. As in Fig. 1, trends that cross y = 0 with a downwards slope show mutual invasibility and therefore coexistence. The environment in (A) contained the base media with low ammonia, (B) contained acetate added to base media, and (C) contained methionine added to the base media. The inset in (C) shows that S. enterica could not invade under ammonia limitation and methionine supplementation, which is consistent with the dynamic genome-scale metabolic modeling. The lines are least-squares linear fits, with the shaded region enclosing 95% confidence intervals.

A simple ecological model shows that competitive exclusion is driven by growth rate differences and strong competition for a communal limiting resource

Next, we explored the generality of these results and controlled for a number of correlated variables which were difficult to study experimentally or with detailed genome-scale metabolic models. For example, in our system, E. coli is the faster grower, but it is also the ‘less generous’ metabolic partner, providing fewer cell-equivalents of acetate per unit of growth than S. enterica provides of methionine (as evidenced by the community being biased towards E. coli when grown in lactose base medium). Second, in a sense, E. coli ‘governs’ the community, because it performs the first step of metabolism of the energy resource, lactose. To disentangle these factors and explore the effects of acetate and methionine addition, nitrogen limitation, and relative growth rate differences, we turned to a theoretical exploration using a system of differential equations.

The initial system of equations contained twelve parameters: a maximum growth rate for each species, a Monod constant and an efficiency term for each resource, and production terms for methionine by S. enterica and acetate by E. coli. Because we were primarily interested in the initial resource values, relative growth rates, and relative rates of nutrient production, we scaled model parameters into the following equations (see Supplemental Methods for scaling procedure):

$$\text{dE}/\text{dt}={\mu }_{\text{E}}$$

$$\text{d}S/\text{dt}={\mu }_{\text{S}}$$

$$\text{dmet}/\text{dt}=-{\mu }_{\text{E}}+{\lambda }_{\text{ met }}{\mu }_{\text{S}}$$

$$\text{dac}/\text{dt}={\lambda }_{\text{ac}}{\mu }_{\text{E}}-{\mu }_{\text{S}}$$

$${\text{dNH}}_3/\text{dt}=-{\mu }_{\text{E}}-{\mu }_{\text{S}}$$

$${\mu }_{\text{E}}={\mu }_{\text{E}}\left(\text{E},{\text{ lcts, met, NH}}_3\right)=(\text{E})\text{min}\left(\text{lcts}/\left({\text{k}}_{\text{lcts}}+\text{lcts}\right),\text{ met }/\left({\text{k}}_{\text{met}}+\text{met}\right)\text{,\hspace{0.17em}}{\text{NH}}_3/\left({\text{k}}_{\text{NH}3}+{\text{NH}}_3\right)\right)$$

$${\mu }_{\text{S}}={\mu }_{\text{S}}\left(\text{S,\hspace{0.17em}}{\mu }_{\text{Smax}},\text{\hspace{0.17em}\hspace{0.17em}ac},{\text{NH}}_3\right)=\left({\mu }_{\text{Smax}}\text{S}\right)\text{min}\left(\text{ac}/\left({\text{k}}_{\text{ac}}+\text{ac}\right),{\text{NH}}_3/\left({\text{k}}_{\text{NH}3}+{\text{NH}}_3\right)\right)$$

Here, E and S are the cell counts of each species. Resources (lcts = lactose, ac = acetate, met = methionine, and NH3 = ammonia) are in units of ‘cell-equivalents’ meaning one resource of each non-substitutable type is used to create one cell. Monod constants (k) are also in units of cells. E’s maximum growth rate was removed by scaling time, and S’s maximum growth rate (μ_Smax) is proportional to E’s (Table S1). Production terms (λ_met and λ_ac) are in units of cells/cell, i.e. are unit-less, and can be considered to be the number of cells of the other species that can be supported by growth of one cell of the focal species. Growth is governed by Monod saturation rates, and a Liebig’s law of the minimum is applied so that only one resource is ever limiting for a species at a time. This scaling allowed us to clearly focus on the initial resource abundances provided the relative growth rates, and the ratesof production of the cross-fed nutrients.

We began with a situation that approximates our experimental system to ensure the model is capable of reproducing our empirical findings. S has a maximum growth rate of 0.5 that of E, and E produces fewer cell-units of acetate than S produces of methionine (based on final population sizes in mutualistic co-cultures), so we set λ_ac = 0.4 and λ_met= 7.3. With these parameters, we were able to recapitulate the experimental and genome-scale simulation results (Fig. S1).

Satisfied that the model can recapitulate our experimental and genome-scale data, we then explored a wider parameter space. To disentangle the correlated difference in cross-fed nutrient production with the difference in growth rates, we set both production terms, λ_ac and λ_met, to 1.5. The product of the production terms must be greater than one to sustain the mutualism (Shou et al. 2007, Fig. S2). We kept S’s growth rate at half of that of E, to be able to test the FFG hypothesis. To understand how different degrees of mutual dependency affected coexistence, we swept through many initial values of methionine supplementation, which reduces E’s dependence on S. To learn how this interacts with co-limitation by NH3, we also swept through different initial values of NH3. To assess coexistence, we started simulations with S rare (1%) and tracked whether S could invadeby observing whether S increased in frequency. Finally, we also ran monoculture simulations to compare final density in the presence vs. absence of a partner, which gave us the qualitative net ecological effect (+,0, or −) that each species had on the other.

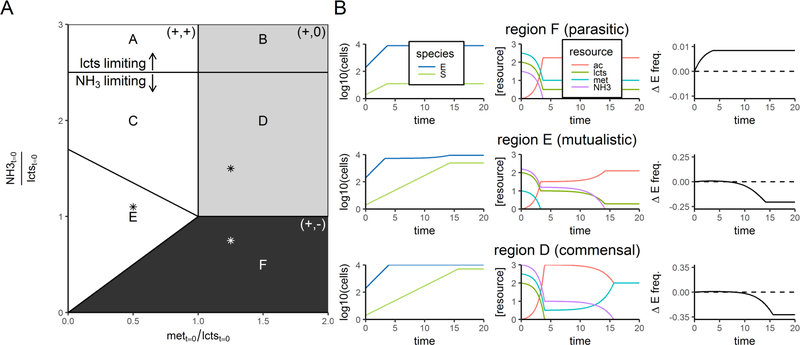
Six qualitatively different results occur when different amounts of nutrients are provided, which are shown in Fig. 4 and summarized in Table 1. Briefly, when there is excess methionine to feed the faster grower, coexistence is prevented when the net interaction is parasitic (+,-), which occurs when E’s total population size becomes limited by NH3 (region F). Coexistence is possible in all other regions, regardless of whether the net interaction is mutualistic or commensal, or whether productivity is low and there is competition for NH3. In regions where coexistence is possible, there are sometimes transient dynamics which reduce S’s frequency (e.g. Fig. 4B, “commensal” region), but after saturation of the batch culture, S’s frequency always increased.

Figure 4: Simulated effect of initial methionine and NH3 concentrations on the abilityof a slower-growing obligate cross-feeding species to coexist with its nutrientsupplier.

A) Diagram showing whether S could increase in frequency when rare, and the net ecological interaction between E and S, for batch culture simulations initiated at many different values of methionine and NH3. In these simulations, μs_max = 0.5, lcts_t=0 = 10000 cell equivalents, λ_met = λ_ac = 1.5, all k = 1e-3 cell equivalents, E_t=0 = 198, and S_t=0 = 2. Different polygons enclose qualitatively different results in terms of what nutrients ran out (see Table 1). Colors indicate the net ecological interaction (the sign of the population density in the presence minus absence of the other species). The first symbol indicates the net effect of E on S, the second symbol the net effect of S on E: white = mutualistic interaction (+/+); gray = commensal interaction (+/0); black = parasitic interaction (+/−). In addition, in the black region, S could not increase from rare, but it could in the white and gray regions. The data used to make this diagram come from 400 simulations, at evenly-spaced x-and-y initial conditions. B) Representative time series from three regions where NH3 limits the system, with initial values taken at the locations marked by asterisks. Resource concentrations, in units of cell equivalents, are 5000 times the y-axis value. The third column shows the change in E frequency, from an initial frequency of 0.99. A negative final change indicates that S can invade from rare, meaning both species can coexist. In the mutualistic and commensal regions, the insets show that there was a transient, small, trend towards an increase in E frequency in early time points, due to E being independent and getting a “head start.”

Table 1: Coexistence potential and interaction type in different nutrient environments.

The regions (column 1) correspond to those depicted in Fig. 4A. Coexistence was measured by invasion-from-rare experiments. The net effect on E was measured by comparison with monoculture. Resource exhaustion was measured when dynamics ceased, and the resource that limits each species’ final population size is indicated.

Region	Coexistence	Net interaction (effect of E on S, effect of S on E]	Resources that run out	E final population size limited by	S final population size limited by	Why the net effect on E?	Does competition for NH3 affect final population size?
A	Yes	(+,+)	lcts	lcts	ac	E gets met from S	No
B	Yes	(+,0)	lcts	lcts	ac	Environment provides sufficient met	No
C	Yes	(+,+)	NH3, lcts	met, then lcts	NH3	E gets met from S	Yes
D	Yes	(+,0)	NH3, lcts	lcts	NH3	Environment provides sufficient met	Yes
E	Yes	(+,+)	NH3, met	met, then NH3	NH3	E gets met from S	Yes
F	No	(+,−)	NH3	NH3	NH3	Competition for NH3	Yes

We observed a different picture when we repeated the initial resource value sweep but provided acetate for slower-growing S, instead of providing methionine for E. Faster-growing E can always invade from rare, showing that E and S coexist, regardless of NH3 levels (Fig. S3). This is despite the fact that there is a region where the net relationship is parasitic, which occurs where there is sufficient acetate to sustain S, yet E competes with S over NH₃ (Fig. S3B, red region). Here, E is benefitted by S but S is harmed by E. In summary, when a faster-growing species obligately depends on a slower-growing species, the obligate species can always invade.

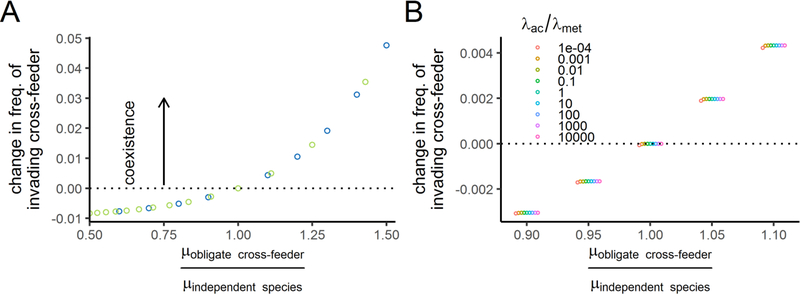
Next, we tested the effect of relative growth rate directly by sweeping across relative growth rates in environments that cause a parasitic interaction (region F in Fig. 4). We also altered which species was obligately dependent upon the other in order to disentangle the effect of E being the lactose metabolizer. We found that there is a hard switch from exclusion to coexistence that occurs when the growth rate of the obligate species is greater than or equal to the growth rate of the independent species (Fig. 5A). This effect is independent of whether E or S is the obligate cross-feeder. The effect also occurs in continuous culture simulations (Fig. S4).

Figure 5: Simulations predict that relative growth rates, but not cross-fed nutrient production rates, determine whether an obligate cross-feeder can coexist with an independent nutrient supplier.

These panels show the results of invasion-from-rare simulations when the net ecological interaction is parasitic. Therefore, all simulations were run under severe NH3 limitation and with excess cross-fed nutrient provided to one species. A) The change in frequency of an invading cross-feeder plotted over the cross-feeder’s relative growth rate. Points above the dotted line indicate successful invasion and therefore coexistence of the cross-feeder with the nutrient provider. The color of the circles indicates which species is the obligate cross-feeder (blue for E, green for S). When E was the cross-feeder, S was provided excess ac, and when S was the cross-feeder, E was provided excess met. B) The change in frequency of an invading cross-feeder as a function of both relative maximum growth rate (x-axis) and the relative “generosity” of the species (relative production terms, λs, colored points). In these simulations, the obligate cross-feeder, S, depends on ac from E, which produces it at a rate of λ_ac. The product of the λ values was held constant at 2.25. In both panels, k = 0.001 cell equivalents. See Figure S5 for simulations with higher k values, which can increase the importance of the production terms.

Finally, we tested the effects of the “generosity” of the two species: specifically, how much resource they provide to the other species (λ_ac and λ_met). In our experiments, λ_ac is lower than λ_met. Does varying this ratio alter coexistence? Surprisingly, even extreme values of this ratio have a negligible effect on coexistence (Fig. 5B). In these simulations, where both species were efficient at taking up all nutrients, only extremely selfish E (low λ_ac/ λ_met) impaired invasion by S, and only when their growth rates are equal. An important caveat is that our simulations used half-saturation constants that were negligibly small (k_x = 0.001cell equivalents, for all resources x), in order to focus on the effect of maximum growth rates. When we relaxed this assumption and re-ran simulations with higher k values, then coexistence of the obligate species could be prevented even if its maximum growth rate was greater than the independent species (Fig. S5, parasitic region). In other words, the obligate species required higher metabolite production by the independent species when half-saturation constants were higher. In the commensal and mutualistic regions, the relative generosity did not affect coexistence (Fig. S5, mutualistic or commensal regions).

Discussion

We explored how changes in the resources in an environment altered the interaction between two cross-feeding bacteria, and the consequences of that altered interaction for coexistence. We started with an obligate cross-feeding mutualism between E. coli and S. enterica. Then, using experiments and models, we made one species metabolically independent, by adding either methionine or acetate, and tested whether both species could continue to coexist. The “feed the faster grower” hypothesis predicts that coexistence will be lost when the faster growing species is released from its dependence on the slower growing species (Hom & Murray 2010, LaSarre et al. 2016). Consistent with the FFG hypothesis, we found that acetate addition, which made the slower growing S. enterica independent, always led to coexistence. However, methionine addition, which made E. coli independent, only sometimes led to competitive exclusion of S. enterica. Competitive exclusion in methionine-rich medium depended upon E. coli having a faster growth rate than S. enterica, and on the productivity of E. coli being set by ammonia rather than lactose. This was because, in addition to the growth-rate difference, ammonia limitation caused the interaction to shift to parasitism when sufficient methionine was added, whereas lactose limitation caused the interaction to shift to commensalism. In other words, the FFG hypothesis only applies when community productivity is strongly limited by a communal nutrient that both species consume. Interestingly, the relative production of cross-fed nutrients had little impact on the prevalence of coexistence, except when the obligate species’ growth rate was high and the resource uptake half-saturation constant was non negligible. Below, we discuss our two key conclusions: First, microbial interactions can readily be shifted from mutualism to commensalism or parasitism by altering nutrient conditions. Second, whether release from mutual dependency leads to coexistence or competitive exclusion is highly context-dependent, depending on both on the type of interaction and relative growth rates.

Whether a cross-feeding mutualism shifts to commensalism or parasitism upon release of a dependency is determined by the nature and relative concentration of the resource that limits system productivity. In our system, productivity was limited either by lactose, which was private to E. coli, or by ammonia, which was communal. The sign and strength of the mutualism (without addition of a cross-fed nutrient) were the same regardless of which metabolite limited system productivity. However, the addition of cross-fed metabolites had categorically different ecological effects under the two limiting resources. Strong ammonia limitation led to parasitism when either species was released, because any growth of the dependent species came at the cost of the independent species’ final population size. In other words, even though the obligate species received a net benefit from the independent species, there was an underlying negative component within the net positive effect, due to ammonia competition. Ammonia competition was also the cause of the negative net effect of the obligate species on the independent species. In contrast, when system productivity was set by the private resource, lactose, there was no underlying competitive interaction, and the interaction only shifted to commensalism. Hoek et al. (2016) also found that the ecological interaction between cross-feeding strains could readily shift upon addition of cross-fed nutrients. In that study, addition of a high concentration of both cross-fed nutrients always led to negative interactions. This finding is consistent with our results, because their cross-feeding organisms were two nearly isogenic strains of Saccharomyces cerevisiae, and therefore every resource except the cross-fed nutrients was communal. In general, as Hoek et al. also suggest, the more similar the metabolism is between cross-feeding strains, the more likely it is that nutrient addition will shift a mutualism to a negative interaction. Consistent with this idea, mathematical predictions suggest that minimizing competition is critical for stabilizing cross-feeding interactions (Doebeli 2002, Pfeiffer & Bonhoeffer 2004, Gudelj & Rosenzweig 2016, McCully et al. 2017). It will be interesting to examine whether stable cross-feeding interactions in natural systems are more common between species with smaller degrees of niche overlap.

Whether an obligate cross-feeder could persist when acting as a parasite was determined by growth rate. When ammonia was sufficiently limiting, our system could be switched to parasitism by adding either acetate or methionine. However, the two additions had distinct outcomes on coexistence: acetate addition allowed coexistence, but methionine addition did not. This divergence in outcomes was determined by the relative maximum growth rate of the species released from metabolic constraint. If the slower growing species (S.enterica) was released, coexistence was maintained because the better competitor for ammonia (E. coli) could not outgrow the species from which it cross-fed. However, when the faster species was released from dependency, the slower grower was outcompeted. This finding is consistent with the FFG hypothesis suggested by Hom and Murray (2010) and LaSarre et al. (2016), though it is important to reiterate that feeding the faster grower did not result in destabilization if the faster grower was not limited by a shared resource. It is also worth noting that the destabilization seen in these previous studies was driven by a different underlying mechanism. In those studies, when the faster-growing species was supplied its cross-fed nutrient in the growth media, it produced toxic organic acids that harmed the slower-growing species and allowed the faster grower to overtake the community (shown in LaSarre et al. 2016, and likely occurring in Hom and Murray 2010). Despite the difference in mechanism, our work agrees with previous studies that changes in nutrients are likely to have much more dramatic effects on community diversity when species differ in their maximum potential growth rates.

Although we conducted our experiments in “seasonal” or batch cultures, our results extend to continuous chemostat cultures as well. A brief test of the FFG hypothesis in a version of our model converted into a continuous culture regime yields the same qualitative results (Fig. S4). Similarly, related work in chemostat models (Miura 1980) or in continuous culture phenomenological models (Hoek et al. 2016; Fig. S6) shows that growth rate is an important determinant of whether an obligate species can coexist with its independent partner. While quantitative predictions will change in continuous culture due to the more constant conditions that the species experience, our qualitative predictions relating to the FFG hypothesis and the influence of limiting nutrients hold true in this environment.

Our resource-explicit model used species traits—rates of resource consumption, production, uptake, and maximal growth—to predict ecological interactions and coexistence. In this model, the net ecological interactions alone (e.g. parasitism) were insufficient to predict the potential for coexistence. This suggests that there will often be limited predictive power in models based on a single interaction term (such as generalized Lotka-Volterra). Phenomenological models of cross-feeding can be improved by using two simultaneous components: the positive, direct effect of resource exchange, and the negative effect of competition for a shared carrying capacity (Estrela et al. 2012, Momeni & Shou, 2013, Muller et al. 2014, Hoek et al. 2016). Separating interaction terms into multiple explicit components allows for a non-monotonic response of one species’ growth rate to the other’s population size. Indeed, these models can predict competitive exclusion of cross-feeders in our system (for example, see Fig. S6). However, even these more complex phenomenological models are limited in their ability to connect changes in resources to changes in system dynamics. A constraint on resource-explicit, trait-based models is that it can be challenging to identify and quantify relevant traits. However, improvement in our ability to predict species’ traits from genomes should reduce this workload (e.g. Machado et al. 2018 for primary metabolic traits, Weber et al. 2015 for secondary metabolic traits). Continued work iterating between different trait-based approaches and phenomenological approaches with varying levels of abstraction will be key for predicting microbial community assembly and dynamics across a range of environments (Momeni et al. 2017).

Finally, our results can inform efforts to manipulate microbial communities. Understanding how communities respond to changing environments is important for managing microbial ecosystems with prebiotics, as prebiotic nutrient addition is unlikely to be sustained indefinitely (Rastall & Gibson 2015). If a beneficial bacterium typically in an obligate cross-feeding mutualism is fed a prebiotic, and its partner is lost, cessation of prebiotic addition will result in the loss of the beneficial species. More broadly, our results demonstrate that a detailed understanding of who cross-feeds what from whom will significantly enhance our ability to manipulate microbiomes using prebiotics, with fewer off-target effects.

Experimental Procedures

Strains and media

We used Escherichia coli strain K12 with a ΔmetB mutation conferring methionineauxotrophy and a Salmonella enterica serovar Typhimurium LT2 strain containingmutations in metA and metJ that cause over-production of methionine (Harcombe 2010; Douglas et al. 2016, 2017). In lactose minimal medium, E. coli consumes lactose andexcretes acetate as a byproduct. S. enterica consumes this acetate and secretes methionine. For all experiments, strains were grown in a modified Hypho minimal medium base with lactose as the primary carbon source, containing 2.78 mM lactose, 14.5 mM K₂HPO4, 16.3mM NaH₂PO₄, 0.814 mM MgSO₄, 3.78 mM Na₂SO₄, trace metals (1.2 uM ZnSO₄, 1 uM MnCl₂, 18 uM FeSO₄, 2 uM (NH₄)₆Mo₇O₂₄, 1 uM CuSO₄, 2 mM CoCl₂, 0.33 um Na₂WO₄, 20 uM CaCl₂) and either 3.78 mM (non-limiting) or 0.378 mM (limiting) [NH4]₂SO₄. Where indicated, 80μM of L-methionine, or 12mM of acetate was added. These concentrations were chosen because preliminary experiments showed they were sufficient to produce similar amounts of growth as observed in obligate, mutualistic co-culture. Furthermore, preliminary experiments showed that this concentration of methionine allowed E. coli to fully consume the available lactose. Before beginning experiments, the strains were streaked from freezer stocks onto Nutrient Broth plates and grown for two days. Single colonies were then picked into 10 mL of Hypho minimal media with methionine supplied for E. coli and 5.56 mM glucose instead of lactose for S. enterica, in flasks, which were grown for two days, shaking at 30°C. Around six hours before beginning experiments, cultures were diluted 10-fold, and once cloudy, diluted into a carbon-free Hypho buffer based on OD600, to equalize cell densities. Experimental cultures were inoculated 1 × 10⁵ CFU/ml for monocultures or 2 × 10⁵ CFU/ml for cocultures, with the desired frequency of E. coli relative to S. enterica. In non-limiting NH₃ media, final population size saturates at around 4 × 10⁸ CFU/mL (11 generations), and in limiting NH3 media, cultures reach population sizes of around 4 × 10⁷ CFU/mL (8 generations) after a four-day growth period. In non-limiting NH3 media, final population size saturates at around 4 × 10⁸ CFU/mL (11 generations), and in limiting NH₃ media, cultures reach population sizes of around 4 × 10⁷ CFU/mL (8 generations) after a four-day growth period.

Growth assays

To measure growth rates in monoculture, methionine was supplied for five replicate E. coli monocultures and acetate was supplied for five replicate S. enterica monocultures. These monocultures were grown in 96-well plates with 200 μl of media per well in a Tecan InfinitePro 200 at 30°C, and measurements of OD600 were taken every 20 minutes, shaking at 432 rpm between readings. To obtain growth rate estimates, we fit growth curves to a Baranyi function (Baranyi & Roberts 1994) by obtaining nonlinear least-square estimates and using the growth rate parameter estimate.

In co-culture experiments, cultures were grown in Hypho media with either no addition (base media), acetate addition, or methionine addition, and with non-limiting or limiting ammonia concentrations, in 96-well plates with 200 μl of media per well at 30°C in a Bellco mini-orbital shaker, shaking at 450 rpm. After four days of growth, the final population size of each species was measured through serial dilution and plating onto species-specific Hypho media with 1% agar. For E. coli, media contained methionine, and for S. enterica, lactose was replaced with 16.6 mM glucose. X-gal (0.05% v/v) was added to plates to further help distinguish E. coli colonies (blue) from S. enterica colonies (white). All co-culture experiments had three or five replicate cultures for each initial frequency.

Invasion-from-rare assays

We used mutual invasibility as our criterion for whether the two species could coexist—coexistence is possible when both species are able to increase in frequency from rare (Chesson 2000, Wright & Vetsigian 2016, Friedman et al. 2017. Starting cultures with a range of species frequencies but the same total density is equivalent to performing serial transfer experiments, but in parallel. If a species is able to increase in frequency when initially rare, this indicates the species would persist in the community if several serial transfers with dilution to fixed density were performed. In contrast, a species that is unable to increase in frequency from rare (even if it increases in density as a result of growth) would ultimately be outcompeted. To perform the invasion-from-rare assays, cells in log phase (see above) were diluted into wells of a 96-well plate with 200 μl of media per wellat different frequencies. The lowest initial frequency of E. coli was 0.012, and the highest was 0.997. After 4 days of growth, the population size of each species was measured by plating, as described above. The E. coli frequency was the number of E. coli cells divided by the total number of cells (E. coli and S. enterica). The change in E. coli frequency was quantified as the E. coli frequency after 4 days of growth minus the initial E. coli frequency, (E / E + S) _final — (E / E + S) _initial.

Genome-scale metabolic modeling

The dynamic, multi-species genome-scale metabolic modeling was carried out in the COMETS platform (Harcombe et al. 2014). Here, we used COMETS to model growth in a well-mixed environment (i.e. a single “box”). COMETS simulates growth of a community by iterating over small time-steps. An environment, which is the abundance and identity of the nutrients the species’ models can use or produce, is pre-defined at the onset of the simulation. In a time-step, flux-balance analysis is used to determine the maximum amount of growth each species is capable of, as well as the nutrients used and produced to obtain this growth. The growth is constrained by the ability of the metabolic model to flow available external resources to the biomass objective reaction, as well as by the maximum uptake possible by that species, which is determined by Michaelis-Menten kinetics (vmax = 10 mmol / g / hr, k = 5e-6 mM for all simulations). Once the flux-balance-analysis is solved in a time-step, the biomass growth and nutrient changes are scaled by the current amountof biomass and by the duration of the time-step, then the environment is adjusted by these changes. The species update sequentially each time step, and the order of species is randomized each time step. See Harcombe et al. (2014) for additional details.

The genome-scale models are previously published modifications of the standard E. coli and S. enterica metabolic models (Harcombe et al. 2014). The E. coli model, ijo1366 (Orth et al 2011), was modified by setting the bounds on the cystathionine gamma-synthase reaction (a reaction in the methionine biosynthetic pathway) to zero, which causes this model to require methionine from the external environment to be able to grow. The S. enterica model, (iRR_1083, Raghunathan et al. 2009), was modified so that for every unit of growth a proportional amount of methionine was excreted into the environment. These models can grow together in a COMETS simulation with lactose, ammonia, oxygen and trace minerals present, but neither can grow alone.

In all simulations, the following compounds were available in unlimited concentrations: Ca2[e], Cobalt2[e], cl[e], cu[e], fe2[e], fe3[e], k[e], mg2[e], mn2[e], mobd[e], ni2[e], o2[e], pi[e], so4[e], and zn2[e] (following BIGG notation). Lactose was supplied at the same concentration as in experiments, 2.78 mM (equivalent to 1 g/L). NH3, methionine, and acetate were also supplied at the same concentrations as experiments, with abundant NH₃= 7.56 mM, scarce NH₃ = 0.378 mM, methionine = 80 μMwhen in excess, and acetate = 12 mM when in excess. In COMETS, molarity is determined by setting the mmols of each resource, and the “spacewidth,” which is the length of a three-dimensional box that determines the experimental volume. To mimic a 200 μl well, spacewidth = 0.5848035cm. Time step = 0.01 hours. Biomass in flux-balance analysis is in units of grams dry weight. Initial total biomass = 5.6e-8 g (roughly 10^Λ4 cells), and divided into E. coli and S. enterica depending on the frequency tested in the given experiment.

Differential equation ecological modeling

The scaled ecological model is shown in the Results, and all relevant parameters / initial values are stated either in results, figure legends, or in Table 2. The ODE system was solved using the deSolve package in R, which used the lsoda solver to numerically integrate. All simulations were solved for sufficient duration to ensure dynamics had ceased. A maximum time step was set at 0.1 time units. During integration, relative tolerance (rtol) was set = 1 × 10⁻¹⁰ and maxsteps = 1 × 10⁶.

Because the resources were abiotic and the system was closed, the resource equations were recast as algebraic equations which improved the stability of the numerical solver. For example, lactose became a function of initial amount and the amount of growth by E: Lactose(time = t) = lactose(time = 0) - (E(time = t) - E(time = 0)). Occasionally, due to the discrete nature of numerical integration, a resource concentration would drop to slightly below zero. These events were tested for and if they occurred, the concentration was set = 0. Such small numerical issues never affected growth more than 1/100 of a cell’s worth of growth.

Statistics

All analysis was done in R. For frequency data, which are bounded by 0 and 1, a logit transformation was used before performing t-tests.