Patient-specific tumor growth trajectories determine persistent and resistant cancer cell populations during treatment with targeted therapies

Abstract

The importance of pre-existing versus acquired drug resistance in cancer patients treated with small molecule tyrosine kinase inhibitors (TKI) remains controversial. The goal of this study is to provide a general estimate of the size and dynamics of a pre-existing, drug-resistant tumor cell population versus a slow-growing persister population that is the precursor of acquired TKI resistance. We describe a general model of resistance development, including persister evolution and pre-existing resistance, solely based on the macroscopic trajectory of tumor burden during treatment. We applied the model to 20 tumor volume trajectories of EGFR-mutant lung cancer patients treated with the TKI erlotinib. Under the assumption of only pre-existing resistant cells or only persister evolution, it is not possible to explain the observed tumor trajectories with realistic parameter values. Assuming only persister evolution would require very high mutation induction rates, while only pre-existing resistance would lead to very large pre-existing populations of resistant cells at the initiation of treatment. However, combining pre-existing resistance with persister populations can explain the observed tumor volume trajectories, and yields an estimated pre-existing resistant fraction varying from 10⁻⁴ to 10⁻¹ at the time of treatment initiation for this study cohort. Our results also demonstrate that the growth rate of the resistant population is highly correlated to the time to tumor progression. These estimates of the size of the resistant and persistent tumor cell population during TKI treatment can inform combination treatment strategies such as multi-agent schedules or a combination of targeted agents and radiotherapy.

Introduction

The emergence of resistance to targeted agents such as small molecule tyrosine kinase inhibitors (TKI) is one of the key challenges in the effort to control cancer. A significant research effort focuses on the mechanisms of resistance (1-4), in order to determine the pathways by which resistance arises and identify strategies to prevent its emergence. An important question of clinical relevance in this context is the temporal evolution of drug resistance. Resistance may arise either from pre-existing sub-clones or de novo during therapy (5-9). This distinction is important for the administration of targeted agents in clinical practice and the combination of targeted agents with other treatment modalities, such as surgery, radiotherapy or thermal ablation in non-metastatic disease.

From a statistical perspective the probability of pre-existing resistance in a macroscopic tumor is high, due to the large number of cell divisions necessary to reach a tumor of detectable size (10-12). This holds when phenomena such as stochastic drift and variations in fitness conferred with mutations are taken into account (13,14). Pre-existing resistance has been well studied in non-small cell lung cancer (NSCLC) patients treated with TKI targeting the epidermal growth factor receptor (EGFR-TKIs) especially for T790M, a common resistance-conferring mutation to first-generation EGFR-TKIs. It can develop via distinct evolutionary paths (5) from a reservoir a drug-tolerant persister cells (8), and has been found in 1–25% of patients pre-treatment and correlated with shorter time to disease progression (15,16). Even though some of these results have been attributed to measurement artifacts (17), it seems beyond doubt that pre-existing resistance occurs in some patients.

In general, a tumor’s genomic instability fosters a genetic diversity which is the underlying driver for its heterogeneity, which in general leads to inferior outcomes when treated with targeted agents. This is not restricted to EGFR/EGFR^T790M, but can be observed in a variety of activating mutations and resistance mechanisms, as recently comprehensively reviewed (18-20). It has been demonstrated that allelic frequencies of specific mutations compared to the abundance of the activating EGFR mutation can predict greater tumor volume response (20,21). Piotrowska et al. recently also showed that EGFR^T790M-positive and -negative clones do co-exist in patients, and that the changes in their relative abundance reflects the response to various targeted therapies (22).

Another path to resistance is through evolution from drug-resistant “persister” cells (23,24), which has been shown to lead to resistance to EGFR-TKIs via the T790M mutation in vitro (5,8). While the evolution of acquired resistance is being thoroughly investigated in vitro, little is known about its prevalence or importance in vivo. There is a continuing debate over the importance of pre-existing versus de novo resistance as the predominant cause of progression in patients on targeted therapy, and there is little clinical evidence to support one hypothesis over the other. One of the main reasons for this uncertainty is the fact that biopsies only provide a limited window, in space as well as in time, into the process of resistance development and are unlikely to detect small populations of resistant clones in vivo. Positron Emission Tomography enables imaging of certain drug targets directly (25), though imaging of microscopic cell populations in patients remains infeasible.

The aim of this work is to provide an estimate of the size of the resistant and persister populations in EGFR-mutant lung cancer patients during treatment with TKIs. We propose a general model and two restricted models describing only pre-existing resistance and only de novo resistance. The goal is to estimate the sizes of these populations in vivo based on the macroscopic behavior of tumor burden, making as few assumptions as possible about the mechanisms of resistance themselves. We apply the models to tumor volume trajectories of NSCLC patients undergoing treatment with EGFR-TKIs and progressing with a T790M mutation.

Materials and Methods

Patient population and data acquisition

We identified metastatic EGFR-mutant patients enrolled on prospective studies treated with erlotinib at our institution between 2006 and 2014. All patients had a pathologically confirmed diagnosis of stage IV adenocarcinoma and the following characteristics:

• intra-thoracic progression, as defined by Response Evaluation Criteria in Solid Tumors (RECIST) 1.1 guidelines (26), at site of previous disease, to ensure a complete tumor trajectory pre-treatment as well as post-progression

• measurable growth of at least one intra-thoracic lesion while on erlotinib, using 3D volume delineation as described below

• presence of EGFR T790M on clinical molecular profiling of tumor biopsy at progression

• Absence of other treatments during the observation period

All lesions were segmented on all CT slices to arrive at a 3D volume estimate. Contouring was performed using clinically commissioned software for radiation treatment planning (MiMvista Corp, Cleveland, OH, USA). Small nodules surrounded by lung tissue were contoured using a low threshold (−400HU), while larger primary tumors were contoured according to clinical standard using soft and lung tissue windows as appropriate. Complex lesions invading the mediastinum or chest wall were contoured and reviewed by a radiation oncologist.

The conversion of tumor volume to cell number was done based on experimental observations in human NSCLC (27). Based on this work the average tumor cell density was calculated to be 2.8*10⁸/cm³. While this parameter can vary from patient to patient, it does not impact the results of this study, as is further discussed below.

As we fit parameters to tumor growth representing volume changes by several factors, the relative difference in contouring error between small and large lesions can become important. To account for this fact we assumed a segmentation error of ±1mm on the entire volume surface, i.e.

$$\mathrm{volume}\mathrm{error}=2\cdot \frac{4}{3}\pi {\left(\frac{d+1}{2}\right)}^3,$$

where d is the diameter in mm along the longest axis of the lesion. This error estimate is designed to attribute a larger relative error to small tumors compared to larger ones. For example, a 1cm nodule in the lung would be attributed a 25% volume error.

Models describing the temporal evolution of resistance

Resistance can be conceived of in two fundamentally distinct ways: as pre-existing resistance stemming from sub-clones already present at initiation of therapy, or de novo resistance, acquired during therapy through evolution of drug-tolerant persister cells (4,5,7). We have implemented these two approaches as special cases of a general model, using a system of ordinary differential equations as outlined in the Guide to Model Equations and Assumptions section.

The de novo approach, represented by our persister-evolution model, assumes a sub-population of drug-tolerant cells that grows slowly in the presence of TKIs and can transform into resistant cells. The pre-existing resistance approach assumes an already completely resistant cell compartment at treatment start, and no persister population. The purpose of this model simplification to two special cases is a reduction in the number of fit parameters from eight (general model) to 5 (pre-existing resistance) and 7 (persister-evolution).

Sequential Model Fitting Process and Data Analysis

For each tumor we extracted a tumor volume trajectory from patient CT scans, starting before treatment with erlotinib throughout progression until discontinuation of erlotinib. We excluded data post-progression in which the patient was no longer on erlotinib, and similarly before initiation of treatment if the patient received another drug. The model parameters were sequentially fit to the tumor volume trajectory according to the following procedure (for more details see supplementary Figure 1).

First, the post-progression growth rates of the resistant population (λ_R) and the pre-treatment growth rate (λ_S) were fitted using only the relevant subset of the CT scans during either regrowth or pre-treatment respectively. The underlying assumption here is that the observed macroscopic growth in these periods is representative of the sensitive and resistant population sizes and their growth rates. In cases where only one pre-treatment scan was available, λ_R was assumed to be the same as λ_S. This is a reasonable assumption for two reasons. First, there is a trend towards correlation between the two, as described in the results. Second, the last pre-treatment CT was on average only 18.5 days before the start of erlotinib, i.e. an erroneous growth rate would only affect a short period of time.

Since we model tumor growth using the Gompertz formalism, we convert the growth parameters (λ) into volume doubling times pre-treatment (VDT_pre) and post-progression (VDT_post) for illustration purposes. The volume doubling time is not constant for Gompertz growth and decreases with increasing size. Consequently, we quote the normalized volume doubling time, which is the doubling time of the tumor at a size of 1cc, to compare growth of tumors of different sizes. This normalized volume doubling time is calculated by solving the un-modified Gompertz growth equation

$$\frac{\mathit{dV}}{\mathit{dt}}=\lambda \mathit{log}\left(\frac{K}{V}\right)V$$

for a given growth parameter λ.

With VDT_pre and VDT_post determined, the remaining parameters were sequentially fit to predict a complete tumor volume trajectory as a function of time using a weighted least-squares formalism. A detailed description of the sequential parameter fitting process for an example patient is outlined in the supplementary material (see supplementary Figure 1). Estimation of parameters and their uncertainties was implemented using the Levenberg–Marquardt method using the lmfit package in Python3.5. The workflow and an example patient are shown in the results section.

Guide to Model Equations and Assumptions

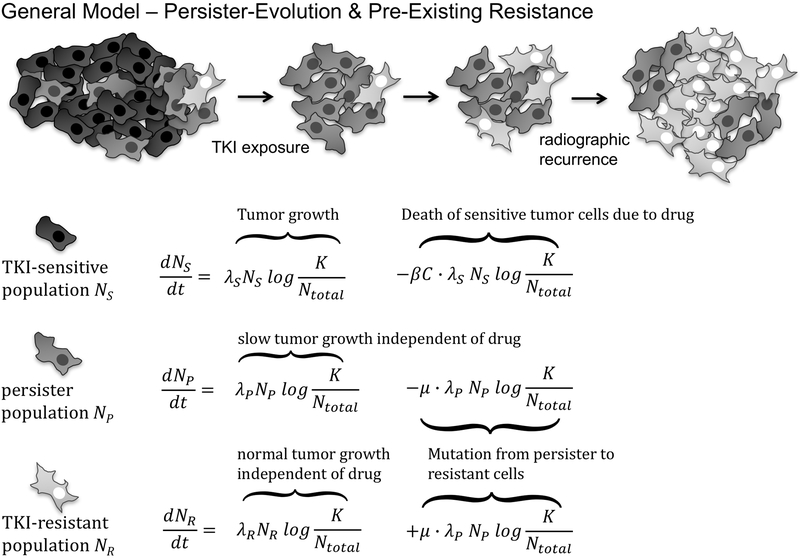
Tumor sub-populations can be modeled in a variety of ways, typically either stochastically as birth-death processes, or deterministically as systems of differential equations (28), and analytical expressions can be found for both approaches (29,30). We describe the evolution of tumor sub-populations using a system of ordinary differential equations (ODEs), similar to previous approaches (28,30,31). The three compartments represented are drug-sensitive cells N_S, drug-tolerant persister cells N_P and the resistant compartment N_R.

A general model describing the dynamics of these compartments is depicted in Figure 1. Cells in the drug-sensitive, persister and resistant compartments grow according to the Gompertz model with the growth rates λ_S, λ_P and λ_R, respectively. N_total represents the total number of cells and the capacity K is set to 4.09*10¹² cells and constant, derived from data of untreated NSCLC cancer patients (32). The robustness of the results towards these assumptions is evaluated and discussed further below. The interaction of the cell compartments via the N_total term in the denominator of the Gompertz growth formulation (see Figure 1) leads to competitive release, i.e. the accelerated emergence of the resistant clone as soon as it faces less competition from other compartments (33-35).

Fig 1.

General Model and system of differential equations describing the temporal evolution of all subpopulations, including both persister-evolution and pre-existing resistance.

Cell loss, i.e. tumor shrinkage, is modeled according to Norton-Simons dynamics (36), i.e. proportional to the growth rate, and is a summary term including cell loss through apoptosis as well as other pathways. This is implemented using the cell loss term featuring the cell loss parameter β and the drug plasma concentration C(t). All patients included in this study received a daily oral dose of 150mg erlotinib, and we modeled plasma concentrations based on measured patient levels for this schedule (36,37). Drug pharmacodynamics are described using a one-compartment model, with an exponential decay from a maximum concentration C_max of 1.136 (μg/mL) with a half live t_1/2 of 20 hours. Lastly, the persister population N_P undergoes a transition to the resistant compartment with a compound mutation probability μ. Note that this compound mutation probability differs from mutation probabilities in birth-death models in the sense that it is applied to the net growth, and not to each cell division in a continuous birth-death process (38). Under these assumptions the general model including persister-evolution and pre-existing resistance takes the form of the coupled set of ODEs displayed in Figure 1.

The general model in Figure 1 contains eight parameters, three population sizes and their corresponding growth rates, the cell loss parameter β and the compound mutation probability μ. Fitting such a large number of parameters simultaneously requires high-dimensional data, which is arguably not the case for the tumor growth, regression and recurrence trajectories at our disposal. To enable model fitting from the tumor trajectory data collected from our patients, we employ two strategies. First, we fit the parameters sequentially, using assumptions about the dynamics of the underlying populations (see methods and supplementary material for a detailed description). Second, we reduce the general model to two special cases, involving either only pre-existing resistance or only persister-evolution. These strategies allow us to arrive at robust parameter estimates.

The model assuming only pre-existing resistance assumes no persistent cells (N_P = 0), and therefore a sizeable pre-existing resistant compartment has to exist at treatment initiation to explain the re-growth trajectory. The model assuming only persister-evolution conversely assumes no resistant cells at treatment start (N_R(t=0) = 0), i.e. the all resistant cells are created through mutation induction from the persistent compartment after treatment initiation.

Results

Clinical Patient Data & Model Fitting

We identified 20 intra-thoracic lesions in 17 patients and analyzed a total of 164 chest CTs (median 7 per patient, interquartile range 5.5–8.5) obtained at a median interval of 8 weeks. The observation period for every patient was determined by the time to RECIST progression: the median progression free survival (PFS) in the population was 12.5 months, ranging from 4.2 to 37.3 months, comparable to published EGFR-mutant populations treated with TKIs (39). The average lesion volume before commencement of erlotinib was 25.1cc. For three patients no pre-treatment volumes could be estimated, in one case due to missing data, in the others due to post-obstructive pneumonitis that rendered exact volume delineation infeasible. These are excluded from the analysis.

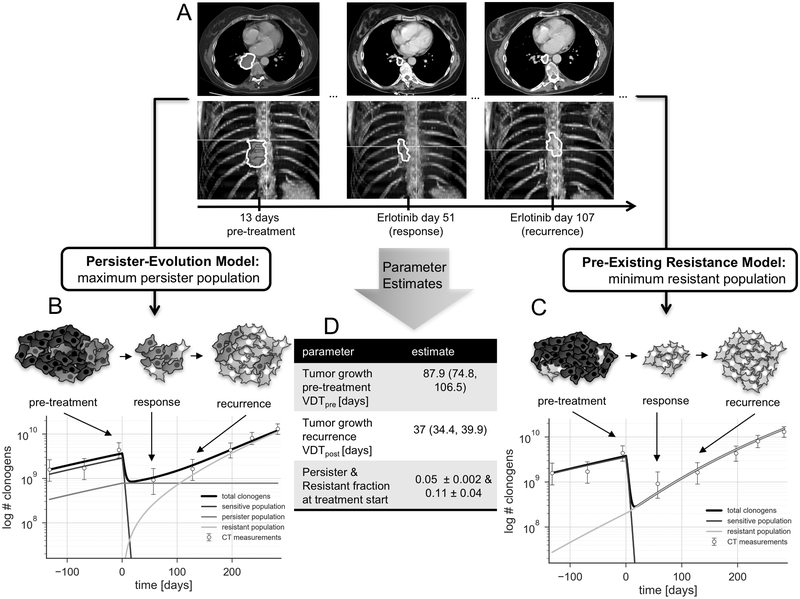
An example patient and model fit is shown in Figure 2: the top part (Figure 2A) shows a sub-set of the available CT scans (pre-treatment, during response and after progression) for one patient. The model fit for the persister evolution model is demonstrated in Figure 2B. The TKI-sensitive population (blue line) first dominates the population, but shrinks quickly after treatment initiation, the persister population stays almost stable, while the resistant population (red line) takes over and repopulates the tumor to match the observed progression trajectory.

Fig 2.

Schematic overview over the model fitting and parameter extraction process. A. tumor volume is extracted by contouring serial CT scans. B. persister-evolution model, C. pre-existing resistance model, both in logarithmic scale. D. overview over the extracted parameters and their range. Error bars represent volume-dependent contouring error as described in the methods section.

Figure 2C demonstrates the case of only pre-existing resistance and no persister population. Figure 2D shows the parameter estimates for the volume doubling time pre- and post-treatment (VDT_pre, VDT_post), and the estimates of the persister and resistant fractions at treatment initiation, in this case 0.05 (pre-existing resistance) and 0.11 (persister-evolution).

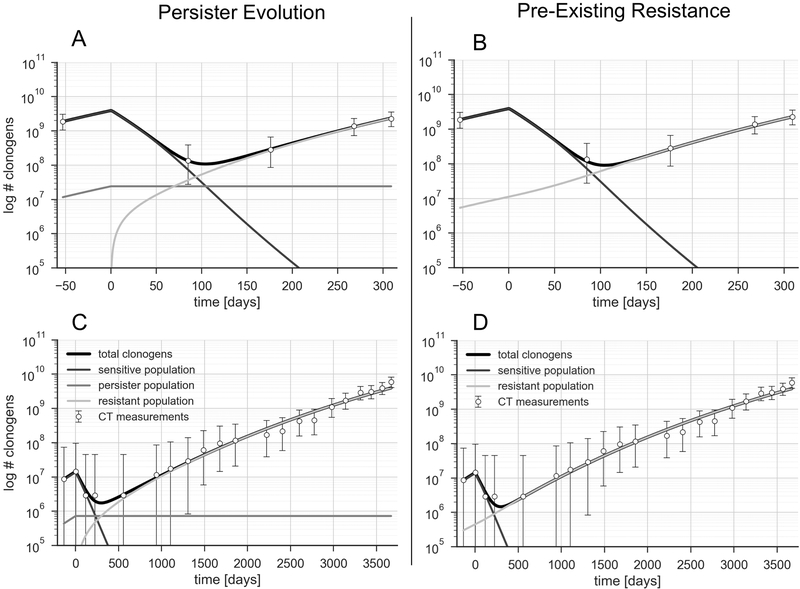
Figure 3 shows data and model fits for two additional patients, one with average PFS and rapid growth (PFS 8 months, 50 days VDT, Figure 3A/B) and one with long PFS and slow growth (PFS 36 months, 327 days VDT, Figure 3C/D).

Fig 3.

A/C: patient with a PFS of 8m, and a fast-growing tumor (VDT 50 days). C/D: patient with long PFS of 36.8m, and very slow tumor growth with a doubling time of 327 days. Only persister-evolution model depicted on the left, only pre-existing resistance on the right.

Tumor Growth

Our model fits tumor growth up to ten years, as evidenced by Figure 3C/D. The pre-treatment volume doubling times observed across the cohort averages 88 days (median 73 days, range 35–261). Post-treatment doubling times were longer with an average of 178 days and a median of 127 days [31–484], though the difference did not reach statistical significance (p=0.085, paired t-test). Assuming normally distributed tumor volumes and growth rates, there was a strong correlation between the tumor volume pre-treatment and the observed volume doubling time (p = 0.005), i.e. larger tumors tended to grow more slowly.

Table 1 shows growth rates pre-treatment and post-progression, together with PFS for all tumors. We found a strong correlation between PFS and the post-treatment doubling time (Spearman’s rank p= 0.005). Three of the patients had two lesions contoured each (marked with symbols in the table). The growth rates of lesions within these patients were more homogeneous than between different patients, the variance being a factor 6 lower than in the group as a whole. It is not possible to draw definite conclusions from this observation, but it indicates that in this cohort different lesions within a patient grow at similar rates.

Table 1.

Growth Rates and progression free survival (PFS) for all patients sorted by PFS. Missing pre-treatment growth rates are due to availability of only one scan pre-treatment. Numbers in brackets reflect the error in the parameter estimate, (−) indicates an uncertainty in volume doubling time (VDT) of < 0.1 day. Note the intervals are asymmetric as the error in the growth rate affects the VDT in a non-linear fashion. The symbols (^¶,§,○) mark tumors in the same patient.

Tumor number	VDTpre [days]	VDTpost [days]	PFS	Tumor number	VDTpre [days]	VDTpost [days]	PFS
1	61.4 (−)	200.2 (−)	4.2	11	-	344.3 (333.8,355.5)	12.1
2	87.9 (74.8, 107)	37 (34.4, 39.9)	4.3	12	-	132.2 (128.8, 135.7)	12.8
3§	-	103.1 (100.6, 105.8)	4.4	13	-	328.5 (229.8, 576)	13.8
4§	-	85.4 (72.3, 104.3)	4.4	14	-	483.7 (−)	16.8
5	-	36.3 (−)	5.8	15	-	99.6 (92.6, 107.7)	20.3
6	-	82.6 (−)	7.5	16	84.1 (−)	243.5 (−)	22.9
7○	96.7 (−)	30.6 (−)	8.6	17	-	355.6 (334.9, 379.1)	25.3
8○	35.2 (−)	72.3 (−)	8.6	18	260.5 (−)	327.4 (−)	36.8
9	-	39.9 (39.4,40.3)	9.3	19¶	45.3 (−)	122.3 (−)	37.3
10	-	209.3 (195.6, 224.9)	12.1	20¶	35.8 (−)	216.9 (−)	37.3

Population Sizes for either only Pre-Existing Resistance or only Persister-Evolution in NSCLC Patients during Treatment with Erlotinib

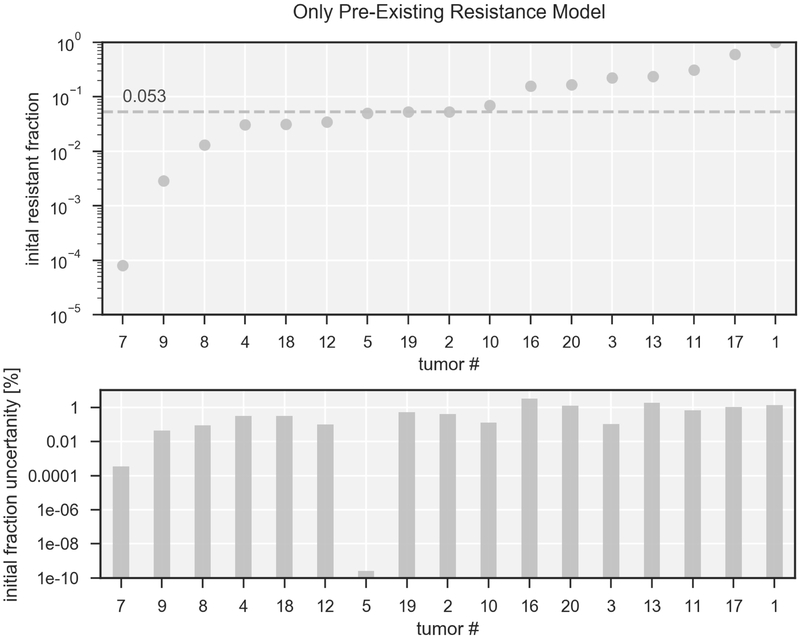
Figure 4 shows the model predictions for the size of the resistant population (top) and their error estimates (bottom) at the initiation of treatment with erlotinib for the model assuming only pre-existing resistance. The fraction of pre-existing resistance (red symbols) ranges from 10⁻⁴ to 0.6, the median across all tumors is 5.3%. The errors estimated in the lower part are expressed as percentage of the total clonogenic population and are on the order of ~1% for most tumors. The error relative to the initial resistant fraction itself is ~10% for most tumors, for details see supplementary Figure 2A.

Fig 4. Population sizes expressed as fractional volume at treatment start assuming only pre-existing resistance.

Top: Fraction of pre-existing resistance in logarithmic scale for 17 tumors, ordered by fraction of pre-existing resistance. The labeling corresponds to Table 1. Bottom: error estimates given by the fitting procedure for the fractional volume, displayed as fraction of the total clonogen number. To view the error expressed as percentage of the initial fraction please consult the supplementary material.

For 5 tumors the predicted fraction of pre-existing resistance is above 20%. These are tumors that demonstrated very little volume decrease and slow growth of the tumor post progression, but still exhibited short progression-free survival. Consequently, the model predicts a very high fraction of pre-existing resistance as likeliest explanation of the observed tumor volume trajectory.

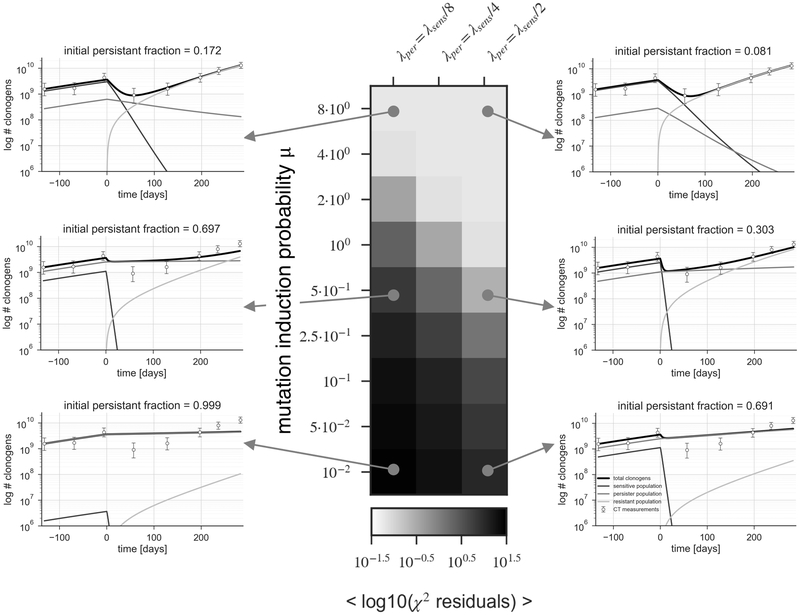
For the persister-evolution model, there is no single optimal choice for the underlying parameters, because of the larger number of variables to fit: the fraction of persister cells N_P, their growth rate λ_R, and the compound mutation induction probability μ. While the size and growth rate of the persister population is not known exactly in a patient, it has been observed in vitro that the persister population grows with four times the volume doubling time of the untreated population (5). Based on these results we conducted a robustness analysis and assumed a range of three values for the growth of the persister population: two, four or eight times slower than the tumor before therapy. We further explore a range of mutation induction probabilities μ, from 8 down to 10^-2. For these combinations we did fit the fraction of persister cells that would result in the observed tumor growth trajectory. The results of this parameter exploration are shown in Figure 5, with the colored panel indicating the goodness of fit achieved for a given choices of persister growth rate λ_P and compound mutation induction probability. The panels to the left and right demonstrate examples of the best fit for the indicated combination of parameter choices. This demonstrates that depending on the growth rate of the persister population, no viable solutions can be found below a specific mutation induction probability. If μ falls below 0.05, the observed trajectories can no longer be explained by the model. The mutation induction probabilities above 1 are not realistic, as they indicate that the rate of resistant cells being created is larger than the net tumor growth, leading to a declining persister population.

Fig 5. Parameter estimation for the persister-evolution model.

The panel represents results for three choices of persister growth rate λ (1/2, 1/4 and 1/8 of the untreated growth rate), and several choices of compound mutation induction probability ranging from 10⁻² to 8. The colorbar represents the goodness of fit quantified by the residuals of the least-square parameter optimization in logarithmic scale.

General Model: Mixed Persister-Resistant Population

As demonstrated above, assuming either only pre-existing resistance or only persister-evolution leads to unrealistic parameter estimates. The former leads to very high estimates (>0.2) for the fraction of pre-existing resistance, while the latter leads to very high estimates for the mutation induction probability (above 0.05).

For the general model we assume that the persister population grows with four times the volume doubling time of the untreated population, as observed in vitro (5), and that the compound mutation induction rate is 10⁻⁷, based on analyses of the rate of accumulation of sub-clonal mutations in lung adenocarcinoma (40). We explored the latter assumption further in a detailed robustness analysis, see below.

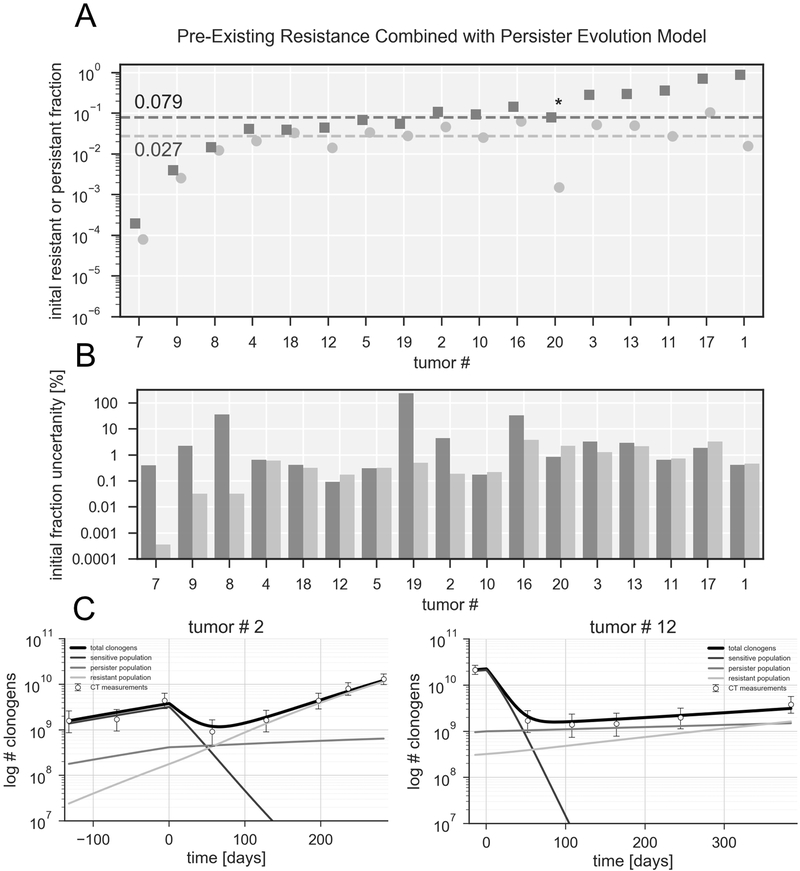
Using this general model we estimated the size of the resistant population at the beginning of treatment, which leads to the mixed population size estimates shown in Figure 6A, together with their error estimates (Figure 6B) and detailed growth curves for two tumors (Figure 6C). The fraction of pre-existing resistance is on average less than half the size compared to the case of pre-existing resistance only, with a median of 0.027 (red line), and a total volume fraction <0.1 for all tumors. In this scenario the function of the persister population is to maintain the tumor volume during the response period, while the resistant population causes the regrowth at progression and beyond. A good example for this is tumor #20, in which the fraction of pre-existing resistance is reduced by several orders of magnitude in the combined model. This also leads to the largest error estimate for this tumor relative to the population size (see supplementary Figure 2B), the error expressed as fraction of total clonogens is however only 2% (see Figure 6B). This tumor had little volume reduction after TKI initiation (~20%) but a relatively long time to progression of 16.8 months. In the pre-existing resistance only case, the model was forced to assume a large fraction to account for the small volume reduction, while in the combined model the persister population can explain this behavior.

Fig 6. Population sizes expressed as fractional volume at treatment start for the combined model.

A. Fraction of pre-existing resistance (circles) and of persister cells (squares) in logarithmic scale for 17 tumors. Dotted lines represent median of persister and resistant fraction among all patients. The order of the tumors is the same as in Figure 5 B. Error estimates for the fractions of pre-existing resistance and persister cells, displayed as fraction of the total clonogen number. For additional details regarding the sequential fitting process see supplementary material C. Combined model growth curves for tumors 2 and 12

The dynamics of relapse are primarily determined by the initial fraction of resistant cells and their growth rate (7). Our cohort shows a strong correlation of the time to progression with post-treatment tumor growth rate, though not with the estimated fraction of resistant cells. This indicates that among those two factors the growth rate of the resistant population is the main determinant for time to progression.

Discussion

Pre-Existing Resistance, Persister-Evolution & the General Model

Assuming solely persister-evolution leads to high estimates for the mutation induction probability, many orders of magnitude higher than those found in the literature ranging from 10⁻⁷ to 10⁻¹¹ (12,41,42). These mutation induction probabilities are a rough estimate within the confines of the model presented, but indicate that in the tumors analyzed in this study it is unlikely that acquired resistance alone was responsible for progression. Some extent of pre-existing resistance must have been present to explain the observed tumor volume trajectories. This is also in line with observations in patients that TKI-resistant clones share a common clonal origin and clonal divergence most likely occurred before initiation of treatment (43,44).

For the case of only pre-existing resistance, the model produces large population estimates for pre-existing resistance in some tumors, up to 60% for tumor #17 (see Figure 4). The reason for these large estimates is that there is no persister population that can explain trajectories with little volume shrinkage. If this would indeed have been the case, such a high fraction of pre-existing T790M cells would certainly have been identified by clinical genotyping, supporting the notion that this model is invalid.

Nevertheless, even though we used a sequential parameter fitting process restricted by several assumptions (see supplementary material for detailed example), we could initially not parameterize the general model because one tumor trajectory does not contain enough information to fit the required parameters for two sub-populations. But with the knowledge that the persister population alone cannot explain the observed progression trajectories with realistic mutation induction rates, we set the mutation induction probability to a realistic value (10⁻⁷) and estimated the amount of pre-existing resistance that would be required to explain the observed clinical data. A robustness analysis (see below), shows that our results do not critically depend on this assumption. In the general model the function of the persister population is to maintain the tumor volume during the response period, while the resistant population causes the regrowth at progression and beyond, as illustrated by the examples in Figure 6.

The relative errors for the estimated resistant population are on the order of 10–50% for many tumors (see supplementary figure 2), which is small relative to the total clonogen number (see Figure 6B). This exemplifies that naturally we cannot estimate the size of these populations very accurately based on microscopic growth dynamics. However, it confirms that based on the model and reasonable assumptions, a pre-existing resistant population of this order of magnitude is necessary to explain the observed recurrence dynamics.

Even though the estimated pre-existing resistant fraction is small, small enough to be undetected in a biopsy that samples only a few locations in the tumor, we do predict a finite amount of resistance present at treatment initiation for all patients in the cohort. However, within our model it is also conceivable that progression occurs exclusively due to resistance arising after initiation of treatment (de novo), even though this was not observed in our cohort. This could be the case in patients that have very long progression-free survival, but nevertheless a rapidly growing resistant population, i.e. a tumor that stays radiographically stable over a long period of time and then grows explosively (volume doubling time <30 days) without changes in treatment.

Co-Existence & Fitness of the Resistant Sub-Population

Our results indicate that a sizeable resistant and persistent sub-population co-exists with the drug-sensitive population at the initiation of treatment, which has recently also been shown in several EGFR-mutant patients (22). We did observe a trend towards slower post- than pre-treatment growth, though the difference did not reach statistical significance. This would indicate that the resistant T790M+ population is at a slight fitness disadvantage, but could also be connected to the fact that the combined growth of persister and resistant populations can appear slower than for a purely resistant population. Slightly deleterious mutations can get fixed in the population even if they reduce the total fitness value of the tumor, if they emerge early enough (45). Leder et al. measured the fitness of different resistance-conferring mutations to different TKIs, and showed that the resistance-conferring mutations decreased fitness in the majority, resulting in growth rates 5–40% lower than in the sensitive population (46). This tendency of the resistant sub-population to exhibit a slower growth rate is in line with other clinical observations (47) and the phenomenon of disease flare after TKI discontinuation (48).

However this observation might not be applicable to other oncogenic drivers, such as NSCLC exhibiting mutations in the anaplastic lymphoma kinase (ALK). In experiments studying the growth rates of ALK-positive cells lines during treatment with Alectinib, it has been observed that also in the absence of drug, resistant cell populations can have higher growth rates than their parental cell lines (49).

Our model only aims at predicting the fraction of persister and resistant cells at the time of treatment initiation. The size of the T790M-positive sub-population at that time is dependent on the interplay of several complex processes such as clonal selection, immune system escape and random drift (50), which are not described by our model. Nevertheless, from time of TKI initiation onwards, our three-population model is a valid description of the underlying dynamics, as the selection pressure exerted by the drug is strong enough to effectively separate the population into three compartments: sensitive – persister – resistant.

The co-existence and relative fraction of pre-existing resistance predicted by our model are in line with models of neutral clonal evolution. Williams et al. (40) have demonstrated in a pan-cancer cohort that within-tumor clonal dynamics are not dominated by strong selection but are consistent with neutral evolutionary dynamics, meaning that individual sub-clones with distinct mutational patterns (such as T790M) will grow at similar rates, coexisting within the tumor for long periods of time without outcompeting one another.

Tumor Growth

The results show that the Gompertz growth formalism is able to simulate the observed size of lung tumors in patients over long periods of time and multiple orders of magnitude, as illustrated in Figure 3C/D. This is an important observation, as we also use the Gompertz model to extrapolate down to microscopic populations, which are not observable by current imaging techniques. The Gompertz model incorporates an increased growth rate for small cell populations and is widely applied in cancer growth modeling (51,52). We have recently shown that this model describes the growth of NSCLC better than the exponential model over all stages of disease (32). Results using an exponential growth model are discussed further below. It can however be argued that all sigmoidal growth models exhibiting decreasing growth rates, such as the Gompertz, Logistic and Bertalanffy approaches, show better agreement with experimental data than exponential growth (51) and would yield similar performance here. Furthermore, other authors have used the assumption of a fixed growth rate and a patient-specific carrying capacity to express inter-patient variation in observed growth (53). We have chosen a constant carrying capacity based on our previous work (54), though it is likely that a similar fit to the observed trajectories can be achieved using a variable carrying capacity.

We demonstrate a significant correlation of post-treatment growth rate to outcome, which has been observed clinically in lung cancer patients (55,56), but no such correlation was observed for the initial fractions of pre-existing resistance. This underscores again that while we are confident that a sizeable population of pre-existing resistance exists in these patients, on the order of 0.01 to a few percent of the total, its exact size is subject to the inherent stochastic nature of interacting cell populations and therefore difficult to estimate using our simplified model.

Robustness towards Assumptions and Limitations

The population estimates are robust towards the exact choice of mutation induction rate. Varying it from 10⁻³ to 10⁻¹¹ does not change the predicted fraction of pre-existing resistance (see supplementary figures 3A/B). Even assuming a very high mutation induction probability does not yield enough resistant cells produced by the persister population in such a short time, and the pre-existing compartment has to explain the clinically observed progression trajectories (see supplementary figure 3C/D for two examples). If the resistant compartment would be populated by many separate mutation events from the persister population, it would also contradict genomic data that the resistant population usually comes from a single clone that transformed, not the accumulation of many clones that transformed independently over time (43,44).

To test the robustness towards the assumption of Gompertzian growth, we have repeated our entire analysis with an exponential growth model instead. This leads to even higher estimates of pre-existing resistance, as small populations grow with the same rate in the exponential model, while they grow faster in the sigmoidal approaches.

The number of CT scans available impacts our ability to perform the sequential model fitting process outlined in the methods. To derive the growth rate and size of the resistant compartment from the post-treatment scans, at least one scan after the detection of recurrence (according to RECIST criteria) is beneficial, but is often not clinically available.

The estimated fractions are also independent of the tumor cell density (we assumed 2.8*10⁸/cm³). There is a range of tumor cell densities reported in the literature, from 10⁵ to 10⁹ (57,58). However, a different choice of density would only shift the tumor trajectory on the log plots displayed, but not affect the VDTs or persister and resistant fractions estimated by the model. It would however impact estimates of the absolute numbers of persister and resistant cells, and relative changes in percentage of tumor cells versus stroma. This makes the results also independent of systematic contouring errors. To test this we contoured several patients using soft-tissue as well as lung windowing, leading to different tumor volumes but without effect on the resulting parameters and fraction sizes.

We have simplified the known heterogeneity of tumors to only three cell compartments, representing resistant, persister and sensitive cells. More realistic descriptions that include a spectrum of drug sensitivity, growth rate, and mutation probability, would require significantly more compartments. The available macroscopic patient data is insufficient to inform such a detailed microscopic description.

We have restricted the study population to patients progressing with a confirmed T790M mutation, to make the sample homogeneous regarding the resistance mechanism. The modeling framework could also capture the dynamics of other, different resistance mechanisms, such as the transition to small-cell lung cancer observed clinically (1). A possible limitation is the retrospective nature of the study, the number of tumors, and the fact that we only used patients in which we could measure tumor volume increase during treatment with erlotinib. While this might have skewed the results towards more indolent tumors, it does not change our conclusions.

Measuring Persister Populations and Pre-Existing Resistance in vivo

There have been studies measuring the fraction of persister and resistant cells in vivo. It has been shown that Fluorothymidine (FLT) PET can detect MET-mediated resistance to EGFR TKIs in NSCLC (59). FLT PET, which has been shown to be a stable marker of cell proliferation, has generally emerged as a predictor of response to EGFR TKIs in NSCLC (60). The existence of a FLT PET signal after initiation of TKIs hints at the presence of a sizeable population of cells that is still proliferating, attributable to the persister/resistant population. Even though FLT PET predicts time to progression, it is not trivial to discern if a given FLT signal comes from a small population proliferating quickly, or a larger population proliferating slowly. Therefore, the model described above could be used to transform semi-quantitative input from imaging modalities such as PET to quantitative estimates for the size of the persistent and resistant cell populations and estimate the temporal dynamics in between imaging timepoints. Imaging the dynamics of resistant sub-populations in patients could also be used to validate the model in itself and enable prediction of patient-specific tumor trajectories based on early tumor imaging.

Liquid biopsies can overcome some of the limitations of traditional tissue biopsies, and lately significant advances have been made specifically in using plasma-based assays to detect T790M mutations (19). They have the potential to become a useful clinical tool to tailor therapy to the specific patient characteristics and could provide the patient-specific input to parameterize models such as the one presented here.

Possible Applications: Exploiting Temporal Evolutions of Subpopulations

Insights into the temporal evolution of resistant sub-populations could yield useful information to design therapeutic approaches. For example, knowledge about the size of sub-populations exhibiting resistance can provide useful information to guide the timing of localized therapeutic interventions, such as radiotherapy. The recent success of adding Durvalumab after chemo-radiation in locally-advanced NSCLC has shown how impactful the integration of new systemic agents can be for earlier stages of disease (61). However, the fact that the addition of Durvalumab yielded an increase in progression-free survival in all patient subgroups except EGFR-mutant tumors highlights the fact that strategies to incorporate EGFR-TKIs into the treatment of locally-advanced disease are urgently needed.

There are multiple trials exploring various approaches of combining targeted agents with radiation (62), in stage III ( NCT01553942, NCT01822496) as well as metastatic disease ( NCT02314364). Especially for locally-advanced NSCLC, there are remaining questions that can be comprehensively investigated using computational modeling, the best example being the length of the TKI induction period before starting concurrent chemo-radiation. There are obvious trade-offs involved: the shorter the induction period, the less we risk competitive release of a dormant sub-population and production of new resistant clones from persister cells. Some induction however is beneficial, as the cell kill in the sensitive sub-population makes the tumor more likely to be controlled by concurrent chemo-radiation and reduces the field size leading to less toxicity and other benefits for the patient. To quantitatively explore such trade-offs using realistic parameters, our model or similar approaches (63), need to be combined with traditional radiation biology models to estimate tumor control probabilities of multi-modality regimen in an integrated fashion.

Conclusion

We have applied two separate, simplified resistance models to clinically observed tumor volume trajectories of EGFR-mutant patients treated with erlotinib and progressing with a T790M mutation. Neither a persister-evolution, nor a pre-existing resistance model alone could explain the observed progression trajectories. Only persister-evolution would require unrealistically high mutation induction rates to explain the observations and would contradict other studies showing the common clonal history of resistant clones. Only pre-existing resistance leads to unrealistically high fractions of resistant cells at treatment initiation for some patients in the cohort, which is not in line with pre-treatment biopsies. However, combining pre-existing resistance with persister cells can explain the observed tumor volume trajectories, and provides robust estimates of the pre-existing resistant fraction in EGFR-mutant lung cancers that progress due to a T790M mutation.

The proposed model can be extended to other resistance conferring mutations and oncogene-drivers and has the potential to inform combination approaches such as the timing of radiotherapy in oligometastatic disease, the integration of targeted agents as induction therapy with radiation in the locally advanced setting, or combinations of targeted agents.

Statement of Significance.

Findings quantify pre-existing resistance and persister cell populations, which is essential for the integration of targeted agents into the management of locally-advanced disease and the timing of radiotherapy in metastatic patients.