Intracellular calcium stores mediate metaplasticity at hippocampal dendritic spines

Abstract

Key points

• Calcium (Ca²⁺) entry mediated by NMDA receptors is considered central to the induction of activity‐dependent synaptic plasticity in hippocampal area CA1; this description does not, however, take into account the potential contribution of endoplasmic reticulum (ER) Ca²⁺ stores.

• The ER has a heterogeneous distribution in CA1 dendritic spines, and may introduce localized functional differences in Ca²⁺ signalling between synapses, as suggested by experiments on metabotropic receptor‐dependent long‐term depression.

• A physiologically detailed computational model of Ca²⁺ dynamics at a CA3–CA1 excitatory synapse characterizes the contribution of spine ER via metabotropic signalling during plasticity induction protocols.

• ER Ca²⁺ release via IP₃ receptors modulates NMDA receptor‐dependent plasticity in a graded manner, to selectively promote synaptic depression with relatively diminished effect on LTP induction; this may temper further strengthening at the stronger synapses which are preferentially associated with ER‐containing spines.

• Acquisition of spine ER may thus represent a local, biophysically plausible ‘metaplastic switch’ at potentiated CA1 synapses, contributing to the plasticity–stability balance in neural circuits.

Abstract

Long‐term plasticity mediated by NMDA receptors supports input‐specific, Hebbian forms of learning at excitatory CA3–CA1 connections in the hippocampus. There exists an additional layer of stabilizing mechanisms that act globally as well as locally over multiple time scales to ensure that plasticity occurs in a constrained manner. Here, we investigated the role of calcium (Ca²⁺) stores associated with the endoplasmic reticulum (ER) in the local regulation of plasticity at individual CA1 synapses. Our study was spurred by (1) the curious observation that ER is sparsely distributed in dendritic spines, but over‐represented in larger spines that are likely to have undergone activity‐dependent strengthening, and (2) evidence suggesting that ER motility at synapses can be rapid, and accompany activity‐regulated spine remodelling. We constructed a physiologically realistic computational model of an ER‐bearing CA1 spine, and examined how IP₃‐sensitive Ca²⁺ stores affect spine Ca²⁺ dynamics during activity patterns mimicking the induction of long‐term potentiation and long‐term depression (LTD). Our results suggest that the presence of ER modulates NMDA receptor‐dependent plasticity in a graded manner that selectively enhances LTD induction. We propose that ER may locally tune Ca²⁺‐based plasticity, providing a braking mechanism to mitigate runaway strengthening at potentiated synapses. Our study provides a biophysically accurate description of postsynaptic Ca²⁺ regulation, and suggests that ER in the spine may promote the re‐use of hippocampal synapses with saturated strengths.

Key points

• Calcium (Ca²⁺) entry mediated by NMDA receptors is considered central to the induction of activity‐dependent synaptic plasticity in hippocampal area CA1; this description does not, however, take into account the potential contribution of endoplasmic reticulum (ER) Ca²⁺ stores.

• The ER has a heterogeneous distribution in CA1 dendritic spines, and may introduce localized functional differences in Ca²⁺ signalling between synapses, as suggested by experiments on metabotropic receptor‐dependent long‐term depression.

• A physiologically detailed computational model of Ca²⁺ dynamics at a CA3–CA1 excitatory synapse characterizes the contribution of spine ER via metabotropic signalling during plasticity induction protocols.

• ER Ca²⁺ release via IP₃ receptors modulates NMDA receptor‐dependent plasticity in a graded manner, to selectively promote synaptic depression with relatively diminished effect on LTP induction; this may temper further strengthening at the stronger synapses which are preferentially associated with ER‐containing spines.

• Acquisition of spine ER may thus represent a local, biophysically plausible ‘metaplastic switch’ at potentiated CA1 synapses, contributing to the plasticity–stability balance in neural circuits.

Introduction

Hebbian synaptic plasticity involves activity‐driven changes in synaptic strengths (Hebb, 1949). This form of plasticity is inherently unstable, as a small change in synaptic strength can promote further change in the same direction, and this positive reinforcement can drive synaptic efficacies to either saturate or reduce to a minimum (Abbott & Nelson, 2000; Honnuraiah & Narayanan, 2013; Hobbiss et al. 2018). It has long been recognized that Hebbian rules need to be supplemented with additional stabilizing mechanisms to curb runaway plasticity and support stable yet flexible neural circuits (Abbott & Nelson, 2000; Zenke & Gerstner, 2017; Keck et al. 2017). The issue of stability is usually addressed within the theoretical Bienenstock–Cooper–Munro (BCM) framework (Bienenstock et al. 1982), which posits an adaptive threshold for long‐term potentiation induction that varies as a function of the history of prior activity of the postsynaptic neuron, concurrently affecting all its afferent synapses. There is, however, limited understanding of biophysical mechanisms implementing such a rule (Gold & Bear, 1994; Bear, 1995; Abraham et al. 2001; Philpot et al. 2003; Xu et al. 2009; Narayanan & Johnston, 2010). This segues to the more general question as to what physiological mechanisms exist, at the cellular and synaptic levels, that could actively regulate the balance of plasticity and stability through appropriate adjustment of the rules of activity‐induced synaptic alterations, thereby shaping the long‐term dynamics of modifiable synapses (Abraham, 2008).

Synaptic plasticity, as a potential neural substrate for learning and memory storage, is particularly well studied in the hippocampal formation (Malenka & Bear, 2004; Neves et al. 2008), and much about its molecular underpinnings has been learned from investigations at the excitatory CA3 to CA1 Schaffer collateral (SC) synapse, an integral component of the neural circuitry supporting spatial learning (Tsien et al. 1996; Heynen et al. 1996; Moser et al. 1998; Sheffield & Dombeck, 2019). These synapses are capable of undergoing bidirectional modification (both long‐term potentiation (LTP) and long‐term depression (LTD)), which relies primarily on the activation of postsynaptic N‐methyl‐d‐aspartate receptors (NMDARs) and the ensuing entry of calcium (Ca²⁺) into the dendritic spine (Malenka & Nicoll, 1993; Lynch et al., 1983; Malenka et al. 1988; Cummings et al. 1996). Given the biophysical requirements of both membrane depolarization and glutamate binding for their activation (Johnston & Wu, 1994), NMDARs are naturally poised to mediate input‐specific, Hebbian forms of synaptic learning (Magee & Johnston, 1997; Song et al. 2000). However, an account of Ca²⁺ signalling based solely around cell surface receptors is incomplete, as another source of Ca²⁺, the endoplasmic reticulum (ER) store, may be available to CA1 spines (Meldolesi & Pozzan, 1998). The ER, which extends into the dendritic processes of hippocampal neurons, has a heterogeneous distribution in individual spines (Spacek & Harris, 1997; Harris et al. 2015). Curiously, it occurs more often in larger spine heads: nearly 80% of the larger mushroom‐shaped spines have ER compared to about 20% of all spines in adult dendrites, as seen in serial EM reconstruction of rat CA1 pyramidal cell dendrites (Cooney et al. 2002).

Here, we consider a synapse‐specific form of metaplasticity due to Ca²⁺ stores associated with the ER in these large dendritic spines. This is in contrast to cell‐wide mechanisms which have been the focus of several previous studies. Our investigation is motivated by the observation that mature spines that have ER are associated with stronger synapses and have most likely been potentiated (Matsuzaki et al. 2001; Holbro et al. 2009; Sun et al. 2014; Chirillo et al. 2015). Further, recent imaging studies on cultured hippocampal neurons from mice reveal a dynamic picture of the ER distribution in spines (Toresson & Grant, 2005); ER can undergo rapid growth in individual spine heads on a time scale of minutes, which was shown to be regulated by NMDAR activation (Ng et al. 2014), and accompanies spine enlargement (Sala et al. 2001; Sala et al. 2005). This local remodelling of the ER in spines correlated with changes in spine morphology suggests an adaptive function for ER specifically at potentiated synapses, providing an interesting context to our investigation.

Several lines of previous experimental work indicate an involvement of the intracellular ER store in neuronal Ca²⁺ regulation (Verkhratsky, 2005), with possible implications for activity‐regulated plasticity processes (Mattson et al. 2000; Rose & Konnerth, 2001; Bardo et al. 2006). This still leaves open important questions regarding the role of stores in microdomain signalling in the context of its uneven distribution in CA1 spines. Given that small spines without ER are capable of undergoing potentiation, what additional functionality does ER introduce in the context of plasticity at individual synapses? Ca²⁺ release from ER is particularly associated with Ca²⁺ signalling underlying synaptic LTD (Malenka & Bear, 2004). Experimental studies on hippocampal/cortical LTD have implicated a requirement for group I metabotropic glutamate receptor (mGluR) signalling (particularly involving the mGluR5 subtype) in the induction of depression by prolonged low frequency synaptic stimulation (Kleppisch et al. 2001; Lüscher & Huber, 2010), and this was shown to depend on release of Ca²⁺ from inositol 1,4,5‐trisphosphate (IP₃)‐sensitive intracellular stores (Stanton et al. 1991; Kato, 1993; Reyes & Stanton, 1996). These earlier findings were based on recordings of synaptic population responses; thus, pointed questions on the synapse specificity of mGluR signalling and Ca²⁺ store contribution could not be directly addressed. Two subsequent imaging‐based studies on plasticity at individual synapses provide more clarity in this regard. Glutamate uncaging at individual CA3–CA1 synapses in rat hippocampal slices (Holbro et al. 2009) was reported to evoke restricted Ca²⁺ release from ER in individual spine heads via IP₃ signalling, and mGluR/store‐dependent depression induced by prolonged low frequency uncaging stimulation was found to be localized to synapses associated with such ER‐bearing spines. Results from a more recent similar study of spine structural plasticity (Oh et al. 2013) show that, at synapses associated with larger spines, the contribution of mGluR/IP₃‐mediated store Ca²⁺ release in these spines is necessary for the induction of synaptic weakening with low frequency input trains. Together, the above findings suggest that, at least at a subset of synapses that are likely to have undergone experience‐dependent potentiation, IP₃‐mediated Ca²⁺ release from spine ER may make a particularly significant contribution under weak stimulation, augmenting the NMDAR‐mediated Ca²⁺ influx to facilitate synaptic depression.

Computational models of hippocampal synapses typically attempt to account for experimental findings on LTP/LTD in terms of the postsynaptic Ca²⁺ elevation mediated by varying levels of NMDAR activation (Shouval et al. 2002; Graupner & Brunel, 2007; Rackham et al. 2010; Kumar & Mehta, 2011; Graupner & Brunel, 2012). These models provide a useful description of a canonical, or generic, synapse. Given that presence of spine ER may be restricted to a small proportion of synapses, the contribution of ER is likely to be ‘washed‐out’ and difficult to disambiguate based on coarse‐grained population readouts. Despite suggestive evidence for the contribution of internal stores to synaptic plasticity in area CA1, a clear description of their relevance to Ca²⁺ signalling in individual spines is lacking. To address this conspicuous gap in our understanding, we have undertaken a detailed characterization of the engagement of the ER Ca²⁺ store at an active CA3–CA1 synapse. Our modelling study of an ER‐bearing CA1 dendritic spine head integrates a detailed kinetic description of mGluR‐regulated Ca²⁺ release from ER with a realistic model for NMDAR Ca²⁺ signalling. Our analysis highlights the synapse‐level differences in Ca²⁺ signalling and plasticity arising from the presence of ER, and provides a novel perspective on the functional role of ER, as an intracellular Ca²⁺ store, in the postsynaptic context.

Methods

We implemented a deterministic, single compartment model of a spine head on a hippocampal CA1 apical dendrite, and characterized the calcium (Ca²⁺) elevation and early long‐term plasticity driven by synaptic activation in the presence of an ER/spine apparatus (Fig. 1). The spine head was modelled as a sphere with fixed volume V _spine = 0.06 μm³, which approximates an average ER‐bearing spine head (ER⁺ spine) found experimentally (Holbro et al. 2009). While ER⁺ spines are on average larger than spines lacking an ER, our canonical spine head lies well within the reported dynamic range of spine sizes/synaptic strengths (Sabatini et al. 2002; Holbro et al. 2009), and thus may be considered potentially capable of undergoing plasticity in both directions (strengthening as well as weakening of synaptic efficacy). ER extending into spines is contiguous with the dendritic ER (Verkhratsky, 2005), and is typically found to occupy only a small fraction of the spine volume (≲5%) (Spacek & Harris, 1997); we assumed an ER‐to‐spine head volume ratio of 0.1. The spine head was assumed to be electrically coupled to its parent dendritic shaft by a thin ‘neck’, modelled as a passive electrical resistance, R _C. Estimates for pyramidal cell dendrites suggest a coupling in the range of a few hundred megaohms (Yuste, 2013); here, we set R _C = 100 MΩ. Diffusive coupling of Ca²⁺ between the spine and dendrite was ignored, in accordance with Ca²⁺ measurements at mushroom spines (Sabatini et al. 2002; Bartol et al. 2015).

Figure 1. Modelling activity‐driven Ca²⁺ dynamics and plasticity at a dendritic spine with ER.

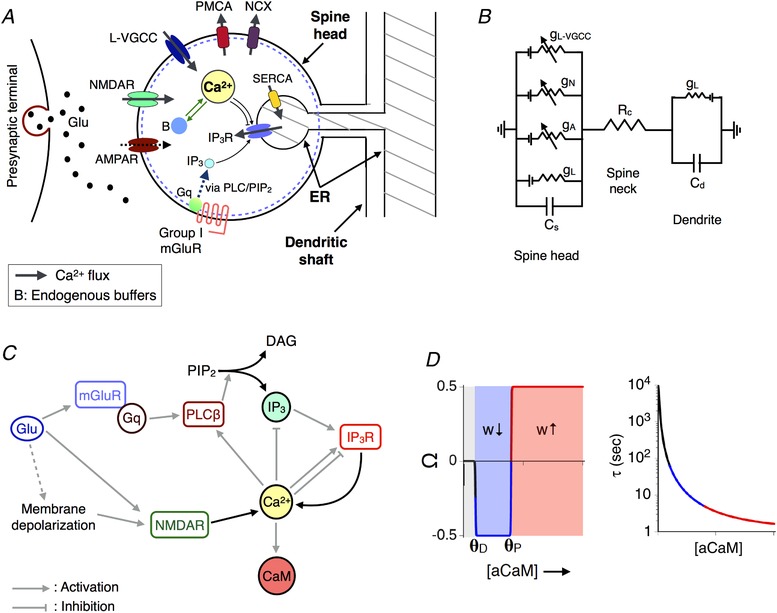
A, schematic representation of an ER⁺ CA1 spine head. Glutamate released into the synaptic cleft activates postsynaptic AMPA and NMDA receptors along with group I metabotropic receptors (mGluR), driving Ca²⁺ increase in the spine due to NMDAR‐gated entry from outside the cell and Ca²⁺ release from the IP₃‐sensitive ER store. B, equivalent circuit diagram representing the spine head resistively coupled to a dendritic compartment by neck resistance R _C. C, summary of the biochemical cascade involved in IP₃ and Ca²⁺‐mediated Ca²⁺ release (ICCR) from ER. Ca²⁺‐activated calmodulin (aCaM) regulates synaptic plasticity at the spine. D, the Ca²⁺–CaM‐based synaptic plasticity model used in the present study. The functions Ω and τ are both functions of aCaM and together shape the dynamics of the synaptic weight (w). [Color figure can be viewed at wileyonlinelibrary.com]

The various biophysical components comprising our model that collectively regulate the electrical and Ca²⁺ dynamics in the spine are described below. All model parameters and molecular concentrations used in our simulations are listed in Tables 1, 2, 3, 4.

Table 1.

Parameters governing membrane voltage dynamics

Parameter	Symbol	Value
Avogadro number	N a	6.023 × 1023 mol−1
Electric charge per Ca2+ ion	q Ca	3.2 × 10−19 C
Volume of (spherical) ER–/ER+ spine head	V spine	0.06 μm3
Resting membrane potential in spine/dendrite	u rest	−70 mV
Resistive coupling between spine head and parent dendrite	R C	100 MΩ
AMPAR conductance parameter	g A	0.5 nS
AMPAR rise time constant	τr A	0.2 ms
AMPAR decay time constant	τd A	2 ms
AMPAR current reversal potential	E A	0 mV
NMDAR conductance parameter	g N	65 pS in model synapse (gives ∆CaEPSP = 0.2 μm)
NMDAR rise time constant	τr N	5 ms
NMDAR decay time constant	τd N	50 ms
NMDAR current reversal potential	E N	0 mV
VGCC activation offset	u m	−20 mV
VGCC activation slope	k m	5 mV
VGCC activation time constant	τm	0.08 ms
VGCC inactivation offset	u h	−65 mV
VGCC inactivation slope	k h	−7 mV
VGCC inactivation time constant	τh	300 ms
Maximum depolarization during BAP in dendritic compartment	V 0	+67 mV
Fast time constant of BAP decay	τf	3 ms
Slow time constant of BAP decay	τs	40 ms
Effective number of co‐active synaptic inputs at dendritic compartment (rate‐dependent plasticity)	ρS	5 × 105 cm−2

Table 2.

Reaction rate parameters for Ca²⁺ buffering and extrusion

Parameter	Symbol	Value
Kinetic rate constants for interaction between Ca2+ and calbindin (CB)	k M0M1 k M1M2 k M1M0 k M2M1 k H0H1 k H1H2 k H1H0 k H2H1	174 μm −1 s−1 87 μm −1 s−1 35.8 s−1 71.6 s−1 22 μm −1 s−1 11 μm −1 s−1 2.6 s−1 5.2 s−1
Kinetic rate constants for interaction between Ca2+ and endogenous immobile buffer (CBP)	$k_{\mathrm{f}}^{\mathrm{CBP}}$ $k_{\mathrm{b}}^{\mathrm{CBP}}$	247 μm −1 s−1 524 s−1
Kinetic rate constants for interaction between Ca2+ and endogenous slow buffer	$k_{\mathrm{f}}^{s\mathrm{low}}$ $k_{\mathrm{b}}^{\mathrm{slow}}$	24.7 μm −1 s−1 52.4 s−1
Kinetic rate constants for interaction between Ca2+ and calmodulin (CaM)	k C0C1 k C1C2 k C1C0 k C2C1 k N0N1 k N1N2 k N1N0 k N2N1	6.8 μm −1 s−1 6.8 μm −1 s−1 68 s−1 10 s−1 108 μm −1 s−1 108 μm −1 s−1 4150 s−1 800 s−1
Kinetic rate constants for PMCA pump	k f PMCA k b PMCA k 3 PMCA k L PMCA	150 μm −1 s−1 15 s−1 12 s−1 3.33 s−1
Kinetic rate constants for NCX	k f NCX k b NCX k 3 NCX k L NCX	300 μm −1 s−1 300 s−1 600 s−1 10 s−1

Table 3.

Reaction parameters for mGluR–IP₃ signalling and ER Ca²⁺ handling (parameter values which have been changed from the original reference ( Doi et al., 2005 ) are highlighted)

Parameter	Symbol	Value
Time constant of glutamate pulse (alpha function)	τglu	1 ms
Max. amplitude of glutamate pulse at mGluR location	G max	300 μm
Kinetic rate constants for mGluR5‐G protein activation	a 1f a 2f a 3f a 4f a1b a2b a 3b a 4b a 5 a 6 a 7 a 8	11.1 μm −1 s−1 11.1 μm −1 s−1 2 μm −1 s−1 2 μm −1 s−1 2 s−1 2 s−1 100 s−1 100 s−1 116 s−1 0.001 s−1 0.02 s−1 6 s−1
Kinetic rate constants for phospholipase C (PLC) activation and production of IP3 and diacylglycerol (DAG)	b 1f b 2f b 3f b 4f b 5f b 1b b 2b b 3b b 4b b 5b b 6 b 7 b 8f b 9f b 8b b 9b b 10 b11 b 12	300 μm −1 s−1 900 μm −1 s−1 800 μm −1 s−1 1200 μm −1 s−1 1200 μm −1 s−1 100 s−1 30 s−1 40 s−1 6 s−1 6 s−1 2 s−1 160 s−1 1 μm −1 s−1 1 μm −1 s−1 170 s−1 170 s−1 8 s−1 2 s−1 8 s−1
Kinetic rate constants for IP3 degradation by IP3 3‐kinase (IP3K)	c 1f c 1b c 2f c 2b c 3	1111 μm −2 s−1 100 s−1 100 μm −1 s−1 80 s−1 20 s−1
Kinetic rate constants for IP3 degradation by IP3 5‐phosphatase (IP3K)	c 4f c 4b c 5	9 μm −1 s−1 72 s−1 18 s−1
Parameters for IP3 receptor kinetics	d 1 d 5 K inh a 2 α	0.8 μm 0.3 μm 0.2 μm 2.7 μm −1 s−1 937.5 μm −1 s−1 (corresponds to an open channel current of 0.15 pA when [Ca2+]ER = 0.5 mm)
Parameters for Hill‐type SERCA kinetics	K S V S	0.2 μm 1 μm s−1

Table 4.

Concentrations of various chemical species in the model

Species	Value
Resting Ca2+ concentration in the spine cytosol ([Ca2+]rest)	50 nm
Resting IP3 concentration in the spine	0.1 μm
Ca2+ concentration in ER lumen (fixed)	250 μm
Fixed extracellular Ca2+ concentration ([Ca2+]ext)	2 mm
Total calbindin (CB) concentration	45 μm
Total concentration of endogenous immobile buffer (CBP)	80 μm
Total concentration of endogenous slow buffer	40 μm
Total calmodulin (CaM) concentration	50 μm
Surface density of PMCA pumps	1000 μm −2
Surface density of NCX molecules	140 μm −2
Total mGluR concentration in the spine	0.3 μm
Total PLC–PIP2 concentration in the spine	0.8 μm
Total PIP2 concentration	4 mm
Total Gq‐GDP concentration in the spine	1 μm
Total IP3 3‐kinase (IP3K) in the spine	0.9 μm
Total IP3 5‐phosphatase (IP5P) in the spine	1 μm
Number of IP3 receptors associated with spine ER (NR)	10–50

Membrane voltage dynamics at the spine

The voltage at the postsynaptic membrane (u) is described by the following Hodgkin–Huxley (HH)‐type ordinary differential equation:

$$\begin{array}{ccc}\hfill A_{\mathrm{spine}}{C}_{\mathrm{m}}\frac{\mathrm{d}u}{\mathrm{d}t}& =& -g_{\mathrm{L}}{A}_{\mathrm{spine}}\left(u-u_{\mathrm{rest}}\right)-I_{\mathrm{A}}\hfill \\ & & -I_{\mathrm{N}}-I_{\mathrm{L}\text{-}\mathrm{VGCC}}-\frac{u-u_{\mathrm{d}}}{R_{\mathrm{C}}}\hfill \end{array}$$ (1)

It includes contributions from a passive leak current (g _L), voltage‐dependent AMPA receptor (AMPAR)/NMDA receptor (NMDAR)‐gated currents (I _A/I _N) in the postsynaptic density (PSD), a high voltage‐activated L‐type Ca²⁺ current (I _L‐VGCC), and passive electrical coupling to the dendritic shaft (R _C) with u _d denoting the voltage of the dendritic compartment (Fig. 1 B). We assumed standard membrane parameters (capacitance C _m = 1 μF cm⁻² and uniform leak conductance density g _L = 0.0002 S cm⁻²), and the resting membrane potential in both the spine and parent dendrite was set to u _rest = −70 mV (Graupner & Brunel, 2007).

AMPAR‐ and NMDAR‐gated currents were assumed to be transiently activated every time a synaptic input arrives, and both were modelled with linear I–V relations (reversal potentials E _A, E _N = 0 mV) (Zador et al. 1990). The AMPAR conductance was modelled as the difference between two exponentials with a rise time constant of ${\tau }_{\mathrm{A}}^{\mathrm{r}}=0.2\mathrm{ms}$ and decay time constant ${\tau }_{\mathrm{A}}^{\mathrm{d}}=2\mathrm{ms}$ (Graupner & Brunel, 2007):

$$g_{\mathrm{AMPAR}}\left(t\right)=g_{\mathrm{A}}\left(e^{-t/{\tau }_{\mathrm{A}}^{\mathrm{d}}}-e^{-t/{\tau }_{\mathrm{A}}^{\mathrm{r}}}\right)$$ (2)

for a glutamate pulse arriving at t = 0. The conductance parameter g _A was fixed at 0.5 nS across all our simulations (Zador et al. 1990). The glutamate dependence of the total NMDAR current was similarly modelled as a difference between exponentials with longer response times (τ^r _N = 5 ms and ${\tau }_{\mathrm{N}}^{\mathrm{d}}=50\mathrm{ms}$) (Narayanan & Johnston, 2010); the NMDAR conductance has an additional (multiplicative) dependence on the membrane potential, describing the Mg²⁺ block, which was modelled as a sigmoid function of the form B(u) = 1/(1 + 0.28 exp(−0.062u)) (Graupner & Brunel, 2007). The NMDAR conductance parameter g _N is a variable in our analysis, and adjusted to obtain different levels of spine Ca²⁺ elevation evoked by unitary synaptic input (see below). Trains of synaptic stimulation have been modelled as the sum of the above conductance waveforms (Zador et al. 1990).

The L‐type voltage‐gated Ca²⁺ current is regulated by a conductance of the form ĝ_L‐VGCC(t) = g _L‐VGCC m ² _u(t)h _u(t), where the time dependence of the HH‐type activation and inactivation gating variables, m _u(t) and h _u(t), respectively, is governed by the following equations (Nowacki et al. 2011):

$${\tau }_{\mathrm{m}}\frac{\mathrm{d}{m}_{\mathrm{u}}}{\mathrm{d}t}=m_{\infty }\left(u\right)-m_{\mathrm{u}},{\tau }_{\mathrm{h}}\frac{\mathrm{d}{h}_{\mathrm{u}}}{\mathrm{d}t}=h_{\infty }\left(u\right)-h_{\mathrm{u}}$$ (3)

where m _∞(u) = 1/(1 + exp(−(u – u _m)/k _m)) and h _∞(u) = 1/(1 + exp(−(u – u _h)/k _h)), with u _m,h, k _m,h and τ_m,h listed in Table 1. The total (i.e., Ca²⁺) current through the L‐VGCC was described by a modified Goldman–Hodgkin–Katz (GHK) relation (De Schutter & Smolen, 1998) in order to correctly account for the large Ca²⁺ concentration gradient between the cytosol ([Ca²⁺]_rest = 50 nm) and the exterior of the cell ([Ca²⁺]_ext = 2 mm) under basal conditions. It is given by:

$$\begin{array}{ccc}\hfill I_{\mathrm{L}-\mathrm{VGCC}}& =& 0.078q_{\mathrm{Ca}}{N}_{\mathrm{a}}{m}_{\mathrm{u}}^2{h}_{\mathrm{u}}{g}_{\mathrm{L}-\mathrm{VGCC}}u\hfill \\ & & \times \left(\frac{\mathrm{Ca}-\mathrm{C}{\mathrm{a}}_{\mathrm{ext}}{e}^{-0.078u}}{1-e^{-0.078u}}\right)\hfill \end{array}$$ (4)

where q _Ca is the electric charge per Ca²⁺ ion, N _a is the Avogadro number, and the conductance parameter g _L‐VGCC is set according to the value of g _N such that the peak L‐VGCC Ca²⁺ influx rate during a backpropagating action potential (bAP) is comparable to that mediated by NMDAR in response to a glutamate pulse (i.e., during an evoked postsynaptic potential; EPSP), consistent with individual spine measurements (Sabatini et al. 2002).

Calcium regulation

We assumed a basal steady‐state Ca²⁺ level of 50 nm in the spine head (Zador et al. 1990). The time course of the averaged, free (i.e. unbound) Ca²⁺ concentration during synaptic activity is described by the following equation:

$$\frac{\mathrm{d}}{\mathrm{d}t}\mathrm{Ca}=J_{\mathrm{N}}+J_{\mathrm{L}-\mathrm{VGCC}}+J_{\mathrm{ER}}+J_{\mathrm{B}}-J_{\mathrm{out}}$$ (5)

The terms J _ER represents the overall contribution of spine ER to Ca²⁺ activity (described in detail in the next two subsections), and was set to zero in the ER⁻ spine head, which in all other respects was identical to the ER⁺ spine. The Ca²⁺ influx through the NMDAR channel cluster, J _N, was also described by a GHK‐type current term, and as in previous studies, we have assumed that the Ca²⁺ current constitutes 10% of the total NMDAR current (De Schutter & Smolen, 1998; Graupner & Brunel, 2007):

$$\begin{array}{c}\hfill J_{\mathrm{N}}=0.078\frac{g_{\mathrm{N}}^{\mathrm{Ca}}B\left(u\right)u}{V_{\mathrm{spine}}}\left(\frac{\mathrm{Ca}-\mathrm{C}{\mathrm{a}}_{\mathrm{ext}}{e}^{-0.078u}}{1-e^{-0.078u}}\right)\left(\mu \mathrm{M}/\mathrm{s}\right)\end{array}$$ (6)

where $g_{\mathrm{N}}^{\mathrm{Ca}}=0.1$ (g_N/[Ca²⁺]_ext)(RT/4F ²), with R denoting the universal gas constant (8.314 J mol⁻¹ K⁻¹), F = 96485 C mol⁻¹ being the Faraday constant, and the temperature T set to 30°C.

The term J _B encapsulates the net effect of cytosolic buffers (Table 2). Calbindin D28‐k (CB) is a prominent fast‐binding mobile buffer in hippocampal neurons (Muller et al. 2005). The interaction of Ca²⁺ with CB is described by a detailed nine‐state kinetic scheme (Bartol et al. 2015) (Fig. 2 A). Each CB molecule carries two high‐affinity and two medium‐affinity binding sites for Ca²⁺. The total concentration of CB was taken to be 45 μm, as measured experimentally in CA1 pyramidal neurons (Muller et al. 2005). Besides CB, we included an endogenous ‘immobile’ Ca²⁺‐binding protein (CBP) with total concentration of 80 μm, as inferred previously from a spatial reaction–diffusion model of spine Ca²⁺ transients fit to single‐spine experimental data (Bartol et al. 2015). Its interaction with Ca²⁺ was described by a first‐order reversible reaction (Fig. 2 B). In addition, we included a slow buffer with a total concentration of 40 μm, the kinetic parameters for which were set 10 times slower than those for the immobile buffer (Naoki et al. 2005). We also included calmodulin (CaM) in our simulations. CaM is known to be present at a high concentration in CA1 dendritic spines (Faas et al. 2011). Due to the slower kinetics of its interaction with Ca²⁺ compared to CB, it has little impact during short Ca²⁺ transients (single synaptic events), but is expected to make a significant contribution to regulating free Ca²⁺ levels on longer time scales during persistent stimulation. We set the total CaM concentration to be 50 μm, which represents an average of several estimates found in the literature (Kakiuchi et al. 1982; Carafoli, 1987; Zador et al. 1990; Kubota & Waxham, 2010). We adopted a kinetic scheme used previously (Keller et al. 2008) to describe the reversible binding of CaM to Ca²⁺. Each CaM molecule comprises a high‐affinity C‐lobe and a low‐affinity N‐lobe, each of which can cooperatively bind up to two Ca²⁺ ions (Fig. 2 C).

Figure 2. Reaction kinetics for various chemical species in the model.

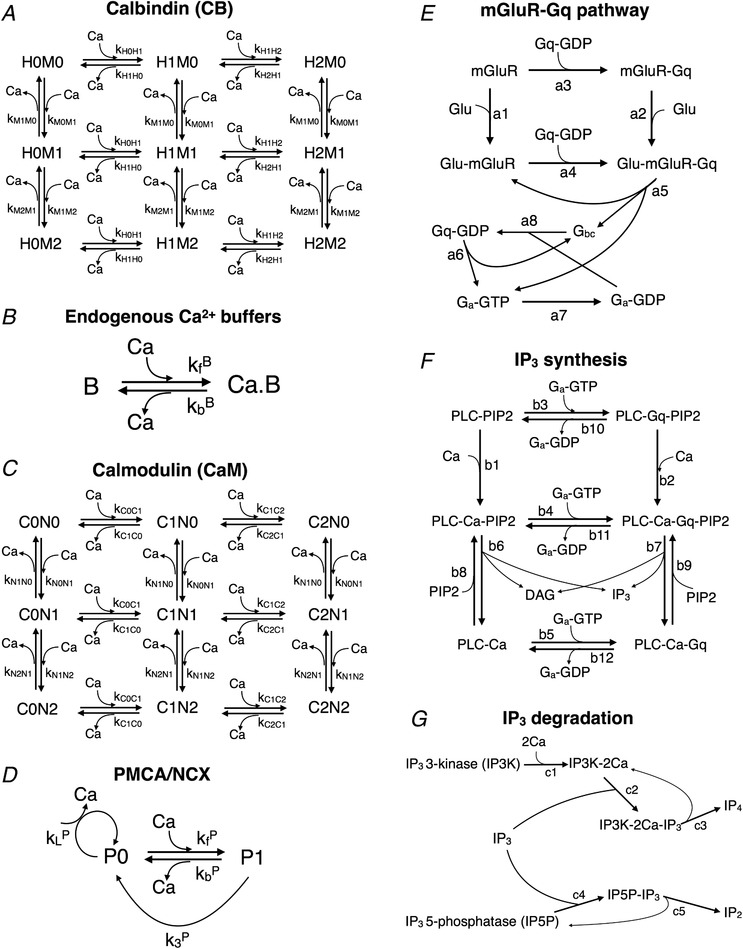
A, nine‐state kinetic scheme for Ca²⁺ interaction with calbindin (CB). Each CB molecule possesses two medium affinity (M) and two high affinity (H) Ca²⁺ binding sites. B, first‐order reversible reaction describing the action of endogenous immobile and slow Ca²⁺ buffers. C, reaction network for the interaction of Ca²⁺ with the N and C lobes of calmodulin (CaM). D, Michaelis–Menten kinetic scheme to describe the action of plasma membrane Ca²⁺ pumps (P = PMCA or NCX). E, biochemical model for G‐protein (Gq) activation by group I metabotropic glutamate receptor (mGluR). F, detailed model describing the G‐protein‐mediated activation of PLC and subsequent production of IP₃ and DAG via hydrolysis of PIP₂. G, reaction steps involved in the enzymatic degradation of IP₃ by IP₃ 3‐kinase (IP3K), which has Ca²⁺‐dependent activity, and IP₃ 5‐phosphatase (IP5P). (Note: several reaction steps in (E–G) are bidirectional (reversible), but have been represented as arrows in a single direction to avoid clutter. The full set of forward and backward kinetic rate constants is listed in Tables 2 and 3.)

In addition to the Ca²⁺ currents and buffers, the Ca²⁺ level in the cytosol is also regulated by efflux mechanisms operating at the plasma membrane (denoted by the J _out term in Eq. (5)), which set the time scale for the decay of Ca²⁺ transients in the spine head. We modelled efflux via plasma membrane Ca²⁺‐ATPase pumps (PMCA) and sodium–calcium exchangers (NCX), both of which were approximated by Michaelis–Menten‐like enzyme kinetics (Fig. 2 D). Surface densities and kinetic parameters for PMCA and NCX were adopted from a previous modelling study of CA1 spines (Bartol et al. 2015). In order to balance the extrusion of Ca²⁺ and ensure that Ca²⁺ in the cytosol can be maintained at a basal level of 50 nm in the absence of stimulation, the transporter equations also included leak terms ($k_{\mathrm{L}}^{\mathrm{PMCA}}$ and $k_{\mathrm{L}}^{\mathrm{NCX}}$), which were set so as to exactly balance the efflux rate per pump molecule when the intracellular Ca²⁺ is held at 50 nm (Table 2).

Model for IP₃‐ and Ca²⁺‐induced calcium release (ICCR) from spine ER store

The intracellular Ca²⁺ store associated with spine ER/spine apparatus is a potential additional source of Ca²⁺ elevation in the spine head during synaptic activation. We modelled Ca²⁺ release from the ER pool evoked by the activation of G protein‐coupled group 1 metabotropic glutamate receptors (mGluR) (assumed to be present on the postsynaptic membrane), subsequent production of the second messenger IP₃, and the downstream activation of IP₃ receptors on the ER membrane (Fig. 2 E–G). We have adapted a previously published kinetic description of mGluR activation leading to phospholipase Cβ (PLCβ)‐mediated hydrolysis of phosphatidylinositol 4,5‐bisphosphate (PIP₂) at cerebellar parallel fibre–Purkinje cell synapses (Doi et al. 2005), which itself borrows heavily from earlier models of metabotropic signalling proposed for generic mammalian neurons (Bhalla & Iyengar, 1999; Mishra & Bhalla, 2002). Glutamate uncaging at individual CA3–CA1 synapses (Holbro et al. 2009) indicates a delay of a few hundred milliseconds in Ca²⁺ release from the spine ER following the presentation of glutamate. A simpler (Hill function‐based) model for mGluR activation and IP₃ turnover is unable to reproduce this experimental delay, prompting us to use the detailed kinetic description, which provides more flexibility in tuning the time course of IP₃ production.

For the purpose of modelling mGluR–Gq activation, we simulated each glutamate pulse (synaptic input) as an α function with a time constant of τ_glu = 1 ms (glutamate is rapidly cleared from the synaptic cleft by the high density of glutamate transporters present on the surrounding astrocytic membrane; Bartol et al. 2015), and a peak concentration of 300 μm at the perisynaptically located mGluR (Doi et al. 2005) (scaled down from ∼1 mm at the PSD). We asked which of the parameters in the detailed mGluR–IP₃ model most affected the latency in IP₃ production. The IP₃ time course was found to be robust to variation in all except a combination of three parameters (a _1b, a _2b and b ₁₁), which were scaled down appropriately (a _1b and a _2b by a factor of 50 and b ₁₁ by a factor of 4) to introduce a few hundred milliseconds delay in the peak of the IP₃ response following the initial input. All other parameter values governing Gq‐mediated PLC activation and IP₃ turnover were taken to be the same as in the original study (Doi et al. 2005) (Table 3).

The gating of IP₃ receptors was modelled with a reduced kinetic scheme adopted from a previous computational study of ER Ca²⁺ dynamics in neuroblastoma cells (Fink et al. 2000). IP₃R activation was assumed to depend on the instantaneous levels of IP₃ and Ca²⁺, modelled by the activation variables m ₁ = [IP₃]/(d ₁ + [IP₃]) and m ₂ = [Ca²⁺]/(d ₅ + [Ca²⁺]), with half‐activation constants d ₁ = 0.8 μm (lower affinity compared to in vitro measurements; Bezprozvanny et al. 1991) and d ₅ = 0.3 μm. IP₃Rs are inactivated at higher calcium levels, which is accounted for by the slower kinetics of a third gating variable, h, given by the following equation:

$$\frac{\mathrm{d}h}{\mathrm{d}t}=a_2\left(K_{\mathrm{inh}}-\left(K_{\mathrm{inh}}+\mathrm{Ca}\right)h\right)$$ (7)

with the dissociation constant for inhibition, K _inh, set equal to 0.2 μm. The Ca²⁺ influx through the IP₃R‐gated channels is given by:

$$J_{\mathrm{ICCR}}=\alpha {\left(m_1{m}_{2}h\right)}^3{N}_{\mathrm{R}}\left(\frac{\mathrm{C}{\mathrm{a}}_{\mathrm{ER}}-\mathrm{Ca}}{N_{\mathrm{a}}{V}_{\mathrm{spine}}}\right)\left(\mu M/s\right)$$ (8)

where N _R is the cluster size of the IP₃R‐gated channels present in the spine head (estimated to be in the range of a few tens (Doi et al. 2005; Shuai et al. 2006; Ullah et al. 2012), and α sets the magnitude of the Ca²⁺ current through an open channel for unit concentration difference across the ER membrane. Single channel measurements suggest a type 3 IP₃R open channel current of ∼0.15 pA at a Ca²⁺ concentration difference of 0.5 mm (Vais et al. 2010). The Ca²⁺ concentration in the ER lumen was assumed to remain constant in our simulations, and we used a value of [Ca²⁺]_ER = 250 μm throughout, which represents an average of several estimates in the literature (Meldolesi & Pozzan, 1998; Solovyova et al. 2002; LaFerla, 2002).

The ER can also contribute to cytosolic Ca²⁺ efflux through the sarco‐endoplasmic reticulum ATPase (SERCA) transporters present on the ER surface, which maintain the steep concentration gradient (∼10³–10⁴) across the ER membrane. The SERCA activity was assumed to have a Hill‐type dependence on the cytosol Ca²⁺ level (Fink et al. 2000), and is given by F _S = V _S[Ca²⁺]²/([Ca²⁺]² + K _S ²), with the half‐activation constant K _S set to 0.2 μm (Yasuda et al. 2004). As with the plasma membrane efflux pumps, we introduced a compensatory leak term at the ER surface, k _S([Ca²⁺]_ER − [Ca²⁺]), where k _S is the SERCA leak rate, which balances the SERCA pump activity to help maintain a cytosolic [Ca²⁺] = 50 nm under resting conditions. The magnitude of maximum SERCA activity in the spine, V _S, depends on the density of SERCA molecules on the ER membrane, ER surface area in the spine head and pump efficiency per molecule. As no estimate appropriate for a spine‐sized region was readily available, we obtained an approximate estimate for V _S by referring to previous experimental measurements on ER refilling rates in rat sensory neurons (Solovyova et al. 2002; Usachev et al. 2006). The refilling time constant there was found to be about 1–5 min. By making reasonable assumptions about the total cell volume, ER volume fraction, SERCA surface density (∼2000 per μm²; Means et al. 2006), and spine ER area (assumed to be 10% of the spine head area; Spacek & Harris, 1997), we arrived at an estimate of V _S = 1 μm s⁻¹, which sets the scale for the contribution of SERCA activity to Ca²⁺ clearance in a typical ER⁺ spine head.

Modelling synaptic activation

Unitary synaptic input at the spine head was modelled as a single pulse of glutamate, which transiently binds to postsynaptic mGluR, and concurrently activates AMPAR/NMDAR currents as described above to produce a small (∼few millivolts) depolarization of the postsynaptic membrane. The amplitude of spine Ca²⁺ evoked by NMDAR current during an EPSP (ΔCa_EPSP) is considered to be in the range of a few hundred nM. For our control synapse (ER⁻ spine) we set the NMDAR conductance parameter g _N to 65 pS, which yields a ΔCa_EPSP = 0.2 μm, consistent with previous studies (Rackham et al. 2010; Kumar & Mehta, 2011). In order to assess the parameter dependence of our results, we also varied g _N to obtain a range of ΔCa_EPSP values (0.1–1 μm). The delay in Ca²⁺ release from the ER following the NMDAR‐mediated Ca²⁺ rise is measured with respect to the time of application of glutamate.

Induction of frequency‐dependent plasticity in ER⁻/ER⁺ spines was simulated with trains of regularly spaced synaptic inputs delivered over a range of different frequencies (0.1–20 Hz). In order to simulate the activation of Schaffer collateral (SC) fibres during the induction of LTP/LTD, we assumed that the local dendritic shaft (modelled as a passive compartment) receives synchronous input from multiple synapses (Zador et al. 1990; Schiegg et al. 1995), which amplifies the depolarization at the spine membrane through the passive resistive coupling (R _C), leading to stronger activation of the NMDAR current at the spine head. The parameter ρ_S, which sets the magnitude of the total number of co‐active synaptic inputs onto the dendritic compartment during SC stimulation, has been adjusted to evoke a depolarization of ∼15 mV at the spine head in response to a single input (Shouval et al. 2002). As the modest depolarization of the spine in this setting is insufficient for L‐VGCC activation, their contribution to the Ca²⁺ response was ignored for simplicity.

We also modelled the pairing of synaptic inputs with the strong depolarization of the postsynaptic membrane induced by backpropagating action potentials (bAPs) in the CA1 neuron, mimicking the conditions for the induction of spike timing‐dependent plasticity (STDP) (Wittenberg & Wang, 2006), which involves the activation of both the NMDAR and L‐VGCC. Dendritic bAPs were modelled as a voltage profile with a peak depolarization of V ₀ = 67 mV, and composed of a fast (τ_f = 3 ms) and a slow (τ_s = 40 ms) exponentially decaying components (Rackham et al. 2010; Kumar & Mehta, 2011):

$$V_{\mathrm{bAP}}\left(t\right)=V_0\theta \left(t\right)\left[0.7e^{-t/{\tau }_{\mathrm{f}}}+0.3e^{-t/{\tau }_{\mathrm{s}}}\right]$$ (9)

where θ(t) = 1 for t ≥ 0, and 0 otherwise, for a bAP arriving at t = 0. A bAP is simulated by feeding the above voltage profile to the dendritic compartment. During repetitive stimulation, each synaptic input is paired with either one or two bAPs (spike doublets/triplets). The timing difference between the pre‐ and postsynaptic firing, Δt, is measured as the interval between the start of the glutamate pulse and peak of the bAP at the dendritic compartment. When a synaptic input is paired with a postsynaptic burst composed of two bAPs (spike triplet), Δt is defined as the interval between the glutamate pulse and the peak of the second bAP; bAPs in a burst are separated by a fixed interval of 10 ms. By convention, glutamate release preceding the bAP is assigned a positive Δt.

Ca²⁺‐based plasticity model

Induction of long‐term modification at hippocampal/cortical synapses is governed by the magnitude and duration of local Ca²⁺ elevation at the dendritic spine (Malenka et al. 1992; Dudek & Bear, 1992; Yang et al. 1999). We adopted a previously proposed model for bidirectional plasticity (Shouval et al. 2002) to describe the induction of both rate and spike timing‐dependent synaptic efficacy changes at the ER‐bearing spine (Fig. 1 D). The model describes the dynamics of a (dimensionless) weight variable, w (a proxy for the postsynaptic AMPAR conductance), and its functional form approximates biophysically plausible descriptions of the regulation of AMPAR number and/or phosphorylation level by a combination of Ca²⁺‐activated kinases and phosphatases (Castellani et al. 2001, 2005). Following some earlier studies (Zador et al. 1990; Naoki et al. 2005; Faas et al. 2011), we modelled the dependence of w on the concentration of active calmodulin (aCaM) instead of the free Ca²⁺. Ca²⁺‐bound CaM is known to regulate the activation of several downstream effectors such as Ca²⁺/CaM‐dependent protein kinase II (CaMKII) (Pepke et al. 2010), PP2B/calcineurin (Kennedy, 2016) and protein kinase A (Chetkovich & Sweatt, 1993; Wang & Storm, 2003), which converge to mediate synaptic changes underlying early LTP/LTD expression (Barria et al. 1997; Derkach et al. 1999; Lee et al. 2000; Esteban et al. 2003). Although earlier models assumed that only the fully activated form of CaM (bound to 4 Ca²⁺ molecules) is relevant, recent studies indicate that even the partially bound forms are capable of regulatory activity (e.g. activation of CaMKII (Pepke et al. 2010)); thus, as a measure of CaM activity, we considered the total Ca²⁺‐bound CaM in the spine (aCaM). The dynamic range of aCaM is restricted by the availability of total CaM in the spine, unlike the Ca²⁺ response, which is not bounded and in principle can grow very large during persistent high‐frequency stimulation. The dynamical equation governing the Ca²⁺ dependence of w is given by

$${\tau }_{\mathrm{w}}\left(\left[\mathrm{aCaM}\right]\right)\frac{\mathrm{d}w}{\mathrm{d}t}=-w+{\mathrm{\Omega }}_{\mathrm{w}}\left(\left[\mathrm{aCaM}\right]\right)$$ (10)

where the function Ω_w is modelled as the difference between two sigmoid functions (Shouval et al. 2002):

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_{\mathrm{w}}\left(\left[\mathrm{aCaM}\right]\right)& =& \frac{1}{1+e^{-{\beta }_{\mathrm{P}}\left(\left[\mathrm{aCaM}\right]-{\theta }_{\mathrm{P}}\right)}}\hfill \\ & & -\frac{0.5}{1+e^{-{\beta }_{\mathrm{D}}\left(\left[\mathrm{aCaM}\right]-{\theta }_{\mathrm{D}}\right)}}\hfill \end{array}$$ (11)

with slopes β_D = 60 μm ⁻¹ and β_P = 60 μm ⁻¹. The offsets θ_P and θ_D (θ_P > θ_D) control the thresholds for the induction of LTP/LTD during synaptic stimulation: no plasticity is induced when aCaM levels remain below θ_D, LTD is induced when aCaM is restricted by and large to the interval (θ_D,θ_P), and LTP induction requires higher levels of aCaM, exceeding the threshold θ_P. The temporal factor τ_w is given by:

$${\tau }_{\mathrm{w}}\left(\left[\mathrm{aCaM}\right]\right)=1+\frac{10}{0.001+{\left({\displaystyle \frac{2\left[\mathrm{aCaM}\right]}{{\theta }_{\mathrm{D}}+{\theta }_{\mathrm{P}}}}\right)}^2}$$ (12)

and its parameters have been set in accordance with experimentally suggested rates for the induction of early LTP (∼seconds) and LTD (∼minutes) and the persistence of synaptic weight changes under resting conditions (∼1–3 h) (Shouval et al. 2002).

Rate‐dependent plasticity was simulated over the 0.1–20 Hz frequency range (in steps of 0.1 Hz) with 900 presynaptic SC inputs applied at each frequency, following earlier studies (Dudek & Bear, 1992; Shouval et al. 2002; Narayanan & Johnston, 2010). STDP induction was mimicked with a train of 100 pairings of pre/postsynaptic spiking presented at 5 Hz (Wittenberg & Wang, 2006), with the spike timing difference Δt varied from −100 ms and 100 ms in steps of 1 ms. The weight variable w (initialized to 0 in all our simulations) integrates over the temporal spine Ca²⁺ signal evoked by these synaptic activation patterns, resulting in a net (cumulative) change Δw at the end of the stimulation period. Spine ER was assumed to contribute to the Ca²⁺ pool in the spine driving changes in w, thereby modulating the induction of NMDAR‐dependent plasticity and giving rise to possible differences in Δw relative to the reference ER⁻ spine. We characterized the nature of this differential effect of spine ER, ΔΔw, as a function of various biophysical model parameters. The plasticity profile obtained in our model synapse is shaped by the choice of θ_P/θ_D (assumed to be same for the ER⁺ and ER⁻ spines), which were appropriately set to have agreement with experimentally obtained plasticity curves. For the rate‐dependent plasticity, θ_P was adjusted such that LTP induction occurs for frequencies ≳15 Hz in the ER⁻ spine head (Dudek & Bear, 1992; Narayanan & Johnston, 2010) (although it represents an average obtained from a large number of synapses, we assigned this threshold to every individual synapse); we also examined the robustness of our results to variation in this parameter (f _P = 10–20 Hz). Different choices of the LTD threshold (θ_D) for the ER⁻ spine have been similarly explored (f _D = 1–6 Hz). In the case of STDP, we referred to a previous experimental study (Wittenberg & Wang, 2006) which reports the average plasticity curve obtained from measurements at a population of CA3–CA1 synapses; here, again, we assigned the plasticity thresholds Δt _D/Δt _P read off from the average curve to our reference synapse associated with an ER⁻ spine (implicitly assuming that only a minor proportion of the synapses recorded from are associated with an ER). We also followed this up by examining the sensitivity of the results to variation in Δt _D and Δt _P over ±10 ms windows.

All numerical simulations and analysis comprising this study were carried out in Python 2.7 using NumPy, SciPy and Matplotlib modules. Python code for running the model simulations is available at GitHub (https://github.com/gmcoderepo/ca1-spine-with-er).

Results

A calibrated kinetic model for mGluR–IP₃ receptor signalling recapitulates salient features of experimental data on Ca²⁺ release from ER in dendritic spines

We considered an average CA1 pyramidal neuron dendritic spine head containing ER (an ER⁺ spine), described by a single‐compartment point model (Methods). The time course of spine Ca²⁺ evoked by synaptic activation is shaped by the coupled electrical and Ca²⁺ dynamics at the spine head, which involves contributions from various biophysical components, and passive electrical coupling with a dendritic compartment (Fig. 1 A–C). The spine ER store, modelled as an intracellular Ca²⁺ pool (fixed luminal concentration of 250 μm), contributes through IP₃ receptor‐gated Ca²⁺ release (IP₃‐ and Ca²⁺‐induced Ca²⁺ release; ICCR) and the uptake of cytosolic Ca²⁺ by SERCA pumps present on the ER membrane.

In order to have a model of mGluR–IP₃ signalling and ICCR that is appropriate for describing hippocampal synapses, we referred to Ca²⁺ imaging data from a previous experimental study of long‐term depression at individual excitatory CA3–CA1 connections (Holbro et al. 2009). Flash photolysis of caged glutamate was reported to evoke mGluR‐ and IP₃‐dependent store Ca²⁺ release which was specific to ER⁺ spines, and trailed the initial NMDAR‐mediated spine Ca²⁺ transient (trial‐averaged delay of ∼470 ms). We adopted a detailed kinetic scheme (Doi et al. 2005) to describe the sequence of biochemical events linking the initial binding of glutamate to postsynaptic Gq‐coupled receptors (expressed on the extrajunctional membrane) to the eventual synthesis of IP₃ and DAG via PIP₂ hydrolysis mediated by activated PLCβ (Methods). We tuned the parameters regulating IP₃ production rate in this model (Table 3) to reproduce the empirical estimate for the timing of the second Ca²⁺ peak relative to the arrival of glutamate (we chose parameters such that for a synapse with N _R = 30 IP₃ receptors and ΔCa_EPSP ∼0.2 μm, the second Ca²⁺ peak occurs with a delay of t ≈ 480 ms). Figure 3 A and B shows the simulated Ca²⁺ response to application of a single pulse of glutamate at t = 0 in our model spine head with ER (coloured curves), which is compared with the reference ER⁻ spine (black curve). The latency as well as magnitude of Ca²⁺ release from ER is dependent on the number of IP₃ receptors present. Although Ca²⁺ at low levels (≲0.3 μm) is a coagonist for IP₃R activation (Finch et al. 1991), release of ER store Ca²⁺ in our calibrated model does not require the initial NMDAR‐mediated Ca²⁺ transient (Fig. 3 C), which, again, is consistent with experimental findings (Holbro et al. 2009).

Figure 3. Glutamate evokes delayed release of Ca²⁺ from dendritic spine ER via mGluR signalling and IP₃R activation.

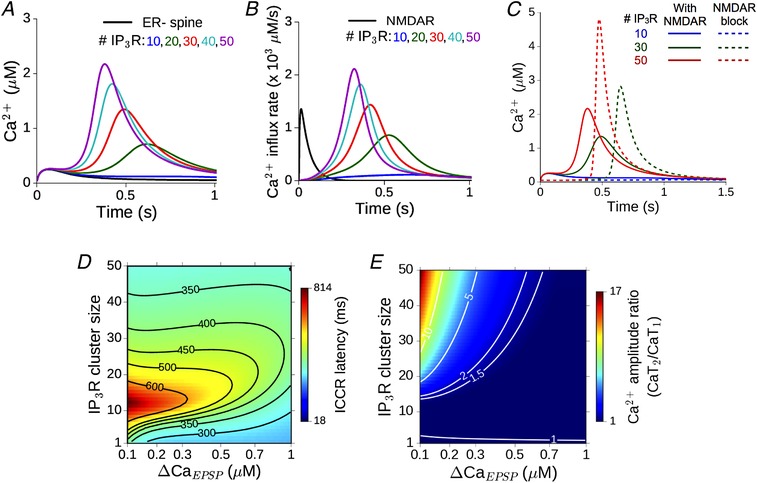
A, response of the reference ER⁻ spine (black) to a single glutamate input is compared with the Ca²⁺ time course in ER⁺ spines with 10–50 IP₃ receptors (coloured curves). The peak of the NMDAR‐mediated Ca²⁺ rise is ΔCa_EPSP = 0.2 μm. B, the underlying Ca²⁺ flux through NMDAR channels (black) and the delayed, temporally restricted flux through IP₃R channels (coloured curves). C, comparison between delayed Ca²⁺ release from ER in the presence of NMDAR (continuous curves) and with NMDAR blocked (dashed curves) for different IP₃R numbers. D, dependence of the delay in ICCR in the ER⁺ spine on the number of IP₃ receptors and amplitude of the initial NMDAR‐evoked Ca²⁺ (ΔCa_EPSP). The horizontal axis is linear in the NMDAR conductance parameter g _N, but parameterized by Ca²⁺ for ease of interpretation; contours correspond to various values of the latency. E, dependence of ratio of the second to the first Ca²⁺ peak (illustrated in A) on the number of IP₃ receptors and ΔCa_EPSP. Contours shown for different values of the amplitude ratio. [Color figure can be viewed at wileyonlinelibrary.com]

The amplitude of the synaptically evoked Ca²⁺ (a direct readout for the NMDAR conductance) and the IP₃ receptor cluster size directly determine the Ca²⁺ signal in the spine. Changes in the ICCR profile in our calibrated model corresponding to changes in these crucial components are summarized as heat maps in Fig. 3 D and E. These represent the dependence of the delay of ICCR (in ms) and the amplitude of the second Ca²⁺ peak relative to the first, respectively, over a biologically realistic range of parameter values. These parameter ranges yield a fairly broad distribution of possible outcomes, and for a small subset of parameter choices, the outcomes are consistent with the averaged experimental estimates (Holbro et al. 2009) (latencies of ∼400–500 ms and a second‐to‐first Ca²⁺ peak ratio of 1–5). Notably, the delay in synaptically evoked release of store Ca²⁺ has a non‐monotonic dependence on the IP₃R cluster size: for a fixed ΔCa_EPSP, the delay first increases, and then decreases with increasing number of IP₃Rs. This dependence may be understood by noting that the IP₃R cluster size sets the strength of the Ca²⁺‐dependent positive feedback loop driving IP₃R activation in the presence of sufficient IP₃. For higher IP₃R numbers, this feedback can drive a self‐sustained burst of Ca²⁺ release from ER. The larger the cluster size, the more swiftly ICCR increases, while also speeding up the suppression of the slower Ca²⁺‐dependent inactivation variable h, which eventually shuts off the IP₃R channel flux. Thus, the temporal profile of the ICCR transient is expected to advance (i.e. follow with a shorter lag) with increasing IP₃R number. At small cluster sizes, on the other hand, the flux through IP₃Rs is inadequate to drive a burst of ICCR even while IP₃ is present. In this regime, there is no discernible second Ca²⁺ peak (e.g. the blue curve corresponding to 10 IP₃Rs in Fig. 3 A), and the kinetics of the IP₃R open fraction (i.e. the ICCR peak location) in this case is primarily shaped by the decaying NMDAR Ca²⁺ transient. The relatively minor contribution of ICCR only adds a small delay to this decay of the total spine Ca²⁺. This additional delay is proportional to the IP₃R number, N _R, thus accounting for the shift of the peak location of IP₃R influx to longer latencies with increasing N _R in the regime of small IP₃R numbers.

mGluR‐mediated Ca²⁺ release from ER can facilitate the induction of synaptic depression with weak stimulation

We next simulated the calcium response in an ER⁺ spine head during the induction of synaptic weakening by low frequency afferent stimulation of the CA3–CA1 pathway. Figure 4 A shows an example of the Ca²⁺ time course evoked by a 1 Hz train of regularly spaced glutamate pulses. Binding of glutamate to postsynaptic AMPARs produces a small depolarization at the spine head (∼few millivolts), resulting in weak NMDAR activation and modest Ca²⁺ entry. Due to little overlap of successive Ca²⁺ events at low input rates, there is no build‐up of Ca²⁺ concentration in the spine over time. Figure 4 A compares the Ca²⁺ signal in the ER⁻ control spine (black curve) with the responses in the ER⁺ spine (coloured curves correspond to different numbers of IP₃R). mGluR‐mediated Ca²⁺ release from spine ER contributes to the common pool of Ca²⁺ in the spine head and augments the NMDAR‐mediated Ca²⁺ signal.

Figure 4. Ca²⁺ release from ER robustly enhances the spine Ca²⁺ signal and facilitates LTD induction at low input rates.

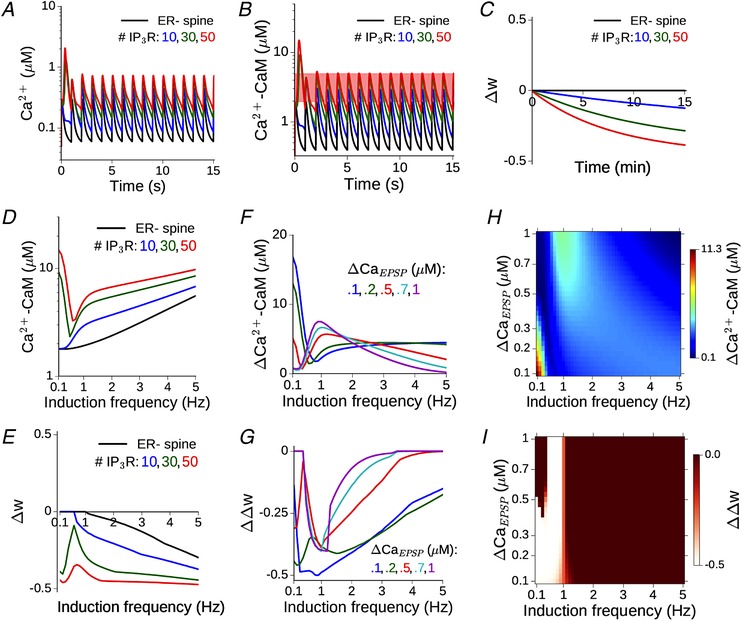
A, time course of Ca²⁺ evoked by repeated synaptic input at 1 Hz in the model ER⁻ spine (black) and an equivalent ER⁺ spine with 10–50 IP₃ receptors. ΔCa_EPSP = 0.2 μM in the ER⁻ spine. B, the corresponding time dependence of Ca²⁺‐bound calmodulin (CaM) in the ER⁻/ER⁺ spine head. Total CaM concentration = 50 μM. C, change in the synaptic weight variable, w, driven by the activated CaM during a 1 Hz input train applied for 15 min (900 spikes). For this specific instantiation of the model, the plasticity threshold θ_D has been set to 2 μM, such that no LTD is induced in the absence of ER contribution, and LTD induction is facilitated with increasing flux through IP₃Rs. D, the amplitude of CaM response to synaptic inputs in the 0.1–5 Hz range is compared between the ER⁻ spine (black) and equivalent ER⁺ spine with 10–50 IP₃ receptors (coloured curves). E, change in the weight variable w at the end of 900 spikes in the ER⁻ (black) and ER⁺ spines (coloured curves), corresponding to D. θ_D is set to give no LTD in the ER⁻ spine for frequencies ≲ 1 Hz. F, the differential CaM response profile in an ER⁺ spine with 30 IP₃Rs relative to the ER⁻ spine for different choices of ΔCa_EPSP (i.e. NMDAR conductance). G, differential LTD induction, ΔΔw, in an ER⁺ spine with 30 IP₃Rs relative to an ER⁻ spine for different choices of ΔCa_EPSP. H, change in maximum CaM activation due to the presence of ER (30 IP₃Rs) as a function of the NMDAR conductance and a range of low induction frequencies. I, difference in synaptic weight change between the ER⁺ and ER⁻ spine, as a function of the NMDAR conductance and induction frequency. Lighter colours indicate enhanced LTD response in the presence of ICCR. [Color figure can be viewed at wileyonlinelibrary.com]

In order to map the Ca²⁺ time course to plasticity, we followed the activation of calmodulin (CaM), which is included in our model and makes a significant contribution to the Ca²⁺ buffering capacity in the spine. Ca²⁺‐bound CaM is known to regulate a number of downstream signalling molecules that collectively determine changes in synaptic strength associated with early LTP/LTD; thus, it provides a suitable choice of input to the dynamical model governing the synaptic weight w (Methods and Fig. 1 D). The parameter θ_D in Eq. (11) decides the Ca²⁺–CaM threshold for LTD induction. For the example in Fig. 4 B, a range of θ_D choices is possible (indicated by the red band running parallel to the time axis) such that LTD can be induced at the ER⁺ spine, whereas the synaptic strength associated with the ER⁻ spine remains unaffected. This is illustrated in Fig. 4 C by a comparison between the time courses of w(t) in the ER⁻ and ER⁺ spines over 900 SC inputs for the specific choice of θ_D = 2 μm. The elevated Ca²⁺–CaM response in the ER⁺ spines (coloured curves) drives a slow induction of synaptic depression (Δw<0) with repeated stimulation, which is absent in the ER⁻ spine (black curve). This particular instantiation of our model thus recapitulates experimental observations regarding the association of mGluR‐mediated store Ca²⁺ release with LTD induction at low stimulation rates (Reyes & Stanton, 1996; Oh et al. 2013).

In order to address the dependence of the results on the model parameters, we repeated our simulations across a range of synaptic input frequencies (0.1–5 Hz) and synaptically evoked spine Ca²⁺ amplitudes (ΔCa_EPSP = 0.1–1 μm). Figure 4 D shows the dependence of the maximum steady‐state amplitude of active CaM during persistent stimulation on the input frequency. The corresponding total change in the weight variable (Δw) at the end of the stimulus train is shown in Fig. 4 E (f _D is fixed at 1 Hz). ICCR robustly enhances CaM activation to facilitate LTD induction over a range of low frequencies, although the contribution of ICCR is non‐monotonic in the input rate. This dependence may be accounted for by noting that the opening of IP₃R is regulated by a combination of two factors: the Ca²⁺‐ and IP₃‐dependent activation, and the level of inhibition (h). At low input rates (≲2 Hz), the IP₃ level increases with the frequency of glutamate application. At the same time, the slowly changing h variable has less time to recover between successive inputs, the more frequently the inputs arrive; therefore, h decreases with increasing input frequency. The balance between these two competing factors (IP₃‐mediated activation and inactivation mediated by h) shapes the overall profile of the IP₃R open probability, and hence the IP₃R Ca²⁺ flux, as a function of the frequency of glutamate input.

Figure 4 F and G compare the responses before and following spine ER acquisition over a range of low frequencies for different choices of the NMDAR conductance parameter (ΔCa_EPSP), with a fixed number of IP₃Rs (N _R = 30). The profiles of the excess CaM activation (Fig. 4 F) and differential plasticity outcome (Fig. 4 G) in the presence of spine ER depend on the amplitude of synaptically evoked Ca²⁺. However, in general, ICCR contribution enhances LTD induction over a range of low‐frequency inputs.

Elaborating on the above results, the heat maps in Fig. 4 H and I summarize the dependence of the maximal Ca²⁺–CaM response and plasticity output in the ER⁺ spine, relative to the ER⁻ reference spine, on the input frequency and NMDAR Ca²⁺ conductance. The vertical axes in both figures are linear in the NMDAR conductance parameter g _N; however, to aid interpretation, they have been parametrized in terms of the NMDAR Ca²⁺ amplitude instead. As before, the frequency threshold for LTD induction is set to f _D = 1 Hz, and all results are for an IP₃R cluster size of N _R = 30. ICCR is found to robustly enhance NMDAR‐driven LTD induction at lower frequencies (f ≲ 1 Hz). The underlying CaM activation in our model exhibits complex dependence on the input rate and ΔCa_EPSP (Fig. 4 H): the excess CaM response in the ER⁺ spine decreases with increasing ΔCa_EPSP at very low input frequencies (f ≲ 0.5 Hz), but this trend reverses at higher frequencies (f ∼ 1–2 Hz).

To see why this difference arises, we first considered the case of very low frequencies (f ≲ 0.5 Hz). Due to the delayed synthesis of IP₃, the initial NMDAR Ca²⁺ elevation only contributes to ICCR by changing the slower inactivation variable h (and not through the activation variable m ₁), which decreases with increasing ΔCa_EPSP. The level of h determines the magnitude of the subsequent ICCR (i.e. the amplitude of the second Ca²⁺ peak), and as h gets smaller with increasing ΔCa_EPSP, so does the maximal IP₃R Ca²⁺ flux (Fig. 4 H). At higher frequencies (∼1–2 Hz), on the other hand, there is insufficient time between one input and the next for IP₃ to decay back to resting levels. As IP₃ is now present at moderate levels when a glutamate input arrives, the NMDAR‐mediated ΔCa_EPSP switches its role: now it directly controls the activation of IP₃Rs (through the instantaneous activation variable m ₁), while the slowly evolving h(t) only has a delayed effect on the IP₃R open probability. Due to this switch in its role from inactivation to activation at higher input rates, an increase in g _N (i.e., ΔCa_EPSP) is now associated with increased IP₃R flux (Fig. 4 H). This explains the increase of ICCR with the NMDAR conductance. In sum, our results demonstrate that store Ca²⁺ contribution regulated by mGluR–IP₃ signalling at a realistic synapse can robustly augment the NMDAR‐mediated Ca²⁺ response to weak synaptic stimulation, providing a basis to understand compromised hippocampal LTD associated with blocking of ER Ca²⁺ stores.

The contribution of ICCR to spine Ca²⁺ dynamics is regulated by NMDAR activation and depends on the rate of synaptic stimulation

Our experimentally constrained model of mGluR–IP₃ signalling indicates that spine ER can make a substantial contribution to the Ca²⁺ response evoked by weak synaptic inputs. Next, we examined the input frequency dependence of the ER contribution to spine Ca²⁺ dynamics during persistent synaptic activation. Higher input rates are associated with stronger NMDAR activation and greater build‐up of Ca²⁺ in the spine head, leading to a switch from LTD to LTP induction above some crossover frequency f _P. We wished to address how the rate‐dependent bidirectional plasticity profile seen in the SC pathway (Dudek & Bear, 1992) is modulated by localized Ca²⁺ release from spine ER.

Gating of IP₃R in the spine can be regulated by the level of synaptic activation. This is summarized in Fig. 5 A, which shows the steady‐state open probability (P _open) of the IP₃R as a joint function of glutamate and spine Ca²⁺ concentration. Increasing the level of glutamate stimulation (e.g. in the context of rate‐based plasticity) has a direct effect on IP₃ synthesis via mGluR–PLCβ activation. At the same time, it also drives increased postsynaptic NMDAR activation. The resulting elevation of spine Ca²⁺ level can affect both the production (via the mGluR pathway) and degradation (via the Ca²⁺ dependence of IP3K activity) of IP₃, besides directly controlling P _open through the m ₁ and h variables (Methods). The broad strokes of this non‐linear dependence on glutamate and Ca²⁺ can be captured by the asymptotic steady‐state response of the IP₃R over a range of (constant) glutamate and Ca²⁺ levels (Fig. 5 A). IP₃R shows maximal activation for a Ca²⁺ concentration of ∼0.3 μm over a range of realistic glutamate levels, and is progressively inhibited with increasing Ca²⁺. Thus, in an ER⁺ spine, the contribution of ICCR is anticipated to diminish progressively with increasing NMDAR activation for a fixed glutamate signal (as in the case of STDP induction protocol). Given the weak dependence of P _open on the glutamate level as suggested by Fig. 5 A, we can also anticipate a similar graded contribution of ICCR with increasing NMDAR‐mediated Ca²⁺ elevation in the context of rate‐dependent plasticity. The interplay between NMDAR‐mediated Ca²⁺ entry, mGluR signalling and IP₃R gating suggested by the above picture is characterized in detail in our synaptic model with realistic parameter settings.

Figure 5. Augmented Ca²⁺–CaM response in a spine head in the presence of ER depends on the synaptic input rate and is suppressed at higher frequencies.

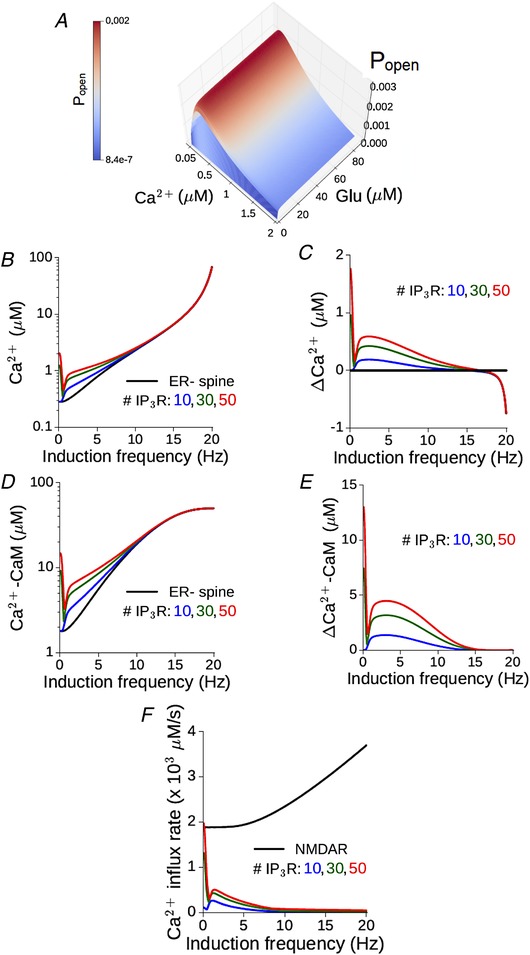
A, the steady state open probability of an IP₃ receptor (P _open) as a function of (constant) glutamate and Ca²⁺ concentrations. B, maximum Ca²⁺ level attained during persistent stimulation at different frequencies in the reference ER⁻ spine (black) and equivalent ER⁺ spine with different numbers of IP₃Rs (coloured curves). C, non‐monotonic dependence of the differential Ca²⁺ responses in the ER⁺ spine on the input rate. D and E, the corresponding results for CaM activation as a function of the input rate. F, the maximum calcium influx rate through NMDA receptors (black) and different numbers of IP₃ receptors (coloured curves) in an ER⁺ spine plotted against the input rate. (All results for the model synapse with peak NMDAR‐mediated Ca²⁺ response ΔCa_EPSP = 0.2 μM.) [Color figure can be viewed at wileyonlinelibrary.com]

We simulated a standard protocol consisting of repeated presynaptic stimulation (900 spikes) of the SC–CA1 pathway at different rates (0.1–20 Hz in steps of 0.1 Hz) (Methods). Figure 5 B compares the frequency–response profile of spine Ca²⁺ elevation (the maximum amplitude attained during the steady state) in the reference ER⁻ spine (black) with the ER⁺ spine for different numbers of IP₃Rs (coloured curves). ICCR enhances the Ca²⁺ responses at lower frequencies, and its contribution steadily diminishes with increasing frequency above f ≈ 5 Hz; this is also highlighted by the profile of the excess Ca²⁺ amplitude in the ER⁺ spine relative to the ER⁻ spine, shown in Fig. 5 C. Similar dependence on the input rate is also observed for the activation of CaM in the ER⁻ and ER⁺ spines (Fig. 5 D and E). The dip in the differential Ca²⁺ signal below zero at higher frequencies (Fig. 5 C) is due to SERCA pump activity in the ER⁺ (but not the ER⁻) spine, which contributes to the extrusion of cytosolic Ca²⁺ and leads to a net lowering of the Ca²⁺ levels in the presence of ER. The action of SERCA Ca²⁺ efflux is revealed only at higher frequencies when ICCR in the spine is suppressed by the Ca²⁺‐dependent inactivation of IP₃R. The inverse dependence of the ER Ca²⁺ contribution on the level of NMDAR activation is also highlighted by a direct comparison between the NMDAR and IP₃R Ca²⁺ current profiles in the ER⁺ spine, which are shown in Fig. 5 F.

Spine Ca²⁺ elevation drives a change in the synaptic weight variable w (Eq. (10)). This is illustrated for the ER⁻ (control) spine in Fig. 6 A, which shows the temporal profile of Ca²⁺–CaM (Fig. 4 A, top) and the corresponding evolution of the w variable (Fig. 6 A, bottom) over 900 spikes at two different input rates, 5 and 17 Hz, associated with LTD and LTP, respectively. (The plasticity thresholds have been adjusted to have f _D = 1 Hz and f _P = 15 Hz at the ER⁻ spine.) The differential effect of ER is displayed separately for the 5 Hz (Fig. 6 B) and 17 Hz (Fig. 6 C) examples. At 5 Hz, ICCR makes an appreciable contribution to the spine Ca²⁺ elevation, and thus to the rate and amplitude of the resulting synaptic changes, with a larger number of IP₃Rs associated with stronger synaptic depression (Fig. 6 B, bottom). In contrast, at 17 Hz, due to the strong suppression of ICCR by the NMDAR‐driven persistent Ca²⁺ elevation, there is little difference in the response in the ER⁻ and ER⁺ spines (Fig. 6 C), resulting in nearly the same plasticity outcome (strong potentiation) at the end of the stimulation (Fig. 6 C, bottom).

Figure 6. Graded contribution of ICCR to spine Ca²⁺ modulates the rate‐dependent bidirectional plasticity profile.

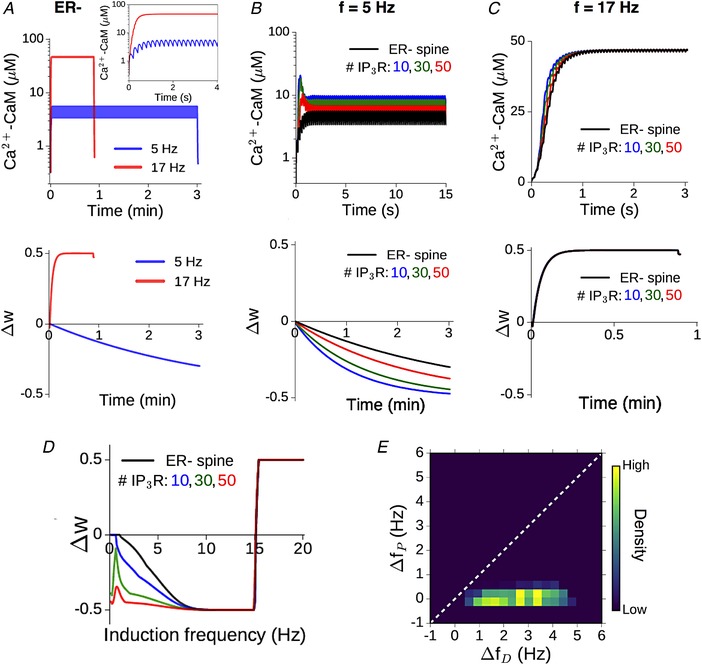
A, illustration of the CaM response (top) and plasticity induction (bottom) at the reference ER⁻ spine for 900 presynaptic spikes applied at two different rates, 5 (blue) and 17 (red) Hz. Inset shows a magnified view of the first 4 s of the Ca²⁺–CaM time course. Plasticity parameters have been adjusted to yield LTD and LTP thresholds f _D = 1 Hz and f _P = 15 Hz, respectively. B, enhancement of NMDAR‐mediated CaM activation (top) and LTD induction (bottom) at 5 Hz stimulation due to ER Ca²⁺ contribution for different IP₃R cluster sizes. C, time course of CaM activation (top) and potentiation (bottom) at 17 Hz stimulation in the ER⁻ spine (black) and ER⁺ spine for different IP₃R cluster sizes (coloured curves). Due to the suppression of ICCR at higher frequencies, the presence of ER makes little difference in this case. In B and C, only the initial phase of the (much longer) Ca²⁺–CaM time course is shown for clarity. D, dependence of the total weight change (Δw) induced by prolonged stimulation (900 spikes) on the synaptic input rate at the ER⁻ spine (black) and corresponding ER⁺ spine for different IP₃R numbers (coloured curves); f _D = 1 Hz and f _P = 15 Hz. Plasticity is enhanced in the ER⁺ spine at low frequencies, with diminished modulation at higher (LTP‐inducing) rates. E, graded contribution of ICCR to the modulation of plasticity is quantified in terms of the relative shifts in the LTD/LTP thresholds in the ER⁺ spine (relative to the ER⁻ control spine). The heat map is a distribution of Δf _D/Δf _P values obtained by random sampling (5000 times) of the plasticity thresholds f _D and f _P (over 1–6 Hz and 10–20 Hz, respectively), and IP₃R number (10–50). (All results for a synapse with NMDAR‐mediated ΔCa_EPSP = 0.2 μM.) [Color figure can be viewed at wileyonlinelibrary.com]

We quantified the induced plasticity profile across the full range of synaptic input rates (0.1–20 Hz), which is shown in Fig. 6 D. The total synaptic weight change (Δw) at the end of the stimulus train is plotted as a function of the input rate f for the reference ER⁻ spine (black) and following ER acquisition for different numbers of IP₃Rs (coloured curves). Consistent with our expectation from Fig. 5 A, we found that ICCR enhances plasticity at lower input frequencies, leading to a broadening of the effective LTD window. Due to the Ca²⁺‐dependent suppression of ICCR at higher frequencies, the profiles of Δw for synapses associated with the ER⁻ and ER⁺ spines are near‐identical above f ≈ 10 Hz.

The differential modulation of LTD and LTP suggested by the above results for our model synapse (ΔCa_EPSP = 0.2 μm) is characterized in terms of the relative broadening of the depression and potentiation windows. A simple way to capture the overall modulation of the plasticity curve is by estimating changes in the threshold frequency for LTD induction (Δf _D) and LTP induction (Δf _P) with the inclusion of ER, relative to the ER⁻ spine. The plasticity thresholds for the ER⁻ spine (f _D and f _P) were repeatedly sampled at random from 1–6 Hz for f _D and 10–20 Hz for f _P to account for experimental uncertainties in these estimates, as well as to as assess the variability in the model output. The resulting distribution of (Δf _D, Δf _P) values (aggregate of 5000 runs over 10–50 IP₃Rs) is visualized as a heat map in Fig. 6 E, and on the whole, it suggests selective enhancement of LTD induction in the presence of ER. In summary, our analysis of the model spine head suggests a graded, frequency‐dependent contribution of ER to spine Ca²⁺ signalling and plasticity, with steadily diminishing contribution of ICCR at higher input frequencies.

Ca²⁺ release from the IP₃‐sensitive ER store selectively enhances synaptic depression during spike timing‐dependent plasticity

We next examined the involvement of ER in spine Ca²⁺ dynamics during trains of pre‐ and postsynaptic action potentials (APs), which simulate the conditions for induction of timing‐ dependent synaptic plasticity (Markram et al. 1997; Nishiyama et al. 2000). In the context of hippocampal CA3–CA1 synapses, pairing of every presynaptic spike with one bAP at theta frequency (5 Hz) was found to induce only synaptic weakening, and LTP induction requires repeated pairing of glutamate release with AP bursts (two bAPs) in the postsynaptic neuron (Wittenberg & Wang, 2006; Tigaret et al. 2016). We made use of these experimental data on STDP, specific to the CA3–CA1 synapse, to constrain our model for spine Ca²⁺ signalling, and examined the contribution of ICCR during this form of plasticity.

We simulated the Ca²⁺ dynamics in our synaptic model during a sequence of pre‐ and postsynaptic spikes. Every glutamate input is separately paired with either one bAP (spike doublets) or two bAPs (spike triplets), and these paired stimuli are presented 100 times at a fixed rate of 5 Hz (Methods). Figure 7 A illustrates the time course of Ca²⁺–CaM (top) and the corresponding change in the synaptic weight (bottom) in the ER⁻ (control) spine head during the triplet stimulation, for three different choices of the pre‐post spike timing difference, Δt. By appropriately adjusting the plasticity thresholds Δ_D and Δ_P, our ER⁻ spine model can show broad agreement with the experimentally reported plasticity profiles. Figure 7 B (top) shows the dependence of the Ca²⁺–CaM amplitude on the spike timing difference (Δt) in the doublet (blue) and triplet (red) cases. The temporal proximity and ordering of pre‐ and postsynaptic inputs, together, control the NMDAR activation level, which in turn decides the maximum Ca²⁺ elevation in the spine during persistent stimulation. The corresponding synaptic weight changes (Δw) induced by the STDP inputs are displayed in Fig. 7 B (bottom). Consistent with experimental data, the doublet protocol only induces synaptic weakening over a restricted range of Δt values (Fig. 7 B, bottom, blue curve). On the other hand, the triplet protocol induces potentiation over an ∼35 ms window of positive Δt values, flanked by two ∼40 ms windows of depression, one for Δt < 0 and a second for causal pre/post pairings with longer time differences (Δt ≥ +35 ms) (Fig. 7 B, bottom, red curve).

Figure 7. Differential Ca²⁺–CaM response in the presence of spine ER depends on NMDAR activation regulated by the spike timing difference.

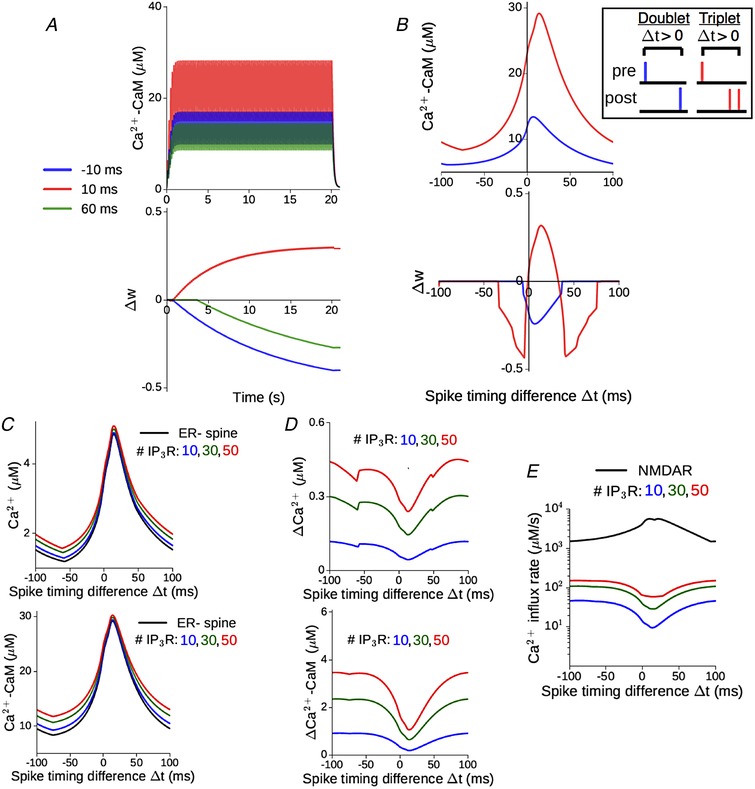
A, illustration of the time course of CaM activation (top) and plasticity induction (bottom) at the reference ER⁻ spine in response to 100 spike triplets (1 EPSP + 2 bAP) at 5 Hz, for three different spike timing differences (Δt): −10, +10 and +60 ms. Plasticity parameters have been chosen so as to yield depression at −10 and +60 ms, and potentiation at +10 ms, consistent with previous measurements (Wittenberg & Wang, 2006). B, top, maximum CaM activation attained during prolonged paired stimulation as a function of Δt, when every synaptic input is paired with either 1 (blue) or 2 (red) bAPs. The inset shows details about the STDP stimulus pattern (doublet vs. triplet pairing, and convention for positive Δt). Bottom, total weight change at the end of the stimulation, plotted as a function of Δt for the doublet (blue) and triplet (red) spike pairings. No potentiation is induced in the former case. Parameters same as in A, in order to have overall consistency with experimental profiles. C, the amplitude of Ca²⁺ (top) and CaM activation (bottom) in the ER⁻ spine (black) vs. ER⁺ spine for different IP₃R numbers (coloured curves), during presentation of 100 spike triplet pairings at 5 Hz over a range of Δt. D, the corresponding excess Ca²⁺ (top) and CaM (bottom) responses in the ER⁺ spine relative to the ER⁻ control. E, maximum rate of Ca²⁺ influx into the ER⁺ spine cytosol through NMDAR channels (black) and different numbers of IP₃Rs during paired stimulation over a range of Δt values. (All results for a synapse with ΔCa_EPSP = 0.2 μM.) [Color figure can be viewed at wileyonlinelibrary.com]

How does ER modulate spine Ca²⁺ signalling during STDP induction? Figure 7 C–E compares the activity‐driven responses of an ER⁺ spine (with different IP₃R cluster sizes) with the ER⁻ reference spine, as a function of the spike timing difference. Release of ER store Ca²⁺ augments both the Ca²⁺ and Ca²⁺–CaM in the spine head (Fig. 7 C), and this excess response in the ER⁺ spine relative to the ER⁻ spine indirectly depends on the spike timing difference, which regulates the NMDAR‐mediated Ca²⁺ entry into the spine (Fig. 7 D). This inverse dependence of the ICCR contribution on NMDAR activation level is reflected in the NMDAR and IP₃R Ca²⁺ current profiles, shown in Fig. 7 E. Stronger NMDAR activation, particularly at small positive spike timing differences (0 < Δt ≤ +40 ms), is associated with reduced ICCR, which follows from the Ca²⁺‐dependent inhibition of IP₃ receptors at sustained Ca²⁺ levels above ∼0.3 μm. These trends broadly agree with the results from our previous simulations of rate‐based plasticity (Fig. 5).

Transient elevation of Ca²⁺–CaM levels drives the induction of plasticity, governed by Eq. (11). The temporal profiles of activated CaM and corresponding plasticity outcomes in the ER⁻/ER⁺ spines are illustrated for two representative spike timing differences in Fig. 8 A and B. For Δt = −35 ms, the amplitude of active CaM in the ER⁻ spine lies just below the threshold for the induction of synaptic depression (Fig. 8 A, black curves). The additional release of ER store Ca²⁺ increases the total CaM activation above the LTD threshold, inducing strong synaptic weakening (Δw < 0) in the presence of ER (Fig. 8 A, coloured curves). When Δt = +10 ms, ICCR makes a relatively modest contribution to the total Ca²⁺ response in the spine head (Fig. 8 B, top), and this yields a small net enhancement of synaptic strengthening compared to the ER⁻ spine (Fig. 8 B, bottom). We simulated STDP inputs to our synaptic model over the full range of allowed spike timing differences (−100 ms ≤ Δt ≤ +100 ms), and the plasticity profiles obtained for the triplet and doublet protocols are shown in Fig. 8 C. Ca²⁺ release from spine ER modulates the overall STDP curve for triplet inputs (Fig. 8 C, top), and synaptic weakening is elicited over a broader range of spike timing differences compared to the ER⁻ spine. Consistent with the reduced contribution of ICCR at small positive Δt (Fig. 7 D and E), presence of ER introduces relatively less broadening of the LTP induction window. In the case of doublet inputs (Fig. 8 C, bottom), ICCR extends the window for induction of synaptic depression over a broader range of spike timing differences relative to the ER⁻ spine, the extent of which scales with the number of IP₃R present.

Figure 8. NMDAR‐dependent contribution of ICCR to spine Ca²⁺ response modulates the STDP profiles.

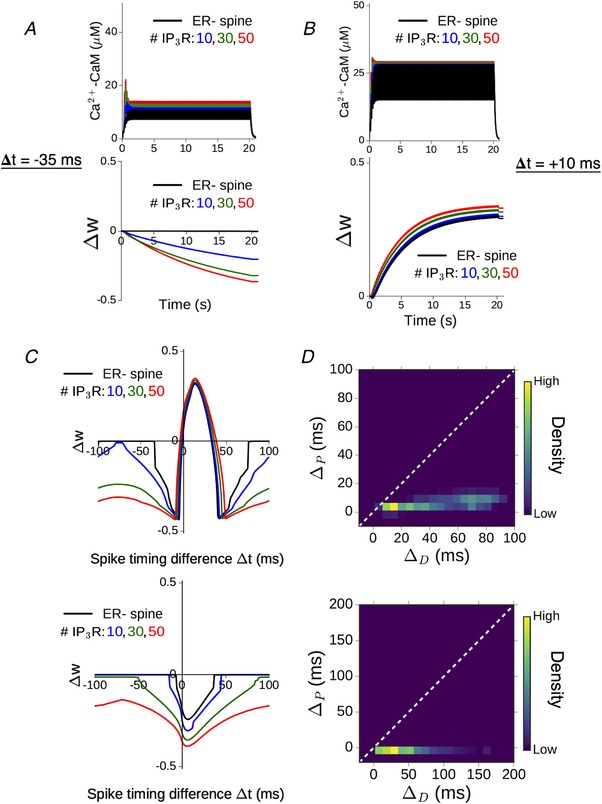
A, time course of the spine CaM activation (top) and plasticity variable Δw (bottom) in response to triplet pairing stimulation with Δt = −35 ms. Results shown for the ER⁻ control spine (black) and ER⁺ spine with different IP₃R numbers (coloured curves). B, results obtained for Δt = +10 ms. (Parameters here are same as in Fig. 5, with no plasticity induced in the ER⁻ spine for Δt = −35 ms.) C, comparison of the plasticity profiles (total weight change Δw) obtained in the absence of ER (black) and with different levels of ICCR (coloured curves) in response to 100 pairings of spike triplets (top) and doublets (bottom). D, quantification of relative changes in LTD and LTP window widths when ICCR is present, for the triplet (top) and doublet (bottom) stimulation patterns. Heat maps represent distributions of (Δ_D, Δ_P) values obtained from random sampling (5000 times) of the STDP thresholds Δt _D and Δt _P in the ER⁻ control spine from 20 ms windows centred on −35 and +35 ms, respectively, and with 10–50 IP₃Rs. [Color figure can be viewed at wileyonlinelibrary.com]

The differential modulation of the depression and potentiation windows seen in the above data was quantified in terms of the relative change in widths of the LTD and LTP windows (Δ_D and Δ_P) in the presence of ER. Repeated random sampling of the STDP thresholds Δt _D/Δt _P for the ER⁻ spine (from ±10 ms windows centred on Δt _D = −35 ms and Δt _P = +35 ms) yields a distribution of possible (Δ_D, Δ_P) pairs. The results (aggregate of 5000 samples, 10–50 IP₃Rs) are represented by separate heat maps for the triplet and doublet input patterns (Fig. 8 D). The overall distribution, which, by and large, is confined to the lower triangle (Δ_D > Δ_P), indicates that the contribution of ICCR can potentially extend the LTD window by several tens of milliseconds, whereas its effect on the LTP window is comparatively less. Taken together, Fig. 8 C and D demonstrates the relative broadening of the LTD window in the presence of ICCR, which is fairly robust to variation of the plasticity thresholds and the IP₃R cluster size. In summary, we found that mGluR‐mediated Ca²⁺ release from spine ER during correlated activation of pre‐ and postsynaptic neurons promotes the induction of synaptic depression over a broader range of temporal activation patterns (Δt), with relatively less influence on LTP induction.

Differential contribution of ICCR to LTD and LTP induction is a general consequence of IP₃ receptor kinetics

The foregoing analysis of our detailed synaptic model highlights the potential contribution of ICCR to activity‐driven Ca²⁺ signalling in the spine, and its regulation by NMDAR‐mediated Ca²⁺ entry. These results were obtained with a specific choice of the NMDAR conductance, a key parameter controlling the dynamic range of NMDAR‐mediated Ca²⁺ responses in the spine. To assess the robustness/sensitivity of our model predictions, we repeated our simulations by varying the conductance parameter g _N so as to span a physiologically plausible range of synaptically evoked Ca²⁺ amplitudes (ΔCa_EPSP = 0.1–1 μm).

Figure 9 A summarizes the differential responses in the ER⁺ spine (for N _R = 30 IP₃Rs) relative to the ER⁻ (control) spine during trains of synaptic (SC) input at different rates. The heat map in Fig. 9 A (left) represents the excess Ca²⁺–CaM amplitude as a function of the input frequency (horizontal axis) and g _N (vertical axis). ER contributes robustly to spine Ca²⁺ elevation at low input frequencies (f ≲ 5 Hz). The contribution of ICCR steadily declines at higher input rates due to Ca²⁺‐dependent inhibition of IP₃ receptors, and this frequency‐dependent suppression of the difference between the ER⁻ and ER⁺ spines is more pronounced at higher ΔCa_EPSP. The corresponding results for the differential induction of plasticity in the ER⁺ spine are displayed as a heat map in Fig. 9 A (right). For each g _N, the plasticity thresholds θ_D and θ_P have been adjusted to have f _D = 1 Hz and f _P = 15 Hz in the ER⁻ spine, and the excess plasticity (ΔΔw) in the presence of ER has been estimated for every input frequency. Figure 9 A (right) indicates that ICCR robustly augments NMDAR‐mediated Ca²⁺ responses to facilitate the induction of synaptic depression at low input frequencies (f ≲ 1 Hz). Due to the inhibition of ICCR with increasing NMDAR activation (Fig. 9 A, left), there is little difference between the plasticity curves for the ER⁻ and ER⁺ spines at higher input frequencies. Except in a limited range of small g _N values (ΔCa_EPSP ≲ 0.15 μm), ICCR is strongly suppressed at stimulation rates above ∼10 Hz, and the LTP threshold (f _P) in the ER⁺ spine remains nearly unchanged relative to the ER⁻ spine.

Figure 9. Differential enhancement of LTD and LTP by spine ER is a general consequence of ICCR kinetics.

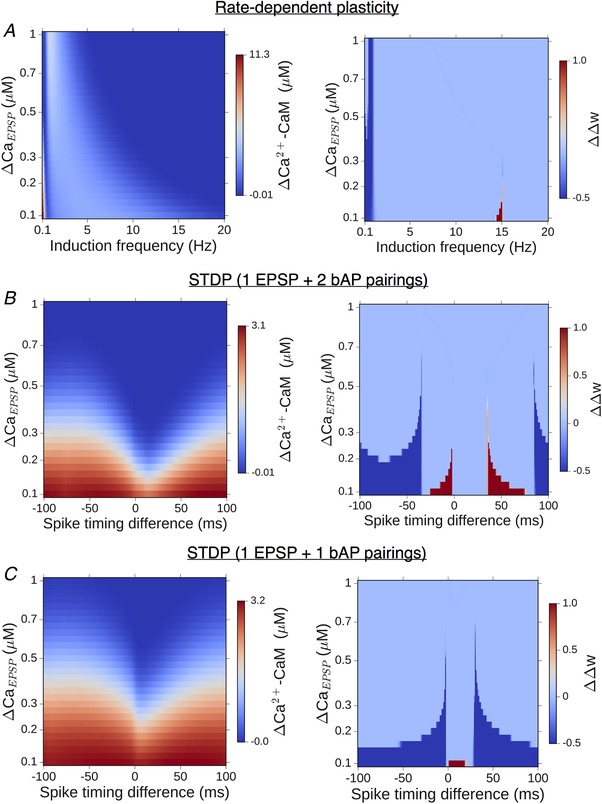
A, left, change in maximum CaM activation due to the presence of ER as a function of the spine NMDAR conductance and induction frequency; right, dependence of the modified plasticity (change in Δw) due to presence of ER on the NMDAR conductance and induction frequency. B and C, parameter sensitivity in the case of STDP inputs for the triplet (B) and doublet (C) spike pairing stimuli. (All results for comparison between ER⁻ control spine and an equivalent ER⁺ spine with 30 IP₃Rs; plasticity thresholds appropriately adjusted to give (in the ER⁻ spine) f _D = 1 Hz and f _P = 15 Hz for rate‐dependent plasticity, and, separately, STDP for −35 ms < Δt < 70 ms.) [Color figure can be viewed at wileyonlinelibrary.com]

We similarly characterized the differential responses and plasticity outcomes in the ER⁺ spine during STDP input patterns (Fig. 9 B and C). For each g _N, the plasticity thresholds θ_D and θ_P in our model were adjusted so as to yield (for spike triplets) an LTD window for −35 ms < Δt < 0 ms and a potentiation window for 0 ms < Δt < 35 ms in the ER⁻ spine. Figure 9 B (left) summarizes the dependence of the excess Ca²⁺–CaM response in the ER⁺ spine (with N _R = 30 IP₃Rs) on g _N and the spike timing difference (Δt) in the triplet case, showing a general reduction in the ICCR‐mediated enhancement of spine Ca²⁺ signals with increasing ΔCa_EPSP. The corresponding differences in the plasticity outcome (ΔΔw, Fig. 9 B, right) show significant broadening of the window of LTD induction over a fairly wide range of g _N values. The ER‐associated broadening of the LTP window is restricted to a comparatively narrow range of g _N values and spike timing intervals. The differential Ca²⁺–CaM response and plasticity outcome in the doublet case (Fig. 9 C) similarly highlight a general broadening of the window of spike timing differences eliciting synaptic depression, the extent of which scales inversely with ΔCa_EPSP.

As the above results were obtained for a specific choice of the plasticity thresholds and IP₃R cluster size, we repeated these comparisons with variable number of IP₃ receptors (N _R = 10–50) and plasticity thresholds, for both frequency‐dependent plasticity and STDP (Methods). For each combination of parameter values (g _N, N _R, θ_D, θ_P), the overall modulation of the NMDAR‐only plasticity curve by ICCR was quantified in terms of the shifts in the LTD and LTP thresholds for rate‐dependent plasticity, and changes in the LTD/LTP window widths in the case of STDP. The summary statistics (Fig. 10 A–C) provide a sense of the variability in model outcomes, and taken together, suggest graded modulation of NMDAR‐based bidirectional plasticity by ICCR, with heightened LTD induction. In sum, our model simulations over realistic parameter ranges provide support for an ER‐linked form of synaptic metaplasticity on the level of individual spines, the nature of which is regulated by mGluR–IP₃ signalling in concert with the temporal profile of NMDAR activation.

Figure 10. Differential enhancement of LTD and LTP by spine ER is broadly reproduced over a range of realistic parameter settings in our model.

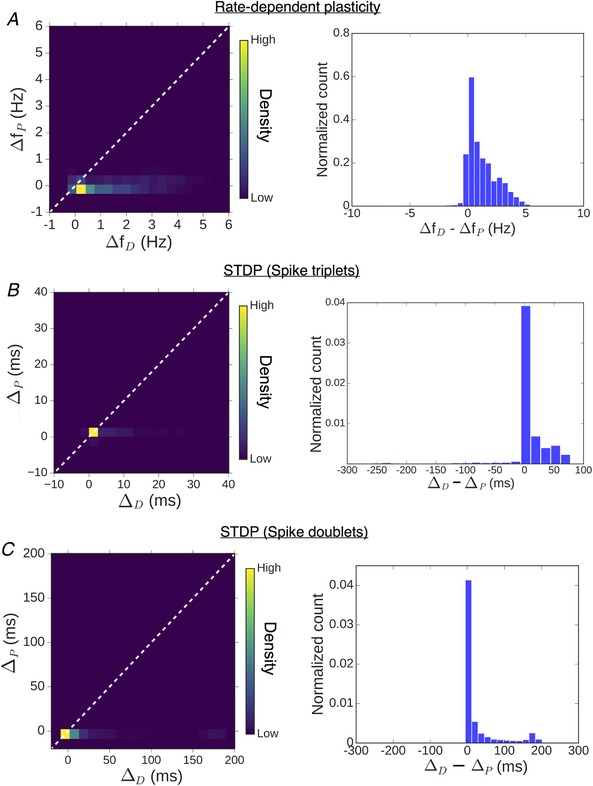
Summary statistics of changes in plasticity windows introduced by ICCR in the case of frequency‐dependent plasticity (A), and for STDP with triplet (B) and doublet (C) spike pairing stimuli. In each case, the left figure is a heat map of the distribution obtained from random sampling of the thresholds at the ER⁻ control spine, over a range of IP₃R cluster sizes (10–50) and NMDAR conductances (ΔCa_EPSP = 0.1–1 μM); the same information is represented as a 1D histogram of the relative differences (depression vs. potentiation) in the right figure. (For frequency‐dependent plasticity, f _D and f _P have been randomly sampled over 1–6 Hz and 10–20 Hz ranges, respectively. For STDP, Δt _D and Δt _P have been sampled from 20 ms windows centered on −35 ms and +35 ms, respectively.) [Color figure can be viewed at wileyonlinelibrary.com]

Discussion

Dendritic spines are specialized structures that facilitate spatially restricted biochemical signalling and enable input‐specific, Hebbian‐type synaptic changes mediated by NMDA receptors (Koch & Zador, 1993; Bourne & Harris, 2008). In the present study, we systematically investigated, with mathematical modelling, how the local reorganization of ER may modulate Ca²⁺‐driven plasticity on the scale of individual excitatory CA1 synapses. Results from our model simulations of rate‐based plasticity and spike timing‐dependent plasticity, taken together, suggest that the presence of ER selectively enhances the propensity for LTD induction with a relatively diminished effect on LTP induction. Targeting of ER to larger spine heads can thus mediate a ‘metaplastic switch’ at stronger synapses that specifically relies on ER Ca²⁺ handling and metabotropic glutamatergic signalling. The graded contribution of the IP₃‐sensitive ER store to spine Ca²⁺ elevation as a function of NMDAR activation that we have characterized here offers a synapse‐specific mechanism to differentially modulate the windows for depression/depotentiation and potentiation, yielding a net enhancement of activity‐driven synaptic depression (Fig. 11). In light of the observed association of ER with more potent synapses (Cooney et al. 2002) and the dynamic acquisition of ER accompanying spine enlargement (Sala et al. 2005; Ng et al. 2014), we propose a regulatory role for ER as a compensatory ‘braking’ mechanism that may temper the propensity for further strengthening at the potentiated synapses. Our findings thus support a novel interpretation for spine ER in adjusting the plasticity profile of a synapse on an as‐needed basis, which may contribute to keeping saturation at bay and maintaining synaptic strengths within a useful dynamic range supporting memory storage and optimal neural network function (Abbott & Nelson, 2000; Abraham, 2008; Keck et al. 2017).

Figure 11. ER Ca²⁺ store introduces a novel form of synaptic metaplasticity at individual CA1 dendritic spines.

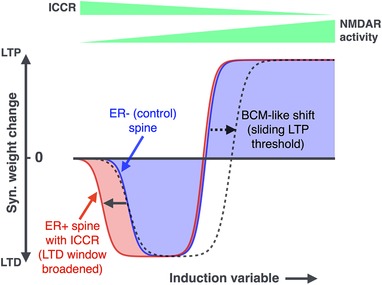
Results from our analysis of frequency‐ and spike timing‐dependent plasticity are summarized by a comparison of the plasticity profiles for the reference ER⁻ spine (blue) and a spine with ER (red). The induction variable (which can stand for the synaptic input frequency f, or spike timing difference Δt) controls the activation of both NMDAR and ICCR, these dependencies being represented by tapering bars at the top. Also shown for comparison is the modified plasticity curve arising from a BCM‐like sliding LTP threshold (dashed curve). [Color figure can be viewed at wileyonlinelibrary.com]

Synapse‐specific LTP in the hippocampal formation is essential for initiation of experience‐dependent learning (Kitamura et al. 2017). This locus is shifted subsequently and cortical neural circuits take over memory consolidation and retrieval after initial memory formation is completed (Kitamura et al. 2017; Eichenbaum, 2017). Spines having undergone experience‐dependent modifications can quickly saturate (runaway effect of LTP) and no longer participate in ongoing learning. Adaptability of the plasticity profile may promote re‐use of strong synapses, enabling saturated synapses to be brought back into the ‘game’. The form of metaplasticity elucidated here is specific to individual CA1 spines, and is likely triggered by the rapid local remodelling of ER that may be a consequence of strong prior synaptic activation (Ng et al. 2014). Our work is of particular relevance to an understanding of the mechanisms in place to overcome possible storage limitations in the CA1 field, given that ER is most likely to be found associated with stronger synapses at the larger CA1 spines. The selective enhancement of synaptic weakening in the presence of ER (Fig. 11) has a direct implication for long‐term stability of the stronger synapses: under ‘natural’ conditions (Klyachko & Stevens, 2006), background synaptic activation may promote a slow resetting of potentiated synapses at the ER‐bearing spines; viewed another way, acquisition of spine ER is anticipated to effectively ‘slow down’ cumulative synaptic strengthening over time. We note that these effects are distinct from a BCM‐like shift of the synaptic LTP threshold (Bienenstock et al. 1982), though at higher SERCA activity levels, ER may introduce such a shift in addition to promoting LTD induction (simulations not shown).

Computational models of Ca²⁺‐based plasticity normally attempt to link NMDAR‐mediated Ca²⁺ entry to downstream signalling events at the postsynaptic locus, and these have provided a meaningful account of the general phenomenology of long‐term plasticity in the hippocampus and neocortex (Zador et al. 1990; Shouval et al. 2002; Graupner & Brunel, 2007; Rackham et al. 2010; Kumar & Mehta, 2011; Graupner & Brunel, 2012). From a neurobiological point of view, though, it is important to go beyond averaged descriptions and consider whether local heterogeneities in microphysiology on the synapse level could introduce functional differences between individual synaptic connections in a population. The role of spine ER in introducing synapse‐specific functional differences in Ca²⁺ signalling may not be clearly discernible from macroscopic measurements of synaptic plasticity properties, or by lumping together and averaging over experimental data from many synaptic contacts only a few of which may be associated with ER‐bearing spines. This situation in hippocampal pyramidal neurons may be contrasted with the case of spines associated with cerebellar parallel fibre to Purkinje cell synapses, which are more homogeneous in terms of the presence of ER (Harris & Stevens, 1988) and where localized Ca²⁺ release from stores is known to be central to the induction of long‐lasting plasticity (Wang et al. 2000; Miyata et al. 2000; Antunes & De Schutter, 2012).

This last aspect, in particular, underlines the utility of a physiologically plausible in silico model which enables systematic characterization of the role of ER in Ca²⁺ signalling at individual spines. The framework presented here is one of the first to weave a quantitative description of metabotropic glutamate signalling into a detailed model of spine Ca²⁺ dynamics driven by NMDAR activation. Delineation of the role of ER Ca²⁺ handling in a spine requires considering mGluR–IP₃ signalling in the backdrop of synaptic NMDAR activation, as NMDAR‐gated Ca²⁺ entry can regulate several aspects of this signalling, including PLCβ activity, IP₃ turnover and IP₃R gating, with dynamic Ca²⁺ feedback from ICCR further adding to the overall system complexity (Fig. 1 C). We calibrated the parameters in our model of ICCR to be consistent with salient features of experimentally reported Ca²⁺ responses in ER‐containing CA1 spines to unitary synaptic events (Holbro et al. 2009), particularly the lag (few hundred milliseconds) in Ca²⁺ release from ER following release of glutamate into the synaptic cleft. Our analysis builds on these observations as we examine the contribution of ER to the spine Ca²⁺ response, and its subsequent shaping of plasticity, in the context of neural activity patterns that mimic the experimental induction of early LTP/LTD.

The response of an ER⁺ spine in our model to low‐frequency glutamate pulses, in particular, highlights the interaction of multiple time scales associated with IP₃ degradation, recovery of IP₃Rs from Ca²⁺‐dependent inactivation, and the input frequency in shaping the profile of ICCR. Our model yields a non‐monotonic rate dependence of the ER Ca²⁺ contribution at low input frequencies (f ≲ 5 Hz) (Fig. 4 D). As noted before, this arises from a balance between the contrasting effects of the input rate on (1) recovery of IP₃Rs from inactivation between inputs (which is lower, the more closely spaced the inputs are), and (2) the availability of IP₃, which increases with input rate and promotes the opening of IP₃R channels. Analogous to the profile of ER Ca²⁺ contribution, our model also predicts a non‐monotonic rate dependence for the time delay in ICCR following glutamate release, which initially increases before decreasing with the input frequency as ICCR gradually synchronizes with the NMDAR‐mediated Ca²⁺ transient. The foregoing properties of spine Ca²⁺ response as functions of the synaptic input frequency, inferred from our numerical simulations, are potentially informative readouts of the model which could be compared with similar readouts from Ca²⁺ imaging experiments at individual CA1 spines. Such a comparison would help validate the interplay of different kinetic time scales in the ER⁺ spine model used in this study and constrain key model parameters.

The contribution of ICCR to spine Ca²⁺ signalling can be broadly understood in terms of NMDAR‐mediated spine Ca²⁺ regulation and the kinetics of IP₃R with its characteristic bell‐shaped dependence on the cytosolic Ca²⁺ level. With repeated low‐frequency stimulation, there is no sustained build‐up of Ca²⁺ evoked by the sequence of glutamate pulses. Every synaptic input triggers transient mGluR activation, evoking a short burst of Ca²⁺ release from ER which is initiated by fast activation (m ₁ and m ₂) of IP₃R influx, followed by the slower Ca²⁺‐dependent inactivation (h) of the IP₃R which brings the Ca²⁺ level down. This allows the IP₃R to recover from inactivation between successive inputs when Ca²⁺ has decayed back to near‐resting levels, and explains the robust augmentation of the NMDAR‐mediated Ca²⁺ signal by ICCR at low stimulation frequencies (Fig. 4). At higher input frequencies, NMDAR‐gated Ca²⁺ transients triggered by successive inputs add up, and there is sustained elevation of Ca²⁺ in the spine, the magnitude of which is set by the input frequency f. As Ca²⁺ is continually maintained at a high level, the Ca²⁺‐dependent inactivation variable h stays small, and keeps the IP₃R persistently inhibited as long as the stimulation is present, despite the concurrent activation of mGluR and availability of IP₃. This underlies the progressive frequency‐dependent suppression of Ca²⁺ flux through IP₃ receptors at higher input frequencies (Fig. 5), and implies a steadily diminishing role for ICCR as LTD switches to LTP according to the Ca²⁺‐based plasticity model governing bidirectional synaptic strength changes (Fig. 6 D and E).

An analogous situation arises during trains of pre‐ and postsynaptic spikes at a constant rate (in the theta band), mimicking the experimental induction of spike timing‐dependent plasticity. The activation of NMDARs in this case is controlled by the relative timing of pre‐ and postsynaptic firing (Δt) on the millisecond scale. The amplitude of the sustained Ca²⁺ elevation driven by NMDA receptor activity is thus a function of the spike timing difference, and it directly controls the extent of inhibition (h) of the IP₃R (Eq. 7). This accounts for the spike timing dependence of the relative contribution of ICCR to the total spine Ca²⁺ signal in Fig. 7, and the overall enhancement of synaptic depression with the addition of ER (Fig. 8 C and D).

The key findings following from our simulations are fairly general, and hold for variation in important model parameters such as NMDAR conductance and number of IP₃Rs within realistic ranges. Other parameters, such as those controlling the spine–dendrite coupling (electrical and diffusional), were kept fixed based on literature estimates; however, our results are not sensitive to these specific values and higher values yield similar plasticity profiles. Further, our main conclusions regarding the contribution of ER to spine Ca²⁺ dynamics are also valid when IP₃Rs are modelled stochastically to account for fluctuations arising from small numbers of receptors.

Regulation of synapse strength is acknowledged to be a complex process, likely involving the coordinated action of several mechanisms that may act over a wide range of time and spatial scales to modulate the rate and direction of ongoing activity‐dependent plasticity. Previously proposed mechanisms include intrinsic plasticity of membrane excitability (Narayanan & Johnston, 2010; Lee & Chung, 2014), compensatory scaling of spine volume to balance synaptic potentiation (Kalantzis & Shouval, 2009; O'Donnell et al. 2011), alterations in the number and/or subunit composition of postsynaptic NMDARs (Xu et al. 2009; Lee et al. 2010), and global synaptic scaling mediated by glial signals (Stellwagen & Malenka, 2006). The present study linking postsynaptic ER to local modulation of Ca²⁺‐based plasticity adds to the repertoire of dynamically regulated biophysical mechanisms that may be in place to control plasticity and function at excitatory hippocampal synapses (Zenke & Gerstner, 2017; Keck et al. 2017).

Although several lines of evidence link group I mGluR activation and ER Ca²⁺ stores to long‐term depression at hippocampal synapses, the involvement of ER, or more generally of mGluR signalling, in synaptic potentiation is less clear. Results from several pharmacological and knockout studies collectively do not implicate an essential role for group I mGluR in LTP or AMPAR‐mediated synaptic transmission in the CA1 region (Bortolotto et al. 1999). Mutant mice lacking a function G protein associated with group I mGluRs were found to be deficient in hippocampal LTD induced by low‐frequency stimulation, but exhibited intact LTP in response to tetanic inputs (Kleppisch et al. 2001). Some studies on mGluR5 knockout mice reported reduced LTP in CA1 neurons (Lu et al. 1997; Jia et al. 1998), but this was shown to involve selective reduction of NMDAR function on both the induction and expression levels, with no effect on the AMPAR component of LTP. Further, there is no direct evidence that the above interaction relies on Ca²⁺ release from stores, or that it is synapse‐specific and restricted to spines containing ER. As noted previously, LTP studies usually examine plasticity on the coarse‐grained level and not at individual synapses; thus, they are of limited utility in addressing the differences in local Ca²⁺ signalling that might arise between ER⁻ and ER⁺ spines during LTP induction. Moreover, the concurrent stimulation of multiple synaptic contacts (as in experimental induction of plasticity) may evoke Ca²⁺ release from ER in the dendritic body as well (Nakamura et al. 1999); this could activate signalling pathways distinct from those associated with early LTP in spines, and trigger plasticity at a large number of synapses (spread out over a wider dendritic region), independent of their association with ER‐bearing spines. The present study is restricted to quantifying the contribution of ER (IP₃‐sensitive stores) to spatially confined Ca²⁺ dynamics in spines, and it is in this specific context that our analysis predicts decreasing ER contribution with stronger synaptic (NMDAR) activation due to the Ca²⁺‐dependent suppression of IP₃R activity. We note that an early experimental study of STDP at CA3–CA1 synapses (Nishiyama et al. 2000) makes a similar suggestion about the suppression of IP₃R activity during LTP (but not LTD) induction, as a possible explanation for the absence of associated heterosynaptic plasticity mediated by regenerative Ca²⁺ release (Ca²⁺ waves) from IP₃‐sensitive stores. The predicted graded effect of spine ER on plasticity curves could be potentially tested by imaging spine Ca²⁺–CaM activity during different forms of persistent stimulation at individual CA3–CA1 synapses contacting ER⁺ spines, and assessing the effect of pharmacological blockade of either stores (SERCA inhibitors such as thapsigargin) or specific inhibition of the IP₃ pathway (e.g. with heparin) on their response profiles. Such a comparison should ideally control for the possible confounding effects of changes in spine volume/synapse strength that may concurrently occur due to activity‐induced plasticity, through targeted inhibition of key effectors downstream of CaM, e.g., CaMKII and calcineurin.

To conclude, we have presented a detailed modelling study, leveraging previous experimental observations, to characterize the local modulation of Ca²⁺ signals and plasticity at hippocampal dendritic spines by ER. Our analysis quantifies a unique role for ER in dynamically altering the long‐term plasticity profile at individual CA1 spines and is supported by experimental evidence (Sala et al. 2005; Holbro et al. 2009; Ng et al. 2014). Our study makes general predictions about a differential effect of ER on LTD and LTP under physiological conditions that is qualitatively distinct from BCM‐like mechanisms, besides providing detailed quantitative characterization of ER Ca²⁺ regulation via metabotropic signalling as a function of the temporal profile of inputs and synaptic NMDAR activation patterns. The synapse‐specific role of ER suggested here adds a new dimension to earlier work on metaplasticity mediated by metabotropic receptors (Cohen & Abraham, 1996; Ireland & Abraham, 2002; Bortolotto et al. 2005; Abraham, 2008). Incidentally, a role for store Ca²⁺ release was also recently implicated in synaptic homeostasis mediated by spontaneous miniature EPSPs (Reese & Kavalali, 2015). The involvement of ER (as a Ca²⁺ store) in biochemical signalling likely extends to other aspects of dendrite function, such as in mediating some forms of heterosynaptic plasticity (Nishiyama et al. 2000), long range (synapse‐to‐nucleus) signalling involved in activity‐dependent transcriptional regulation (Bading, 2013), and spatiotemporal integration of synaptic inputs (Lee et al. 2016); recent studies also link perturbations of the pathways considered here to early pathological events reported in some forms of Alzheimer's disease and fragile X syndrome (Bear et al. 2004; Nakamoto et al. 2007; Cheung et al. 2008; Pchitskaya et al. 2018). The approach presented here provides a framework for future modelling studies aimed at investigating these diverse questions. On a more general note, the potential contribution of ER to microscale signalling elucidated here highlights the need to move beyond ‘average’ accounts of synaptic signalling, and consider the implications of local physiological differences between synapses for their plasticity and function.

Additional information

Competing interests

The authors declare that no competing interests exist.

Author contributions

G.M. and S.N. conceived the study and designed the experiments. G.M. performed the experiments and analysed the data; G.M. and S.N. wrote the paper. All authors have read and approved the final version of this manuscript and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

S.N.: Wellcome Trust/DBT India Alliance (grant number IA/I/12/1/500529). G.M.: Wellcome Trust/DBT India Alliance (grant number IA/I/12/1/500529) and Science & Engineering Research Board, India (grant number PDF/2017/001803)

Biography

Gaurang Mahajan obtained a PhD in physics from IUCAA, Pune. He is currently a postdoctoral fellow in computational neuroscience at the Indian Institute of Science Education and Research, Pune. He studies various aspects of synaptic function using mathematical models, and is broadly interested in addressing biological questions using theoretical/computational approaches.