Abstract
Spontaneous pattern formation in Turing systems relies on feedback. Patterns in cells and tissues however often do not form spontaneously, but are under control of upstream pathways that provide molecular guiding cues. The relationship between guiding cues and feedback in controlled biological pattern formation remains unclear. We explored this relationship during cell polarity establishment in the one-cell-stage C. elegans embryo. We quantified the strength of two feedback systems that operate during polarity establishment, feedback between polarity proteins and the actomyosin cortex, and mutual antagonism amongst polarity proteins. We characterized how these feedback systems are modulated by guiding cues from the centrosome. By coupling a mass-conserved Turing-like reaction-diffusion system for polarity proteins to an active gel description of the actomyosin cortex, we reveal a transition point beyond which feedback ensures self-organized polarization even when cues are removed. Notably, the baton is passed from a guide-dominated to a feedback-dominated regime significantly beyond this transition point, which ensures robustness. Together, this reveals a general criterion for controlling biological pattern forming systems: feedback remains subcritical to avoid unstable behaviour, and molecular guiding cues drive the system beyond a transition point for pattern formation.
Cell polarity establishment in C. elegans zygotes is a prototypical example for cellular pattern formation that depends both on feedback between two classes of pattern-forming proteins and on upstream guiding cues provided by the centrosomal polarity trigger [1–3]. Posterior PAR proteins (pPARs: PAR-1, PAR-2, and LGL-1) and anterior PAR proteins (aPARs: PAR-6, PAR-3, and PKC-3) interact via antagonistic feedback while bound to the cell cortex [4], which gives rise to stably unpolarized and polarized states [5–7]. The formation of PAR polarity domains involves actomyosin cortical flows that transport PAR proteins [6, 8–11]. In addition PAR proteins regulate the actomyosin cortex [8, 12–16], implying mechanochemical feedback [17]. Two centrosomal polarity triggers act as guiding cues for the polarization process [1–3]. First, centrosomal microtubules protect PAR-2 from PKC-3-mediated antagonism [5]. Second, contractility in the actomyosin cortex is increased via RhoA activation [18], and a local down-regulation of non-muscle myosin II (NMY-2, referred to as myosin) at the posterior pole [19] initiates cortical flows [8, 20]. The relationship between guiding cues and feedback in PAR polarity establishment remains unclear. To address this issue, we first focus on feedback and later shift our attention to the guiding cues and their relation to the mechanisms of feedback.
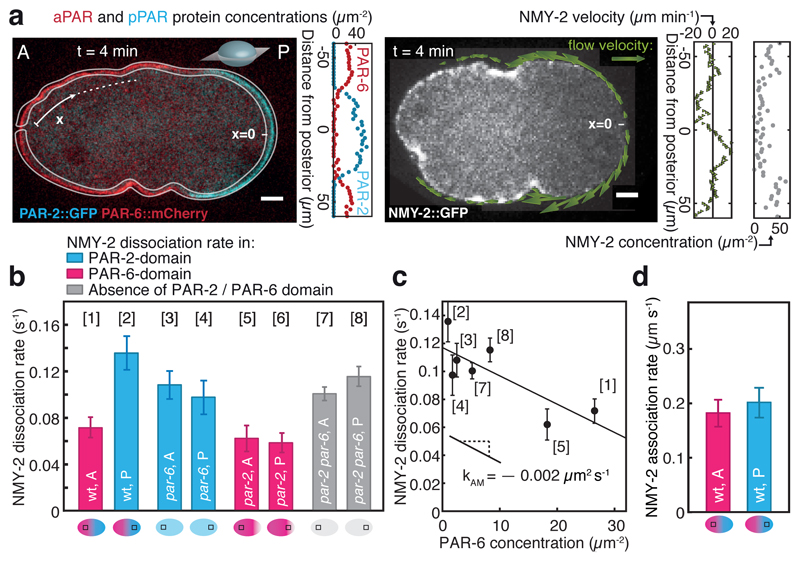
Previous work has investigated antagonistic feedback between the two PAR species [4, 6, 21]. We set out to characterize mechanochemical feedback from PAR proteins onto actomyosin contractility. Cortical myosin is regulated by PAR domains [8, 12–16], but the strength of this regulation in terms of changes of myosin association and dissociation rates remains unknown. Fluorescence Recovery After Photobleaching (FRAP) is a technique for determining dissociation rates at steady-state [22, 23] (Supplementary Fig. 1, Supplementary Discussion 1.2). Performing FRAP during maintenance where myosin appears to reach a steady state (Supplementary Fig. 2a,c, Supplementary Discussion 1.2), we found that the rate of NMY-2 dissociation from the cortex is about two-fold higher in the posterior compared to the anterior PAR domain (posterior, kdiss= 0.14 ± 0.01 s−1; anterior, kdiss= 0.072 ± 0.009 s−1) (Fig. 1b). The spontaneous dissociation rate of myosin in anterior during maintenance is similar to the one reported during cortical flows, as measured via co-moving mass-balance imaging (COMBI; [24]). This indicates that myosin reaction kinetics do not change much over these stages of the cell cycle. We next determined the rate of NMY-2 association to the cortex by considering that the steady-state surface concentration of NMY-2 is set by the ratio of this association rate and the dissociation rate from the cortex. To this end, we developed a fluorescence-based image quantification technique (MACE: Membrane-Associated Concentration Evaluation) that determines the spatiotemporal concentration fields of labeled proteins at the cell surface (Fig. 1a, see also [25]). We find that the rates of association of NMY-2 to the cortex are similar in both PAR domains (anterior: kon = 0.19 ± 0.03 µm s−1, posterior: kon = 0.21 ± 0.03 µm s−1) (Fig. 1d), indicating that NMY-2 association to the cortex is independent of PARs. However, changing the local PAR state of the cortex via RNAi changes the local NMY-2 dissociation rate (Fig. 1b, Supplementary Fig. 2k), indicating that the PAR domain state controls NMY-2 dissociation from the cortex. We next asked if the posterior or the anterior PAR complex regulates the NMY-2 dissociation rate. To this end, we measured the NMY-2 dissociation rate during par-2 and par-6 double-RNAi (Supplementary Fig. 2j). Under this condition, the NMY-2 dissociation rate is not significantly different from the one measured in the posterior domain of unperturbed embryos (Fig. 1b), indicating that the anterior PAR complex is the dominant regulator of the myosin dissociation rate [26]. Indeed, by combining FRAP data with MACE analysis we find that the dissociation rate kdiss of NMY-2 decreases with increasing PAR-6 concentration approximately as kdiss = (koff,M + kAMA), where koff,M is the spontaneous dissociation rate of NMY-2 in the absence of PARs, A is the anterior PAR-6 concentration and kAM is a coupling coefficient (kAM = (-2.0 ± 0.7) · 10−3 µm2 s−1; Fig. 1c, Supplementary Fig. 2k). Thus, anterior PAR complexes control the amount of cortical myosin by regulating its dissociation rate. This gives rise to mechanochemical feedback since controlling myosin levels controls actomyosin flows, and thus flow-based PAR complex transport [6, 8–11, 20].
Fig. 1. Mechanochemical feedback in PAR polarity establishment.
a, Example of PAR and myosin protein concentration and velocity fields obtained at a single time point during polarity establishment from confocal medial sections using MACE (4 minutes after flow onset; blue, PAR-2::GFP representing pPARs; red, PAR-6::mCherry representing aPARs; grey, NMY-2::GFP; see Methods). Scale bar, 5 µm. A and P denote the anterior and posterior, respectively. x indicates the position along the circumference, with the posterior pole at x = 0. b, Average NMY-2 dissociation rates as measured by FRAP for unperturbed, par-2, par-6 and par-2 / par-6 double RNAi embryos as a function of position and cortical PAR state (see schematics at the bottom); see Supplementary Fig. 2d-g for statistics. c, NMY-2 dissociation rates as a function of PAR-6 concentration. Solid line represents a linear fit with slope kAM = -0.002 ± 0.0007 µm2 s−1 and intercept koff,M = 0.117 ± 0.009 s−1. Due to uncertainties in the determining the PAR-6 concentration, condition [6] (par-2 RNAi, posterior side) was not included (Supplementary Fig. 2h). d, NMY-2 association rates as a function of position and cortical PAR state (see schematics at the bottom). Error bars are standard error of the mean.
Feedback structures allow non-equilibrium systems to spontaneously break symmetry and form self-organized patterns [27–29]. However, external signals can couple to self-organized Turing-like systems, for breaking symmetry and for guiding mechanisms of pattern formation to realize appropriate spatiotemporal profiles of constituents [30–37]. We next set out to investigate the relationship between feedback and guidance in PAR polarization, and develop a theory of guided mechanochemical self-organization where PAR distributions, myosin distribution and cortical flow pattern are all interdependent and respond to guiding cues. We aimed for a description that is simple enough to capture all relevant processes, but still contains enough detail to be of predictive power. Two feedback mechanisms are included: antagonism between anterior and posterior PAR proteins is captured by a mass-conserved Turing-like system [6, 38, 39], and mechanochemical feedback is captured by coupling the Turing-like system to an active fluid to describe the mechanics of the actomyosin cortex [20, 40]. In addition, two guiding cues modify PAR and myosin concentration fields over space and time to steer the polarization process. We write reaction-advection-diffusion equations for the cell surface concentration fields of PAR-2 (P), PAR-6 (A), and myosin (M) as representatives for the posterior PAR complex, the anterior PAR complex, and the contractile actomyosin cortex, respectively (Fig. 2a). We consider azimuthal symmetry around the long axis of the egg, and pursue a 1D description with periodic boundary conditions, where the spatial coordinate x denotes the distance along the surface to the posterior pole (−L/2 < x < L/2, with L denoting the circumference of the embryo; Fig. 1a).
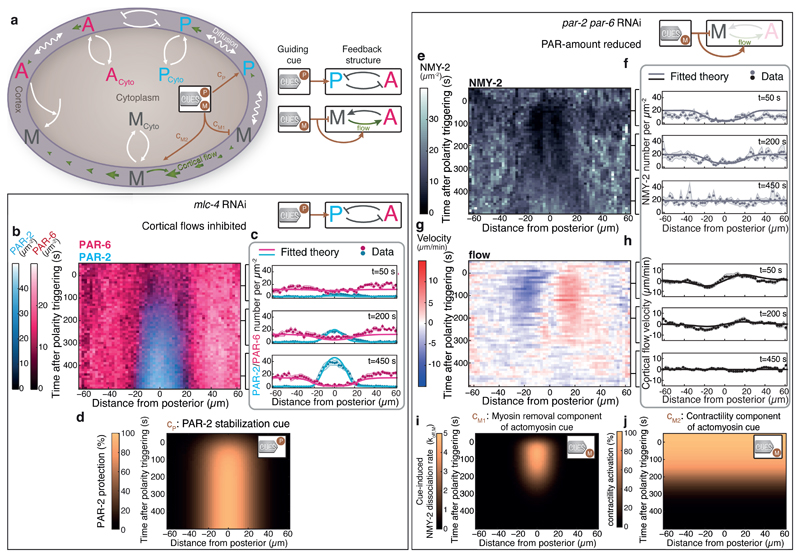
Fig. 2. Isolating both guiding cues by RNAi and determining their spatiotemporal profiles.
a, M, A, P, represent myosin, aPARs and pPARs, respectively. These are located either in the cytoplasm or at the cortex where they are subjected to lateral diffusion and advective transport by cortical flow. We consider spontaneous association and dissociation to and from the cortex, mutual inhibitory interactions between the aPARs and the pPARs in the cortex-associated state, as well as an aPAR-dependent regulation of cortical myosin concentration. Two polarity triggers steer the polarization process, one impacts on the cortical pPAR concentration (cP: PAR-2-stabilization cue, see text for details), and one impacts on the actomyosin cortex with two components (cM1: myosin removal cue component, cM2: contractility cue component, see text for details). b, Average spatiotemporal distributions of aPARs (PAR-6::mCherry) and pPARs (PAR-2::GFP) over the time-course of polarity establishment obtained by MACE and with mlc-4 RNAi to inhibit cortical flows (N=8 embryos, Supplementary Fig. 7b). c, Best fits from theory (displayed at t = 50 s, 200 s and 450 s; solid lines; Supplementary Video 1) to MACE data (dots, shaded regions represent standard error of the mean) are used to determine d, the spatiotemporal profile of the PAR-2 stabilization cue cP, which reduces the anterior PAR complex-dependent inhibition of PAR-2. e, Average spatiotemporal profile of myosin (NMY-2::GFP) during par-2 and par-6 double RNAi to inactivate the PAR system (N = 8 embryos, Supplementary Discussion and Supplementary Fig. 10,11). g, Corresponding average myosin flow field (N = 10 embryos, see Methods). f,h, Best fits from theory (displayed at t = 50 s, 200 s and 450 s; Supplementary Video 2) to MACE data (dots, shaded regions represent standard error of the mean) are used to determine i, the spatiotemporal profile of the myosin removal cue component cM1, which increases the myosin dissociation rate, and j, the spatiotemporal profile of the actomyosin contractility cue component cM2, which controls the mechanical contractility of the cortex.
| (1) |
| (2) |
| (3) |
Here, v denotes the cortical flow velocity, and DA, DP, and DM describe the respective diffusion coefficients of the three species in the cortex-associated state. Antagonistic feedback between the two PAR species is controlled by kAP and kPA [6, 21], and mechanochemical feedback arises from the regulation of the myosin dissociation rate by aPARs via kAM (Fig. 1c). Note that our experimental measurement of the PAR-6 dependent dissociation rate of myosin does not rule out additional regulatory interactions between the PAR proteins and the actomyosin cortex. Spontaneous binding and unbinding rates of S ∈ {A, P, M} are denoted by kon,S and koff,S, respectively. Oligomerization states of aPAR and pPAR complexes [9–11, 41] are captured via effective coefficients, nonlinear interactions and the stoichiometric coefficients α, β [6]. All species obey mass-conservation, and cytoplasmic concentrations Acyto, Pcyto, and Mcyto are determined by where ρSV is the total number of molecules of type S ∈ {A, P, M}. Cytoplasmic volume is denoted by V, and ψ is the surface-to-volume ratio. Finally, we consider two guiding cues, the PAR-2 stabilization cue cP (reducing the inhibition of aPARs onto pPARs) and the actomyosin cue. The latter consists of two cue components, a myosin removal component cM1 (increasing the spontaneous NMY-2 dissociation rate), and a contractility component cM2 (modifying overall contractility):
| (4) |
| (5) |
Here FP(x) and FM(x) characterize the impact of the respective cues in a region around the posterior pole with a gaussian profile, while fP(t), fM(t), and fC(t) characterize the respective time-dependent behaviors of cues and cue components, smoothly transitioning between off- and onstates (Supplementary Equations (28-32), Supplementary Fig. 6). κP and κM scale the amplitudes of the respective cues. Contractility C depends on myosin concentration M, and gradients in C drive cortical flows, which are resisted by an effective cortex viscosity η and frictional drag γ with membrane and cytoplasm according to [20]:
| (6) |
with a hydrodynamic length-scale [42], C* a proportionality constant, and M* a contractility saturation constant. Supplementary Fig. 12 provides an analysis how sensitive this theory is to changes in each of the 28 parameters. Seven of these parameters are known (Supplementary Table 2, [6, 23, 42, 43]). In this study, we directly measured ten more parameters (Supplementary Tables 2,3, Fig. 1c,d, Supplementary Fig. 3-6). We determined the remaining eleven parameters by a systematic parameter inference procedure, where numerical solutions are compared to the experimental dynamics of Figure 2 (Supplementary Fig. 13-15, see and Supplementary Information, section 2.6 for details), With this approach, we i) characterized spatiotemporal activity profiles of guiding cues, and ii) calibrated our theory by determining all interactions and parameters of the PAR - actomyosin patterning system.
We first determined the spatiotemporal activity profiles of guiding cues, by fitting measured distributions of aPARs, pPARs, and myosin together with the cortical flow to our theoretical description (Supplementary Information, section 2.6). For each cue we utilized RNAi to perform our analysis in a reduced system, where a guiding cue is singled out. First, we isolated the PAR-2 stabilization cue (cP, Fig. 2a) by suppressing cortical flows via RNAi of the regulatory myosin light chain mlc-4, which inhibits advective transport of PAR proteins (Supplementary Fig. 7a,b). Using MACE, we showed that PAR domains still form under mlc-4 RNAi (Fig. 2b), consistent with previous work [5, 15]. Here, the spatiotemporal dynamics of PAR proteins (Fig. 2b) are driven by the PAR-2 stabilization cue and PAR-reaction-chemistry-dependent feedback alone. Applying a systematic parameter inference procedure, we quantified four kinetic parameters of the PAR interaction network (the antagonistic interaction strengths kAP, kPA and the association rates kon,A, kon,P; eqs. 1,2,5, Supplementary Information, section 2.6, Supplementary Tables 1,2) together with the spatiotemporal activity profile of the PAR-2 stabilization cue onto the PAR system (Fig. 2d, Supplementary Information, section 2.4-2.6). With this, we can quantitatively account for the measured PAR distributions over the entire polarization process under mlc-4 RNAi (Fig. 2c, Supplementary Video 1). We find that the PAR-2 stabilization cue is turned on with a characteristic time scale of 74 ± 4 seconds, acts over almost half the surface of the embryo (width: 57.2 ± 0.3 µm) and protects approximately 95% of the PAR-2 proteins from aPAR-dependent antagonism [5] near the posterior pole (Fig. 2d, Supplementary Table 2). To conclude, we have quantified the spatiotemporal activity profile of the PAR-2 stabilization cue.
Second, we characterized the actomyosin guiding cue, which triggers cortical flows. This cue consists of two components: First, a contractility component initially increases myosin activity throughout the entire cortex in preparation for polarity establishment, and later globally down-regulates myosin activity when PAR domains are established [18]. Second, a myosin removal component locally removes myosin in the vicinity of the centrosome at the posterior pole for a transient period of time, to generate a contractile imbalance that initiates cortical flows [19]. Since both the PAR system (Fig. 1c) and this two-component actomyosin guiding cue impact on myosin, we set out to render the PAR system ineffective in order to isolate the actomyosin cue. Double-RNAi of par-2 and par-6 reduced the PAR-2 and PAR-6 amounts to a degree that the regulation of PARs on myosin is negligible (see Supplementary Discussion, section 1.1 and Supplementary Fig. 10,11). An active-fluid description of actomyosin (eqs. 3,4,6; Supplementary Table 1) together with a systematic parameter inference procedure (Supplementary Information, section 2.4-2.6) allowed us to quantify two physical parameters of the actomyosin system (C* and M*, which control the relation between myosin concentrations and contractility, Supplementary Information, section 2.6, Supplementary Tables 1,2) together with the activity profile of both components of the actomyosin cue. With this, our theory describes at a quantitative level the measured NMY-2 distribution and cortical flow field under double RNAi of par-2 and par-6 (Fig. 2f,h, Supplementary Video 2). We find that the myosin removal component of the actomyosin cue down-regulates NMY-2 by increasing its dissociation rate by a factor of about 6 in a restricted region close to the posterior pole (width: 31.7 ± 1.2 µm) for a time of 204 ± 10 s (Fig. 2i) [19]. The contractility component of the actomyosin cue is active even before polarity initiation at t = 0 s, and its time of inactivation appears to coincide with the inactivation of the myosin removal component (Fig. 2j, Supplementary Fig. 5). To summarize, we have inactivated mechanochemical feedback to isolate both the PAR and the actomyosin subsystems in order to i) determine the strength of all unknown interactions in our theoretical description and ii) quantify the spatiotemporal profile of both guiding cues.
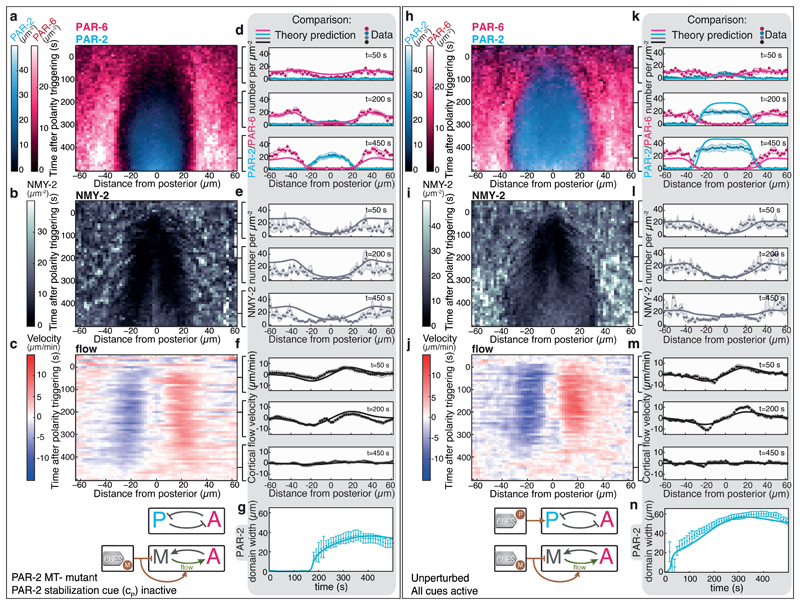
We next tested if our theory correctly describes how feedback structures and guiding cues together orchestrate PAR polarity establishment. To this end, we set out to predict the spatiotemporal evolution of PAR polarization in the full system and in presence of mechanochemical feedback (Fig. 1c), starting from the unpolarized state that is perturbed by both cues (Fig. 2). We investigated two conditions, unperturbed PAR polarity establishment (Fig. 3h-j) as well as PAR polarity establishment for a PAR-2 mutant with an inactive PAR-2 stabilization cue [5] (referred to as PAR-2 MT-; Fig. 3a-c). We obtained a theoretical prediction for both conditions by numerically solving equations 1-6 (Supplementary Table 1) using above-determined parameter values (Supplementary Tables 2,3) and setting the strength of the PAR-2 stabilization cue to zero for the PAR-2 MT-condition. We find good agreement between theoretical predictions and experimental data for all fields measured (Fig. 3d-g, k-n, Supplementary Videos 3,4). PAR-2 dynamics are captured better for PAR-2 MT- as compared to the unperturbed case, which is indicative of an alteration of the spatiotemporal dynamics of the PAR-2 stabilization cue between the unperturbed and the mlc-4 RNAi condition we have not considered (Supplementary Fig. 9, Supplementary Video 5). Hence, we are able to account for the spatiotemporal dynamics of the full PAR - actomyosin system, and we conclude that our theory appropriately captures both guidance and feedback.
Fig. 3. Predicting PAR and myosin dynamics in the presence of guiding cues and feedback structures.
a-c, Average spatiotemporal distributions of a, aPARs (PAR-6::mCherry) and pPARs (PAR-2::GFP) (both N = 9 embryos), b, myosin (NMY-2::mKate2; N = 6 embryos) together with c, the myosin flow field (N = 9 embryos) during polarity establishment for the PAR-2 MT-mutant. d-f, Comparison of MACE data for the PAR-2 MT-mutant (dots, shaded regions represent standard error of the mean) to theory predictions (displayed at t = 50 s, 200 s and 450 s; see Supplementary Video 3). h-j, Average spatiotemporal distributions of h, aPARs (PAR-6::mCherry) and pPARs (PAR-2::GFP) (both N = 6 embryos), i, myosin (NMY-2::GFP; N = 8 embryos) together with j, the myosin flow field (N = 12 embryos) during polarity establishment of the unperturbed condition. k-m, Comparison of MACE data for the unperturbed condition (dots, shaded regions represent standard error of the mean) to theory predictions (displayed at t = 50 s, 200 s and 450 s; solid lines); see Supplementary Video 4. g,n, Comparison of the measured and predicted PAR-2 domain width for the unperturbed condition (n) and the PAR-2 MT-mutant (g). Error bars are standard error of the mean.
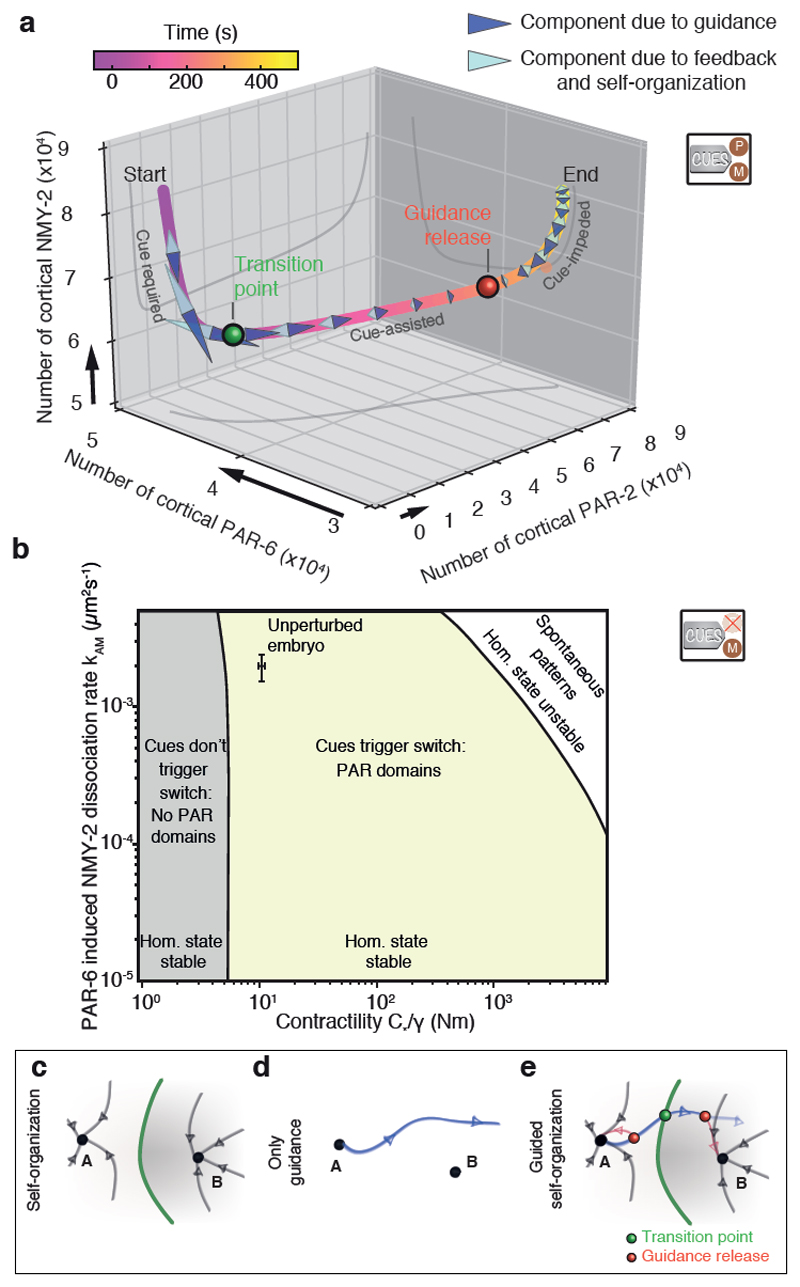
We next set out to investigating the relationship between feedback and guidance. For this, we studied the temporal evolution of the full system in terms of the total numbers of proteins of PAR-2, PAR-6, and NMY-2 associated to the cortex, respectively. We set out to reveal in our theory which interactions drive the system from the unpolarized to the polarized state, differentiating between terms associated to guidance and terms associated to feedback (see Methods; Fig. 2a). We make two observations: first, instantaneously setting to zero all terms associated with guidance prior to approximately 60 s results in the system returning back to the initial and unpolarized state, while the system continues to progress towards the polarized state when these terms are set to zero beyond this point in time (Supplementary Fig. 8). Second, the contribution of guidance terms to the time evolution of the trajectory switches from assisting to impeding (Fig. 4a, light blue arrowheads; also see Methods) at about 260 s. Together, this reveals three phases of polarity establishment: guiding cues are required in the initial phase up to 60 s (transition point, Fig. 4a,e, Supplementary Fig. 8), guiding cues are no longer required but assist the polarization process in a second phase up to 260 s (guidance release, Fig. 4a,e), and guiding cues impedes the process and self-organization takes over in determining the systems’ dynamics in the final phase (Fig. 4a,e).
Fig. 4. Handover from cue-driven to mechanochemically self-organized dynamics.
a, Evolution of the total numbers of cortical PAR-2, PAR-6 and NMY-2 with both cues active, as determined by numerical evaluation of eqs. 1-6. Black arrows denote an increase in protein numbers by 104. Arrowheads indicate projections of time-rate changes induced by guidance (dark blue) and self-organization (light blue) onto the tangent of the trajectory (see Methods). Guidance release (red point at T ≈ 260 s) occurs when the guiding cue component of the evolution dynamics switches from assisting (i.e. pulling forwards along the trajectory) to impeding (pulling backwards along the trajectory). Guiding cues need to be active only up to the transition point at T ≈ 60 s (green dot) to achieve polarization (Supplementary Fig. 8). b, Stability diagram of the homogeneous aPAR-high state as a function of both the contractility strength C*/γ and the aPAR-myosin coupling coefficient kAM. The system is unable to polarize in response to the actomyosin cue (cM1 together with cM2) in the grey region, polarizes in response to the actomyosin cue in the yellow region, and undergoes spontaneous pattern formation in absence of any cue in the white region. c-e, Schematic of the mechanisms of pattern formation via guided mechanochemical self-organization.
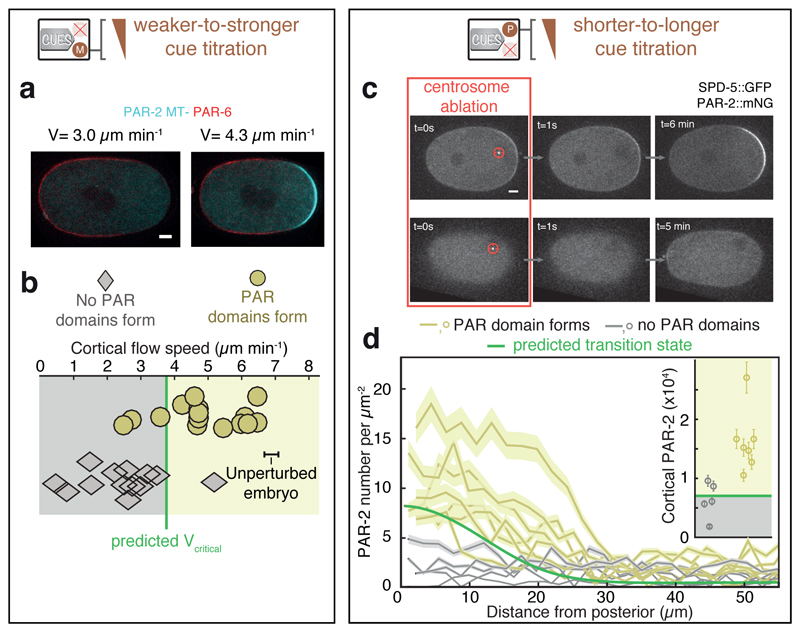
Our analysis indicates that two features are important for achieving controllability and robustness. First, feedback remains subcritical throughout to avoid unstable behaviour and spontaneous pattern formation. Consistent with this, C. elegans zygotes have not been observed to polarize in the absence of cues [1, 5, 44, 45], but how far the PAR - actomyosin patterning system is placed away from a mechanochemical instability is not known [24, 40]. We tested for subcritical feedback in our theory by performing a linear stability analysis of the homogeneous state. We find that the system is poised far away from the unstable regime (Fig. 4b, white region), which allows for control of pattern formation since the system will only polarize in response to guiding cues. Second, to achieve robustness guiding cues need to be strong enough and active long enough to drive the system significantly beyond the ’barrier to polarization’ (i.e. the transition point at 60 s, Fig. 4a). For example, our theoretical analysis suggests that the actomyosin guiding cue is not strong enough to to drive the system beyond the transition state when contractility drops below a critical threshold (Fig. 4b, grey region), and predicts a critical flow speed of 3.7 µm min−1 required for polarization (Fig. 5b). To test this, we isolated the actomyosin cue (PAR-2 MT- mutant condition, Fig. 5a) and gradually reduced cortical flow speeds by performing a series of milder-to-stronger mlc-4 RNAi experiments. Consistent with our prediction, embryos failed to polarize when cortical flow speeds dropped to about half the flow speed of unperturbed embryos (6.9 ± 0.3 µm min−1; Fig. 5b). Hence, the actomyosin cue generates cortical flows that are approximately twice the critical speed required for successful polarization, which provides robustness. Next, we experimentally investigated how long the PAR-2 stabilization cue needs to be active to achieve polarization. We laser-ablated centrosomes at different times ([45]; Fig. 5c), recorded the spatial profiles of the nucleated PAR-2 domain at the moment of ablation and for each experiment, and assessed if embryos continued to evolve towards the polarized state afterwards, or returned back to the unpolarized state (Fig. 5c, see Methods). We found that the minimal PAR-2 domain required for polarization in the experiment (Fig. 5d) was similar to the PAR-2 domain at the transition point as predicted from theory (Fig. 5d, Fig. 4a). Notably, while approximately 70,000 PAR-2 proteins are cortex-associated at the time of guidance release (t=260 s, Fig. 4a), only about 10,000 PAR-2 proteins are required to reach the transition point that needs to be passed for achieving polarization (Fig. 5d). Hence, the PAR-2 stabilization cues drives the system far beyond the ’barrier to polarization’, which provides robustness.
Fig. 5. Robust PAR polarization breaks down close to the transition point.
a, Two individual PAR-2 MT-mutant embryos that were exposed to different mlc-4 RNAi feeding times, resulting in reduced peak cortical flow velocities v (Supplementary Fig. 7c). left: no PAR domains, right: PAR domains form. Scale bar, 5 µm. b, Cortical flow velocities for 28 zygotes, exposed to weaker-to-stronger mlc-4 RNAi. Upper row and yellow circles, embryos successfully polarized (N=15); bottom row and grey diamonds, embryos failed to polarize (N=13). Green vertical line indicates the theoretically predicted critical velocity (vcritical) required for polarization by the actomyosin cue (cM1 together with cM2). The peak cortical flow velocity of unperturbed zygotes (mean ± SEM) is also indicated. c, Inhibition of the centrosomal polarity trigger via laser-ablation. Both centrosomes were ablated, while t =0 s represents the ablation of the second and final centrosome. Dependent on the time-point of ablation, the posterior PAR domain formed (upper row) or failed to form (lower row). Scale bar, 5 µm. d The PAR-2 domain at the moment of the final centrosome ablation. Green line: theoretically predicted transition state. Yellow: zygotes that formed a posterior PAR domain after centrosome ablation (N=7); grey: zygotes that did not form a domain (N=5). Insert: Integrated number of cortical PAR-2 for all zygotes from panel d. Yellow, right column: posterior PAR domain formed (N=7), grey, left column: posterior PAR domain failed to form (N=5), green: transition state.
A fundamental challenge for patterning system is that they typically involve unstable behaviors that are hard to control. Our analysis indicates that polarity pattern formation in C. elegans avoids local instabilities. Feedback structures are subcritical but generate basins of attraction around (at least) two states, one corresponding to the unpatterned and one to the patterned state (Fig. 4c). Guiding cues drive the system away from the unpatterned state (Fig. 4d) and beyond its basin of attraction, and into the vicinity of the patterned state. Finally, self-organization can take over in shaping the time evolution of the system near the patterned state (Fig. 4e). Thus, guiding cues are active for a significant fraction of the trajectory, rendering PAR polarization deterministic and likely conferring robustness. Note that guiding cues can be either temporary and functioning only in triggering pattern formation (as is the case for the actomyosin cue, Fig. 2i, j) or permanent and with a possible role in shaping the final patterned state (PAR-2 stabilization cue, Fig. 2d). Interestingly, two guiding cues shape the self-organized dynamics of the system, and these dynamics are generated by two distinct feedback structures (PAR antagonism, mechanochemical feedback). We speculate that combining several feedback structures and controlling each one with its own guiding cue is a general mechanism for providing specificity and robustness in controlled biological pattern formation.
Methods
C. elegans strains and growth conditions
All strains were maintained at 18°C and imaged at room temperature. Prior to imaging, C. elegans was transferred to 24°C for 12-16 h. To obtain embryos, adult worms were dissected in M9 buffer (22 mM KH2PO4, 42 mM Na2HPO4, 86 mM NaCl) and mounted on agarose pads for imaging. All C. elegans strains, used in this study, are described in Supplementary Table 4. RNA interference was performed using the feeding method, as described in [46]. Feeding times were standardized for each condition, and were typically between 16 h to 24 h.
Image acquisition
All spinning-disk confocal movies of C. elegans zygotes were, except otherwise noted, acquired at room temperature, using a Zeiss axiovert observer Z1 equipped with a CSU-X1 Yokogawa spinning disk head using a 63X / 1.2 NA PlanApochromat objective and a Andor iXon emCCD camera. Measurements of the threshold velocity for polarity establishment were performed using the same system equipped with a Hamamatsu ORCA-Flash4.0 V2 CMOS camera. Concentration measurements were performed by acquiring one confocal stack in the mid-plane of the C. elegans zygote with a frame rate of 10 seconds, to reduce photobleaching to below 5 % for 500 seconds. Given a typical number of frames per movie of about 70, we estimate the effect of photobleaching to about 5 % over the course of our experiments (Supplementary Fig. 3d). NMY-2 GFP movies used for flow measurements were obtained in the mid-plane with a frame rate of 1 second, while NMY-2 mKate movies were captured with a frame rate of 2 seconds. Fluorescent Correlation Spectroscopy measurements were acquired with a Zeiss LSM 780 confocal microscope.
FRAP on NMY-2
We performed the Fluorescence Recovery After Photobleacing experiments using an Andor FRAPPA system. We acquired the images as cortical Z-stacks of three planes at 0.5 µm spacing with an interval time of 2 sec between individual stacks (iQ software, Andor Technology). We performed FRAP on GFP-labeled NMY-2 by bleaching a square of (9 µm X 9 µm) with a laser dwell time of 20 µs per pixel. We monitored the recovery for a subsquare (6 µm X 6 µm) at the center of the bleach square. We fitted the recovery curves of each FRAP experiment and determined the characteristic recovery time by fitting the fluorescence-intensity data with an exponential function, from which the mean as well as the standard error of the mean was calculated (Supplementary Fig. 2d-g). In case that the protein reached a steady-state concentration before the FRAP event, this recovery time scale is identical to the dissociation time scale of the bleached protein (Supplementary Discussion 1.2, Supplementary Fig. 1).
Membrane-associated concentration evaluation (MACE)
The fluorescence intensity for GFP, mCherry and mKate2 was calibrated as follows. Initially, we determined the concentration of an in vitro stock solution of GFP, mCherry and mKate2, using a Varian Cary 4000 UV-Vis Spectrophotometer. We then measured the fluorescence intensity of these solutions with known fluorophore concentration, for six concentration values, ranging typically from 500 nM to 10 µM. For each concentration value, we recorded between six to twelve individual intensity measurements, always using a freshly prepared sample. After correcting for camera flatness, we determined the average fluorescence for each measurement as well as the standard deviation between measurements for the same concentration. The corresponding calibration curves are shown in Supplementary Fig. 3e. The calibration factor w was extracted using linear fitting. For a homogeneous fluorophore concentration, the confocal intensity readout per pixel is given by: I = i · N, with i as the intensity per fluorophore and N the number of fluorophores in the confocal volume. This leads to: I = iV ρsolution = w · ρsolution, with V the confocal volume and ρsolution the fluorescence volume density. We obtained w= 21.7 ± 2.2 counts· µm3 for eGFP, w= 10.7 ± 2.0 counts· µm3 for mCherry, w= 14.6 ± 1.4 counts· µm3 for mNeonGreen, and w= 22.5 ± 3.6 counts· µm3 for mKate2. Errors are the 95% confidence interval of a linear regression.
Measuring cytoplasmic concentration over time
The cytoplasmic concentration of PAR-2 (or PAR-2 MT-) and PAR-6 was measured as follows. Initially, for each movie, we subtracted the background intensity and the autofluorescence of N2 C. elegans zygotes. The average fluorescence intensity per pixel of the cytoplasm was determined by averaging between the mean fluorescence intensity of three 4.34 X 4.34 µm ROI’s inside the zygote. The average fluorescence intensity was converted to concentration using the measured conversion factor w, as explained above (see also [25]).
Determining the point-spread function
Quantifying the fluorescence intensity, originating from the membrane-bound protein fraction, requires the characterization of the broadening of the emitted fluorescent light due to diffraction and scattering inside the C. elegans zygote. Therefore, we measured the point-spread function of GFP and mCherry tagged PH-domain as membrane-bound reporter. In Supplementary Fig. 3g,h, we show the fluorescence intensity of PH::GFP and PH::mCherry in the maintenance phase. The intensity profile, perpendicular to the membrane was extracted around the cell-periphery, using image segmentation via the Matlab KoreTechs package [47]. For each intensity profile along the membrane, we fitted a Gaussian function added to an error function, which accounts for the higher cytoplasmic concentration, compared to the cell exterior,
with C as the background, Ig and σg as the amplitude and width of the Gaussian, Icyto the intensity of the cytoplasm and x0 as the position of the membrane. We fitted each individual profile along the membrane (typically around 300 profiles per frame) and determined the average width per embryo, which we repeated for several embryos. This yielded σg = 329.6 nm ± 7.3 nm (STD) (PH::GFP, N=8) and σg = 320.7 nm ± 18.9 nm (STD) (PH::mCherry, N=9). We compared this width to the width of the point spread function of individual 100 nm TetraSpeck fluorescence beads (Invitrogen) to σ = 185 nm in x and y and 510 nm in z (N=6) (Supplementary Fig. 3k). We assume that the dominating factor of the broadening of the membrane-associated signal originates from light scattering inside the C. elegans zygote, which explains the slightly larger width of the diffraction signal for light with shorter wavelength.
Measuring kymographs of protein concentration at the membrane
In short, spatiotemporal concentration measurements were performed in two steps. First, kymographs for NMY-2, PAR-2 and PAR-6 were determined, using custom-developed MATLAB code (see also [48]), which, similar to deconvolution, recovers the integrated, diffraction-corrected fluorescence intensity coming from fluorescently tagged proteins, which in our case are membrane-associated. Second, we used this fluorescence intensity to infer protein concentrations using a calibration procedure similar to [25]. In detail, all movies were background- and autofluorescence subtracted. Then, each frame of individual movies was segmented, using the KoreTechs Package [47]. Each segmentation was converted in a Bezier-smoothed curve with a separation of one pixel size between adjacent segmentation points. For all frames and all segmentation points, the fluorescence intensity profile perpendicular to the cell membrane was determined, for a length of 4.3 µm. The fluorescence signal of membrane-bound proteins is broadened due to diffraction, with a point spread function
Since σ characterizes the length where the amplitude drops by e−0.5, the PSF volume is characterized by
with a volume of
and an illuminated area of a membrane in the x-z plane
This implies that the surface concentration is given by:
Here, σ denotes the surface concentration, N the number of proteins in the confocal volume, APSF the surface of the membrane, illuminated by the confocal microscope, VPSF the volume of the point-spread function, σy the width of the point-spread function in the y-direction, ρ the fluorophore density, w the fluorescence calibration factor (Supplementary Fig. 3e) and I the intensity. Note that we choose the coordinate system such that x and z lie in the membrane plane and y is perpendicular to the membrane. The fluorescence intensity I was obtained by, for each individual profile along the membrane, fitting the intensity profile with:
We binned these resulting kymographs over 2.17 µm in space (10 pixel).
Generating ensemble-averaged concentration and flow fields
We synchronized individual kymographs in space and time using the geometric posterior pole and the beginning of cortical flows as reference points (x = 0, t = 0). For PAR concentration fields for mlc-4 RNAi, we synchronized individual kymographs in time to the onset of cytokinesis. We then characterized the time between polarity establishment and cytokinesis to typically 850 s, and then generated ensemble averaged PAR concentration fields where t = 0 denotes triggering of polarity establishment. For creating an ensemble averaged concentration field, we discarded all measurements that show non-stereotypic initiation of cortical flows, away from the posterior pole (with a tolerance of 10 µm).
Determining total protein amounts
We determine the total protein amount as the sum of the cortical and the cytoplasmic amount. The cytoplasmic amount was determined by determining the average cytoplasmic concentration, as explained above, and integration over the ellipsoidal zygote, using a=27 µm, b=15 µm and c=15 µm as semi-axis of the ellipsoid. The cortical amount was determined by first generating calibrated kymographs of the protein of interest. We then integrated the protein amount over the ellipsoid. Therefore we first reparameterized the kymographs from distance to the posterior to angle with respect to the anterior-posterior axis. Simplifying the embryonic shape as ellipsoid, we can then integrate the protein amount using:
with Ptotal(t) the protein amount on the cell surface and P(ϕ,Θ) as the protein concentation on the cell surface. Assuming azimuthal symmetry, a kymograph along Θ provides sufficient information on the total cortical bound protein fraction (Supplementary Fig. 3i,j,l-q).
FCS measurement of the total protein amounts
We first determined the confocal volume of the Zeiss LSM 780 confocal microscope. Therefore we measured autocorrelation spectra for GFP in solution, with 4 different concentrations (300 nM, 100 nM, 10 nM, 3 nM). Fitting each autocorrelation allows for the determination of the number of fluorophores in confocal volume, which translates to a confocal volume in the case that the fluorophore concentration is known [49], yielding Vconf = 3.2994e−16l. Next we determined the number of PAR-2::GFP molecules inside the confocal volume, in the one-cell C. elegans embryo by measuring autocorrelation spectra, for six embryos at a total of 21 different locations. We calculated the concentration, measured by FCS by dividing the number of PAR-2::GFP by the confocal volume (Supplementary Fig. 3a-c).
Determining the NMY-2 association rate
The association rate of NMY-2 from the cytoplasm to the actin cortex was calculated, assuming local binding equilibrium (Supplementary Figure 2a,c), such that with M the cortical NMY-2 concentration, kon,M,eff the effective association rate and koff,M,eff the effective dissociation rate. Using FRAP, we measured koff,M,eff (Fig. 1b), while using MACE, we measured M (Supplementary Fig. 2a,b) in the anterior and the posterior domain. We thus calculated the effective association rate in both domains to: posterior: kon,M,eff,P = 2.1 ± 0.4 µm−2s−1, anterior: kon,M,eff,A = 1.9 ± 0.4 µm−2s−1. Thus, the effective association rate appears identical, in both domains, with an average of kon,M,eff = 2.0 ± 0.4 µm−2s−1. The effective association rate and the association rate of NMY-2 (kon,M) are related via kon,M,eff = kon,MMCyto, with MCyto the cytoplasmic NMY-2 concentration. We measured the average NMY-2 cytoplasmic concentration for the wild type to MCyto = 10.4 ± 1.4 µm−3 (Supplementary Fig. 3m). We therefore obtained the NMY-2 association rate kon,M = 0.199 ± 0.04 µms−1.
Determining the ratio of labeled to unlabeled protein
For our quantification of the PAR-2 and PAR-6 amount, we used strains that posses a fluorescently tagged transgene and the endogenous, untagged gene. We quantified the ratio of labeled to unlabeled protein by western blotting C. elegans embryos against PAR-2 and PAR-6 (Supplementary Fig. 3f). We found a ratio of GFP labeled to unlabeled PAR-2 of 0.91 and a ratio of mCherry labeled to unlabeled PAR-6 to 0.71.
Determining the width of the posterior domain
The posterior PAR domain width was determined at each time point, by fitting the function P1 [erf ((x − P2)/P4) − erf ((x − P3)/P4)] + P5, to the ensemble-averaged concentration of PAR-2 as well as the theoretical prediction of the PAR-2 concentration. The domain width was then given by P3 − P2. The experimental error was obtained by also fitting the above function to each individual movie of polarity establishment of the ensemble (N=6, unperturbed, N=9, PAR-2 MT-) and calculating the standard error of the mean of the quantity P3 − P2. For very small domains, this fitting routine becomes sensitive to the experimental noise profile. We thus restrained domain fitting of the experimental profiles to time-points where the fitting procedure detected a finite domain in the theoretical prediction.
NMY-2 diffusion constant bound to the actomyosin cortex
We measured the diffusion constant of GFP-labeled NMY-2 mini-filaments by analyzing individual mini-filament trajectories. We imaged C. elegans zygotes with a frame rate of 5 Hz and analyzed these movies using u-track [50]. During the flow-phase, we found that the mean square displacement grows quadratic in time, as expected for directed movement (Supplementary Fig. 4a). We inhibited cortical flows and thus the directed motion of NMY-2 using ect-2 RNAi. Then the mean square displacement grew linear in time, indicating diffusive motion (Supplementary Fig. 4b,c). We analyzed 7 movies of GFP-tagged NMY-2 under the ect-2 RNAi condition. We restricted our analysis to NMY-2 tracks with a minimum length of 3 seconds, resulting in 657 tracks in total. Fitting the mean square displacement with a linear function yields DM = (0.054 ± 0.08) µm2s−1. Here the uncertainty was evaluated by quantifying the standard deviation of the diffusion constant among the 657 tracks.
Trajectory analysis of the PAR-myosin system
We represent the temporal evolution of the PAR - actomyosin patterning system by the trajectory of the total number of cortical or membrane-bound PAR-2, PAR-6 and NMY-2, which change in time according to equations 1-6. Practically, we integrated the theoretical prediction for the unperturbed PAR-myosin system over the entire cortex (Fig. 3k,l). We observe that the membrane-bound PAR-6 numbers reduce marginally, that NMY-2 numbers decrease for an interval of about 350 seconds and that the PAR-2 numbers increase in time – a characteristic of the formation of the posterior PAR domain (Fig. 4a). We investigated the transition point of this pattern forming system, which characterizes the following: Initially the system is in a stable, homogeneous state and the cues drive the system towards the patterned state. If the cues are all inactivated shortly after their activation, the self-organized interactions carry the PAR - actomyosin system back to the homogeneous state. If the cues are however active for a longer time, the system can cross the transition point, from which point on the self-organized interactions will carry the system to the patterned state, even when the cues are inactivated (Supplementary Fig. 8a).
Separating guidance from self-organized components during trajectory analysis
In Supplementary Equations (33-35), we separated interactions that give rise to PAR polarity establishment into self-organized (Supplementary Equations (22-24)) and guidance interactions (Supplementary Equations (25,26)). These interactions give rise, at each time-point, to a change in the number of cortical PAR-2, PAR-6 and NMY-2. In Fig. 4a, we display the projection of the guidance-dynamics and the self-organized dynamics on the trajectory of the PAR - actomyosin system. Notably, we observed that initially the cues drive the system from the unpolarized system to the domain state, while the self-organized dynamics aims to drive the system back to the unpolarized state. This situation changes at around t = 260 s. From then on, the self-organized dynamics dominates over the guidance dynamics and drives the zygote to the polarized state.
Determining the critical flow velocity for polarization via flows
To measure the threshold velocity for polarity establishment, we monitored the fluorescently tagged PAR-2 and PAR-6 (using the SWG025 strain) in the confocal mid-plane of the zygote. These embryos were exposed to a range of different feeding times of mlc-4 RNAi. We determined cortical flow velocities for mlc-4 RNAi by investigating the displacement-field of yolk granules adjacent to the actomyosin cortex, using the freely available PIVlab MATLAB algorithm [51]. 2D velocity fields were obtained as in [20] (Supplementary Fig. 7c). Each embryo then was classified as polarized or unpolarized by monitoring the occurrence of a posterior PAR domain close to cytokinesis and an asymmetric cell division. We determined the theoretical prediction by calculating the spatiotemporal solutions of the PAR - actomyosin system for different values of the scaled contractility strength C*/γ. For each solution, we monitored the peak actomyosin flow velocity and the maximum PAR-2 concentration 500 seconds after polarity triggering. We determined the critical flow velocity by fitting the data to CP2(v) = A · tanh(B · (v−vcrit))+1)+C, with A the saturation value, B the steepness, C the offset and vcrit the critical flow velocity.
Determining the transition-state PAR-2 domain size by centrosome laser ablation
Laser ablation of the centrosome was performed in a C. elegans strain with SPD-2 labeled with GFP and PAR-2 labeled with mNeonGreen, while using mlc-4 RNAi. We conducted centrosome ablation using methods similar to those in [20].We performed ablation by applying 10 ultraviolet pulses at 1 kHz on the circumference of a circle with a diameter of 0.5 µm at 9 equidistant sites. We ablated both centrosomes at different time-points during the first cell stage, when their distance to the membrane was larger than typically 2 µm, to avoid membrane rupture. After ablation, we imaged the zygote for typically 5 minutes. We scanned for the re-appearance of the centrosome, which occurs in case the centrosome was only bleached, for cell rupture or for membrane damage, resulting in cytoplasmic leakage, and excluded all these from our data-set. From 72 centrosome ablation experiments, 12 were considered successful. At the time-point of the second centrosome ablation, we used MACE to measure the spatial profile of the PAR-2 domain as well as the integrated number of cortical PAR-2.
Supplementary Material
Acknowledgments
P.G. acknowledges a EMBO Long-Term Fellowship for funding. K.V.K.’s research is supported by the Department of Biotechnology, India through a Ramalingaswami re-entry fellowship, and the Max Planck Society and the Department of Science and Technology, India through a Max Planck Partner Group at ICTS-TIFR. N.W.G. was supported by the Francis Crick Institute, which receives its core funding from Cancer Research UK (FC001086), the UK Medical Research Council (FC001086), and the Wellcome Trust (FC001086) and is a member of the GENiE network supported by COST Action BM1408 and EMBO. S.W.G was supported by the DFG (SPP 1782, GSC 97, GR 3271/2, GR 3271/3, GR 3271/4), the European Research Council (grant No 281903 and 742712), ITN grants 281903 and 641639 from the EU, the Max-Planck-Society as a Max-Planck-Fellow, and the Human Frontier Science Program (RGP0023/2014). J.S.B. acknowledges the Human Frontier Science Program for funding. We thank Dan Dickinson, Bob Goldstein, Fumio Motegi, and Geraldine Seydoux for sharing C. elegans strains. We thank Pierre Gönczy, Lars Hubatsch, Tony Hyman, Karsten Kruse, and Michel Labouesse for discussion and insightful comments on the manuscript.
Footnotes
Data and Code Availability Statement
All data generated or analyzed in this study, as well as code to analyze data and perform numeric simulations is available upon request.
Authors Contribution:
P.G. performed experiments and K.V.K. developed the theory, with help from all authors. Data was analyzed together with input from all authors, and P.G., K.V.K., F.J. and S.W.G. wrote the manuscript.
Competing Interests:
The authors declare no competing interests.
References
- [1].Motegi Fumio, Seydoux Geraldine. The PAR network: redundancy and robustness in a symmetry-breaking system. Philosophical Transactions of the Royal Society B: Biological Sciences. 2013;368(1629) doi: 10.1098/rstb.2013.0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Hoege Carsten, Hyman Anthony A. Principles of PAR polarity in Caenorhabditis elegans embryos. Nature Reviews Molecular Cell Biology. 2013;14(5):315–322. doi: 10.1038/nrm3558. [DOI] [PubMed] [Google Scholar]
- [3].Lang Charles F, Munro Edwin. The PAR proteins: from molecular circuits to dynamic self-stabilizing cell polarity. Development. 2017;144(19):3405–3416. doi: 10.1242/dev.139063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Goldstein Bob, Macara Ian G. The PAR proteins: Fundamental players in animal cell polarization. Developmental Cell. 2007;13(5):609–622. doi: 10.1016/j.devcel.2007.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Motegi Fumio, Zonies Seth, Hao Yingsong, Cuenca Adrian A, Griffin Erik, Seydoux Geraldine. Microtubules induce self-organization of polarized PAR domains in Caenorhabditis elegans zygotes. Nature Cell Biology. 2011;13(11):1361–1367. doi: 10.1038/ncb2354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Goehring Nathan W, Trong Philipp Khuc, Bois Justin S, Chowdhury Debanjan, Nicola Ernesto M, Hyman Anthony A, Grill Stephan W. Polarization of PAR Proteins by Advective Triggering of a Pattern-Forming System. Science. 2011;334(6059):1137–1141. doi: 10.1126/science.1208619. [DOI] [PubMed] [Google Scholar]
- [7].Trong Philipp Khuc, Nicola Ernesto M, Goehring Nathan W, Kumar K Vijay, Grill Stephan W. Parameter-space topology of models for cell polarity. New Journal Of Physics. 2014;16 [Google Scholar]
- [8].Munro Edwin, Nance Jeremy, Priess James R. Cortical flows powered by asymmetrical contraction transport PAR proteins to establish and maintain anterior-posterior polarity in the early C. elegans embryo. Developmental Cell. 2004;7(3):413–424. doi: 10.1016/j.devcel.2004.08.001. [DOI] [PubMed] [Google Scholar]
- [9].Wang Shyi-Chyi, Low Tricia Yu Feng, Nishimura Yukako, Gole Laurent, Yu Weimiao, Motegi Fumio. Cortical forces and CDC-42 control clustering of PAR proteins for Caenorhabditis elegans embryonic polarization. Nature Cell Biology. 2017;19(8):988–995. doi: 10.1038/ncb3577. [DOI] [PubMed] [Google Scholar]
- [10].Rodriguez Josana, Peglion Florent, Martin Jack, Hubatsch Lars, Reich Jacob, Hirani Nisha, Gubieda Alicia G, Roffey Jon, Fernandes Artur Ribeiro, Johnston Daniel, St, Ahringer Julie, et al. aPKC Cycles between Functionally Distinct PAR Protein Assemblies to Drive Cell Polarity. Developmental Cell. 2017;42:400–415. doi: 10.1016/j.devcel.2017.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Dickinson Daniel J, Schwager Francoise, Pintard Lionel, Gotta Monica, Goldstein Bob. A Single-Cell Biochemistry Approach Reveals PAR Complex Dynamics during Cell Polarization. Developmental Cell. 2017;42(4):416–434. doi: 10.1016/j.devcel.2017.07.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Schneider Stephan Q, Bowerman Bruce. Cell polarity and the cytoskeleton in the Caenorhabditis elegans zygote. Annual Review of Genetics. 2003;37:221–249. doi: 10.1146/annurev.genet.37.110801.142443. [DOI] [PubMed] [Google Scholar]
- [13].Cheeks Rebecca J, Canman Julie C, Gabriel Willow N, Meyer Nicole, Strome Susan, Goldstein Bob. C. elegans PAR proteins function by mobilizing and stabilizing asymmetrically localized protein complexes. Current Biology. 2004;14(10):851–862. doi: 10.1016/j.cub.2004.05.022. [DOI] [PubMed] [Google Scholar]
- [14].Beatty Alexander, Morton Diane G, Kemphues Kenneth. PAR-2, LGL-1 and the CDC-42 GAP CHIN-1 act in distinct pathways to maintain polarity in the C. elegans embryo. Development. 2013;140(9):2005–2014. doi: 10.1242/dev.088310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Zonies Seth, Motegi Fumio, Hao Yingsong, Seydoux Geraldine. Symmetry breaking and polarization of the C. elegans zygote by the polarity protein PAR-2. Development. 2010;137(10):1669–1677. doi: 10.1242/dev.045823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Nance Jeremy, Zallen Jennifer A. Elaborating polarity: PAR proteins and the cytoskeleton. Development. 2011;138(5):799–809. doi: 10.1242/dev.053538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Gross Peter, Kumar K Vijay, Grill Stephan W. How active mechanics and regulatory biochemistry combine to form patterns in development. Annual Review of Biophysics. 2017;46(1):337–356. doi: 10.1146/annurev-biophys-070816-033602. [DOI] [PubMed] [Google Scholar]
- [18].Tse Yu Chung, Werner Michael, Longhini Katrina M, Labbe Jean-Claude, Goldstein Bob, Glotzer Michael. RhoA activation during polarization and cytokinesis of the early Caenorhabditis elegans embryo is differentially dependent on NOP-1 and CYK-4. Molecular Biology of the Cell. 2012;23(20):4020–4031. doi: 10.1091/mbc.E12-04-0268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Motegi Fumio, Sugimoto Asako. Sequential functioning of the ECT-2 RhoGEF, RHO-1 and CDC-42 establishes cell polarity in Caenorhabditis elegans embryos. Nature Cell Biology. 2006;8(9):978–985. doi: 10.1038/ncb1459. [DOI] [PubMed] [Google Scholar]
- [20].Mayer Mirjam, Depken Martin, Bois Justin S, Juülicher Frank, Grill Stephan W. Anisotropies in cortical tension reveal the physical basis of polarizing cortical flows. Nature. 2010;467(7315):617–621. doi: 10.1038/nature09376. [DOI] [PubMed] [Google Scholar]
- [21].Sailer Anne, Anneken Alexander, Li Younan, Lee Sam, Munro Edwin. Dynamic Opposition of Clustered Proteins Stabilizes Cortical Polarity in the C. elegans Zygote. Developmental Cell. 2015;35(1):131–142. doi: 10.1016/j.devcel.2015.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Goehring Nathan W, Chowdhury Debanjan, Hyman Anthony A, Grill Stephan W. FRAP Analysis of Membrane-Associated Proteins: Lateral Diffusion and Membrane-Cytoplasmic Exchange. Biophysical Journal. 2010;99(8):2443–2452. doi: 10.1016/j.bpj.2010.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Goehring Nathan W, Hoege Carsten, Grill Stephan W, Hyman Anthony A. PAR proteins diffuse freely across the anterior-posterior boundary in polarized C. elegans embryos. Journal of Cell Biology. 2011;193(3):583–594. doi: 10.1083/jcb.201011094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Nishikawa Masatoshi, Naganathan Sundar Ram, Juülicher Frank, Grill Stephan W. Controlling contractile instabilities in the actomyosin cortex. eLife. 2017;6 doi: 10.7554/eLife.19595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Wu JQ, Pollard TD. Counting cytokinesis proteins globally and locally in fission yeast. Science. 2005;310(5746):310–314. doi: 10.1126/science.1113230. [DOI] [PubMed] [Google Scholar]
- [26].David Daryl JV, Tishkina Alisa, Harris Tony JC. The PAR complex regulates pulsed actomyosin contractions during amnioserosa apical constriction in Drosophila. Development. 2010;137(10):1645–1655. doi: 10.1242/dev.044107. [DOI] [PubMed] [Google Scholar]
- [27].Turing Alan M. The Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society of London Series B-Biological Sciences. 1952;237(641):37–72. [Google Scholar]
- [28].Kondo Shigeru, Miura Takashi. Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation. Science. 2010;329(5999):1616–1620. doi: 10.1126/science.1179047. [DOI] [PubMed] [Google Scholar]
- [29].Marcon Luciano, Sharpe James. Turing patterns in development: what about the horse part? Current Opinion in Genetics & Development. 2012;22(6):578–584. doi: 10.1016/j.gde.2012.11.013. [DOI] [PubMed] [Google Scholar]
- [30].Mikhailov Alexander S, Showalter Kenneth. Control of waves, patterns and turbulence in chemical systems. Physics Reports-Review Section of Physics Letters. 2006;425(2–3):79–194. [Google Scholar]
- [31].Prokopenko Mikhail. Guided self-organization. HFSP Journal. 2009;3(5):287–289. doi: 10.2976/1.3233933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Otsuji Mikiya, Ishihara Shuji, Co Carl, Kaibuchi Kozo, Mochizuki Atsushi, Kuroda Shinya. A mass conserved reaction-diffusion system captures properties of cell polarity. PLOS Computational Biology. 2007;3(6):1040–1054. doi: 10.1371/journal.pcbi.0030108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Jilkine Alexandra, Edelstein-Keshet Leah. A Comparison of Mathematical Models for Polarization of Single Eukaryotic Cells in Response to Guided Cues. PLOS Computational Biology. 2011;7(4) doi: 10.1371/journal.pcbi.1001121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Wu Fabai, Halatek Jacob, Reiter Matthias, Kingma Enzo, Frey Erwin, Dekker Cees. Multistability and dynamic transitions of intracellular Min protein patterns. Molecular Systems Biology. 2016;12(6) doi: 10.15252/msb.20156724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Raspopovic J, Marcon L, Russo L, Sharpe J. Digit patterning is controlled by a bmp-sox9-wnt turing network modulated by morphogen gradients. Science. 2014;345:566–570. doi: 10.1126/science.1252960. [DOI] [PubMed] [Google Scholar]
- [36].Corson Francis, Couturier Lydie, Rouault Herve, Mazouni Khalil, Schweisguth Francois. Self-organized Notch dynamics generate stereotyped sensory organ patterns in Drosophila. Science. 2017;356(6337):501–508. doi: 10.1126/science.aai7407. [DOI] [PubMed] [Google Scholar]
- [37].Zagorski Marcin, Tabata Yoji, Brandenberg Nathalie, Lutolf Matthias P, Tkačik Gašper, Bollenbach Tobias, Briscoe James, Kicheva Anna. Decoding of position in the developing neural tube from antiparallel morphogen gradients. Science. 2017;356(6345):1379–1383. doi: 10.1126/science.aam5887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Lee Sungrim Seirin, Shibata Tatsuo. Self-organization and advective transport in the cell polarity formation for asymmetric cell division. Journal of Theoretical Biology. 2015;382:1–14. doi: 10.1016/j.jtbi.2015.06.032. [DOI] [PubMed] [Google Scholar]
- [39].Halatek Jacob, Frey Erwin. Rethinking pattern formation in reaction–diffusion systems. Nature Physics. 2018;14:507–514. [Google Scholar]
- [40].Bois Justin S, Juülicher Frank, Grill Stephan W. Pattern Formation in Active Fluids. Physical Review Letters. 2011;106(2) doi: 10.1103/PhysRevLett.106.028103. [DOI] [PubMed] [Google Scholar]
- [41].Arata Yukinobu, Hiroshima Michio, Chan-Gi Pack, Ravikrishna Ramanujam, Motegi Fumio, Nakazato Kenichi, Shindo Yuki, Wiseman Paul W, Sawa Hitoshi, Kobayashi Tetsuya J, Brandāo Hugo B, et al. Cortical Polarity of the RING Protein PAR-2 Is Maintained by Exchange Rate Kinetics at the Cortical-Cytoplasmic Boundary. Cell Reports. 2016;16(8):2156–2168. doi: 10.1016/j.celrep.2016.07.047. [DOI] [PubMed] [Google Scholar]
- [42].Saha Arnab, Nishikawa Masatoshi, Behrndt Martin, Heisenberg Carl-Philipp, Juülicher Frank, Grill Stephan W. Determining Physical Properties of the Cell Cortex. Biophysical Journal. 2016;110(6):1421–1429. doi: 10.1016/j.bpj.2016.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Robin Francois B, McFadden William M, Yao Baixue, Munro Edwin M. Single-molecule analysis of cell surface dynamics in Caenorhabditis elegans embryos. Nature Methods. 2014;11(6):677–682. doi: 10.1038/nmeth.2928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Munro Edwin, Bowerman Bruce. Cellular Symmetry Breaking during Caenorhabditis elegans Development. Cold Spring Harbor Perspectives in Biology. 2009;1(4) doi: 10.1101/cshperspect.a003400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Cowan Carrie R, Hyman Anthony A. Centrosomes direct cell polarity independently of microtubule assembly in C. elegans embryos. Nature. 2004;431(7004):92–96. doi: 10.1038/nature02825. [DOI] [PubMed] [Google Scholar]
- [46].Kamath RS, Ahringer J. Genome-wide RNAi screening in Caenorhabditis elegans. Methods. 2003;30(4):313–321. doi: 10.1016/s1046-2023(03)00050-1. [DOI] [PubMed] [Google Scholar]
- [47].Sedzinski Jakub, Biro Mate, Oswald Annelie, Tinevez Jean-Yves, Salbreux Guillaume, Paluch Ewa. Polar actomyosin contractility destabilizes the position of the cytokinetic furrow. Nature. 2011;476(7361):462–466. doi: 10.1038/nature10286. [DOI] [PubMed] [Google Scholar]
- [48].Blanchoud Simon, Busso Coralie, Naef Felix, Goenczy Pierre. Quantitative Analysis and Modeling Probe Polarity Establishment in C. elegans Embryos. Biophysical Journal. 2015;108(4):799–809. doi: 10.1016/j.bpj.2014.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Ruettinger S, Buschmann V, Kraemer B, Erdmann R, Macdonald R, Koberling F. Comparison and accuracy of methods to determine the confocal volume for quantitative fluorescence correlation spectroscopy. Journal of Microscopy. 2008;232(2):343–352. doi: 10.1111/j.1365-2818.2008.02105.x. [DOI] [PubMed] [Google Scholar]
- [50].Jaqaman Khuloud, Loerke Dinah, Mettlen Marcel, Kuwata Hirotaka, Grinstein Sergio, Schmid Sandra L, Danuser Gaudenz. Robust single-particle tracking in live-cell time-lapse sequences. Nature Methods. 2008;5(8):695–702. doi: 10.1038/nmeth.1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Thielicke William, Stamhuis Eize J. PIVlab - Towards User-friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. Journal of Open Research Software. 2014;2(1) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.