Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2018 Feb 2;3(2):1425–1436. doi: 10.1021/acsomega.7b01862

High-Throughput Acoustofluidic Self-Assembly of Colloidal Crystals

Meghana Akella 1, Jaime J Juárez 1,*
PMCID: PMC6641480  PMID: 31458472

Abstract

graphic file with name ao-2017-018629_0009.jpg

Colloidal crystals are encountered in a variety of energy-harvesting applications, where they serve as waveguides or filters for electromagnetic and electro-optic energy. Techniques such as electric or magnetic assembly are used to assemble colloidal crystals, but are limited by crystal size, yield, and throughput. This article demonstrates the continuous, high-throughput assembly of two-dimensional (2D)-colloidal crystals in an acoustofluidic flow cell. The device is fabricated using off-the-shelf components and does not require a clean-room access. An experimental state diagram shows how the fluid flow rate and voltage applied to the piezoelectric element in our device can tune the crystal microstructure. Highly ordered colloidal crystals are continuously assembled in less than a minute with a throughput yield of several hundred particles per minute using this device. The acoustically assembled ordered 2D crystals are immobilized using a UV-curable resin and extracted as ordered polymer–particle fibers, demonstrating the ability of using acoustic fields to assemble ordered structures embedded in bulk materials. Particle tracking is used to construct the cross-channel particle distribution to understand the effect of acoustic compression on colloidal crystal assembly. Microparticle image velocimetry data is compared to a theoretical transport model to quantify the effect fluid flow and acoustic trapping has on the colloidal crystal ensemble.

Introduction

Manufacturing defect-free ordered materials are immensely important for producing materials with applications to energy-harvesting1−4 components for subdiffraction limited imaging5 or as waveguides6 for electromagnetic energy due to their unique physical and chemical properties, when compared to their bulk counterparts.7−9 Assembling ordered structures using individual colloidal particles as building blocks is a bottom-up manufacturing process, where colloids form ordered microstructures in the presence of an externally applied field (e.g., electric,10−12 magnetic,13−16 and acoustic17−20). External fields offer a pathway toward mediating self-assembly due to short assembly time scales and controllability. Externally driven self-assembly processes can form single crystals in a short span of time,21 typically ranging from a few seconds to a few hours.22 Particles can be controlled and positioned individually using feedback methods or annealing techniques, allowing for external control of crystal growth.23,24 However, the assembly is conducted in small batches with limited material throughput,18,21,23,25 making it difficult to produce bulk materials at the scale required for many applications. Producing ordered materials in bulk using batch production increases the manufacturing time and complexity of production, as materials are processed in small batches and then assembled separately to form bulk materials. External fields require specific material properties (e.g., dielectric, ferro- or paramagnetic) to drive the assembly of sedimented microparticles in solution to form two-dimensional (2D) ordered structures. Many of the external field techniques require photolithography to fabricate electrodes to generate the required external field patterns, which increases cost and device complexity due to the clean-room operations and expensive equipment required for lithography techniques and to conduct the experiment.

In comparison to other directed techniques, acoustically driven self-assembly can be done on a variety of materials, as sound waves exert a mechanical force on the particles and do not require specific electrical, magnetic, or chemical material properties. An acoustically driven system only requires a difference in density and material compressibility between the colloidal particles and solution to drive assembly.17,26 Complex microstructures can be obtained using acoustic wave interference that can be created using off-the-shelf piezoelectric elements, eliminating the need for photolithography.17,18,27 Particles assemble at the nodes (or antinodes) in the acoustic field, irrespective of the geometry of the experimental assembly chamber or electrodes. Hence, an acoustically directed assembly does not require electrodes with complex geometries for assembly, eliminating the need for complex photolithography equipment and clean-room settings.28 Acoustically driven assembly can be done using off-the-shelf devices, making the process affordable and accessible.29 Acoustic fields act over large areas (∼1000 mm2), enabling large-scale assembly of colloidal particles,30−32 as opposed to the nano- or micrometer-sized batch assemblies demonstrated using other externally directed assemblies. Acoustic fields drive particles to assemble over short time periods,17,18,28 making the process suitable for continuous throughput production of colloidal crystals.

This article presents a continuous, high-throughput process for producing ordered 2D colloidal crystal structures using acoustofluidic self-assembly of microparticles, using off-the-shelf components, without the need to access a clean room. Fifteen micrometer, non-Brownian polystyrene microparticles dispersed in water are continuously introduced to a glass capillary microfluidic flow cell with a syringe pump. A piezoelectric element attached to the side of the capillary generates an acoustic standing wave inside the microfluidic flow cell. We image the particles at approximately 20 mm from the inlet, by which point sedimentation has caused the particles to settle on the bottom of the capillary. The acoustic standing wave drives sedimented microparticles to assemble at acoustic nodes. Acoustofluidic devices based on glass capillaries have been used to trap Brownian particles31 (∼6 μm) and nanoparticles down to 500 nm.33

An experimental state diagram shows the effect that the fluid flow rate and applied acoustic pressure have on the assembled microstructure. Highly ordered, continuous crystals observed to assemble in less than a minute with a yield throughput rate of several hundred particles per minute were observed under various pressures and flow rates. Finally, the ability to fabricate a bulk material using an acoustically directed assembly is demonstrated by freezing the acoustically assembled particles in a UV-curable resin continuously through the acoustic cell to form ordered microparticle–polymer threadlike structures.

Particle tracking software is used to identify the location of microparticles assembled in ordered structures. This data is used as part of a cross-channel distribution analysis to understand the compressive influence that the acoustic pressure has on the observed structures. The flow cell throughput is quantified using the microparticle image velocimetry (PIV) analysis of optical video microscopy data. The degree of order within the assembled structures is quantified by calculating the experimental order parameter and comparing the number of nearest neighbors to theoretical expectations for an ideal ordered structure.

The approach described in the article can be used to support materials applications for non-Brownian microparticles. Microparticles on the 15 μm diameter scale can influence the optical transmission of white light as long as the particles themselves are part of a superassembly (i.e., composed of other, smaller particles).34 The use of larger particles also offers the possibility of manipulating longer wavelength electromagnetic energy (e.g., near IR emissions), which can only be done by fabricating inverse opal structures.35 This is a challenge due to the fast sedimentation times associated with large diameter colloids. Assembled non-Brownian microparticles are used as a scaffold support material to fabricate immunoassays for the detection of biological molecules.36 Non-Brownian microparticles can act as filler material for polymer composites for enhancing mechanical properties.37 The mechanical properties can be tuned over a wide range of Young’s modulus if the particles are internally ordered.38

Unlike previous demonstrations of batch self-assembly driven by acoustic fields,17,30 the flow-through reactor platform we describe here is capable of using acoustic fields to continuously assemble colloidal particles on the order of several hundred particles per minute. The flow-through reactor configuration of our microfluidic cell lends itself well to additive manufacturing and rapid prototyping platforms, leading to an increase in throughput, material yield, reduced operating costs, and improved production time. Future work will focus on mitigating defects in assembled structures and applying this platform to additive manufacturing of polymer–particle composites, where the degree of order between particles can influence composite mechanical38 or optical39 properties.

Results

Acoustic Force

Acoustic waves produced by a mechanically oscillating force will transport particles to nodes (or antinode) depending on differences in particle–fluid density and compressibility. In our experiment, colloidal crystals are assembled in a capillary using an acoustic standing wave generated by a piezoelectric element. Upon applying the acoustic field, the colloidal particles assemble at the acoustic node (i.e., the region of minimum acoustic energy), forming colloidal crystals. The acoustic cell fabrication and setup are discussed in the Experimental Setup section.

Acoustic energy is dominantly influenced by the compressibility and density of the fluid–particle system. The acoustic energy exerted on a small particle by an acoustic wave is given by17,40

graphic file with name ao-2017-018629_m001.jpg 1
graphic file with name ao-2017-018629_m002.jpg 2
graphic file with name ao-2017-018629_m003.jpg 3

where Ucomp represents the energy contribution due to the compressibility mismatch between the particle and solution resulting from the local acoustic pressure and Udens models how the acoustic energy acts on the fluid–solid system when there is a density mismatch, whereas P is the acoustic wave pressure, Vp is the volume of the particle, ρ is the density, c is the velocity of sound, β is the compressibility, λ is the wavelength, and k = 2π/λ is the wavenumber. The subscripts s and f represent the solid particle and fluid, respectively. The angled brackets represent the time-averaged pressure, where P(x) = Po cos(kx) sin(ωt) represents a model for acoustic pressure distribution our device. The prefactor, Po, is the pressure wave magnitude, and ω is the pressure wave frequency. Colloidal particles in an acoustic field assemble at the node or antinode, depending on the acoustic contrast factor of the particle–fluid system. The acoustic contrast factor is defined by eq 4

graphic file with name ao-2017-018629_m004.jpg 4

where ρ is the density, β is the compressibility. The subscripts s and f represent the solid particle and fluid, respectively.

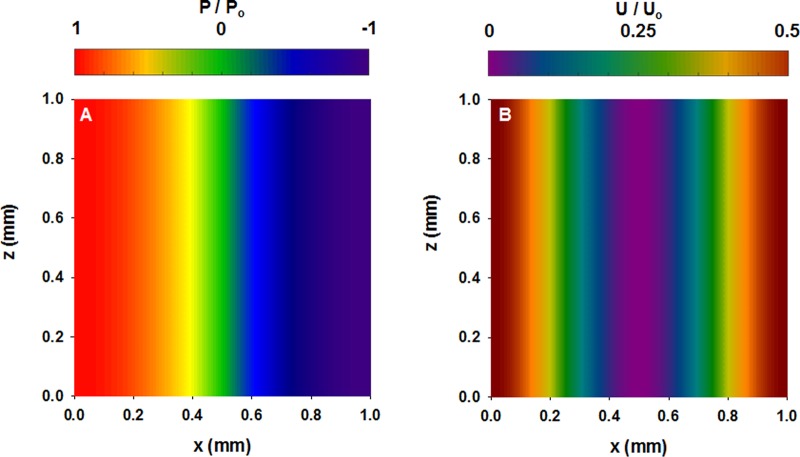
The normalized acoustic pressure distribution and the corresponding normalized acoustic energy distribution in our capillary system are shown in Figure 1A,B, respectively. A detailed explanation of the energy and pressure equations defined to simulate the field distribution is described in the Supporting Information. In our experiment, a single node is formed in the center of the capillary using a sine wave, creating at the point of 0 acoustic pressure and minimum energy point within the capillary. This minimum energy zone in the center of the capillary occupies the full length of the capillary, which helps assemble the colloidal particles into ordered crystals.

Figure 1.

Figure 1

Open in a new tab

(A) Acoustic pressure distribution normalized by the pressure amplitude and (B) the acoustic energy arising from the pressure distribution normalized by the acoustic energy amplitude.

State Diagram

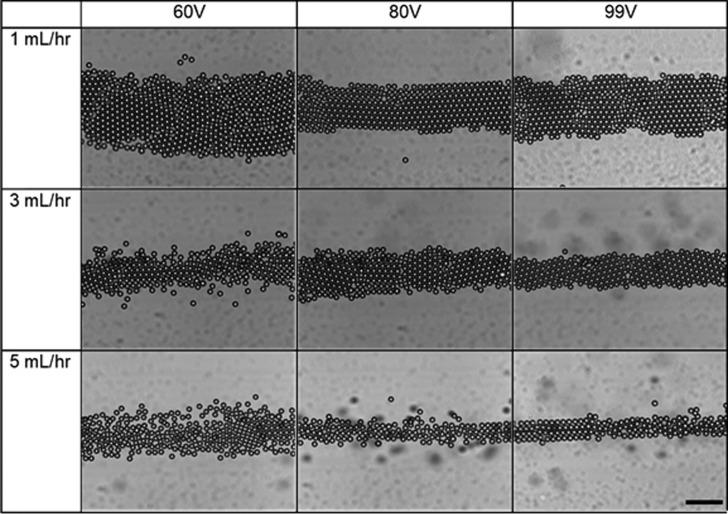
The acoustic contrast factor is positive for the system examined in this work (Φ = 0.393) on the basis of the density and compressibility values of water and polystyrene stated in the Supporting Information. The larger effect of density over compressibility based on the acoustic contrast factor leads particles to assemble at the standing wave node located in the center of the capillary. The particles’ assembly time varied from 30–40 s to up to 2–3 min, depending on the applied acoustic pressure and flow conditions. The assembly was examined at three different voltages (60, 80, and 99 Vpp) and flow rates (1, 3, and 5 mL/h) to understand the effect of acoustic compression and flow rate on microstructure, as shown in the state diagram in Figure 2 for a fixed nominal resonance frequency of 830 kHz.

Figure 2.

Figure 2

Open in a new tab

State diagram of the assembled microstructures observed at various applied voltages (60, 80, and 99 Vpp) and flow rates (1, 3, and 5 mL/h). Scale bar is 100 μm.

In this experiment, because we are using non-Brownian microparticles, nucleation and 2D crystal formation occur solely due to the packing of spherical particles induced by acoustophoretic transport to the acoustic node. Nucleation of non-Brownian microparticles into hexagonally close-packed structures was previously observed as a result of ultrasound energy input.41 Péclet numbers calculated in Table S1 also indicate that transport is primarily convection driven as opposed to Brownian motion. As the applied voltage increases, the increasing acoustic pressure on the colloidal particles induces hexagonal close-packing. Particles form crystals but have line and point defects in the 1 mL/h case when voltage is applied at 60 Vpp. At 80 Vpp and 1 mL/h, we observe the formation of a colloidal crystal with less defects, as shown in Movie 1, Supporting Information. Increasing the voltage to 99 Vpp resulted in an ordered crystal that was acoustically trapped at the node. The crystal did not flow as seen in the 60 and the 80 Vpp cases, as shown in Movie 2, Supporting Information. Because of the high compression, the particles did not have time to rearrange and the defects were formed.

Similar behavior was observed at several other flow rates. At a flow rate of 3 mL/h, particles formed a partially close-packed system. As we increased the voltage further, crystals with line defects were formed at 80 Vpp. Upon increasing the voltage to 99 Vpp, a close-packed structure was observed. At a flow rate of 5 mL/h, particles do not form a close-packed structure at 60 Vpp, as the applied acoustic compression is not sufficient to form a close-packed structure with the increased flow rate. As we increase the applied acoustic pressure, a partially formed crystal and a close-packed microstructure can be observed at 80 and 99 Vpp, respectively.

We observed that as the flow rate increases, the order decreases. A clear demonstration of the effect of the flow rate can be observed at 60 Vpp case in the 1, 3, and 5 mL/h cases. A crystal microstructure is observed at 1 mL/h. At 3 mL/h, a randomly ordered microstructure is formed and at 5 mL/h, a random aggregate is formed, showing that the degree of crystallinity decreases with an increase in the flow rate. The effect of increase in the flow rate on the crystal structure from 1 to 5 mL/h at 99 Vpp can be seen in Movies 2–4, Supporting Information. The crystal formation behaves similar to the crystal kinetics observed previously in results for shear flow colloidal crystal kinetics.42 The 80 Vpp case has behavior similar to that in the 60 Vpp case where a crystalline microstructure is formed at 1 mL/h, followed by a randomly close-packed microstructure at 3 mL/h and finally, a random aggregate for the 5 mL/h case. At 99 Vpp, the 1 and 3 mL/h cases show a close-packed crystal and the 5 mL/h case shows the formation of a small crystallite, demonstrating that acoustic compression is the dominating force compared with the fluid flow at increased applied voltage.

An increased flow rate also increases the rate of crystal formation due to enhanced mass transport. However, above a critical flow rate, it was observed that the crystal formation rate decreases as the flow rate increases. This is a result of flow-displaced crystallized microstructures, where incoming particles do not have adequate time to assemble into close-packed structures. This leads to a decrease in the degree of hexagonal close-packing. We observe this in the case of acoustic assembly at 7 mL/h, where assembly does not occur at 60, 80, or 99 Vpp. When the acoustic field is switched on, an ordered structure can form given sufficient time and particle concentration. However, the fluid flow transports particles faster than they are able to nucleate into crystalline structures, leading to random dispersions like the one shown in Figure S1, Supporting Information.

Polystyrene bead concentration varied due to stochastic addition of particles to the acoustofluidic device during pumping. A decreasing concentration tends to a decreased degree of hexagonal close-packing and increased assembly time. Particles are transported to the acoustic node irrespective of how low the particle concentration is at all of the voltages and flow rates. Although sample concentration affects crystallization, the acoustic field driving particles to assemble at the node acting to locally concentrate the particles is the most critical factor in determining the degree of hexagonal close-packing.

Defect Formation

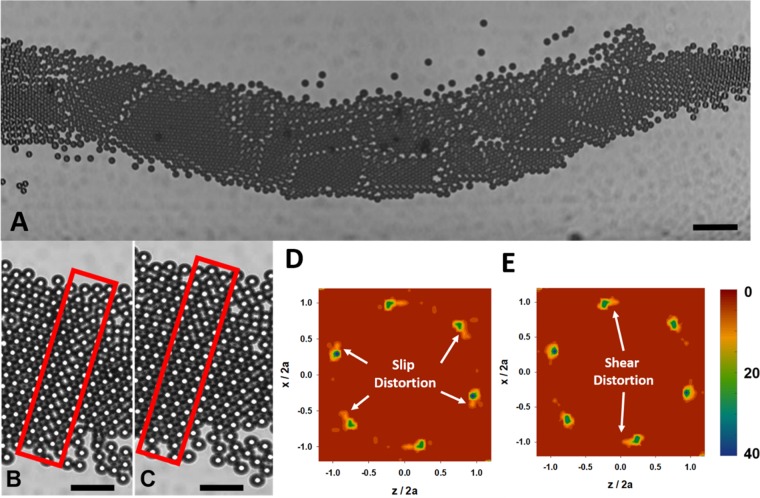
During assembly, we observe defects (e.g., grain boundaries, line, or point defects) and occasionally, curved microstructures, as shown in Figure 3A. Some of these defects arise temporarily from shear slip planes while the crystals assemble and dynamically reach equilibrium under flow. Figure 3B shows the formation of one slip plane as it reorients into a crystalline grain in Figure 3C. Figure 3D shows the radial distribution graph of the slip plane shown in Figure 3B. Tail-like structures can be observed on the region showing the nearest neighbors, denoting a slip plane. Figure 3E shows the radial distribution curve of the reoriented crystal, and the tail-like structures are not found on the nearest neighbors, except in the case of the top and bottom distribution points, denoting the recombination of the slip plane. The tail seen in the top and bottom distribution points is due to the shear flow distortion in the microstructure.43 The slip planes that form in this way influence the placement of incoming particles and crystal grain orientations, which leads to the observed crystal curvature. The formation and reorientation of the slip plane can be seen in Movie 5, Supporting Information.

Figure 3.

Figure 3

Open in a new tab

(A) Various defects (point and line) and grain boundaries form in a crystal assembled at 1 mL/h and 60 Vpp. The scale bar is 100 μm. (B) A slip plane (red box) forms while the colloidal crystal is subject to shear flow. (C) The slip plane reorients itself with a kink in the microstructure observed at the top of the red box, indicating a change in grain orientation. The scale bar for (B) and (C) is 50 μm. (D) A two-dimensional radial distribution of the microstructure shows secondary peaks distorting the microstructure of the colloidal crystal while the slip plane is present. (E) The two-dimensional radial distribution shows that the secondary peaks have subsided, leaving only peaks distorted by the flow.

Crystal Formation in UV-Curable Resin

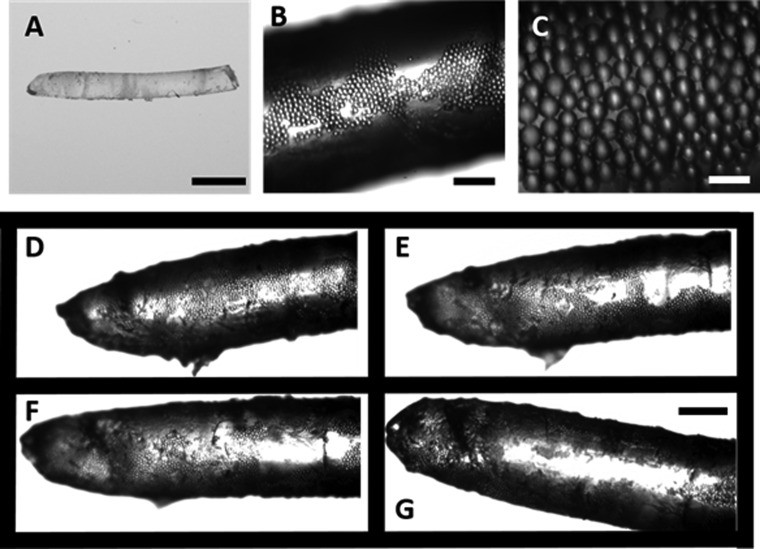
To demonstrate the ability to fabricate composite materials using our acoustic assembly approach, we assemble microparticles in a UV-curable resin. The polystyrene beads are stored in an aqueous solution, and these beads will not form a stable mixture when dispersed in the resin. For demonstration purposes, we used poly(methyl methacrylate) (PMMA) microparticles drawn from a powder and dispersed in the UV resin. The PMMA microparticles suspended in the UV-resin solution assemble at a flow rate of 2 mL/h, an applied voltage of 85 Vpp, and a frequency of 848 kHz. The UV resin is cured in UV light for 2 min and 30 s to freeze the crystals, as shown in Figure 4A. We extracted a sample polymer fiber that is 7.8 mm in length and 0.94 mm in diameter. The resin–particle structures were extracted continuously because the UV curing was done at the end of the tubing. So the UV resin inside the tubing was not cured at any point and was flowing out continuously.

Figure 4.

Figure 4

Open in a new tab

(A) Polymer fiber with ordered microparticles at 1×, which was extruded as a threadlike structure. The scale bar is 2 mm. (B) Ordered PMMA microparticles embedded in the polymer fiber at 10×. The scale bar is 250 μm. (C) A monolayer of ordered microparticles assembled in the polymer at 40×. The scale bar is 50 μm. The PMMA particles form a monolayer of ordered structures on the resin surface (D) due to acoustic assembly and not due to particle concentration, which is demonstrated by sample rotation. On rotation, the particle layer gradually disappears (E, F) and no particles are visible on the opposite face of the sample (G). The scale bar for figures (D)–(G) is 500 μm.

Figure 4B shows a 10× magnified image of the acoustically assembled particle assembly in the resin. Continuous close-packed structures can be observed to form a single layer around the polymer fiber, as shown in a 180° view of the sample shown in Movie 6, Supporting Information. We observe that particles assembled only across a part of the sample and are not distributed randomly across the surface area of the sample. The 40× magnified image of the assembly shows the resin seep in between particles, demonstrating the interparticle bonding of the beads, as shown in Figure 4C. Figure 4D–G shows various rotated positions of the resin fiber, demonstrating a single layer of assembled particles. Figure 4D shows the assembled particles on the surface of the string. Upon rotation, two sections of the polymer and assembled beads can be observed, as shown in Figure 4E,F, showing that the close-packing of particles is due to the acoustic force and not due to fluid shear or particle concentration effects. Upon further rotation, as shown in Figure 4G, the assembled particles are no longer visible and only the resin along with a few random particles is visible, showing that the particles are assembled in a single layer around the resin structure. The position of the particles around the resin demonstrates that the assembly occurs at the bottom of the capillary in the acoustic cell due to sedimentation.

The particle assembly demonstrated using PMMA beads is not as uniform as seen in the polystyrene bead assembly as the dry, unfunctionalized PMMA particles are suspended in the resin solution, and so they do not form a stable solution, as opposed to the functionalized polystyrene solution we used. The PMMA beads are not monodisperse, and the difference in particle sizes causes a nonhexagonal packing of the packing, as shown in Figure 4C.

Discussion

Order Parameters

The average degree of hexagonal close-packing, ⟨C6⟩, is defined as the average number of nearest neighbors of a particle in an ensemble.23 The number of nearest neighbors, Nic, for the particle, i, surrounded by nearest neighbors, j, is calculated within a coordination distance, rc. The ensemble is considered to be crystalline if the crystalline connectivity, χ6 ≥ 0.32. So the nearest neighbors for a given particle can be calculated using44

graphic file with name ao-2017-018629_m005.jpg 5

where χ6ij is defined in the Supporting Information. The average order parameter for the ensemble containing N particles, ⟨C6⟩ is given by

graphic file with name ao-2017-018629_m006.jpg 6

Equations 5 and 6 are used to calculate the experimental ensemble order parameter ⟨C6⟩ for the experiments shown in Figure 2. A detailed derivation of eq 6 is given in the Supporting Information.

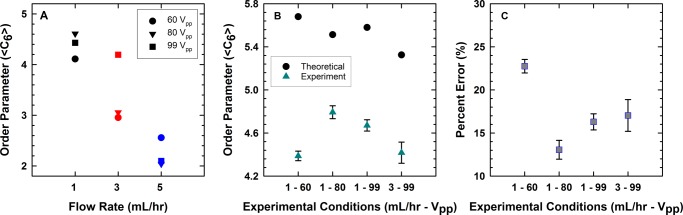
In an ideal infinite two-dimensional crystal composed of particles in a hexagonally close-packed configuration, each particle will have six nearest neighbors. This would yield an average ⟨C6⟩ value of 6 for the crystal. However, a crystal of a limited size and aspect ratio reduces the ideal value of ⟨C6⟩ for the crystals assembled in this work. The theoretical maximum value of ⟨C6⟩ for each of the conditions examined in our state diagram was evaluated using eqs S31 and S32 in the Supporting Information. The values for ideal ⟨C6⟩ range from 5 to 5.7 on the basis of the number of particles assembled under the experimental conditions examined here. Our results from this analysis (Figure 5A) indicate that only four cases (1 mL/h-60 Vpp, 1 mL/h-80 Vpp, 1 mL/h-99 Vpp, and 3 mL/h-99 Vpp) have a high degree of hexagonal order (⟨C6⟩ ∼ 4 or greater), whereas the remainder either exhibit significant polycrystalline order or are completely random. The order parameters shown in Figure 5A have an error of less than 5% and are not represented in the graphs.

Figure 5.

Figure 5

Open in a new tab

(A) Average degree of hexagonal close-packing observed during experimental conditions. The experimental standard deviation was less than 5% of the observed average. (B) Average order parameter with error bars for the four best experimental conditions compared to the expected order parameter theoretically expected on the basis of spherical packing. (C) The percent error between the theoretical and expected values from (B).

The order parameter generally increases with an increased applied voltage and a decreased flow rate, as shown in Figure 5A. At 1 mL/h, the experimentally observed microstructures have an average ⟨C6⟩ that ranges from 4.39 to 4.67, exhibiting crystalline order at all of the flow conditions. At 80 Vpp, the microstructure undergoes rearrangement, which leads to highly ordered colloidal crystals under these conditions. When the colloidal particles become acoustically trapped at 99 Vpp, the acoustic compression immobilizes the grains to form the observed microstructure. At these conditions, the colloids do not have time to assemble into low-defect configurations, leading to a polycrystalline microstructure. At 3 mL/h, ⟨C6⟩ increases with an increase in the applied voltage, as the particles form a crystalline structure due to acoustic compression, whereas at 5 mL/h, ⟨C6⟩ is the highest for the 60 Vpp case compared to that in the 80 and 99 Vpp cases under the same flow rate conditions. The numerical value for the ideal ⟨C6⟩ value is compared with the experimental results for 1 mL/h-60 Vpp, 1 mL/h-80 Vpp, 1 mL/h-99 Vpp, and 3 mL/h-99 Vpp in Figure 5B. The error between the theoretical and experimental values was found to range between 10 and 20%, as shown in Figure 5C. The error observed in our experimental cases arises from point defects, line defects, and grain boundaries. Acoustic trapping and flow effects also play a role in determining the degree of order in observed structures.

Bead Distribution across the Channel

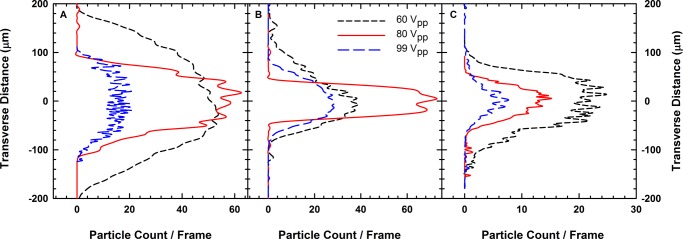
We examine the particle count distribution per captured frame across the capillary to understand the degree of acoustic compression. The transverse x-locations for each particle center identified through image analysis are used to construct a cross-channel bead distribution histogram for all voltages and flow rates examined here. To compensate for differences in optical position of the microscope stage and compare histograms between experiments, we translated the coordinates of each crystal data set. We did this by fitting a Gaussian distribution to each histogram and translating each graph by the mean value.

As shown in Figure 6, at least 600–1300 particles can be assembled to form close-packed structures in the acoustic cell at any given instant within the region of observation, as opposed to the few tens of particles assembled using externally directed assembly batch production techniques. The number of particles in the capillary was obtained from the particle tracking data histograms and is represented by the area under the curves shown in Figure 6A–C. As the pressure of acoustic compression increases, the transverse width of the observed microstructures decreases with an increasing flow rate (Figure 6). Increasing acoustic compression drives colloidal particles to form hexagonally close-packed crystals, which explains the reduction in the width observed at 1 mL/h with increasing voltage (Figure 6A). At 3 and 5 mL/h, the microstructures undergo a reduction in width as the fluid flow stretches the entrained crystals. The trend with increasing voltage observed at 1 mL/h is also observed with 5 mL/h. The voltage trend deviates at 3 mL/h with 80 Vpp, exhibiting a thinner microstructure than with 99 Vpp. We attribute this deviation to the stochastic nature of particle addition to the capillary during the experiment and variations in bead concentration during sample preparation. The crystal curvature will also cause deviations in the observed particle distribution.

Figure 6.

Figure 6

Open in a new tab

Transverse colloidal bead distribution across the x-direction of the capillary flow cell at voltages of 60, 80, and 99 Vpp at (A) 1 mL/h, (B) 3 mL/h, and (C) 5 mL/h.

Effect of the Flow Rate on Crystallization

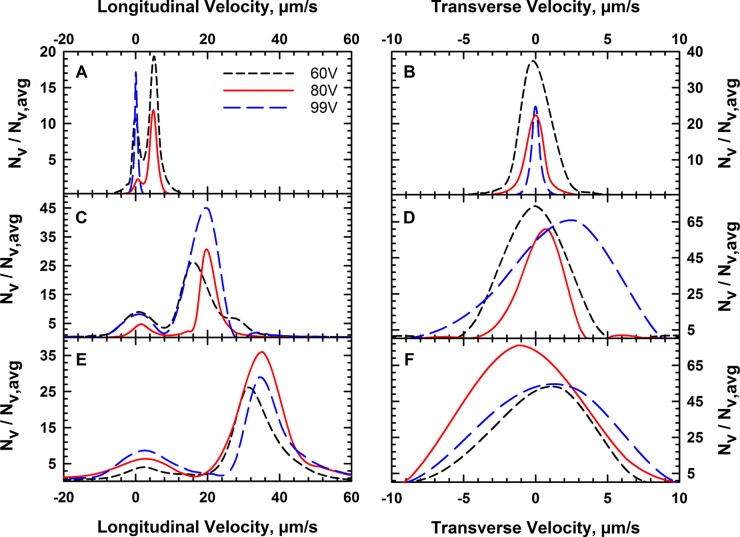
Microparticle image velocimetry was used to evaluate the velocity of the colloids that make up the crystals for the voltage and flow rate conditions examined in Figure 2. The histogram count in the transverse velocity analysis shown in Figure 7B represents the number of vectors of a given magnitude. The velocity vector distribution (Nv) obtained by a PIV analysis was normalized by the average number of velocity vectors for each case to obtain the vector density (Nv,avg). PIV analysis of each case shows that the average velocity increases with the flow rate, as we see an average velocity of 5.7, 18.93, and 33.06 μm/s for 1, 3, and 5 mL/h, respectively. The velocity for each of the nine cases obtained from the micro-PIV analysis is tabulated in Table S1. The distribution of these velocities in the direction of flow (Figure 7A) indicates that the input voltage does not appear to have a strong effect on transport at 3 and 5 mL/h. The input voltage has the strongest effect at 1 mL/h, where the crystal is acoustically trapped at the node and longitudinal velocity is negligible. In a few instances during our experiments, particles stuck to the capillary wall caused other particles to move in the opposite direction of flow as they tried to move around the obstacle. This situation sometimes leads to negative values for longitudinal velocity.

Figure 7.

Figure 7

Open in a new tab

Velocity distribution measured by particle image velocimetry for the cases shown in Figure 3. The longitudinal (z) and transverse (x) velocity distribution for 1 mL/h (A, B), 3 mL/h (C, D), and 5 mL/h (E, F).

On the basis of the width of the crystal and the velocity of the particles in the direction of fluid flow, we estimated the particle throughput per minute, (i.e., new particles being added to the flowing crystal) to range from 300 to 1300 particles, as shown in Table S2 using eq S39 from the Supporting Information. The width of the crystal shown in Figure 6 was accurate in most cases when compared to the number of rows observed in the state diagram and was considered to calculate the throughput using the calculations described in the Supporting Information. However, in a several cases, the crystal was bent, resulting in a slightly higher width than seen experimentally. In such cases, the average number of rows seen in the experimental results was considered to calculate the particle throughput.

The velocities observed here are lower in comparison to what might be expected at the flow rates examined here. Sedimentation within the capillary occurs as the particles are non-Brownian. The Péclet numbers evaluated for each case (Table S2) indicate that convection dominates the transport of particles in our system. Sedimentation causes particles to settle near the capillary wall, where hydrodynamic interactions with the capillary wall hinder particle transport. The average height above the capillary wall is estimated using eq 8, which allows us to estimate the separation between the particle surface and the wall.

The work by Goldman et al. provides us with a way to interpret microparticle image velocimetry data near the wall of the capillary.45 The particle translation velocity, up,z, is measured using optical video microscopy and normalized by a factor of

graphic file with name ao-2017-018629_m007.jpg 7

where Γ is the effective shear rate in the capillary. The dimensionless height, y/a, is a function of B, and we can use the data from Goldman et al. to estimate this functional form as

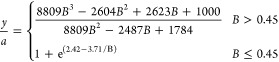graphic file with name ao-2017-018629_m008.jpg 8

Equation 8 provides us with a way to connect the measured translation velocity with the particle’s height above the capillary wall. Equations 7 and 8 are based on hydrodynamic calculations from Goldman et al.45 As the particles settle in flow, they achieve a mechanical equilibrium between sedimentation and electrostatics (see eq S1 in the Supporting Information). Measuring the particle velocity and calculating the effective shear yields the equilibrium height of the particle if eqs 7 and 8 are used. This approach was used to measure the electrostatic interaction between a glass surface and a non-Brownian particle entrained in flow.46 A detailed derivation of the expression is discussed in the Supporting Information.

The analysis suggests that the wall separation varies between ∼3 and 30 nm, as tabulated in Table S1. On average, the wall separation increases with increasing flow rate, suggesting that lift causes the particles to come off the wall. We would expect the wall separation to be an order of magnitude higher on the basis of similar hydrodynamic measurements in the literature;46 however, we attribute the discrepancy to several factors. First, the hindrance factors reported here are for single particles translating above a plane wall and the analysis neglects the effects of hydrodynamics in the presence of multiple particles, which would reduce particle mobility.

Second, our data suggests that an acoustically generated force maybe present normal to the capillary wall, as evidenced by the trapping behavior at 1 mL/h and 99 Vpp. This component likely drives particles down toward the wall, which also reduces particle mobility. This normal force maybe present due to the fact that the piezoelectric element is at a slight angle and is not perfectly perpendicular to the capillary wall as a result of the manufacturing process. The piezoelectric element tilts slightly as the epoxy used to glue the element dries.

Third, it has been shown theoretically that acoustic streaming effects push the particles downward, which may push particles toward the capillary wall, reducing the expected theoretical height.47 The combination of these effects slow particles down and make them to appear as though they have a separation of ∼3–30 nm. The height in the 1 mL/h-99 Vpp case is not calculated as the particles are trapped and no longer flow.

Acoustic Streaming

The transverse component of the velocity (Figure 7B) averages ∼0 μm/s with a negligible standard deviation. This indicates that there is no detectable transport in the transverse direction (i.e., perpendicular to the direction of flow) at steady state, which indicates that significant flows driven by acoustic streaming are not present in this direction. Rayleigh and Eckart streaming are two mechanisms that may contribute to acoustic streaming effects in our device scale. Fluid jets due to Eckart streaming are negligible because our device is small and operates at a low frequency, which reduces the fluid momentum generated by acoustic.48 Rayleigh streaming produces vortices, which we would expect to have significant effect on crystal formation. Literature results from a computational analysis found that the acoustic streaming effect is more significant in the transverse x-direction rather than in the longitudinal z-direction, where the flow of fluid in the capillary is a more significant effect.47 It is possible that the velocity measured in the longitudinal direction is a result of fluid flow due to pumping and acoustic streaming; however, a more detailed study is necessary to decouple the effect of these combined mechanisms.

Conclusions

We demonstrate a continuous flow colloidal crystal fabrication system using acoustofluidic-driven self-assembly. The crystal microstructures observed in this device arise from the combined effects of acoustic compression and hydrodynamic stresses. As acoustic compression increases, the colloidal particles hexagonally close pack to form ordered structures while entrained in a fluid flow. However, we show that it is possible to acoustically trap a crystal structure despite the presence of flow. Microparticle image velocimetry is used to examine the transport of colloidal crystals subject to fluid flow. The average particle velocity and colloidal crystal throughput increase with the flow rate. However, flow rates of 5 mL/h and higher increase particle velocity such that crystalline microstructure is difficult or impossible to maintain under the acoustic field conditions examined in this work. We compare the observed and expected degree of hexagonal close-packing using an order parameter analysis. Overall, the degree of hexagonal close-packing increases with applied acoustic field strength and decreases with the flow rate. We find that experimental structures have a degree of order that deviates from expectations on the basis of spherical packing by 10–20%. This deviation arises from the presence of point and line defects, grain boundaries, acoustic trapping, and flow effects.

The approach demonstrated here can serve as a continuous flow reactor to produce colloidal crystals with energy-harvesting applications. Unlike batch assembly techniques, where the number of input particles is fixed, our platform has a high-throughput yield of several hundred particles per second. The use of off-the-shelf components to fabricate the acoustofluidic cell is advantageous as the device costs less than $20 and does not require any special processes like photolithography. Experiments were done in normal lab conditions instead of a clean-room setting, making it suitable for many applications while using minimal laboratory equipment. The relatively small footprint of the device makes it easy to integrate into complex fluid systems.

Future work will focus on studying the optimum conditions necessary to obtain uniform crystals cured in the resin and design the experimental setup to obtain the resin–particle bonding without the excess polymer demonstrated in this article. Integration of the platform described here with additive manufacturing techniques will enable the production of self-assembled materials on demand with unique material properties. Our experimental setup does not allow us to directly observe nucleation during assembly. We plan to streamline our experimental cell to help us observe this process. Given the defects observed during the experiment, it is necessary to understand the interplay between forces (e.g., acoustic, hydrodynamic, and surface) and how these forces influence assembly kinetics. A more detailed study of dislocation dynamics using an updated experimental cell will allow us to develop real-time annealing techniques to remove defects during crystal formation.

Materials and Methods

Acoustic Cell Fabrication

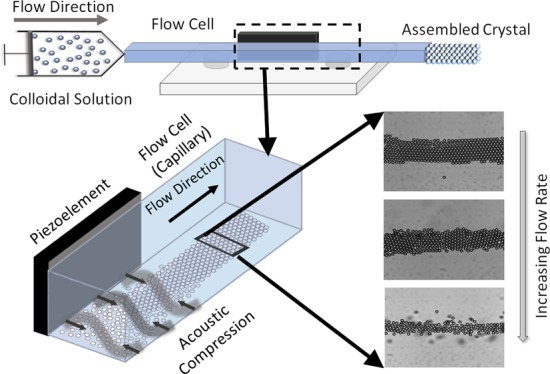
The acoustic cell was prepared using off-the-shelf components without the use of a clean room (Figure 8). A square borosilicate glass capillary (Vitrocom, Catalog# 8100-100) with an inner side dimension of 1 mm and wall thickness of 0.2 mm was cleaned using protocols established for removing contaminants from glass capillaries.49 The glass capillary was immersed in 1% Sparkleen (Fisher Scientific, Catalog# 04-320-4) solution at 80 °C for 30 min. Sparkleen immersion is followed with immersion of the glass capillary in deionized water for 30 min and drying using air. A lead zirconate titanate piezoelement (APC International Inc., P-30.00 mm-5.00 mm-1.00 mm-841 WFB) was attached to the capillary using high-strength epoxy (JB Weld Epoxy Steel Resin) and cured for 24 h at room temperature.

Figure 8.

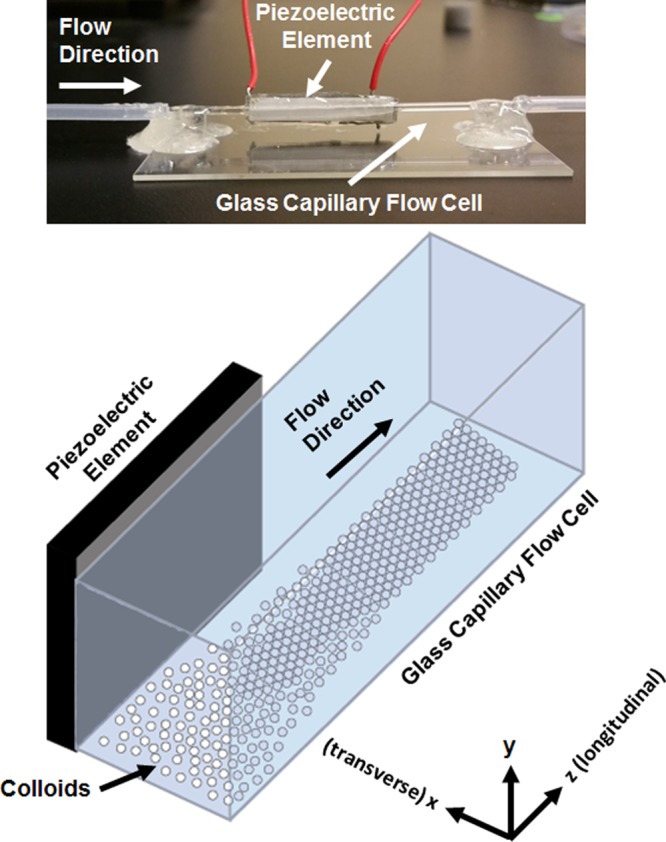
Figure 8

Open in a new tab

(Top) Photographic image of the acoustofluidic device used to assemble colloidal crystals. (Bottom) A schematic representation of the acoustofluidic device during operation.

The acoustofluidic device was fixed on a microscope slide (Fisher Scientific, 12-550-A3) using two poly(dimethylsiloxane) (PDMS) (Ellsworth Adhesives, Part# 184 SIL ELAST KIT 0.5 kG) pillars, 5 mm in diameter and 4 mm high, with epoxy to serve as the supporting element for the capillary. First, the capillary is glued to the PDMS pillars using epoxy (Devcon home 5-minute Epoxy) and is allowed to cure for 24 h. Next, the tubing is glued to the ends of the capillary on both sides and is allowed to cure for 24 h. The setup was allowed to cure for an additional 24 h to ensure that epoxy (Devcon home 5-minute Epoxy) completely bonded the acoustofluidic device to the PDMS pillars. Silicone tubing (VWR International, Catalog# 16211-316) was attached on both ends of the capillary using epoxy. The capillary and tubing are glued at an interval of 24 h and are not glued immediately (as epoxy needs only 15–20 min to set), as attaching the tubing to the capillary immediately causes the capillary to bend, casting a shadow when viewed through the microscope and affecting the imaging process.

Sample Preparation

Polystyrene beads with a 15 μm diameter (Polysciences Inc., Cat# 18328) were used as building blocks to form colloidal crystals. One hundred microliters of polystyrene bead solution was suspended per 1 mL of deionized water sourced from an ARIES High Purity Water System with a 0.2 μm filter (Aries Filterworks).

UV-Resin–Microparticle Solution

Unfunctionalized, dry PMMA particles (27–32 μm diameter) were purchased from Cospheric (PMPMS-1.2 27–32 μm). The UV-curable resin was purchased from Sigma-Aldrich (CPS 1030 UV-A). The resin was diluted using acetone and isopropyl alcohol using a 1:1:1 ratio of the resin and solvents to reduce the viscosity of the resin. The PMMA microparticles were then added to the diluted resin solution.

Experimental Setup

The acoustic cell was fixed to an optical microscope stage. The piezoelement on the acoustic cell was driven with a sine function wave input using a wave function generator (Agilent 33220A). A radio frequency (RF) amplifier (Electronics & Innovation, 210L) with a maximum input of 1 Vrms was used to amplify the signal input into the piezoelement. The amplitude and frequency of the signal from the amplifier was monitored continuously using an oscilloscope (Tektronix, TBS 1052B-EDU). A signal attenuator (Tektronix P2220 Voltage Probe) was used on the oscilloscope to reduce the possibility of damage on the oscilloscope due to high voltage inputs. Two dummy loads of 1 W (Tektronix 011-0049-01) and 50 W (Pasternack PE6234) were used with the wave function generator and the RF amplifier, respectively, to ensure that the circuit remained closed at all times.

The polystyrene bead dispersion was interfaced with the acoustofluidic device through the silicone tubing and introduced into the device with a syringe pump (Lucca Technologies, GenieTouch). The acoustic pressure was generated by applying various voltages to the piezoelement. All experiments were conducted at peak-to-peak voltages of 60, 80, and 99 Vpp as a direct input from the RF amplifier at a fixed frequency of 830 kHz. The colloidal throughput was varied by introducing the dispersion at flow rates of 1, 3, and 5 mL/h using the syringe pump.

At the outlet of the tubing, a 48 W UV-light source (SUNUV SUN2C 48 W LED UV lamp) ranging from 355 to 405 nm was set up and the device was manually operated to be lit up for 4.5 min continuously to obtain continuously cured resin structures. The assembly is cured while the suspension is flowing. The UV lamp is placed at the end of the tubing, and the flow rate and UV exposure time used in this experiment was empirically determined so that the flowing UV resin with the acoustic assembly was cured as it flowed out of the tubing. Our method works as the resin is cured at the exit of the tubing and is not cured while the resin is inside the tubing (which would lead to blocking). The resin–polymer composite cure can be extracted as a continuous process. The flow does not have to stop to extract the cured fibers.

Optical Microscopy and Analysis

An inverted optical microscope (Olympus IX70) was used to observe the assembly process at 10× magnification. Videos were recorded using a scientific complementary metal-oxide-semiconductor camera (QImaging, Optimos). Five hundred frames of video were taken at a frame rate of 10 frames/s. Each pixel in the recorded video was measured to be 885.6 nm with a stage micrometer. The videos were processed and analyzed using the MATLAB Image Processing Toolbox (Mathworks). Each frame was filtered to remove noise before identifying centroid locations. The centroid locations are written to a text file and saved for bead distribution analysis. The images and video for the particle–resin sample were taken using a Lumenera Infinity3 6UR camera mounted on an upright microscope (Leica DM3000).

An open source particle image velocimetry (PIV) package, PIVLab,50−52 was used to identify particle velocity distributions. PIVLab uses a cross-correlation algorithm to calculate particle displacement between two images. Before our images are processed by PIVLab, we crop the frames to remove areas not occupied by beads to eliminate spurious velocity vectors that arise from local intensity variations caused by fluctuations in the light source. Seeding densities below 10 particles per interrogation area within an image will produce faulty vectors for velocimetric data analysis.53 The cropped images are then filtered using a highpass filter and a Wiener denoise filter prior to analysis. The PIV algorithm then divides a frame into smaller interrogation areas and performs a correlation between these areas and the same areas on a consecutive frame to calculate the displacement of particles.

Acknowledgments

M.A. and J.J.J. acknowledge the Iowa State University Microelectronics Research Center through the Catron Fellowship and the College of Engineering Graduate Recruitment Initiative Fellowship for financial support. We also thank Max Noack from the Microelectronics Research Center, Iowa State University for help with the experiment setup.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b01862.

  • List of supporting videos with descriptions of each, a more detailed discussion of the theoretical underpinnings of the platform described here, figures that describe model spherical packing in our device, and tables with information on hydrodynamic measurements conducted by μ-PIV measurements (PDF)

  • Optimum crystal formation at 1 mL/h and 80 Vrms without any defects (AVI)

  • Crystal formation at 1 mL/h and 99 Vrms (AVI)

  • Crystal formation at 3 mL/h and 99 Vrms (AVI)

  • Crystal formation at 5 mL/h and 99 Vrms (AVI)

  • Formation and reorientation of slip plane in a crystal formed at 1 mL/h and 60 Vpp (AVI)

  • Acoustically-assembled particles cured in a UV-curable resin to form bulk material (AVI)

The authors declare no competing financial interest.

Supplementary Material

ao7b01862_si_001.pdf (700.2KB, pdf)
ao7b01862_si_002.avi (4.4MB, avi)
ao7b01862_si_003.avi (5MB, avi)
ao7b01862_si_004.avi (4.8MB, avi)
ao7b01862_si_005.avi (5MB, avi)
ao7b01862_si_006.avi (1.1MB, avi)
ao7b01862_si_007.avi (4MB, avi)

References

  1. Parviz B. A.; Ryan D.; Whitesides G. M. Using Self-Assembly for the Fabrication of Nano-Scale Electronic and Photonic Devices. IEEE Trans. Adv. Packag. 2003, 26, 233–241. 10.1109/TADVP.2003.817971. [DOI] [Google Scholar]
  2. Xia Y.; Gates B.; Li Z.-Y. Self-Assembly Approaches to 3-Dimensional Photonic Crystals. Adv. Mater. 2001, 13, 409–413. . [DOI] [Google Scholar]
  3. Ozin G. A.; Yang S. M. The Race for the Photonic Chip: Colloidal Crystal Assembly in Silicon Wafers. Adv. Funct. Mater. 2001, 11, 95–104. . [DOI] [Google Scholar]
  4. Joannopoulos J. D. Photonics: Self-Assembly Lights up. Nature 2001, 414, 257–258. 10.1038/35104718. [DOI] [PubMed] [Google Scholar]
  5. Lee J. Y.; Hong B. H.; Kim W. Y.; Min S. K.; Kim Y.; Jouravlev M. V.; Bose R.; Kim K. S.; Hwang I.-C.; Kaufman L. J.; et al. Near-Field Focusing and Magnification through Self-Assembled Nanoscale Spherical Lenses. Nature 2009, 460, 498–501. 10.1038/nature08173. [DOI] [Google Scholar]
  6. Takazawa K.; Kitahama Y.; Kimura Y.; Kido G. Optical Waveguide Self-Assembled from Organic Dye Molecules in Solution. Nano Lett. 2005, 5, 1293–1296. 10.1021/nl050469y. [DOI] [PubMed] [Google Scholar]
  7. Brust M.; Schiffrin D. J.; Bethell D.; Kiely C. J. Novel Gold-dithiol Nano-networks with Non-metallic Electronic Properties. Adv. Mater. 1995, 7, 795–797. 10.1002/adma.19950070907. [DOI] [Google Scholar]
  8. Link S.; El-Sayed M. Shape and Size Dependence of Radiative, Non-Radiative and Photothermal Properties of Gold Nanoparticles. Int. Rev. Phys. Chem. 2000, 19, 409–453. 10.1080/01442350050034180. [DOI] [Google Scholar]
  9. Hwang J.-H.; McLachlan D. S.; Mason T. O. Brick Layer Model Analysis of Nanoscale-to-Microscale Cerium Dioxide. J. Electroceram. 1999, 3, 7–16. 10.1023/A:1009998114205. [DOI] [Google Scholar]
  10. Juárez J. J.; Feicht S. E.; Bevan M. A. Electric Field Mediated Assembly of Three Dimensional Equilibrium Colloidal Crystals. Soft Matter 2012, 8, 94–103. 10.1039/C1SM06414B. [DOI] [Google Scholar]
  11. Juárez J. J.; Bevan M. A. Interactions and Microstructures in Electric Field Mediated Colloidal Assembly. J. Chem. Phys. 2009, 131, 134704 10.1063/1.3241081. [DOI] [PubMed] [Google Scholar]
  12. Edwards T. D.; Bevan M. A. Controlling Colloidal Particles with Electric Fields. Langmuir 2014, 30, 10793–10803. 10.1021/la500178b. [DOI] [PubMed] [Google Scholar]
  13. Fang W.-X.; He Z.-H.; Xu X.-Q.; Mao Z.-Q; Shen H. Magnetic-Field-Induced Chain-like Assembly Structures of Fe3O4 Nanoparticles. EPL 2007, 77, 68004 10.1209/0295-5075/77/68004. [DOI] [Google Scholar]
  14. Wang M.; He L.; Yin Y. Magnetic Field Guided Colloidal Assembly. Mater. Today 2013, 16, 110–116. 10.1016/j.mattod.2013.04.008. [DOI] [Google Scholar]
  15. Zerrouki D.; Baudry J.; Pine D.; Chaikin P.; Bibette J. Chiral Colloidal Clusters. Nature 2008, 455, 380–382. 10.1038/nature07237. [DOI] [PubMed] [Google Scholar]
  16. Byrom J.; Han P.; Savory M.; Biswal S. L. Directing Assembly of DNA-Coated Colloids with Magnetic Fields To Generate Rigid, Semiflexible, and Flexible Chains. Langmuir 2014, 30, 9045–9052. 10.1021/la5009939. [DOI] [PubMed] [Google Scholar]
  17. Owens C. E.; Shields C. W.; Cruz D. F.; Charbonneau P.; Lopez G. P. Highly Parallel Acoustic Assembly of Microparticles into Well-Ordered Colloidal Crystallites. Soft Matter 2016, 12, 717–728. 10.1039/C5SM02348C. [DOI] [PubMed] [Google Scholar]
  18. Caleap M.; Drinkwater B. W. Acoustically Trapped Colloidal Crystals That Are Reconfigurable in Real Time. Proc. Natl. Acad. Sci. U.S.A. 2014, 111, 6226–6230. 10.1073/pnas.1323048111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Yang Y.; Pham A. T.; Cruz D.; Reyes C.; Wiley B. J.; Lopez G. P.; Yellen B. B. Assembly of Colloidal Molecules, Polymers, and Crystals in Acoustic and Magnetic Fields. Adv. Mater. 2015, 27, 4725–4731. 10.1002/adma.201500462. [DOI] [PubMed] [Google Scholar]
  20. Wollmann S.; Patel R. B.; Wixforth A.; Krenner H. J. Ultrasonically Assisted Deposition of Colloidal Crystals. Appl. Phys. Lett. 2014, 105, 031113 10.1063/1.4891171. [DOI] [Google Scholar]
  21. Juárez J. J.; Mathai P. P.; Liddle J. A.; Bevan M. A. Multiple Electrokinetic Actuators for Feedback Control of Colloidal Crystal Size. Lab Chip 2012, 12, 4063–4070. 10.1039/c2lc40692f. [DOI] [PubMed] [Google Scholar]
  22. Shah A. A.; Ganesan M.; Jocz J.; Solomon M. J. Direct Current Electric Field Assembly of Colloidal Crystals Displaying Reversible Structural Color. ACS Nano 2014, 8, 8095–8103. 10.1021/nn502107a. [DOI] [PubMed] [Google Scholar]
  23. Juárez J. J.; Bevan M. A. Feedback Controlled Colloidal Self-Assembly. Adv. Funct. Mater. 2012, 22, 3833–3839. 10.1002/adfm.201200400. [DOI] [Google Scholar]
  24. Kim S.; Asmatulu R.; Marcus H. L.; Papadimitrakopoulos F. Dielectrophoretic Assembly of Grain-Boundary-Free 2D Colloidal Single Crystals. J. Colloid Interface Sci. 2011, 354, 448–454. 10.1016/j.jcis.2010.11.023. [DOI] [PubMed] [Google Scholar]
  25. Demirörs A. F. Magnetophoretic Assembly of Anisotropic Colloids for Spatial Control of Reinforcement in Composites. J. Phys. Chem. B 2016, 120, 9759–9765. 10.1021/acs.jpcb.6b05935. [DOI] [PubMed] [Google Scholar]
  26. Gor’kov L. P. On the Forces Acting on a Small Particle in an Acoustical Field in an Ideal Fluid. Phys.-Dokl. 1962, 6, 773. [Google Scholar]
  27. Marzo A.; Seah S. A.; Drinkwater B. W.; Sahoo D. R.; Long B.; Subramanian S. Holographic Acoustic Elements for Manipulation of Levitated Objects. Nat. Commun. 2015, 6, 8661 10.1038/ncomms9661. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Piyasena M. E.; Austin Suthanthiraraj P. P.; Applegate R. W.; Goumas A. M.; Woods T. A.; López G. P.; Graves S. W. Multinode Acoustic Focusing for Parallel Flow Cytometry. Anal. Chem. 2012, 84, 1831–1839. 10.1021/ac200963n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Walsh D. I. III; Kong D. S.; Murthy S. K.; Carr P. A. Enabling Microfluidics: From Clean Rooms to Makerspaces. Trends Biotechnol. 2017, 35, 383–392. 10.1016/j.tibtech.2017.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Thomas M. L.-J.; Drinkwater W. B.; Trask S. T. 3D Printed Components with Ultrasonically Arranged Microscale Structure. Smart Mater. Struct. 2016, 25, 02LT01 10.1088/0964-1726/25/2/02LT01. [DOI] [Google Scholar]
  31. Austin Suthanthiraraj P. P.; Piyasena M. E.; Woods T. A.; Naivar M. A.; Lόpez G. P.; Graves S. W. One-Dimensional Acoustic Standing Waves in Rectangular Channels for Flow Cytometry. Methods 2012, 57, 259–271. 10.1016/j.ymeth.2012.02.013. [DOI] [PubMed] [Google Scholar]
  32. Goddard G.; Martin J. C.; Graves S. W.; Kaduchak G. Ultrasonic Particle-Concentration for Sheathless Focusing of Particles for Analysis in a Flow Cytometer. Cytometry, Part A 2006, 69A, 66–74. 10.1002/cyto.a.20205. [DOI] [PubMed] [Google Scholar]
  33. Mao Z.; Li P.; Wu M.; Bachman H.; Mesyngier N.; Guo X.; Liu S.; Costanzo F.; Huang T. J. Enriching Nanoparticles via Acoustofluidics. ACS Nano 2017, 11, 603–612. 10.1021/acsnano.6b06784. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Vogel N.; Utech S.; England G. T.; Shirman T.; Phillips K. R.; Koay N.; Burgess I. B.; Kolle M.; Weitz D. A.; Aizenberg J. Color from Hierarchy: Diverse Optical Properties of Micron-Sized Spherical Colloidal Assemblies. Proc. Natl. Acad. Sci. U.S.A. 2015, 112, 10845–10850. 10.1073/pnas.1506272112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Askar K.; Leo S.-Y.; Xu C.; Liu D.; Jiang P. Rapid Electrostatics-Assisted Layer-by-Layer Assembly of near-Infrared-Active Colloidal Photonic Crystals. J. Colloid Interface Sci. 2016, 482, 89–94. 10.1016/j.jcis.2016.07.076. [DOI] [PubMed] [Google Scholar]
  36. Zhao Y.; Zhao X.; Sun C.; Li J.; Zhu R.; Gu Z. Encoded Silica Colloidal Crystal Beads as Supports for Potential Multiplex Immunoassay. Anal. Chem. 2008, 80, 1598–1605. 10.1021/ac702249a. [DOI] [PubMed] [Google Scholar]
  37. Cho J.; Joshi M. S.; Sun C. T. Effect of Inclusion Size on Mechanical Properties of Polymeric Composites with Micro and Nano Particles. Compos. Sci. Technol. 2006, 66, 1941–1952. 10.1016/j.compscitech.2005.12.028. [DOI] [Google Scholar]
  38. Tsai P. J.; Ghosh S.; Wu P.; Puri I. K. Tailoring Material Stiffness by Filler Particle Organization. ACS Appl. Mater. Interfaces 2016, 8, 27449–27453. 10.1021/acsami.6b10895. [DOI] [PubMed] [Google Scholar]
  39. Sumioka K.; Kayashima H.; Tsutsui T. Tuning the Optical Properties of Inverse Opal Photonic Crystals by Deformation. Adv. Mater. 2002, 14, 3.. [DOI] [Google Scholar]
  40. Barnkob R.; Augustsson P.; Laurell T.; Bruus H. Measuring the Local Pressure Amplitude in Microchannel Acoustophoresis. Lab Chip 2010, 10, 563–570. 10.1039/b920376a. [DOI] [PubMed] [Google Scholar]
  41. Lash M. H.; Fedorchak M. V.; Little S. R.; McCarthy J. J. Fabrication and Characterization of Non-Brownian Particle-Based Crystals. Langmuir 2015, 31, 898–905. 10.1021/la501511s. [DOI] [PubMed] [Google Scholar]
  42. Holmqvist P.; Lettinga M. P.; Buitenhuis J.; Dhont J. K. G. Crystallization Kinetics of Colloidal Spheres under Stationary Shear Flow. Langmuir 2005, 21, 10976–10982. 10.1021/la051490h. [DOI] [PubMed] [Google Scholar]
  43. Morris J. F.; Katyal B. Microstructure from Simulated Brownian Suspension Flows at Large Shear Rate. Phys. Fluids 2002, 14, 1920–1937. 10.1063/1.1476745. [DOI] [Google Scholar]
  44. Nelson D. R.; Halperin B. I. Dislocation-Mediated Melting in Two Dimensions. Phys. Rev. B 1979, 19, 2457–2484. 10.1103/PhysRevB.19.2457. [DOI] [Google Scholar]
  45. Goldman A. J.; Cox R. G.; Brenner H. Slow Viscous Motion of a Sphere Parallel to a Plane wall—II Couette Flow. Chem. Eng. Sci. 1967, 22, 653–660. 10.1016/0009-2509(67)80048-4. [DOI] [Google Scholar]
  46. Alexander B. M.; Prieve D. C. A Hydrodynamic Technique for Measurement of Colloidal Forces. Langmuir 1987, 3, 788–795. 10.1021/la00077a038. [DOI] [Google Scholar]
  47. Liu Z.; Kim Y.-J.; Wang H.; Han A. Effects of Fluid Medium Flow and Spatial Temperature Variation on Acoustophoretic Motion of Microparticles in Microfluidic Channels. J. Acoust. Soc. Am. 2016, 139, 332–349. 10.1121/1.4939737. [DOI] [PubMed] [Google Scholar]
  48. Wiklund M.; Green R.; Ohlin M. Acoustofluidics 14: Applications of Acoustic Streaming in Microfluidic Devices. Lab Chip 2012, 12, 2438–2451. 10.1039/c2lc40203c. [DOI] [PubMed] [Google Scholar]
  49. Bowman C. L. Quantifying the Cleanliness of Glass Capillaries. Cell Biochem. Biophys. 1998, 29, 203–223. 10.1007/BF02737895. [DOI] [PubMed] [Google Scholar]
  50. Thielicke W.; Stamhuis E. J.. PIVlab - Time-Resolved Digital Particle Image Velocimetry Tool for MATLAB. https://figshare.com/articles/PIVlab_version_1_35/1092508.
  51. Thielicke W.; Stamhuis E. J. PIVlab – Towards User-Friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. J. Open Res. Software 2014, 2 (1), e30. 10.5334/jors.bl. [DOI] [Google Scholar]
  52. Thielicke W.The Flapping Flight of Birds - Analysis and Application; Rijksuniversiteit Groningen, 2014. [Google Scholar]
  53. Keane R. D.; Adrian R. J. Theory of Cross-Correlation Analysis of PIV Images. Appl. Sci. Res. 1992, 49, 191–215. 10.1007/BF00384623. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao7b01862_si_001.pdf (700.2KB, pdf)
ao7b01862_si_002.avi (4.4MB, avi)
ao7b01862_si_003.avi (5MB, avi)
ao7b01862_si_004.avi (4.8MB, avi)
ao7b01862_si_005.avi (5MB, avi)
ao7b01862_si_006.avi (1.1MB, avi)
ao7b01862_si_007.avi (4MB, avi)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES