Summary
Navigation engages many cortical areas, including visual, parietal, and retrosplenial cortices. These regions have been mapped anatomically and with sensory stimuli, and studied individually during behavior. Here, we investigated how behaviorally-driven neural activity is distributed and combined across these regions. We performed dense sampling of single-neuron activity across the mouse posterior cortex and developed unbiased methods to relate neural activity to behavior and anatomical space. Most parts of posterior cortex encoded most behavior-related features. However, the relative strength with which features were encoded varied across space. Therefore, posterior cortex could be divided into discriminable areas based solely on behaviorally-relevant neural activity, revealing functional structure in association regions. Multimodal representations combining sensory and movement signals were strongest in posterior parietal cortex, where gradients of single-feature representations spatially overlapped. We propose that encoding of behavioral features is not constrained by retinotopic borders and instead varies smoothly over space within association regions.
INTRODUCTION
During visually guided navigation, sensory information is processed and transformed into motor plans to achieve rewarding outcomes. This processing involves the dorsal posterior part of cortex, which includes visual, parietal, and retrosplenial areas. These areas represent visual stimuli (Glickfeld and Olsen, 2017), combine visual and locomotion information for predictive coding (Keller et al., 2012; Saleem et al., 2013), transform sensory cues into motor plans (Goard et al., 2016; Harvey et al., 2012; Licata et al., 2017; Pho et al., 2018), and maintain navigation-related signals such as heading direction and route progression (Alexander and Nitz, 2015; Nitz, 2006). Despite progress in understanding these processes in individual areas, a high resolution spatial map of navigation-related features across posterior cortex has not been established. Here we investigated how the representations that support visually guided navigation are distributed and combined across cortical space. To what degree is information localized or distributed? How do representations relate to known area boundaries? Where are visual and movement information combined to inform task-relevant behaviors?
Pioneering studies have mapped and segmented mouse posterior cortex using anatomical features and retinotopy. Tract tracing studies have identified a number of visual areas (V1, PM, AM, AL, LM) (Glickfeld and Olsen, 2017; Wang and Burkhalter, 2007). These areas represent retinotopic copies of the visual space, and functional boundaries between them can be defined based on reversal of the visual field sign (Garrett et al., 2014; Marshel et al., 2011). Although retinotopic copies suggest discrete areas, anatomical studies using cyto- and chemoarchitecture have, in some cases, identified transitions shifted relative to retinotopic boundaries (Zhuang et al., 2017), or have found smooth anatomical gradients at sharp retinotopic borders (Allen Institute, 2017; Gămănuţ et al., 2018). Also, the organization within parietal and retrosplenial areas has been challenging to identify because these areas are not well driven by simple visual stimuli (Zhuang et al., 2017) and lack internal anatomical boundaries (Gămănuţ et al., 2018).
It is therefore not fully understood how the organization of posterior cortex may impact the encoding of behavioral variables and the emergence of multimodal representations for navigation. In particular, it is unclear if posterior cortex, especially higher association regions, encodes behavioral information in functionally discrete areas, as suggested by retinotopic mapping. Alternatively, secondary and higher regions could form a smooth continuum of functional properties, as suggested by anatomical studies. Much work on the function of secondary visual areas has emphasized the differences between their responses to simple visual stimuli such as drifting gratings (Andermann et al., 2011; Glickfeld et al., 2013; Juavinett and Callaway, 2015; Marshel et al., 2011). However, some of these studies also provided evidence that nearby regions of cortex tend to be functionally more similar than distant ones (Andermann et al., 2011; Marshel et al., 2011). This is consistent with recent work that has revealed that areas in mouse posterior cortex are highly interconnected. Retrograde tracing has found nearly all-to-all inter-area connectivity (Gămănuţ et al., 2018). Also, most V1 neurons broadcast information to multiple areas via branching axon collaterals (Han et al., 2018). Theoretical models have proposed that these connectivity patterns are consistent with an organization in which the probability of connectivity between cortical locations decays smoothly with distance, such that similarity in encoding decreases gradually over space (Song et al., 2014). A smooth functional organization could explain apparent discrepancies in area boundaries and suggest spatial proximity as a simple principle for the emergence of multimodal representations.
Here, we mapped behavior-related cortical activity in mice during a visually guided navigation task using dense sampling with single-neuron resolution. We developed analyses to relate neural activity to behavior and cortical space in an unbiased manner. Representations of individual task-related features were highly distributed across posterior cortex, with each area encoding most features of the task, consistent with reports in anterior brain regions (Allen et al., 2017; Chen et al., 2017; Makino et al., 2017). Except for sharp transitions between primary visual, parietal, and retrosplenial areas, representations were spatially organized as gradients of encoding similarity. As a result, despite the lack of sharp boundaries, posterior cortex could be divided into discriminable areas based on quantitative differences in the encoding of task features. Multimodal sensory-motor representations emerged where gradients for the encoding of optic flow and locomotion overlapped, specifically near posterior parietal cortex (PPC). Our results add a map of encoding of task-related information to existing maps based on anatomical or simple functional properties and improve our understanding of distinctions and divisions between association areas.
RESULTS
A visually guided locomotion task that engages posterior cortex
We developed a task for mice with the goal to engage the visual and navigation-related networks in the dorsal posterior cortex. Mice interacted with a visual virtual reality environment comprised of dots displayed on a screen at randomized locations in 3D space (Methods; Figure 1A and Supplemental Video). The running velocity of the mouse on a spherical treadmill (ball), measured as the pitch and roll velocity of the ball, controlled linear and angular movement in the virtual environment (Harvey et al., 2009).
Figure 1. A visually guided locomotion task that engages posterior cortex.
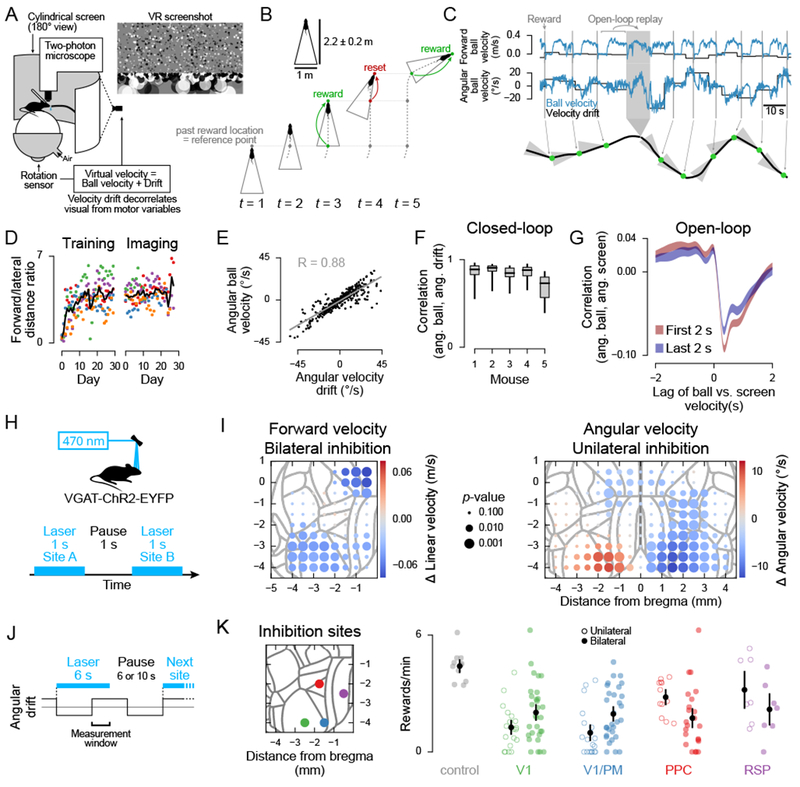
(A) Experimental setup and screenshot of the virtual reality environment.
(B) Schematic of the reward condition in the task (top-down view). Dashed lines, path taken by the mouse. Solid gray triangle, invisible boundaries used to determine reward delivery (Methods).
(C) Top: Example velocity traces. Bottom: Corresponding top-down view of the path taken by the mouse. Green dots indicate reward times.
(D) Task performance during training and imaging. The ratio between the forward distance to the lateral distance covered by the mouse was used to assess the efficiency of the mouse’s behavior. Each dot is one session; colors indicate different mice. Black line, mean across mice (n = 5).
(E) Correlation between angular ball velocity and velocity offset for one session. Each dot shows the mean velocity during a single epoch with a single drift value. Only closed-loop segments are included. Gray line, least squares fit; R, Pearson correlation coefficient. (n = 386 drift epochs)
(F) Boxplot of the correlation between angular velocity and drift as in (E), for all sessions for each mouse. Line, median; box, first to third quartile; whiskers, range (23.6 ± 5.99 sessions per mouse, mean ± s.d).
(G) Cross-correlation between angular screen and ball velocity during open-loop segments. Red line, first 2 s of segment; blue line, last 2 s of segment; shading, mean ± s.e.m. across sessions (n = 118).
(H) Schematic of optogenetics setup during the task, with the drift velocity set to zero.
(I) Effect of targeted inhibition on locomotion velocity. Each dot represents an inhibition site that was randomly targeted. Dot color represents the difference between pre- and post-inhibition velocity, and dot size represents significance based on hierarchical bootstrap (Methods). Effects were smoothed with a 1 mm square window. Gray outlines, area parcellation from the Allen Mouse CCF (22,384 unilateral and 10,661 bilateral trials; 158.87 ± 21.14 per location, mean ± s.d.; 19 sessions; 3 mice).
(J) Protocol for targeted inhibitions during the full task (with velocity drift).
(K) Left: Map of targeted sites. Right: Each dot represents the average reward rate during inhibition after a drift switch (see “measurement window” in (J)) for a single session. In the control condition, the laser was on, but targeted to a site on the metal headplate. Black dots, mean; error bars, 5th and 95th percentile of a bootstrap distribution of the mean. Conditions vs. control: p < 10−4, except for RSP, p = 0.056. Unilateral vs. bilateral: p < 0.01 for V1, V1/PM, PPC, p = 0.21 for RSP. The difference between unilateral and bilateral mean effects was significantly different for V1 and PPC (p = 0.0016), V1/PM and PPC (p = 0.001), V1 and RSP (p = 0.038), and V1/PM and RSP (p = 0.023), but not for V1 and V1/PM (p = 0.717), and PPC and RSP (p = 0.939). Two-tailed p-values based on 104 resampling iterations.
See also Supplemental Video.
Mice were trained to run approximately two meters straight forward, in virtual world coordinates, from an invisible reference point to obtain a reward. The reference point was reset to the current position of the mouse after a reward or if the mouse did not maintain a straight path (Methods; Figure 1B–C). A random offset (drift) velocity was added to the linear and angular movement of the dots on the screen and changed every 6-12 seconds, independently of reward times. To obtain rewards, mice therefore continuously needed to adjust their running to compensate for the drift and run straight in the virtual world. This task required training, and mice reached steady state performance after about two weeks (Figure 1D–F).
In addition, we periodically switched to open-loop playback of a visual stimulus that was identical to a visual stimulus previously generated by the mouse’s behavior (Figure 1C). During open-loop segments, as expected, the instantaneous correlation between the angular ball and screen velocities was low. However, there was a strong cross-correlation, with the ball velocity lagging the screen velocity by about 360 ms (Figure 1G). Mice thus remained engaged and attempted to correct angular motion even during the open-loop playback.
A key feature of this task was the use of virtual reality to decorrelate optic flow and locomotion using drift and open-loop periods (Chen et al., 2013; Keller et al., 2012; Minderer et al., 2016). The same locomotor actions resulted in distinct optic flow patterns and vice versa. This made it possible to dissociate neural encoding of visual signals, locomotion signals, and visual-motor interactions.
To test whether activity in dorsal posterior cortex had a causal relationship with the behavior required for the task, we inhibited small volumes of cortex by optogenetically activating GABAergic interneurons (Guo et al., 2014; Zhao et al., 2011). We first tested the effect of inhibition on locomotion by setting the drift velocity to zero, thus fixing visual-motor relationships (Figure 1H). We mapped inhibition across a grid on each hemisphere. Cortical inhibition affected both forward and angular running velocity. Forward velocity was reduced when inhibiting either V1 or posterior motor cortex bilaterally (Figure 1I, left). Unilateral inactivation of medial V1 and PM caused an ipsiversive increase in angular velocity (Figure 1I, right). This effect was consistent with a blinding in the contralateral visual hemifield. Such blinding would create a net ipsiversive optic flow during forward running and an expected compensatory ipsiversive locomotor shift.
We also tested the effect of cortical inhibition in the full task, which included velocity drift, to understand if cortical regions were required to adapt to changing visual-motor mappings (Figure 1J). Around the times of drift switches, we inhibited four locations individually that showed different effects in the no-drift case: central V1, medial V1/PM, PPC, and retrosplenial cortex (RSP) (Figure 1K, left). As expected from the no-drift experiments, both unilateral and bilateral inhibition of V1 or PM reduced the reward rate. Also, although inhibition of either PPC or RSP had little effect on locomotion in the absence of drift, inhibition of these areas decreased the reward rate in the presence of drift (Figure 1I, 1K, right). Unilateral inhibition had a stronger effect than bilateral inhibition for V1 and PM, whereas bilateral effects were stronger for PPC and RSP. Together with the no-drift experiments and prior work on PPC and RSP (Buneo and Andersen, 2006; Cho and Sharp, 2001), these findings suggest that, in our task, V1/PM activity might be compared across hemispheres to determine locomotion direction and that PPC and RSP might be involved in adjusting behavior for changing sensorimotor mappings.
Unbiased recordings of cortical activity
While mice performed the task, we imaged the activity of cortical neurons (either layer 2/3 or layer 5) in transgenic mice that expressed GCaMP6s in a subset of excitatory neurons (Dana et al., 2014). In each session, we imaged a 650 μm by 650 μm field-of-view (Figure 2A). Over multiple sessions, we systematically tiled fields-of-view to cover dorsal posterior cortex, including areas identified in the Allen Institute Mouse Common Coordinate Framework (CCF) v.3: V1 (VisP), secondary visual areas (AL, AM, PM), parietal areas (RL, A), retrosplenial areas (RSPagl/MM, RSPd) and trunk somatosensory cortex (SSPd-tr) (Allen Institute, 2017) (Figure 2B–D).
Figure 2. Relating neural activity, behavior, and cortical anatomy using a deep neural network model.
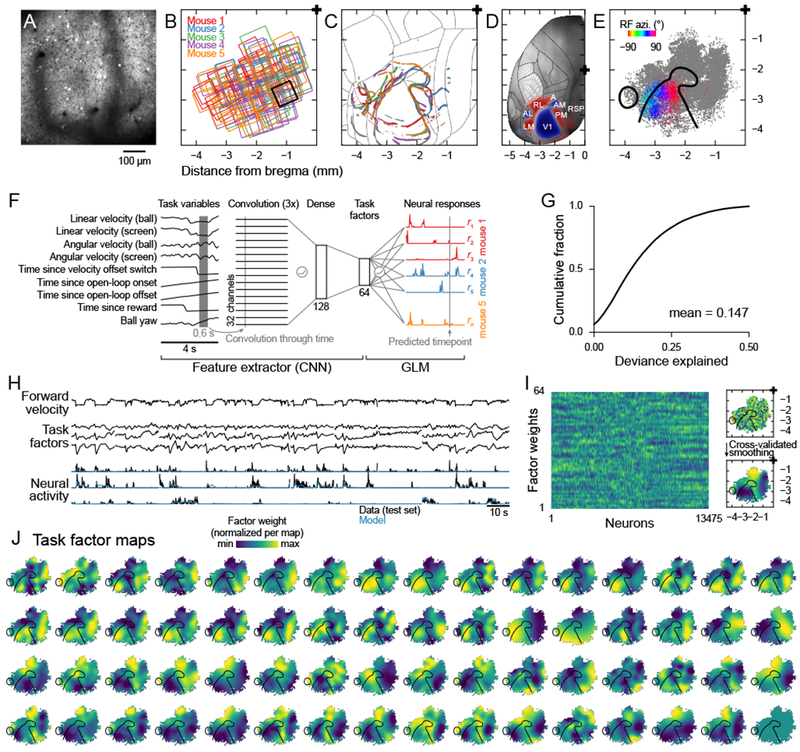
(A) Mean fluorescence image from one session.
(B) Overview of all fields-of-view. Each square represents one session, colors represent mice. Black square, example session in (A). 118 sessions from 5 mice, 23.6 ± 5.99 sessions per mouse, mean ± s.d.
(C) Field sign reversals (Methods) for all five mice, based on widefield epifluorescence imaging. Thin gray lines, area parcellation from the Allen Mouse CCF.
(D) Overlay of the brain template, area parcellation, and average field sign maps (across 79 mice), all obtained from the Allen Institute.
(E) All 23,213 detected neurons, registered with the Allen Mouse CCF. Gray dots, neuron location; colored dots, sources with significant visual receptive field fits; color indicates azimuth of the receptive field in the visual field; black lines, field sign reversals (zero field sign) based on map in (C).
(F) Schematic of the encoding model consisting of three convolutional layers (each with 32 channels), followed by two fully connected layers (128 units and 64 units), all connected through rectification nonlinearities. The response of each neuron was modeled as a linear combination of the final layer activations, passed through an output nonlinearity (the exponential function).
(G) Cumulative histogram of the fit quality (fraction of Poisson deviance explained) of all 23,213 neurons.
(H) Example traces for timepoints that were not used to fit the model. Top: Example task input variable (forward running velocity). Middle: Three example task factors, i.e. activations of the “Task factors” layer in (F). Bottom: Black lines, neural activity (deconvolved fluorescence); Blue lines, model prediction. Traces are discontinuous because data was split into 20 s long chunks and every fifth chunk was held out for testing.
(I) Left: Factor weights for all well-fit sources (fraction of deviance explained > 0.1). Sources were ordered to maximize the weight correlation between neighbors. Right: Schematic of smoothing procedure. Weight values at the location of the corresponding source were smoothed with a Gaussian filter whose width was determined by cross-validation across mice to maximize the prediction performance for the map of the held out mouse.
(J) Optimally smoothed maps for all 64 task factors. Black outlines indicate the field sign reversals based on map in (C).
See also Figure S1.
Posterior cortex was sampled without regard to anatomical boundaries to allow an unbiased analysis of activity distributions across cortical space. Also, we sampled densely at single-neuron resolution to uncover functionally distinct, but spatially overlapping, single-neuron properties and potential heterogeneities that might be obscured with spatial averaging, such as with wide-field imaging.
We identified time-varying fluorescence sources automatically (Pnevmatikakis et al., 2016) and then deconvolved the fluorescence traces (Friedrich et al., 2017) (Methods; Figure S1H–M). We included putative apical dendrites (Figure S1K), which have been shown to follow the activity of L5 somata (Peron et al., 2015). Our dataset comprised 18,127 somata (layer 2/3: 14,377; layer 5: 3,750) and 5,086 putative apical dendrites (Figure 2E). We refer to both somata and putative apical dendrites as “neurons”.
In each mouse, under the same imaging window, we also mapped retinotopy with wide-field calcium imaging. Visual field sign maps were aligned to the two-photon data using blood vessels (Figure S1A–D). Each mouse was registered to the Allen Institute CCF by aligning the field sign map to a CCF-aligned reference field sign map (www.brain-map.org) (Figure 2C–2D, S1E). This registration identified the position of each neuron within the CCF. We estimated the error of our alignment procedure using Allen Institute field sign maps that contained ground-truth CCF coordinates. Our procedure resulted in errors less than 130 μm (Figure 2C, S1E–F), which was smaller than the smallest posterior brain regions and less than the length scales for most of our analyses (see Methods for details on alignment).
Relating neural activity and complex behavior with a deep neural network model
We wanted to understand how the relationship between neural activity and task information varied across cortical space. To relate neural activity to behavior, we considered common approaches to model a neuron’s activity as a function of measured task variables (Peron et al., 2015; Pillow et al., 2008; Runyan et al., 2017). In these approaches, the experimenter defines and evaluates a small set of potential relationships between neural activity and task features. A benefit of these approaches is that they allow the experimenter to focus on specific encoding relationships.
However, our aim was to compare encoding across diverse cortical regions. We therefore considered it important to use an approach that did not rely on strong prior assumptions about the relationships between neural activity and task features. For example, in parietal and retrosplenial areas, there is little agreed-upon expectation for these relationships. Because these regions are far removed from the sensory periphery, encoding could include complex temporal patterns and nonlinear transformations of task variables. Further, to reveal the organization of encoding across cortical space, we considered it initially not critical to understand which aspects of the task were encoded in particular regions; this question is considered later. We initially asked how, rather than which, encoding properties changed across cortex.
We built an automated feature extractor that identified neural-activity-relevant features of task variables in a way that required minimal assumptions about encoding relationships (Figure 2F). The task feature extractor took the form of a convolutional neural network (CNN) that received as input 4 s long temporal snippets of each measured task variable. The convolutions were applied in the temporal dimension. The input task variables were the linear and angular locomotion (ball) velocity, the linear and angular optic flow (screen) velocity, the time since the last drift switch, the times since the last open-loop onset and offset, the time since the last reward, and rotation of the ball in yaw (yaw was not used to control the virtual environment).
The feature extractor was trained to reduce the input snippet to a set of 64 “task factors” that optimally describe neural activity. Each task factor was not constrained to represent an individual task variable and could represent a nonlinear combination of task variables, including complex temporal dependencies. The task factors were then used as the predictors in a regression model (Poisson-distributed generalized linear model, GLM) to explain the activity of each neuron (a linear visual receptive field estimate was added as an additional predictor, see Methods). The task factors were shared across and optimized for all neurons, but separate GLM weights were fit for each neuron. The GLMs predicted the deconvolved fluorescence activity of the given neuron at a time point 3 s into the 4 s input snippet. A neuron’s encoding could thus be described by its set of GLM weights across the task factors.
Importantly, the CNN and the GLMs were trained jointly on the entire dataset. Therefore, the predictors in our model were identified by the CNN based on an objective optimization procedure, rather than being manually specified. Each task factor corresponded to some aspect of the task that was relevant for neural activity. We chose 64 task factors because this number maximized the prediction quality on held-out data. We designed the model to ensure that each factor represented a different aspect of the task (Methods). Consequently, correlations between factors were low (Figure S1N), and factors were not well described by a lower-dimensional linear subspace (Figure S1O).
Our model captured a substantial amount of the neural activity variance (mean fraction of Poisson deviance explained: 0.147, Figure 2G). 78.1% of activity sources had fit qualities that were significantly higher than chance (false discovery rate of 0.001 (Benjamini and Hochberg, 1995)). Several versions of more traditional GLMs performed worse (e.g. Figure S8B).
Encoding maps revealed functional relationships between areas
We created encoding maps for each of the 64 task factors obtained from our model. In these maps, at each neuron’s anatomical location, we plotted that neuron’s weight for the given factor. The map for a given factor showed the spatial distribution of a factor’s weights and thus the importance across space of a particular aspect of the task for neural activity. We smoothed the maps using a Gaussian kernel chosen with cross-validation to give the best prediction performance across mice (Figure 2I).
The encoding of most task factors (63 of 64 factors) had structure across cortical space, indicating that task features were not uniformly represented across all areas (Figure 2J). This initial visualization indicated that we were able to capture functional relationships between cortical areas based solely on task-related neural activity. We note that the identity of the individual factors shown in Figure 2J depended on the initialization of the CNN (Methods, section Factor non-identifiability controls). However, the high dimensional encoding structure described by all factors collectively was unaffected by the initialization (Figure S2). We used this high dimensional structure for all analyses.
Cortical regions could be finely discriminated based solely on their task tuning
To analyze how the encoding of task features changed across cortical space, we examined the average spatial rate of change of the encoding maps (Figure 3A). The rate-of-change map showed sharp transitions in the encoding properties that divided the analyzed region into three areas: V1, RSP, and a secondary visual/parietal area. These boundaries did not align precisely with the retinotopic field sign borders and were better aligned with the boundaries defined by the Allen Institute, which are based on cyto- and chemoarchitecture (Figure 3A, S3) (Allen Institute, 2017). In particular, the peak rate of change in encoding at the lateral side of V1 was displaced laterally from the visual field sign border (Figure 3A, S3A–D) (Zhuang et al., 2017). Further, the rate of change of encoding did not reveal sharp transitions within the secondary visual/parietal area. For example, the anterior boundary of AM in the field sign map did not correspond to a peak in the rate of change of encoding properties of neurons (Figure S3E–F).
Figure 3. Cortical regions were discriminable based on task-related encoding properties.
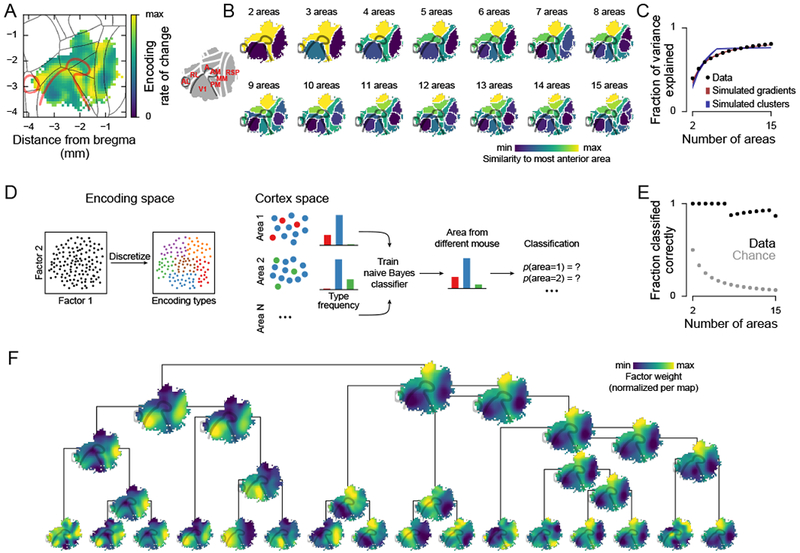
(A) Average spatial rate of change of the encoding maps in Figure 2J. The rate of change (magnitude of central differences between neighboring points) was computed for each factor map and normalized by its maximum before averaging across factors.
(B) k-means clustering of factor maps from Figure 2J. Colors are based on a one-dimensional embedding of the cluster centroids.
(C) Black dots show fraction of map variance explained by the clusterings in (B). Shaded areas show variance explained ± s.d. across 100 simulations for two simulated datasets: random gradients (red) and maps with consistent clusters (blue; gradient model fits better than clustered model, p < 10−4; see Methods).
(D) Schematic of the area classifier. Neurons were grouped into 100 encoding types by k-means clustering in the factor weight space. To test area discriminability at a given number of areas, the frequency of each encoding type in each area was used to train a naïve Bayes classifier on four mice. The classifier was then used to compute the area probabilities based on the type frequencies in the fifth mouse. The process was repeated for all mice and the probabilities were averaged before maximum-likelihood classification.
(E) Fraction of areas classified correctly (n = 5 mice).
(F) Agglomerative hierarchical clustering of the 64 factors (only the top four levels are shown). The clustering metric was the correlation of the weights between the factors. The map of each cluster is the average of the maps in Figure 2J for all factors within the cluster.
See also Figures S2, S3 and S4.
To test whether the three main divisions contained sub-regions with different encoding properties, we grouped regions based on encoding similarity by applying k-means clustering to the encoding maps (Figure 3B). The fraction of variance explained increased smoothly with the number of clusters and was more similar to simulations of smooth maps than to simulations of clustered maps (Figure 3C). This suggested that there was no optimal number of clusters beyond the three main divisions and that clustering likely subdivided a continuum.
However, despite the lack of sharp boundaries, sub-regions within the three main divisions were statistically discriminable based on their encoding properties. To show this, we grouped neurons into encoding types based on their weights for task factors. Each spatial cluster (“areas” in Figure 3B) could then be characterized by the distribution of encoding types it contained. We trained a naïve Bayes classifier on this distribution from four mice and, in a fifth mouse, predicted the area identities based on the encoding type distributions (Figure 3D). For up to seven areas, each area in a map was discriminable from each other area. Even for 15 areas, only two confusions occurred (Figure 3E). This discriminability suggested that encoding properties varied consistently across mice within the three main areas apparent in the map of the rate of change of encoding (Figure 3A).
The order in which subdivisions emerged at increasingly finer map resolutions provided insights into the functional relationships between areas (Figure 3B). To highlight these relationships, we performed hierarchical clustering on the encoding maps (Figure 3F), and we overlaid the areas identified from clustering with the areas defined by the Allen Institute (Figure S4). Multiple interesting observations emerged from the k-means and hierarchical clustering. First, parietal regions clustered with medial secondary visual areas. Parietal regions could be subdivided into: a medial strip including area A, part of area AM, and area PM; a lateral region overlapping with RL; and, an anterior region close to somatosensory cortex. Second, RSP could be divided into separate clusters along the anterior-posterior axis, indicating that it may not be a functionally uniform region (see left branch of clustering hierarchy in Figure 3F). Third, AL was functionally more similar to the AM/MM clusters than to RL, which was consistent with connectivity (Gămănuţ et al., 2018) but differed from tuning preferences for simple visual stimuli (Marshel et al., 2011). Fourth, even at fine clustering resolution (15 clusters), we did not observe a cluster aligned with the retinotopically defined part of area AM. Finally, the most consistent boundaries in all maps were at the divisions between primary visual, parietal, and retrosplenial areas, but the boundaries within these main divisions differed substantially across maps.
Cortical areas were therefore statistically discriminable based on their functional relationship with task features at a resolution comparable to anatomical and retinotopic maps. However, except for the boundaries between V1, parietal, and retrosplenial areas, encoding properties varied gradually.
Neurons within an area had diverse encoding properties
Given that posterior cortex could be divided into discriminable areas, we wanted to understand the underlying structure of the discriminability at the resolution of single neurons. We initially hypothesized that the discriminability of cortical areas was due to a spatial compartmentalization of encoding properties across areas, such that each area would be characterized by neurons with encoding properties that were unique to that area.
We analyzed how neurons in each area were distributed across the space of encoding properties. The encoding properties of a neuron were defined as the neuron’s weights for the task factors. For visualization, we reduced the 64-dimensional weights into two dimensions with t-distributed stochastic neighbor embedding (t-SNE) (Figure 4A). For the following analyses, we used the parcellation into five areas for ease of display (Figure 4B), but similar results were found with ten areas or with the areas defined by the Allen Institute (Figure S5). If each area had unique encoding properties, neurons in encoding space would segregate by cortical area. Instead, each of the five cortical areas contained neurons in most parts of encoding space (Figure 4C).
Figure 4. Anatomically defined populations showed diverse encoding properties.
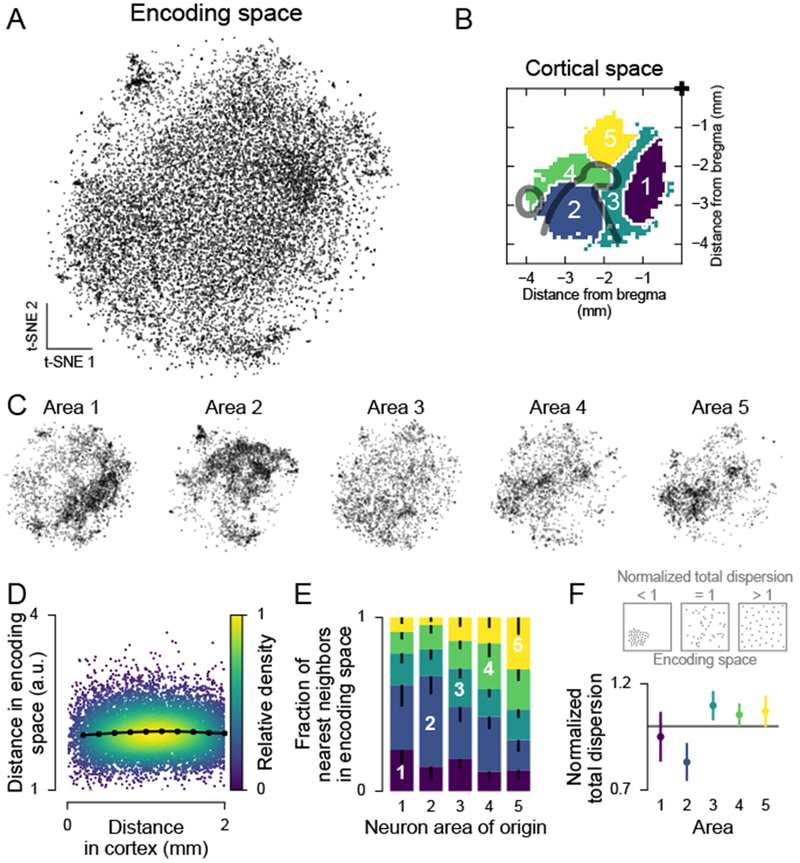
(A) t-SNE of the factor weights for all neurons.
(B) Parcellation of cortex used in (C). From Figure 3B.
(C) Same embedding as in (A), but split by areas in (B).
(D) Relationship between anatomical and encoding-space distance. Each dot is one neuron pair. Black line, mean (computed in 200 μm bins). Pearson correlation for 0-500 μm: 0.032 (greater than zero, p < 10−323, n = 10,977,961 neuron pairs).
(E) Anatomical location of nearest-encoding-space-neighbors for neurons in all areas in (B). Neurons were randomly subsampled to match neuron numbers across areas. Colors as in (B). Error bars (only lower tail is drawn), fifth percentile of hierarchical bootstrap of the mean.
(F) Top: Schematic of the normalized total dispersion statistic. A normalized total dispersion value less (greater) than one means less (more) dispersion in weight space than the overall population. Bottom: Normalized total dispersion for the areas in (B). Error bars, 5th and 95th percentile of hierarchical bootstrap of the mean. The mean is different from 1 with: area 1, p = 0.256, n = 3518; area 2, p < 10−3, n = 3407; area 3, p = 0.018, n = 2389; area 4, p = 0.059, n = 2065; area 5, p = 0.075, n = 1959 neurons.
See also Figure S5.
We quantified these observations by analyzing the distribution of the full 64-dimensional encoding weights. The relationship between cell-cell anatomical distance and cell-cell distance in encoding space was weakly positive (Pearson correlation 0.031 over 0-500 μm cortical distance, p < 10−323, Figure 4D). Anatomically nearby neurons had a wide range of similarity in encoding, similar to anatomically far apart neurons. Consequently, a neuron in one cortical area often had a nearest neighbor in encoding space that was located in another area, indicating that areas overlapped in their encoding properties (Figure 4E). This overlap was extensive: for all areas except V1, most nearest-encoding neighbors were located in different areas. We also quantified the dispersion of the encoding weights of the neurons in an area by summing the variances of each of the 64 encoding dimensions (“total dispersion”). We then normalized each area’s total dispersion by the total dispersion across all areas. If areas had specialized single-neuron encoding properties, each area was expected to have a normalized total dispersion less than one. This was the case only for V1 (Figure 4F). In contrast, the area comprising parietal and secondary visual regions (PM, AM, A, MM) had a normalized total dispersion greater than one and thus tiled encoding space more evenly than the overall population (Figure 4F).
Therefore, each cortical region had diverse encoding properties that overlapped with those from different regions, indicating that encoding properties in our task were not spatially compartmentalized. The even tiling of encoding space by parietal and secondary visual areas indicated a diversity of encoding that was consistent with a role of these areas in the integration of information across the surrounding regions.
Neurons with similar encoding properties were distributed across cortex
Our results so far indicated that cortical areas were discriminable based on their encoding properties, but also that encoding properties were distributed across areas. Therefore, we considered that encoding properties could be distributed without regard to area boundaries, but non-randomly, such that areas were discriminable based on their characteristic profile of encoding properties. We tested whether distributed encoding properties were more likely than area-specific properties to be informative about the identity of a cortical area. We identified neurons with similar encoding properties by discretizing the encoding weight space into encoding types (Methods; Figure 3D). An inspection of the distribution of each of the encoding types across cortical space revealed that neurons from a single encoding type were typically highly distributed and found in many regions (Figure S6C).
We quantified to what degree particular encoding types were under- or over-represented in different areas. We used the joint probability distribution of cortical areas and encoding types to compute the pointwise mutual information (PMI) between each area and encoding type (Figure 5A–B). The PMI measured how much the probability of observing a particular encoding type in a particular area deviated from statistical independence, that is, from a situation in which the encoding type was uninformative about the cortical area. The PMI was positive if the encoding type was enriched in the area and negative if it was selectively excluded from the area.
Figure 5. Neurons with similar encoding properties were distributed across cortex.
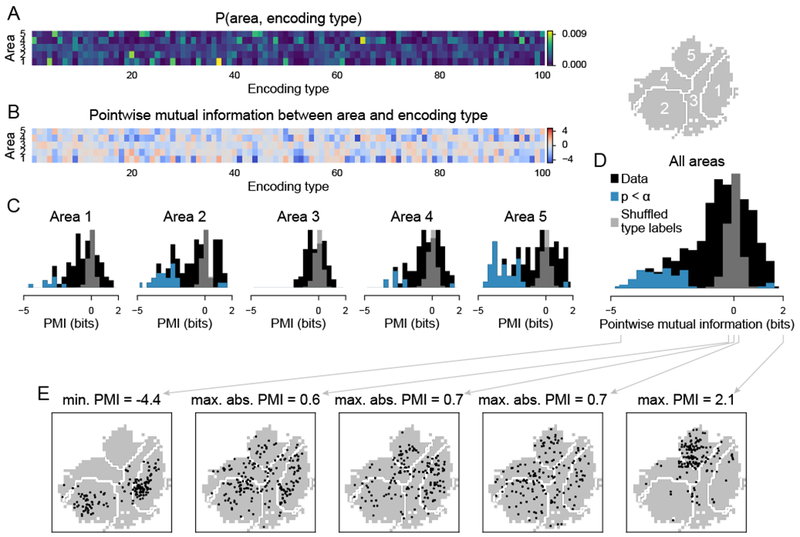
Encoding types were defined by applying k-means clustering to the weight space, as in Figure 3. Areas were defined based on the five-area parcellation shown in Figures 3B.
(A) Joint probability distribution of all areas and encoding types.
(B) Pointwise mutual information between area and encoding type (), based on the frequency of neurons of each type in each area.
(C) Histograms of the data in (B). Each histogram shows the PMI values of all encoding types with respect to one area. Gray, control distribution (shuffled type labels); blue, PMI values that were significantly different from zero; black, non-significant datapoints. Significance based on bootstrap estimate of PMI (hierarchically resampled data 104 times and re-computed probabilities). The significance threshold α was corrected for multiple comparisons by controlling the false discovery rate at 0.01. n = 500 encoding type/area pairs.
(D) Histogram of PMI values for all encoding type/area pairs. Colors as in (C). 64 pairs are significantly less than zero, 5 are significantly greater.
(E) Distribution across cortex of five example encoding types with strongest exclusion from one area (left), least informative about cortical location (middle), strongest specificity to one area (right).
See also Figure S6.
Few encoding types were significantly specific to a single cortical area. Only 5 of 100 encoding types had a PMI significantly greater than zero for any area (Figure 5B–D). Instead, neurons of the same encoding type were typically distributed across several areas. Most pairs of encoding type and area had PMI values near zero, indicating that the presence of an encoding type in a given area provided little information about the identity of the area (Figure 5E, middle three panels). However, a fair number of pairs of encoding type and cortical area (64 of 500) had PMI values that were significantly less than zero (Figure 5C–D). Neurons of these encoding types were significantly excluded from certain areas (Figure 5E, left). Consequently, these encoding types were informative about their cortical location without being specifically localized to a certain area. Similar results were obtained when using the Allen Institute-defined areas (Figure S6A).
Therefore, cortical areas were distinct because they had different relative profiles of encoding properties and not because of encoding types that were specific to individual areas. Areas were separable at the population scale but with many similarities at the level of individual neurons. For a given neuron with known encoding properties, it was difficult to identify in which area it resided (Figure 5E and S6). Similarly, for a given area, it was difficult to predict the encoding properties of a neuron chosen from that area (Figure 4C,E).
Encoding of measured task variables
Above, we analyzed encoding relationships using unsupervised methods to gain insights into the functional organization of cortex without relying on the interpretability of the encoded task features. Next, we considered how the encoding of explicitly measured task variables varied across cortical space.
First, to visualize the large-scale involvement of cortex in the task, we considered how activity changed around the time of the reward (Figure 6A). In the visual-retrosplenial regions, activity was high during ongoing behavioral actions, including fast running prior to a reward, and activity was low when the mouse stopped following a reward (Figure 6A). The pattern was reversed in the parietal region. Parietal region activity was high during periods of acceleration and deceleration (Figure 6A). These patterns were consistent with a role for the visual-retrosplenial group in the maintenance of a straight locomotion trajectory. The activity in the parietal group was consistent with an involvement in the adjustment of behavior in response to task events (Buneo and Andersen, 2006).
Figure 6. Encoding of task variables.
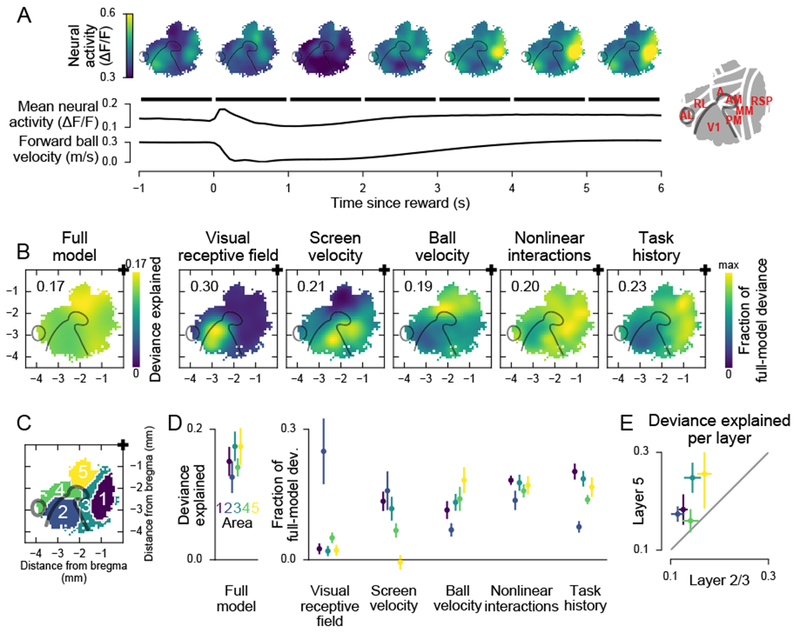
(A) Mean neural activity, aligned to the reward. Top: Smoothed activity maps for 1 s bins. Bottom: Mean activity trace and forward ball velocity trace. Black bars indicate extent of map bins.
(B) Maps of encoding strength. Left: Map of full model fit quality across cortex. Right: Maps of unique contributions of different features to the full model fit. Fraction of full-model deviance was computed, separately for each neuron, as 1 − (Dnull − Dreduced)/(Dnull − Dfull), where Dreduced was the deviance of a model lacking the indicated feature, Dfull was the deviance of the full model, and Dnull was the deviance of a null model (Methods). All maps are scaled from zero to the value indicated in the top left corner.
(C) Parcellation of cortex used in (D). From Figure 3B.
(D) Data from (B), binned by areas in (C). Colors as in (C). Error bars, 5th and 95th percentile of hierarchical bootstrap of the mean. Number of neurons: area 1, 6318; area 2, 6256; area 3, 3820; area 4, 3708; area 5, 2882. Mean deviance explained is greater than zero in all areas with p < 10-3. Mean fraction of full-model deviance is greater than zero for all areas and conditions with p < 0.009 except for area 5, screen velocity (p = 0.610).
(E) Mean full-model deviance explained, split by layer. Error bars, 5th and 95th percentile of hierarchical bootstrap of the mean. Number of neurons: layer 2/3, 11639, layer 5, 3717.
See also Figure S7.
We next used our encoding model (Figure 2) to understand how encoding of specific task variables varied across cortex (Figures 6 and S7). For each neuron, we quantified how well the full model, with all task variables included, could explain the neuron’s activity (measured as deviance explained). From the full-model deviance, we subtracted the deviance explained by a model that included all variables except the variable of interest (Figure 6B,D). The difference in the performance of these models provided a conservative estimate of a variable’s contribution to a neuron’s activity (Methods).
The primary variables relevant for the task were locomotion velocity (ball velocity) and movement velocity through the virtual environment (screen velocity), which were decorrelated by adding drift and open-loop periods. Encoding of these variables varied mainly along the anterior-posterior axis (Figure 6B,D). Screen velocity encoding was strongest in medial V1 and PM, which correspond to the temporal visual field, where optic flow is strongest during forward locomotion. In contrast, locomotion velocity encoding was strongest in a region corresponding to the Allen CCF area VisA. As expected, linear visual receptive fields were restricted to V1 (Figure 6B,D).
In addition, we tested for the encoding of more complex features, including nonlinear combinations of task variables and task history (Methods). Nonlinear interactions between task variables were encoded almost equally strongly in all areas (Figure 6B,D). To test for encoding of task history, we compared models that had access to either 3 s or 0.3 s of past task variables. We found that task history was encoded most strongly in RSP and in the parietal areas (areas 3 and 5, Figure 6D). This finding is consistent with work showing long timescales and integration of navigationally-relevant variables in RSP and parietal areas (Alexander and Nitz, 2015; Morcos and Harvey, 2016; Runyan et al., 2017).
We also compared encoding in layer 2/3 and layer 5. The types of task variables encoded were similar across layers (Figure S7D). Also, the differences in encoded features between areas were consistent for both layers. However, encoding was generally stronger in layer 5 than in layer 2/3 (Figure 6E).
Although encoding of task features was not uniform across cortical space, it was striking that at least some neural activity in most areas could be explained by any given feature. Except for screen velocity in the most anterior area, the fraction of explainable deviance for any task feature in any of the five areas was significantly greater than zero (Figure 6D). Thus, if an experiment focused solely on a single area, it would likely find encoding of most task parameters of interest. Here, by analyzing a large portion of cortical space in a single study, we were able to find that areas differed not in terms of which features they encoded, but rather in the relative strength with which they encoded those features.
Distributedness of information across cortex depended on encoded features
Our maps of encoding properties suggested that the distribution of information may be related to the type of feature that is encoded. It appeared that simpler features, such as visual receptive fields, screen velocity, and ball velocity, were more spatially confined than more complex features, such as nonlinear feature interactions and task history. To test this idea, we grouped neurons by their encoding properties into encoding types (as in Figure 3D). We then asked how the features encoded by the neurons of a given type related to the spread of those neurons in cortex, quantified as the area of an ellipse fit to the cortical locations of all neurons of that type (Figure 7A).
Figure 7. Distributedness of information across cortex depended on encoded feature.

(A) Schematic of distributedness analysis. Encoding types were defined as in Figures 3 and 5. The spread in cortex (distributedness) of each encoding type was defined as the area of a 1-standard-deviation-contour of a Gaussian distribution fit to the cortical locations of the neurons with this type. The fraction of full-model deviance was defined as in Figure 6B and averaged for each neuron type.
(B) Distributedness versus fit quality for the full model. The three encoding types with highest fraction of full-model deviance are colored. Error bars, 5th and 95th percentile of hierarchical bootstrap of the mean. Error bars were only plotted for the colored types, to maintain visibility. Gray line, 5th and 95th percentile of hierarchical bootstrap of a linear regression fit. The regression slope was not different from zero (p = 0.14).
(C) Cortical locations of the neurons belonging to each of the colored types in (B).
(D) As in (B), but for the unique contributions of different features to the full model fit. Gray dots represent encoding types that were not significantly different from zero by bootstrap. The three types with the highest deviance explained for each feature are colored. The regression slopes were significantly different from zero (p < 10−4) for screen velocity, ball velocity, and nonlinear interactions, but not for task events (p = 0.058) or task history (p = 0.995). The slopes for both task history and task events were significantly different from the other features (p < 0.001). All p-values were determined by bootstrap (104 repeats).
(E) As in (C), but for the types colored in (D).
Encoding types with the strongest encoding of either visual or locomotion velocity had some of the smallest spreads in cortex (Figure 7D–E, see colored encoding types). For the encoding of nonlinear interactions and task history, the types with the strongest encoding had intermediate spreads (Figure 7D–E, see colored encoding types). We also tested specific encoding of task events, such as rewards, open-loop onset and offset, and drift switches. The few encoding types that had significant event-specific encoding were highly distributed across cortex (Figure 7D–E, see colored encoding types).
Therefore, encoding types associated with relatively simple stimuli appeared more localized, which is consistent with area specialization for simple visual stimuli (Andermann et al., 2011; Glickfeld et al., 2013; Marshel et al., 2011). However, most encoding types showed a wide spread across cortical space (Figure S6C). Neurons that were task-related in more complex, but nevertheless reliable, ways, such as nonlinear combinations of sensory, movement, and task features, tended to be highly distributed across cortex.
Multimodal representations emerged where encoding maps overlapped
We wanted to understand where task-relevant information, in particular the relationship between visual and locomotion information, was represented in a format that could be best decoded by a downstream region to solve the task. We focused on decoding of linear combinations of signals because theory suggests that linear representations allow optimal inference in the context of multimodal integration (Ma et al., 2006; Pitkow and Angelaki, 2017). We developed a simplified version of our encoding model in which task variables did not interact nonlinearly and therefore remained invariant to each other (Figure 8A; Methods). As above, the model took the form of a GLM, but rather than using the CNN-based feature extractor, we specified manually which task variable combinations and transformations to relate to neural activity.
Figure 8. Population decoding reveals that multimodal representations emerge where modalities overlap.

(A) Schematic of the encoding model and decoding. A separate encoding model was fit for each neuron. Population decoding was performed on local groups of ~50 neurons. A prior model was used to account for correlations between the decoded variable and other task variables (Methods).
(B) Maps of decoding accuracy for the modalities that were explicitly decorrelated in this study: angular and linear screen and ball velocity. Left and center-left: Decoding maps for the single-modality (screen and ball) features. Center-right: to illustrate where decoding accuracy of the screen and ball single-modality maps overlapped, the screen and ball maps were multiplied pixel-wise. Right: maps for the multi-modal feature (drift).
(C) Mean decoding performance (), split by layer. Error bars, 5th and 95th percentile of hierarchical bootstrap of the mean. Number of neurons: layer 2/3, 11639, layer 5, 3717. Colors indicate area as in legend below.
(D) Maps as in (B), but showing decoding accuracy for open-loop timepoints using an encoding model fit on closed-loop timepoints. Plots next to maps show mean by area. For these plots, closed-loop accuracy was computed using only the timepoints that were later replayed during open-loop segments. Error bars, 5th and 95th percentile of hierarchical bootstrap of the mean.
(E) Maps of decoding accuracy for long-timescale integration features.
See also Figure S8.
We used Bayes’ rule to invert the GLM and to measure how well individual features could be decoded from the neural activity of small local populations (~50 neurons; Methods). To assess decoding accuracy, we isolated the portion of task variance explained that was due to the neural activity and not due to correlations between the decoded variable and other task variables (Methods). Since features only interacted linearly in the GLM, a high decoding accuracy meant that the neural activity encoded the feature of interest in a manner invariant to other features.
The main reward-relevant task variables were the angular optic flow (screen) velocity and angular locomotion (ball) velocity. Optic flow and locomotion velocity were related by the drift velocity. Screen, ball, and drift velocity therefore formed a set of visual, motor, and visual-motor-integration variables. The visual component (angular screen velocity) could be decoded predominantly from the MM region medial to area PM (Figure 8B). The motor component (angular ball velocity) could be decoded from a mediolateral strip that overlapped with the parietal region A (Figure 8B). The visual-motor-integration component (angular drift) could be decoded best in a location that was anterior and medial of the retinotopically defined area AM. This location corresponded to the zone of maximal overlap between the visual and locomotion velocity decoding regions (Figure 8B). Similarly, linear velocity drift could be decoded best where linear visual and locomotion velocity decoding overlapped.
These results indicate two significant points. First, the best angular drift decoding was in a location that matched what our previous work has studied as PPC (Driscoll et al., 2017; Harvey et al., 2012; Morcos and Harvey, 2016; Runyan et al., 2017). Second, our data suggested that representations formed overlapping maps and that multimodal information could be decoded where the representations of component features overlapped.
To test how the combination of multimodal information depended on coherence between sensory and motor signals, we compared decoding performance during the task to decoding performance in the open-loop segments, during which the animal was not in control of the virtual environment (Figure 8D). Using an encoding model fit to closed-loop time points, we decoded task variables during open-loop times. If representations depended on behavioral control, the decoding performance of the closed-loop model was expected to be low during open-loop times. Decoding of angular velocity, the most task-relevant variable, was reduced during open-loop segments for both visual and motor components (Figure 8D, top). Decoding performance of linear visual and drift velocity was reduced in secondary and higher areas, but improved in primary visual cortex (Figure 8D, bottom). This suggests a disengagement of secondary and higher areas, and reduction in multimodal representations, when the animal was not in control of the environment. There was no decrease in mean activity in any area during open-loop segments (Figure S8E). Together with our optogenetic inhibition results (Figure 1I,K), our findings suggest that V1 represents visual-motor mismatch in a task-independent way, whereas higher areas such as PPC and RSP integrate sensory, motor and task information in a way that depends on coherent interactions with the environment.
We further found that the best decoding of higher order task features was broadly present in association areas (Figure 8E). All of the temporally or spatially integrated features that we considered were best decoded from RSP, consistent with a role for this region in integration of visual information during navigation (Alexander and Nitz, 2015; Cho and Sharp, 2001). Interestingly, however, decoding was not uniform across RSP. Rather, decoding of heading since the last reward was specific to posterior portions of RSP. RSP may therefore have important functional subdivisions.
The patterns of decoding across cortical space were broadly consistent for neurons in layer 2/3 and layer 5. However, decoding performance for nearly all features of the task was superior in layer 5 populations (Figure 8C, S8D).
DISCUSSION
Unbiased and unsupervised comparison of encoding properties during navigation
Both our experimental design and analysis approach were developed to address the challenges of comparing activity in a wide range of cortical areas. The use of a navigation task likely engages posterior cortex more strongly than passive viewing of stimuli (Andermann et al., 2011; Marshel et al., 2011). Our task was self-guided and continuous, potentially allowing more natural cooperation between brain areas than in rigid trial-based tasks. Also, the space of task variables was sampled densely, rather than at a few pre-defined states, which could help understand the distribution of encoding properties.
We developed a neural-network-based feature extractor and combined it with a linear encoding model (Batty et al., 2017; McIntosh et al., 2016) to relate neural activity to behavior in a way that requires few prior assumptions about the considered encoding relationships. Instead of relating activity directly to explicitly measured task variables, we started with unsupervised analyses. This approach allowed us to consider relationships that were based on hard-to-interpret features, such as nonlinear interactions or long temporal dependencies. These methodological advances helped us to compare task-related activity across widely varying cortical areas within a single experimental paradigm.
The spatial organization of behaviorally relevant information in cortex
In the context of our visually guided navigation task, encoding properties formed smooth gradients across large parts of posterior cortex. The only functional discontinuities in posterior cortex were found at the major anatomical borders between V1, parietal, and retrosplenial areas. Despite the lack of further discontinuities, different regions could be distinguished based on population-level differences in encoding profiles. On a cellular level, however, encoding properties were strikingly distributed, and most task features were encoded in most areas.
Our data appear consistent with a distributed architecture without sharp distinctions between local and long-range connectivity, in which functional similarity is related smoothly to cortical distance. A distributed architecture, in this sense, has been suggested by theoretical work. Modeling has shown that the inter-area connectivity of both primate and rodent cortex can be explained by an organizational rule that acts on the level of single axons (Song et al., 2014). According to this rule, the probability of a neuron to send an axon into any part of cortex decays smoothly (exponentially) with wiring distance. Networks based on this rule thus form a spatial continuum and lack discrete areas (Song et al., 2014). Such networks may appear modular in larger brains, such as those of primates, and distributed in smaller brains, such as from rodents, even with the same underlying principle.
Emergence of multimodal information between primary areas
These models make predictions for the formation and location of multimodal representations. Due to the rule of connectivity decay with distance, multimodal representations are expected to emerge at cortical locations between the peaks of encoding for individual features. We found that multimodal representations were common across posterior cortex, with most areas having significant encoding of both visual and locomotion signals. This finding is consistent with work showing movement-related signals in primary sensory cortices (Keller et al., 2012; Saleem et al., 2013). However, in our data, multimodal representations emerged to the greatest extent at locations where visual and movement gradients overlapped, most saliently in the location we have studied in depth as PPC, which is anterior and medial to the boundaries of retinotopic area AM (Driscoll et al., 2017; Harvey et al., 2012; Morcos and Harvey, 2016; Runyan et al., 2017). At this location, we found an overlap of angular screen and ball velocity encoding and the highest decoding accuracy for the most action-relevant task variable, angular drift.
More generally, our study shows that task-related activity can be used to identify functional structure in association areas that have been challenging to map with sensory stimuli. While angular drift could be decoded best in the location we have called PPC, other multimodal signals were present in a large group of areas including PM, MM, A, AM, and RL (as defined in the Allen CCF). This group was active during behavioral change-points (Figure 6) and encoded visual-motor integration features (Figures 6 and 8). A sub-region extending along the anterior-posterior direction (area 3) had the most diverse encoding of all regions (Figure 4) and strongly encoded nonlinear interactions of visual and locomotion features (Figure 6D). We hypothesize that functions typically ascribed to parietal cortex extend throughout this region, potentially in a posterior to anterior gradient from visual-motor integration to learned visually-guided motor planning. In addition, our results indicate that area PM has an important role in navigation (Andermann et al., 2011; Roth et al., 2012). Furthermore, RSP had prominent functional subdivisions along the anterior-posterior axis.
Beyond multimodal mixing, redundant and recurrently connected neural populations are thought to be requirements for other features of cortical processing. The prevalence of complex nonlinear stimulus transformations and their distributed representation in our data may be a signature of processing for probabilistic inference (Pitkow and Angelaki, 2017). Also, the widespread integration signals we found across secondary and association areas are consistent with the sharing of information between neural populations at different stages of a processing stream, as needed for predictive coding (Keller et al., 2012; Marques et al., 2018).
Implications for the future study of posterior dorsal cortex during behavior
The areas we identified based on the encoding of task information did not line up exactly with retinotopic boundaries. In the secondary visual regions, we found gradients of task encoding, in contrast to the sharp boundaries suggested by retinotopic mapping. Our results also suggested that the spatial structure of encoding may depend on the features considered. Future studies comparing cortical areas should consider the caveats associated with sampling and binning neural activity based on area boundaries defined by specific features, such as retinotopy.
Despite the distributed representations we observed, it is possible that computations in cortex could be localized. For example, computations to generate or transform representations could occur selectively in a specialized area and then this information could be broadcast widely. It will thus be of interest to develop experimental approaches that extend beyond encoding to test if computation is localized or distributed.
STAR METHODS
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Christopher Harvey (harvey@hms.harvard.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Mice
All experimental procedures were approved by the Harvard Medical School Institutional Animal Care and Use Committee and were performed in compliance with the Guide for the Care and Use of Laboratory Animals. All imaging data were obtained from five male C57BL/6J-Tg(Thy1-GCaMP6s) GP4.12Dkim/J mice. For the optogenetic inactivation experiments, three male VGAT-ChR2-YFP mice were used (The Jackson Laboratory). All mice were 8-10 weeks old at the start of behavioral training, 12-24 weeks old during imaging and optogenetic experiments, and had not undergone previous procedures. Mice were kept on a reversed 12 h dark/light cycle and housed in groups of up to four littermates per cage. Mouse health was checked daily.
METHOD DETAILS
Behavior
Virtual reality system
The virtual reality system was programmed in MATLAB using the Psychophysics Toolbox 3. A PicoPro laser projector (Celluon Inc.) back-projected the virtual environment onto a half-cylindrical screen (24 inch diameter) at a framerate of 60 Hz. The luminance of the image was gamma-corrected and adjusted to account for the curvature of the screen.
The virtual environment was updated in response to the mouse’s locomotion on a custom-made open-cell Styrofoam ball (8 inch diameter, ~135 g). Two optical sensors (ADNS-9800, Avago Technologies) positioned 45° below the equator of the ball and separated by 90° in azimuth were connected to a Teensy-3.2 microcontroller (PJRC.COM) to measure the 3-dimensional rotation velocity of the ball. The pitch and roll velocity components controlled the linear and angular velocity in the virtual environment. The velocity gain was adjusted such that the distance travelled in the virtual environment equaled the distance traveled on the surface of the ball.
The virtual environment consisted of 6,000 dots placed uniformly at random in a 4 m by 4 m wide and 5 m high virtual arena. Movement of the mouse on the ball caused corresponding translation of the dots through the arena. The arena had continuous boundary conditions such that dots leaving the bounds on one side reappeared on the other. The viewpoint of the mouse was located in the center of the arena. Only dots within a radius of 2 m from the viewpoint of the mouse were visible. All dots had a diameter of 63 mm in the virtual world, corresponding to 1.8° of visual space at a distance of 2 m. Dots closer than 1 m from the mouse were collapsed in height onto the floor of the arena. The dots were either black or white, on a gray background. Each dot had a lifetime of 1 s, after which it vanished and a new dot was generated at a random location.
Task description
Mice were trained to run along a straight path for a fixed distance (“goal distance”) away from an invisible reference point to obtain a reward (4 μl of 10% sweetened condensed milk in water). The goal distance was adjusted daily to maintain the reward rate between 2 and 5 rewards per minute and was 2.21 ± 0.23 m (mean ± s.d.) for the imaging sessions.
To detect deviation from a straight path, we continuously measured the position of the reference point in relation to a triangular reward detection zone (Figure 1B). The reward detection zone was an isosceles triangle whose apex was at the mouse’s current position and whose base was behind the mouse and orthogonal to the mouse’s current heading direction. The goal distance defined the height of the triangle and the base had a fixed length of 1 m. When the reference point crossed any edge of the triangle due to the mouse’s locomotion, the point was reset to the current position of the mouse. If the point left the triangle by crossing its base, a reward was delivered. This mechanism rewarded the mouse for moving away from the current reference point in a straight path. The triangular reward detection zone ensured that more recent path segments were weighted more heavily than segments further in the past in determining the straightness of the mouse’s path.
To decorrelate the locomotion velocity from the optic flow on the screen, we added a drift to the movement of the mouse through the virtual environment. The drift velocity remained constant for 6-12 seconds (interval chosen uniformly at random). Then, new values were randomly drawn from a normal distribution, independently for the forward and angular directions. The standard deviation of the angular drift component was 18°/s. For comparison, the standard deviation of the angular running velocity during the task was 15.6°/s (after subtracting the drift). The standard deviation of the forward drift component was 0.06 m/s (s.d. of forward running velocity after subtracting drift, 0.17 m/s). To obtain data where locomotion and optic flow were completely decorrelated, we included a segment of open-loop playback after every ninth drift segment. During open-loop playback, we displayed a visual stimulus that was identical to the preceding 6-12 seconds of closed-loop behavior. No rewards were delivered during the open-loop segments.
Behavioral training
Before behavioral training, a titanium headplate was affixed to the skull of each mouse using dental cement (Metabond, Parkell). The center of the headplate was positioned over left posterior cortex (2.25 mm lateral and 2.50 mm posterior from bregma). To allow for an imaging plane parallel to the surface of cortex, the headplate was tilted by 16° from horizontal around the anterior-posterior axis. While performing the task, mice were head-restrained so that the headplate was tilted at 16° and the skull was level.
Starting three days before the first training session, mice were put on a water restriction schedule which limited their total consumption to 1 ml per day. The weight of each mouse was monitored daily and additional water was given if the weight fell below 80% of the pre-training weight. Mice were trained daily for 45-60 min at approximately the same time each day. Initially, the drift velocity was set to zero and the goal distance was set to a low value such that any movement on the ball would result in a reward. The goal distance was increased automatically after each reward within a session, and the initial and maximal goal distance were adjusted between sessions to maintain the reward rate between 2 and 5 rewards per minute. Once mice reached a goal distance of 2 m, drift was gradually introduced over several sessions. Training took approximately 2 weeks.
Optogenetic inactivation experiments
Three male VGAT-ChR2-YFP mice were used for the optogenetic inactivation experiments (The Jackson Laboratory). For these experiments, we followed the procedures described in (Guo et al., 2014).
Clear skull cap
The mouse was anaesthetized with isoflurane (1-2% in air). The scalp was resected to expose the entire dorsal surface of the skull. The periosteum was removed but the bone was left intact. A thin layer of cyanoacrylate glue was applied to the bone (Insta-Cure, Bob Smith Industries), followed by a layer of transparent dental acrylic (Jet Repair Acrylic, Lang Dental, P/N 1223-clear). A bar-shaped head plate was affixed to the skull posterior to the lambdoid suture using dental cement (Metabond, Parkell). Mice were then trained to perform the task.
Once mice reached steady state performance, they were anesthetized again and their skull cap was polished with a polishing drill (Model 6100, Vogue Professional) using denture polishing bits (HP0412, AZDENT). After polishing, clear nail polish was applied (Electron Microscopy Sciences, 72180). Fiducial marks were made on the skull cap to aid in laser alignment. An aluminum ring was then affixed to the skull using dental cement mixed with India ink to prevent stimulation light from reaching the mouse’s eyes.
Photostimulation
Light from a 470 nm collimated diode laser (LRD-0470-PFR-00200, Laserglow Technologies) was coupled into a pair of galvanometric scan mirrors (6210H, Cambridge Technology) and focused onto the skull by an achromatic doublet lens (f=300 mm, AC508-300-A-ML, Thorlabs). The laser (analog power modulation, off to 95% power rise time, 50 μs) and mirrors (<5 ms step time for steps up to 20 mm) allowed simultaneous stimulation of several sites by rapidly moving the beam between them. The beam of the diode laser had a top-hat profile with a diameter at the focus of approximately 200 μm.
For the grid-based inhibition mapping, stimulation trials were performed continuously throughout the behavioral session. For each stimulation trial, we randomly selected which hemisphere to stimulate (left, right or both), and then randomly selected one of 72 stimulation sites (per hemisphere) (Figure 1I). All sites were stimulated once before the first site was stimulated again. Sites were spaced in a regular grid at 500 μm intervals. During these experiments, we set the drift velocity in the task to zero.
For the inhibitions during the full task (with drift), two drift values were used (18°/s and −18°/s) and were switched every four seconds. The laser onset was aligned to the drift switch and the laser was on for six seconds. Inhibition trials were performed randomly at every second or third drift switch. The coordinates of the targeted sites, in millimeters lateral and posterior from bregma, were 2.5, −4 (V1), 1.5, −4 (V1/PM), 1.75, −2 (PPC), and 0.5, −2.5 (RSP) (Figure 1K). For control trials, the laser was targeted at a location on the metal headplate. Unilateral and bilateral trials were randomly interleaved.
Following Guo et al., the laser power at each stimulation site had a near-sinusoidal temporal profile (40 Hz) and time average of 5.7 mW. To ensure identical stimulus properties and mirror sounds, for unilateral stimulations, we still moved the laser between two sites, but the second site targeted the head-plate so that the light did not reach the brain.
Chronic cranial windows for imaging
After mice reached steady task performance, the cranial window surgery was performed. Twelve hours before the surgery, mice received a dose of dexamethasone (2 μg per g body weight). For the surgery, mice were anesthetized with isoflurane (1-2% in air). The dental cement covering the skull was removed and a circular craniotomy with a diameter slightly greater than 4 mm was made over the left hemisphere (centered 2.25 mm lateral and 2.50 mm posterior from bregma). The dura was removed. A glass plug consisting of two 4 mm diameter coverslips and one 5 mm diameter coverslip (#1 thickness, CS-4R and CS-5R, Warner Instruments), glued together with optical adhesive (NOA68, Norland), was inserted into the craniotomy and fixed in place with dental cement. India ink was mixed into the dental cement to prevent light contamination from the visual stimulus. An aluminum ring was then affixed to the head plate with dental cement. During imaging, this ring interfaced with light shielding around the microscope objective to prevent light contamination.
Widefield retinotopic mapping
Retinotopic maps were collected for the mice used for calcium imaging. Mapping was performed as described before (Driscoll et al., 2017). Mice were lightly anaesthetized with isoflurane (0.5 – 1.0% in air). GCaMP fluorescence (excitation, 455 nm; emission, 469 nm) was collected with a tandem-lens macroscope. A periodic visual stimulus consisting of a spherically corrected black and white checkered moving bar (Marshel et al., 2011) was presented on a 27 inch IPS LCD monitor (MG279Q, Asus). The monitor was positioned in front of the right eye at an angle of 30 degrees from the mouse’s midline.
Retinotopic maps were computed by taking the temporal Fourier transform of the imaging data at each pixel and extracting the phase of the signal at the stimulus frequency (Kalatsky and Stryker, 2003). The phase images were smoothed using a Gaussian filter (100 μm s.d.) and the field sign was computed (Sereno et al., 1994).
Two-photon imaging
Two-photon microscope design
Data were collected using a custom-build rotating two-photon microscope. The entire scan head of the microscope was mounted on a gantry that could be translated along two axes (dorsal-ventral and medial-lateral with respect to the mouse). The objective and collection optics were attached to the scan head assembly and could be rotated around the third axis, such that the objective could be positioned freely within the coronal plane of the mouse. Additionally, the spherical treadmill was mounted on a three-axis translation stage (Dover Motion) to position the mouse with respect to the objective. We positioned the objective such that the image plane was parallel to the left hemisphere of dorsal posterior cortex (approximately 16 degrees from horizontal). The head of the mouse remained in its natural position.
Excitation light (920 nm) from a titanium sapphire laser (Chameleon Ultra II, Coherent) was coupled into the scan head via periscopes aligned with the gantry. The scan head consisted of a resonant and a galvanometric scan mirror, separated by a scan lens-based relay telescope, and allowed for fast scanning. Average power at the sample was 60–70 mW. The collection optics were housed in an aluminum box to block light from the visual display. Emitted light was filtered (525/50 nm, Semrock) and collected by a GaAsP photomultiplier tube. The microscope was controlled by ScanImage 2016 (Vidrio Technologies).
Image acquisition
Images were acquired at 30 Hz at a resolution of 512 × 512 pixels (650 μm × 650 μm). The imaging depth below the dura was either between 120 μm and 170 μm (layer 2/3) or between 300 μm and 500 μm (layer 5). Imaging was continuous for the duration of the behavioral session, lasting between 55 and 70 min. We found that there was slow axial drift of approximately 6 μm/h, possibly due to physiological changes as the animal consumed liquid rewards. To compensate for the drift, the stage was moved continuously at a similar rate. The rate was adjusted between sessions based on residual drift observed between the beginning and end of each session. To synchronize imaging and behavioral data, the imaging frame clock and projector frame clock were recorded.
Registration to the Allen CCF
Before each two-photon imaging session, an image of the surface vasculature was recorded directly above the coordinates of the imaging session. To align each two-photon session to the retinotopic map for each mouse, matching features in the vasculature were identified manually between the two-photon surface vasculature image and an image of the vasculature obtained during retinotopic mapping. Using the features as control points, a similarity transformation (translation, rotation and scaling) was computed to align the two-photon imaging data to the retinotopic map (Figure S1A–D).
To combine data across mice, we aligned the field sign map of each mouse to a CCF-aligned reference field sign map available from the Allen Institute (www.brain-map.org) (Figure 2D and S1E). For each mouse, we first obtained outlines of V1 and AM, which were defined as pixels in the field sign map with an absolute value less than 0.06 (the field sign ranges from −1.0 to 1.0). We then manually determined the rotation and translation that best aligned the outlines of V1 and area AM to the CCF-aligned reference map (Figure S1E). This registration provided a position for each neuron in coordinates from the CCF.
Since two-photon imaging and widefield-imaging for retinotopic mapping were performed through the same imaging window, the alignment error between two-photon sessions within each mouse was expected to be very small. However, greater errors could be introduced during the registration to the CCF. We therefore estimated the potential error in identifying a neuron’s position due to the alignment procedure by using data from the Allen Institute that included, for individual mice, field sign maps with ground-truth CCF coordinates. To mimic our alignment procedure, we registered a field sign map from a single Allen Institute mouse to the average field sign map from their other mice. We estimated the CCF coordinates from the alignment and compared these coordinates to the real positions known for that mouse. This procedure was identical to the methods we used to align data across mice and to register our data to the CCF. This alignment introduced errors in the range of 100 to 130 μm (Figure S1F), which is smaller than the smallest posterior brain regions and less than the relevant length scales for most of our analyses.
Pre-processing of imaging data
All image processing was performed in MATLAB. Before source extraction, in-plane motion was corrected using a hierarchical approach. First, fast motion artefacts were corrected within blocks of 1000 frames using the Lucas-Kanade method (Greenberg and Kerr, 2009). Then, the average images of each corrected 1000-frame block were aligned to the average image of the middle block of the session to correct for slow changes. In three consecutive steps, we found a rigid, then an affine, and finally a nonrigid transformation using MATLAB functions imregtform and imregdemons. The successive transformations were combined into one displacement field using cubic interpolation and applied to the image data in a single step to minimize interpolation artefacts. We found the stepwise motion correction procedure to be necessary for robust nonrigid motion correction. Preprocessing code is available at https://github.com/HarveyLab/Acquisition2P_class/.
Fluorescence source extraction
After motion correction, the spatial footprints of fluorescence sources were identified using a modified version of the constrained non-negative matrix factorization (CNMF) framework (Pnevmatikakis et al., 2016). For CNMF, we used down-sampled image data to conserve space and reduce noise (from 30 Hz to 1.2 Hz). We used three unregularized background components to model temporally and spatially varying neuropil fluorescence. The procedure to initialize source footprints was modified compared to the original CNMF. We used an approach that identified sources independently of their anatomical shape and could identify both cell bodies and neurites. First, the field of view was divided into overlapping tiles (52 pixels edge length, 6 pixels overlap). The temporal correlation matrix C between all pixels in a tile was computed and used to construct a graph with edge weights between pixels i and j. Spectral clustering was then applied to the graph to segment the pixels within the tile into a pre-determined number of subregions with high temporal correlations between the pixels of each subregion (Ding et al., 2005). Subregions with temporal correlations greater than 0.9 were assumed to be fragments of the same source and merged. The subregions were used to initialize the CNMF algorithm.
The fluorescence traces returned by CNMF were then normalized by their baseline fluorescence. The CNMF approach absorbs both out-of-focus neuropil fluorescence and the true baseline fluorescence of each source into the background components. We therefore used nonnegative regression (MATLAB lsqnonneg) to separate the background fluorescence at the pixels occupied by each source into a component that varied spatially like the source footprint, and an offset that modeled diffuse fluorescence. The regression coefficient of the source-shaped background component was used as the baseline. The fluorescence trace of each source was divided by its baseline to obtain the change over baseline (F−F0)/F0. Finally, traces were deconvolved using the OASIS algorithm with a first-order autoregressive model and individually optimized decay constants (Friedrich et al., 2017).
Source classification
Our version of CNMF did not impose a spatial prior on the extracted fluorescence sources and therefore returned sources with irregular spatial footprints, in addition to soma-shaped footprints. We used a simple convolutional neural network (CNN) in MATLAB to classify source footprints by shape into somata, transverse processes (small dot-shaped sources), and artefacts (Figure S1H–L). The CNN took as input a 25-by-25 pixel image of the source footprint returned by CNMF. The input was processed by three convolutional layers (filter size, 5×5; channels, 6; stride, 1), followed by a fully connected layer (64 units) and a softmax output layer. All layers were connected by rectified linear units. The training data consisted of 1884 manually labeled source images, augmented by random rotation and translation to 300,000 samples. The network was trained using stochastic gradient descent with momentum (batch size, 512; learning rate 0.03; L2 regularization, 0.0001, otherwise default settings of sgdm in MATLAB). Classification accuracy was confirmed using held-out data to be similar to manual classification.
We used a similar approach to classify fluorescence traces into traces with calcium transients, traces with low signal-to-noise ratio, and traces containing artefacts (Figure S1H–L). The trace-classification CNN took as input the normalized fluorescence trace. The input was processed by two convolutional layers (filter size, 1×16; channels, 4 and 8; stride, 1), followed by a max-pooling layer that reduced the trace to 8 points per channel, a fully connected layer (64 units), and a softmax output layer. All layers were connected by rectified linear units. The network was trained using stochastic gradient descent with momentum (batch size, 64; learning rate 0.01; L2 regularization, 0.001, otherwise default settings of sgdm in MATLAB). The training data consisted of 1586 manually labeled traces. Classification accuracy was confirmed using held-out data to be similar to manual classification.
The only sources used for further analyses were those that had either soma or transverse-process shapes and traces that contained calcium transients (total, 23,213; soma, 18,127; transverse process, 5,086). In the text we refer to both soma-shaped and transverse-process-shaped fluorescence sources as “neurons”.
QUANTIFICATION AND STATISTICAL ANALYSES
Data preprocessing was performed in MATLAB (MathWorks) and all main analyses were performed using Python 3. Except for the CNN and GLM, which used TensorFlow, most analyses used the Scikit-learn Python library. Data and analysis pipelines were organized using DataJoint.
Statistical confidence and significance were generally computed by hierarchical bootstrapping. To estimate the uncertainty of a statistic (e.g. the mean) of a sample, the statistic was recomputed many times for resampled datasets. The datasets were generated by random sampling with replacement, first of the mice, then of the imaging sessions within the sample of mice, and then of the neurons within the sample of sessions. Resampled datasets had the same size as the original dataset. 1000 resampled datasets were generated unless noted otherwise. The resampling of mice was constrained such that at least two different mice were in each resampled population. The hierarchical procedure was used to account for the fact that sources from the same session and sessions from the same mouse were statistically not fully independent. We reported the 5th and 95th percentile of the bootstrap distribution as the confidence intervals. For significance testing, we computed the empirical probability that a bootstrap sample was greater or less than the null hypothesis value, whichever was smaller. The reported two-tailed p-value was twice this probability.
Unless indicated otherwise, the significance threshold was set at 0.05. Where indicated, we accounted for multiple comparisons by controlling the false discovery rate with the Benjamini-Hochberg procedure (Benjamini and Hochberg, 1995): For a given false discovery rate α and ascending list of p-values p corresponding to the m hypotheses that were tested, we found the largest k such that . We then rejected the null hypothesis for all hypotheses up to k.
The number of samples (n) and p-values were reported in the figure legends. For behavior analyses (Figure 1), n typically referred to the number of mice. For analyses of neuronal properties, n typically referred to the number of neurons. No statistical methods were used to predetermine sample size. For each experiment, all mice received the same experimental treatment. Therefore, there was no stratification, subject-level randomization or experimenter blinding during any stage of the study. Behavioral sessions were excluded from analysis if the animal did not receive at least 1.5 rewards per minute for at least 20 minutes. Imaging sessions were excluded if there was noticeable drift after motion correction.
Optogenetic inactivation experiments
We assessed the effect of optogenetic perturbation at each cortical location on the locomotion velocities and reward rate. Perturbation trials were only included if the mouse was performing the task (greater than 1.5 rewards per minute, computed in a four-minute running average).
For the mapping experiments (Figure 1I), we obtained 33,045 trials (158.87 ± 21.14 per location, mean ± s.d.) in 19 sessions from three mice. Although mice were trained on the full task (randomized drift velocity), no drift was used for the mapping sessions since we wanted to assess the effect of inhibition on locomotion without the additional complexity of changing visual-motor mappings. For analysis, to increase the number of trials, we pooled trials across neighboring positions in the 500 μm grid. Therefore, each point in Figure 1I is based on the trials at the indicated location and the up to eight immediate neighbors. In each trial, we computed the change in locomotion velocity between 300 ms before laser onset and the time of laser offset. The resulting values constituted the test distribution. To obtain a null distribution, we computed the change in the task variable between equally spaced timepoints in the preceding inter-trial-interval. Even though there might be residual effects from previous trials, due to the randomization of stimulation locations, we assumed these effects to be zero on average. We then computed the difference between the test value and the null value for each trial, and used hierarchical bootstrapping to obtain a p-value for the null hypothesis that the mean of the difference was zero. These p-values were reported in Figure 1I.
For the targeted experiments (Figure 1K), we obtained 10,596 trials (815.08 ± 505.86 per location, mean ± s.d.) in 30 sessions (same three mice as for the mapping experiments). The average reward rate was computed for the final two seconds of each inhibition trial, i.e. the period after the drift switch.
Neural network encoding model
The encoding of task variables was analyzed by fitting a convolutional neural network (CNN) that predicted the activity of all recorded neurons simultaneously, based on the measured task variables. The model was programmed in Python 3 using TensorFlow 1.3.0.
Inputs and outputs
The input to the model consisted of a 4 s long snippet of task and behavioral information. Based on this input, the neural activity at a single timepoint 3 s into the snippet was predicted. Therefore, neurons whose activity was related to task features up to 3 s in the past and up to 1 s into the future could be modeled. The length of the snippet was chosen to approximately match the longest task events. For example, the time taken by the mouse to stop running for a reward, consume the reward, and re-accelerate was approximately 4 s (Figure 6A). One snippet was created for each timepoint, i.e. adjacent snippets overlapped.
All data (task variables and fluorescence activity) were resampled at 10 Hz for the model to reduce the amount of data. Only timepoints in which the mouse performed the task (greater than 1.5 rewards per minute, computed in a four-minute running average) were included, and only sessions with at least 20 minutes of task performance were included (118 sessions in total, 23.6 ± 5.99 sessions per mouse, 60.52 ± 9.02 minutes of task performance per session, mean ± s.d.).
Nine task variables were used as inputs in the full model: Linear ball velocity (ball pitch), angular ball velocity (ball roll), ball yaw (not used to control virtual reality), linear screen velocity, angular screen velocity, time since last reward, time since last drift switch, time since last open-loop onset and time since last open-loop offset. The inclusion of the temporal variables meant that activity related to these task events could be modeled even beyond the 4 s length of the input snippet.
The measured ball pitch, roll and yaw velocities were normalized by scaling with a session-specific factor. The factor was optimized such that the velocity histogram of each session best matched (in a least-squares sense) the velocity histogram of all sessions combined. The same factors were applied to ball and screen velocities. Scale factors were small (range, 0.62 – 1.77, 5th to 95th percentile, 0.76 – 1.28), but were included to ensure that variations in average locomotion speed would not lead to trivial differences in the encoding weights between sessions.
The output of the model was the predicted deconvolved fluorescence trace, in units of ΔF/F0.
Architecture
The model consisted of a nonlinear stage (CNN) that was shared across all sessions and neurons, and a neuron-specific linear readout stage (GLM, Figure 2F). The input layer was followed by three 1d-convolutional layers that convolved the input snippet across time with learned filters of size 6 (0.6 s). Each convolutional layer had 32 channels. The output of the last convolutional layer was flattened and connected densely to a layer with 128 units, which was connected to another dense layer with 64 units (“Task factors” layer in Figure 2F). This was the last layer in the shared stage. Between the layers in the shared stage, a leaky rectification nonlinearity of the form max(x, 0.1x) was applied to the activations.
The neuron-specific stage consisted of a single readout layer that computed a linear combination of the activations in the bottleneck layer. This layer had a separate set of weights for each neuron. The output of this layer modeled the logarithm of the deconvolved fluorescence trace.
The nonlinear (shared) stage of the model therefore reduced the high-dimensional task information into 64 variables (“task factors”) that were most relevant for explaining the neural activity. The task factors were the same for all modeled neurons. The second stage then formed a separate generalized linear model for each neuron that used the 64 task factors as predictors.
In addition to the task factors, two further features were included as predictors in the second stage (GLM) of the model. The first was the output of a separately fitted model of visual receptive fields (see section Visual Receptive Fields). Therefore, the CNN was trained to fit only the residual activity that was not already explained by the visual receptive field. The second was a time-varying offset designed to capture slow, behavior-independent fluctuations in neural activity throughout the session. The offset was modeled as a cubic polynomial of the normalized time within the session. The parameters of the polynomial were fitted jointly with all other network parameters.
Training
Network weights were initialized with normally distributed random values. Random values that fell more than two standard deviations from zero were dropped and redrawn (tensorflow.truncated_normal). The standard deviation was set to , where n was the number of inputs to that layer. Biases were initialized with zero.
The network was trained to minimize a loss function based on the Poisson likelihood of the neural activity, given the prediction (tensorflow.nn.log_poisson_loss). To prevent overfitting, the sum of the squared weights of all main network layers was added to the loss function, scaled by 9.17 × 10−7 (this and other hyperparameters were optimized, see below). In addition, dropout with a probability of 0.5 was applied during training to the convolutional and first densely connected layer. The visual receptive field input and the time-varying offset were not regularized. Fitting was done by stochastic gradient descent using the Adam optimizer with the following parameters: learning rate, 0.0027; β1, 0.89; β2, 0.9999, batch size 4096. Each batch contained a random sample of all sessions, such that each weight update included contributions from most sessions. Randomization was performed such that all sessions contributed to the weight updates equally on average.
For training, 80 percent of the data was used, with the remaining 20 percent held out for model evaluation. The split between training and test set was done in 20-second-long segments, which was longer than the autocorrelation time of the data. Every fifth segment was assigned to the test set. Care was taken to ensure that no test data were included in the training set. Model fit quality was always reported for the test set. Model fit quality was quantified using the Poisson deviance,
between data y and prediction μ at timepoints t. We reported the fit quality in terms of the fraction of Poisson deviance explained by the model, compared to a null model that predicts the mean of the data at all datapoints: 1 − Dmodel/Dnull. We only included activity sources with fits explaining at least 10% of the deviance in subsequent analyses.
The following hyperparameters were optimized using the Bayesian Optimization Python package (https://github.com/fmfn/BayesianOptimization): learning rate, batch size, number of convolutional layers, number of channels in convolutional layers, size of the first densely connected layer, size of the bottleneck layer, size of the convolutional filter, degree of the time-varying offset polynomial, Adam parameters. The model performance was robust to most of these parameters and varied mostly in the time to reach convergence, rather than the fit quality at convergence. Based on extensive hyperparameter optimization, we believe that the fit quality we obtained was close to the optimum attainable with the general nonlinear-linear-exponential architecture we used. In separate tests (data not shown), we found that the model fit could be improved slightly by adding a separate nonlinear readout network for each neuron, but at the cost of not being able to compare readout weights across neurons easily.
Reduced models
To measure the unique contribution of different input variables to the overall fit quality (Figure 6), we constructed reduced models that lacked a variable. For each neuron, we computed the difference between the deviance explained by the full model and the deviance explained by the reduced model. This difference describes the deviance uniquely attributable to the variable that was missing in the reduced model. We reported this value as a fraction of the full-model deviance: 1 − (Dnull − Dreduced)/(Dnull − Dfull). For the variables shown in Figures 6 and 7, the reduced models were modified from the full model as follows:
For visual receptive fields, the visual receptive field input was removed.
For ball velocity, the linear ball velocity, angular ball velocity, and ball yaw inputs were removed.
For screen velocity, the linear screen velocity and angular screen velocity were removed.
For nonlinear interactions, the convolutional layers were changed to “depthwise” convolutions, which apply a different filter to each input channel without cross-channel mixing. Also, the nonlinearity between the first densely connected layer and the bottleneck layer was removed. Therefore, there was no nonlinear mixing between the nine task variables in this model.
For task history, the length of the input snippet was reduced from 3 s past and 1 s future task information with respect to the predicted neural activity timepoint, to 0.3 s past and 0.1 s future task information.
For task features (Figure 7), the time since last reward, time since last drift switch, time since last open-loop onset and time since last open-loop offset inputs were removed. These variables accounted for a significant amount of deviance in only a small number of neurons and were therefore not included as a map in Figure 6.
Factor non-identifiability controls
Similar to non-identifiability in classical factor analysis, the factors obtained from the encoding model were not uniquely identifiable: theoretically, certain linearly transformed versions of the readout weight vectors could provide equally good model fits. Therefore, re-fitting the model with different random initializations of the neural network weights could lead to factors that appear different when considering individual factors. However, linear transformations (e.g. rotations) of the factor space do not change the intrinsic structure (relative positions) of the data points in this space. We performed controls to show that our main analyses captured properties of this structure that were robust to the non-identifiability (Figure S2). We re-fit the full model 100 times with different random initializations of the neural network weights. For each initialization, we recomputed the encoding maps, average encoding map rate of change, k-means clustering of encoding maps, and cluster discriminability scores (Figure S2C). To assess variability in the location of cluster boundaries for the k-means clustering of encoding maps, we defined pixels to be at a boundary if at least one of its neighbors belonged to a different cluster than itself. For each pixel, we then computed the probability of it being a boundary pixel (Figure S2D).
Visual Receptive Fields
We estimated a linear visual receptive field for each neuron and included the receptive field prediction in the CNN. This had two purposes. First, we wanted to ensure that we did not incorrectly attribute velocity tuning to neurons with simple linear visual receptive fields. Second, linear visual receptive fields are a well-studied encoding property that served as a useful comparison for the encoding maps in Figure 6.
Visual receptive fields were estimated based on the neural activity and screen content recorded while mice performed the task. The images displayed on the screen were downsampled to 79 by 107 pixels and reshaped into a pixels-by-timepoints visual stimulus matrix. The visual stimulus was shifted in time by 100 ms to account for various lags between the stimulus display and the detection of fluorescence activity. The linear visual receptive field was estimated for each neuron using a spike-triggered average based on a regularized pseudo-inverse (Smyth et al., 2003),
where S is the visual stimulus matrix that has been augmented with a regularization matrix, r is the neural response that has been normalized and augmented with zeros, and X+ is the Moore-Penrose pseudoinverse of matrix X. The regularization matrix was a second-derivative matrix designed to penalize differences between adjacent points in the receptive field map and therefore encouraged smoothness (Smyth et al., 2003). The strength of the regularization was chosen to maximize prediction performance on a held-out test set (same train/test split as for the CNN). To reduce background noise, a Gabor filter was fit to the receptive field map using a grid search over 36 evenly spaced orientations and 10 log-spaced spatial frequencies from 0.02 to 0.3 cycles per degree, and the receptive field map was scaled by the envelope of the best-fit Gabor filter. The fit quality of the receptive field map was assessed by fitting a Poisson generalized linear model to the deconvolved fluorescence activity, with the linear prediction of the receptive field estimate as its sole input. For neurons where the receptive field did not explain any of their activity (fraction of deviance explained on the test set ≤ 0), the receptive field estimate was set to zero.
The activity prediction based on the visual receptive field estimate was used in the CNN along with the 64 task factors from the shared stage of the CNN to predict the activity of each neuron. A single weight was fitted as part of the CNN training to scale the visual prediction. We estimated the visual receptive fields separately from the CNN because the high dimensionality of the visual stimulus made joint fitting infeasible.
Encoding weight maps
The area of cortex covered by our imaging data was divided into a pixel grid with 100 μm spacing. Only pixels containing data from at least two imaging sessions were shown. Maps were based on the CNN encoding weights of all neurons with a fraction of explained deviance greater than 0.1. Weights for each task factor were z-scored by subtracting the mean and dividing by the standard deviation across neurons.
Map computation and smoothing
Each pixel in the maps was a weighted average of the normalized encoding weights of all neurons, where the averaging weight of each source decayed with the distance between the source and the pixel according to a Gaussian kernel. The smoothness (standard deviation of the Gaussian) was optimized by cross-validation across mice. A map was computed with the data from four mice, and used to predict the weights of the fifth mouse. This was repeated for all five mice and for 20 smoothness values from 0.2 to 3.0 mm. The least-squares fit quality was averaged across mice and the smoothness value with the best fit quality was chosen for the map. If the best value was 3.0 mm, the map was considered to have no spatial structure and was shown as a flat image. For regularization, pseudo-data were added to each pixel that had the value of the global mean of all data points and amounted in weight to one tenth of the number of data points in the pixel with the most data points. The regularization reduced noise in areas of low neuron density (e.g. at the edge of the recorded area) by biasing the maps to their mean value.
Maps of rate of change of encoding weight
To test whether there were consistent spatial locations at which encoding weights changed, we computed the spatial rate of change of pixel values in each of the encoding weight maps. The rate of change was computed using the central difference between pixels along the rows and columns of the map. From the 2-dimensional gradient vector at each pixel, the magnitude was computed. The resulting map of encoding rate of change was normalized between zero and one and the maps for all task factors were averaged.
Clustering of encoding weight maps
Area parcellations based on encoding properties were created by applying k-means clustering (sklearn.cluster.KMeans) to the pixels of the 64 encoding maps. Each map pixel represented a datapoint in a 64-dimensional space. For each value of k, 300 random initializations and up to 1000 iterations were used. The cluster order and color was determined by applying metric multidimensional scaling (sklearn.manifold.MDS) to the cluster centroids to embed them into a one-dimensional space. The clusters were then ordered and colored according to their distance in the embedding from the most anterior area. Similarity in color therefore reflected similarity in encoding properties. The fraction variance explained by each clustering was computed as 1 − Dcluster/Dnull, where Dcluster was the sum of squared distances of data points (map pixels) to their nearest cluster centroid, and Dnull was the sum of squared distances from the mean of all data points.
For comparison, the same clustering analysis was applied to maps simulated according to two simple models (Figure 3C): In the “simulated gradients” model, each map consisted of a radial gradient centered at a random map location. In the “simulated clusters” model, each map contained the same clustered structure (taken from the Allen Institute parcellation, six clusters), but with a different, normally distributed random intensity for each cluster in each map. Simulated maps were scaled to match the range of the real encoding maps. To match the explainable variance of the simulated maps to the real data, normally distributed random noise was added independently to each map pixel. The standard deviation of the noise was chosen to minimize the squared difference in the variance-explained curve (Figure 3C) between the models and the real data. 100 simulation repeats were performed for each model. Significance of the difference in model fit quality for the variance-explained curve was tested by bootstrap. For each of 10−4 iterations, 100 samples were drawn with replacement from each model’s simulation repeats, the mean variance-explained curve was computed for each model, and their squared difference from the real data. The p-value was computed as the fraction of bootstrap samples in which the “simulated clusters” model had a lower error than the “simulated gradients” model.
Area discriminability classifier
For the area discriminability classifier, neurons were first clustered (sklearn.cluster.KMeans) into “encoding types” based on their encoding vectors (normalized to unit length). The goal of this step was to discretize encoding properties to simplify the subsequent analyses. The number of clusters was set to 100. This number approximately maximized the area discriminability. However, results were not very sensitive to the number of clusters for values between 50 and 1000.
We used a naïve Bayes classifier (sklearn.naive_bayes.MultinomialNB) to test how discriminable the areas were from each other in each of the parcellations in Figure 3B. Each area was characterized by how many neurons of each encoding type it contained. Based on these counts, the classifier modeled the probability that a given population of neurons (also characterized by its type frequencies) originated from each of the areas.
To test the discriminability of areas in a parcellation, encoding types were obtained and a classifier was trained based on the data from four mice, and used to compute the probability that the population in each area from the fifth mouse came from each of the areas. This was repeated for all five mice and the confusion probabilities were averaged across mice. For each true area, the predicted area was the area to which the classifier assigned the highest probability. For each parcellation in Figure 3B, the fraction of correctly classified areas was computed and reported in 1/k, where k was the number of areas, i.e. probability of choosing the correct one out of k areas when choosing uniformly at random.
Dendrogram
Agglomerative clustering was used to visualize major patterns in the spatial distribution of encoding weights. The 64-dimensional encoding weight vector of each neuron was normalized to unit length, such that the clustering depended only on the encoding properties (vector direction) of the neurons, rather than also on their activity levels (vector length). The 64 task factors were agglomeratively clustered using the correlations between the weights of each factor across all neurons as the clustering metric, with the average as the linkage method. This meant that factors that had high weights for similar subsets of the neurons were clustered together. To generate the map for a cluster of factors, the weight maps (as computed for Figure 2J) for all factors in that cluster were averaged.
Encoding space analyses
To visualize the distribution of neurons across weight space, the 64-dimensional encoding vectors were reduced to two dimensions using t-distributed stochastic neighbor embedding (t-SNE; sklearn.manifold.TSNE). The output of t-SNE depends strongly on the perplexity parameter. We therefore tested perplexities between 50 and 1600 and chose 200, which was the value that produced the most pronounced structure in the visualization. We computed the t-SNE embedding 10 times with perplexity 200 at different values for the learning rate, and chose the one that had the lowest Kullback-Leibler divergence between the low-dimensional embedding and the high-dimensional data. The same embedding was used for Figures 4A, 4C, S5B and S5F.
The fraction of nearest neighbors in encoding space in each area (Figure 4E) was computed using the full 64-dimensional encoding vectors. Neurons were first randomly subsampled to obtain the same number of sources from each area. Then, for each remaining neuron in one mouse, the nearest neighbor in encoding space among the sources from the other four mice was found. This was repeated for each of the mice. To obtain confidence intervals, this entire process was repeated 200 times on hierarchically resampled datasets. Figure 4E shows the mean across resampled datasets and the 5th percentile. The upper confidence interval was omitted for clarity of visualization.
The normalized total encoding-weight dispersion of the neurons in each area (Figure 4F) was computed by summing the variances of the encoding weights along each of the 64 dimensions and dividing by the total dispersion of the whole population. Confidence intervals (5th and 95th percentile) were based on hierarchical bootstrap (500 iterations).
Distribution of encoding types across cortex
Encoding types and area parcellations in Figure 5 were defined as for Figure 3. The empirical prior area probability p(area) (i.e. the number of neurons in each area, divided by the total number of neurons) and the empirical likelihood of encoding types in each area p(type|area) were used to compute the joint probability of areas and types p(area, type) = p(type|area)p(area). Empirical distributions were smoothed by adding one to the counts before normalization. The pointwise mutual information (PMI) between areas and types was then computed as
The PMI quantifies how much the actual probability of observing a neuron of a particular type in a particular area differs from a case in which the type and area distributions are statistically independent. A positive PMI means that the combination of area and type is over-represented, and a negative PMI means it is under-represented in the data. To test whether PMI-values were significantly different from zero, PMI values were recomputed 104 times using hierarchically resampled data, and a p-value was computed for each PMI value as the fraction of resampled values greater than or less than zero, whichever was smaller. The significance threshold α was adjusted to account for multiple comparisons by controlling the false-discovery rate at 0.01 using the Benjamini-Hochberg procedure as described above. 64 of 500 PMI values were significantly less than zero and 5 were significantly greater. The shuffle distribution in Figures 5C–D was computed by randomly shuffling the type labels of the neurons to break the relationship between encoding type and location in cortex.
Relating neural activity to task variables
For the reward-aligned activity maps (Figure 6A), fluorescence activity of all sources was grouped into 1 s long bins based on reward times. Data in each bin were averaged, and maps across cortex were computed for each bin using a Gaussian smoothing kernel (0.3 mm s.d.).
When relating neural activity to task variables, it is essential to consider correlations between task variables to avoid inferring a relationship between neural activity and a task variable when the activity actually depends on a different, but correlated, variable. We therefore took a conservative approach based on nested models. Our approach identified how much additional explanatory power about the neural activity a variable contributed after all other variables had been accounted for. Concretely, for the maps in Figure 6B, we fit a full model including all variables and reported how much more deviance it explained than models lacking one of the variables (see section Reduced models). As with the maps of task factor weights in Figure 2, we used cross-validation to determine the amount of smoothing for the encoding maps to ensure that the observed structure was consistent across mice. For the “Full model” map (Figure 6B, left), all recorded neurons were included. For the single-variable maps, only well-fit sources (CNN deviance explained > 0.1) were included.
To relate encoding to spread in cortex (Figure 7), neurons were grouped by encoding type as defined for Figure 3. The spread of neurons across cortex within each type was quantified as the area of the ellipse described by the 1 s.d. contour of a Gaussian distribution fit to the cortical location of the sources. The y-axis shows the fraction of deviance uniquely attributable to each variable (see section “Reduced models”), averaged within each encoding type. Confidence intervals (5th and 95th percentile, only displayed for the top three types) were computed by hierarchical bootstrap (104 iterations). Types whose confidence interval did not include zero were considered significant (plotted in black); non-significant points were plotted in gray. Regression lines were computed by fitting a simple linear regression to the hierarchically resampled datasets; shaded area indicates 5th and 95th percentile of the resulting distribution of lines. The significance of regression slopes was tested using the two-tailed bootstrap p-value defined above.
Population decoding
To test whether task-relevant information was present in local populations, we built a decoder that estimated the probability distribution over each task variable at each timepoint, given the recorded neural responses. The core of the decoder was an encoding model that took the form of a generalized linear model (GLM). The GLM was fit to the fluorescence activity of every source independently and estimated the probability of the neural response, given the task variables. Manual feature selection was used instead of the CNN feature extractor because our goal was to test where task variables were represented in disentangled representations. The ability of the CNN to transform and combine input variables nonlinearly would have confounded this analysis.
Generalized linear model
The GLM predicted the deconvolved fluorescence activity r as
where fi is a static pointwise nonlinearity for feature si, parametrized as a weighted sum of 16 raised cosine “bumps”:
with each bj given by
The basis function centers ϕ were chosen such that they covered the range of the feature and were spaced by π/2. (Peron et al., 2015; Pillow et al., 2008).
In addition to the nine variables used in the CNN, the inputs to the GLM used here included the following variables because their untangled representation across cortex was of interest: linear and angular drift, multiplicative interaction terms (linear ball velocity × linear screen velocity and angular ball velocity × angular screen velocity), and linear and angular acceleration. To measure acceleration at behaviorally relevant timescales, the velocity traces were smoothed (Gaussian window, 100 ms s. d.). Acceleration was defined as the difference between the current timepoint and the next in the smoothed trace. As in the CNN-based model, the prediction based on the separately fitted visual receptive field estimate was supplied as a separate feature to the model. This feature did not undergo the raised cosine basis expansion.
The model was implemented in TensorFlow and fit using batch gradient descent (Adam optimizer; learning rate, 0.001; β1, 0.8; β2, 0.9). Like the CNN-based model, the model was trained to minimize a loss function based on the Poisson likelihood. To prevent overfitting, the following penalty was added to the loss function:
where λ is a parameter to tune regularization strength, wi is the vector of basis function weights for task feature i, and P is the second derivative matrix (a matrix with values 2 and −1 on the main an off-diagonals, respectively). The first term encouraged smoothness in the feature nonlinearities by placing a Gaussian prior on the parameters for each nonlinearity (Peron et al., 2015). The second term adds a group lasso penalty that encourages sparsity on the level of task variables (Yuan and Lin, 2006). Together with the first term, this results in an elastic net penalty (Zou and Hastie, 2005), which prevents model degeneracy for variables that are correlated or linearly dependent (e.g. linear velocity, angular velocity, and drift) while also encouraging sparsity. The regularization strength λ was optimized for each neuron by fitting separate models for a series of 50 λ-values logarithmically spaced between 10−8 and 10-1. For the final model, the largest (most regularizing) λ was chosen that yielded a fraction of deviance explained that was within 0.01 of the best model, on a held-out dataset (20% of the data).
Decoding
To measure the information about task variables that was decodable from different parts of cortex, we first grouped neurons into small local populations. Each population contained approximately 50 nearby neurons that were recorded simultaneously. Populations were chosen by evenly tiling the cortical space covered in a recording session with points (“population centers”), and then assigning neurons to the nearest center. The number of centers per session was chosen to result in approximately 50 neurons per population. Each neuron belonged to exactly one population and populations covered non-overlapping regions of cortex.
To decode the value of a task variable, given the local population activity, we used the encoding model (GLM) to estimate the probability of the population responses, given the task variables, and then inverted the model according to Bayes theorem. This approach allowed us to isolate the information contained in the neural activity about a specific task variable, while accounting for information about other, correlated, task variables. Let s be the decoded task variable and the other task variables (both s and are parametrized in the GLM in terms of the cosine basis functions). The probability of observing the response rn of neuron n can be written as . For each decoded task variable, at each timepoint in the test set, we used the GLM fitted on the training set to compute for a range of 20 values for s linearly spaced between the minimum and maximum of s in the training set. Assuming fluorescence responses to be conditionally independent given the task variables, we then computed the probability of observing the population activity as follows:
Using Bayes’ rule, we obtained a quantity ps, which is proportional to the posterior probability of observing each of the 20 tested values of s, as , where were the true values that were observed for the other task variables. We modeled as a Gaussian mixture (sklearn.mixture.GaussianMixture with five components, each with its own full covariance parameters) that was fitted to the training data. When decoding the drift variables, we did not include screen velocity in the prior model because this would have led to a degeneracy (drift is a linear combination of ball and screen velocity). As the decoded value of s, we used its expected value .
Our goal was to assess how much information about the task variable was present in the neural activity. To assess decoding accuracy, we therefore first computed Dtotal, the sum of squared errors between the true task variable and the decoding estimate. Dtotal contained contributions from the correlations between the decoded task variable s and the other variables in addition to the information provided by the neural responses. To isolate the contribution of the neural response, we computed Dneural = Dtotal − Dprior, where Dprior was the sum of squared errors between the true task variable and a decoding estimate based only on the relationship between the decoded variable and the other variables, , without any neural information. We then computed the fraction of variance explained by the neural responses as , where Dnull was the sum of squares of the decoded task variable. Maps of decoding accuracy (Figure 8) were computed by assigning each neuron the decoding performance of the population that this source was a member of, and then applying cross-validated Gaussian smoothing as described above. To provide a notion of the uncertainty of the estimate of decoding accuracy, for the maps, we reported the accuracy in units of standard errors above zero. The standard error was computed from the average variance of decoding performance at each pixel in the map, based on the maps from n = 5 mice.
For the open-loop analysis (Figure 8D), an encoding model was fit to all timepoints except the open-loop timepoints and those closed-loop timepoints that were replayed during the open-loop segments. This model was then used to decode the task variables at open-loop timepoints (for the maps and the “Open loop” points in Figure 8D) and at the replayed closed-loop timepoints (for the “Closed loop” points). The error bars show 5th and 95th percentile confidence intervals of the mean across neurons (hierarchical bootstrap).
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited Data | ||
| Allen Mouse Common Coordinate Framework | Allen Institute for Brain Science | http://help.brain-map.org/display/mousebrain/Documentation |
| Retinotopic field sign maps | Allen Institute for Brain Science | http://api.brain-map.org/api/v2/well_known_file_download/501586803 and 78 further “well known file” IDs. |
| Experimental Models: Organisms/Strains | ||
| C57BL/6J-Tg(Thy1-GCaMP6s)GP4.12Dkim/J | The Jackson Laboratory | Stock No: 025776 |
| VGAT-ChR2-EYFP | The Jackson Laboratory | Stock No: 014548 |
| Software and Algorithms | ||
| MATLAB 2014b+ | The MathWorks | https://www.mathworks.com |
| ScanImage 2016 | Vidrio Technologies | http://scanimage.vidriotechnologies.com/display/SIH/ScanImage+Home |
| Image preprocessing and motion correction code | Driscoll et al., 2017 | https://github.com/HarveyLab/Acquisition2P_class |
| OASIS algorithm for deconvolution of calcium imaging data | Friedrich et al., 2017 | https://github.com/zhoupc/OASIS_matlab |
| TensorFlow 1.3.0 | Google Inc. | https://github.com/tensorflow/tensorflow |
| Benjamini-Hochberg procedure | Benjamini and Hochberg, 1995 | N/A |
Acknowledgements
We thank Mark Andermann, Jerry Chen, Jan Drugowitsch, Bernardo Sabatini and members of the Harvey lab for helpful discussions. We thank the Research Instrumentation Core and machine shop at Harvard Medical School (supported by grant P30 EY012196). This work was supported by a Burroughs-Wellcome Fund Career Award at the Scientific Interface, the Searle Scholars Program, the New York Stem Cell Foundation, NIH grants from the NIMH BRAINS program (R01 MH107620), NINDS (R01 NS089521), and the BRAIN Initiative (R01 NS108410), an Armenise-Harvard Foundation Junior Faculty Grant, a Herchel Smith Fellowship, and a Boehringer-Ingelheim Fellowship. The Titan X Pascal used for this research was donated by the NVIDIA Corporation.
Footnotes
Declaration of Interests
The authors declare no competing interests.
REFERENCES
- Alexander AS, and Nitz DA (2015). Retrosplenial cortex maps the conjunction of internal and external spaces. Nature Neuroscience 18, 1143–1151. [DOI] [PubMed] [Google Scholar]
- Allen WE, Kauvar IV, Chen MZ, Richman EB, Yang SJ, Chan K, Gradinaru V, Deverman BE, Luo L, and Deisseroth K (2017). Global Representations of Goal-Directed Behavior in Distinct Cell Types of Mouse Neocortex. Neuron 94, 891–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Institute Allen (2017). Allen Mouse Common Coordinate Framework v.3 technical white paper (Allen Institute for Brain Science). http://help.brain-map.org/download/attachments/8323525/Mouse_Common_Coordinate_Framework.pdf?version=3
- Andermann ML, Kerlin AM, Roumis DK, Glickfeld LL, and Reid RC (2011). Functional Specialization of Mouse Higher Visual Cortical Areas. Neuron 72, 1025–1039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batty E, Merel J, Brackbill N, Heitman A, Sher A, Litke A, Chichilnisky EJ, and Paninski L (2017). Multilayer Recurrent Network Models of Primate Retinal Ganglion Cell Responses In International Conference on Learning Representations. [Google Scholar]
- Benjamini Y, and Hochberg Y (1995). Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society. Series B (Methodological) 57, 289–300. [Google Scholar]
- Buneo CA, and Andersen RA (2006). The posterior parietal cortex: Sensorimotor interface for the planning and online control of visually guided movements. Neuropsychologia 44, 2594–2606. [DOI] [PubMed] [Google Scholar]
- Chen G, King JA, Burgess N, and O’Keefe J (2013). How vision and movement combine in the hippocampal place code. PNAS 110, 378–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen T-W, Li N, Daie K, and Svoboda K (2017). A Map of Anticipatory Activity in Mouse Motor Cortex. Neuron 94, 866–879. [DOI] [PubMed] [Google Scholar]
- Cho J, and Sharp PE (2001). Head direction, place, and movement correlates for cells in the rat retrosplenial cortex. Behav. Neurosci. 115, 3–25. [DOI] [PubMed] [Google Scholar]
- Dana H, Chen T-W, Hu A, Shields BC, Guo C, Looger LL, Kim DS, and Svoboda K (2014). Thy1 -GCaMP6 Transgenic Mice for Neuronal Population Imaging In Vivo. PLOS ONE 9, e108697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding C, He X, and Simon HD (2005). On the equivalence of nonnegative matrix factorization and spectral clustering. In Proceedings of the 2005 SIAM International Conference on Data Mining, (SIAM), pp. 606–610. [Google Scholar]
- Driscoll LN, Pettit NL, Minderer M, Chettih SN, and Harvey CD (2017). Dynamic Reorganization of Neuronal Activity Patterns in Parietal Cortex. Cell 170, 986–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedrich J, Zhou P, and Paninski L (2017). Fast online deconvolution of calcium imaging data. PLOS Computational Biology 13, e1005423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gămănuţ R, Kennedy H, Toroczkai Z, Ercsey-Ravasz M, Essen DCV, Knoblauch K, and Burkhalter A (2018). The Mouse Cortical Connectome, Characterized by an Ultra-Dense Cortical Graph, Maintains Specificity by Distinct Connectivity Profiles. Neuron 97, 698–715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrett ME, Nauhaus I, Marshel JH, and Callaway EM (2014). Topography and Areal Organization of Mouse Visual Cortex. J. Neurosci. 34, 12587–12600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glickfeld LL, and Olsen SR (2017). Higher-Order Areas of the Mouse Visual Cortex. Annu. Rev. Vis. Sci. 3, 251–273. [DOI] [PubMed] [Google Scholar]
- Glickfeld LL, Andermann ML, Bonin V, and Reid RC (2013). Cortico-cortical projections in mouse visual cortex are functionally target specific. Nature Neuroscience 16, 219–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goard MJ, Pho GN, Woodson J, and Sur M (2016). Distinct roles of visual, parietal, and frontal motor cortices in memory-guided sensorimotor decisions. ELife Sciences 5, e13764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenberg DS, and Kerr JND (2009). Automated correction of fast motion artifacts for two-photon imaging of awake animals. Journal of Neuroscience Methods 176, 1–15. [DOI] [PubMed] [Google Scholar]
- Guo ZV, Li N, Huber D, Ophir E, Gutnisky D, Ting JT, Feng G, and Svoboda K (2014). Flow of Cortical Activity Underlying a Tactile Decision in Mice. Neuron 81, 179–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han Y, Kebschull JM, Campbell RAA, Cowan D, Imhof F, Zador AM, and Mrsic-Flogel TD (2018). The logic of single-cell projections from visual cortex. Nature 556, 51–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Collman F, Dombeck DA, and Tank DW (2009). Intracellular dynamics of hippocampal place cells during virtual navigation. Nature 461, 941–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Coen P, and Tank DW (2012). Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juavinett AL, and Callaway EM (2015). Pattern and Component Motion Responses in Mouse Visual Cortical Areas. Current Biology 25, 1759–1764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalatsky VA, and Stryker MP (2003). New Paradigm for Optical Imaging: Temporally Encoded Maps of Intrinsic Signal. Neuron 38, 529–545. [DOI] [PubMed] [Google Scholar]
- Keller GB, Bonhoeffer T, and Hübener M (2012). Sensorimotor Mismatch Signals in Primary Visual Cortex of the Behaving Mouse. Neuron 74, 809–815. [DOI] [PubMed] [Google Scholar]
- Licata AM, Kaufman MT, Raposo D, Ryan MB, Sheppard JP, and Churchland AK (2017). Posterior Parietal Cortex Guides Visual Decisions in Rats. J. Neurosci. 37, 4954–4966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma WJ, Beck JM, Latham PE, and Pouget A (2006). Bayesian inference with probabilistic population codes. Nat Neurosci 9, 1432–1438. [DOI] [PubMed] [Google Scholar]
- Makino H, Ren C, Liu H, Kim AN, Kondapaneni N, Liu X, Kuzum D, and Komiyama T (2017). Transformation of Cortex-wide Emergent Properties during Motor Learning. Neuron 94, 880–890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marques T, Nguyen J, Fioreze G, and Petreanu L (2018). The functional organization of cortical feedback inputs to primary visual cortex. Nature Neuroscience 21, 757–764. [DOI] [PubMed] [Google Scholar]
- Marshel JH, Garrett ME, Nauhaus I, and Callaway EM (2011). Functional Specialization of Seven Mouse Visual Cortical Areas. Neuron 72, 1040–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh L, Maheswaranathan N, Nayebi A, Ganguli S, and Baccus S (2016). Deep learning models of the retinal response to natural scenes. In Advances in Neural Information Processing Systems, 1361–1369. [PMC free article] [PubMed] [Google Scholar]
- Minderer M, Harvey CD, Donato F, and Moser EI (2016). Neuroscience: Virtual reality explored. Nature 533, 324–325. [DOI] [PubMed] [Google Scholar]
- Morcos AS, and Harvey CD (2016). History-dependent variability in population dynamics during evidence accumulation in cortex. Nature Neuroscience 19, 1672–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nitz DA (2006). Tracking Route Progression in the Posterior Parietal Cortex. Neuron 49, 747–756. [DOI] [PubMed] [Google Scholar]
- Peron SP, Freeman J, Iyer V, Guo C, and Svoboda K (2015). A Cellular Resolution Map of Barrel Cortex Activity during Tactile Behavior. Neuron 86, 783–799. [DOI] [PubMed] [Google Scholar]
- Pho GN, Goard MJ, Woodson J, Crawford B, and Sur M (2018). Task-dependent representations of stimulus and choice in mouse parietal cortex. Nature Communications 9, 2596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pillow JW, Shlens J, Paninski L, Sher A, Litke AM, Chichilnisky EJ, and Simoncelli EP (2008). Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature 454, 995–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitkow X, and Angelaki DE (2017). Inference in the Brain: Statistics Flowing in Redundant Population Codes. Neuron 94, 943–953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pnevmatikakis EA, Soudry D, Gao Y, Machado TA, Merel J, Pfau D, Reardon T, Mu Y, Lacefield C, Yang W, et al. (2016). Simultaneous Denoising, Deconvolution, and Demixing of Calcium Imaging Data. Neuron 89, 285–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth MM, Helmchen F, and Kampa BM (2012). Distinct Functional Properties of Primary and Posteromedial Visual Area of Mouse Neocortex. J. Neurosci. 32, 9716–9726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Runyan CA, Piasini E, Panzeri S, and Harvey CD (2017). Distinct timescales of population coding across cortex. Nature 548, 92–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saleem AB, Ayaz A, Jeffery KJ, Harris KD, and Carandini M (2013). Integration of visual motion and locomotion in mouse visual cortex. Nature Neuroscience 16, 1864–1869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sereno MI, McDonald CT, and Allman JM (1994). Analysis of Retinotopic Maps in Extrastriate Cortex. Cereb. Cortex 4, 601–620. [DOI] [PubMed] [Google Scholar]
- Smyth D, Willmore B, Baker GE, Thompson ID, and Tolhurst DJ (2003). The Receptive-Field Organization of Simple Cells in Primary Visual Cortex of Ferrets under Natural Scene Stimulation. J. Neurosci. 23, 4746–4759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song HF, Kennedy H, and Wang X-J (2014). Spatial embedding of structural similarity in the cerebral cortex. PNAS 111, 16580–16585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q, and Burkhalter A (2007). Area map of mouse visual cortex. The Journal of Comparative Neurology 502, 339–357. [DOI] [PubMed] [Google Scholar]
- Yuan M, and Lin Y (2006). Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 68, 49–67. [Google Scholar]
- Zhao S, Ting JT, Atallah HE, Qiu L, Tan J, Gloss B, Augustine GJ, Deisseroth K, Luo M, Graybiel AM, et al. (2011). Cell type-specific channelrhodopsin-2 transgenic mice for optogenetic dissection of neural circuitry function. Nature Methods 8, 745–752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhuang J, Ng L, Williams D, Valley M, Li Y, Garrett M, and Waters J (2017). An extended retinotopic map of mouse cortex. ELife 6, e18372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H, and Hastie T (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 67, 301–320. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


