Abstract
The numerical model HydratiCA was used to simulate the reaction kinetics of alkali-activated metakaolin, a material belonging to a class of sustainable binders alternative to Portland cement. The full chemistry of the system, including solid phases and aqueous species, is taken into account in these simulations. Specifically, metakaolin dissolution, reaction product nucleation and growth, and ion speciation, and diffusion in solution are simulated. The sodium aluminosilicate (N–A–S–H), formed by the reaction of metakaolin in alkaline solution, is implemented in the model as a combination of co-precipitating pseudo-zeolitic phases, with variable stoichiometry. The results show how variations of the reaction pathways, occurring when alkaline activators of different composition and concentration are used, can be associated with different macroscopic behaviors in terms of mechanical performance and durability. Reconciling these macroscopic properties with the basic chemical processes will be a fundamental technological challenge for the deployment of sustainable technologies in the construction industry.
1. Introduction
The sustainable development goals outlined in the United Nations 2030 Agenda include actions oriented at mitigating climate change, building resilient infrastructures, and promoting the development of sustainable cities.1 This need of imagining a sustainable future has boosted cement chemistry research aimed at defining a new generation of green building materials. Among the possible innovative alternatives to Portland cement, alkali-activated materials (also named geopolymers) represent a viable solution, with a consolidated scientific literature. Lack of internationally recognized standards and regulations2 has so far hindered the use of alkali-activated cements in practical applications, although actions are being taken in this direction.3
The concept beyond this class of cements is the replacement of limestone (impure CaCO3), as a primary raw material, with aluminosilicates from various sources. The production of Portland cement by CaCO3 calcination bears a huge environmental footprint because one mole of CO2 is emitted for each mole of processed CaCO3.
In alkali-activated cements, reaction products are formed by alkaline hydrolysis of precursor aluminosilicates. In this context, clay is a widely available and economically viable raw material for the supply of Al–Si reactants to be used for alkali activation. The simplest clay mineral, in terms of chemistry, is kaolinite (Al2Si2O5(OH)4), which upon calcination over a temperature range of 550–800 °C releases water vapor and transforms to the dehydroxylated form Al2Si2O7, commonly referred to as metakaolin (although metakaolinite would be a more appropriate definition). Partial or total loss of its crystalline structure, subsequent to thermal treatment, enhances its reactivity in alkaline environment. Extensive literature on the properties of alkali-activated metakaolin can be found in review papers.4−7
Despite the extensive research performed on such materials, specific details of the reaction pathways leading to the formation of a hardened material from the dissolution of metakaolin in alkaline solution remain uncertain and are still a matter of debate. The implementation of mathematical models may bridge the gap between the empirical knowledge of the macroscopic properties of alkali-activated metakaolin and the associated physical and chemical processes operating at small scales. A knowledge-based approach will likely drive a faster and more robust innovation in the design of such materials.
Progress in this direction has been made by a number of studies that used atomistic simulations to quantitatively assess, at small space and time scales, structural breakup during metakaolin dissolution,8 clustering of Al–Si units,9 and nanostructural details of the product of aluminosilicate alkali activation.10,11 The reaction kinetics of alkali-activated systems has been simulated by empirical models,12,13 which, however, did not explicitly describe the full chemistry and mineralogy of the system.
In this study, the dissolution–precipitation kinetics of metakaolin in alkali solution is simulated using the cellular automaton reaction–diffusion model HydratiCA. By defining a database of chemical reactions, each described by a specific stoichiometry, with direct and inverse rates, the time-dependent concentration of metakaolin, reaction product, and aqueous species is tracked over a time interval of hours.
The implementation of this numerical model is intended to provide possible answers to questions such as:
What are the underlying mechanisms inducing the observed differences in terms of macroscopic properties (e.g., setting time, mechanical strength) when different alkali activators are used?
How do the rates of nucleation and growth and stoichiometry of the reaction product change when the alkali concentration is varied?
This numerical study represents a starting point for the definition of a detailed quantitative description of the chemical kinetics inherent to alkali activated systems.
2. Computational Methods
2.1. Overview
The HydratiCA model was developed at the National Institute of Standards and Technology on the basis of a cellular automaton algorithm for the simulation of reaction-transport processes.14,15 HydratiCA has been successfully used for the simulation of systems related to Portland cement;16−20 however, the flexibility of this model allows different chemical systems to be simulated.21,22
The computational domain is built by mapping the phases present in the system as discrete units of concentration, called cells, onto a mesh of lattice sites with a given lattice spacing λ. At each discrete time step τ, the system’s evolution is simulated by changing the number of cells of each component at each lattice site according to a set of stochastic rules that model the diffusive transport of the aqueous species and the chemical reactions occurring between components within a given neighborhood of a lattice site. These stochastic reaction-transport equations converge to the continuum standard rate laws and the diffusion equation in the limit λ, τ → 0.
The user defines the physicochemical properties of the phases present in the system as well as the thermodynamic and kinetic parameters governing diffusive transport and chemical reactions.
A generic dissolution–precipitation equilibrium of the type
| 1 |
is simulated by assigning an equilibrium constant (or solubility product) Keq and a rate constant k+ for the direct reaction (dissolution in the case of eq 1). At each time step, the occurrence of dissolution or precipitation depends on the value of the supersaturation S at each lattice site. The value of the rate constant for the inverse reaction is simply k– = k+/Keq.
Precipitation of a new solid phase can occur, provided that this has previously nucleated at locations of the spatial domain where the supersaturation is high enough. The nucleation rate is defined, based on classical nucleation theory, by the following equation
| 2 |
The pre-exponential factor A is defined as
| 3 |
and the dimensionless parameter W is
| 4 |
The parameters present in eqs 3 and 4 are the volume occupied by a molecule of the newly formed phase in the nucleus (v0), the surface energy at the interface nucleus/solution (σ), the diffusion coefficient of the solute species (D), and the thermal energy kBT (with kB being the Boltzmann constant).
A detailed description of the algorithm, along with its validation, can be found in the literature cited at the beginning of this section.
2.2. System Definition
The system simulated in this study consists of a single metakaolin platelet having a size of 9 × 9 × 3 μm3, in aqueous solution, with a water/metakaolin mass ratio of 0.56. Periodic boundary conditions are applied to the computational domain of 11 × 11 × 5 voxels (1 μm/voxel). Such an idealized small system was chosen to minimize computational time, considering that the focus of this investigation is to understand the reaction kinetics rather than the microstructural evolution of the system. The alkaline activators used in the simulations were sodium silicate (Na2SiO3) and sodium hydroxide (NaOH). Three different runs were performed, each with a different combination of activator and molar concentration (Table 1). The selected molar concentrations are close to those typically used in experiments and correspond to bulk molar Na/Al ratios ≤1, which are commonly recommended to avoid efflorescence.23
Table 1. Mix Design for the Simulated Systems.
| run | H2O/MK | activator | reaction time (h) |
|---|---|---|---|
| 1 | 0.56 | 8 mol/L Na2SiO3 | 12 |
| 2 | 0.56 | 4 mol/L Na2SiO3 | 12 |
| 3 | 0.56 | 8 mol/L NaOH | 12 |
The reaction product of alkali-activated metakaolin consists in a sodium aluminosilicate hydrate, named N–A–S–H, following the convention used for Portland cement phases (N = Na2O; A = Al2O3; S = SiO2; H = H2O). This phase is characterized by an X-ray diffraction pattern typical of amorphous or semi-amorphous matter and, in the published literature, is also referred to as N–A–S–H gel, aluminosilicate gel, or geopolymer gel, although the use of the term “gel” is too generic and does not provide a clear picture about the small-scale structural nature of this phase. The bulk chemical composition of N–A–S–H is affine to that of sodium zeolites and, although the exact nature, composition, structure, and even nomenclature of this phase is still debated, recent evidence based on atomistic models and total scattering data10 confirmed the hypothesis that this phase consists of defective nanocrystalline zeolitic domains.24 On the basis of the above considerations, N–A–S–H is implemented in the model as a solid with variable stoichiometry, in which the chemical variability is simulated by co-precipitation of four zeolitic end-members, similar to the approach used to simulate calcium-silicate hydrates (C–S–H) precipitation in Portland cement systems.16 This allows a reaction product of variable chemical composition to precipitate, depending on the aqueous solution composition. In the absence of thermodynamic and kinetic data relative to the N–A–S–H product, the use of a combination of zeolitic phases represents a valid approximation, given the chemical and structural affinity of these phases. A similar approach was used to simulate the formation of N–A–S–H at thermodynamic equilibrium, in a thermodynamic model of alkali-activated cement.25 The selected end-members include zeolite phases that are commonly observed in Na-activated systems, such as zeolite A, Na-faujasite, and zeolites of the sodalite series.24,26 Other commonly occurring zeolites in such systems are natrolite27,28 and analcime.29 Although other zeolitic phases may form under a variety of chemical compositions and curing conditions, it is stressed here that the phases selected are not intended to cover the whole range of crystalline zeolite phases, but rather to span a wide enough compositional interval for the N–A–S–H model. The properties of the solid phases and the set of reactions implemented in the model are reported in Tables 2 and 3.
Table 2. Solid Phases Used in the Numerical Model.
| phase | formula | molar mass (g/mol) | density (g/cm3) |
|---|---|---|---|
| metakaolin | Al2Si2O7 | 222.13 | 2.60 |
| N–A–S–Ha | Na2Al2Si2O8·5H2O | 246.05 | 1.99 |
| N–A–S–Hb | NaAlSi2O6·nH2O | 202.14 + n × 18.02 | 1.98 (n = 4) – 2.29 (n = 1) |
| N–A–S–Hc | Na2Al2Si3O10·2H2O | 380.22 | 2.25 |
| N–A–S–Hd | Na4Al3Si3O12(OH)·2H2O | 501.18 | 2.31 |
Table 3. List of Chemical Reactionsa.
| reaction | log Keq | k+ |
|---|---|---|
| Al2Si2O7 + 4OH– + 5H2O → 2Al(OH)4– + 2H3SiO4 | 19.52 | 1.43 × 10–4 |
| Na2A2lSi2O8·5H2O + 2OH– + H2O → 2Na+ + 2Al(OH)4– + 2H3SiO4 | –9.55 | 5.50 × 10–15 |
| NaAlSi2O6·H2O + 2OH– + 3H2O → Na+ + Al(OH)4– + 2H3SiO4 | –7.70 | 5.50 × 10–15 |
| NaAlSi2O6·4H2O + 2OH– → Na+ + Al(OH)4– + 2H3SiO4 | –4.14 | 5.50 × 10–15 |
| Na2Al2Si3O10·2H2O + 3OH– + 5H2O → 2Na+ + 2Al(OH)4– + 3H3SiO4 | –17.66 | 5.50 × 10–15 |
| Na4Al3Si3O12(OH)·2H2O + 2OH– + 7H2O → 4Na+ + 3Al(OH)4– + 3H3SiO4 | –3.64 | 5.50 × 10–15 |
| H3SiO4– + OH– → H2SiO4 + H2O | 0.90 | 6.03 × 10–2 |
Keq: equilibrium constant; k+: rate constant, expressed as mol m–2 s–1.
The first reaction listed in Table 3 accounts for metakaolin dissolution. Quantitative data on metakaolin solubility are not available, and the equilibrium constant was calculated using the formation enthalpy and entropy data retrieved from literature.30 Strictly speaking, the equilibrium constant obtained from this reaction does not represent a solubility product. However, written in this form, this chemical equation stresses the dependence of metakaolin solubility upon solution pH.
Al(OH)4– was observed to be the dominant Al species in strongly alkaline solutions.31 H3SiO4 and H2SiO42– are the two dominant Si species in alkali-activated metakaolin systems,32 with the pH-dependent equilibrium between these two species being controlled by the speciation equation reported in Table 3. The equilibrium constant for this reaction was calculated from geochemical databases.33 In the absence of published data on the reaction rate k+, the reported value was assumed on the basis of the one used in a previous HydratiCA model for the formation of Ca complexes in solution.17
The rate constant for metakaolin dissolution was calculated using literature data from dissolution experiments34 performed at a liquid/metakaolin mass ratio of 100, considering that at high dilution, the dissolution rate approximates the value of the rate constant.
The equilibrium constants for the dissolution–precipitation equilibrium of N–A–S–H were calculated from solubility data for end-member N–A–S–Ha (zeolite A35), end-member N–A–S–Hb (analcime;36 zeolite Y37), and end-member N–A–S–Hc (natrolite37). The equilibrium constant for end-member N–A–S–Hd (hydro-sodalite) was calculated from a value of the Gibbs free energy of the formation reported elsewhere.38
The values of the dissolution rate constants for the N–A–S–H end-members were assigned on the basis of the data from a study on zeolite dissolution.39 Although this value is relative to zeolites with heulandite composition, in the absence of more specific data, this value is assumed to be valid for all N–A–S–H end-members. This selected dissolution rate constant k+ = 5.50 × 10–15 is in the range of values relative to other Na-tectosilicates.40
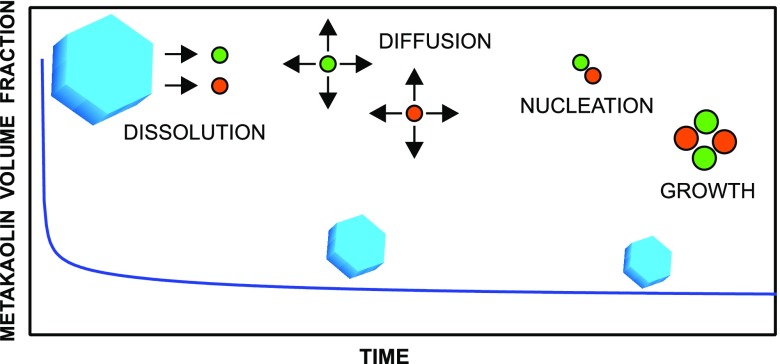
The formation of aqueous Al–Si complexes subsequent to metakaolin dissolution, which is often postulated on the basis of NMR data,32,41,42 is not explicitly simulated. Such Si–Al entities are broadly defined “oligomers” in the literature, relying on a model dating back to 1959.43 However, this term is a fairly generic one and is more often used in the field of organic chemistry. Here, it is preferred to adopt the term “nucleus” to describe nano-sized entities formed from the aggregation of aqueous species. Therefore, the formation of Al–Si species, as precursors of the final reaction product (a process that is generally referred to as “oligomer condensation” in the literature) is here regarded as a nucleation event and simulated using the mathematical formalism expressed by eqs 2–4. This “nucleation” formalism is considered more suitable for the description of the precipitation of inorganic solids and is in line with the current views on phase separation from aqueous solutions.44−46 In the present simulations, the occurrence of N–A–S–H nucleation is restricted to the surface of metakaolin (heterogeneous nucleation), based on previous experimental evidence.41,42,47
The pre-exponential factor A and the energy barrier W present in eq 2 were obtained by using values of the molecular volume v0 obtained from the molar mass and density48,49 of the N–A–S–H end-members. The diffusion coefficient D was set to 1 × 10–9 m2/s on the basis of the data from silica diffusivity.50 The value of the surface energy σ was set to 0.20 J/m2, which is in the range of suggested values for amorphous silica.51
3. Results and Discussion
3.1. Metakaolin Dissolution
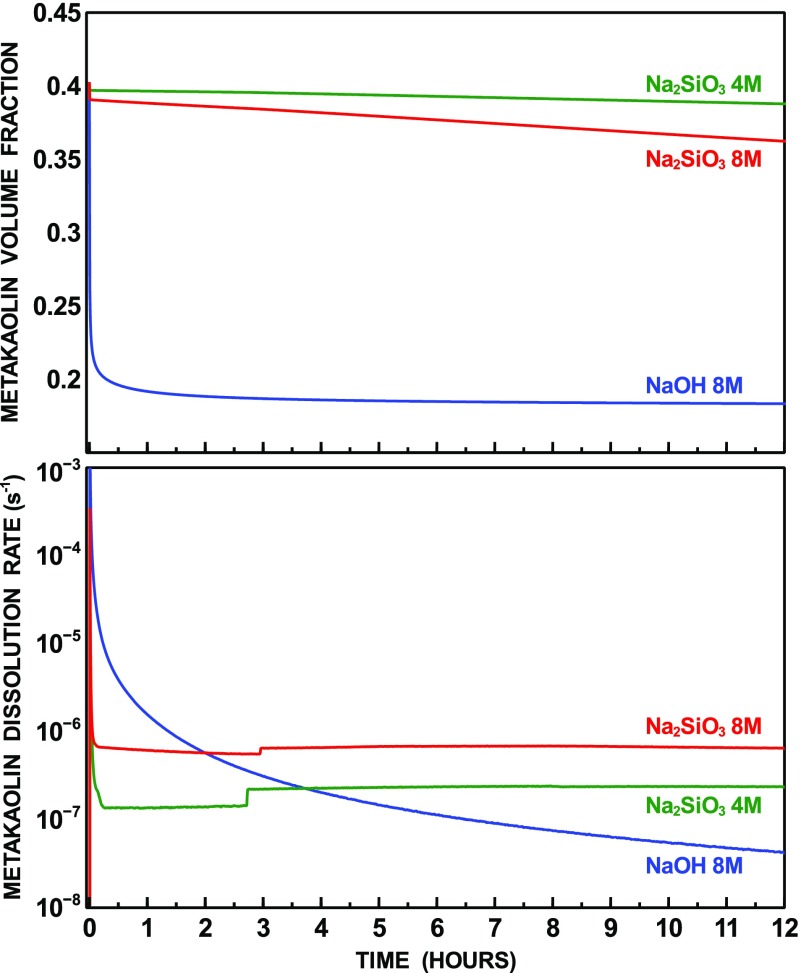
The time-dependent volume fraction and dissolution rate of metakaolin after 12 h of simulated reaction are displayed in Figure 1. Dissolution initially occurs at a fast rate, which quickly decays within the first 30 min. Such a fast reaction, restricted to the very early stage and followed by a much slower rate of reaction, is commonly observed in indirect experimental methods based on calorimetry performed on alkali-activated metakaolin and other calcined clays.52−54
Figure 1.
Volume fraction and dissolution rate for the three simulated systems.
The results show that during this stage, dissolution occurs at a faster rate for the system activated by sodium hydroxide, compared to those activated by sodium silicate. The initial faster rate of dissolution for hydroxide-activated metakaolin is due to the absence of silicate ions in the solution at time zero, when metakaolin is mixed with the alkaline solution, which makes the aqueous solution more undersaturated with respect to metakaolin. For the silicate-activated system, the rate of dissolution is proportional to the activator concentration and hence the solution pH.
At 12 h of reaction, the amount of metakaolin, in volume, decreased from 40 to 18% for the hydroxide-activated system. A much smaller decrease is predicted for the silicate-activated systems, with the amount of metakaolin at 12 h being 36 and 39% for the 8 and 4 M solutions, respectively. However, after 12 h of reaction, metakaolin dissolution for the silicate-activated systems proceeds at a nearly constant rate, which is significantly higher compared to the dissolution rate of the hydroxide-activated system, which conversely keeps decreasing due to limited availability of Si in the solution, which hinders N–A–S–H precipitation. Even assuming a constant rate of dissolution for the hydroxide-activated system, after 12 h, it can be predicted that a crossover in the amount of consumed metakaolin occurs approximately after 4 days for the 8 M Na2SiO3 system and after 13 days for the 4 M Na2SiO3.
3.2. N–A–S–H Precipitation
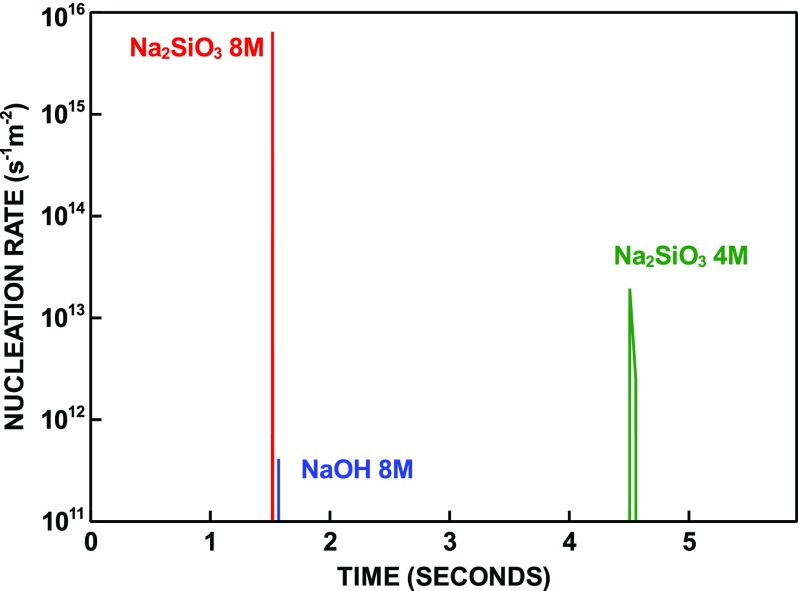
Fast metakaolin dissolution during the very early stage of reaction releases Si and Al ions, which, in combination with Na ions present in the alkaline activator, leads to a supersaturation of the aqueous solution with respect to N–A–S–H. Figure 2 shows that, for all three simulated systems, nucleation occurs within a few seconds from contact between metakaolin and alkaline solution over a narrow time interval resembling the site-saturation regime, i.e., nucleation can be approximately described as a single event occurring at the very beginning of the reaction. This nucleation behavior is analogous to the one suggested for Portland cement, based on experimental evidence55 and numerical simulations.16 The total amount of N–A–S–H nuclei formed, normalized to the metakaolin surface, is 3.22 × 1014 m–2 for the 8 mol/L Na2SiO3 system, 1.09 × 1012 m–2 for 4 mol/L Na2SiO3 and 2.06 × 1010 m–2 for 8 mol/L NaOH. The number of nuclei formed is proportional to the solution supersaturation. During the first few seconds, saturation with respect to N–A–S–H is the lowest for the hydroxide-activated system because Si ions are not initially present in the solution. For comparison, the number of nuclei formed in Portland cement systems was estimated by kinetic modeling to amount to 4.55 × 1011 m–2.56
Figure 2.
Rate of N–A–S–H nucleation for the three simulated systems.
After the rapid formation of nuclei at the interface between metakaolin and aqueous solution, N–A–S–H precipitation proceeds by growth. Given the lack of long-range order in the N–A–S–H product, the term growth here does not refer to the incorporation of structural units along specific crystallographic direction, but rather to the attachment of multi-ion clusters to the bulk N–A–S–H phase to form aggregates of poorly crystalline, highly defective nano-sized entities. This process has been postulated to be an intermediate precipitation step leading to the formation of disordered precursors of crystalline phases.44
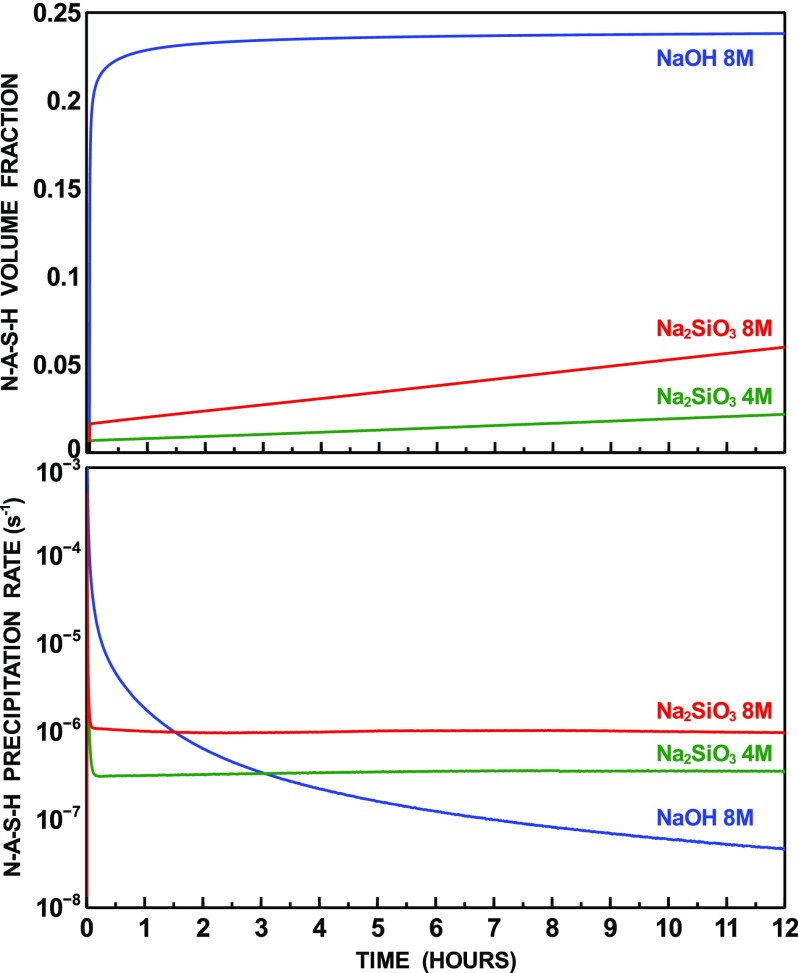
Figure 3 displays the time-dependent N–A–S–H volume fraction and the rate of precipitation for the simulated systems. In analogy to what was observed for metakaolin dissolution, fast early stage precipitation of N–A–S–H occurs for the hydroxide-activated system. Even in the presence of a smaller amount of nuclei, for the hydroxide-activated system, N–A–S–H precipitation occurs at a faster rate during the 1 h of the reaction as a consequence of the fast release of chemical species by metakaolin dissolution. However, at later stages, while N–A–S–H precipitation in the silicate-activated system proceeds nearly at steady state, a significant decrease in the rate of precipitation is observed for the hydroxide-activated system, consistent with the predicted decaying rate of metakaolin dissolution (Figure 1). Assuming that the precipitation rates remain constant after 12 h, the amount of N–A–S–H formed is predicted to become larger than that precipitated in the hydroxide-activated system after 3 days for the systems activated by 8 mol/L Na2SiO3 and 9 days for the one activated by 4 mol/L Na2SiO3.
Figure 3.
N–A–S–H volume fraction and precipitation rate for the three simulated systems.
The predicted faster early-stage rate of reaction in the presence of sodium hydroxide may induce a quicker set, in agreement with previous experimental observations performed on alkali-activated metakaolin, suggesting that setting time is proportional to the activator Si/Na ratio.57,58 On the other hand, the predicted faster rate of N–A–S–H precipitation at later stage, using Na2SiO3 as alkaline activator, is consistent with the better mechanical performance commonly observed in the presence of sodium-silicate as compared to sodium hydroxide for metakaolin and other alkali-activated materials.5,52,59
The N–A–S–H composition predicted by the simulations is dominated, for all systems, by the N–A–S–Hc end-member (Table 2). Growth of the other end-members is kinetically hindered during the first 12 h, when their volume fraction is of the order of 10–8 or smaller. No significant change was observed when the stoichiometry and equilibrium constant of the N–A–S–Hb end-member were changed to reflect analcime or zeolite Y chimico-physical properties (see Table 2). Therefore, the predicted chemical composition of the reaction product tends to that of a phase with Na/Al = 1 and Si/Al = 1.5.
3.3. Aqueous Phase
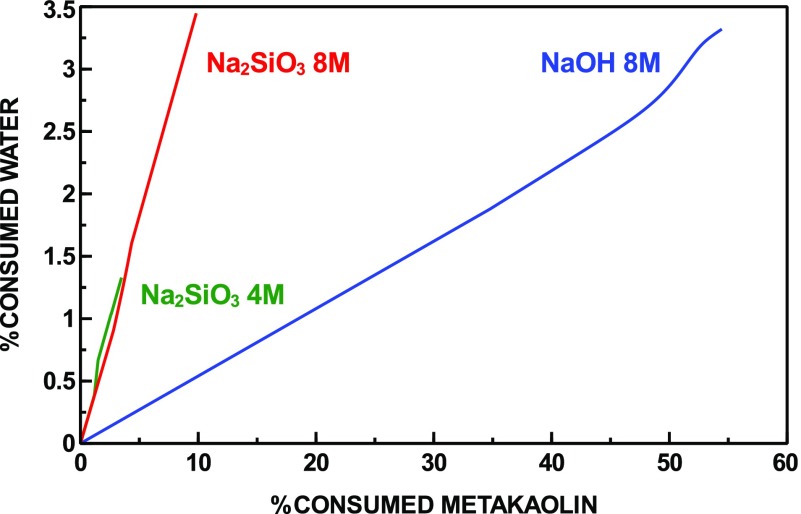
Interestingly, the simulation results show that although early-stage reaction kinetics are faster for the hydroxide-activated system, the amount of water consumed after 12 h does not vary significantly compared to the silicate-activated system. This behavior is illustrated in Figure 4, which shows that for a given amount of dissolved metakaolin, the amount of water consumed is significantly smaller for the hydroxide-activated system. The different amount of water consumed during the reaction, depending on the activator used, is a consequence of the reaction stoichiometry, and this point will be illustrated in more detail later in this section. This result, moreover, agrees with previous investigation showing that denser, less porous microstructures develop as the Si/Na ratio of the alkaline activator is increased.60 Therefore, the better mechanical performance in the presence of sodium silicate, compared to sodium hydroxide, can be attributed to both a faster late-stage rate of N–A–S–H precipitation, as shown in the previous Section 3.2, and enhanced water consumption, leading to the formation of a denser microstructure.
Figure 4.
Percentage of water consumed as a function of the percentage of dissolved metakaolin.
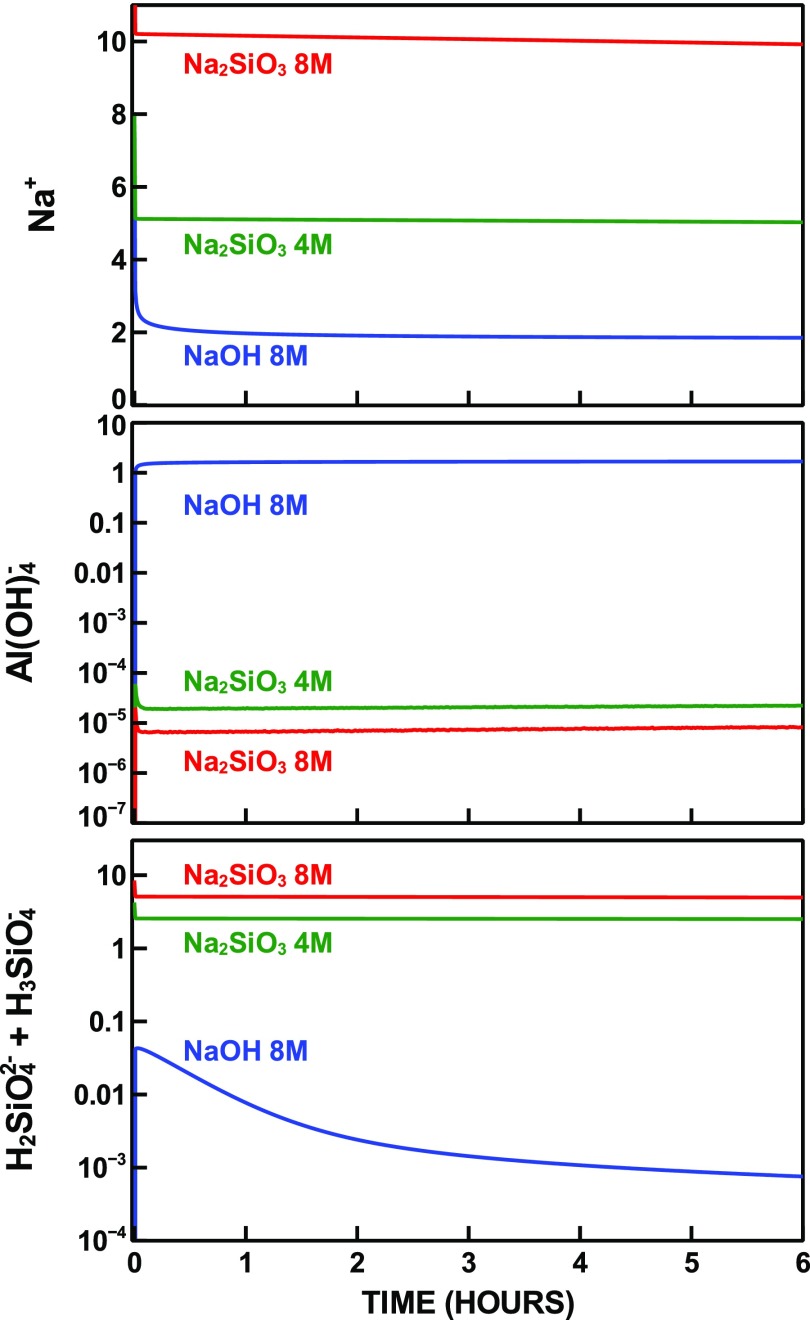
The time-dependent concentrations of Na, Al, and Si ionic species in aqueous solution are displayed in Figure 5. The pH of the pore solution after 12 h is 13.67 for 8 mol/L Na2SiO3, 13.47 for 4 mol/L Na2SiO3, and 13.12 for 8 mol/L NaOH (14.90, 14.60, and 14.90 at time zero), in agreement with the pH range measured experimentally for alkali-activated metakaolin.61
Figure 5.
Concentration of aqueous species expressed as mol/L.
Fast early-stage N–A–S–H precipitation in the hydroxide-activated system is associated with a larger amount of Na and Si aqueous species removed from the pore solution. However, although the concentration of Al(OH)4– in the silicate-activated systems reaches values as low as a few tens μmol, a much higher concentration is predicted for the hydroxide-activated system. Interestingly, this behavior was experimentally observed by NMR spectroscopy of alkali-activated metakaolin.62 The results of those measurements suggested the presence of Al(OH)4 in the pore solution only for hydroxide-activated metakaolin, whereas no aqueous Al species could be detected in silicate-activated systems. Additionally, the results indicated the presence of Na+ in the solution as a charge-balancing ion for Al(OH)4–.
Although the simulations predict a lower amount of Na+ at 12 h, the rate of Na+ consumption is 5–13 times bigger for the silicate-activated systems at the end of the simulations.
To better understand these observations, it is convenient to write chemical equations for silicate and hydroxide-activated systems with Na/Al = 1, dominated by the precipitation of a N–A–S–H product with Na/Al = 1 and Si/Al = 1.5, as predicted by the simulations
| 5 |
| 6 |
These equations imply that
for each mole of metakaolin consumed, more product is formed in the silicate-activated system;
for each mole of metakaolin consumed, more water is consumed in the silicate-activated system;
excess Al(OH)4– and Na+ are present in the pore solution of the hydroxide-activated system.
The presence of excess Na in the pore solution may induce enhanced carbonation for hydroxide-activated metakaolin. Indeed, this behavior was observed in an alkali-activated calcined smectite system, in which the formation of alkali carbonates was detected by XRD only when NaOH was used as an activator.54
3.4. Role of Keq and k+
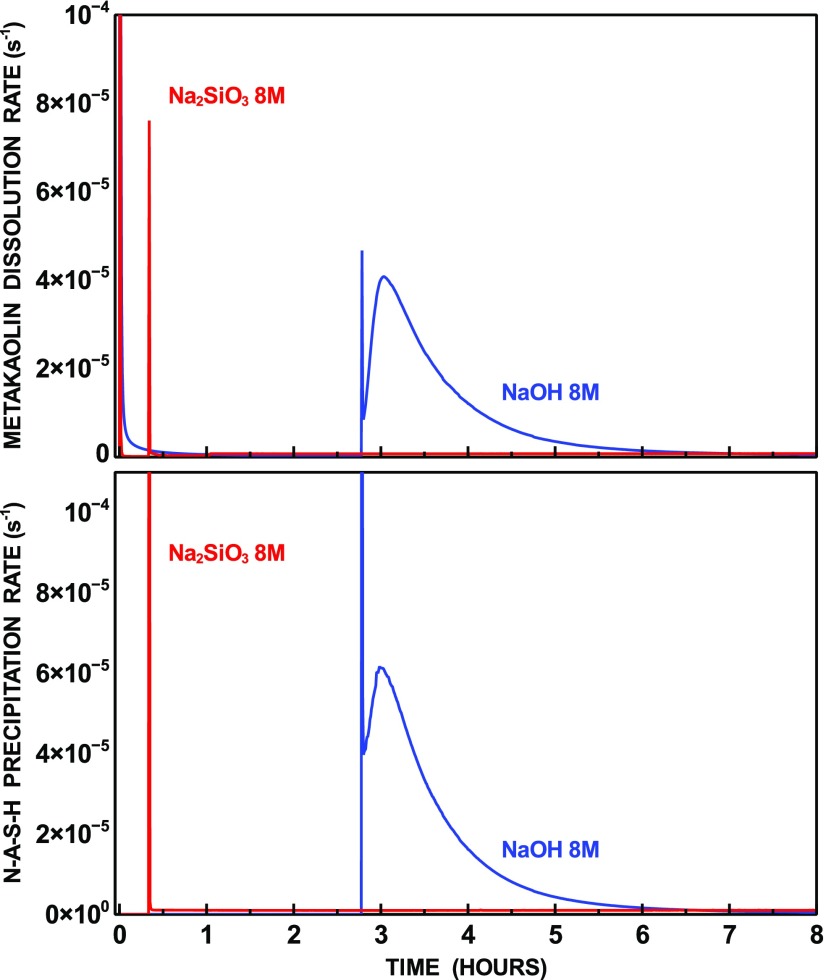
The effect of modifying the values of the N–A–S–H end-members dissolution–precipitation equilibrium constants and dissolution rate constants was investigated by running an additional set of simulations for the three modeled systems. The criteria adopted for varying these values were based on the selection of amorphous, rather than crystalline end-members, as being representative of N–A–S–H. Solubility studies on zeolite A showed that the solubility of the ionic species increased up to 1 order of magnitude for the amorphous precursor, compared to the crystalline phase.35 Based on this observation, the values of Keq were recalculated accordingly for all N–A–S–H end-members. Moreover, based on the measured differences between quartz and amorphous silica, the value of k+ was increased by an order of magnitude.40 The densities of the N–A–S–H end-members did not vary compared to the previous simulations, based on the evidence from atomistic models of N–A–S–H structures, which displayed small variations in the density of crystalline, defective, and amorphous structures, for stoichiometries with Si/Al ≤ 2.10 The values of Keq and k+ adopted for this set of simulations are summarized in Table 4. The time-dependent rates of metakaolin dissolution and N–A–S–H precipitation are displayed in Figure 6. The most notable difference is the delayed N–A–S–H nucleation, which occurs after about 20 min for the 8 mol/L Na2SiO3 system and after nearly 3 h for the 8 mol/L NaOH system. Nucleation does not occur during the first 12 h for the 4 mol/L Na2SiO3 system.
Table 4. Equilibrium Constant and Dissolution Rate Constant for Amorphous N–A–S–H End-Membersa.
| phase | log Keq | k+ |
|---|---|---|
| N–A–S–Ha | –5.55 | 5.50 × 10–14 |
| N–A–S–Hb | –5.70 | 5.50 × 10–14 |
| N–A–S–Hc | –13.66 | 5.50 × 10–14 |
| N–A–S–Hd | +4.36 | 5.50 × 10–14 |
Keq: equilibrium constant; k+: rate constant, expressed as mol m–2 s–1.
Figure 6.
Rates of metakaolin dissolution and N–A–S–H precipitation for the system with amorphous end-members.
Such a delayed N–A–S–H nucleation affects the rate of metakaolin dissolution, which in this case presents two distinct peaks: one at the beginning of the reaction and the other immediately after the nucleation event.
The occurrence of two distinct exothermic peaks, measured by isothermal calorimetry, was observed in a previous investigation on the activation of metakaolin by sodium hydroxide and sodium silicate. These peaks were located at the beginning and after a few hours from the beginning of the reaction. The separation between the two peaks was more pronounced at lower temperatures, whereas the peaks became nearly overlapping at a temperature of 40 °C, when the overall rate of reaction is faster.63,64
4. Conclusions
The HydratiCA model proved to be a promising tool for simulating the reaction kinetics of alkali-activated systems. The possibility of tracking the time-dependent evolution of the amount of solid phases and aqueous species present in the system represents a powerful resource for a better understanding of the basic chemical processes associated with alkali-activated materials.
The results of the numerical simulations presented in this study provided a picture of the influence of different alkaline activators on the reaction pathways of metakaolin-based cement.
The main findings of this numerical study suggest the following:
The use of NaOH as alkaline activator is associated with a fast early-stage rate of dissolution–precipitation, which may explain the experimental observations suggesting that the setting time depends on the Si/Na ratio of the alkaline activator.
Alkaline activation by Na2SiO3, in turn, induces a faster late-stage rate of metakaolin dissolution and N–A–S–H precipitation, as well as a significantly larger amount of water consumption. These predictions can be reconciled with the macroscopic experimental observation that products characterized by better mechanical strength and reduced porosity are formed when sodium silicate is used as activator.
The N–A–S–H phase, which nucleates immediately after the contact of metakaolin with the alkaline solution, is chemically affine to natrolite, with Na/Al = 1 and Si/Al = 1.5. This stoichiometric constraint, and equilibrium of this phase with the aqueous solution, may explain the experimental observation that Al aqueous species are more easily detected when no Si is present in the alkaline activator. Moreover, the presence of excess Na as a charge-balancing ion may induce enhanced formation of alkaline carbonates in hydroxide-activated metakaolin.
HydratiCA relies on classical nucleation theory for simulating the formation of new phases in solution. One possible improvement in the modeling of alkali-activated materials may consist in the implementation of nonclassical nucleation pathways. Recent research suggested that the formation of new solid phases in the aqueous solution may occur by the aggregation of prenucleation clusters to form stable nuclei. This process has been especially observed during the precipitation of amorphous or defective materials.65,66 Recently, results of small angle X-ray scattering (SAXS) experiments have shown that the nucleation of calcium-silicate hydrates (C–S–H) in Portland cement occurs by aggregation of prenucleation amorphous entities.67 Similar results were obtained for metal–organic frameworks topologically affine to zeolites.68 SAXS experiments performed on alkali-activated metakaolin showed analogous results with the formation of 2 nm clusters, defined as oligomers by the authors, by the aggregation of smaller particles,69 suggesting an analogy between condensation of oligomers and nucleation.
One potentially viable numerical approach for the implementation of nonclassical nucleation pathways in alkali-activated system is “population balance modeling”. This numerical scheme can track the time variation in the size distribution of particles present in a given system, similarly to what can be experimentally achieved by SAXS methods. Population balance modeling was recently implemented to the simulation of C–S–H formation by the aggregation of defective crystallites.70
It is also important to stress that experimental efforts, oriented at measuring the rate of metakaolin dissolution and N–A–S–H precipitation, as well as the definition of specific N–A–S–H thermodynamic models, will be necessary for developing more accurate numerical models.
The final message of this work is that the use of kinetic, thermodynamic, and multiscale microstructural models of alkali-activated systems should be encouraged, as it will certainly be beneficial to a deeper understanding of the basic chemical aspects of this class of sustainable binders.
Acknowledgments
The calculations were performed on the C3P (Computational Chemistry Community in Padua) High-Performance Computing facility of the Department of Chemical Sciences (University of Padua).
The author declares no competing financial interest.
References
- United Nations General Assembly . Transforming Our World: The 2030 Agenda for Sustainable Development; Resolution Adopted by the General Assembly, 2015. [Google Scholar]
- Douglas Hooton R. D. Current developments and future needs in standards for cementitious materials. Cem. Concr. Res. 2015, 78, 165–177. 10.1016/j.cemconres.2015.05.022. [DOI] [Google Scholar]
- Provis J.; Duxson P.; Kavalerova E.; Krivenko P.; Pan Z.; Puertas F.; van Deventer J. In Alkali-Activated Materials: State-of-the-Art Report, RILEM TC 224-AAM; Provis J., van Deventer J., Eds.; Springer: Dordrecht, 2014; pp 11–57. [Google Scholar]
- Li C.; Sun H.; Li L. A review: The comparison between alkali-activated slag (Si+Ca) and metakaolin (Si+Al) cements. Cem. Concr. Res. 2010, 40, 1341–1349. 10.1016/j.cemconres.2010.03.020. [DOI] [Google Scholar]
- Rashad A. M. Alkali-activated metakaolin: A short guide for civil Engineer An overview. Constr. Build. Mater. 2013, 41, 751–765. 10.1016/j.conbuildmat.2012.12.030. [DOI] [Google Scholar]
- Liew Y.-M.; Heah C.-Y.; Mustafa A. B. M.; Kamarudin H. Structure and properties of clay-based geopolymer cements: A review. Prog. Mater. Sci. 2016, 83, 595–629. 10.1016/j.pmatsci.2016.08.002. [DOI] [Google Scholar]
- Davidovits J. In Ceramic Engineering and Science Proceedings, Proceedings of the 41st International Conference on Advanced Ceramics and Composites; Wiley-Blackwell, 2018; pp 201–214.
- Yunsheng Z.; Wei S. Semi-empirical AM1 calculations on 6-memebered alumino-silicate rings model: implications for dissolution process of metakaoline in alkaline solutions. J. Mater. Sci. 2007, 42, 3015–3023. 10.1007/s10853-006-0521-x. [DOI] [Google Scholar]
- Yang C.; Mora-Fonz J.; Catlow C. Modeling the polymerization of aluminosilicate clusters. J. Phys. Chem. C 2012, 116, 22121–22128. 10.1021/jp3049197. [DOI] [Google Scholar]
- Lolli F.; Manzano H.; Provis J.; Bignozzi M.; Masoero E. Atomistic simulations of geopolymer models: the impact of disorder on structure and mechanics. ACS Appl. Mater. Interfaces 2018, 10, 22809–22820. 10.1021/acsami.8b03873. [DOI] [PubMed] [Google Scholar]
- Zhang M.; Deskins N.; Zhang G.; Cygan R.; Tao M. Modeling the polymerization process for geopolymer synthesis through reactive molecular dynamics simulations. J. Phys. Chem. C 2018, 122, 6760–6773. 10.1021/acs.jpcc.8b00697. [DOI] [Google Scholar]
- Provis J.; van Deventer J. Geopolymerisation kinetics. 2. Reaction kinetic modelling. Chem. Eng. Sci. 2007, 62, 2318–2329. 10.1016/j.ces.2007.01.028. [DOI] [Google Scholar]
- Yang K.; White C. Modeling the formation of alkali aluminosilicate gels at the mesoscale using coarse-grained Monte Carlo. Langmuir 2016, 32, 11580–11590. 10.1021/acs.langmuir.6b02592. [DOI] [PubMed] [Google Scholar]
- Karapiperis T.; Blankleider B. Cellular automation model of reaction-transport porcesses. Phys. D 1994, 78, 30–64. 10.1016/0167-2789(94)00093-X. [DOI] [Google Scholar]
- Karapiperis T. Cellular automaton model of precipitation/dissolution coupled with solute transport. J. Stat. Phys. 1995, 81, 165–180. 10.1007/BF02179974. [DOI] [Google Scholar]
- Bullard J. W. A determination of hydration mechanisms for tricalcium silicate using a kinetic cellular automaton model. J. Am. Ceram. Soc. 2008, 91, 2088–2097. 10.1111/j.1551-2916.2008.02419.x. [DOI] [Google Scholar]
- Bullard J. W.; Enjolras E.; George W. L.; Satterfield S. G.; Terrill J. E. A parallel reaction-transport model applied to cement hydration and microstructure development. Modell. Simul. Mater. Sci. Eng. 2010, 18, 025007 10.1088/0965-0393/18/2/025007. [DOI] [Google Scholar]
- Bullard J. W.; Flatt R. J. New insights into the effect of calcium hydroxide precipitation on the kinetics of tricalcium silicate hydration. J. Am. Ceram. Soc. 2010, 93, 1894–1903. 10.1111/j.1551-2916.2010.03656.x. [DOI] [Google Scholar]
- Oey T.; Kumar A.; Bullard J. W.; Neithalath N.; Sant G. The filler effect: the influence of filler content and surface area on cementitious reaction rates. J. Am. Ceram. Soc. 2013, 96, 1978–1990. 10.1111/jace.12264. [DOI] [Google Scholar]
- Bullard J. W.; Hagedorn J.; Ley M. T.; Hu Q.; Griffin W.; Terrill J. E. A critical comparison of 3D experiments and simulations of tricalcium silicate hydration. J. Am. Ceram. Soc. 2018, 101, 1453–1470. 10.1111/jace.15323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullard J. W. Approximate rate constants for nonideal diffusion and their application in a stochastic model. J. Phys. Chem. A 2007, 111, 2084–2092. 10.1021/jp0658391. [DOI] [PubMed] [Google Scholar]
- Bullard J. W. A three-dimensional microstructural model of reactions and transport in aqueous mineral systems. Modell. Simul. Mater. Sci. Eng. 2007, 15, 711–738. 10.1088/0965-0393/15/7/002. [DOI] [Google Scholar]
- Luukkonen T.; Abdollahnejad Z.; Yliniemi J.; Kinnunen P.; Illikainen M. One-part alkali-activated materials: A review. Cem. Concr. Res. 2018, 103, 21–34. 10.1016/j.cemconres.2017.10.001. [DOI] [Google Scholar]
- Provis J.; Lukey G.; van Deventer J. Do geopolymers actually contain nanocrystalline zeolites? A reexamination of existing results. Chem. Mater. 2005, 17, 3075–3085. 10.1021/cm050230i. [DOI] [Google Scholar]
- Myers R. J.; Lothenbach B.; Bernal S. A.; Provis J. L. Thermodynamic modelling of alkali-activated slag cements. Appl. Geochem. 2015, 61, 233–247. 10.1016/j.apgeochem.2015.06.006. [DOI] [Google Scholar]
- Ofer-Rozovsky E.; Arbel Haddad M.; Bar Nes G.; Katz A. The formation of crystalline phases in metakaolin-based geopolymers in the presence of sodium nitrate. J. Mater. Sci. 2016, 51, 4795–4814. 10.1007/s10853-016-9767-0. [DOI] [Google Scholar]
- Slaty F.; Khoury H.; Wastiels J.; Rahier H. Characterization of alkali activated kaolinitic clay. Appl. Clay Sci. 2013, 75–76, 120–125. 10.1016/j.clay.2013.02.005. [DOI] [Google Scholar]
- Slaty F.; Khoury H.; Rahier H.; Wastiels J. Durability of alkali activated cement produced from kaolinitic clay. Appl. Clay Sci. 2015, 104, 229–237. 10.1016/j.clay.2014.11.037. [DOI] [Google Scholar]
- Hajimohammadi A.; Provis J. L.; van Deventer J. S. The effect of silica availability on the mechanism of geopolymerisation. Cem. Concr. Res. 2011, 41, 210–216. 10.1016/j.cemconres.2011.02.001. [DOI] [Google Scholar]
- Schieltz N.; Soliman M. In Thermodynamics of the Various High Temperature Transformations of Kaolinite, Proceedings of the 13th National Conference on Clays and Clay Minerals; Pergamon Press: NY, 1966; pp 419–428.
- Sipos P. The structure of Al(III) in strongly alkaline aluminate solutions. A review. J. Mol. Liq. 2009, 146, 1–14. 10.1016/j.molliq.2009.01.015. [DOI] [Google Scholar]
- Weng L.; Sagoe-Crentsil K. Dissolution processes, hydrolysis and condensation reactions during geopolymer synthesis: Part I-Low Si/Al ratio systems. J. Mater. Sci. 2007, 42, 2997–3006. 10.1007/s10853-006-0820-2. [DOI] [Google Scholar]
- Walther J.Essentials of Geochemistry; Jones & Bartlett Learning: Burlington, 2009. [Google Scholar]
- Hajimohammadi A.; van Deventer J. S. Dissolution behaviour of source materials for synthesis of geopolymer binders: A kinetic approach. Int. J. Min. Process. 2016, 153, 80–86. 10.1016/j.minpro.2016.05.014. [DOI] [Google Scholar]
- Ejaz T.; Jones A. G.; Graham P. Solubility of Zeolite A and Its Amorphous Precursor under Synthesis Conditions. J. Chem. Eng. Data 1999, 44, 574–576. 10.1021/je980164j. [DOI] [Google Scholar]
- Wilkin R.; Barnes H. Solubility and stability of zeolites in aqueous solution: I. Analcime, Na-, and K-clinoptilolite. Am. Mineral. 1998, 83, 746–761. 10.2138/am-1998-7-807. [DOI] [Google Scholar]
- Lothenbach B.; Bernard E.; Mader U. Zeolite formation in the presence of cement hydrates and albite. Phys. Chem. Earth 2017, 99, 77–94. 10.1016/j.pce.2017.02.006. [DOI] [Google Scholar]
- Moloy E. C.; Liu Q.; Navrotsky A. Formation and hydration enthalpies of the hydrosodalite family of materials. Microporous Mesoporous Mater. 2006, 88, 283–292. 10.1016/j.micromeso.2005.09.020. [DOI] [Google Scholar]
- Aradottir E. S. P.; Sigfusson B.; Sonnenthal E.; Bjornsson G.; Jonsson H. Dynamics of basaltic glass dissolution - Capturing microscopic effects in continuum scale models. Geochim. Cosmochim. Acta 2013, 121, 311–327. 10.1016/j.gca.2013.04.031. [DOI] [Google Scholar]
- Palandri J.; Kharaka Y.. A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling; U.S. Geological Survey: Menlo Park, CA, 2004; Vol. 1068, pp 1–64. [Google Scholar]
- Favier A.; Habert G.; d’Espinose de Lacaillerie J.; Roussel N. Mechanical properties and compositional heterogeneities of fresh geopolymer pastes. Cem. Concr. Res. 2013, 48, 9–16. 10.1016/j.cemconres.2013.02.001. [DOI] [Google Scholar]
- Chen X.; Sutrisno A.; Zhu L.; Struble L. J. Setting and nanostructural evolution of metakaolin geopolymer. J. Am. Ceram. Soc. 2017, 100, 2285–2295. 10.1111/jace.14641. [DOI] [Google Scholar]
- Glukhovsky V.Soil Silicates; State Publishing House of Literature on Building and Architecture of Ukrainian SSR: Kiev, Ukraine, 1959. [Google Scholar]
- De Yoreo J. J.; Gilbert P. U. P. A.; Sommerdijk N. A. J. M.; Penn R. L.; Whitelam S.; Joester D.; Zhang H.; Rimer J. D.; Navrotsky A.; Banfield J. F.; Wallace A. F.; Michel F. M.; Meldrum F. C.; Cölfen H.; Dove P. M. Crystallization by particle attachment in synthetic, biogenic, and geologic environments. Science 2015, 349, aaa6760 10.1126/science.aaa6760. [DOI] [PubMed] [Google Scholar]
- Zahn D. Thermodynamics and kinetics of prenucleation clusters, classical and non-classical nucleation. ChemPhysChem 2015, 16, 2069–2075. 10.1002/cphc.201500231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karthika S.; Radhakrishnan T. K.; Kalaichelvi P. A review of classical and nonclassical nucleation theories. Cryst. Growth Des. 2016, 16, 6663–6681. 10.1021/acs.cgd.6b00794. [DOI] [Google Scholar]
- Rouyer J.; Poulesquen A. Evidence of a fractal percolating network during geopolymerization. J. Am. Ceram. Soc. 2015, 98, 1580–1587. 10.1111/jace.13480. [DOI] [Google Scholar]
- Deer W. A.; Howie R. A.; Zussman J.. An Introduction to the Rock-Forming Minerals, 3rd ed.; The Mineralogical Society: London, 2013. [Google Scholar]
- Jha B.; Singh D. N.. Fly Ash Zeolites; Springer: Singapore, 2016. [Google Scholar]
- Wollast R.; Garrels R. Diffusion coefficient of silica in seawater. Nat. Phys. Sci. 1971, 229, 94 10.1038/physci229094a0. [DOI] [Google Scholar]
- Mizele J.; Dandurand J.; Schott J. Determination of the surface energy of amorphous silica from solubility measurements in micropores. Surf. Sci. 1985, 162, 830–837. 10.1016/0039-6028(85)90986-0. [DOI] [Google Scholar]
- Granizo M. L.; Alonso S.; Blanco-Varela M. T.; Palomo A. Alkaline activation of metakaolin: effect of calcium hydroxide in the products of reaction. J. Am. Ceram. Soc. 2004, 85, 225–231. 10.1111/j.1151-2916.2002.tb00070.x. [DOI] [Google Scholar]
- Yao X.; Zhang Z.; Zhu H.; Chen Y. Geopolymerization process of alkali-metakaolinite characterized by isothermal calorimetry. Thermochim. Acta 2009, 493, 49–54. 10.1016/j.tca.2009.04.002. [DOI] [Google Scholar]
- Valentini L.; Contessi S.; Dalconi M. C.; Zorzi F.; Garbin E. Alkali-activated calcined smectite clay blended with waste calcium carbonate as a low-carbon binder. J. Cleaner Prod. 2018, 184, 41–49. 10.1016/j.jclepro.2018.02.249. [DOI] [Google Scholar]
- Garrault S.; Behr T.; Nonat A. Formation of the C-S-H layer during early hydration of tricalcium silicate grains with different sizes. J. Phys. Chem. B 2006, 110, 270–275. 10.1021/jp0547212. [DOI] [PubMed] [Google Scholar]
- Valentini L.; Favero M.; Dalconi M. C.; Russo V.; Ferrari G.; Artioli G. Kinetic model of calcium-silicate hydrate nucleation and growth in the presence of PCE superplasticizers. Cryst. Growth Des. 2016, 16, 646–654. 10.1021/acs.cgd.5b01127. [DOI] [Google Scholar]
- Silva P. D.; Sagoe-Crenstil K.; Sirivivatnanon V. Kinetics of geopolymerization: Role of Al2O3 and SiO2. Cem. Concr. Res. 2007, 37, 512–518. 10.1016/j.cemconres.2007.01.003. [DOI] [Google Scholar]
- Arnoult M.; Perronnet M.; Autef A.; Rossignol S. How to control the geopolymer setting time with the alkaline silicate solution. J. Non-Cryst. Solids 2018, 495, 59–66. 10.1016/j.jnoncrysol.2018.02.036. [DOI] [Google Scholar]
- Bernal S.; Provis J.; Fernandez-Jimenez A.; Krivenko P.; Kavalerova E.; Palacios M.; Shi C. In Alkali Activated Materials, State-of-the-Art Report, RILEM TC 224-AAM; Provis J., van Deventer J., Eds.; Springer: Dordrecht, 2014; pp 59–91. [Google Scholar]
- Duxson P.; Provis J. L.; Lukey G. C.; Mallicoat S. W.; Kriven W. M.; van Deventer J. S. Understanding the relationship between geopolymer composition, microstructure and mechanical properties. Colloids Surf., A 2005, 269, 47–58. 10.1016/j.colsurfa.2005.06.060. [DOI] [Google Scholar]
- Pouhet R.; Cyr M. Carbonation in the pore solution of metakaolin-based geopolymer. Cem. Concr. Res. 2016, 88, 227–235. 10.1016/j.cemconres.2016.05.008. [DOI] [Google Scholar]
- Duxson P.; Lukey G. C.; Separovic F.; van Deventer J. S. J. Effect of alkali cations on aluminum incorporation in geopolymeric gels. Ind. Eng. Chem. Res. 2005, 44, 832–839. 10.1021/ie0494216. [DOI] [Google Scholar]
- Zhang Z.; Wang H.; Provis J. L.; Bullen F.; Reid A.; Zhu Y. Quantitative kinetic and structural analysis of geopolymers. Part 1. The activation of metakaolin with sodium hydroxide. Thermochim. Acta 2012, 539, 23–33. 10.1016/j.tca.2012.03.021. [DOI] [Google Scholar]
- Zhang Z.; Provis J. L.; Wang H.; Bullen F.; Reid A. Quantitative kinetic and structural analysis of geopolymers. Part 2. Thermodynamics of sodium silicate activation of metakaolin. Thermochim. Acta 2013, 565, 163–171. 10.1016/j.tca.2013.01.040. [DOI] [Google Scholar]
- Gebauer D.; Völkel A.; Cölfen H. Stable prenucleation calcium carbonate clusters. Science 2008, 322, 1819–1822. 10.1126/science.1164271. [DOI] [PubMed] [Google Scholar]
- Raiteri P.; Gale J. D. Water is the key to nonclassical nucleation of amorphous calcium carbonate. J. Am. Chem. Soc. 2010, 132, 17623–17634. 10.1021/ja108508k. [DOI] [PubMed] [Google Scholar]
- Krautwurst N.; Nicoleau L.; Dietzsch M.; Lieberwirth I.; Labbez C.; Fernandez-Martinez A.; Van Driessche A. E. S.; Barton B.; Leukel S.; Tremel W. Two-step nucleation process of calcium silicate hydrate, the nanobrick of cement. Chem. Mater. 2018, 30, 2895–2904. 10.1021/acs.chemmater.7b04245. [DOI] [Google Scholar]
- Cravillon J.; Schroder C. A.; Nayuk R.; Gummel J.; Huber K.; Wiebcke M. Fast nucleation and growth of ZIF-8 nanocrystals monitored by time-resolved in situ small-angle and wide-angle X-ray scattering. Angew. Chem., Int. Ed. 2011, 50, 8067–8071. 10.1002/anie.201102071. [DOI] [PubMed] [Google Scholar]
- Steins P.; Poulesquen A.; Diat O.; Frizon F. Structural evolution during geopolymerization from an early age to consolidated material. Langmuir 2012, 28, 8502–8510. 10.1021/la300868v. [DOI] [PubMed] [Google Scholar]
- Andalibi M. R.; Kumar A.; Srinivasan B.; Bowen P.; Scrivener K.; Ludwig C.; Testino A. On the mesoscale mechanism of synthetic calcium-silicate-hydrate precipitation: a population balance modeling approach. J. Mater. Chem. A 2018, 6, 363–373. 10.1039/C7TA08784E. [DOI] [Google Scholar]