Effect of Surface Functionalization and Physical Properties of Nanoinclusions on Thermal Conductivity Enhancement in an Organic Phase Change Material

Abstract

We probe the role of surface functionalization and physical properties of nanoinclusions in thermal conductivity enhancement during liquid–solid phase transition in a hexadecane-based phase change material (PCM). Hexadecane-based PCM is loaded with six different nanoinclusions: carbon black nanopowder (CBNP), nickel nanoparticles (NiNPs), copper nanoparticles, silver nanowires (AgNWs), multiwalled carbon nanotubes, and graphene nanoplatelets (GNPs). The nanoinclusions CBNP, NiNP, AgNW, and GNP are surface-functionalized with oleic acid. Nanoinclusion-loaded PCM showed a large enhancement in thermal conductivity, which was more prominent in the solid state. Interestingly, a maximum thermal conductivity enhancement of ∼122% was observed in the solid state for the PCM loaded with 0.01 wt % CBNP. Higher thermal conductivity enhancement in the solid state is attributed to the formation of a nanocrystalline network structure during freezing of the PCM, consisting of a needlelike microstructure, which is confirmed by optical phase contrast microscopy. During solidification, the nanoinclusions are driven toward the grain boundaries, thereby forming a quasi-two-dimensional network of percolating structures with high thermal transport efficiency due to the enhancement of phonon-mediated heat transfer and near-field radiative heat transfer. Thermal conductivity increases with the increased loading of the nanoinclusions due to the formation of more interconnecting aggregates. Among the carbon-based nanoinclusions, the highest thermal conductivity enhancement is obtained for the PCM loaded with CBNP, which is attributed to the low fractal dimensions and volume-filling capability of CBNP aggregates. In the case of metallic nanoinclusions, the highest thermal conductivity enhancement is obtained for the PCM loaded with AgNW, which is due to the large aspect ratio of AgNW. The carboxylic group of oleic acid attached to the nanoinclusions is found to provide better steric stability with insignificant aggregation and improved thermal stability, which are beneficial for practical applications. Our results indicate that the initial thermal conductivity of carbon-based nanoinclusions has an insignificant role in the thermal conductivity enhancement of the PCM but the volume-filling capability of the nanoinclusion has a prominent role. The findings from the present study will be beneficial for tailoring the properties of nanoinclusion-loaded organic PCM for thermal energy storage and reversible thermal switching applications at room temperature.

Introduction

The quest for efficient cooling materials for diverse technologies drive the current research activities on thermal properties of new materials.¹⁻⁴ Organic phase change materials (PCMs) are being developed as efficient agents for thermal energy storage and management to reduce the global energy consumption and for intermediate storage of thermal energy from renewable energy sources like solar energy and waste heat recovery.⁵⁻⁹ Thermal energy storage can be classified into three categories, viz., sensible heat storage, latent heat storage, and thermochemical heat storage.¹⁰ Among these three techniques, latent heat thermal energy storage (LHTES) using organic phase change materials (PCMs) is particularly advantageous due to higher energy storage density at a relatively constant temperature corresponding to the phase transition temperature of the PCM.¹¹ Sharma et al.¹² reported a 3–4 times higher energy storage per unit volume for a LHTES system, as compared to that for a sensible heat storage system for a temperature difference of 20 °C, which shows the efficacy of PCM-based thermal energy storage for practical applications. Although PCMs with various types of phase transitions have been experimentally studied,^11,13 PCMs with liquid–solid first-order phase transition are particularly beneficial for practical applications due to smaller volume changes during phase transition (<10%), ease of incorporation in the host matrix, and economic viability.¹⁰ In liquid–solid phase transition, energy is stored during melting, which is subsequently recovered during solidification, and the heat storage capacity of a typical PCM across liquid–solid first-order phase transition can be expressed by the following equation¹²

1

Here H_st, c_ps, c_pl, T_m, T₁, T₂, m, f_m, and Δh_m indicate the heat storage capacity, specific heat in the solid and liquid states, melting point of the PCM, initial operating temperature (<T_m), final operating temperature (>T_m), mass of the PCM, melting fraction, and specific enthalpy change, respectively. Equation 1 clearly shows that the heat storage capacity of a PCM is primarily determined by the associated phase transition temperature and enthalpy change.

Compared with inorganic PCMs, organic PCMs have several advantages such as lower vapor pressure during melting, reduced degree of supercooling, high latent heat, lower cost, chemical inertness, nontoxicity, and higher thermal stability after repeated melting/freezing cycles.¹⁴ Organic PCMs have found widespread applications in various industries, viz., thermal management of buildings, domestic and commercial refrigeration, concentrated solar thermal plants, and solar energy storage.^{5−9,14−16}

Applicability of organic PCMs for efficient thermal energy storage is severely restricted by the lower thermal conductivity of these materials⁹ and hence, various strategies have been developed for enhancing the thermal conductivity of these organic PCMs, viz., dispersing high-thermal-conductivity nanoinclusions,^8,9,17 inserting a metal framework, encapsulation and impregnating with porous materials.^11,17 Among these methods, nanoinclusion-assisted enhancement in the thermal conductivity of organic PCMs has been the most popular due to the ease of sample preparation and cost efficiency. Nanoinclusion-assisted enhancement in thermal conductivity has been reported for a wide range of organic PCMs loaded with various kinds of nanoinclusions, viz., graphene/1-octadecanol,⁹ oleylamine-functionalized reduced graphene oxide/palmitic acid,¹⁴ single-walled carbon nanotube/n-octadecane,⁷ etc.

Zheng et al.¹⁸ reported reversible thermal switching across the liquid–solid phase transition of graphite/hexadecane PCM at T = 18 °C and observed ∼3.2 times enhancement in the thermal conductivity of the PCM loaded with 0.8 vol % graphite nanoinclusions, in the solid state. Sun et al.¹⁹ reported ∼3 times enhancement in the thermal conductivity of functionalized multiwalled carbon-nanotube-loaded hexadecane, in the solid state, for 0.4 vol % loading. Schiffres et al.²⁰ reported 2.3–3 times enhancement in the thermal conductivity of multilayer graphene/hexadecane PCM, in the solid state, for loading concentration of 1 vol %. Such large thermal conductivity enhancement for nanoinclusion-loaded hexadecane, in the solid state, was attributed to the formation of needlelike microstructures during solidification and aggregation of the nanoinclusions along the grain boundaries, forming a percolating network with a higher thermal transport efficiency.¹⁸⁻²⁰ Recently, significant enhancement in the thermal conductivity of n-hexadecane was achieved by inverse miceller templating and loading with various nanoinclusions such as graphene nanoplatelets (GNPs), multiwalled carbon nanotubes (MWCNTs), and copper nanowires.^8,17

Although nanoinclusion-assisted thermal conductivity enhancement of hexadecane is well studied, the effect of aggregation and cluster formation is not fully understood.^21,22 Eapen et al.²³ discussed the effects of percolating structures on thermal conductivity enhancement beyond the classical Maxwell limit. Moreover, earlier studies on hexadecane-based nanoinclusions were primarily focused on carbon-based nanoinclusions and reports on the effects of metallic nanoinclusions (apart from copper nanowire¹⁷) on thermal conductivity enhancement during liquid–solid phase transition are scarce. Furthermore, the effect of surface functionalization of the nanoinclusions on thermal conductivity enhancement and long-term stability in hexadecane-based PCM is not known. Xia et al.²⁴ reported that surface functionalization results in superior stability but adversely affects the thermal conductivity enhancement. Hermida-Merino et al.⁶ also reported that surface functionalization decisively influences the transport properties.

Hexadecane-based PCMs are technologically important candidates for room temperature (phase transition temperature near 18 °C) thermal energy storage and reversible thermal switching applications. Here, we probe the effects of various types of nanoinclusions on the thermal conductivity enhancement and the effects of surface functionalization and aggregation on thermal conductivity and thermal stability of such PCM, which are important to tailor nanoinclusion-loaded PCMs for practical applications.

In the present study, enhancement in the thermal conductivity of hexadecane-based PCM loaded with three different carbon-based nanoinclusions, viz., carbon black nanopowder (CBNP), multiwalled carbon nanotubes, and graphene nanoplatelets, and three metallic nanoinclusions, viz., silver nanowire (AgNW), nickel nanoparticles (NiNPs), and copper nanoparticles (CuNPs) is systematically studied. In the case of carbon-based nanoinclusions, multiwalled carbon nanotube has a larger aspect ratio with respect to the graphene nanoplatelets, which are two-dimensional (2D) structures with fractal morphology. Additionally, a comparatively cheaper alternative, viz., carbon black nanopowder, is selected to compare the thermal conductivity enhancement at similar concentrations. Among the metallic nanoinclusions, silver nanowire has a larger aspect ratio as compared to that of the other two metallic nanoinclusions (nickel and copper nanoparticles), which are of spherical shapes, but with widely varying bulk thermal conductivity. Thermal conductivity enhancements are experimentally measured using a transient hot-wire probe. The sample temperature, during liquid–solid phase transition, is remotely monitored using infrared thermography (IRT). The gain in freezing time for nanoinclusion-loaded PCM is determined from the normalized temperature decay curves, obtained from infrared thermography, for the first time. In addition, the effect of surfactant capping on thermal conductivity enhancement and thermal stability is also studied. Thermal stability of the nanoinclusion-loaded PCM is probed by repeated thermal cycling. Optical phase contrast microscopy is used to obtain insight into the microscale aggregation phenomena during consecutive thermal cycling.

Mechanism of Thermal Conductivity Enhancement

Thermal conductivity enhancement of nanoinclusion-loaded organic phase change materials is primarily governed by the aggregation phenomena.^25,26 The nanoinclusions, when dispersed within a matrix of PCM, form clusters, which act as efficient percolating structures for heat transfer.²² Moreover, during solidification, the clusters are squeezed toward the grain boundaries, forming a network of percolating structures, which results in large enhancement of thermal conductivity in the solid state.^18,19

Effect of Cluster Formation

The aggregation dynamics and the effects of cluster formation on thermal conductivity enhancement in nanoinclusion-loaded PCM are explained on the basis of a three-level homogenization model of Prasher and Evans.²⁵ The nanoinclusions form aggregates due to van der Waals interaction, and these aggregates grow in size with the increasing concentration of the nanoinclusions, resulting in an enhancement of thermal conductivity, as the nanoinclusions of higher thermal conductivity, as compared to that of the PCM, are in physical contact with each other within the aggregates with a radius of gyration several times larger than that of the individual nanoinclusions.²² Formation of larger aggregates (but within the limit of well-dispersed aggregates) is beneficial for thermal conductivity enhancement of the nanoinclusion-loaded PCM primarily due to three reasons, viz., phonon-mediated efficient heat conduction through a larger network of percolating structure, reduced interfacial thermal resistance due to improved contact between the nanoinclusions within an aggregate, and increased near-field radiative heat transfer between the closely packed nanoinclusions with interparticle separation lower than the typical dimensions of the individual nanoinclusions.^22,23,27

The aggregates or clusters have fractal morphologies consisting of a backbone and dead ends.²² The backbone is a quasi-continuous network of percolating nanoinclusions, spanning the entire aggregate volume with characteristic length scale equal to the radius of gyration of the aggregate. On the other hand, the randomly placed nanoinclusions form dead ends within the aggregates.²² Under such a scenario, the effective thermal conductivity of a cluster is attributed to two different sources, viz., the thermal conductivity of the homogenized medium with dead ends alone (first-level homogenization) and superimposition of the backbone over this homogenized medium (second-level homogenization).²⁵ Finally, the effective thermal conductivity of the entire system is obtained from homogenization of the clusters with the medium (third level of homogenization).²⁵

Let k, k_f, k_de, k_p, and k_c indicate the effective thermal conductivity of the nanoinclusion-loaded PCM (entire system), thermal conductivity of the PCM in liquid state, thermal conductivity of the cluster with dead ends alone, total thermal conductivity of the cluster, and bulk thermal conductivity of the nanoinclusions, respectively. Then according to the Bruggeman model, the thermal conductivity of the cluster with dead ends alone can be expressed by the following equation^22,25

2

Here, ϕ_de indicates the volume fraction of the nanoinclusions belonging to the dead ends alone and ϕ_de = ϕ_c – ϕ_bb, where ϕ_c and ϕ_bb indicate the volume fraction of the nanoinclusion within a cluster and the volume fraction of nanoinclusions belonging to the backbone, respectively.²⁵Section S1, in the Supporting Information, describes the calculations of ϕ_bb, ϕ_de, and ϕ_c in terms of the fractal dimension of the clusters. The total thermal conductivity of the clusters (k_c) is estimated with an assumption that the backbone is superimposed on a medium with homogenized thermal conductivity k_de.²⁵²⁵ The total thermal conductivity of the cluster is obtained from the following equation originally proposed by Nan et al.²⁸

3

Here L₃₃ = 1 – 2L₁₁, where L₁₁ = 0.5m²/(m² – 1) – 0.5m cosh^–1[m(m² – 1)^−1.5] and m is the aspect ratio of the cluster with respect to the nanoinclusions, defined as m = R_g/a, where R_g and a indicate the radius of gyration of the cluster and size of the nanoinclusions, respectively.²⁸ The term β_ii (i = 1 and 3) is expressed by the following equations²⁸

4

5

Here ω = (2 + 1/m) × (δ_R/a), where δ_R indicates the hypothetical Kaptiza radius, which signifies the length scale in the host matrix over which the temperature drop is comparable to the temperature drop at the nanoinclusion/host interface.^25,28 Finally, the effective thermal conductivity of the entire sample (nanoinclusion-loaded PCM) is obtained from the Maxwell-Garnett model using the following equation²⁵

6

Nanoinclusion-aided enhancement in the thermal conductivity of the PCM is calculated from eq 6 in the liquid state. However, thermal conductivity enhancement drastically increases in the solid state and during the liquid–solid phase transition, which is attributed to the squeezing of nanoinclusions toward the grain boundaries, as explained in the following section.

Network of Clusters in Solid State

When crystal-forming liquids are loaded with nanoinclusions, the nanoinclusions are driven toward the intercrystal regions or grain boundaries during freezing.^18,20 Internal stress field is generated within the PCM (considering linear viscoelastic properties) during freezing, which is expressed by the following relation²⁹

7

Here S(r,t), E(t), e₀(τ), T(r,τ), ν, and α_l indicate the stress field at location r and time t, relaxation modulus function at time t, instantaneous mean strain at time t = τ, temperature profile at a particular location (r) at instantaneous time t = τ, Poisson’s ratio, and coefficient of thermal expansion, respectively.²⁹

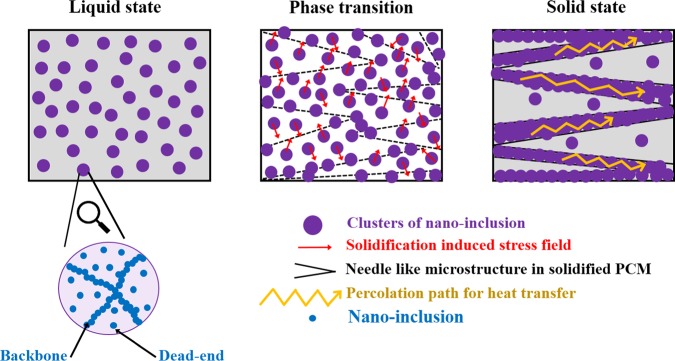
The solidification-induced internal stress squeezes the nanoinclusions toward the grain boundaries and increases the contact area between the nanoinclusions, thereby reducing the thermal contact resistance (Kapitza resistance), which results in an enhancement in the thermal conductivity of the nanoinclusion-loaded PCM due to the formation of a quasi-2D network of percolation pathways with a high heat-transfer efficiency.^{7,18,19,22,30}Figure 1 schematically shows the solidification-induced formation of a 2D network of percolating structures with enhanced heat-transfer properties.

Figure 1.

Schematic representation of the solidification-induced formation of a 2D network of percolating structures with enhanced heat-transfer properties. In the liquid state (left figure), the clusters are randomly dispersed. During phase transition (middle figure), needlelike structures develop and the clusters experience a stress field, which drives them toward the grain boundaries. The formation of a quasi-2D percolating network is complete in the solid state (right figure), which causes a large enhancement in thermal conductivity. The inset shows the expanded view of a cluster, where the backbones and dead ends consisting of individual nanoinclusions are seen. Thermal conductivity enhancement within a cluster is primarily through phonon-mediated heat transfer via the interconnected backbones, which span the entire length of a cluster.

Domingues et al.²⁷ proposed that stress-induced squeezing of the nanoinclusions also leads to substantially lower interparticle separation distances, as compared to the typical dimensions of the nanoinclusions, which results in an enhancement of near-field radiative heat transfer.

Results and Discussion

Characterization of the Nanoinclusions

Section S2, in the Supporting Information, describes the characterization results for the nanoinclusions in detail. Only the essential features are discussed below. From transmission electron microscopy (TEM) image analyses, the average sizes of NiNP and CuNP were obtained as ∼23.4 ± 2.3 and 12.8 ± 2.8 nm, respectively. The room temperature powder X-ray diffraction (XRD) pattern indicated the presence of face-centered cubic (FCC) Ni (JCPDS 04-0850)³¹ and FCC elemental Cu (JCPDS 71-4610)³² phases, and the average crystallite sizes were found to be ∼29 ± 3 and 13 ± 2 nm for NiNP and CuNP, respectively, which were in good agreement with the sizes obtained from TEM. Small-angle X-ray scattering (SAXS) studies³³ indicated the most probable sizes of CBNP and GNP as ∼21 ± 2 and ∼12 ± 2 nm, respectively. Analyses of the scattering intensity at a high q (wave vector) region, i.e., Porod’s region,³³ indicated the fractal dimension of GNP, which was in agreement with the earlier reported results.^6,34 The average hydrodynamic sizes were 295 ± 59, 296 ± 82, and 615 ± 141 nm for NiNP, CuNP, and CBNP, respectively, which were significantly higher than the sizes obtained from XRD, TEM, and SAXS. This indicated significant aggregation of the nanoinclusions on dispersion in hexadecane. The larger hydrodynamic size of CBNP nanoinclusions was attributed to the formation of aciniform aggregates of the primary particles (nodules).³⁵ In the Fourier transform infrared (FTIR) spectra, the strong absorption band, at 1716 cm^–1, for the pure oleic acid, corresponding to the stretching of the carbonyl group,³⁶ was missing for the oleic acid-capped nanoinclusions, where two new absorption bands appeared at 1667 and 1598 cm^–1, which corresponded to the asymmetric and symmetric stretching of −COO^–, respectively.³⁷ The difference between the symmetric and asymmetric bands was found to be ∼69 cm^–1, indicating the formation of chelating bidentate on the surface of the nanoinclusions, upon coating with oleic acid due to strong electronic interaction of the polar carboxylic head group of oleic acid with the nanoinclusions.³⁷ FTIR spectra confirmed that the major absorption bands were not shifted for the PCM loaded with various nanoinclusions,³⁶⁻³⁸ which clearly indicated the absence of any chemical reaction between the PCM and the nanoinclusions.

Characterization of the PCM

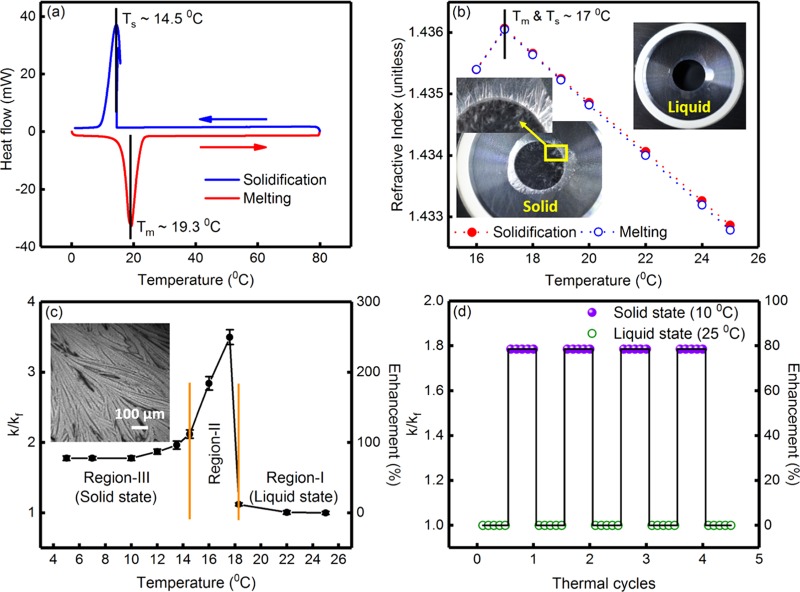
Figure 2a shows the heat flow curves, during solidification and melting of the PCM (hexadecane), obtained from differential scanning calorimetry (DSC) studies. The solidification (T_s) and melting (T_m) temperatures were found to be 14.5 and 19.3 °C, respectively. These values are in good agreement with the phase transition temperature of ∼17–18 °C reported by Vélez et al.,¹⁰ Sun et al.,¹⁹ Zheng et al,¹⁸ and Su et al.¹³ The latent heat values were found to be ∼238.6 and 241.4 kJ kg^–1 during solidification and melting, respectively, which were also in agreement with the values reported elsewhere (∼236 kJ kg^–1 by Vélez et al.,¹⁰ ∼238 kJ kg^–1 by Su et al.,¹³ etc.). The degree of supercooling (difference between T_s and T_m) was found to be ∼4.8 °C, which was higher than the value of ∼1 °C reported by Vélez et al.¹⁰Figure 2b shows the variation of refractive index of the PCM as a function of temperature during solidification and melting. Table S2, in the Supporting Information, shows the experimental data for variation of refractive index, as a function of temperature. It can be seen from Figure 2b that refractive index increased with decreasing temperature up to the phase transition temperature of the PCM and beyond that refractive index decreased. Due to absorption and re-emission of light along the traveling path, speed of light in a medium is lower than that in a vacuum. With decreasing temperature, the density of the PCM increases, leading to a decreased speed of light in the medium, resulting in an increase in refractive index. The phase transition temperature of the PCM was found to be ∼17 °C, which was in agreement with the results obtained from differential scanning calorimetry studies. It can be further seen from Figure 2b that the refractive index decreased sharply below the phase transition temperature, which was attributed to the cracking of the solidified pellets, which allowed the light to pass through. Extensive cracking of the solidified pellets was observed due to the formation of a needlelike microstructure after freezing.^18,19 The insets of Figure 2b show the photograph of the PCM in the liquid and solid states and the presence of a needlelike microstructure and cracks in the solidified pellet is clearly discernible from the photographs. Figure 2c shows the variation of k/k_f as a function of temperature for the PCM. Here, k and k_f indicate the temperature-dependent thermal conductivity of the PCM and the thermal conductivity of the PCM at T = 25 °C (=0.140 ± 0.002 W m^–1 K^–1), respectively. The percentage enhancement in thermal conductivity [=100 × (k – k_f)/k_f] is also shown in Figure 2c. Table S3, in the Supporting Information, shows the experimental data for variation of thermal conductivity and k/k_f as a function of temperature. The thermal conductivity enhancement was insignificant in the liquid state, whereas significant enhancement in thermal conductivity was observed in the phase transition region and solid state. In the solid state, thermal conductivity decreased slightly with decreasing temperature but remained constant below 10 °C. The thermal conductivity of the PCM in the solid state, at T = 10 °C, was found to be 0.249 (±0.003) W m^–1 K^–1, which was slightly higher than the earlier reported value of 0.21 W m^–1 K^–1.¹³ The increase in thermal conductivity in the solid state was attributed to the formation of a closely packed nanocrystalline structure. A similar enhancement in thermal conductivity in the solid state has been experimentally reported by Sun et al.¹⁹ and Zheng et al.¹⁸ for n-hexadecane. Using molecular dynamics simulation, Babaei et al.³⁹ confirmed the formation of a nanocrystalline phase during solidification of PCM, which caused an enhancement in thermal conductivity due to the phonon-mediated heat transfer. It has been reported that hexadecane crystals exhibit strong anisotropic growth kinetics, resulting in the formation of a needlelike microstructure and ice templating.¹⁸⁻²⁰ The inset of Figure 2c shows a phase contrast optical micrograph of hexadecane in the solid state, where the presence of needlelike microstructures is clearly discernible (indicated by the arrows). For establishing repeatability and thermal stability of the PCM, thermal cycling was carried out and five thermal conductivity measurements were performed at regular time intervals in the solid (at T = 10 °C) and liquid (at T = 25 °C) states. Figure 2d shows the variation of k/k_f during thermal cycling of the PCM, where it can be seen that freezing and melting cycles were reversible, even after four cycles. The k/k_f in the solid state (at T = 10 °C) was ∼1.779, indicating a thermal conductivity enhancement of 77.9% for the PCM, which was significantly higher than the earlier reported values of ∼28% by Sun et al.¹⁹ and ∼50% by Su et al.¹³ The observed reversible thermal cycles indicated the superior thermal stability and efficacy of hexadecane-based PCM for thermal energy storage applications.

Figure 2.

(a) Heat flow curves, during solidification and melting of the PCM (hexadecane), obtained from differential scanning calorimetry studies. The solidification (T_s) and melting (T_m) temperatures were ∼14.5 and 19.3 °C, respectively, as indicated in the figure. (b) The variation of refractive index of the PCM as a function of temperature during solidification and melting. The phase transition temperature was ∼17 °C. (Inset) typical photographs of the PCM in the liquid and solid states. The presence of needlelike microstructures and cracks in the solidified pellet of the PCM is clearly discernible. (c) Variation of k/k_f and percentage enhancement in thermal conductivity, as a function of temperature, for the PCM, without any nanoinclusions. Here, k and k_f indicate the temperature-dependent thermal conductivity of the PCM and the thermal conductivity of the PCM at T = 25 °C (=0.140 ± 0.002 W m^–1 K^–1), respectively. The variation of k/k_f can be divided into three regions, viz., region-I (liquid state), region-II (phase transition), and region-III (solid state). (Inset) optical phase contrast microscopy image of the PCM in solid state, where the needlelike microstructure is clearly discernible. (d) Variation of k/k_f and percentage enhancement in thermal conductivity during thermal cycling of the PCM, without any nanoinclusions.

Nanoinclusion-Assisted Thermal Conductivity Enhancement of the PCM

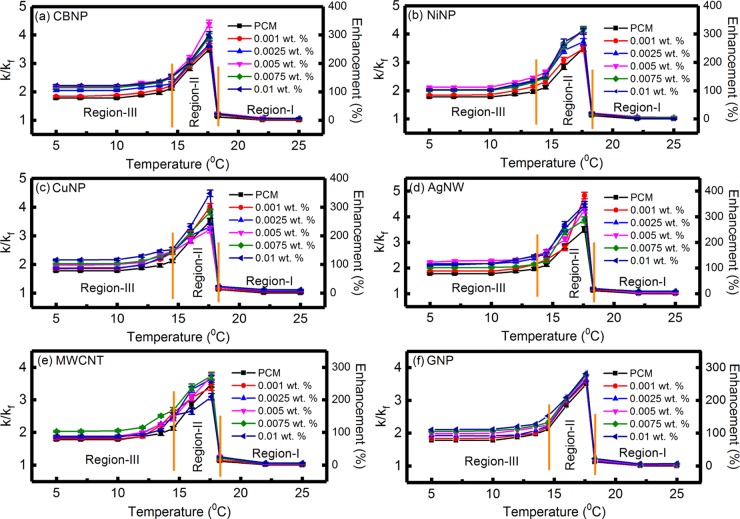
Figure 3a–f shows the variation of k/k_f and percentage (%) enhancement in thermal conductivity, as a function of temperature, for the PCM loaded with various concentrations of CBNP, NiNP, CuNP, AgNW, MWCNT, and GNP nanoinclusions, respectively. Tables S4–S9, in the Supporting Information, show the experimental data for the variations of thermal conductivity and k/k_f as a function of temperature for the PCM loaded with various concentrations of CBNP, NiNP, CuNP, AgNW, MWCNT, and GNP, respectively. For comparison, the variation of k/k_f in the case of PCM without any nanoinclusions is also shown in the figures. It can be clearly seen from Figure 3a–f that the variation of k/k_f as a function of temperature can be divided into three distinct regions, which were indicated as regions I, II, and III, respectively. For T > 18.3 °C, the PCM, with or without nanoinclusions, was found to be in the liquid state, and this region was categorized as region-I. Region-II indicated the phase transition region for 14.5 °C < T < 18.3 °C, and region-III corresponded to the temperature range well below the freezing point, where the PCM, with or without nanoinclusions, was in the solid state.

Figure 3.

Variation of k/k_f and percentage enhancement in thermal conductivity, as a function of temperature, for the PCM loaded with various concentrations of (a) CBNP, (b) NiNP, (c) CuNP, (d) AgNW, (e) MWCNT, and (f) GNP nanoinclusions. For comparison, the variation of k/k_f in the case of PCM, without any nanoinclusions, is also shown in the figures. The variation of k/k_f can be divided into three regions, viz., region-I (liquid state), region-II (phase transition), and region-III (solid state).

Figure 3a shows that the thermal conductivity enhancements in the liquid state (at T = 25 °C) were ∼1.4, 5.0, 5.5, 5.5, and 6.4% for 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % CBNP loading, respectively. Figure S4a, in the Supporting Information, shows the enlarged view of the variation of k/k_f and percentage enhancement in thermal conductivity, as a function of temperature, for the PCM loaded with various concentrations of CBNP, in the liquid state. In the phase transition region (region-II), maximum enhancements of thermal conductivity were ∼260, 267, 339, 293, and 300% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % CBNP, respectively. Figure 3a further shows that the thermal conductivity enhancement decreased with temperature in the solid state (region-III) and attained a steady value below 10 °C. In the solid state, thermal conductivity enhancements were ∼87.9, 105.0, 117.4, 115.5, and 121.4% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % CBNP, respectively. Figure S5a, in the Supporting Information, shows the enlarged view of the variation of k/k_f and percentage enhancement in thermal conductivity, as a function of temperature, for the PCM loaded with various concentrations of CBNP, in the solid state.

The higher thermal conductivity in the solid state (region-III) as compared to that in the liquid state (region-I) was due to the formation of a crystalline structure of the PCM after freezing and phonon-assisted efficient heat transfer in the solid state.^18,19 The maximum enhancement in thermal conductivity was observed in the phase transition region, which was attributed to the strong anisotropic growth kinetics-induced formation of a continuous networking structure during liquid–solid phase transition in hexadecane.¹⁷⁻¹⁹ The formation of such needlelike microstructures during liquid–solid phase transition has been reported experimentally.¹⁷⁻²⁰ Schiffres et al.²⁰ reported that a slower cooling rate results in the formation of a microstructure with thicker and longer needles, leading to a comparatively larger thermal conductivity enhancement due to anisotropic templating. Zheng et al.¹⁸ mapped the internal stress distribution in frozen hexadecane and reported an uneven stress distribution with an average pressure of ∼160 psi, which was attributed to the anisotropic growth kinetics and formation of a needlelike microstructure in frozen hexadecane. The formation of needlelike microstructures during liquid–solid phase transition of hexadecane is also confirmed in the present study from optical phase contrast microscopy images (inset of Figure 2c). During freezing, due to internal stress fields, the nanoinclusions are driven toward the intercrystal regions or grain boundaries.^18,20,29 This results in an enhancement in the thermal conductivity of the nanoinclusion-loaded PCM due to the formation of a quasi-2D network of percolation pathways with high heat-transfer efficiency.^7−19,22,30 Increased near-field radiative heat transfer due to low interparticle separation distance (spatially localized near the grain boundaries) also leads to an enhancement of thermal conductivity.²⁷ On the other hand, the lowering of thermal conductivity enhancements in region-III, well below the freezing point, was attributed to the microstructural changes, where longer needles were broken down to shorter needles, probably due to the solidification-induced residual stress fields.^18,29

It can be seen from Figure 3b that in region-I, thermal conductivity enhancements were ∼2.1, 4.3, 5.7, 5.0, and 2.1% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % NiNPs, respectively. Figure S4b, in the Supporting Information, shows the enlarged view of the variation of k/k_f and percentage increase in thermal conductivity, as a function of temperature, for the PCM loaded with various concentrations of NiNPs, in the liquid state. In the phase transition region, the maximum enhancements in thermal conductivity were ∼248, 273, 313, 316, and 310% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % NiNPs, respectively. In region-III, the enhancements in thermal conductivity were ∼85.7, 102.1, 112.9, 101.4, and 102.9% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % NiNPs, respectively. Figure S5b, in the Supporting Information, shows the enlarged view of variation of k/k_f and percentage enhancement in thermal conductivity, as a function of temperature, for the PCM loaded with various concentrations of NiNPs, in the solid state. Figure 3c shows the variation of k/k_f and percentage enhancement in thermal conductivity, as a function of temperature for the PCM loaded with CuNP, where it can be seen that the enhancements in thermal conductivity in the liquid state were ∼2.9, 5.7, 9.3, 10.0, and 11.4% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % CuNPs, respectively. Thermal conductivity enhancements in the phase transition region were ∼301, 231, 221, 283, and 348% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % CuNPs, respectively. On the other hand, in region-III, thermal conductivity enhancements (at T = 10 °C) were ∼85.5, 87.9, 100.7, 102.9, and 117.1% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % CuNPs, respectively. Thermal conductivity enhancements for CuNP-loaded PCM were found to be higher than the earlier reported values of ∼3 and 182% enhancement in the liquid and phase transition regions, respectively, for hexadecane loaded with 0.01 wt % copper nanowires (outer diameter and length ∼50 nm and 1–50 μm, respectively).¹⁷ On the other hand, in the solid state, the thermal conductivity enhancement was higher (∼130%) in the case of PCM loaded with 0.01 wt % copper nanowires¹⁷ as compared to that with CuNP nanoinclusions used in the present study (maximum enhancement ∼117.1%). This was probably due to the higher aspect ratio of the copper nanowires that formed efficient percolating trajectories along the grain boundaries during freezing.

Figure 3d shows that the thermal conductivity enhancements, in the liquid state, were ∼2.9, 7.1, 2.9, 8.6, and 9.3% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % AgNWs, respectively. In region-II, thermal conductivity enhancements were ∼382, 337, 326, 287, and 348% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % AgNWs, respectively. On the other hand, 87.9, 117.1, 129.3, 102.1, and 117.9% enhancements in thermal conductivity were observed in the solid state (at T = 10 °C) for AgNW loading of 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt %, respectively. Figure 3e shows the variation of thermal conductivity enhancement for the PCM loaded with MWCNTs, where it can be seen that the thermal conductivity enhancements in the liquid state were ∼1.4, 2.9, 4.3, 5.0, and 5.7% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % MWCNT. Thermal conductivity enhancements in the phase transition region were ∼238, 264, 273, 274, and 209% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % MWCNTs, respectively. In the solid state, thermal conductivity enhancements were ∼80.0, 85.0, 87.9, 105.0, and 87.9% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % MWCNTs. In the present study, the maximum thermal conductivity enhancement in the solid state (at T = 10 °C) was ∼105% for the PCM loaded with 0.0075 wt % MWCNT, which was lower than the ∼200% enhancement in thermal conductivity reported by Sun et al.¹⁹ for hexadecane loaded with carboxylic acid-functionalized MWCNTs (loading = 0.4% volume fraction). On the other hand, our results indicated a maximum enhancement in thermal conductivity of ∼274% for the PCM loaded with 0.0075 wt % MWCNTs in the phase transition region, which was substantially higher than the values reported by Sun et al.¹⁹ It can be seen from Figure 3f that the thermal conductivity enhancements in the liquid state were ∼1.4, 2.9, 4.3, 5.7, and 7.1% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % GNP, respectively. Thermal conductivity enhancements in the phase transition region were ∼257, 263, 271, 278, and 282% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % GNP, respectively. Thermal conductivity enhancements of ∼84.3, 91.4, 100.0, 107.1, and 111.4% were observed for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % GNP, respectively, in the solid state. The maximum enhancement in thermal conductivity in the phase transition region was found to be ∼282% for the PCM loaded with 0.01 wt % GNP, which was higher than the enhancement values of ∼220 and 110–160% reported by Zheng et al.¹⁸ and Schiffres et al.,²⁰ respectively. Figures S4c–f and S5c–f, in the Supporting Information, show the enlarged views of the variation of k/k_f and percentage enhancements in thermal conductivity as a function of temperature for the PCM loaded with various concentrations of CuNPs, AgNWs, MWCNTs, and GNPs in the liquid and solid states, respectively.

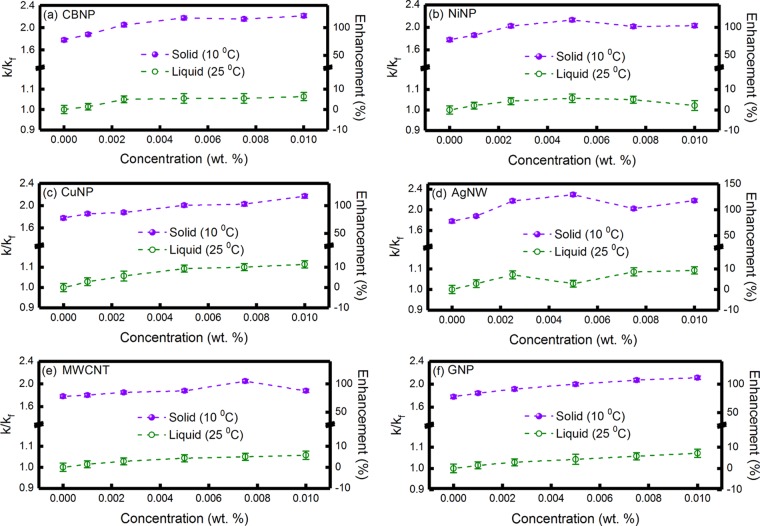
Figure 4a–f shows the variation of k/k_f and percentage enhancement in thermal conductivity as a function of sample concentration in the solid (T = 10 °C) and liquid (T = 25 °C) states for the PCM loaded with six different nanoinclusions, viz., CBNP, NiNP, CuNP, AgNW, MWCNT, and GNP. In the liquid state, maximum enhancements in thermal conductivity were ∼6.4, 5.7, 11.4, 9.3, 5.7, and 7.1% for the PCM loaded with 0.01 wt % CBNP, 0.005 wt % NiNPs, 0.01 wt % CuNPs, 0.01 wt % AgNWs, 0.01 wt % MWCNTs, and 0.01 wt % GNPs, respectively. It can be clearly seen from Figure 4 that for the PCM loaded with CBNP, CuNPs, MWCNTs, and GNPs, thermal conductivity increased with the concentration of the nanoinclusions in the liquid state. On the other hand, for the PCM loaded with NiNPs and AgNWs, thermal conductivity decreased at higher concentrations of the nanoinclusions, which was due to the sedimentation of the larger aggregates at higher concentrations of the nanoinclusions. The sedimentation velocity (V_s) of a concentrated solution is expressed as 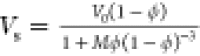.²¹ Here M and ϕ indicate a numerical constant (M ∼ 4.6) and effective volume fraction of the solute, respectively. V₀ indicates the sedimentation velocity at infinite dilution, which is linearly proportional to the density difference of the solute and the solvent.²¹ Due to higher density of AgNW and NiNP (density ∼10.5 and 8.9 g cc^–1, respectively), these nanoinclusions were prone to form unstable aggregates at higher concentrations, which resulted in the decrease of thermal conductivity enhancements at higher concentrations, as can be seen from Figure 4b,d.

Figure 4.

Variation of k/k_f and percentage enhancement in thermal conductivity as a function of sample concentration in the solid (T = 10 °C) and liquid (T = 25 °C) states for the PCM loaded with (a) CBNP, (b) NiNP, (c) CuNP, (d) AgNW, (e) MWCNT, and (f) GNP nanoinclusions.

It can be further seen from Figure 4a–f that the thermal conductivity enhancement was substantially higher for the nanoinclusion-loaded PCM in the solid state, which was attributed to the formation of the crystalline structure of the PCM on freezing and phonon-mediated efficient heat transfer through the quasi-2D network of percolating structures.¹⁷⁻¹⁹ In the present study, the maximum thermal conductivity enhancements in the solid state were ∼121.4, 112.9, 117.1, 129.3, 105.0, and 111.4% for the PCM loaded with 0.01 wt % CBNP, 0.005 wt % NiNPs, 0.01 wt % CuNPs, 0.005 wt % AgNWs, 0.0075 wt % MWCNTs, and 0.01 wt % GNPs, respectively. The aggregates grow in size with the increasing concentration of the nanoinclusions due to van der Waals interaction, resulting in an enhancement of thermal conductivity. As discussed earlier in the theoretical section, the formation of such larger aggregates is beneficial for thermal conductivity enhancement due to phonon-mediated efficient heat conduction through a larger network of percolating structure with reduced interfacial thermal resistance and increased near-field radiative heat transfer.^22,23,27 Initial increase in thermal conductivity enhancement of the nanoinclusion-loaded PCM with increasing loading fraction has also been reported earlier for hexadecane-based PCM.¹⁷⁻¹⁹Figure S6a–f, in the Supporting Information, shows the variation of k/k_f in the liquid state as a function of concentration (in volume fraction) for the PCM loaded with CBNP, NiNP, CuNP, AgNW, MWCNT, and GNP nanoinclusions, respectively. The theoretical plots for the effective medium theory (k/k_f = 1 + 3ϕ, ϕ being the effective volume fraction of the nanoinclusions, which is considered as the theoretical upper limit of eq 6 after three-level homogenization following the Prasher and Evans model²⁵) are also shown in the figures. It can be clearly seen from Figure S6a–f that the experimentally measured k/k_f values were higher than the theoretically predicted values, which indicated the presence of agglomeration in these systems.^4,17

It has been reported that the thermal conductivity of nanofluids initially increases with the aggregate size and attains an optimal value for the well-dispersed aggregates due to the formation of a high-efficiency percolation network and beyond that thermal conductivity decreases for larger aggregates.²² The formation of such large aggregates causes a saturation or a slight decrease in thermal conductivity enhancements at higher concentrations of the nanoinclusions, as can be seen from Figure 4a–f. This was attributed to the fractal morphologies of the aggregates consisting of a backbone and dead ends, as discussed earlier in the theoretical section and schematically shown in Figure 1.²⁵ Thermal conductivity enhancement occurs via phonon-mediated effective heat transport through the backbone, and the dead ends are, in general, insignificant toward enhancement of thermal transport.²² This is also evident from eq 2 (after first-order homogenization involving dead ends only), where considering the highest volume fraction as 7.33 × 10^–6 for 0.01 wt % loading of AgNWs and thermal conductivities of Ag and PCM (in solid state) as 427⁴ and 0.249 W m^–1 K^–1, respectively, the effective thermal conductivity of AgNW-loaded PCM was found to be ∼0.252 W m^–1 K^–1. This shows that if the contributions from only dead ends are considered, the maximum thermal conductivity enhancement is ∼1.2%, which was approximately 2 orders of magnitude lower than the experimentally measured value of ∼120%. In larger aggregates, the number of dead ends increases, which does not contribute toward thermal conductivity enhancement, and moreover, such larger aggregates are not well dispersed and prone to sedimentation, causing a saturation or decrease in thermal conductivity of the nanoinclusion-loaded PCM at higher loading fractions. A decrease in thermal conductivity for higher concentrations of MWCNT loading in hexadecane-based PCM was experimentally reported by Angayarkanni and Philip¹⁷ and Sun et al.,¹⁹ which is in good agreement with the findings of the present study.

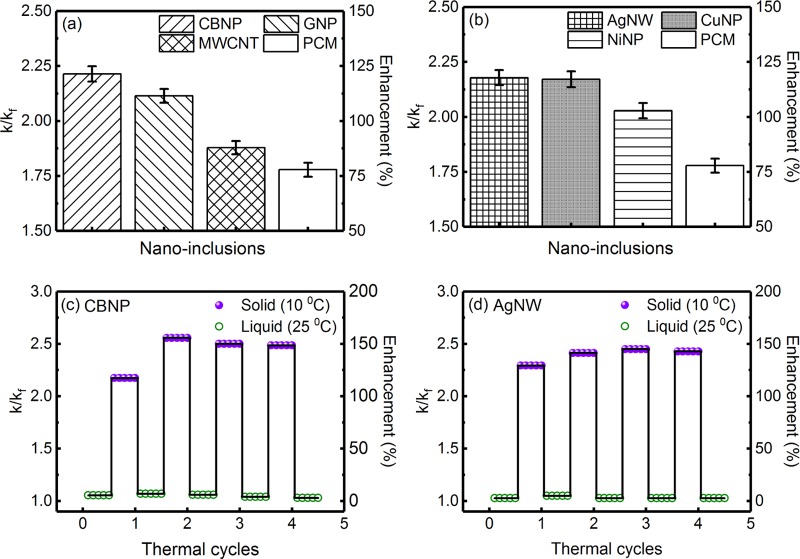
The six different nanoinclusions used in the present study were classified into two groups, viz., carbon-based nanoinclusions (CBNP, GNP, and MWCNT) and metallic nanoinclusions (AgNW, CuNP, and NiNP). Figure 5a,b shows the bar charts comparing the k/k_f and percentage enhancement in thermal conductivity in the solid state at a loading concentration of 0.01 wt % for the carbon-based and metallic nanoinclusions, respectively. For comparison, the thermal conductivity enhancement of the PCM (without any nanoinclusions) is also shown in Figure 5a,b. Among the three carbon-based nanoinclusions, bulk thermal conductivity is the highest for MWCNTs (∼6600 W m^–1 K^–1), followed by GNPs (∼3000 W m^–1 K^–1) and CBNP (∼0.25–0.4 W m^–1 K^–1).⁴ Nevertheless, it can be clearly seen from Figure 5a that the highest enhancement in thermal conductivity was for the PCM loaded with CBNP, followed by GNPs and MWCNTs, in the decreasing order. This was attributed to the variations in morphology and Kapitza resistance of the nanoinclusions. For the nanoinclusion-loaded PCM in the solid state, the enhancement in thermal conductivity is due to the formation of percolation trajectories along the intercrystallite regions, and GNP, being two-dimensional, forms better percolation pathways with comparatively larger networking structures.⁴⁰ Using molecular dynamics simulations, Yang et al.⁴¹ showed that carbon nanotubes and graphene nanoplatelets act as nucleation sites during freezing, which leads to orientational ordering near the PCM/nanoinclusions interface, resulting in an enhanced phonon coupling.⁴⁰ It was further shown by Yang et al.⁴¹ that the nucleation rate is lower for the PCM loaded with GNP. In the case of hexadecane-based PCM, a lower freezing rate leads to the formation of a longer and thicker needlelike microstructure with improved heat-transfer efficiency.²⁰ The higher thermal conductivity enhancement in the case of PCM loaded with GNPs was also attributed to the lower Kapitza resistance of GNP, as compared to that of MWCNT.⁴⁰ On the other hand, the PCM loaded with CBNP nanoinclusions showed the highest thermal conductivity enhancement, which was attributed to the fractal nature of the aggregates of CBNP, consisting of nodules of primary particles. An earlier study showed that CBNP loading in PCM leads to the formation of high thermal conductivity percolation trajectories with reduced interaggregate gaps.⁴² The higher thermal conductivity for CBNP-loaded octadecane-based PCM was reported by Wu et al.,⁴³ which was attributed to the low fractal dimensions and volume-filling capability of the CBNP aggregates. Thermal conductivity enhancement through the percolating network of the nanoinclusions loaded within a PCM is limited due to the interfacial thermal resistance of the aggregate/aggregate and aggregate/PCM interfaces and phonon mismatch due to the random curvatures of the aggregate/aggregate interfaces.^44,45 CBNP, due to its aciniform structure and low fractal dimension, forms tightly packed aggregates with improved aggregate/aggregate interactions, leading to higher-thermal-conductivity trajectories, which explains the highest thermal conductivity enhancement for the PCM loaded with CBNP, as shown in Figure 5a.

Figure 5.

Bar charts comparing the k/k_f and percentage enhancement in thermal conductivity in the solid state at a loading concentration of 0.01 wt % for the (a) carbon-based and (b) metallic nanoinclusions. For comparison, the thermal conductivity enhancement of the PCM, without any nanoinclusions, is also shown in the figures. Variation of k/k_f and percentage enhancement in thermal conductivity during thermal cycling for the PCM loaded with 0.005 wt % (c) CBNP and (d) AgNWs.

On the other hand, it is evident from Figure 5b that in the case of metallic nanoinclusions the highest thermal conductivity enhancement was obtained for the PCM loaded with AgNWs, followed by CuNPs and NiNPs, in the decreasing order. Among the three metallic nanoinclusions, bulk thermal conductivity is the highest for AgNWs (∼427 W m^–1 K^–1) followed by CuNPs (∼385 W m^–1 K^–1) and NiNPs (∼91 W m^–1 K^–1).⁴ Although the thermal conductivity enhancements for the PCM loaded with metallic nanoinclusions showed a similar trend, other physical factors, viz., larger aspect ratio of AgNW and larger size of NiNP (average crystallite sizes of NiNP and CuNP were ∼29 ± 3 and 13 ± 2 nm, respectively) also played a significant role according to earlier studies,⁴⁶ which showed a higher thermal conductivity enhancement for lower particle size and larger aspect ratios of the dispersed phase. On the other hand, an increase in the effective thermal conductivity of the PCM loaded with metallic nanoinclusions as a function of the bulk thermal conductivity of the nanoinclusions suggested a series or parallel ordering, under aggregation in these systems.⁴⁷Figure S7a,b, in the Supporting Information, shows the bar charts comparing the thermal conductivity enhancements in the liquid state for the PCM loaded with carbon-based and metallic nanoinclusions, respectively. It can be seen from Figure S7a,b that the thermal conductivity enhancements were not significant in the liquid state, which was in agreement with the observations made from Figures 3 and S4.

Figure 5c,d shows the results of thermal cycling for the PCM loaded with 0.005 wt % CBNP and AgNWs, respectively. During thermal cycling, several thermal conductivity measurements were performed in the liquid state (at T = 25 °C, well above the freezing point), then the samples were frozen well below the phase transition temperature, and several thermal conductivity measurements were performed in the solid state (at T = 10 °C). In the case of pure PCM (without any nanoinclusions), the melting and freezing cycles were perfectly reversible (as can be seen from Figure 2d), whereas some deviations were observed for the PCM loaded with 0.005 wt % CBNP and AgNWs. In the case of PCM loaded with CBNP, thermal conductivity enhancements in the liquid state were ∼7.0, 6.0, 4.0, and 3.0% after first, second, third, and fourth cycles, respectively. On the other hand, thermal conductivity enhancements in the solid state were ∼117.4, 155.7, 150.0, and 148.6% after first, second, third, and fourth cycles, respectively. In the case of the PCM loaded with AgNWs, thermal conductivity enhancements in the liquid state were ∼5.0, 2.9, 2.9, and 2.9% after first, second, third, and fourth cycles, respectively. In the solid state, for the PCM loaded with AgNWs, thermal conductivity enhancements were ∼129.3, 141.4, 145.0, and 142.9% after first, second, third, and fourth cycles, respectively. It can be seen from Figure 5c,d that the variations in thermal conductivity enhancements, during thermal cycling, were negligible in the liquid state but significant in the solid state. This was attributed to the difference in aggregate sizes and aggregate numbers after subsequent melting/freezing cycles. The individual nanoinclusions form aggregates due to van der Waals interaction, and after subsequent thermal cycles, the aggregates do not redisperse reversibly.¹⁹ Phase contrast optical microscopy studies were carried out to ascertain the microstructural evolution after subsequent thermal cycles, and Figure 6a–d shows the optical phase contrast microscopy images for the PCM loaded with 0.005 wt % CBNP after first, second, third, and fourth cycles, respectively, in the liquid sate. The formation of micron-sized aggregates of CBNP (encircled in the figure for better visualization) after the second freezing cycle is clearly discernible from Figure 6b, which resulted in a larger thermal conductivity enhancement in the second cycle (as can be seen from Figure 5c). On the other hand, Figure 6c clearly shows that after the third thermal cycle, larger aggregates were formed with lower number density, which caused a slight decrease in thermal conductivity enhancement in the third thermal cycle (thermal conductivity enhancement ∼150.0% at the third cycle, against ∼155.7% after the second cycle). Figure 6d shows the phase contrast microscopy image after the fourth cycle, where lower number of aggregates were visible, as larger aggregates were prone to sedimentation, causing a further decrease in thermal conductivity enhancement in the fourth cycle, as can be seen from Figure 5c.

Figure 6.

Optical phase contrast microscopy images for the PCM loaded with 0.005 wt % CBNP after (a) first, (b) second, (c) third, and (d) fourth cycles in the liquid sate. The formation of micron-sized aggregates of CBNP are clearly discernible from the images. A few aggregates are encircled in the figures for easy identification.

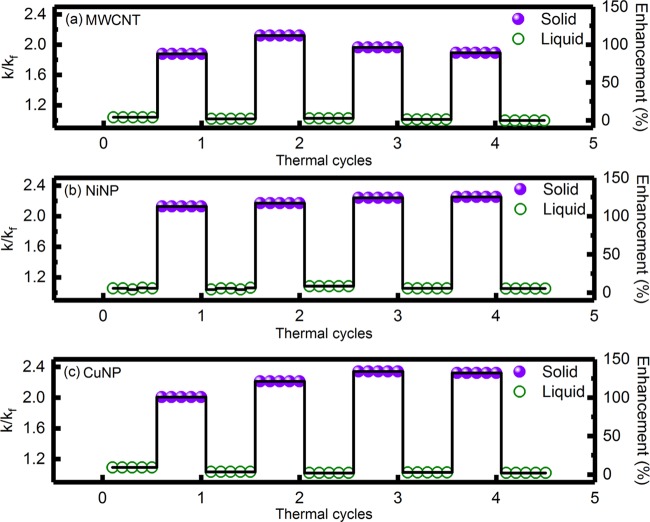
Figure 7a–c shows the results of thermal cycling for the PCM loaded with 0.005 wt % MWCNTs, NiNPs, and CuNPs, respectively. In the case of the PCM loaded with MWCNTs, thermal conductivity enhancements in the liquid state were ∼2.1, 2.9, 1.4, and 0.0% after first, second, third, and fourth cycles, respectively. On the other hand, thermal conductivity enhancements in the solid state were ∼87.9, 112.1, 96.4, and 89.3% after first, second, third, and fourth cycles, respectively. For the PCM loaded with NiNP nanoinclusions, thermal conductivity enhancements were ∼4.3, 8.6, 5.7, and 5.5% after first, second, third, and fourth cycles, respectively, in the liquid state and 112.9, 117.1, 124.3, and 125.2% after first, second, third, and fourth cycles, respectively, in the solid state. For CuNP nanoinclusion-loaded PCM, thermal conductivity enhancements in the liquid state were ∼3.6, 2.1, 2.9, and 2.1% after first, second, third, and fourth cycles, respectively. Thermal conductivity enhancements in the solid state were ∼100.7, 121.4, 134.3, and 132.1% after first, second, third, and fourth cycles, respectively. The variations in the thermal conductivity enhancements in the solid state during thermal cycling were attributed to the irreversible aggregation dynamics after subsequent melting/freezing cycles. A similar variation in thermal conductivity enhancements was reported for hexadecane-based PCM loaded with MWCNTs and graphite suspensions by Sun et al.,¹⁹ Zheng et al.,¹⁸ and Angayarkanni and Philip,¹⁷ where the variations were attributed to irreversible aggregation dynamics and weak solid–fluid interaction induced negative thermal conductivity enhancement for positive Kapitza lengths.

Figure 7.

Variation of k/k_f and percentage enhancement in thermal conductivity during thermal cycling of the PCM loaded with 0.005 wt % (a) MWCNT, (b) NiNP and (c) CuNP nanoinclusions.

Effect of Surface Functionalization on Thermal Conductivity Enhancement

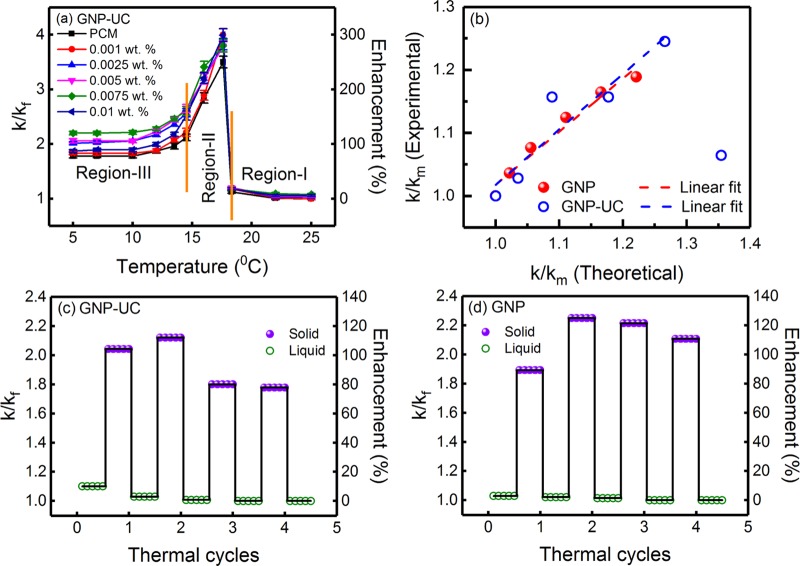
To study the effect of surface functionalization on thermal conductivity enhancement, experiments were performed using uncoated graphene nanoplatelet (GNP-UC)-loaded PCM. Figure 8a shows the variation of k/k_f and percentage enhancement in thermal conductivity as a function of temperature for the PCM loaded with five different concentrations (viz., 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt %) of GNP-UC. For comparison, thermal conductivity variation of the PCM (without any nanoinclusion) is also shown in Figure 8a. Table S10, in the Supporting Information, shows the experimental data for the variation of thermal conductivity and k/k_f as a function of temperature. It can be clearly seen from Figure 8a that the variation of k/k_f as a function of temperature can be divided into three regions, viz., region-I (liquid state, for T > 18.3 °C), region-II (phase transition region, 14.5 °C < T < 18.3 °C), and region-III (solid state, for T < 14.5 °C), which is in agreement with our earlier observations. Thermal conductivity enhancements in the liquid state (at T = 25 °C) were ∼0.0, 2.9, 4.3, 7.9, and 5.7% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % GNPs-UC. In the phase transition region, thermal conductivity enhancements were ∼300, 283, 279, 280, and 299% for loading concentrations of 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt %. On the other hand, thermal conductivity enhancements decreased in the solid state and became constant below 10 °C. Thermal conductivity enhancements in the solid state (at T = 10 °C) were ∼82.9, 105.7, 105.7, 121.4, and 89.3% for the PCM loaded with 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt % GNPs-UC. Table 1 shows the comparison of the k/k_f values as a function of loading concentration for the PCM loaded with GNPs and GNPs-UC in the liquid and solid states, where it can be seen that the variation of k/k_f in the liquid state is insignificant, whereas in the solid state, k/k_f was slightly higher for the PCM loaded with GNPs-UC. Nevertheless, at the highest concentration of 0.01 wt %, k/k_f, in the case of GNP-UC, was substantially lower, which was attributed to the intense agglomeration for the uncoated nanoinclusions.

Figure 8.

(a) Variation of k/k_f and percentage enhancement in thermal conductivity as a function of temperature for the PCM loaded with five different concentrations of uncoated GNPs (GNPs-UC). For comparison, thermal conductivity variation of the PCM, without any nanoinclusion, is also shown in the figure. The variation of k/k_f can be divided into three regions, viz., region-I (liquid state), region-II (phase transition), and region-III (solid state). (b) Variation of experimentally measured k/k_m as a function of theoretically calculated k/k_m values for the PCM loaded with various concentrations of oleic acid-functionalized GNPs and uncoated GNPs (GNPs-UC). Here, k_m indicates the thermal conductivity of the PCM, without any inclusions, in the solid state. The experimental and theoretical data were found to be linearly correlated, and the linear regression analyses are also shown in the figure. The errors associated with the theoretical values were less than ±5%. Variation of k/k_f and percentage enhancement in thermal conductivity during thermal cycling of the PCM loaded with 0.005 wt % (c) uncoated GNPs (GNPs-UC) and (d) oleic acid-functionalized GNPs.

Table 1. Comparison of k/k_f as a Function of Loading Concentration for the PCM Loaded with GNPs and GNPs-UC.

	GNP				GNP-UC
	liquid state (T = 25 °C)		solid state (T = 10 °C)		liquid state (T = 25 °C)		solid state (T = 10 °C)
loading (wt %)	k/kf	error	k/kf	error	k/kf	error	k/kf	error
0.001	1.01	0.02	1.84	0.03	1.00	0.02	1.83	0.03
0.0025	1.03	0.02	1.91	0.03	1.03	0.02	2.06	0.03
0.005	1.04	0.02	2.00	0.03	1.04	0.02	2.06	0.03
0.0075	1.06	0.02	2.07	0.03	1.08	0.02	2.21	0.04
0.01	1.07	0.02	2.11	0.03	1.06	0.02	1.89	0.04

The presence of an organic coating on the surface of the GNP increases the interfacial thermal resistance (Kapitza resistance) of the nanoinclusions, leading to a lower effective thermal transport efficiency due to phonon scattering at the nanoinclusion/coating/PCM interfaces, which is partially specular and partially diffusive depending on the local curvature and roughness of the interface.⁴⁸ This is more evident in the solid state, where the thermal transport is primarily through the percolating network of the aggregates, which resulted in comparatively lower thermal conductivity enhancements for the PCM loaded with oleic acid-functionalized graphene nanoplatelets (GNPs). Vales-Pinzon et al.⁴⁹ also reported an effective decrease in thermal conductivity of ethylene glycol-based nanofluid containing iron nanoparticles after surface capping with carbon. On the other hand, Li et al.⁵⁰ reported an increase in the thermal conductivity of the water-based SiO₂-coated graphene nanofluid, which was attributed to the increased hydrophilic interaction of silica-coated graphene, resulting in lower interfacial thermal resistance and larger stability in the aqueous medium. The significant influence of surface functionalization and the role of adsorbing moieties on thermal conductivity enhancement is studied in detail.^51,52

Effective thermal conductivity enhancements in the PCM loaded with GNPs and GNPs-UC were analyzed using the model proposed by Chu et al.⁵³Section S3, in the Supporting Information, describes the model and the calculations in detail. Theoretical values of k/k_m, in the case of PCM loaded with GNPs and GNPs-UC, were computed using this model, where the value of R_K (interfacial thermal resistance) was considered as 5 × 10^–8 m² K W^–1 for GNP-UC.⁵⁴ Here, k_m indicates the thermal conductivity of the PCM, without any inclusions, in the solid state. Figure 8b shows the variation of experimentally measured k/k_m as a function of theoretically calculated k/k_m values. It can be seen that the experimentally measured values were linearly correlated with the theoretical values and the data was fitted with linear regression analysis. The slope and adjusted R² for the linear regression analyses were ∼0.9 ± 0.2 and 0.85, respectively, indicating quantitative agreement between the experimental and theoretical values. It can be further seen from Figure 8b that the experimentally measured k/k_m for the highest loading concentration of 0.01 wt % was significantly lower than the theoretically calculated value, which was attributed to the sedimentation of the large unstable aggregates of GNPs-UC, which was also confirmed from the optical phase contrast microscopy images, as subsequently discussed.

On the other hand, due to the presence of oleic acid capping on the surface, the Kapitza resistance of the surface-functionalized GNP nanoinclusions was expected to be higher, and based on the thermal conductivity model for coated nanospheres,⁴⁹ the value was estimated as ∼8 × 10^–8 m² K W^–1 (Section S4, in the Supporting Information, describes the calculations in detail), which was then fitted into the model proposed by Chu et al.⁵³ to obtain the theoretical values of k/k_m for the oleic acid-coated GNP nanoinclusions. Figure 8b shows the variation of the experimentally measured k/k_m values as a function of theoretically calculated k/k_m values for the PCM loaded with oleic acid-functionalized GNPs, where it can be seen that the experimental and theoretical values were linearly correlated. The slope and adjusted R² of the linear regression analysis were ∼0.8 ± 0.1 and 0.96, respectively, which indicated quantitative agreement between the calculated and experimental values. It can be further seen from Figure 8b that the agreement between the experimental and theoretical values was superior in the case of the PCM loaded with oleic acid-functionalized GNPs as compared with the PCM containing uncoated nanoinclusions, which was attributed to the lower aggregation probability of the former.

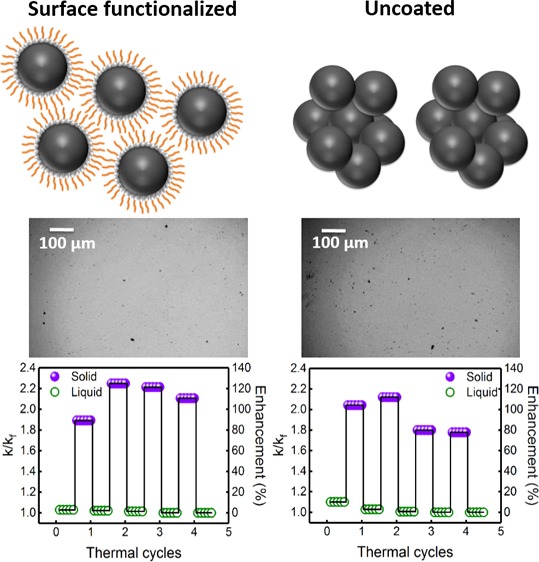
Figure 8c,d shows the results of the thermal cycling for the PCM loaded with 0.005 wt % GNPs-UC and surface-functionalized GNPs. In the case of PCM loaded with GNPs-UC, thermal conductivity enhancements in the liquid state were ∼2.9, 0.7, 0, and 0% after first, second, third, and fourth cycles, respectively. In the solid state, thermal conductivity enhancements were 104.3, 112.1, 80, and 77.9% after first, second, third, and fourth cycles, respectively. On the other hand, in the case of the PCM loaded with oleic acid-functionalized GNPs, thermal conductivity enhancements in the liquid state were ∼2.1, 1.4, 0, and 0% after first, second, third, and fourth cycles, whereas in the solid state, thermal conductivity enhancements were ∼89.3, 125.0, 121.4, and 110.7% after first, second, third, and fourth cycles, respectively. It can be seen from Figure 8c,d that the thermal conductivity enhancements decreased after repeated thermal cycling, which was attributed to the irreversible aggregation dynamics during subsequent melting and freezing cycles.¹⁹ For the PCM loaded with uncoated GNPs (GNPs-UC), due to intense aggregation during third and fourth thermal cycles, a significant decrease in thermal conductivity enhancement was seen. For increasing domain size in the case of larger aggregates, the acoustic mismatch model for long-wavelength phonons predicts a lowering of interfacial heat flux, leading to a reduced effective thermal conductivity.⁵⁵ Moreover, surface roughness increases with aggregate size, which leads to enhancement in interfacial scattering of high-frequency phonons (diffuse mismatch model), leading to an effective lowering of thermal conductivity for very large aggregates.⁵⁶

Optical phase contrast microscopy was carried out on the PCM loaded with GNPs and GNPs-UC to probe the microstructural evolution during thermal cycling. Figure 9a–h shows the phase contrast microscopy images for the PCM loaded with GNPs and GNPs-UC, respectively, in the liquid state, after first, second, third, and fourth thermal cycles. For the PCM loaded with GNPs, it can be clearly seen from Figure 9a–d that the size and number density of the aggregates increased during the second thermal cycle and that in the case of third and fourth cycles aggregate numbers were nearly constant. Nevertheless, the number density was the highest during second cycles and decreased during subsequent cycling due to slight agglomeration. This resulted in a small decrease in the thermal conductivity enhancement in the solid state for the PCM loaded with GNPs during third and fourth cycles, as shown in Figure 8d. On the other hand, it can be seen from Figure 9e–h that for the PCM loaded with GNPs-UC, intense agglomeration occurred during third and fourth thermal cycles, resulting in sedimentation of the larger aggregates, which were not visible in Figure 9h. This caused a large decrease in thermal conductivity for the PCM loaded with GNPs-UC during third and fourth thermal cycles, as can be seen from Figure 8c.

Figure 9.

(a–d) Optical phase contrast microscopy images of the PCM loaded with 0.005 wt % oleic acid-functionalized GNPs, in the liquid state, after first, second, third, and fourth thermal cycles, respectively. (e–h) Optical phase contrast microscopy images of the PCM loaded with 0.005 wt % uncoated GNPs (GNPs-UC), in the liquid state, after first, second, third, and fourth thermal cycles, respectively. A few aggregates are encircled in the figures for easy identification.

Our studies clearly show that the presence of a surfactant (oleic acid) capping on the surface of the GNP increased the stability of the nanoinclusions, resulting in good thermal stability under cycling, without significant reduction in thermal conductivity, which is beneficial for practical applications. The carboxylic acid group of oleic acid is bound to the surface of the nanoinclusions, whereas the aliphatic chain is extended into the nonpolar matrix of hexadecane (PCM), which reduced the aggregation probability of the coated nanoinclusions by providing additional steric stabilization.⁵⁷ Similarly, Zeng et al.⁵⁸ reported a superior stability of stearic acid-capped MoS₂ in cyclohexane, which was attributed to the extension of the long aliphatic chains of stearic acid in the organic medium. Moreover, it has been reported that for surfactant-capped nanoinclusions the thickness of the solvation monolayer is larger (determined by the chain length of the surfactant as compared to a few atomic distances in the case of uncoated nanoinclusions), which enhances the coupling of the nanoinclusions with the host matrix.⁵⁹ Xia et al.²⁴ also reported that surfactant capping increased the stability of the nanoinclusions. They also reported a slight reduction in thermal conductivity for surface-capped nanoinclusions, especially for surfactants with longer chain lengths, which was attributed to the increase in Kapitza resistance upon surface functionalization. These observations are in good agreement with the experimental findings obtained from the present study.

Infrared-Thermography-Based Studies on the PCM

Infrared-thermography (IRT)-based studies were carried out to map the surface temperature distribution of the PCM (with or without nanoinclusions) during freezing, and the results were compared with the cooling curve of deionized water. For IRT-based studies, the samples (initial temperature ∼29 °C, i.e., well above the phase transition temperature) were placed in a recirculating water bath maintained at T = 8 (±0.1) °C and the sample temperature was monitored as a function of time. Figure 10a–d shows the typical infrared images during cooling of water at t = 0, 500, 1000, and 1500 s, respectively. The pseudo-color-coded temperature scale is also shown along with the images. Figure 10e–h shows the typical infrared images during freezing of the PCM (without any nanoinclusions) at t = 0, 500, 1000, and 1500 s, respectively. The infrared images were emissivity-corrected to reflect the correct temperature of the sample. Figure 10 shows that the sample temperature decreased with time but the rate of temperature fall was lower in the case of PCM (see Figure 10b,f, for comparison). For quantitative analyses, a region of interest (ROI) was selected and the average temperature, as a function of time, was determined by spatial averaging over several pixel locations within the ROI. Caution was exercised to avoid the edge pixels within the ROI to minimize temperature fluctuations.

Figure 10.

(a–d) Typical infrared images during cooling of water at t = 0, 500, 1000, and 1500 s, respectively. (e–h) Typical infrared images during freezing of the PCM, without any nanoinclusions, at t = 0, 500, 1000, and 1500 s, respectively. The pseudo-color-coded temperature scale is also shown along with the images.

Figure 11 shows the variation of normalized temperature difference [(T – T₀)/T₀, where T₀ is the initial temperature] as a function of normalized time (t/t_m, where t_m is the maximum observation time = 2000 s) for water, PCM without any nanoinclusions, and PCM loaded with 0.0025 and 0.0075 wt % GNPs. Figure 11 shows that water temperature decreased exponentially with time and attained the surrounding temperature very rapidly, whereas the PCM (with and without nanoinclusions) underwent phase transition near the freezing point and hence the surrounding temperature was attained at a much longer time, as compared to that for water, which is beneficial for practical applications in thermal energy storage and management. The presence of humps (the regions of the temperature–time curves with negligible slope) in the normalized temperature decay curves indicated the phase transition regions for the PCM (with or without nanoinclusions). The slight variations in the freezing temperatures of the PCM, with or without nanoinclusions, were attributed to the convection losses from the top surface, which was kept exposed to the surrounding to ensure obstructed field of view for thermal mapping.

Figure 11.

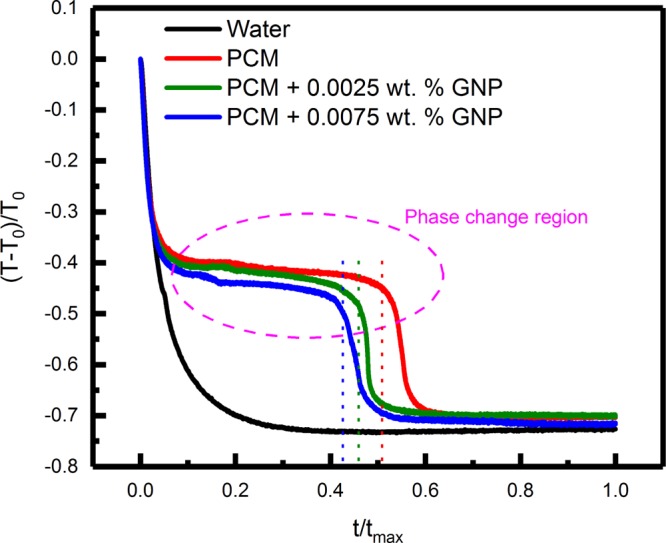
Variation of the normalized temperature difference [(T – T₀)/T₀, where T₀ is the initial temperature] as a function of normalized time (t/t_m, where t_m is the maximum observation time = 2000 s) for water, PCM without any nanoinclusions, and PCM loaded with 0.0025 and 0.0075 wt % GNP nanoinclusions. The presence of phase transition regions for the PCM (with or without nanoinclusions) is also indicated in the figure.

It can be further seen from Figure 11 that the freezing process was the fastest for the PCM loaded with 0.0075 wt % GNPs, followed by the PCM loaded with 0.0025 wt % GNPs and the PCM without any nanoinclusions, in the decreasing order. This was attributed to the higher thermal conductivity of the PCM loaded with GNPs. The freezing time was estimated as ∼1014 (±1), 921 (±1), and 846 (±1) s for the PCM without any nanoinclusions and PCM loaded with 0.0025 and 0.0075 wt % GNPs, respectively. For the PCM loaded with 0.0075 wt % GNPs, the gain in freezing time was ∼16.5%, which indicated a proportionate increase in the charging/discharging rate, which is immensely beneficial for practical applications of the nanoinclusion-loaded PCM for thermal energy storage.⁴ Faster freezing time was also reported by Harikrishnan et al.⁶⁰ for stearic acid-TiO₂-based PCM, where the gain in freezing time was ∼7.03% for 0.05 wt % TiO₂ loading. Sarı and Karaipekli⁶¹ reported ∼21.4% gain in freezing time for palmitic acid/expanded graphite-based PCM with loading concentration of 20 wt %. On the other hand, in the present study, a moderately high gain (∼16.5%) in freezing time was achieved for an extremely low concentration of nanoinclusion loading (0.0075 wt %), which is beneficial from cost factor point of view for practical applications.

Our results clearly show the efficacy of IRT-based studies to remotely map the surface temperature distribution of PCM during liquid–solid phase transition, where freezing time can be obtained in a noncontact way. Additional advantages of IRT-based temperature measurements include simultaneous measurement over a wide area, noncontact and noninvasive temperature mapping, real-time temperature acquisition, and pseudo-color-coded images for easy representation and data analyses.

Conclusions

We studied the thermal conductivity enhancement across the liquid–solid phase transition of hexadecane-based PCM, loaded with six different nanoinclusions, viz., CBNP, NiNP, CuNP, AgNW, MWCNT, and GNP. The phase transition temperature was determined from differential scanning calorimetry studies, and the refractive index of the PCM, in the liquid state, was found to increase with decreasing sample temperature due to an increase in density. After liquid–solid phase transition, the refractive index was found to decrease due to solidification-induced cracking of the pellets. The loading of nanoinclusions caused an enhancement in thermal conductivity of the PCM, which was more prominent in the solid state. The higher thermal conductivity in the solid state was attributed to the formation of a nanocrystalline phase on solidification, consisting of a needlelike microstructure, which was confirmed from optical phase contrast microscopy. In the solid state, the nanoinclusions were squeezed toward the intercrystallite grain boundaries, forming a quasi-2D network of percolating structures with high thermal transport efficiency due to the enhancement of phonon-mediated heat transfer and near-field radiative heat transfer along the thermal trajectories. For the PCM loaded with CBNP, CuNP, MWCNT, and GNP nanoinclusions, thermal conductivity enhancements increased with the concentration of the nanoinclusions due to the formation of larger-sized aggregates with improved conduction path. On the other hand, for the PCM loaded with NiNPs and AgNWs, thermal conductivity decreased at higher concentrations of the nanoinclusions due to the formation of larger aggregates, which were prone to sedimentation. Among the carbon-based nanoinclusions, the highest enhancement in thermal conductivity was obtained for the PCM loaded with CBNP nanoinclusions, which was attributed to the low fractal dimensions and volume-filling capacity of CBNP aggregates with efficient phonon coupling. In the case of metallic nanoinclusions, the highest thermal conductivity enhancement was obtained for the PCM loaded with AgNW nanoinclusions, which was attributed to the large aspect ratio of AgNWs. Our findings indicated that surface functionalization of the GNP nanoinclusions with oleic acid resulted in better thermal stability of the nanoinclusion-loaded PCM, without significant reduction in thermal conductivity, which is beneficial for practical applications. The carboxylic group of oleic acid was bound to the nanoinclusions, whereas the long aliphatic chain was extended into the nonpolar matrix of hexadecane (PCM), thereby providing additional steric stability that prevented the formation of large and unstable aggregates at a higher loading concentration or after repeated thermal cycling, which was also confirmed from optical phase contrast microscopy images. The increased interfacial thermal resistance for the surface-functionalized nanoinclusions was also studied theoretically, and the theoretical and experimental results were found to be in good agreement. Infrared-thermography-based experiments were carried out to monitor the sample temperature during phase transition in a noncontact way, and freezing time gain for the nanoinclusion-loaded PCM was quantified remotely using infrared thermography. Our study clearly shows the significant role of aggregation and volume-filling networks in thermal conductivity enhancement and thermal stability of nanoinclusion-loaded hexadecane. The findings from the present study will be beneficial for tailoring the properties of nanoinclusion-loaded hexadecane-based PCM for thermal energy storage and reversible thermal switching applications at room temperature.

Materials and Methods

Materials

In the present study, hexadecane (C₁₆H₃₄) was used as a phase change material (PCM). Hexadecane was purchased from Sigma-Aldrich (99% purity). Six different nanoinclusions were used in the present study, viz., carbon black nanopowder (CBNP), nickel nanoparticles (NiNPs), copper nanoparticles (CuNPs), silver nanowires (AgNWs), multiwalled carbon nanotubes (MWCNTs), and graphene nanoplatelets (GNPs). CBNP, AgNWs, and GNPs were obtained from Reinste, whereas NiNPs, CuNPs, and MWCNT were purchased from NanoAmor. The materials received from the suppliers were used without any further purifications.

Experimental Methods

Characterization of Nanoinclusions

Room temperature powder X-ray diffraction (XRD), small-angle X-ray scattering, and dynamic light scattering studies were carried out to measure the size distributions and stability of the nanoinclusions. Fourier transform infrared (FTIR) spectroscopy was carried out to ascertain possible interactions between the PCM and nanoinclusions. The solidification and melting temperatures and latent heat of fusion of the PCM were determined from differential scanning calorimetry (DSC) studies using Q200 (TA Instruments) in the temperature range of 0.1–80 °C with heating and cooling rates of 3 °C min^–1 under a nitrogen atmosphere. Variations of refractive index of the PCM as a function of temperature were measured using an automatic refractometer (J357 series, Rudolph Research Analytical). Section S5, in the Supporting Information, describes the characterization techniques in detail.

Preparation of Nanoinclusion-Loaded PCM

Before adding to the PCM (hexadecane), CBNP, NiNPs, AgNWs, and GNPs were surface-functionalized with oleic acid. An appropriate quantity of CBNP, NiNP, AgNW, and GNP was added in 2 mL of oleic acid, and the samples were sonicated for 20 min, followed by magnetic stirring for 40 min at a temperature of ∼70 °C for completion of the coating process. Thereafter, the samples were washed multiple times with acetone and centrifuged at 4000 rpm to remove the excess oleic acid. The surface-functionalized nanoinclusions were dispersed in the PCM using a horn sonicator (Sonics Vibra-Cell), operating at 30% power for 5 min.

CuNP and MWCNT nanoinclusions of various concentrations were directly dispersed in the PCM using the horn sonicator, operating at 30% power for 25 min. To compare the effect of surface functionalization on thermal conductivity enhancement and thermal stability after consecutive thermal cycling, experiments were also performed on the PCM loaded with uncoated (GNPs-UC) and coated graphene nanoplatelets (GNPs). GNPs-UC were directly dispersed in the PCM using the horn sonication technique. Five different concentrations of the nanoinclusions were used, viz., 0.001, 0.0025, 0.005, 0.0075, and 0.01 wt %.

Microscopic images of the PCM loaded with different nanoinclusions, in the liquid state, were acquired using an inverted phase contrast microscope (Carl Zeiss) equipped with a 10× objective.

Measurement of Thermal Conductivity Using a Transient Hot-Wire Probe

A transient hot-wire probe (KD2) was used for thermal conductivity measurement of the PCM (with or without nanoinclusions). In the transient hot-wire technique, thermal conductivity is quantified on the basis of heat dissipation from a linear heat source, where the temperature rise is expressed by the following equation⁸

8

Here T, T₀, q, k, t, γ, d_r, and α indicate time-dependent temperature, initial temperature, heat flux per unit length, thermal conductivity of the medium, time, Euler’s constant (=0.5772), radial distance from the probe, and thermal diffusivity of the medium, respectively. For distances close to the hot-wire probe, i.e., small values of d_r, the thermal conductivity of the medium is quantified from the slope of the variation of temperature rise (ΔT = T – T₀) curve, as a function of natural logarithm of time, which can be expressed by the following equation⁴

9

Here ΔT₁ and ΔT₂ indicate the temperature rise at times t₁ and t₂, respectively. Thermal conductivity measurements on the PCM at different temperatures were carried out by placing the sample holder along with the hot-wire probe in a recirculating water bath with precise temperature control (±0.1 °C). The sample assembly was thermally insulated using a custom-made arrangement, and thermal conductivity measurements were carried out in the steady state, after a time delay of ∼600 s, for ensuring temperature homogeneity. To ensure a proper contact between the hot-wire probe and the sample, the sample–probe assembly was also isolated from mechanical vibrations. Before proceeding with quantitative measurements, the KD2 probe was calibrated for three standard liquids, viz., water, kerosene, and ethylene glycol and the data was also validated using hot disk thermal constant analyzer (model: TPS-2500s, Sweden).⁸Section S6, in the Supporting Information, describes the standardization procedure in detail. All thermal conductivity measurements were repeated three times, and data is represented as mean ± standard deviation (n = 3). Standard deviations around the mean values were considered as the standard uncertainties in thermal conductivity values. The standard uncertainty in the thermal conductivity ratio (k/k_f) was calculated from the law of error propagation, i.e., u(k/k_f) = (k/k_f) × [(u(k)/k)² + (u(k_f)/k_f)²]^0.5. To probe the thermal stability of the nanoinclusion-loaded PCM, thermal cycling studies, for at least four cycles, were performed by successive solidification and melting of the PCM (with or without nanoinclusions).

Noncontact Temperature Measurement Using Infrared Thermography

Infrared thermography (IRT) is a noncontact temperature measurement methodology, where the infrared rays emitted from the surface of the object under investigation are detected using a suitable infrared detector and the object temperature is measured from the intensity of the infrared radiation using the following radiometric equation⁶²

10

Here M_cam is the radiance received by the infrared detector, which is housed inside a suitable infrared camera along with the appropriate electronics, optics, and cooling mechanisms. M_obj, M_env, and M_atm are the radiance emitted by the object under investigation, surrounding environment, and atmosphere, respectively. τ and ε indicate atmospheric transmittance and surface emissivity, respectively. For laboratory experiments, τ ∼ 1, and for real objects, ε < 1 (for a hypothetical perfect blackbody, ε = 1). Under these assumptions, eq 10 can be simplified as M_cam = εM_obj + (1 – ε)M_env. The radiance received by the infrared detector is converted into an electrical signal, and object temperature is obtained from suitable calibration curves. Detailed description and numerous applications of various IRT-based experimental techniques can be found elsewhere.^62,63Section S7, in the Supporting Information, describes the essential features of the infrared camera used in the present study.

For IRT-based experiments, the liquid samples (the initial temperature is higher than the phase transition temperature) were placed in a recirculating water bath, whose temperature was kept constant at 8.0 (±0.1) °C and the decay in sample temperature was monitored using the infrared camera, which was placed vertically above the sample surface to minimize the viewing angle errors. The camera-to-sample distance was maintained at 0.35 m. At a distance of 0.35 m, the horizontal and vertical spatial resolution was found to be ∼0.4 mm per pixel. In the present study, for recording infrared images, the reflected background temperature and atmospheric transmittance were considered as 28.45 °C and 1, respectively. The surface emissivity values were kept constant at 0.98 and 0.95 for water and hexadecane, respectively. The acquired infrared images were later analyzed using Altair software. Figure S8, in the Supporting Information, shows a typical schematic of the experimental setup, where the infrared camera, transient hot-wire probe (KD2 probe), sample, and recirculating water bath are clearly indicated.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b01084.

• Characterization results of the nanoinclusions, model for thermal conductivity enhancement of GNP nanoinclusions and effect of oleic acid coating, Kaptiza resistance for coated nanoinclusions, description of the characterization techniques, standardization of the transient hot-wire method, description of the infrared camera used in the present study, experimental data sets for refractive index and thermal conductivity measurements, additional graphs showing thermal conductivity enhancements, and schematic of the experimental setup (PDF)

Author Contributions

A.K.M. and B.B.L. performed the experiments and data analyses. J.P. supervised the project and provided guidance and comments. All authors contributed equally to the manuscript preparation.

The authors declare no competing financial interest.