Abstract
Knowledge-based design of extracting agents for selective binding of actinides is essential in stock-pile stewardship, environmental remediation, separations, and nuclear fuel disposal. Robust computational protocols are critical for in depth understanding of structural properties and to further advance the design of selective ligands. In particular, rapid radiochemical separations require predictive capabilities for binding in the gas phase. This study focuses on gas-phase binding preferences of cyclic imide dioximes to uranyl, neptunyl, plutonyl, and americyl. Structural properties, electron withdrawing effects, and their effects on binding preferences are studied with natural bond-order population analysis. The aromatic amidoximes are found to have a larger electron-donation effect than the aliphatic amidoximes. It is also found that plutonyl is more electron withdrawing than uranyl, neptunyl, and americyl when bound to the cyclic imide dioximes studied.
Introduction
All of the actinides are radioactive, with a broad range of half-lives. Selective ligand binding for separation of U, Np, Pu, and Am is critical in various applications for nuclear fuel disposal, reprocessing and stock-pile stewardship, and in environmental remediation.1−3 In particular, optimization of separations in nuclear fuel disposal and remediation is essential due to the large amount of radioactive material that is generated including rare earth elements, actinides, and light fission fragments.4−6 Industrial scale separations largely focus on utilizing the PUREX process to separate Pu from a mixture of U, Np, Am, and rare earth fission fragments.7 Although this process is efficient, it produces mixed organic radioactive waste as a product. Furthermore, PUREX is inherently not proliferation resistant, which makes the process less ideal for countries seeking to process their own fuels. Better understanding of extracting agents’ selectivity is needed for improved proliferation resistant fuel cycles. Moreover, selective binding to the uranyl cation for sequestering U from seawater as a possible source of uranium for power production has been heavily investigated, with emphasis on dioximes as extracting agents.8−12 These efforts continue to be explored as a possible synergistic operation with desalinization plants or by direct seawater “mining” with subsequent recovery of U.
Although traditional solvent extraction and ion-exchange techniques have been largely used for separations of lanthanides and actinides, gas-phase studies are critical for rapid radiochemical separations13−19 and efficient capabilities for the prediction of binding selectivity in the gas phase are essential to optimize and design separation agents. Calculations of differences in Gibbs free energy of reaction allow for the prediction of likelihood of binding selectivity and further possible separation selectivity, however, fundamental understanding of complexation preferences from structural characteristics and electron-withdrawing effects can be insightful for the design of targeted extracting agents. In particular, understanding binding preferences from electron-withdrawing effects and further structural changes can be essential to optimize rapid separations in the gas phase. Developing new protocols or improving current methodologies is critical to accelerate the optimization of separations of actinides. Computational knowledge-based design of separation agents for selective binding of actinides is particularly appealing due to its ability to screen various ligands for separation efficiency while reducing experimental trial and error, which is a limiting factor when working with radioactive elements.
Binding agents for uranium extraction have been extensively studied by Rao, Hay, and others.8,9,20−31 Previous studies have also investigated uranyl bound to cyclic imide dioximes, including computational predictions aiding experimental findings.9,20,24,26,31−35 Although there have been many studies in this area, the methods of choice have varied greatly among studies.
This study provides a systematic computational analysis focusing on the correlation between electron withdrawing effects predicted with natural bond orbital (NBO) analysis, structural characteristics, and possible implications in binding strength of uranyl, neptunyl, plutonyl, and americyl complexed with chelating amidoxime ligands [AnO2(HA)(NO3)(CH3OH) (Figure 1a), AnO2(HB)(NO3)(CH3OH) (Figure 1b), AnO2(HC)(NO3)(CH3OH) (Figure 1c), AnO2(HA)2 (Figure 1d), AnO2(HB)2 (Figure 1e), and AnO2(HC)2 (Figure 1f), with H2A = acenaphtho[1,2-c][1,2,5]thiadiazole 8,8-dioxide (Np-CAO-H2)U(O)2(NO3)(CH3OH), H2B = phthalimidedioxime, H2C = glutarimidedioxime, and An = U, Np, Pu, and Am.] The proposed compounds contain cyclic imide dioximes with the same backbone differing in the number and aromaticity character of the rings. Population analyses are calculated with NBO, as it was shown that the NBO population analyses of [An(NO3)]2+ structures were largely independent of the level of theory of choice.36 The same study indicated that Mulliken and Lowdin population analyses for the [An(NO3)]2+ compounds across the entire actinide series showed a large dependence on the level of theory of choice.36 The focus of this work is to provide relative characteristics among the compounds studied addressing structural properties and electron-withdrawing effects. The associated Gibbs free energies of reaction obtained with density functional theory (DFT) are reported as reference only, as other considerations, including multireference and spin–orbit relativity, would need to be addressed for accurate energetic predictions. A T1/D1 diagnostic in a study of [An(NO3)]2+ structures36 predict the T1 coefficients to be 0.023 for [U(NO3)]2+, 0.024 for [Np(NO3)]2+ and [Am(NO3)]2+, and 0.025 for [Pu(NO3)]2+, with D1 coefficients of 0.067 for [U(NO3)]2+ and [Np(NO3)]2+, 0.074 for [Pu(NO3)]2+, and 0.065 for [Am(NO3)]2+. However, no set limits have been established for T1/D1 diagnostics thresholds to establish multireference character of actinide compounds. UO2(HA)(NO3)(CH3OH) was synthesized by Jenkins and co-workers,37 UO2(HB)2, UO2(HC)2, and NpO2(HC)2a complexes were studied by Rao and co-workers.8,24,38
Figure 1.
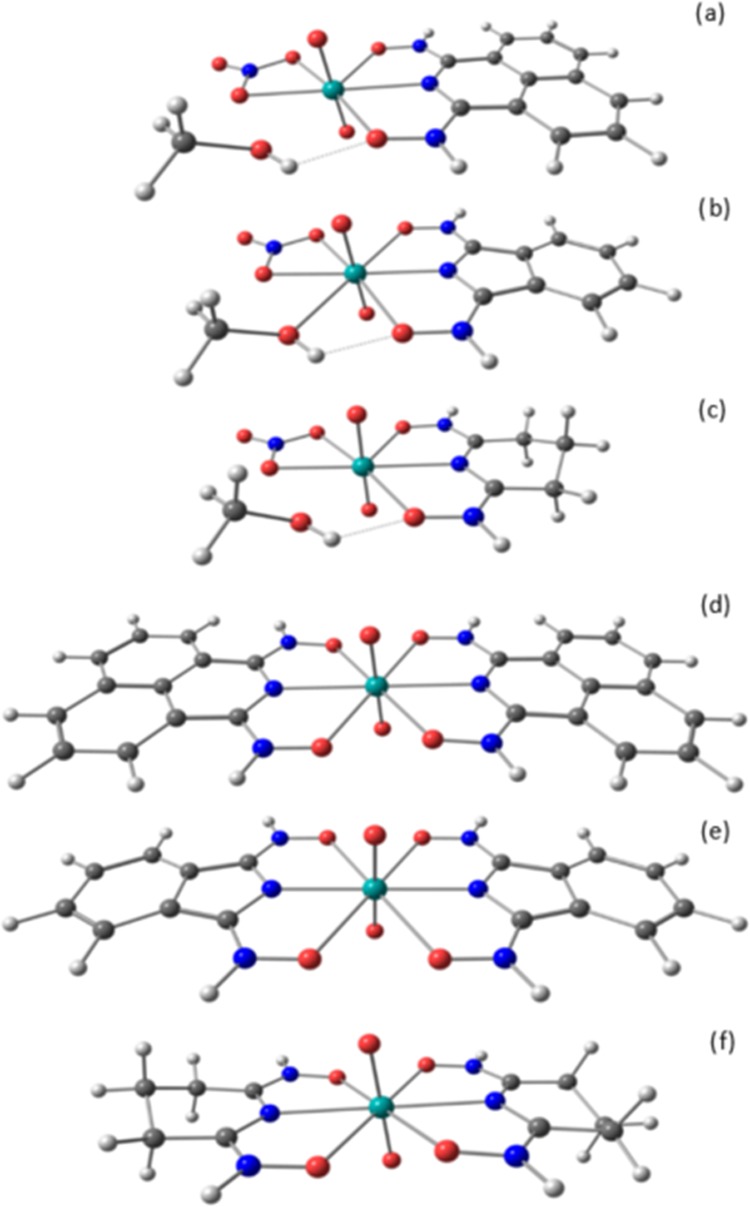
(a) AnO2(HA)(NO3)(CH3OH), (b) AnO2(HB)(NO3)(CH3OH), (c) AnO2(HC)(NO3)(CH3OH), (d) AnO2(HA)2, (e) AnO2(HB)2, (f) AnO2(HC)2. [Green = U, Np, Pu, and Am; red = oxygen; blue = nitrogen; gray = carbon; white = hydrogen.]
Results
Findings reported in this section correspond to calculations performed with the B3LYP functional. Properties studied with the strongly constrained and appropriately normed semilocal (SCAN) functional are included in the Supporting Information (SI).
Population Analysis
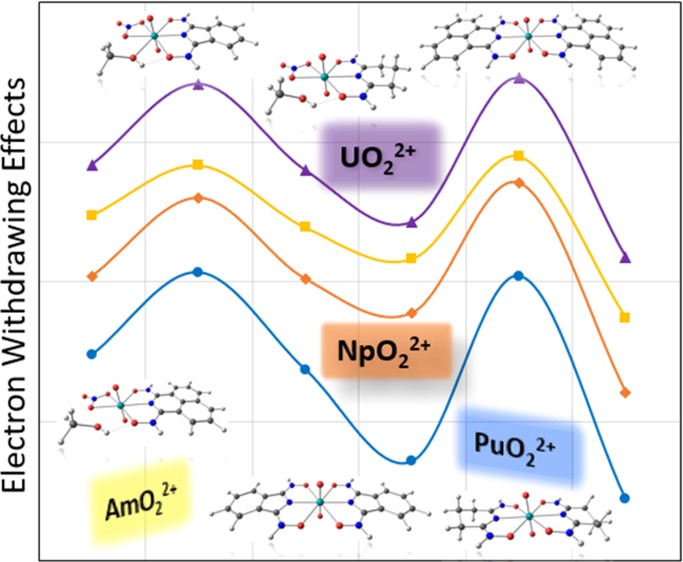
The partial charges predicted with NBO for the fragments in the compounds studied indicate plutonyl is more electron withdrawing than neptunyl, followed by americyl, and uranyl in the compounds studied (shown in Figure 2 and Table S.4 in the SI). Consequently, a larger electron donation from the ligand (for HX = HA, HB, and HC) backbone is observed for plutonyl than neptunyl and americyl, followed by uranyl, for all compounds proposed in this study. A higher electron donation is observed in the ligand backbone in AnO2(HX)2 compounds than in the AnO2(HX)(NO3)(CH3OH) counterpart (within 0.06 units). Additionally, the backbone from the HA ligand is more electron donating than in HB, which is also more electron donating than HC for the AnO2(HX)(NO3)(CH3OH) and AnO2(HX)2 compounds.
Figure 2.
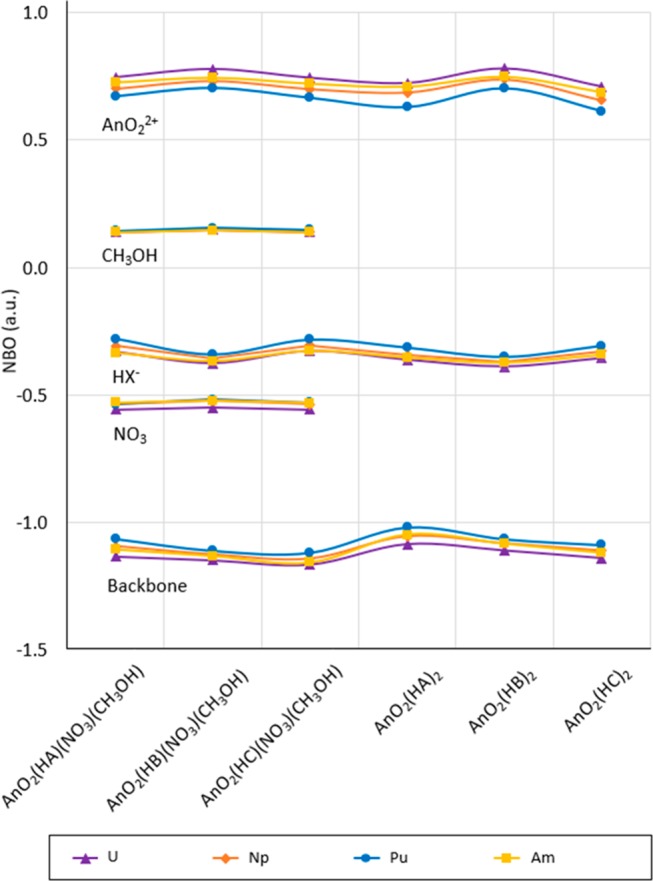
Partial charges predicted with NBO for the AnO22+, HX-, backbone (O3–N1–C1–N2–C2–N3–O4), NO3– and CH3OH fragments in AnO2(HX)(NO3)(CH3OH), AnO2(HX)2, with An = U, Np, Pu, and Am and HX = HA, HB, and HC.
The NO3– segment reveals a slightly lower electron donation in the uranyl compounds than the corresponding neptunyl, plutonyl, and americyl compounds, and it is found to be less electron donating than HX– in all AnO2(HX)(NO3)(CH3OH) compounds. Electronic density for the CH3OH segment seems independent of the HX character of the ligand. NBO populations calculated for the CH3OH segment show no significant difference in electron-withdrawing effects among the compounds studied. Figure 2 shows calculated NBO partial charges for AnO22+, backbone (O3–N1–C1–N2–C2–N3–O4),b NO3–, and CH3OH segments in all compounds. Identifying labels for atoms in the compounds studied are shown in Figure 3. All NBO values are included in Table S.4 in the Supporting Information (SI).
Figure 3.
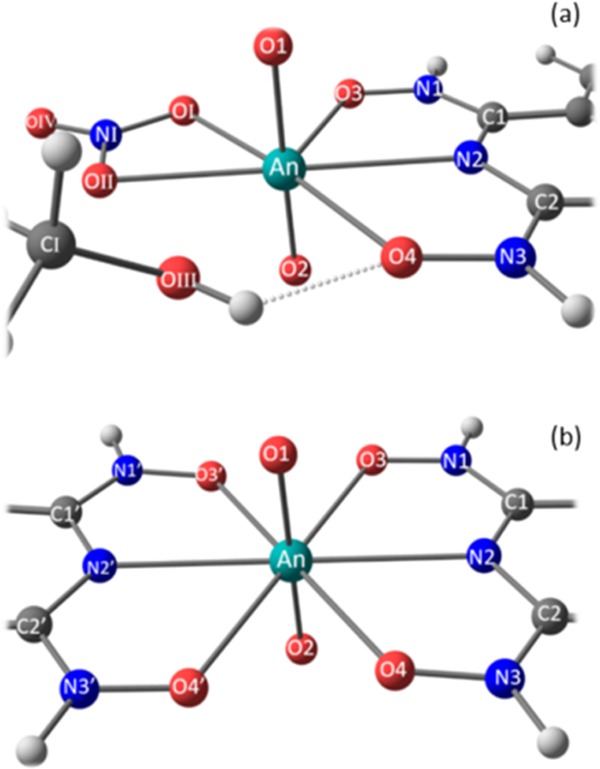
Reference atomic labels. (a) AnO2(HX)(NO3)(CH3OH), (b) AnO2(HX)2, with An = U, Pu, and X = A, B, C.
The natural electron configuration in the compounds studied reveals a 5f occupancy between 2.60 and 2.64 for U, between 3.84 and 3.88 for Np, between 4.96 and 5.01 for Pu, and between 6.09 and 6.12 for Am. The natural charge observed in the proposed compounds for U is between 1.60 and 1.67, between 1.35 and 1.41 for Np, between 1.19 and 1.26 for Pu, and 1.16 and 1.22 for Am. The natural 7s, 5f, 6d, and 7p electron configurations as well as the An charge for U, Np, Pu, and Am in AnO2(HX)(NO3)(CH3OH) and AnO2(HX)2 compounds are shown in Table 1.
Table 1. Natural Electron Configurations of U, Np, Pu, and Am in AnO2(HA)(NO3)(CH3OH) and AnO2(HX)2 Calculated with NBO.
| compound | 7s | 5f | 6d | 7p | An charge |
|---|---|---|---|---|---|
| UO2(HA)(NO3)(CH3OH) | 0.20 | 2.64 | 1.47 | 0.01 | 1.60 |
| UO2(HB)(NO3)(CH3OH) | 0.20 | 2.63 | 1.46 | 0.01 | 1.63 |
| UO2(HC)(NO3)(CH3OH) | 0.20 | 2.64 | 1.47 | 0.01 | 1.60 |
| UO2(HA)2 | 0.20 | 2.62 | 1.48 | 0.01 | 1.61 |
| UO2(HB)2 | 0.20 | 2.60 | 1.46 | 0.01 | 1.67 |
| UO2(HC)2 | 0.20 | 2.62 | 1.47 | 0.01 | 1.62 |
| NpO2(HA)(NO3)(CH3OH) | 0.20 | 3.88 | 1.46 | 0.01 | 1.35 |
| NpO2(HB)(NO3)(CH3OH) | 0.20 | 3.87 | 1.45 | 0.01 | 1.37 |
| NpO2(HC)(NO3)(CH3OH) | 0.20 | 3.88 | 1.45 | 0.01 | 1.35 |
| NpO2(HA)2 | 0.21 | 3.86 | 1.46 | 0.01 | 1.37 |
| NpO2(HB)2 | 0.21 | 3.84 | 1.44 | 0.01 | 1.41 |
| NpO2(HC)2 | 0.20 | 3.87 | 1.45 | 0.01 | 1.36 |
| PuO2(HA)(NO3)(CH3OH) | 0.21 | 5.01 | 1.46 | 0.01 | 1.19 |
| PuO2(HB)(NO3)(CH3OH) | 0.21 | 5.00 | 1.45 | 0.01 | 1.22 |
| PuO2(HC)(NO3)(CH3OH) | 0.21 | 5.01 | 1.46 | 0.01 | 1.19 |
| PuO2(HA)2 | 0.21 | 5.00 | 1.47 | 0.01 | 1.19 |
| PuO2(HB)2 | 0.21 | 4.96 | 1.45 | 0.01 | 1.26 |
| PuO2(HC)2 | 0.21 | 4.99 | 1.47 | 0.01 | 1.20 |
| AmO2(HA)(NO3)(CH3OH) | 0.21 | 6.12 | 1.40 | 0.01 | 1.16 |
| AmO2(HB)(NO3)(CH3OH) | 0.21 | 6.12 | 1.38 | 0.01 | 1.18 |
| AmO2(HC)(NO3)(CH3OH) | 0.21 | 6.12 | 1.39 | 0.01 | 1.17 |
| AmO2(HA)2 | 0.21 | 6.10 | 1.40 | 0.01 | 1.18 |
| AmO2(HB)2 | 0.21 | 6.09 | 1.38 | 0.01 | 1.22 |
| AmO2(HC)2 | 0.21 | 6.10 | 1.39 | 0.01 | 1.20 |
Structural Analysis
This study focuses on differences observed among the proposed complexes. For validation purposes, the differences between bond lengths reported for known crystal structures of UO2(HA)(NO3)(CH3OH)37 and UO2(HC)28 are calculated.
Table 2 shows differences between bond lengths obtained with X-ray crystallography and with computational predictions for U–O1, U–O3, U–O4, U–N2, and N3–O4 in UO2(HA)(NO3)(CH3OH) and UO2(HC)2. The U–O1 bond length in UO2(HA)(NO3)(CH3OH) is observed to be 0.004 Å shorter than in UO2(HC)2, and computational results predict this difference to be 0.006 Å. Similarly, the U–N2 bond length is observed to be 0.049 Å shorter in UO2(HA)(NO3)(CH3OH) than in UO2(HC)2, with a computational prediction of 0.041 Å. All bond lengths and differences obtained from crystal structures and computational predictions are reported in Table S.5 in the SI.
Table 2. Difference between Bond Lengths in UO2(HA)(NO3)(CH3OH)37 and UO2(HC)2,8 (in Å)a.
| experimental | calculated | difference | |
|---|---|---|---|
| U–O1 | –0.004 | –0.006 | –0.002 |
| U–O3 | –0.137 | –0.075 | 0.062 |
| U–O4 | –0.010 | –0.006 | 0.004 |
| U–N2 | –0.049 | –0.041 | 0.008 |
| N3–O4 | 0.009 | 0.007 | –0.002 |
Experimental = bond length in UO2(HA)(NO3)(CH3OH) – bond length in UO2(HC)2 (from X-ray data); calculated = bond length in UO2(HA)(NO3)(CH3OH) – bond length in UO2(HC)2 (from computational prediction); difference = calculated – experimental.
The An–O distance in the actinyl group is the same between An–O1 and An–O2 in all of the AnO2(HX)2 compounds. Differences between the An–O1 and An–O2 bond lengths in the AnO2(HX)(NO3)(CH3OH) compounds are within 0.001 and 0.005 Å. The An–O1 bond length is found to be longest for uranyl compounds, followed by neptunyl compounds, plutonyl compounds, and shortest in americyl compounds. On average, among the compounds tested, the U–O1 bond is 0.022 Å longer than Np–O1, 0.032 Å longer than Pu–O1, and 0.039 Å longer than Am–O1. The An–O bond length is longer in the AnO2(HX)2 configuration than in AnO2(HX)(NO3)(CH3OH). Differences between An–O1 among the compounds tested are shown in Tables 3 and 5.
Table 3. Difference in An–O1 Bond Length between AnO2(HX)(NO3)(CH3OH) and AnO2(HX)2 with HX = HA, HB, and HC; in Å.
| AnO2(HX)2–AnO2(HX)(NO3)(CH3OH) |
|||
|---|---|---|---|
| HA | HB | HC | |
| U | 0.004 | 0.002 | 0.005 |
| Np | 0.004 | 0.002 | 0.005 |
| Pu | 0.002 | 0.006 | 0.006 |
| Am | 0.003 | 0.002 | 0.005 |
Table 5. Difference in An–O1 Bond Length in AnO2(HX)(NO3)(CH3OH) and AnO2(HX)2 between U and Np Compounds [U–Np], Np and Pu Compounds [Np–Pu], and Pu and Am Compounds [Pu–Am]; in Å.
| U–Np | Np–Pu | Pu–Am | |
|---|---|---|---|
| AnO2(HA)(NO3)(CH3OH) | 0.022 | 0.008 | 0.009 |
| AnO2(HB)(NO3)(CH3OH) | 0.022 | 0.011 | 0.006 |
| AnO2(HC)(NO3)(CH3OH) | 0.022 | 0.012 | 0.005 |
| AnO2(HA)2 | 0.022 | 0.010 | 0.007 |
| AnO2(HB)2 | 0.022 | 0.006 | 0.011 |
| AnO2(HC)2 | 0.022 | 0.011 | 0.006 |
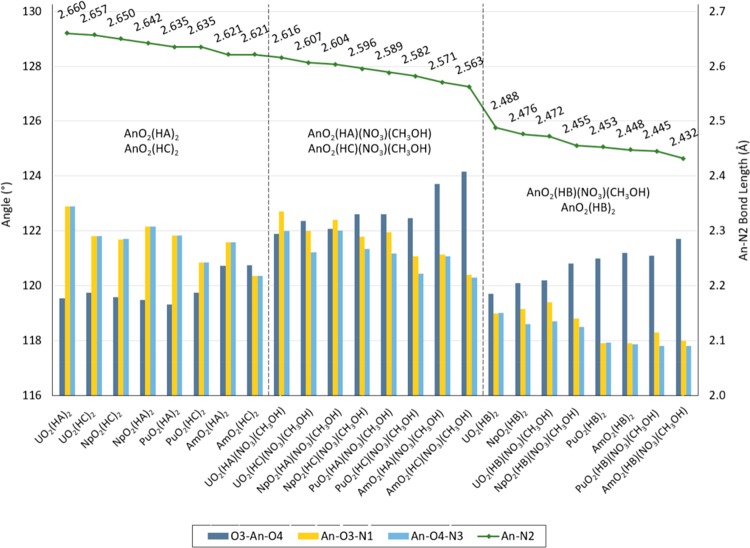
The An–N2 distance amongst the compounds studied is between 2.660 and 2.432 Å. The An–N2 bond length is between 2.660 and 2.482, 2.650 and 2.455, 2.635 and 2.445, and 2.621 and 2.432 Å for An = U, Np, Pu, and Am, respectively. Americyl compounds with the HB ligand present the shortest An–N2 bond length among the AmO2(HX)(NO3)(CH3OH) and AnO2(HX)2 compounds, with lengths of 2.432 and 2.448 Å, respectively. Similarly, the longest An–N2 bond length is observed for uranyl with the HA ligand, in both the UO2(HA)(NO3)(CH3OH) and UO2(HA)2 configurations, with 2.616 and 2.660 Å bond lengths, respectively. The An–N2 bond length for the AnO2(HA)2 and AnO2(HC)2 compounds is found to be between 2.660 and 2.621 Å, whereas this length for the AnO2(HA)(NO3)(CH3OH) and AnO2(HC)(NO3)(CH3OH) compounds is between 2.616 and 2.563 Å. A noticeable decrease of 0.075 Å in the An–N2 bond length is observed for the HB compounds, with respect to the HA and HC compounds. The An–N2 bond length for AnO2(HB)(NO3)(CH3OH) and AnO2(HB)2 is between 2.488 and 2.432 Å. Figure 4 shows the An–N2 bond length for all compounds. Overall, as shown in Figure 5, the U–N2 bond length is longer than Np–N2, which is longer than the Pu–N2, with the Am–N2 bond length being the shortest amongst the compounds studied [i.e., AnO2(HX)(NO3)(CH3OH) and AnO2(HX)2, with HX = HA, HB, and HC.]
Figure 4.
An–N2 bond length, O3–An–O4, An–O3–N1, and An–O4–N3 angles in AnO2(HX)(NO3)(CH3OH), AnO2(HX)2, with An = U, Np, Pu, and Am and HX = HA, HB, and HC.
Figure 5.
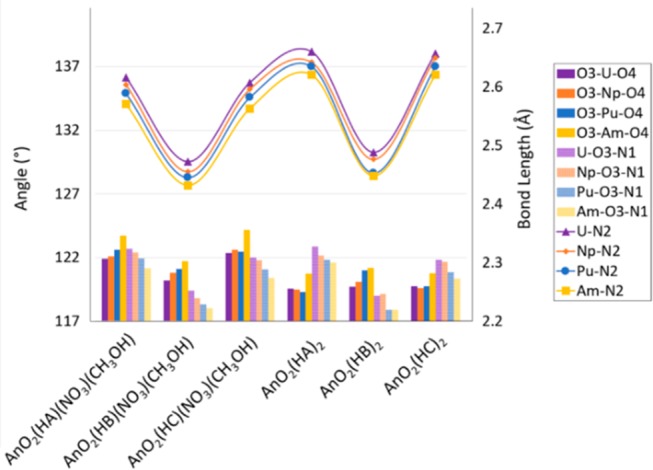
An–N2 bond length, O3–An–O4, and An–O3–N1 angle in AnO2(HX)(NO3)(CH3OH), AnO2(HX)2, with An = U, Np, Pu, and Am and HX = HA, HB, and HC.
As the An–N2 bond length decreases, the O3–An–O4 angle increases and the An–O3–N1 and An–O4–N3 angles decrease. Furthermore, the O3–An–O4 angle is predicted to be smallest for U compounds and largest for Am compounds. The An–O3–N1 angle is predicted to be largest for U compounds and smallest for Am compounds. It is important to notice that even though the An–N2 bond length decreases as the O3–An–O4 angle increases, a distinct break is observed between the compound with HA and HC ligands versus those with the HB ligand. Figures 4 and 5 show the predicted trends.
On average, the interatomic distances in the backbone (O3–N1–C1–N2–C2–N3–O4) are 1.328 Å for all compounds tested (with 1.309 and 1.352 Å being the shortest and longest distance, respectively). The H2A, H2B, and H2C compounds not bound to AnO22+ show average bond lengths of 1.418, 1.286, 1.384, 1.384, 1.286, and 1.418 Å for O3–N1, N1–C1, C1–N2, N2–C2, C2–N3, and N3–O4, respectively. Calculated bond lengths in the backbone are shown in Table S.6 in the SI. This bond length distribution of approximately 1.3 Å along the backbone of the HX ligands bound to AnO22+ while being a 1.4/1.2 Å in the unbound ligands is consistent to findings presented by Bernstein et al. for UO2(HA)(NO3)(CH3OH)c37 and Tian et al. for UO2(HC)2,d8 which suggests an O–N–C–N–C–N–O configuration advantageous for an electronic delocalization likely contributing to strong coordination to AnO22+.
Gibbs Free Energies of Reaction
The proposed compounds [AnO2(HX)(NO3)(CH3OH) and AnO2(HX)2 with An = U, Np, Pu, and Am and HX = HA, HB, and HC] are found to be most stable with plutonyl and least stable with americyl. As shown in Figure 6, all configurations studied present a lower Gibbs free energy of reaction for the complexation of plutonyl than for uranyl, neptunyl, and americyl for the reactions indicated in eqs 1a, 1b and 2a, 2b, with An(VI).
Figure 6.
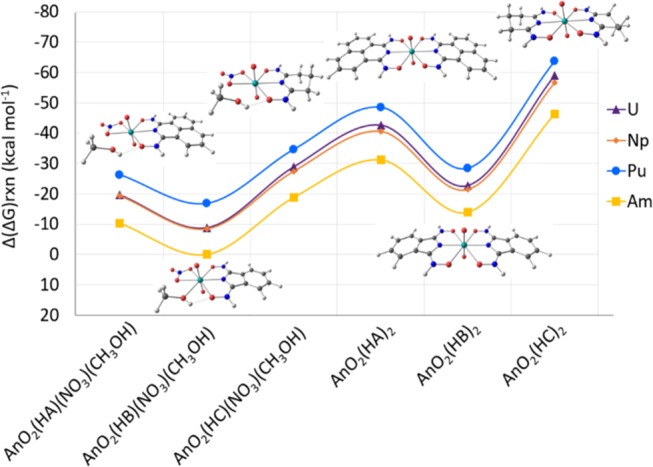
Calculated Δ(ΔG)rxn according to eqs 1a, 1b and 2a, 2b for AnO2(HX)(NO3)(CH3OH) and AnO2(HX)2, with An = U, Np, Pu, Am and HX = HA, HB, and HC. Results are relative to AmO2(HB)(NO3)(CH3OH) and shown in kcal mol–1. The continuous lines are shown as a visual aid and do not represent an interpolation. Y-axis oriented with increasing stability.
The Gibbs free energy of reaction for the plutonyl compounds is between 8.07 and 4.60 kcal mol–1 lower than for the corresponding uranyl compounds. Similarly, the neptunyl compounds show a difference in Gibbs free energy of reaction between 10.41 and 7.52 kcal mol–1 lower than for the corresponding americyl compounds. A smaller difference is observed between uranyl and neptunyl compounds, where the uranyl compounds present a Gibbs free energy of reaction between 2.40 and 0.21 kcal mol–1 lower than the corresponding neptunyl compounds. Differences in Gibbs free energy of reaction for all compounds are included in Table S.7 in the SI.
Overall, the AnO2(HX)2 compounds have a lower Gibbs free energy of reaction than their respective AnO2(HX)(NO3)(CH3OH) compounds (for HX = HA, HB, and HC). The UO2(HX)2 compounds present Gibbs free energies of 23.05, 13.94, and 30.17 kcal mol–1 lower than the equivalent UO2(HX)(NO3)(CH3OH) compounds, for HA, HB, HC, respectively. Similarly, the NpO2(HX)2 compounds present Gibbs free energies of 21.18, 12.93, and 29.19 kcal mol–1 lower than the equivalent NpO2(HX)(NO3)(CH3OH) compounds, with HX = HA, HB, and HC, respectively. The PuO2(HX)2 compounds show Gibbs free energies of 22.23, 11.55, and 29.05 kcal mol–1 lower than the equivalent PuO2(HX)(NO3)(CH3OH) compounds for HX = HA, HB, and HC, respectively. Finally, the Gibbs free energies of formation of the AmO2(HX)2 compounds are 20.84, 13.90, and 27.44 kcal mol–1 lower than for the AmO2(HX)(NO3)(CH3OH) compounds, for HX = HA, HB, and HC, respectively.
The largest difference between contiguous actinides is calculated to be between Pu and Am, followed by Np and Pu, with the smallest difference between U and Np in both AnO2(HX)2 and AnO2(HX)(NO3)(CH3OH) configurations (shown in Figure 7). The difference in Gibbs free energy of reaction between contiguous actinides is between 0.21 and 17.35 kcal mol–1 for AnO2(HA)(NO3)(CH3OH) and AnO2(HA)2, between 0.23 and 16.80 for AnO2(HB)(NO3)(CH3OH) and AnO2(HB)2, and between 1.43 and 17.42 for AnO2(HC)(NO3)(CH3OH) and AnO2(HC)2 (Tables 4 and 6).
Figure 7.
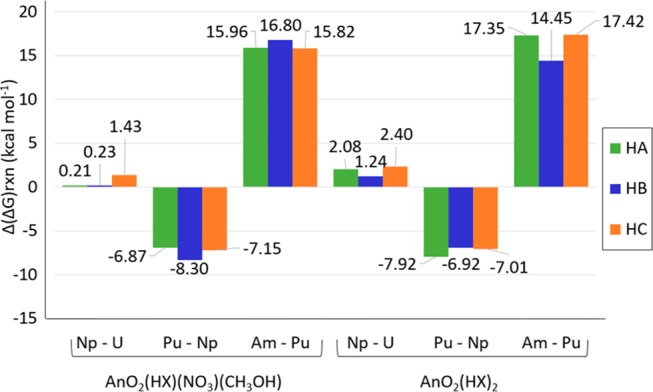
Δ(ΔG)rxn predicted for AnO2(HX)(NO3)(CH3OH) and AnO2(HX)2 [with HX = HA (green), HB (blue), and HC (orange)] between contiguous actinides [between U and Np indicated as “Np–U”; between Np and Pu indicated as “Pu–Np”; and between Pu and Am indicated as “Am–Np”], in kcal mol–1.
Table 4. Δ(ΔG)rxn for Uranyl Compounds Normalized to UO2(HB)(NO3)(CH3OH) Calculated with DFT (B3LYP) and MP2, in kcal mol–1a.
| compound | DFT | MP2 | DFT – MP2 |
|---|---|---|---|
| UO2(HA)(NO3)(CH3OH) | –10.86 | –9.45 | –1.41 |
| UO2(HC)(NO3)(CH3OH) | –20.11 | –20.77 | 0.66 |
| UO2(HA)2 | –33.91 | –32.48 | –1.43 |
| UO2(HB)2 | –13.94 | –14.07 | 0.13 |
| UO2(HC)2 | –50.28 | –51.86 | 1.57 |
DFT – MP2 = Δ(ΔG)rxn calculated with DFT – Δ(ΔG)rxn calculated with MP2.
Table 6. Δ(ΔG)rxn for Plutonyl Compounds Normalized to PuO2(HB)(NO3)(CH3OH) Calculated with DFT and MP2, in kcal mol–1a.
| compound | DFT | MP2 | DFT – MP2 |
|---|---|---|---|
| PuO2(HA)(NO3)(CH3OH) | –9.45 | –7.85 | –1.60 |
| PuO2(HC)(NO3)(CH3OH) | –17.77 | –17.96 | 0.19 |
| PuO2(HB)2 | –11.55 | –12.36 | 0.81 |
| PuO2(HC)2 | –46.82 | –47.08 | 0.26 |
DFT – MP2 = Δ(ΔG)rxn calculated with DFT – Δ(ΔG)rxn calculated with MP2.
To evaluate possible differences in energetics due to the computational methodology of choice, Gibbs free energies of reaction for the uranyl and plutonyl compounds are calculated with DFT and MP2 and relative to AnO2(HB)(NO3)(CH3OH) to show relative Gibbs free energies with respect to the least stable compound amongst the uranyl and plutonyl compounds tested. Overall, it is observed that the differences in relative Gibbs free energies of formation predicted with DFT are between 0.13 and 1.60 kcal mol–1 from those predicted with MP2. UO2(HA)(NO3)(CH3OH) shows a ΔGrxn 10.86 and 9.45 kcal mol–1 lower than UO2(HB)(NO3)(CH3OH) when calculated with DFT and MP2, respectively. Similarly, UO2(HC)(NO3)(CH3OH) presents a ΔGrxn 20.11 and 20.77 kcal mol–1 lower than UO2(HB)(NO3)(CH3OH), when calculated with DFT and MP2, respectively. The ΔGrxn of UO2(HA)2 are 33.91 and 32.48 kcal mol–1 lower than UO2(HB)(NO3)(CH3OH) calculated with DFT and MP2, respectively. UO2(HB)2 gives ΔGrxn 13.94 and 14.07 kcal mol–1 lower than UO2(HB)(NO3)(CH3OH) with DFT and MP2, respectively. Finally, the ΔGrxn of UO2(HC)2 are 50.28 and 51.86 kcal mol–1 lower than UO2(HB)(NO3)(CH3OH) calculated with DFT and MP2, respectively. Differences in predicted Gibbs free energies of reaction calculated with DFT and MP2 are shown in Tables 4 and 6.
Sun et al. studied similar compounds with a single HA and HB ligand and two water molecules bound to uranyl and predicted the AnO2(HC)(OH2)2e compound to be more stable than AnO2(HB)(OH2)2.24 Ansari et al. found that NpO2(HC)2f was weaker than UO2(HC)2.38 Both findings are consistent to our predicted results.
Discussion
Overall, it is observed that the An–N2 bond length in compounds with the HB ligand is shorter than with HA and HC. Moreover, no distinct difference in An–N2 bond length is observed in the compounds with the HA ligand with respect to those with the HC ligand, which correlates to the compounds with the HB ligand having a lower Gibbs free energy of reaction than the compounds with HA and HC ligands. This trend is observed for both the AnO2(HX)(NO3)(CH3OH) and AnO2(HX)2 configurations. Furthermore, the HB ligand shows a higher electron-withdrawing effect than HA and HC. In summary, an increase in An–N2 bond length and an increase in electron donation from the dioxime ligands correlates to stronger complexation of the actinyls with the HA and HC ligands than with the HB ligand. All three atoms (O3, O4, and N2) contribute to the binding energy. Therefore, if the nitrogen is closer to the actinide, as seen for HB, this causes the oxygen atoms to be in less favorable angles, which may disrupt their binding to the actinide effectively causing the total ligand binding energy to be lower.
Uranyl, neptunyl, plutonyl, and americyl present a stronger binding in the AnO2(HC)2 configuration, followed by AnO2(HA)2, AnO2(HC)(NO3)(CH3OH), AnO2(HB)2, AnO2(HA)(NO3)(CH3OH), and the weakest binding in the AnO2(HB)(NO3)(CH3OH) configuration. This result is in parallel with the calculated electron-donating effects of the ligand with HC– and HA– to be the most electron-donating ligands, followed by HB– being the least electron donating. Not surprisingly, the electron-donating effects from NO3– were less than those of HX–, which is in line with the result that the AnO2(HX)(NO3)(CH3OH) compounds are less stable than the corresponding UO2(HA)2 compounds.
Calculated Gibbs free energies of reaction for AnO2(HX)(NO3)(CH3OH) and AnO2(HX)2, with An = U, Np, Pu, and Am and HX = HA, HB, and HC following the proposed formation reaction indicated in eqs 1a, 1b and 2a, 2b show that the most stable compounds are found when complexing Pu(VI), least stable when complexing Am(VI), and present similar stability for U(VI) with respect to Np(VI). Overall, all of the configurations studied show a stronger binding to plutonyl, followed by uranyl and neptunyl, and with americyl having the weakest binding. None of the configurations presented would be efficient at separating uranyl from neptunyl in an environment as proposed in eqs 1a, 1b and 2a, 2b.
In conclusion, the compounds with aliphatic amidoximes form more stable complexes than the aromatic amidoximes. The An–N2 bond length increases as the binding strength increases. The HA and HC ligands show a larger electron donation than the HB ligands, and all ligands are more electron donating than NO3–, supporting the finding that the AnO2(HX)2 compounds have a stronger binding between the ligands and the actinyl cation than the corresponding AnO2(HX)(NO3)(CH3OH) compounds.
Additionally, the plutonyl cation is the most electron-withdrawing actinyl within the compounds studied, while presenting the strongest binding. Moreover, the improved conjugation through the five-membered ring containing the nitrogen in HB as opposed to the six-membered ring in HA is likely a significant factor to be considered in ligand design, as the double bond on the back of the five-membered ring contributes to the aromatic stabilization as an anion. This effect is seen for all other five-membered heterocycles (such as imidazole or triazole) when they are anionic. Consequently, we would suggest that for designing future ligands a six-membered backbone is preferred to five-membered example since this “decouples” the conjugation from the backbone of the ligand.
Methods
Structural properties and Gibbs free energies of reaction are calculated in the gas phase for the uranyl, neptunyl, plutonyl and americyl cations complexed with acenaphtho[1,2-c][1,2,5]thiadiazole 8,8-dioxide (Np-CAO-H2)U(O)2(NO3)(CH3OH) (H2A), phthalimidedioxime (H2B), and glutarimidedioxime (H2C). Two motifs are proposed, AnO2(HX)(NO3)(CH3OH) and AnO2(HX)2, where HX represents the singly deprotonated ligand (with X = A, B, and C corresponding to H2A, H2B, and H2C) and An includes U, Np, Pu, and Am. The proposed structures are shown in Figure 1.
The reactions studied for the formation of the proposed compounds are shown in eqs 1a and 1b.
| 1a |
| 1b |
The Gibbs free energy of reaction for eqs 1a, 1b and 2a, 2b is calculated as indicated in eqs 2a and 2b, respectively.
| 2a |
| 2b |
The differences in Gibbs free energy of reaction [Δ(ΔG)rxn] values shown are relative to those corresponding to AmO2(HB)(NO3)(CH3OH) and are calculated as indicated in eqs 3a and 3b, with An = U, Np, and Pu and HX = HA, HB, and HC.
| 3a |
| 3b |
The protocol followed in this study begins with geometry optimizations obtained with density functional theory (DFT), using the B3LYP39 functional, the Stuttgart RSC 1997 ECP and associated basis set for U, Np, Pu, and Am, and the 6-311++G** basis set for O, N, C, and H, with tight tolerances and extra fine grid. The ECP on the actinide atom accounts for scalar relativistic effects by replacing 60 electrons with a relativistic pseudopotential. The molecules were optimized without imposing symmetry constraints explicitly to avoid enforcing a preconceived symmetry onto the systems studied. Therefore, the initial orbitals utilized in the optimization would not have been exactly degenerate as the starting point did not have high symmetry. Thermochemical corrections are calculated at 298.15 K. Gibbs free energies of reaction are calculated on structures optimized with DFT. MP2 calculations are single point energy calculations utilizing the thermochemical corrections obtained with DFT. The correlation space considered in the MP2 calculations included all electrons and orbitals that are not included in the ECP.
Following the geometry optimizations, NBO analysis is included in the protocol to establish orbital occupancies and electron-withdrawing and -donation effects and partial charges of the fragments in the compounds studied. Structural characteristics are then correlated to electron-withdrawing and -donation effects to provide information of the selectivity preferences and compounds’ stability from a structural perspective. Finally, the protocol includes the calculation of Gibbs free energies of reaction as a complement to binding preferences predicted from structural and electronic effects.
Utilizing the B3LYP functional, the Stuttgart RSC 1997 ECP and basis set for U and the 6-311++G** basis set for the non-U atoms is commonly accepted to provide accurate geometries for uranyl compounds.40−50 A previous study of [An(NO3)]2+ structures established that utilizing the 6-31G*, cc-pVDZ, 6-311++G**, cc-pVTZ, and cc-pVQZ basis set for non-An atoms, the Stuttgart RSC 1997 ECP and associated basis set for the actinides include all of the basis functions in the basis set, while changing the functional (LDA, TPSS, B3LYP, PBE0, and B972) predicted structures with an An–O distance of less than 0.03 Å and an O–An–O angle difference of less than 1°.36 In the current study, the strongly constrained and appropriately normed semilocal (SCAN)51 density functional is also included as it had not yet been tested for actinides. The SCAN functional is utilized to analyze structural characteristics, population analysis, and differences in predicted Gibbs free energies of reaction of the uranyl compounds with relative to those predicted with B3LYP.
All DFT geometry optimizations and vibrational frequencies calculations are obtained with the NWChem 6.5 and 6.6 package (for B3LYP only studies).52 The NBO53 population analysis is obtained with the natural bond orbital 6.0 (NBO6) program.54 Molpro201555 is used for MP2 calculations. The uranyl structures for the B3LYP and SCAN comparison are obtained with NWChem 6.8.52 NWChem calculations used default convergence criteria of 10–7 for energy and 10–5 for density. Basis sets are obtained from the Environmental Molecular Sciences Laboratory (EMSL) database.56,57
Vibrational frequency calculations reveal some complex frequencies (with magnitude no larger than 77 cm–1). Visualization of the vibrational modes reveals that none of the complex frequency modes represents significant modes likely to affect the structural characteristics discussed in this study, as complex frequencies stem from in-and-out of plane bending modes of the molecular structure, which do not affect the bond lengths and angles discussed in this study. From the vibrational modes in each compound [108, 90, 87, 153, 117, and 111 for AnO2(HA)(NO3)(CH3OH), AnO2(HB)(NO3)(CH3OH), AnO2(HC)(NO3)(CH3OH), AnO2(HA)2, AnO2(HB)2, and AnO2(HC)2, respectively], no more than two complex modes were found per compound. The zero-point energy (ZPE) contribution is less than 0.02% of the Gibbs free energy of the compound, which indicates that there is a small contribution to the 0 K zero-point vibrational correction and that omitting these modes from the vibrational analysis the thermal correction to the energy would be slightly underestimated. Moreover, the entropy contribution is less than 0.0002% of the Gibbs free energy of the compounds. Consequently, it can be established that the effect of the complex modes onto the analysis provided in this manuscript is inconsequential. The effect of numerical error increases from finite differences, which explains that the larger compounds having larger magnitudes of complex frequencies than the smaller compounds. The magnitude of all complex frequencies for all compounds is included in Table S.1 in the SI. The ZPE and entropy contribution to the Gibbs free energy for all compounds are shown in Tables S.2 and S.3, respectively, in the SI.
The maximum spin contaminations from the unrestricted DFT wavefunction are 0.00, 0.01, 0.13, 0.17 for the U, Np, Pu, and Am compounds, respectively. Restricted and unrestricted DFT calculations for the UO2(HA)(NO3)(CH3OH) compound give a difference of 5.3 × 10–4 kcal mol–1 in total energy, 0.797 kcal mol–1 in ZPE, 0.067 kcal mol–1 for the thermal correction to the enthalpy, and 1.30 × 10–5 kcal mol–1 for the entropy. The MP2 calculations are obtained with a restricted open shell.
Conclusions
Effective calculations can accelerate the design of efficient extracting agents for actinide separations, which is critical for multiple industrial processes. Predictive capabilities, including analysis of structural characteristics with electron-donation and -withdrawing effects, are a useful aid to predict binding selectivity. We have studied a series of ligands and actinides that are relevant for separations based on previous experimental studies. Variations in predicted characteristics obtained when altering the functional of choice suggest that researchers can apply the protocol used in this study to predict binding preferences through analysis of structural characteristics affected by electron-withdrawing effects, however, cautious conclusions must be made from calculations of Gibbs free energies of reaction. Future work includes studying higher levels of theory and multireference character, relativistic effects, and effects of solvation on the structures in this study for future application in liquid separations.
Acknowledgments
The authors gratefully acknowledge Dr. Robert J. Hinde for guidance and useful discussions. This work was supported in part by the National Nuclear Security Administration (grant DOE-NNSA-DE-NA0001983) under the Stewardship Science Academic Alliance Program (D.A.P., J.D.A., H.L.H.). The views expressed here are those of the authors and do not necessarily reflect those of NNSA. This work was also supported by the National Science Foundation grant ACI-0904972 (D.A.P., R.J.H.), grant ACI-1450300 (R.J.H.), and grant CHE-1709881 (J.P.C.). This work was also supported by the Y-12 National Security Complex project PD15N610 (D.M.J., J.P.C., J.A.B.). R.J.H. acknowledges support from the NWChem-Ex Exascale Computing Project from the U.S. Department of Energy (DOE) at Brookhaven National Laboratory under Contract No. DE-SC0012704. This material is based upon work performed using computational resources supported by the University of Tennessee and Oak Ridge National Laboratory Joint Institute for Computational Sciences (http://www.jics.tennessee.edu). Results in this paper were obtained using the high-performance Handy computing system at the Institute for Advanced Computational Science at Stony Brook University. Computational resources were provided by UNT’s High Performance Computing Services, a division of the University Information Technology with additional support from UNT Office of Research and Economic Development. This work used the Extreme Science and Engineering Discovery Environment (XSEDE),58 which is supported by National Science Foundation grant number ACI-1548562. This research used resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357. This research also used resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Partial results were previously reported and are copyrighted by the University of Tennessee.59
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b02068.
Partial charges, structural characteristics, contribution to thermochemical calculations, and magnitudes of complex vibrational frequencies corresponding to the structures (PDF)
The authors declare no competing financial interest.
Footnotes
Note that NpO2(HC)2 in this study was considered Np(V).
The backbone (O3–N1–C1–N2–C2–N3–O4) and backbone′ (O3′–N1′–C1′–N2′–C2′–N3′–O4′) showed the same NBO population analysis.
UO2(HA)(NO3)(CH3OH) is the nomenclature used in this study. Bernstein et al.37 refer to this compound as (Np-CAO-H2)U(O)2(NO3)(CH3OH).
UO2(HC)2 is the nomenclature utilized in this study. Tian et al.8 refer to this compound as UO2(HA)2·H2O.
The nomenclatures used by Sun et al. are UO2(IL)(OH2)21+ and UO2(IIL)(OH2)21+.24 For naming consistency throughout this paper, we renamed these structures to AnO2(HC)(OH2)2 and AnO(HB)(OH2)2, respectively.
Ansari et al. utilized the HA as the nomenclature for the ligand. For consistency throughout this paper, these compounds are instead referred to as UO2(HC)2 and NpO2(HC)2.
Supplementary Material
References
- Grenthe I.; Drozdzynski J.; Fujino T.; Buck E. C.; Albrecht-Schmitt T. E.; Wolf S. F.. Uranium. In The Chemistry of the Actinides and Transactinide Elements; Springer: Netherlands, 2011; pp 253–698. [Google Scholar]
- Runde W. H.; Schulz W. W.. Americium. In The Chemistry of the Actinide and Transactinide Elements; Springer: Netherlands, 2011; pp 1265–1395. [Google Scholar]
- Choppin G.; Ekberg C.; Liljenzin J.-O.; Rydberg J.. Origin of Nuclear Science. In Radiochemistry and Nuclear Chemistry; Elsevier Science & Technology: Oxford, U.K., 2013; pp 1–14. [Google Scholar]
- Romanchuk A. Y.; Kalmykov S. N.; Kersting A. B.; Zavarin M. Behaviour of Plutonium in the Environment. Russ. Chem. Rev. 2016, 85, 995–1010. 10.1070/RCR4602. [DOI] [Google Scholar]
- Tinnacher R. M.; Begg J. D.; Mason H.; Ranville J.; Powell B. A.; Wong J. C.; Kersting A. B.; Zavarin M. Effect of Fulvic Acid Surface Coatings on Plutonium Sorption and Desorption Kinetics on Goethite. Environ. Sci. Technol. 2015, 49, 2776–2785. 10.1021/es505120s. [DOI] [PubMed] [Google Scholar]
- Begg J. D.; Zavarin M.; Kersting A. B. Desorption of Plutonium from Montmorillonite: An Experimental and Modeling Study. Geochim. Cosmochim. Acta 2017, 197, 278–293. 10.1016/j.gca.2016.10.006. [DOI] [Google Scholar]
- Sullens T. A.; Almond P. M.; Albrecht-Schmitt T. E. Ethylenediammonium Decafluorodineptunate(IV). Acta Crystallogr., Sect. E: Struct. Rep. Online 2004, 60, m973–m975. 10.1107/S1600536804014217. [DOI] [Google Scholar]
- Tian G.; Teat S. J.; Zhang Z.; Rao L. Sequestering Uranium from Seawater: Binding Strength and Modes of Uranyl Complexes with Glutarimidedioxime. Dalton Trans. 2012, 41, 11579–11586. 10.1039/c2dt30978e. [DOI] [PubMed] [Google Scholar]
- Kang S. O.; Vukovic S.; Custelcean R.; Hay B. P. Cyclic Imide Dioximes: Formation and Hydrolytic Stability. Ind. Eng. Chem. Res. 2012, 51, 6619–6624. 10.1021/ie300492z. [DOI] [Google Scholar]
- Leggett C. J.; Parker B. F.; Teat S. J.; Zhang Z.; Dau P. D.; Lukens W. W.; Peterson S. M.; Cardenas A. J. P.; Warner M. G.; Gibson J. K.; et al. Structural and Spectroscopic Studies of a Rare Non-Oxido V(v) Complex Crystallized from Aqueous Solution. Chem. Sci. 2016, 7, 2775–2786. 10.1039/C5SC03958D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endrizzi F.; Leggett C. J.; Rao L. Scientific Basis for Efficient Extraction of Uranium from Seawater. I: Understanding the Chemical Speciation of Uranium under Seawater Conditions. Ind. Eng. Chem. Res. 2016, 55, 4249–4256. 10.1021/acs.iecr.5b03679. [DOI] [Google Scholar]
- Das S.; Brown S.; Mayes R. T.; Janke C. J.; Tsouris C.; Kuo L. J.; Gill G.; Dai S. Novel Poly(Imide Dioxime) Sorbents: Development and Testing for Enhanced Extraction of Uranium from Natural Seawater. Chem. Eng. J. 2016, 298, 125–135. 10.1016/j.cej.2016.04.013. [DOI] [Google Scholar]
- Hall H. L.; Auxier J. D. Exploring Rapid Radiochemical Separations at the University of Tennessee Radiochemistry Center of Excellence. J. Radioanal. Nucl. Chem. 2016, 307, 1723–1727. 10.1007/s10967-015-4570-y. [DOI] [Google Scholar]
- Stratz S. A.; Jones S. J.; Mullen A. D.; Mathuthu M.; Oldham C. J.; Auxier J. D.; Hall H. L. Gas Chemical Adsorption Characterization of Lanthanide Hexafluoroacetylacetonates. J. Radioanal. Nucl. Chem. 2017, 312, 355–360. 10.1007/s10967-017-5232-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahbazi S.; Stratz S. A.; Auxier J. D.; Hanson D. E.; Marsh M. L.; Hall H. L. Characterization and Thermogravimetric Analysis of Lanthanide Hexafluoroacetylacetone Chelates. J. Radioanal. Nucl. Chem. 2017, 311, 617–626. 10.1007/s10967-016-5005-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stratz S. A.; Jones S. A.; Oldham C. J.; Mullen A. D.; Jones A. V.; Auxier J. D.; Hall H. L. Gas-Phase Detection of Solid-State Fission Product Complexes for Post-Detonation Nuclear Forensic Analysis. J. Radioanal. Nucl. Chem. 2016, 310, 1273–1276. 10.1007/s10967-016-4920-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auxier J. D. II; Jordan J. A.; Stratz S. A.; Shahbazi S.; Hanson D. E.; Cressy D.; Hall H. L. Thermodynamic Analysis of Volatile Organometallic Fission Products. J. Radioanal. Nucl. Chem. 2016, 307, 1621–1627. 10.1007/s10967-015-4653-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichler R.; Eichler B.. Thermochemical Data from Gas-Phase Adsorption and Methods of Their Estimation. In The Chemistry of Superheavy Elements; Springer-Verlag: Berlin, 2013; pp 375–413. [Google Scholar]
- Gaggeler H. W.; Turler A.. Gas-Phase Chemistry of Superheavy Elements. In The Chemistry of Superheavy Elements; Springer-Verlag: Berlin, 2014; pp 415–483. [Google Scholar]
- Vukovic S.; Hay B. P. De Novo Structure-Based Design of Bis-Amidoxime Uranophiles. Inorg. Chem. 2013, 52, 7805–7810. 10.1021/ic401089u. [DOI] [PubMed] [Google Scholar]
- Sellin R.; Alexandratos S. D. Polymer-Supported Primary Amines for the Recovery of Uranium from Seawater. Ind. Eng. Chem. Res. 2013, 52, 11792–11797. 10.1021/ie401979e. [DOI] [Google Scholar]
- Thompson R. C.; Olsen Y.; Mitchell R. P.; Davis A.; Rowland S. J.; John A. W. G.; McGonigle D.; Russell A. E. Lost at Sea: Where Is All the Plastic?. Science 2004, 304, 838. 10.1126/science.1094559. [DOI] [PubMed] [Google Scholar]
- Rochman C. M.; Hoh E.; Kurobe T.; Teh S. J. Ingested Plastic Transfers Hazardous Chemicals to Fish and Induces Hepatic Stress. Sci. Rep. 2013, 3, 3263 10.1038/srep03263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun X.; Tian G.; Xu C.; Rao L.; Vukovic S.; Kang S. O.; Hay B. P. Quantifying the Binding Strength of U(VI) with Phthalimidedioxime in Comparison with Glutarimidedioxime. Dalton Trans. 2014, 43, 551–557. 10.1039/C3DT52206G. [DOI] [PubMed] [Google Scholar]
- Sun X.; Xu C.; Tian G.; Rao L. Complexation of Glutarimidedioxime with Fe(III), Cu(II), Pb(II), and Ni(II), the Competing Ions for the Sequestration of U(VI) from Seawater. Dalton Trans. 2013, 42, 14621–14627. 10.1039/c3dt51767e. [DOI] [PubMed] [Google Scholar]
- Vukovic S.; Watson L. A.; Kang S. O.; Custelcean R.; Hay B. P. How Amidoximate Binds the Uranyl Cation. Inorg. Chem. 2012, 51, 3855–3859. 10.1021/ic300062s. [DOI] [PubMed] [Google Scholar]
- Tian G.; Teat S. J.; Rao L. Thermodynamic Studies of U(VI) Complexation with Glutardiamidoxime for Sequestration of Uranium from Seawater. Dalton Trans. 2013, 42, 5690. 10.1039/c3dt32940b. [DOI] [PubMed] [Google Scholar]
- Kim J.; Tsouris C.; Mayes R. T.; Oyola Y.; Saito T.; Janke C. J.; Dai S.; Schneider E.; Sachde D. Recovery of Uranium from Seawater: A Review of Current Status and Future Research Needs Recovery of Uranium from Seawater: A Review of Current Status and Future Research Needs. Sep. Sci. Technol. 2013, 48, 367–387. 10.1080/01496395.2012.712599. [DOI] [Google Scholar]
- Schneider E.; Sachde D. The Cost of Recovering Uranium from Seawater by a Braided Polymer Adsorbent System. Sci. Global Secur. 2013, 21, 134–163. 10.1080/08929882.2013.798993. [DOI] [Google Scholar]
- Barber P. S.; Kelley S. P.; Griggs C. S.; Wallace S.; Rogers R. D. Surface Modification of Ionic Liquid-Spun Chitin Fibers for the Extraction of Uranium from Seawater: Seeking the Strength of Chitin and the Chemical Functionality of Chitosan. Green Chem. 2014, 16, 1828–1836. 10.1039/C4GC00092G. [DOI] [Google Scholar]
- Carboni M.; Abney C. W.; Liu S.; Lin W. Highly Porous and Stable Metal–organic Frameworks for Uranium Extraction. Chem. Sci 2013, 4, 2396–2402. 10.1039/c3sc50230a. [DOI] [Google Scholar]
- Scanlan J. P. Equilibria in Uranyl Carbonate Systems - II: The Overall Stability Constant of UO2(CO3)22- and the Third Formation Constant of UO2(CO3)34. J. Inorg. Nucl. Chem. 1977, 39, 635–639. 10.1016/0022-1902(77)80578-2. [DOI] [Google Scholar]
- Bross D. H.; Peterson K. A. Composite Thermochemistry of Gas Phase U(VI)-Containing Molecules. J. Chem. Phys. 2014, 141, 244308 10.1063/1.4904721. [DOI] [PubMed] [Google Scholar]
- Abney C. W.; Liu S.; Lin W. Tuning Amidoximate to Enhance Uranyl Binding: A Density Functional Theory Study. J. Phys. Chem. A 2013, 117, 11558–11565. 10.1021/jp408460x. [DOI] [PubMed] [Google Scholar]
- Wang C. Z.; Lan J. H.; Wu Q. Y.; Luo Q.; Zhao Y. L.; Wang X. K.; Chai Z. F.; Shi W. Q. Theoretical Insights on the Interaction of Uranium with Amidoxime and Carboxyl Groups. Inorg. Chem. 2014, 53, 9466–9476. 10.1021/ic500202g. [DOI] [PubMed] [Google Scholar]
- Penchoff D. A.; Peterson C. C.; Quint M. S.; Auxier J. D.; Schweitzer G. K.; Jenkins D. M.; Harrison R. J.; Hall H. L. Structural Characteristics, Population Analysis, and Binding Energies of [An(NO3)]2+ [with An = Ac - Lr]. ACS Omega 2018, 10.1021/acsomega.8b01800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein K. J.; Do-Thanh C.-L.; Penchoff D. A.; Alan Cramer S.; Murdock C. R.; Lu Z.; Harrison R. J.; Camden J. P.; Jenkins D. M. The Synthesis and Spectroscopic Characterization of an Aromatic Uranium Amidoxime Complex. Inorg. Chim. Acta 2014, 421, 374–379. 10.1016/j.ica.2014.06.023. [DOI] [Google Scholar]
- Ansari S. A.; Bhattacharyya A.; Zhang Z.; Rao L. Complexation of Neptunium(V) with Glutaroimide Dioxime: A Study by Absorption Spectroscopy, Microcalorimetry, and Density Functional Theory Calculations. Inorg. Chem. 2015, 54, 8693–8698. 10.1021/acs.inorgchem.5b01319. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Perspective: Fifty Years of Density-Functional Theory in Chemical Physics. J. Chem. Phys. 2014, 140, 18A301 10.1063/1.4869598. [DOI] [PubMed] [Google Scholar]
- Schreckenbach G.; Hay P. J.; Martin R. L. Theoretical Study of Stable Trans and Cis Isomers in [UO2(OH)4]2-Using Relativistic Density Functional Theory. Inorg. Chem. 1998, 37, 4442–4451. 10.1021/ic980057a. [DOI] [PubMed] [Google Scholar]
- Schreckenbach G.; Jeffrey Hay P.; Martin R. L. Density Functional Calculations on Actinide Compounds: Survey of Recent Progress and Application to [UO2X4]2- (X = F, Cl, OH) and AnF6 (An = U, Np, Pu). J. Comput. Chem. 1999, 20, 70–90. . [DOI] [Google Scholar]
- Bühl M.; Sieffert N.; Chaumont A.; Wipff G. Water versus Acetonitrile Coordination to Uranyl. Density Functional Study of Cooperative Polarization Effects in Solution. Inorg. Chem. 2011, 50, 299–308. 10.1021/ic101950d. [DOI] [PubMed] [Google Scholar]
- Sonnenberg J. L.; Hay P. J.; Martin R. L.; Bursten B. E. Theoretical Investigations of Uranyl-Ligand Bonding: Four- and Five-Coordinate Uranyl Cyanide, Isocyanide, Carbonyl, and Hydroxide Complexes. Inorg. Chem. 2005, 44, 2255–2262. 10.1021/ic048567u. [DOI] [PubMed] [Google Scholar]
- De Jong W. A.; Aprà E.; Windus T. L.; Nichols J. A.; Harrison R. J.; Gutowski K. E.; Dixon D. A. Complexation of the Carbonate, Nitrate, and Acetate Anions with the Uranyl Dication: Density Functional Studies with Relativistic Effective Core Potentials. J. Phys. Chem. A 2005, 109, 11568–11577. 10.1021/jp0541462. [DOI] [PubMed] [Google Scholar]
- Vallet V.; Macak P.; Wahlgren U.; Grenthe I. Actinide Chemistry in Solution, Quantum Chemical Methods and Models. Theor. Chem. Acc. 2006, 115, 145–160. 10.1007/s00214-005-0051-7. [DOI] [Google Scholar]
- Gutowski K. E.; Cocalia V. A.; Griffin S. T.; Bridges N. J.; Dixon D. A.; Rogers R. D. Interactions of 1-Methylimidazole with UO2(CH3CO2)2 and UO2(NO3)2: Structural, Spectroscopic, and Theoretical Evidence for Imidazole Binding to the Uranyl Ion. J. Am. Chem. Soc. 2007, 129, 526–536. 10.1021/ja064592i. [DOI] [PubMed] [Google Scholar]
- Shamov G. A.; Schreckenbach G.; Martin R. L.; Hay P. J. Crown Ether Inclusion Complexes of the Early Actinide Elements, [AnO2(18-Crown-6)]N+, An ) U, Np, Pu and n) 1, 2: A Relativistic Density Functional Study. Inorg. Chem. 2008, 47, 1465–1475. 10.1021/ic7015403. [DOI] [PubMed] [Google Scholar]
- Spencer L. P.; Yang P.; Scott B. L.; Batista E. R.; Boncella J. M. Oxidative Addition to U(V)-U(V) Dimers: Facile Routes to Uranium(VI) Bis(Imido) Complexes. Inorg. Chem. 2009, 48, 11615–11623. 10.1021/ic901581r. [DOI] [PubMed] [Google Scholar]
- Bühl M.; Schreckenbach G. Oxygen Exchange in Uranyl Hydroxide via Two “Nonclassical” Ions. Inorg. Chem. 2010, 49, 3821–3827. 10.1021/ic902508z. [DOI] [PubMed] [Google Scholar]
- Ončák M.; Schröder D.; Slavíček P. Theoretical Study of the Microhydration of Mononuclear and Dinuclear Uranium(VI) Species Derived from Solvolysis of Uranyl Nitrate in Water. J. Comput. Chem. 2010, 31, 2294–2306. 10.1002/jcc.21521. [DOI] [PubMed] [Google Scholar]
- Sun J.; Ruzsinszky A.; Perdew J. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402 10.1103/PhysRevLett.115.036402. [DOI] [PubMed] [Google Scholar]
- Valiev M.; Bylaska E. J.; Govind N.; Kowalski K.; Straatsma T. P.; Van Dam H. J. J.; Wang D.; Nieplocha J.; Apra E.; Windus T. L.; et al. NWChem: A Comprehensive and Scalable Open-Source Solution for Large Scale Molecular Simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. 10.1016/j.cpc.2010.04.018. [DOI] [Google Scholar]
- Reed A. E.; Weinstock R. B.; Weinhold F. Natural Population Analysis. J. Chem. Phys. 1985, 83, 735–746. 10.1063/1.449486. [DOI] [Google Scholar]
- Glendening E.; Badenhoop J. K.; Reed A. E.; Carpenter J. E.; Bohmann J. A.; Morales C. M.; Landis C. R.; Weinhold F.. NBO 6.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, 2013.
- Werner H.-J.; Knowles P. J.; Knizia G.; Manby F. R.; Schütz M. Molpro: A General Purpose Quantum Chemistry Package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. 10.1002/wcms.82. [DOI] [Google Scholar]
- Feller D. The Role of Databases in Support of Computational Chemistry Calculations. J. Comput. Chem. 1996, 17, 1571–1586. . [DOI] [Google Scholar]
- Schuchardt K. L.; Didier B. T.; Elsethagen T.; Sun L.; Gurumoorthi V.; Chase J.; Li J.; Windus T. L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. 10.1021/ci600510j. [DOI] [PubMed] [Google Scholar]
- Towns J.; Cockerill T.; Dahan M.; Foster I.; Gaither K.; Grimshaw A.; Hazlewood V.; Lathrop S.; Lifka D.; Peterson G. D.; et al. XSEDE: Accelerating Scientific Discovery. Comput. Sci. Eng. 2014, 16, 62–74. 10.1109/MCSE.2014.80. [DOI] [Google Scholar]
- Penchoff D. A.Computational Studies for Optimization and Design of Extracting Agents for Separation of Lanthanides and Actinides; The University of Tennessee, 2014. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.