Abstract
The sequence fitness of a llama single-domain antibody with an unusually high thermal stability is explored by a combined computational and experimental study. Starting with the X-ray crystallographic structure, RosettaBackrub simulations were applied to model sequence–structure tolerance profiles and identify key substitution sites. From the model calculations, an experimental site-directed mutagenesis was used to produce a panel of mutants, and their melting temperatures were determined by thermal denaturation. The results reveal a sequence fitness of an excess stability of approximately 12 °C, a value taken from a decrease in the melting temperature of an electrostatic charge-reversal substitution in the CRD3 without a deleterious effect on the binding affinity to the antigen. The tolerance for the disruption of antigen recognition without loss in the thermal stability was demonstrated by the introduction of a proline in place of a tyrosine in the CDR2, producing a mutant that eliminated binding. To further assist the sequence design and the selection of engineered single-domain antibodies, an assessment of different computational strategies is provided of their accuracy in the detection of substitution “hot spots” in the sequence tolerance landscape.
1. Introduction
A combinatorial optimization of amino acid sequences to fit a topological protein fold takes place on comparability landscapes with the fitness measured by scaling factors.1 From an experimental perspective, sequence–structure tolerance is typically probed by site-directed mutagenesis studies, and the landscape is thermal stability and conservation of function. A common observation of mutational studies is the remarkable plasticity of protein structures to amino acid changes and how large the sequence envelope is for particular fold families.
A well-known class of protein folds that occupies a superfamily of sequences is the N-terminal domains of both the heavy and light chains of the variable region of antibodies. A popular construct of the heavy chain is single-domain antibody (sdAb) chains derived from camelids. The interest in sdAbs lies in their biotechnological applications that require an evaluated thermal stability and reversible folding as well as a high affinity and singularity of molecular recognition.2−7
Typical sdAbs have melting transition temperatures (Tm) in the range of 60–70 °C.2−5 An outlier is a llama sdAb specific for Staphylococcus aureus enterotoxin B (SEB), which has a reported Tm of 85 °C.2 The first available X-ray crystallographic structure of this unusually stable sdAb (designated as A3) revealed an asymmetrical homodimeric assembly of conformers displaying differences in the secondary structure geometry and local connectivity.8 The fold topology of each chain is the common assembly of two β sheets with a β-sandwich arrangement. Structural alignment search with Protein Data Bank (PDB) entries shows strong neighbors in the fold space with high Z-score matches with other antibody structures.
From a computational perspective, the effect of a mutation on Tm can be calculated from all-atom simulations of the thermodynamic folding–unfolding dynamics that govern the heat capacity or melting curve.1,9−11 Alternatively, an alchemical process of residue mutation can be modeled by using the free energy perturbation theory applied to a cycle of the folded and unfolded states to determine changes in the free energy of the folding stability.12−14 Although both modeling methods are rigorous, they are computationally prohibitive when applied to a large set of mutants for proteins of moderate size or larger. Because of this drawback, algorithms have been developed with energy functions specifically parameterized to predict differences in the folding free energy due to point mutations. Examples include Site-Directed Mutator (SDM),15 I-Mutant3.0,16 FoldX,17 PoPMuSiC,18 and PreTherMut,19 among others.20,21 Typically, these algorithms are empirically weighted using the data obtained from protein engineering experiments, and their predicted free energy changes are correlated to experimental differences in the folding free energy.
Here, this work presents a combined computational and experimental study of identifying residue contributions that govern the unusually high Tm of A3. Our earlier study reported several alanine substitutions and their application in comparative modeling methods to assess predictions of the thermal stability.22 The computational strategy here is different and is based on RosettaBackrub simulations23,24 to model the sequence–structure tolerance landscape and generate conformations for a set of amino acid substitutions including nonalanine mutations. Ranking of the mutants and their conformations is based on the application of the empirical energy function Rosetta and an alternative all-atom statistical potential. From our computational analysis, we apply site-directed mutagenesis to generate a panel of mutants that occupy structural regions identified as possible sequence “hot spots” and to evaluate the accuracy of modeling stability. Each mutant is experimentally characterized by their change in Tm relative to the wild-type (WT) A3 monomer and, unlike previous work,22 their binding affinity to the protein target SEB is reported. The latter is important in understanding the sequence tolerance of conserving protein function.
As a part of our computation design study of A3, we provide an assessment of knowledge-based and empirical prediction methods. Rather than the more conventional approach of predicting the correlation between an energy function and experimental folding free energies, we focus primarily on the often occurring case where the only available experimental data from protein engineering are Tm measurements for selected mutations. The observed nature of constructing a relationship between the Tm and the folding free energy (measured near or below 300 K) is nicely illustrated by the experimental study on the miniprotein Trp-cage with multiple sequence mutations.25 The relationship depends on the condition of unfolding–folding reversibility, an observation derived from the intrinsic physical properties of each protein under investigation as well as the experimental conditions of the denaturation.
Although our assessment of computational prediction schemes is not an exhaustive study, the analysis includes several widely popular web-based methods for modeling changes in the thermal stability and will be helpful to researchers working on similar problems on designing sdAb constructs. Included in our analysis is the rescoring of structures generated by the RosettaBackrub simulations using a highly benchmarked statistical potential function. Building upon the conformational ensemble produced from the RosettaBackrub, we also examine an approximation that corrects the statistical potential for molecular electrostatics of solvent interactions and their changes arising from the mutations by the addition of a weighted implicit solvent model. Taken together, our study of mutations of an sdAb offers an excellent assessment of the benefits and limitations of in silico methods applied to the rational design of antibody fragments.
2. Results and Discussion
2.1. Structural Features of A3
The X-ray crystallographic structure of the llama A3 sdAb in a homodimeric form is illustrated in Figure 1. The structure displays an unusual asymmetric assembly of two conformers (denoted as A and B chains) that differ in their secondary structure and, as noted in the published report, the dimerization has important implications for conformational misfolding.8 Additional crystallographic structures of A3 as monomeric chains have been determined, and the set includes several site-specific mutations.8 As reported in the crystallographic work, the protein production of the homodimer as opposed to the monomer is attributed to the cytoplasmic expression versus periplasmic.8 Structural differences among the conformers are centered primarily within the α-helical region containing residue F29 of the highly variable complementarity determining region CDR1 and residues S50–Y60 of the region linking the β-strands of the CDR2. The dimeric interface consists of residues 113–121 of the CDR3 loop as well as E44 and R45 of a variable β-hairpin and Y98 of the framework.
Figure 1.
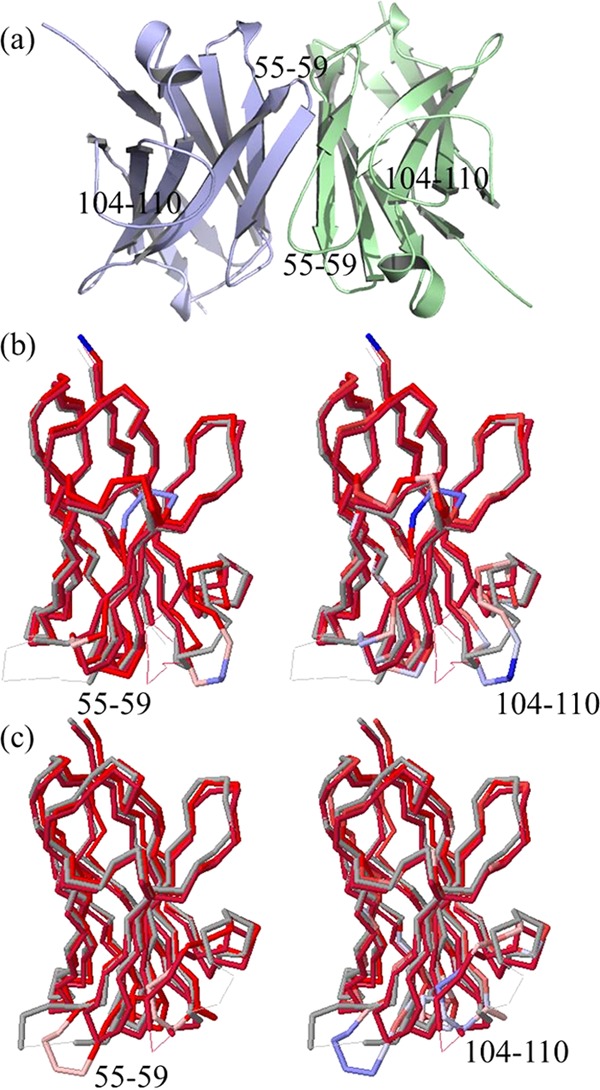
X-ray crystallographic structure of the asymmetric homodimeric A3 (PDB 4TYU) and structural neighbors from a Dali search of the single-chain conformers of the assembly. (a) Conformers of A3 where the color green denotes the A-chain and blue color the B-chain. (b) Structure–structure alignment of the A-chain with sdAbs 3STB and 1I3V, where on the left shows structural differences and the right sequence differences. The color spectrum runs from red to blue, where red designates structural and/or sequence conservation, whereas blue shows divergence. (c) Alignments of the B-chain with sdAbs 3STB and 1I3V.
A structural alignment search of the A and B chains was performed by the Dali algorithm26 to detect regions of the structural and sequence divergence. The significance of these regions is they offer substitution sites for exploring the sequence fitness that underlie the high Tm. The choice of applying chains from the dimeric assembly rather than a monomer is to capture a wider range of conformational plasticity among the crystallographic conformers. The search finds, as anticipated from the large data set of known immunoglobulins, greater than 1000 structural neighbors with high Z-scores and sequence identities that span the range from a high of 77% to a low 6%. Shown in Figure 1b,c are the high Z-score ranking sdAb hits of PDB entries 3STB and 1I3V with sequence identities of roughly 77 and 66%, respectively. Among the multiple neighbors observed from Dali, the pairwise alignments show a structural variability in the length and placement of the α-helix for residues 26–32, β-turn region centered at P55, and the loop region of roughly 98–110.
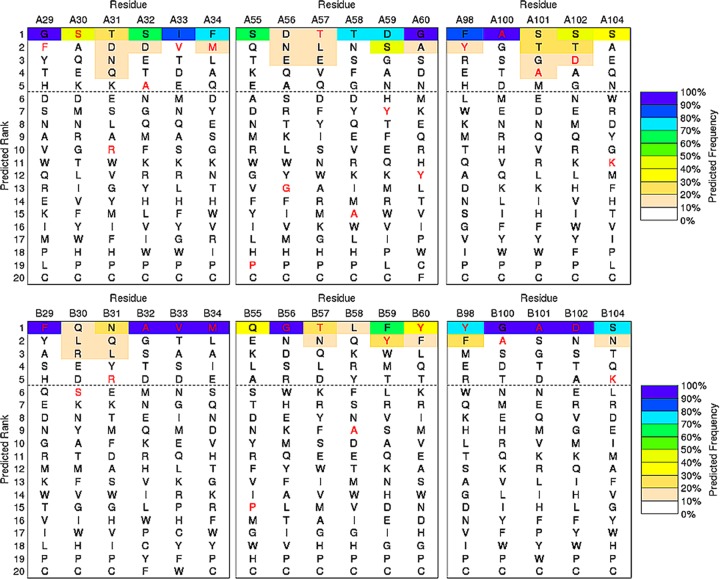
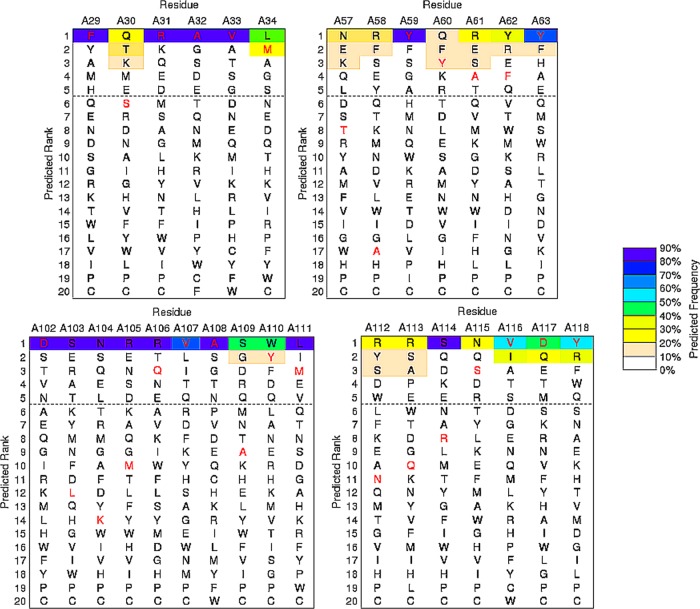
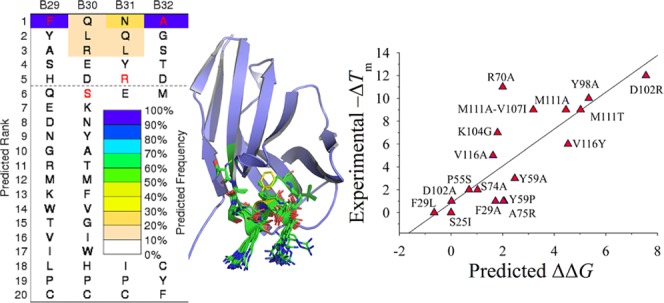
To explore the relationship between the Dali search results and the sequence fitness of structural regions to amino acid substitutions, we calculated the sequence–tolerance profiles that contribute to the fold stability of the conformers by the RosettaBackrub simulation method.23,24 RosettaBackrub is a structure-based modeling approach where the sequence tolerance is depended on the structural details surrounding a selected sequence location site. Unlike many coarse-grained simulation strategies, the RosettaBackrub models the protein chain at a resolution that detects local conformational differences on the sequence fitness. Illustrated in Figure 2 is a subset of the residue-specific profiles determined for the A and B conformers taken from the dimer. Shown are regions F29–M34, P55–Y60, and Y98–K104 that model the sequence tolerance between the conformers near or within the CDRs.22 Additional profiles are shown in Figure 3 for an alternative starting conformer and includes extended regions D102–M111 and N112–Y118. The profiles report the ranking of amino acids for each sequence position by a predicted frequency of site population. Wild-type (WT) residues are shown in red, and the dashed line indicates a cutoff of picking the top five amino acid choices at each position.
Figure 2.
Selected sequence–tolerance profiles of the A-chain conformer (top graph) and B-chain conformer (bottom graph) of A3 determined by the RosettaBackrub method. Sequences colored red denote the wild-type residue. The color spectrum of each profile designates the predicted frequency of the sequence-site placement along the A- or B-chain conformers. The horizontal line is arbitrarily positioned to highlight the five top-ranking sequences.
Figure 3.
Sequence–tolerance profiles for an alternative single-chain conformer of A3 to further illustrate the effect of the variability arising from different conformations. Added profile regions include D102–M111 and N112–Y118. The description is similar to that given in Figure 2.
The profiles show the variation between the conformers at specific sequence sites where structural differences are most evident. One example is the Y59–Y60 segment shown in Figure 2, where the aromatic rings are less favorable in population for the A-chain conformer and are located in an unstructured topology, whereas a β-strand is found for the B-chain. Similarly, Figure 3 shows Y59–Y60 to populate high-frequency placements at their conformational positions along the chain. Despite the structural differences between the conformers, WT residues with high favorable ranking are observed for many sites, suggesting a strong sequence-fold comparability fitness. For example, the structural topology at position F29 is a helical fold populated among the conformers with the only exception being the dimeric A-chain, yet the WT phenylalanine is nearly equivalent in the sequence ranking for all chains. Conversely, the WT residue P55, which is located in a β-turn region of the high structural divergence among the Dali search results, shows low population frequency for both A and B conformers (Figure 2). Contrasting rankings are observed for charged residues D102 and K104, where the negative charge is among the top-ranked populations for the set of conformers, whereas the positive charge varies in the sequence ranking (Figures 2 and 3).
2.2. Experimental Site-Directed Mutagenesis
To test the computed tolerance profiles and the effect of structural variability observed from the Dali search results, a panel of substitutions for experimental site-directed mutagenesis was designed and included 18 mutations (listed in Table 1). The criteria for which sites to select for substitution and the residue type was based on the output of RosettaBackrub simulations of evaluating an exhaustive number of substitutions. The final set was down selected for exploring the following: (1) destabilization of the helical-connecting region between S25 and F29 of CDR1; (2) conformational flexibility of CDR2 positioned at P55 and its poor tolerance score; (3) divergent placement of Y59 in the A and B chains and overall rank; (4) placement of charged and nonpolar groups in the largely unstructured CDR3 of residues D102–V116; and (5) overall sequence conservation. Although the mutants are nearly all single-point substitutions, the selection provides a sufficient probe into the sequence tolerance of function and stability. Substitutions outside of the predicted profiles were modeled from the crystallographic structures.
Table 1. Measured Tm and KD for Wild-Type (WT) A3 and Mutants.
| A3 clone | Tm (°C) | KD (nM) | structural region |
|---|---|---|---|
| WT | 85 | 0.23 | |
| S25I | 85 | 0.19 | CDR1 |
| F29A | 84 | 0.20 | CDR1 |
| F29L | 85 | 0.18 | CDR1 |
| P55S | 83 | 3.30 | CDR2 |
| Y59A | 82 | 0.45 | CDR2 |
| Y59P | 84 | no binding | CDR2 |
| R70A | 74 | 0.33 | FR3 |
| S74A | 83 | 0.21 | FR3 |
| A75R | 84 | 0.52 | FR3 |
| Y98A | 75 | 0.34 | FR3 |
| D102A | 84 | 0.09 | CDR3 |
| D102R | 73 | 0.29 | CDR3 |
| K104G | 78 | 0.21 | CDR3 |
| M111A | 76 | 0.25 | CDR3 |
| M111T | 76 | 0.50 | CDR3 |
| M111A/V107I | 76 | 0.60 | CDR3 |
| V116A | 80 | 0.14 | CDR3 |
| V116Y | 79 | 0.13 | CDR3 |
Thermal denaturation curves were determined for each protein mutant along with their binding kinetics to SEB to ensure proper folding, as determined by their ability to recognize the antigen. The WT and all mutant proteins were produced as monomers, thus eliminating possible complications arising from the dimerization. Representative circular dichroism (CD) and surface plasmon resonance (SPR) data are shown in Figure 4 (see also the Supporting Information). With the exception of the Y59P, all of the mutants retained their binding function and most recognized SEB with near wild-type affinities. The mutations at P55 and Y59 may affect the conformation of CDR2 (see Figure 1), which was previously shown to provide critical interactions between A3 and SEB.3 The melting transition temperatures were compared to the WT form.
Figure 4.
Representative experimental data. The top graph shows denaturation curves of A3 mutants F29L (blue) and Y98A (green). Vertical lines have been drawn through the inflection points, dotted for Y98A and solid for F29L. Middle and lower graphs are SPR data for mutants P55S and D102R. The on rate, off rate and calculated dissociation constant (KD) of A3 binding the target SEB are shown above the data for these mutants.
Although the tolerance profiles from RosettaBackrub are not absolute in ranking sequence frequencies, it is of interest to generally place the experimental measured results in the context of the computed profiles and apply the ideas of protein fitness.1 Among the mutants, an asymptotic margin or threshold robustness of excess configurational stability can be estimated from the substitutions which retained the functional property of native-like binding to the antigen SEB. The most remarkable outcome is the electrostatic charge-reversal D102R in CDR3, which showed a significant drop of 12 °C in the Tm compared to the WT form and demonstrated a native-like KD (Table 1). The D102R Tm brings the stability excess near the upper bound that is typical of other sdAbs. Additional mutants with an excess stability of ∼10 °C include R70A and Y98A, both positioned in FR3. In contrast to D102R, the elimination of the atomic charge with D102A showed a negligible ΔTm and binds with an equal affinity to the antigen, as observed with the WT form. Figures 2 and 3 report that the WT residue of an Asp at 102 is placed in the high-frequency selection for the conformers, and the D102A mutant was predicted to be among the top-ranked substitutions, although still susceptible to a loss in the thermal stability (Table 1). The substitution D102 → R was predicted to be outside the top-ranked frequency, and the experimental data reports a more significant decrease in the stability greater than anticipated from its ranking among substitutions.
In contrast to D102R, the limit of conserving function from sequence tolerance is observed by the introduction of a proline in place of a tyrosine (Y59P) in CDR2, producing a mutant where the binding was eliminated, whereas the thermal stability remained near the WT form. Figure 2 shows that the placement of a proline in the CDR2 is a rare occurrence in the sequence landscape and is likely due to restraints in the backbone torsional flexibility. The interplay of stability and function of the CDR2 is further established by the P55S mutant where the KD is significantly decreased and the loss in stability is negligible. Overall, the low sequence consensus of prolines in the CDRs is predicted by the RosettaBackrub.
The mutant Y98A with an experimental measurement of −ΔTm ∼ 3 °C suggests the tolerance profile for the B-chain to be more accurate in describing the configurational stability than that of the A-chain, which is thought to be a kinetically trapped chain in the dimeric form.8,27 A similar observation can be made for mutants F29A, F29L, and K104G. Simulation studies have been reported22 for comparing the WT B-conformer with mutants F29A and Y98A and support the ranking of residue substitutions given in Figure 2.
2.3. Assessment of Structure-Based Stability Predictions
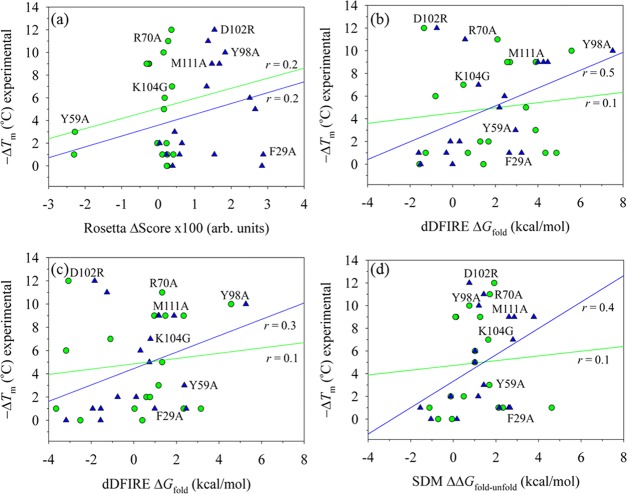
As an initial step in constructing an empirical relationship between the experimental Tm and a predictive model at the molecular level, RosettaBackrub simulations were applied to calculate the effects of residue substitutions on changes in the Rosetta scoring28 of conformers (denoted by a free energy change ΔG). Figure 5a reports the correlation of using both conformers A and B as input structures to calculate conformational ensembles for each mutation. Although it is important to note that the RosettaBackrub calculations only model the folded conformations and do not reproduce the thermodynamic co-existence between the folded and unfolded states as in the experimental Tm, the correlation is nevertheless of general interest to test whether simple models can detect significant outliners in changes of the fold stability. The computed Rosetta score is an average over the ensemble and is relative to the WT form taken from the crystallographic assembly. The calculated correlation coefficient of Figure 4a for evaluating 18 mutants using either the A or B-conformer is only r = ∼0.2.
Figure 5.
Scatter plots of scoring the effect of 18 residue substitutions relative to the wild-type structure and their relationship to the experimentally determined changes in melting temperatures (ΔTm). To account for differences in physical units between the computed ΔG and the experimental ΔTm, the free energy coordinate can be arbitrarily scaled by a “reference-state.” For illustrations (a)–(c), conformations were generated by the RosettaBackrub simulation method24 starting with either the crystallographic A-chain conformer (denoted as green-colored circles) or the B-chain conformer (blue triangles). The first two plots were computed as statistical averages over each modeled conformational ensemble. (a) Application of the Rosetta 3.1 scoring function to the mutations, yielding linear regression correlation coefficients of r = 0.2 for both chains. (b) Scoring of the generated ensemble by dDFIRE, yielding r = 0.1 for the A-chain and r = 0.5 for the B-chain. (c) The first-order rank conformer determined by dDFIRE scoring for the two chains (r ∼ 0 for the A-chain and r = 0.3 for the B-chain). (d) Application of the SDM modeling method15 using the starting crystallographic A-chain and B-chain conformers to calculate changes in free energies and their relationship to Tm (r ∼ 0 for A-chain and r = 0.3 for the B-chain).
Given the poor performance of approximating the observed experimental changes, the conformational ensembles that were generated by the RosettaBackrub for each mutation were rescored using the statistical potential dDFIRE.29 The selection of dDFIRE rather than other popular statistical potentials (see, e.g., RWplus35 and GOAP36) is based on previous simulation studies of A3 and protein structure refinement studies.22,30−34
The results shown in Figure 5b report a correlation of r = 0.1 for the A conformer and 0.5 for the B-conformer. Although calculations for the B-conformer yielded a slight improvement, there are several significant outliers that unfavorably deter an accurate correlation (e.g., F29A, D102R, and K104G). Rather than using the ensemble of conformations in computing the relative differences, the top scoring conformations determined by dDFIRE were only analyzed. Figure 5c shows the correlation r = ∼ 0 for the A conformer and r = 0.3 for the B-conformer. For additional comparison purposes, the application of the SDM server15 was applied to both conformers. SDM is a two-state model calculation and uses a statistical potential energy function that incorporates environment-specific amino acid substitution frequencies within homologous protein families to calculate a stability score. Figure 5d reports the SDM results and their relationship to ΔTm. We find a correlation for the A conformer of r = 0.1 and 0.4 for the B-conformer.
Modeled structures for several mutants and their reorganization from the WT B-chain conformer predicted by RosettaBackrub simulations are highlighted in Figure 6. The structure for F29A shows the distortion in the backbone conformation from the WT form and disrupts the α-helix formation for many of the ensemble. This modeling result combined with sequence–tolerance profiles given in Figures 2 and 3 suggests that the helix is not a determinant of the stability but rather a poor scoring by statistical potentials of the generated conformations. Noticeable backbone displacements are likewise observed for M111A, and to a lesser extent, D102R. Overall, the examination of the predicted structures proves difficult to resolve the differences between modeling and experiments.
Figure 6.
Molecular illustrations of the modeled folded structure of the wild-type sdAb conformation and selected mutants determined by RosettaBackrub simulations. The structures are (a) wild-type B-chain conformer showing CDR1 (colored cyan), CDR2 (green), CDR3 (yellow) and several mutational sites; (b) mutant F29A; (c) D102R; and (d) M111A. For figures (b)–(d), the wild-type conformation surrounding a selected sequence position is shown in blue, the top-rank-ordered dDFIRE structure from the generated ensemble is shown in green, and the lowest-rank ordered dDFIRE conformation is shown in red. Surrounding local side-chains are highlighted in the respective colors.
Figure 7 presents predictions from additional servers as a part of the assessment of modeling methods. The servers include mCSM,37 PoPMuSiC,18 and I-Mutant3.0.16 The mCSM strategy is a complementary approach to SDM and specifically applies a novel graph-based signature approach which extends the concept of the interatomic distance patterns to a residue-environment description for the modeling of residue substitutions. The PoPMuSiC predictor uses statistical potentials and is based on a formalism that models a linear combination of energy functions, where proportionality coefficients are fitted and vary with the solvent accessibility of the mutated residue. The third web server is the I-Mutant3.0, which is based on a support vector machine algorithm and applies a statistical potential to score mutations.
Figure 7.
Modeling 18 sequence substitutions of the B-chain conformer of A3. (a) mCSM server37 predictions showing r ∼ 0.5. (b) PoPMuSiC server18 with r ∼ 0.3. (c) I-Mutant3.0 server16 predictions showing r ∼ 0.4. (d) Linear scaling approximation of scoring mutations by a combined dDFIRE statistical potential and a weighted generalized Born (GB) implicit solvent model applied to a two-state model of the folded and unfolded conformations; the linear regression correlation coefficient is r ∼ 0.8.
Although the results from the three servers show poor correlations to experimentally measured values of ΔTm, the modeling strategies do detect one or two hot spots in the sequence–tolerance landscape. The three top-ranked substitutions from mCSM and PoPMuSiC are Y98A, M111A/V107I (or M111A), and F29A. From I-Mutant3.0, the three are R70A, Y98A, and F29A. All three servers failed to detect D102R and incorrectly modeled F29A as a false positive.
To help resolve why the charge-reversal D102R and several hydrophobic substitutions are difficult to predict, a linear scaling approximation was constructed as a model system to explore if a more accurate solvent description can correct the difficulties of modeling changes in polarization effects. The model system is assembled by the addition to dDFIRE a linearly weighted generalized Born implicit solvent model (GBMV2).38 The GBMV2 model has been successfully applied to modeling A3 for calculating thermal unfolding profiles of the wild-type form and template-based homology models22 and the conformational transition of A → B upon unfolding.27
The linear scaling model is given by the following net sum
| 1 |
where ΔΔGfold–unfolddDFIRE is the energy difference between a mutant conformation and the wild-type structure computed for both the folded (RosettaBackrub) and unfolded (simulations) forms using the dDFIRE potential function. The term ΔGfold is the GBMV2 solvent free energy for the folded conformation computed as the difference between the mutant and WT form, and similarly, ΔGunfoldGB is for the unfolded conformation. Unfolded conformations are modeled chains with large measures of the radius of gyration and overall lack of secondary structure.22,27 The terms εf and εu are scaling parameters determined from a linear fit to the experimentally obtained ΔTm for each mutant.
Using only the B-chain conformer, Figure 7d reports the linear scaling model with εf fitted to ∼20 and εu ∼ 10 for 18 mutants selected from the experimental data set. We find the correlation coefficient to be r = ∼0.8, a significant improvement from the routine application of simulations of modeling only the folded state. We should note that merely including the unfolded state scored by dDFIRE is not adequate to improve the correlation, particularly that of D102R and K104G. Conversely, the GBMV2 energies for charge deletions when properly weighted contribute favorably to yielding a more accurate correlation. In general, the importance of contributions from dDFIRE and GBMV2 depends on the change in the solvent exposure at the substitution site of the native conformation versus the unfolded form.
The reweighting of the solvent terms in predictive models is not a new idea and has been the subject of many investigations of continuum models for computing solvent energies of protein structures.39−44 For the ideal model, εf = εu = 1, which describes a condition suitable for modeling substitutions that do not alter the ionization or induce significant conformational changes of the surface polarity. For the work presented here, the high value of εf reflects structural changes not adequately captured when conformations generated by the RosettaBackrub simulations are introduced to the GBMV2 reaction field for mutations that affect the dipolar reorganization. Likewise, εu accounts for the lack of an extensive conformational ensemble generated for the mutants.
From the plot of Figure 7d, achieving good universality in the fitted parameters appears noticeably weak for several single-point mutants, particularly the charge deletions R70A and K104G. These two ion-pair breaking mutants are better modeled by allowing the scaling parameters to account for local environment-specific effects along the protein chain as well as amino acid type and substitution, namely, the form of εf → εf(xi, α → β), where xi is the spatial location of the residue i of type α to be mutated to type β. To test this idea, we increased the contribution of ΔGfoldGB by setting εf = 12. The net result improves −ΔTm predictions for R70A ∼ 10 °C and K104G ∼ 8 °C, suggesting that the fitting accuracy of mutants that alter ion-pairs should be treated differently in a structure-based approach.
The last set of calculations is from the published strategy developed by Rooman and co-workers45 and is designated as HoTMuSiC. This method applies statistical potentials and unlike the empirical relationship given above of modeling the linear correspondence between the experimentally measured ΔTm versus the predicted ΔΔG, the method HoTMuSiC allows a direct comparison between ΔTm values from measurements and predictions. Using the HoTMuSiC web server,45Figure 8 reports a scatter plot of the experimental ΔTm versus predicted ΔTm and shows an r = 0.4. Similar to the other predictions, HoTMuSiC detects correctly hot spots at positions Y98 and M111, however showing a false positive for F29A. Also, as observed with other web-based predictions, the method fails to detect D102R and R70A as outliers.
Figure 8.
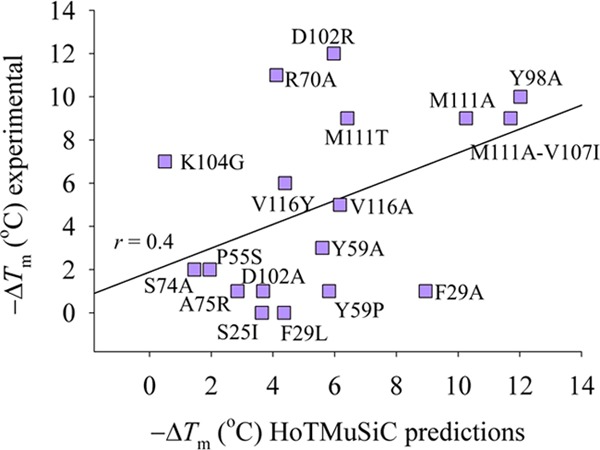
Modeling sequence substitutions of the B-chain conformer of A3 using the server HoTMuSiC.45 Comparison is presented of experimental measurements ΔTm vs predictions. The linear regression correlation coefficient is r = 0.4.
3. Conclusions
The sequence tolerance of the sdAb A3 with an unusually high thermal stability was investigated by a combined computational and experimental study. The experimental results demonstrated several hot spots in the sequence fitness landscape of A3 and provided insights into why this particular sequence mapped onto an sdAb scaffold is highly stable in the folded conformation. Complementary to the experimental study, the mutagenesis results provide a data set for evaluating different computational strategies aimed at the structure-based design of single-domain antibodies. Toward this end, an assessment of prediction methods was provided in determining a relationship between calculations and experimental changes in melting temperatures. The analysis showed that different methods were able to detect outliers in fitness space; however, the predictions generally suffered in accuracy when modeling a selective set of electrostatic and hydrophobic mutations. To understand the limitations in applying statistical potentials and knowledge-based scoring functions in ranking mutations, a computational model was tested of combining an all-atom statistical potential with a scaled implicit solvent model to calculate the net contribution from the two-state model of folded and unfolded conformations. The results showed that integrating a weighted contribution of solvent molecular electrostatics with a statistical potential function may offer improvements in the rank order of sequence substitutions. As with any scaling function, a poor universality in the fitted constants for different protein systems may arise and require a readjustment for an optimal fit. Relative to the computationally fast empirical methods, the proposed model requires an increase in the computational demand due to the sampling of conformational space (folded and unfolded) and the scoring of structures with a physics-based implicit solvent model. For future protein designs of sdAbs, a hybrid approach is likely the best strategy of applying the scaling model as a refinement tool for modeling charge deletions and/or substitutions that lack consensus among the available empirical models.
4. Computational and Experimental Methods
4.1. Computational Approach
Starting conformations for modeling were taken from the recently reported crystallographic structure of the A3 sdAb determined to a resolution of 2.13 Å (PDB 4TYU).8 The structure is a dimeric assembly of two distinctive chains, one denoted as the A conformer and the other the B-conformer. Because of the lack of a fully formed disulfide bond in the electron density maps of each chain, the S–S bond was modeled. Other modeled A3 conformations were taken from the crystallographic structures PDB 4W70, 4TYU, 4U7S, 4W68, 4W81, and 4U05. Sequence tolerance profiles for each conformer were generated by the RosettaBackrub simulation method developed by Smith and Kortemme.23 The RosettaBackrub protocol consisted of Monte Carlo simulations of a flexible backbone, and the side-chain moves in the Rosetta modeling program. The simulations were followed by a combination of simulated annealing and genetic algorithm optimization methods in the RosettaBackrub to enrich for low-energy sequences.
For the application presented here, we selected to model the sequence–fitness profiles for regions F29–M34, P55–Y60, Y98–K104, D102–M111, and N112–Y118, where amino acids were ranked individually for each sequence position by a predicted frequency of tolerance.23 The regions were selected to model the sequence and structurally variability of the CDRs. It should be noted that the number of residues in a sampling window for computing a tolerance profile is limited due to the computational task of modeling sequence permutations. The generalized Rosetta modeling version26 was applied, and the number of generated conformations was set to 20 for each residue position, the Boltzmann factor set to 0.228, and the fitness score reweighting was given a value of 0.4.24 Sampling convergence from RosettaBackrub was established by noting a little change from increasing the number of generated conformations to 50 for a selected set of mutations. Simulation parameters were set similar to that of computing the sequence–fitness profiles. Two scoring functions were applied to the generated ensembles and consisted of the Rosetta 3.1 energy function28 and the statistical potential dDFIRE.29
The set of 20 folded conformations generated from the RosettaBackrub (WT and mutants) plus the corresponding X-ray crystal structures were subjected to the energy minimization by the method of steepest descent minimization for 50 steps using the CHARMM22 + CMAP potential energy function46 combined with the GBMV2 implicit solvent model. For generating the unfolded states of the WT form, parallel-tempering simulations were carried out by using the self-guided Langevin dynamics (SGLD) simulation method to sample the conformational space.47 A set of conformations were extracted at the upper bound ensemble temperature of 475 K with the selection criteria of satisfying large values of radius of gyration and having minimum residual secondary structure content.22 An integration time step of 2 fs was used for all simulations. The GBMV2 parameters for the simulations and all scoring were set to values of β = −12 and P3 = 0.65 to smooth the energy surface. The hydrophobic cavitation term was modeled by applying the solvent-exposed surface area of the protein solute with a surface tension coefficient set to a value of 0.015 kcal/(mol Å2).
SGLD parameters of the friction constant were set to γ of 1 ps–1 for all heavy atoms, the guiding factor λ set to a value of 1, and the averaging time tL was set to 1 ps. The selection of these values was taken from previous studies of the SGLD model.22,27,32 Nonbonded interaction cutoff parameters for electrostatics and van der Waals terms were set at a radius of 22 Å with a 2 Å potential switching function. Covalent bonds between the heavy atoms and hydrogen atoms were constrained by the SHAKE algorithm.48 Simulations were performed using the Multiscale Modeling Tools for Structural Biology49 and the CHARMM simulation program50 (version c35b2). Simulations were carried out using 32 replica clients, and the frequency of exchanges was set to every 1 ps of simulation.
For generating the mutants in the unfolded conformations, side-chains of the WT unfolded conformations were replaced in the ensemble by using the SCWRL modeling program51 and were subjected to energy minimization using the same CHARMM22/GBMV2 force field. All ensembles were eventually scored with dDFIRE and GBMV2 for final analysis.
4.2. Mutagenesis and Characterization Methods
Site-directed mutagenesis for the construction of 18 mutants of the A3 sdAb was performed using the QuikChange site-directed mutagenesis kit (Agilent); mutations were confirmed by sequencing (Operon). Protein was expressed and purified from the periplasm as a monomer using a combination of osmotic shock, immobilized metal affinity chromatography, and size exclusion chromatography, as described previously.2,4 The purified protein used for all experiments was in a monomeric form. The protein concentration was determined based on the absorbance at 280 nm using a nanodrop 1000 spectropolarimeter (ThermoFisher). Samples were stored refrigerated in phosphate-buffered saline until characterization.
The Tm of each mutant was measured by CD using a Jasco J-815 CD Spectropolarimeter equipped with a PTC-423S Peltier for temperature control, as previously described.3,4 The CD measurements were done at least in duplicate, often with several different preparations of the protein. The Tm values estimated from replicate measurements made by CD were all within less than a half degree of each other.
Surface plasmon resonance utilizing a ProteOn XPR36 (Bio-Rad) was employed to determine the binding of each mutant to surface-immobilized SEB antigen.2,4 All SPR measurements were done at least in duplicate, often with several different preparations of each mutant as a monomer. The KD determined by SPR for replicates agreed within at least a factor of 3. Other than the mutants at P55, the KD values were considered to be essentially equivalent to wild-type, as KD determinations can be problematic when off rates are so slow.
Acknowledgments
This work was funded by the U.S. Department of Defense Threat Reduction Agency JSTO award CBCALL12-LS6-2-0036 (E.R.G.). The funding support for K.B.T. was from the American Society for Engineering Education Postdoctoral Fellowship. The opinions or assertions contained herein belong to the authors and are not necessarily the official views of the U.S. Army, U.S. Navy or the U.S. Department of Defense.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b00730.
Representative size exclusion chromatography data obtained from the purification of the sdAbs (Figure S1); surface plasmon resonance data to determine binding affinities from A3 wild-type and variants (Figure S2); circular dichroism data to determine the melting point from A3 wild-type and mutants (Figure S3) (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Tokuriki N.; Tawfik D. S. Stability effects of mutations and protein evolvability. Curr. Opin. Struct. Biol. 2009, 19, 596–604. 10.1016/j.sbi.2009.08.003. [DOI] [PubMed] [Google Scholar]
- Graef R. R.; Anderson G. P.; Doyle K. A.; Zabetakis D.; Sutton F. N.; Liu J. L.; Serrano-González J.; Goldman E. R.; Cooper L. A. Isolation of a highly thermal stable lama single domain antibody specific for Staphylococcus aureus enterotoxin B. BMC Biotechnol. 2011, 11, 86 10.1186/1472-6750-11-86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zabetakis D.; Anderson G. P.; Bayya N.; Goldman E. R. Contributions of the complementarity determining regions to the thermal stability of a single-domain antibody. PLoS One 2013, 8, e77678 10.1371/journal.pone.0077678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner K. B.; Zabetakis D.; Goldman E. R.; Anderson G. P. Enhanced stabilization of a stable single domain antibody for SEB toxin by random mutagenesis and stringent selection. Protein Eng., Des. Sel. 2014, 27, 89–95. 10.1093/protein/gzu001. [DOI] [PubMed] [Google Scholar]
- Turner K. B.; Zabetakis D.; Legler P.; Goldman E. R.; Anderson G. P. Isolation and epitope mapping of staphylococcal enterotoxin B single-domain antibodies. Sensors 2014, 14, 10846–10863. 10.3390/s140610846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muyldermans S. Nanobodies: natural single-domain antibodies. Annu. Rev. Biochem. 2013, 82, 775–797. 10.1146/annurev-biochem-063011-092449. [DOI] [PubMed] [Google Scholar]
- Eyer L.; Hruska K. Single-domain antibody fragments derived from heavy-chain antibodies: A review. Vet. Med. 2012, 57, 439–513. 10.17221/6336-VETMED. [DOI] [Google Scholar]
- George J.; Compton J. R.; Leary D. H.; Olson M. A.; Legler P. M. Structural and mutational analysis of a monomeric and dimeric form of a single domain antibody with implications for protein misfolding. Proteins 2014, 82, 3101–3116. 10.1002/prot.24671. [DOI] [PubMed] [Google Scholar]
- Yeh I.-C.; Lee M. S.; Olson M. A. Calculation of protein heat capacity from replica-exchange molecular dynamics simulations with different implicit solvent models. J. Phys. Chem. B 2008, 112, 15064–15073. 10.1021/jp802469g. [DOI] [PubMed] [Google Scholar]
- Lee M. S.; Olson M. A. Comparison of two adaptive temperature-based replica exchange methods applied to a sharp phase transition of protein unfolding-folding. J. Chem. Phys. 2011, 134, 2444111 10.1063/1.3603964. [DOI] [PubMed] [Google Scholar]
- Lee M. S.; Olson M. A. Protein folding simulations combining self-guided Langevin dynamics and temperature-based replica exchange. J. Chem. Theory Comput. 2010, 6, 2477–2487. 10.1021/ct100062b. [DOI] [PubMed] [Google Scholar]
- Zwanzig R. W. High temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954, 22, 1420–1426. 10.1063/1.1740409. [DOI] [Google Scholar]
- Straatsma T. P.; McCammon J. A. Computational alchemy. Annu. Rev. Phys. Chem. 1992, 43, 407–435. 10.1146/annurev.pc.43.100192.002203. [DOI] [Google Scholar]
- Tidor B.; Karplus M. Simulation analysis of the stability mutant R96H of T4 lysozyme. Biochemistry 1991, 30, 3217–3228. 10.1021/bi00227a009. [DOI] [PubMed] [Google Scholar]
- Worth C. L.; Preissner R.; Blundell T. L. SDM--a server for predicting effects of mutations on protein stability and malfunction. Nucleic Acids Res. 2011, 39, W215–W222. 10.1093/nar/gkr363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan S.; Vihinen M. Performance of protein stability predictors. Hum. Mutat. 2010, 31, 675–684. 10.1002/humu.21242. [DOI] [PubMed] [Google Scholar]
- Schymkowitz J.; Borg J.; Stricher F.; Nys R.; Rousseau F.; Serrano L. The FoldX web server: an online force field. Nucleic Acids Res. 2005, 33, W382–W388. 10.1093/nar/gki387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehouck Y.; Kwasigroch J. M.; Gilis D.; Rooman M. PoPMuSiC 2.1: A web server for the estimation of protein stability changes upon mutation and sequence optimality. BMC Bioinf. 2011, 12, 151 10.1186/1471-2105-12-151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian J.; Wu N.; Chu X.; Fan Y. Predicting changes in protein thermostability brought about by single- or multi-site mutations. BMC Bioinf. 2010, 11, 370 10.1186/1471-2105-11-370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia L.; Yarlagadda R.; Reed C. C. Structure based thermostability prediction models for protein single point mutations with machine learning tools. PLoS One 2015, 10, e0138022 10.1371/journal.pone.0138022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panigrahi P.; Sule M.; Ghanate A.; Ramasamy S.; Suresh C. G. Engineering Proteins for thermostability with iRDP web server. PLoS One 2015, 10, e0139486 10.1371/journal.pone.0139486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson M. A.; Zabetakis D.; Legler P. M.; Turner K. B.; Anderson G. P.; Goldman E. R. Can template-based protein models guide the design of sequence fitness for enhanced thermal stability of single domain antibodies?. Protein Eng., Des. Sel. 2015, 28, 395–402. 10.1093/protein/gzv047. [DOI] [PubMed] [Google Scholar]
- Lauck F.; Smith C. A.; Friedland G. F.; Humphris E. L.; Kortemme T. RosettaBackrub--a web server for flexible backbone protein structure modeling and design. Nucleic Acids Res. 2010, 38, W569–W575. 10.1093/nar/gkq369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith C. A.; Kortemme T. Predicting the tolerated sequences for proteins and protein interfaces using RosettaBackrub flexible backbone design. PLoS One 2011, 6, e20451 10.1371/journal.pone.0020451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barua B.; Lin J. C.; Williams V. D.; Kummler P.; Neidigh J. W.; Andersen N. H. The Trp-cage: optimizing the stability of a globular miniprotein. Protein Eng., Des. Sel. 2008, 21, 171–185. 10.1093/protein/gzm082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm L.; Sander C. Protein structure comparison by alignment of distance matrices. J. Mol. Biol. 1993, 233, 123–138. 10.1006/jmbi.1993.1489. [DOI] [PubMed] [Google Scholar]
- Olson M. A.; Legler P. M.; Goldman E. R. Comparison of replica exchange simulations of a kinetically trapped protein conformational state and its native form. J. Phys. Chem. B 2016, 120, 2234–2240. 10.1021/acs.jpcb.6b00233. [DOI] [PubMed] [Google Scholar]
- RosettaCommons 2010. http://www.rosettacommons.org (accessed March 06, 2019).
- Zhou H.; Zhou Y. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci. 2002, 11, 2714–2726. 10.1110/ps.0217002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson M. A.; Lee M. S. Evaluation of unrestrained replica-exchange simulations using dynamic walkers in temperature space for protein structure refinement. PLoS One 2014, 9, e96638 10.1371/journal.pone.0096638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson M. A.; Lee M. S. Application of replica exchange umbrella sampling to protein structure refinement of nontemplate models. J. Comput. Chem. 2013, 34, 1785–1793. 10.1002/jcc.23325. [DOI] [PubMed] [Google Scholar]
- Olson M. A.; Lee M. S. Structure refinement of protein model decoys requires accurate side-chain placement. Proteins 2013, 81, 469–478. 10.1002/prot.24204. [DOI] [PubMed] [Google Scholar]
- Olson M. A.; Chaudhury S.; Lee M. S. Comparison between self-guided Langevin dynamics and molecular dynamics simulations for structure refinement of protein loop conformations. J. Comput. Chem. 2011, 32, 3014–3022. 10.1002/jcc.21883. [DOI] [PubMed] [Google Scholar]
- Lee M. S.; Olson M. A. Assessment of detection and refinement strategies for de novo protein structures using force field and statistical potentials. J. Chem. Theory Comput. 2007, 3, 312–324. 10.1021/ct600195f. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Zhang Y. A novel side-chain orientation dependent potential derived from random-walk reference state for protein fold selection and structure prediction. PLoS One 2010, 5, e15386 10.1371/journal.pone.0015386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H.; Skolnick J. GOAP: a generalized orientation-dependent, all-atom statistical potential for protein structure prediction. Biophys. J. 2011, 101, 2043–2052. 10.1016/j.bpj.2011.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pires D. E.; Ascher D. B.; Blundell T. L. mCSM: predicting the effects of mutations in proteins using graph-based signatures. Bioinformatics 2014, 30, 335–342. 10.1093/bioinformatics/btt691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee M. S.; Feig M.; Salsbury F. R. Jr.; Brooks C. L. 3rd New analytic approximation to the standard molecular volume definition and its application to generalized Born calculations. J. Comput. Chem. 2003, 24, 1348–1356. 10.1002/jcc.10272. [DOI] [PubMed] [Google Scholar]
- Warshel A.; Papazyan A. Electrostatic effects in macromolecules: fundamental concepts and practical modeling. Curr. Opin. Struct. Biol. 1998, 8, 211–217. 10.1016/S0959-440X(98)80041-9. [DOI] [PubMed] [Google Scholar]
- Sham Y. Y.; Muegge I.; Warshel A. The effect of protein relaxation on charge-charge interactions and dielectric constants of proteins. Biophys. J. 1998, 74, 1744–1753. 10.1016/S0006-3495(98)77885-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson M. A. Mean-field analysis of protein-protein interactions. Biophys. Chem. 1998, 91, 219–229. 10.1016/S0301-4622(01)00172-7. [DOI] [PubMed] [Google Scholar]
- Olson M. A.; Reinke L. T. Modeling implicit reorganization in continuum descriptions of protein-protein interactions. Proteins 2000, 38, 115–119. . [DOI] [PubMed] [Google Scholar]
- Li L.; Li C.; Zhang Z.; Alexov E. On the dielectric “constant” of proteins: smooth dielectric function for macromolecular modeling and its implementation in DelPhi. J. Chem. Theory Comput. 2013, 9, 2126–2136. 10.1021/ct400065j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cumberworth A.; Bui J. M.; Gsponer J. Free energies of solvation in the context of protein folding: Implications for implicit and explicit solvent models. J. Comput. Chem. 2016, 37, 629–640. 10.1002/jcc.24235. [DOI] [PubMed] [Google Scholar]
- Pucci F.; Bourgeas R.; Rooman M. Predicting protein thermal stability changes upon point mutations using statistical potentials: Introducing HoTMuSiC. Sci. Rep. 2016, 6, 23257 10.1038/srep23257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackerell A. D. Jr.; Feig M.; Brooks C. L. 3rd Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004, 25, 1400–1415. 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- Wu X.; Brook B. R. Self-guided Langevin dynamics simulation method. Chem. Phys. Lett. 2003, 381, 512–518. 10.1016/j.cplett.2003.10.013. [DOI] [Google Scholar]
- Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- Feig M.; Karanicolas J.; Brooks C. L. 3rd MMTSB Tool Set: Enhanced sampling and multiscale modeling methods for applications in structural biology. J. Mol. Graphics Modell. 2004, 22, 377–395. 10.1016/j.jmgm.2003.12.005. [DOI] [PubMed] [Google Scholar]
- Brooks B. R.; Brooks C. L. 3rd; Mackerell A. D. Jr.; Nilsson L.; Petrella R. J.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krivov G. G.; Shapovalov M. V.; Dunbrack R. L. Jr. Improved prediction of protein side-chain conformations with SCWRL4. Proteins 2009, 77, 778–795. 10.1002/prot.22488. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.