Abstract
Although methodology articles have increasingly emphasized the need to analyze data from two members of a dyad simultaneously, the most popular method in substantive applications is to examine dyad members separately. This might be due to the underappreciation of the extra information simultaneous modeling strategies can provide. Therefore, the goal of this study was to compare multiple growth curve modeling approaches for longitudinal dyadic data (LDD) in both structural equation modeling and multilevel modeling frameworks. Models separately assessing change over time for distinguishable dyad members are compared to simultaneous models fitted to LDD from both dyad members. Furthermore, we compared the simultaneous default versus dependent approaches (whether dyad pairs’ Level 1 [or unique] residuals are allowed to covary and differ in variance). Results indicated that estimates of variance and covariance components led to conflicting results. We recommend the simultaneous dependent approach for inferring differences in change over time within a dyad.
Keywords: longitudinal dyadic data analysis, multilevel modeling, separate modeling, simultaneous modeling, structural equation modeling
Often, in longitudinal studies, our objectives are to study how an individual changes over time as well as differences in how individuals change over time (e.g., McArdle & Nesselroade, 2014; Singer & Willett, 2003). The former is called intraindividual change, whereas the latter is called interindividual differences in intraindividual changes (Baltes & Nesselroade, 1979). An example of each type of objective in the developmental literature is emotion regulation. Kopp (1989) found that infants’ ability to regulate their emotions gets better as they get older; this is intraindividual change. However, not all infants change in the same way, such that some get better more rapidly and some improve less rapidly; this is interindividual differences in intraindividual changes. In the specific case of emotion regulation, we can examine both how infants change in emotion regulation over age and how individual trajectories differ across infants.
LONGITUDINAL DATA
To study changes over time, one can measure the same individuals across multiple time points on the same measures or constructs. The data are called repeated measures, multiwave, or longitudinal. In a longitudinal study, each individual acts as his or her own control and thus the aforementioned objectives of the analysis of change can be fulfilled by analyzing the longitudinal data. One important feature of longitudinal data is that the data from different time points are nested within an individual and thus are more or less correlated within an individual (Fitzmaurice, Laird, & Ware, 2011). Considering the nested data feature, researchers fit multilevel models (MLM) or latent growth curve models in the structural equation modeling (SEM) framework to analyze longitudinal data for the analysis of change (e.g., Grimm, Steele, Ram, & Nesselroade, 2013; McArdle, 2009; Singer & Willett, 2003).
DYADIC DATA
In a different line of investigation, psychological research often examines how related people are similar or different from each other in their behaviors and attitudes. For example, family researchers might be interested in studying the extent to which a husband and wife’s marital satisfaction levels relate within a couple. To examine this research question, one needs to collect data from dyads of two related individuals (i.e., both husband and wife). The collected data are called dyadic data. There are two kinds of dyadic data, depending on dyadic distinguishability, whether the two individuals comprising a dyad possess a distinctive characteristic to identify them (i.e., distinguishable dyads) or not (i.e., indistinguishable dyads; e.g., Kenny, Kashy, & Cook, 2006). For our example, the husband and the wife in a dyad can be distinguished based on their gender or role and thus form a distinguishable dyad. In contrast, identical twins can be considered to form indistinguishable dyads. In this article, we focus on studying distinguishable dyads.
When examining dyadic data, it is important to account for the possibility that one member’s responses to questions might be related to the other member’s responses. That is, the data from two members of a dyad are nested within a dyad and thus might be correlated. For example, in the case of marital relationships, two members of a dyad are inherently reporting on the same relationship. Therefore, dyadic data often encounter the problem of nonindependence (e.g., Gonzalez & Griffin, 2012; Kenny et al., 2006). To account for nonindependence in the data, we need to allow the observations from a member of a dyad to be related to the corresponding observations from the other member of the dyad in statistical analyses. However, one assumption underlying many basic statistical analyses (e.g., regression analysis and analysis of variance [ANOVA]) is that observations are independent. Thus, more advanced analyses such as MLM and SEM have been proposed and studied for cross-sectional dyadic data analysis to account for interdependence in the data (e.g., Du & Wang, 2016; Kenny et al., 2006; Ledermann, Macho, & Kenny, 2011; Newsom, 2002; Sayer & Klute, 2005; Wendorf, 2002).
LONGITUDINAL DYADIC DATA
When dyads are repeatedly measured, we have longitudinal dyadic data (LDD). For LDD, data from different time points are nested within a dyad member and data from dyad members are nested within a dyad. Thus, LDD are three-level data. There are two kinds of nonindependence in LDD: nonindependence from repeated measures over time and nonindependence from related members in a dyad at a given time point. This could make the data analysis more complicated. Specifically, there are three kinds of intraclass correlations (ICCs) for which to account in analyses: an ICC for each dyad member over time (how strongly data from different time points correlate for each dyad member) and a third kind of ICC for the relation between dyad members at each time point (how strongly data from the two dyad members correlate at each time point).
Several techniques have been proposed and used to account for nonindependence in LDD. These techniques answer different research questions. For example, growth curve modeling (e.g., Atkins, 2005; Kashy & Donnellan, 2008; Kashy, Donnellan, Burt, & McGue, 2008; Lyons & Sayer, 2005; Peugh, DiLillo, & Panuzio, 2013; Whittaker, Beretvas, & Falbo, 2014) can be used to address questions related to intraindividual change over time, whereas cross-lagged models (e.g., Bolger & Laurenceau, 2013; Ferrer & Nesselroade, 2003) are considered as longitudinal actor–partner models to study how a dyad member at time t – 1 influences the other dyad member at time t and thus do not address intraindividual change (Kenny et al., 2006). In this article, we focus on discussing how to apply growth curve modeling to LDD for the analysis of change.
As stated by Kenny et al. (2006), “The analysis of over-time data from individuals is very complex. … Adding the complications of dyadic data analysis makes a difficult topic even more challenging. Moreover, methodologists have not yet come to a complete consensus on which data-analytic techniques are most appropriate” (p. 343). Inspired by this comment, we explicitly compare six growth modeling approaches for LDD analysis with distinguishable dyads: 2 Modeling Framework (MLM vs. SEM) × 3 Modeling Approach (separate vs. simultaneous “default” vs. simultaneous “dependent”). By comparing methodologies in both the MLM and SEM frameworks, we hope to provide researchers with the tools necessary to conduct these analyses independently. Furthermore, we assess change over time for distinguishable dyad members separately and simultaneously using the default or a dependent Level 1 (unique) residual covariance approach. The simultaneous default approach does not allow dyad pairs’ Level 1 (unique) residuals to covary and differ in variance whereas the simultaneous dependent approach does. The approaches are explained in detail later.
Researchers have discussed and compared different growth curve modeling approaches for LDD analysis with distinguishable dyads. However, none has explicitly compared all six approaches. For example, Atkins (2005) focused on discussing MLM with the separate or simultaneous default approach for conducting LDD analysis in family research but not within the SEM framework or in comparison to the simultaneous dependent approach. Kashy and Donnellan (2008) illustrated MLM and SEM growth models with the simultaneous dependent approach for LDD analysis with distinguishable dyads but did not compare them to the separate and simultaneous “default” approaches. More recently, Peugh et al. (2013) articulated the use of SEM models with the simultaneous dependent approach but not within the MLM framework or in comparison to the separate and simultaneous default approaches for LDD analysis with distinguishable dyads. Furthermore, Whittaker et al. (2014) described how to use the curve of factor analysis in the SEM framework to analyze LDD and discussed the measurement invariance over time issue but did not compare various error covariance structure approaches.
Therefore, the purpose of this study is to apply three growth curve modeling approaches in both MLM and SEM frameworks to analyze a real LDD set with distinguishable dyads to show (a) differences in the research questions that can be answered by different modeling approaches, and (b) similarities and differences in the results of using different approaches. SAS PROC MIXED or Mplus code for implementing each of the six (2 × 3) approaches is provided and recommendations are made and discussed on growth curve modeling for LDD analysis with distinguishable dyads.
OUR REAL DATA AND SUBSTANTIVE RESEARCH QUESTIONS
The data are from a longitudinal study exploring infant development in 135 parent–infant triads and include a measure of marital satisfaction completed by both mothers and fathers at five waves of data collection. The data are both longitudinal and dyadic in nature. More specifically, families attended six laboratory visits when the infants were 3, 5, 7, 12, 14, and 20 months of age (±14 days). Only mothers and infants attended the 12-month visit, and only fathers and infants attended the 14-month visit, resulting in five time points of data collection each for mothers and fathers.
Before each laboratory visit, parents completed a measure of marital satisfaction measured using the Short Marital Satisfaction Test (SMAT; Locke & Wallace, 1959), a 15-item questionnaire assessing global marital satisfaction and how the couple agrees on various matters that arise in marriage (i.e., recreation, finances, and the handling of disagreements). Parents completed the questionnaire separately. Scores on the SMAT ranged from 29.89 to 157 for fathers and 26 to 156 for mothers. Cronbach’s alphas assessing internal consistency for fathers’ SMAT responses ranged from .75 to .89 across the five time points and ranged from .73 to .86 for mothers’ responses. See Appendix A for a subset of the data in various forms.
Descriptive statistics for mother and father marital satisfaction are presented in Table 1. The correlations among mothers’ data over time (the M block in Table 1) ranged from .55 to .78, with higher correlations from repeated measures data with shorter time intervals. A very similar range (.59–.79) and pattern were observed for the correlations among fathers’ data over time (the F block in Table 1). The correlations between mother and father reports of marital satisfaction (the M&F block in Table 1) indicated that they were related at each time point (.52–.65) and across time (.43–.52) as well. Thus, data used for this empirical example are related over time for each dyadic member, between the two dyadic members at each time point and across time, as would be expected for typical longitudinal dyadic data. More information about the sample and the measure can be found in Planalp, Braungart-Rieker, Lickenbrock, and Zentall (2013).
TABLE 1.
Descriptive Statistics of Mother and Father Marital Satisfaction
| Time | MMS1 3 months |
MMS2 5 months |
MMS3 7 months |
MMS4 12 months |
MMS5 20 months |
FMS1 3 months |
FMS2 5 months |
FMS3 7 months |
FMS4 14 months |
FMS5 20 months |
|
|---|---|---|---|---|---|---|---|---|---|---|---|
| M | 119.69 | 118.01 | 117.73 | 117.03 | 115.10 | 117.03 | 117.15 | 117.87 | 117.16 | 115.26 | |
| SD | 18.27 | 19.62 | 19.99 | 22.58 | 22.09 | 21.03 | 20.39 | 19.83 | 20.76 | 21.29 | |
| Correlations | |||||||||||
| M | |||||||||||
| MMS1 | 1.00 | ||||||||||
| MMS2 | .73 | 1.00 | |||||||||
| MMS3 | .66 | .79 | 1.00 | ||||||||
| MMS4 | .61 | .7,3 | .69 | 1.00 | |||||||
| MMS5 | .55 | .62 | .63 | .74 | 1.00 | ||||||
| M&F | F | ||||||||||
| FMS1 | .57 | .52 | .48 | .39 | .50 | 1.00 | |||||
| FMS2 | .62 | .64 | .57 | .48 | .58 | .77 | 1.00 | ||||
| FMS3 | .51 | .52 | .52 | .50 | .49 | .65 | .79 | 1.00 | |||
| FMS4 | .46 | .48 | .49 | .57 | .58 | .59 | .70 | .66 | 1.00 | ||
| FMS5 | .43 | .45 | .43 | .49 | .65 | .59 | .71 | .70 | .77 | 1.00 | |
Note. MMS = mother marital satisfaction; FMS = father marital satisfaction. The correlations were all significant at the .001 significance level. The correlations are from three blocks. The M block contains the correlations among mothers over time, the F block contains the correlations among fathers over time, and the M&F block contains the correlations between mothers and fathers at each time point and over time.
ICCs were calculated for mothers’ repeated measures over time, fathers’ repeated measures over time, and between mothers and fathers at each time point. SAS syntax for calculating the three types of ICCs is included in Appendix B. ICCs for measuring the nonindependence from the repeated measures data of mothers and fathers over time were .67 and .71, respectively. These two ICCs summarize the correlations in the M and F blocks of Table 1, respectively. At each time point, the ICCs for measuring the nonindependence between mothers and fathers ranged from .52 to .67 (.56 at 3 months, .64 at 5 months, .52 at 7 months, .60 at 12 and 14 months, .67 at 20 months), which are corresponding to the correlations in the M&F block of Table 1. The calculated ICC values indicated that the data were highly dependent over time within a dyadic member and were also highly dependent between mothers and fathers at each time point. High ICCs from LDD suggest and require the use of models that can handle nonindependence among observations.
With a focus on studying intraindividual changes, intraindividual variability, and interindividual differences and relations in them (Baltes & Nesselroade, 1979), we are interested in answering the following substantive research questions:
How do mothers’ (or fathers’) reports of marital satisfaction change over time, on average, respectively?
How do mothers (or fathers) differ in changes in marital satisfaction over time?
How do mothers differ from fathers in changes in marital satisfaction over time, on average?
How do couples differ in the mother versus father differences in changes over time?
How do mothers’ changes relate to fathers’ changes?
How much average intraindividual variability is there for mothers (or fathers) after controlling the individual fitted trends?
How much difference in the average intraindividual variability is there between mothers and fathers after controlling for the individual fitted trends?
How do intraindividual fluctuations of mothers relate to those of fathers after controlling for the individual fitted trends?
Also see Table 2 for the list of substantive research questions, which is long. However, with LDD and an appropriate modeling approach, we are able to answer them, which is demonstrated in what follows.
TABLE 2.
Research Questions That Can Be Answered by the Various Modeling Approaches Considered in This Study for Our Example
| Type of Research Questions | Related Parameters to Be Estimated and Tested | How to Deal With the Data From Two Members of a Dyad | ||
|---|---|---|---|---|
| (1) Separate Modeling | (2) Simultaneous Modeling With a Default Error Covariance Structure | (3) Simultaneous Modeling With a Dependent Error Covariance Structure | ||
| 1. How do mothers’ (or fathers’) reports of marital satisfaction change over time, on average? | Fixed effects (e.g., β10 in Equation 2 and β20 in Equation 3) | Y | Y | Y |
| 2. How do mothers (or fathers) differ in changes in marital satisfaction over time? | Level 2 variance components (e.g., and in Equation 5) | Y | Y | Y |
| 3. How do mothers differ from fathers in changes in marital satisfaction over time, on average? | Fixed effects (e.g., β30 in Equation 9 and β40 in Equation 10) | N | Y | Y |
| 4. How do couples differ in the mother versus father differences in changes over time? | Level 2 variance components (e.g. and in Equation 11) | N | Y | Y |
| 5. How do mothers’ changes relate to fathers’ changes? Or how do mothers’ changes relate to mother versus father differences in the changes? | Level 2 covariances (e.g., covariances in Equation 11) | N | Y | Y |
| 6. How much average intraindividual variability is there for mothers (or fathers) after controlling the individual fitted trends? | Level 1 residual variances (e.g., in Equations 4 or 12; and in Equation 13) | Y | Y | Y |
| 7. How much difference in the average intraindividual variability is there between mothers and fathers after controlling the individual fitted trends? | Difference in Level 1 residual variances (e.g., compare and in Equation 13) | N | N | Y |
| 8. How do intraindividual fluctuations of mothers relate to those of fathers after controlling the individual fitted trends? | Level 1 residual covariance (e.g., σmf in Equation 13) | N | N | Y |
Note. Each model can be fitted in either the multilevel modeling or structural equation modeling framework. Y = the research question can be answered by the approach; N = the research question cannot be answered by the approach. For the statistical tests, the Wald test can be used for testing the fixed effects and covariances. For testing the variances, we recommend the specific one-sided Wald test or the generalized likelihood ratio test (see Ke & Wang, 2015, for more details).
MODELING APPROACHES FOR LONGITUDINAL DYADIC DATA ANALYSIS
A non-exhaustive literature review was conducted to gather modeling information about how substantive researchers have been analyzing LDD. We used the keywords longitudinal (or repeated measures) and dyad (dyadic or pair) for searching post-2000 peer-reviewed articles in several psychology journals including, but not limited to Child Development, Developmental Psychology, Infancy, Development and Psychopathology, British Journal of Developmental Psychology, Journal of Abnormal Child Psychology, Journal of Family Psychology, and Journal of Marriage and Family. Models such as MLM, latent growth curve models in the SEM framework, and repeated measures ANOVAs were widely used for the analysis of change using LDD. Given that traditional repeated measures ANOVAs are generally less flexible and less capable in handling missing data for longitudinal data analysis (Hedeker & Gibbons, 2006), we focus on studying MLM and SEM for LDD analysis in this article. These two frameworks for the analysis of change perform the same or nearly identically, given that the specified models are the same (e.g., Bauer, 2003; Kashy & Donnellan, 2008; Kenny et al., 2006; MacCallum, Kim, Malarkey, & Kiecolt-Glaser, 1997). Thus, one purpose of this study is to illustrate the similarity, differences, advantages, and limitations of conducting LDD analysis in the two frameworks.
Surprisingly, our literature review showed that few substantive studies (less than 20%) modeled longitudinal dyadic data from both dyad members simultaneously. In other words, substantive researchers often model the longitudinal data from each dyad member separately, resulting in two separate models, and verbally compare the results from the two models. Although this provides information on each dyad member’s behavior of interest, it is impossible to infer comparisons statistically. Use of this popular but perhaps less appropriate practice might be due to the lack of understanding of negative consequences of the separate modeling strategy and the underappreciation of the extra information and flexibility a simultaneous modeling strategy can provide. If the question of interest includes a comparison between dyad members, researchers should use a modeling approach that accurately answers that question, namely a simultaneous approach. Based on the results of our limited search, this was often not the case. Thus, another goal of this study is to discuss the separate versus simultaneous modeling approaches for LDD analysis and demonstrate the similarities and differences in the estimates of both fixed effects and variance parameters from both approaches.
In addition, for the simultaneous modeling approach, we compare two methods for modeling the error covariance structure: the default method, which does not allow Level 1 (or unique) residuals to covary and their variances to be different versus a dependent method allowing Level 1 residuals to covary and their variances to differ. Note that the default and dependent approaches are also called the standard and alternative error covariance structures in the MLM literature (e.g., Singer & Willett, 2003).
In sum, we examine and compare 2 (MLM vs. SEM) × 3 (separate vs. simultaneous default vs. simultaneous dependent) modeling approaches for LDD analysis. We focus on examining what research questions can be answered by each modeling approach (see Table 2 for a summary), how the estimates of fixed effects and variance–covariance parameters differ between approaches, and which modeling technique might yield more informative and accurate results.
Data Structures for MLM and SEM
We fit the multilevel models using SAS 9.3 (SAS Institute, 2011) and the SEM models using Mplus 6.0 (Muthén & Muthén, 1998–2010) to the real LDD. We had different data structures for the two frameworks (Singer & Willett, 2003). When using SAS PROC MIXED for multilevel models, data were set up in a long data format, in which each dyad has multiple records or rows of data for one outcome variable, in our case marital satisfaction (SMAT). Using our real data example, for the separate mother and father analyses, there are five variables: a dyad or family ID variable, a time variable (age: infant age) for each dyad, and the outcome variables (msmat: mothers’ marital satisfaction; fsmat: fathers’ marital satisfaction) in the data set. For the simultaneous analyses, there are six variables: a dyad or family ID variable, a time variable (age: infant age), a dyad member identifier (mom: whether the member is mother or father), the outcome (smat: marital satisfaction data from both mothers and fathers), and two additional variables (time and role) that are explained later. Appendix A shows examples of the long data format used in our separate and simultaneous modeling analyses.
When using Mplus for SEM analyses, data are in a wide data format, such that each dyad has one row of data and multiple variables: each variable for each dyad member at each time point. For our example, there is a dyad or family ID variable, five mother variables, and five father variables for each dyad. Appendix A also shows an example of the wide data format used in our analyses.
Because our data are from mothers and fathers reporting on marital satisfaction, we use the terms mother and father to indicate two distinguishable members of a dyad in the following descriptions of modeling strategies. The models can be applied to other longitudinal data with distinguishable dyads.
Separate MLM Models for Each Dyad Member
MLM allows the examination of both intraindividual changes and interindividual differences in changes (Singer & Willett, 2003). MLM models for this study used a Level 1 model for intraindividual changes over time and a Level 2 model for interindividual differences in such change (Singer & Willett, 2003).
We compared models with no change, linear change, and quadratic change functions (Singer & Willett, 2003). Model comparison results indicated that the linear model fit the data adequately. Thus in this article, we focus on models with a linear change function at the first level.
Two separate two-level MLM models were fit to the data for mothers and fathers, respectively. Equations for the separate MLM models are, for Level 1, intraindividual changes over time:
| (1) |
and for Level 2, between-person differences in such changes
| (2) |
| (3) |
where yit is the observed score in the outcome variable (marital satisfaction) for individual i at time t. Different centering and scaling approaches of the time variable (infant age at a mother–child or father–child visit), ageit, yield different meanings of the random effects: b1i and b2i. In our example, we centered the infant age variable at the child’s birth date with year as the time unit and thus the values for ageit were 3/12, 5/12, 7/12, 12/12, 20/12 for mothers and 3/12, 5/12, 7/12, 14/12, 20/12 for fathers. Random coefficient b1i represents the level of marital satisfaction (at the child’s birth) of individual i, or intercept, and random effect b2i represents the linear rate of change over the observation period in marital satisfaction of individual i, or linear slope. eit is the deviation of the observed response score from individual i’s fitted curve for individual i at time t. The default covariance structure of the Level 1 residuals in MLM is a diagonal matrix with equal residual variances across time, and off-diagonal elements constrained to be zero. For our example, it is the 5 × 5 diagonal matrix in Equation 4. measures the average intraindividual variability of the observed responses around each individual’s fitted curve.
| (4) |
At the second level, β10 and β20 represent the average initial level and linear slope across individuals. The covariance matrix of Level 2 residuals ζ1i and ζ2i, matrix G1, usually includes the variances for the intercept and slope as well as the covariance between intercepts and slopes (σ12).
| (5) |
Separate SEM Models for Each Dyad Member
SEM is a widely used tool for examining relationships between multiple variables in one pathway model (Bollen, 1998), and can also be used to examine LDD (Kashy & Donnellan, 2008). In particular, latent growth curve modeling is a highly recommended method for studying levels and changes of a behavior with repeated-measures data over time, as well as the relation between the growth of several variables over time (Ferrer & McArdle, 2003; McArdle, 2009; Meredith & Tisak, 1990). For a linear latent growth curve model, two latent variables, intercept and change, can be defined to model the individual change trajectories over time. Depending on the factor loadings, different meanings of the intercept and change latent variables can be obtained.
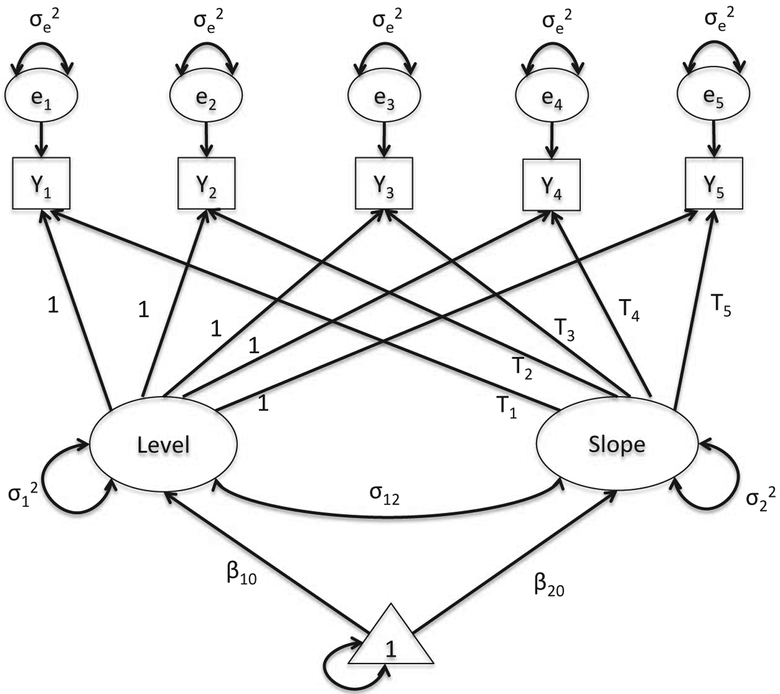
Using the same example as with the MLM models earlier, we specified two separate models for mothers’ and fathers’ marital satisfaction. See Figure 1 for a path diagram. By constraining all paths from the latent intercept variable to the manifest (observed) marital satisfaction variable at each time point to be one and to the latent change variable to be the age values of the infant (unit: year) at the visit such as 3/12, 5/12, 7/12, 12/12, 20/12 for mothers and 3/12, 5/12, 7/12, 14/12, 20/12 for fathers, this allows the latent intercept variable to represent individual initial levels for marital satisfaction, corresponding to b1i in MLM, and the latent change variable to represent individual yearly linear rate of change in marital satisfaction, corresponding to b2i in MLM. The means of the level and linear slope latent variables correspond to fixed effects β10 and β20 in MLM, representing the average initial level and linear slope across individuals, respectively. In addition, the residual or unique variance of the observed variables is set to be equal across time, , to be consistent with the standard setting in the MLM framework. It should be noted that this constraint is not necessary for latent growth curve modeling. For the two latent variables, a 2 × 2 covariance structure is specified to model the variances of the latent level and linear slope variables and their covariance, corresponding to the G1 matrix (Equation 5) in MLM. The model specification in the SEM framework, therefore, is the same as that in the MLM framework.
FIGURE 1.
Path diagram of separate SEM models for mothers and fathers. T1, T2, T3, T4, and T5 are 3/12, 5/12, 7/12, 12/12, and 20/12 for mothers and 3/12, 5/12, 7/12, 14/12, and 20/12 for fathers for our example.
To examine whether and how fathers’ change trajectories differ from those of mothers, we need to model the longitudinal data from both mothers and fathers simultaneously. Next, we discuss the simultaneous models in both MLM and SEM frameworks.
Simultaneous MLM Models for Both Dyad Members
To answer our research question on whether mothers and fathers differ from each other in their initial levels and changes over time in marital satisfaction, we need to analyze the data from both mothers and fathers simultaneously. Simultaneous modeling methods allow us to statistically test for the differences between mothers and fathers. Although the longitudinal data from both mothers and fathers are three-level, we analyze them using a two-level MLM because the role within a dyad (e.g., mother vs. father) is a fixed (not random) factor. In other words, a conceptual three-level model can be represented but only two levels show random variation (also see Chapter 8 in Bolger & Laurenceau, 2013). Thus, the two-level MLM equations for the simultaneous modeling method, for Level 1, intraindividual changes over time:
| (6) |
and for Level 2, between-person differences in change:
| (7) |
| (8) |
| (9) |
| (10) |
In Equation 6, yidt represents the observed outcome (marital satisfaction) for member i of dyad d at time t. momid indicates whether a datum is from the mother or the father of dyad d with 1 indicating from the mother and 0 indicating from the father. For the random effects, b1d represents the initial status in marital status and b2d represents the linear slope for the father in dyad d. In addition, b3d represents the difference in the initial status between the father and the mother of dyad d, and b4d is the difference in the linear slopes between the father and the mother of dyad d. It should be noted that we could specify the model to allow b3d and b4d to represent the initial status and linear slope for the mother in dyad d. In this case, another indicator variable (e.g., dad) needs to be added. For example, we have, for Level 1, intraindividual changes over time:
The two specifications are mathematically equivalent. However, the specification in Equation 6 allows us to directly compare mothers and fathers in their initial levels and changes over time. Therefore, we use the specification in Equation 6 in this article.
Following the regular assumptions in MLM, the random effects are assumed to have a multivariate normal distribution with COV (b1d; b2d; b3d; b4d) = COV(ζ1d; ζ2d; ζ3d; ζ4d) for this unconditional MLM model. Diagnostics of the normality assumption and alternative (or robust) methods for general growth curve modeling have been discussed in the literature (e.g., Pan & Fang, 2012; Tong & Zhang, 2012) and are not discussed in this article due to the scope limits. The covariance matrix of the random effects, G2, is
| (11) |
The main diagonal elements in G2 measure interindividual variation in fathers’ initial levels, fathers’ linear slopes, differences in the initial levels between mothers and fathers, and differences in the linear slopes between mothers and fathers, respectively. β10; β20; β30; and β40 are the corresponding fixed effects, representing the average initial level for fathers, the average linear slope for fathers, the average difference in the initial levels between mothers and fathers, and the average difference in the linear slopes between mothers and fathers, respectively.
For the Level 1 residual variable eidt, we compare two ways of modeling its covariance structure: the default error covariance structure and the dependent error covariance structure. The former sets the residual variances to be equal for mothers and fathers and assumes all the covariances to be 0, resulting a diagonal homogeneous covariance matrix (see Equation 12). Using our specific example, the default covariance structure implies that mother and father reports of marital satisfaction, after controlling for the individual linear trends, are unrelated and have the same amount of intraindividual variability. In other words, after controlling for the individual linear trends, mothers’ and fathers’ reports of marital satisfaction are not correlated at a given time point and the amount of intraindividual variability in mothers’ reports of marital satisfaction is assumed to be the same as that in fathers’ reports of marital satisfaction ( in Equation 12).
| (12) |
An alternative to this default error covariance structure is to account for interdependence in the Level-1 residuals of two members of a dyad at a given time point. An appropriate dependent error covariance structure for Level 1 residuals in LDD analysis is the heterogeneous compound symmetry covariance structure (e.g., Fitzmaurice et al., 2011; Kashy & Donnellan, 2008; Singer & Willett, 2003). That is, the Level 1 residual variances for mothers and fathers are allowed to differ from each other, and the Level 1 errors of the mother and the father of a dyad are allowed to covary at a given time point (see Equation 13). Again, using our specific example, the dependent covariance structure implies that mother and father reports, after controlling for the individual linear trends, are allowed to covary at a given time point and have different amounts of average intraindividual variability between mothers and fathers.
In Equation 13, σmf represents the covariance between the Level 1 residuals of mothers and fathers at a given time point. In addition, σmf is assumed to be the same across different dyads and different time points. represents the Level 1 residual variance for mothers and represents the Level 1 residual variance for fathers, which are also assumed to be same across dyads and across different time points, respectively. The dependent specification gives us extra information, especially about differences and relations between dyadic members. Using our specific example, we can test whether to study whether mothers and fathers have the same amount of average intraindividual variability in reports of marital satisfaction around their individual fitted trajectories. Furthermore, we can test whether σmf = 0 to investigate whether the intraindividual fluctuations in reports of marital satisfaction around the individual fitted trajectories covary between mothers and fathers at a given time point. In other words, after controlling the linear trends, σmf could inform us whether when a mother has a higher level of marital satisfaction, the father tends to have a higher level of marital satisfaction as well.
| (13) |
Simultaneous SEM Models for Both Dyad Members
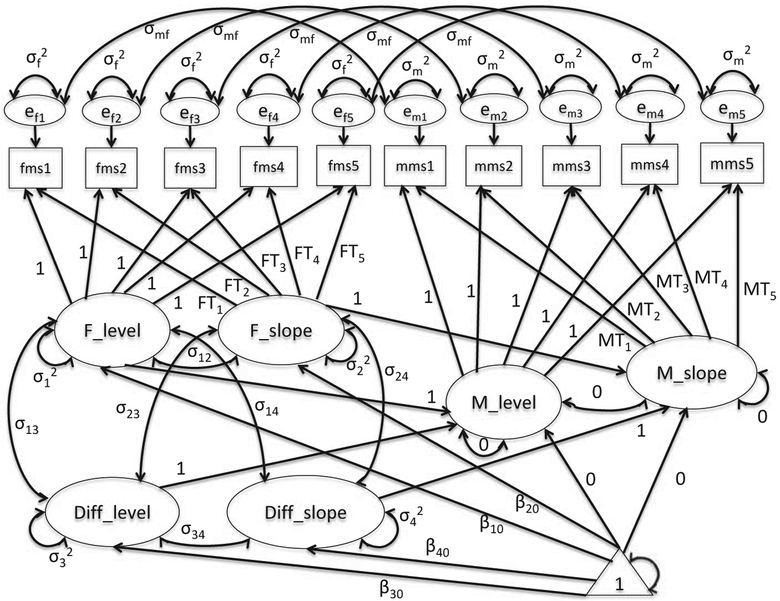
To specify models in the SEM framework that mimic the MLM models for simultaneously modeling data from both mothers and fathers, two sets of latent variables, latent intercepts and slopes for mothers and fathers, respectively, are included. They are M_level, M_slope, F_level, and F_slope. To compare mothers and fathers, difference score variables (Diff_level and Diff_slope) are also generated. More specifically, we have Diff_level = M_level – F_level and Diff_slope = M_slope – F_slope, where the means and variances of both M_level and M_slope are set to be 0 because we want to estimate the means and variances of Diff_level and Diff_slope. The means and variances of both F_level and F_slope are freely estimated. By using those constraints, we set fathers in the reference group, which mimics the MLM framework. The four latent variables, including F_level, F_slope, Diff_level, and Diff_slope, corresponding to the random effects b1d; b2d; b3d; and b4d in Equation 6, are assumed to follow a multivariate normal distribution with a 4 × 4 freely estimated covariance matrix. This matrix is equivalent to the G2 matrix in Equation 11 in the MLM framework. Under the default residual covariance structure method, residuals em1 to em5 and ef1 to ef5 are assumed to follow a multivariate normal distribution with a 10 × 10 homogeneous diagonal covariance matrix (see Equation 12). The path diagram for the simultaneous SEM model with the default error covariance structure is depicted in Figure 2. As illustrated, the unique residual variances are constrained to be equal across the time points and between mothers and fathers, and the covariance between mother and father unique residuals at each time point is constrained to 0.
FIGURE 2.
Path diagram of simultaneous SEM models with the default error covariance structure. T1, T2, T3, T4, and T5 are 3/12, 5/12, 7/12, 12/12, and 20/12 for mothers and 3/12, 5/12, 7/12, 14/12, and 20/12 for fathers for our example.
We can also specify the simultaneous model with the dependent error covariance structure (i.e., heterogeneous compound symmetry error covariance structure) in the SEM framework (see Figure 3). In contrast to the simultaneous model with the default error covariance structure, the unique residual variance of mothers (variance of em1 to em5; ) are allowed to be different from the unique residual variance of fathers (variance of ef1 to ef5; ). In addition, the covariance between mother unique residuals and father unique residuals at each time point (σmf) is freely estimated.
FIGURE 3.
Path diagram of simultaneous SEM models with the dependent error covariance structure. T1, T2, T3, T4, and T5 are 3/12, 5/12, 7/12, 12/12, and 20/12 for mothers and 3/12, 5/12, 7/12, 14/12, and 20/12 for fathers for our example.
EMPIRICAL RESULTS FROM THE MODELS
Results From the Separate Modeling Strategies
Using the separate modeling strategies, we can answer the first two research questions:
How do mothers’ (or fathers’) reports of marital satisfaction change over time, on average?
How do mothers (or fathers) differ in changes in marital satisfaction over time?
First, we examined the estimates of fixed effects (or estimated means of latent variables) from each MLM or SEM model (see Table 3). As expected, fixed effects estimates and their standard error estimates are identical from the two modeling frameworks, for both mother and father models. Substantively, mothers’ average initial level of marital satisfaction was 119.31, and decreased by approximately 3.5 points per year. Fathers’ average initial level of marital satisfaction was 117.19 and decreased at approximately1.89 points per year, although this slope estimate is not significantly different from 0. The initial levels of marital satisfaction are similar between mothers and fathers and there were decreasing patterns over time for both, although mothers’ changes were significant and fathers’ changes were not. For the estimates of the variance parameters, again MLM and SEM had nearly identical results because the models were specified in the same way. This is consistent with our expectation that both MLM and SEM can be used to examine longitudinal data and yield the same results given the same model specification. The results from variance tests were all significant, indicating that there was sufficient variation in mothers’ and fathers’ initial levels and changes in marital satisfaction over time. Furthermore, the estimates of the average intraindividual variability after accounting for the individual fitted linear trends were 108.66 and 106.00 for mothers and fathers, respectively (Research Question 6). However, based on results from the separate modeling of mothers’ and fathers’ data, we are not able to statistically infer whether fathers’ change trajectories differ from those of mothers. The trajectories looked similar, but there is no statistical comparison, because we examined each dyad member using a separate model.
TABLE 3.
Separate Mother and Father Modeling Results: Estimates of Fixed Effects and Variance Components Using MLM and SEM
| Mother | Father | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MLM | SEM | MLM | SEM | |||||||||
| Fixed Effects | ||||||||||||
| Estimate | SE | p value | Estimate | SE | p value | Estimate | SE | p value | Estimate | SE | p value | |
| β10 | 119.31 | 1.66 | < .001 | 119.31 | 1.66 | < .001 | 117.19 | 1.79 | < .001 | 117.19 | 1.79 | < .001 |
| β20 | −3.45 | 1.24 | 0.006 | −3.45 | 1.24 | 0.006 | −1.89 | 1.16 | 0.105 | −1.89 | 1.16 | 0.104 |
| Variance Components | ||||||||||||
| Estimate | SE | p value | Estimate | SE | p value | Estimate | SE | p value | Estimate | SE | p value | |
| 282.91 | 45.67 | < .001 | 282.91 | 45.67 | < .001 | 347.39 | 53.19 | < .001 | 347.39 | 53.19 | < .001 | |
| 91.55 | 25.53 | < .001 | 91.55 | 25.53 | < .001 | 76.13 | 23.13 | < .001 | 76.13 | 23.13 | .001 | |
| σ12 | −23.20 | 26.27 | .377 | −23.20 | 26.27 | .377 | −49.52 | 28.26 | .080 | −49.51 | 28.25 | .080 |
| 108.67 | 8.29 | < .001 | 108.67 | 8.29 | < .001 | 103.00 | 8.05 | < .001 | 103.00 | 8.06 | < .001 | |
Note. β10 = average initial level; β20 = average linear slope; = variance of initial levels; = variance of linear slopes; σ12 = covariance of initial levels and linear slopes; = residual variance.
Results From the Simultaneous Modeling Strategies
To address our substantive research questions, especially on whether mothers and fathers differ in their initial levels and changes over time in marital satisfaction, we fit the simultaneously modeling models (2 MLM and 2 SEM models) to the data and the results are displayed in Table 4. First, fixed effects estimates and their standard error estimates from the MLM and SEM models were very similar, regardless of the different specifications of the error covariance structures. In addition, the estimates were also similar to those from the models that were separately fitted to the data for fathers and mothers. Although the fixed effects results were similar, we can conduct additional statistical tests on β30 and β40 for comparing estimates between mothers and fathers using the simultaneous models (Research Question 3). The differences between mothers and fathers were nonsignificant based on the Wald tests, indicating that the average initial levels and linear slopes in marital status for mothers and fathers were not significantly different from each other in this sample. For the covariances and correlations among the random-effects (latent) changes (Equation 11, Research Question 5), the correlation between fathers’ initial levels of marital satisfaction and the differences in the initial levels between fathers and mothers was significantly negative (the estimates were −.47 and −.50 from the default and dependent approaches with ps ≤ .002 from the Wald tests, respectively), indicating that the higher the fathers’ initial levels, the lower the differences in the initial levels between fathers and mothers. The other covariances and correlations were not significantly different from 0. This information, however, cannot be obtained from the separate modeling approach. Therefore, the simultaneous models allow us to statistically infer differences and relations between mothers and fathers, whereas this cannot be done from the models with separately modeled data from fathers and mothers.
TABLE 4.
Estimates of Fixed Effects and Variance–Covariance Parameters From Simultaneous Modeling Mothers’ and Fathers’ Data Using MLM and SEM
| Default Error Covariance Structure | Dependent Error Covariance Structure | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MLM | SEM | MLM | SEM | |||||||||
| Fixed Effects | Estimate | SE | p value | Estimate | SE | p value | Estimate | SE | p value | Estimate | SE | p value |
| Father intercept β10 | 117.22 | 1.79 | < .001 | 117.22 | 1.79 | < .001 | 117.21 | 1.79 | < .001 | 117.21 | 1.79 | < .001 |
| Father slope β20 | −2.15 | 1.17 | 0.070 | −2.15 | 1.18 | 0.070 | −2.12 | 1.16 | 0.071 | −2.12 | 1.17 | 0.071 |
| Difference in M vs. F intercept β30 | 2.09 | 1.56 | 0.182 | 2.09 | 1.56 | 0.180 | 2.09 | 1.56 | 0.181 | 2.09 | 1.56 | 0.179 |
| Difference in M vs. F slope β40 | −1.43 | 1.27 | 0.263 | −1.43 | 1.28 | 0.265 | −1.41 | 1.27 | 0.267 | −1.41 | 1.28 | 0.269 |
| Variance Components | Estimate | SE | p value | Estimate | SE | p value | Estimate | SE | p value | Estimate | SE | p value |
| Father intercept | 345.91 | 52.99 | < .001 | 345.92 | 52.99 | < .001 | 346.21 | 53.05 | < .001 | 346.21 | 53.05 | < .001 |
| Father slope | 80.71 | 23.76 | < .001 | 80.75 | 23.77 | < .001 | 78.95 | 23.78 | < .001 | 78.95 | 23.78 | < .001 |
| Difference in M vs. F intercept | 165.19 | 41.03 | < .001 | 165.20 | 41.03 | < .001 | 189.82 | 41.34 | < .001 | 189.80 | 41.34 | < .001 |
| Diff in M vs. F slope | 22.91 | 26.61 | 0.195 | 22.93 | 26.61 | 0.195 | 49.72 | 27.44 | 0.035 | 49.72 | 27.44 | 0.035 |
| Cov (Father intercept, Father slope) σ12 | −50.83 | 28.32 | 0.073 | −50.84 | 28.33 | 0.073 | −50.35 | 28.27 | 0.075 | −50.35 | 28.27 | 0.075 |
| Cov (Father intercept, Difference in intercept) σ13 | −114.09 | 36.96 | < .001 | −114.09 | 36.96 | .002 | −127.63 | 37.20 | 0.001 | −127.64 | 37.21 | 0.001 |
| Cov (Father intercept, Difference in slope) σ14 | 31.59 | 29.07 | 0.277 | 31.60 | 29.07 | 0.277 | 44.89 | 29.44 | 0.127 | 44.89 | 29.44 | 0.127 |
| Cov (Father slope, Difference in intercept) σ23 | 12.06 | 24.01 | 0.615 | 12.09 | 24.02 | 0.615 | 21.66 | 24.09 | 0.369 | 21.66 | 24.09 | 0.369 |
| Cov (Father slope, Difference in slope) σ24 | −2.12 | 19.68 | 0.914 | −2.14 | 19.68 | 0.913 | −17.57 | 20.29 | 0.387 | −17.57 | 20.29 | 0.387 |
| Cov (Difference in intercept, Diff in slope) σ34 | −16.33 | 28.16 | 0.562 | −16.34 | 28.16 | 0.562 | −37.33 | 28.56 | 0.191 | −37.33 | 28.56 | 0.191 |
| Level 1 residual | 105.47 | 5.74 | < .001 | 105.46 | 5.75 | < .001 | NA | NA | NA | NA | NA | NA |
| Residual variance Mother | NA | NA | NA | NA | NA | NA | 108.58 | 8.28 | < .001 | 108.58 | 8.28 | < .001 |
| Residual variance Father | NA | NA | NA | NA | NA | NA | 103.36 | 8.11 | <.001 | 103.36 | 8.11 | < .001 |
| Correlation between Mother and Father residuals ρmf | 0 | N/A | N/A | 0 | NA | NA | .170 | .054 | .002 | .170 | .054 | .002 |
Note. M = mother; F = father; NA = not available; SE = standard error estimate. The variance tests are one-sided (H0: variance = 0 vs. Ha: variance > 0), which is the default of SAS PROC MIXED. One-sided Wald variance tests are recommended by Fitzmaurice et al. (2011) because two-sided Wald variance tests are too conservative due to the boundary issue (also see Ke & Wang, 2015). The default of Mplus is two-sided tests, so for testing the variance components, the p values in the Mplus columns are the two-sided p values from Mplus divided by 2.
In terms of the estimates of Level-1 (or unique) residual variance–covariance components, the results from the simultaneous default and simultaneous dependent methods differed, in line with our expectations that allowing mother and father residuals to covary would alter some variance and covariance estimates (see Table 4). Although the simultaneous default method allows us to compare fixed effects (or means in SEM) estimates between mothers and fathers, it does not account for interdependence between dyadic members of a dyad within a time point after controlling the individual linear trends and does not allow different Level-1 (or unique) residual variances between mothers and fathers. The simultaneous dependent method, however, does account for these. Consequently, in terms of variance–covariance parameter estimates, there were some differences in the results from the default and dependent methods.
Specifically, the correlation between mother and father residuals in the simultaneous default method is fixed at zero, and in the dependent method is estimated. As can be seen in Table 4, there was indeed a significant correlation between mother and father Level-1 (or unique) residuals at a given time point (rmf = .170 with p = .002 from both MLM and SEM), indicating nonindependence in the Level-1 (or unique) residuals of a dyad and implying that after controlling the linear trends, when a mother had a higher marital satisfaction, the father tended to have a higher marital satisfaction (Research Question 8).
In addition, to answer Research Question 6, the simultaneous default method gives the same Level-1 (or unique) residual variance estimate for both mothers and fathers (estimate = 105.47 and 105.46 from MLM and SEM, respectively), whereas the dependent method allows us to estimate separate Level-1 (or unique) residual variances for mothers and fathers (108.58 vs. 103.36 from both MLM and SEM). Although the two residual variances were not significantly different from each other, χ2(1) = 0.20, p = .655, from both MLM and SEM, using these data (Research Question 7), the dependent method gives us more information about mothers’ and fathers’ residual variances and allows a statistical test for comparing them.
With regard to Research Question 4, the variance estimate of the differences in slopes between mothers and fathers differed between the default and dependent methods. For example, using the default method, the variance estimates were 22.91 and 22.93 from MLM and SEM, respectively, and were not significant (p = .195) from the MLM. In contrast, using the dependent method, the variance estimates were 49.72 and 49.71 from MLM and SEM, respectively, and were significant (p = .034). This has some practical implications. For example, when the default method was used, the insignificant variance test results might lead a researcher not to examine possible predictors of the differences in linear slopes (e.g., Ke & Wang, 2015; Singer & Willett, 2003). When the dependent method was used, the researcher would examine possible predictors of the differences in linear slopes. Again, the dependent method could give us more information.
Finally, we compared the model fits of the simultaneous models with default or dependent error covariance structures using the likelihood ratio test. The −2LL for the simultaneous default model was 9696.3, and for the simultaneous dependent model was 9686.6. With two degrees of freedom, the dependent model fit the data significantly better than the standard model. The SAS PROC MIXED and Mplus code for fitting the aforementioned models is included in Appendix B.1 In addition, R lme code for MLM modeling and R lavaan code for SEM is also included in the online supplementary document.
DISCUSSION
Our study was motivated by the fact that the separate modeling strategy is still the most widely used method in LDD analysis. Researchers might not be aware of the limitations of the separate modeling strategy nor appreciate the extra information and flexibility the simultaneous models can provide. Therefore, the goal of this study was to compare multiple modeling methods of analyzing LDD for studying change differences within distinguishable dyads, illustrate the similarities and differences in the results from the models, and provide our recommendations. Specifically, we compared the separate modeling to simultaneous modeling strategies, and also a default method with a dependent method for the error covariance structure under the simultaneous modeling strategy. We analyzed real LDD in both the MLM and SEM frameworks. Results showed that, although estimates of fixed effects were similar from the different modeling approaches, estimates of variance components substantially differed.
MLM Versus SEM
Researchers have long understood that MLM and SEM can and will provide identical or nearly identical results if the underlying models are specified in the same way. For example, Newsom (2002) and Wendorf (2002) showed that identical or nearly identical results were obtained from analyzing cross-sectional dyadic data in the two frameworks. Kashy and Donnellan (2008) analyzed longitudinal dyadic data using both MLM and SEM and showed that identical results were also obtained. In this study, we showed how to specify models for LDD analysis in the same way in both MLM and SEM frameworks and demonstrated that identical or nearly identical results can be obtained from the two frameworks. Although the two frameworks could yield identical results, there are advantages and limitations for LDD analysis using each framework.
On the one hand, SEM is useful and flexible when multiple manifest variables are used for measuring a latent construct and thus latent variables need to be generated to define latent constructs (e.g., Grimm, Kuhl, & Zhang, 2013). As shown in our examples, it is also flexible and easy to form latent variables from latent variables such as Diff_level and Diff_slope for various interesting comparisons. Furthermore, it is more flexible to test longitudinal and dyadic measurement invariance using the SEM framework, as shown in Whittaker et al. (2014). On the other hand, MLM is more straightforward in terms of handling unbalanced data. In this study, at Wave 3, mothers were measured at 12 months and fathers at 14 months. Although the data look unbalanced between mothers and fathers, within each maternal or paternal group, the data are balanced. Thus, we can handle the differences in the age values between mothers and fathers in both frameworks (exact age values are used in MLM and different sets of factor loadings for the linear slope latent variable for mothers and fathers in SEM). When the data are unbalanced within each maternal or paternal group, however, it is more straightforward for MLM to handle the unbalanced nature of the data by including the exact age values for different individuals.
Separate Modeling Versus Simultaneous Default Versus Simultaneous Dependent
More important, we also examined multiple modeling methods for LDD analysis in both MLM and SEM frameworks. Although methodology articles have been emphasizing the need for analyzing dyadic data simultaneously, our nonexhaustive literature review showed that the separate modeling strategy is still the most popular method. Conceptually, it is impossible to compare changes between dyad members when the separate modeling strategy is used, so the simultaneous modeling strategy can give us much more informative results, especially in terms of the meaningful comparisons between dyad members (see Table 2 for a summary). Under the simultaneous modeling strategy, our results demonstrated the importance of considering all different kinds of interdependence. The difference between simultaneous default and dependent error covariance structures lies in how we treat the interdependence of the two dyad members at a given time point. Quantitatively, our results showed that although the fixed effect estimates were similar from different modeling methods, the estimates and statistical inference of variance–covariance components could be very different. For multilevel models, the maximum likelihood estimates of fixed effects are unbiased as long as the mean structure is correctly specified, even when the covariance structure is misspecified (e.g., Liang & Zeger, 1986). Therefore, it is not surprising to see that the fixed-effects estimates in our study were similar to each other from the models with different specifications for the covariance structure because the mean structures were the same across the models. However, it should also be noted that different covariance structures could empirically influence estimates of fixed effects and their standard error estimates, as emphasized by statisticians and methodologists such as Bamia, White, and Kenward (2013) and Liu, Rovine, and Molenaar (2012). Substantively, allowing the residual covariances at both levels to be nonzero in the simultaneous dependent approach appropriately reflects the fact that dyadic members (e.g., mother and father) could be dependent at a given time point due to shared experiences at the time point that are not captured by the predictor variables such as the time variable in our example (see Bolger & Shrout, 2007, for a more detailed discussion and examples). Therefore, it is important to have an appropriate covariance structure specified for LDD analysis given the different kinds of interdependence in LDD.
Because the default model is a reduced model of the dependent model, we can fit both to LDD and compare model fits. If the dependent error covariance structure fits the data significantly better, it should be used. The extra parameters in the model with the dependent error covariance structure shed light on differences in intraindividual variability and relations in intraindividual fluctuations between dyadic members after controlling trends.
To allow the use of the simultaneous approaches, data from both dyad members over time need to be collected (e.g., Kenny et al., 2006). Depending on the shape of the change trajectory, different numbers of time points are needed for capturing the change pattern accurately (e.g., Singer & Willett, 2003). Generally speaking, at least three time points are needed for estimating linear curves, four for quadratic curves, and five for cubic and other nonlinear curves. The simultaneous models can also be viewed as bivariate growth curve models. Power to detect fixed effects, variances, and covariances between latent slopes for univariate and bivariate growth curve models has been discussed in the literature (e.g., Bolger & Laurenceau, 2013; Fitzmaurice et al., 2011; Hertzog, Lindenberger, Ghisletta, & Oertzen, 2006; Rast & Hofer, 2014; Satorra & Saris, 1985). An adequate amount of data needs to be collected to ensure both estimation accuracy and statistical power in LDD analysis. Future studies are needed to examine the data requirements for LDD analysis.
Conclusion and Recommendations
In conclusion, if one wants to compare changes over time between dyad members, we recommend repeatedly collecting data from both dyad members over time and using a model with simultaneously modeling data from both dyad members to statistically infer differences in changes between dyad members. The default error covariance structure (homogeneous diagonal error covariance structure) fails to take all kinds of interdependence in dyadic data into account. A dependent error covariance structure, heterogeneous compound symmetry error covariance structure, allows heterogeneity and interdependence in the data from members of a dyad at a given time point and thus we recommend the use of dependent error covariance structures for LDD analysis. We hope this article helps researchers better analyze their longitudinal dyadic data with distinguishable dyads.
Supplementary Material
FUNDING
Funding for Elizabeth M. Planalp was awarded by the National Institute of Mental Health of the National Institutes of Health under Award Number T32MH018931. Data collection was supported by National Institute of Child Health and Development 5R03 HD39802 awarded to Julie M. Braungart-Rieker. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
All the materials in the appendices can be found at http://www3.nd.edu/~lwang4/LDD-SEM/.
REFERENCES
- Atkins DC (2005). Using multilevel models to analyze couple and family treatment data: Basic and advanced issues. Journal of Family Psychology, 19, 98–110. doi: 10.1037/0893-3200.19.1.98 [DOI] [PubMed] [Google Scholar]
- Baltes BP, & Nesselroade JR (1979). History and rationale of longitudinal research In Nesselroade JR & Baltes BP (Eds.), Longitudinal research in the study of behavior and development (pp. 1–39). London, UK: Academic Press. [Google Scholar]
- Bamia C, White IR, & Kenward MG (2013). Some consequences of assuming simple patterns for the treatment effect over time in a linear mixed model. Statistics in Medicine, 32, 2585–2594. doi: 10.1002/sim.5707 [DOI] [PubMed] [Google Scholar]
- Bauer DJ (2003). Estimating multilevel linear models as structural equation models. Journal of Educational and Behavioral Statistics, 28, 135–167. doi: 10.3102/10769986028002135 [DOI] [Google Scholar]
- Bolger N, & Laurenceau J-P (2013). Intensive longitudinal methods: An introduction to diary and experience sampling research. New York, NY: Guilford. [Google Scholar]
- Bolger N, & Shrout PE (2007). Accounting for statistical dependency in longitudinal data on dyads In Little TD, Bovaird JA, & Card NA (Eds.), Modeling contextual effects in longitudinal studies (pp. 285–298). Mahwah, NJ: Erlbaum. [Google Scholar]
- Bollen KA (1998). Structural equation models. New York, NY: Wiley. [Google Scholar]
- Card NA, Selig JP, & Little T (Eds.). (2011). Modeling dyadic and interdependent data in the developmental and behavioral sciences. London, UK: Routledge. [Google Scholar]
- Du H, & Wang L (2016). The impact of the number of dyads on estimation of dyadic data analysis using multilevel modeling. Methodology, 12(1), 21–31. doi: 10.1027/1614-2241/a000105 [DOI] [Google Scholar]
- Ferrer E, & McArdle JJ (2003). Alternative structural models for multivariate data analysis. Structural Equation Modeling, 10, 493–524. doi: 10.1207/S15328007SEM1004_1 [DOI] [Google Scholar]
- Ferrer E, & Nesselroade JR (2003). Modeling affective processes in dyadic relations via dynamic factor analysis. Emotion, 3, 344–360. doi: 10.1037/1528-3542.3.4.344 [DOI] [PubMed] [Google Scholar]
- Fitzmaurice GM, Laird NM, & Ware JH (2011). Applied longitudinal analysis. New York, NY: Wiley. [Google Scholar]
- Gonzalez R, & Griffin D (2012). Dyadic data analysis. Washington, DC: American Psychological Association. [Google Scholar]
- Grimm KJ, Kuhl AP, & Zhang Z (2013). Measurement models, estimation, and the study of change. Structural Equation Modeling, 20, 504–517. doi: 10.1080/10705511.2013.797837 [DOI] [Google Scholar]
- Grimm KJ, Steele JS, Ram N, & Nesselroade JR (2013). Exploratory latent growth models in the structural equation modeling framework. Structural Equation Modeling, 20, 568–591. doi: 10.1080/10705511.2013.824775 [DOI] [Google Scholar]
- Hedeker D, & Gibbons RD (2006). Longitudinal data analysis (Vol. 451). New York, NY: Wiley. [Google Scholar]
- Hertzog C, Lindenberger U, Ghisletta P, & Oertzen TV (2006). On the power of multivariate latent growth curve models to detect correlated change. Psychological Methods, 11, 244–252. doi: 10.1037/1082-989X.11.3.244 [DOI] [PubMed] [Google Scholar]
- Kashy DA, & Donnellan MB (2008). Comparing MLM and SEM approaches to analyzing developmental dyadic data: Growth curve models of hostility in families In Card N, Selig J, & Little T (Eds.), Modeling dyadic and interdependent data in the developmental and behavioral sciences (pp. 165–190). New York, NY: Routledge/Taylor & Francis Group. [Google Scholar]
- Kashy DA, Donnellan MB, Burt SA, & McGue M (2008). Growth curve models for indistingishable dyads using multilevel modeling and structural equation modeling: The case of adolescent twins’ conflict with their mothers. Developmental Psychology, 44, 316–329. [DOI] [PubMed] [Google Scholar]
- Ke Z, & Wang L (2015). Detecting individual differences in change: Methods and comparisons. Structural Equation Modeling, 22, 382–400. doi: 10.1080/10705511.2014.936096 [DOI] [Google Scholar]
- Kenny DA, Kashy DA, & Cook WL (2006). Dyadic data analysis. New York, NY: Guilford. [Google Scholar]
- Kopp CB (1989). Regulation of distress and negative emotions: A developmental view. Developmental Psychology, 25, 343–354. [Google Scholar]
- Laursen BP, Little TD, & Card NA (Eds.). (2012). Handbook of developmental research methods. New York, NY: Guilford. [Google Scholar]
- Ledermann T, Macho S, & Kenny DA (2011). Assessing mediation in dyadic data using the actor-partner interdependence model. Structural Equation Modeling, 18, 595–612. doi: 10.1080/10705511.2011.607099 [DOI] [Google Scholar]
- Liang K-Y, & Zeger SL (1986). Longitudinal data analysis using generalized linear models. Biometrika, 73, 13–22. doi: 10.1093/biomet/73.1.13 [DOI] [Google Scholar]
- Liu S, Rovine MJ, & Molenaar PC (2012). Selecting a linear mixed model for longitudinal data: Repeated measures analysis of variance, covariance pattern model, and growth curve approaches. Psychological Methods, 17(1), 15–30. doi: 10.1037/a0026971 [DOI] [PubMed] [Google Scholar]
- Locke HJ, & Wallace KM (1959). Short marital-adjustment and prediction tests: Their reliability and validity. Marriage and Family Living, 21, 251–255. [Google Scholar]
- Lyons KS, & Sayer AG (2005). Longitudinal dyad models in family research. Journal of Marriage and Family, 67, 1048–1060. doi: 10.1111/j.1741-3737.2005.00193.x [DOI] [Google Scholar]
- MacCallum RC, Kim C, Malarkey WB, & Kiecolt-Glaser JK (1997). Studying multivariate change using multilevel models and latent curve models. Multivariate Behavioral Research, 32, 215–253. doi: 10.1207/s15327906mbr3203_1 [DOI] [PubMed] [Google Scholar]
- McArdle JJ (2009). Latent variable modeling of differences and changes with longitudinal data. Annual Review of Psychology, 60, 577–605. doi: 10.1146/annurev.psych.60.110707.163612 [DOI] [PubMed] [Google Scholar]
- McArdle JJ, & Nesselroade JR (2014). Longitudinal data analysis using structural equation models. Washington, DC: American Psychological Association. [Google Scholar]
- Meredith W, & Tisak J (1990). Latent curve analysis. Psychometrika, 55, 107–122. doi: 10.1007/BF02294746 [DOI] [Google Scholar]
- Muthén LK, & Muthén BO (1998–2010). Mplus user’s guide (6th ed.). Los Angeles, CA: Muthén & Muthén. [Google Scholar]
- Newsom JT (2002). A multilevel structural equation model for dyadic data. Structural Equation Modeling, 9, 431–447. doi: 10.1207/S15328007SEM0903_7 [DOI] [Google Scholar]
- Pan JX, & Fang KT (2012). Growth curve models and statistical diagnostics. New York, NY: Springer Science & Business Media. [Google Scholar]
- Peugh JM, DiLillo D, & Panuzio J (2013). Analyzing mixed-dyadic data using structural equation models. Structural Equation Modeling, 20, 314–337. doi: 10.1080/10705511.2013.769395 [DOI] [Google Scholar]
- Planalp EM, Braungart-Rieker JM, Lickenbrock DM, & Zentall S (2013). Trajectories of parenting during infancy: The role of infant temperament and marital adjustment for mothers and fathers. Infancy, 18(Suppl. 1), E16–E45. doi: 10.1111/infa.12021 [DOI] [Google Scholar]
- Rast P, & Hofer SM (2014). Longitudinal design considerations to optimize power to detect variances and covariances among rates of change: Simulation results based on actual longitudinal studies. Psychological Methods, 19(1), 133–154. doi: 10.1037/a0034524 [DOI] [PMC free article] [PubMed] [Google Scholar]
- SAS Institute. (2011). SAS® 9.3 system options: Reference (2nd ed.). Cary, NC: Author. [Google Scholar]
- Satorra A, & Saris WE (1985). Power of the likelihood ratio test in covariance structure analysis. Psychometrika, 50, 83–90. [Google Scholar]
- Sayer AG, & Klute MM (2005). Analyzing couples and families: Multilevel methods In Bengtson VL, Acock AC, Allen KR, Dilworth-Anderson P, & Klein DM (Eds.), Sourcebook of family theory and research (pp. 289–313). Thousand Oaks, CA: Sage. [Google Scholar]
- Singer JD, & Willett JB (2003). Applied longitudinal data analysis: Methods for studying change and event occurrence. New York, NY: Oxford University Press. [Google Scholar]
- Tong X, & Zhang Z (2012). Diagnostics of robust growth curve modeling using Student’s t distribution. Multivariate Behavioral Research, 47, 493–518. doi: 10.1080/00273171.2012.692614 [DOI] [PubMed] [Google Scholar]
- Wendorf CA (2002). Comparisons of structural equation modeling and hierarchical linear modeling approaches to couples’ data. Structural Equation Modeling, 9, 126–140. doi: 10.1207/S15328007SEM0901_7 [DOI] [Google Scholar]
- Whittaker TA, Beretvas SN, & Falbo T (2014). Dyadic curve-of-factors model: An introduction and illustration of a model for longitudinal nonexchangeable dyadic data. Structural Equation Modeling, 21, 303–317. doi: 10.1080/10705511.2014.882695 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.