Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2019 Jan 16;4(1):1375–1385. doi: 10.1021/acsomega.8b02403

Establishing Cost-Effective Computational Models for the Prediction of Lanthanoid Binding in [Ln(NO3)]2+ (with Ln = La to Lu)

Charles C Peterson †,‡, Deborah A Penchoff ‡,*, John D Auxier II §, Howard L Hall ‡,∥,§,⊥,*
PMCID: PMC6649180  PMID: 31459405

Abstract

graphic file with name ao-2018-02403r_0008.jpg

Evaluating the efficiency of predictive methods is critical to the processes of upscaling laboratory processes to full-scale operations on an industrial scale. With regard to separation of lanthanoids, there is a considerable motivation to optimize these processes because of immediate use in nuclear fuel cycle operations, nuclear forensics applications, and rare-earth metal recovery. Efficient predictive capabilities in Gibbs free energies of reaction are essential to optimize separations and ligand design for selective binding needed for various radiochemical applications such as nuclear fuel disposition and recycling of lanthanoid fission products into useful radioisotope products. Ligand design is essential for selective binding of lanthanoids, as separating contiguous lanthanoids is challenging because of the similar behavior these elements exhibit. Modeling including electronic structure calculations of lanthanoid-containing compounds is particularly challenging because of the associated computational cost encountered with the number of electrons correlated in these systems and relativistic considerations. This study evaluates the predictive capabilities of various ab initio methods in the calculation of Gibbs free energies of reaction for [Ln(NO3)]2+ compounds (with Ln = La to Lu), as nitrates are critical in traditional separation processes utilizing nitric acid. The composite methodologies evaluated predict Gibbs free energies of reaction for [Ln(NO3)]2+ compounds within 5 kcal mol–1 in most cases from the target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3+SO] at a fraction of the computational cost.

Introduction

Nuclear operations involve handling of fission products (many of which are lanthanoids) and the partitioning for inclusion for other industrial processes such as radioisotope source production, nuclear forensics measurements, or waste disposition. Efficient and cost-effective methods of partitioning fission products into useful waste or product streams require specialized chemical processes that are well-suited for these unique applications. Development of these processes to separate fission products also requires careful selection of ligands to selectively extract useful elements (such as rare-earth metals) from bulk materials. These ligands are often selected based on radiation tolerance because degradation of chemical components from irradiation may result in a decrease of process efficiency.1 Design of selective ligands to optimize separation processes often involves hazardous experiments that could greatly benefit from additional information regarding the suitability of a given ligand. Furthermore, lanthanoids are often used as surrogates for complexation and structural analysis of actinoid compounds as it was recently highlighted in a study by Corbey and co-workers for americium compounds.2

Although there have been many advances in separation science, efficient and highly selective binding to lanthanoids and actinoids continues to be present challenges.3,4 Consequently, developing effective computational protocols to model lanthanoid-binding characteristics can aid researchers in nuclear operations to design new and improved methods of separating lanthanoids from bulk materials. Traditional electronic structure modeling of lanthanoid-containing compounds can be computationally expensive and inefficient for rapid predictive capabilities of large fully complexed compounds. Increasing the efficiency of these methods can provide a means of further optimizing chemical processes while providing guidance in laboratory experiments (i.e., preselection of potentially efficient ligands) without requiring the use of extensive computational resources, thus providing tools to optimize separation processes to a wider segment of the community. Benchtop chemical processes are often focused on determining if a particular method is possible and less on the efficiency of the chemical process. Although this is adequate for exploratory laboratory exercises, the question of efficiency in upscaling must be considered for any wide adoption of a process. To this end, determination of the thermochemical characteristics and prediction of how these may affect larger industrial processes is a significant consideration. Providing engineers with predictive capabilities to perform low-cost (both computationally and monetarily) simulations of complex lanthanoid systems and predictions of separation efficiency reduce the overall cost of industrial process design. Cost reduction stems from the ability to prototype systems in a virtual environment such that primary and alternate designs may be evaluated for further, often costlier, exploration.5

Among electronic structure methods in computational modeling, density functional theory (DFT) methods have been widely used to describe the thermochemical properties of lanthanoid-containing compounds. DFT can describe electron correlation at a reasonable computational cost; however, the predicted thermochemical characteristics can be largely dependent on the choice of level of theory as it was recently shown in a systematic study of 5f elements in an actinoid nitrate study.6 Furthermore, ab initio7 and composite methods8 have been used for thermochemical predictions, but these methodologies vary in computational cost and accuracy. Utilizing ab initio methods for lanthanoid-containing compounds can be challenging because of the number of electrons and basis functions needed to describe these systems, which increase the computational cost. Composite methods, such as f-ccCA9 (which follows the correlation consistent Composite Approach, ccCA, methodology10,11) and Feller–Peterson–Dixon (FPD),12 have been developed to describe the thermochemical properties of lanthanoid systems with the accuracy of methods such as coupled cluster with perturbative doubles and triples [CCSD(T)] at a lower computational cost. Both of these methods describe dynamical electron correlation, outer-core electron correlation, and effects due to special relativity including spin–orbit (SO) coupling. There have also been studies which utilized ab initio methods for thermochemical9,13 and spectroscopic13 analysis of small lanthanoid compounds.

Establishing accurate and cost-effective predictive computational models for selective binding of lanthanoids and actinoids is essential for the optimization and design of separations agents; and as previously indicated, reliable predictive capabilities for lanthanoid compounds are not only needed for fission products but also as surrogates for actinoid studies. Large systematic analysis of lanthanoid-containing complexes performed with ab initio methods can become highly restricted by the size of the compounds because of the computational constraints. This study focuses on lanthanoid mononitrate as this is a highly important system in lanthanoid- and actinoid-separation because of the common binding of one or more nitrates stemming from the often use of nitric acid in the separation process14,15—as also noted by Glatz in cataloguing all of the industrial processing for handling spent nuclear fuel.16 Because of the presence of nitric acid, nitrates bound to lanthanoids and actinoids have been observed in multiple separations, and synthesis and characterization studies with bis[(phosphino)methyl]pyridine-1-oxide (NOPOPO),2 1,2-phenylenediphosphonates,17 2,6-bis[(diphenylphosphino)methyl]pyridine N,P,P′-trioxide,18 2-((diphenylphosphino) methyl)pyridine, dioxide and 2,6-bis((diphenylphosphino)methyl)pyridineiV,P,P′-trioxide,19 decorated pyridine and pyridine n-oxide platforms,3 tetra-n-donor extractants,20 undiluted quaternary ammonium ionic liquid,21 cyclic dilactams,22 bis-1,2,3-triazolebipyridine,23 and cyclic imide dioximes,24 among others.

This work evaluates the performance of ab initio methodologies including MP2 and CCSD(T) calculations, along with composite methods to predict the Gibbs free energy of reaction involving the binding of nitrates to lanthanoid ions across the lanthanoid series (namely [Ln(NO3)]2+, with Ln = La to Lu). Additionally, the proposed method A and method B (as described in the Methods section) are evaluated for the prediction of Gibbs free energies of reaction of [Ln(OH)]2+. The [Ln(OH)]2+ model system is chosen as a secondary test set for the proposed methods because of hydroxyl anions bound to lanthanoids being important in separations of lanthanoids and actinoids, as illustrated in separations of americium from lanthanoids.25

Methods

The ab initio methods, MP226,27 and CCSD(T),27 are used to calculate the Gibbs free energies of reaction of [Ln(NO3)]2+ (where Ln = La–Lu). These methods are also used to determine the accuracy of the composite methodologies utilized in this study. Correlation-consistent basis sets are used throughout this study. The cc-pVnZ-DK312 basis set is used for the lanthanoids, whereas cc-pVnZ-DK28 is used for the N and O atoms (where n = ζ level). Also, the weighted core valence (cc-pwCVnZ-DK3 for Ln atoms; cc-pCVnZ-DK for N and O atoms)12,28 is used when accounting for core correlation. The third-order Douglas–Kroll–Hess Hamiltonian29 is used to describe scalar relativistic effects.

The model reaction for this study is described by eq 1.

graphic file with name ao-2018-02403r_m001.jpg 1

Six ab initio methods are used to compute Gibbs free energies of the reaction of [Ln(NO3)]2+ compounds [with Ln = La–Lu]. These methods are CCSD(T)-FSI/cc-pVTZ-DK3, MP2-FSI/cc-pVTZ-DK3, CCSD(T)-FSII/cc-pwCVTZ-DK3, MP2-FSI/cc-pV∞Z-DK3, CCSD(T)-FSI/cc-pV∞Z-DK3, and CCSD(T)-FSII/cc-pwCV∞Z-DK3. The description of the correlation space is indicated with the “FS” labels (for “frozen shell”), with FSI and FSII referring to the electrons in the correlation space. The FSI calculations include the valence electrons in the correlation space (4f5s5p for Ln atoms and 2s2p for N and O atoms). The FSII calculations add the outer-core electrons (FSI + 4s4p4d for Ln atoms and FSI + 1s for N and O atoms). The cc-pV∞Z-DK3 cc-pwCV∞Z-DK3 refers to the basis sets used to calculate at the complete basis set (CBS)8 limit. For the CBS calculations, the Hartree–Fock extrapolations use a two-point formula developed by Karton and Martin,30 described by eq 2

graphic file with name ao-2018-02403r_m002.jpg 2

where n is 3 and 4 for triple- and quadruple-ζ basis sets (cc-pVTZ-DK3 and cc-pVQZ-DK3),12,28 respectively. The correlation energy is extrapolated using a two-point extrapolation formula31 described by eq 3, with n = 2 and 3 (as utilized by Lu and Peterson12 for lanthanoid-containing systems).

graphic file with name ao-2018-02403r_m003.jpg 3

The accuracy of predictive capabilities of these methods is evaluated with respect to CCSD(T)-FSII/cc-pwCV∞Z-DK3 (i.e., target method included in this study) as it contains the highest amount of dynamic electronic correlation, outer-core correlation, and extrapolation to the CBS limit.

Various composite schemes have also been utilized, including f-ccCA9 and newly proposed variations (method A and method B). The total energy described by f-ccCA9 is shown by eq 4.

graphic file with name ao-2018-02403r_m004.jpg 4

The reference energy (Eref) is described by MP2-FSI/cc-pV∞Z-DK3. The ΔEcc term describes higher dynamic electronic correlation from CCSD(T)-FSI/cc-pVTZ-DK3. The ΔECV term describes the electronic correlation from the outer-core electronic correlation from CCSD(T)-FSII/cc-pwCVTZ-DK3. The ΔEspin term describes the SO interactions from the four-component Dirac–Hartree–Fock and triple-ζ basis set developed by Dyall,32 and it is calculated as shown in previous work.33

Another composite scheme, similar to f-ccCA9 except that the ΔEspin term is removed, is shown by eq 5. This composite method is referred throughout this article as method A.

graphic file with name ao-2018-02403r_m005.jpg 5

Last, the composite scheme described by eq 6 removes the ΔECC term and utilizes CCSD(T)-FSI/cc-pV∞Z-DK3 in the reference energy (instead of MP2). This composite method is referred to as method B throughout this article.

graphic file with name ao-2018-02403r_m006.jpg 6

The Gibbs free energy for the proposed reaction (ΔGrxn) for eq 1 is calculated as shown in eq 7, with the total energy obtained with the methods described in eqs 4–6, and thermochemical corrections obtained with DFT at 298.15 K (for the optimized structures as indicated in the Methods section). This approach was recently utilized in a similar study of [An(NO3)]2+ compounds, for which the thermochemical corrections for the Gibbs free energies of reaction are obtained at each level of theory utilized for the geometry and vibrational frequency calculations.6

graphic file with name ao-2018-02403r_m007.jpg 7

Although the focus of this study is on nitrate binding to lanthanoids, methods A and B are also evaluated against the target methodology for Gibbs free energies of reaction for hydroxyl anion binding to lanthanoids (namely [Ln(OH)]2+) for method-verification purposes.

The geometry optimizations are performed utilizing DFT following a protocol in previous work,34 with the B3LYP35,36 functional, the Stuttgart RSC Segmented ECP and associated basis set for the lanthanoid atoms, and the 6-311++G**37 basis set for O and N atoms with tight tolerances and extra fine grid. The ECP accounts for scalar relativistic effects by replacing 28 electrons with a relativistic pseudopotential. The compounds are optimized without imposing symmetry constraints. Thermochemical corrections are calculated at 298.15 K. No imaginary frequencies were found. The geometry optimizations and vibrational frequency calculations calculated with the B3LYP functional are obtained with the NWChem 6.8 package.38 All single-point calculations (except for Dirac–Hartree–Fock) are performed with MOLPRO2015.39 The DIRAC1640 software package was used for Dirac–Hartree–Fock calculations. Basis sets for non-lanthanoids are obtained from the Environmental Molecular Sciences Laboratory (EMSL) database.41,42

Results and Discussion

Unless otherwise indicated, the results discussed in this section correspond to an Ln IV configuration in the gas phase. This notation follows the NIST Atomic Spectra Database spectra name classifications which correspond to a defined electronic structure associated with each state, as shown in Table 1.43

Table 1. Electronic Configuration for Ln IV and Ln III43.

Ln Ln IV Ln III
La [Cd]5p6 [Xe]5d
Ce [Xe]4f [Xe]5f2
Pr [Xe]4f2 [Xe]4f3
Nd [Xe]4f3 [Xe]4f4
Pm [Xe]4f4 [Xe]4f5
Sm [Xe]4f5 [Xe]4f6
Eu [Xe]4f6 [Xe]4f7
Gd [Xe]4f7 [Xe]4f75d
Tb [Xe]4f8 [Xe]4f9
Dy [Xe]4f9 [Xe]4f10
Ho [Xe]4f10 [Xe]4f11
Er [Xe]4f11 [Xe]4f12
Tm [Xe]4f12 [Xe]4f13
Yb [Xe]4f13 [Xe]4f14
Lu [Xe]4f14 [Xe]4f147s
Open in a new tab

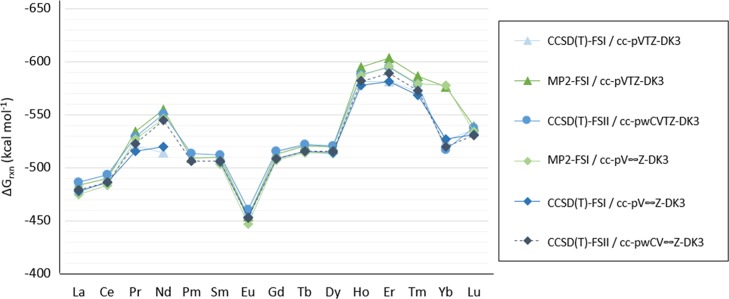
The Gibbs free energies of reaction (ΔGrxn) for the [Ln(NO3)]2+ complexes are calculated with the proposed methods described in the Methods section [namely CCSD(T)-FSI/cc-pVTZ-DK3, MP2-FSI/cc-pVTZ-DK3, CCSD(T)-FSII/cc-pwCVTZ-DK3, MP2-FSI/cc-pV∞Z-DK3, CCSD(T)-FSI/cc-pV∞Z-DK3, and CCSD(T)-FSII/cc-pwCV∞Z-DK3]. The predicted ΔGrxn of the [Ln(NO3)]2+ compounds for the lanthanoid series calculated by these methods are shown by Figure 1. All predicted ΔGrxn are tabulated in Table S1 in the Supporting Information.

Figure 1.

Figure 1

Open in a new tab

Predicted Gibbs free energies of reaction (ΔGrxn) for the [Ln(NO3)]2+ complexes calculated with CCSD(T)-FSI/cc-pVTZ-DK3, MP2-FSI/cc-pVTZ-DK3, CCSD(T)-FSII/cc-pwCVTZ-DK3, MP2-FSI/cc-pV∞Z-DK3, CCSD(T)-FSI/cc-pV∞Z-DK3, and CCSD(T)-FSII/cc-pwCV∞Z-DK3.

To assess the chemical accuracy of the computational methods used, the differences of the predicted ΔGrxn with each method are compared among the options studied. Accuracy between the MP2 and CCSD(T) methods is shown by comparing the difference in the predicted ΔGrxn, calculated with the CCSD(T)-FSI/cc-pVTZ-DK3 and MP2-FSI/cc-pVTZ-DK3 along with the difference between predicted ΔGrxn with CCSD(T)-FSI/cc-pV∞Z-DK3 and MP2-FSI/cc-pV∞Z-DK3. Throughout the lanthanoid series, the differences in predicted ΔGrxn between MP2-FSI and CCSD(T)-FSI are all under 15 kcal mol–1, except for [Nd(NO3)]2+, [Er(NO3)]2+, and [Yb(NO3)]2+ compounds, where the difference in predicted ΔGrxn is 40.0, 21.8, and 50.5 kcal mol–1, respectively. Using the cc-pVTZ-DK3 and cc-pV∞Z-DK3, basis sets show little effect in the difference in predicted ΔGrxn between MP2-FSI and CCSD(T)-FSI except for [Nd(NO3)]2+ and [Er(NO3)]2+ for which utilizing the cc-pV∞Z-DK3 basis set showed a decrease of 13.5 and 8.0 kcal mol–1, respectively.

The predicted ΔGrxn obtained with CCSD(T)-FSI/cc-pVTZ-DK3 and CCSD(T)-FSII/cc-pCVTZ-DK3 are compared with those calculated with CCSD(T)-FSI/cc-pV∞Z-DK3 and CCSD(T)-FSII/cc-pwCV∞Z-DK3 to show the effects of outer-core electron correlation to the predicted ΔGrxn. These effects on the predicted ΔGrxn are under 10 kcal mol–1 throughout the lanthanoid series with [Nd(NO3)]2+ and [Er(NO3)]2+ being the only compounds for which the difference is over 10 kcal mol–1. The differences in ΔGrxn between considering an FSI and FSII level at the CBS limit and at the triple-ζ basis set level were similar except for [Nd(NO3)]2+ and [Er(NO3)]2+, where predicted ΔGrxn from the CBS limit decrease by 11.5 and 5.9 kcal mol–1, respectively.

Overall, all of the ab initio methods predict the same binding trends for the [Ln(NO3)]2+ complexes throughout the series, except for Nd with CCSD(T)-FSI/cc-pVTZ-DK3 and CCSD(T)-FSI/cc-pV∞Z-DK3 which show a slight increase (of about 5 kcal mol–1) to the ΔGrxn from [Pr(NO3)]2+ to [Nd(NO3)]2+, whereas all other methods show a decrease of about 20 kcal mol–1.

Throughout the lanthanoid series, the lanthanoid in the [Ln(NO3)]2+ compound has been shown to have an Ln IV configuration except for Yb in which the predicted ground state has a Yb III configuration, where Yb has a fully occupied 4f shell (instead of a partly filled shell with 13 f electrons as in the Yb IV configuration). Because the Yb 4f shell is closed in this configuration, the open shell electron is in an N–O orbital. All of the computational methods tested for the proposed system in this study predict Yb III to be lower in energy except with CCSD(T)-FSI/cc-pVTZ-DK3 which predicts the Yb IV configuration to be 2.1 kcal mol–1 higher in energy than Yb III configuration. The CCSD(T)-FSII/cc-pwCVTZ-DK3 and CCSD(T)-FSI/cc-pV∞Z-DK3 methods predict the Yb III configuration to be 1.1 and 4.5 kcal mol–1 lower, respectively. The target method, CCSD(T)-FSII/cc-pwCV∞Z-DK3, shows that the Yb III configuration is more stable by 9.6 kcal mol–1. The MP2 methods show a wider gap between the two configurations, where MP2-FSI/cc-pVTZ and MP2-FSI/cc-pV∞Z-DK3 show that the Yb III configuration is more stable by having a lower energy by 52.0 and 59.9 kcal mol–1, respectively. A recent study on [An(NO3)]2+ compounds where An = Ac–Lr has also shown a ground state of an An III configuration instead of a An IV configuration for Fm, Md, and No atoms in the gas phase (but Fm IV and Md IV in the aqueous phase).6

Composite Results

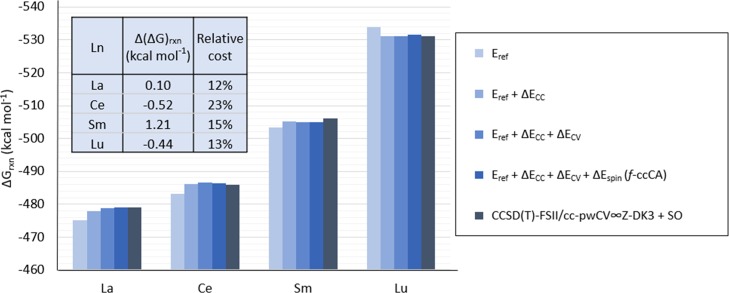
The ΔGrxn for [La(NO3)]2+, [Ce(NO3)]2+, [Pr(NO3)]2+, [Sm(NO3)]2+, and [Lu(NO3)]2+ is calculated with the composite methods described in eq 4 (f-ccCA), eq 5 (method A), and eq 6 (method B). Table 2 shows the difference between the predicted ΔGrxn calculated with the f-ccCA method and the target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3+SO]. In this case, the target method contains an SO correction calculated as indicated in the ΔEspin33 correction included in f-ccCA.9 The difference between the predicted ΔGrxn calculated utilizing the f-ccCA method (for the enthalpy calculation) and the target method is shown to be small, between 0.10 and 1.21 kcal mol–1 throughout the [La(NO3)]2+, [Ce(NO3)]2+, [Pr(NO3)]2+, [Sm(NO3)]2+, and [Lu(NO3)]2+ compounds tested. The breakdown of the contribution to the predicted energy with f-ccCA and with the target methodology is shown in Figure 2.

Table 2. Relative Energy of [La(NO3)]2+, [Gd(NO3)]2+, and [Lu(NO3)]2+ (Δ(ΔG)rxn) Calculated with Method A and B, Relative to CCSD(T)-FSII/cc-pwCV∞Z-DK3 and Associated Relative Computational Costa.

  method A Eref[MP2] + ΔECC + ΔECV
 method B Eref[CCSD(T)] + ΔECV
  Δ(ΔG)rxn (kcal mol–1) relative cost (%) Δ(ΔG)rxn (kcal mol–1) relative cost (%)
La 0.11 10 0.32 25
Gd –0.21 10 –0.30 34
Lu –0.44 11 –0.21 70
Open in a new tab
a

Relative computational cost is shown as a percentage and it is calculated as relative cost = (CPU hours with method A or B)/(CPU hours with CCSD(T)-FSII/cc-pwCV∞Z-DK3) × 100; Δ(ΔG)rxn = ΔGrxn(method A or B) – ΔGrxn(CCSD(T)-FSII/cc-pwCV∞Z-DK3).

Figure 2.

Figure 2

Open in a new tab

Predicted ΔGrxn for [Ln(NO3)]2+ calculated with f-ccCA and target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3 + SO]. The contribution from each term in the f-ccCA formulation [Eref, Eref + ΔEcc, Eref + ΔEcc + ΔEcv, and Eref + ΔEcc + ΔEcv + ΔEspin] is also shown. The relative computational cost and difference in predicted ΔGrxn calculated with f-ccCA and the target method is shown in the table (inset). [Relative computational cost is shown as a percentage and it is calculated as relative cost = (CPU units with f-ccCA)/(CPU units with target method) × 100; Δ(ΔG)rxn = ΔGrxn(f-ccCA) – ΔGrxn(target method)].

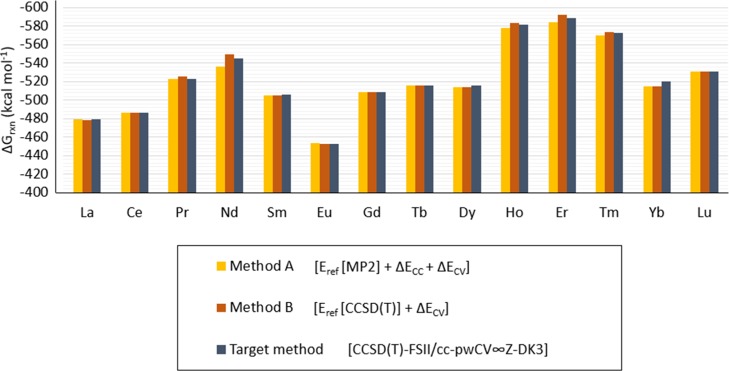
Moreover, the SO contribution to the overall ΔGrxn, as described by the ΔEspin term in f-ccCA, is found to be very small, under 0.49 kcal mol–1, except for [Pr(NO3)]2+, where this contribution is predicted to be 3.8 kcal mol–1. The predicted ΔGrxn obtained with the composite methods A and B does not include corrections for SO coupling because it was shown that the SO correction for the reaction proposed in eq 1 is under 3 kcal mol–1 and therefore, incurring the additional computational cost for adding this term for the reaction was unnecessary. In method A, the reference energy is obtained at the MP2-FSI level; a higher dynamic electronic correlation term, ΔEcc, is added to the CCSD(T)-FSI level; an additional outer-core electron correlation term, ΔEcv, is obtained at the CCSD(T)-FSII level, which is similar to f-ccCA except for the inclusion of SO effects. For the composite method B, the ΔEcc term is removed and the reference energy is computed at the CCSD(T)-FSI level which does not affect the ΔEcv term with CCSD(T)-FSII. Predicted ΔGrxn calculated with method A and method B is shown in Figure 3 for all of the lanthanoid compounds which shows a similar trend between ΔGrxn and the target method, CCSD(T)-FSII/cc-pwCV∞Z-DK3 (without SO), across the lanthanoid series.

Figure 3.

Figure 3

Open in a new tab

Predicted ΔGrxn for [Ln(NO3)]2+ calculated with composite method A (eq 5) and method B (eq 6), along with the target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3].

The predicted ΔGrxn with f-ccCA (eq 4) is within 2 kcal mol–1 from the ΔGrxn predicted with the target (CCSD(T)-FSII/cc-pwCV∞Z-DK3+SO) except for [Nd(NO3)]2+ where the difference is 8.6 kcal mol–1. The difference between the predicted ΔGrxn calculated with the composite methods from method A (eq 5) and B (eq 6) are shown to be small, under 1 kcal mol–1 in most of the systems, and between 3 and 13 kcal mol–1 for [Nd(NO3)]2+, [Ho(NO3)]2+, [Er(NO3)]2+, and [Tm(NO3)]2+. The difference between the predicted ΔGrxn calculated with the composite methods described by f-ccCA (eq 4) with CCSD(T)-FSII/cc-pwCV∞Z-DK3+SO and CCSD(T)-FSII/cc-pwCV∞Z-DK3 (target method for f-ccCA, method A and method B, respectively) are shown in the Supporting Information in Table S2.

The f-ccCA method shows a relative computational cost between 12 and 23% for prediction of the ΔGrxn of the [Ln(NO3)]2+ compounds over the target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3+SO], as shown in Figure 2. The impact to the predicted ΔGrxn is shown to be less than 1.5 kcal mol–1 from using f-ccCA. As expected, because composite method A has a reference energy computed with MP2, instead of CCSD(T), it has a lower computational cost than that when calculated with method B. Furthermore, the cost is lower (compared to the target method) for method A than for method B with less than a kcal mol–1 difference in the predicted ΔGrxn (as shown in Table 2).

Evaluation of Method A and Method B for [Ln(NO3)]2+ and [Ln(OH)]2+ Compounds

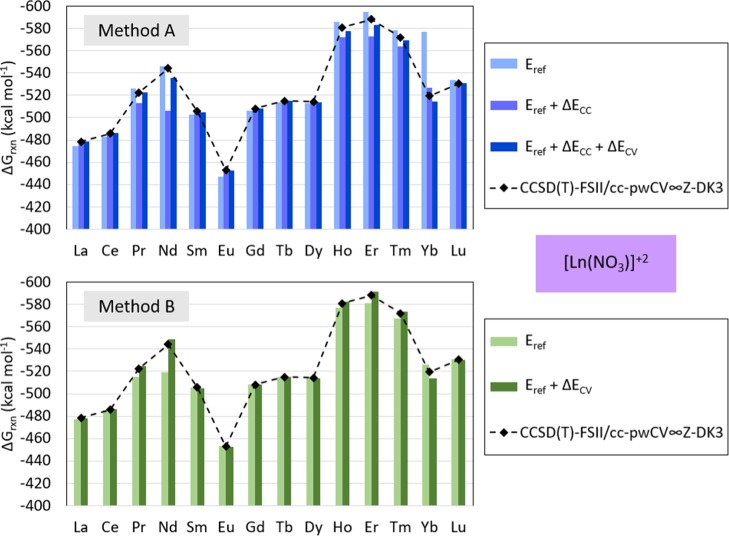
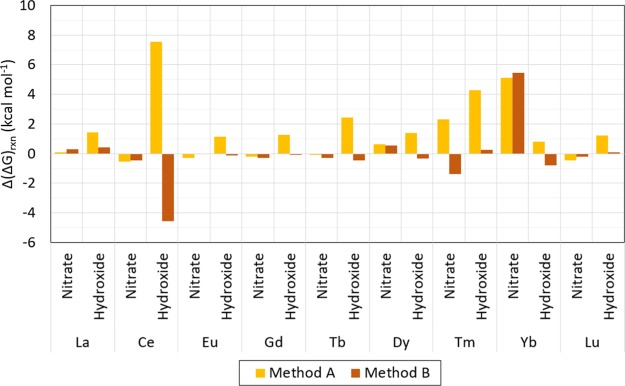
The predicted Gibbs free energy of reaction for Ln(NO3)]2+ with method A is within 0.10 and 8.59 kcal mol–1 from those predicted by the target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3]. With method B, this difference is between 0.05 and 5.47 kcal mol–1. With method A, the predicted Gibbs free energy of reaction calculated for [La(NO3)]2+ is 0.10 kcal mol–1 higher than predicted with the target method, 0.52 kcal mol–1 lower for Ce(NO3)]2+, 0.25 kcal mol–1 lower for [Pr(NO3)]2+, 8.59 kcal mol–1 higher for [Nd(NO3)]2+, 1.21 kcal mol–1 higher for [Sm(NO3)]2+, 0.29 kcal mol–1 lower for [Eu(NO3)]2+, 0.21 kcal mol–1 lower for Gd(NO3)]2+, 0.10 kcal mol–1 lower for Tb(NO3)]2+, 0.65 kcal mol–1 higher for Dy(NO3)]2+, 3.24 kcal mol–1 higher for [Ho(NO3)]2+, 4.97 kcal mol–1 higher for [Er(NO3)]2+, 2.30 kcal mol–1 higher for [Tm(NO3)]2+, 5.11 kcal mol–1 higher for [Yb(NO3)]2+, and 0.44 kcal mol–1 lower for [Lu(NO3)]2+. Comparably, with method B, the predicted Gibbs free energy of reaction calculated for [La(NO3)]2+ is 0.32 kcal mol–1 higher than predicted with the target method, 0.44 kcal mol–1 lower for [Ce(NO3)]2+, 2.47 kcal mol–1 lower for [Pr(NO3)]2+, 4.99 kcal mol–1 lower for [Nd(NO3)]2+, 0.79 kcal mol–1 higher for [Sm(NO3)]2+, 0.05 kcal mol–1 lower for [Eu(NO3)]2+, 0.30 kcal mol–1 lower for [Gd(NO3)]2+, 0.30 kcal mol–1 lower for [Tb(NO3)]2+, 0.56 kcal mol–1 higher for Dy(NO3)]2+, 1.39 kcal mol–1 lower for [Ho(NO3)]2+, 3.08 kcal mol–1 lower for [Er(NO3)]2+, 1.38 kcal mol–1 lower for [Tm(NO3)]2+, 5.47 kcal mol–1 higher for [Yb(NO3)]2+, and 0.21 kcal mol–1 lower for [Lu(NO3)]2+. These results are shown in Figure 4 and Table 3.

Figure 4.

Figure 4

Open in a new tab

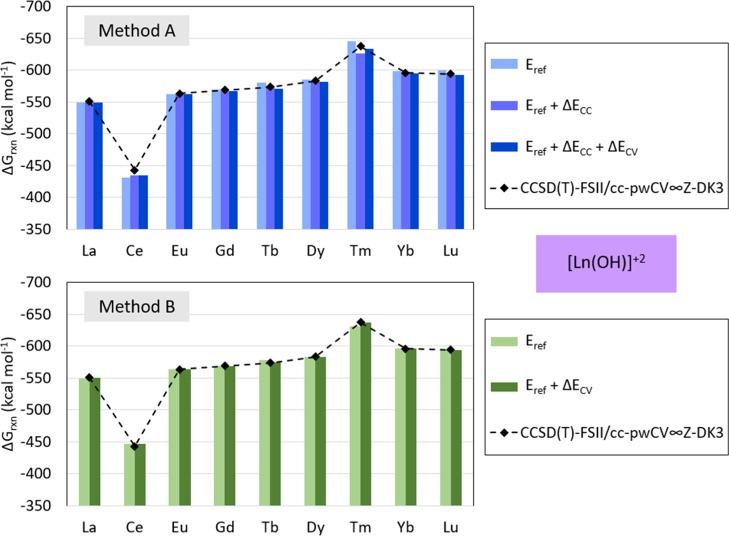
Predicted ΔGrxn for [Ln(NO3)]2+ calculated with method A (top) and method B (bottom) and target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3]. The contribution from each term in method A and method B formulation [Eref, Eref + ΔECC, and Eref + ΔECC + ΔECV for method A; and Eref and Eref + ΔEcV for method B). As indicated in eqs 5 and 6, method A is defined with Eref[MP2], ΔECC[CCSD(T)], and ΔECV[CCSD(T)], and method B with Eref[CCSD(T)] and ΔECV[CCSD(T)].

Table 3. Predicted Δ(ΔG)rxn for [Ln(NO3)]2+ Calculated with Method A and Method B with Respect to the Target Method [CCSD(T)-FSII/cc-pwCV∞Z-DK3].

  method A method B
La 0.10 0.32
Ce –0.52 –0.44
Pr –0.25 –2.47
Nd 8.59 –4.99
Sm 1.21 0.79
Eu –0.29 –0.05
Gd –0.21 –0.30
Tb –0.10 –0.30
Dy 0.65 0.56
Ho 3.24 –1.39
Er 4.97 –3.08
Tm 2.30 –1.38
Yb 5.11 5.47
Lu –0.44 –0.21
Open in a new tab

The calculated Gibbs free energy of reaction with method A for [Ln(OH)]2+ is within 0.08 and 7.54 kcal mol–1 from those predicted by the target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3] and between 0.07 and 4.57 kcal mol–1 with method B. The predicted Gibbs free energy of reaction calculated with method A for [La(OH)]2+ is 1.41 kcal mol–1 higher than predicted with the target method, 7.54 kcal mol–1 higher for [Ce(OH)]2+, 1.14 kcal mol–1 higher for [Eu(OH)]2+, 1.28 kcal mol–1 higher for [Gd(OH)]2+, 2.44 kcal mol–1 higher for [Tb(OH)]2+, 1.38 kcal mol–1 higher for [Dy(OH)]2+, 4.29 kcal mol–1 higher for [Tm(OH)]2+, 0.08 kcal mol–1 higher for [Yb(OH)]2+, and 1.23 kcal mol–1 higher for [Lu(OH)]2+. These results are shown in Figure 5 and Table 4. Similarly, the predicted Gibbs free energy of reaction for [Ln(OH)]2+ calculated with method B is within 0.10 and 8.59 kcal mol–1 from those predicted by the target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3] and is shown in Figure 5 and Table 4. The predicted Gibbs free energy of reaction with method B for [La(OH)]2+ is 0.43 kcal mol–1 higher than predicted with the target method, 4.57 kcal mol–1 lower for [Ce(OH)]2+, 0.11 kcal mol–1 lower for [Eu(OH)]2+, 0.09 kcal mol–1 lower for [Gd(OH)]2+, 0.44 kcal mol–1 lower for [Tb(OH)]2+, 0.32 kcal mol–1 lower for [Dy(OH)]2+, 0.24 kcal mol–1 higher for [Tm(OH)]2+, 0.74 kcal mol–1 lower for [Yb(OH)]2+, and 0.07 kcal mol–1 higher for Lu.

Figure 5.

Figure 5

Open in a new tab

Predicted ΔGrxn for [Ln(OH)]2+ calculated with method A (top) and method B (bottom) and target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3]. The contribution from each term in method A and method B formulation [Eref, Eref + ΔECC, Eref + ΔECC + ΔECV for method A; and Eref, Eref + ΔEcV for method B) are calculated as indicated in eqs 5 and 6. Method A is defined with Eref[MP2], ΔECC[CCSD(T)], and ΔECV[CCSD(T)], and method B with Eref[CCSD(T)] and ΔECV[CCSD(T)]. (Note Yb is in a Yb III state).

Table 4. Predicted Δ(ΔG)rxn for [Ln(OH)]2+ Calculated with Method A and Method B with Respect to the Target Method [CCSD(T)-FSII/cc-pwCV∞Z-DK3 ].

  method A method B
La 1.41 0.43
Ce 7.54 –4.57
Eu 1.14 –0.11
Gd 1.28 –0.09
Tb 2.44 –0.44
Dy 1.38 –0.32
Tm 4.29 0.24
Yb 0.80 –0.79
Lu 1.23 0.07
Open in a new tab

Comparison of Method A and Method B

A direct comparison of predicted Gibbs free energies of reaction calculated with method A and method B is performed for [Ln(NO3)]2+ and [Ln(OH)]2+ (with Ln = La, Ce, Eu, Gd, Tb, Dy, Tm, Yb, and Lu). Although the complete lanthanoid series is evaluated with method A and method B for [Ln(NO3)]2+, only compounds with La, Ce, Eu, Gd, Tb, Dy, Tm, Yb, and Lu are included in this discussion because of [Ln(OH)]2+ with Ln = Pr, Nd, Sm, Ho, and Er being unavailable.

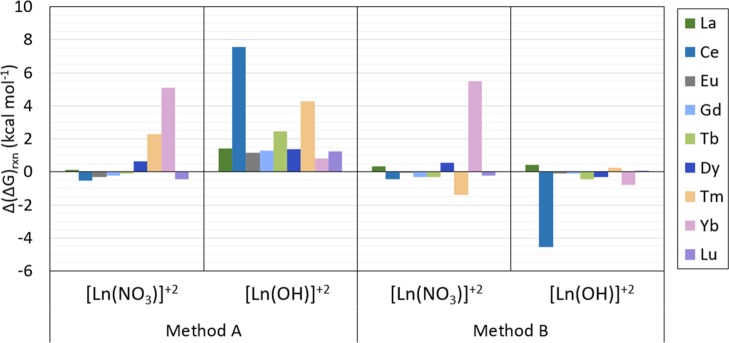
When considering all compounds included in this evaluation, on average method A and method B predict Gibbs free energies of reaction 1.73 and 0.89 kcal mol–1 from those calculated with the target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3], respectively. The range with method B is approximately 2 kcal mol–1 smaller than that with method A (with method A predicting Gibbs free energies of reaction between 0.10 and 1.73 kcal mol–1 from the target method, and method B between 0.05 and 5.47 kcal mol–1), as shown in Table 5.

Table 5. Absolute Difference between ΔGrxn Calculated with Method A and Method B w.r.t. the Target Method [CCSD(T)-FSII/cc-pwCV∞Z-DK3] Evaluated for All Compounds Tested in the Comparison Study [i.e., Ln(NO3)]2+ and Ln(OH)]2+ (with Ln = La, Ce, Eu, Gd, Tb, Dy, Tm, Yb, and Lu)]a.

  method A
 method B
  [Ln(NO3)]2+ [Ln(OH)]2+ [Ln(NO3)]2+ [Ln(OH)]2+
(a)
La 0.10 1.41 0.32 0.43
Ce 0.52 7.54 0.44 4.57
Eu 0.29 1.14 0.05 0.11
Gd 0.21 1.28 0.30 0.09
Tb 0.10 2.44 0.30 0.44
Dy 0.65 1.38 0.56 0.32
Tm 2.30 4.29 1.38 0.24
Yb 5.11 0.80 5.47 0.79
Lu 0.44 1.23 0.21 0.07
average 1.08 2.39 1.00 0.78
range 5.01 6.74 5.42 4.50
  method A method B
(b)
average 1.73 0.89
range 7.45 5.42
Open in a new tab
a

Results shown per compound (a) and overall compounds per method (b) are in kcal mol–1.

Method B predicts Gibbs free energies of reaction within 1.4 kcal mol–1 from those predicted with the target method for all compounds in this analysis except for [Yb(NO3)]2+ and [Ce(OH)]2+ with differences of 5.47 and 4.57 kcal mol–1. For the same compounds, method A predicts Gibbs free energies of reaction within 4.3 kcal mol–1, except for [Yb(NO3)]2+ and Ce(OH)]2+ for which the differences are 5.1 and 7.5 kcal mol–1, respectively. Absolute differences are shown in Table 5.

In general, Gibbs free energies of reaction calculated with method B are closer to those predicted with the target method than when calculated with method A, as shown in Table 5, Figures 6, and 7. Also, the predicted Gibbs free energies of reaction calculated with method B are often higher than those predicted with the target method, whereas those predicted with method A are often lower than those predicted by the target method. As shown in Figure 6, the predicted Gibbs free energy of reaction of [Ln(NO3)]2+ calculated with method A is less than 0.65 kcal mol–1 for all compounds in this analysis except for [Tm(NO3)]2+ and [Yb(NO3)]2+, which have a predicted energy 2.30 and 5.11 kcal mol–1 higher than the target method, respectively, whereas with method B the predicted Gibbs free energies are all within 0.56 kcal mol–1 from those predicted with the target method except for [Tm(NO3)]2+ and [Yb(NO3)]2+ which have a predicted energy 1.38 kcal mol–1 lower and 5.47 kcal mol–1 higher than the target method, respectively. The Gibbs free energy of reaction of the [Ln(OH)]2+ compounds calculated with method A is between 0.80 and 7.54 kcal mol–1 higher than those predicted with the target method, whereas when calculated with method B, all predicted Gibbs free energies are within 0.79 kcal mol–1 from those predicted by the target method, except for [Ce(NO3)]2+ with a predicted ΔGrxn 4.57 kcal mol–1 lower than predicted by the target method. All values are shown in Figures 6 and 7.

Figure 6.

Figure 6

Open in a new tab

Difference between ΔGrxn calculated with method A and method B w.r.t. the target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3] evaluated for all compounds tested in the comparison study (that is, Ln(NO3)]2+ and Ln(OH)]2+ (with Ln = La, Ce, Eu, Gd, Tb, Dy, Tm, Yb, and Lu)). Results shown are in kcal mol–1.

Figure 7.

Figure 7

Open in a new tab

Difference between ΔGrxn calculated with method A and method B w.r.t. the target method [CCSD(T)-FSII/cc-pwCV∞Z-DK3] evaluated for all compounds tested in the comparison study (i.e., Ln(NO3)]2+ and Ln(OH)]2+ (with Ln = La, Ce, Eu, Gd, Tb, Dy, Tm, Yb, and Lu)). Results shown are in kcal mol–1.

Conclusions

Computational predictive capabilities are essential to optimize the design of ligands for selective binding of lanthanoids. In particular, cost-efficient methods are critical for industrial applications, as processes at industrial scales can greatly benefit from robust and efficient computational protocols. In this study, the Gibbs free energy of reaction of a nitrate ion bound to lanthanoid ions is calculated with ab initio methods including CCSD(T) and composites. Finding computationally efficient methods for predictive capabilities of nitrate ligands bound to lanthanoids is essential because of the importance of nitric acid use in the separation process and subsequent nitrate complexation to lanthanoids.

The SO contribution to the proposed reaction is small (less than 0.45 kcal mol–1) for the compounds tested, and therefore found unnecessary in the evaluation of the Gibbs free energy in the studied binding reaction. All lanthanoid ions in this study presented a behavior corresponding to an Ln IV configuration except for Yb, which presented a Yb III configuration similar to No in previous studies of actinoid nitrate systems (following the NIST nomenclature indicated in Table 1). The effects of higher electron correlation beyond MP2 ranges from 2 to 50 kcal mol–1 through the lanthanoid series, whereas the effects of outer-core correlation are less than 10 kcal mol–1 (except for Nd and Eu, where it is 24.6 and 7.2 kcal mol–1, respectively). All composites included in this study predict Gibbs free energies of reaction within approximately 3 kcal mol–1 from each other at a fraction of the cost of the target methodology [CCSD(T)-FSII/cc-pwCV∞Z-DK3 for method A and B, and CCSD(T)-FSII/cc-pwCV∞Z-DK3+SO for f-ccCA]. The composite method A [where Eref is described by MP2] predicts Gibbs free energies of reaction between 0.09 and 8.59 kcal mol–1 from those predicted by the target method at a computational cost between 10 and 32% of the target method. The Gibbs free energy predicted utilizing f-ccCA between 0.11 and 1.21 kcal mol–1 from those predicted by the target method at a computational cost between 12 and 23% of the target method. The Gibbs free energy of reaction predicted with the composite method B (where Eref is described by CCSD(T)) is between 0.05 and 5.47 kcal mol–1 from those predicted by the target method at a computational cost between 22 and 70% of the target method.

This study provides options for ab initio methods that can predict Gibbs free energies of reaction for the binding of nitrates to lanthanoids at a lower computational cost than CCSD(T). Although the focus of the study is on [Ln(NO3)]2+, the proposed method A and method B are also evaluated on [Ln(OH)]2+, showing promising future extensions of these methods to other lanthanoid-containing compounds. Future work will include expanding the application of these methods to fully complexed systems of interest in separation technologies.

Acknowledgments

This work was supported in part by the National Nuclear Security Administration (grant DOE-NNSA-DE-NA0001983) under the Stewardship Science Academic Alliance Program (D.A.P., J.D.A., and H.L.H.). D.A.P. thanks Dr. J. F. Corbey and Dr. M. T. Cook for useful discussions. The views expressed here are those of the authors and do not necessarily reflect those of NNSA. Computational resources were provided by UNT’s High Performance Computing Services, a division of the University Information Technology with additional support from UNT Office of Research and Economic Development. This material is based upon work performed using computational resources supported by the University of Tennessee and Oak Ridge National Laboratory Joint Institute for Computational Sciences (http://www.jics.tennessee.edu). This work used the Extreme Science and Engineering Discovery Environment (XSEDE),44 which is supported by National Science Foundation grant number ACI-1548562. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract no. DE-AC02-05CH11231. The f-ccCA9 methodology has been included in full or in part in presentations at American Chemical Society Meetings,45 among other professional meetings.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b02403.

  • Predicted Gibbs free energy of reaction for [Ln(NO3)]2+ calculated with CCSD(T)-FSI/cc-pVTZ-DK3, MP2-FSI/cc-pVTZ-DK3, CCSD(T)-FSII/cc-pwCVTZ-DK3, MP2-FSI/cc-pV∞Z, CCSD(T)-FSI/cc-pV∞Z-DK3, and CCSD(T)-FSII/cc-pwCV∞Z-DK3; method A and method B described in the Methods section; and relative computational cost (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao8b02403_si_001.pdf (646.2KB, pdf)

References

  1. Mincher B. J.; Modolo G.; Mezyk S. P. Review Article: The Effects of Radiaton Chemistry on Solvent Extraction: 2. A Review of Fission-Product Extraction. Solvent Extr. Ion Exch. 2009, 27, 331–353. 10.1080/07366290902821263. [DOI] [Google Scholar]
  2. Corbey J. F.; Rapko B. M.; Wang Z.; McNamara B. K.; Surbella R. G.; Pellegrini K. L.; Schwantes J. M. Crystallographic and Spectroscopic Characterization of Americium Complexes Containing the Bis[(Phosphino)Methyl]Pyridine-1-Oxide (NOPOPO) Ligand Platform. Inorg. Chem. 2018, 57, 2278–2287. 10.1021/acs.inorgchem.7b03154. [DOI] [PubMed] [Google Scholar]
  3. Rosario-Amorin D.; Ouizem S.; Dickie D. A.; Wen Y.; Paine R. T.; Gao J.; Grey J. K.; de Bettencourt-Dias A.; Hay B. P.; Delmau L. H. Synthesis, Lanthanide Coordination Chemistry, and Liquid-Liquid Extraction Performance of CMPO-Decorated Pyridine and Pyridine N-Oxide Platforms. Inorg. Chem. 2013, 52, 3063–3083. 10.1021/ic3025342. [DOI] [PubMed] [Google Scholar]
  4. Tian G.; Shuh D. K.; Beavers C. M.; Teat S. J. A Structural and Spectrophotometric Study on the Complexation of Am(III) with TMOGA in Comparison with the Extracted Complex of DMDOOGA. Dalton Trans. 2015, 44, 18469–18474. 10.1039/c4dt02882a. [DOI] [PubMed] [Google Scholar]
  5. Hirshorn S. R.NASA System Engineering Handbook, 2nd ed.; National Aeronautics and Space Administration: Washington, DC, 2007. [Google Scholar]
  6. Penchoff D. A.; Peterson C. C.; Quint M. S.; Auxier J. D.; Schweitzer G. K.; Jenkins D. M.; Harrison R. J.; Hall H. L. Structural Characteristics, Population Analysis, and Binding Energies of [An(NO3)]2+ [with An = Ac - Lr]. ACS Omega 2018, 3, 14127–14143. 10.1021/acsomega.8b01800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Szabo A.; Ostlund N. S.. Modern Quantum Chemistry, 1st ed.; Dover Publications, Inc.: Mineola, NY, 1982. [Google Scholar]
  8. Jensen F.Relativistic Methods. Introduction to Computational Chemistry; John Wiley & Sons: West Sussex, England, 2007; pp 277–292. [Google Scholar]
  9. Peterson C. C.Accurate Energetics Across the Periodic Table Via Quantum Chemistry; University of North Texas, 2015. [Google Scholar]
  10. DeYonker N. J.; Cundari T. R.; Wilson A. K. The Correlation Consistent Composite Approach (CcCA): An Alternative to the Gaussian-n Methods. J. Chem. Phys. 2006, 124, 114104. 10.1063/1.2173988. [DOI] [PubMed] [Google Scholar]
  11. Peterson C.; Penchoff D. A.; Wilson A. K.. Prediction of Thermochemical Properties Across the Periodic Table: A Review of the Correlation Consistent Composite Approach (CcCA) Strategies and Applications, 2016.
  12. Lu Q.; Peterson K. A. Correlation Consistent Basis Sets for Lanthanides: The Atoms La-Lu. J. Chem. Phys. 2016, 145, 054111. 10.1063/1.4959280. [DOI] [PubMed] [Google Scholar]
  13. Solomonik V. G.; Smirnov A. N. Toward Chemical Accuracy in Ab Initio Thermochemistry and Spectroscopy of Lanthanide Compounds: Assessing Core–Valence Correlation, Second-Order Spin–Orbit Coupling, and Higher Order Effects in Lanthanide Diatomics. J. Chem. Theory Comput. 2017, 13, 5240. 10.1021/acs.jctc.7b00408. [DOI] [PubMed] [Google Scholar]
  14. Madic C.; Lecomte M.; Baron P.; Boullis B. Separation of Long-Lived Radionuclides from High Active Nuclear Waste. Compt. Rendus Phys. 2002, 3, 797–811. 10.1016/s1631-0705(02)01370-1. [DOI] [Google Scholar]
  15. Hudson M.; Lewis F.; Harwood L. Development of Highly Selective Ligands for Separations of Actinides from Lanthanides in the Nuclear Fuel Cycle. Synlett 2011, 18, 2609–2632. 10.1055/s-0030-1289557. [DOI] [Google Scholar]
  16. Glatz J.-P.Spent Fuel Dissolution and Reprocessing Processes. Comprehensive Nuclear Materials; Elsevier, 2012; pp 343–366. [Google Scholar]
  17. Diwu J.; Wang S.; Liao Z.; Burns P. C.; Albrecht-Schmitt T. E. Cerium(IV), Neptunium(IV), and Plutonium(IV) 1,2-Phenylenediphosphonates: Correlations and Differences between Early Transuranium Elements and Their Proposed Surrogates. Inorg. Chem. 2010, 49, 10074–10080. 10.1021/ic1015912. [DOI] [PubMed] [Google Scholar]
  18. Bond E. M.; Duesler E. N.; Paine R. T.; Neu M. P.; Matonic J. H.; Scott B. L. Synthesis and Molecular Structure of a Plutonium(IV) Coordination Complex: [Pu(NO3)2{2,6-[(C6H5)2P(O)CH2]2C5H3NO}2](NO3)2·1.5H2O·0.5MeOH. Inorg. Chem. 2000, 39, 4152–4155. 10.1021/ic000146z. [DOI] [PubMed] [Google Scholar]
  19. Rapko B. M.; Duesler E. N.; Smith P. H.; Paine R. T.; Ryan R. R. Chelating Properties of 2-((Diphenylphosphino)Methyl)Pyridine N,P-Dioxide and 2,6-Bis((Diphenylphosphino)Methyl)Pyridine N,P,P′-Trioxide toward f-Element Ions. Inorg. Chem. 1993, 32, 2164–2174. 10.1021/ic00062a047. [DOI] [Google Scholar]
  20. Whittaker D. M.; Griffiths T. L.; Helliwell M.; Swinburne A. N.; Natrajan L. S.; Lewis F. W.; Harwood L. M.; Parry S. A.; Sharrad C. A. Lanthanide Speciation in Potential SANEX and GANEX Actinide/Lanthanide Separations Using Tetra-N-Donor Extractants. Inorg. Chem. 2013, 52, 3429–3444. 10.1021/ic301599y. [DOI] [PubMed] [Google Scholar]
  21. Van de Voorde M.; Van Hecke K.; Binnemans K.; Cardinaels T. Separation of Samarium and Europium by Solvent Extraction with an Undiluted Quaternary Ammonium Ionic Liquid: Towards High-Purity Medical Samarium-153. RSC Adv. 2018, 8, 20077–20086. 10.1039/c8ra03279c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lavrov H. V.; Ustynyuk N. A.; Matveev P. I.; Gloriozov I. P.; Zhokhov S. S.; Alyapyshev M. Y.; Tkachenko L. I.; Voronaev I. G.; Babain V. A.; Kalmykov S. N.; et al. A Novel Highly Selective Ligand for Separation of Actinides and Lanthanides in the Nuclear Fuel Cycle. Experimental Verification of the Theoretical Prediction. Dalton Trans. 2017, 46, 10926–10934. 10.1039/c7dt01009e. [DOI] [PubMed] [Google Scholar]
  23. Muller J. M.; Galley S. S.; Albrecht-Schmitt T. E.; Nash K. L. Characterization of Lanthanide Complexes with Bis-1,2,3-Triazole-Bipyridine Ligands Involved in Actinide/Lanthanide Separation. Inorg. Chem. 2016, 55, 11454–11461. 10.1021/acs.inorgchem.6b02005. [DOI] [PubMed] [Google Scholar]
  24. Bernstein K. J.; Do-Thanh C.-L.; Penchoff D. A.; Cramer S. A.; Murdock C. R.; Lu Z.; Harrison R. J.; Camden J. P.; Jenkins D. M. The Synthesis and Spectroscopic Characterization of an Aromatic Uranium Amidoxime Complex. Inorg. Chim. Acta. 2014, 421, 374–379. 10.1016/j.ica.2014.06.023. [DOI] [Google Scholar]
  25. Chen J.; Wang S.; Xu C.; Wang X.; Feng X. Separation of Americium from Lanthanides by Purified Cyanex 301 Countercurrent Extraction in Miniature Centrifugal Contactors. Procedia Chem. 2012, 7, 172–177. 10.1016/j.proche.2012.10.029. [DOI] [Google Scholar]
  26. Møller C.; Plesset M. S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. 10.1103/physrev.46.618. [DOI] [Google Scholar]
  27. Cramer C. J.Essentials of Computational Chemistry; Wiley, 2002. [Google Scholar]
  28. de Jong W. A.; Harrison R. J.; Dixon D. A. Parallel Douglas-Kroll Energy and Gradients in NWChem: Estimating Scalar Relativistic Effects Using Douglas-Kroll Contracted Basis Sets. J. Chem. Phys. 2001, 114, 48–53. 10.1063/1.1329891. [DOI] [Google Scholar]
  29. Reiher M.Relativistic Douglas-Kroll-Hess Theory; Wiley Interdisciplinary Reviews: Computational Molecular Science, 2012; pp 139–149. [Google Scholar]
  30. Karton A.; Martin J. M. L. Comment on: “Estimating the Hartree–Fock Limit from Finite Basis Set Calculations” [Jensen F (2005) Theor Chem Acc 113:267]. Theor. Chem. Acc. 2006, 115, 330–333. 10.1007/s00214-005-0028-6. [DOI] [Google Scholar]
  31. Martin J. M. L. Ab Initio Total Atomization Energies of Small Molecules — towards the Basis Set Limit. Chem. Phys. Lett. 1996, 259, 669–678. 10.1016/0009-2614(96)00898-6. [DOI] [Google Scholar]
  32. Gomes A. S. P.; Dyall K. G.; Visscher L. Relativistic Double-Zeta, Triple-Zeta, and Quadruple-Zeta Basis Sets for the Lanthanides La–Lu. Theor. Chem. Acc. 2010, 127, 369–381. 10.1007/s00214-009-0725-7. [DOI] [Google Scholar]
  33. Peterson C.; Penchoff D. A.; Wilson A. K. Ab Initio Approaches for the Determination of Heavy Element Energetics: Ionization Energies of Trivalent Lanthanides (Ln = La-Eu). J. Chem. Phys. 2015, 143, 194109. 10.1063/1.4935809. [DOI] [PubMed] [Google Scholar]
  34. Penchoff D. A.; Peterson C. C.; Camden J. P.; Bradshaw J. A.; Auxier J. D.; Schweitzer G. K.; Jenkins D. M.; Harrison R. J.; Hall H. L. Structural Analysis of the Complexation of Uranyl, Neptunyl, Plutonyl, and Americyl with Cyclic Imide Dioximes. ACS Omega 2018, 3, 13984–13993. 10.1021/acsomega.8b02068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Becke A. D. Perspective: Fifty Years of Density-Functional Theory in Chemical Physics. J. Chem. Phys. 2014, 140, 18A301. 10.1063/1.4869598. [DOI] [PubMed] [Google Scholar]
  36. Becke A. D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  37. Krishnan R.; Binkley J. S.; Seeger R.; Pople J. A. Self-consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. 10.1063/1.438955. [DOI] [Google Scholar]
  38. Valiev M.; Bylaska E. J.; Govind N.; Kowalski K.; Straatsma T. P.; Van Dam H. J. J.; Wang D.; Nieplocha J.; Apra E.; Windus T. L.; et al. NWChem: A Comprehensive and Scalable Open-Source Solution for Large Scale Molecular Simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. 10.1016/j.cpc.2010.04.018. [DOI] [Google Scholar]
  39. Werner H.-J.; Knowles P. J.; Knizia G.; Manby F. R.; Schütz M. A General Purpose Quantum Chemistry Package. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 242–253. 10.1002/wcms.82. [DOI] [Google Scholar]
  40. Bast R.; Saue T.; Visscher L.; Jensen H. J. A.; Bakken V.; Dyall K. G.; Dubillard S.; Ekstroem U.; Eliav E.; Enevoldsen T.; Fasshauer E.; et al. DIRAC, a Relativistic Ab Initio Electronic Structure Program. Realease DIRAC15; Dirac, 2015.
  41. Feller D. The Role of Databases in Support of Computational Chemistry Calculations. J. Comput. Chem. 1996, 17, 1571–1586. . [DOI] [Google Scholar]
  42. Schuchardt K. L.; Didier B. T.; Elsethagen T.; Sun L.; Gurumoorthi V.; Chase J.; Li J.; Windus T. L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. 10.1021/ci600510j. [DOI] [PubMed] [Google Scholar]
  43. Kramida A.; Ralchenko Y.; Reader J. .; Team N. A.. NIST Atomic Spectra Database. (Ver. 5.5.2), [Online], Gaithersburg, MD, 2018.
  44. Towns J.; Cockerill T.; Dahan M.; Foster I.; Gaither K.; Grimshaw A.; Hazlewood V.; Lathrop S.; Lifka D.; Peterson G. D.; et al. XSEDE: Accelerating Scientific Discovery. Comput. Sci. Eng. 2014, 16, 62–74. 10.1109/mcse.2014.80. [DOI] [Google Scholar]
  45. a Peterson C. C.; Wilson A. K.. Ab Initio Approaches for Accurate Predictions of Lanthanide Thermochemistry. Abstracts of Papers, 249th ACS National Meeting & Exposition; Denver, CO, United States, 2015; PHYS-488.; b Penchoff D.; Peterson C.; Schweitzer G.; Wilson A.. Optimization of Separations of Rare Earths and Actinides through Computational Approaches. Abstracts of Papers, 251st ACS National Meeting & Exposition; San Diego, CA, Unites States, 2016; EC-147.; c Penchoff D.; Peterson C.; Auxier J.; Hall H.; Wilson A.. Optimization of Selective Separations of Lanthanides: An Integrated Computational and Experimental Study. Abstracts of Papers, 251st ACS National Meeting & Exposition; San Diego, CA, Unites States, 2016; NUCL-126.; d Peterson C.; Penchoff D.; Wilson A.. Composite Approach towards Accurate Predictions of Lanthanide and Actinide Thermochemistry. Abstracts of Papers, 251st ACS National Meeting & Exposition; San Diego, CA, Unites States, 2016; COMP-626.; e Penchoff D.; Peterson C.; Auxier J.; Hall H.; Wilson A.. Improving Rapid Separations for Nuclear Forensics through Computational Techniques. Abstracts of Papers, 252nd ACS National Meeting & Exposition; Philadelphia, PA, Unites States, 2016; NUCL-14.; f Penchoff D.; Peterson C.; Schweitzer G.; Wilson A.. Computational Predictions for Separations of Lanthanides and Actinides. Abstracts of Papers, 252nd ACS National Meeting & Exposition; Philadelphia, PA, Unites States, 2016; INOR-61.; g Peterson C.; Penchoff D.; Wilson A.. Composite Approaches for Accurate Predictions of Lanthanide and Actinide Chemistry. Abstracts of Papers, 252nd ACS National Meeting & Exposition; Philadelphia, PA, Unites States, 2016; COMP-76.; h Penchoff D. A.; Peterson C.; Wilson A. K.. Thermochemical and Structural Predictions of Lanthanide- and Actinide-Containing Compounds: A Computational Perspective. Abstracts of Papers, 253rd ACS National Meeting & Exposition; San Francisco, CA, United States, 2017; INOR-1135.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao8b02403_si_001.pdf (646.2KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES