Cell sensing and decision-making in confinement: The role of TRPM7 in a tug of war between hydraulic pressure and cross-sectional area

TRPM7 senses hydraulic pressure and modulates cortical actomyosin to guide migrating cells towards the path of lower resistance.

Abstract

How cells sense hydraulic pressure and make directional choices in confinement remains elusive. Using trifurcating Ψ-like microchannels of different hydraulic resistances and cross-sectional areas, we discovered that the TRPM7 ion channel is the critical mechanosensor, which directs decision-making of blebbing cells toward channels of lower hydraulic resistance irrespective of their cross-sectional areas. Hydraulic pressure–mediated TRPM7 activation triggers calcium influx and supports a thicker cortical actin meshwork containing an elevated density of myosin-IIA. Cortical actomyosin shields cells against external forces and preferentially directs cell entrance in low resistance channels. Inhibition of TRPM7 function or actomyosin contractility renders cells unable to sense different resistances and alters the decision-making pattern to cross-sectional area–based partition. Cell distribution in microchannels is captured by a mathematical model based on the maximum entropy principle using cortical actin as a key variable. This study demonstrates the unique role of TRPM7 in controlling decision-making and navigating migration in complex microenvironments.

INTRODUCTION

Cell migration through interstitial tissues is a key step for the dissemination of cancerous cells from a primary tumor to distant metastatic sites in the body. In vivo, cancer cells migrate either by degrading their surrounding three-dimensional (3D) extracellular matrix (ECM) or by traveling through 3D channel-like tracks created intrinsically by various anatomical structures or generated by the enzymatic activity of “leader” cancer cells or cancer-associated stromal cells (1). Advances in multiphoton microscopy reveal that the tissue microenvironment contains confining pores varying from 1 to 20 μm in diameter or fiber- and channel-like tracks ranging from 3 to 30 μm in width and up to 600 μm in length (2). The confining cross-sectional areas of 3D channel-like tracks create a tight seal between the cell and the track walls (3–5). Hence, neutrophil-like cells migrating inside such confining channels exclusively push the column of water ahead of them, thereby generating hydraulic pressure (5). In addition to pushing water, metastatic tumor cells can also uptake and discharge water during confined migration (4).

Cells sense, integrate, and interpret the diverse chemical and physical cues of the local microenvironment, such as chemotactic and/or adhesion site gradients, ECM stiffness and composition, confinement, and hydraulic pressure, to define a direction of migration and the underlying motility mechanisms. Plasticity broadens the repertoire of migration modes and mechanisms used by tumor cells (i.e., mesenchymal versus bleb-based migration) and enables them to optimize their directed locomotion in different microenvironments (6, 7). Directional dilemmas imposed by intersections of confining channel-like tracks in vivo present an additional layer of complexity in the directional decision and migratory mechanisms of cells. Neutrophil-like cells are capable of sensing small changes of hydraulic pressure on the order of ~1 Pa and display a bias toward the path of lower hydraulic resistance when presented with multiple confining paths (5).

It is currently unknown how cells detect such a small pressure differential and make decisions at intersections. When cells are subjected to hydraulic pressure perturbations, force balance at the cell surface suggests that the effective membrane tension (8, 9) will change, which will, in turn, alter the conformation of mechanosensitive ion channels and trigger mechanoresponses. Using trifurcating Ψ-like microchannels coated with collagen I, we investigated the decision-making process of MDA-MB-231 breast adenocarcinoma and HT1080 fibrosarcoma cells as a function of hydraulic resistance and cross-sectional area of branch channels. We discovered that the transient receptor potential cation channel subfamily M member 7, also known as TRPM7, is a key mechanosensor, which directs decision-making toward branch channels of lower hydraulic resistance irrespective of their cross-sectional area. Cell exposure to low (3 Pa) hydrostatic pressure differentials selectively activated TRPM7, which, in turn, induced rapid calcium uptake. Pharmacological inhibition or functional knockout of TRPM7 abolished hydrostatic pressure–induced intracellular calcium increase. Similarly, hydraulic pressure induced differential calcium signal intensities at bleb-based protrusions inside branch channels of different resistances. TRPM7 knockout abrogated these differences and altered the decision-making pattern to cross-sectional area–based partition. We found that the myosin IIA (MIIA)–green fluorescent protein (GFP) signal of the bleb-based protrusions of untreated control cells in each of the three branch channels correlated with the relative magnitude of the respective channel’s hydraulic resistance. TRPM7 knockout abolished this correlation. Together, these data suggest that TRPM7 is a mechanosensor of hydraulic resistance, whereas MIIA serves as the effector. In distinct contrast to the faster extension protrusion rate along the lower resistance channel observed for neutrophil-like HL60 cells (5), tumor cells display a lower protrusion growth rate in channels of lower resistance, which is in line with the lower MIIA-GFP signal in these channels. Last, we demonstrate that cell distribution in branch channels of different hydraulic resistances and cross-sectional areas is captured by a mathematical model based on the maximum entropy principle (MEP).

RESULTS

Cell decision-making strategies and protrusion dynamics at trifurcating microchannels of different hydraulic resistances

To study the decision-making strategy of migrating cells when presented with different paths, we fabricated a polydimethylsiloxane (PDMS)–based microfluidic device consisting of an array of trifurcating Ψ-like microchannels coated with collagen I (Fig. 1A and fig. S1A). In this configuration, cells entered from a cell-seeding reservoir (3, 10) and migrated inside a 200-μm-long feeder microchannel before reaching a trifurcation. The height, H, and width, W, of the feeder microchannels are 3 and 10 μm, respectively, thereby forcing MDA-MB-231 breast cancer cells and HT1080 fibrosarcoma cells to occupy the entire 30-μm² cross-sectional area. The dimensions of the three branch channels are distinct (Fig. 1A and fig. S1A), thereby enabling us to expose cells to different hydraulic resistances (Fig. 1B and fig. S1B) (11). Specifically, the cross-sectional area of the right branch channel (H = 3 μm × W = 20 μm) was set to be twice as large as that of the left or straight branches (H = 3 μm × W = 10 μm). The hydraulic resistance of the right branch channel varied from lowest (fig. S1, A and B) to highest (Fig. 1, A and B) simply by tuning its length from 320 to 2240 μm. Moreover, the hydraulic resistance of the left branch channel was always larger than that of the straight branch due to its longer path (L = 320 μm versus 200 μm). In all microfluidic designs, the majority of both MDA-MB-231 breast adenocarcinoma and HT1080 fibrosarcoma cells chose to enter the branch channel of least hydraulic resistance irrespective of this being the straight (Fig. 1C) or the right branch channel (fig. S1C). Eighty percent of MDA-MB-231 breast adenocarcinoma cells (or more) exhibited membrane blebs, which were identified as discrete, spherical-like bulges localized at the cell poles, whereas only a small fraction of cells displayed finger-like protrusions regardless of the trifurcating Ψ-like microchannels used (fig. S1, D and E). Similar observations were made for HT1080 cells inside these short (H = 3 μm) channels (fig. S1F). Note that cells displaying blebbing as opposed to mesenchymal phenotypes occupied the entire cross-sectional area even of the large right branch channel (Fig. 1D and fig. S1D). Thus, we focused our analysis on blebbing cells, which constituted the predominant cell population inside these microchannels.

Fig. 1. Decision-making strategy and cell dynamics at trifurcating Ψ-like branch channels of different hydraulic resistances.

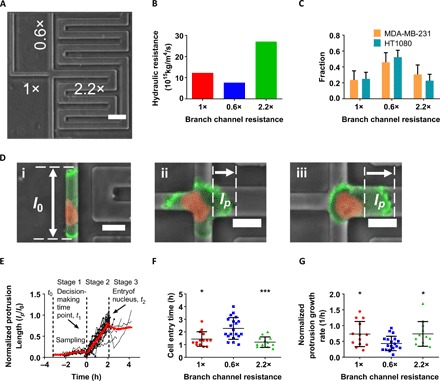
(A) Phase contrast image of a Ψ-like trifurcating microfluidic device. The relative hydraulic resistance of each branch channel is indicated. Scale bar, 50 μm. (B) Absolute values of the hydraulic resistance of each branch channel shown in (A). (C) Distribution pattern of MDA-MB-231 and HT1080 cells in branch channels of different hydraulic resistances (n > 70 from three independent experiments for each cell line). Data represent the mean with 95% confidence interval. (D) Evaluation of protrusion dynamics of LifeAct-GFP H2B-mCherry MDA-MB-231 cells at the trifurcation. (i) Representative cell in the feeder channel before reaching the intersection. l₀ is defined as the overall cell front-rear length. (ii) Representative cell at the intersection. l_p is defined as the protrusion length inside the branch. (iii) Representative cell entering the right branch channel after decision is made. l_p is defined as the distance between the leading edge of the cell and the nucleus. Scale bars, 20 μm. The contrast of the fluorescent signals has been increased in all images uniformly for visualization purposes. (E) Normalized protrusion length (l_p/l₀) for cells choosing the straight branch channel (n = 14) over time. Red line represents the moving average. At t₀, cells first reached the intersection; at t₁, the decision was made; and at t₂, the nucleus fully entered the branch channel at the trifurcation. (F) Cell entry time, t₂ − t₁, in branch channels of different hydraulic resistances (n > 10 cells for each branch from >3 independent experiments). Data represent the means ± SD; Kruskal-Wallis with post hoc Dunn was performed, *P < 0.05 and ***P < 0.001 relative to the cells choosing the straight branch. (G) Normalized leading protrusion growth rate for cells entering branch channels of different hydraulic resistances (n > 10 for each branch from >3 independent experiments). Data represent the means ± SD; one-way analysis of variance (ANOVA) with post hoc Tukey was performed, *P < 0.05 relative to the cells choosing the straight branch.

We next studied cell protrusion dynamics at the trifurcations. When blebbing cells reached the intersection, they sampled the local microenvironment by extending wide, bleb-based protrusions, which occupied the entire cross section of each of the three branch channels (Fig. 1D). We tracked the protrusion dynamics in each branch by measuring the protrusion length, l_p, which was defined as the distance between leading edges of the cell and the nucleus provided that the nucleus had already emerged into the branch channel (Fig. 1D, iii). If not, l_p simply corresponded to the protrusion length inside the branch (Fig. 1D, ii). The protrusion length l_p was then normalized by the cell front-rear length, l₀, inside the feeder channel (Fig. 1D, i) and plotted as a function of time for individual cells and for the moving average of the cell population (fig. S1G and Fig. 1E). Decision-making was preceded by competition among protrusions sampling all three distinct branches (fig. S1G and stage 1 of Fig. 1E). A final choice of direction was made at t₁, called the decision-making time point, when fast growth was initiated in one of these protrusions (stage 2), thereby rendering it dominant (Fig. 1E and fig. S1G). This fast protrusion growth stopped at t₂ (stage 3) when the nucleus had fully entered the branch channel (Fig. 1E). At this stage, the cell typically relaxed to a more compact shape or further elongated, which was rather infrequent. Cell migration speed did not predict the directional decision, as cells moved with the same speed in the feeder channel before entering any of the three different branches (fig. S1H). Together, these data illustrate that the onset of formation of a dominant protrusion marked the cell’s directional decision.

The decision-making time, t₂ − t₀, defined as the duration from the first encounter at the intersection at t₀ till full cell entry into a branch channel at t₂ (stages 1 and 2 of Fig. 1E), was significantly longer for MDA-MB-231 than for HT1080 cells (fig. S1I). Because of the slower MDA-MB-231 migration speeds (fig. S1J), both cell types required similar time scales to complete their decisions (fig. S1K). A markedly longer entry time, t₂ − t₁ (stage 2 of Fig. 1E), was required for cell entry into the branch channel of lowest hydraulic resistance (Fig. 1F and fig. S1L). This counterintuitive observation is further corroborated by findings showing that the protrusion growth rate is lower in lowest hydraulic resistance channels (Fig. 1G and fig. S1M). Together, these observations suggested that cells chose paths of lower hydraulic resistance despite taking a longer time to enter them. These data prompted us to hypothesize that high hydraulic resistance triggers cytoskeletal alterations, which affect actin filament dynamics and potentially decision-making in confined channels.

Cortical actomyosin regulates decision-making in response to hydraulic resistance

Actin filament dynamics is regulated by actin-binding proteins, which control the nucleation, elongation, branching, and disassembly of actin filaments. The Arp2/3 complex nucleates actin filament branching at the cell leading edge and the formation of a perinuclear actin network that facilitates nuclear deformation and migration of dendritic cells through confined spaces (12). Arp2/3 inhibition via MDA-MB-231 cell treatment with CK666 (100 μM) failed to alter the distribution of cells in branch channels of different hydraulic resistances relative to vehicle control (Fig. 2A). Similar observations were made for the RhoA effector mDia1, which facilitates the polymerization of long parallel actin filaments into stress fibers, as mDia1 knockdown (KD) (fig. S2A) did not affect the statistical pattern of cell entry into different branch channels (Fig. 2A). Arp2/3 inhibition or mDia1 KD delayed MDA-MB-231 cell decision-making (Fig. 2B). Because neither of these interventions altered cell migration speeds (fig. S2B), the longer decision times reflected prolonged sampling periods (stage 1 of Fig. 1E) rather than extended cell entry times (stage 2) (fig. S2C). This is further substantiated by confocal microscopy images showing that CK666 treatment or mDia1 KD failed to efficiently realign stress fibers inside branch channels in a direction perpendicular to the feeder channel (fig. S2D).

Fig. 2. Cortical actomyosin regulates cell decision-making in response to hydraulic resistance.

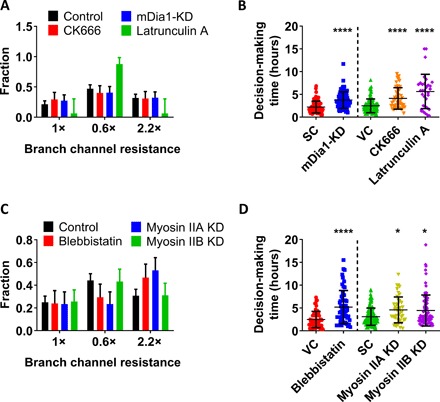
(A) Distribution pattern of MDA-MB-231 cells in branch channels of different hydraulic resistances in response to different pharmacological [(CK666 and Latrunculin A (LatA)] or molecular interventions (mDia1-KD) (n > 70 cells from three independent experiments for CK666 and mDia1-KD experiments and n > 20 cells from three independent experiments for LatA experiments). Data represent the mean with 95% confidence interval. P < 0.01 for the distribution of LatA-treated cells versus controls as indicated by χ² test. (B) Decision-making times of MDA-MB-231 cells in response to different pharmacological (CK666 and LatA) or molecular interventions (mDia1-KD) (n > 30 cells from three independent experiments for each condition). Data represent the means ± SD. Mann-Whitney U test was performed, ****P < 0.0001 relative to scramble control (SC). Kruskal-Wallis with post hoc Dunn was performed, ****P < 0.0001 relative to vehicle control (VC). (C) Distribution pattern of MDA-MB-231 cells in branch channels of different hydraulic resistances in response to different pharmacological (blebbistatin) or molecular interventions (myosin-IIA or myosin-IIB KD) (n > 70 cells from three independent experiments for each condition). Data represent the mean with 95% confidence interval. P < 0.01 and P < 0.0001 for the distribution of blebbistatin-treated and myosin-IIA–KD cells, respectively, relative to controls as indicated by χ² test. (D) Decision-making times of MDA-MB-231 cells in response to different pharmacological (blebbistatin) or molecular interventions (myosin-IIA or myosin-IIB KD) (n > 40 cells from three independent experiments for each condition). Data represent the means ± SD. Kruskal-Wallis with post hoc Dunn was performed, *P < 0.05 relative to scramble control. Mann-Whitney U test was performed, ****P < 0.0001 relative to vehicle control.

Inhibition of actin polymerization via cell treatment with a high dose of Latrunculin A (LatA; 2 μM) caused a pronounced change in the distribution of cells in different branch channels, with the vast majority (70 to 90%) choosing to enter the channel of lowest hydraulic resistance (Fig. 2A and fig. S2E). Note that, although LatA-treated cells continued to move inside the feeder channel albeit with a reduced speed (fig. S2B), most of these cells stalled at the intersection, with only 10% of them choosing to enter a branch channel (fig. S2F). Along these lines, the decision-making time of LatA-treated cells was markedly prolonged (fig. 2B).

Hydraulic resistance serves as an energy barrier or a pressure head that cells need to overcome to move inside confining channels (5, 6). Because cortical actomyosin contractions can generate spatiotemporally localized variations in intracellular hydrostatic pressure (13), we examined the effect of actomyosin contractility in the decision-making process by treating MDA-MB-231 cells with the myosin-II ATPase (adenosine triphosphatase) cycle inhibitor blebbistatin (50 μM). This pharmacological intervention markedly altered cell decision-making, as blebbistatin-treated cells no longer followed the path of lower resistance but instead preferred to enter the branch channel of higher cross-sectional area despite its markedly elevated hydraulic resistance (Fig. 2C). Of the two major nonmuscle myosin II isoforms, MIIA KD (fig. S2G) cells also preferentially entered the larger branch channel (Fig. 2C). On the other hand, MIIB KD (fig. S2G) did not change the statistical distribution of cells in different branch channels relative to scramble controls (Fig. 2C). Of note, individual MIIA or MIIB KD or blebbistatin treatment markedly delayed cell decision-making at the intersection (Fig. 2D) without altering migration speeds at the feeder channels (fig. S2H).

The cortical actomyosin complex is linked to the membrane through ezrin-radixin-moesin (ERM) to generate membrane tension (14). Cells treated with a selective inhibitor of ezrin phosphorylation (NSC668394; 10 μM) displayed a distribution pattern in branch channels of different hydraulic resistances similar to that of myosin II inhibition or MIIA KD (fig. S2I). Although inhibitors of microtubule dynamics reduce the directionality of confined MDA-MB-231 cells (3), colchicine, which promotes microtubule disassembly, failed to affect cell decision-making in branch channels relative to vehicle controls (fig. S2J), although it suppressed migration in the feeder channel (fig. S2K). Together, our data reveal the key role of cortical actomyosin in cell decision-making in confining channels.

Hydrostatic pressure induces intracellular calcium increase via TRPM7 activation

The question that arises next is how cells sense hydraulic pressure. It is well established that calcium-mediated signaling is rapidly generated in response to mechanical stimulation of cells and is key to diverse cellular functions including motility (15). Since both hydraulic (see below) and hydrostatic pressure change membrane curvature (16), we first examined the effects of hydrostatic pressure on calcium uptake using the fluorescent Ca²⁺ indicator, Fluo-4 Direct. To control the hydrostatic pressure on cells, we generated cylindrical wells of prescribed dimensions (D = 6 mm, H = 1 cm) by bonding PDMS-based walls to a glass slide that was then coated with collagen I. Hydrostatic pressure differentials ranging from 3 to 30 Pa were applied by adding prescribed amounts of media atop the cells seeded on the collagen I glass surface. Application of a 3-Pa hydrostatic pressure differential was sufficient to transiently elevate intracellular calcium intensity (Fig. 3A and fig. S3A). Hydrostatic pressure–induced calcium increase was completely abolished by 5 mM EGTA (Fig. 3A). The magnitude of intracellular calcium intensity was further elevated upon applying higher (10 or 20 Pa) hydrostatic pressure differentials (fig. S3B). Moreover, intracellular calcium concentration followed the repetitive increases and decreases of hydrostatic pressure (fig. S3C).

Fig. 3. Hydrostatic pressure induces intracellular calcium increase via TRPM7 activation.

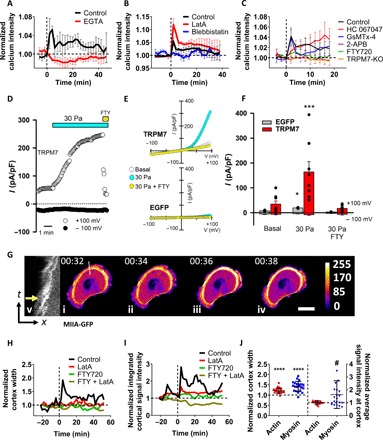
(A to C) Normalized calcium signal intensity of vehicle control and drug-treated or TRPM7 knockout (KO) MDA-MB-231 cells on 2D following the application of a 3-Pa hydrostatic pressure differential at t = 0 min (n > 30 cells from three independent experiments). All signal intensities are normalized to those of the respective unstimulated controls. Data represent means ± SEM. (D) Time course of whole-cell TRPM7 cationic currents recorded at +100 and −100 mV in a HEK293 cell transfected with mouse TRPM7 and exposed to a 30-Pa increase in hydrostatic pressure followed by exposure to 10 μM FTY720. (E) Current-voltage relationships of whole-cell cationic currents in HEK293 cells expressing mouse TRPM7 (top) or enhanced green fluorescent protein (EGFP; bottom) under basal conditions and after the application of a 30-Pa hydrostatic pressure differential in the presence or absence of FTY720. (F) Mean current densities measured under the different experimental conditions shown in (E). TRPM7-expressing cells (n = 8) and EGFP-expressing cells (n = 3). *P < 0.05, ***P < 0.002 for 30 Pa versus any other condition by Kruskal-Wallis followed by Dunn’s post hoc test. (G) Representative image sequence depicting the MIIA-GFP signal of an MDA-MB-231 cell before and after the application of a 3-Pa hydrostatic pressure differential. Pressure is applied right after (ii). Scale bar, 20 μm. (v) Kymograph of the line scan shown in (i) to (iv). The yellow arrow indicates the first frame after the application of a hydrostatic pressure differential. In (i) to (iv), following image segmentation, each pixel’s intensity value was assigned a color according to ImageJ’s fire heat map for visualization purposes. (H) Normalized cortex width and (I) normalized integrated cortical signal intensity of MIIA-GFP–labeled MDA-MB-231 cells following the application of a 3-Pa hydrostatic pressure differential at t = 0 min in response to vehicle control (n > 20 cells from three independent experiments), LatA, and/or FTY720 treatments (n > 5 cells for each condition from two experiments). Data are normalized to the initial (treated or untreated) values at t = −22 min before the application of hydrostatic pressure. (J) Normalized width and average fluorescence intensity of cortical actin and myosin measured by LifeAct-Ruby2– and MIIA-GFP–labeled MDA-MB-231 cells, respectively, immediately after the application of a 3-Pa hydrostatic pressure differential (n > 20 cells from three independent experiments). Data are normalized to the values right before the hydrostatic pressure exposure. Mann-Whitney U test was performed, ****P < 0.0001 relative to width of actin or myosin cortex before hydrostatic pressure exposure and #P < 0.05 relative to signal intensity of cortical myosin before the application of hydrostatic pressure.

In light of the markedly stronger dependence of the decision-making pattern on hydraulic resistance upon inhibition of actin polymerization (Fig. 2A and fig. S2E), we examined the effect of LatA (2 μM) on hydrostatic pressure–mediated calcium uptake. Figure 3B reveals that LatA-treated cells exhibited a pronounced increase in intracellular calcium intensity following exposure to 3 Pa relative to vehicle controls. This sensitivity is attributed to the markedly reduced capacity of LatA-treated cells (essentially their lipid bilayer) to counteract an external force. In contrast to LatA, inhibition of actomyosin contractility by blebbistatin abolished calcium uptake following cell exposure to hydrostatic pressure (Fig. 3B), thereby suggesting that actomyosin cytoskeleton is linked to the generation of Ca²⁺ signals in response to increased hydrostatic pressure.

We next used a panel of selective pharmacological inhibitors to pinpoint the potential candidate responsible for transducing hydrostatic pressure into calcium uptake. Possible Ca²⁺-permeable mechanosensitive ion channels expressed in MDA-MB-231 cells are Piezo1 and Piezo2 and transient receptor potential (TRP) channels TRPV4, TRPC1, and TRPM7 (17). MDA-MB-231 cell treatment with 2-aminoethoxydiphenylborate (2-APB; 100 μM), which inhibits the function of TRPC1 and TRPM7 as well as the inositol 1,4,5-trisphosphate receptor, blocked hydrostatic pressure–induced calcium uptake (Fig. 3C). Use of HC 067047 (5 μM) to selectively inhibit TRPV4 (18) or GsMTX-4 (20 μM) to inhibit Piezo1/2 (19), TRPC1, and TRPC6 (20) failed to suppress calcium uptake in response to hydrostatic pressure (Fig. 3C). Specific inhibition of TRPM7 with Fingolimod (FTY720) (2 μM) (21) abolished the hydrostatic pressure–induced intracellular calcium increase (Fig. 3C). Inhibition of TRPM7 via the use of FTY720 also abrogated the increased hydrostatic pressure–mediated calcium signal in LatA-treated cells (fig. S3D). The use of TRPM7 knockout cells generated via CRISPR-Cas9 (fig. S3E) verified the role of TRPM7 in the generation of hydrostatic pressure–induced Ca²⁺ signals (Fig. 3C). To confirm and extend our findings, we quantified calcium uptake using Fura2 in human embryonic kidney (HEK) 293 cells ectopically expressing human TRPV4, human Piezo1, mouse Piezo2, or mouse TRPM7 in response to a hydrostatic pressure differential of 30 Pa. In accord with our findings using MDA-MB-231 cells, only TRPM7, but not TRPV4, Piezo1, or Piezo2, expressing HEK293 cells responded to the application of a hydrostatic pressure differential (fig. S3, F and G). Moreover, blebbistatin treatment abolished hydrostatic pressure–mediated calcium uptake in TRPM7-expressing HEK293 cells (fig. S3G). Of note, GFP-expressing HEK293 cells exhibited no Ca²⁺ response to hydrostatic pressure (fig. S3F).

Whole-cell patch-clamp recordings reveal that application of a 30-Pa hydrostatic pressure differential also activated large outwardly rectifying cationic currents in TRPM7–yellow fluorescent protein (YFP)–transfected HEK293 cells (Fig. 3, D to F). Time course of hydrostatic pressure–induced cationic current activation in a TRPM7-expressing HEK293 cell and its inhibition by the TRPM7 inhibitor FTY720 are shown in Fig. 3D. The corresponding current/voltage curves obtained from HEK293 cells transfected with TRPM7-YFP are shown in Fig. 3E (top). As a control, green fluorescent protein (EGFP)–transfected HEK293 cells exhibited low basal currents that modestly increased upon increasing hydrostatic pressure (Fig. 3E, bottom), consistent with the low basal expression of TRPM7 in these cells (22). Mean normalized currents obtained from EGFP- and TRPM7-YFP–transfected HEK293 cells are shown in Fig. 3F. Treatment of HEK293 cells with blebbistatin (10 μM) significantly increased basal TRPM7 currents but prevented further activation following the increase in hydrostatic pressure (fig. S3H). Together, our data identify TRPM7 as a sensor of hydrostatic pressure and mechanochemical transducer. Moreover, the response of TRPM7 to hydrostatic pressure appears to be tuned by maneuvers that modify plasma membrane tension.

Next, we analyzed the interplay between actomyosin cytoskeleton and TRPM7 in the cell response to hydrostatic pressure. Live cell imaging using MIIA-GFP reveals that application of a hydrostatic pressure differential (3 Pa) to MDA-MB-231 cells rapidly increased the cortical width of myosin and its average signal intensity (Fig. 3, G to J, and fig. S3, I and J), which is in line with the reported effects of compression on myosin II in zebrafish progenitor cells (23). These hydrostatic pressure–mediated changes were abolished upon blockade of TRPM7 function and/or inhibition of actin polymerization via LatA (2 μM) (Fig. 3, H and I), thereby further illustrating the cross-talk between TRPM7 and actomyosin contractility. Only the cortical width of actin but not its average signal intensity measured by LifeAct-Ruby2 increased with the application of 3-Pa hydrostatic pressure differential (Fig. 3J and fig. S3, K and L). Cumulatively, these data illustrate that a cell’s response to hydrostatic pressure results in a thicker cortical actin meshwork containing a markedly elevated density of myosin motors.

TRPM7 is a key mechanosensor that directs decision-making in channels of lower hydraulic resistance

In light of our findings showing that hydrostatic pressure induces calcium uptake via the activation of TRPM7, we tracked the calcium dynamics of each of the three protrusions inside the branch channels of the trifurcating device using Fluo-4 Direct. When the cell occluded the intersection for the first time and started sensing the resistances of branch channels, the calcium signal intensity positively correlated with hydraulic resistance (Fig. 4, A and B). This correlation was lost in TRPM7 knockout cells or wild-type cells treated with para-nitroblebbistatin (Fig. 4, A and B). Since TRPM7 is activated via membrane stretching (24) and regulates intracellular calcium levels in response to hydrostatic pressure (Fig. 3F and fig. S3B) or hydraulic resistance (Fig. 4, A and B), we measured changes in the membrane curvature of each protrusion in branches of different hydraulic resistances (fig. S4A). When the cell first occluded the intersection, membrane curvature was modified in all three branches relative to that of the feeder channel. Quantitative analysis illustrates that the changes in membrane curvature correlate with the hydraulic resistance of the branch channels irrespective of their cross-sectional areas (fig. S4B). We next assessed how modulation of intracellular calcium levels and of TRPM7 function affect cell decision-making in branch channels of different hydraulic resistances. MDA-MB-231 cells treated with Bapta-AM (25 μM), which is a cell-permeable calcium chelator, preferentially entered the branch channel of the largest cross-sectional area despite its markedly elevated hydraulic resistance (Fig. 4C). Of note, this treatment did not alter the migration speed of cells in the feeder channel (fig. S4C). Similarly, 2-APB and the selective TRPM7 inhibitor FTY720 altered the decision-making pattern from hydraulic resistance–based to cross-sectional area–based partition (Fig. 4C). This finding was further confirmed using TRPM7 knockout cells (Fig. 4C). Although these pharmacological (Bapta-AM, 2-APB, and FTY720) or molecular interventions (TRPM7 knockout) changed the distribution pattern of cells in different branch channels, they did not affect decision-making times (fig. S4D). On the other hand, GsMTX-4 and HC 067047 failed to alter the statistical distribution of preferential cell entry into branch channels of lower hydraulic resistance (fig. S4E), thereby suggesting that Piezo1/2, TRPC1, TRPC6, and TRPV4 are not involved in hydraulic resistance sensing. Cumulatively, our data identify TRPM7 as the key mechanosensor, which directs decision-making in channels of lower hydraulic resistance.

Fig. 4. TRPM7 is a key mechanosensor that directs decision-making in channels of lower hydraulic resistance.

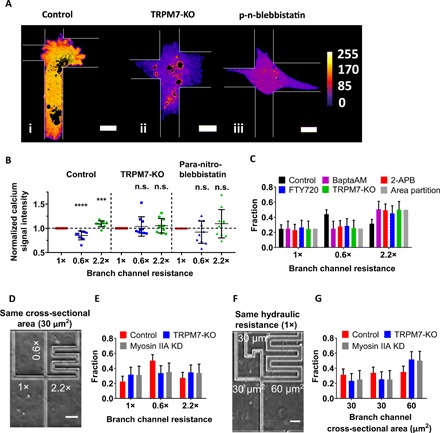
(A) Representative images of calcium signal intensity of (i) control, (ii) TRPM7-KO, and (iii) para-nitroblebbistatin–treated cells once they first reached and occupied the entire intersection of 1×-0.6×-2.2× devices. Following image segmentation, oversaturated pixels indicating high calcium intensity within vacuoles/organelles were blackened, and then each pixel’s intensity value was assigned a color according to ImageJ’s fire heat map for visualization purposes. The borders of the microchannels are depicted by thin white lines. (B) Normalized calcium signal intensity within each protrusion of MDA-MB-231 control, TRPM7-KO, and para-nitroblebbistatin-treated cells in branches of different hydraulic resistances (n = 10 cells from >3 independent experiments). Data represent the means ± SD. Kruskal-Wallis with post hoc Tukey was performed. *P < 0.05, ****P < 0.0001 relative to cells in 1× channel. n.s., not statistically significant relative to 1× channel. (C) Distribution pattern of MDA-MB-231 cells in branch channels of different hydraulic resistances in response to different pharmacological (BaptaAM, 2-APB, and FTY720) or molecular interventions (TRPM7 KO) as compared to the pattern predicted by the branch channel cross-sectional area partition (n > 70 cells from three independent experiments for each condition). Data represent the mean with 95% confidence interval. P < 0.05 for all treatments relative to controls as indicated by χ² test. (D) Phase contrast image of a Ψ-like trifurcating microfluidic device with branches of identical cross-sectional areas but distinct hydraulic resistances. The relative hydraulic resistance of each branch channel is indicated. Scale bar, 50 μm. (E) Distribution pattern of scramble control, TRPM7-KO, and MIIA-KD MDA-MB-231 cells in branch channels of the device shown in (D) (n > 70 cells from three independent experiments). Data represent the mean with 95% confidence interval. P < 0.05 for all treatments relative to controls as indicated by χ² test. (F) Phase contrast image of a Ψ-like trifurcating microfluidic device with branches of identical hydraulic resistances but different cross-sectional areas. The cross-sectional area of each branch channel is indicated. Scale bar, 50 μm. (G) Distribution pattern of scramble control, TRPM7-KO, and MIIA-KD MDA-MB-231 cells in branch channels of the device shown in (F) (n > 60 cells from three independent experiments). Data represent the mean with 95% confidence interval. P < 0.05 for all treatments relative to controls as indicated by χ² test.

To further establish the critical role of TRPM7 in the tug of war between hydraulic pressure and cross-sectional area in cell decision-making, we fabricated additional microfluidic devices with two distinct designs. In the first design, the cross-sectional area of all three branch channels was identical (30 μm²), but their respective hydraulic resistances were different (Fig. 4D). As expected, control untreated cells preferentially entered the branch of lower hydraulic resistance (Fig. 4E). Because the cross-sectional area was the same in all three branches, TRPM7 knockout or MIIA-KD cells entered each of these channels with an equal probability (Fig. 4E). In the second design, the hydraulic resistances of all three branches were set to be the same, whereas their cross-sectional areas were different (Fig. 4F). Because of the identical hydraulic resistances, control untreated cells distributed equally to each of the branch channel (Fig. 4G). In contrast, TRPM7 knockout or MIIA-KD cells entered the branch of the larger cross-sectional area (Fig. 4G).

Cell distribution in branch channels of different hydraulic resistances and cross-sectional areas is described by MEP-based partition

Cortical actomyosin plays a critical role in the distribution of cells to branch channels of different hydraulic resistances and cross-sectional areas, as evidenced by the use of blebbistatin-treated and MIIA-KD cells. To further investigate the relationship between actin/myosin and hydraulic resistance, we quantified the intensity of LifeAct-GFP and MIIA-GFP signals in all three bleb-based protrusions (see boxed areas) at the intersection (Fig. 5A) and subtracted the intensity of the respective signal at the central part of the cell where only cytosolic actin and myosin were present. We next integrated the signal intensity for each bleb-based protrusion as a function of time during the decision-making process. We discovered that, at the decision-making time point, the normalized intensity of the LifeAct-GFP signals was the lowest on the protrusion inside the branch of least hydraulic resistance, whereas it was similar on the protrusions inside the other two branches (Fig. 5B). The normalized MIIA-GFP signal of untreated control cells in each of the three branch channels directly correlated with the relative magnitude of the respective channel’s hydraulic resistance (Fig. 5C). TRPM7 KO abolished these correlations for both actin and myosin. The finding that the LifeAct-GFP and MIIA-GFP signals are lowest inside the branch channel of least hydraulic resistance may help explain the counterintuitive result of the lowest protrusion growth rate detected in this branch channel (Fig. 1G).

Fig. 5. Cell distribution in branch channels of different hydraulic resistances and cross-sectional areas is described by MEP-based partition.

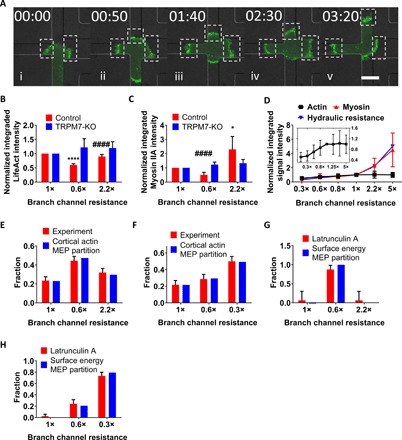
(A) Representative image sequence depicting the cortical actin signal of a LifeAct-GFP–labeled MDA-MB-231 cell in each branch (dashed boxed area). Cell makes a decision right after (iv). The contrast of the fluorescent signals has been increased in all images uniformly for visualization purposes. (B) Normalized integrated actin signal intensity at the decision-making time point measured by LifeAct-GFP in scramble control and TRPM7-KO MDA-MB-231 cells (n > 10 cells, three independent experiments). Actin intensity was normalized to the signal of the left branch channel (1×). Data represent the means ± SD. One-way ANOVA with post hoc Tukey was performed. ****P < 0.0001 relative to control in 1× channel. ####P < 0.0001 relative to control in 0.6× channel. (C) Normalized integrated myosin-IIA signal intensity at the decision-making time point measured by MIIA-GFP in scramble control and TRPM7-KO MDA-MB-231 cells (n > 10 cells, three independent experiments). MIIA intensity was normalized to the signal of the left branch (1×). Data represent the means ± SD. One-way ANOVA with post hoc Tukey was performed. *P < 0.05 relative to control in 1× channel. ####P < 0.0001 relative to control in 2.2× channel. (D) Normalized integrated actin and myosin-IIA signal intensity at the decision-making time point measured in LifeAct-GFP– or MIIA-GFP–labeled MDA-MB-231 cells, respectively, as a function of hydraulic resistance (n > 10 cells for each data point). Inset: Normalized integrated actin signal intensity as a function of hydraulic resistance. Data are normalized to the 1× resistance and represent the means ± SD. (E) Prediction of probability distribution of MDA-MB-231 cells by cortical actin signal–based MEP partition in the trifurcating microfluidic device shown in Fig. 1A (1×-0.6×-2.2×) (n > 400 cells from >3 independent experiments). Data represent the mean with 95% confidence interval. (F) Prediction of probability distribution of MDA-MB-231 cells by cortical actin signal–based MEP partition in the trifurcating microfluidic device shown in fig. S1A (1×-0.6×-0.3×) (n > 300 cells from >3 independent experiments). Data represent the mean with 95% confidence interval. (G) Prediction of probability distribution of LatA-treated MDA-MB-231 cells by the surface energy MEP partition for the 1×-0.6×-2.2× microfluidic design (n > 20 cells from three independent experiments). Data represent the mean with 95% confidence interval. (H) Prediction of probability distribution of LatA-treated MDA-MB-231 cells by surface energy MEP partition for the 1×-0.6×-0.3× microfluidic design (n > 150 cells from three independent experiments). Data represent the mean with 95% confidence interval.

To extend our observations, we tracked the intensity of LifeAct-GFP and MIIA-GFP signals in bleb-based protrusions as a function of a wide range of hydraulic resistances in different microfluidic designs (fig. S5A and table S1). While LifeAct-GFP intensity increased monotonically with increasing hydraulic resistance, it plateaued at the resistance threshold of 1× (channel of W × H × L = 10 μm × 3 μm × 320 μm) (Fig. 5D, inset). On the other hand, the MIIA-GFP signal intensity correlated directly and quantitatively with hydraulic resistance over the entire range of resistances examined in this work (Fig. 5D). We also tracked two additional parameters as a function of the branch channel’s hydraulic resistance: (i) the migration speed inside the branch channel after nuclear entry (stage 3 of Fig. 1E) and (ii) the protrusion growth rate measured during cell entry (stage 2 of Fig. 1E). While the protrusion growth rate plateaued at the hydraulic resistance threshold of 1×, the migration speed continued to increase at higher magnitudes of resistance (fig. S5B). The trend of the protrusion growth rate with increasing hydraulic resistance matched that of the LifeAct-GFP signal intensity (Fig. 5D and fig. S5B). Moreover, the integrated LifeAct-GFP signal intensity (Fig. 5B) inversely correlated with the statistical pattern of cell entry into branch channels (Fig. 1C). Together, these data suggest that the ability of cells to enter branch channels of different hydraulic resistances is regulated by cortical actin, which determines the statistical distribution of cells in different channels.

Bleb formation and growth are the result of physical instability across the plasma membrane, which may originate from nonequilibration of hydrostatic pressure or from intrinsic or force-induced rupture of the cortex (13). Given that the vast majority of cells migrating inside the feeder/branch channels displayed membrane blebs (fig. S1, D and E), we examined the maximum size of blebs present in all three protrusions at the intersection (Fig. 5A). The deviation of the maximum bleb size dropped to a minimum value at the decision-making time point (fig. S5C), thereby suggesting the application of a roughly equal pressure differential (P_out − P_in) across all three membrane protrusions. Using the consecutive frame subtraction method, we next quantified the integrated LifeAct-GFP intensity as a function of time and found it to also reach a minimum at the decision-making time point (fig. S5D). Bleb size and integrated actin intensity measurements are shown for several other cells in fig. S5 (E to G). Cumulatively, these data suggest that a cell makes a directional decision at a critical time point at which an internal and external physical balance occurs. This balance is encountered by all cells, yet their decision is dictated by the hydraulic resistance of the branch channel.

We next sought to understand how the hydraulic resistance quantitatively shapes the distribution of cells in different branch channels. In general, the direction of cell polarization (and therefore the direction of migration) is a fluctuating variable that stochastically changes in time and therefore can be described by a probability function. In the absence of external chemical gradients or hydraulic pressure cues, the cell polarization is equally likely to orient in any direction. Therefore, the probability of migrating into any channel would be proportional to the cross-sectional area of the channel. This is observed when TRPM7 is disrupted. Our data show that TRPM7 senses hydraulic pressure and alters the probability of entering into the trifurcated channels. To define the probability function of the cell decision-making process, we used the MEP to phenomenologically link hydraulic variations with experimental migration outcomes. When MEP was applied, we found that the probability distribution function in different branches has the form

$$p_i=\frac{e^{\frac{-M_i}{\langle M\rangle }}}{{\displaystyle \sum _i^{\mathit{N}}}{e}^{\frac{-M_i}{\langle M\rangle }}}$$ (1)

where M_i denotes the integrated LifeAct signal of the bleb-based protrusion in a branch channel and 〈M〉 is obtained from data fitting (table S2). Data from the cortical actin–based MEP partition model are in excellent agreement with experimental results (Fig. 5, E and F, and table S3).

In experimental conditions where the actomyosin cortex is completely disrupted [e.g., following treatment with a high concentration of LatA (2 μM)], the hydraulic resistance is essentially counteracted by the membrane (lipid) bilayer. This surface energy is calculated by a force balance across the membranes in each of the three branch channels. The pressure drop, ΔP, generated by the hydraulic resistance was calculated as described in (11). From mechanical force balance considerations (9), we obtained the expression of excess surface tension, ΔT, due to hydraulic resistance

$$\mathrm{\Delta }T=\frac{\mathrm{\Delta }P}{2}{(\frac{1}{W}+\frac{1}{H})}^{-1}$$ (2)

Therefore, in the absence of actomyosin cortex, we argue that ΔT is the critical variable that responds to hydraulic resistance, and the tension integrated over the cell surface area (ΔT_iA_i, or the surface energy) should serve in place as M_i in Eq. 1. Data obtained using the surface energy MEP partition model match our experimental data (Fig. 5, G and H).

The MEP probability model is assumption free and straightforward. Although it cannot predict the decision-making strategy of individual cells, this theoretical framework connects cell mechanical variables with migration decision and captures the overall statistical distribution of a cell population to branches of different hydraulic resistances and cross-sectional areas. Note that this MEP model is limited to cells exhibiting a blebbing phenotype at the trifurcation, which represents the vast majority of cells in most microfluidic designs that we used in our work.

DISCUSSION

Previous work has shown that neutrophil-like cells preferentially choose the path of lower hydraulic resistance when presented with multiple confining paths (5). However, the underlying mechanism by which cells sense and respond to hydraulic pressure is unknown. Similar to neutrophil-like cells, we herein show that both human breast cancer (MDA-MB-231) and fibrosarcoma (HT-1080) cells exhibit a bias toward the path of lower hydraulic resistance. We identify TRPM7 as a key mechanosensor of hydraulic resistance, which drives hydraulic resistance–based decision-making in confinement. Hydrostatic pressure– or hydraulic resistance–mediated TRPM7 activation triggers calcium influx and supports a thicker cortical actin meshwork containing an elevated density of myosin motors (Fig. 6), which preferentially directs cell entrance in low resistance channels. Inhibition of TRPM7 function or actomyosin contractility alters the decision-making pattern from hydraulic resistance–based to cross-sectional area–based partition.

Fig. 6. Schematic summarizing how blebbing cells sense and respond to hydraulic resistance.

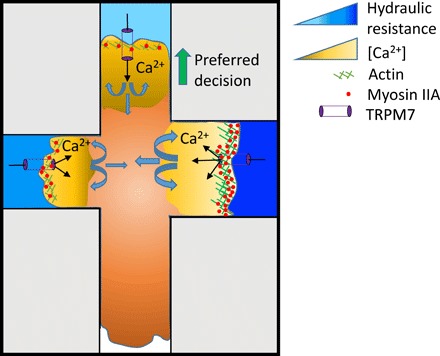
Hydraulic resistance triggers TRPM7 activation in a magnitude-dependent manner, which, in turn, mediates calcium influx and supports a thicker cortical actomyosin meshwork, which preferentially directs cell entrance in low resistance channels. MIIA-GFP signal intensity correlates quantitatively with the hydraulic resistance of each branch channel, whereas the integrated LifeAct-GFP signal intensity correlates inversely with the cell distribution pattern into branches. Variations in bleb size and cortical actin intensity reach a minimum at the decision-making time point, suggesting a physical balance between internal and external cell forces. Inhibition of TRPM7 function or actomyosin contractility alters the decision-making pattern from hydraulic resistance–based to cross-sectional area–based partition.

TRPM7 preferentially permeates divalent cations at negative membrane potentials, thereby contributing to Ca²⁺ influx while allowing monovalent ion flux at depolarized voltages. TRPM7 is a constitutively active cation channel whose gating is further influenced by free intracellular Mg²⁺ (and Mg·ATP) (22) and mechano/osmotic stimulation (24). Thus, the involvement of TRPM7 in hydraulic resistance/pressure sensing and cell decision-making in confining spaces is in agreement with its reported responses to mechanical stress. However, this finding is intriguing for two reasons. First, how is TRPM7 activated by hydrostatic/hydraulic pressure and, second, what makes TRPM7 uniquely suited to respond to hydraulic pressure compared to other well-known mechanosensitive channels, such as TRPV4 or Piezo1/2, which are also expressed in MDA-MB-231 cells (17)?

Piezo channels directly respond to membrane tension (25, 26), while TRPV4 channel’s direct mechanical activation is not that clear. On the one hand, previous studies suggest that osmotic (27) and mechanical (28) sensitivity of TRPV4 depends on the activation of phospholipase A2 and subsequent production of the arachidonic acid metabolite 5′-6′-epoxyeicosatrienoic acid (EET) (29). On the other hand, EET-independent TRPV4 activation by membrane stretching has also been described (30). In the case of TRPM7, direct activation by membrane stretching has been reported for native and ectopically expressed channels (24, 31).

Considering that membrane tension is the primary stimulus gating mechanosensitive ion channels (32), hydrostatic pressure/hydraulic resistance presumably activates these channels through deformation of the plasma membrane, thereby changing its tension. Another structure that may also be in the first line of the cellular response to pressure is the cytoskeleton. The cortical actomyosin cytoskeleton supports and constrains the lipid bilayer, as well as exerts an active modulation of the membrane tension through the specific interactions between the membrane and cytoskeleton at ERM-anchoring elements (8, 33, 34). Accordingly, mechanosensitive channels can be modulated by actions that alter the actomyosin cytoskeleton (26, 32). Blebbistatin, which decreases cytoskeletal tension but increases membrane tension (33), also augments the basal activity of ectopically expressed TRPM7 channels, as evidenced by patch-clamp experiments, but abolishes their response to Ca²⁺ increases via the application of hydrostatic pressure differentials. The fact that no increases in basal intracellular Ca²⁺ levels were detected in the presence of blebbistatin may be related to the Mg²⁺ blockade of inward currents reported for the TRPM7 channel (22). Together, these findings support the hypothesis that membrane tension is the primary stimulus for the channel activation and that cellular responses to pressure, according to the tensegrity model, may differ depending on the previous level of tension in the cell (34). That is, pre-existing membrane tension induced by blebbistatin impairs further activation of TRPM7 with increases in hydrostatic pressure.

One possible explanation for the preferential involvement of TRPM7 in hydrostatic pressure–induced cell responses over the other mechanosensitive ion channels is the high sensitivity of TRPM7 to mechanical deformation of the membrane. The pressure sensitivity (measured as the pressure applied through a patch pipette to achieve half maximal channel activation) of Piezo and TRPV4 channel ranges from 4000 to 5000 Pa (25, 26, 30), whereas that of TRPM7 is 10-fold lower (500 Pa) (24, 31). Thus, mechanosensitive channels with a lower mechanical threshold, such as TRPM7, would be better suited to respond to the small changes in hydrostatic pressure or hydraulic resistance. Another characteristic that may influence the key participation of TRPM7 in hydrostatic pressure/hydraulic resistance sensing is its close physical interaction with different elements of the actomyosin cytoskeleton, including proteins of the Arp2/3 complex, cofilin-1, F-actin–capping proteins, scaffold proteins, regulatory proteins such as calmodulin, and motor proteins, particularly myosin-II (35). Besides, TRPM7 interacts with and modulates the activity of myosin-IIA in a Ca²⁺- and kinase-dependent way (36).

Cells at the intersection regulate the distribution of cortical actomyosin independently in each protrusion in response to the hydraulic resistance of each branch channel. A higher hydraulic resistance triggers an elevated calcium influx via TRPM7 activation, which, in turn, supports a thicker cortical actin meshwork containing an elevated density of myosin motors. The cell next evaluates the relative abundance of cortical actomyosin in each branch channel and makes the decision following a partition pattern based on the MEP. Thus, a higher probability of cell entry occurs in branch channels of lower resistance, which require lower energy expenditure for cortical actin polymerization. Previous observations indicate that membrane tension is critical for coupling motility and membrane protrusion. Membrane tension is inversely related to cell protrusion expansion (33). During the decision-making process, MIIA redistributes from the recessive protrusions to the cell trailing edge (fig. S5H), which has now reached the intersection, thereby helping push the cell into the branch channel irrespective of the hydraulic resistance.

Cortical actomyosin is required to generate adequate tension to balance the external hydrostatic pressure/hydraulic resistance. Although both cortical actin and myosin contribute to the membrane tension (8), the individual inhibition of their functions leads to markedly different decision-making patterns. Disruption of cortical actin reduces the effective membrane tension (8), and hence, the hydraulic resistance/hydrostatic pressure is solely balanced by the lipid bilayer. As described by the MEP, upon actin disruption, the surface tension/energy of the lipid bilayer is not sufficient by itself to counteract high external forces, thereby strengthening the preference of cells for entering branch channels of lower hydraulic resistance. Of note, disruption of actin does not suppress TRPM7-mediated calcium uptake. On the other hand, myosin inhibition increases membrane tension (33), and as such, cells can counteract hydraulic resistance more effectively than LatA-treated cells. Moreover, myosin inhibition increases the basal activity of ectopically expressed TRPM7 channels but abolishes their response to hydrostatic or hydraulic pressure and thus alters the decision-making pattern from hydraulic resistance–based to cross-sectional area–based partition.

In this study, we have used PDMS-based microchannels to investigate how cells sense hydraulic resistance and make directional choices in confinement. Since PDMS is not permeable to water, confined cells need to push a full column of water ahead of them during confined migration (5); as such, the microchannels provide significant hydraulic resistance that can be readily calculated from the channel geometry (11). Cells in vivo migrate through collagen matrices that display varying degrees of permeability to water. In this case, the cells do not push a column of water but rather hydrodynamically interact with the 3D environment (37). Depending on the permeability and geometry of the 3D collagen matrices, the hydraulic resistance in the matrices can be comparable to or even higher than the hydraulic resistance in microchannels (37). Therefore, the findings of this work are also relevant to cell migration in 3D collagen matrices.

In summary, we herein identified TRPM7 as a key mechanosensor of hydraulic resistance, which drives cell decision-making in branch channels of lower resistance that require lower energy expenditure for cortical actin polymerization. TRPM7 may thus represent the link between cell decision-making and cell energy levels, as TRPM7 is a mechanosensitive ion channel regulated by intracellular Mg·ATP (22).

MATERIALS AND METHODS

Cell culture

Human MDA-MB-231 adenocarcinoma, HT1080 fibrosarcoma, and HEK293 cells were cultured in Dulbecco’s modified Eagle’s medium (DMEM) containing glucose (4.5 g/liter), l-glutamine, and sodium pyruvate (Gibco) and supplemented with 10% heat-inactivated fetal bovine serum (FBS; Gibco) and 1% penicillin/streptomycin (10,000 U/ml; Gibco). Cells were grown in an incubator maintained at 37°C and 5% CO₂ and passaged every 2 to 4 days.

Cloning, lentivirus preparation, and transduction

Target sequences were subcloned into pLVTHM (plasmid no. 12247; Addgene, Cambridge, MA; a gift from D. Trono) using Mlu I and Cla I as restriction sites or pLKO.1 (plasmid no. 8453; Addgene, Cambridge, MA; a gift from B. Weinberg) using Age I and Eco RI as restriction sites. The target sequences are as follows: scramble control sh1, GCACTACCAGAGCTAACTCAGATAGTACT; human MYH9 sh1, ACGGAGATGGAGGACCTTATG; human MYH10 sh1, GGATCGCTACTATTCAGGA; human DIA1 sh1, GCATGCCCTATCAAGAGATTA; human DIA1 sh2, GCCGCTGCTGGATGGATTAAA. The pLenti.PGK.LifeAct-GFP.W (plasmid no. 51010; a gift from R. Lansford), pLenti.PGK.H2B-mCherry (plasmid no. 51007; a gift from R. Lansford), pLenti.PGK.LifeAct-Ruby2.W (plasmid no. 51009; a gift from R. Lansford), and MYH9-GFP (plasmid no. 11347; a gift from Robert Adelstein) plasmids were purchased from Addgene. The pcDNA3.1 plasmid expressing mouse TRPM7 tagged with YFP was a gift from T. Gudderman (Ludwig-Maximilians Universitat, Munich, Germany).

For lentivirus production, 293T/17 cells were cotransfected with psPAX2, pMD2.G, and the lentiviral plasmid containing the target sequences. Lentivirus was harvested and purified after 48-hour transfection via centrifugation (50,000g for 2 hours at 4°C). Subsequently, cells were transduced for 24 hours with medium containing lentiviral particles.

To generate MYH9-GFP–labeled cells, 60 to 80% confluent MDA-MB-231 cells were transfected with MYH9-GFP plasmid using Lipofectamine 3000 reagent according to the manufacturer’s recommendations, followed by G418 selection (1 mg/ml).

Photolithography and device fabrication

PDMS-based microfluidic devices consisting of an array of trifurcating Ψ-like microchannels were fabricated as described previously (3, 10). All design dimensions used are summarized in table S1: The dimensions were verified using a laser profilometer. In migration assays, all channels were coated with collagen I (20 μg/ml; Collagen I Rat Protein, Tail, Thermo Fisher Scientific).

Microfluidic device seeding, live cell imaging, and cell treatment

Cells were collected from culture dishes using 0.05% trypsin-EDTA (Gibco), followed by 5-min centrifugation at 300g and resuspended in DMEM supplemented with 1% penicillin/streptomycin and 10% FBS to a concentration of 5 × 10⁶ cells/ml. Twenty microliters of cell suspension was added to the device inlet, generating a pressure gradient for cells to enter the device. The pressure was then balanced by transferring 7 to 8 μl of cell suspension from the inlet to the outlet. Cells were allowed to adhere and spread outside of the channel entrances for 20 to 40 min. All wells of the device were then filled with 120 μl of DMEM supplemented with 1% penicillin/streptomycin and 10% FBS. Devices were incubated at 37°C and 5% CO₂ before imaging.

Cells were imaged every 10 min for at least 20 hours on an inverted Nikon Eclipse Ti microscope (Nikon, Tokyo, Japan) with automated controls (NIS-Elements, Nikon) and a 10×/0.45 numerical aperture Ph1 objective using time-lapse microscopy. During the experiments, cells were maintained on a stage top incubator (Okolab, Pozzuoli, Italy, or Tokai Hit, Shizuoka-hen, Japan) at 37°C and 5% CO₂. For select experiments, cells were imaged using fluorescein isothiocyanate and tetramethyl rhodamine isothiocyanate filters.

Cells were treated with the following pharmacological agents or their corresponding vehicle controls: blebbistatin (50 μM; Sigma-Aldrich), para-nitroblebbistatin (20 μM; Optopharma), colchicine (125 μM; Sigma-Aldrich), CK666 (100 μM; Sigma-Aldrich), LatA (2 μM; Sigma-Aldrich), 2-APB (100 μM; Tocris Biosciences), Bapta-AM (25 μM; Sigma-Aldrich), GsMTx4 (20 μM; Abcam), FTY720 (2 μM; Tocris Biosciences), HC 067047 (5 μM; Tocris Biosciences), ionomycin (500 nM; Sigma-Aldrich), and EGTA (5 mM; Sigma-Aldrich).

Decision-making analysis

For decision-making tracking, a successful decision was acknowledged when the nucleus and at least 90% volume of the cell entered one branch channel at the trifurcation.

Protrusion dynamics measurements

Live cell videos were exported to ImageJ (National Institutes of Health, Bethesda, MD), and the protrusion length was measured manually. A protrusion, l_p, was defined as the distance between leading edges of the cell and the nucleus provided that the nucleus had already emerged into the branch channel (Fig. 1D, iii). If not, l_p simply corresponded to the protrusion length inside the branch (Fig. 1D, ii). The protrusion length l_p was then normalized by the cell front-rear length, l₀, inside the feeder channel (Fig. 1D, i).

Cell entry time measurements

Live cell videos were exported to ImageJ (National Institutes of Health, Bethesda, MD), and cell entry times were calculated manually. The cell entry time was defined as the time period from the decision-making time point t₁ until complete nuclear entry to one of the branch channels t₂ (t₂ − t₁).

Protrusion growth rate measurements

The protrusion growth rate was determined as (l_p/l₀)/(t₂ − t₁).

Decision-making time measurements

Live cell videos were exported to ImageJ (National Institutes of Health, Bethesda, MD), and decision-making times were calculated manually. The decision-making time was defined as the time period from the first cell contact with the trifurcation t₀ until complete nuclear entry to one of the branch channels t₂ (t₂ − t₀). The decision-making time was rendered dimensionless by multiplying it with the cell speed at the feeder channel and dividing the product by the characteristic length scale of 10 μm.

Hydraulic resistance measurements

Absolute value of hydraulic resistance for each channel was calculated as previously described (11). The calculation is as follows:

$$\text{Hydraulic resistance} (\text{fluidic resistance})=\frac{\mathrm{\alpha }\mathrm{\mu }\mathit{L}}{{\mathit{WH}}^3}$$ (3)

where μ is the viscosity of the fluid inside the channel, and L, W, and H are the length, width, and height of the microchannel (W/H << 1), respectively. α is a dimensionless parameter provided by Eq. 4

$$\mathrm{\alpha }={[1-\frac{192H}{{\mathrm{\pi }}^{5}W}\text{tanh}(\frac{\mathit{\pi }\mathit{W}}{2H}\left)\right]}^{-1}$$ (4)

Speed/persistence measurements

Live cell videos were analyzed via ImageJ (National Institutes of Health, Bethesda, MD). The MTrackJ plugin was used for cell path tracking. The cell tracks were recorded from the time of complete entry into the feeder channel until contact with the trifurcation was made. Cell speed and persistence were calculated on the basis of a custom-made MATLAB script (MathWorks, Natick, MA).

Migration phenotype classification

Cells were examined with an inverted Nikon Eclipse Ti microscope (Nikon, Tokyo, Japan) using a 40× air objective. Cell migration phenotype was tabulated manually. Blebbing cells were defined as those displaying membrane blebs, which were identified as discrete, spherical-like bulges localized at the cell poles. Mesenchymal cells were defined as those exhibiting finger-like protrusions.

Calcium assay

The calcium assay was performed using the Fluo-4 Direct Calcium Assay Kit according to the manufacturer’s protocol (F10471, Invitrogen). Briefly, cells at ~80% confluency were incubated with a 0.4× reagent at 37°C and 5% CO₂ for 45 min and then at room temperature for 15 min. Subsequently, cells were trypsinized and seeded into the devices for imaging. A 0.4× reagent was included in the medium during the experiments. Intracellular calcium imaging in transfected HEK293 cells was carried out in cells loaded with 4.5 μM Fura2-AM (Fura-2-acetoxymethyl ester) (Invitrogen) as previously described (28).

Whole-cell patch-clamp recordings

HEK293 cells were seeded onto poly-l-lysine–coated 25-mm glass coverslips. Cells were transfected using 9 equivalents of homemade polyethylenimine with mouse pcDNA3.1-YFP-TRPM7 or control pEGFP plasmids. Recordings were done 24 to 72 hours after transfection. Cells were held at 0 mV, and ramps from −100 to +100 mV (400 ms) were applied at a frequency of 0.2 Hz. Ramp data were acquired at 10 kHz and low-pass–filtered at 1 kHz. Experiments were performed at room temperature (22° to 26°C). Whole-cell TRPM7 cationic currents were measured using pipettes (1.6 to 2 megohms) filled with a solution containing 140 mM CsCl, 10 mM Hepes, 1 mM EGTA, 4 mM Na₂ATP, and 0.3 mM Na₃GTP (pH 7.2 to 7.3 and 295 to 300 mosmol/liter). The external solution, which was also used for calcium experiments in HEK293 cells, contained 110 mM NaCl, 5 mM KCl, 1.8 mM CaCl₂, 0.5 mM MgCl₂, 10 mM Hepes, and 5 mM glucose (pH 7.3 to 7.4 and 305 to 310 mosmol/liter).

Generation of hydrostatic pressure differential

Cylindrical wells of prescribed dimensions (D = 6 mm, H = 1 cm) were generated by bonding PDMS-based walls to a glass slide through oxygen plasma treatment and were subsequently coated with collagen I. Hydrostatic pressure differentials ranging from 3 to 20 Pa were applied by adding (or removing in select experiments) 10- to 70-μl volumes of medium atop the cells seeded in the wells. For control (unstimulated) cases, no medium was added or removed.

Calcium intensity analysis

The videos were analyzed by a custom MATLAB script. The location of the cells was identified by image segmentation involving thresholding and subsequent conversion of the images to a binary format. The pixel intensities (indicating calcium binding to the fluorophore) within the cell regions, as indicated by the binary image, were obtained over the entire field of view and normalized to the total area of fluorescent cells for 2D experiments. In microchannel assays, intensity of each protrusion was normalized to that of the protrusion in the 1× branch. Total signal intensity per area was averaged over multiple fields of view per time point and normalized to the average total calcium intensity per area of the unstimulated cells (no addition/removal of medium) at the same time point for the 2D experiments. Oversaturated pixels indicating high calcium intensity within vacuoles and/or organelles were blackened.

Membrane curvature analysis

Videos of LifeAct-GFP– or Fluo-4 Direct–stained MDA-MB-231 cells were analyzed by a custom MATLAB script. Cells were identified using image segmentation. Membrane protrusions in each branch channel at the time point when cells fully occluded the intersection were fitted by a second-order polynomial, and the prefactor (a) of the second order representing the membrane curvature was used. The original membrane curvature (a_o) was obtained by the same method during cell migration inside the feeder channel and averaged over >10 consecutive time points. The percent change of membrane curvature was calculated by taking the absolute value of (a − a_o)/a_o.

Cortical actin and myosin signal quantification for 2D hydrostatic pressure experiments

Videos of MDA-MB-231 LifeAct-Ruby2 or MIIA-GFP cells were analyzed by a custom MATLAB script. Cortical actin and MIIA were identified by image segmentation involving thresholding and subsequent conversion of the images to a binary format. For calculating the width of cortical actin and MIIA, the sum of the pixels of high intensity around the perimeter of a cell was normalized to its contour length. The contour length was obtained via Canny edge detection of the binary images, followed by image dilation and thinning. For the integrated cortical signal intensity measurements, after using the same image thresholding and binary conversion to track the location of the high-intensity signals around the perimeter of the cells, the sum of those pixel intensities from the original images was acquired. These values were normalized to those of the first frame (t = 0). For the percentage increase of the width/integrated signal, the width/integrated signal of the first time point after stimulation was normalized to the values before stimulation (before medium addition).

Cortical actin and myosin signal quantification in confinement

Videos of MDA-MB-231 LifeAct-Ruby2 or MIIA-GFP cells were analyzed by a custom MATLAB script. In short, the cortical actin and myosin signals of the protrusions within each branch channel were obtained after background subtraction of the fluorescence signal of each cell. For the normalized integrated signal intensity over a range of hydraulic resistances, all values were normalized to the signal on the 1× relative resistance branch.

Integrated actin signal difference quantification

The actin signal throughout MDA-MB-231 LifeAct-GFP cells of each time frame was subtracted from the succeeding one. All negative values were rounded to 0. Thus, a value of 0 indicated either no change in the actin signal from one frame to another or a smaller signal intensity of the following time point.

Maximum bleb size measurements

First, every bleb in each cell extension within the branch channels was fitted to an ellipse. Second, the largest bleb in each branch channel was determined by comparing the diameter of the circles with the same area as the fitted ellipses. SD was calculated between the largest blebs of each branch.

Confocal imaging

Cells were imaged using a Nikon A1 confocal microscope (Nikon, Tokyo, Japan) with a 63× oil objective.

CRISPR-Cas9–mediated knockout of TRPM7

CRISPR-Cas9–mediated knockout was performed using an established methodology (38). The short guide RNA (sgRNA) sequence (5′-AAATTTGTCAGCAACTCGTC-3′) from the GeCKO library (39) was cloned into the Bbs I restriction site of the SpCas9-2A-Puro V2.0 vector, which was a gift from F. Zhang (Addgene plasmid no. 62988). MDA-MB-231 cells were transiently transfected with the sgRNA plasmid, grown for 48 hours, and selected with puromycin (0.5 μg/ml; Invitrogen). Surviving cells were plated as single-cell colonies in a 96-well plate (1 cell per well) and expanded. Knockout of TRPM7 in expanded cells was confirmed by Western blotting with an anti-TRPM7 antibody (clone N74/25, Abcam).

Western blotting

Western blots were performed as previously described (40), using NuPage 3 to 8% or 4 to 12% gels and the following antibodies:

Primary antibodies: anti-MIIA antibody (rabbit) (1:1000; M8064, Sigma Aldrich), anti-MIIB antibody (N-17) (rabbit) (1:1000; 3404S, Cell Signaling), and anti-DIA1 antibody (E-4) (mouse) (1:100; SC-373807, Santa Cruz Biotechnology). β-Actin was used as a loading control (1:10,000; 612656; Purified Mouse Anti-Actin Ab-5, BD Biosciences).

Secondary antibodies: anti-mouse immunoglobulin G (IgG), horseradish peroxidase (HRP)–linked antibody (1:2000; 7076S, Cell Signaling), and anti-rabbit IgG, HRP-linked antibody (1:2000; 7074S, Cell Signaling).

MEP modeling

By using the MEP, we can estimate the probability, p_i, of cells entering one of the three possible paths/branch channels at the intersection.

The general expression of “entropy” is given by

$$\mathit{S}=-{\displaystyle \sum _{\mathit{i}}^{\mathit{N}}}{\mathit{p}}_{\mathit{i}}\text{log}{\mathit{p}}_{\mathit{i}}$$ (5)

where N is the total number of branch channels at the trifurcation and p_i is the probability of the cell entering into each branch. The normalization constraint is

$${\displaystyle \sum _{\mathit{i}}^{\mathit{N}}}{\mathit{p}}_{\mathit{i}}=1$$ (6)

If M is a variable that depends on key parameters of our system including the hydraulic resistance, R, the cortical actin intensity, I, and the projected area of a cell, A, M = M(R, I, A), then our general macroscopic constraint should also obey Eq. 7

$${\displaystyle \sum _{\mathit{i}}^{\mathit{N}}}{\mathit{p}}_{\mathit{i}}{\mathit{M}}_{\mathit{i}}=\langle \mathit{M}\rangle$$ (7)

thereby following a linear dependence on p_i.

If α and β are the Lagrange multipliers that enforce the constraints, the equation that has to be maximized, is

$$\mathit{G}=-{\displaystyle \sum _{\mathit{i}}^{\mathit{N}}}{\mathit{p}}_{\mathit{i}}\text{log}{\mathit{p}}_{\mathit{i}}-\mathrm{\alpha }({\displaystyle \sum _{\mathit{i}}^{\mathit{N}}}{\mathit{p}}_{\mathit{i}}-\mathsf{1})-\mathrm{\beta }({\displaystyle \sum _{\mathit{i}}^{\mathit{N}}}{\mathit{p}}_{\mathit{i}}{\mathit{M}}_{\mathit{i}}-\langle \mathit{M}\rangle )$$ (8)

By setting

$$\frac{\mathrm{\partial }\mathit{G}}{\mathrm{\partial }{\mathit{p}}_{\mathit{i}}}=-\text{log}{\mathit{p}}_{\mathit{i}}-\mathsf{1}-\mathrm{\alpha }-\mathrm{\beta }{\mathit{M}}_{\mathit{i}}=\mathsf{0}$$ (9)

taking into consideration the constraint (Eq. 6) and deriving β = 1/〈M〉 from the average probability distribution, we conclude with the probability distribution function over all paths

$$p_i=\frac{e^{\frac{-M_i}{\langle M\rangle }}}{{\displaystyle \sum _i^N}{e}^{\frac{-M_i}{\langle M\rangle }}}$$

The term ${\displaystyle \sum _i^N}{e}^{\frac{-M_i}{\langle M\rangle }}$ in the denominator represents the typical or dynamical partition function, and thus, p_i indicates the relative probability of the cells entering one microchannel over another.

From our experimental data, we found that the cortical actin intensity in each channel, I_i, depends on the hydraulic resistance of that channel, I_i = I(R_i). The total amount of cortical actin in each channel is I_iA_i, where A_i is the projected cortical area of a protrusion in that microchannel. In each trifurcation design, there is a reference branch channel where the hydraulic resistance is 1×, while the resistances in the other two channels vary. Since the actin intensities also vary from cell to cell, the absolute values of intensity cannot be used across different cells. Thus, we normalized the actin intensity of each protrusion of a cell within each branch channel to the intensity value of the protrusion within the reference channel.

We used two designs (1×-0.6×-0.17× and 1×-0.6×-0.3×) to find the expression of 〈M〉 and M_i. Letting M_i = I_iA_i and 〈M〉 = 0.6, we get a good fitting of the theoretical to the experimental probability of cells entering the left, straight, or right branch channels at the trifurcations. The fitted values are summarized in table S2. The difference between the experimental and the predicted probability of cell entrance to a branch channel is less than 3%. By using the fitted M_i and 〈M〉, we succeeded in predicting the probability distributions in three more designs with less than 3% difference (table S3).

Statistical analysis

Directional choices in trifurcations are presented as means ± 95% confidence intervals. All other data represent the means ± SD or means ± SEM from ≥3 independent experiments for each condition unless stated otherwise. Two-tailed unpaired t test, Mann-Whitney U test, one-way analysis of variance (ANOVA; with post hoc Tukey) test, Kruskal-Wallis (with post hoc Dunn) test, and χ² test were used, wherever appropriate, to determine statistical significance. Statistical significance was identified as P < 0.05. Analysis was performed using GraphPad Prism 6 and OriginPro 9 software.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/7/eaaw7243/DC1

Fig. S1. Characterization of cell decision-making at trifurcating Ψ-like branch channels of different hydraulic resistances.

Fig. S2. Effects of different cytoskeletal constituents on cell decision-making in response to hydraulic resistance.

Fig. S3. Hydrostatic pressure induces intracellular calcium increase and a thicker cortical actin meshwork.

Fig. S4. High hydraulic resistance results in larger changes of membrane curvature.

Fig. S5. Variations in bleb size and cortical actin intensity reach a minimum at the decision-making time point, suggesting a physical balance between internal and external cell forces.

Table S1. Dimensions of the different trifurcated designs.

Table S2. Comparison between the experimental and theoretical probabilities of cells entering branches in two different devices.

Table S3. Comparison between the experimental and theoretical probabilities of cells entering branches in multiple devices.