Quantitative imaging of electric surface potentials with single-atom sensitivity

Abstract

Because materials consist of positive nuclei and negative electrons, electric potentials are omnipresent at the atomic scale. However, due to the long range of the Coulomb interaction, large-scale structures completely outshine small ones. This makes the isolation and quantification of the electric potentials that originate from nanoscale objects such as atoms or molecules very challenging. Here we report a noncontact scanning probe technique which addresses this challenge. It exploits a quantum dot sensor and the joint electrostatic screening by tip and surface, thus enabling quantitative surface potential imaging across all relevant length scales down to single atoms. We apply the technique to the characterization of a nanostructured surface, thereby extracting work function changes and dipole moments for important reference systems. This authenticates the method as a versatile tool to study the building blocks of materials and devices down to the atomic scale.

Electrostatic interactions are a key element in the functionality of many nanoscale materials and systems. For example, the performance of organic and inorganic semiconductor devices is affected by electric dipoles at the relevant interfaces [1–4]. Since both, established and novel device concepts aim for the few-nanometre scale [5–8], the relevance of microscopic electric potentials in functional materials and devices increases continually. On a more fundamental level, the measurement of electric potentials can also give valuable insights into primary mechanisms at surfaces and interfaces, such as reconstruction or relaxation, mechanical distortion, charge transfer and chemical interaction [9], which all create electric potentials at the atomic scale. But the importance of electrostatic interactions is not limited to semiconductor and solid state materials. Also the structure and aggregation of biomolecules, for example, is steered by the interactions between polarized functional groups [10, 11], and electrostatic interactions play an important role in catalysis, too [12].

In many contexts, surfaces are the natural environment to study nanoscale electric potentials, either because of their intrinsic importance (semiconductor devices, catalysis), or because they offer a convenient substrate for immobilisation and accessibility (biomolecules). The state of the art in electric potential imaging at surfaces is Kelvin Probe Force Microscopy (KPFM). KPFM is suitable for structure sizes of several tens of nanometres [4,13–16]. For smaller structures, in the realm of single atoms or molecules [17] and cutting-edge semiconductor devices [5], KPFM is problematic since high resolution can only be reached at small tip-surface distances where chemical forces start acting. Their influence hampers a quantitative interpretation of the data [18]. KPFM images with sub-molecular resolution obtained with carbon-monoxide-decorated tips [19, 20] suffer from the same limitation, notwithstanding continuous efforts to improve the data analysis [20, 21], and are moreover slow and limited to small surface areas (typically one single molecule). Thus, a versatile, fast and quantifiable scanning probe method for imaging electric potentials at the atomic scale is lacking.

Recently we reported that a single molecule, when attached to the tip of a non-contact atomic force / scanning tunnelling microscope (NC-AFM/STM) by controlled manipulation [22, 23], may act as a quantum dot (QD) and can be used as a sensor to detect and image electric potentials, resulting in scanning quantum dot microscopy (SQDM) [24, 25]. Here, we present a rigorous analysis of the corresponding imaging mechanism and show that SQDM can be used to map out surface potential distributions and dielectric surface topographies quantitatively. Most notably, we find that the screening action of the combined tip/surface system induces an exponential decay of electric potentials with lateral distance from the probing tip. This effect occasions the exceptionally high lateral resolution of SQDM. A detailed investigation of this exponential screening leads us to an image deconvolution algorithm which, in conjunction with far-reaching instrumental developments [26], transforms SQDM into a powerful imaging technique for electric surface potential imaging in ever smaller nanostructures and novel materials.

Principle and Formalism of SQDM imaging

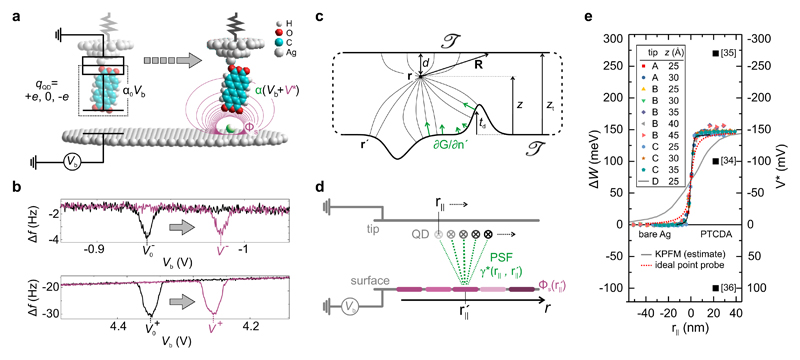
A schematic drawing of the molecular QD at the tip apex of a NC-AFM/STM is shown in Fig. 1a [24, 25]. This setup can be considered as a single-electron box consisting of two capacitances in series [27], but it can also be understood as an electrostatic boundary value problem where the potential Φ_QD at the QD at r is determined by the shape of the confining boundary 𝒯 (the conductive surfaces of tip and sample connected at infinity; Fig.1c) and by the potential distribution Φ_s(r′) on it.

Figure 1. Principle and quantitative nature of SQDM.

a, Principle of electric potential sensing with a molecular QD. When placed above a bare surface, the QD changes its charge by ±e if its potential Φ_QD = α₀V_b reaches the threshold values Φ^± at $V_{\text{b}}=V_0^{\text{±}}.$ The local topography (green) and the surface potential Φ_s (violet) of a nanostructure (here: adatom) change the QD potential Φ_QD, as α₀ changes to α and V* is added to V_b. In the equivalent circuit diagram superimposed on the left, the QD is marked by a dashed box. b, Δf (V_b) = −dF_z/dz × f₀/(2k₀) curves (qPlus type NC-AFM with k₀ = 1800 N/m, f₀ = 31200 Hz, amplitude A = 0.2 Å) in the V_b ranges where the QD changes its charge state (upper panel V⁻, lower panel V⁺), measured above the empty surface (black) and above a nanostructure (violet). The change from α₀ to α and the additional contribution V* (see Panel a) leads to a shift from $V_0^{\pm }$ to V^±. c, Illustration of SQDM as a boundary value problem with the QD at r. Tip and surface are connected at infinity. d, The PSF γ* describes the contribution of the potential ${\Phi }_{\text{s}}({\text{r}}_{||}^{\prime })$ (shades of violet illustrate magnitude) to Φ_QD at all possible positions r_|| (visualized by green lines). For flat surfaces, reciprocally, Φ_QD at a certain lateral position r_|| is the sum over all local potentials on the sample surface at positions ${\text{r}}_{||}^{\prime }$ weighted with γ*. e, Series of V* profiles across a PTCDA/Ag(111) island edge measured with different tips and tip heights as indicated. The expected profiles for corresponding measurements with KPFM [13] and with an ideal point probe (z = 25 Å) are shown for comparison. The measured work function change for a PTCDA layer corresponds to ΔW = −eV* at positive r_||. Values for ΔW reported in literature are indicated as black squares.

It is the principle of SQDM to compensate the local variations of Φ_s and of the sample topography beneath the QD encountered during scanning by adjusting (and recording) the sample bias V_b. The condition Φ_QD = const indicates a correct compensation. This does not put special requirements on the choice of the QD and on its theoretical description. Hence, we may use the approximation of a point-like QD. Since compensation is verified at r, this is the point where the influence of the surface potential is measured. We can relate the information in this imaging plane back to the properties of the surface itself by defining a specific 𝒯 which approximates the experimental situation and solving the corresponding boundary value problem. For Dirichlet boundary conditions we obtain [28]

$${\Phi }_{\text{QD}}(\text{r})=-\frac{{ϵ}_0}{e}\left[{\displaystyle \underset{\text{sample}}{\iint }({\Phi }_{\text{s}}(\text{r}\prime )+V_{\text{b}})\frac{\partial G(\text{r},\text{r}\prime )}{\partial \text{n}\prime }{d}^2\text{r}\prime +{\displaystyle \underset{\text{tip}}{\iint }{\Phi }_{\text{s}}(\text{r}+\text{R})\frac{\partial G(\text{r},\text{r}+\text{R})}{\partial \text{n}\prime }{d}^2\text{R}}}\right],$$ (1)

while we discuss the case of non-conductive surfaces elsewhere [29]. Here, n′ is the surface normal at r′ or r + R, respectively, and G is the Green’s function which encodes the boundary shape via G(r, r′) = 0 ∀ r′ ∈ 𝒯 (Fig. 1c). All adsorbate-related charges which are slightly inside the volume enclosed by 𝒯 create, together with their image charges, the locally varying surface potential Φ_s in Eq. 1. Since tip and QD have a fixed spatial relation and are sufficiently far from the sample, we can assume that ∂G(r, r + R)/∂n′ barely varies with r (during scanning) and consequently the second integral in Eq. 1 is a constant Φ_T. Thus, from now on, Φ_s refers to the sample surface potential only and we describe the shape of 𝒯 on the sample side as a topography of height t_d superimposed onto a plane such that r = (r_||, z) and ${\text{r}}^{\prime }=({\text{r}}_{||}^{\prime },t_{\text{d}}).$

Eq. 1 is central since it relates data on Φ_QD in the imaging plane at z to the desired surface properties. For a chosen shape of $𝒯,{\Phi }_{\text{s}}({\text{r}}_{||}^{\prime })$ as calculated by inversion of Eq. 1 corresponds to the potential distribution which, if applied to 𝒯, would reproduce the Φ_QD data in the imaging plane. Thus, a more accurate representation of 𝒯 yields a better recovery of ${\Phi }_{\text{s}}({\text{r}}_{||}^{\prime }).$ As it turns out, the approximation of a planar surface with t_d = 0, which we will adopt in the following, provides excellent results for the systems investigated here, where generally t_d ≪ z. A discussion of alternative approximations for t_d and their consequences is given in Ref. [29]. Moreover, we adopt the reasonable assumption of an axially symmetric tip.

For these conditions, ∂G/∂n′ depends only on the relative distance $|{\text{r}}_{||}-{\text{r}}_{||}^{\prime }|$ and is the point spread function (PSF) $\gamma (|{\text{r}}_{||}-{\text{r}}_{||}^{\prime }|,z)\equiv -{ϵ}_0/e\times \partial G/\partial n^{\prime }$ of SQDM (Fig. 1d). Then, Eq. 1 becomes (from now on we drop the explicit reference to z)

$${\Phi }_{\text{QD}}({\text{r}}_{||})=(V^{\ast }({\text{r}}_{||})+V_{\text{b}})\alpha ({\text{r}}_{||})+{\Phi }_{\text{T}}$$ (2)

with the following definitions for α and V*

$$\alpha \left({\text{r}}_{||}\right)={\displaystyle \underset{\mathrm{sample}}{\iint }\text{γ}(|{\text{r}}_{||}-{\text{r}}_{||}^{\prime }|)d^2{\text{r}}_{||}^{\prime }=\frac{\partial {\Phi }_{\text{QD}}}{\partial V_{\text{b}}}}$$ (3)

$$V^{\ast }\left({\text{r}}_{||}\right)={\displaystyle \underset{\mathrm{sample}}{\iint }{\Phi }_{\text{s}}({\text{r}}_{||}^{\prime }){\text{γ}}^{\ast }}(|{\text{r}}_{||}-{\text{r}}_{||}^{\prime }|)d^2{\text{r}}_{||}^{\prime }$$ (4)

Analogous equations can be derived for a more general 𝒯 with t_d ≠ 0 [29]. Here, α is the gating efficiency, γ* = γ/α is the PSF normalized to one, and V* quantifies the effect of the surface potential distribution Φ_s on Φ_QD expressed in the form of an equivalent (additional) bias potential. For extended, homogeneous objects with constant Φ_s, V* is in fact the surface potential: Φ_s = V*. Inhomogeneous potential distributions ${\Phi }_{\text{s}}({\text{r}}_{||}^{\prime })$ can be obtained from V* via a deconvolution with the PSF γ* (Eq. 4) as we will discuss later. First we demonstrate how α and V* can be extracted from an actual SQDM measurement.

At two specific Φ_QD values Φ⁺ and Φ⁻ the QD charge state changes as an electron tunnels across the contact between tip and QD [24]. These charging events cause sharp drops in the frequency shift Δf(V_b) of the NC-AFM (Fig. 1b), corresponding to steps in the tip-surface force [30, 31]. These drops at V_b = V^±(r_||) are indicators that the charging condition Φ_QD = Φ^± has been reached and that the compensation of V* was hence successful. Thus, V^± are the primary measurands of SQDM. To image V^±, we have developed a feedback controller which maintains the charging condition either for V⁺ or for V⁻ as the surface is scanned twice at constant height [26] (see Methods).

After some algebra we can derive the following two relations from Eq. 2 and the charging conditions:

$${\alpha }_{\text{rel}}\left({\text{r}}_{||}\right)=\frac{\alpha \left({\text{r}}_{||}\right)}{{\alpha }_0}=\frac{V_0^{+}-V_0^{-}}{V^{+}\left({\text{r}}_{||}\right)-V^{-}\left({\text{r}}_{||}\right)}$$ (5)

and

$$V^{*}\left({\text{r}}_{||}\right)=\frac{V_0^{-}}{{\alpha }_{\text{rel}}\left({\text{r}}_{||}\right)}-V^{-}\left({\text{r}}_{||}\right).$$ (6)

Since SQDM measures variations in Φ_s and α, we have selected a reference point on the surface where we define z, Φ_s ≡ 0, α ≡ α₀, and denote the measured V^± values as $V_0^{\pm }.$ With this, we have established V*(r_||) and α_rel(r_||) as the secondary SQDM measurands. Note that the absolute value of α can be determined from V^±(z) and corresponding force change datasets [32], which is, however, not required for SQDM.

Measuring work function changes

We demonstrate the quantitative measurement of the surface potential Φ_s for a homogeneous sample by looking at work function changes. The corresponding experiment was carried out on PTCDA (3,4,9,10-perylene-tetracarboxylic dianhydride) adsorbed on the Ag(111) surface with a PTCDA molecule as SQDM sensor [24, 25] using a qPlus NC-AFM. Although PTCDA/Ag(111) is an extremely well-studied benchmark system [33], no consensus has yet been reached regarding the work function change ΔW upon adsorption of PTCDA on Ag(111). In fact, values between −0.1 eV and +0.27 eV have been reported from photoemission experiments [34–36] (black squares in Fig. 1e). In Fig. 1e we show line profiles of V*, measured from the bare Ag(111) surface across PTCDA island edges deep into a compact PTCDA island for different tip preparations, tip heights, and even different NC-AFM tuning forks. Remarkably, the line scans collapse practically onto a single curve, proving that work function changes as determined by SQDM are robust and reproducible, and yield a value of ΔW = −eΦ_s = −eV* = (145 ± 10) meV from Ag(111) to PTCDA/Ag(111).

We compare the work function determined by SQDM to results obtained from density functional theory (DFT) calculations. We employ a fully self-consistent implementation, ${\text{vdW}}_{\text{sc}}^{\text{surf}}$ [37], of the Tkatchenko-Scheffler vdW^surf functional [38], in combination with PBE [39] (see Methods). The calculated work function shift between Ag(111) and PTCDA/Ag(111) is ΔW = 90 meV. Compared to PBE, which predicts a value of 240 meV, ${\text{vdW}}_{\text{sc}}^{\text{surf}}$ yields an improved though not perfect agreement with the experimental value. This result stresses the fundamental importance of van der Waals interactions for electronic processes at molecule/metal interfaces and, on a more general note, shows that SQDM is able to set benchmarks for the development of ab-initio theory.

Turning back to the experiment, the curves in Fig. 1e also reveal the sharpness with which we measure the potential distribution at the island edge. To put our experimental V*(r_||) curve into perspective, we compare it with two extreme cases: First, a simulated estimate for a corresponding classical KPFM experiment [13] (grey solid curve) in which the entire tip acts as a sensor for the electric potential, and second, a simulation of the measurement with an idealized hypothetical point-like sensor for electrostatic potentials (red dotted curve in Fig. 1e, compare also Fig. 2a). While it is expected that the V* resolution of SQDM, because of its nanoscopic sensor, is superior to KPFM, the profile we observe in experiment is even sharper than that of the ’ideal’ point probe. This surprising finding asks for a closer analysis of the physics behind the PSF γ* which, according to Eq. 4, determines how a step in the surface potential Φ_s is smeared into V*. Knowing γ* will ultimately allow the reconstruction of arbitrary potential distributions ${\Phi }_{\text{s}}({\text{r}}_{||}^{\prime })$ via Eq. 4.

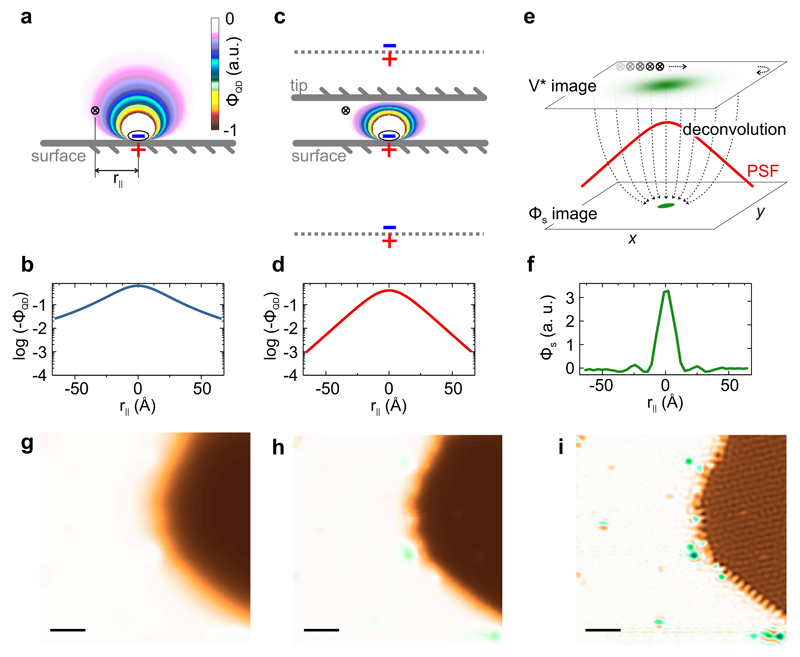
Figure 2. Electrostatic screening and image deconvolution in SQDM.

a, Simulated potential Φ_QD above a charge/image-charge dipole on a conductive surface. A point-like potential probe at a lateral distance r_|| is indicated by a cross. b, Cross-section through the potential Φ_QD at the height of the point probe in Panel a. c, Same as in Panel a, but with a second conductive plane (”tip”) above the point probe. The potential distribution can now be simulated via an infinite series of image dipoles. Two images are indicated as dashed lines. The potential Φ_QD at the point probe position is reduced compared to Panel a. d, Cross-section through the potential Φ_QD at the height of the probe in Panel c. The log-scale plot reveals the exponential decay of Φ_QD with lateral distance from the dipole. e, Illustration of the deconvolution process in which the Φ_s image is recovered from the measured V* image using Φ_QD(r_||) from Panel d as the PSF γ*. f, Cross-section through the Φ_s image of a CO molecule on Ag(111) as obtained from deconvolution. The full width at half maximum is only 1.6 nm. g, Simulation of an SQDM V* image for the hypothetical setup without a tip (Panel a). Simulation based on the image in Panel i. h, Measured SQDM V* image (STC controller) of a complex surface with extended PTCDA islands and smaller nanostructures (compare Fig. 3). i, SQDM Φ_s image as obtained from the V* image in Panel h via deconvolution (see Methods). All nanostructures are now equally well visible. The scale bar size in Panels g-i is 10 nm.

The functional form of γ* and image deconvolution

To analyse the shape of γ*, we must solve the boundary value problem for the chosen shape of 𝒯. To reach a generic solution, we approximate also the tip as planar which is justified since the PtIr tips used in our experiments are rather blunt on the mesoscopic scale, which is also confirmed by our experimental results. Other tip shapes would not invalidate the general conclusions drawn here [29].

For Dirichlet conditions, the gradient $\partial G({\text{r}}_{||},{\text{r}}_{||}^{\prime })/\partial n\prime$ and thus γ* is proportional to the potential at r_|| of a test charge placed at ${\text{r}}_{||}^{\prime }$ and shifted slightly into the volume enclosed by the grounded surface 𝒯, which creates a minimal perturbation of ${\Phi }_{\text{s}}({\text{r}}_{||}^{\prime }).$ The respective ${\gamma }_{\text{pp}}^{*}$ for grounded parallel planes separated by z_t = z+d can then be calculated via an infinite series of image charges (Fig. 2c) which screen the test charge placed at $({\text{r}}_{||}^{\prime }=0,z_{\text{c}}\ll z).$ This series has no closed solution [40], but there exists an asymptotic expression for large r_|| that clearly reveals an (even faster than) exponential decay of ${\gamma }_{\text{pp}}^{*}$ with |r_||| [41]

$${\gamma }_{\text{pp}}^{*}\left(\left|{\text{r}}_{||}\right|,z,z_{\text{t}}\right)\propto \sqrt{\frac{8}{\left|{\text{r}}_{||}\right|z_{\text{t}}}}\sin \left(\frac{z}{z_{\text{t}}}\pi \right)\sin \left(\frac{z_c}{z_{\text{t}}}\pi \right)e^{-\frac{\pi }{z_{\text{t}}}\left|{\text{r}}_{||}\right|}.$$ (7)

To put this result into perspective, we compare it with the PSF of a hypothetical ideal point probe (instead of tip and QD) (Fig. 2a) which behaves as $\text{p}\cdot \widehat{\text{r}}/r^{\text{2}}$ (Fig. 2b), as expected for the test-charge/image-charge dipole.

The exponential decay of the PSF γ* (which is not exclusive to the parallel-plane approximation) puts the sensing of electrostatic potentials via SQDM in line with STM, for which the tunnelling probability also decays exponentially with distance. In both cases the result is a superior lateral resolution, since the influence of objects which are not right beneath the probe is strongly suppressed (compare Figs. 2g and h). Remarkably, in SQDM this is achieved in spite of the long range of electrostatic fields, while the tunnelling in STM is intrinsically short-ranged. Perpendicular to the surface there is, however, no exponential decay in SQDM. This preserves its superior sensitivity at large tip heights. Beyond the tip height dependence (Eq. 7), γ* depends only weakly on details of the tip. If anything, blunter tips yield a higher resolution, since their screening is stronger. This is in marked contrast to KPFM [42]. Knowing ${\gamma }_{\text{pp}}^{*},$ we can now obtain Φ_s by a deconvolution of V* (Eqs. 4 and 6, Fig. 2e, f, i, see Methods).

The second SQDM measurement quantity α_rel (Eq. 5) is not related to Φ_s but to the shape of 𝒯 via Eq. 3. Considerations summarized in the Methods and detailed in Ref. [29] show that the dielectric topography $t_{\text{d}}\left({\text{r}}_{||}^{\prime }\right)$ can be obtained from α_rel(r_||) via deconvolution, in the same way as Φ_s is obtained from V*.

An example image and its interpretation

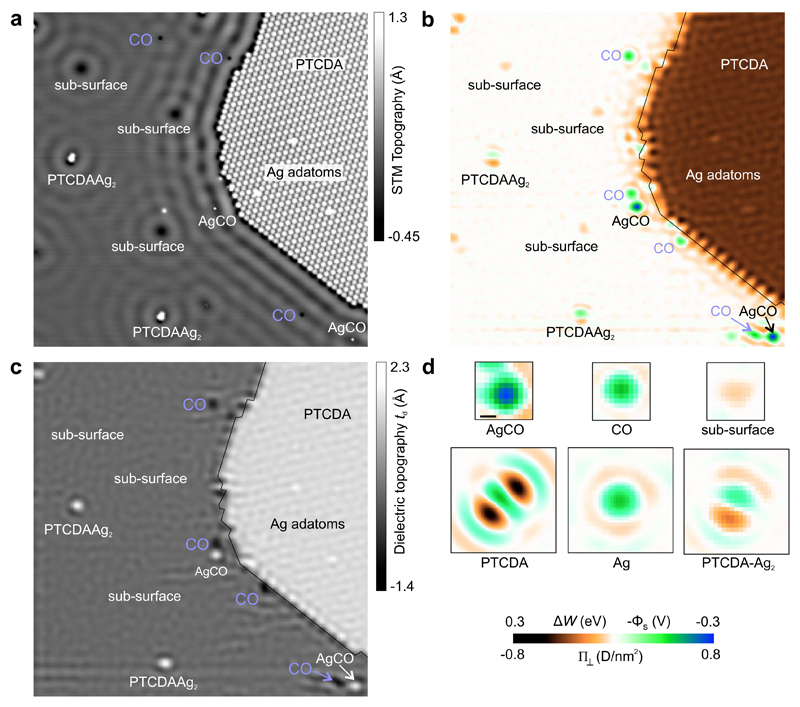
We demonstrate the quantitative imaging of electric surface potentials and dielectric topography for a Ag(111) surface on which Ag adatoms, CO molecules and PTCDA molecules have been deposited. As the STM image Fig. 3a reveals, the surface (in a manner of speaking a ’nanotechnology construction site’) contains various types of nanostructures: CO molecules, AgCO complexes, subsurface defects, a compact PTCDA monolayer, Ag adatoms on the PTCDA layer, and PTCDA-Ag₂ complexes that were made by controlled manipulation [43].

Figure 3. SQDM images of nanostructures on Ag(111).

Image size for a-c is 60×60 nm². a, STM image (V_b = 20 mV) showing various adsorbates and defects on a Ag(111) surface. b, SQDM Φ_s image (STC controller) of the area in Panel a. All features from Panel a are visible, however, the mobile CO molecules have moved to different locations. The thin black line traces the PTCDA island edge from Panel a. The rows of inequivalent PTCDA molecules on the island edges and within the island are resolved. See Supplementary Information for corresponding V^± images. c, SQDM dielectric topography image of the area in Panel a. The absolute scale t_d is obtained from calibration measurements of α_rel(z). The subsurface defects do not exhibit any topographic feature. d, Cutouts from several SQDM Φ_s images of individual nanostructures including a PTCDA-Ag₂ complex [43]. The colour scale refers to Panels b and d. The scale bar in d is 1 nm.

The surface potential Φ_s obtained by deconvolution (Fig. 3b) reveals a rich electrostatic landscape in which all features of the STM image appear as sources of complex patterns. Particularly remarkable is the deeply structured edge of the PTCDA island, and even inside the PTCDA layer a regular pattern is discernible. The fringes and granular structures are deconvolution artefacts which arise since deconvolution is an ill-posed problem. Note that the colour scale in Fig. 3b,d is calibrated as the surface potential Φ_s, as the work function change ΔW, and as the surface dipole density Π_⊥, all measured relative to the bare Ag surface. The three quantities are related straightforwardly by ΔW = −eΦ_s = −eΠ_⊥/ϵ₀, where the second equality is the Helmholtz equation [44].

The surface potential of individual objects in Fig. 3d reveals, in addition to the vertical dipole density Π_⊥ that is colour-coded, lateral multipoles such as the quadrupole moment of PTCDA and the dipole moment of PTCDA-Ag₂. Evidently, this information that is not available from STM helps with the identification of nanoscale objects. Their identification is further supported by the dielectric topography in Fig. 3c. We note that the dielectric topography of all nanostructures has the same sign as in the STM image (protrusion or depression compared to bare Ag(111)). This confirms our interpretation of t_d as a (dielectric) topography. In fact, the absence of a topographic signal for certain defects allows us to classify them as subsurface defects which by their electric potential (clearly imaged in Fig. 3b) scatter surface state electrons (as obvious from Fig. 3a). We also note the appearance of CO molecules as depressions in the dielectric topography image. This is a direct consequence of the push-back effect by which the molecule depletes the spill-out electron density of the metal substrate. The dielectric topography, as well as the surface potential, also show a number of small adsorbates on the edge of the PTCDA island that are barely visible in the STM image.

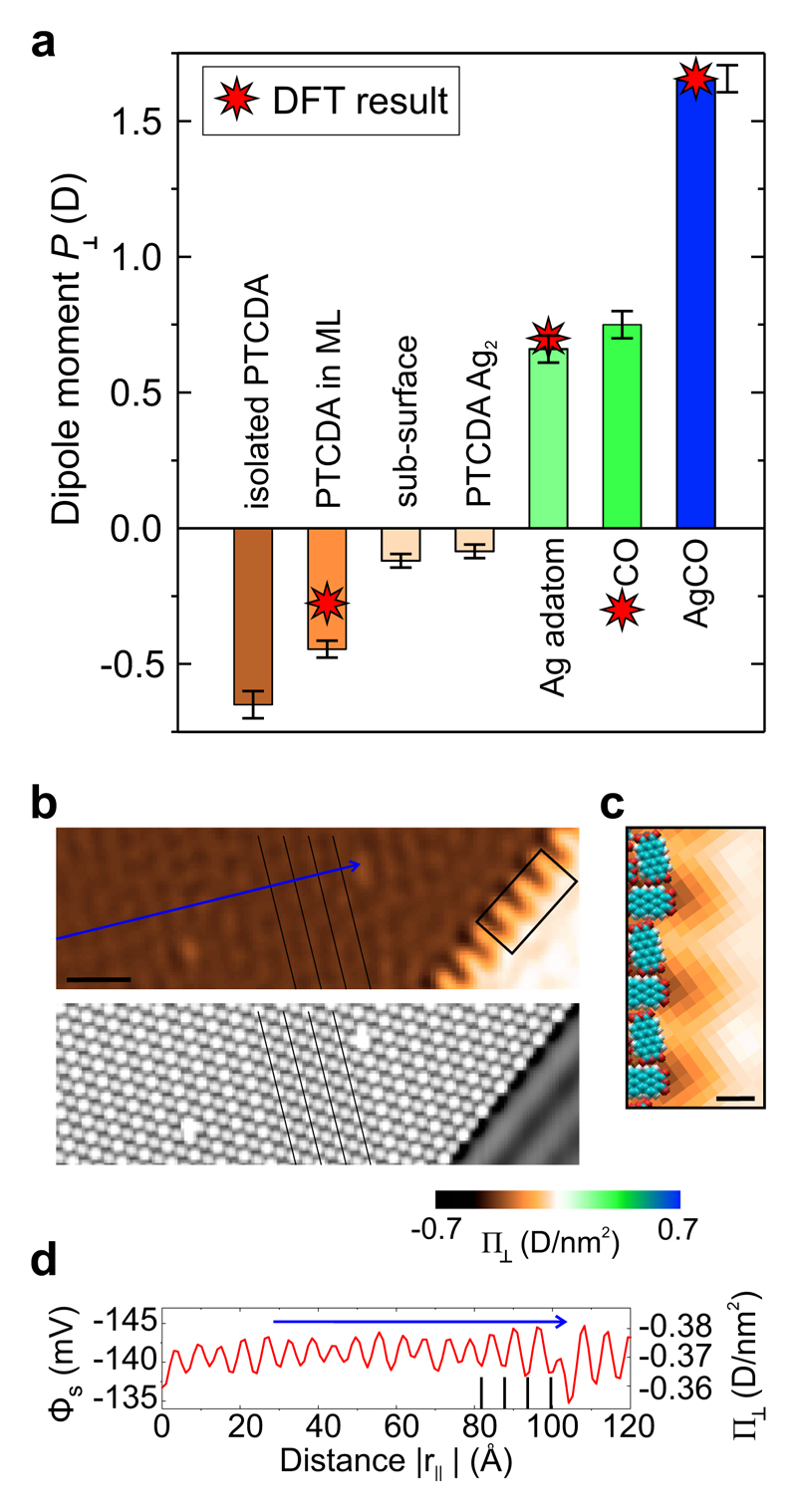
On the basis of high resolution images such as the ones in Fig. 3d we have calculated surface dipole moments P_⊥ of individual nanostructures by two-dimensional integration. The results are shown in Fig. 4a. We find that adsorption of CO on Ag(111) increases the dipole of CO to 0.75 D beyond its gas-phase value of 0.12 D, while CO adsorption on an Ag adatom on Ag(111) (which itself has a dipole of 0.66 D) results in a complex with a dipole moment of 1.65 D. The large positive dipole for the AgCO complex is of particular relevance, because this structure comes very close to the situation when a CO molecule is attached to the apex of an SPM tip, a common method to enhance image resolution [45, 46]. It has been conjectured before that the dipole of this CO-functionalized tip plays a crucial role for the correct interpretation of the corresponding images [21, 47–49]. Here we report a measurement of the dipole moment in a situation that closely resembles the adsorption of CO on the exposed tip apex. Another interesting effect in Fig. 4a is the depolarization of the PTCDA surface dipole once a molecular island is formed. The interaction between the parallel dipoles leads to a mutual reduction from -0.65 D for an isolated PTCDA molecule to -0.45 D as the intermolecular distance is decreased to ≃ 1 nm.

Figure 4. Surface dipoles of selected nanostructures and dipole density within a layer.

a, Surface dipole moments of adatoms, molecules or complexes with indicated error bars and DFT simulation results. The error bars approximate the uncertainty due to fringing artefacts in the deconvolved images. b, Cutout STM (bottom) and SQDM Φ_s image (top) from Fig. 3. Black lines indicate adjacent rows of identically adsorbed PTCDA molecules. The scale bar is 5 nm. c Zoom of the island border region marked in Panel b. The orientation and size of PTCDA molecules at the border is indicated. The scale bar is 1 nm. d The line profile through the Φ_s image along the blue arrow in Panel b reveals a modulation caused by rows of inequivalent PTCDA molecules. Black vertical lines correspond to the rows marked in Panel b.

Dipoles that are created by an adsorbate on a metal surface result from a delicate interplay between the original charge distribution in the adsorbate, (de)polarization effects, charge transfers and the deformation of the metal charge density. Their measurement thus provides a sensitive benchmark to validate our ability to describe these processes quantitatively. Therefore, we compare our experimental results with DFT simulations. The dipoles computed with the $\text{PBE}+{\text{vdW}}_{\text{sc}}^{\text{surf}}$ functional for CO, the Ag adatom and the AgCO complex, adsorbed on Ag(111), are -0.30 D, +0.70 D and +1.66 D, respectively, in good overall agreement with experiment, with the well-known exception of CO [50, 51].

The close-up image in Fig. 4b reveals a modulation of the surface potential Φ_s above the PTCDA island. Its periodicity of 1.7 nm matches the arrangement of inequivalent molecules in the PTCDA/Ag(111) unit cell. In the STM image in Fig. 3a the inequivalent molecules appear with different brightnesses. From scanning tunnelling spectroscopy it is known that charge transfer upon adsorption into the LUMO (Lowest Unoccupied Molecular Orbital) is smaller for the bright molecule than for the dark one [52]. However, since it is also known that the brighter molecule adsorbs at a larger height above the surface [53], it is not clear which of the two has the larger dipole in the end (a larger charge transfer has the tendency to increase the charge transfer dipole, but so does a larger adsorption height, which moreover will lead to a smaller pushback dipole of opposite direction). The line profile and the lateral grid in Fig. 4b reveal that the bright molecule has a lower inward pointing dipole density than the dark one. This shows that the charge transfer dipole at the PTCDA/Ag(111) interface is stronger than the push-back dipole, and that the larger charge transfer into the dark molecule overcompensates the effect of its smaller adsorption height.

A further striking feature of the PTCDA island is the strong modulation of the surface potential at its boundary. Comparing to a real-space model of the molecular layer, we can assign this structure to the uncompensated quadrupoles of PTCDA at the border where molecules alternatingly expose positively (hydrogen) or negatively (oxygen) charged groups. This strong electrostatic corrugation is an important reason for the preferential adsorption of small contaminants at the island edges, as found in Fig. 3.

Outlook

SQDM offers a fresh way to look at the nanoscale world. The formalism of SQDM, based on a Dirichlet boundary value problem, is now fully clarified. We illustrate the power of the method by presenting work function, surface dipole and electric potential measurements. A dedicated SQDM controller simplifies the recording of SQDM images to a point where SQDM requires no more effort than other atomic resolution scanning probe techniques. SQDM with a PTCDA quantum dot can easily be applied to other materials like NaCl which can be prepared with sub monolayer coverage on Ag [54] (see Supplementary Information). An even wider range of applications can be reached through the use of quantum dots that are lithographically fabricated at the end of the tip. The large tip-surface separations at which SQDM can operate make it particularly promising also for the study of rough surfaces or, for example, biomolecules with a distinct 3D structure.

Methods

SQDM Controller

SQDM imaging requires two images (V⁺ and V⁻) of the same sample area to be recorded one after another (compare Fig. 1b). We developed and used two different types of controllers for SQDM which both provide a voltage ΔV that is added to V_b to track and compensate the changes in V⁺ or V⁻ as the tip scans the surface. Both were implemented on a commercial rapid control prototyping hardware from dSPACE GmbH. They are two-degree-of-freedom (2DOF) controllers with a feedback and a feedforward (FF) part which mainly differ in the type of the tracked feature of each Δf dip. For the first 2DOF controller, the feedback part is an extremum seeking controller (ESC) [55] tracking the minimum in Δf (V_b + ΔV), while the second controller is an integral controller which tracks a specific Δf value at the slope of each peak (slope tracking controller, STC).

The ESC computes the derivative dΔf/dV_b via a small modulation of V_b with a frequency f_mod and adjusts ΔV such that the derivative remains zero. The advantage of this controller is its robustness. The disadvantage is its slower speed since the small Δf detection bandwidth requires f_mod to be equally small. The STC tracks a Δf reference value on the slope of the dip and uses the Δf deviation from this reference as the error signal to an integral controller. It is significantly faster than the ESC but could potentially introduce small systematic errors when the dips change their position on a non-constant background (Kelvin parabola). In the experiments presented here this error was, however, estimated to be below 1 mV.

In order to maximize the scanning speed, the FF part of both controllers uses the previous scan line as a reference for the current line. In this way, the feedback controller has to regulate only the difference between the previous and the current line to zero. Since at least one scan line (the reference) has to be acquired without the FF and thus more slowly, the scan speed can be adjusted during image acquisition. Using the STC, the total acquisition time of the V^± image information for Fig. 3 was two hours. More details on the 2DOF are given elsewhere [26].

DFT simulations

All the calculations presented in this work are obtained with a fully self-consistent implementation of the Tkatchenko-Scheffler ${\text{vdW}}_{\text{sc}}^{\text{surf}}$ functional [37], in combination with PBE in the full-potential all-electron code FHI-aims. The metal surfaces presented in this work are built with six Ag layers. A vacuum of 60 Å is used in order to prevent spurious interactions between periodic images. We used a (6 × 6) unit cell with a total number of 216 silver atoms. The molecule/atom is placed in the centre. Several unit cells have been tested, the one that we employ prevents any spurious lateral interaction. During the relaxation the topmost metal layer and the molecule were allowed to relax. We set the convergence criterion to 0.01 eVÅ⁻¹ for the maximum force and employ a Monkhorst-Pack grid of (2 × 2 × 1). The energy calculations are performed with a grid of (4 × 4 × 1) k-points. We use a radius of 5 Å for the cut-off potential to ensure an accurate treatment of long-ranged vdW interactions. For all calculations, we set a convergence criteria of 10⁻⁵ electrons for the electron density, 10⁻⁶ eV for the total energy and 10⁻³ eV for the sum of eigenvalues. Our calculations include scalar relativistic effects via the scaled zeroth-order regular approximation (ZORA).

The value of the dipole is linked to the change in electron density due to molecular adsorption. First, we compute the induced electron density as a function of z. This is the (2D integrated) difference between the electron density of the whole system and the densities of the isolated components, that is the metallic surface and the molecule/atom. Second, the delocalized charge is defined as the integral of the induced density along the z-axis. Finally, the change in the potential energy is computed with a second integration along the same direction. In other words, the induced dipole is obtained by solving the 1D Poisson equation along the z-direction.

Dielectric topography

To analyze variations in α_rel, we drop the assumption of a planar surface. Recalling the boundary value problem, topographic features in the region around r′ affect the screening of the test charge (at r′) and thus its potential at r, which is proportional to γ. For example, more material around r′ (if r′ itself is in a depression) increases the screening and thus decreases γ (Fig. 1c). Since the screening depends on the given material’s polarizability, dielectric nanostructures screen more weakly than metallic ones. Because modifications of the substrate’s metallic charge density by an adsorbate are effectively modifications in the metallic topography, they must be added to the screening effect of the (typically dielectric) adsorbate itself. Adsorbates which push back the metal charge density could thus effectively appear as depressions as it is reported for CO molecules in Fig. 3c. Leaking of metallic charge into the adsorbate via hybridization has the opposite effect. We lump all screening effects, originating from variations in real topography and dielectric properties, into a single dielectric topography t_d which equals the effective metallic surface topography that would cause the observed variations in α_rel. To obtain t_d from α_rel, we need to analyse the properties of γ (Eq. 3).

The non-local screening of the test charge makes $\gamma ({\text{r}}_{||},{\text{r}}_{||}^{\prime })$ a functional of $t_{\text{d}}({\text{r}}_{||}^{″})$ which depends on t_d in an entire region of the surface. Here, we disregard this aspect, while a comprehensive analysis is given elsewhere [29]. Without nonlocality, γ can be expressed as a function $\gamma ({\text{r}}_{||},{\text{r}}_{||}^{\prime })=f({\text{r}}_{||},{\text{r}}_{||}^{\prime },t_{\text{d}}({\text{r}}_{||}^{\prime })).$ Inserting the first order Taylor expansion of f with respect to t_d into Eq. 3 and dividing by α₀ yields the desired relation in which α_rel is a convolution of t_d with a point spread function ${\gamma }_{\text{topo}}=\partial f/\partial t_{\text{d}}{|}_{t_{\text{d}}=0}.$

$${\alpha }_{\text{rel}}\left({\text{r}}_{||}\right)=\frac{1}{{\alpha }_0}{\displaystyle \underset{\text{sample}}{\iint }f({\text{r}}_{||},{\text{r}}_{||}^{\prime },0)d^2{\text{r}}_{||}^{\prime }+\frac{1}{{\alpha }_0}{\displaystyle \underset{\text{sample}}{\iint }{\gamma }_{\text{topo}}({\text{r}}_{||},{\text{r}}_{||}^{\prime })t_{\text{d}}({\text{r}}_{||}^{\prime })}}{d}^2{\text{r}}_{||}^{\prime }.$$

Since $f({\text{r}}_{||},{\text{r}}_{||}^{\prime },0)$ corresponds to γ in the absence of any topography t_d, the first integral equals α₀ and the first term is therefore simply one. We can obtain the shape of γ_topo from the consideration that a local topographic feature (that is, a small polarizable object) in the homogeneous field above the otherwise flat sample (Taylor expansion of f) represents nothing else but a local dipole with a moment proportional to V_b. Hence, the contribution of such a feature to α is similar to that of an actual dipole to Φ_QD. Therefore, γ_topo has the same shape as ${\gamma }_{\text{pp}}^{*}\left({\gamma }_{\text{topo}}\propto {\gamma }_{\text{pp}}^{*}\right),$ which is fully borne out by a finite element simulation [29]. The norm of γ_topo is found by using a calibration function g ≈ (α_rel(z + Δz) − α_rel(z))/Δz which is experimentally obtained by varying z by Δz. Typical experimental values are in the range of g ≈ 0.03 Å⁻¹.

Data acquisition: from V^± to V* and α_rel

The V⁺ and V⁻ images of the same sample area are recorded consecutively (”2 pass”) in constant height mode, typically at tip heights between 20 and 30 Å using the STC or ESC discussed above. To determine the calibration curve α_rel = g × (z − t) at the chosen QD height z which is required for the correct normalization of γ_topo, we measure $V_0^{\pm }$ at one point of the reference area at heights z and z + 1 Å. This allows a linear estimate of α_rel(z) = 1 + c(z) × t which is sufficiently accurate if the maximum of t is t_max ≪ z. After recording the V^± images, standard image correction procedures like linear drift correction are applied if necessary. Finally, the V* and α_rel images are computed from the V^± images via Eqs. 5 and 6. For this procedure, a reference $V_0^{\pm }$ is chosen on an empty part of the metal substrate.

Deconvolution

For the deconvolution of V* we calculate the PSF ${\gamma }^{*}(|{\text{r}}_{||}-{\text{r}}_{||}^{\prime }|,z).$ To be suitable for deconvolution on an m × n image, the PSF is stored as a k × k kernel matrix K with k = 2l + 1 where k and l are integers. To enable a correct treatment of pixels close to image borders, we expand the (deconvolved) image to a size of (m + 2l) × (n + 2l) by adding l rows or columns on each side of the original image. Rows of K correspond to the x component of $|{\text{r}}_{||}-{\text{r}}_{||}^{\prime }|,$ columns to the y component. Note that the value of matrix elements in K only depends on the distance $|{\text{r}}_{||}-{\text{r}}_{||}^{\prime }|.$ The kernel matrix always has the same mesh size as the SQDM V* and α_rel images to be deconvolved (here typically 1-3 Å/pixel). The sum over all k² kernel matrix elements is normalized to 1 as required for γ*. The size k of the kernel matrix is chosen such that the values at its edges are sufficiently close to zero (K_0l ≲ 5 × 10⁻⁵K_ll). Due to the exponential decay of the PSF with lateral distance this is the case already for kernels that measure only 150 × 150 Ų. The elements of $\mathit{\text{K}}(|{\text{r}}_{||}-{\text{r}}_{||}^{\prime }|,z)$ are computed via the image charge method as discussed in the text (Fig. 2c). We use a point charge placed 1 Å above the surface and 100,000 image charges, which results in a full convergence of the potential between the tip and surface planes in the relevant lateral distance range. The matrix elements are then calculated as the lateral potential distribution d = 7 Å beneath the tip plane [24].

Since SQDM scans are constant height scans, the effective QD-sample separation z − t_d(r_||) varies with t_d, which, in turn, leads to variations of the actual PSF (cf. Eq. 7). As one consequence, identical nanostructures on substrate terraces of different height will not show the same V* image contrast. We compensate this effect during deconvolution by dynamically adjusting the PSF to the local t_d(r_||) value. To allow this, we calculate an entire set of K matrices for a range of tip-surface distances. We assume a locally planar surface of height t_d which can then be obtained by inverting the relation α_rel = 1 + gt_d with a value for g given above. This t_d(r_||) = (α_rel(r_||) − 1)/g is then used with the given z to select the correct K for each pixel in the V* image. Thus, we retain the model of a planar sample surface for which γ* can be easily computed and has axial symmetry, but we appropriately adjust the separation between both planes when determining the PSF for each pixel. A rigorous derivation of the underlying formalism is given elsewhere [29].

We deconvolve V* and α_rel images using an iterative non-linear deconvolution algorithm with a Tikhonov-Phillips regularization term to suppress over-amplification of noise and other deconvolution artefacts. We found in empirical tests that for our SQDM images, regularization based on the L₂ norm (like Tikhonov-Phillips) leads to better results than regularization using the L₁ norm (like the popular total variation minimization approach). To apply the Tikhonov-Phillips regularization we modify the expression for χ² and add a term that measures the squared variation between neighbouring pixels in the deconvolved image as

$${\chi }^2={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n(P_{ij}^{\exp }-P_{ij}^{\text{conv}})+\lambda \left[{(P_{ij}-P_{\left(i+1\right)j})}^2+{\left(P_{ij}-P_{i\left(j+1\right)}\right)}^2\right].}}$$

We have found that good deconvolution results are obtained with a value of λ = 0.0036/s², where s measures the image resolution in Å/pixel. This scaling is applied to enable deconvolution results that are independent of image resolution, since images with higher resolution are automatically smoother on a pixel-by-pixel level.

Supplementary Material

Supplementary information is available in the online version of the paper.