A Comprehensive Framework for Physiologically‐Based Pharmacokinetic Modeling in Matlab

Abstract

Physiologically‐based pharmacokinetic (PBPK) models are useful tools to predict clinical scenarios for special populations for whom there are high hurdles to conduct clinical trials such as children or the elderly. However, the coding of a PBPK model in a mathematical programming language can be challenging. This tutorial illustrates how to build a whole‐body PBPK model in Matlab to answer specific pharmacological questions involving drug disposition and magnitudes of drug–drug interactions in different patient populations.

Background

Physiologically‐based pharmacokinetic (PBPK) models have been applied with significant impact during drug development and postmarketing phases and have achieved regulatory acceptance1 as shown by the recent guidelines of the US Food and Drug Administration2 and the European Medicines Agency.3 PBPK models are useful for the prediction of drug–drug interaction (DDI) magnitudes4 and drug disposition in special populations such as pediatrics,5 pregnant and breastfeeding women,6, 7 and patients with liver cirrhosis8 or renal impairment,9 for all of whom there are high hurdles to design and conduct clinical trials. In addition, PBPK models have been successfully applied to simulate different routes of administration10 and for the design of novel formulations.

A PBPK model describes the absorption, distribution, metabolism, and elimination of a drug in a physiologically relevant compartmental structure, where each compartment represents an organ or tissue.11 The organs and tissues are connected via arteries and veins, which themselves merge in the lung. Dynamic drug movement through regional blood flows to the different organs and tissues is described by ordinary differential equations (ODEs). Tissue distribution can be predicted by a PBPK model that is of high relevance to most drugs because the drug targets are usually in specific populations of cells in an organ or tissue. The distribution into a compartment can either be limited by perfusion (well‐stirred models) or by the cell membrane (permeability‐limited models).12

An important characteristic of the PBPK modeling approach is the separation of system data (where the term system refers to the population of interest) from drug metabolism and pharmacokinetic data and the trial design.12 System data contain all relevant information to build a population of virtual individuals such as demographics, organ weights, and regional blood flows. It is of tremendous importance that the system data used to parameterize the PBPK system components reflects the “true” (meaning observed) population to produce reliable predictions.13 The incorporated physiological, biochemical, and genetic variability of system parameters allows the identification of certain subpopulations with high risks for DDIs (e.g., poor metabolizers for the enzyme cytochrome P450 (CYP) 2D6), where clinical data are often lacking.14 However, variability is often underestimated in PBPK models because of missing parameters or processes involved with physiological changes caused by diseases or specific patient characteristics, all of which add uncertainty and variability.15

Drug metabolism and pharmacokinetic data describe the information related to physicochemical properties (e.g., molecular weight), absorption (e.g., intestinal permeability), distribution (e.g., binding to plasma proteins), metabolism (e.g., kinetic parameters for an enzyme), and excretion (e.g., renal clearance).16 Usually drug characteristics, such as the intrinsic clearance of an enzyme, are quantified through laboratory‐based experiments that are then scaled to the in vivo clearance under the consideration of system parameters such as the enzyme abundance in the liver per gram protein, the protein content per gram liver, the liver weight, and the hepatic blood flow.17 By considering variability in these system parameters, it is possible to obtain reliable population predictions of drug clearance.14 System and drug data can be combined in the trial design component, considering parameters such as dose, dosing regimen, route of administration, number of individuals, and duration of administration to simulate clinical scenarios of interest.

Several commercial PBPK software platforms, such as SimCYP,18 PK‐Sim,19 and GastroPlus20 simplify the model management for unexperienced modelers and are based on structural PBPK models. However, they are limited in flexibility to simulate specific pharmacological questions. In this tutorial, a general framework on how to build a whole‐body PBPK model in Matlab (MathWorks, Natick, MA) is described for scientists and users with interest in mathematical modeling and its application in pharmacology. The general development can also be adapted in other programming languages such as R or other Matlab packages such as Simbiology.

Five Steps to Build a PBPK Model in Matlab

Matlab offers a powerful mathematical programming language with matrix‐based operations (https://uk.mathworks.com/products/matlab.html). The basic principles of Matlab are extensively described in the documentation by MathWorks (https://uk.mathworks.com/help/matlab/index.html). This tutorial illustrates the different steps necessary to build a PBPK model to simulate specific clinical scenarios with examples of pseudo code separated by lines from the main text. The entire code and tables listing the abbreviation and units for all used parameters can be found in the supplement (Tables S1 and S2). The Statistic and Machine Learning Toolbox is a required Add‐On to the Matlab suite to execute the code.

A “building block” system is used for separating system, drug, and trial design data to inform the PBPK model.12 The advantages are that each block can be used for a different purpose (e.g., the generated population could be used in a different model), and each block can be exchanged (e.g., aging white population vs. pediatric population21). Each building block described in this tutorial is a Matlab function. Matlab requires one script indicating the order in which the functions should be executed, which in this tutorial is called the main function.

%Main function: Calls each function of a PBPK model

 

Define the model structure and the model parameters

Generation of the virtual population

Load the drug files and perform the in vitro to in vivo extrapolation

solve the ordinary differential equations (ODEs)

process the data from the ODE solution and output the results

The variables used in different functions in Matlab need either to be passed onto the next function or to be defined as globals using the “global” command. However, it is good practice to scope variables as local if they are only used within a specific script.

Step 1: Define the parameters of the model

The modeling process is started by defining the objective and the purpose of the model, identifying the pharmacological scenario to be simulated. The model structure proposed can vary based on the overall purpose of the simulations, and a representative compartmental model is shown in Figure 1.22 As an example, it would be of scientific interest to simulate clinical scenarios in aging HIV‐infected patients because clinical data of antiretroviral drug disposition and DDI magnitudes between antiretroviral agents and comedications are currently lacking. When simulating anti‐HIV therapy, drug penetration into viral reservoirs, such as the testis and the brain,23 and into the lymphatic system being the target site for antiretroviral drugs can represent a relevant pharmacokinetic factor. The flexible computational structure supports the inclusion of the lymphatic system, dividing each compartment into the vascular, interstitial, and intracellular spaces (Figure 2) with lymph fluid flowing from the interstitial space of each organ to a central lymph‐node compartment and further to the venous blood pool. Organs not being simulated are lumped into a remaining organ compartment.13 In our example, the model is used to simulate the effect of the CYP3A4 inhibitor ritonavir, used as a pharmacokinetic enhancer to boost the concentrations of coadministered HIV protease inhibitors such as darunavir, on the disposition of the anticoagulant rivaroxaban being metabolized by CYP3A4 in aging white subjects.

Figure 1.

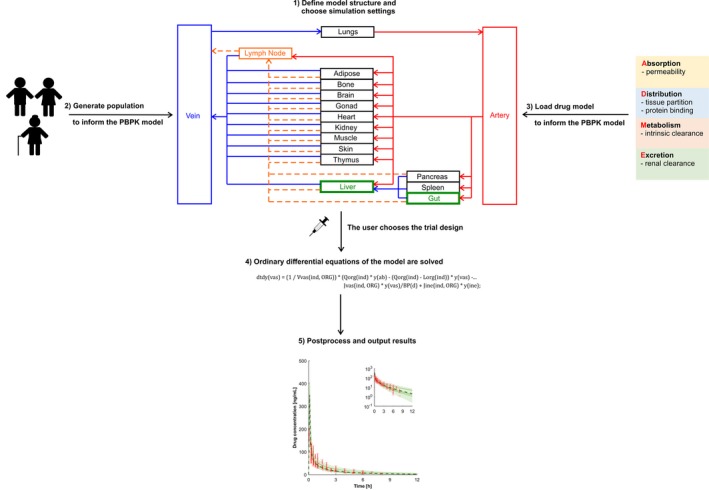
Schematic illustration of the five steps to build a physiologically‐based pharmacokinetic model.

Figure 2.

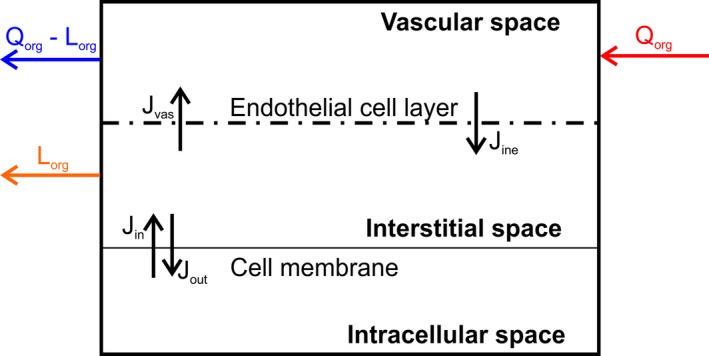
Structure of an organ in the model. J _in, flux into the cell; J _ine, flux from the interstitial to the vascular space; J _out, flux out of the cell; J _vas, flux from the vascular to the interstitial space; L _org, regional lymph flow; Q _org, regional blood flow.

First, the model structure and model variables, including populations, compartments, drugs, and routes of administration are defined by a number because Matlab is a numerical software tool. The number assigned to each variable (e.g., drugs) refers to the column in each matrix containing specific data (e.g., if darunavir is defined by a one, the data of darunavir would be in the first column; Figure 3). Each variable is also defined by a string defining its name for the outputs.

Figure 3.

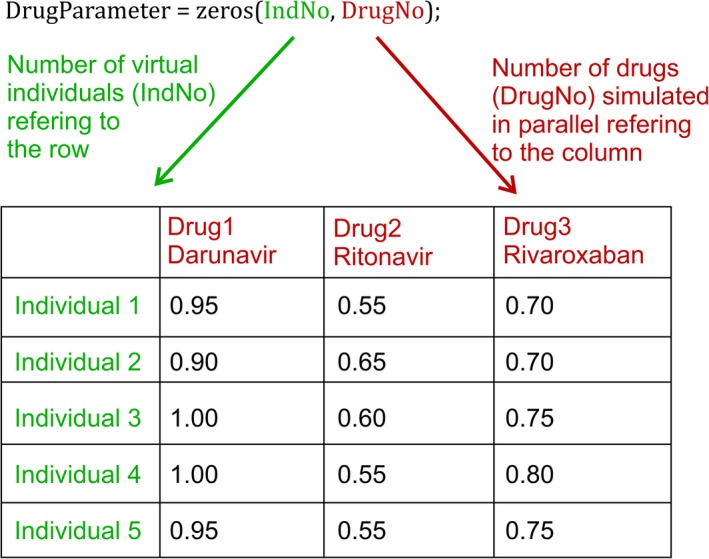
Example of the organization of drug parameters with variability. Each row contains data for an individual, and each column contains data for a drug. Parameter clues are illustrative only. IndNo, number of virtual individuals. DrugNo, number of drugs.

After defining all necessary variables of the model, the target population and the drugs to be used in a specific simulation need to be entered. The virtual trial design can be described by first indicating the number of virtual individuals in the simulation. The appropriate number of individuals depends on the variability of system data involved to describe the pharmacokinetics of the simulated drug (e.g., enzymatic vs. total clearance) and the number of patients included in clinical trials to verify the model. To come to the “true” population mean for most anatomical, physiological, and biological parameters, a sample size of at least 100 individuals is recommended. Of note, for system parameters with high variability, such as enzyme and transporter abundance, a virtual population containing 500 individuals might be more appropriate.24 Therefore, if observed clinical data are available for six patients, it is recommended to run 20 trials times six patients, resulting in 120 virtual individuals. The split into different trials allows the comparison of the mean predicted concentration of each trial with the mean observed data. The mean observed is used because often observed concentration from individuals are not published or available. Observed data from six individuals may not be representative of the whole patient population taking the drug of interest; thus, it is important to recognize that the mean prediction obtained might be different and far from the mean of the six observed subjects, but it might be close to the “true” population of patients. Therefore, if the observed data from six subjects fit the prediction of one trial, even when its prediction should be on the upper or lower end of all simulations, this is still considered to be a “successful” outcome.

Next the proportion of men and women in the simulated population and the age range of the virtual individuals can be specified. In addition, the resolution of each simulated time unit needs to be given for the outputs.

Once the individual characteristics are described, the dosing regimen for each drug can be defined, indicating the route of administration, the number of doses (1 for a single dose and n for multiple doses), the dose, and the dosing interval. After entering the trial design, a dose event matrix can be set up to allow the simultaneous simulations of darunavir, ritonavir, and rivaroxaban alone and in combination to investigate DDIs. The matrix contains five columns with the start and the end time of each dose, the dose, the route of administration, and the resolution for each dosing event. Only unique start and end times for each dosing event are needed, which need to be extracted.

The code to define the model parameters and choose the simulation settings is given by:

function[] = DefineParameters()

 

%This function defines the population, model structure (PBPK compartments),

%the drugs, the virtual trial design and the simulation settings to be used

 

%=======================================================

 

Define the populations saved on the hard drive by a number and a string

 

Define the compartments of the model by a number and a string

Define enzymes for the dynamic abundance calculation in case of DDIs by a number and a string

Define the number of subcompartments

 

Define the drugs saved on the hard drive by a number and a string

Define plasma‐binding proteins by a number and a string

 

Define the route of administration by a number and a string

 

%=======================================================

 

User sets the population to be simulated (if more than one is saved on the hard drive)

 

User sets the number of drugs to be simulated

Initialize drug name

 

Define a case for each simulated drug

 define a drug name for each drug to be simulated

end

 

Define the number of trials

Define the number of virtual individuals per trial

Calculate the number of all virtual individuals to be simulated

 

Ask the user for the proportion of women in the virtual population

Ask the user for the minimal and maximal age of the virtual population to be simulated

 

Ask the user for the resolution of each time step

 

Initialize the route of administration, the number of doses, the dose, the dose interval, the start timepoint for the dose, and the prolongation of the terminal elimination phase.

 

Define a case for each drug to be simulated

 Define the route of administration to be an iv bolus or oral

 Define the number of doses and dose given in mg

 Define the dose interval in h

 Set a start time for the drug to be administered in h

 Set the prolongation for the terminal elimination phase in h

end

 

%=======================================================

 

Define the name of the columns for the dose event matrix

Calculate the number of columns of the dose event matrix

 

Initialize a matrix containing the regimen for each drug

Define a case for each drug

 Define a case for each dose being administered

 Calculate the start time for the first dosing event

 Calculate the end time for the first dosing event

 

 Calculate the start time for all dosing events

 Calculate the end time for all dosing events

 

 Consider the prolongation of the terminal elimination phase

 end

end

 

Define a case for each drug

 sort the regimen matrix based on the start time of each drug

 delete zero values

end

 

Define a case for each drug

 combine the dosing regimens for different drugs

 use a function to find unique dosing events for each drug

 set dose, route of administration, and resolution for the other drugs to be zero

 sort the matrix according to the start time

 find unique start times

 output the dose event matrix for each drug based on the unique start times

 end

end

 

Calculate the number of events

Put together the dose event matrix

 

end

Step 2: Generation of the population

A repository summarizing the anatomical, physiological, and biological system parameters required to inform a PBPK model has been recently published.13 The described continuous, age‐dependent equations and the variability for each system parameter can be directly entered in Matlab:

function[] = Population()

 

%This function generates the virtual population based on the user settings

%Attention: the normrnd command needs the Statistics and Machine Learning Toolbox

 

Calculate age from a Weibull distribution for each virtual individual

 while age of an individual is smaller or larger than the minimal or maximal user‐defined age

 Resample age from the Weibull distribution

 end

end

 

Calculate number of virtual female individuals

Assign randomly a zero (defined as “male”) or one (defined as “female”) to each virtual subject

 

Calculate system parameters as described in ref: [13]

Add random variability to the system parameters by using a normal described

 

end

Step 3: Calculation of the required drug parameters

In the next step, the user‐defined drug file is loaded from the library containing all developed drug files. The string defining the drug (e.g., “darunavir”) is converted to the function in the drug library to load the drug‐dependent data to inform the PBPK model (Figure 4):

Figure 4.

Steps from the user‐defined drug to be simulated to the drug parameter that are loaded to inform the physiologically‐based pharmacokinetic model.

function[] = Drug()

 

%This function loads the relevant drug files from the drug library and

%performs the in vitro‐to‐in vivo extrapolation

 

Define a case for each drug

 load the Matlab file containing the drug parameter by converting the string defining the…

 drug to the function in the drug library

end

 

end

Drug parameters incorporated in a drug file are shown in Table 1. The measured drug properties included in the drug file can be derived through experimental in vitro methods and integrated into specific equations for drug absorption, distribution, and elimination as described in the following sections.

Table 1.

Parameters required for a drug file to inform the physiologically‐based pharmacokinetic model

Parameter	Typical units	Explanation
Physicochemical properties
MW	g/mol	Molecular weight
logP	–	Octanol‐water partition coefficient
Compound type	–	Important property to predict tissue distribution according to Rodgers and Rowland
pKa	–	Acid dissociation constant
BP	–	Blood‐to‐plasma ratio
fuPL	–	Fraction unbound in plasma
Absorption
P app	×10−6 cm/s	Apparent permeability
Distribution
Kp scalar	–	Scalar to alter predicted partition coefficient
Elimination
V max/K m or CLint	pmol/minute/pmol enzyme/μM or μmol/minute/mg protein	Kinetic parameters per enzyme and metabolic pathway
CLr	L/h	Renal clearance
CLad	L/h	Additional plasma clearance
Transporter
CLpd	μL/minute/Mio cells	Passive diffusion flux
V max/K m or CLint	pmol/minute/pmol transporter/μM or μmol/minute/Mio cells	Kinetic parameters for transporters
Interactions
K i	μM	Inhibition constant for competitive inhibition
K app	μM	Apparent enzyme inhibition constant for mechanism‐based inhibition
k inact	1/h	Maximum inactivation rate constant
IndMax	–	Maximum fold of induction
IC50	μM	Half maximum inhibitory concentration

Absorption

The compartmental absorption and transit model proposed by Yu and Amidon25 about 20 years ago is used as a basis. The assumptions of the original compartmental absorption and transit model are the following:

1. The drug is immediately dissolved

2. Absorption occurs primarily in the small intestine and not in the stomach or the colon

3. Transit time and radii are similar for each compartment

4. Intestinal metabolism is negligible

5. Only passive diffusion occurs through the gut wall

It can be assumed that assumption 1 holds true for antiretroviral drugs because they are often given as an immediate‐release tablet. Formulation and dissolution play a crucial role when simulating capsules or delayed‐release tablets, and more complex absorption models can be built into the model as previously described.26, 27 The compartmental absorption and transit model consists of five different compartments, namely, the stomach, duodenum, jejunum, ileum, and colon. The stomach serves as an entry compartment for the orally administered drug. It is assumed that the drug can only move further to the duodenum and no absorption or other processes occur in the stomach. Movement between different compartments representing the intestine can be described by first‐order rate constants calculated from the gastric emptying and the intestinal transit time.25

Permeability into enterocytes and further into the systemic circulation can be mediated by passive or active processes. Drug transporters are present on the apical and basolateral site of the small intestine.28 An established experimental model such as human epithelial colorectal adenocarcinoma cells seeded as a monolayer can be used to measure the apparent permeability (P _app) in vitro and depending on the experimental conditions, the measured flux into the cell can be the sum of passive and active. The measured P _app can be converted to the effective permeability in man (P _eff,man) describing the flux of the drug from the lumen into the enterocytes in humans29 as follows:

$$P_{\mathrm{eff},\mathrm{man}}={10}^{0.6795*\text{log}(P_{\mathrm{app}})-0.3355},$$ (1)

where P _app is in 10⁻⁶ cm/s and P _eff,man is in 10⁻⁴ cm/s. P _eff,man needs to be multiplied by the available enterocyte surface for drug absorption (permability surface area PSA) to arrive at the absorption clearance (CL_ab) (please note that the flux between two compartments can be written as a clearance), namely:

$${\text{CL}}_{\mathrm{ab}}=P_{\mathrm{eff},\mathrm{man}}*\text{PSA}*0.001*3,600$$ (2)

where CL_ab is in L/h. The PSA can be calculated by assuming that the gut has a cylindric shape, namely:

$$\text{PSA}=2*\mathrm{\pi }*r*\text{Le}*F_{\mathrm{Villi}}$$ (3)

where r is the radius of each intestinal segment in centimeters, Le is the length of each intestinal segment in centimeters, and F _villi is a fold expansion factor for the villi surface area. The length and the expansion factors for the different gastrointestinal segments has been extensively described previously.30, 31 Drugs penetrate through the intestinal wall mainly by the transcellular pathway because of the tight junctions between enterocytes. Paracellular transport is only possible for drugs with a molecular weight <300 Da being positively charged and with an octanol‐water partition coefficient (logP) > 0.32

To estimate the concentration in the enterocyte, the volume of the enterocytic cell layer needs to be determined. A jejunal biopsy was undertaken in 11 healthy controls (five women) aged younger than 30 years, and 3,040 enterocytes were found in the sample. The volume of one enterocyte is 770 μm³, calculated as a cylinder from the measured height and radius.33 The surface of the small intestine can be calculated by assuming a cylindric shape and the radius and length of 2.25 cm and 280/260 cm for an average male/female subject, respectively.31 The resulting surface area of the small intestine is 3,958/3,676 cm². Scaling the number of enterocytes from the biopsy sample to the entire small intestine leads to 1.20 × 10¹¹/1.12 × 10¹¹ cells. The total volume of all enterocytes in the small intestine is therefore 0.093/0.086 L.

The drug distributes further from the enterocytes to the interstitial space and could move further either via the systemic or the lymphatic circulation. The potential strategies for antiretroviral drugs include manipulating the formulation in such a way so that more drug gains access into the lymphatic system because (i) it is the relevant target site, (ii) there will be no first‐pass metabolism, and (iii) the drug stays longer in the body because intestinal lymph flow is about 600‐fold slower than intestinal blood flow.31, 34 To move preferentially into the lymph circulation rather than into the systemic circulation, a drug needs to be highly lipophilic and positively charged and should have a high molecular weight.35 However, there are no quantitative relationships in the literature. A manual restriction factor can be implemented into the model defining a proportion of the drug going via the lymphatic system to test new formulations. The rest of the drug will distribute via systemic circulation.

Distribution—passive and active pathways

The prediction of tissue distribution is important in a PBPK model. Intracellular concentrations cannot be easily obtained, particularly in humans, but most drug targets are in cells. In addition, metabolism occurs in hepatocytes and enterocytes, and therefore intracellular concentration is important to predict metabolism and DDI magnitudes adequately. Several models are described in the literature to predict distribution into tissue.36, 37, 38, 39, 40, 41 Poulin and Theil36, 37 assume homogenous distribution in a tissue, which does not hold true if the cell membrane is a tight barrier. Therefore, the approach of Rodgers et al.³⁸ and Rodgers and Rowland^39,40 is used in this model.38, 39, 40 In contrast to Poulin and Theil, Rodgers et al. consider binding to different constituents of the cell, such as lipids and proteins.

Calculation of partition coefficients

Mono protic‐ and diprotic basic drugs with an acid dissociation constant > 7 interact preferentially with acidic phospholipids in the tissue through electrostatic interactions. Binding to extracellular proteins may not play an important role because basic drugs preferentially bind to alpha‐acidic glycoprotein, which is mostly restricted to plasma. Therefore, an affinity constant for acidic phospholipids (KaAP) is calculated for red blood cells. The partition coefficient for the unbound drug into red blood cells can be calculated from the blood‐to‐plasma (BP) ratio, which itself can be measured in vitro. It is assumed that KaAP is similar for all tissues. Generally, the tissue partition coefficient of the unbound drug (Kpu) for muscle should be preferred as there is a good correlation between distribution into muscle and distribution into other tissues. The unbound drug partition coefficient for erythrocytes is given by ref. 38:

$${\text{Kpu}}_{\mathrm{RBC}}=\frac{C_{\mathrm{RBC}}}{C_{\mathrm{PL}}*{\mathrm{fu}}_{\mathrm{PL}}}=\frac{\text{BP}*\text{HCT}+(1-\text{HCT})}{{\text{fu}}_{\mathrm{PL}}}$$ (4)

where C = concentration, fu = fraction unbound in plasma, HCT = hematocrit, PL = plasma, and RBC = red blood cells. The affinity constant for acidic phospholipids is given by ref. 38:

$$\begin{array}{cc}\hfill {\text{KaAP}}_{\mathrm{RBC}}=& [{\text{Kpu}}_{\mathrm{RBC}}-\left(\left(\frac{K_{\mathrm{io},\mathrm{RBC}}}{K_{\mathrm{io},\mathrm{PL}}}\right)*f_{\mathrm{IW},\mathrm{RBC}}\right)\hfill \\ & -\left(\frac{\text{log}P*f_{\mathrm{NL},\mathrm{RBC}}+(0.3*\text{log}P+0.7)*f_{\mathrm{NP},\mathrm{RBC}}}{K_{\mathrm{io},\mathrm{PL}}}\right)]\hfill \\ & *\left[\frac{K_{\mathrm{io},\mathrm{PL}}}{{[\text{AP}]}_{\mathrm{RBC}}*(K_{\mathrm{io},{\mathrm{RBC}}^{-1}})}\right]\hfill \end{array}$$ (5)

$$\begin{array}{cc}\hfill {\text{Kpu}}_{\mathrm{org}}=& \\ & \left(\frac{K_{\mathrm{io},\mathrm{IW}}*f_{\mathrm{IW},\mathrm{org}}}{K_{\mathrm{io},\mathrm{PL}}}\right)+f_{\mathrm{EW},\mathrm{org}}+\left(\frac{{\text{KaAP}}_{\mathrm{RBC}}*{[\text{AP}]}_{\mathrm{org}}*(K_{\mathrm{io},{\mathrm{IW}}^{-1}})}{K_{\mathrm{io},\mathrm{PL}}}\right)\hfill \\ & +\left(\frac{\text{log}P*f_{\mathrm{NL},\mathrm{org}}+(0.3*\text{log}P+0.7)*f_{\mathrm{NP},\mathrm{org}}}{K_{\mathrm{io},\mathrm{PL}}}\right)\hfill \end{array}$$ (6)

where K _io = ionized form according to Henderson‐Hasselbalch,39 f _IW = fraction of intracellular water, f _EW = fraction of extracellular water, f _NL = fraction of neutral lipids, f _NP = fraction of neutral phospholipids, and AP = acidic phospholipids. The subscript org represents organ. For the partitioning into the adipose tissue, it is more accurate to use the vegetable oil:water partition coefficient (logD _vo:w) rather than logP, namely36:

$$\text{log}{D}_{\mathrm{vo}:w}=(1.115*\text{log}P-1.35)-\text{log}(K_{\mathrm{io},\mathrm{PL}})$$ (7)

Binding to extracellular albumin should be considered for drugs that are not moderate to strong bases thus requiring the determination of the affinity constant for binding proteins (KaPR). The calculation is done for plasma because albumin concentration in plasma is known, and the unbound fraction in plasma can be determined in in vitro experiments. It is assumed that KaPR_PL holds true for all tissues,39 namely:

$$\begin{array}{c}\hfill {\text{KaPR}}_{\mathrm{PL}}=\\ & \left[\frac{1}{{\text{fu}}_{\mathrm{PL}}}-1-\left(\frac{\text{log}P*f_{\mathrm{NL},\mathrm{PL}}+(0.3*\text{log}P+0.7)*f_{\mathrm{NP},\mathrm{PL}}}{K_{\mathrm{io},\mathrm{PL}}}\right)\right]*\frac{1}{{\text{PR}}_{\mathrm{PL}}}\hfill \end{array}$$ (8)

where PR_PL is the binding protein concentration in plasma in g/L. The unbound drug partition coefficient is given by ref. 39:

$$\begin{array}{cc}\hfill {\text{Kpu}}_{\mathrm{org}}=& \left(\frac{K_{\mathrm{io},\mathrm{IW}}*f_{\mathrm{IW},\mathrm{org}}}{K_{\mathrm{io},\mathrm{PL}}}\right)+f_{\mathrm{EW},\mathrm{org}}+({\text{KaPR}}_{\mathrm{PL}}*{\text{KpPR}}_{\mathrm{org}}*{\text{PR}}_{\mathrm{PL}})\hfill \\ & +\left(\frac{\text{log}P*f_{\mathrm{NL},\mathrm{org}}+(0.3*\text{log}P+0.7)*f_{\mathrm{NP},\mathrm{org}}}{K_{\mathrm{io},\mathrm{PL}}}\right)\hfill \end{array}$$ (9)

where KpPR_org is the partition coefficient of plasma‐binding proteins in different organs.

The apparent volume of distribution in steady state (V _ss) can be calculated as follows40:

$$V_{\mathrm{ss}}=\frac{V_{\mathrm{PL}}}{{\text{fu}}_{\mathrm{PL}}}+\sum V_{\mathrm{org}}*{\text{Kp}}_{\mathrm{org}}$$ (10)

where V is the volume and Kp is the total tissue partition coefficient, which is defined as38:

$$\text{Kp}=\frac{C_{\mathrm{org}}}{C_{\mathrm{PL}}}=\text{fu}*\text{Kpu}.$$ (11)

A Kp scalar can be introduced to the model, which multiplies the predicted Kp

$${\text{Kp}}_{\mathrm{used}}=\text{Kp}*\text{Kp scalar}$$ (12)

and can be used to correct for insufficient tissue partition prediction. One such example is the extensive lysosomal trapping or binding to intracellular constituents such as DNA (e.g., doxorubicin).38

When splitting every compartment of the PBPK model into the subcompartment vascular, interstitial, and intracellular spaces, the distribution through the endothelial cell layer and through the cell membrane are required to inform the PBPK model. The endothelial cell layer is not a tight barrier for small molecule drugs, thus it can be assumed that the extracellular water is almost instantaneously in equilibrium. Under physiological conditions, blood comes with high pressure into the capillaries, and its content is pushed against the endothelial cell layer and through the small and large pores into the interstitial space.42 There is a partial fluid loss, the lymph, which is recycled back to the venous blood pool via the lymph nodes. Erythrocytes cannot cross the endothelial cell layer, and hence the lymph is colorless.

The calculated Kp is used to estimate the flux through the cell membrane between the interstitial and the intracellular spaces, when experimental data about cell membrane permeability are not available. It holds true that the concentration in plasma equals the concentration in the vascular space, which is considered to belong to the blood, namely:

$$\text{Kp}=\frac{C_{\mathrm{org}}}{C_{\mathrm{PL}}}=\frac{C_{\mathrm{ine}}+C_{\mathrm{cel}}}{C_{\mathrm{vas}}}=\frac{C_{\mathrm{ine}}}{C_{\mathrm{vas}}}+\frac{C_{\mathrm{cel}}}{C_{\mathrm{vas}}}$$ (13)

where the subscripts vas, ine, and cel represent vascular, interstitial and intracellular, respectively. Kp is determined in steady state and under steady‐state conditions, the vascular and interstitial space concentration differ by the drug concentration in erythrocytes, and the interstitial and intracellular drug concentration differ by the fraction unbound and the flux through the membrane, namely:

$$\text{Kp}=\frac{1}{\text{BP}}+\frac{J_{\mathrm{in}}*{\text{fu}}_{\mathrm{ine}}}{J_{\mathrm{out}}*{\text{fu}}_{\mathrm{cel}}}.$$ (14)

Kp can only be described by the ratio of influx (J _in) and efflux (J _out) of the cell.

Fraction unbound in the interstitial and intracellular spaces

A critical parameter for the distribution of a drug is fu in each compartment. Usually, fu is only measured in plasma samples, but the site of metabolism or efflux transporters is intracellular, making it necessary to know fu_cel. In a first step, the age dependency of fu is calculated for each virtual individual based on the measured fu in vitro and the main binding protein. “Ref” refers to a 30‐year‐old adult who is arbitrarily used to represent a “young” subject. It is assumed that the binding affinity does not change with age, and therefore fu for plasma is given by ref. 9:

$${\text{fu}}_{\mathrm{PL}}=\frac{1}{1+{\text{PR}}_{\mathrm{PL}}*\left(\frac{\frac{1}{{\mathrm{fu}}_{\mathrm{Ref}}}-1}{{\text{PR}}_{\mathrm{PL},\mathrm{Ref}}}\right)}.$$ (15)

In a second step, fu in the interstitial space of each organ is estimated based on the known partition coefficient for the plasma‐binding proteins in each tissue.38 It is assumed that the binding affinity is the same as in plasma. Thus, fu_ine is calculated as follows:

$${\text{fu}}_{\mathrm{ine},\mathrm{org}}=\frac{1}{\frac{{\text{KpPR}}_{\mathrm{org}}}{f_{\mathrm{EW},\mathrm{org}}}*\left(\frac{1}{{\text{fu}}_{\mathrm{PL}}}-1\right)+1}.$$ (16)

fu_cel is calculated according to Rodgers and Rowland,39 namely:

$${\text{fu}}_{\mathrm{cel},\mathrm{org}}=\frac{1}{\begin{array}{cc}\hfill 1& +\left[\left(\frac{\text{log}P*f_{\mathrm{NL},\mathrm{org}}+(0.3*\text{log}P+0.7)*f_{\mathrm{NP},\mathrm{org}}}{K_{\mathrm{io},\mathrm{PL}}}\right)+{\text{KpPR}}_{\mathrm{org}}*{\text{PR}}_{\mathrm{PL}}\right]\hfill \end{array}}.$$ (17)

Active drug transporters

Drug transporters can theoretically be implemented into any compartment of the model to represent active distribution into cells, but absolute transporter abundance values to inform the PBPK model are only available for the liver.43 There are some important points to consider before implementing a transporter into a PBPK model. Each transporter has a direction, and its impact will depend on whether the transporter is expressed on the apical or basolateral site. Passive permeability can occur besides active transport for given compounds, and therefore it is important to define the contribution of each of these transport processes. The overall contribution of uptake transporter is likely to be negligible for compounds characterized by a high passive permeability. Conversely, efflux transporters will have a pronounced impact for compounds characterized by a slow passive diffusion. Importantly, uptake and efflux transporters are exposed to different drug concentrations and thus the unbound drug concentration in the interstitial and intracellular spaces should be used for uptake and efflux transporters, respectively.44 Transporter functionality can be described by Michaelis–Menten kinetics; however, V _max,T/K _m,T = CL_u,int,T,45 where V _max,T is the maximum transport rate, K _m,T is the Michaelis–Menten constant for a transporter, and CL_u,int,T is the intrinsic transport clearance of the unbound drug, only holds true if the unbound concentration is much smaller than K _m (fu x C ≪ K _m). This is the case under physiological conditions in the cell but might not hold true for uptake transporters being exposed to the interstitial concentration. In addition, Michaelis–Menten assume one binding site per transporter, which is questionable, for instance, for the organic anion‐transporting polypeptide 1B1.46 Active hepatic drug transporters can be described by ref. 45:

$$\begin{array}{cc}\hfill {\text{CL}}_{\mathrm{int},T,\mathrm{tot},\mathrm{hep}}=& \left[\sum _{u=1}^m\left(\left(\frac{V_{\max ,\mathrm{up},\mathrm{hep},u}}{K_{\mathrm{m},\mathrm{up},\mathrm{hep},u}+C_{\mathrm{ine}}*{\text{fu}}_{\mathrm{ine}}}+{\text{CL}}_{\mathrm{int},\mathrm{up},\mathrm{hep},u}\right)*{\text{AB}}_{\mathrm{up},\mathrm{hep},u}\right)-\sum _{e=1}^m\left(\left(\frac{V_{\max ,\mathrm{ef},\mathrm{hep},e}}{K_{\mathrm{m},\mathrm{ef},\mathrm{hep},e}+C_{\mathrm{cel}}*{\text{fu}}_{\mathrm{cel}}}+{\text{CL}}_{\mathrm{int},\mathrm{ef},\mathrm{hep},e}\right)*{\text{AB}}_{\mathrm{ef},\mathrm{hep},e}\right)\right]\hfill \\ & *\text{HPGL}*\text{liver weight}\hfill \end{array}$$ (18)

where HPGL is the hepatocellularity, and AB is the abundance. The subscripts T, tot, hep, up, eff, u, and e stand for transporter, total, hepatic, uptake, efflux, uptake, and efflux transporter isoform, respectively.

Metabolism and elimination

The following four different options are described to represent drug clearance in the model:

1. Enzymatic intrinsic clearance

2. Intrinsic hepatic clearance not assigned to a specific enzyme

3. Renal clearance

4. Additional plasma clearance

Enzymatic intrinsic clearance can be either represented as CL_int,E or through V _max,E and K _m,E, where CL_int,E is the intrinsic clearance, V _max,E is the maximum metabolism rate for each enzyme, and K _m,E is the Michaelis–Menten constant for each enzyme. Different pathways can be implemented considering active metabolic pathways,47 namely:

$$\begin{array}{c}\hfill {\text{CL}}_{\mathrm{int},E,\mathrm{tot},\mathrm{hep}}\\ & =\sum _{j=1}^J\left(\sum _{i=1}^I\left(\left(\frac{V_{\max E,\mathrm{hep},j,i}}{K{m}_{E,\mathrm{hep},j,i}}\right)+{\text{CLint}}_{E,\mathrm{hep},j,i}\right)*A{B}_{E,\mathrm{hep},j}\right)\hfill \\ & *\text{MPPGL}*\text{liver weight}\hfill \end{array}$$ (19)

$${\text{CL}}_{\mathrm{int},E,\mathrm{tot},\mathrm{gut}}=\left[\sum _{j=1}^J\left(\sum _{i=1}^I\left(\left(\frac{V_{\max E,\mathrm{gut},j,i}}{K_{\mathrm{m}E,\mathrm{gut},j,i}}\right)+{\text{CL}}_{\mathrm{int},E,\mathrm{gut},j,i}*{\text{AB}}_{E,\mathrm{gut},j}\right)\right)\right]$$ (20)

where MPPGL is the microsomal protein per gram liver. The subscript E stands for enzyme, i stands for the metabolic pathway, and j represents the enzyme isoform.

The intrinsic hepatic clearance not assigned to a specific enzyme has the units μmol/minute/mg and is scaled via MPPGL and liver weight but not CYP abundance (which is not a problem for geriatric but would be for Japanese, pediatrics, etc.), namely:

$${\text{CL}}_{\mathrm{int}},\mathrm{tot},\mathrm{hep}={\text{CL}}_{\mathrm{int},E,\mathrm{tot},\mathrm{hep}}+{\text{CL}}_{\mathrm{int},\mathrm{hep}}*\text{MPPGL}*\text{liver weight}.$$ (21)

The well‐stirred liver model is used to calculate the hepatic clearance from the intrinsic clearance48 and is given by:

$${\text{CL}}_{\mathrm{hep}}=\frac{Q_{\mathrm{LI}}*{\text{fu}}_{\mathrm{BL}}*{\text{CL}}_{\mathrm{int},\mathrm{tot},\mathrm{LI}}}{Q_{\mathrm{LI}}+{\text{fu}}_{\mathrm{BL}}*{\text{CL}}_{\mathrm{int},\mathrm{tot},\mathrm{LI}}}$$ (22)

where CL_hep is the total hepatic clearance in L/h, Q _LI is the hepatic blood flow, and fu_BL is the fraction unbound in blood.

The renal clearance is scaled via the glomerular filtration rate (GFR) and ignores tubular secretion and active transport processes, which would require a more mechanistic PBPK model49 and is given by50:

$${\text{CL}}_{\mathrm{R}}={\text{CL}}_{\mathrm{R},\mathrm{Ref}}*\frac{\text{GFR}}{{\text{GFR}}_{\mathrm{Ref}}}*\frac{\text{fu}}{{\text{fu}}_{\mathrm{Ref}}},$$ (23)

where CL_R is the renal clearance in L/h.

The fourth clearance option in the PBPK model is the additional plasma clearance (CL_ad). This parameter is always used as a fixed value, not scaled to any population, but it offers the possibility to enter an in vivo clearance value if clearance mechanism pathways are completely unknown. In cases when there are no measured in vitro values for enzymatic kinetic parameters or CL_int,tot,hep but the in vivo clearance and the different contributions of metabolism and elimination pathways are known, a retrograde calculation can be performed to inform the PBPK model.51

The total clearance can be written as follows:

$${\text{CL}}_{\mathrm{tot}}=\frac{Q_{\mathrm{LI}}*{\text{fu}}_{\mathrm{BL}}*{\text{CL}}_{\mathrm{int},\mathrm{tot},\mathrm{LI}}}{Q_{\mathrm{LI}}+{\text{fu}}_{\mathrm{BL}}*{\text{CL}}_{\mathrm{int},\mathrm{tot},\mathrm{LI}}}+{\text{CL}}_{\mathrm{R}}+{\text{CL}}_{\mathrm{ad}}.$$ (24)

DDI

The PBPK framework allows simulation of competitive inhibition (whereby the inhibitor binds to the active site of the enzymes and blocks its activity), mechanism‐based inhibition (whereby the inhibitor represses the transcription or translation of the metabolizing enzyme leading to a loss of enzyme concentration), and induction. The enzymatic intrinsic clearance (Eq. (19) for the liver and Eq. 20 for the gut) needs to be modified accordingly:52

$$\sum _{j=1}^J\left(\sum _{i=1}^I\left(\left(\frac{V_{{\max }_{E,x,j,i,}}*[\text{Sub}]}{K_{{\mathrm{m}}_{E,x,j,i}}*\left(1+{\sum }_{c=1}^C\frac{{[\text{Inh}]}_c}{K{i}_c}\right)+[\text{Sub}]}\right)\right)*{\text{ABt}}_{E,x,j}\right)$$ (25)

where [Sub] represents the substrate concentration, [Inh] is the concentration of the cth competitive inhibitor, Ki stands for the inhibition constant, ABt is the time‐dependent enzyme abundance, and the subscript x represents either the liver or the gut. In the case of mechanism‐based inhibition or induction, the enzyme concentration changes with time. The basal state can be described by ref. 52:

$$\frac{{\text{dABt}}_E}{\mathrm{d}t}=k_{\mathrm{deg},E}*{\text{AB}}_E-k_{\mathrm{deg},E}*{\text{ABt}}_E=k_{\mathrm{deg},E}*({\text{AB}}_{\mathrm{cyp}}-{\mathrm{ABt}}_{\mathrm{cyp}})$$ (26)

where k _deg represents the degradation rate. It holds that ABt(0) = AB. In the case of mechanism‐based inhibition, Eq. (26) changes as follows52:

$$\frac{{\text{dABt}}_E}{\mathrm{d}t}=k_{\mathrm{deg},E}*{\text{AB}}_E-\left(k_{\mathrm{deg},E}+\sum _{m=1}^M\frac{k_{\mathrm{inact},E,m}*{[\text{Inh}]}_m}{K_{\mathrm{app},E,m}+{[\text{Inh}]}_m}\right)*{\text{ABt}}_E$$ (27)

where k _inact and K _app are the inactivation rate of an enzyme and the apparent enzyme inhibition constant of the mth mechanism‐based inhibitor. In the case of induction, the syntheses rate changes as follows52:

$$\frac{{\text{dABt}}_E}{\mathrm{d}t}=k_{\mathrm{deg},E}*{\text{AB}}_E*\left(1+\sum _{i=1}^I\frac{{\text{IndMax}}_{E,i}*{[\text{Inh}]}_i}{I{C}_{50,E,i}+{[\text{Inh}]}_i}\right)-k_{\mathrm{deg},E}*{\text{ABt}}_E$$ (28)

where IndMax and IC₅₀ are the maximum fold of induction and the half maximal inducer concentration of the ith inducer. All DDI mechanisms are accounted for in Eq. (25).

Step 4: Bridge system and drug data—the ODE solver

After generating the population and drugs to inform the PBPK model, the ODEs are set up. ODEs are solved for each individual (ind) and each dose event (n) by the build‐in stiff ODE solver ode15s53 to ensure efficient running times of the code:

function[] = Solve ODE()

 

%This function solves the ordinary differential equations

 

Convert variables from global to local

 

Calculate the number of ODE equations

Get the number of simulated timepoints

Get the number of simulated timepoints for each dosing event

 

Initialize a vector for the simulated timepoints

Initialize a matrix for the simulated concentration

 

Run the ODE system for each virtual individual separately

 Set the initial concentration for the first / single dose

 

 Run the ODE system for each dosing event separately

 Set the initial concentration for multiple dosing events

 Solve the ODEs

 

 Generate time steps for each dosing event with the user‐defined resolution

 Evaluate the solution from the ODE system for each given timepoint

 

 Combine timepoints for each dosing event in the time vector

 Combine concentrations for each dosing event

 end

end

 

end

The function defining the initial concentration C0 for single doses and M0 for multiple dosing events needs to consider the drug concentration in a compartment at the timepoint of the nth multiple dose and is given by:

function C0 = Initialize_C();

 Set the initial concentration of each compartment to zero

 

 Set the initial CYP abundance in the liver and intestine according to [54,55]

 

 Define a case for each drug

 switch the route of administration for each drug

 in case the route of administration is an iv bolus

 then venous blood concentration is the dose divided by the venous volume

 in case the route of administration is oral

 then stomach concentration is the dose divided by the stomach volume

 end

 end

end

function M0 = Initialize_M(C0)

 if the first dose is administered

 then M0 has been defined by C0

 

 else

 M0 is defined by the calculated concentration of the last dosing event

 

 Define a case for each drug

 switch the route of administration for each drug

 in case the route of administration is an iv bolus

 dose divided by the venous volume is added to the venous conc.

 in case the route of administration is oral

 dose divided by the stomach volume is added to the stomach conc.

 end

 end

end

A relevant element is to define the right‐hand site (rhs) of the differential equations to describe the drug movement from and to each compartment. The differential equations can be written as follows for the vascular, interstitial, and intracellular spaces of a generic compartment:

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{vas},\mathrm{org}}}{\mathrm{d}t}=& \frac{1}{V_{\mathrm{vas},\mathrm{org}}}*[Q_{\mathrm{org}}*C_{\mathrm{ab}}-(Q_{\mathrm{org}}-L_{\mathrm{org}})\hfill \\ & *C_{\mathrm{vas},\mathrm{org}}-J_{\mathrm{vas},\mathrm{org}}*\left(\frac{C_{\mathrm{vas},\mathrm{org}}}{\text{BP}}\right)\hfill \\ & +J_{\mathrm{ine},\mathrm{org}}*C_{\mathrm{ine},\mathrm{org}}],\hfill \end{array}$$ (29)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{ine},\mathrm{org}}}{\mathrm{d}t}=& \frac{1}{V_{\mathrm{ine},\mathrm{org}}}*[J_{\mathrm{vas},\mathrm{org}}*\left(\frac{C_{\mathrm{vas},\mathrm{org}}}{\text{BP}}\right)-J_{\mathrm{ine},\mathrm{org}}*C_{\mathrm{ine},\mathrm{org}}-L_{\mathrm{org}}\hfill \\ & *C_{\mathrm{ine},\mathrm{org}}-J_{\mathrm{in},\mathrm{org}}*C_{\mathrm{ine},\mathrm{org}}*{\text{fu}}_{\mathrm{ine},\mathrm{org}}+J_{\mathrm{out},\mathrm{org}}\hfill \\ & *C_{\mathrm{cel},\mathrm{org}}*{\text{fu}}_{\mathrm{cel},\mathrm{org}}],\hfill \end{array}$$ (30)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{cel},\mathrm{org}}}{\mathrm{d}t}=& \frac{1}{V_{\mathrm{cel},\mathrm{org}}}*[J_{\mathrm{in},\mathrm{org}}*C_{\mathrm{ine},\mathrm{org}}*{\text{fu}}_{\mathrm{ine},\mathrm{org}}-J_{\mathrm{out},\mathrm{org}}\hfill \\ & *C_{\mathrm{cel},\mathrm{org}}*{\text{fu}}_{\mathrm{cel},\mathrm{org}}]\hfill \end{array}$$ (31)

where Q is the blood flow, L is the lymph flow, J is a flux, and the subscript ab represents the arterial blood pool. The Matlab function defining the rhs of the differential Eqs. (29), (30), (31) is written in the following way:

function dtdy = rhs(~, y)

 initialize the output as a column vector containing only zeros

 

 define subcompartments by a number

 

 write the differential equations

end

Some organs require a more detailed differential equation than the generic equations described in Eqs. (29), (30), (31). Blood flows from the venous blood pool into the lungs and after being loaded with oxygen, the blood returns to the arterial blood pool. Therefore, the differential equation of the vascular space of the lungs is given by:

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{vas},\mathrm{LU}}}{\mathrm{d}t}=& \frac{1}{V_{\mathrm{vas},\mathrm{LU}}}*[\text{CO}*C_{\mathrm{vb}}-(\text{CO}-L_{\mathrm{LU}})*C_{\mathrm{vas},\mathrm{LU}}-J_{\mathrm{vas},\mathrm{LU}}\hfill \\ & *\left(\frac{C_{\mathrm{vas},\mathrm{LU}}}{\mathrm{BP}}\right)+J_{\mathrm{ine},\mathrm{LU}}*C_{\mathrm{ine},\mathrm{LU}}]\hfill \end{array}$$ (32)

where CO is the cardiac output, and the subscripts LU and vb represent the lung and the venous blood pool, respectively.

In the kidney, the CL_R should be considered. A mechanistic kidney model including renal transporters is not described in this tutorial.

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{vas},\mathrm{KI}}}{\mathrm{d}t}=& \frac{1}{V_{\mathrm{vas},\mathrm{KI}}}*[Q_{\mathrm{KI}}*C_{\mathrm{ab}}-(Q_{\mathrm{KI}}-L_{\mathrm{KI}})*C_{\mathrm{vas},\mathrm{KI}}-J_{\mathrm{vas},\mathrm{KI}}\hfill \\ & *\left(\frac{C_{\mathrm{vas},\mathrm{KI}}}{\text{BP}}\right)J_{\mathrm{ine},\mathrm{KI}}*C_{\mathrm{ine},\mathrm{KI}}-{\text{CL}}_{\mathrm{R}}*C_{\mathrm{vas},\mathrm{KI}}*\frac{{\text{fu}}_{\mathrm{PL}}}{\text{BP}}]\hfill \end{array}$$ (33)

where the subscript KI stands for the kidney.

In the liver, active drug transporters and hepatic metabolism by enzymes are included and given by:

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{vas},\mathrm{LI}}}{\mathrm{d}t}=& \frac{1}{V_{\mathrm{vas},\mathrm{LI}}}*[Q_{\mathrm{ha}}*C_{\mathrm{ab}}+Q_{\mathrm{PVBY}}*C_{\mathrm{ab}}+(Q_{\mathrm{GU}}-L_{\mathrm{GU}})\hfill \\ & *C_{\mathrm{vas},\mathrm{GU}}+Q_{\mathrm{SP}}*C_{\mathrm{vas},\mathrm{SP}}+(Q_{\mathrm{PA}}-L_{\mathrm{PA}})\hfill \\ & *C_{\mathrm{vas},\mathrm{PA}}-(Q_{\mathrm{LI}}-L_{\mathrm{LI}})*C_{\mathrm{vas},\mathrm{LI}}-J_{\mathrm{vas},\mathrm{LI}}\hfill \\ & *\left(\frac{C_{\mathrm{vas},\mathrm{LI}}}{\text{BP}}\right)+J_{\mathrm{ine},\mathrm{LI}}*C_{\mathrm{ine},\mathrm{LI}}],\hfill \end{array}$$ (34)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{ine},\mathrm{LI}}}{\mathrm{d}t}=& \frac{1}{V_{\mathrm{ine},\mathrm{LI}}}*[J_{\mathrm{vas},\mathrm{LI}}*\left(\frac{C_{\mathrm{vas},\mathrm{LI}}}{\text{BP}}\right)-J_{\mathrm{ine},\mathrm{LI}}*C_{\mathrm{ine},\mathrm{LI}}-L_{\mathrm{LI}}\hfill \\ & *C_{\mathrm{ine},\mathrm{LI}}-J_{\mathrm{in},\mathrm{LI}}*C_{\mathrm{ine},\mathrm{LI}}*{\text{fu}}_{\mathrm{ine},\mathrm{LI}}+J_{\mathrm{out},\mathrm{LI}}\hfill \\ & *C_{\mathrm{cel},\mathrm{LI}}*{\text{fu}}_{\mathrm{cel},\mathrm{LI}}-\sum _{u=1}^m(\frac{V_{\max ,\mathrm{up},\mathrm{hep},u}*C_{\mathrm{ine},\mathrm{LI}}*{\text{fu}}_{\mathrm{ine},\mathrm{LI}}}{K_{\mathrm{m},\mathrm{up},\mathrm{hep},u}+C_{\mathrm{ine},\mathrm{LI}}*{\text{fu}}_{\mathrm{ine},\mathrm{LI}}}+{\text{CL}}_{\mathrm{int},\mathrm{up},\mathrm{hep},u}\hfill \\ & *C_{\mathrm{ine},\mathrm{LI}}*{\text{fu}}_{\mathrm{ine},\mathrm{LI}})*A{B}_{\mathrm{up},\mathrm{hep},u}*\text{HPGL}*W_{\mathrm{LI}}\hfill \\ & +\sum _{e=1}^m\left(\frac{V_{\max ,\mathrm{eff},\mathrm{hep},e}*C_{\mathrm{cel},\mathrm{LI}}*{\text{fu}}_{\mathrm{cel},\mathrm{LI}}}{K_{\mathrm{m},\mathrm{eff},\mathrm{hep},e}+C_{\mathrm{cel},\mathrm{LI}}*{\text{fu}}_{\mathrm{cel},\mathrm{LI}}}+{\text{CL}}_{\mathrm{int},\mathrm{eff},\mathrm{hep},e}*C_{\mathrm{ine},\mathrm{LI}}*{\text{fu}}_{\mathrm{ine},\mathrm{LI}}\right)\hfill \\ & *{\text{AB}}_{\mathrm{eff},\mathrm{hep},e}*\text{HPGL}*W_{\mathrm{LI}}],\hfill \end{array}$$ (35)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{cel},\mathrm{org}}}{\mathrm{d}t}=& \frac{1}{V_{\mathrm{cel},\mathrm{org}}}*[J_{\mathrm{in},\mathrm{LI}}*C_{\mathrm{ine},\mathrm{LI}}*{\text{fu}}_{\mathrm{ine},\mathrm{LI}}-J_{\mathrm{out},\mathrm{LI}}*C_{\mathrm{cel},\mathrm{LI}}*{\text{fu}}_{\mathrm{cel},\mathrm{LI}}\hfill \\ & +\sum _{u=1}^m\left(\frac{V_{\max ,\mathrm{up},\mathrm{hep},u}*C_{\mathrm{int},\mathrm{LI}}*{\text{fu}}_{\mathrm{int},\mathrm{LI}}}{K_{\mathrm{m},\mathrm{up},\mathrm{hep},u}+C_{\mathrm{int},\mathrm{LI}}*{\text{fu}}_{\mathrm{int},\mathrm{LI}}}+{\text{CL}}_{\mathrm{int},\mathrm{up},\mathrm{hep},u}*C_{\mathrm{ine},\mathrm{LI}}*{\text{fu}}_{\mathrm{ine},\mathrm{LI}}\right)\hfill \\ & *{\text{AB}}_{\mathrm{up},\mathrm{hep},u}*\text{HPGL}*W_{\mathrm{LI}}-\sum _{e=1}^m\left(\frac{V_{\max ,\mathrm{eff},\mathrm{hep},e}*C_{\mathrm{cel},\mathrm{LI}}*{\text{fu}}_{\mathrm{cel},\mathrm{LI}}}{K_{\mathrm{m},\mathrm{eff},\mathrm{hep},e}+C_{\mathrm{cel},\mathrm{LI}}*{\text{fu}}_{\mathrm{cel},\mathrm{LI}}}+{\text{CL}}_{\mathrm{int},\mathrm{eff},\mathrm{hep},e}*C_{\mathrm{ine},\mathrm{LI}}*{\text{fu}}_{\mathrm{ine},\mathrm{LI}}\right)\hfill \\ & *{\text{AB}}_{\mathrm{eff},\mathrm{hep},e}*\text{HPGL}*W_{\mathrm{LI}}\hfill \\ & -\left[\sum _{j=1}^J\left(\sum _{i=1}^I\left(\frac{V_{\max ,E,\mathrm{hep},j,i}}{K_{\mathrm{m},E,\mathrm{hep},i,j}*(1+\mathrm{\Sigma }[\text{Inh}]/Ki)+C_{\mathrm{cel},\mathrm{LI}}*{\text{fu}}_{\mathrm{cel},\mathrm{LI}}}+{\text{CL}}_{\mathrm{int},E,\mathrm{hep},j,i}\right)*{\text{ABt}}_{E,\mathrm{hep},j}\right)+{\text{CL}}_{\mathrm{int},\mathrm{hep}}\right]*\text{MPPGL}*W_{\mathrm{LI}}*C_{\mathrm{cel},\mathrm{LI}}]\hfill \end{array}$$ (36)

where HPGL is the hepatocellularity, and the subscripts LI, ha, PVBY, GU, SP, PA, up, and eff represent the liver, hepatic arterial, portal vein bypass, gut, spleen, pancreas, uptake, and efflux, respectively.

Lymph fluid flows through afferent lymph vessels from the interstitial space of organs to the central lymph‐node compartment and further to the venous blood pool, given by:

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{vas},\mathrm{LN}}}{\mathrm{d}t}=& \frac{1}{V_{\mathrm{vas},\mathrm{LN}}}*[Q_{\mathrm{LN}}*(C_{\mathrm{ab}}-C_{\mathrm{vas},\mathrm{LN}})+L_{\mathrm{tot}}\hfill \\ & *(C_{\mathrm{ine},\mathrm{LN}}-C_{\mathrm{vas},\mathrm{LN}})],\hfill \end{array}$$ (37)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{ine},\mathrm{LN}}}{\mathrm{d}t}=& {\frac{1}{V}}_{\mathrm{ine},\mathrm{LN}}*[\sum _{\mathrm{org}=1}^O(L_{\mathrm{org}}*C_{\mathrm{ine},\mathrm{org}})-L_{\mathrm{tot}}*C_{\mathrm{ine},\mathrm{LN}}-J_{\mathrm{in},\mathrm{LN}}\hfill \\ & *C_{\mathrm{ine},\mathrm{LN}}*{\text{fu}}_{\mathrm{ine},\mathrm{LN}}+J_{\mathrm{out},\mathrm{LN}}*C_{\mathrm{cel},\mathrm{LN}}*{\text{fu}}_{\mathrm{cel},\mathrm{LN}}]\hfill \end{array},$$ (38)

where L _tot is the total lymph flow, and the subscript LN represents the central lymph‐node compartment.

The differential equations for the venous and arterial blood compartments are given by:

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{vb}}}{\mathrm{d}t}& =\frac{1}{V_{\mathrm{vb}}}*[C_{\mathrm{vas},\mathrm{AD}}*(Q_{\mathrm{AD}}-L_{\mathrm{AD}})+C_{\mathrm{vas},\mathrm{BO}}*Q_{\mathrm{BO}}+C_{\mathrm{vas},\mathrm{BR}}\hfill \\ & *(Q_{\mathrm{BR}}-L_{\mathrm{BR}})+C_{\mathrm{vas},\mathrm{GO}}*(Q_{\mathrm{GO}}-L_{\mathrm{GO}})+C_{\mathrm{vas},\mathrm{HE}}\hfill \\ & *(Q_{\mathrm{HE}}-L_{\mathrm{HE}})+C_{\mathrm{vas},\mathrm{KI}}*(Q_{\mathrm{KI}}-L_{\mathrm{KI}})+C_{\mathrm{vas},\mathrm{MU}}\hfill \\ & *(Q_{\mathrm{MU}}-L_{\mathrm{MU}})+C_{\mathrm{vas},\mathrm{SK}}*(Q_{\mathrm{SK}}-L_{\mathrm{SK}})+C_{\mathrm{vas},\mathrm{TH}}\hfill \\ & *(Q_{\mathrm{TH}}-L_{\mathrm{TH}})+C_{\mathrm{vas},\mathrm{LI}}*(Q_{\mathrm{LI}}-L_{\mathrm{LI}})+C_{\mathrm{vas},\mathrm{LN}}\hfill \\ & *(Q_{\mathrm{LN}}+L_{\mathrm{tot}})+C_{\mathrm{vas},\mathrm{RE}}*(Q_{\mathrm{RE}}-L_{\mathrm{RE}})-\text{CO}*C_{\mathrm{vb}}],\hfill \end{array}$$ (39)

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{C}_{\mathrm{ab}}}{\mathrm{d}t}=& \frac{1}{V_{\mathrm{ab}}}*[(\text{CO}-L_{\mathrm{LU}})*C_{\mathrm{vas},\mathrm{LU}}\hfill \\ & -\sum _{o=1}^O(Q_{\mathrm{org},o}*C_{\mathrm{ab}})-{\text{CL}}_{\mathrm{ad}}*C_{\mathrm{ab}}*\frac{{\text{fu}}_{\mathrm{PL}}}{\text{BP}}]\hfill \end{array}$$ (40)

where the subscripts AD, BO, BR, GO, HE, MU, SK, TH, and RE represent adipose, bone, brain, gonads, heart, muscle, skin, thymus, and remaining organ, respectively.

The solution of the different equation needs to be evaluated in Matlab using the implemented deval function over a predefined number of timepoints (NumPoints). The solution for the drug concentration of each compartment is saved in the matrix Conc, and the corresponding timepoint to the concentration is saved in the vector Time as described previously.

Step 5: Work with the simulated data—the postprocessing step

The solution of the differential equation solver has been saved into one single matrix. The first step of postprocessing is therefore to extract the concentration for each compartment of the model from the solution matrix of the ODE solver. Different statistics can now be calculated with the extracted concentrations, such as the mean and the 5 and 95 percentiles with predefined Matlab commands, which require the Statistics and Machine Learning Toolbox as an add‐on to the Matlab suite.

One important aspect of postprocessing is to ensure mass balance of the model. The concentration of each compartment is multiplied by the compartmental volume, and the drug amount cleared by a specific pathway as well as the amount not being absorbed are integrated and added together. The product should be equivalent to the dose entered in the study design.

Pharmacokinetic parameters, such as the maximal concentration (C_max), the timepoint of the maximal concentration (T_max), the area under the curve (AUC), the apparent clearance (CL/F), and the apparent volume of distribution (VD/F) can be calculated for each compartment. The elimination rate is used to extrapolate the AUC to infinity and to calculate the clearance and the volume of distribution.

function[] = PostProcessing()

 

%This function processes the data from the ODE solution and outputs the results

%Attention: Some statistical calculations (geomean, prctile) require

%the Statistical and Machine Learning Toolbox

 

Initialize Cmax

Initialize Tmax

Initialize AUCt

 

Calculate PK parameters for each simulated drug

 Calculate PK parameters for each virtual individual

 if the venous concentration at timepoint t is bigger than Cmax

 than the venous concentration at timepoint t is the new Cmax

 than the timepoint t is the new Tmax

 end

 

 Calculate the AUC according to the linear trapezoidal rule

 end

end

 

take the logarithm of the concentration for extrapolation

 

Initialize the slope and beta

 

Calculate the slope and beta for each simulated drug

 Calculate the slope and beta for each virtual individual

 linear regression of the last four timepoints

 beta is the slope of the regression

 end

end

LogVenousConc = log10(VenousConc);

 

half‐life is the natural logarithm of two divided by beta

AUC extrapolated to infinity is the AUCt plus the venous concentration at the last simulated timepoint divided by beta

Clearance is the dose divided by the AUC extrapolated to infinity

Volume of distribution is the clearance divided by beta

 

end

As shown above for the concentration, the mean and percentiles or other statistics can be calculated for pharmacokinetic parameters.

The results can be either output graphically using the built‐in plot function or can be exported to Excel (Microsoft, Redmond, WA) using the xlswrite command.

Simulation of the DDI Magnitude Between Rivaroxaban and Darunavir/Ritonavir

To illustrate the steps of PBPK model development, the DDI magnitude between a single dose of rivaroxaban and darunavir boosted with ritonavir under steady‐state conditions will be simulated. The rivaroxaban PBPK model was developed combining published in vitro data (bottom‐up approach) with clinical clearance data (top‐down approach). Validated PBPK models for darunavir and ritonavir were used.56 Ritonavir has an impact on the CL_R of rivaroxaban,57 which was considered in the model. The parameters of the drug models can be found in the model code (Supplementary Material S1). A clinical DDI investigating the effect of 600 mg ritonavir twice daily on a single 10 mg dose of oral rivaroxaban in 12 healthy men aged 18–44 years was used to verify the rivaroxaban model.57 A total of 10 virtual trials with 12 men (proportion of women is set to zero) aged 20–44 years were simulated. Afterward, the effect of 800/100 mg darunavir/ritonavir once daily (qd) on a single oral dose of 10 mg rivaroxaban was simulated because the boosted protease inhibitor is given in clinical practice.

The simulation of 10 mg rivaroxaban with and without 600 mg of oral ritonavir were in good agreement with the observed clinical data (Figure 5 a). T_max of rivaroxaban was underpredicted by twofold because T_max was achieved 1.5 hours later in the clinical study compared with the simulation. However, the predicted T_max ratio of rivaroxaban administered with 600 mg ritonavir twice daily and rivaroxaban given without a perpetrator was within 1.25‐fold of the observed data. The elimination half‐life of rivaroxaban was overpredicted by twofold, but C_max and AUC were predicted within 1.25‐fold (bioequivalence criterion; Table 2). The effect of 100 mg ritonavir qd used to boost darunavir in clinical practice is predicted to be similar to 600 mg of ritonavir twice daily (Figure 5 b) because full inhibition of CYP CYP3A4 and CYP2J2 is already achieved.

Figure 5.

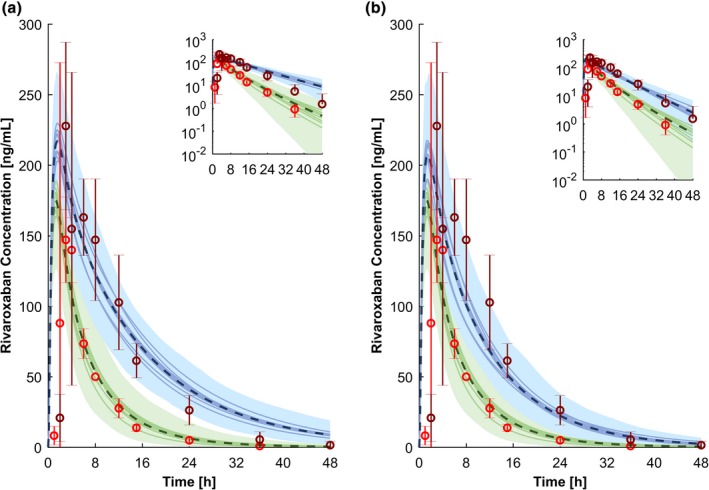
Physiologically‐based pharmacokinetic simulations for a single dose of 10 mg rivaroxaban administered with 600 mg ritonavir twice daily in steady state (a) and 800/100 mg darunavir/ritonavir once daily in steady state (b). Green represents the prediction of rivaroxaban alone, and blue shows the prediction of rivaroxaban administered with the perpetrators. The dashed line and the shaded area are the mean and the 95% confidence interval for the prediction of all virtual individuals, respectively. The solid lines show the mean of each virtual trial (10 trials with 12 virtual subjects per trial have been simulated). The red and the dark red circles show the observed clinical data of 10 mg rivaroxaban alone and coadministered with 600 mg ritonavir twice daily.57 Conc., concentration; h, hour.

Table 2.

Observed vs. predicted pharmacokinetic parameters

Pharmacokinetic parameter	Cmax (ng/mL)		Tmax (h)		AUC (ng × h/mL)		t 1/2 (h)
	Observed	Predicted	Observed	Predicted	Observed	Predicted	Observed	Predicted
Rivaroxaban 10 mg	153.7 ± 23.7	162.7 ± 26.9	3.0 ± 0.5	1.5 ± 0.1	1,000 ± 161	1,208 ± 268	5.7 ± 1.8	12.5 ± 3.3
Rivaroxaban 10 mg + Ritonavir 600 mg twice daily	238.0 ± 55.7	197.4 ± 32.6	4.0 ± 2.2	1.6 ± 0.2	2,529 ± 425	2,761 ± 875	6.9 ± 2.2	20.2 ± 4.7
Ratio	1.55 ± 0.43	1.21 ± 0.28	1.33 ± 0.77	1.09 ± 0.14	2.53 ± 0.59	2.29 ± 0.88	1.21 ± 0.53	1.62 ± 0.57
Rivaroxaban 10 mg + Darunavir/r 800/100 mg once daily	NA	190.0 ± 31.2	NA	1.7 ± 0.2	NA	2,510 ± 685	NA	19.9 ± 5.2
Ratio	NA	1.17 ± 0.27	NA	1.16 ± 0.15	NA	2.08 ± 0.73	NA	1.60 ± 0.60
Darunavir/r 800/100 mg once daily	6,803 ± 1,618	5,432 ± 1,929	3.6 ± 1.6	3.1 ± 0.5	75,780 ± 22,102	75,002 ± 56,887	14.4 ± 5.2	10.9 ± 5.7
Ritonavir 100 mg once daily	606 ± 281	531 ± 280	3.1 ± 2.0	1.8 ± 0.5	5,296 ± 4,664	5,470 ± 3,132	6.3 ± 1.5	5.4 ± 1.4

Data are presented as mean +/‐ standard deviation. Observed data are published in ref. 57 for rivaroxaban, refs. 58, 59, 60 for darunavir, and refs.59, 61 for ritonavir.

C_max, maximal concentration; T_max, timepoint of the maximal concentration; AUC, area under the curve; t1/2 = elimination half‐life; NA = not applicable.

The predicted concentrations of the two perpetrators darunavir (800 mg qd) and ritonavir (100 mg qd) are in accordance with observed clinical data from various studies (Figure 6). The T_max of ritonavir was underpredicted by twofold, but all pharmacokinetic parameters of boosted darunavir and ritonavir were within the 1.25‐fold interval of the observed clinical data (Table 2).

Figure 6.

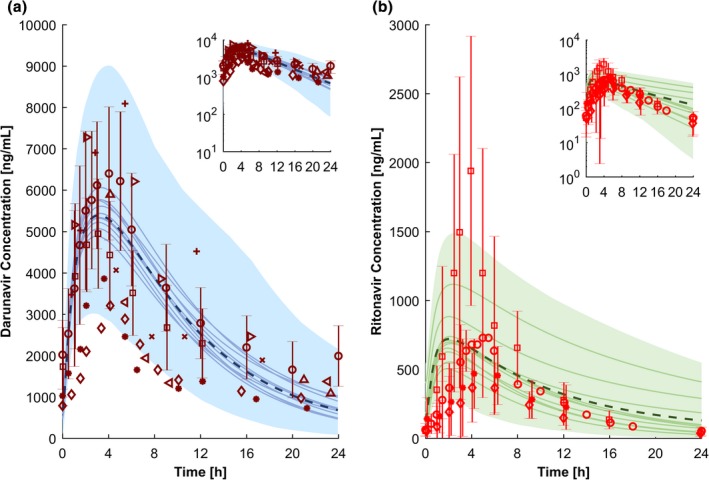
Physiologically‐based pharmacokinetic simulations for 800 mg darunavir once daily boosted with 100 mg ritonavir once daily (a) and 100 mg ritonavir once daily (b). The dashed line and the shaded area are the mean and the 95% confidence interval for the prediction of all virtual individuals, respectively. The solid lines how the mean of each virtual trial (10 trials with 12 virtual subjects per trial have been simulated). The red markers show observed clinical data (a: refs. 58, 59, 60 b: refs. 59, 61, 62). Conc., concentration; h, hour.

Conclusion

We have described a comprehensive strategy to develop and code a PBPK model in Matlab with potential applications in other pharmacological scenarios. Of interest, PBPK models are increasingly accepted for the prediction of DDIs and drug disposition in special populations such as pediatrics and the elderly. Furthermore, this type of computational framework can be integrated with pharmacodynamic models, which can be easily added to custom build PBPK models in Matlab.

Funding

The study was supported by the Swiss National Foundation (Grant 166204), the OPO Foundation, and the Isaac Dreyfus Foundation. Melissa Penny was additionally supported by the Swiss National Science Foundation Professorship (PP00P3_170702).

Conflict of Interest

The authors declared no competing interests for this work.

Supporting information

Table S1. Parameters and their abbreviation and units used to build a physiologically‐based pharmacokinetic model.

Table S2. Subscripts and their abbreviation used to build the physiologically‐based pharmacokinetic model.

Supplementary Material S1. Model code.