Abstract
Organismal adaptations to new environments often begin with plastic phenotypic changes followed by genetic phenotypic changes, but the relationship between the two types of changes is controversial. Contrary to the view that plastic changes serve as steppingstones to genetic adaptations, recent transcriptome studies reported that genetic gene expression changes more often reverse than reinforce plastic expression changes in experimental evolution. However, it was pointed out that this trend could be an artifact of the statistical nonindependence between the estimates of plastic and genetic phenotypic changes, because both estimates rely on the phenotypic measure at the plastic stage. Using computer simulation, we show that indeed the nonindependence can cause an apparent excess of expression reversion relative to reinforcement. We propose a parametric bootstrap method and show by simulation that it removes the bias almost entirely. Analyzing transcriptome data from a total of 34 parallel lines in 5 experimental evolution studies of Escherichia coli, yeast, and guppies that are amenable to our method confirms that genetic expression changes tend to reverse plastic changes. Thus, at least for gene expression traits, phenotypic plasticity does not generally facilitate genetic adaptation. Several other comparisons of statistically nonindependent estimates are commonly performed in evolutionary genomics such as that between cis- and trans-effects of mutations on gene expression and that between transcriptional and translational effects on gene expression. It is important to validate previous results from such comparisons, and our proposed statistical analyses can be useful for this purpose.
Keywords: estimation error, evolution, phenotypic plasticity, parametric bootstrap, transcriptome
Introduction
Organismal adaptations to new environments often follow a two-phase process. The first phase is characterized by plastic phenotypic changes induced by environmental shifts without the involvement of mutations, whereas the second phase is characterized by genetic phenotypic changes driven by Darwinian selection. Discerning the relationship between the two phases is critical to understanding adaptive evolution. Recent years have seen a rise in the appreciation of the role of phenotypic plasticity in evolution (West-Eberhard 2003; Pigliucci et al. 2006; Pfennig et al. 2010; Levis and Pfennig 2016), especially by the school of extended evolutionary synthesis (Laland et al. 2014, 2015). In particular, it has been argued that, when organisms move to a new environment, plasticity serves as a steppingstone, moving the organismal phenotype closer to the optimum in the new environment and hence easing the subsequent genetic adaptation (Price et al. 2003). Although this model was supported by a few studies of small numbers of traits (Suzuki and Nijhout 2006; Ledon-Rettig et al. 2008), it was refuted by the analyses of expression changes of thousands of genes in experimental evolution (Fong et al. 2005; Sandberg et al. 2014; Ghalambor et al. 2015; Rodriguez-Verdugo et al. 2016; Ho and Zhang 2018). Specifically, these researchers measured the expression level (i.e., relative mRNA concentration) of each gene from the organisms in the original environment (Lo, where the subscript stands for the original stage), immediately after they move to the new environment (Lp, where the subscript stands for the plastic stage), and after long-term experimental evolution in the new environment (La, where the subscript stands for the adapted stage). They then computed the plastic change (PC) in gene expression level by Lp–Lo and the genetic change (GC) in gene expression level by La–Lp. They found that GC and PC are more often of opposite signs than of the same sign, and therefore concluded that plastic expression changes are generally reversed rather than reinforced by genetic expression changes during environmental adaptations (Ho and Zhang 2018).
Nevertheless, it was recently pointed out that the reported prevalence of expression reversion (RV) can be a statistical artifact (Mallard et al. 2018). In particular, because of the addition of Lp in estimating PC but deduction of Lp in estimating GC, any estimation error of Lp has antagonistic effects on PC and GC, which could have generated the observed preponderance of expression RVs. In the present work, we first use computer simulation to examine the severity of the bias caused by this statistical nonindependence between PC and GC estimates. We then propose remedies of this problem and examine their performance using simulation. After confirming their performance, we apply them to the actual transcriptome data previously analyzed. In addition to discussing the implications of our results for the relationship between plastic and genetic phenotypic changes in environmental adaptations, we discuss the potential of applying our proposed remedies in other common evolutionary genomic analyses where nonindependent estimates are compared.
Results
The Severity of the Statistical Problem Varies Depending on Several Factors
To examine the impact of the interdependency between PC and GC estimates on the observed preponderance of gene expression RV relative to reinforcement (RI), we conducted a computer simulation of M genes where the true expression levels at the three stages for each gene are Ko = Kp = Ka = μ. Because the true PC = GC = 0, any observation of expression RV or RI in the simulation is a false positive. Let l be the expression level measurement for a gene from one replicate at a particular stage. We assume that l is a Gaussian random variable with a mean of μ and a coefficient of variation of CV, which equals the standard deviation of the random variable divided by μ. For any gene, let Lo, La, and Lp be the estimates of Ko, Ka, Kp, based on no, np, and na independent measurements, respectively. Lo is computed by averaging l across the no replicates; Lp and La are similarly estimated. We followed a previous study (Ho and Zhang 2018) in defining expression RV and RI. Specifically, we focus on genes whose absolute values of estimated PC and GC are both larger than the cutoff (c) of 0.2Lo. A gene is then said to exhibit RI if the estimated PC and GC have the same sign; otherwise, the gene is said to exhibit RV. The proportion of all genes exhibiting RI (CRI) and that exhibiting RV (CRV) are then estimated.
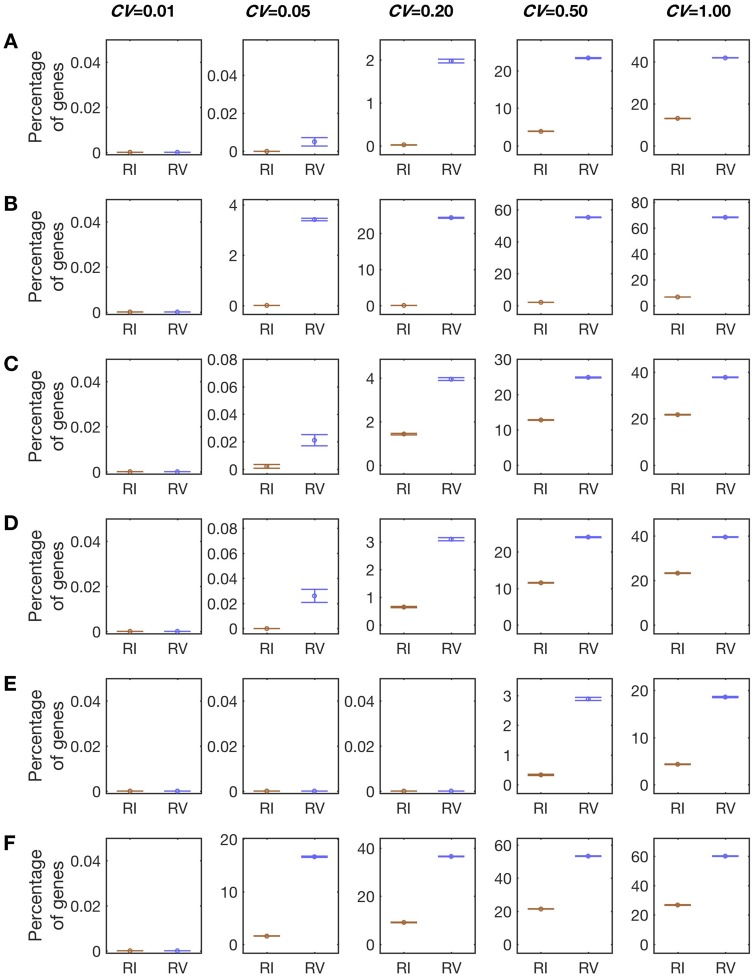
Under each set of simulation parameters, we investigated M = 1,000 genes and repeated the simulation 100 times. We found that the false positive rate of RV is generally greater than that of RI (fig. 1). For example, when μ = 100, CV = 0.2, and no = np = na = 6, we found that CRV = 2 ± 0.04% (mean ± standard error) of genes exhibit RV, whereas CRI = 0.023 ± 0.005% of genes exhibit RI; their difference δ = CRV − CRI = 1.98 percentage points (fig. 1A). Therefore, random estimation errors of expression levels can cause an apparent excess of RV over RI. In other words, the comparison between RV and RI is biased.
Fig. 1.
Rates of false identification of gene expression RV and RI estimated by computer simulation. The mean expression level (μ) used = 100. The CV used is marked on the top of each column. Each row has a different combination of the cutoff (c) and numbers of replicates at the original (no), plastic (np), and adapted (na) stages. Results shown are means and standard errors estimated from 100 rounds of simulation, each containing 1,000 hypothetical genes with the same μ and CV. See main text for definitions of RV and RI. (A) Simulation results under no = 6, np = 6, na = 6, and c = 0.2Lo, where Lo is the observed mean expression level at stage o. (B) Simulation results under no = 6, np = 1, na = 6, and c = 0.2Lo. (C) Simulation results under no = 1, np = 6, na = 6, and c = 0.2Lo. (D) Simulation results under no = 6, np = 6, na = 1, and c = 0.2Lo. (E) Simulation results under no = 6, np = 6, na = 6, and c = 0.5Lo. (F) Simulation results under no = 6, np = 6, na = 6, and c = 0.05Lo.
To investigate factors impacting the severity of the above bias, we performed the same simulation using different combinations of μ and CV. As expected, we did not see any noticeable impact of μ (μ = 10 in supplementary fig. S1, Supplementary Material online, and μ = 1,000 in supplementary fig. S2, Supplementary Material online) but found a positive correlation between CV and both CRV and CRI. Specifically, when CV decreases to 0.05, CRV and CRI reduce to 0.005 ± 0.002% and 0 ± 0%, respectively (fig. 1A). When CV = 0.01, both CRV and CRI become 0. However, when CV increases to 0.50, CRV and CRI respectively rise to 23 ± 0.1% and 3.9 ± 0.06%, with δ = 19 percentage points. The increase of CV to 1.0 further enlarges δ to 29 percentage points. Clearly, the bias in the comparison between RV and RI is negligible when CV is small (i.e., expression measures l’s are precise) but becomes a severe problem when CV is large (i.e., l’s are imprecise).
It is also of interest to study how the experimental design affects the severity of the bias. In particular, because the bias is caused by the use of Lp in both PC and GC estimations, having a precise Lp estimate is likely the most important. To confirm this prediction, we respectively reduced no, np, and na to 1 in a set of otherwise identical simulations. Indeed, when we reduced np to 1, CRV increases as long as CV ≥ 0.05 (fig. 1B). Furthermore, the impact of reducing np to 1 enlarges with CV. For example, when CV = 0.05, CRV = 3.4 ± 0.05% and CRI = 0 ± 0%, with δ = 3.4 percentage points. But when CV = 1.00, CRV = 68 ± 0.2% and CRI = 6.5 ± 0.08%, with δ = 62 percentage points. As predicted, reducing no or na to 1 does not have any noticeable impact (fig. 1C and D). Hence, to reduce the bias in the comparison between RV and RI, one should consider increasing np instead of no or na, especially when the total number of replicates is constrained for example by the research budget.
We used the cutoff c = 0.2Lo in all simulations so far. To evaluate how the cutoff choice affects the bias in the comparison between RV and RI, we repeated the simulation using either c = 0.5Lo or 0.05Lo as the cutoff while keeping other parameters unchanged. As expected, using c = 0.5Lo substantially lowers CRV and CRI (fig. 1E). Specifically, when CV ≤ 0.20, CRV = CRI = 0. Even when CV = 1.0, δ = 14 percentage points, only one half that when c = 0.2Lo. Hence, raising the cutoff can guard against the bias for RV. Of course, using too high of a cutoff is expected to reduce the sensitivity in detecting any potential difference between CRV and CRI. By contrast, using c = 0.05Lo increases CRV and CRI (fig. 1F). For example, even when CV = 0.20, δ becomes 3.4 percentage points. Therefore, low cutoffs should be used with caution.
An Improved Method for Comparing RV and RI
Our extensive simulation demonstrates that the current analytical pipeline tends to yield an artificial excess of RV over RI. One method to remedy this problem is to use one half of the np replicates to estimate one Lp that is used to compute PC and the other half of the np replicates to estimate another Lp to compute GC. Although this method removes the interdependency between PC and GC, it effectively uses only one half of the np replicates in Lp estimation so the estimation is relatively imprecise. We thus propose an alternative method that is based on parametric bootstrap. Parametric bootstrap assumes that the data come from a known distribution with unknown parameters. One estimates the parameters from the available data and then uses the estimated distributions to simulate samples for statistical analysis. In our case, the mean expression level of a gene at stage o follows a Gaussian distribution with the mean equal to the observed mean expression of the gene at stage o (i.e., Lo) and the standard deviation equal to the estimated standard error of Lo. We can thus draw a random variable from the above Gaussian distribution to represent an observation of the mean expression level of the gene at stage o. We can similarly draw random variables representing the mean expression level of the gene at stage p and that at stage a, respectively. These three random variables allow the computation of PC and GC and the determination of RV, RI, or neither. This process is repeated 1,000 times. If at least 950 repeats show RV, this gene is considered to exhibit RV. Similarly, if at least 950 repeats show RI, the gene is considered to exhibit RI.
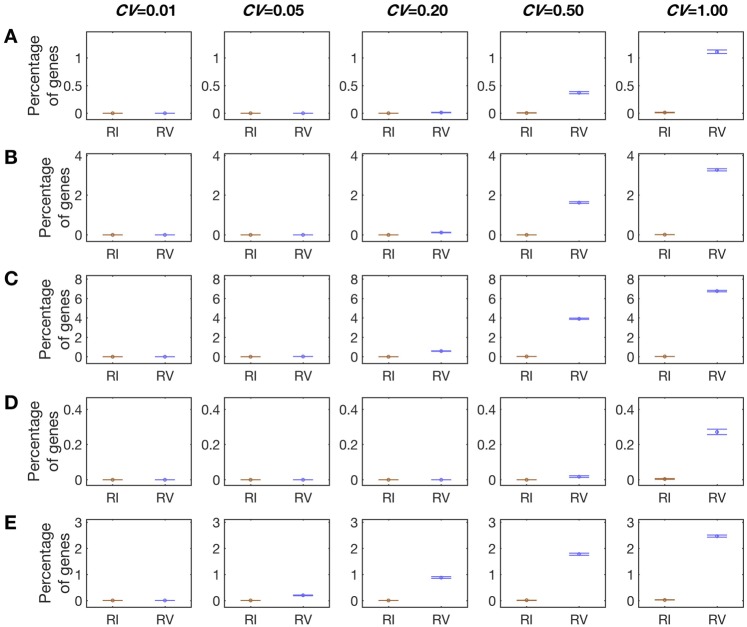
We used computer simulation to examine the performance of this new method. When μ = 100, CV = 0.2, and no = np = na = 6, CRV = 0.01 ± 0.003%, whereas CRI = 0 ± 0% (fig. 2A). Even when CV rises to 1.0, CRV = 1.1 ± 0.03%, whereas CRI = 0.01 ± 0.004%. Therefore, this new method substantially decreases the false identification of RV and RI and reduces the bias. Even when np is as small as 3, the new method performs reasonably well (fig. 2B). For instance, when CV = 0.2, CRV and CRI are 0.1 ± 0.01% and 0 ± 0%, respectively. Even when CV = 1.0, CRV and CRI are 3.3 ± 0.005% and 0.009 ± 0.003%, respectively. However, the performance worsens when np = 2, because CRV and CRI respectively equal to 6.8 ± 0.08% and 0.02 ± 0.005% when CV = 1.0 (fig. 2C). When a higher cutoff (c = 0.5Lo) is used, CRV and CRI are further reduced (fig. 2D). By contrast, using a lower cutoff (c = 0.05Lo) can increase the bias (fig. 2E).
Fig. 2.
Rates of false identification of expression RV and RI when the newly proposed parametric bootstrap method is used. The mean expression level (μ) used = 100. The CV used is marked on the top of each column. Each row has a different combination of the cutoff (c) and numbers of replicates at the original (no), plastic (np), and adapted (na) stages. Results shown are means and standard errors estimated from 100 rounds of simulation, each containing 1,000 hypothetical genes with the same μ and CV. See main text for definitions of RV and RI. (A) Simulation results under no = 6, np = 6, na = 6, and c = 0.2Lo. (B) Simulation results under no = 6, np = 3, na = 6, and c = 0.2Lo. (C) Simulation results under no = 6, np = 2, na = 6, and c = 0.2Lo. (D) Simulation results under no = 6, np = 6, na = 6, and c = 0.5Lo. (E) Simulation results under no = 6, np = 6, na = 6, and c = 0.05Lo.
The Excess of RV over RI Holds in the Absence of Methodological Bias
We now apply this new method to empirical data. Because the new method requires the information of the standard error of the mean expression estimate of each gene, no, np, and na must each be ≥2. Among the six data sets of experimental evolution recently analyzed for the comparison between RV and RI (Ho and Zhang 2018), we reanalyzed the five data sets that satisfy the above requirement. Three of them have a relatively large np, including Escherichia coli adapting to a glycerol medium from a glucose medium (no = 3, np = 5, and na = 3), E. coli adapting to a lactate medium from a glucose medium (no = 3, np = 6, and na = 3), and guppies adapting to low-predation streams from high-predation streams (no = 5, np = 5, and na = 4). Furthermore, most of the genes in these three data sets have CV < 1.0 (supplementary fig. S3A–C, Supplementary Material online). Therefore, according to our simulation results, δ upon the parametric bootstrap test should not exceed 1 percentage point in these cases if the null hypothesis of CRV = CRI holds. The other two cases, E. coli adapting to 42 °C from 37 °C (no = 3, np = 2, and na = 2) and budding yeast adapting to a xylulose medium from a glucose medium (no = 2, np = 2, and na = 2), have a much smaller np and higher CV (supplementary fig. S3D and E, Supplementary Material online). Therefore, δ could be inflated in these two cases.
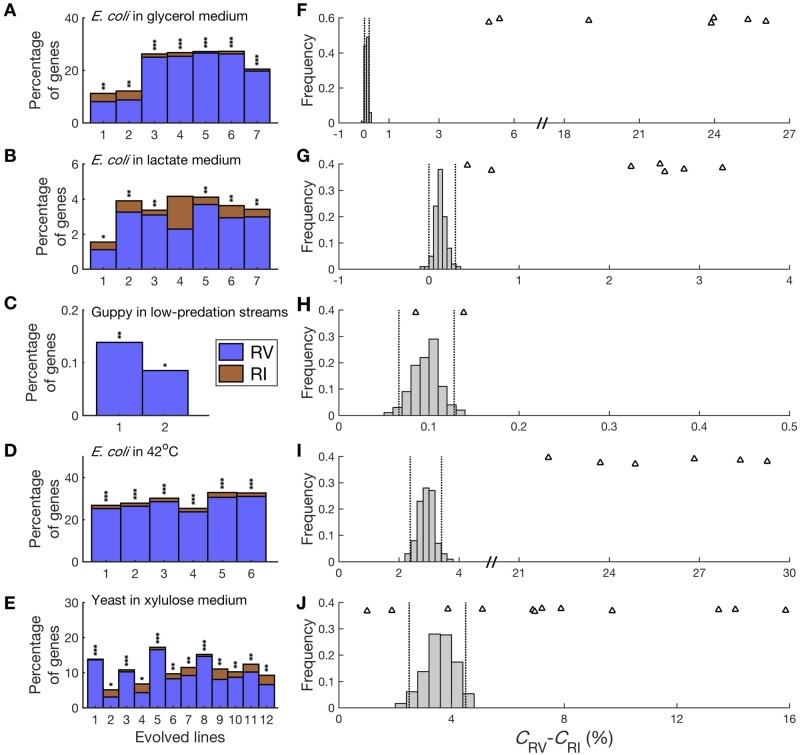
We start by investigating the first three cases. When applying the new method to the case of E. coli adapting to the glycerol medium, we found a significant excess of CRV over CRI in each of the seven parallel experiments (nominal P value < 0.05, two-tailed binomial test; fig. 3A). More importantly, δ is between 5 and 26 percentage points, which cannot be explained by the slight bias of the method. In the seven parallel lines of E. coli adapting to the lactate medium, six have a significantly positive δ (nominal P value < 0.05, two-tailed binomial test; fig. 3B). Among the six, five have a δ between 2.2 and 3.2 percentage points, whereas the “evolved line #1” has δ = 0.69 percentage point. In the two parallel lines of guppies adapting to low-predation streams, both show a significantly positive δ (nominal P value < 0.05, two-tailed binomial test; fig. 3C), but the δ values are small (0.09 and 0.14 percentage points).
Fig. 3.
Observed or simulated fractions of genes showing expression reversion (CRV) and reinforcement (CRI), respectively. (A) Observed CRV and CRI in seven parallel experiments of Escherichia coli undergoing laboratory evolution in a glycerol medium. The equality in the percentage of RI and RV genes in each adaptation is tested by a two-tailed binomial test. *, P < 0.05; **, P < 10−10; ***, P < 10−100. (B) Observed CRV and CRI in seven parallel experiments of E. coli undergoing laboratory evolution in a lactate medium. (C) Observed CRV and CRI in two parallel experiments of guppies undergoing evolution in low-predation streams. (D) Observed CRV and CRI in six parallel experiments of E. coli undergoing laboratory evolution in 42 °C. (E) Observed CRV and CRI in 12 parallel experiments of yeast undergoing laboratory evolution in a xylulose medium. (F) Observed CRV − CRI in E. coli adaptations to a glycerol medium, compared with the expected values under the null hypothesis of no gene expression changes. The observed values from 7 parallel experiments are indicated by triangles, whereas the expected values estimated by 100 simulations are presented as frequency distributions using bars. The simulations use the distributions of mean (μ) and CV estimated from the actual data. Two dashed lines depict the 2.5th and 97.5th percentiles in the distribution. (G) Observed CRV − CRI in E. coli adaptations to a lactate medium, compared with the expected values under the null hypothesis of no gene expression changes. (H) Observed CRV − CRI in guppy adaptations to low-predation streams, compared with the expected values under the null hypothesis of no gene expression changes. (I) Observed CRV − CRI in E. coli adaptations to 42 °C, compared with the expected values under the null hypothesis of no gene expression changes. (J) Observed CRV − CRI in yeast adaptations to a xylulose medium, compared with the expected values under the null hypothesis of no gene expression changes.
Because some of the above observed δ values are small, it is important to assess whether they could be due to the remaining minor bias of the new method. To this end, we performed additional simulations using the observed distributions of CV (supplementary fig. S3, Supplementary Material online) and μ (supplementary fig. S4, Supplementary Material online) specific to each data set. In each simulation, the number of replicates (no, np, and na) and the number of genes also follow the actual numbers in each data set. Again, we assumed no difference in true expression level among the three stages in the simulation. We found that δ is mostly <1 percentage point in the simulation (fig. 3F–H). More importantly, compared with the distribution of δ from the simulation, δ from all seven parallel experimental evolution lines of E. coli in the glycerol medium (fig. 3F), five of the seven parallel experimental evolution lines of E. coli in the lactate medium (fig. 3G), and one of the two parallel experimental evolution lines of guppies in low-predation streams (fig. 3H) are significantly larger (in the right 2.5% of the distribution of δ resulting from the simulation). Therefore, the observed preponderance of transcriptomic RV in these three data sets is largely genuine.
In the two data sets where np = 2, it is even more critical to perform simulations using the observed distributions of CV (supplementary fig. S3, Supplementary Material online) and μ (supplementary fig. S4, Supplementary Material online) to guard against potential inflations of δ. In the six lines of E. coli adapting to 42 °C, each shows a significantly positive δ (nominal P value < 0.05, two-tailed binomial test; fig. 3D). More importantly, each has a δ larger than 21 percentage points, which is larger than any δ observed in the 100 simulations (fig. 3I). In the 12 lines of budding yeast adapting to the xylulose medium, all have a significantly positive δ (nominal P value < 0.05, two-tailed binomial test; fig. 3E). In addition, nine of them have δ values significantly larger than what the simulation under the null hypothesis shows (fig. 3J). Therefore, the prevalence of RV in these two data sets is also mostly genuine.
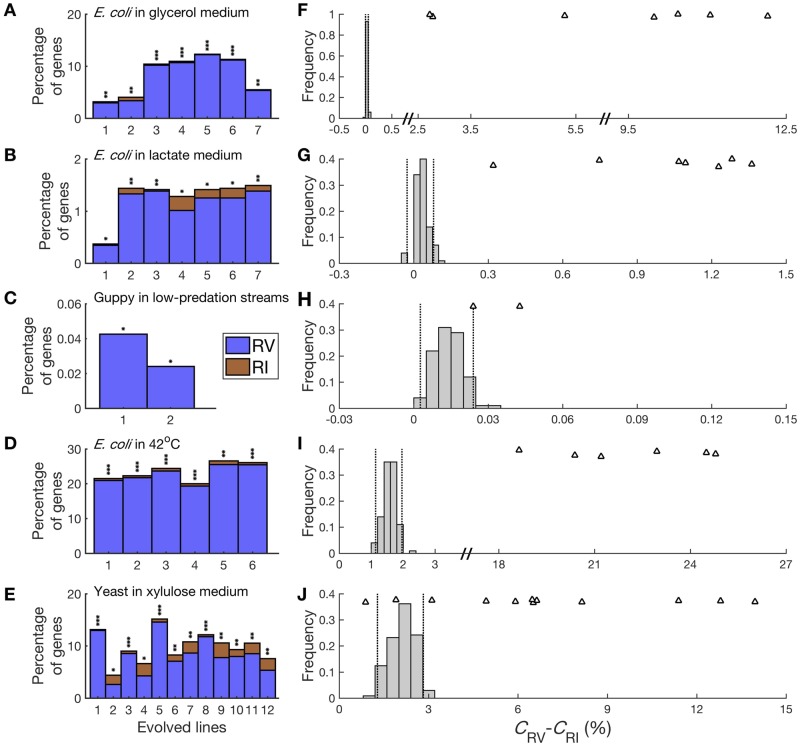
Because using higher cutoffs can minimize the bias, we repeated the analysis of these five data sets using c = 0.5Lo instead of 0.2Lo. We found all 34 cases in the five data sets show significantly positive δ values (nominal P value < 0.05, two-tailed binomial test; fig. 4A–E). Furthermore, 32 of 34 observed δ’s are in the right 2.5% of the corresponding distribution of simulated δ’s (fig. 4F–J). These results further establish that the observed preponderance of transcriptomic RV in these data sets is not statistical artifacts.
Fig. 4.
Observed or simulated fractions of genes showing expression reversion (CRV) and reinforcement (CRI), respectively, under a more stringent cutoff (c = 0.5Lo). (A) Observed CRV and CRI in seven parallel experiments of Escherichia coli undergoing laboratory evolution in a glycerol medium. The equality in the percentage of RI and RV genes in each adaptation is tested by a two-tailed binomial test. *, P < 0.05; **, P < 10−10; ***, P < 10−100. (B) Observed CRV and CRI in seven parallel experiments of E. coli undergoing laboratory evolution in a lactate medium. (C) Observed CRV and CRI in two parallel experiments of guppies undergoing evolution in low-predation streams. (D) Observed CRV and CRI in six parallel experiments of E. coli undergoing laboratory evolution in 42 °C. (E) Observed CRV and CRI in 12 parallel experiments of yeast undergoing laboratory evolution in a xylulose medium. (F) Observed CRV − CRI in E. coli adaptations to a glycerol medium, compared with the expected values under the null hypothesis of no gene expression changes. The observed values from seven parallel experiments are indicated by triangles, whereas the expected values estimated by 100 simulations are presented as frequency distributions using bars. The simulations use the distributions of mean (μ) and CV estimated from the actual data. Two dashed lines depict the 2.5th and 97.5th percentiles in the distribution. (G) Observed CRV − CRI in E. coli adaptations to a lactate medium, compared with the expected values under the null hypothesis of no gene expression changes. (H) Observed CRV − CRI in guppy adaptations to low-predation streams, compared with the expected values under the null hypothesis of no gene expression changes. (I) Observed CRV − CRI in E. coli adaptations to 42 °C, compared with the expected values under the null hypothesis of no gene expression changes. (J) Observed CRV − CRI in yeast adaptations to a xylulose medium, compared with the expected values under the null hypothesis of no gene expression changes.
Discussion
Using computer simulation, we confirmed that previous transcriptomic studies of PC and GC are biased such that expression RV tends to be observed more often than RI artificially. The severity of the bias depends on several factors. In general, the bias is stronger when the expression measures are less precise (i.e., higher CV), the number of measurements per gene at stage p is smaller (i.e., lower np), and the cutoff for calling PC and GC is lower (i.e., lower c). In our simulation, we assumed that the expression levels of a gene are the same at stages o, p, and a, rendering all observed RV and RI cases false positives. In reality, the expression levels at the three stages are unlikely to be the same for most genes. Consequently, only some of the observed RV and/or RI events may be false. That is, our simulation tends to overestimate the bias in the comparison between RV and RI. Considering this fact and the simulation results under realistic parameters, the bias is generally minor.
Statistical artifacts owing to nonindependence between variables have long been known (Pearson 1897). Historically, population biologists proposed the use of permutation to address this problem (Jackson and Somers 1991), and permutation tests were performed in Ghalambor et al. (2015) and Rodriguez-Verdugo et al. (2016). Specifically, they first measured the linear or rank correlation between PC and GC among genes. They then randomized the stage labels (o, p, or a) among all replicate measurements of each gene before recomputing Lo, Lp, and La and reestimating PC and GC. This randomization was performed for all genes and the correlation between PC and GC among genes was reestimated after the randomizations. This was repeated many times to derive a null distribution of the correlation. The authors found that the observed negative correlations are significant when compared with their null distributions, so concluded that the negative correlations between PC and GC are genuine. Although Mallard et al. (2018) challenged the suitability of the permutation test in Ghalambor et al. (2015) and claimed that permutation is sometimes insufficient for removing statistical artifacts, this criticism was rejected by Ghalambor and coworkers (Ghalambor et al. 2018; Hoke et al. 2018) because they found Mallard et al.’s simulated data rarely matched the criteria required in the original analysis (Ghalambor et al. 2015). We note that, even if the permutation test can guard against the artificial correlation, as what appears to be the case here, this test does not allow estimating δ or accurately identifying the genes that show RV or RI. Instead, we proposed in this work a parametric bootstrap method to compare PC and GC and demonstrated by computer simulation that its bias is minimal. Thus, to estimate δ and identify genes exhibiting RV or RI, the parametric bootstrap method is preferred. This said, the difference in focal statistics between the parametric bootstrap method and the permutation method makes it difficult to compare their performances directly.
Using the parametric bootstrap method, we reanalyzed a total of 34 cases of 5 evolutionary experiments of E. coli, yeast, and guppies. Under a high cutoff of c = 0.5Lp, δ, the difference between the percentage of genes showing RV and that showing RI, is significantly positive in all cases and significantly greater than the expected bias in 32 cases. These results confirm the previous finding that genetic adaptations to new environments more often reverse than reinforce plastic gene expression changes.
In addition to gene expression changes, we recently studied metabolic flux changes in E. coli’s environmental adaptations, using computational metabolic analysis including flux balance analysis (FBA) and minimization of metabolic adjustment (MOMA) (Ho and Zhang 2018). We showed that the metabolic flux changes also exhibit an excess of RV over RI, regardless of whether the same computational method (MOMA) or different computational methods (FBA and MOMA) are used to predict fluxes at the three stages. Although computational flux predictions are certainly not error free, the type of error is fundamentally different from the random error in gene expression measurement studied here. It is likely that the potential error of a computational flux prediction arises mainly from mismatches between the reality and the assumed metabolic model. Because a similar mismatch occurs in each of the three stages, the effect of the mismatch is probably canceled out when the flux differences between stages o and p and those between stages p and a are computed to obtain PC and GC, respectively. We thus believe that the previous finding of an excess of metabolic flux RV over RI would probably hold if such mismatches are minimized. Future experimental fluxomic analysis is needed to confirm this prediction. Note that our simulation results can guide the design of future fluxomic studies and our new method can be deployed to deal with the nonindependence between the experimentally measured plastic and genetic flux changes. Notwithstanding, phenotypic traits of different levels of the biological organization (e.g., organismal, cellular, and molecular traits) may have different evolutionary patterns (Zhang 2018). Whether the predominance of RV over RI revealed at the transcriptomic and fluxomic levels hold at other phenotypic levels awaits future exploration.
Regarding the biological reason why RV is more prevalent than RI, previous metabolic flux analysis revealed that, even in the presence of plasticity, organismal fitness drops substantially after an environmental shift but largely recovers through subsequent adaptive evolution (Ho and Zhang 2018). Thus, the overall physiological state of the organism may be quite similar between the adapted stages in the original and new environments but is much different in the low-fitness plastic stage right after the environmental shift. Such disturbances and subsequent recoveries in overall physiology and fitness explain why plastic phenotypic changes are mostly genetically compensated rather than strengthened. In short, PCs in gene expression and metabolic flux represent emergency stress responses that may be important for organismal survival in new environments but are otherwise not steppingstones for genetic adaptations. In the case of guppies adapting from a high- to a low-predation environment, the new environment appears less stressful than the original one. It has been suggested that RV would still be more prevalent than RI in this case because a trait with a plastic phenotypic change away from the new optimum is presumably under a stronger directional selection than a trait with a plastic phenotypic change toward the new optimum (Price et al. 2003; Ghalambor et al. 2015).
We found that δ varies substantially among the five data sets of experimental evolution. Why some environmental adaptations show a higher excess of RV over RI than others is unclear. In theory, a higher δ may result when the new environment is more stressful. This said, how stressful a new environment is depends not only on the environment per se but also on the evolutionary history of the population, because adaptive plasticity may exist if the population experienced similar environments as the new environment in the past. That δ is exceptionally low in guppies may be simply because their new environment is not stressful or because animals differ from microbes in the relative abundances of RV and RI. To find the exact cause requires further investigations.
Although our study is designed and conducted to address the nonindependence between the estimates of PCs and GCs in gene expression, the lessons learned and methods developed are useful for dealing with other comparisons of nonindependent estimates, which are common in evolutionary genomics. Below, we highlight two such examples in the study of gene expression evolution. The first involves the comparison between the contributions of cis- and trans-regulatory mutations to gene expression evolution. The standard approach (Wittkopp et al. 2004) is to first measure the expression levels of a gene in two strains or closely related species that can be crossed. The observed expression difference is referred to as the total difference, which is the sum of cis- and trans-regulatory differences. One then measures the expression levels of the two alleles in the hybrid of the two strains/species. Because the two alleles in the hybrid have the same trans-regulatory environment, their expression difference must be due to the cis-regulatory difference. One can then estimate the trans-regulatory difference by subtracting the cis-regulatory difference from the total difference. It was reported that when both cis- and trans-regulatory differences exist for the same gene, they more often have effects in opposite directions than in the same direction, which could mean widespread compensatory changes underlying the evolution of gene expression (Coolon et al. 2014; Metzger et al. 2017). But because one estimates the trans-regulatory difference by subtracting the cis-regulatory difference from the total difference, the above result could be a statistical artifact of the nonindependence between the estimates of cis- and trans-regulatory differences. Another example is the comparison between transcriptional and translational differences underlying gene expression differences between strains or species. The transcriptional activity of a gene is typically approximated by the mRNA concentration measured by RNA sequencing, whereas the translational activity is typically measured by the ratio between the protein concentration (or ribo-seq read number in ribosome profiling) and mRNA concentration. It is reported that transcriptional differences and translational differences between species tend to have opposite directions (Artieri and Fraser 2014; McManus et al. 2014). Again, because the estimates of translational and transcriptional activities are not independent from each other, the above result could be a statistical artifact. It will be important to confirm that these and other previous results hold after the correction for the statistical problem.
Materials and Methods
All simulations and analyses were performed in MATLAB codes. Random normal variables were generated by the function “normrnd.” The transcriptomic data sets of E. coli, guppies, and yeast were originally from Fong et al. (2005), Ghalambor et al. (2015), Rodriguez-Verdugo et al. (2016), and Tamari et al. (2016). Data processing followed Ho and Zhang (2018). Specifically, in the study of E. coli K-12 undergoing experimental evolution in glycerol (Fong et al. 2005), the transcriptomes of 1) the ancestral line in glucose, 2) ancestral line in glycerol, and 3) seven parallel evolution lines in glycerol on day 44 were profiled by Affymetrix E. coli Antisense Genome Arrays. The number of replicates for (1) and each line of (3) is 3, whereas the number of replicates for (2) is 5. In the study of E. coli K-12 undergoing experimental evolution in lactate (Fong et al. 2005), the transcriptomes of 1) the ancestral line in glucose, 2) ancestral line in lactate, and 3) seven parallel evolution lines in lactate on day 60 were also profiled by Affymetrix E. coli Antisense Genome Arrays. The number of replicates for (1) and each line of (3) is 3, whereas the number of replicates for (2) is 6. In the study of the guppy Poecilia reticulata undergoing experimental evolution in low-predation streams (Ghalambor et al. 2015), RNA-seq was used for profiling the transcriptomes of 1) guppies caught from streams with high predation and exposed to chemical cues of predators in the lab, 2) guppies caught from streams with high predation and not exposed to chemical cues of predators in the lab, and 3) two independently evolved groups of guppies in streams with no predators. The number of replicates is 5 for (1) and (2), respectively, and the number of replicates is 4 for either group of (3). All expression levels were provided by the authors. In the experimental evolution of E. coli in 42 °C (Rodriguez-Verdugo et al. 2016), RNA-seq was performed in 1) the ancestral line at 37 °C, 2) ancestral line at 42 °C, 3) two evolved lines at 42 °C and four lines each carrying a distinct adaptive mutation at 42 °C. The number of replicates for (1) is 3, and the number of replicates for either group of (2) or (3) is 2. The reads were downloaded from Sequence Read Archive (SRA) database and mapped by the instruction of the original paper. Expression levels were measured by Reads Per Kilobase of transcript per Million mapped reads (RPKM). In the experimental evolution of 12 different strains of the budding yeast Saccharomyces cerevisiae in a xylulose medium (Tamari et al. 2016), RNA-seq was used for profiling the transcriptomes of 1) 12 ancestral lines in a glucose medium, 2) 12 ancestral lines in the xylulose medium, and 3) 12 evolved lines in the xylulose medium. Each line has two replicates. The reads were downloaded from SRA database and mapped following the original study. Expression levels were measured by RPKM. In all data sets, the gene expression measures in (1), (2), and (3) represent the phenotypes at the original, plastic, and adapted stages, respectively.
Supplementary Material
Supplementary data are available at Molecular Biology and Evolution online.
Supplementary Material
Acknowledgments
We thank three anonymous reviewers for valuable comments. This work was supported in part by U.S. National Institutes of Health grant GM120093 to J.Z.
References
- Artieri CG, Fraser HB.. 2014. Evolution at two levels of gene expression in yeast. Genome Res. 243:411–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coolon JD, McManus CJ, Stevenson KR, Graveley BR, Wittkopp PJ.. 2014. Tempo and mode of regulatory evolution in Drosophila. Genome Res. 245:797–808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fong SS, Joyce AR, Palsson BO.. 2005. Parallel adaptive evolution cultures of Escherichia coli lead to convergent growth phenotypes with different gene expression states. Genome Res. 1510:1365–1372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghalambor CK, Hoke KL, Ruell EW, Fischer EK, Reznick DN, Hughes KA.. 2015. Non-adaptive plasticity potentiates rapid adaptive evolution of gene expression in nature. Nature 5257569:372–375. [DOI] [PubMed] [Google Scholar]
- Ghalambor CK, Hoke KL, Ruell EW, Fischer EK, Reznick DN, Hughes KA.. 2018. Ghalambor et al. reply. Nature 5557698:E23.. [DOI] [PubMed] [Google Scholar]
- Ho W-C, Zhang J.. 2018. Evolutionary adaptations to new environments generally reverse plastic phenotypic changes. Nat Commun. 91:350.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoke K, Hughes KA, Fischer EK, Ghalambor CK.. 2018. Untangling the role of selection and drift in population divergence via transcriptional network simulations: extended analysis of Ghalambor et al. (2015). bioRxiv 277830. [Google Scholar]
- Jackson DA, Somers KM.. 1991. The specter of spurious correlations. Oecologia 861:147–151. [DOI] [PubMed] [Google Scholar]
- Laland K, Uller T, Feldman M, Sterelny K, Müller GB, Moczek A, Jablonka E, Odling-Smee J, Wray GA, Hoekstra HE, et al. 2014. Does evolutionary theory need a rethink?—POINT yes, urgently. Nature 5147521:161–164. [DOI] [PubMed] [Google Scholar]
- Laland KN, Uller T, Feldman MW, Sterelny K, Muller GB, Moczek A, Jablonka E, Odling-Smee J.. 2015. The extended evolutionary synthesis: its structure, assumptions and predictions. Proc Biol. Sci. 2821813:20151019.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ledon-Rettig CC, Pfennig DW, Nascone-Yoder N.. 2008. Ancestral variation and the potential for genetic accommodation in larval amphibians: implications for the evolution of novel feeding strategies. Evol Dev. 103:316–325. [DOI] [PubMed] [Google Scholar]
- Levis NA, Pfennig DW.. 2016. Evaluating ‘plasticity-first’ evolution in nature: key criteria and empirical approaches. Trends Ecol Evol. 317:563–574. [DOI] [PubMed] [Google Scholar]
- Mallard F, Jaksic AM, Schlotterer C.. 2018. Contesting the evidence for non-adaptive plasticity. Nature 5557698:E21–E22. [DOI] [PubMed] [Google Scholar]
- McManus CJ, May GE, Spealman P, Shteyman A.. 2014. Ribosome profiling reveals post-transcriptional buffering of divergent gene expression in yeast. Genome Res. 243:422–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzger BPH, Wittkopp PJ, Coolon JD.. 2017. Evolutionary dynamics of regulatory changes underlying gene expression divergence among Saccharomyces species. Genome Biol Evol. 94:843–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearson K. 1897. Mathematical contributions to the theory of evolution—On a form of spurious correlation which may arise when indices are used in the measurement of organs. Proc R Soc Lond. 60:489–498. [Google Scholar]
- Pfennig DW, Wund MA, Snell-Rood EC, Cruickshank T, Schlichting CD, Moczek AP.. 2010. Phenotypic plasticity’s impacts on diversification and speciation. Trends Ecol Evol. 258:459–467. [DOI] [PubMed] [Google Scholar]
- Pigliucci M, Murren CJ, Schlichting CD.. 2006. Phenotypic plasticity and evolution by genetic assimilation. J Exp Biol. 209(Pt 12):2362–2367. [DOI] [PubMed] [Google Scholar]
- Price TD, Qvarnstrom A, Irwin DE.. 2003. The role of phenotypic plasticity in driving genetic evolution. Proc R Soc Lond [Biol]. 2701523:1433–1440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez-Verdugo A, Tenaillon O, Gaut BS.. 2016. First-step mutations during adaptation restore the expression of hundreds of genes. Mol Biol Evol. 331:25–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandberg TE, Pedersen M, LaCroix RA, Ebrahim A, Bonde M, Herrgard MJ, Palsson BO, Sommer M, Feist AM.. 2014. Evolution of Escherichia coli to 42 degrees C and subsequent genetic engineering reveals adaptive mechanisms and novel mutations. Mol Biol Evol. 3110:2647–2662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki Y, Nijhout HF.. 2006. Evolution of a polyphenism by genetic accommodation. Science 3115761:650–652. [DOI] [PubMed] [Google Scholar]
- Tamari Z, Yona AH, Pilpel Y, Barkai N.. 2016. Rapid evolutionary adaptation to growth on an ‘unfamiliar’ carbon source. BMC Genomics. 17:674.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West-Eberhard MJ. 2003. Developmental plasticity and evolution. New York: Oxford University Press. [Google Scholar]
- Wittkopp PJ, Haerum BK, Clark AG.. 2004. Evolutionary changes in cis and trans gene regulation. Nature 4306995:85–88. [DOI] [PubMed] [Google Scholar]
- Zhang J. 2018. Neutral theory and phenotypic evolution. Mol Biol Evol. 356:1327–1331. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.