Marine ice sheet instability amplifies and skews uncertainty in projections of future sea-level rise

Significance

The potential for collapse of the Antarctic ice sheet remains the largest single source of uncertainty in projections of future sea-level rise. This uncertainty comes from an imperfect understanding of ice sheet processes and the internal variability of climate forcing of ice sheets. Using a mathematical technique from statistical physics and large ensembles of state-of-the-art ice sheet simulations, we show that collapse of ice sheets widens the range of possible scenarios for future sea-level rise. We also find that the collapse of marine ice sheets makes worst-case scenarios of rapid sea-level rise more likely in future projections.

Abstract

Sea-level rise may accelerate significantly if marine ice sheets become unstable. If such instability occurs, there would be considerable uncertainty in future sea-level rise projections due to imperfectly modeled ice sheet processes and unpredictable climate variability. In this study, we use mathematical and computational approaches to identify the ice sheet processes that drive uncertainty in sea-level projections. Using stochastic perturbation theory from statistical physics as a tool, we show mathematically that the marine ice sheet instability greatly amplifies and skews uncertainty in sea-level projections with worst-case scenarios of rapid sea-level rise being more likely than best-case scenarios of slower sea-level rise. We also perform large ensemble simulations with a state-of-the-art ice sheet model of Thwaites Glacier, a marine-terminating glacier in West Antarctica that is thought to be unstable. These ensemble simulations indicate that the uncertainty solely related to internal climate variability can be a large fraction of the total ice loss expected from Thwaites Glacier. We conclude that internal climate variability alone can be responsible for significant uncertainty in projections of sea-level rise and that large ensembles are a necessary tool for quantifying the upper bounds of this uncertainty.

In marine ice sheets, the grounding line is a critical boundary where ice flowing from the ice sheet interior becomes thin enough to float in ocean water. The grounding line location and ice flux are sensitive functions of the depth of the surrounding ocean (1–3). When the bedrock beneath the grounding line is reverse sloping (i.e., deepens toward the ice sheet interior), a small retreat of the grounding line onto deeper bed leads to greater ice flux and therefore more retreat. This positive flux feedback leads to the potential for rapid and irreversible retreat wherever the bed is reverse sloping, which has been termed the “marine ice sheet instability” (4). Rapid ice loss from the Antarctic ice sheet through this instability will likely drive sea-level rise beyond the next century (5, 6). However, projections of future sea-level rise are uncertain due to imperfect representation of ice sheet processes in models, unknown future anthropogenic emissions, and the internal variability of future climate forcing of ice sheets. Even with improvements in ice sheet models and climate projections, there will always remain a component of sea-level projection uncertainty that cannot be reduced due to the fundamentally unpredictable internal variability of the climate system which causes ice sheet change. This fundamental lower bound in the uncertainty of projections due to internal climate variability (for ice sheets and other elements of the climate system) has been termed “irreducible uncertainty” (7). The inevitability of uncertainty remaining in sea-level projections necessitates robust modeling of the ice sheet dynamical factors which produce uncertainty in future ice sheet projections, for which there is no existing theoretical framework. In particular, it is critically important to constrain the upper bounds of uncertainty in sea-level rise projections, which have a disproportionate influence on planning for coastal adaptation measures (8).

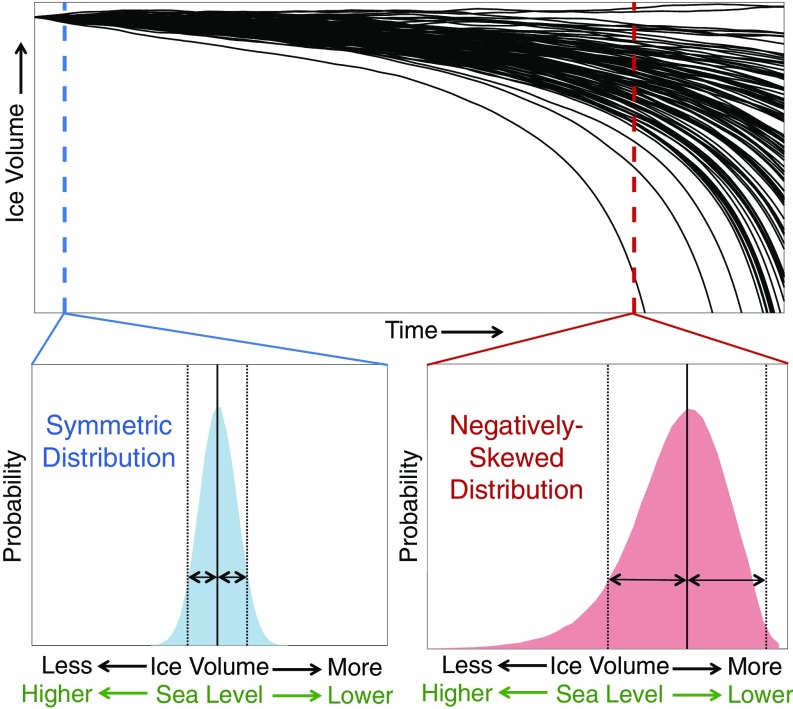
Ice sheets evolve in response to changes in climate variables (i.e., climate “forcing”), such as snowfall and ocean temperature. The amount and structure of uncertainty in projections of the future ice sheet contribution to sea-level rise can thus be determined through large ensembles of ice sheet model simulations, which are plausible realizations of the future evolution of an ice sheet in response to climate forcing (see Fig. 1, Upper for a conceptual illustration of an ensemble). Each ensemble member is distinguished by selecting either a unique set of model parameters or one realization of future variable climate forcing from a distribution of possibilities. At a particular point in time, the statistical properties of the full ensemble represent the probability distribution of ice sheet state, represented by a variable such as extent or volume (conditioned on the probability of the model parameters or climate variability having particular values). The spread (or standard deviation [SD]) of the probability distribution quantifies the amount of uncertainty in the projection. In a probability distribution that is symmetric, the skewness is 0, and the projected change in ice sheet volume is equally likely to fall above or below the mostly likely projection (Fig. 1, Lower Left). A negative skewness of the probability distribution indicates that the probability of ice sheet volume turning out to be below the most likely projection is greater than that of ice sheet volume turning out to be above the most likely projection (and vice versa for positive skewness). Put another way, a negative skewness indicates that the probability of worst-case scenarios (i.e., more ice sheet mass loss and corresponding sea-level rise than is expected from the highest-likelihood projection) is greater than the probability of best-case scenarios (of less sea-level rise than the highest-likelihood projection).

Fig. 1.

(Upper) Conceptual illustration of an evolving ensemble of ice sheet model simulations, where each solid line is a single plausible realization of the future ice sheet evolution. Dashed colored lines indicate two time slices, for which probability distributions are provided (Lower Left and Lower Right). The statistical properties of the probability distribution of ensemble simulations change with time from a narrow, symmetric distribution at early times (blue dashed line, Lower Left) to a wide, asymmetric distribution with negative skewness (red dashed line, Lower Right), making the probability of ice sheet volumes below the most likely projection many times greater than that of ice sheet volumes above the most likely projection (arrows show example of ice sheet volumes above and below the most likely ice sheet volume projection).

In this study, we develop a framework for determining how marine ice sheet processes produce uncertainty in projections of future sea level. We do so using 2 complementary approaches: 1) Stochastic perturbation analysis of a simple model of marine ice sheet evolution with one evolving quantity and 2) statistical analysis of a large number of simulations of the future evolution of a West Antarctic glacier using a state-of-the-art numerical ice sheet model with many thousands of evolving quantities. These 2 approaches represent end members of the hierarchy of modern ice sheet models. They provide both a theoretical framework for understanding the sources of uncertainty in projections of the future ice sheet contribution to sea level and an application of this framework to an actual glacier that is thought to be undergoing the marine ice sheet instability.

Stochastic Perturbation Theory

Over the past several decades, much of the observed increase in Antarctic ice loss has been caused by ocean-driven ice sheet melting (9). Our goal in this study is thus to quantify the uncertainty in projected ice sheet state that is caused by uncertainty in ocean-induced ice sheet melt, although the principles involved are extendable to uncertainty in other climate forcing (or uncertainty in glaciological parameters). We start by mathematically and numerically analyzing the uncertainty in ice sheet state simulated by a minimal model of grounding-line migration for a glacier under climate forcing (10, 11)

$$\frac{dL}{dt}=P{h}_g^{-1}L-\gamma h_g^{\beta -1}+\eta ,$$ [1]

where $L$ is the distance of the grounding line from the glacier onset, and $h_g=-\frac{{\rho }_w}{{\rho }_i}{b}_g$ is the thickness of ice at the grounding line, which depends on the ratio of seawater (${\rho }_w$) and ice (${\rho }_i$) densities and the local bedrock depth ($b_g$). This model, which is derived and discussed in more detail in Robel et al. (11), tracks the total mass balance of the glacier, captured in 3 processes. The first term captures ice entering as snowfall over the glacier surface at accumulation rate $P$ (averaged through glacier geometry: $L$ and $h_g$). The second term captures ice leaving the glacier due to ice flow through the grounding line ($\gamma h_g^{\beta -1}$). The third term captures ocean-induced melt at the grounding line ($\eta$). The parameters $\beta$ and $\gamma$ are related to the balance of glaciological processes which contribute to setting the velocity of ice at the grounding line (e.g., gravitational driving stress, basal sliding, and ice shelf buttressing). Observations (12), mathematical analyses (1–3, 13), and numerical simulations (11, 14, 15) have all shown that grounding-line velocity is generally a nonlinear function of grounding-line ice thickness (as we assume in Eq. 1), even during periods of transient grounding-line migration, although there is perhaps some variation in the exact value of $\beta$ that applies in such a situation. Still, this minimal model is meant as a tool to understand the processes which drive uncertainty in simulations of marine ice sheet instability, not a means for making actual predictions of ice sheet change. As we show later on, the conclusions drawn from this minimal model are reproduced in a state-of-the-art ice sheet model which does not make the same simplifying assumptions.

In Eq. 1, the rate at which the grounding line migrates in response to ocean-induced melting (or freezing) is $\eta =\overline{\eta }+{\eta }^{\prime }\left(t\right)$, consisting of a time-averaged component ($\overline{\eta }$) and a time-variable component (${\eta }^{\prime }\left(t\right)$). The time-averaged ocean forcing may be uncertain and so is drawn from a Gaussian distribution with SD ${\sigma }_P$. The time-variable ocean forcing is a first-order autoregressive Gaussian noise process with interannual SD ${\sigma }_F$, and decorrelation timescale ${\tau }_F$. Other studies have shown using a complex spatially resolved model that ocean-induced grounding-line variability is filtered through the frequency-dependent response of the ice shelf to ocean forcing (16). In this minimal model, we assume a simpler form for $\eta$ in which all ocean-induced grounding-line migration is the result of melting directly at the grounding line and neglects effects from sub-ice shelf melt and buttressing. While this assumption will likely produce some quantitative difference than that of a model which includes sub-ice shelf melt beyond the grounding line, the more complicated ice-shelf–resolving simulations in the next section show that the qualitative aspects of our mathematical analysis do not appear to be changed by such detailed considerations.

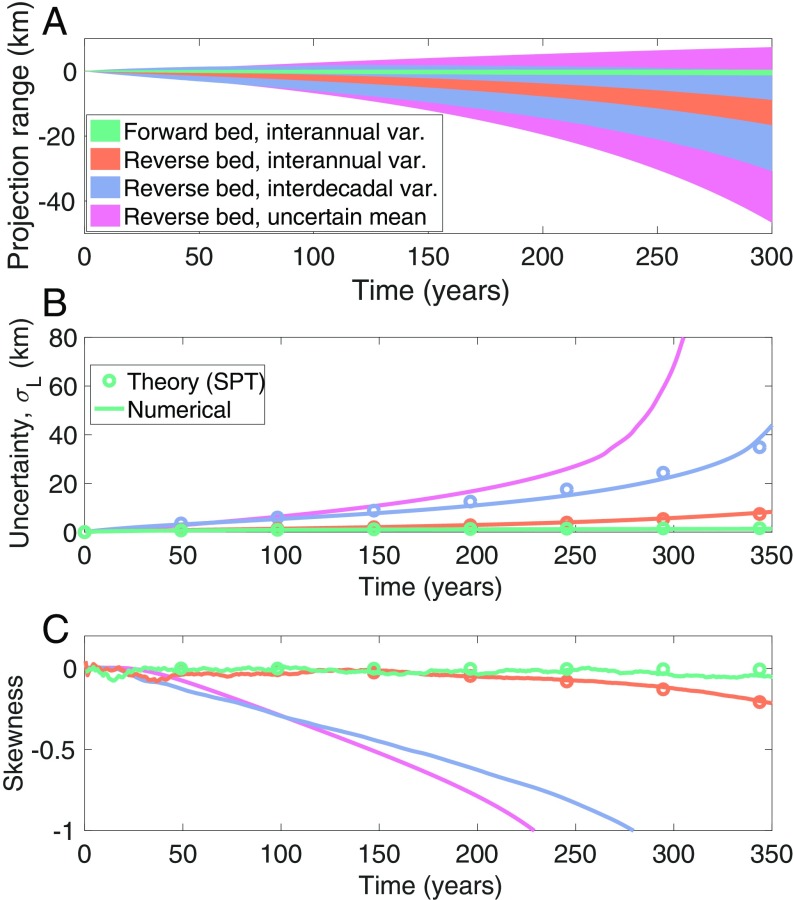
Fig. 2 shows ensembles (with 10,000 simulations each) of simulated grounding-line migration over a bed of constant slope, calculated using Eq. 1 (details in Materials and Methods). The only forcing during the simulation period shown is ocean-induced grounding-line migration ($\eta$). The ensemble spread (represented in Fig. 2 by the interquartile range) captures the uncertainty in projected grounding-line position due to uncertainty in ocean forcing. On a forward-sloping bed (green shading/lines), small interannual forcing in the grounding-line position (${\sigma }_F=100$ m/y, $\overline{\eta }=0$) produces an ensemble spread that remains small, bounded, and symmetric. For the same stochastic forcing on a reverse-sloping bed (orange shading/lines), all ensemble members retreat, as the ensemble spread grows rapidly without bound and becomes skewed (negatively) toward more retreat.

Fig. 2.

Evolution of a 10,000-member ensemble of minimal model (Eq. 1) simulations of grounding-line retreat over idealized constant-slope bed topography and variability in ocean forcing. (A) Ensemble interquartile range (shading spans 25th percentile to 75th percentile). (B) SD derived from numerically calculated ensemble statistics (solid lines) and analytic predictions from stochastic perturbation theory (circles). (C) Skewness derived from numerically calculated ensemble statistics (solid lines) and analytic predictions from stochastic perturbation theory (circles). Negative skew indicates more retreated grounding line. There is no analytic approximation available for skewness under autocorrelated forcing (see SI Appendix for discussion of stochastic perturbation theory). Pink shading and lines are simulations on a reverse-sloping bed ($b_x=4\times 10^{-3}$) with constant ocean forcing, selected from a Gaussian distribution. Blue shading and lines are simulations on a reverse-sloping bed ($b_x=4\times 10^{-3}$) with interdecadal variability in ocean forcing (${\tau }_F=10$ y). Orange shading and lines are simulations on a reverse-sloping bed ($b_x=3.5\times 10^{-3}$) with interannual variability in ocean forcing (${\tau }_F=1$ y). Green shading and lines are simulations on a forward-sloping bed ($b_x=-10^{-3}$) with interannual variability in ocean forcing (${\tau }_F=1$ y). In all simulations, $P=0.35$ m/y, $\gamma =7.8\times 10^{-9}$ m^−2.75⋅y⁻¹, and $\beta =4.75$. In simulations with variable ocean forcing (blue, orange, green), $\overline{\eta }=0$ and ${\sigma }_F=100$ m/y. In simulations with uncertainty in constant ocean forcing (pink), ${\sigma }_P=50$ m/y.

The growth in ensemble spread (i.e., uncertainty) occurs because the marine ice sheet instability amplifies (rather than damps) small perturbations from stochastic ocean forcing. These growing perturbations accumulate over time, leading to a divergence between ensemble members, which each experience a different series of perturbations from ocean forcing. The skewness of the ensemble can be understood physically and from an analysis of Eq. 1. For a retreating ice sheet, the rate of retreat is set by the difference between two fluxes: The accumulation flux and the grounding-line flux. If the grounding-line flux is more sensitive to the position of the grounding line than the accumulation (which it is for sufficiently nonlinear grounding-line flux), the net effect will be that the rate of retreat of more-retreated ensemble members will be greater than the rate of retreat of the less-retreated ensemble members. The result is that the retreat of the ensemble becomes progressively more negatively skewed with time. In ensembles where all simulations are advancing, the most advanced ensemble members accelerate faster, producing a positive skew.

Observations indicate that climate forcing of glaciers in Antarctica (and elsewhere) exhibits strong variability on decadal timescales (17, 18). In our minimal model, when stochastic forcing has decadal persistence, the ensemble spread and skewness grow considerably faster (blue shading/lines in Fig. 2). Such an amplified glacier response to temporal persistence in forcing agrees with previous model studies of mountain glaciers (19) and periodically forced ice streams (16, 20, 21).

For temporal ocean variability, stochastic perturbation theory (22) (SI Appendix) provides a theoretical framework for determining the physical processes which control the amplification and skewing of uncertainty in ice sheet projections. Analytic approximations for the spread and skewness of ensembles derived from stochastic perturbation theory (circles in Fig. 2 B and C) match well with numerically calculated ensemble statistics. This theoretical framework shows that ensemble spread grows exponentially with a rate that is proportional to the bed slope and the nonlinearity in grounding-line ice flux ($\beta$ in Eq. 1). Thus, when the bed is forward sloping (negative), the ensemble spread remains bounded. When the bed is reverse sloping (positive), the marine ice sheet instability causes the ensemble spread to grow exponentially without bound. The ensemble variance is also proportional to the decorrelation timescale of the forcing, implying greater uncertainty in projections when climate forcing is persistent on longer timescales.

As alluded to above, the skewness of the ensemble is caused by the changing rate of grounding-line migration over a reverse-sloping bed. It can be shown analytically (see SI Appendix for details) that when the grounding-line ice flux is sufficiently nonlinear with respect to ice thickness ($\beta >3$ in Eq. 1), then ensembles of a retreating grounding line will tend to be skewed toward more retreat. Conversely, when grounding-line ice flux is linear or weakly nonlinear ($\beta <3$), then ensembles will tend to be skewed toward less retreat. In a wide range of realistic settings, we expect ensembles to skew toward more retreat during the retreating phase of the marine ice sheet instability because of the high-degree nonlinearity of grounding-line ice flux ($\beta =4.75$ in ref. 1, $\beta =5$ in ref. 2, $\beta =4$ in ref. 3). In other words, the fact that the probability distribution is skewed in the direction of more sea-level rise is a fundamental consequence of the strong nonlinearity inherent in grounding-line dynamics.

Uncertainty in the time-averaged ocean forcing ($\overline{\eta }$; pink shading/lines in Fig. 2) produces even more ensemble spread (for relatively less uncertainty, ${\sigma }_P=50$ m/y) and further indicates the importance of the marine ice sheet instability for amplifying and skewing uncertainty in ice sheet projections. Uncertainty in the time-averaged climate forcing can be thought of as a limiting case of the response to an initial impulse with an infinite decorrelation time (${\tau }_F\to \infty$). However, for such a nonstochastic case, there is no formal limit from stochastic perturbation theory in which the ensemble spread can be predicted.

Large Ensembles of Thwaites Glacier Instability.

To demonstrate that the intuition gained from the theoretical framework developed in the previous section applies to realistic glacier models, we simulate ensembles of the future retreat of Thwaites Glacier in West Antarctica using the Ice Sheet System Model (ISSM), a state-of-the-art finite-element model of ice sheet flow (23). Thwaites Glacier rests on a reverse-sloping bed and is currently retreating rapidly, which is argued to be the result of the marine ice sheet instability (24, 25). In ISSM, as in other models, ocean-induced ice sheet melting is parameterized with a depth-dependent melt rate, with maximum melt rate, $M_{max}$, prescribed at some depth (25). We treat $M_{max}$ as a first-order autoregressive noise process that varies monthly with a prescribed decorrelation timescale (${\tau }_F$), a mean of 80 m/y, no long-term trend, and no variation in space. Many observations and models indicate that subice shelf melt rates at glaciers in the Amundsen Sea, and elsewhere in Antarctica, exhibit strong variability on decadal (and longer) timescales (17, 26, 27). A short run of a regional ocean model simulation for the Amundsen Sea region (SI Appendix) produces variability in $M_{max}$ with interannual SD of 1.4 m/y. This estimate of variability is likely an underestimate since the ocean simulation was run for only 15 y (the time period over which reanalysis forcing is available) and did not include coupled ocean–atmosphere feedbacks. Thus, for our baseline ensemble of Thwaites Glacier, our conservative estimate for the statistics of ocean-induced melt variability is ${\tau }_F=10$ y and ${\sigma }_M=1.4$ m/y. In reality, we also expect that $M_{max}$ varies in space, due to (for example) the Coriolis effect on ocean circulation in the subshelf cavity, which would quantitatively (but not necessarily qualitatively) affect our results.

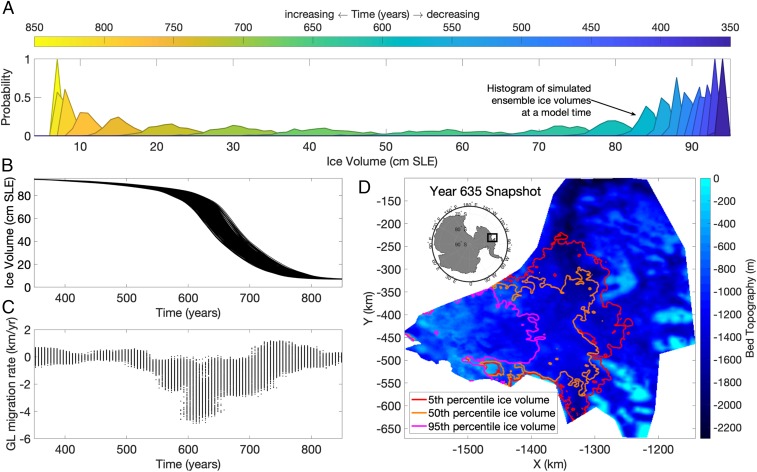
Fig. 3A shows the evolution of the probability distribution of a 500-member ensemble of ISSM-simulated ice volume at Thwaites Glacier in response to decadal variability in subice shelf melt rate. All ensemble members initialized with the modern state of Thwaites Glacier eventually reach complete deglaciation (Fig. 3B), in agreement with previous studies (24, 25). The rate of grounding-line migration (Fig. 3C) experiences significant variability over the course of the retreat due to the stochastic ocean forcing and the presence of forward-sloping “speed bumps” in the bed topography, both of which can slow the rate of retreat or even cause advance for short durations (28). Even with the relatively conservative assumption that there is no variability in surface mass balance and a small amplitude of subshelf melt variability (representing $<2\%$ of the time-averaged subshelf melt), the spread in the ensemble spans $\sim$20 cm of uncertainty in projected sea-level rise during periods of fast retreat (i.e., the green probability distribution functions [PDFs] in Fig. 3A), with a probability distribution skewed in the direction of lower ice volume (greater contribution to sea level). This uncertainty is over 25% of the entire sea-level rise due to deglaciation of Thwaites Glacier and 50% of the median sea-level rise achieved during those periods of fast retreat. This spread between simulations amounts to instantaneous differences of hundreds of kilometers in the grounding-line position (Fig. 3D). Following this growth of uncertainty during the centuries of most rapid retreat, the ensemble then contracts and skews in the opposite direction as individual ensemble members achieve complete deglaciation of Thwaites Glacier, due to the limited model domain used in our simulations. In simulations of the entire Antarctic Ice Sheet in which the marine ice sheet instability spreads to other glaciers (5, 6), we would expect even faster amplification of uncertainty as multiple glaciers become involved in deglaciation.

Fig. 3.

Evolution of a 500-member ensemble of ISSM simulations of Thwaites Glacier evolution over 500 y (where year 0 in model time is the modern glacier state) in response to decadal variability and constant average in maximum subice shelf melt rate. (A) Evolution of ensemble PDF over time, plotted every 25 y, with probability on the y axis and Thwaites Glacier ice volume (in cm sea-level equivalent [SLE]) on the x axis. (B) Black lines are simulated ice volume contained in Thwaites Glacier catchment in cm SLE for all ensemble members. (C) Black dots are evolving grounding-line migration rates for all ensemble members (based on the centroid of the 2D grounding line). (D) Snapshots (red, orange, and pink lines) of grounding-line positions at year 635 in model time, from 5th percentile, 50th percentile, and 95th percentile ice volume ensemble members.

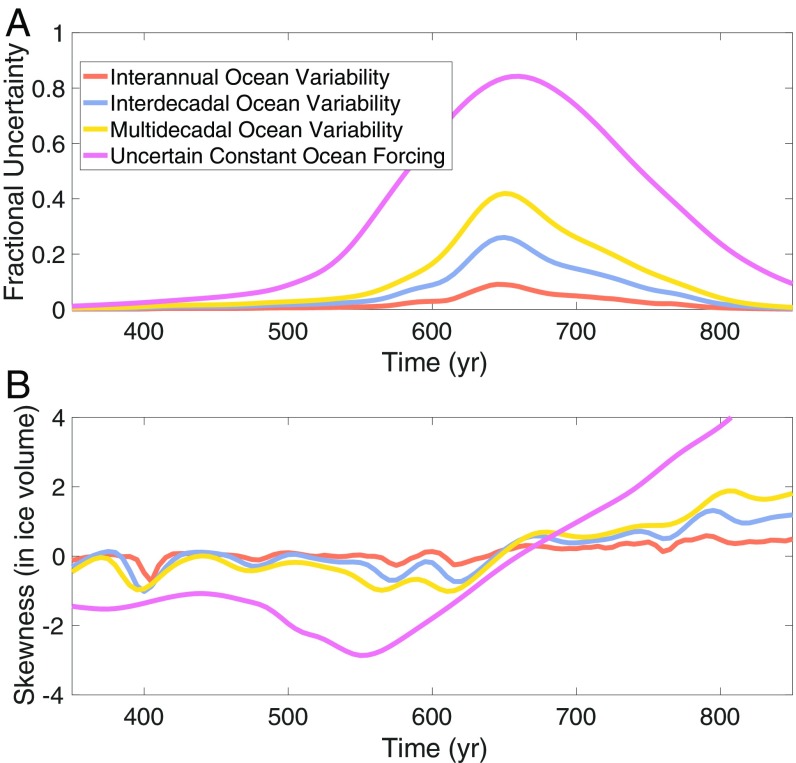
In Fig. 4, we compare Thwaites Glacier ensemble statistics, given a comparable amplitude (${\sigma }_M=1.4$ m/y) of variability in $M_{max}$, but differing degrees of temporal persistence. As predicted by theory, ensemble spread (Fig. 4A) increases with longer persistence in forcing variability (proportional to $\sqrt{{\tau }_F}$; SI Appendix). During the century of fastest retreat, multidecadal ocean variability (yellow line; ${\tau }_F=30$ y) produces skewed uncertainty that is nearly 50% of the total ice loss from Thwaites glacier or $\sim$40 cm of uncertainty in projected sea-level rise. Some studies have suggested that Antarctic glaciers may be subject to such multidecadal variability in forcing through low-frequency coupled modes of the ocean–atmosphere system (26) or sporadic detachment of very large tabular icebergs (29).

Fig. 4.

Evolution of uncertainty and skewness of uncertainty in four Thwaites Glacier ensembles (500 simulations each). Three of the ensembles have variability in ocean forcing specified using a first-order autoregressive model: Including variability at interannual (${\tau }_F=1.1$ y, blue line), interdecadal (${\tau }_F=10$ y, red line; Fig. 3), and multidecadal (${\tau }_F=30$ y, yellow line) timescales. One ensemble has no temporal variability, but the constant maximum subshelf melt rate is uncertain and so drawn from a Gaussian distribution (with ${\sigma }_M=5$ m/y and the same mean as other ensembles, purple line). (A) “Fractional projection uncertainty” given by the ratio of ensemble spread (measured by $\pm 2\sigma$ of ensemble) to total ice loss at the end of simulation: $4{\sigma }_{vol}/{\mu }_{vloss}$. (B) Ensemble skewness, with negative skewness representing a distribution skewed toward lower total ice volume (more ice loss and more sea-level rise).

Poorly constrained subice shelf properties [such as roughness (30)] and the small scale of the turbulent ice–ocean boundary layer make it difficult to accurately simulate even the time-averaged subice shelf melt rate given some change in global climate. Consequently, we also consider uncertainty in the time-averaged subshelf basal melt rate (which may also result from uncertainties in future anthropogenic emissions) by keeping $M_{max}$ constant in time, but varying it between ensemble members (drawing from a Gaussian distribution with SD of 5 m/y). As in the minimal model, this ensemble (purple line in Fig. 4) has a very strong amplification of skewed uncertainty due to the accumulation of differences in subshelf basal melt rate among ensemble members over the course of the instability. For several centuries, the spread in this ensemble amounts to nearly the entire signal of ice loss from Thwaites Glacier (i.e., some ensemble members have retreated completely while others have lost almost no ice at all), skewed in the direction of more ice loss throughout most of the early period of the simulation.

Discussion and Conclusions

Studies of the future evolution of the Antarctic Ice Sheet have estimated the uncertainty in future sea-level rise due to poorly constrained model parameters (5, 6, 31–34). Other studies (35) have investigated the role of internal climate variability in the Greenland Ice Sheet contribution to sea-level rise, but with simulations that were too short to capture much of the marine ice sheet instability that may occur in the future. No study has provided a theoretical framework explaining the role of ice sheet dynamics in setting the amount and structure of uncertainty in sea-level rise projections. We provide such a theoretical framework in this study and find that ice sheet instabilities are amplifiers of uncertainty, which is a common mathematical property of unstable nonlinear systems (22). Although there are processes not considered here that might stabilize (36) or further destabilize (6) an ice sheet, our analysis shows that we should expect more rapid instability (of any kind) to cause more rapid uncertainty growth. Indeed, the theoretical framework developed in this study applies to a sufficiently broad set of assumptions regarding ice sheet dynamics, such that we expect that any type of ice sheet instability, regardless of the processes involved, will experience rapid growth in the ice sheet projection uncertainty during periods of most rapid instability. Integrating the contribution of marine ice sheet instability over many glaciers also integrates the uncertainty of each glacier’s future evolution, potentially leading to considerable uncertainty in sea-level projections, as has been seen in ensemble studies of total ice sheet contribution to future sea-level rise (5, 6, 32, 34, 35). We have shown that model ensembles can be used to quantify a range of possible scenarios for future sea-level rise, including potentially catastrophic scenarios of rapid sea-level rise. However, large model ensembles can be prohibitively expensive when extended to the entire Antarctic Ice Sheet. To fully capture the complete range of possible Antarctic futures, we will need efficient methods for uncertainty quantification (32, 37) and model order reduction that captures the complexities of ice sheet dynamics (31, 34). Such sophisticated methods will ensure that we can make the most useful sea-level projections beyond 2100 for those stakeholders who depend on them.

Materials and Methods

Numerical Solution of Minimal Model.

The ensemble simulations using the minimal model (Eq. 1), and plotted in Fig. 2, are solved numerically using the Euler–Maruyama method. All simulations begin from the same initial condition, a steady state with parameters indicated in the Fig. 2 legend, bed depth of $b\left(x\right)=-0.002x$, and steady-state $L=250$ km. The bed topography is then modified with a new bed slope just behind the steady-state grounding-line position. A small perturbation is added to the accumulation rate ($\mathrm{\Delta }P=-0.006$ m/y) during an initial 500-y spin-up period. At the end of that period, the grounding line is very near a steady state at $t=0$, which is when stochastic perturbations ($\eta \left(t\right)$) begin. All code used to run these ensemble simulations and produce Fig. 2 is available as a public repository on GitHub: https://github.com/aarobel/StochasticMISI.

ISSM.

ISSM is a finite-element software package which is used to solve the 2D shelfy-stream approximation for this study (23), publicly available for download from https://issm.jpl.nasa.gov/. The model solves for ice velocity, surface and base elevation, and grounding-line position at 1-km resolution everywhere in the Thwaites catchment on each 2-wk time step. In our simulations, basal friction follows a linear viscous law and ice rigidity is a function of ice temperature, and both are inverted on the basis of modern velocities using data assimilation (38). Ice temperature, basal friction, and basin boundaries (covering the Thwaites Glacier catchment) are held fixed throughout the simulation to reduce computational load and facilitate the large ensemble simulations. Subice shelf basal melt follows a simple function of depth $M\left(z\right)=M_{max}-M_{max}\left(z_{max}-z\right)$, where $M_{max}$ is the maximum melt rate that occurs at a depth $z_{max}$. Perturbations in $M_{max}$ are varied every month and renormalized to ensure that the SD of monthly $M_{max}$ is always 5 m/y, regardless of the long-term persistence. Surface mass balance and surface temperatures averaged over the 1979 to 2010 period from RACMO2 (39) are applied at the surface of the domain and held constant in time.